Compatibility Between OLCI Marine Remote-Sensing Reflectance from Sentinel-3A and -3B in European Waters
Abstract
1. Introduction
2. Data and Methods
2.1. Satellite Data
2.2. Field Data
2.3. Validation Statistics and Uncertainties
2.4. Analysis of Compatibility
3. Results
3.1. Validation Results and Uncertainty Estimates
3.2. Comparison Between S-3A and S-3B
3.3. Analysis of Compatibility
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Le Traon, P.Y. Satellites and operational oceanography. In New Frontiers in Operational Oceanography; Chassignet, E., Pascual, A., Tintoré, J., Verron, J., Eds.; GODAE Ocean View; Florida State University: Tallahassee, FL, USA, 2018; Chapter 7; pp. 161–189. [Google Scholar]
- Casey, K.; Brandon, T.; Cornillon, P.; Evans, R. The past, present and future of the AVHRR Pathfinder SST program. In Oceanography from Space: Revisited; V. Barale, J.G., Alberotanza, L., Eds.; Springer: Heidelberg, Germany, 2010; Chapter 16; pp. 273–287. [Google Scholar]
- Goldberg, M.D.; Kilcoyne, H.; Cikanek, H.; Mehta, A. Joint Polar Satellite System: The United States next generation civilian polar-orbiting environmental satellite system. J. Geophys. Res. 2013, 118, 13463–13475. [Google Scholar] [CrossRef]
- EU. Regulation(EU) No 377/2014 of the European Parliament and of the Council of 3 April 2014 Establishing the Copernicus Programme; Official Journal of the European Union: Luxembourg, 2014; 23p. [Google Scholar]
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.H.; Féménias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C.; et al. The Global Monitoring for Environment and Security (GMES) Sentinel-3 mission. Remote Sens. Environ. 2012, 120, 37–57. [Google Scholar] [CrossRef]
- Bojinski, S.; Verstraete, M.; Peterson, T.; Richter, C.; Simmons, A.; Zemp, M. The concept of Essential Climate Variables in support of climate research, applications, and policy. Bull. Am. Meterol. Soc. 2014, 95, 1431–1443. [Google Scholar]
- GCOS. Systematic Observation Requirements for Satellite-Based Products for Climate; GCOS-154, Supplemental Details to the Satellite-Based Component of the “Implementation Plan for the Global Observing System for Climate in Support of the UNFCC”; World Meteorological Organization: Geneva, Switzerland, 2011; 138p. [Google Scholar]
- Morel, A.; Antoine, D.; Gentili, B. Bidirectional reflectance of oceanic waters: Accounting for Raman emission and varying particle scattering phase function. Appl. Opt. 2002, 41, 6289–6306. [Google Scholar] [CrossRef]
- Gordon, H. Atmospheric correction of ocean color imagery in the Earth Observing System era. J. Geophys. Res. 1997, 102, 17081–17106. [Google Scholar]
- IOCCG. Why Ocean Colour? The Societal Benefits of Ocean-Colour Technology, Reports of the International Ocean Colour Coordinating Group; Platt, T., Hoepffner, N., Stuart, V., Brown, C., Eds.; No. 7; IOCCG: Dartmouth, NS, Canada, 2008. [Google Scholar]
- McClain, C.; Feldman, G.; Hooker, S. An overview of the SeaWiFS project and strategies for producing a climate research quality global ocean bio-optical time series. Deep Sea Res. 2004, 51, 5–42. [Google Scholar]
- Brewin, R.; Sathyendranath, S.; Kulk, G.; Rio, M.H.; Concha, J.; Bell, T.; Bracher, A.; Fichot, C.; Frölicher, T.; Galí, M.; et al. Ocean carbon from space: Current status and priorities for the next decade. Earth-Sci. Rev. 2023, 240, 104386. [Google Scholar] [CrossRef]
- Henson, S.; Sarmiento, J.; Dunne, J.; Bopp, L.; Lima, I.; Doney, S.; John, J.; Beaulieu, C. Detection of anthropogenic climate change in satellite records of ocean chlorophyll and productivity. Biogeosciences 2010, 7, 621–640. [Google Scholar]
- Yoder, J.; Kennelly, M.; Doney, S.; Lima, I. Are trends in SeaWiFS chlorophyll time-series unusual relative to historic variability? Acta Oceanol. Sin. 2010, 29, 1–4. [Google Scholar]
- Cael, B.; Bisson, K.; Boss, E.; Dutkiewicz, S.; Henson, S. Global climate-change trends detected in indicators of ocean ecology. Nature 2023, 619, 551–554. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, C.; Shang, S.; Muller-Karger, F.; Li, Y.; Dai, M.; Huang, S.; Ning, X.; Hong, H. Bridging between SeaWiFS and MODIS for continuity of chlorophyll-a concentration assessments off Southeastern China. Remote Sens. Environ. 2006, 102, 250–263. [Google Scholar] [CrossRef]
- Djavidnia, S.; Mélin, F.; Hoepffner, N. Comparison of global ocean colour data records. Ocean Sci. 2010, 6, 61–76. [Google Scholar] [CrossRef]
- Mélin, F.; Zibordi, G.; Djavidnia, D. Merged series of normalized water leaving radiances obtained from multiple satellite missions for the Mediterranean Sea. Adv. Space Res. 2009, 43, 423–437. [Google Scholar] [CrossRef]
- Mélin, F. Global distribution of the random uncertainty associated with satellite derived Chla. IEEE Geosci. Remote Sens. Lett. 2010, 7, 220–224. [Google Scholar] [CrossRef]
- Barnes, B.; Hu, C. Cross-sensor continuity of satellite-derived water clarity in the Gulf of Mexico: Insights into temporal aliasing and implications for long-term water clarity assessment. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1761–1772. [Google Scholar] [CrossRef]
- Mélin, F. Impact of inter-mission differences and drifts on chlorophyll-a trend estimates. Int. J. Remote Sens. 2016, 37, 2061–2079. [Google Scholar] [CrossRef]
- Mélin, F.; Vantrepotte, V.; Chuprin, A.; Grant, M.; Jackson, T.; Sathyendranath, S. Assessing the fitness-for-purpose of satellite multi-mission ocean color climate data records: A protocol applied to OC-CCI chlorophyll-a data. Remote Sens. Environ. 2017, 203, 139–151. [Google Scholar] [CrossRef]
- VIM. International Vocabulary of Metrology—Basic and General Concepts and Associated Terms; JCGM 200; Joint Committee for Guides in Metrology, Bureau International des Poids et Mesures: Sévres, France, 2012; 108p. [Google Scholar]
- Kyryliuk, D.; Kratzer, S. Evaluation of Sentinel-3A OLCI products derived using the Case-2 Regional CoastColour processor over the Baltic Sea. Sensors 2019, 19, 3609. [Google Scholar] [CrossRef]
- Mograne, M.; Jamet, C.; Loisel, H.; Vantrepotte, V.; Mériaux, X.; Cauvin, A. Evaluation of five atmospheric correction algorithms over French optically-complex waters for the Sentinel-3A OLCI ocean color sensor. Remote Sens. 2019, 11, 668. [Google Scholar] [CrossRef]
- Li, J.; Jamet, C.; Zhu, J.; Han, B.; Li, T.; Yang, A.; Guo, K.; Jia, D. Error budget in the validation of radiometric products derived from OLCI around the China Sea from open ocean to coastal waters compared with MODIS and VIIRS. Remote Sens. 2019, 11, 2400. [Google Scholar] [CrossRef]
- Giannini, F.; Hunt, B.; Jacoby, D.; Costa, M. Performance of OLCI Sentinel-3A satellite in the Northeast Pacific coastal waters. Remote Sens. Environ. 2021, 256, 112317. [Google Scholar] [CrossRef]
- Liu, H.; He, X.; Li, Q.; Hu, X.; Ishizaka, J.; Kratzer, S.; Yang, C.; Shi, T.; Hu, S.; Zhou, Q.; et al. Evaluation of ocean color atmospheric correction methods for Sentinel-3 OLCI using global automatic in situ observations. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4206319. [Google Scholar] [CrossRef]
- Arena, M.; Pratolongo, P.; Loisel, H.; Tran, M.; Schaffer Ferreira Jorge, D.; Delgado, A. Optical water characterization and atmospheric correction assessment of estuarine and coastal waters around the AERONET-OC Bahia Blanca. Front. Remote Sens. 2024, 5, 1305787. [Google Scholar] [CrossRef]
- González Vilas, L.; Brando, V.; Di Cicco, A.; Colella, S.; D’Alimonte, D.; Kajiyama, T.; Attila, J.; Schroeder, T. Assessment of ocean color atmospheric correction methods and development of a regional ocean color operational dataset for the Baltic Sea based on Sentinel-3 OLCI. Front. Mar. Sci. 2024, 10, 1256990. [Google Scholar] [CrossRef]
- Gordon, H.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: A preliminary algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar]
- Franz, B.; Bailey, S.; Werdell, P.; McClain, C. Sensor-independent approach to the vicarious calibration of satellite ocean color radiometry. Appl. Opt. 2007, 46, 5068–5082. [Google Scholar]
- Ahmad, Z.; Franz, B.; McClain, C.; Kwiatkowska, E.; Werdell, P.; Shettle, E.; Holben, B. New aerosol models for the retrieval of aerosol optical thickness and normalized water-leaving radiances from the SeaWiFS and MODIS sensors over coastal regions and open oceans. Appl. Opt. 2010, 49, 5545–5560. [Google Scholar] [CrossRef]
- EUMETSAT. Sentinel-3 Product Notice—OLCI Level-2 Ocean Colour. In S3.PN-OLCI-L2M.003.00; 2021; 10p. Available online: https://user.eumetsat.int/s3/eup-strapi-media/S3_PN_OLCI_L2_M_003_00_Sentinel_3_Product_Notice_OLCI_Level_2_Ocean_Colour_be36d5b00c.pdf (accessed on 17 March 2025).
- EUMETSAT. Ocean Colour Standard Atmospheric Correction, Algorithm Theoretical Basis, v4.2. EUM/21/SAC/ATBD. 2022. 114p. Available online: https://www-cdn.eumetsat.int/files/2022-11/EUMETSAT_OC-SAC_ATBD_v4.2_web.pdf (accessed on 17 March 2025).
- Zibordi, G.; Kwiatkowska, E.; Mélin, F.; Talone, M.; Cazzaniga, I. Assessment of OLCI-A and OLCI-B radiometric data products across European seas. Remote Sens. Environ. 2022, 272, 112911. [Google Scholar]
- Mélin, F. Validation of ocean color remote sensing reflectance data: Analysis of results at European coastal sites. Remote Sens. Environ. 2022, 280, 113153. [Google Scholar] [CrossRef]
- EUMETSAT. Recommendations for Sentinel-3 OLCI ocean colour product validations in comparison with in situ measurements—Match-up protocols. In UM/SEN3/DOC/19/1092968; EUMETSAT: Darmstadt, Germany, 2019; 12p, Available online: https://user.eumetsat.int/s3/eup-strapi-media/Recommendations_for_Sentinel_3_OLCI_Ocean_Colour_product_validations_in_comparison_with_in_situ_measurements_Matchup_Protocols_V8_B_e6c62ce677.pdf (accessed on 17 March 2025).
- Barnes, B.; Cannizzaro, J.; English, D.; Hu, C. Validation of VIIRS and MODIS reflectance data in coastal and oceanic waters: An assessment of methods. Remote Sens. Environ. 2019, 220, 110–123. [Google Scholar]
- Clerc, S.; Donlon, C.; Borde, F.; Lamquin, N.; Hunt, S.; Smith, D.; McMillan, M.; Mittaz, J.; Woolliams, E.; Hammond, M.; et al. Benefits and lessons learnt from the Sentinel-3 tandem phase. Remote Sens. 2020, 12, 2668. [Google Scholar] [CrossRef]
- Lamquin, N.; Clerc, S.; Donlon, C. OLCI A/B tandem phase analysis, Part 1: Level-1 homogenisation and harmonisation. Remote Sens. 2020, 12, 1804. [Google Scholar] [CrossRef]
- Holben, B.; Eck, T.; Slutker, I.; Tanré, D.; Buis, J.; Setzer, A.; Vermote, E.; Reagan, J.; Kaufman, Y.; Nakajima, T.; et al. AERONET: A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Zibordi, G.; Holben, B.; Talone, M.; D’Alimonte, D.; Slutsker, I.; Giles, D.; Sorokin, M. Advances in the Ocean Color component of the Aerosol Robotic Network (AERONET-OC). J. Atmos. Ocean. Technol. 2021, 38, 725–746. [Google Scholar] [CrossRef]
- Zibordi, G.; Hooker, S.; Berthon, J.F.; D’Alimonte, D. Autonomous above-water radiance measurements from an offshore platform: A field assessment experiment. J. Atmos. Ocean. Technol. 2002, 19, 808–819. [Google Scholar] [CrossRef]
- Zibordi, G.; Strömbeck, N.; Mélin, F.; Berthon, J.F. Tower-based radiometric observations at a coastal site in the Baltic Proper. Estuarine Coast. Shelf Sci. 2006, 69, 649–654. [Google Scholar] [CrossRef]
- Zibordi, G.; Berthon, J.F.; Mélin, F.; D’Alimonte, D.; Kaitala, S. Validation of satellite ocean color primary products at optically complex coastal sites: Northern Adriatic Sea, northern Baltic Proper, Gulf of Finland. Remote Sens. Environ. 2009, 113, 2574–2591. [Google Scholar] [CrossRef]
- Zibordi, G.; Holben, B.; Slutsker, I.; Giles, D.; D’Alimonte, D.; Mélin, F.; Berthon, J.F.; Vandemark, D.; Feng, H.; Schuster, G.; et al. AERONET-OC: A network for the validation of ocean color primary products. J. Atmos. Ocean. Technol. 2009, 26, 1634–1651. [Google Scholar] [CrossRef]
- Zibordi, G.; Mélin, F.; Berthon, J.F.; Talone, M. In situ autonomous optical raiometry measurements for satellite ocean color validation in the Western Black Sea. Ocean Sci. 2015, 11, 275–286. [Google Scholar] [CrossRef]
- Cazzaniga, I.; Mélin, F. How representative are AERONET-OC sites of European marine waters? Remote Sens. 2024, 16, 1793. [Google Scholar] [CrossRef]
- Cazzaniga, I.; Zibordi, G.; Mélin, F. Spectral features of ocean colour radiometric products in the presence of cyanobacteria blooms in the Baltic Sea. Remote Sens. Environ. 2023, 287, 113464. [Google Scholar]
- Cazzaniga, I.; Zibordi, G.; Mélin, F. Spectral variations of the remote sensing reflectance during coccolithophore blooms in the Western Black Sea. Remote Sens. Environ. 2021, 264, 112607. [Google Scholar]
- Thuillier, G.; Hersé, M.; Labs, D.; Foujols, T.; Peetermans, W.; Gillotay, D.; Simon, P.; Mandel, H. The solar spectral irradiance from 200 to 2400 nm as measured by the SOLSPEC spectrometer from the ATLAS and EURECA missions. Sol. Phys. 2003, 214, 1–22. [Google Scholar] [CrossRef]
- Zibordi, G.; D’Alimonte, D.; Kajiyama, T. Automated quality control of AERONET-OC LWN data. J. Atmos. Ocean. Technol. 2022, 39, 1961–1972. [Google Scholar] [CrossRef]
- Cazzaniga, I.; Zibordi, G. AERONET-OC LWN uncertainties: Revisited. J. Atmos. Ocean. Technol. 2023, 40, 411–425. [Google Scholar] [CrossRef]
- Smirnov, A.; Holben, B.; Eck, T.; Dubovik, O.; Slutker, I. Cloud-screening and quality control algorithms for the AERONET database. Remote Sens. Environ. 2000, 73, 337–349. [Google Scholar]
- Giles, D.; Sinyuk, A.; Sorokin, M.; Schafer, J.; Smirnov, A.; Slutsker, I.; Eck, T.; Holben, B.; Lewis, J.; Campbell, J.; et al. Advancements in the Aerosol Robotic Network (AERONET) Version 3 database—Automated near-real-time quality control algorithm with improved cloud screening for Sun photometer aerosol optical depth (AOD) measurements. Atmos Meas. Tech. 2019, 12, 169–209. [Google Scholar]
- Mélin, F.; Clerici, M.; Zibordi, G.; Holben, B.; Smirnov, A. Validation of SeaWiFS and MODIS aerosol products with globally-distributed AERONET data. Remote Sens. Environ. 2010, 114, 230–250. [Google Scholar]
- Mélin, F.; Zibordi, G.; Holben, B. Assessment of the aerosol products from the SeaWiFS and MODIS ocean color missions. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1185–1189. [Google Scholar]
- Mélin, F.; Franz, B. Assessment of satellite ocean colour radiometry and derived geophysical products. In Optical Radiometry for Oceans Climate Measurements; Zibordi, G., Donlon, C., Parr, A., Eds.; Experimental Methods in the Physical Sciences; Academic Press: Waltham, MA, USA, 2014; Volume 47, pp. 609–638. [Google Scholar]
- IOCCG. Uncertainties in Ocean Colour Remote Sensing, Reports of the International Ocean Colour Coordinating Group; Mélin, F., Ed.; No. 18; IOCCG: Dartmouth, NS, Canada, 2019. [Google Scholar]
- Mélin, F. From validation statistics to uncertainty estimates: Application to VIIRS ocean color radiometric products at European coastal locations. Front. Mar Sci. 2021, 8, 790948. [Google Scholar]
- GUM. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurements; JCGM 100; Joint Committee for Guides in Metrology, Bureau International des Poids et Mesures: Sèvres, France, 2008; 134p. [Google Scholar]
- Immler, F.; Dykema, J.; Gardiner, T.; Whiteman, D.; Thorne, P.; Vömel, H. Reference quality upper-air measurements: Guidance for developing GRUAN data products. Atmos. Meas. Tech. 2010, 3, 1217–1231. [Google Scholar] [CrossRef]
- Mélin, F.; Zibordi, G.; Berthon, J.F.; Bailey, S.; Franz, B.; Voss, K.; Flora, S.; Grant, M. Assessment of MERIS reflectance data as processed by SeaDAS over the European Seas. Opt. Exp. 2011, 19, 25657–25671. [Google Scholar]
- Mélin, F.; Zibordi, G.; Berthon, J.F. Uncertainties in remote sensing reflectance from MODIS-Terra. IEEE Geosci. Remote Sens. Lett. 2012, 9, 432–436. [Google Scholar]
- Hooker, S.; Esaias, W.; Feldman, G.; Gregg, W.; McClain, C. An overview of SeaWiFS and ocean color. In NASA Technical Memorandum 104566; Hooker, S., Firestone, E., Eds.; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 1992; Volume 1, SeaWiFS Prelaunch Technical Report Series; 24p. [Google Scholar]
- Rast, M.; Bézy, J.; Bruzzi, S. The ESA Medium Resolution Imaging Spectrometer MERIS—A review of the instrument and its mission. Int. J. Remote Sens. 1999, 20, 1681–1702. [Google Scholar] [CrossRef]
- Esaias, W.; Abbott, M.; Barton, I.; Brown, O.; Campbell, J.; Carder, K.; Clark, D.; Evans, R.; Hoge, F.; Gordon, H.; et al. An overview of MODIS capabilities for ocean science observations. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1250–1265. [Google Scholar]
- Cao, C.; Xiong, J.; Blonski, S.; Liu, Q.; Uprety, S.; Shao, X.; Bai, Y.; Weng, F. Suomi NPP VIIRS sensor data record verification, validation, and long-term performance monitoring. J. Geophys. Res. 2013, 118, 11664–11678. [Google Scholar] [CrossRef]
- Ångström, A. The parameters of atmospheric turbidity. Tellus 1964, 26, 64–75. [Google Scholar]
- McKinna, L.; Cetinić, I.; Chase, A.; Werdell, P. Approach for propagating radiometric data uncertainties through NASA ocean color algorithms. Front. Earth Sci. 2019, 7, 176. [Google Scholar] [CrossRef]
- EUMETSAT. Ocean Colour Bright Pixel Correction, Algorithm Theoretical Basis, v1.3. EUM/18/BPC/ATBD. 2021, p. 68. Available online: https://www.eumetsat.int/OC-BPC (accessed on 17 March 2025).
- Lamquin, N.; Déru, A.; Clerc, S.; Bourg, L.; Donlon, C. OLCI A/B tandem phase analysis, Part 2: Benefits of sensors harmonisation for level-2 products. Remote Sens. 2020, 12, 2702. [Google Scholar] [CrossRef]
- Mikelsons, K.; Wang, M.; Kwiatkowska, E.; Jiang, L.; Dessailly, D.; Gossn, J. Statistical evualtion of Sentinel-3 OLCI ocean color data retrievals. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4212119. [Google Scholar] [CrossRef]
- Hu, C.; Lee, Z.P.; Franz, B. Chlorophyll a algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. 2012, 117, C01011. [Google Scholar] [CrossRef]
- Druon, J.N.; Gascuel, D.; Gibin, M.; Zanzi, A.; Fromentin, J.M.; Colloca, F.; Hélaouët, P.; Coll, M.; Mannini, A.; Bluemel, J.; et al. Mesoscale productivity fronts and local fishing opportunities in the European seas. Fish Fish. 2021, 22, 1227–1247. [Google Scholar] [CrossRef]

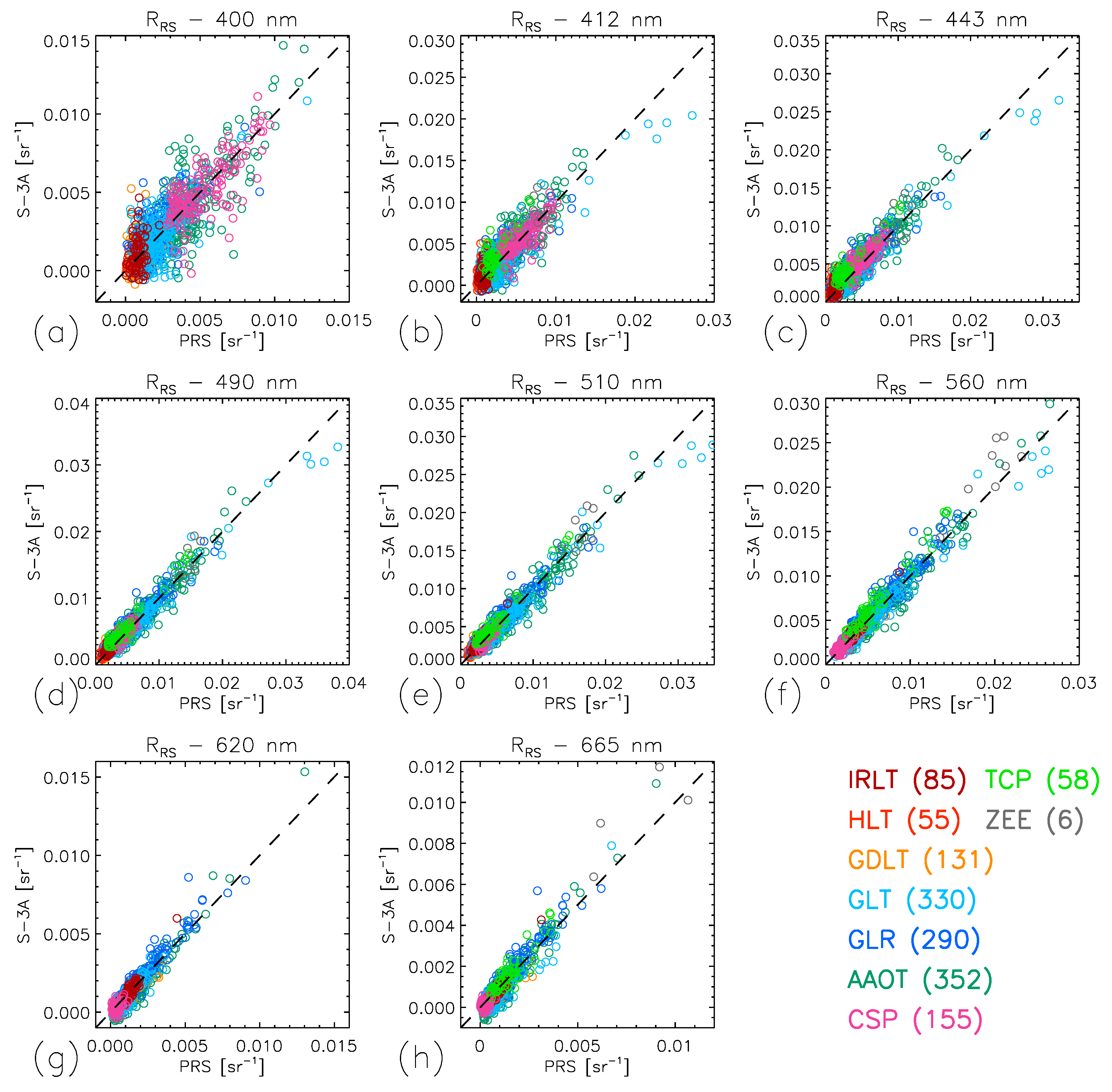


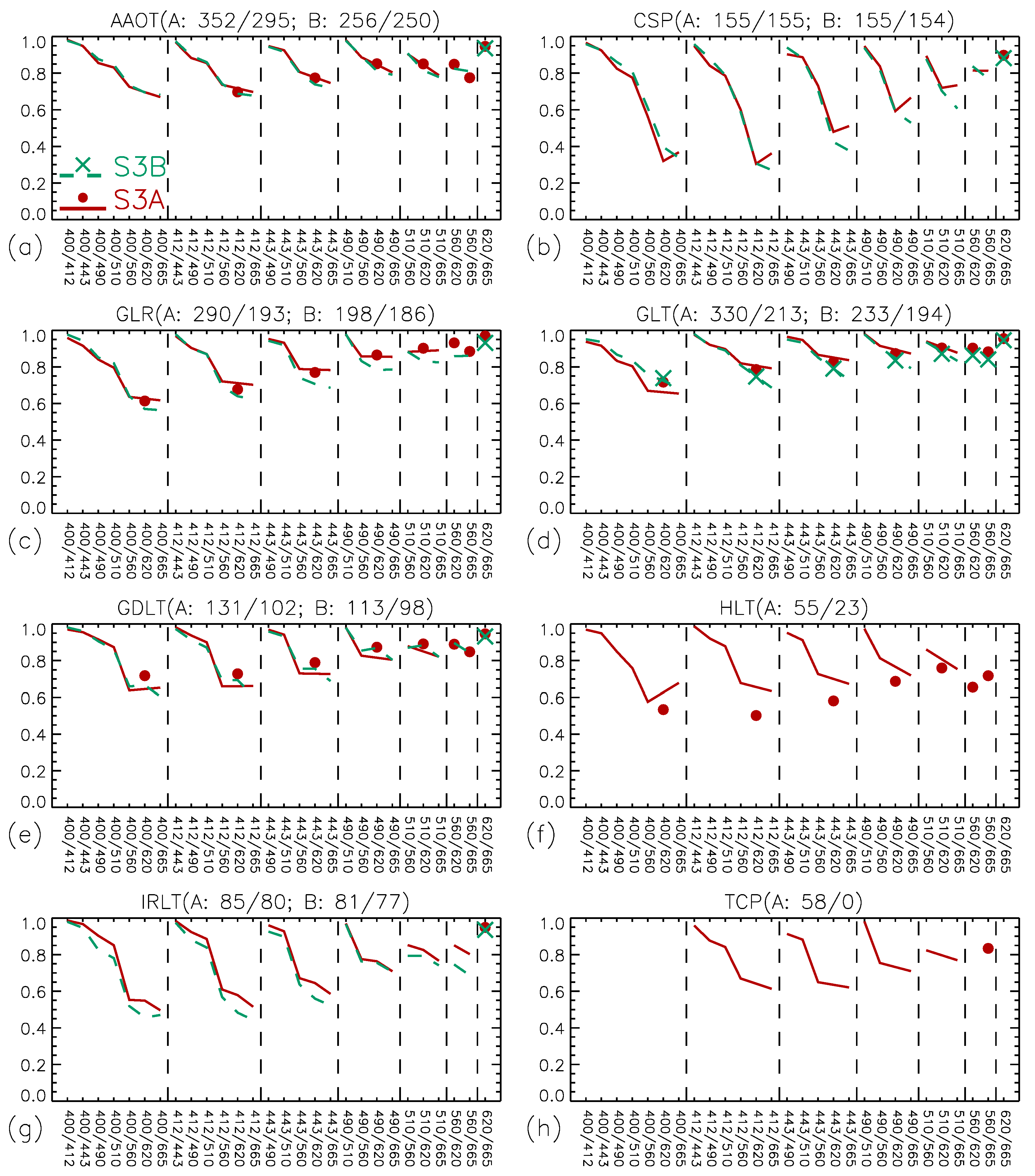
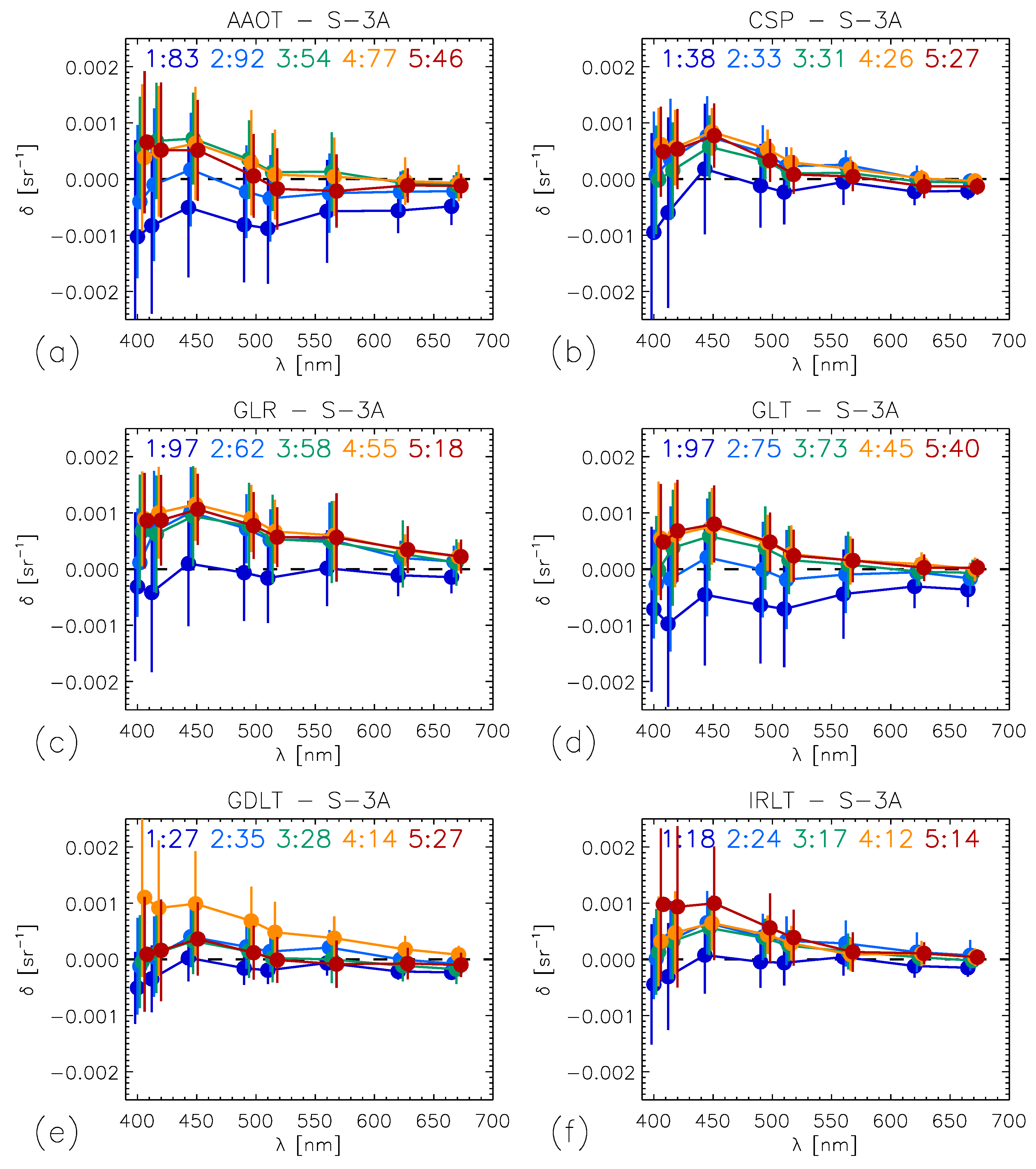

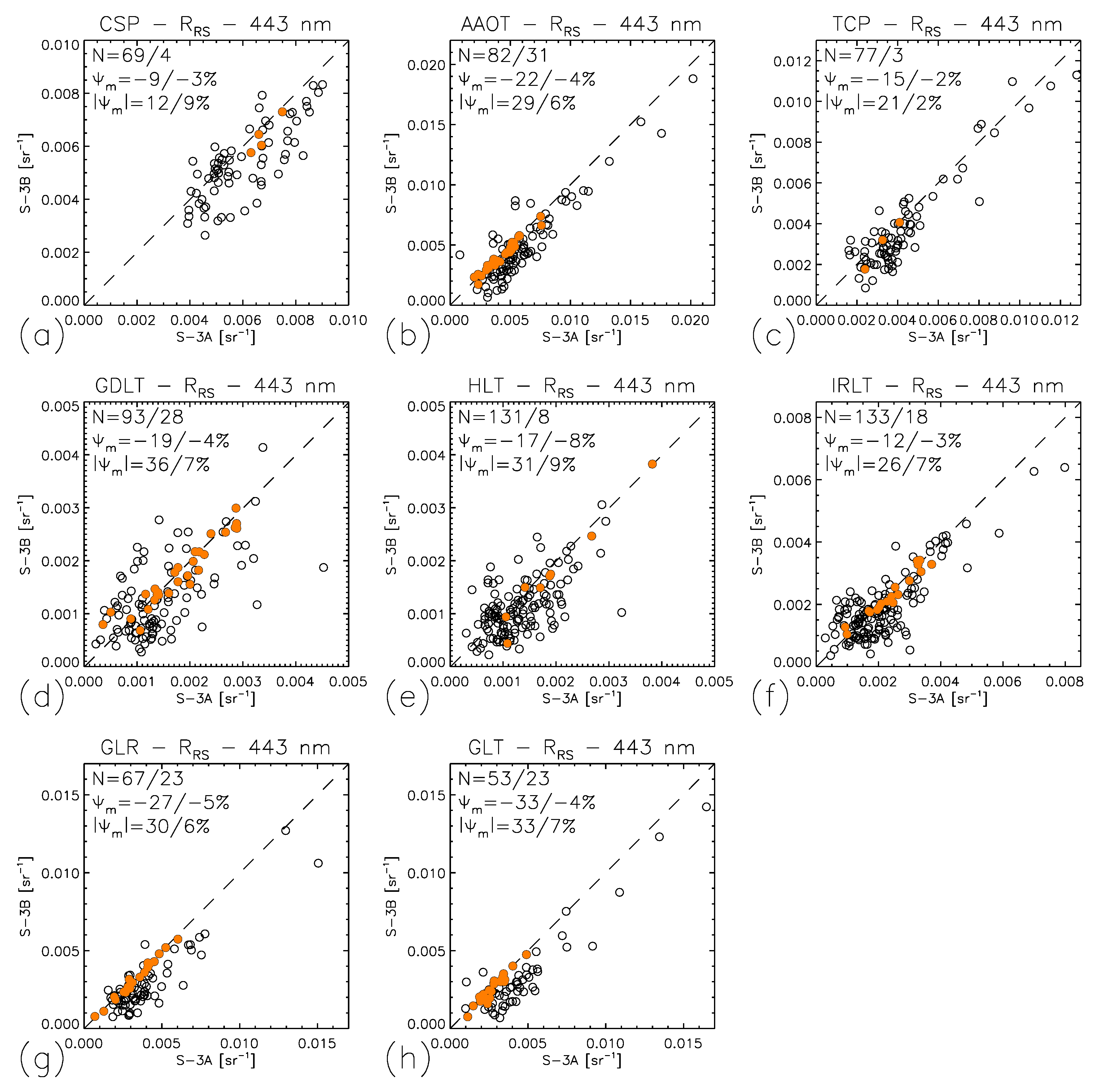

| Acronym | Name | Latitude (°) | Longitude (°) | Years |
|---|---|---|---|---|
| AAOT | Acqua Alta Oceanographic Tower | 45.314N | 12.508E | 2002–2023 |
| CSP | Casablanca Platform | 40.717N | 1.358E | 2019–2022 |
| GLR * | Gloria Platform | 44.600N | 29.360E | 2011–2019 |
| Section-7 Platform | 44.546N | 29.447E | 2019–2022 | |
| GLT | Galata Platform | 43.45N | 28.193E | 2014–2023 |
| GDLT | Gustav Dalen Lighthouse Tower | 58.594N | 17.467E | 2005–2022 |
| HLT | Helsinki Lighthouse Tower | 59.949N | 24.926E | 2006–2017, 2019 |
| IRLT | Irbe Lighthouse Tower | 57.751N | 21.723E | 2018–2022 |
| TCP | Thornton_C-Power | 51.532N | 2.955E | 2015–2018 † |
| ZEE | Zeebrugge-MOW1 | 51.362N | 3.120E | 2014–2019 ‡ |
| Site | N | 400 | 412 | 443 | 490 | 510 | 560 | 620 | 665 | (443) | (865) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CSP | 69 | 45 | 42 | 52 | 58 | 46 | 55 | 51 | 49 | 68 | 49 |
| 80 | 75 | 81 | 81 | 78 | 84 | 80 | 80 | 93 | 80 | ||
| AAOT | 82 | 45 | 48 | 49 | 33 | 33 | 40 | 40 | 32 | 70 | 68 |
| 77 | 91 | 91 | 89 | 81 | 93 | 93 | 88 | 96 | 89 | ||
| GLR | 67 | 45 | 31 | 34 | 34 | 37 | 39 | 42 | 40 | 79 | 57 |
| 81 | 67 | 73 | 79 | 76 | 78 | 79 | 82 | 96 | 90 | ||
| GLT | 53 | 40 | 19 | 21 | 23 | 32 | 38 | 34 | 36 | 83 | 66 |
| 72 | 58 | 58 | 64 | 72 | 87 | 87 | 89 | 91 | 91 | ||
| GDLT | 93 | 53 | 65 | 69 | 72 | 69 | 82 | 83 | 80 | 73 | 76 |
| 76 | 97 | 97 | 97 | 96 | 97 | 94 | 97 | 95 | 92 | ||
| IRLT | 133 | 70 | 71 | 71 | 73 | 70 | 61 | 72 | 66 | 77 | 74 |
| 93 | 98 | 97 | 95 | 94 | 88 | 94 | 92 | 90 | 90 |
| S-3A → | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| S-3B ↓ | |||||
| 1 | 0 | 0/0/0/0/2/10 | 11/4/8/12/13/17 | 29/43/34/19/7/19 | 21/20/7/11/0/0 |
| 2 | 0 | 0 | 0 | 0/0/0/0/8/11 | 8/8/17/8/29/27 |
| 3 | 0 | 0 | 0 | 0 | 0/0/0/0/8/6 |
| 4 | 0/0/0/0/9/18 | 0 | 0 | 0 | 0 |
| 5 | 0/7/1/3/17/25 | 0 | 0 | 0 | 0 |
| Site | 400 | 412 | 443 | 490 | 510 | 560 | 620 | 665 | (443) | (865) |
|---|---|---|---|---|---|---|---|---|---|---|
| CSP | 61 | 67 | 68 | 65 | 55 | 61 | 59 | 54 | 71 | 55 |
| 87 | 91 | 93 | 88 | 84 | 91 | 93 | 91 | 97 | 88 | |
| AAOT | 48 | 55 | 57 | 48 | 48 | 62 | 40 | 44 | 83 | 66 |
| 82 | 98 | 95 | 98 | 99 | 96 | 93 | 94 | 100 | 88 | |
| GLR | 60 | 48 | 54 | 60 | 66 | 79 | 73 | 78 | 88 | 55 |
| 85 | 94 | 94 | 94 | 93 | 93 | 91 | 93 | 96 | 90 | |
| GLT | 53 | 34 | 43 | 40 | 38 | 43 | 40 | 58 | 85 | 66 |
| 85 | 94 | 94 | 92 | 92 | 94 | 91 | 92 | 94 | 91 | |
| GDLT | 55 | 78 | 85 | 80 | 83 | 88 | 86 | 87 | 73 | 74 |
| 82 | 98 | 98 | 98 | 98 | 97 | 99 | 99 | 95 | 90 | |
| IRLT | 74 | 77 | 79 | 78 | 77 | 76 | 80 | 78 | 73 | 70 |
| 94 | 99 | 98 | 98 | 95 | 96 | 96 | 98 | 89 | 89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mélin, F.; Cazzaniga, I.; Sciuto, P. Compatibility Between OLCI Marine Remote-Sensing Reflectance from Sentinel-3A and -3B in European Waters. Remote Sens. 2025, 17, 1132. https://doi.org/10.3390/rs17071132
Mélin F, Cazzaniga I, Sciuto P. Compatibility Between OLCI Marine Remote-Sensing Reflectance from Sentinel-3A and -3B in European Waters. Remote Sensing. 2025; 17(7):1132. https://doi.org/10.3390/rs17071132
Chicago/Turabian StyleMélin, Frédéric, Ilaria Cazzaniga, and Pietro Sciuto. 2025. "Compatibility Between OLCI Marine Remote-Sensing Reflectance from Sentinel-3A and -3B in European Waters" Remote Sensing 17, no. 7: 1132. https://doi.org/10.3390/rs17071132
APA StyleMélin, F., Cazzaniga, I., & Sciuto, P. (2025). Compatibility Between OLCI Marine Remote-Sensing Reflectance from Sentinel-3A and -3B in European Waters. Remote Sensing, 17(7), 1132. https://doi.org/10.3390/rs17071132






