The First Experimental Validation of a Communication Base Station as a Ground-Based SAR for Deformation Monitoring
Abstract
1. Introduction
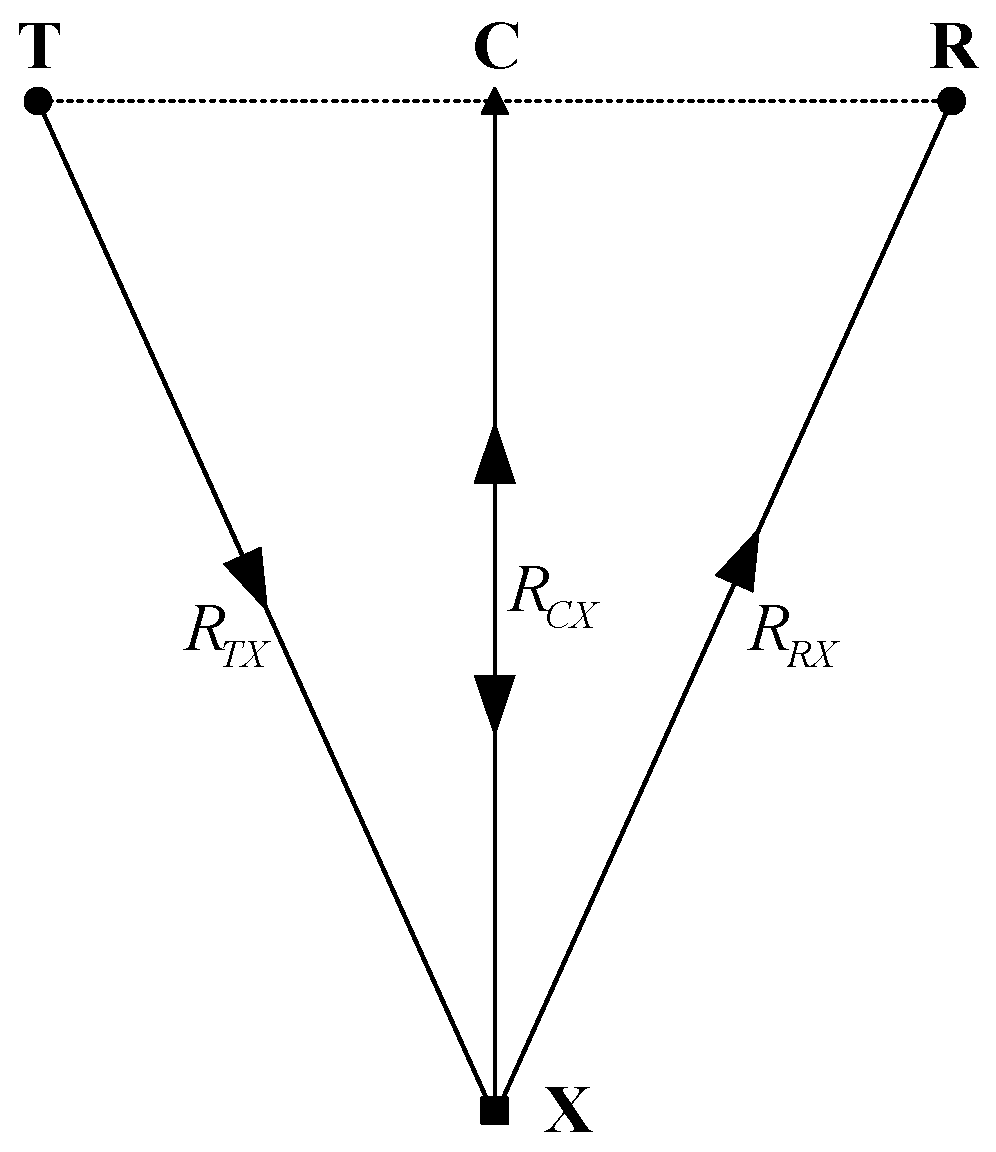
2. A CBS System Model with an EPC
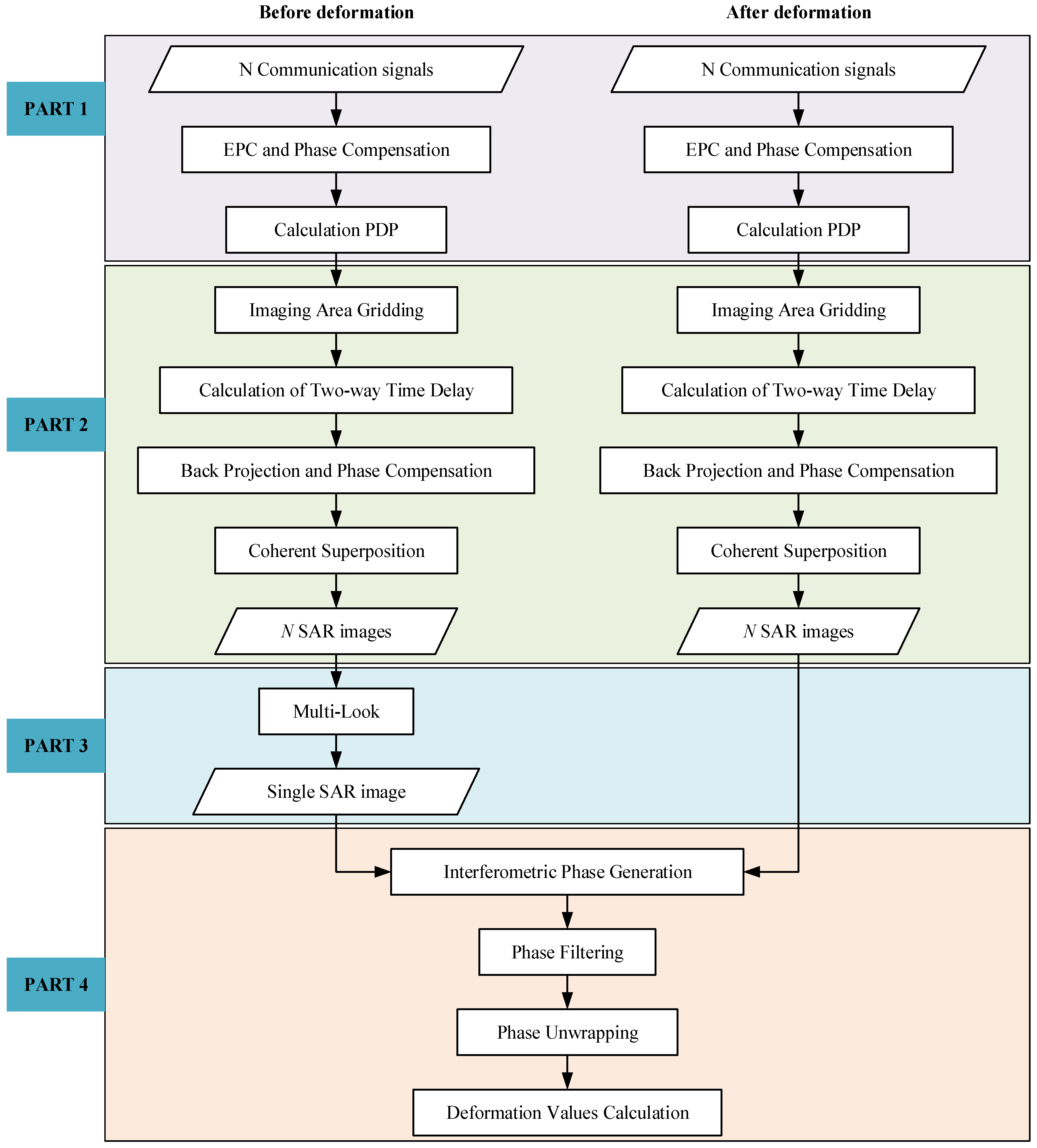
3. Data Processing Methods
3.1. Communication Echo Signals Achievement with an EPC
3.2. SAR Images Formulation Based on ULA Communication Signals with the BPA
3.2.1. Availability Analysis of the BPA
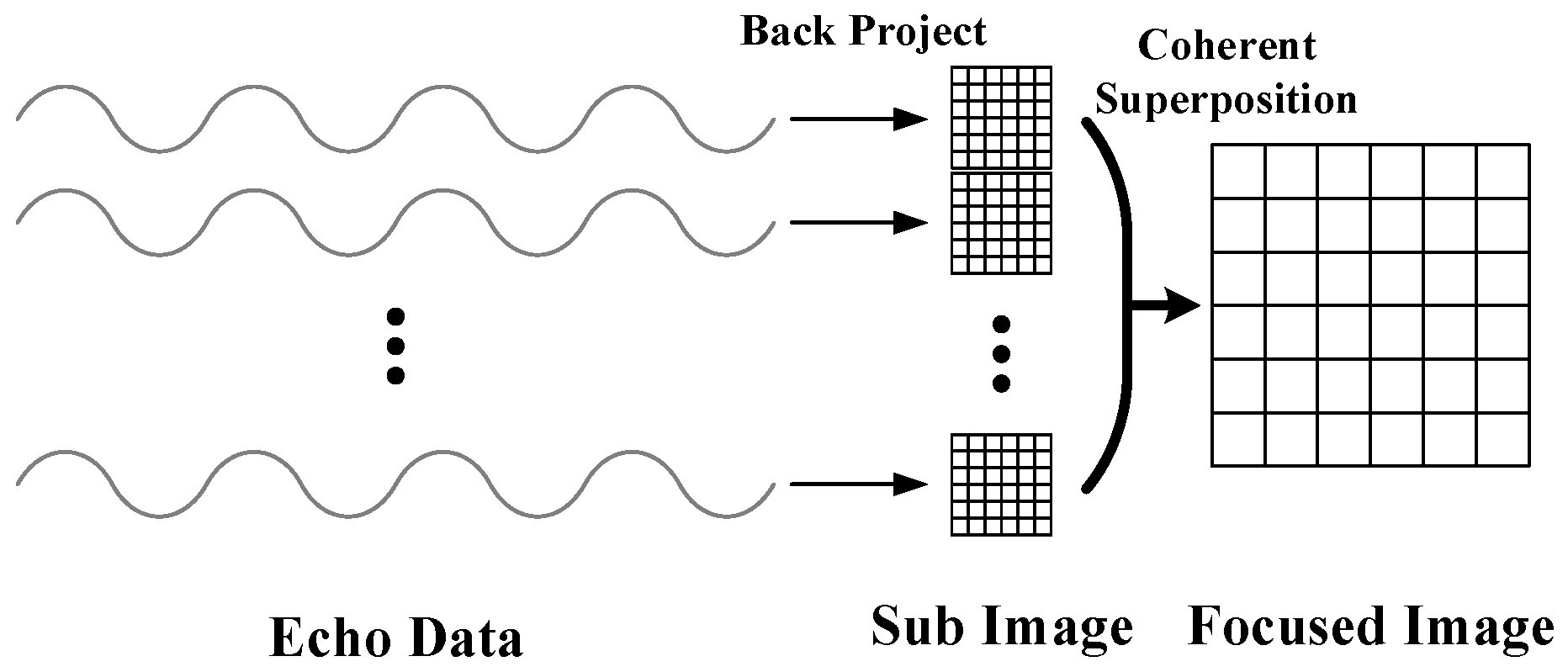
3.2.2. The Principle and Procedure of the BPA
- (i).
- Range compression: Pulse compression processing is applied to the echo data in the range direction to achieve high resolution. This is typically accomplished using a matched filter. In this experiment, the PDP of the communication signal is equivalent to the result obtained from the radar echo signal after pulse compression, thereby rendering this step unnecessary.
- (ii).
- Imaging area gridding: The imaging area is divided into a grid under an appropriate coordinate system, with the grid size being slightly smaller than the resolution unit of the system.
- (iii).
- Calculation of the two-way time delay: The two-way slant range and time delay between each grid point and the antenna phase center are calculated for all azimuth times.
- (iv).
- Back projection and phase compensation: Based on the time delay for each grid point, the echo data at each point are interpolated from the corresponding azimuth echo, and phase compensation is applied to all points. The phase compensation term is dependent on the two-way slant range between the grid point and the antenna phase center at the current azimuth time. Ultimately, the echo data at each azimuth time are back projected to produce a sub-image.
- (v).
- Coherent superposition: The focused SAR image is obtained by coherently superposing the sub-images generated at all azimuth times
3.3. Multi-Look Processing of the SAR Images
3.3.1. The Principle of Multi-Look Processing
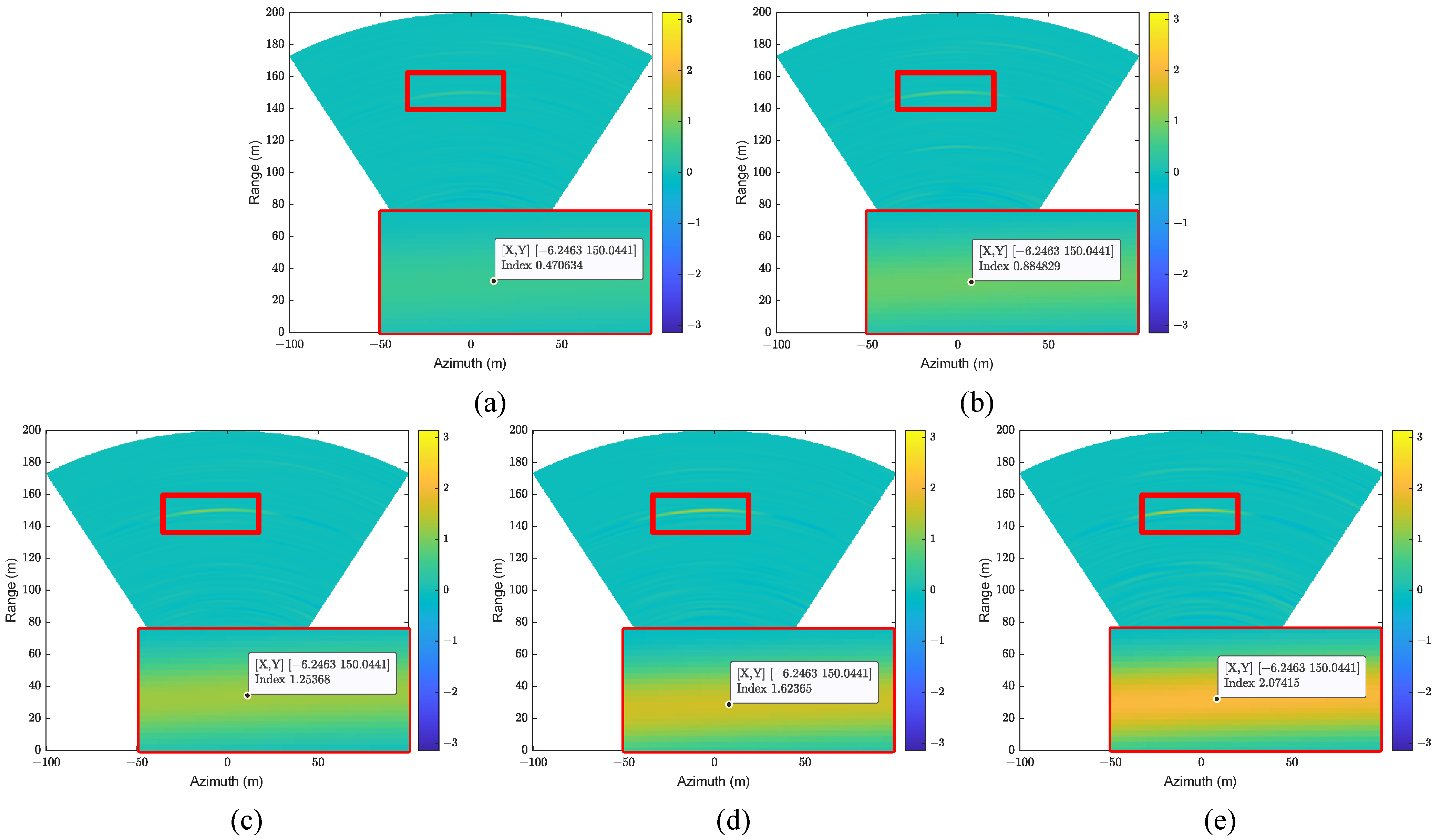
3.3.2. The Experiment of Multi-Look Processing
3.4. GB-SAR Deformation Detection with SAR Images
3.4.1. The GB-SAR Deformation Detection Principle
- (i).
- Interferometric Phase Generation: An interferometric phase map, or interferogram, is generated by conjugate multiplying two GB-SAR images, which encapsulates the deformation information of the target area.
- (ii).
- Phase filtering: Phase noise can adversely affect the accuracy of phase measurements; thus, this issue is typically addressed using techniques such as mean filtering. When processing a large number of interferograms, temporal window filtering is employed. Conversely, for a smaller number of interferograms, spatial window filtering is preferred.
- (iii).
- Phase unwrapping: Since the interferometric phase value is wrapped within a certain range, it must be adjusted by adding integer multiples of . Phase unwrapping is a critical step in obtaining the true phase value of the target. Commonly used methods for this process include the branch-cut method and the region-growing algorithm.
- (iv).
- Deformation value calculation: Upon completion of the phase unwrapping process, the LOS deformation value of the target area can be computed from the true interferometric phase value using Equation (14).
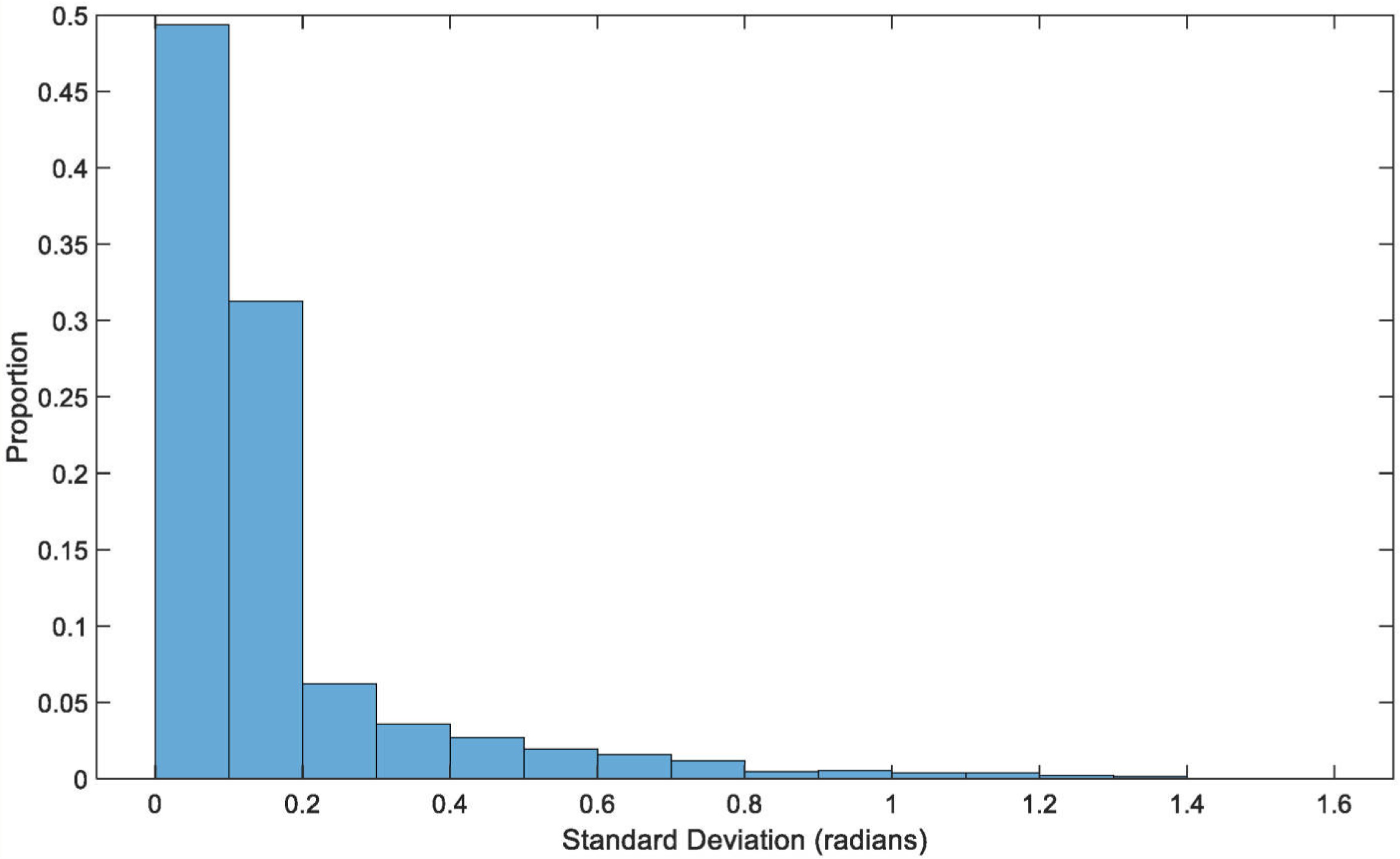
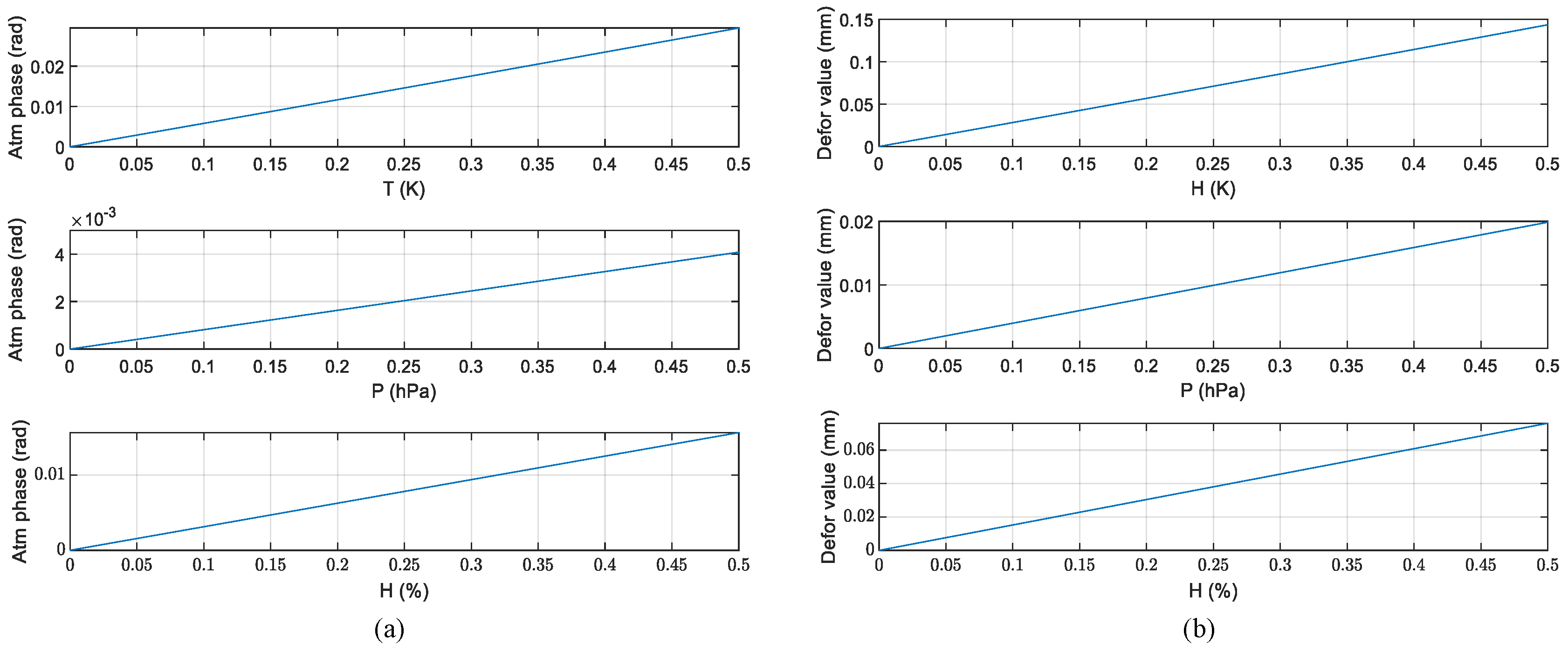
3.4.2. Atmospheric Phase Analysis and Simulation
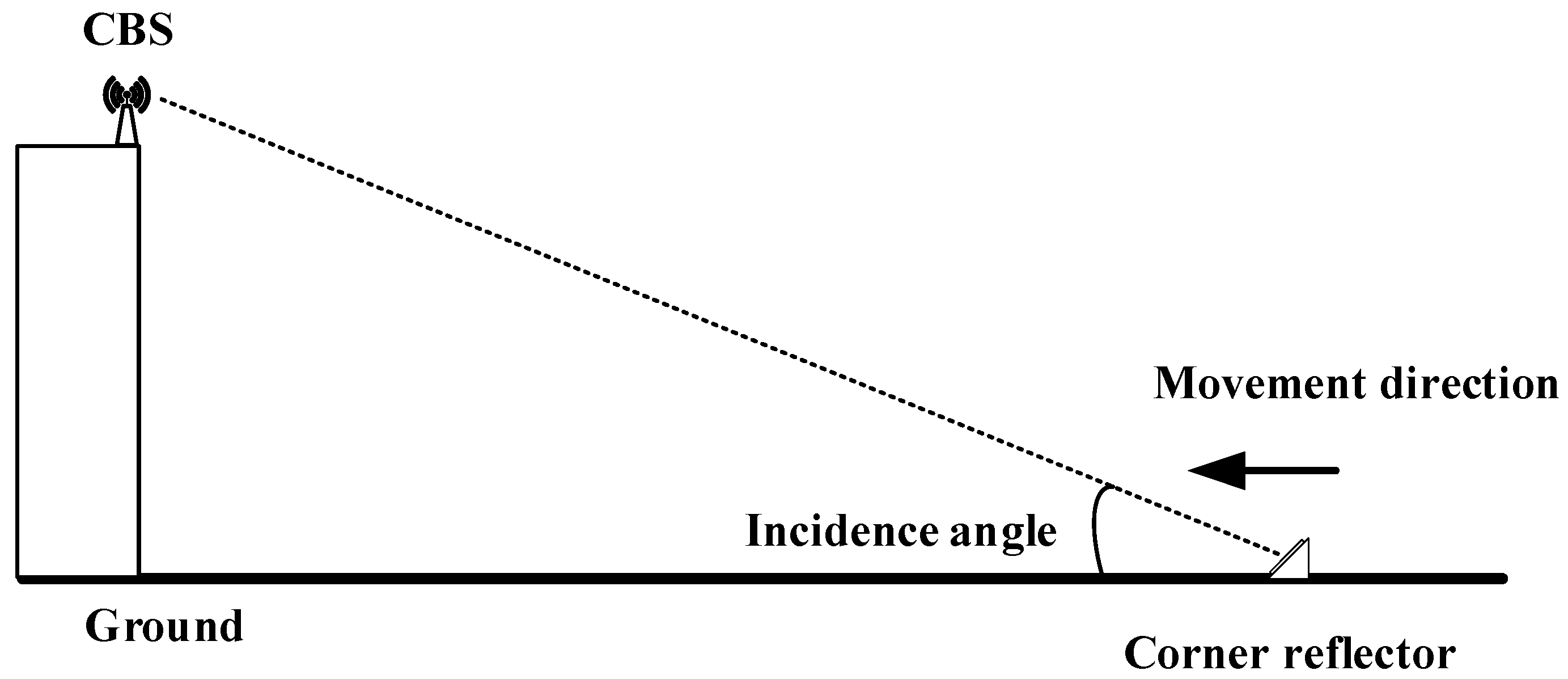
3.4.3. Observation Geometry Analysis
4. The Deformation Detection Experiment and Results
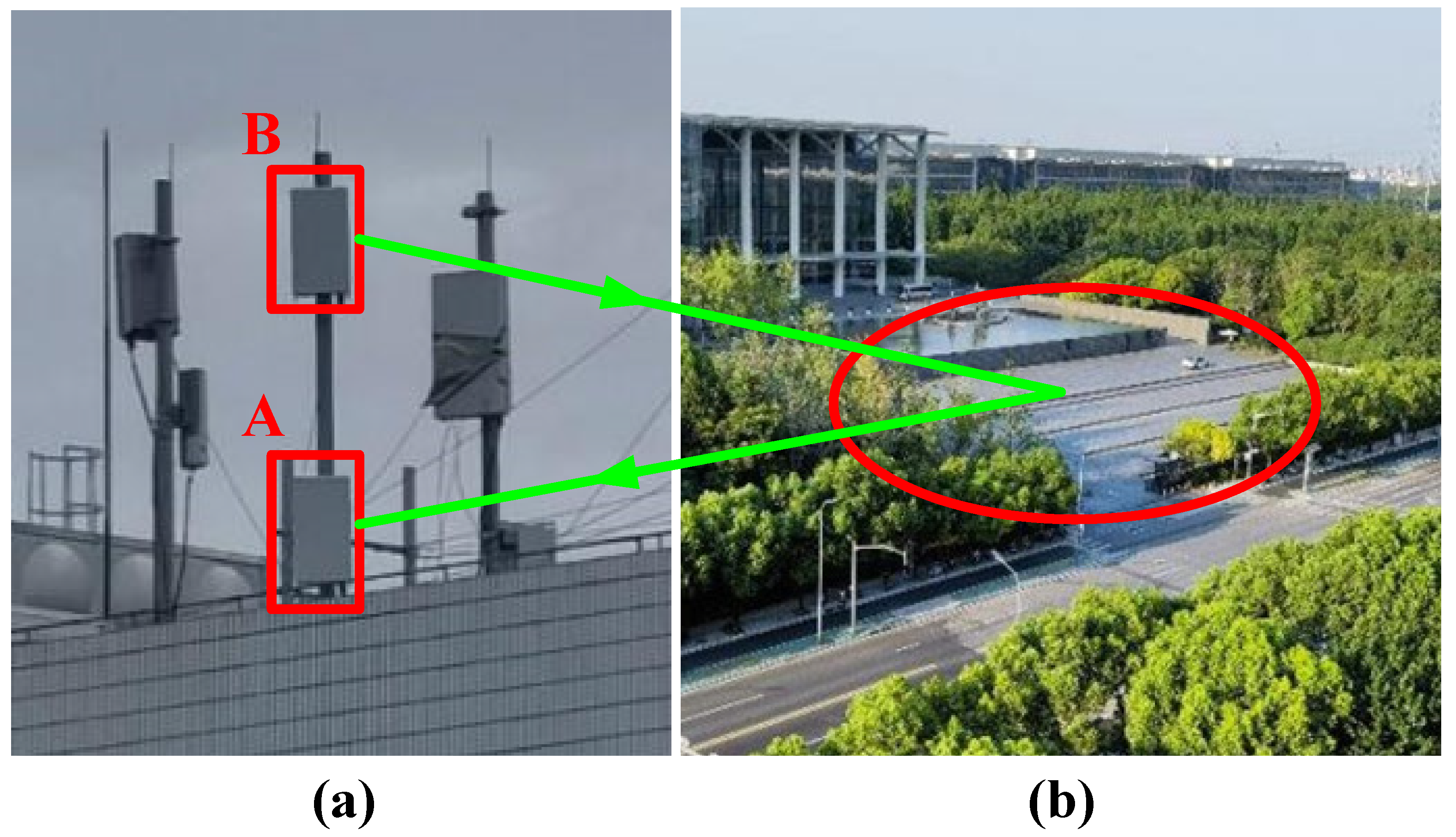
4.1. Deformation Detection Experiment Conditions
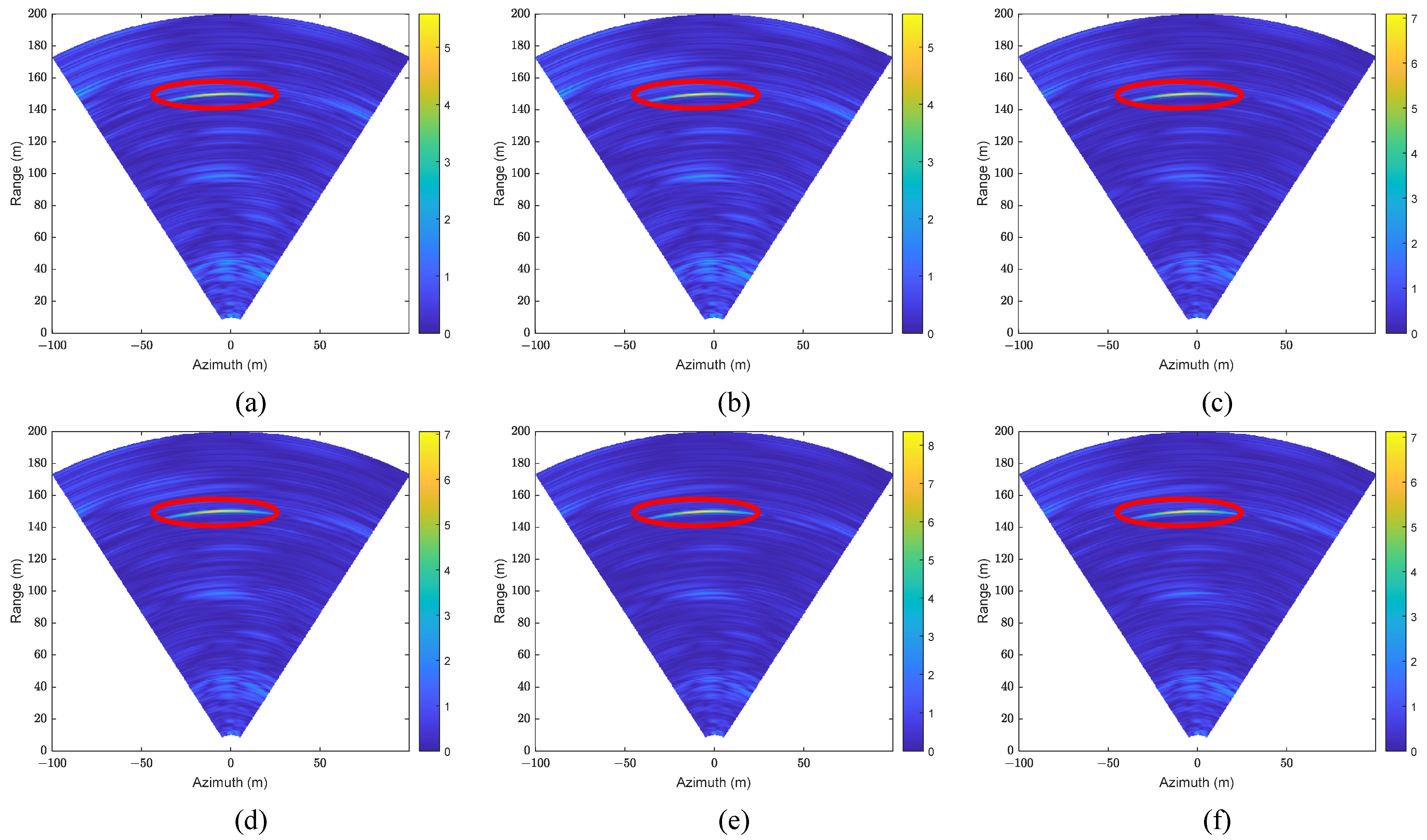
4.2. The Deformation Detection Experiment Results
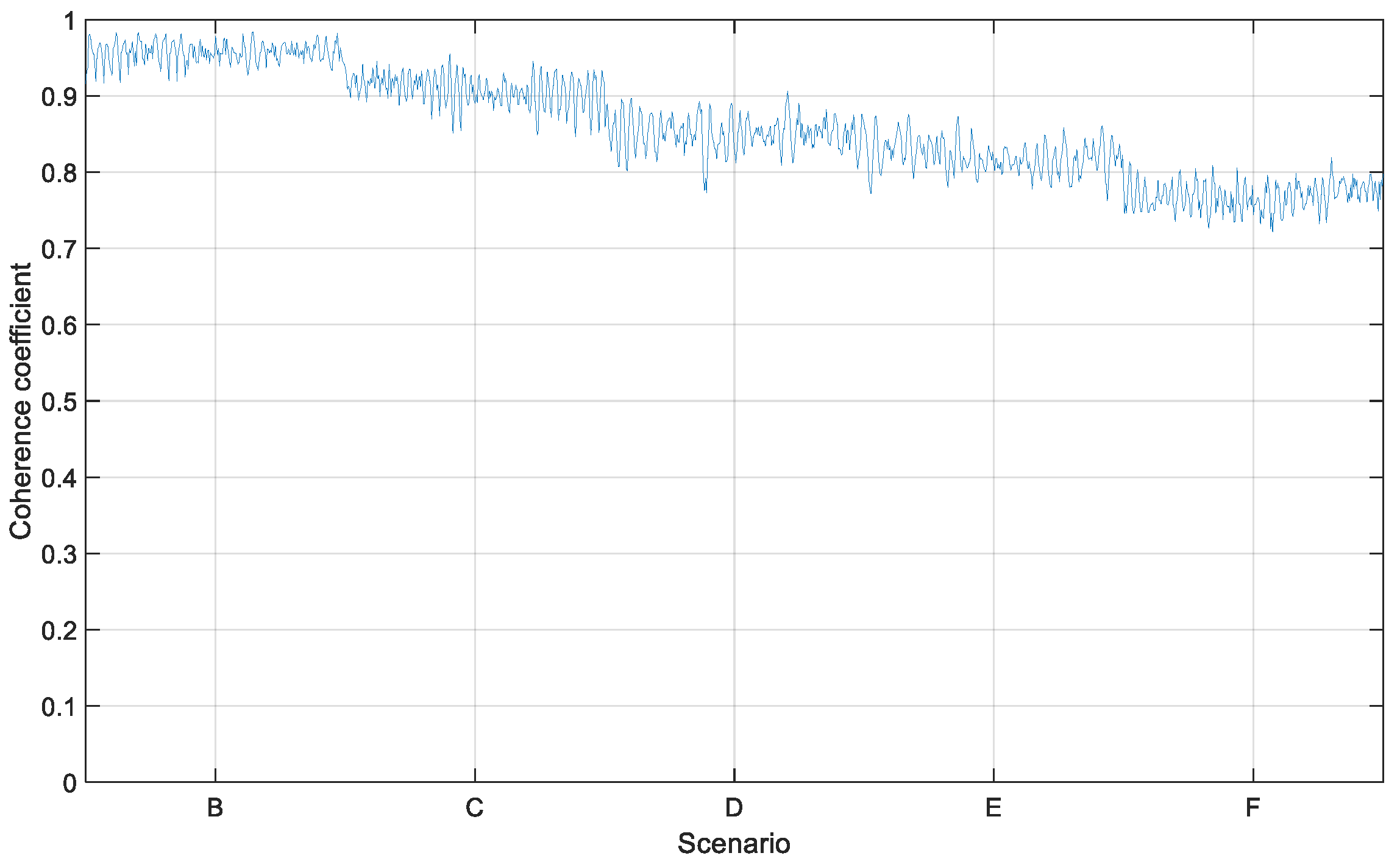
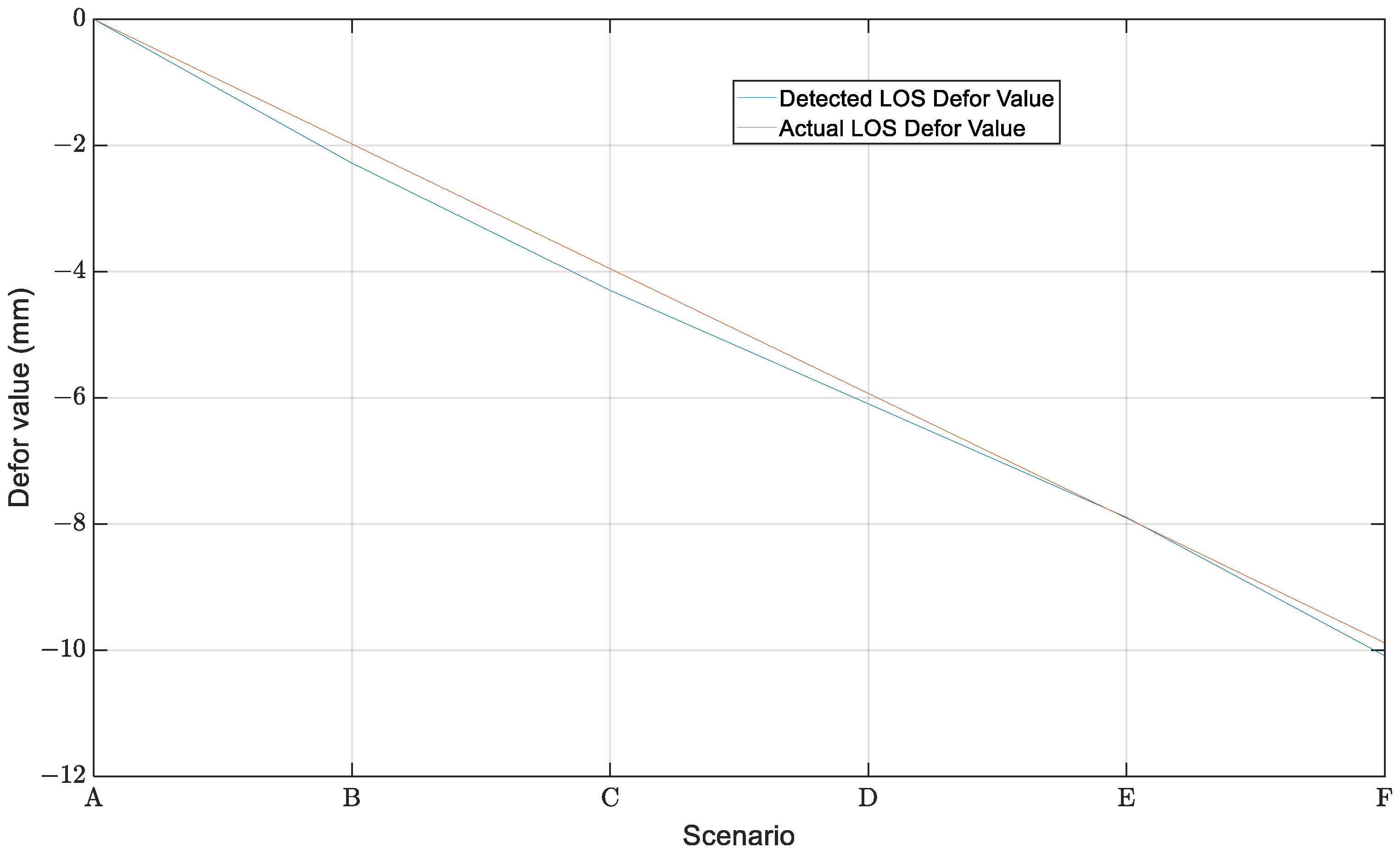
4.3. Error Analysis
4.4. Comparison with Traditional Deformation Monitoring Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Tan, D.K.P.; He, J.; Li, Y.; Bayesteh, A.; Chen, Y.; Zhu, P.; Tong, W. Integrated Sensing and Communication in 6G: Motivations, Use Cases, Requirements, Challenges and Future Directions. In Proceedings of the 2021 1st IEEE International Online Symposium on Joint Communications & Sensing (JC&S), Dresden, Germany, 23–24 February 2021; pp. 1–6. [Google Scholar]
- Liu, M.; Yang, M.; Zhang, Z.; Li, H.; Liu, F.; Nallanathan, A.; Hanzo, L. Sensing-Communication Coexistence vs. Integration. IEEE Trans. Veh. Technol. 2023, 6, 8158–8163. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Fei, Z.; Liu, P.; Wang, R.; Xia, F. Physical Layer Security in Integrated Sensing and Communication Systems: Opportunities and Challenges. Mob. Commun. 2023, 3, 55–61. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Z.; Hao, S.; Chen, X.; Zhang, R. OTFS Waveform Design Based on WFRFT for Integrated Sensing and Communication. In Proceedings of the 2023 IEEE/CIC International Conference on Communications in China (ICCC), Dalian, China, 10–12 August 2023; pp. 1–6. [Google Scholar]
- Zhang, Z.; Xiao, Y.; Ma, Z.; Xiao, M.; Ding, Z.; Lei, X.; Karagiannidis, G.K.; Fan, P. 6G Wireless Networks: Vision, Requirements, Architecture, and Key Technologies. IEEE Veh. Technol. Mag. 2019, 3, 28–41. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, G.; Xu, L.; Sun, S. Towards 6G: Integrated sensing and communication. Appl. Electron. Tech. 2023, 5, 30–34. [Google Scholar] [CrossRef]
- Zhu, G.; Li, Y.; Chen, Y.; Chai, S.; Shi, Q.; Luo, Z. Global Competitive Situation of 6G Key Technology R&D and China’s Countermeasures. Strateg. Study CAE 2023, 6, 9–17. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, R.; Chen, G.; Wu, W. Integrated Sensing and Communication Waveform Design: A Survey. IEEE Open J. Commun. Soc. 2022, 3, 1930–1949. [Google Scholar] [CrossRef]
- Zhang, R.; Shim, B.; Yuan, W.; Renzo, M.D.; Dang, X.; Wu, W. Integrated Sensing and Communication Waveform Design with Sparse Vector Coding: Low Sidelobes and Ultra Reliability. IEEE Trans. Veh. Technol. 2022, 4, 4489–4494. [Google Scholar] [CrossRef]
- Xiao, Z.; Zeng, Y. Full-Duplex Integrated Sensing and Communication: Waveform Design and Performance Analysis. In Proceedings of the 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP), Changsha, China, 20–22 October 2021; pp. 1–5. [Google Scholar]
- Liu, Y.; Liao, G.; Xu, J.; Yang, Z.; Zhang, Y. Adaptive OFDM Integrated Radar and Communications Waveform Design Based on Information Theory. IEEE Commun. Lett. 2017, 10, 2174–2177. [Google Scholar] [CrossRef]
- Xiao, Z.; Zeng, Y. Waveform Design and Performance Analysis for Full-Duplex Integrated Sensing and Communication. IEEE J. Sel. Areas Commun. 2022, 6, 1823–1837. [Google Scholar] [CrossRef]
- Yuan, W.; Wei, Z.; Li, S.; Yuan, J.; Ng, D.W.K. Integrated Sensing and Communication-Assisted Orthogonal Time Frequency Space Transmission for Vehicular Networks. IEEE J. Sel. Top. Signal Process. 2021, 6, 1515–1528. [Google Scholar] [CrossRef]
- Hieu, N.Q.; Hoang, D.T.; Luong, N.C.; Niyato, D. iRDRC: An Intelligent Real-Time Dual-Functional Radar-Communication System for Automotive Vehicles. IEEE Wirel. Commun. Lett. 2020, 12, 2140–2143. [Google Scholar] [CrossRef]
- Wang, X.; Fei, Z.; Zhang, J.A.; Huang, J.; Yuan, J. Constrained Utility Maximization in Dual-Functional Radar-Communication Multi-UAV Networks. IEEE Trans. Commun. 2021, 4, 2660–2672. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, A.; Wei, Z.; Lai, M.; Pan, C.; Feng, Z.; Liu, J. Improve Sensing and Communication Performance of UAV via Integrated Sensing and Communication. In Proceedings of the 2021 IEEE 21st International Conference on Communication Technology (ICCT), Tianjin, China, 13–16 October 2021; pp. 644–648. [Google Scholar]
- Zhang, K.; Shen, C. UAV Aided Integrated Sensing and Communications. In Proceedings of the 2021 IEEE 94th Vehicular Technology Conference (VTC2021-Fall), Norman, OK, USA, 27–30 September 2021; pp. 1–6. [Google Scholar]
- Wu, Q.; Xu, J.; Zeng, Y.; Ng, D.W.K.; Al-Dhahir, N.; Schober, R.; Swindlehurst, A.L. A Comprehensive Overview on 5G-and-Beyond Networks with UAVs: From Communications to Sensing and Intelligence. IEEE J. Sel. Areas Commun. 2021, 10, 2912–2945. [Google Scholar] [CrossRef]
- Hu, Y.; Tang, L.; Zhuo, X.; Li, Z.; Wu, W.; Zhao, Y.; Bu, Z. Imaging Based on Communication-Assisted Sensing for UAV-Enabled ISAC. In Proceedings of the 2023 IEEE 98th Vehicular Technology Conference (VTC2023-Fall), Hong Kong, 10–13 October 2023; pp. 1–5. [Google Scholar]
- Zhou, L.; Gui, S.; Li, L.; Tian, Z. Bistatic OFDM ISAR Imaging Method for Non-cooperative Moving Target in ISAC Area. In Proceedings of the 2023 IEEE 11th Asia-Pacific Conference on Antennas and Propagation (APCAP), Guangzhou, China, 22–24 November 2023; pp. 1–2. [Google Scholar]
- Wang, C.; Li, Y.; Li, Z.; Zeng, K.; He, J.; Wang, G. A 3D imaging method for future communication and imaging integrated terminal. In Proceedings of the 2021 CIE International Conference on Radar (Radar), Haikou, China, 15–19 December 2021; pp. 774–777. [Google Scholar]
- Liu, F.; Cui, Y.; Masouros, C.; Xu, J.; Han, T.X.; Eldar, Y.C.; Buzzi, S. Integrated Sensing and Communications: Toward Dual-Functional Wireless Networks for 6G and Beyond. IEEE J. Sel. Areas Commun. 2022, 6, 1728–1767. [Google Scholar] [CrossRef]
- Xie, C. Research of Resources Allocation and Handover Technique Based on MIMO Ultra Dense Heterogeneous Network. Ph.D. Thesis, School of Microelectronics and Communication, Engineering of Chongqing University, Chongqing, China, 2018. [Google Scholar]
- Wei, Z.; Qu, H.; Wang, Y.; Yuan, X.; Wu, H.; Du, Y.; Han, K.; Zhang, N.; Feng, Z. Integrated Sensing and Communication Signals Toward 5G-A and 6G: A Survey. IEEE Internet Things J. 2023, 13, 11068–11092. [Google Scholar] [CrossRef]
- Tigrek, R.F.; De Heij, W.J.A.; Van Genderen, P. OFDM Signals as the Radar Waveform to Solve Doppler Ambiguity. IEEE Trans. Aerosp. Electron. Syst. 2012, 1, 130–143. [Google Scholar] [CrossRef]
- Wang, W.-Q. Mitigating Range Ambiguities in High-PRF SAR With OFDM Waveform Diversity. IEEE Geosci. Remote Sens. Lett. 2013, 1, 101–105. [Google Scholar] [CrossRef]
- Cui, Y.; Jing, X.; Mu, J. Integrated Sensing and Communications Via 5G NR Waveform: Performance Analysis. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; pp. 8747–8751. [Google Scholar]
- Li, P.; Guo, X. Key Technologies and Application of ISAC. ZTE Technol. J. 2023, 2, 72–78. [Google Scholar] [CrossRef]
- Zheng, Y. Research on OFDM-based Radar Communication Sharing Method. Master’s Thesis, Information and Communication Engineering, Harbin Engineering University, Harbin, China, 2023. [Google Scholar]
- Hu, C.; He, Q.; Tian, W.; Deng, Y.; Dong, X. A performance analysis of typical imaging algorithms in Ground-Based Synthetic aperture radar. In Proceedings of the 2017 XXXIInd General Assembly and Scientific Symposium of the International Union of Radio Science (URSI GASS), Montreal, QC, Canada, 19–26 August 2017; pp. 1–4. [Google Scholar]
- Zhang, W.; Li, C.; Shi, Y.; Wang, H.; Li, H.; Shang, Y.; Zhou, M. A new portable 2D ground-based synthetic aperture radar system for micro-deformation monitoring and SAR imaging. In Proceedings of the 2023 35th Chinese Control and Decision Conference (CCDC), Yichang, China, 20–23 May 2023; pp. 5338–5342. [Google Scholar]
- Zhang, X.; Ge, D.; Zhang, L.; Wang, Y.; Qin, K.; Li, M.; Guo, X. Subsidence deformation monitoring in KaiLuan mining area by D- InSAR technique. In Proceedings of the World Automation Congress 2012, Puerto Vallarta, Mexico, 24–28 June 2012; pp. 1–4. [Google Scholar]
- Wang, Y.; Hong, W.; Zhang, Y.; Lin, Y.; Li, Y.; Bai, Z.; Zhang, Q.; Lv, S.; Liu, H.; Song, Y. Ground-Based Differential Interferometry SAR: A Review. IEEE Geosci. Remote Sens. Mag. 2020, 1, 43–70. [Google Scholar] [CrossRef]
- Qi, Y.; Zhang, M.; Qi, L.; Tan, W.; Sun, J.; Huang, P.; Xu, W. Application of Ground-based Deformation Monitoring Radar in Mine Slope Monitoring-Taking a mine in Inner Mongolia as an example. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–4. [Google Scholar]
- Herrera, G.; Tomas, R.; Lopez-Sanchez, J.M.; Delgado, J.; Mallorqui, J.J.; Duque, S.; Mulas, J. Advanced DInSAR analysis on mining area: La Union case study (Murcia, SE Spain). Eng. Geol. 2007, 90, 148–159. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, S.; Liu, D.; Wang, W.; Peng, J. Research on application of GB-SAR in slope deformation monitoring. Sci. Surv. Mapp. 2021, 5, 58–65. [Google Scholar]
- Florentino, A.; Charapaqui, S.; Jara, C.; Milla, M. Implementation of a ground based synthetic aperture radar (GB-SAR) for landslide monitoring: System description and preliminary results. In Proceedings of the IEEE XXIII International Congress on Electronics, Electrical Engineering and Computing, Piura, Peru, 2–5 August 2016; pp. 1–6. [Google Scholar]
- Dick, G.J.; Eberhardt, E.; Cabrejo-Liévano, A.G.; Stead, D.; Rose, N.D. Development of an early-warning time-of-failure analysis methodology for open-pit mine slopes utilizing ground-based slope stability radar monitoring data. Can. Geotech. J. 2015, 4, 515–529. [Google Scholar] [CrossRef]
- Traglia, F.; Intrieri, E.; Nolesini, T.; Bardi, F.; Del Ventisette, C.; Ferrigno, F.; Frangioni, S.; Frodella, W.; Gigli, G.; Lotti, A.; et al. The ground-based InSAR monitoring system at Stromboli volcano: Linking changes in displacement rate and intensity of persistent volcanic activity. Bull. Volcanol. 2014, 2, 786. [Google Scholar] [CrossRef]
- Farina, P.; Leoni, L.; Babboni, F.; Coppi, F.; Mayer, L.; Coli, N.; Thompson, C. Monitoring engineered and natural slopes by ground-based radar: Methodology, data processing and case studies review. In Proceedings of the SHIRMS2012: Southern Hemisphere International Rock Mechanics Symposium, Sun City, South Africa; pp. 15–17.
- Huang, Q.; Yue, J.; Gong, J. Monitoring of Geheyan Dam deformation using GBInSAR technology GBInSAR. Adv. Sci. Technol. Water Resour. 2016, 36, 47–51. [Google Scholar]
- Gao, Z.; Jia, Y.; Liu, S.; Zhang, X. Experimental study of SFCW interferometry radar applied to vehicle-bridge coupling vibration monitoring of high-speed railway bridge. China Meas. Test 2023, 3, 135–141. [Google Scholar]
- Liu, L.; Meng, X.; Xie, W. Research on 5G Base Station to Satellite Earth Station Interference and Mitigation Methods. In Proceedings of the 2023 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB), Beijing, China, 14–16 June 2023; pp. 1–6. [Google Scholar]
- Zhang, H. Broadband Base Station Antenna and its MIMO Array Design. Master’s Thesis, School of Electronic and Information Engineering, Anhui University, Hefei, China, 2023. [Google Scholar]
- Xing, M.; Li, Z.; Bao, Z.; Wang, T. Study of Distributed Microsatellites Radar Space-Time-Frequency Imaging Method. J. Astronaut. 2005, B10, 70–76+82. [Google Scholar]
- Wang, L.; Xu, J.; HuangFu, K.; Peng, Y.N. Analysis and Compensation of Equivalent Phase Center Error in MIMO-SAR. Acta Electron. Sin. 2009, 12, 2688–2693. [Google Scholar] [CrossRef]
- Shan, W.; Wang, J.; Xiang, K.; Wang, J.; Guan, J. Research on uniform linear array output signal and beamforming. In Proceedings of the 2020 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Macau, China, 21–24 August 2020; pp. 1–4. [Google Scholar]
- Lellouch, G.; Mishra, A.; Inggs, M. Impact of the Doppler modulation on the range and Doppler processing in OFDM radar. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 0803–0808. [Google Scholar]
- Liang, D. Imaging Experimental System Design and Algorithm Implementation for MIMO Radar. Master’s Thesis, Master of Engineering, Harbin Engineering University, Harbin, China, 2015. [Google Scholar]
- Pasternak, Y.G.; Pendyurin, V.A.; Popov, I.V.; Fedorov, S.M. Extrapolated Virtual Antenna Array for Enhancement of Resolution of Uniform Linear Array. In Proceedings of the 2022 Photonics & Electromagnetics Research Symposium (PIERS), Hangzhou, China, 25–29 April 2022; pp. 1045–1052. [Google Scholar]
- Han, G.; Cong, W.; Zhu, B. An Azimuth High Resolution Algorithm Based on Virtual Array and Spatial Resampling. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–4. [Google Scholar]
- Shang, T. Research and Implementation of LEO Satellite Random Access Technology for 5G. Master’s Thesis, School of Telecommunciations Engineering, XiDian University, Xi’an, China, 2023. [Google Scholar]
- Gao, Y. Research on Key Technologies of Post-Disaster Search and Rescue Equipment Based on Mobile Communication. Ph.D. Thesis, School of Electronic Engineering Bupt, Beijing University of Posts and Telecommunications, Beijing, China, 2022. [Google Scholar]
- Yao, J. A LTE-PRACH Receiver Design and Implementation Based on TMS320C6670. Electron. Eng. Prod. World 2012, 8, 35–37. [Google Scholar]
- Wu, G. SAR Imaging Simulation and Detection of Ship Targets on Sea Surface. Master’s Thesis, School of Physics and Electronic Information, Yan’an University, Yan’an, China, 2024. [Google Scholar]
- McCorkle, J.W.; Rofheart, M. Order N2 log(N) backprojector algorithm for focusing wide-angle wide-bandwidth arbitrary-motion synthetic aperture radar. In Proceedings of the SPIE—The International Society for Optical Engineering, Orlando, FL, USA, 17 June 1996. [Google Scholar]
- Munson, D.C.; O’Brien, J.D.; Jenkins, W.K. A tomographic formulation of spotlight-mode synthetic aperture radar. Proc. IEEE 1983, 8, 917–925. [Google Scholar] [CrossRef]
- Yang, L.; Kuang, L. Multi-core DSP-based Acceleration of SAR BP Algorithm Imaging. In Proceedings of the 2022 2nd International Conference on Computer Science, Electronic Information Engineering and Intelligent Control Technology (CEI), Nanjing, China, 23–25 September 2022; pp. 728–731. [Google Scholar]
- Sun, G.; Zhang, F. Convolutional Neural Network (CNN)-Based Fast Back Projection Imaging with Noise-Resistant Capability. IEEE Access 2020, 8, 117080–117085. [Google Scholar] [CrossRef]
- Sowjanya, L.S.L.; Kumar, P.K. Performance comparison of DAS and BP algorithms for Synthetic Aperture Radar Imaging. In Proceedings of the 2022 IEEE Microwaves, Antennas, and Propagation Conference (MAPCON), Bangalore, India, 12–16 December 2022; pp. 1726–1731. [Google Scholar]
- Wang, G.; Qi, F.; Liu, Z.; Liu, C.; Xing, C.; Ning, W. Comparison Between Back Projection Algorithm and Range Migration Algorithm in Terahertz Imaging. IEEE Access 2020, 8, 18772–18777. [Google Scholar] [CrossRef]
- Liu, B. Research on Motion Compensation and GPU Parallel Implemetion of BP Algorithm Imaging for Airborne SAR. Master’s Thesis, School of Electronic Science and Engineering, University of Electronic Science and Technology of China, Chengdu, China, 2014. [Google Scholar]
- Hu, X.; Wang, B.; Xiang, M.; Wang, Z. InSAR elevation inversion method based on backprojection model with external DEM. J. Radars 2021, 3, 391–401. [Google Scholar] [CrossRef]
- Zhu, B.; Liu, T. Performance Evaluation in Subaperture Measurement of Synthetic Aperture Radar. Ship Electron. Eng. 2016, 2, 46–49. [Google Scholar] [CrossRef]
- Lee, J.S.; Hoppel, K.W.; Mango, S.A. Intensity and Phase Statistics of Multilook Polarimetric and Interferometric SAR Imagery. IEEE Trans. Geosci. Remote Sens. 1994, 5, 1017–1027. [Google Scholar]
- Chan, Y.-K.; Koo, V.-C.; Hii, W.H.-H.; Lim, C.-S. A Ground-Based Interferometric Synthetic Aperture Radar Design and Experimental Study for Surface Deformation Monitoring. IEEE Aerosp. Electron. Syst. Mag. 2021, 10, 4–15. [Google Scholar] [CrossRef]
- Dong, J.; Dong, Y. Atmospheric artifact compensation for deformation monitoring with ground-based radar. Eng. Surv. Mapp. 2014, 10, 72–75. [Google Scholar] [CrossRef]





| L | 1 | 4 | 8 | 16 | 32 |
|---|---|---|---|---|---|
| Mean(rad) | −1.7175 | −1.7173 | −1.7171 | −1.7171 | −1.7173 |
| STD | 0.0730 | 0.0580 | 0.0464 | 0.0417 | 0.0387 |
| Scenarios | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| Displacement | 0 mm | 2 mm | 4 mm | 6 mm | 8 mm | 10 mm |
| Scenarios | B | C | D | E | F |
|---|---|---|---|---|---|
| Actual LOS Deformation Value (mm) | −1.9770 | −3.9540 | −5.9310 | −7.9080 | −9.8850 |
| Detected LOS Deformation Value (mm) | −2.2802 | −4.2977 | −6.0963 | −7.8961 | −10.0894 |
| Error (mm) | −0.3032 | −0.3437 | −0.1653 | 0.0119 | −0.2044 |
| Characteristic | CBSs | Satellite SAR Platforms | GB-SAR Platforms |
|---|---|---|---|
| Cost | Low | Extreme | High |
| Flexibility | High | Low | Medium |
| Scalability | High | Low | Medium |
| Temporal Sampling Rate | Extreme | Low | High |
| Temporal Decorrelation | Slight | Severe | Moderate |
| Observation Range | Moderate | Extensive | Moderate |
| Accuracy | High | Moderate | High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, J.; Suo, Z.; Ti, J. The First Experimental Validation of a Communication Base Station as a Ground-Based SAR for Deformation Monitoring. Remote Sens. 2025, 17, 1129. https://doi.org/10.3390/rs17071129
Xi J, Suo Z, Ti J. The First Experimental Validation of a Communication Base Station as a Ground-Based SAR for Deformation Monitoring. Remote Sensing. 2025; 17(7):1129. https://doi.org/10.3390/rs17071129
Chicago/Turabian StyleXi, Jiabao, Zhiyong Suo, and Jingjing Ti. 2025. "The First Experimental Validation of a Communication Base Station as a Ground-Based SAR for Deformation Monitoring" Remote Sensing 17, no. 7: 1129. https://doi.org/10.3390/rs17071129
APA StyleXi, J., Suo, Z., & Ti, J. (2025). The First Experimental Validation of a Communication Base Station as a Ground-Based SAR for Deformation Monitoring. Remote Sensing, 17(7), 1129. https://doi.org/10.3390/rs17071129





