Evaluation of Scale Effects on UAV-Based Hyperspectral Imaging for Remote Sensing of Vegetation
Abstract
1. Introduction
2. Materials and Methods
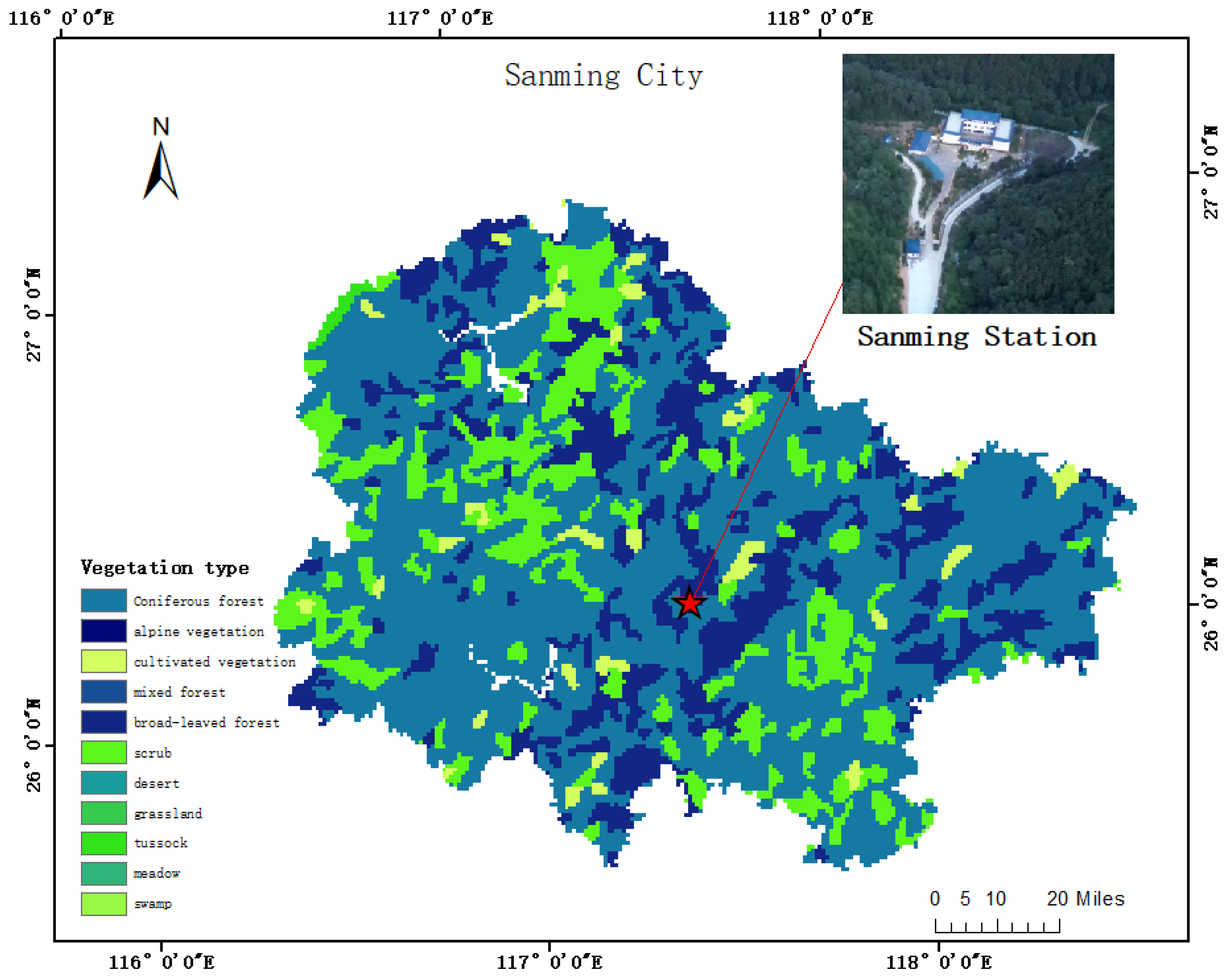
2.1. Study Area
2.2. UAV Hyperspectral Image Acquisition
2.3. Data Processing
3. Results
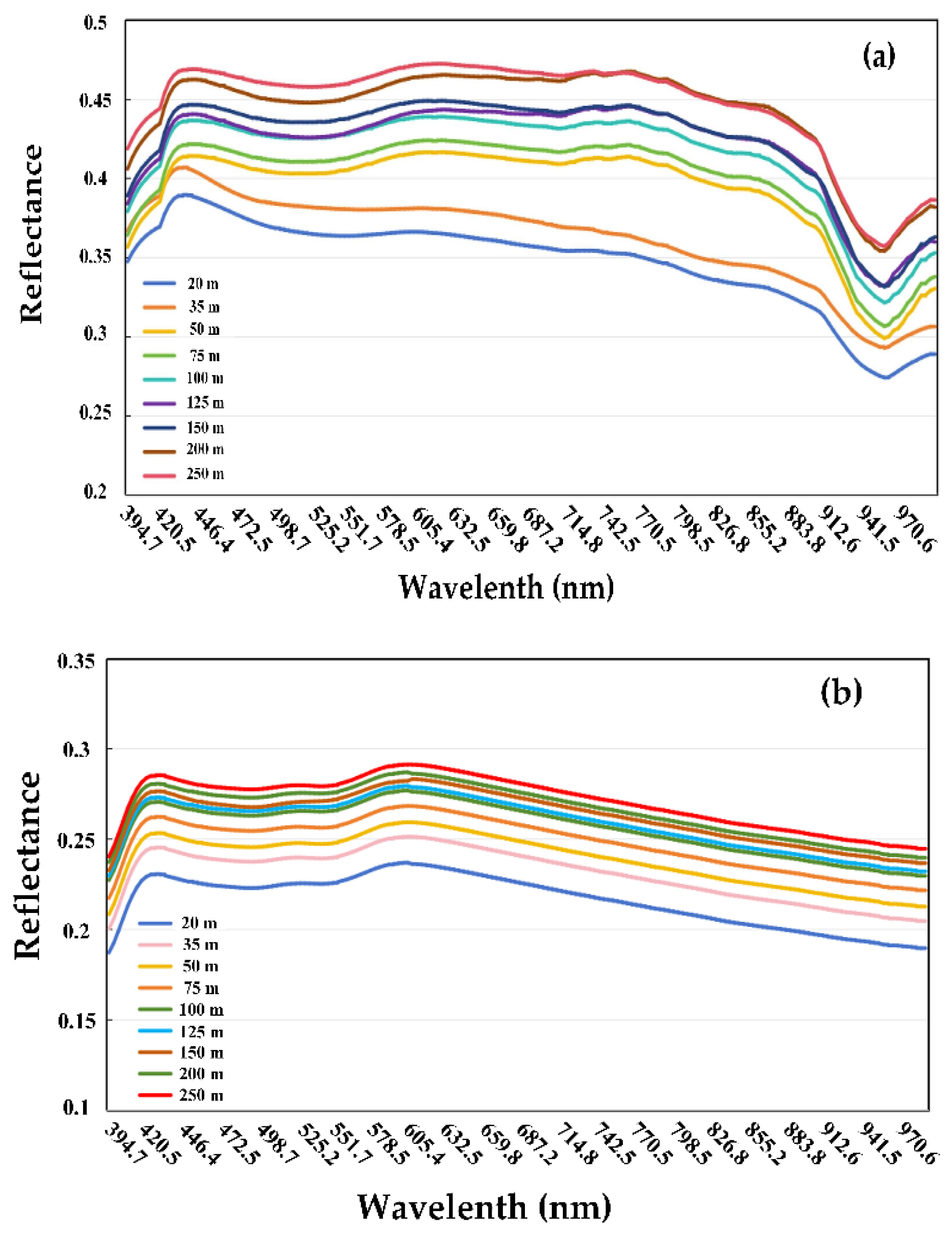
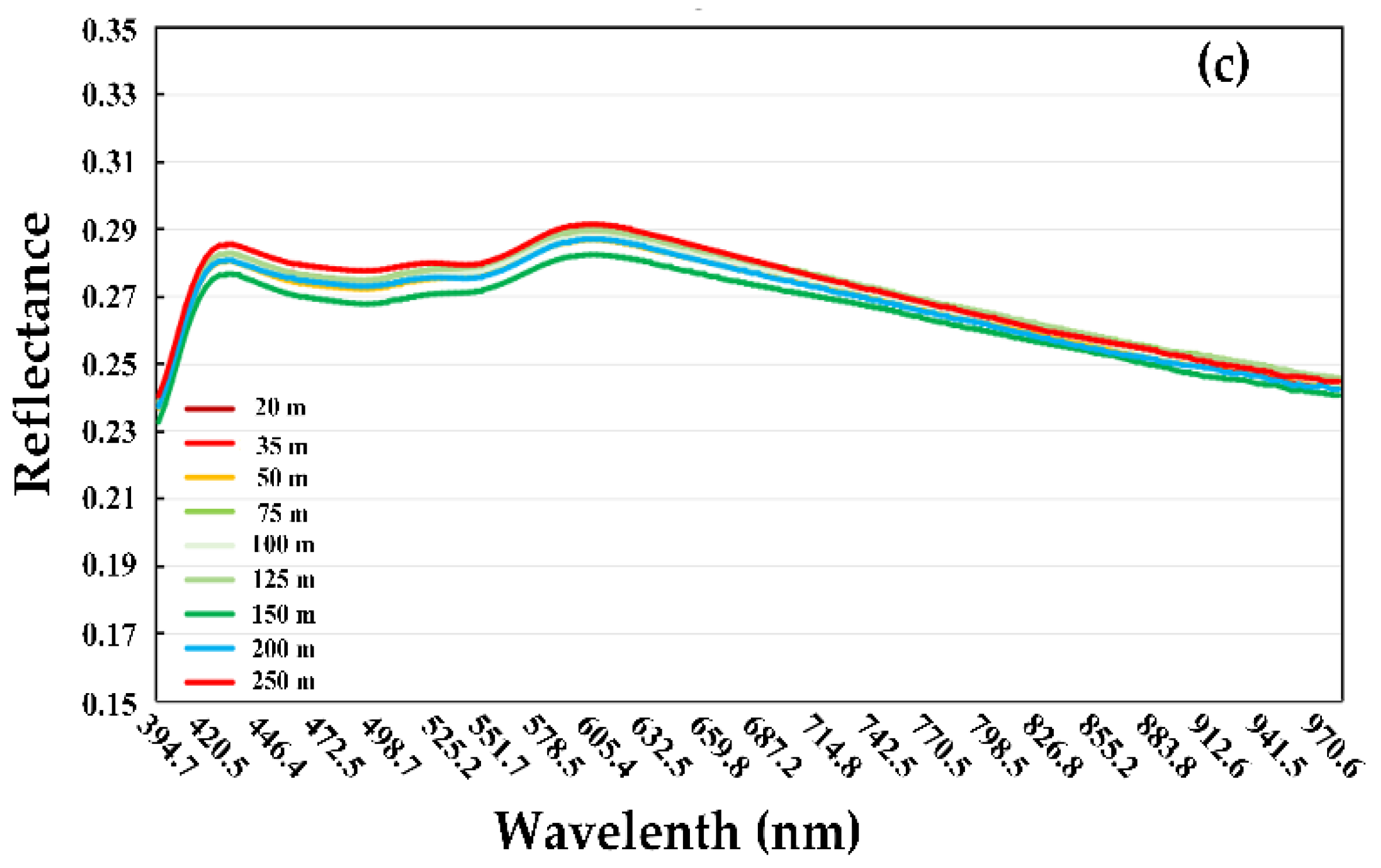
3.1. Atmospheric Correction Methods on Reflectance with Grey Reference
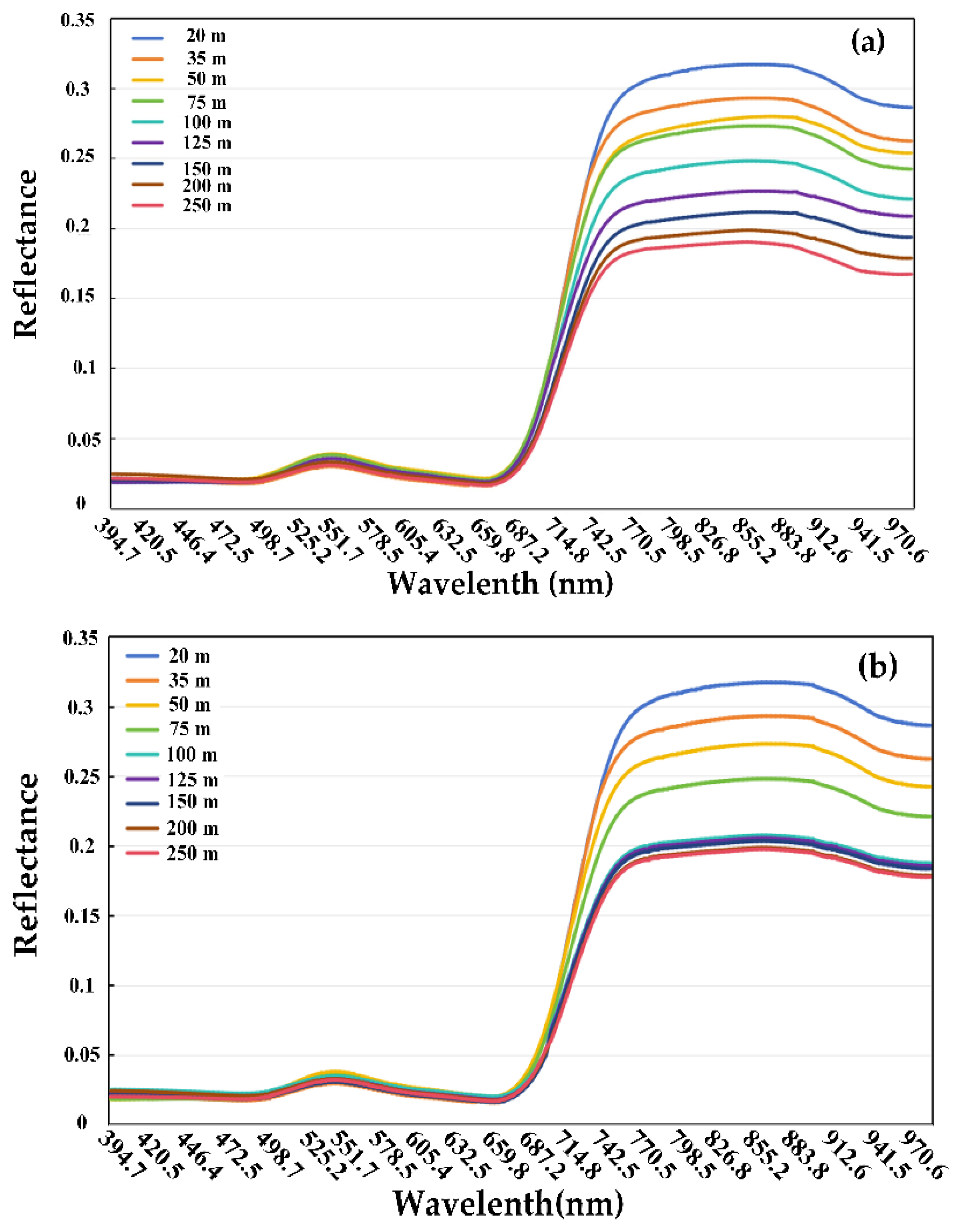
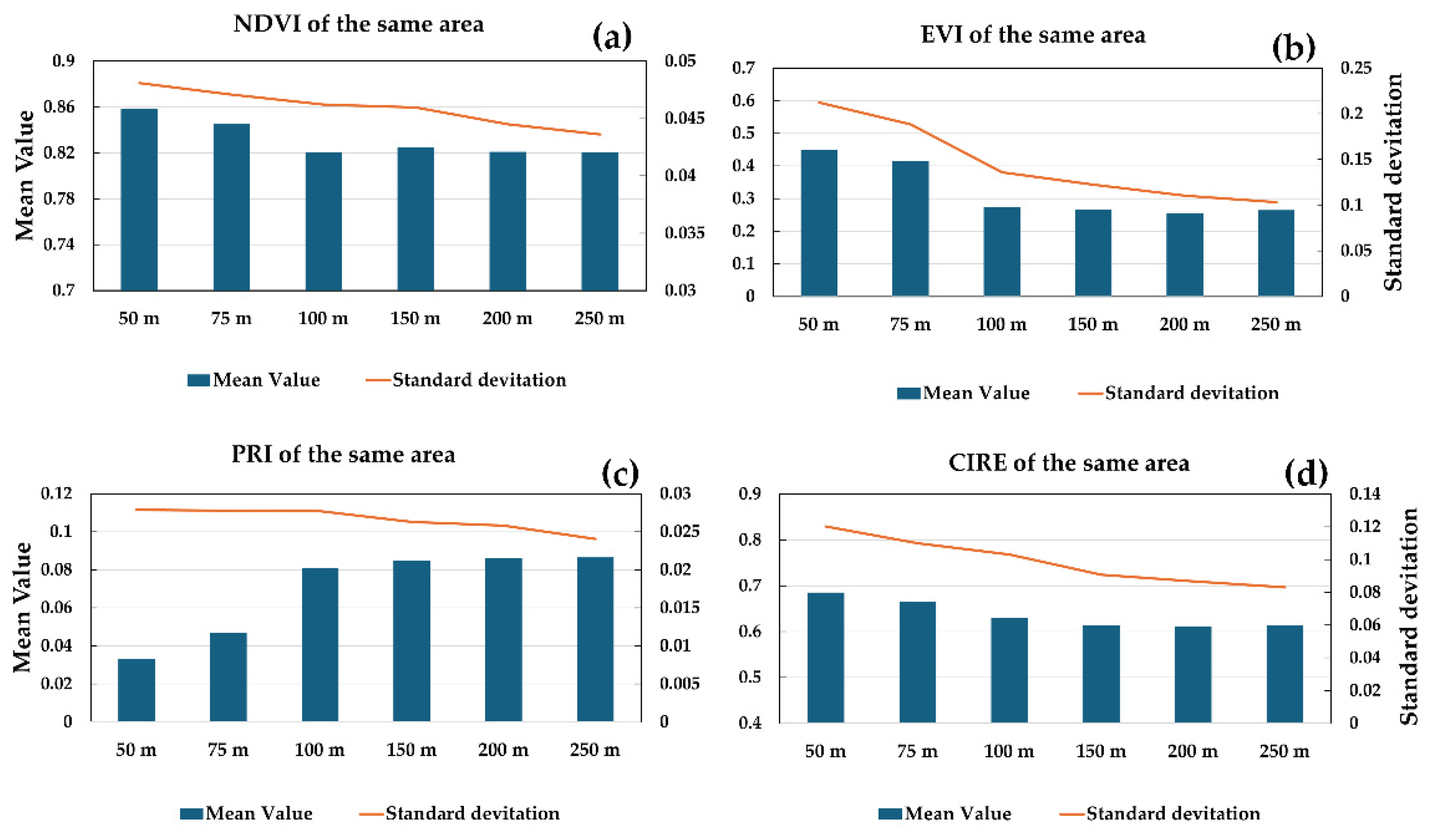
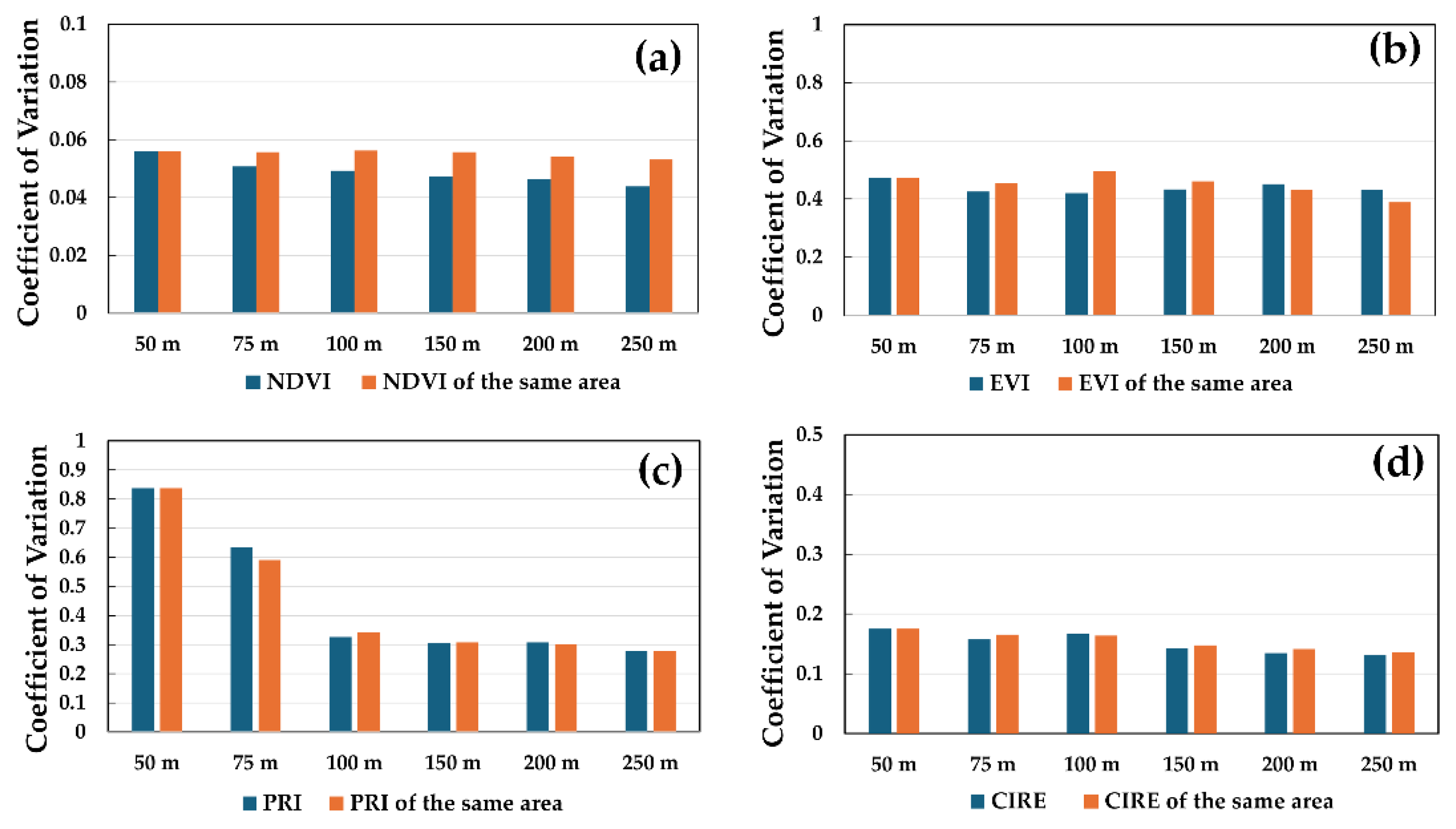
3.2. Impact of Observed Canopy Heterogeneity on Remote Sensing of Forest Canopy
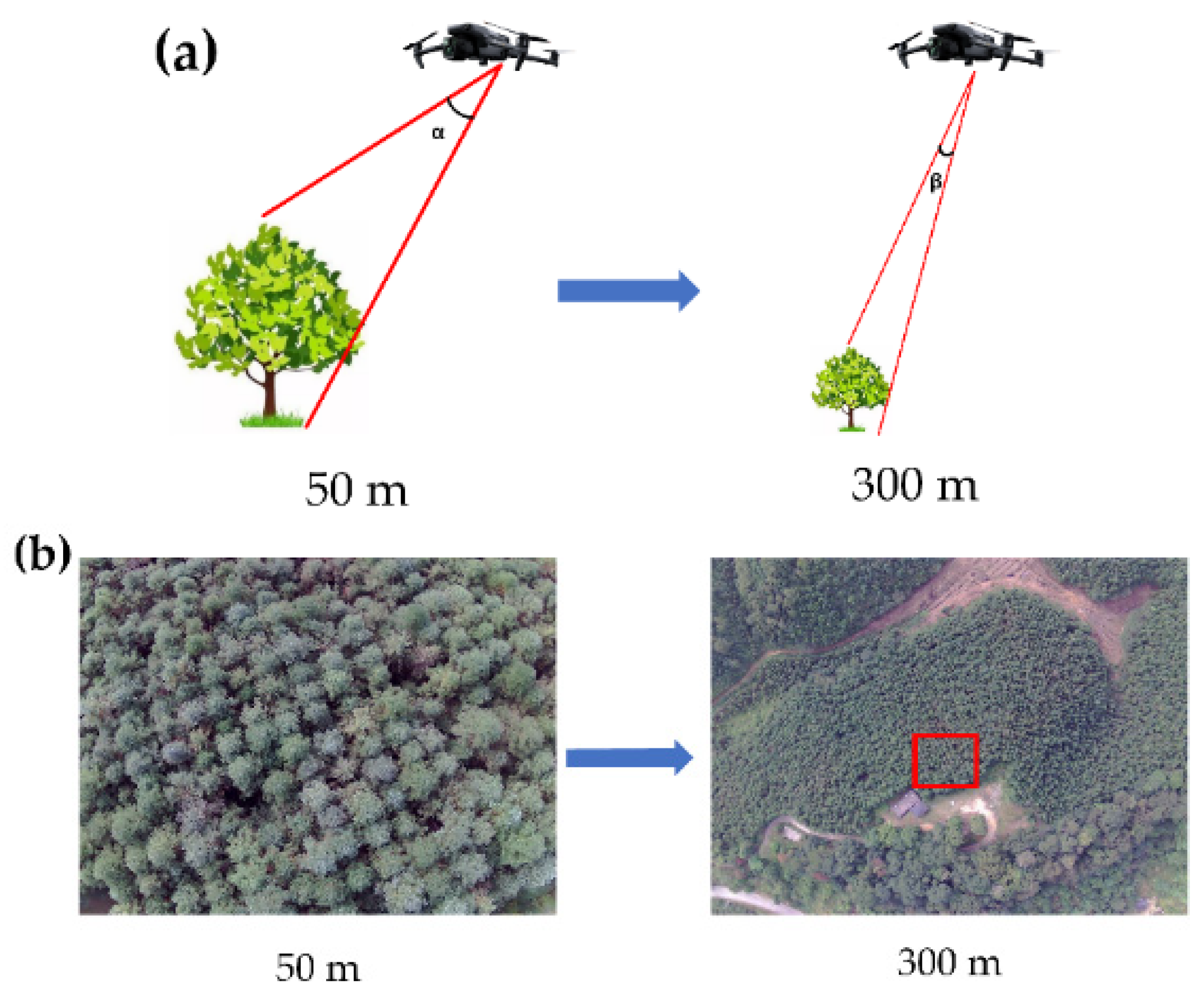
3.3. Impact of Viewer Geometry on Vegetation Indices of Forest Canopy
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karteris, M.; Theodoridou, I.; Mallinis, G.; Tsiros, E.; Karteris, A. Towards a green sustainable strategy for Mediterranean cities: Assessing the benefits of large-scale green roofs implementation in Thessaloniki, Northern Greece, using environmental modelling, GIS and very high spatial resolution remote sensing data. Renew. Sustain. Energy Rev. 2016, 58, 510–525. [Google Scholar] [CrossRef]
- Cao, C.; Lam, N.S.-N. Understanding the scale and resolution effects in remote sensing and GIS. In Scale in Remote Sensing and GIS; Routledge: London, UK, 2023; pp. 57–72. [Google Scholar]
- Zhu, Q.; Guo, X.; Deng, W.; Shi, S.; Guan, Q.; Zhong, Y.; Zhang, L.; Li, D. Land-use/land-cover change detection based on a Siamese global learning framework for high spatial resolution remote sensing imagery. ISPRS J. Photogramm. Remote Sens. 2022, 184, 63–78. [Google Scholar] [CrossRef]
- Peng, D.; Zhang, X.; Zhang, B.; Liu, L.; Liu, X.; Huete, A.R.; Huang, W.; Wang, S.; Luo, S.; Zhang, X.; et al. Scaling effects on spring phenology detections from MODIS data at multiple spatial resolutions over the contiguous United States. ISPRS J. Photogramm. Remote Sens. 2017, 132, 185–198. [Google Scholar] [CrossRef]
- Woodcock, C.E.; Strahler, A.H. The factor of scale in remote sensing. Remote Sens. Environ. 1987, 21, 311–332. [Google Scholar] [CrossRef]
- Wen, D.; Huang, X.; Bovolo, F.; Li, J.; Ke, X.; Zhang, A.; Benediktsson, J.A. Change detection from very-high-spatial-resolution optical remote sensing images: Methods, applications, and future directions. IEEE Geosci. Remote Sens. Mag. 2021, 9, 68–101. [Google Scholar] [CrossRef]
- Hengl, T. Finding the right pixel size. Comput. Geosci. 2006, 32, 1283–1298. [Google Scholar] [CrossRef]
- Tian, Y.; Wu, Z.; Li, M.; Wang, B.; Zhang, X. Forest fire spread monitoring and vegetation dynamics detection based on multi-source remote sensing images. Remote Sens. 2022, 14, 4431. [Google Scholar] [CrossRef]
- You, Y.; Cao, J.; Zhou, W. A survey of change detection methods based on remote sensing images for multi-source and multi-objective scenarios. Remote Sens. 2020, 12, 2460. [Google Scholar] [CrossRef]
- Aasen, H.; Honkavaara, E.; Lucieer, A.; Zarco-Tejada, P.J. Quantitative remote sensing at ultra-high resolution with UAV spectroscopy: A review of sensor technology, measurement procedures, and data correction workflows. Remote Sens. 2018, 10, 1091. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, L. A review on unmanned aerial vehicle remote sensing: Platforms, sensors, data processing methods, and applications. Drones 2023, 7, 398. [Google Scholar] [CrossRef]
- Yao, H.; Qin, R.; Chen, X. Unmanned aerial vehicle for remote sensing applications—A review. Remote Sens. 2019, 11, 1443. [Google Scholar] [CrossRef]
- Feng, L.; Chen, S.; Zhang, C.; Zhang, Y.; He, Y. A comprehensive review on recent applications of unmanned aerial vehicle remote sensing with various sensors for high-throughput plant phenotyping. Comput. Electron. Agric. 2021, 182, 106033. [Google Scholar] [CrossRef]
- Guimarães, N.; Pádua, L.; Marques, P.; Silva, N.; Peres, E.; Sousa, J.J. Forestry remote sensing from unmanned aerial vehicles: A review focusing on the data, processing and potentialities. Remote Sens. 2020, 12, 1046. [Google Scholar] [CrossRef]
- Iizuka, K.; Itoh, M.; Shiodera, S.; Matsubara, T.; Dohar, M.; Watanabe, K. Advantages of unmanned aerial vehicle (UAV) photogrammetry for landscape analysis compared with satellite data: A case study of postmining sites in Indonesia. Cogent Geosci. 2018, 4, 1498180. [Google Scholar] [CrossRef]
- Pajares, G. Overview and current status of remote sensing applications based on unmanned aerial vehicles (UAVs). Photogramm. Eng. Remote Sens. 2015, 81, 281–330. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Sam, L.; Akanksha; Martín-Torres, F.J.; Kumar, R. UAVs as remote sensing platform in glaciology: Present applications and future prospects. Remote Sens. Environ. 2016, 175, 196–204. [Google Scholar] [CrossRef]
- Salamí, E.; Barrado, C.; Pastor, E. UAV flight experiments applied to the remote sensing of vegetated areas. Remote Sens. 2014, 6, 11051–11081. [Google Scholar] [CrossRef]
- Guo, Y.; Yin, G.; Sun, H.; Wang, H.; Chen, S.; Senthilnath, J.; Wang, J.; Fu, Y. Scaling effects on chlorophyll content estimations with RGB camera mounted on a UAV platform using machine-learning methods. Sensors 2020, 20, 5130. [Google Scholar] [CrossRef]
- Pascucci, S.; Pignatti, S.; Casa, R.; Darvishzadeh, R.; Huang, W. Special issue “hyperspectral remote sensing of agriculture and vegetation”. Remote Sens. 2020, 12, 3665. [Google Scholar] [CrossRef]
- Li, Z.; Guo, X. Remote sensing of terrestrial non-photosynthetic vegetation using hyperspectral, multispectral, SAR, and LiDAR data. Prog. Phys. Geogr. Earth Environ. 2016, 40, 276–304. [Google Scholar] [CrossRef]
- Hyperspectral Remote Sensing of Agriculture on JSTOR. Available online: https://www.jstor.org/stable/24216514 (accessed on 15 January 2025).
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J.J. Hyperspectral imaging: A review on UAV-based sensors, data processing and applications for agriculture and forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef]
- Zhang, Y.; Migliavacca, M.; Penuelas, J.; Ju, W. Advances in hyperspectral remote sensing of vegetation traits and functions. Remote Sens. Environ. 2021, 252, 112121. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Lyon, J.G.; Huete, A. Advances in hyperspectral remote sensing of vegetation and agricultural crops. In Fundamentals, Sensor Systems, Spectral Libraries, and Data Mining for Vegetation; CRC Press: Boca Raton, FL, USA, 2018; pp. 3–37. [Google Scholar]
- Lu, B.; Dao, P.D.; Liu, J.; He, Y.; Shang, J. Recent advances of hyperspectral imaging technology and applications in agriculture. Remote Sens. 2020, 12, 2659. [Google Scholar] [CrossRef]
- Näsi, R.; Honkavaara, E.; Lyytikäinen-Saarenmaa, P.; Blomqvist, M.; Litkey, P.; Hakala, T.; Viljanen, N.; Kantola, T.; Tanhuanpää, T.; Holopainen, M. Using UAV-based photogrammetry and hyperspectral imaging for mapping bark beetle damage at tree-level. Remote Sens. 2015, 7, 15467–15493. [Google Scholar] [CrossRef]
- Cao, J.; Leng, W.; Liu, K.; Liu, L.; He, Z.; Zhu, Y. Object-based mangrove species classification using unmanned aerial vehicle hyperspectral images and digital surface models. Remote Sens. 2018, 10, 89. [Google Scholar] [CrossRef]
- Du, B.; Zhao, R.; Zhang, L.; Zhang, L. A spectral-spatial based local summation anomaly detection method for hyperspectral images. Signal Process. 2016, 124, 115–131. [Google Scholar] [CrossRef]
- Liu, T.; Gu, Y.; Chanussot, J.; Dalla Mura, M. Multimorphological superpixel model for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6950–6963. [Google Scholar] [CrossRef]
- Akinyoola, J.A.; Oluleye, A.; Gbode, I.E. A Review of Atmospheric Aerosol Impacts on Regional Extreme Weather and Climate Events. Aerosol Sci. Eng. 2024, 8, 249–274. [Google Scholar] [CrossRef]
- Seinfeld, J.H.; Bretherton, C.; Carslaw, K.S.; Coe, H.; DeMott, P.J.; Dunlea, E.J.; Feingold, G.; Ghan, S.; Guenther, A.B.; Kahn, R.; et al. Improving our fundamental understanding of the role of aerosol−cloud interactions in the climate system. Proc. Natl. Acad. Sci. USA 2016, 113, 5781–5790. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, G.; Liu, J.; Zhang, X.; Xu, B.; Wang, Y.; Zhao, C.; Gai, J. Estimation of soybean breeding yield based on optimization of spatial scale of UAV hyperspectral image. Trans. Chin. Soc. Agric. Eng. 2017, 33, 110–116. [Google Scholar]
- Comerón, A.; Muñoz-Porcar, C.; Rocadenbosch, F.; Rodríguez-Gómez, A.; Sicard, M. Current research in lidar technology used for the remote sensing of atmospheric aerosols. Sensors 2017, 17, 1450. [Google Scholar] [CrossRef]
- Archer-Nicholls, S.; Lowe, D.; Schultz, D.M.; McFiggans, G. Aerosol–radiation–cloud interactions in a regional coupled model: The effects of convective parameterisation and resolution. Atmos. Chem. Phys. 2016, 16, 5573–5594. [Google Scholar] [CrossRef]
- Lyu, X.; Li, X.; Dang, D.; Dou, H.; Wang, K.; Lou, A. Unmanned aerial vehicle (UAV) remote sensing in grassland ecosystem monitoring: A systematic review. Remote Sens. 2022, 14, 1096. [Google Scholar] [CrossRef]
- Sankey, T.T.; McVay, J.; Swetnam, T.L.; McClaran, M.P.; Heilman, P.; Nichols, M. UAV hyperspectral and lidar data and their fusion for arid and semi-arid land vegetation monitoring. Remote Sens. Ecol. Conserv. 2018, 4, 20–33. [Google Scholar] [CrossRef]
- Yan, Y.; Deng, L.; Liu, X.; Zhu, L. Application of UAV-based multi-angle hyperspectral remote sensing in fine vegetation classification. Remote Sens. 2019, 11, 2753. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, J.; Zhang, J. Analysis of Unmanned Aerial Vehicle (UAV) hyperspectral remote sensing monitoring key technology in coastal wetland. In Proceedings of the Selected Papers of the Photoelectronic Technology Committee Conferences held November 2015, Various, China, 15–28 November 2015; Volume 2016, pp. 721–729. [Google Scholar]
- Du, X.; Zhou, Z.; Huang, D. Influence of Spatial Scale Effect on UAV Remote Sensing Accuracy in Identifying Chinese Cabbage (Brassica rapa subsp. Pekinensis) Plants. Agriculture 2024, 14, 1871. [Google Scholar] [CrossRef]
- Ma, S.; Shao, X.; Xu, C. Landslides triggered by the 2016 heavy rainfall event in Sanming, Fujian Province: Distribution pattern analysis and spatio-temporal susceptibility assessment. Remote Sens. 2023, 15, 2738. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, A.; Duan, A.; Wu, H.; Zhang, J. Responses to subtropical climate in radial growth and wood density of Chinese fir provenances, southern China. For. Ecol. Manag. 2022, 521, 120428. [Google Scholar] [CrossRef]
- Cao, S.; Duan, H.; Sun, Y.; Hu, R.; Wu, B.; Lin, J.; Deng, W.; Li, Y.; Zheng, H. Genome-wide association study with growth-related traits and secondary metabolite contents in red-and white-heart Chinese fir. Front. Plant Sci. 2022, 13, 922007. [Google Scholar] [CrossRef]
- Wang, H.; Sun, J.; Duan, A.; Zhu, A.; Wu, H.; Zhang, J. Dendroclimatological analysis of chinese fir using a long-term provenance trial in Southern China. Forests 2022, 13, 1348. [Google Scholar] [CrossRef]
- Yu, X.; Liu, Q.; Liu, X.; Liu, X.; Wang, Y. A physical-based atmospheric correction algorithm of unmanned aerial vehicles images and its utility analysis. Int. J. Remote Sens. 2017, 38, 3101–3112. [Google Scholar] [CrossRef]
- Schläpfer, D.; Popp, C.; Richter, R. Drone data atmospheric correction concept for multi-and hyperspectral imagery–the DROACOR model. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIII-B3-2, 473–478. [Google Scholar] [CrossRef]
- Eisfelder, C.; Asam, S.; Hirner, A.; Reiners, P.; Holzwarth, S.; Bachmann, M.; Gessner, U.; Dietz, A.; Huth, J.; Bachofer, F.; et al. Seasonal Vegetation Trends for Europe over 30 Years from a Novel Normalised Difference Vegetation Index (NDVI) Time-Series—The TIMELINE NDVI Product. Remote Sens. 2023, 15, 3616. [Google Scholar] [CrossRef]
- Fan, X.; Liu, Y. Multisensor Normalized Difference Vegetation Index Intercalibration: A comprehensive overview of the causes of and solutions for multisensor differences. IEEE Geosci. Remote Sens. Mag. 2018, 6, 23–45. [Google Scholar] [CrossRef]
- Gopinath, G.; Ambili, G.K.; Gregory, S.J.; Anusha, C.K. Drought risk mapping of south-western state in the Indian peninsula—A web based application. J. Environ. Manag. 2015, 161, 453–459. [Google Scholar] [CrossRef] [PubMed]
- Song, B.; Park, K. Detection of aquatic plants using multispectral UAV imagery and vegetation index. Remote Sens. 2020, 12, 387. [Google Scholar] [CrossRef]
- Kong, D.; Zhang, Y.; Gu, X.; Wang, D. A robust method for reconstructing global MODIS EVI time series on the Google Earth Engine. ISPRS J. Photogramm. Remote Sens. 2019, 155, 13–24. [Google Scholar] [CrossRef]
- Alexandridis, T.K.; Ovakoglou, G.; Clevers, J.G.P.W. Relationship between MODIS EVI and LAI across time and space. Geocarto Int. 2020, 35, 1385–1399. [Google Scholar] [CrossRef]
- Wang, C.; Wu, Y.; Hu, Q.; Hu, J.; Chen, Y.; Lin, S.; Xie, Q. Comparison of vegetation phenology derived from solar-induced chlorophyll fluorescence and enhanced vegetation index, and their relationship with climatic limitations. Remote Sens. 2022, 14, 3018. [Google Scholar] [CrossRef]
- Shi, H.; Li, L.; Eamus, D.; Huete, A.; Cleverly, J.; Tian, X.; Yu, Q.; Wang, S.; Montagnani, L.; Magliulo, V.; et al. Assessing the ability of MODIS EVI to estimate terrestrial ecosystem gross primary production of multiple land cover types. Ecol. Indic. 2017, 72, 153–164. [Google Scholar] [CrossRef]
- Hikosaka, K.; Tsujimoto, K. Linking remote sensing parameters to CO2 assimilation rates at a leaf scale. J. Plant Res. 2021, 134, 695–711. [Google Scholar] [CrossRef] [PubMed]
- Sukhova, E.; Zolin, Y.; Popova, A.; Yudina, L.; Sukhov, V. The influence of soil salt stress on modified photochemical reflectance indices in pea plants. Remote Sens. 2023, 15, 3772. [Google Scholar] [CrossRef]
- Zhang, C.; Filella, I.; Garbulsky, M.F.; Peñuelas, J. Affecting factors and recent improvements of the photochemical reflectance index (PRI) for remotely sensing foliar, canopy and ecosystemic radiation-use efficiencies. Remote Sens. 2016, 8, 677. [Google Scholar] [CrossRef]
- Delegido, J.; Verrelst, J.; Meza, C.M.; Rivera, J.P.; Alonso, L.; Moreno, J. A red-edge spectral index for remote sensing estimation of green LAI over agroecosystems. Eur. J. Agron. 2013, 46, 42–52. [Google Scholar] [CrossRef]
- Kimes, D.S. Dynamics of directional reflectance factor distributions for vegetation canopies. Appl. Opt. 1983, 22, 1364–1372. [Google Scholar] [CrossRef]
- Asner, G.P. Biophysical and biochemical sources of variability in canopy reflectance. Remote Sens. Environ. 1998, 64, 234–253. [Google Scholar] [CrossRef]
- Hilker, T.; Hall, F.G.; Coops, N.C.; Lyapustin, A.; Wang, Y.; Nesic, Z.; Grant, N.; Black, T.A.; Wulder, M.A.; Kljun, N.; et al. Remote sensing of photosynthetic light-use efficiency across two forested biomes: Spatial scaling. Remote Sens. Environ. 2010, 114, 2863–2874. [Google Scholar] [CrossRef]
- Moravec, D.; Komárek, J.; López-Cuervo Medina, S.; Molina, I. Effect of atmospheric corrections on NDVI: Intercomparability of Landsat 8, Sentinel-2, and UAV sensors. Remote Sens. 2021, 13, 3550. [Google Scholar] [CrossRef]
- Crusiol, L.G.T.; Nanni, M.R.; Furlanetto, R.H.; Cezar, E.; Silva, G.F.C. Reflectance calibration of UAV-based visible and near-infrared digital images acquired under variant altitude and illumination conditions. Remote Sens. Appl. Soc. Environ. 2020, 18, 100312. [Google Scholar]
- Fahey, T.; Islam, M.; Gardi, A.; Sabatini, R. Laser beam atmospheric propagation modelling for aerospace LIDAR applications. Atmosphere 2021, 12, 918. [Google Scholar] [CrossRef]
- Stuhl, B.K. Atmospheric refraction corrections in ground-to-satellite optical time transfer. Opt. Express 2021, 29, 13706–13714. [Google Scholar] [CrossRef]
- Mobley, C.D.; Werdell, J.; Franz, B.; Ahmad, Z.; Bailey, S. Atmospheric Correction for Satellite Ocean Color Radiometry; No. GSFC-E-DAA-TN35509; NASA: Washington, DC, USA, 2016.
- van der Tol, C.; Vilfan, N.; Dauwe, D.; Cendrero-Mateo, M.P.; Yang, P. The scattering and re-absorption of red and near-infrared chlorophyll fluorescence in the models Fluspect and SCOPE. Remote Sens. Environ. 2019, 232, 111292. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Ryu, Y.; Dechant, B.; Eichelmann, E.; Hemes, K.; Ma, S.; Sanchez, C.R.; Shortt, R.; Szutu, D.; Valach, A.; et al. Outgoing Near-Infrared Radiation from Vegetation Scales With Canopy Photosynthesis Across a Spectrum of Function, Structure, Physiological Capacity, and Weather. JGR Biogeosci. 2020, 125, e2019JG005534. [Google Scholar] [CrossRef]
- Badgley, G.; Field, C.B.; Berry, J.A. Canopy near-infrared reflectance and terrestrial photosynthesis. Sci. Adv. 2017, 3, e1602244. [Google Scholar] [CrossRef] [PubMed]
- Yang, P. Exploring the interrelated effects of soil background, canopy structure and sun-observer geometry on canopy photochemical reflectance index. Remote Sens. Environ. 2022, 279, 113133. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant Remote Sensing Vegetation Indices: A Review of Developments and Applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef]
- Zou, X.; Mõttus, M. Sensitivity of common vegetation indices to the canopy structure of field crops. Remote Sens. 2017, 9, 994. [Google Scholar] [CrossRef]
- Gao, L.; Wang, X.; Johnson, B.A.; Tian, Q.; Wang, Y.; Verrelst, J.; Mu, X.; Gu, X. Remote sensing algorithms for estimation of fractional vegetation cover using pure vegetation index values: A review. ISPRS J. Photogramm. Remote Sens. 2020, 159, 364–377. [Google Scholar] [CrossRef]
- Zeng, Y.; Hao, D.; Huete, A.; Dechant, B.; Berry, J.; Chen, J.M.; Joiner, J.; Frankenberg, C.; Bond-Lamberty, B.; Ryu, Y.; et al. Optical vegetation indices for monitoring terrestrial ecosystems globally. Nat. Rev. Earth Environ. 2022, 3, 477–493. [Google Scholar] [CrossRef]
- Canto-Sansores, W.G.; López-Martínez, J.O.; González, E.J.; Meave, J.A.; Hernández-Stefanoni, J.L.; Macario-Mendoza, P.A. The importance of spatial scale and vegetation complexity in woody species diversity and its relationship with remotely sensed variables. ISPRS J. Photogramm. Remote Sens. 2024, 216, 142–153. [Google Scholar] [CrossRef]
- Huang, S.; Tang, L.; Hupy, J.P.; Wang, Y.; Shao, G.F. A commentary review on the use of normalized difference vegetation index (NDVI) in the era of popular remote sensing. J. For. Res. 2021, 32, 1–6. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, J.M.; Ju, W.; Wang, H.; Qiu, F.; Yang, F.; Fan, W.; Huang, Q.; Wang, Y.-P.; Feng, Y.; et al. Improving the ability of the photochemical reflectance index to track canopy light use efficiency through differentiating sunlit and shaded leaves. Remote Sens. Environ. 2017, 194, 1–15. [Google Scholar] [CrossRef]
- Biriukova, K.; Celesti, M.; Evdokimov, A.; Pacheco-Labrador, J.; Julitta, T.; Migliavacca, M.; Giardino, C.; Miglietta, F.; Colombo, R.; Panigada, C.; et al. Effects of varying solar-view geometry and canopy structure on solar-induced chlorophyll fluorescence and PRI. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102069. [Google Scholar] [CrossRef]
- Zhang, Q.; Ju, W.; Chen, J.M.; Wang, H.; Yang, F.; Fan, W.; Huang, Q.; Zheng, T.; Feng, Y.; Zhou, Y.; et al. Ability of the photochemical reflectance index to track light use efficiency for a sub-tropical planted coniferous forest. Remote Sens. 2015, 7, 16938–16962. [Google Scholar] [CrossRef]
- Rogers, C.A.; Chen, J.M.; Zheng, T.; Croft, H.; Gonsamo, A.; Luo, X.; Staebler, R.M. The Response of Spectral Vegetation Indices and Solar-Induced Fluorescence to Changes in Illumination Intensity and Geometry in the Days Surrounding the 2017 North American Solar Eclipse. JGR Biogeosci. 2020, 125, e2020JG005774. [Google Scholar] [CrossRef]
- Stow, D.; Nichol, C.J.; Wade, T.; Assmann, J.J.; Simpson, G.; Helfter, C. Illumination geometry and flying height influence surface reflectance and NDVI derived from multispectral UAS imagery. Drones 2019, 3, 55. [Google Scholar] [CrossRef]
- Zhang, X.; Qiu, F.; Zhan, C.; Zhang, Q.; Li, Z.; Wu, Y.; Huang, Y.; Chen, X. Acquisitions and applications of forest canopy hyperspectral imageries at hotspot and multiview angle using unmanned aerial vehicle platform. J. Appl. Remote Sens. 2020, 14, 022212. [Google Scholar] [CrossRef]
- Petri, C.A.; Galvão, L.S. Sensitivity of seven MODIS vegetation indices to BRDF effects during the Amazonian dry season. Remote Sens. 2019, 11, 1650. [Google Scholar] [CrossRef]
- Elbaz, S.; Sheffer, E.; Lensky, I.M.; Levin, N. The Impacts of Spatial Resolution, Viewing Angle, and Spectral Vegetation Indices on the Quantification of Woody Mediterranean Species Seasonality Using Remote Sensing. Remote Sens. 2021, 13, 1958. [Google Scholar] [CrossRef]
- Roth, L.; Aasen, H.; Walter, A.; Liebisch, F. Extracting leaf area index using viewing geometry effects—A new perspective on high-resolution unmanned aerial system photography. ISPRS J. Photogramm. Remote Sens. 2018, 141, 161–175. [Google Scholar] [CrossRef]
- Kganyago, M.; Ovakoglou, G.; Mhangara, P.; Adjorlolo, C.; Alexandridis, T.; Laneve, G.; Beltran, J.S. Evaluating the contribution of Sentinel-2 view and illumination geometry to the accuracy of retrieving essential crop parameters. Gisci. Remote Sens. 2023, 60, 2163046. [Google Scholar] [CrossRef]
- Guo, Y.; Mu, X.; Chen, Y.; Xie, D.; Yan, G. Correction of Sun-View Angle Effect on Normalized Difference Vegetation Index (NDVI) with Single View-Angle Observation. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–13. [Google Scholar] [CrossRef]
- Poley, L.G.; McDermid, G.J. A systematic review of the factors influencing the estimation of vegetation aboveground biomass using unmanned aerial systems. Remote Sens. 2020, 12, 1052. [Google Scholar] [CrossRef]
- Tian, B.; Yu, H.; Zhang, S.; Wang, X.; Yang, L.; Li, J.; Cui, W.; Wang, Z.; Lu, L.; Lan, Y.; et al. Inversion of cotton soil and plant analytical development based on unmanned aerial vehicle multispectral imagery and mixed pixel decomposition. Agriculture 2024, 14, 1452. [Google Scholar] [CrossRef]
- Milton, E.J.; Blackburn, G.A.; Rollin, E.M.; Danson, F.M. Measurement of the spectral directional reflectance of forest canopies: A review of methods and a practical application. Remote Sens. Rev. 1994, 10, 285–308. [Google Scholar] [CrossRef]
- Luo, S.; Jiang, X.; Yang, K.; Li, Y.; Fang, S. Multispectral remote sensing for accurate acquisition of rice phenotypes: Impacts of radiometric calibration and unmanned aerial vehicle flying altitudes. Front. Plant Sci. 2022, 13, 958106. [Google Scholar] [CrossRef]
- Chen, J.M.; Leblanc, S.G. A four-scale bidirectional reflectance model based on canopy architecture. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1316–1337. [Google Scholar] [CrossRef]





| Flight | Target | Flight Heights (m) | Flight Time |
|---|---|---|---|
| 1 | Forest Canopy | 20, 35, 50, 75, 100, 125, 150, 200, 250 | 23/11/15 12:33 |
| 2 | Grey Panel | 20, 35, 50, 75, 100, 125, 150, 200, 250 | 23/11/15 12:36 |
| Flight Height (m) | Resolution (cm) |
|---|---|
| 50 | 2.50 |
| 75 | 3.70 |
| 100 | 5.00 |
| 125 | 6.00 |
| 150 | 7.40 |
| 200 | 9.80 |
| 230 | 11.30 |
| 300 | 14.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Guan, T.; Qiu, F.; Liu, L.; Zhang, X.; Zeng, H.; Zhang, Q. Evaluation of Scale Effects on UAV-Based Hyperspectral Imaging for Remote Sensing of Vegetation. Remote Sens. 2025, 17, 1080. https://doi.org/10.3390/rs17061080
Wang T, Guan T, Qiu F, Liu L, Zhang X, Zeng H, Zhang Q. Evaluation of Scale Effects on UAV-Based Hyperspectral Imaging for Remote Sensing of Vegetation. Remote Sensing. 2025; 17(6):1080. https://doi.org/10.3390/rs17061080
Chicago/Turabian StyleWang, Tie, Tingyu Guan, Feng Qiu, Leizhen Liu, Xiaokang Zhang, Hongda Zeng, and Qian Zhang. 2025. "Evaluation of Scale Effects on UAV-Based Hyperspectral Imaging for Remote Sensing of Vegetation" Remote Sensing 17, no. 6: 1080. https://doi.org/10.3390/rs17061080
APA StyleWang, T., Guan, T., Qiu, F., Liu, L., Zhang, X., Zeng, H., & Zhang, Q. (2025). Evaluation of Scale Effects on UAV-Based Hyperspectral Imaging for Remote Sensing of Vegetation. Remote Sensing, 17(6), 1080. https://doi.org/10.3390/rs17061080





