Multispectral Land Surface Reflectance Reconstruction Based on Non-Negative Matrix Factorization: Bridging Spectral Resolution Gaps for GRASP TROPOMI BRDF Product in Visible
Abstract
1. Introduction
2. Data
2.1. GRASP TROPOMI BRDF Product
2.2. USGS/ASTER Spectral Libraries
3. Methods
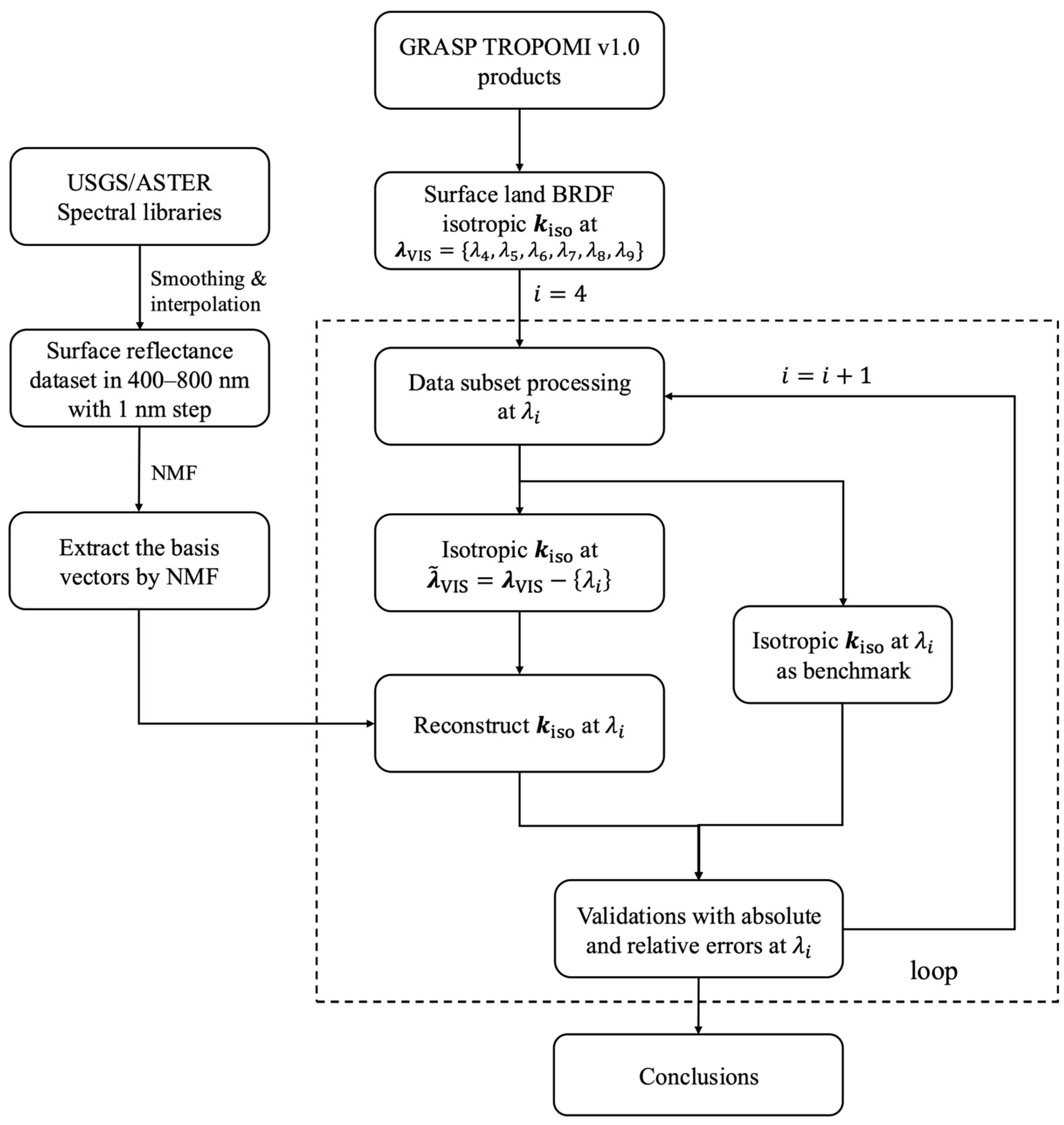
3.1. Flowchart of Research Strategy
- (1)
- Using the USGS/ASTER spectral libraries as reference data for spectral analysis, we smooth and interpolate the surface reflectance dataset in the 400–800 nm range to encompass the visible (VIS) spectrum and part of the NIR, with a resolution of 1 nm per step. This interpolation process reduces noise, fills in missing values, and ensures a continuous dataset, enabling the capture of more detailed and accurate spectral information.
- (2)
- Basis vectors (endmember vectors) are extracted using non-negative matrix factorization (NMF) method, which is crucial for reducing dimensionality and finding meaningful patterns in the spectral dataset.
- (3)
- We select the wavelength-dependent isotropic parameters of land surface BRDF at six VIS and NIR wavelength bands from the GRASP TROPOMI v1.0 product for surface reflectance reconstruction. These wavelength bands are defined as:corresponding to 416, 440, 494, 670, 747, and 772 nm, respectively, from the GRASP TROPOMI BRDF product.
- (4)
- To quantitatively evaluate the effect of surface reflectance reconstruction, the selected isotropic coefficient dataset is dynamically divided into two subsets during each iteration of a loop. One subset,is used to calculate the mixing coefficient vector for reconstructing the isotropic parameters at . The other subset, containing , serves as a benchmark to validate the reconstructed results by comparing absolute and relative errors.
- (5)
- By iterating through these six VIS and NIR wavelength bands in the loop, the accuracy of surface reflectance construction method can be systematically evaluated.
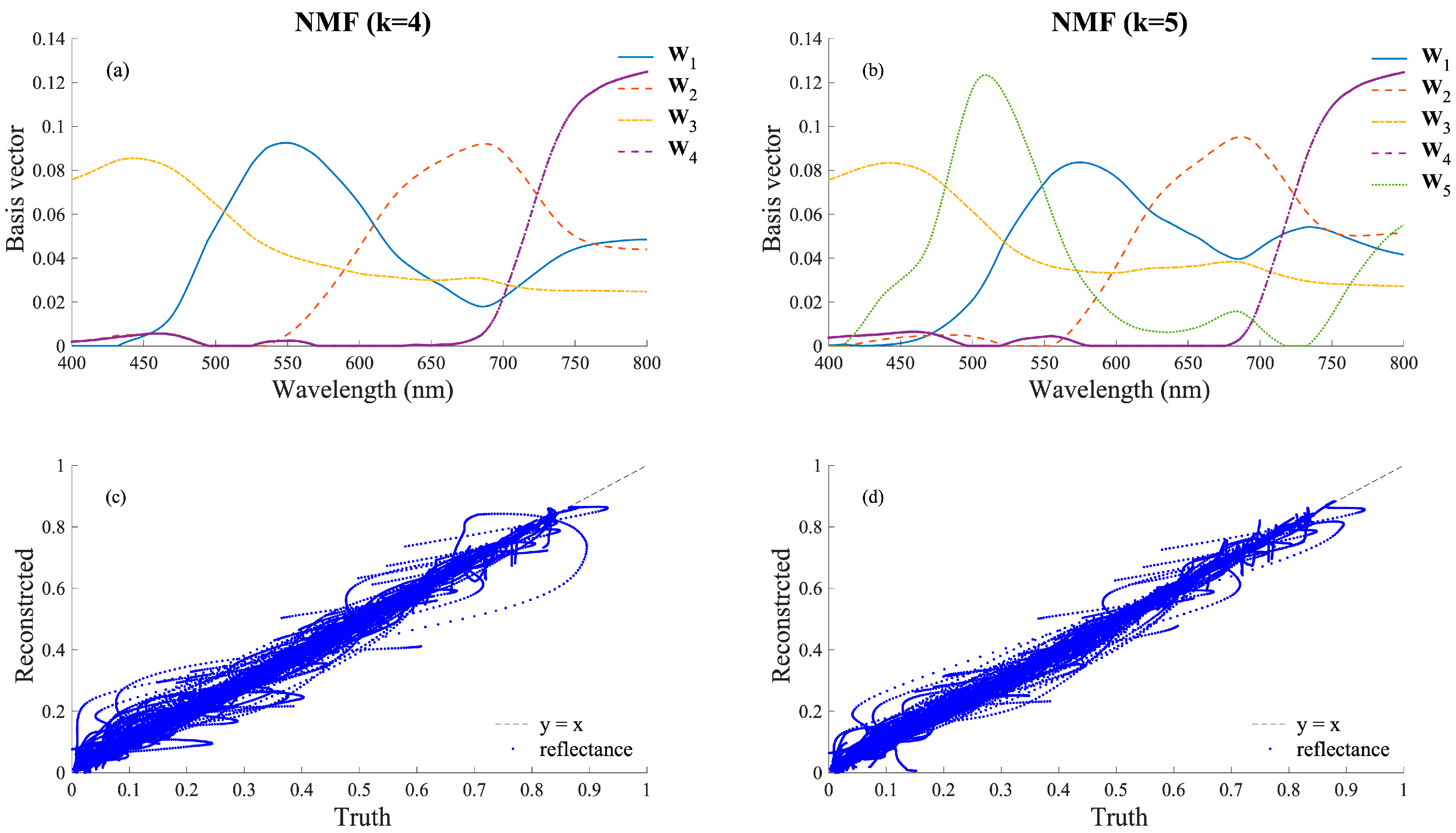
3.2. Extracted Basis Vectors
3.3. Surface Reflectance Reconstruciton
4. Results
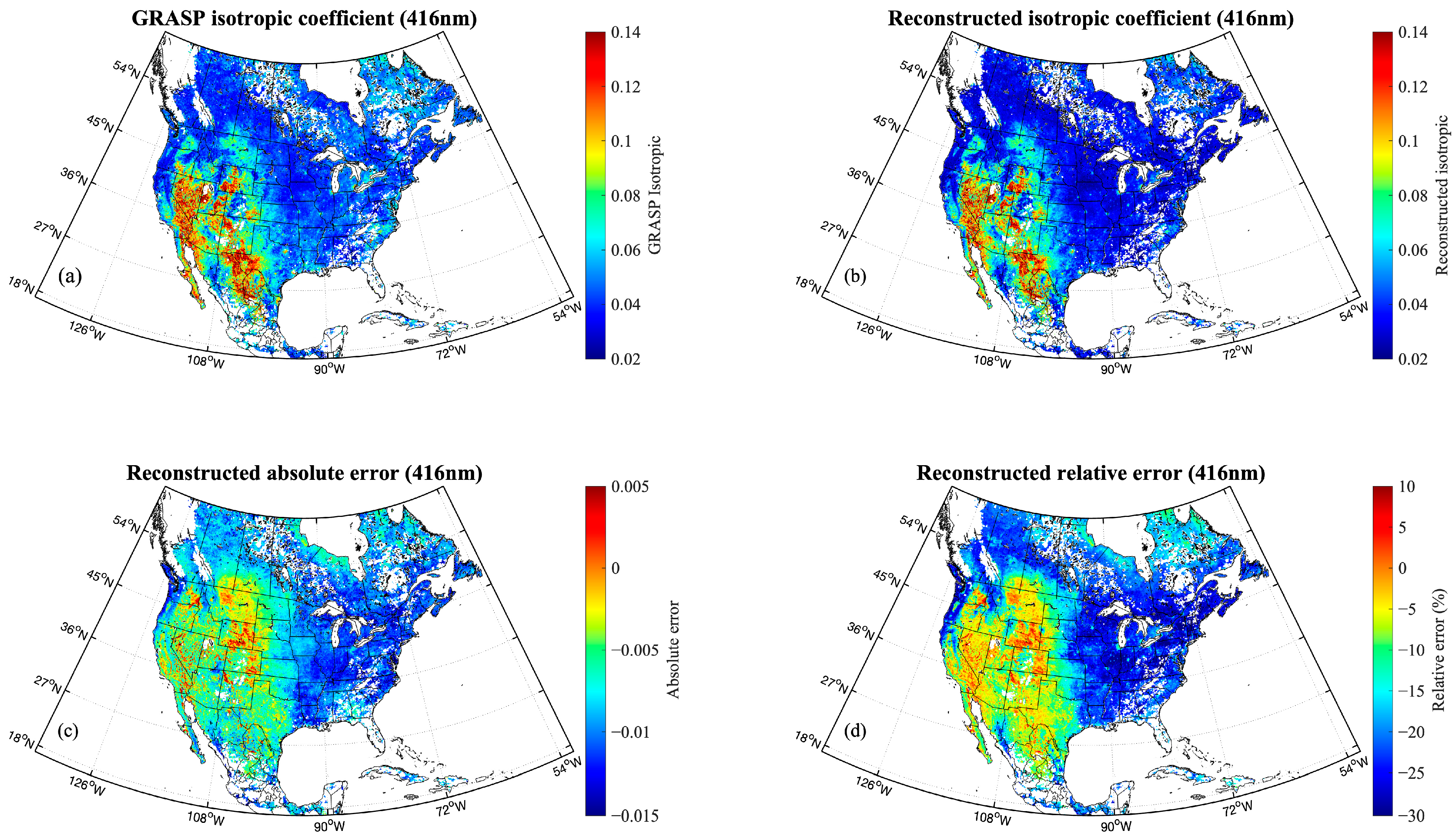
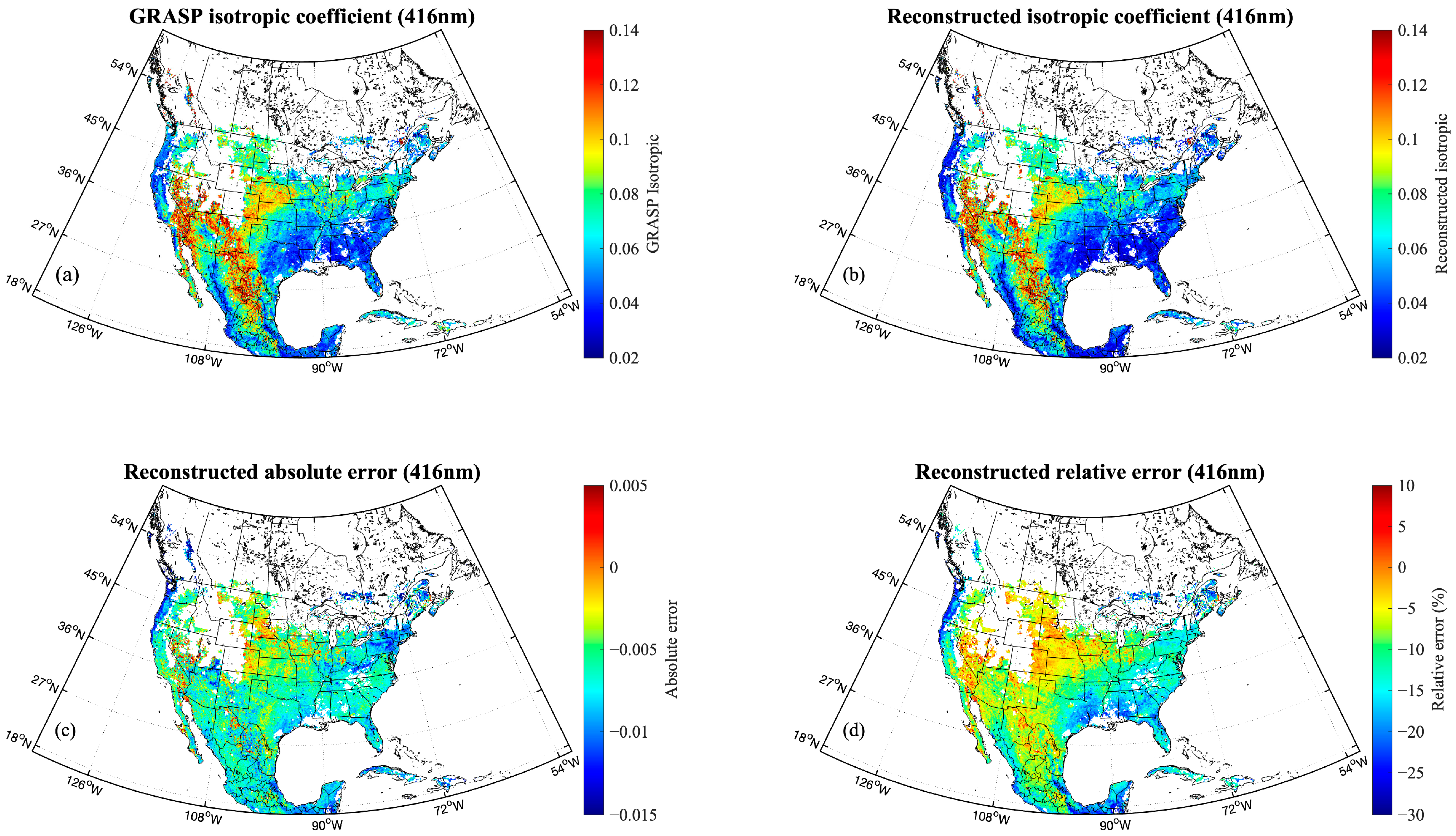
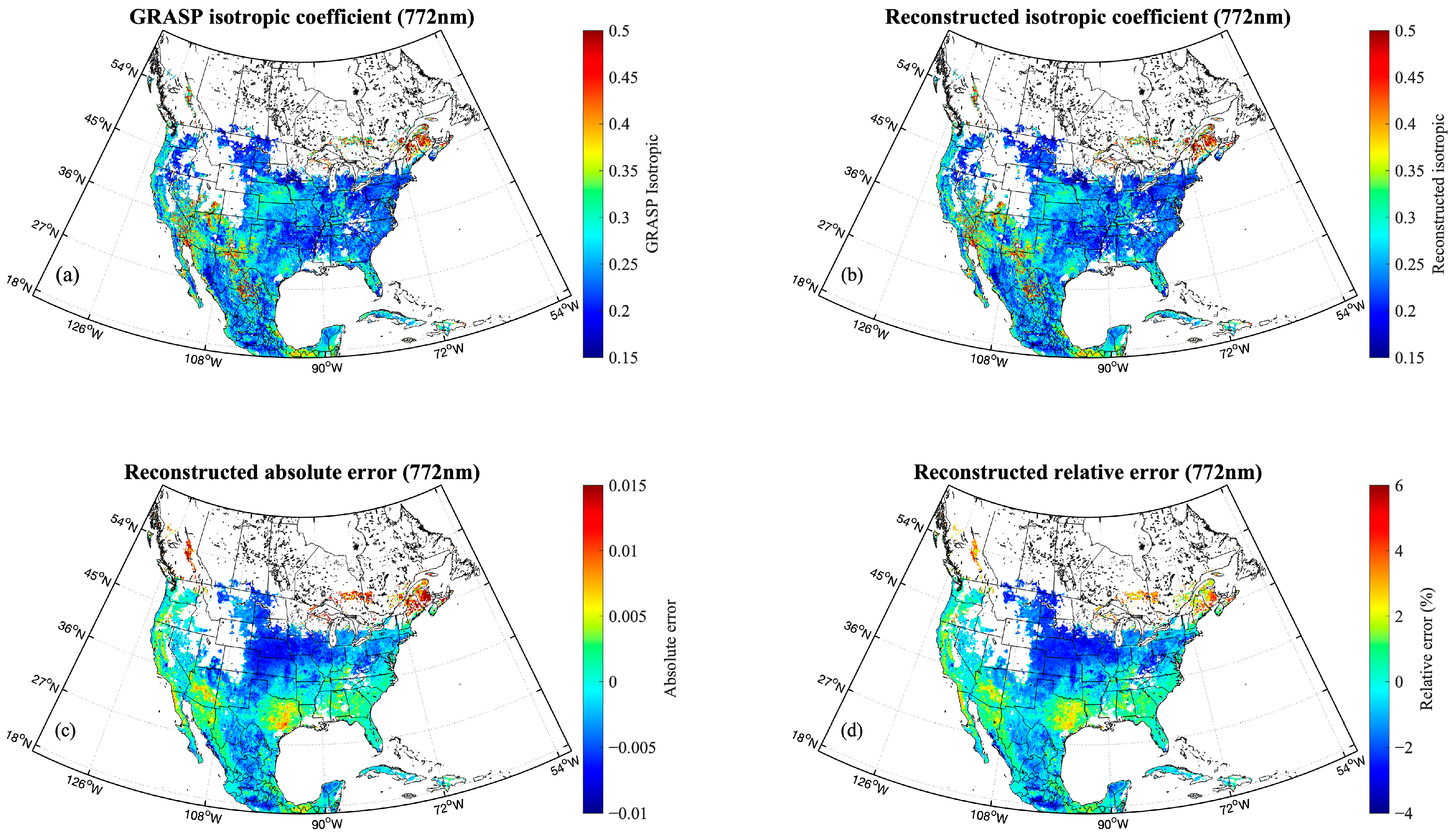
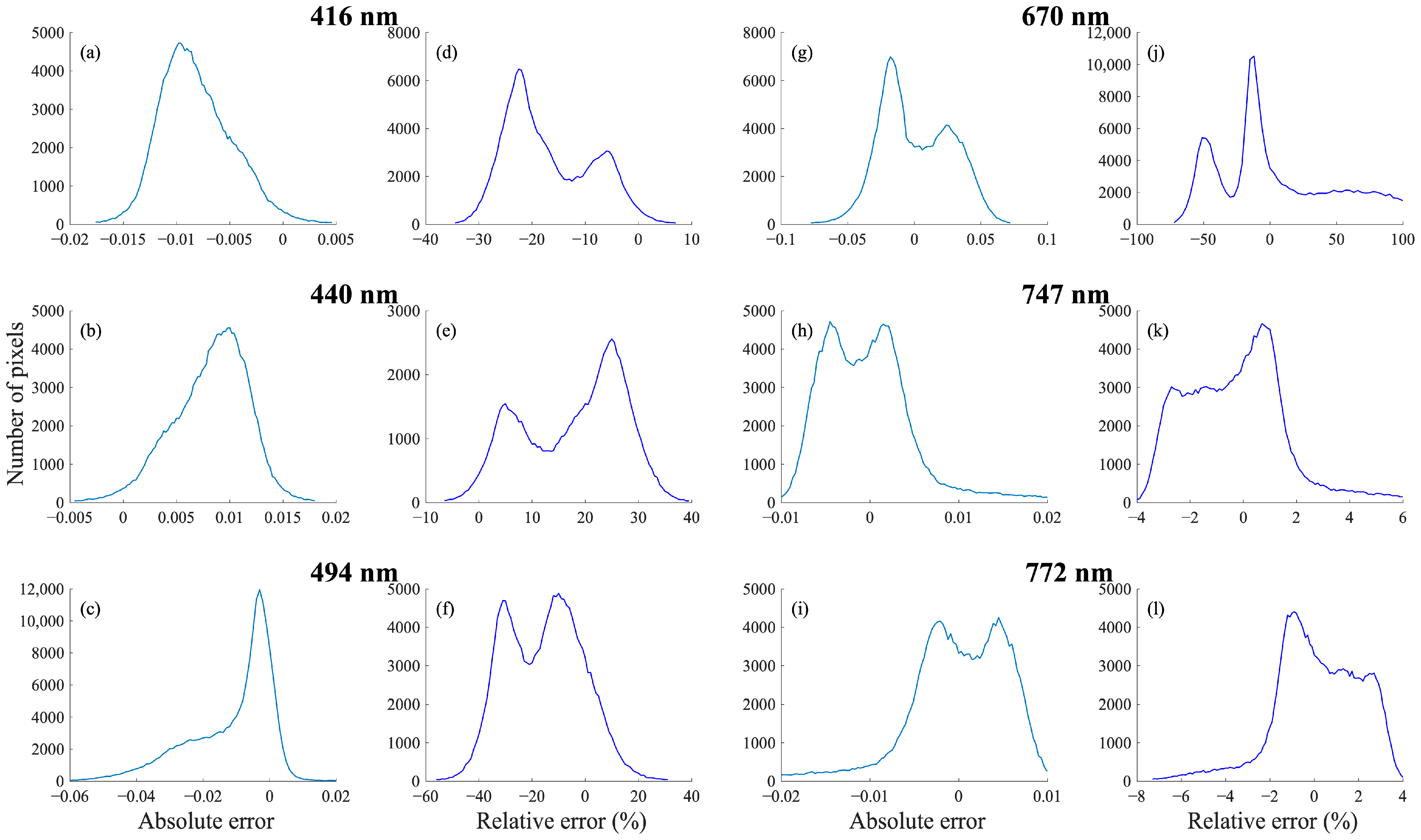
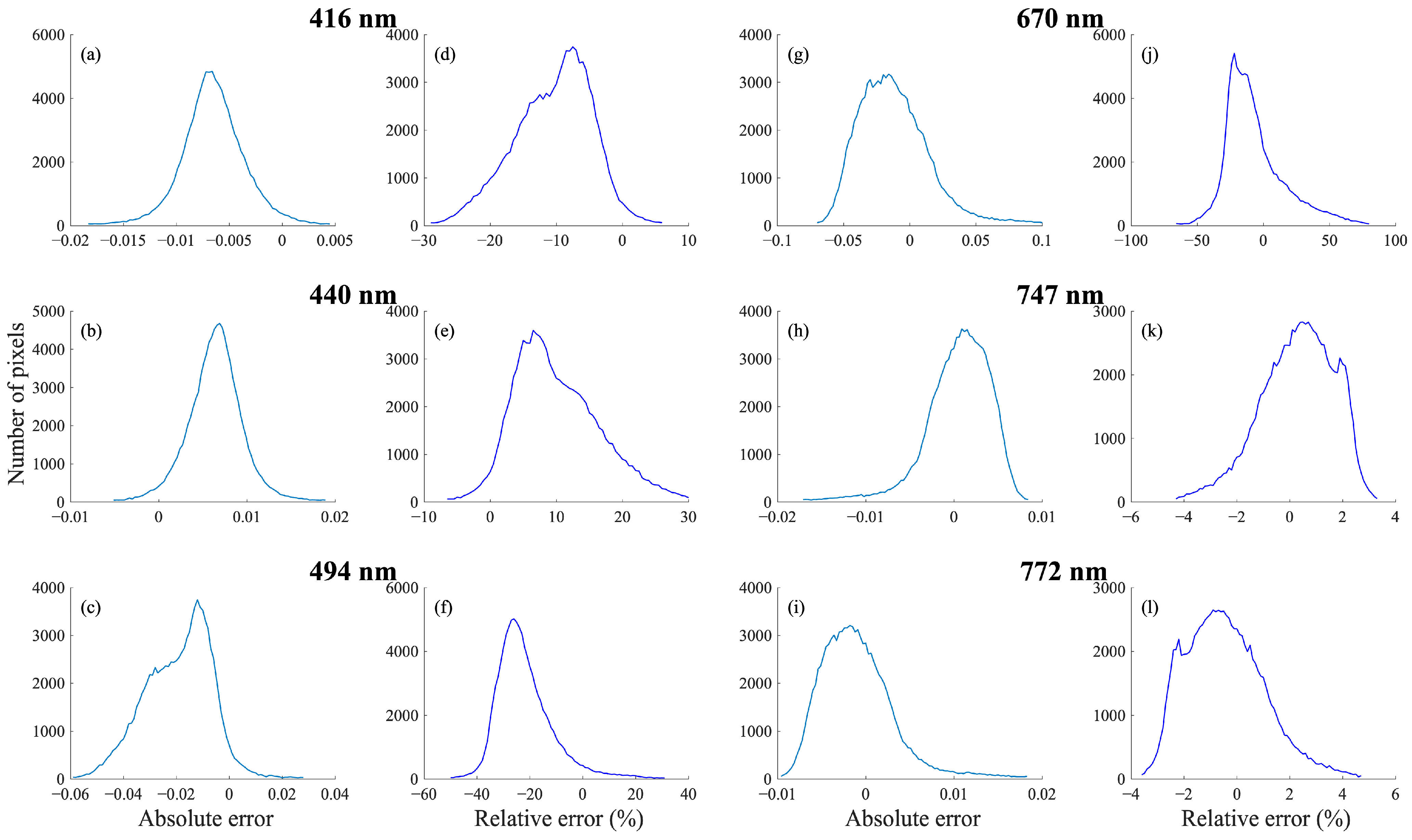
4.1. Reconstructed Spatial Distribution and Error Histogram
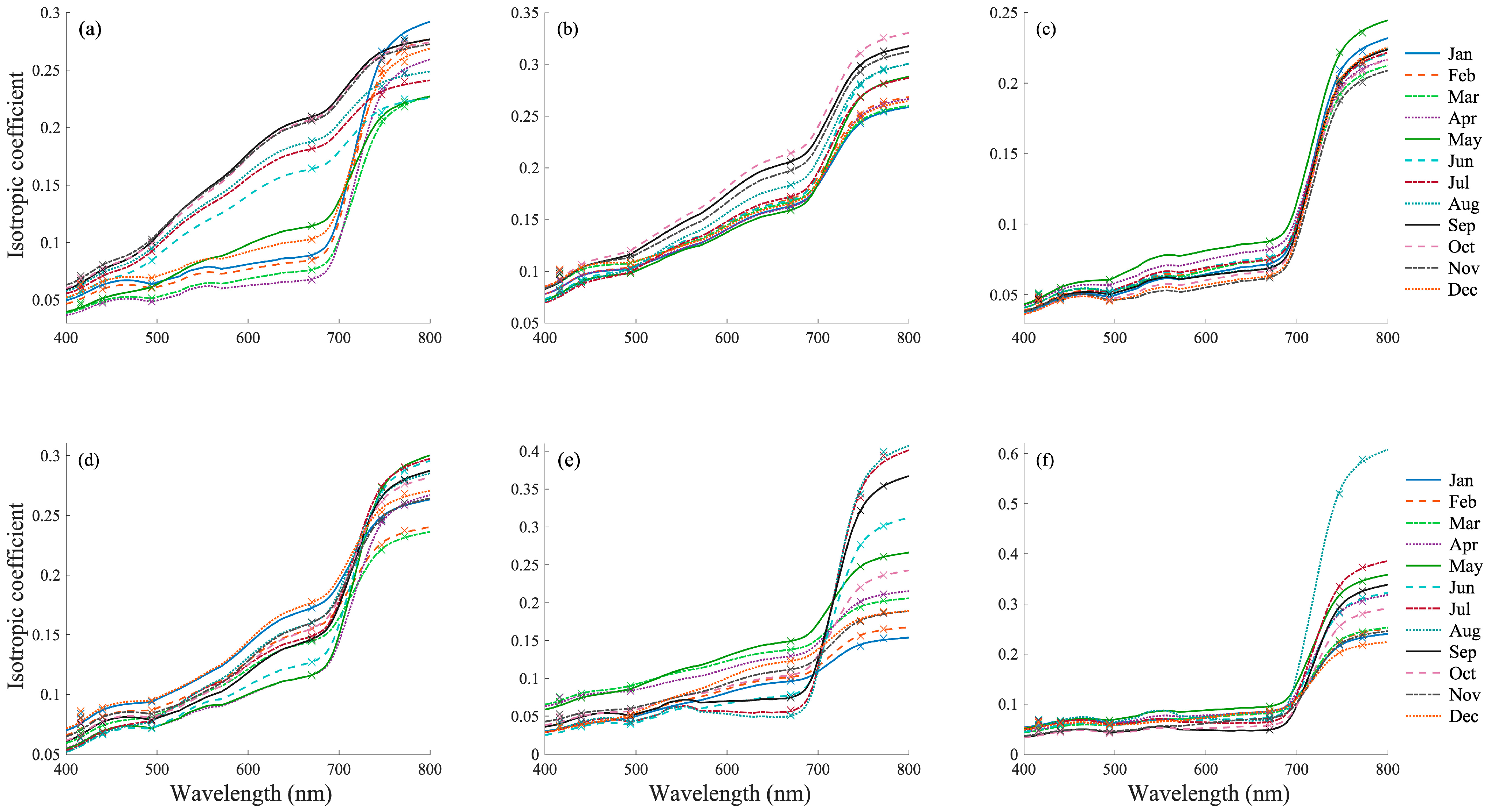
4.2. Reconstructed Spectral Features in the 400–800 nm Range
4.3. Reconstructed Spectral Features in the 400–2400 nm Range
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Macarringue, L.S.; Bolfe, É.L.; Pereira, P.R.M. Developments in land use and land cover classification techniques in remote sensing: A review. J. Geogr. Inf. Syst. 2022, 14, 1–28. [Google Scholar] [CrossRef]
- Atzberger, C. Advances in remote sensing of agriculture: Context description, existing operational monitoring systems and major information needs. Remote Sens. 2013, 5, 949–981. [Google Scholar] [CrossRef]
- Li, J.; Pei, Y.; Zhao, S.; Xiao, R.; Sang, X.; Zhang, C. A review of remote sensing for environmental monitoring in China. Remote Sens. 2020, 12, 1130. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Sun, Q.; Erb, A.M.; Li, Z.; Schaaf, C.B.; Zhang, X.; Román, M.O.; Scott, R.L.; Zhang, Q.; et al. Evaluation of the VIIRS BRDF, Albedo and NBAR products suite and an assessment of continuity with the long term MODIS record. Remote Sens. Environ. 2017, 201, 256–274. [Google Scholar] [CrossRef]
- Claverie, M.; Vermote, E.F.; Franch, B.; Masek, J.G. Evaluation of the Landsat-5 TM and Landsat-7 ETM+ surface reflectance products. Remote Sens. Environ. 2015, 169, 390–403. [Google Scholar] [CrossRef]
- Chen, C.; Dubovik, O.; Fuertes, D.; Litvinov, P.; Lapyonok, T.; Lopatin, A.; Ducos, F.; Derimian, Y.; Herman, M.; Tanré, D.; et al. Validation of GRASP algorithm product from POLDER/PARASOL data and assessment of multi-angular polarimetry potential for aerosol monitoring. Earth Syst. Sci. Data 2020, 12, 3573–3620. [Google Scholar] [CrossRef]
- Zhang, H.; Kondragunta, S.; Laszlo, I.; Zhou, M. Improving GOES Advanced Baseline Imager (ABI) aerosol optical depth (AOD) retrievals using an empirical bias correction algorithm. Atmos. Meas. Tech. 2020, 13, 5955–5975. [Google Scholar] [CrossRef]
- Wang, W.; Dungan, J.; Genovese, V.; Shinozuka, Y.; Yang, Q.; Liu, X.; Poulter, B.; Brosnan, I. Development of the Ames Global Hyperspectral Synthetic Data Set: Surface Bidirectional Reflectance Distribution Function. J. Geophys. Res. Biogeosci. 2023, 128, e2022JG007363. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, X.; Wu, W. A Hyperspectral Bidirectional Reflectance Model for Land Surface. Sensors 2020, 20, 4456. [Google Scholar] [CrossRef]
- Li, Z.; Sun, D.; Qiu, Z.; Xi, H.; Wang, S.; Perrie, W.; Li, Y.; Han, B. A Reconstruction Method for Hyperspectral Remote Sensing Reflectance in the Visible Domain and Applications. J. Geophys. Res. Ocean. 2018, 123, 4092–4109. [Google Scholar] [CrossRef]
- Roccetti, G.; Bugliaro, L.; Gödde, F.; Emde, C.; Hamann, U.; Manev, M.; Sterzik, M.F.; Wehrum, C. HAMSTER: Hyperspectral Albedo Maps dataset with high Spatial and TEmporal Resolution. Atmos. Meas. Tech. 2024, 17, 6025–6046. [Google Scholar] [CrossRef]
- Ahmed, M.T.; Villordon, A.; Kamruzzaman, M. Comparative analysis of hyperspectral Image reconstruction using deep learning for agricultural and biological applications. Results Eng. 2024, 23, 102623. [Google Scholar] [CrossRef]
- Zhang, J.; Su, R.; Fu, Q.; Ren, W.; Heide, F.; Nie, Y. A survey on computational spectral reconstruction methods from RGB to hyperspectral imaging. Sci. Rep. 2022, 12, 11905. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.; Sun, J.; Chen, Y.; Lu, H.; Duan, F.; Zhu, L.; Fan, T. M2H-Net: A reconstruction method for hyperspectral remotely sensed imagery. ISPRS J. Photogramm. Remote Sens. 2021, 173, 323–348. [Google Scholar] [CrossRef]
- Zhao, E.; Qu, N.; Wang, Y.; Gao, C. Spectral Reconstruction from Thermal Infrared Multispectral Image Using Convolutional Neural Network and Transformer Joint Network. Remote Sens. 2024, 16, 1284. [Google Scholar] [CrossRef]
- Shen, H.-L.; Cai, P.-Q.; Shao, S.-J.; Xin, J.H. Reflectance reconstruction for multispectral imaging by adaptive Wiener estimation. Opt. Express 2007, 15, 15545–15554. [Google Scholar] [CrossRef]
- Zhang, X.; Cui, G.; Ruan, X.; Cui, D.; Gao, X.; Chen, Q.; Yao, Y.; Melgosa, M.; Sueeprasan, S. Spectral reflectance reconstruction based on wideband multi-illuminant imaging and a modified particle swarm optimization algorithm. Opt. Express 2024, 32, 2942–2958. [Google Scholar] [CrossRef]
- Yao, P.; Wu, H.; Xin, J.H. Improving Generalizability of Spectral Reflectance Reconstruction Using L1-Norm Penalization. Sensors 2023, 23, 689. [Google Scholar] [CrossRef]
- Zoogman, P.; Liu, X.; Chance, K.; Sun, Q.; Schaaf, C.; Mahr, T.; Wagner, T. A climatology of visible surface reflectance spectra. J. Quant. Spectrosc. Radiat. Transf. 2016, 180, 39–46. [Google Scholar] [CrossRef]
- Yu, W.; Li, J.; Liu, Q.; Zeng, Y.; Zhao, J.; Xu, B.; Yin, G. Global Land Cover Heterogeneity Characteristics at Moderate Resolution for Mixed Pixel Modeling and Inversion. Remote Sens. 2018, 10, 856. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral Unmixing Overview: Geometrical, Statistical, and Sparse Regression-Based Approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Du, P.; Liu, S.; Liu, P.; Tan, K.; Cheng, L. Sub-pixel change detection for urban land-cover analysis via multi-temporal remote sensing images. Geo-Spat. Inf. Sci. 2014, 17, 26–38. [Google Scholar] [CrossRef]
- Hu, Z.; Chu, Y.; Zhang, Y.; Zheng, X.; Wang, J.; Xu, W.; Wang, J.; Wu, G. Scale matters: How spatial resolution impacts remote sensing based urban green space mapping? Int. J. Appl. Earth Obs. Geoinf. 2024, 134, 104178. [Google Scholar] [CrossRef]
- Clark, R.N.; Swayze, G.A.; Livo, K.E.; Kokaly, R.F.; King, T.V.; Dalton, J.B.; Vance, J.S.; Rockwell, B.W.; Hoefen, T.; McDougal, R.R. Surface reflectance calibration of terrestrial imaging spectroscopy data: A tutorial using AVIRIS. In Proceedings of the 10th Airborne Earth Science Workshop, Pasadena, CA, USA, 27 February–2 March 2001. [Google Scholar]
- Song, X.; Zou, L.; Wu, L. Detection of Subpixel Targets on Hyperspectral Remote Sensing Imagery Based on Background Endmember Extraction. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2365–2377. [Google Scholar] [CrossRef]
- Miao, L.; Qi, H. Endmember Extraction From Highly Mixed Data Using Minimum Volume Constrained Nonnegative Matrix Factorization. IEEE Trans. Geosci. Remote Sens. 2007, 45, 765–777. [Google Scholar] [CrossRef]
- Fan, F.; Deng, Y. Enhancing endmember selection in multiple endmember spectral mixture analysis (MESMA) for urban impervious surface area mapping using spectral angle and spectral distance parameters. Int. J. Appl. Earth Obs. Geoinf. 2014, 33, 290–301. [Google Scholar] [CrossRef]
- Gómez-Sánchez, A.; Marro, M.; Marsal, M.; Zacchetti, S.; Rocha de Oliveira, R.; Loza-Alvarez, P.; de Juan, A. Linear unmixing protocol for hyperspectral image fusion analysis applied to a case study of vegetal tissues. Sci. Rep. 2021, 11, 18665. [Google Scholar] [CrossRef]
- Févotte, C.; Dobigeon, N. Nonlinear Hyperspectral Unmixing With Robust Nonnegative Matrix Factorization. IEEE Trans. Image Process. 2015, 24, 4810–4819. [Google Scholar] [CrossRef]
- Rajabi, R.; Ghassemian, H. Spectral Unmixing of Hyperspectral Imagery Using Multilayer NMF. IEEE Geosci. Remote Sens. Lett. 2015, 12, 38–42. [Google Scholar] [CrossRef]
- Akhtar, N.; Mian, A. RCMF: Robust Constrained Matrix Factorization for Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3354–3366. [Google Scholar] [CrossRef]
- Liu, R.; Du, B.; Zhang, L. Hyperspectral Unmixing via Double Abundance Characteristics Constraints Based NMF. Remote Sens. 2016, 8, 464. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 6755, 788–791. [Google Scholar] [CrossRef]
- Fathi Hafshejani, S.; Moaberfard, Z. Initialization for non-negative matrix factorization: A comprehensive review. Int. J. Data Sci. Anal. 2023, 16, 119–134. [Google Scholar] [CrossRef]
- Hou, W.; Wang, J.; Xu, X.; Reid, J.S.; Han, D. An algorithm for hyperspectral remote sensing of aerosols: 1. Development of theoretical framework. J. Quant. Spectrosc. Radiat. Transf. 2016, 178, 400–415. [Google Scholar] [CrossRef]
- Hou, W.; Wang, J.; Xu, X.; Reid, J.S.; Janz, S.J.; Leitch, J.W. An algorithm for hyperspectral remote sensing of aerosols: 3. Application to the GEO-TASO data in KORUS-AQ field campaign. J. Quant. Spectrosc. Radiat. Transf. 2020, 253, 107161. [Google Scholar] [CrossRef]
- Hou, W.; Mao, Y.; Xu, C.; Li, Z.; Li, D.; Ma, Y.; Xu, H. Study on the spectral reconstruction of typical surface types based on spectral library and principal component analysis. SPIE 2019, 11023, 702–711. [Google Scholar]
- Ferrero, A.; Campos, J.; Rabal, A.M.; Pons, A.; Hernanz, M.L.; Corróns, A. Principal components analysis on the spectral bidirectional reflectance distribution function of ceramic colour standards. Opt. Express 2011, 19, 19199–19211. [Google Scholar] [CrossRef]
- Hou, W.; Wang, J.; Xu, X.; Reid, J.S. An algorithm for hyperspectral remote sensing of aerosols: 2. Information content analysis for aerosol parameters and principal components of surface spectra. J. Quant. Spectrosc. Radiat. Transf. 2017, 192, 14–29. [Google Scholar] [CrossRef]
- Pauca, V.P.; Piper, J.; Plemmons, R.J. Nonnegative matrix factorization for spectral data analysis. Linear Algebra Its Appl. 2006, 416, 29–47. [Google Scholar] [CrossRef]
- Hassani, A.; Iranmanesh, A.; Mansouri, N. Text mining using nonnegative matrix factorization and latent semantic analysis. Neural Comput. Appl. 2021, 33, 13745–13766. [Google Scholar] [CrossRef]
- Qian, Y.; Jia, S.; Zhou, J.; Robles-Kelly, A. Hyperspectral Unmixing via L1/2 Sparsity-Constrained Nonnegative Matrix Factorization. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4282–4297. [Google Scholar] [CrossRef]
- Feng, X.-R.; Li, H.-C.; Wang, R.; Du, Q.; Jia, X.; Plaza, A. Hyperspectral unmixing based on nonnegative matrix factorization: A comprehensive review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 4414–4436. [Google Scholar] [CrossRef]
- Lee, D.; Seung, H.S. Algorithms for non-negative matrix factorization. Adv. Neural Inf. Process. Syst. 2000, 13. [Google Scholar]
- Lin, C.-J. Projected Gradient Methods for Nonnegative Matrix Factorization. Neural Comput. 2007, 19, 2756–2779. [Google Scholar] [CrossRef]
- Kim, H.; Park, H. Sparse non-negative matrix factorizations via alternating non-negativity-constrained least squares for microarray data analysis. Bioinformatics 2007, 23, 1495–1502. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Park, H. Nonnegative Matrix Factorization Based on Alternating Nonnegativity Constrained Least Squares and Active Set Method. SIAM J. Matrix Anal. Appl. 2008, 30, 713–730. [Google Scholar] [CrossRef]
- Kim, J.; Park, H. Toward Faster Nonnegative Matrix Factorization: A New Algorithm Comparisons. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 353–362. [Google Scholar] [CrossRef]
- Kim, J.; Park, H. Fast Nonnegative Matrix Factorization: An Active-Set-Like Method and Comparisons. SIAM J. Sci. Comput. 2011, 33, 3261–3281. [Google Scholar] [CrossRef]
- Cichocki, A.; Zdunek, R. Regularized alternating least squares algorithms for non-negative matrix/tensor factorization. In Advances in Neural Network—ISNN 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 793–802. [Google Scholar]
- Hoyer, P.O. Non-negative matrix factorization with sparseness constraints. J. Mach. Learn. Res. 2004, 5, 1457–1469. [Google Scholar]
- Gillis, N.; Glineur, F. Using underapproximations for sparse nonnegative matrix factorization. Pattern Recognit. 2010, 43, 1676–1687. [Google Scholar] [CrossRef]
- Schmidt, M.N.; Winther, O.; Hansen, L.K. Bayesian non-negative matrix factorization. In Proceedings of the Independent Component Analysis and Signal Separation: 8th International Conference, ICA 2009, Paraty, Brazil, 15–18 March 2009; Proceedings 8. pp. 540–547. [Google Scholar]
- Zafeiriou, S.; Tefas, A.; Buciu, I.; Pitas, I. Exploiting discriminant information in nonnegative matrix factorization with application to frontal face verification. IEEE Trans. Neural Netw. 2006, 17, 683–695. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, Z.-H.; Chen, S. Non-negative matrix factorization on kernels. In Proceedings of the PRICAI 2006: Trends in Artificial Intelligence: 9th Pacific Rim International Conference on Artificial Intelligence, Guilin, China, 7–11 August 2006; Proceedings 9. pp. 404–412. [Google Scholar]
- Liu, H.; Wu, Z. Non-negative matrix factorization with constraints. In Proceedings of the AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010; pp. 506–511. [Google Scholar]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A.; Liu, L. Robust Collaborative Nonnegative Matrix Factorization for Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6076–6090. [Google Scholar] [CrossRef]
- Wang, Y.-X.; Zhang, Y.-J. Nonnegative matrix factorization: A comprehensive review. IEEE Trans. Knowl. Data Eng. 2012, 25, 1336–1353. [Google Scholar] [CrossRef]
- Gillis, N. The why and how of nonnegative matrix factorization. Regul. Optim. Kernels Support Vector Mach. 2014, 12, 257–291. [Google Scholar]
- Dubovik, O.; Lapyonok, T.; Litvinov, P.; Herman, M.; Fuertes, D.; Ducos, F.; Torres, B.; Derimian, Y.; Huang, X.; Lopatin, A.; et al. GRASP: A versatile algorithm for characterizing the atmosphere. SPIE Newsroom 2014, 25, 2-1201408. [Google Scholar] [CrossRef]
- Torres, B.; Dubovik, O.; Fuertes, D.; Schuster, G.; Cachorro, V.E.; Lapionak, T.; Goloub, P.; Blarel, L.; Barreto, A.; Mallet, M.; et al. Advanced characterization of aerosol properties from measurements of spectral optical depth using the GRASP algorithm. Atmos. Meas. Tech. Discuss. 2016, 10, 3743–3781. [Google Scholar] [CrossRef]
- Dubovik, O.; Fuertes, D.; Litvinov, P.; Lopatin, A.; Lapyonok, T.; Doubovik, I.; Xu, F.; Ducos, F.; Chen, C.; Torres, B.; et al. A Comprehensive Description of Multi-Term LSM for Applying Multiple a Priori Constraints in Problems of Atmospheric Remote Sensing: GRASP Algorithm, Concept, and Applications. Front. Remote Sens. 2021, 2, 706851. [Google Scholar] [CrossRef]
- Litvinov, P.; Chen, C.; Dubovik, O.; Bindreiter, L.; Matar, C.; Fuertes, D.; Lopatin, A.; Lapyonok, T.; Lanzinger, V.; Hangler, A.; et al. Extended aerosol and surface characterization from S5P/TROPOMI with GRASP algorithm. Part I: Conditions, approaches, performance and new possibilities. Remote Sens. Environ. 2024, 313, 114355. [Google Scholar] [CrossRef]
- Chen, C.; Litvinov, P.; Dubovik, O.; Bindreiter, L.; Matar, C.; Fuertes, D.; Lopatin, A.; Lapyonok, T.; Lanzinger, V.; Hangler, A.; et al. Extended aerosol and surface characterization from S5P/TROPOMI with GRASP algorithm. Part II: Global validation and Intercomparison. Remote Sens. Environ. 2024, 313, 114374. [Google Scholar] [CrossRef]
- Chen, C.; Litvinov, P.; Dubovik, O.; Fuertes, D.; Matar, C.; Miglietta, F.; Pepe, M.; Genesio, L.; Busetto, L.; Bindreiter, L.; et al. Retrieval of aerosol and surface properties at high spatial resolution: Hybrid approach and demonstration using sentinel-5p/TROPOMI and PRISMA. J. Geophys. Res. Atmos. 2024, 129, e2024JD041041. [Google Scholar] [CrossRef]
- Veefkind, J.P.; Aben, I.; McMullan, K.; Förster, H.; De Vries, J.; Otter, G.; Claas, J.; Eskes, H.; De Haan, J.; Kleipool, Q.; et al. TROPOMI on the ESA Sentinel-5 Precursor: A GMES mission for global observations of the atmospheric composition for climate, air quality and ozone layer applications. Remote Sens. Environ. 2012, 120, 70–83. [Google Scholar] [CrossRef]
- Litvinov, P.; Hasekamp, O.; Cairns, B. Models for surface reflection of radiance and polarized radiance: Comparison with airborne multi-angle photopolarimetric measurements and implications for modeling top-of-atmosphere measurements. Remote Sens. Environ. 2011, 115, 781–792. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Waring, R.; Coops, N.; Fan, W.; Nightingale, J. MODIS enhanced vegetation index predicts tree species richness across forested ecoregions in the contiguous USA. Remote Sens. Environ. 2006, 103, 218–226. [Google Scholar] [CrossRef]
- Matsushita, B.; Yang, W.; Chen, J.; Onda, Y.; Qiu, G. Sensitivity of the enhanced vegetation index (EVI) and normalized difference vegetation index (NDVI) to topographic effects: A case study in high-density cypress forest. Sensors 2007, 7, 2636–2651. [Google Scholar] [CrossRef]
- Kokaly, R.F.; Clark, R.N.; Swayze, G.A.; Livo, K.E.; Hoefen, T.M.; Pearson, N.C.; Wise, R.A.; Benzel, W.M.; Lowers, H.A.; Driscoll, R.L.; et al. USGS Spectral Library Version 7; 1035; U.S. Geological Survey: Reston, VA, USA, 2017; p. 68.
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER spectral library version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Sridhar, M.; Muthukumar, M. Spectral Library for Various Rocks and Minerals of Salem District: A Comparative Study and Validation with ASTER Data. In On a Sustainable Future of the Earth’s Natural Resources; Ramkumar, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 149–157. [Google Scholar]
- Hou, W.; Li, Z.; Dong, X.; Zhou, Z.; Ge, B.; Zheng, Y.; Yao, Q.; Fan, C.; Shi, Z. Hyperspectral surface reflectance reconstruction based on non-negative matrix factorization and multispectral results. Proc. SPIE 2021, 12064, 86–92. [Google Scholar] [CrossRef]
- Yang, Y.; Nan, R.; Mi, T.; Song, Y.; Shi, F.; Liu, X.; Wang, Y.; Sun, F.; Xi, Y.; Zhang, C. Rapid and Nondestructive Evaluation of Wheat Chlorophyll under Drought Stress Using Hyperspectral Imaging. Int. J. Mol. Sci. 2023, 24, 5825. [Google Scholar] [CrossRef]
- Fang, H.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An Overview of Global Leaf Area Index (LAI): Methods, Products, Validation, and Applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar] [CrossRef]
- Hunt, E.R.; Doraiswamy, P.C.; McMurtrey, J.E.; Daughtry, C.S.T.; Perry, E.M.; Akhmedov, B. A visible band index for remote sensing leaf chlorophyll content at the canopy scale. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 103–112. [Google Scholar] [CrossRef]
- Galieni, A.; D’Ascenzo, N.; Stagnari, F.; Pagnani, G.; Xie, Q.; Pisante, M. Past and Future of Plant Stress Detection: An Overview From Remote Sensing to Positron Emission Tomography. Front. Plant Sci. 2021, 11, 609155. [Google Scholar] [CrossRef]
- Qian, B.; Ye, H.; Huang, W.; Xie, Q.; Pan, Y.; Xing, N.; Ren, Y.; Guo, A.; Jiao, Q.; Lan, Y. A sentinel-2-based triangular vegetation index for chlorophyll content estimation. Agric. For. Meteorol. 2022, 322, 109000. [Google Scholar] [CrossRef]
- Bell, I.E.; Baranoski, G.V.G. Reducing the dimensionality of plant spectral databases. IEEE Trans. Geosci. Remote Sens. 2004, 42, 570–576. [Google Scholar] [CrossRef]
- Fabre, S.; Briottet, X.; Lesaignoux, A. Estimation of Soil Moisture Content from the Spectral Reflectance of Bare Soils in the 0.4–2.5 µm Domain. Sensors 2015, 15, 3262–3281. [Google Scholar] [CrossRef]
- Govender, M.; Chetty, K.; Bulcock, H. A review of hyperspectral remote sensing and its application in vegetation and water resource studies. Water Sa 2007, 33, 145–151. [Google Scholar] [CrossRef]
- Booysen, R.; Lorenz, S.; Thiele, S.T.; Fuchsloch, W.C.; Marais, T.; Nex, P.A.M.; Gloaguen, R. Accurate hyperspectral imaging of mineralised outcrops: An example from lithium-bearing pegmatites at Uis, Namibia. Remote Sens. Environ. 2022, 269, 112790. [Google Scholar] [CrossRef]
- Shammi, S.A.; Meng, Q. Use time series NDVI and EVI to develop dynamic crop growth metrics for yield modeling. Ecol. Indic. 2021, 121, 107124. [Google Scholar] [CrossRef]
- Okujeni, A.; Canters, F.; Cooper, S.D.; Degerickx, J.; Heiden, U.; Hostert, P.; Priem, F.; Roberts, D.A.; Somers, B.; van der Linden, S. Generalizing machine learning regression models using multi-site spectral libraries for mapping vegetation-impervious-soil fractions across multiple cities. Remote Sens. Environ. 2018, 216, 482–496. [Google Scholar] [CrossRef]
- Li, T.; Liu, T.; Wang, Y.; Li, X.; Gu, Y. Spectral reconstruction network from multispectral images to hyperspectral images: A multitemporal case. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Adam, E.; Mutanga, O.; Rugege, D. Multispectral and hyperspectral remote sensing for identification and mapping of wetland vegetation: A review. Wetl. Ecol. Manag. 2009, 18, 281–296. [Google Scholar] [CrossRef]
- Yokoya, N.; Grohnfeldt, C.; Chanussot, J. Hyperspectral and multispectral data fusion: A comparative review of the recent literature. IEEE Geosci. Remote Sens. Mag. 2017, 5, 29–56. [Google Scholar] [CrossRef]



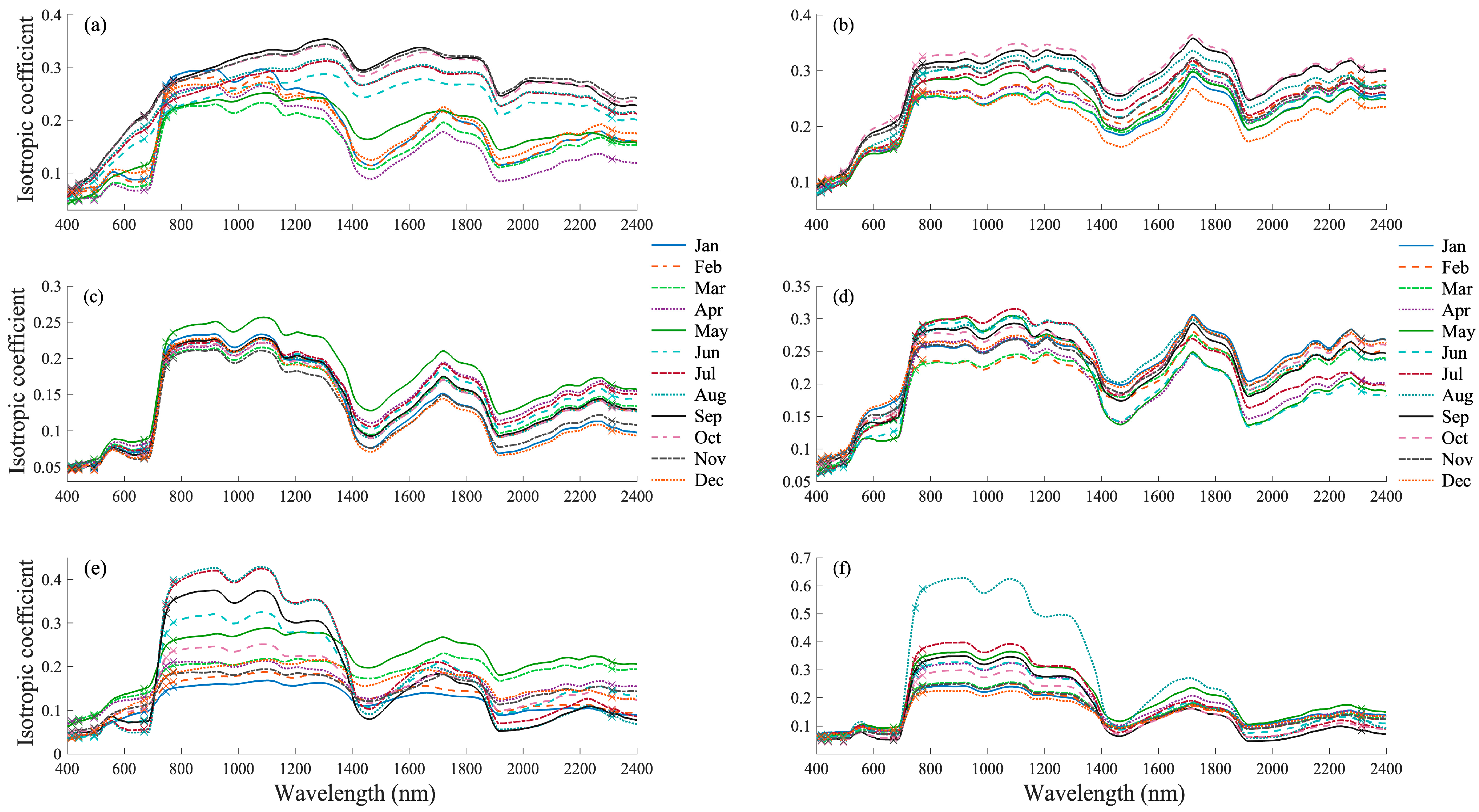

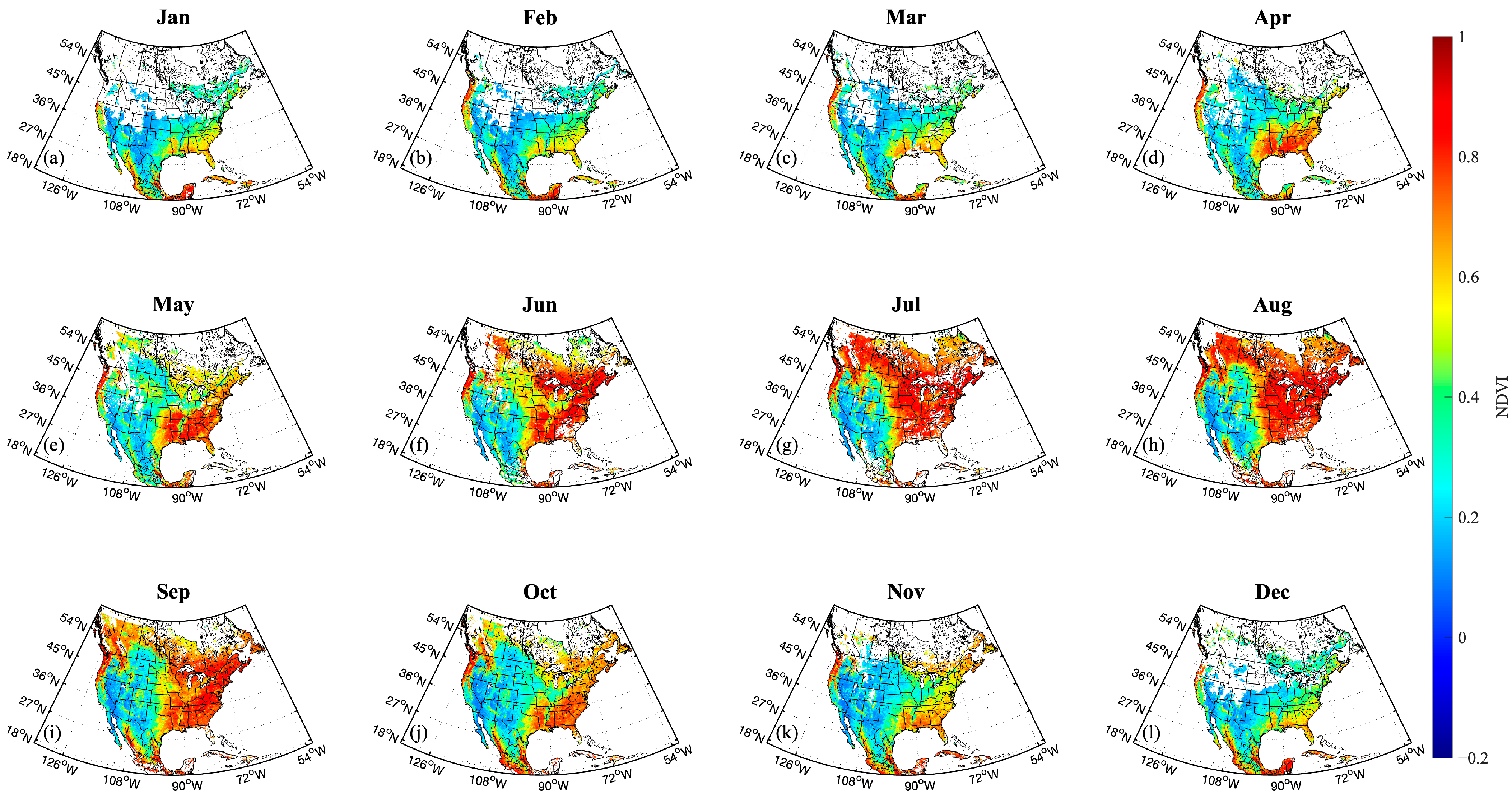
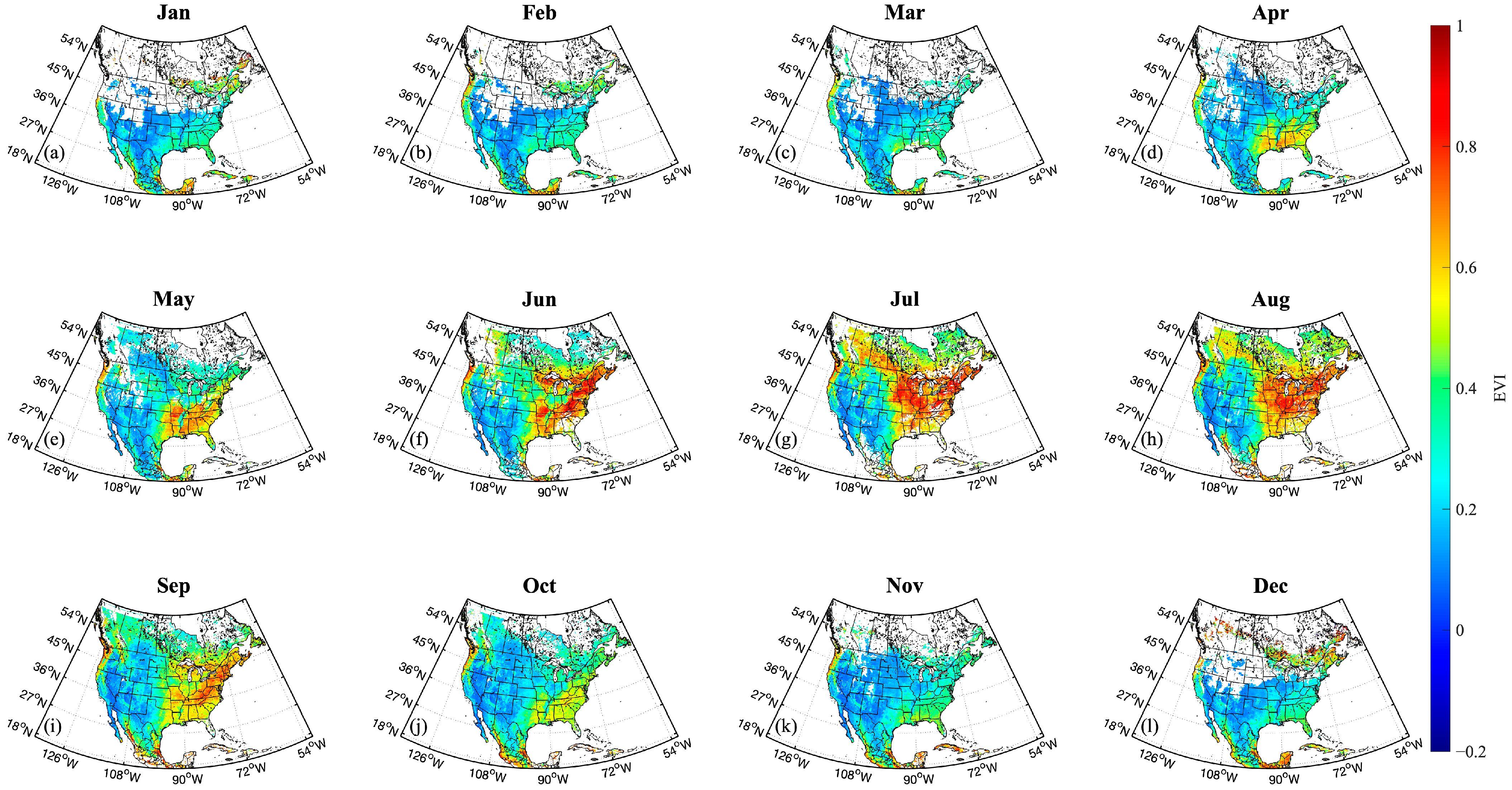
| Parameter | Value |
|---|---|
| Wavelength (nm) | 340, 367, 380, 416, 440, 494, 670, 740, 772, 2313 |
| L1B spatial sampling (km) | 5.5 × 3.5 (340–772 nm), 5.5 × 7.0 only for 2313 nm |
| Spectral resolution (nm) | 1.0 |
| Spatial resolution (°) | 0.09 |
| Auxiliary information | ECMWF’s wind speed information |
| Cloud masking | S5P NPP-VIIRS cloud mask |
| Data Date | Wavelength | Reconstructed Absolute Error | Reconstructed Relative Error | ||
|---|---|---|---|---|---|
| Mean | Std. Dev. | Mean | Std. Dev. | ||
| August 2020 | 416 nm | −0.0080 | 0.0036 | −16.62% | 8.27% |
| 440 nm | 0.0083 | 0.0037 | 18.04% | 9.65% | |
| 494 nm | −0.0039 | 0.0492 | −4.45% | 123.35% | |
| 670 nm | 0.0020 | 0.0273 | 16.39% | 54.91% | |
| 747 nm | 0.0001 | 0.0057 | −0.20% | 1.94% | |
| 772 nm | −0.0002 | 0.0065 | 0.20% | 1.96% | |
| March 2020 | 416 nm | −0.0065 | 0.0038 | −10.22% | 6.22% |
| 440 nm | 0.0067 | 0.0040 | 10.47% | 6.85% | |
| 494 nm | −0.0141 | 0.0385 | −21.96% | 38.17% | |
| 670 nm | −0.0092 | 0.0321 | −4.93% | 24.05% | |
| 747 nm | 0.0005 | 0.0042 | 0.33% | 1.44% | |
| 772 nm | −0.0007 | 0.0048 | −0.38% | 1.55% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, W.; Liu, X.; Wang, J.; Chen, C.; Xu, X. Multispectral Land Surface Reflectance Reconstruction Based on Non-Negative Matrix Factorization: Bridging Spectral Resolution Gaps for GRASP TROPOMI BRDF Product in Visible. Remote Sens. 2025, 17, 1053. https://doi.org/10.3390/rs17061053
Hou W, Liu X, Wang J, Chen C, Xu X. Multispectral Land Surface Reflectance Reconstruction Based on Non-Negative Matrix Factorization: Bridging Spectral Resolution Gaps for GRASP TROPOMI BRDF Product in Visible. Remote Sensing. 2025; 17(6):1053. https://doi.org/10.3390/rs17061053
Chicago/Turabian StyleHou, Weizhen, Xiong Liu, Jun Wang, Cheng Chen, and Xiaoguang Xu. 2025. "Multispectral Land Surface Reflectance Reconstruction Based on Non-Negative Matrix Factorization: Bridging Spectral Resolution Gaps for GRASP TROPOMI BRDF Product in Visible" Remote Sensing 17, no. 6: 1053. https://doi.org/10.3390/rs17061053
APA StyleHou, W., Liu, X., Wang, J., Chen, C., & Xu, X. (2025). Multispectral Land Surface Reflectance Reconstruction Based on Non-Negative Matrix Factorization: Bridging Spectral Resolution Gaps for GRASP TROPOMI BRDF Product in Visible. Remote Sensing, 17(6), 1053. https://doi.org/10.3390/rs17061053










