Research on the Preprocessing Method of Laser Ranging Data with Complex Patterns Based on a Novel Spline Function
Abstract
1. Introduction
2. Method
2.1. Novel Spline Fitting Filtering Method
2.1.1. Adaptive Segmentation of Data
2.1.2. Determination of the Optimal Trend Function for Each Subinterval
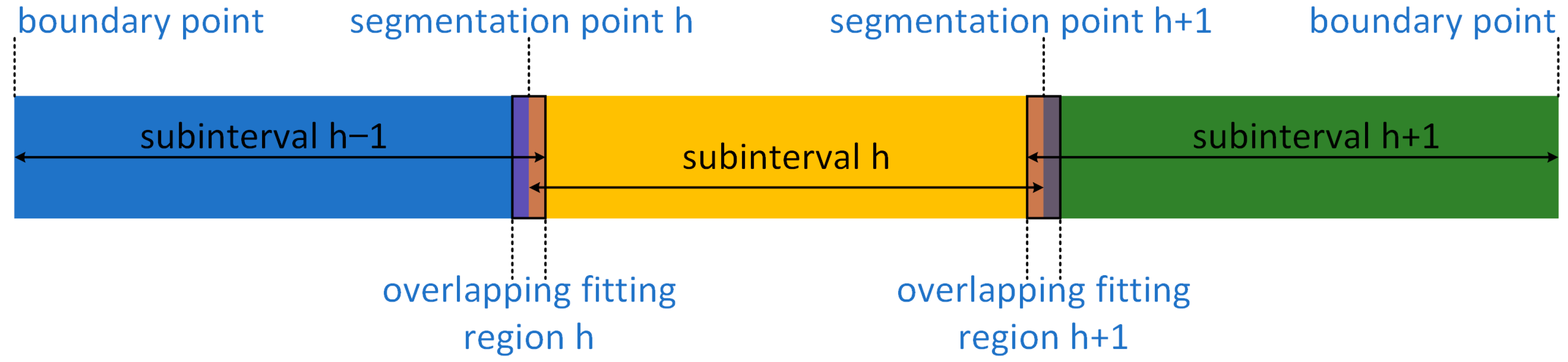
2.1.3. Smooth Transition of Trend Functions Between Adjacent Subintervals
- (1)
- Divide the data into multiple subintervals with overlapping parts.
- (2)
- Fit the data within each subinterval independently.
- (3)
- Combine the fitting results of adjacent subintervals within the overlapping region by means of a weight function.
- a.
- Smoothness: Both functions are constructed based on sinusoidal function, ensuring good continuity and derivability.
- b.
- Symmetry: The two functions are symmetric about w = 1/2.
- c.
- Complementarity: Both functions have a value range of [0, 1] and their sum is constant at 1.
- d.
- Normalization: The two functions complement each other; when one function decreases from 1 to 0, the other increases from 0 to 1.
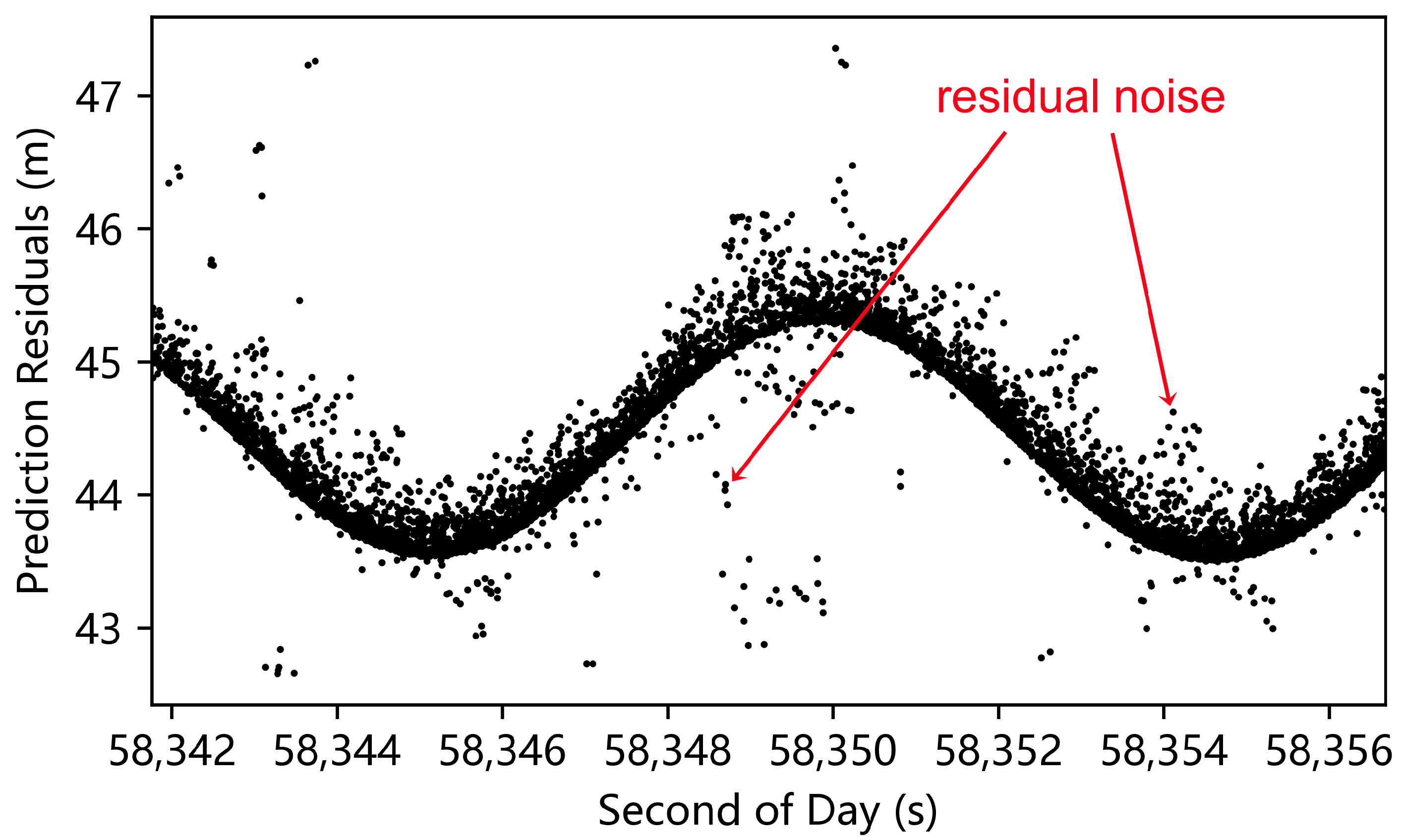
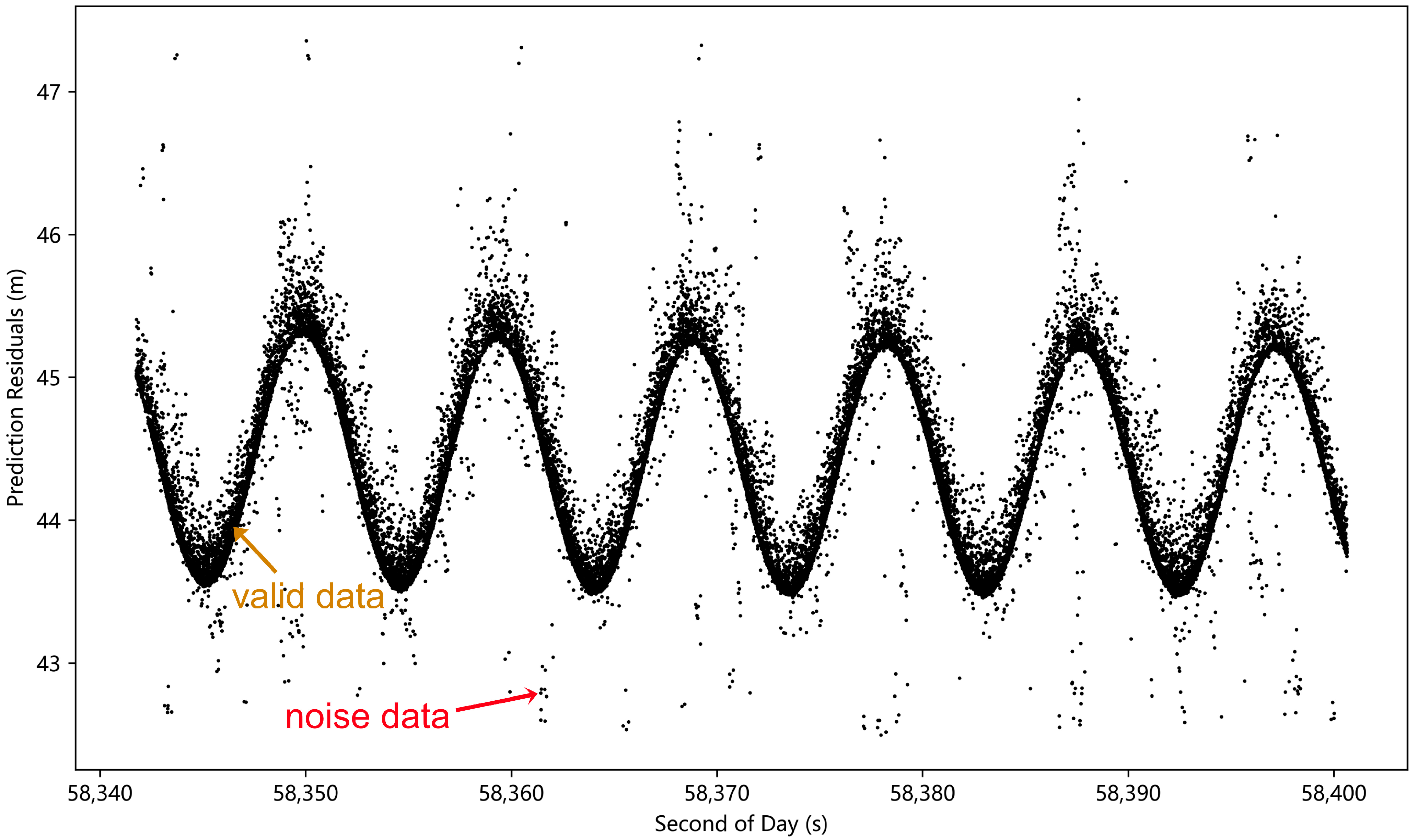
2.1.4. Filtering of Noise Data
2.2. Laser Ranging Data Preprocessing Flow Based on Novel Spline Fitting
- (1)
- Calculate the prediction residual PR, i.e., the difference between the observed value O and the computed value C (Observed-Computed), using high-precision prediction and measured data;
- (2)
- Remove outliers from the prediction residual PR by manual or automatic data identification techniques;
- (3)
- Solve the trend function f(t) of the prediction residuals using a novel spline fitting method;
- (4)
- Calculate the fit residual FR, i.e., the difference between PR and f(t), and solve the RMS of the fit residual;
- (5)
- Identify the noise by setting the threshold window β × RMS, remove the noise data outside the threshold window, and use the remaining data for the next iteration;
- (6)
- Repeat steps (3) to (5) until the RMS meets the preset requirements and save the preprocessed data.
3. Results
3.1. Preprocessing of Data with Good Characteristics
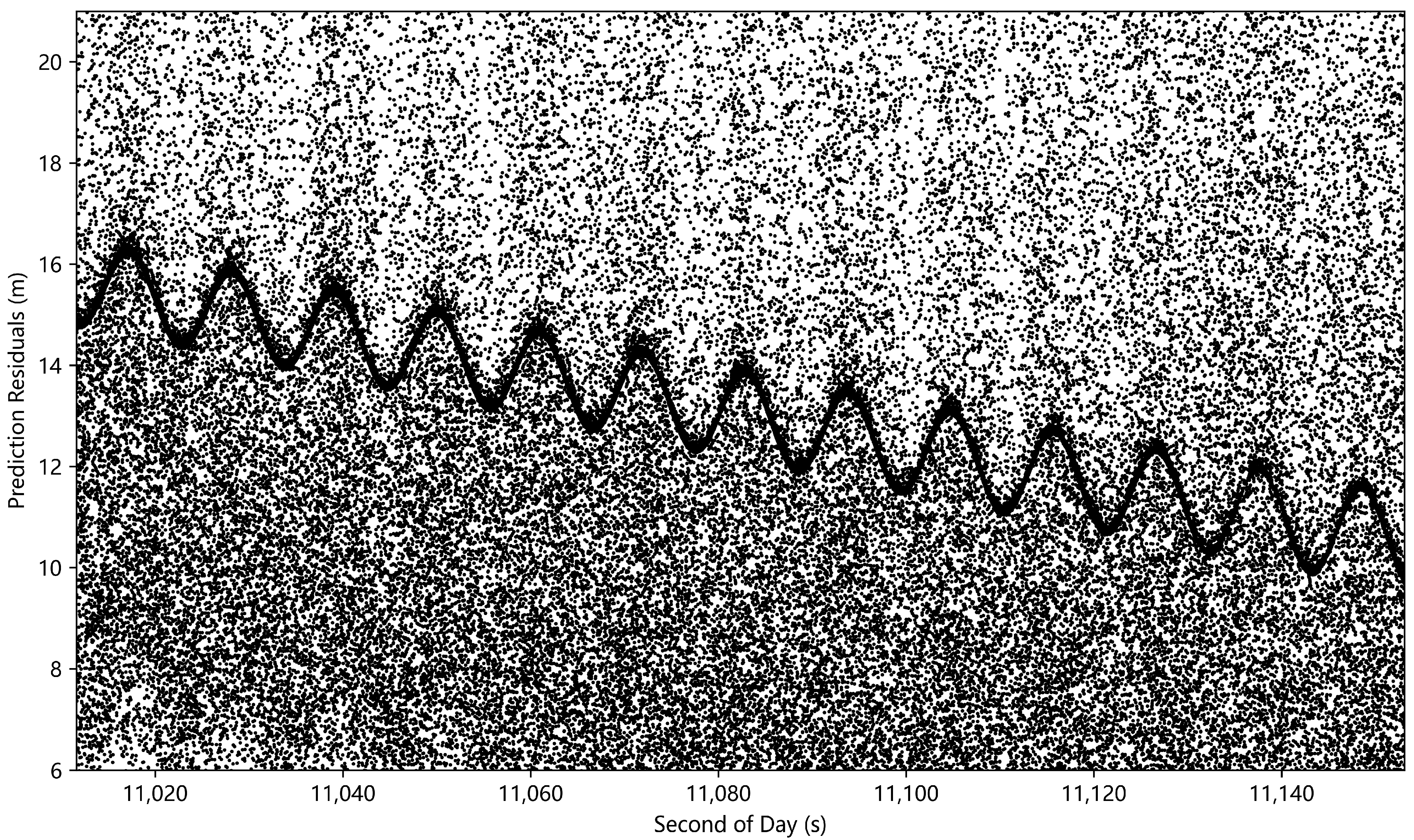
3.2. Preprocessing of Low Signal-to-Noise Ratio Data
3.3. Preprocessing of High-Frequency Fluctuation Data
3.4. Preprocessing of Data with Amplitude Variation Characteristics
3.5. Preprocessing of Discontinuous Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SLR | Satellite laser ranging |
| ILRS | International Laser Ranging Service |
| EOP | Earth orientation parameters |
| RMSE | Root mean squared error |
References
- Pearlman, M.; Arnold, D.; Davis, M.; Barlier, F.; Biancale, R.; Vasiliev, V.; Ciufolini, I.; Paolozzi, A.; Pavlis, E.C.; Sośnica, K.; et al. Laser Geodetic Satellites: A High-Accuracy Scientific Tool. J. Geod. 2019, 93, 2181–2194. [Google Scholar] [CrossRef]
- Sośnica, K.; Bury, G.; Zajdel, R. Contribution of Multi-GNSS Constellation to SLR-Derived Terrestrial Reference Frame. Geophys. Res. Lett. 2018, 45, 2339–2348. [Google Scholar] [CrossRef]
- Maier, A.; Krauss, S.; Hausleitner, W.; Baur, O. Contribution of Satellite Laser Ranging to Combined Gravity Field Models. Adv. Space Res. 2012, 49, 556–565. [Google Scholar] [CrossRef]
- Lemoine, F.G. The Contribuons of Satellite Laser Ranging to Satellite Altimetry. In Proceedings of the 20th International Workshop on Laser Ranging, Potsdam, Germany, 9–14 October 2016; p. 40. [Google Scholar]
- Kirchner, G.; Koidl, F. Graz kHz SLR System: Design, Experiences and Results. Available online: https://ilrs.cddis.eosdis.nasa.gov/lw14/docs/papers/adv4_gkm.pdf (accessed on 12 January 2025).
- Wu, Z.; Zhang, H.; Zhang, Z.; Yang, F.; Chen, J.; Li, P. kHz repetition Satellite Laser Ranging system with high precision and measuring results. Chin. Sci. Bull. 2011, 56, 1177–1183. [Google Scholar] [CrossRef]
- Gibbs, P.; Potter, C.; Sherwood, R.; Wilkinson, M.; Benham, D.; Smith, V.; Appleby, G. Some Early Results of Kilohertz Laser Ranging at Herstmonceux. Available online: https://ilrs.gsfc.nasa.gov/lw15/docs/papers/Some%20Early%20Results%20of%20Kilohertz%20Laser%20Ranging%20at%20Herstmonceux.pdf (accessed on 6 January 2025).
- Fan, Z.; Liu, X.; Zhang, Z.; Meng, W.; Long, M.; Bai, Z. 10 kHz Repetition Rate Picosecond Green Laser for High-Accuracy Satellite Ranging. Front. Phys. 2023, 10, 1115330. [Google Scholar] [CrossRef]
- Cheng, S.; Long, M.; Zhang, H.; Wu, Z.; Qin, S.; Zhang, Z. Research on satellite laser ranging at pulse repetition frequency of 100 kHz. Infrared Laser Eng. 2022, 51, 20220121. [Google Scholar] [CrossRef]
- Hampf, D.; Wagner, P.; Schafer, E.; Riede, W. Concept for a New Minimal SLR System. Available online: https://ilrs.gsfc.nasa.gov/lw21/docs/2018/papers/Session8_Hampf_Paper.pdf (accessed on 21 January 2025).
- Courde, C.; Mariey, H.; Chabé, J.; Phung, D.-H.; Torre, J.-M.; Aimar, M.; Maurice, N.; Samain, E.; Tosi, A.; Buttafava, M. High Repetition Rate SLR at GRSM. Available online: https://ilrs.gsfc.nasa.gov/2019_Technical_Workshop/docs/2019/abstracts/session4_Courde_abstract.pdf (accessed on 19 January 2025).
- Wang, P.; Steindorfer, M.A.; Koidl, F.; Kirchner, G.; Leitgeb, E. Megahertz Repetition Rate Satellite Laser Ranging Demonstration at Graz Observatory. Opt. Lett. 2021, 46, 937–940. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, M.; Schreiber, U.; Procházka, I.; Moore, C.; Degnan, J.; Kirchner, G.; Zhongping, Z.; Dunn, P.; Shargorodskiy, V.; Sadovnikov, M.; et al. The next Generation of Satellite Laser Ranging Systems. J. Geod. 2019, 93, 2227–2247. [Google Scholar] [CrossRef]
- Tang, R.; Li, Y.; Li, X.; Li, R.; Huang, K. Spin Rate Determination of AJISAI Based on High Frequency Satellite Laser Ranging. Chin. J. Lasers 2015, 42, 287–292. [Google Scholar]
- Liu, T.; Chen, H.; Shen, M.; Gao, P.; Zhao, Y. Spinning Satellite Laser Ranging Data Analysis and Processing. Chin. J. Lasers 2017, 44, 0504001. [Google Scholar] [CrossRef]
- Kucharski, D.; Kirchner, G.; Otsubo, T.; Lim, H.-C.; Bennett, J.; Koidl, F.; Kim, Y.-R.; Hwang, J.-Y. Confirmation of Gravitationally Induced Attitude Drift of Spinning Satellite Ajisai with Graz High Repetition Rate SLR Data. Adv. Space Res. 2016, 57, 983–990. [Google Scholar] [CrossRef]
- Kessler, D.J.; Cour-Palais, B.G. Collision Frequency of Artificial Satellites: The Creation of a Debris Belt. J. Geophys. Res. Space Phys. 1978, 83, 2637–2646. [Google Scholar] [CrossRef]
- Liou, J.-C.; Johnson, N.L. Risks in Space from Orbiting Debris. Science 2006, 311, 340–341. [Google Scholar] [CrossRef]
- Krag, H.; Serrano, M.; Braun, V.; Kuchynka, P.; Catania, M.; Siminski, J.; Schimmerohn, M.; Marc, X.; Kuijper, D.; Shurmer, I.; et al. A 1 Cm Space Debris Impact onto the Sentinel-1A Solar Array. Acta Astronaut. 2017, 137, 434–443. [Google Scholar] [CrossRef]
- Kirchner, G.; Koidl, F.; Friederich, F.; Buske, I.; Völker, U.; Riede, W. Laser Measurements to Space Debris from Graz SLR Station. Adv. Space Res. 2013, 51, 21–24. [Google Scholar] [CrossRef]
- Liang, Z.; Dong, X.; Ibrahim, M.; Song, Q.; Han, X.; Liu, C.; Zhang, H.; Zhao, G. Tracking the Space Debris from the Changchun Observatory. Astrophys. Space Sci. 2019, 364, 201. [Google Scholar] [CrossRef]
- Steindorfer, M.A.; Kirchner, G.; Koidl, F.; Wang, P.; Jilete, B.; Flohrer, T. Daylight Space Debris Laser Ranging. Nat. Commun. 2020, 11, 3735. [Google Scholar] [CrossRef]
- Smagło, A.; Lejba, P.; Schillak, S.; Suchodolski, T.; Michałek, P.; Zapaśnik, S.; Bartoszak, J. Measurements to Space Debris in 2016–2020 by Laser Sensor at Borowiec Poland. Artif. Satell. 2021, 56, 119–134. [Google Scholar] [CrossRef]
- Kucharski, D.; Kirchner, G.; Koidl, F.; Fan, C.; Carman, R.; Moore, C.; Dmytrotsa, A.; Ploner, M.; Bianco, G.; Medvedskij, M.; et al. Attitude and Spin Period of Space Debris Envisat Measured by Satellite Laser Ranging. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7651–7657. [Google Scholar] [CrossRef]
- Kirchner, G.; Kucharski, D.; Cristea, E. Gravity Probe-B: New Methods to Determine Spin Parameters from kHz SLR Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 370–375. [Google Scholar] [CrossRef]
- Kucharski, D.; Kirchner, G.; Bennett, J.C.; Lachut, M.; Sośnica, K.; Koshkin, N.; Shakun, L.; Koidl, F.; Steindorfer, M.; Wang, P.; et al. Photon Pressure Force on Space Debris TOPEX/Poseidon Measured by Satellite Laser Ranging. Earth Space Sci. 2017, 4, 661–668. [Google Scholar] [CrossRef]
- Liu, T.; Shen, M.; Gao, P.; Zhao, Y. Tumbling Motion Estimation of Rocket Body Based on Diffuse Reflection Laser Ranging. Chin. J. Lasers 2019, 46, 0104007. [Google Scholar] [CrossRef]
- Guo, J.; Wang, Y.; Shen, Y.; Liu, X.; Sun, Y.; Kong, Q. Estimation of SLR Station Coordinates by Means of SLR Measurements to Kinematic Orbit of LEO Satellites. Earth Planets Space 2018, 70, 201. [Google Scholar] [CrossRef]
- Rutkowska, M.; Jagoda, M. SLR Technique Used for Description of The Earth Elasticity. Artif. Satell. 2015, 50, 127–141. [Google Scholar] [CrossRef]
- Tang, R.; Zhai, D.; Zhang, H.; Pi, X.; Li, C.; Fu, H.; Li, R.; Li, Z.; Li, Y. Research Progress in Space Debris Laser Ranging. Space Debris Res. 2020, 20, 21–30. [Google Scholar]
- Greene, B. Laser Tracking of Space Debris. Available online: https://ilrs.cddis.eosdis.nasa.gov/lw13/docs/papers/adv_greene_1m.pdf (accessed on 26 January 2025).
- Kucharski, D.; Kirchner, G.; Jah, M.K.; Bennett, J.C.; Koidl, F.; Steindorfer, M.A.; Wang, P. Full Attitude State Reconstruction of Tumbling Space Debris TOPEX/Poseidon via Light-Curve Inversion with Quanta Photogrammetry. Acta Astronaut. 2021, 187, 115–122. [Google Scholar] [CrossRef]
- Cordelli, E.; Mira, A.D.; Flohrer, T.; Setty, S.; Zayer, I.; Scharring, S.; Dreyer, H.; Wagner, G.; Kästel, J.; Schafer, E.; et al. Ground-Based Laser Momentum Transfer Concept for Debris Collision Avoidance. J. Space Saf. Eng. 2022, 9, 612–624. [Google Scholar] [CrossRef]
- Hall, A.; Steele, P.; Moulin, J.; Ferreira, E. Airbus Active Debris Removal Service. Adv. Astronaut. Sci. Technol. 2021, 4, 1–10. [Google Scholar] [CrossRef]
- Phipps, C.R.; Baker, K.L.; Libby, S.B.; Liedahl, D.A.; Olivier, S.S.; Pleasance, L.D.; Rubenchik, A.; Trebes, J.E.; Victor George, E.; Marcovici, B.; et al. Removing Orbital Debris with Lasers. Adv. Space Res. 2012, 49, 1283–1300. [Google Scholar] [CrossRef]
- Ibrahim, M.; Hanna, Y.S.; Samwel, S.W. Statistical and Comparative Studies for the Observations of Helwan-SLR Station. Int. J. Nonlinear Sci. Numer. Simul. 2004, 5, 135–148. [Google Scholar] [CrossRef]
- Kucharski, D.; Otsubo, T.; Kirchner, G.; Lim, H.-C. Spectral Filter for Signal Identification in the kHz SLR Measurements of the Fast Spinning Satellite Ajisai. Adv. Space Res. 2013, 52, 930–935. [Google Scholar] [CrossRef]
- Ma, T.; Zhao, C.; He, Z.; Zhang, H. Realtime recognition method of weak signal in space debris laser ranging. Acta Geod. Cartogr. Sin. 2022, 51, 87–94. [Google Scholar]
- Moore, C. Development of Automated SLR Data Processing at Mt Stromlo SLR Station. In Proceedings of the 21st International Workshop on Laser Ranging, Canberra, Australia, 5–9 November 2018; p. 22. [Google Scholar]
- Hiener, M.; Schreiber, U.; Brandl, N. Recursive Filter Algorithm for Noise Reduction in SLR. In Proceedings of the 15th International Workshop on Laser Ranging, Canberra, Australia, 15–20 October 2006; p. 6. [Google Scholar]
- Fang, Q.; Zhao, Y. The research progress in data processing algorithm of satellite laser ranging. Laser Technol. 2008, 32, 417–419. [Google Scholar]
- Li, Y.; Fu, H.; Li, R.; Tang, R.; Li, Z.; Zhai, D.; Zhang, H.; Pi, X.; Ye, X.; Xiong, Y. Research and Experiment of Lunar Laser Ranging in Yunnan Observatories. Chin. J. Lasers 2019, 46, 0104004. [Google Scholar] [CrossRef]
- Kucharski, D.; Kirchner, G.; Otsubo, T.; Koidl, F. A Method to Calculate Zero-Signature Satellite Laser Ranging Normal Points for Millimeter Geodesy—A Case Study with Ajisai. Earth Planets Space 2015, 67, 34. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, G.; Feng, X.; Zhang, Z.; Li, S.; Hu, B. High Precision Centroid Location Algorithm Based on Cubic Spline Fitting and Interpolation. Acta Opt. Sin. 2021, 41, 1212004. [Google Scholar] [CrossRef]
- Tao, T. Stability Analysis and Application of Cubic Spline Interpolation Function; Chengdu University of Technology: Chengdu, China, 2023. [Google Scholar]
- Hu, J. Research of Dual-Wavelength Satellite Laser Ranging, Shanghai Astronomical Observatory; Chinese Academy of Sciences: Shanghai, China, 2003. [Google Scholar]
- Sinclair, A.T. Re-Statement of Herstmonceux Normal Point Recommendation. Available online: https://ilrs.gsfc.nasa.gov/data_and_products/data/npt/npt_algorithm.html (accessed on 24 December 2024).
- Torrence, M.H.; Klosko, S.M. The Construction and Testing of Normal Points at Goddard Space Flight Center; NASA: Washington, DC, USA, 1984; pp. 506–516. [Google Scholar]




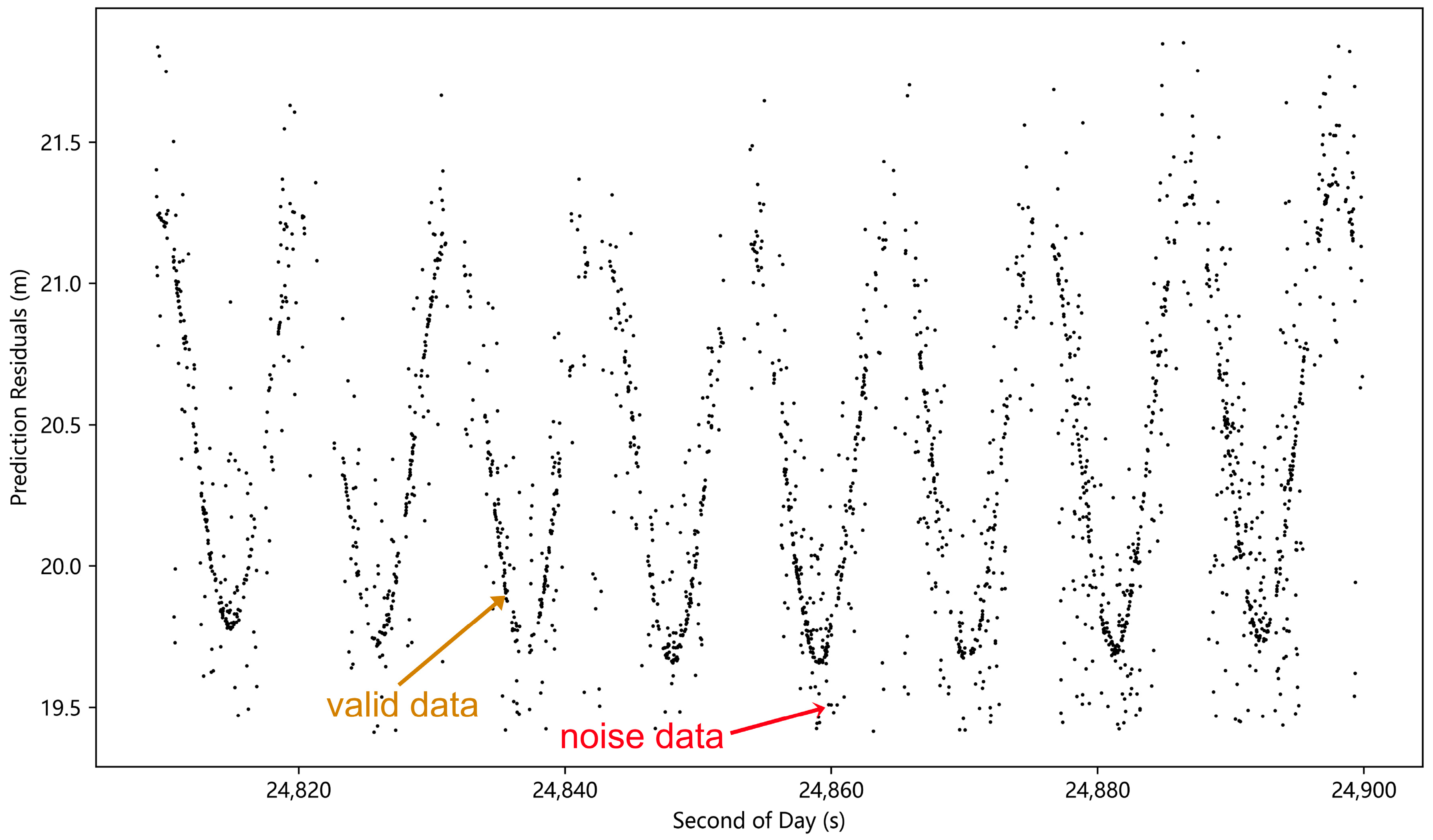


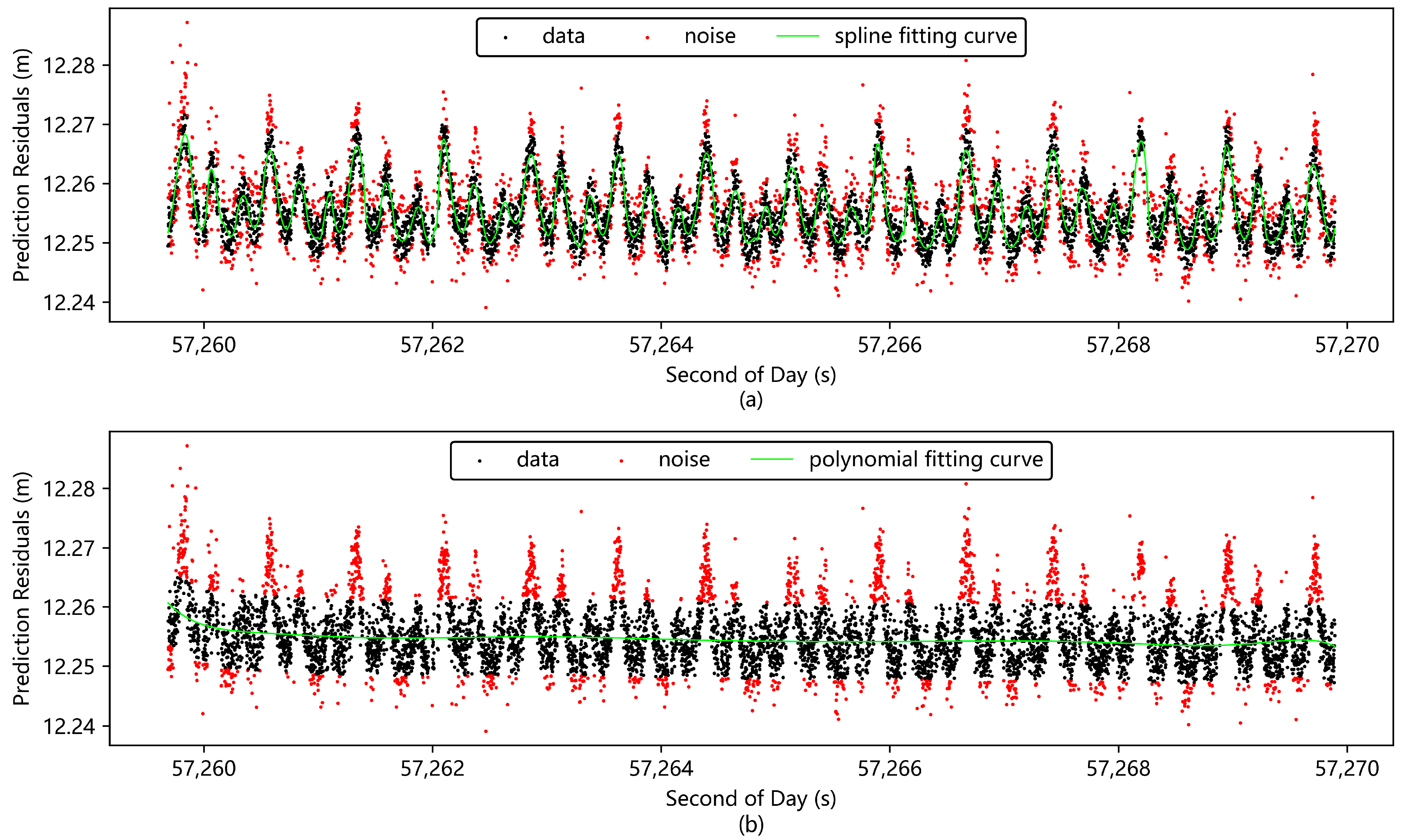
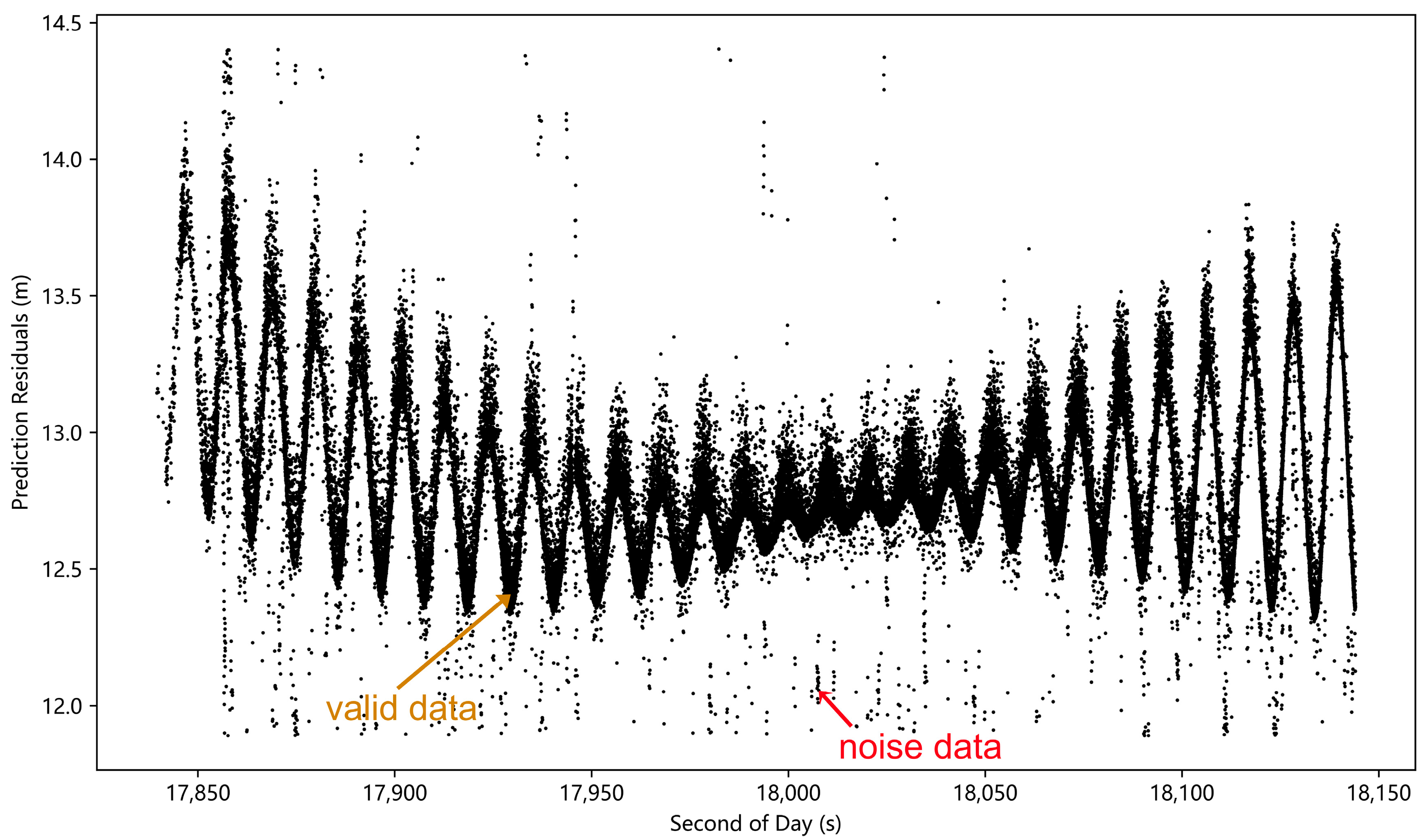


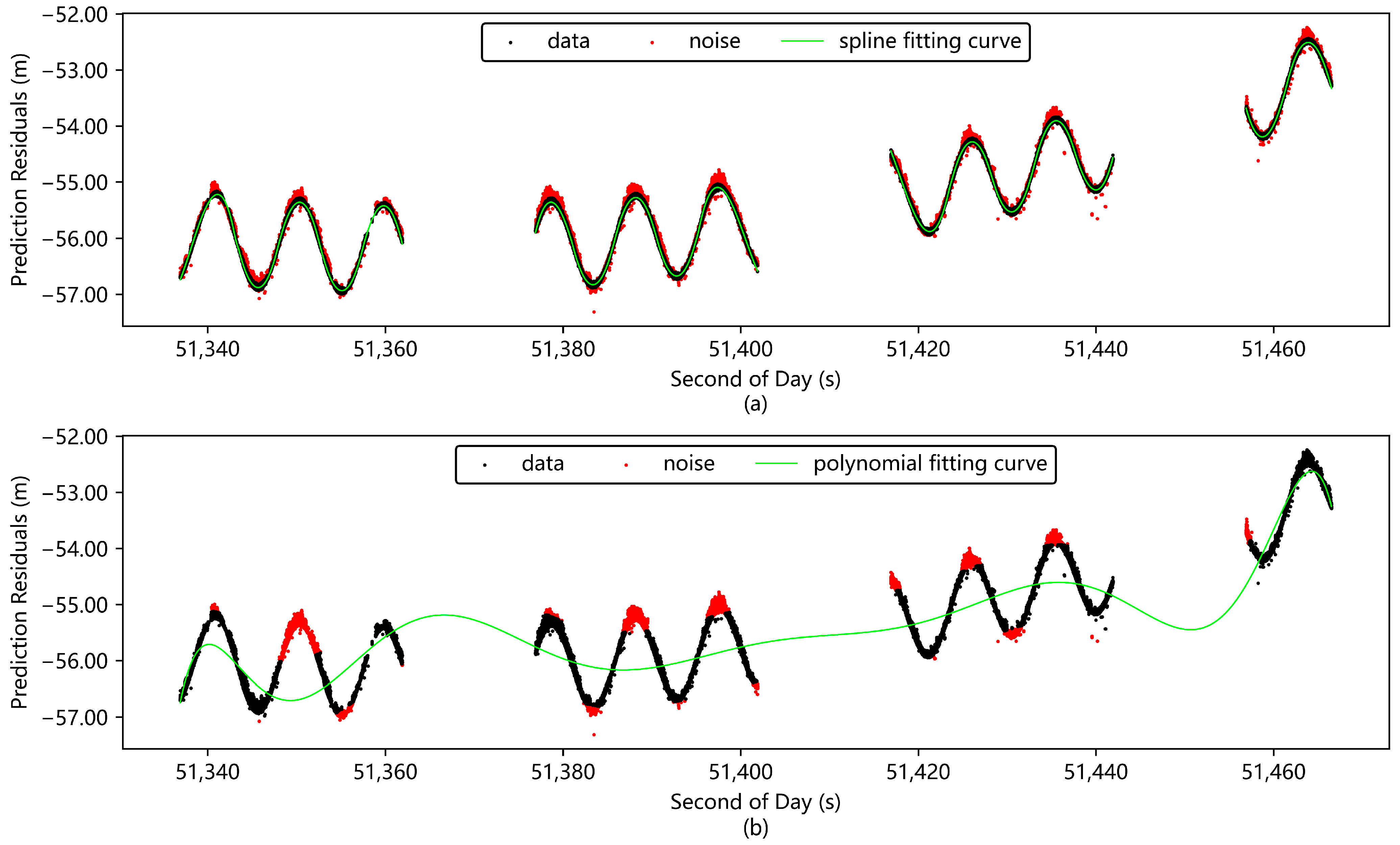
| Method | RMS Before Denoising/mm | RMS After Denoising/mm | RMS Decrease | Mistaken Deletion of Valid Data |
|---|---|---|---|---|
| novel spline fitting | 225.3 | 55.2 | Yes | No |
| polynomial fitting | 574.6 | 399.3 | Yes | Yes |
| Method | RMS Before Denoising/mm | RMS After Denoising/mm | RMS Decrease | Mistaken Deletion of Valid Data |
|---|---|---|---|---|
| novel spline fitting | 282.3 | 78.4 | Yes | No |
| polynomial fitting | 491.2 | 321.7 | Yes | Yes |
| Method | RMS Before Denoising/mm | RMS After Denoising/mm | RMS Decrease | Mistaken Deletion of Valid Data |
|---|---|---|---|---|
| novel spline fitting | 3.3 | 1.8 | Yes | No |
| polynomial fitting | 5.7 | 3.2 | Yes | Yes |
| Method | RMS Before Denoising/mm | RMS After Denoising/mm | RMS Decrease | Mistaken Deletion of Valid Data |
|---|---|---|---|---|
| novel spline fitting | 112.2 | 33.1 | Yes | No |
| polynomial fitting | 258.0 | 146.5 | Yes | Yes |
| Method | RMS Before Denoising/mm | RMS After Denoising/mm | RMS Decrease | Mistaken Deletion of Valid Data |
|---|---|---|---|---|
| novel spline fitting | 41.6 | 20.4 | Yes | No |
| polynomial fitting | 483.4 | 372.5 | Yes | Yes |
| Method | Result | Good Characteristic Data | Low S/N Ratio Data | High-Frequency Fluctuation Data | Amplitude Variation | Discontinuous Data |
|---|---|---|---|---|---|---|
| novel spline fitting | RMS before denoising/mm | 225.3 | 282.3 | 3.3 | 112.2 | 41.6 |
| RMS after denoising/mm | 55.2 | 78.4 | 1.8 | 33.1 | 20.4 | |
| Mistaken deletion of valid data | No | No | No | No | No | |
| polynomial fitting | RMS before denoising/mm | 574.6 | 491.2 | 5.7 | 258.0 | 483.4 |
| RMS after denoising/mm | 399.3 | 321.7 | 3.2 | 146.5 | 372.5 | |
| Mistaken deletion of valid data | Yes | Yes | Yes | Yes | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Dong, X.; Liang, Z.; Gao, J.; Liu, Y.; Song, Q.; Han, X.; Dong, H. Research on the Preprocessing Method of Laser Ranging Data with Complex Patterns Based on a Novel Spline Function. Remote Sens. 2025, 17, 1043. https://doi.org/10.3390/rs17061043
Zheng Y, Dong X, Liang Z, Gao J, Liu Y, Song Q, Han X, Dong H. Research on the Preprocessing Method of Laser Ranging Data with Complex Patterns Based on a Novel Spline Function. Remote Sensing. 2025; 17(6):1043. https://doi.org/10.3390/rs17061043
Chicago/Turabian StyleZheng, Yanning, Xue Dong, Zhipeng Liang, Jian Gao, Yang Liu, Qingli Song, Xingwei Han, and He Dong. 2025. "Research on the Preprocessing Method of Laser Ranging Data with Complex Patterns Based on a Novel Spline Function" Remote Sensing 17, no. 6: 1043. https://doi.org/10.3390/rs17061043
APA StyleZheng, Y., Dong, X., Liang, Z., Gao, J., Liu, Y., Song, Q., Han, X., & Dong, H. (2025). Research on the Preprocessing Method of Laser Ranging Data with Complex Patterns Based on a Novel Spline Function. Remote Sensing, 17(6), 1043. https://doi.org/10.3390/rs17061043






