Rapid Laser Ranging Method for Compact LiDAR Systems
Abstract
1. Introduction
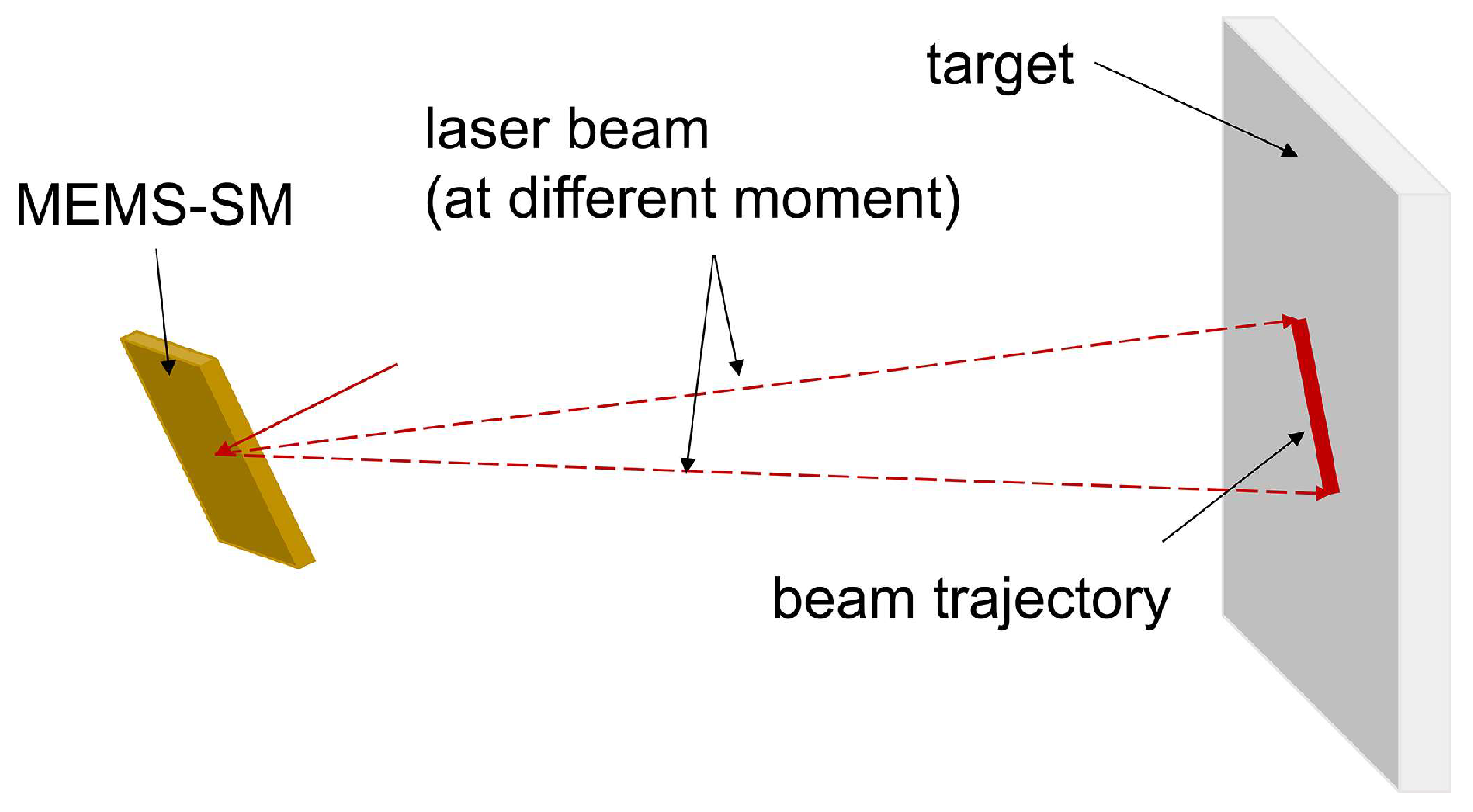
2. Principles
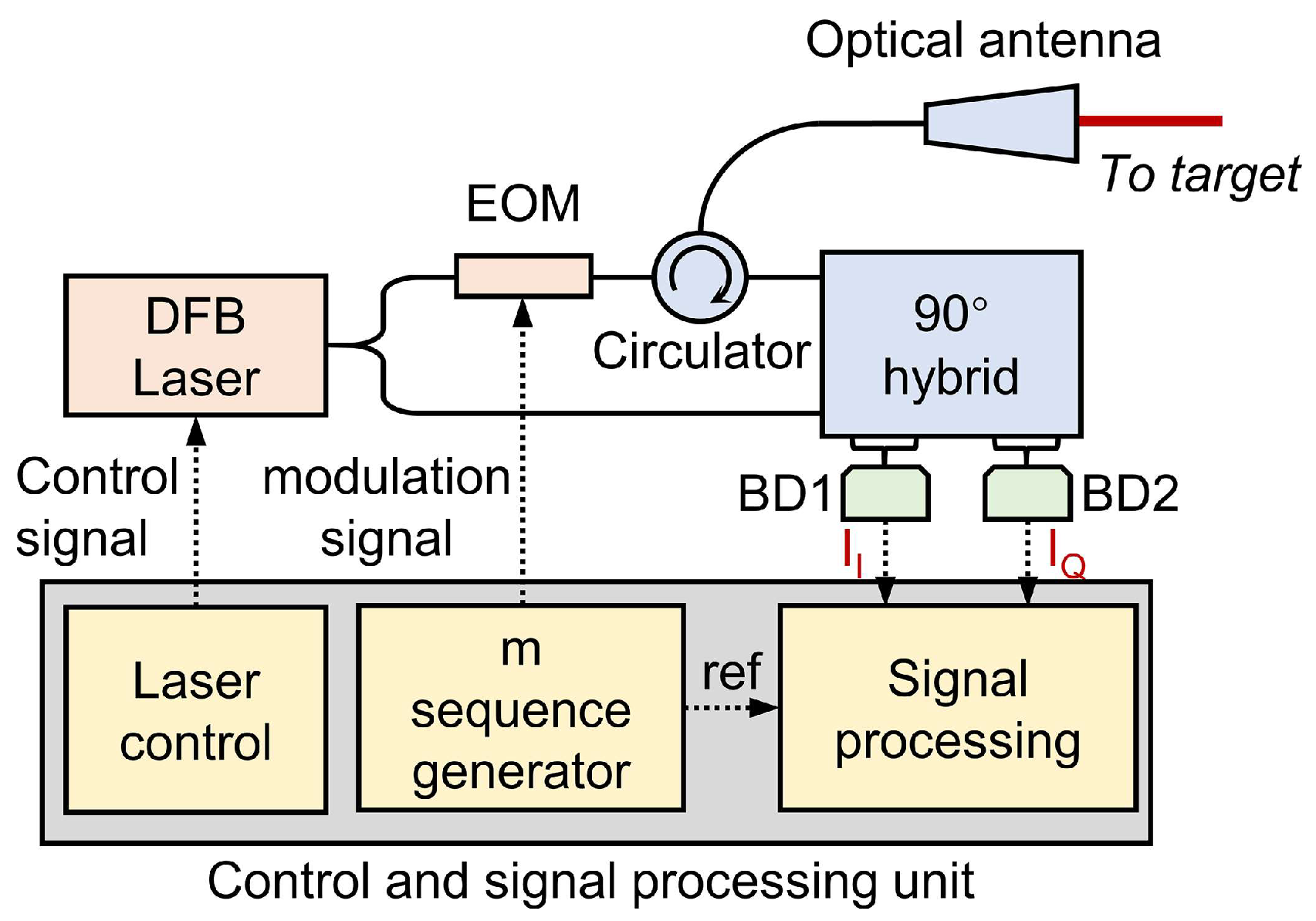
2.1. Coherent Detection with LD-PRPM
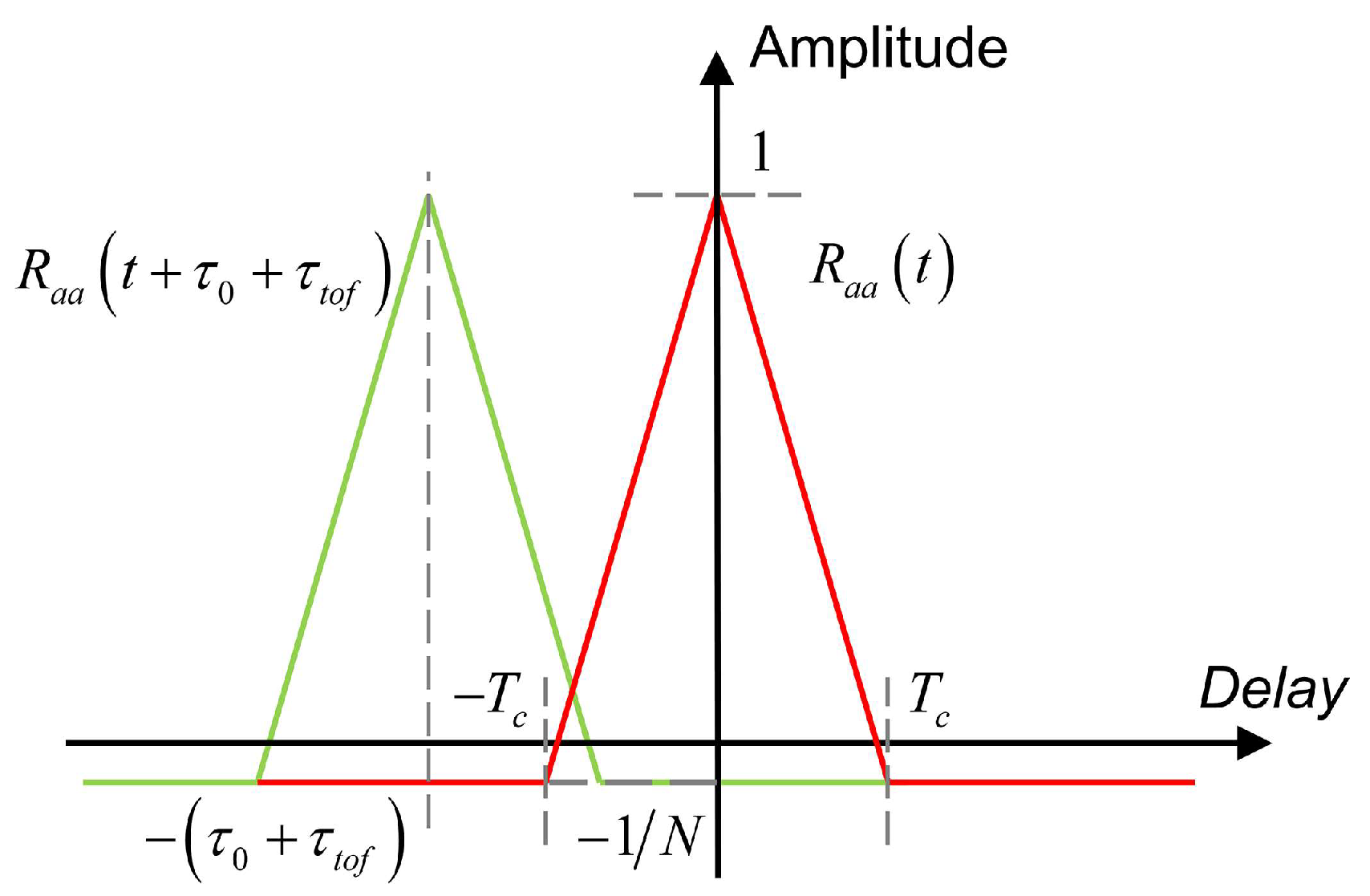
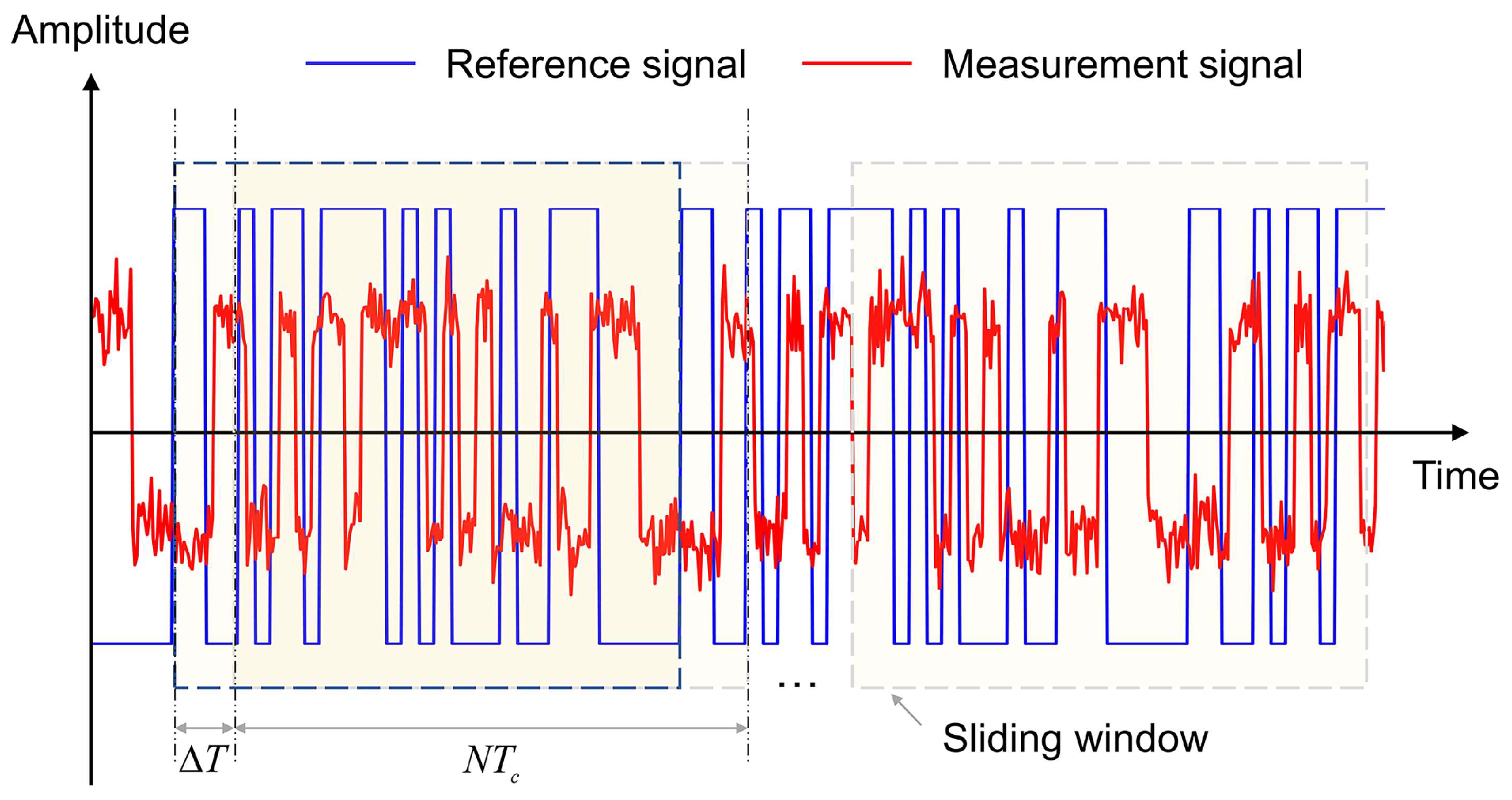
2.2. Sliding Window Analysis
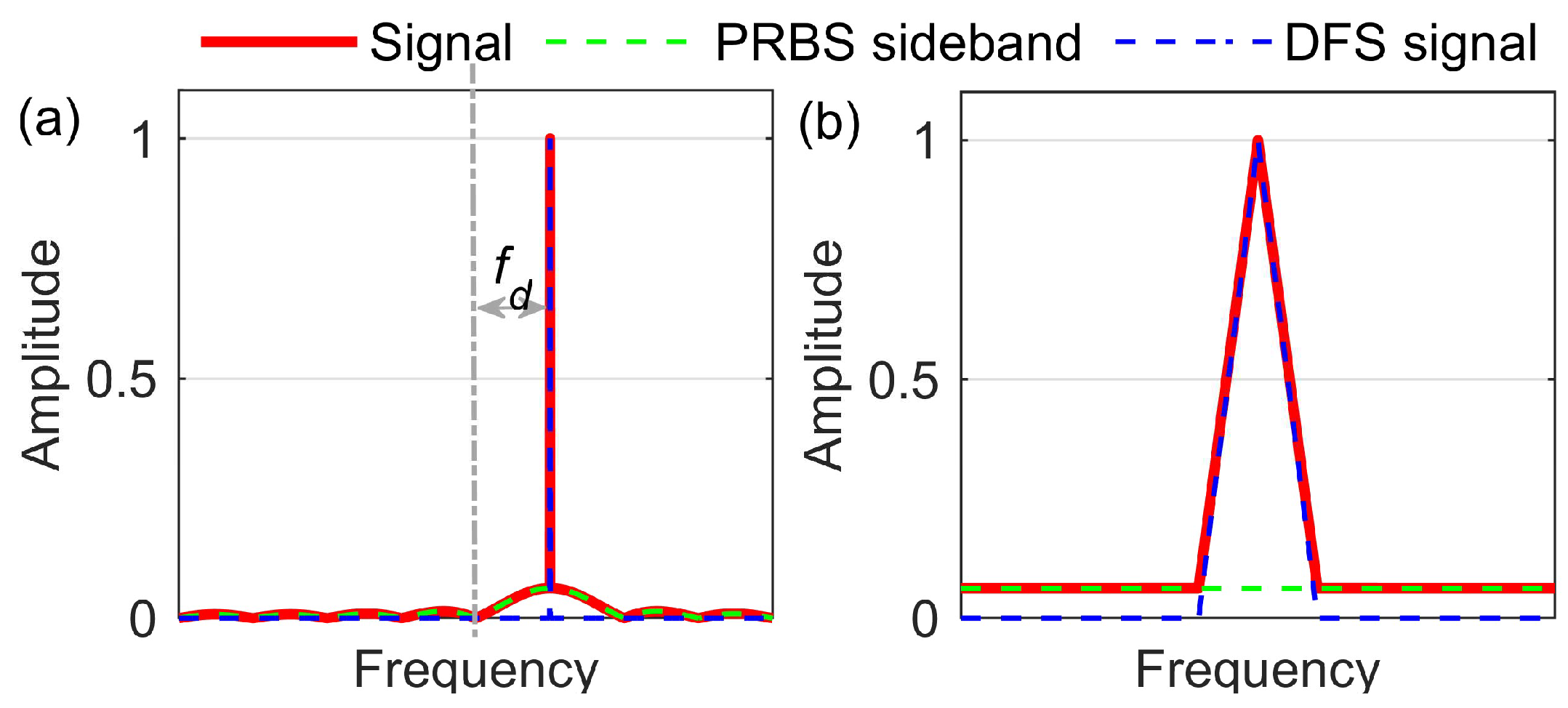
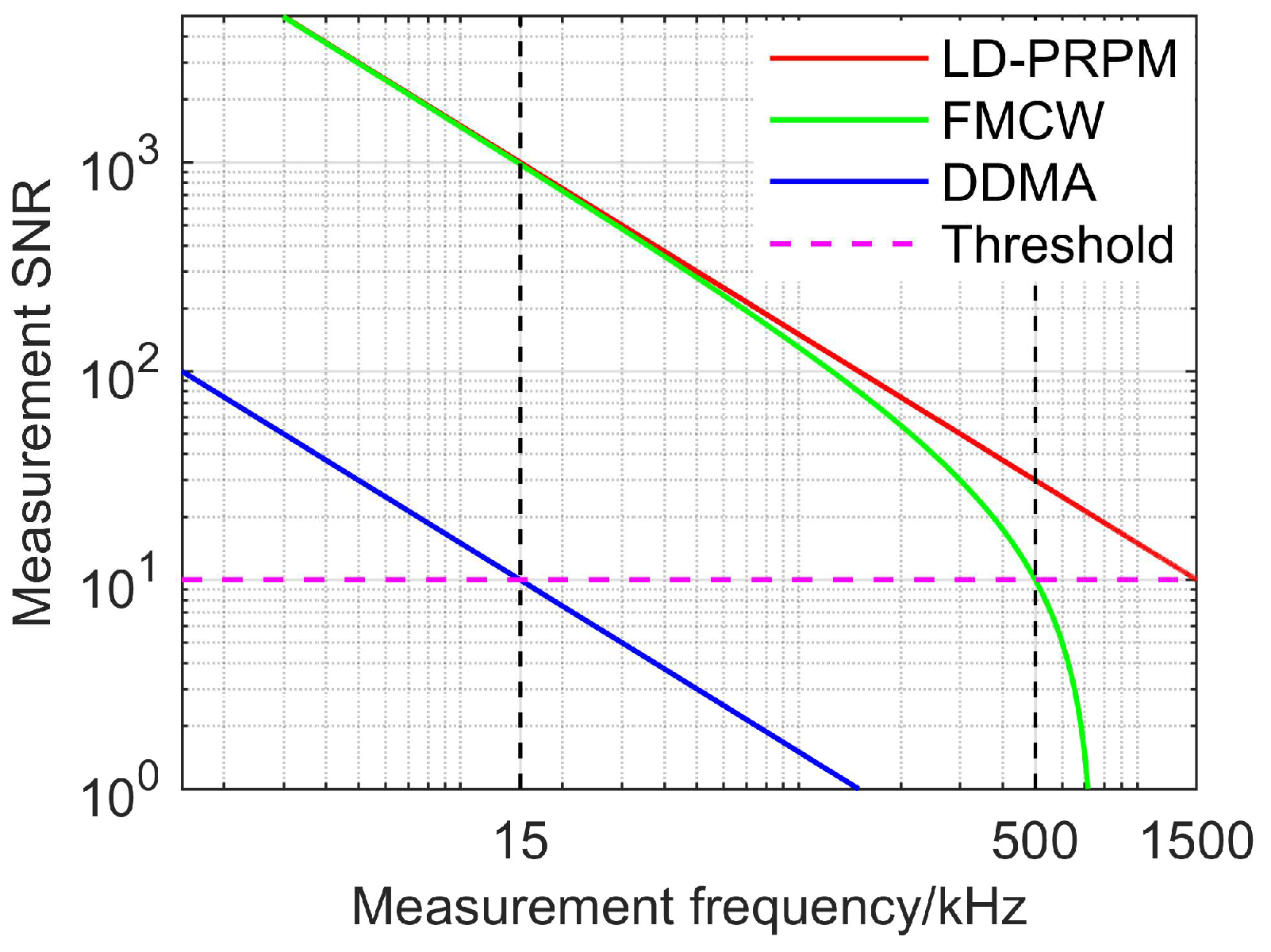
3. Comparisons
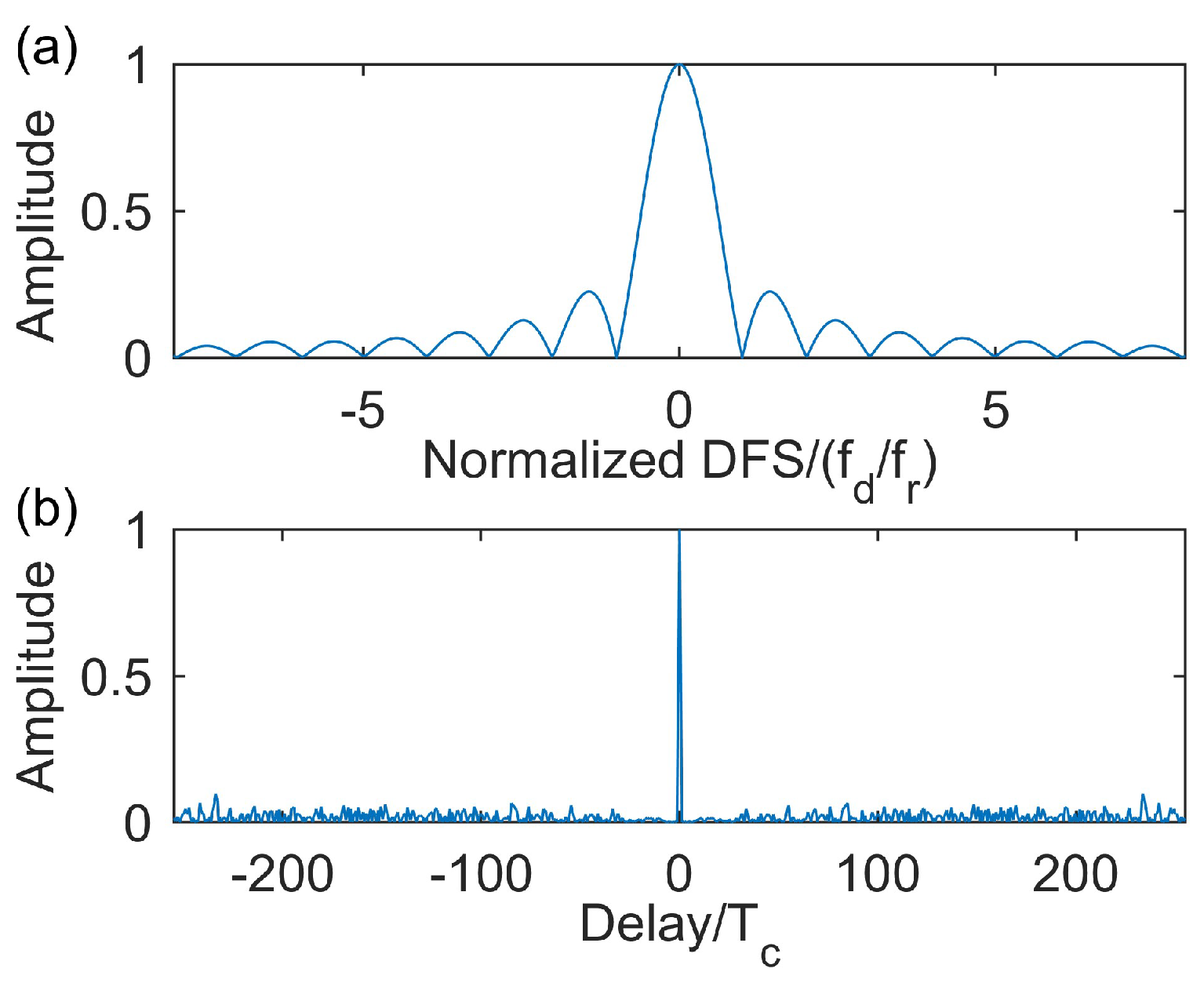
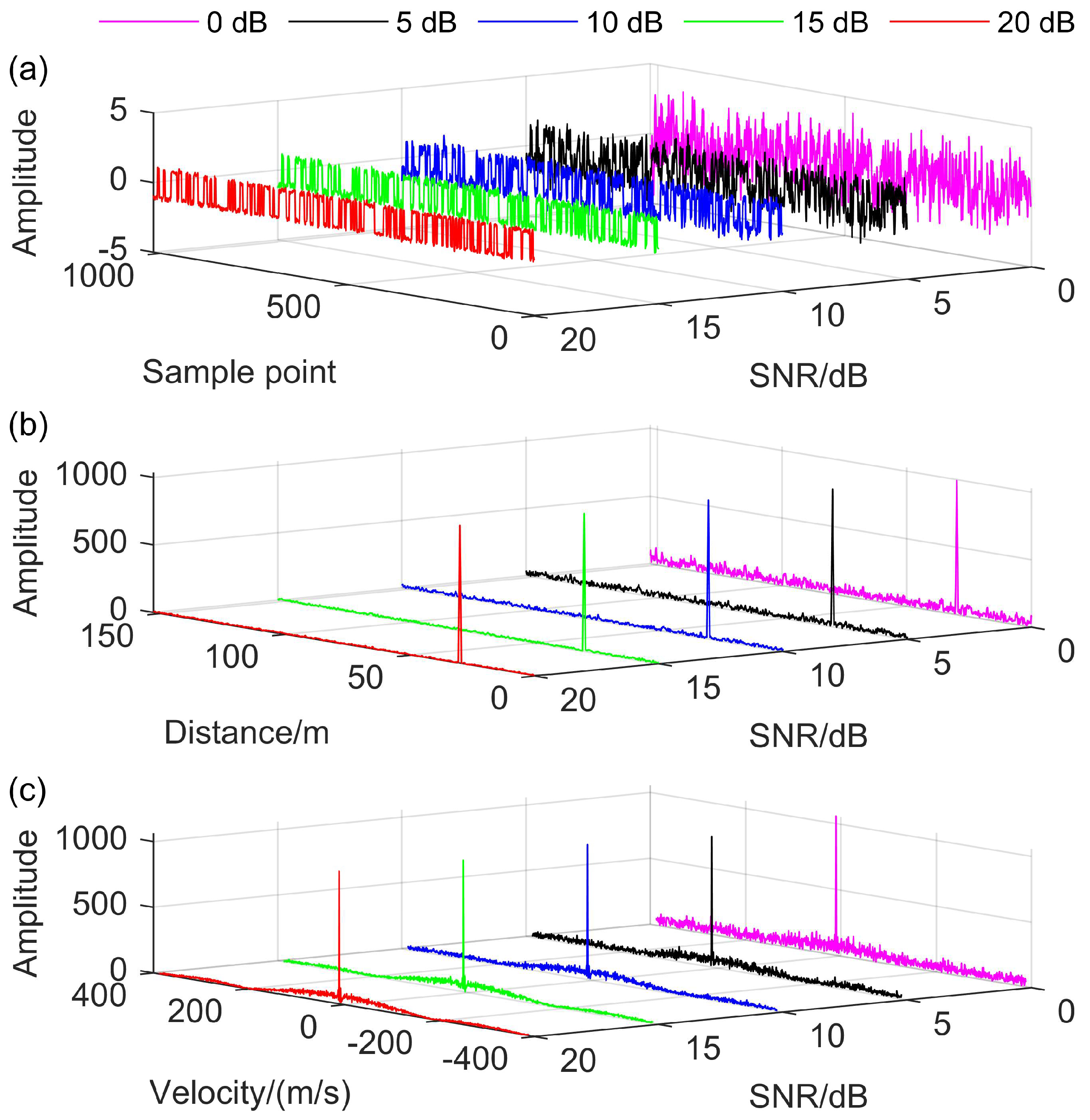
4. Simulations
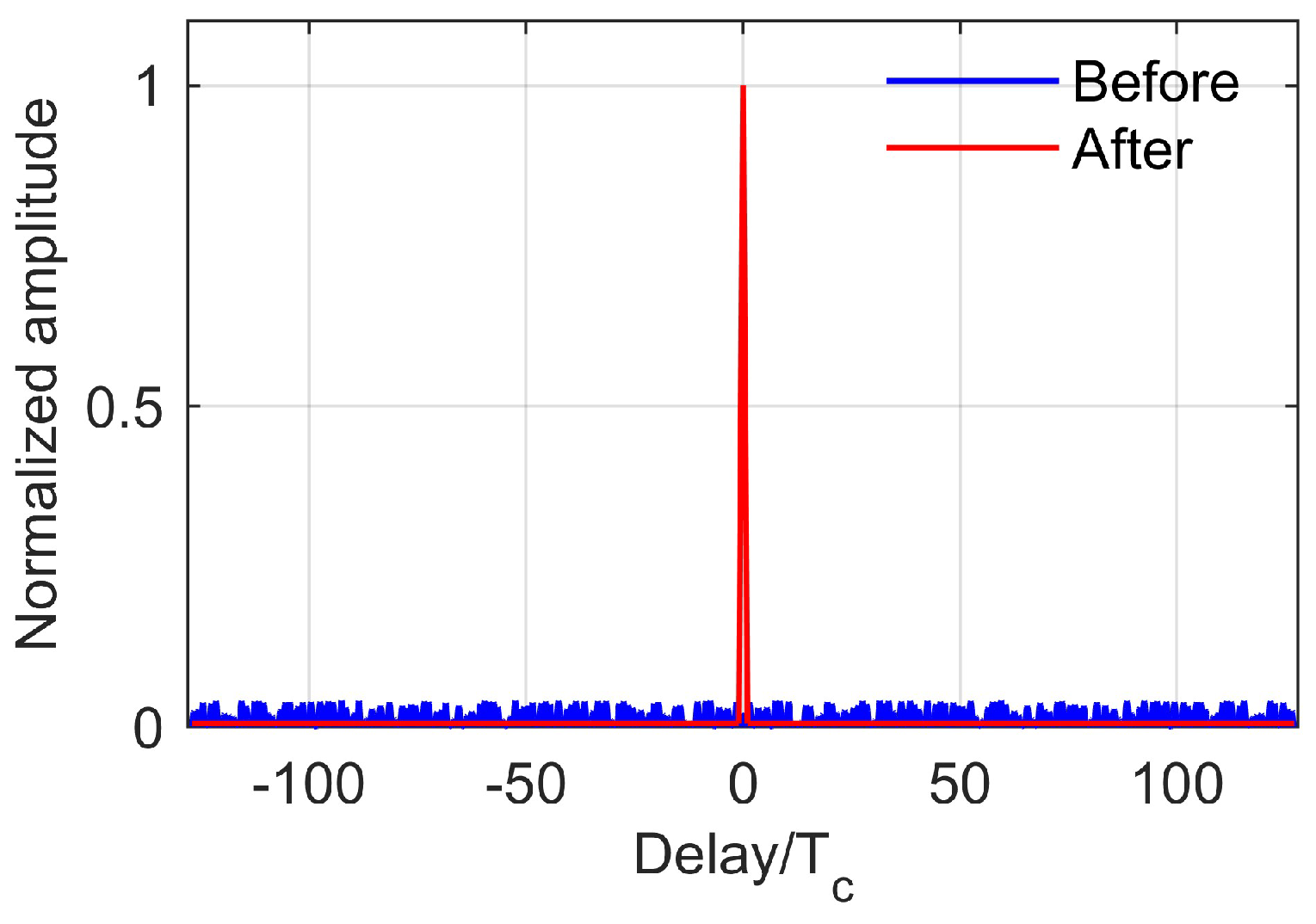
4.1. Coherent Detection with LD-PRPM
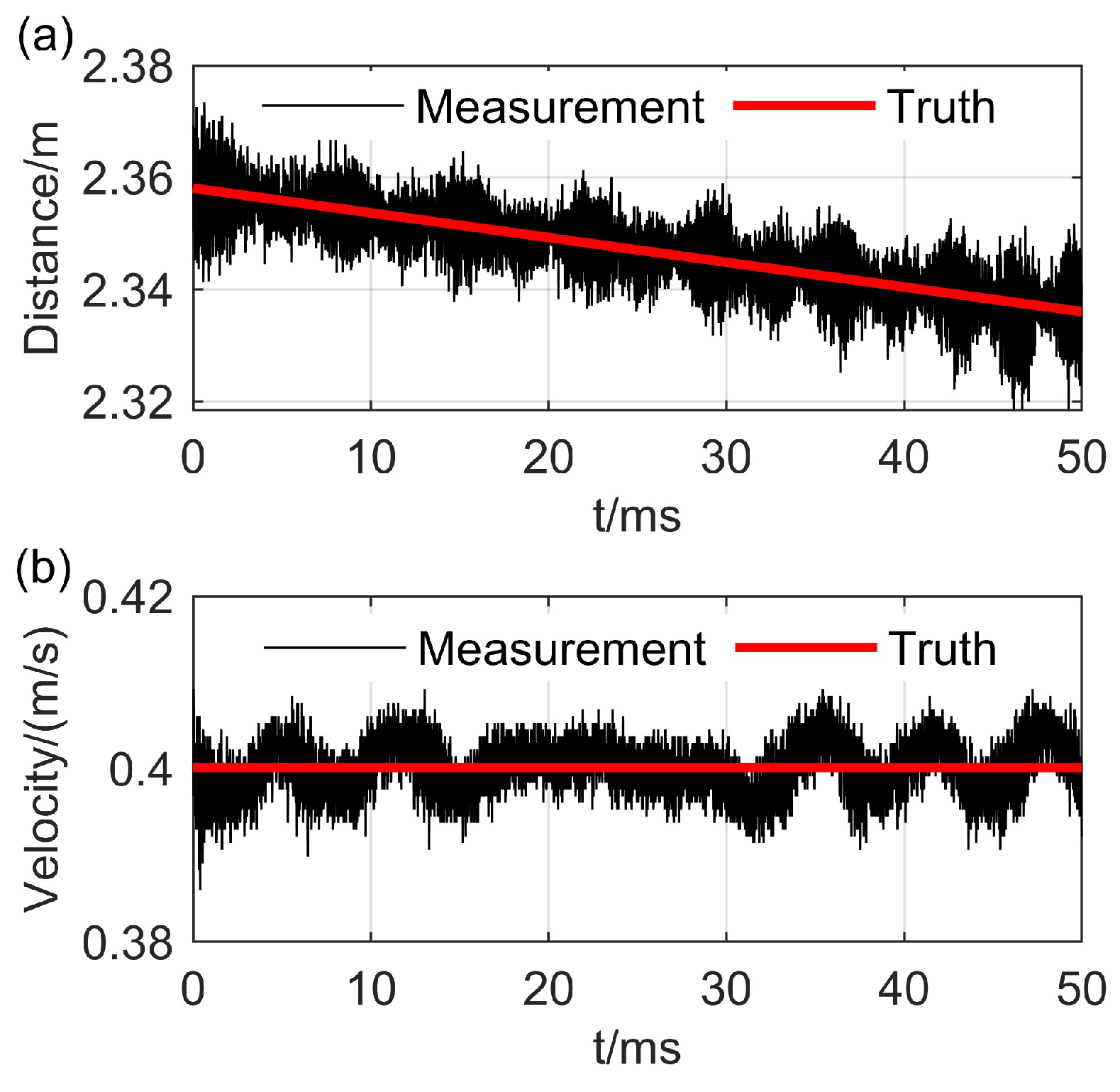
4.2. Sliding Window Analysis
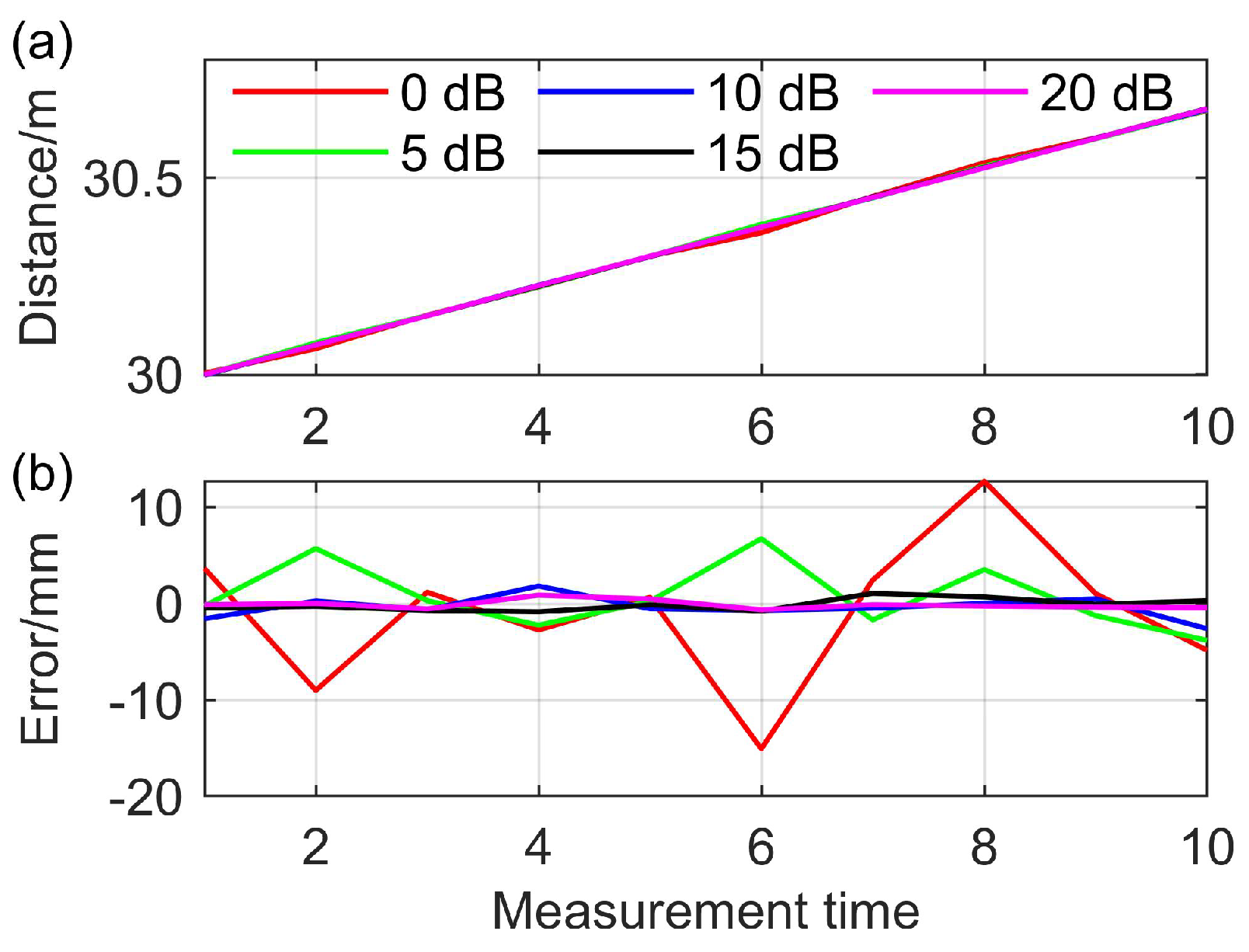
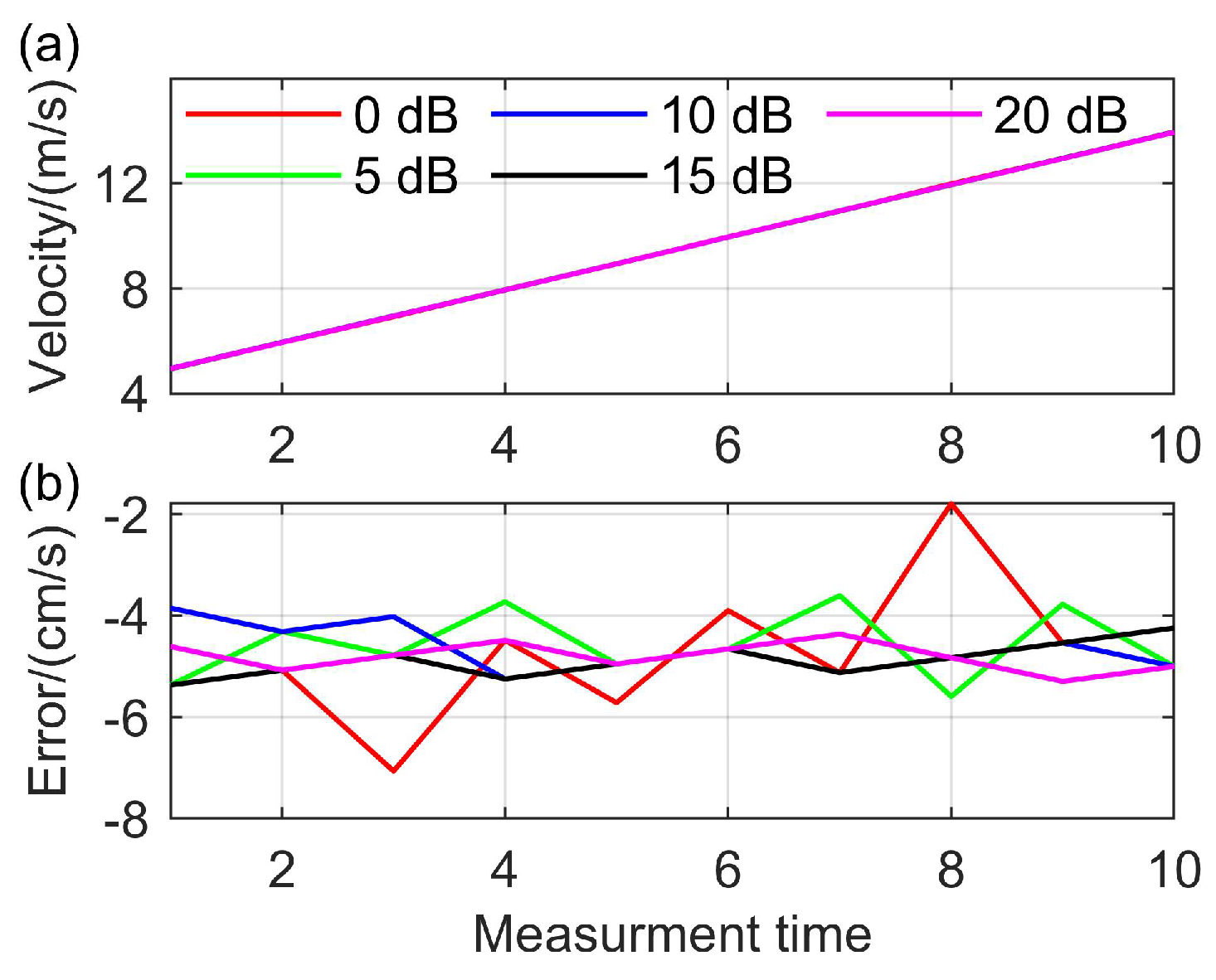
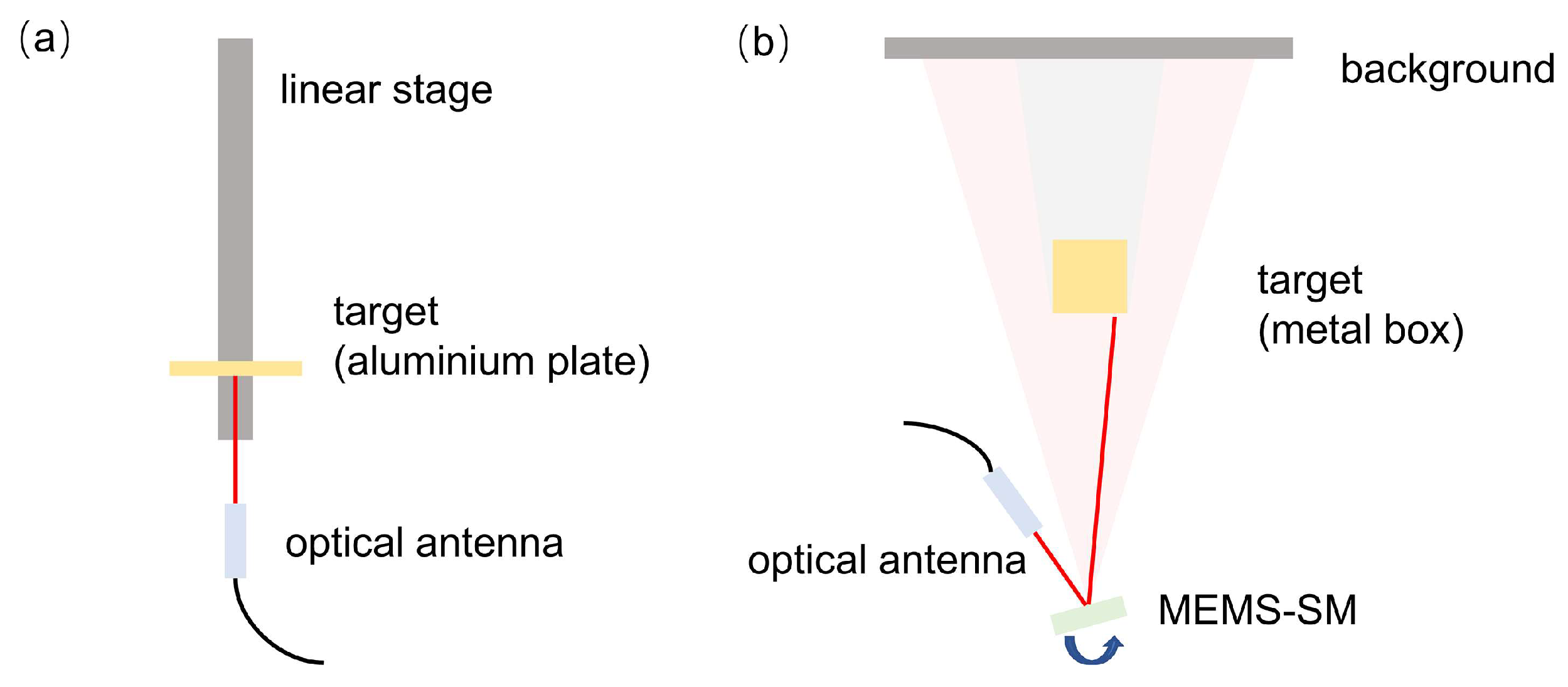
5. Experiments
5.1. Coherent Detection with LD-PRPM
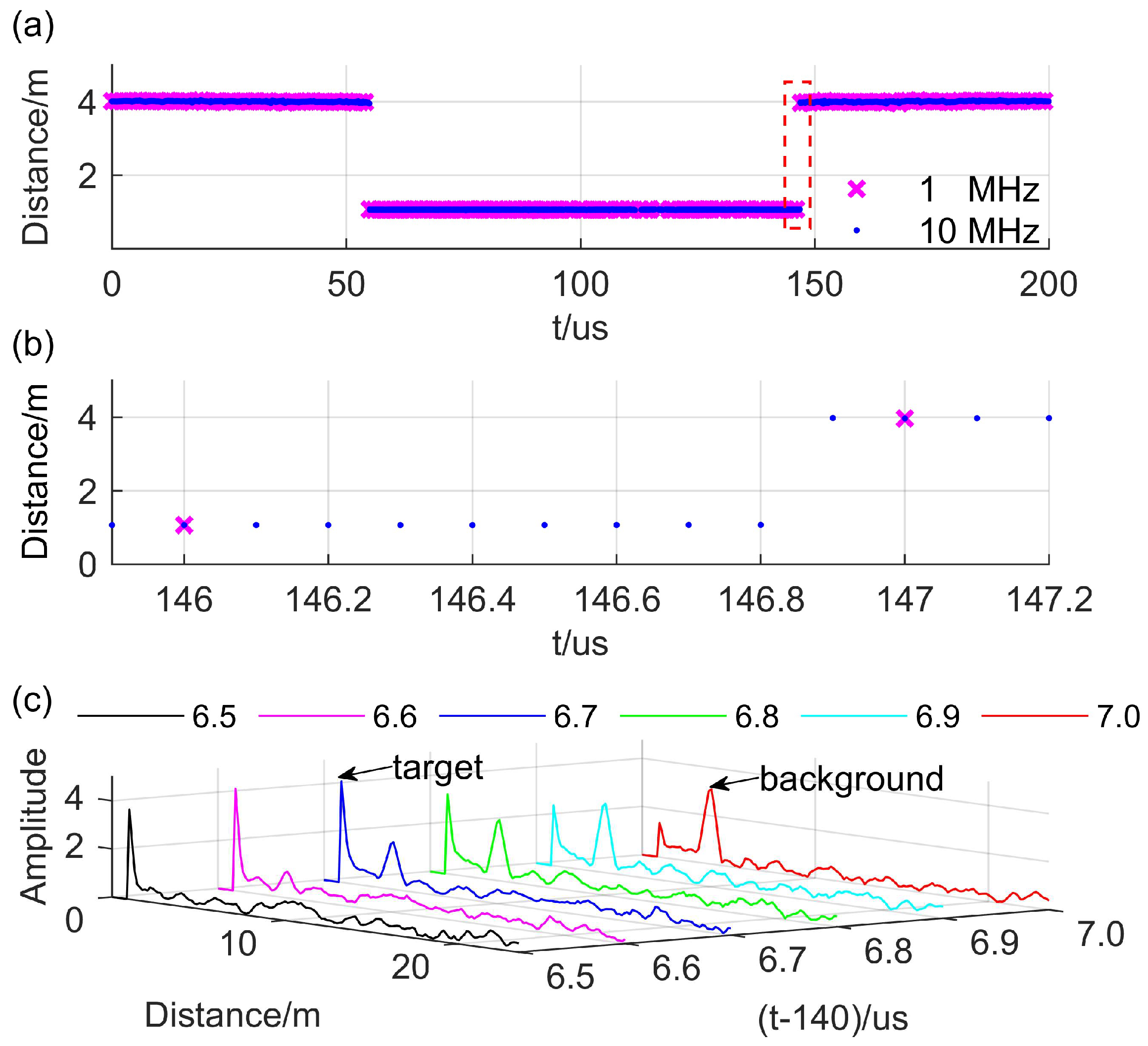
5.2. Sliding Window Analysis
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lukashchuk, A.; Riemensberger, J.; Karpov, M.; Liu, J.; Kippenberg, T.J. Dual Chirped Microcomb Based Parallel Ranging at Megapixel-Line Rates. Nat. Commun. 2022, 13, 3280. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Karpf, S.; Jalali, B. Time-Stretch LiDAR as a Spectrally Scanned Time-of-Flight Ranging Camera. Nat. Photonics 2020, 14, 14–18. [Google Scholar] [CrossRef]
- Riemensberger, J.; Lukashchuk, A.; Karpov, M.; Weng, W.; Lucas, E.; Liu, J.; Kippenberg, T.J. Massively Parallel Coherent Laser Ranging Using a Soliton Microcomb. Nature 2020, 581, 164–170. [Google Scholar] [CrossRef]
- Bastos, D.; Brandao, A.; Lorences-Riesgo, A.; Monteiro, P.P.; Oliveira, A.S.R.; Pereira, D.; Olyaei, H.Z.; Drummond, M.V. Time-Frequency Range Estimation Method for Pulsed LiDAR. IEEE Trans. Veh. Technol. 2023, 72, 1429–1437. [Google Scholar] [CrossRef]
- Park, Y.; Kim, G. LIDAR Pulse Coding for High Resolution Range Imaging at Improved Refresh Rate. Opt. Express 2016, 24, 23810–23828. [Google Scholar] [CrossRef]
- Kim, G.; Eom, J.; Park, Y. Concurrent Transmitting LiDAR Sensor with Bipolar Optical Codes. In Proceedings of the Wireless Telecommunications Symposium, Boston, MA, USA, 24 May 2023. [Google Scholar]
- Wang, J.; Zhang, G.; You, Z. High-Resolution LiDAR Using Random Modulated Continuous Wave with a Low Code Rate. Measurement 2022, 202, 111719. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, G.; You, Z. Improved Sampling Scheme for LiDAR in Lissajous Scanning Mode. Microsyst. Nanoeng. 2022, 8, 64. [Google Scholar] [CrossRef]
- Li, Z.-P.; Ye, J.-T.; Huang, X.; Jiang, P.-Y.; Cao, Y.; Hong, Y.; Yu, C.; Zhang, J.; Zhang, Q.; Peng, C.-Z.; et al. Single-Photon Imaging over 200 Km. Optica 2021, 8, 344–349. [Google Scholar] [CrossRef]
- Lihachev, G.; Riemensberger, J.; Weng, W.; Liu, J.; Tian, H.; Siddharth, A.; Snigirev, V.; Shadymov, V.; Voloshin, A.; Wang, R.N.; et al. Low-Noise Frequency-Agile Photonic Integrated Lasers for Coherent Ranging. Nat. Commun. 2022, 13, 1–10. [Google Scholar] [CrossRef]
- Snigirev, V.; Riedhauser, A.; Lihachev, G.; Churaev, M.; Riemensberger, J.; Wang, R.N.; Siddharth, A.; Huang, G.; Möhl, C.; Popoff, Y.; et al. Ultrafast Tunable Lasers Using Lithium Niobate Integrated Photonics. Nature 2023, 615, 411–417. [Google Scholar] [CrossRef]
- Li, M.; Chang, L.; Wu, L.; Staffa, J.; Ling, J.; Javid, U.A.; Xue, S.; He, Y.; Lopez-rios, R.; Morin, T.J.; et al. Integrated Pockels Laser. Nat. Commun. 2022, 13, 5344. [Google Scholar] [CrossRef] [PubMed]
- Behroozpour, B.; Sandborn, P.A.M.; Quack, N.; Seok, T.J.; Matsui, Y.; Wu, M.C.; Boser, B.E. Electronic-Photonic Integrated Circuit for 3D Microimaging. IEEE J. Solid-State Circuits 2017, 52, 161–172. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Y.; Yao, J. Rapid Linear Frequency Swept Frequency-Modulated Continuous Wave Laser Source Using Iterative Pre-Distortion Algorithm. Remote Sens. 2022, 14, 3455. [Google Scholar] [CrossRef]
- Jiang, S.; Liu, B.; Wang, H. FMCW Laser Ranging Method Based on a Frequency Multiplier. Appl. Opt. 2021, 60, 918. [Google Scholar] [CrossRef]
- Zhang, X.; Pouls, J.; Wu, M.C. Laser Frequency Sweep Linearization by Iterative Learning Pre-Distortion for FMCW LiDAR. Opt. Express 2019, 27, 9965. [Google Scholar] [CrossRef]
- Cheng, X.; Liu, J.; Zhang, Y.; Zhang, F.; Qu, X. Simultaneous Measurement of Distance and Speed via Frequency-Modulated Continuous-Wave LIDAR System Based on H13C14N Gas Cell. Opt. Lasers Eng. 2022, 159, 107193. [Google Scholar] [CrossRef]
- Qian, R.; Zhou, K.C.; Zhang, J.; Viehland, C.; Dhalla, A.H.; Izatt, J.A. Video-Rate High-Precision Time-Frequency Multiplexed 3D Coherent Ranging. Nat. Commun. 2022, 13, 1476. [Google Scholar] [CrossRef]
- Yang, H.J.; Deibel, J.; Nyberg, S.; Riles, K. High-Precision Absolute Distance and Vibration Measurement with Frequency Scanned Interferometry. Appl. Opt. 2005, 44, 3937–3944. [Google Scholar] [CrossRef]
- Martinez, J.J.; Campbell, M.A.; Warden, M.S.; Hughes, E.B.; Copner, N.J.; Lewis, A.J. Dual-Sweep Frequency Scanning Interferometry Using Four Wave Mixing. IEEE Photonics Technol. Lett. 2015, 27, 733–736. [Google Scholar] [CrossRef]
- Xu, Z.; Tang, L.; Zhang, H.; Pan, S. Simultaneous Real-Time Ranging and Velocimetry via a Dual-Sideband Chirped Lidar. IEEE Photonics Technol. Lett. 2017, 29, 2254–2257. [Google Scholar] [CrossRef]
- Cheng, L.; Ziyi, X.; Guodong, L.; Bingguo, L.; Binghui, L. FSI Combined with Heterodyne Interferometer for Non-Cooperative Targets Distance Measurement. IEEE Photonics Technol. Lett. 2022, 34, 85–88. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Z.; Tian, K.; Zhang, H. Frequency-Scanning Interferometry for Dynamic Measurement Using Adaptive Sage-Husa Kalman Filter. Opt. Lasers Eng. 2023, 165, 107545. [Google Scholar] [CrossRef]
- Trocha, P.; Karpov, M.; Ganin, D.; Pfeiffer, M.H.P.; Kordts, A.; Wolf, S.; Krockenberger, J.; Marin-Palomo, P.; Weimann, C.; Randel, S.; et al. Ultrafast Optical Ranging Using Microresonator Soliton Frequency Combs. Science 2018, 359, 887–891. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Shu, H.; Shen, B.; Chang, L.; Xie, W.; Liao, W.; Tao, Z.; Bowers, J.E.; Wang, X. Breaking the Temporal and Frequency Congestion of LiDAR by Parallel Chaos. Nat. Photonics 2023, 17, 306–314. [Google Scholar] [CrossRef]
- Lukashchuk, A.; Riemensberger, J.; Tusnin, A.; Liu, J.; Kippenberg, T.J. Chaotic Microcomb-Based Parallel Ranging. Nat. Photonics 2023, 17, 814–821. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, K.; Zhang, H.; Pan, S. Multifunction Lidar System Based on Polarization-Division Multiplexing. J. Light. Technol. 2019, 37, 2000–2007. [Google Scholar] [CrossRef]
- Esteban, J.J.; García, A.F.; Barke, S.; Peinado, A.M.; Cervantes, F.G.; Bykov, I.; Heinzel, G.; Danzmann, K. Experimental Demonstration of Weak-Light Laser Ranging and Data Communication for LISA. Opt. Express 2011, 19, 15937–15946. [Google Scholar] [CrossRef]
- Albuquerque, D.F.; Vieira, J.M.N.; Lopes, S.I.; Aguilera, T.; Álvarez, F.J. Doppler Resilient Modulation in a Cdma-Based Acoustic Local Positioning System. In Proceedings of the 2016 International Conference on Indoor Positioning and Indoor Navigation IPIN, Alcala de Henares, Spain, 4–7 October 2016. [Google Scholar]
- Zhang, Y.; Wu, Y.; Xia, H. Spatial Resolution Enhancement of Coherent Doppler Lidar by Pseudo-Random Phase Coding. J. Light. Technol. 2022, 40, 4467–4473. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Gao, B.; Liu, X.; Wang, J.; You, Z. Rapid Laser Ranging Method for Compact LiDAR Systems. Remote Sens. 2025, 17, 1002. https://doi.org/10.3390/rs17061002
Guo J, Gao B, Liu X, Wang J, You Z. Rapid Laser Ranging Method for Compact LiDAR Systems. Remote Sensing. 2025; 17(6):1002. https://doi.org/10.3390/rs17061002
Chicago/Turabian StyleGuo, Jiahui, Bo Gao, Xiaojun Liu, Junya Wang, and Zheng You. 2025. "Rapid Laser Ranging Method for Compact LiDAR Systems" Remote Sensing 17, no. 6: 1002. https://doi.org/10.3390/rs17061002
APA StyleGuo, J., Gao, B., Liu, X., Wang, J., & You, Z. (2025). Rapid Laser Ranging Method for Compact LiDAR Systems. Remote Sensing, 17(6), 1002. https://doi.org/10.3390/rs17061002






