Estimation of Forest Canopy Height Using ATLAS Data Based on Improved Optics and EEMD Algorithms
Abstract
1. Introduction
2. Study Area and Datasets
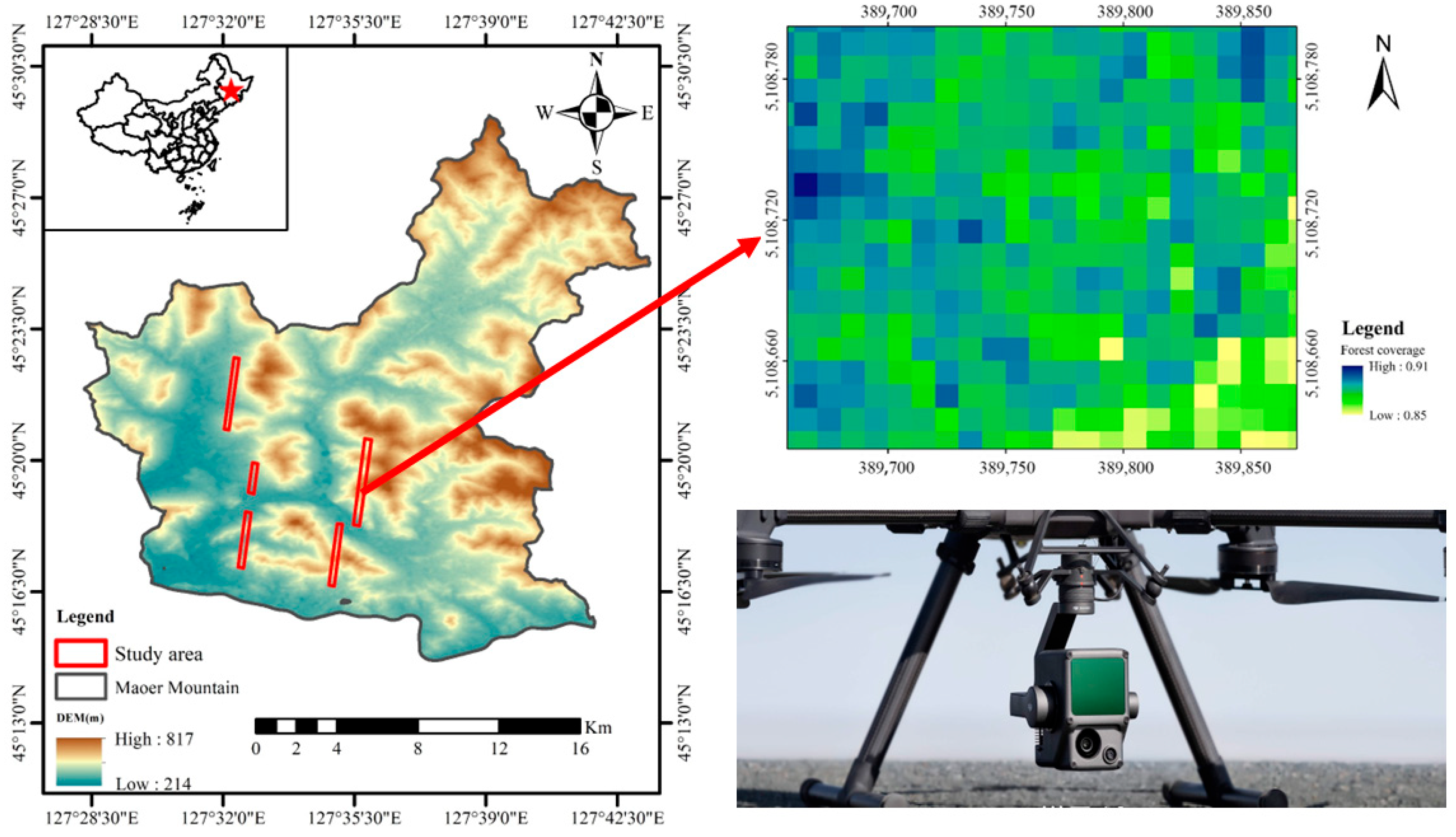
2.1. Study Area
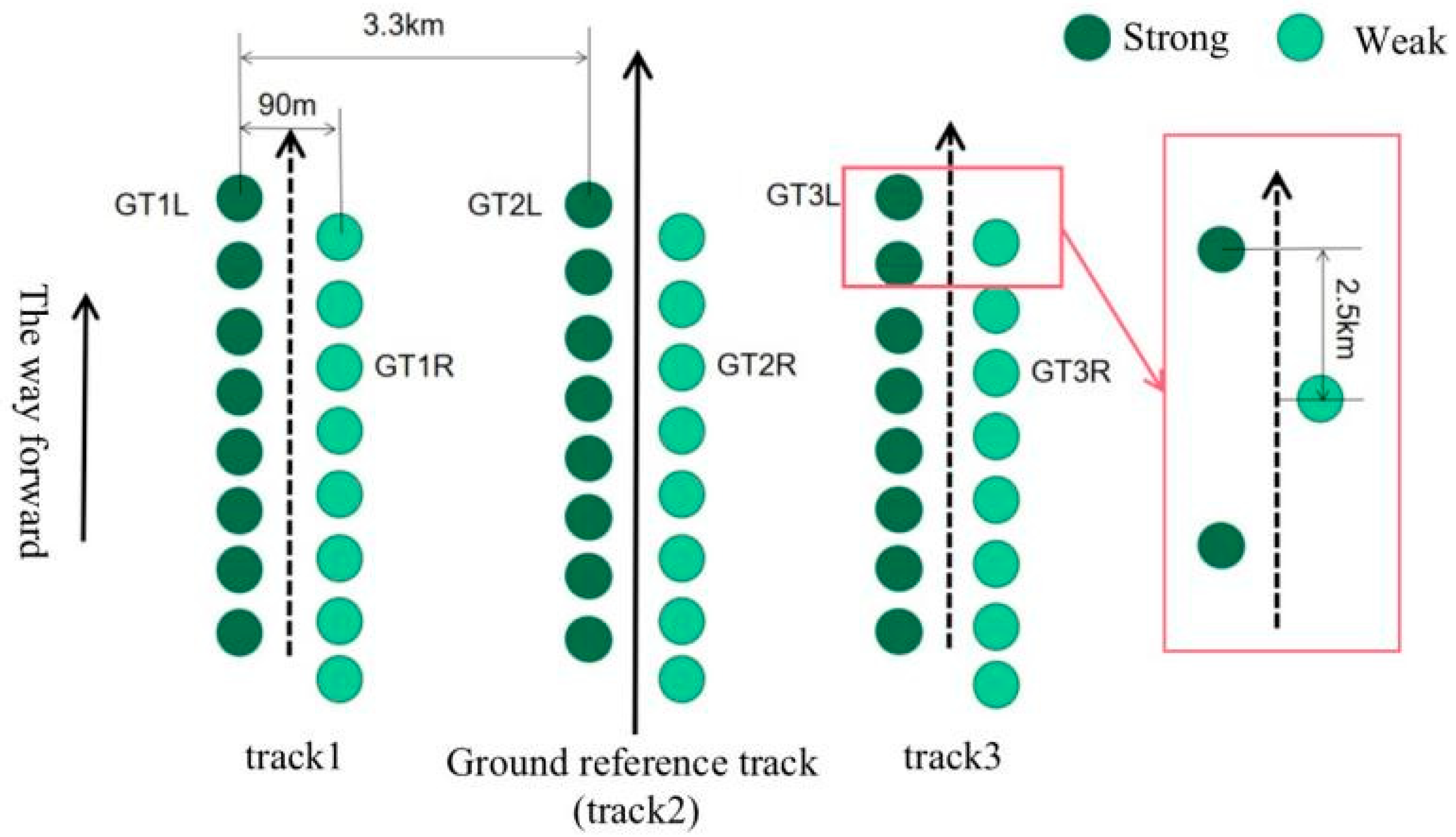
2.2. ATLAS Data
2.3. Airborne Lidar Data
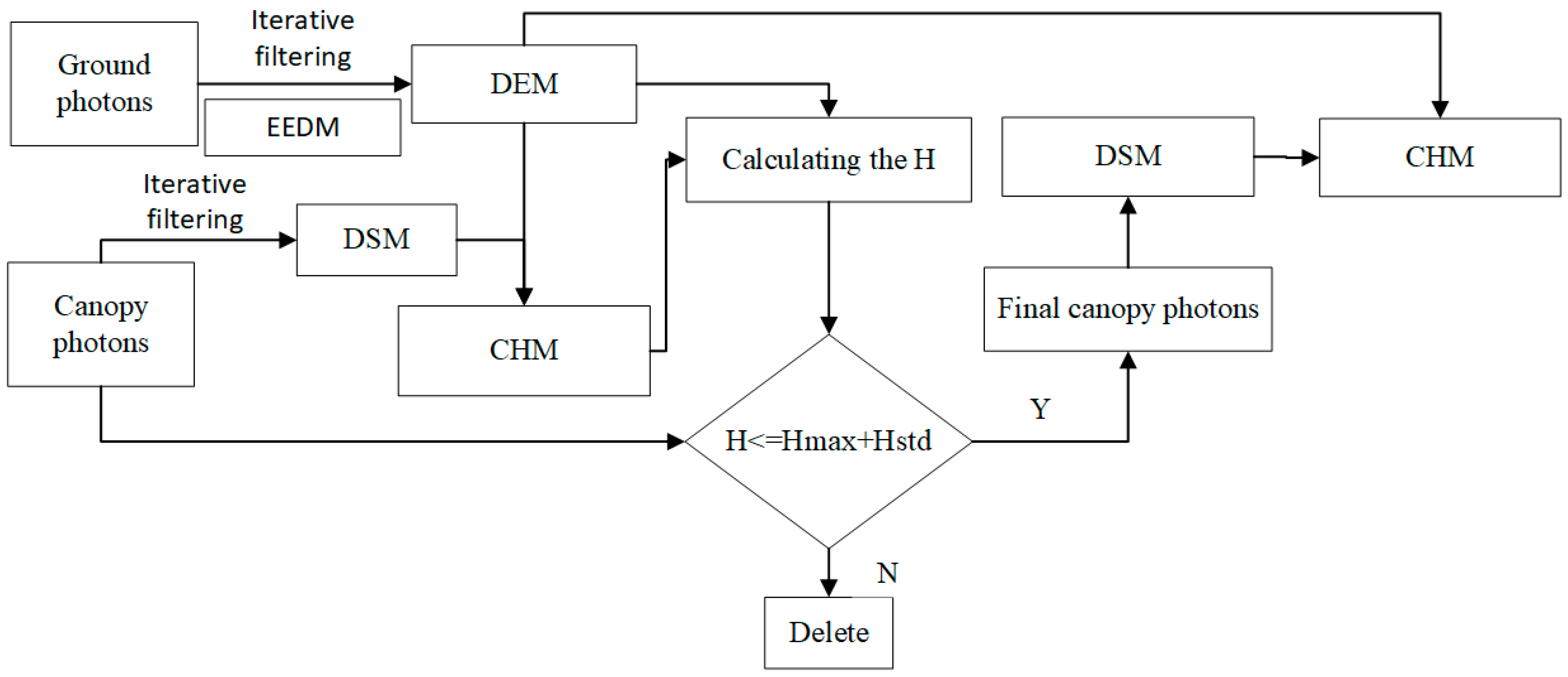
3. Methodology
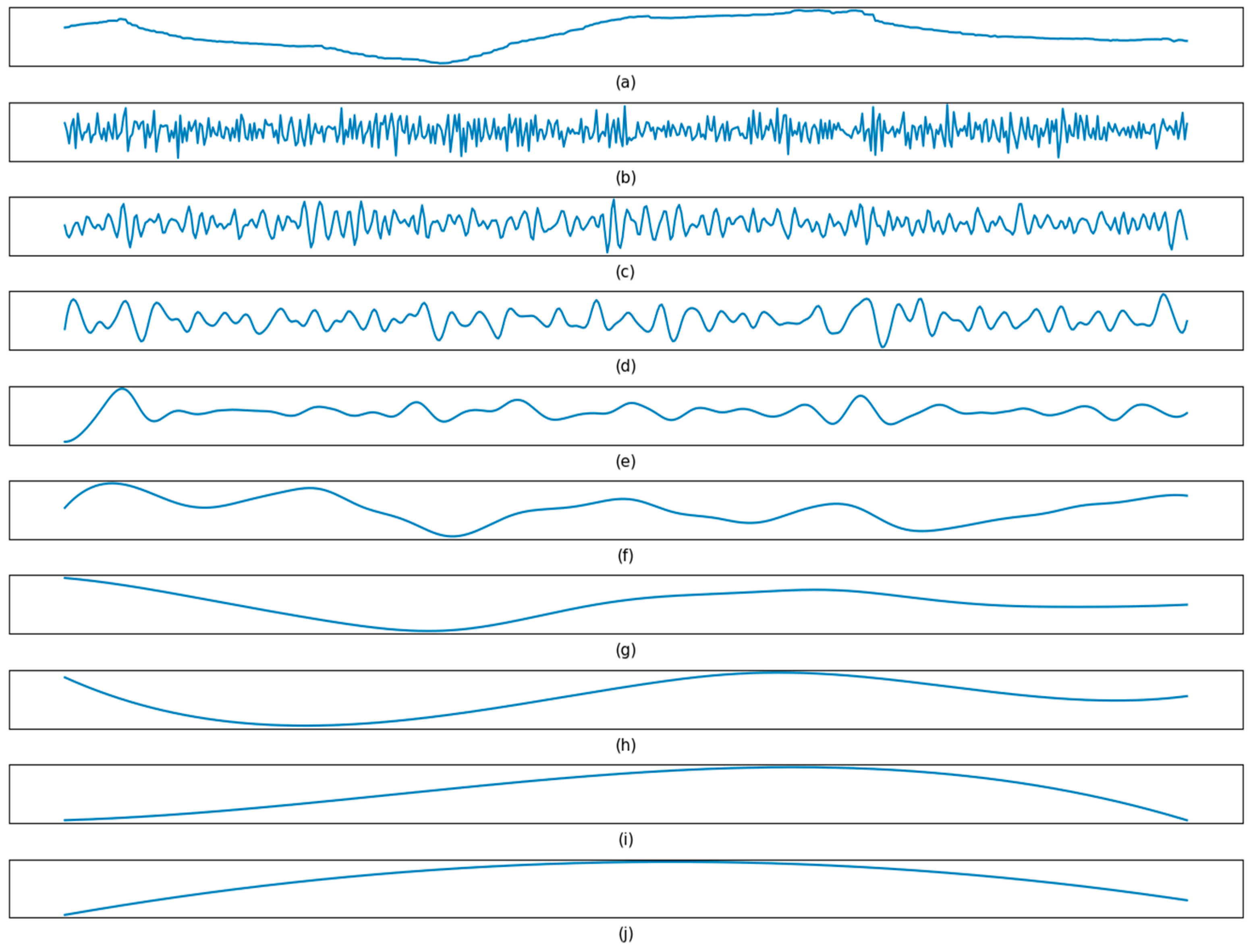
3.1. Denoising
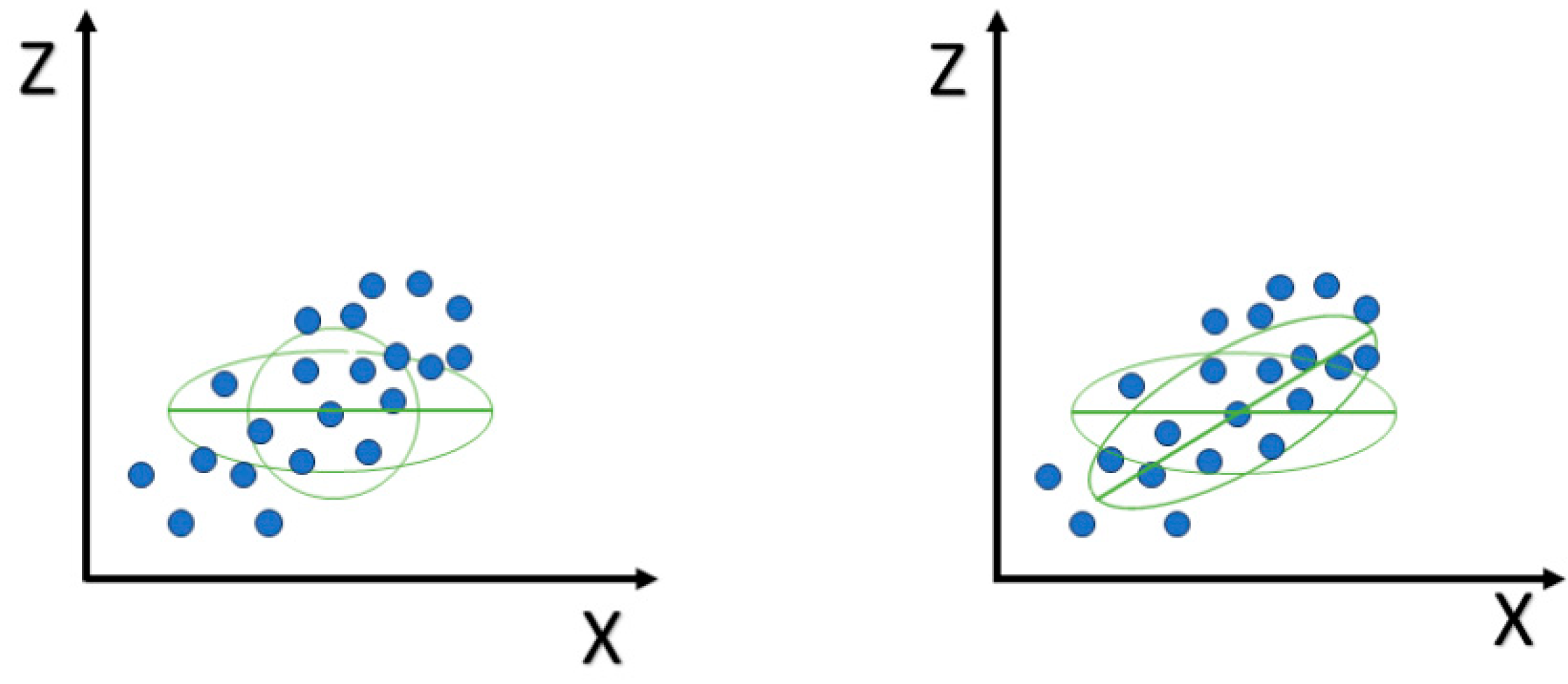
3.2. Photon Points Classification
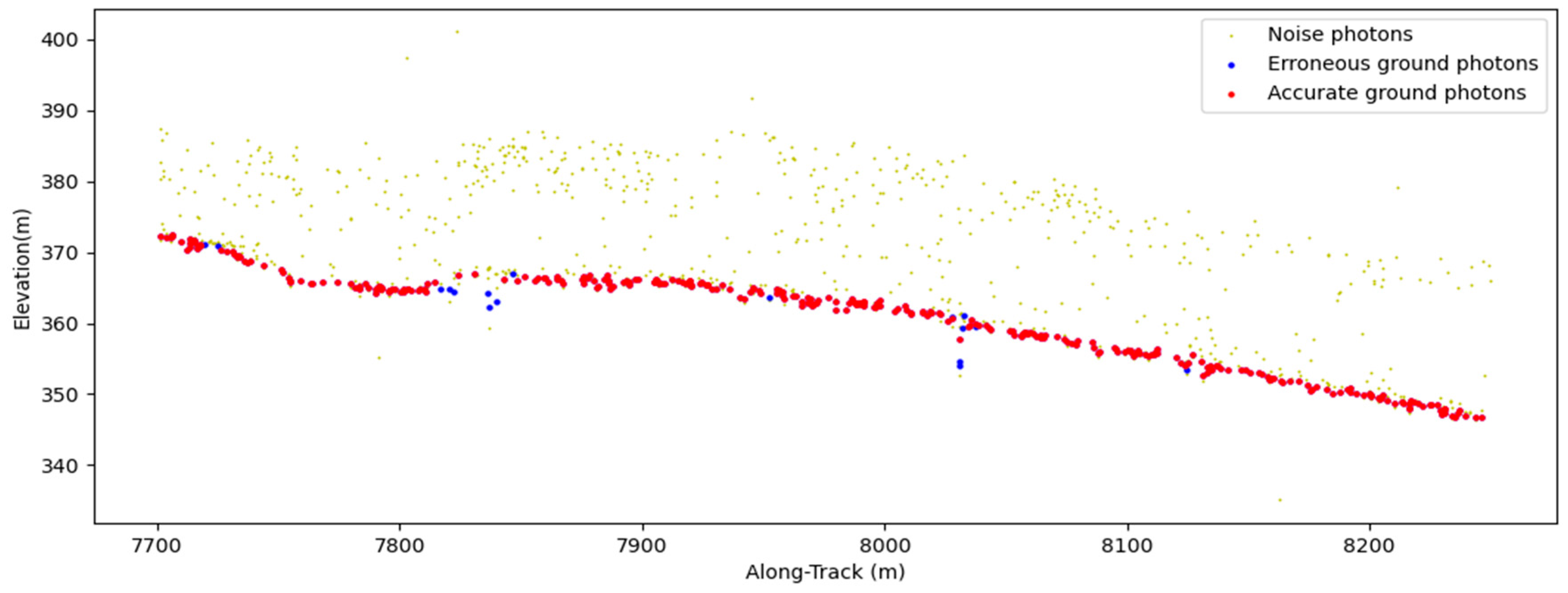
3.2.1. Classification of Ground Points
3.2.2. Classification of Canopy Points
3.3. Estimation and Verification of Canopy Height
4. Results
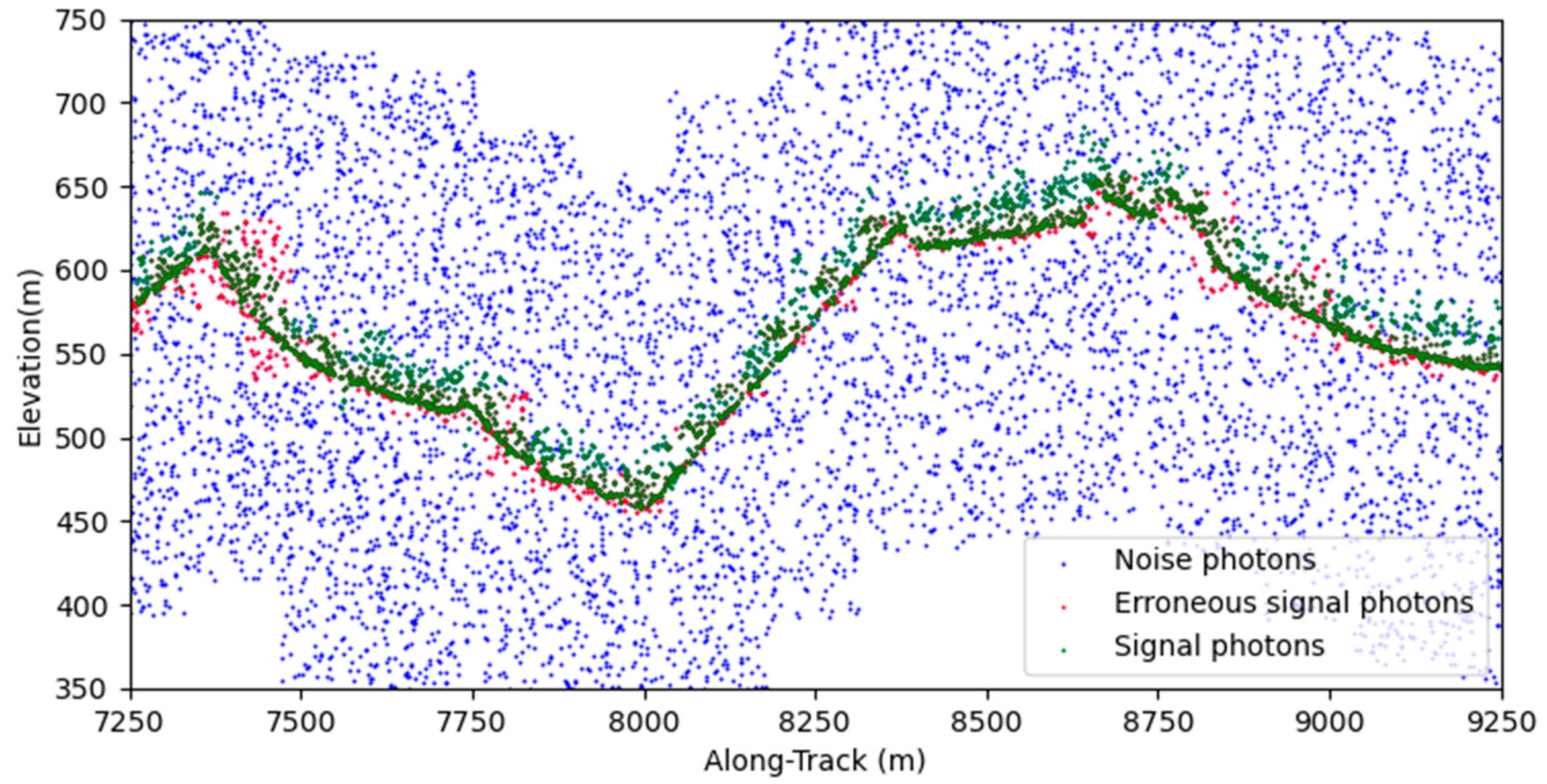
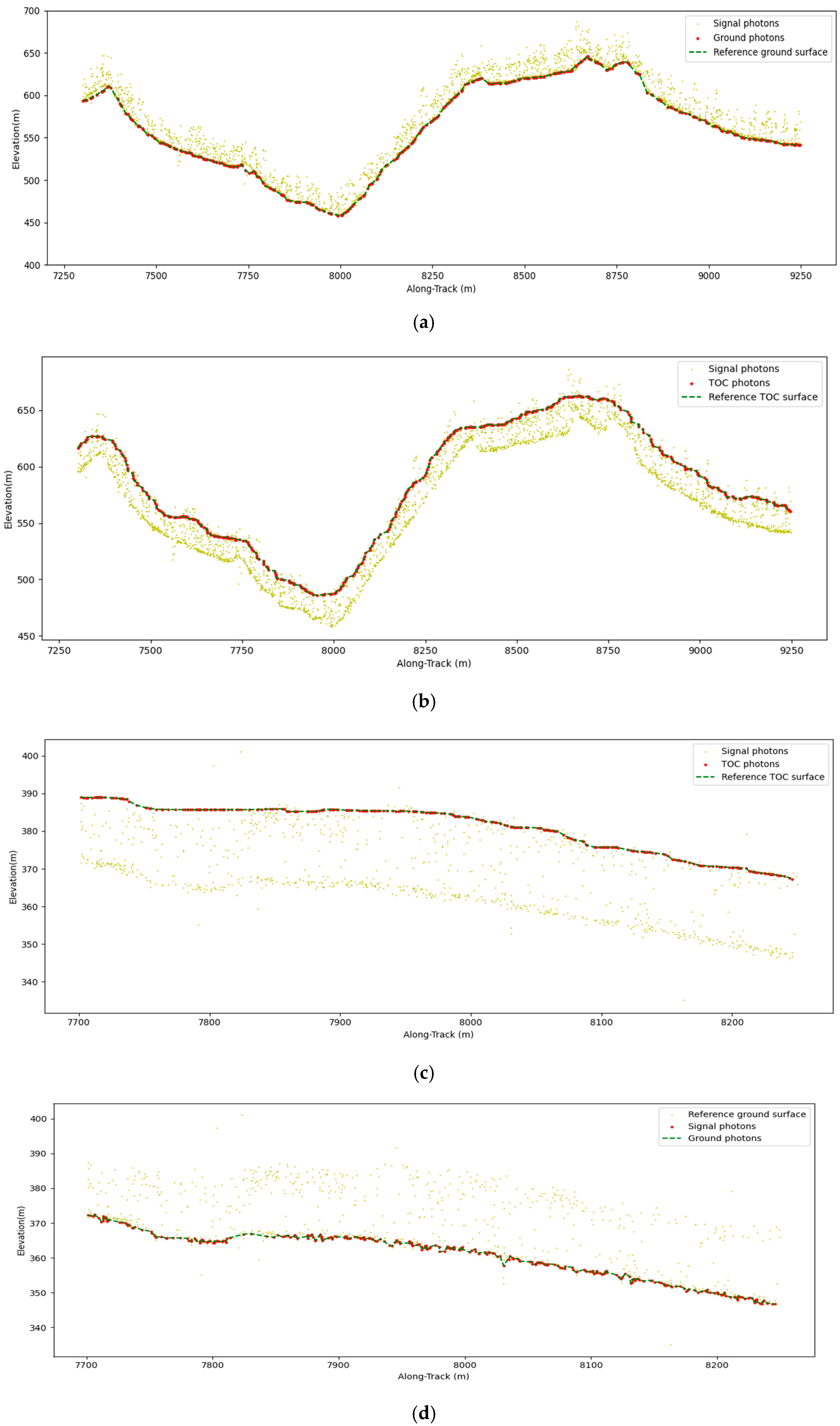
4.1. Noise Removal
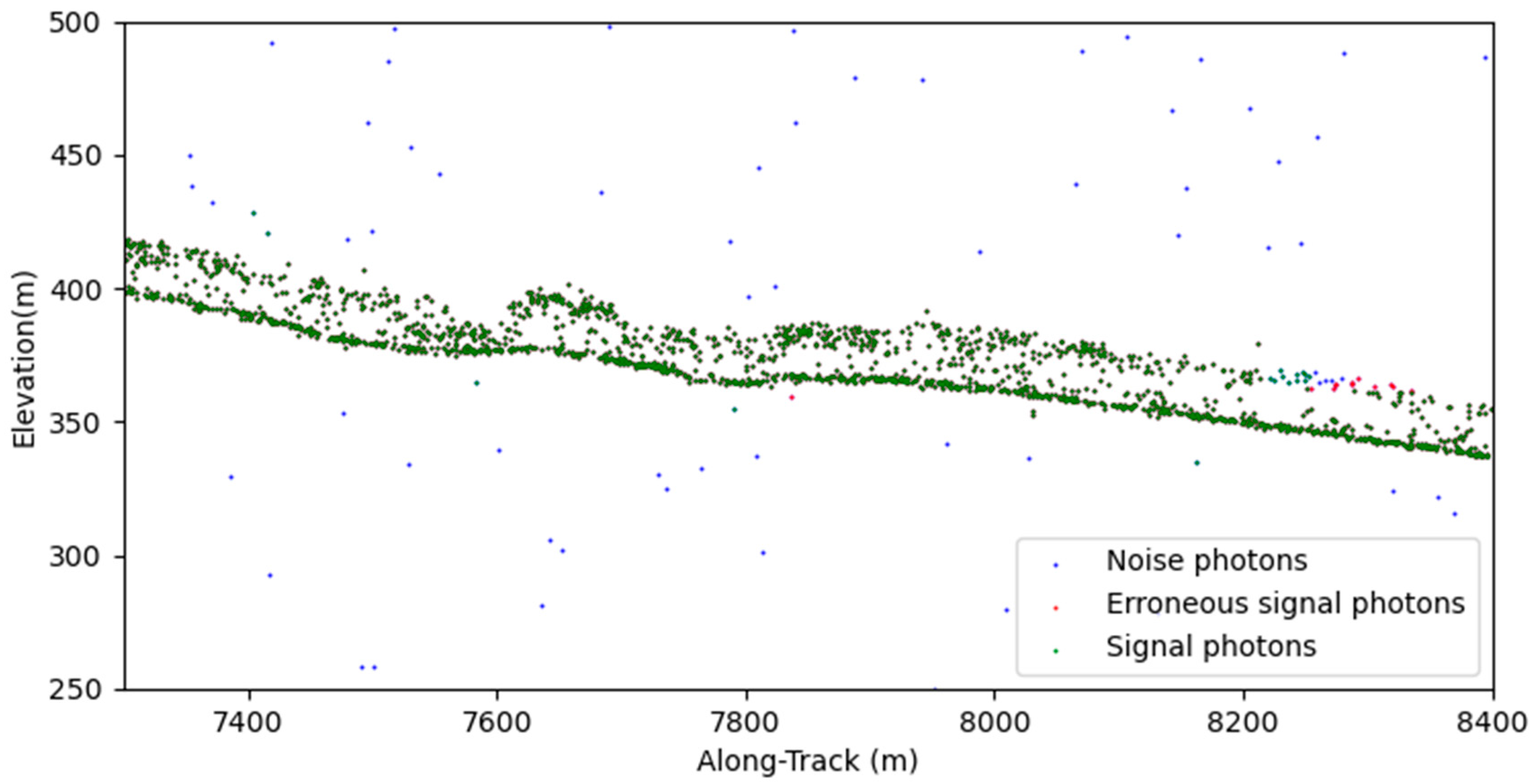
4.2. Photon Classification
5. Discussion
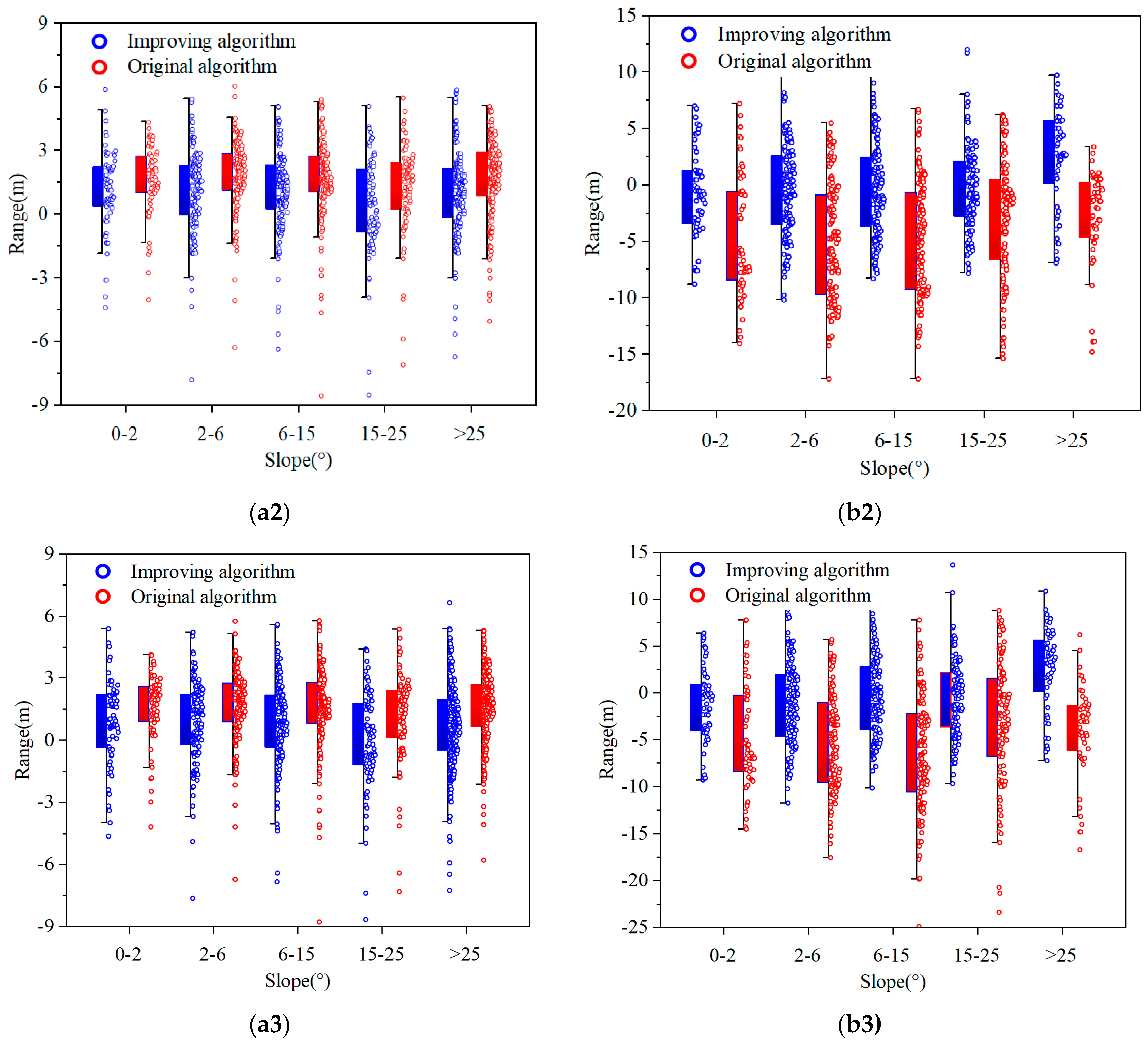
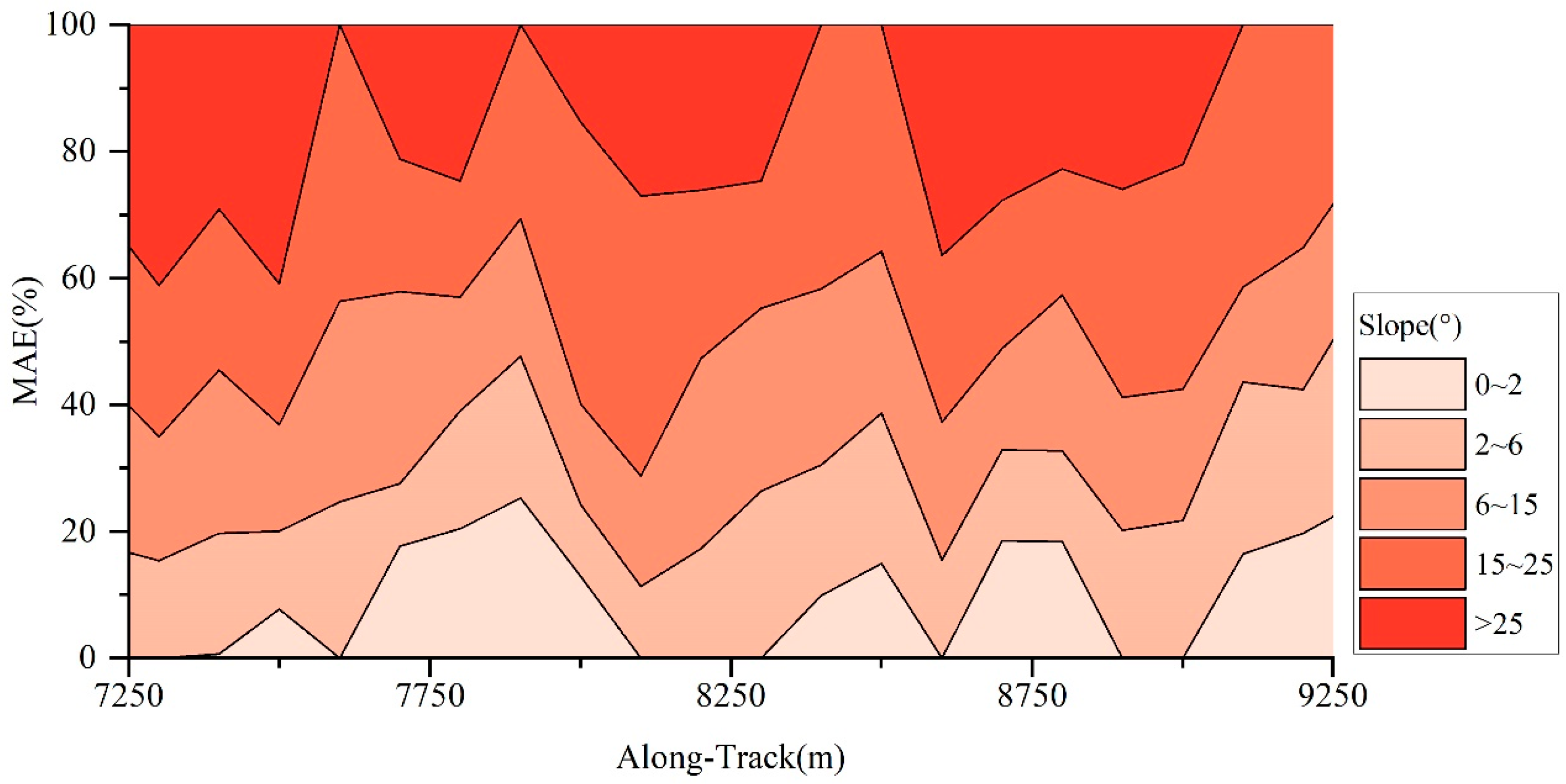
5.1. Effect of Slope
5.2. Effect of Forest Cover
5.3. Other Effects
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, G.; Ganguly, S.; Nemani, R.R.; White, M.A.; Milesi, C.; Hashimoto, H.; Wang, W.; Saatchi, S.; Yu, Y.; Myneni, R.B. Estimation of Forest Aboveground Biomass in California Using Canopy Height and Leaf Area Index Estimated from Satellite Data. Remote Sens. Environ. 2014, 151, 44–56. [Google Scholar] [CrossRef]
- Chen, Q. Retrieving Vegetation Height of Forests and Woodlands over Mountainous Areas in the Pacific Coast Region Using Satellite Laser Altimetry. Remote Sens. Environ. 2010, 114, 1610–1627. [Google Scholar] [CrossRef]
- Kelly, M.; Su, Y.; Di Tommaso, S.; Fry, D.; Collins, B.; Stephens, S.; Guo, Q. Impact of Error in Lidar-Derived Canopy Height and Canopy Base Height on Modeled Wildfire Behavior in the Sierra Nevada, California, USA. Remote Sens. 2017, 10, 10. [Google Scholar] [CrossRef]
- Sačkov, I.; Kardoš, M. Forest Delineation Based on LiDAR Data and Vertical Accuracy of the Terrain Model in Forest and Non-Forest Area. Ann. For. Res. 2014, 57, 119–136. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y.; Shen, M.; Chen, X.; Chen, R. Spatiotemporal Variation of Net Primary Productivity and Response to Climatic Factors in the Yangtze River Basin. Water Resour. Hydropower Eng. 2022, 53, 165–176. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, K.; Du, T. Research of Vegetation Cover Variations in Reservoir Areas Based on Satellite Remote Sensing: A Case Study of Sanhekou Reservoir Area. Water Resour. Hydropower Eng. 2024, 55, 134–147. [Google Scholar] [CrossRef]
- Li, Y.; Shang, R.; Qu, Y. Assessment of the Dynamics of Vegetation Net Primary Productivity and Its Response to Environmental Chan-Ges before and after the Grain for Green Project: A Case Study Form the Loess Plateau of Northern Shaanxi. Water Resour. Hydropower Eng. 2023, 54, 156–166. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E.; et al. Mapping Global Forest Canopy Height through Integration of GEDI and Landsat Data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- Fu, H.; Zhu, J.; Wang, C.; Wang, H.; Zhao, R. Underlying Topography Estimation over Forest Areas Using High-Resolution P-Band Single-Baseline PolInSAR Data. Remote Sens. 2017, 9, 363. [Google Scholar] [CrossRef]
- Niemi, M.; Vauhkonen, J. Extracting Canopy Surface Texture from Airborne Laser Scanning Data for the Supervised and Unsupervised Prediction of Area-Based Forest Characteristics. Remote Sens. 2016, 8, 582. [Google Scholar] [CrossRef]
- Parker, G.G.; Russ, M.E. The Canopy Surface and Stand Development: Assessing Forest Canopy Structure and Complexity with near-Surface Altimetry. For. Ecol. Manag. 2004, 189, 307–315. [Google Scholar] [CrossRef]
- González-Jaramillo, V.; Fries, A.; Zeilinger, J.; Homeier, J.; Paladines-Benitez, J.; Bendix, J. Estimation of Above Ground Biomass in a Tropical Mountain Forest in Southern Ecuador Using Airborne LiDAR Data. Remote Sens. 2018, 10, 660. [Google Scholar] [CrossRef]
- Nie, S.; Wang, C.; Zeng, H.; Xi, X.; Xia, S. A Revised Terrain Correction Method for Forest Canopy Height Estimation Using ICESat/GLAS Data. ISPRS J. Photogramm. Remote Sens. 2015, 108, 183–190. [Google Scholar] [CrossRef]
- Qin, H.; Wang, C.; Xi, X.; Tian, J.; Zhou, G. Estimation of Coniferous Forest Aboveground Biomass with Aggregated Airborne Small-Footprint LiDAR Full-Waveforms. Opt. Express 2017, 25, A851. [Google Scholar] [CrossRef]
- Yamamoto, K.H.; Powell, R.L.; Anderson, S.; Sutton, P.C. Using LiDAR to Quantify Topographic and Bathymetric Details for Sea Turtle Nesting Beaches in Florida. Remote Sens. Environ. 2012, 125, 125–133. [Google Scholar] [CrossRef]
- Ballhorn, U.; Jubanski, J.; Siegert, F. ICESat/GLAS Data as a Measurement Tool for Peatland Topography and Peat Swamp Forest Biomass in Kalimantan, Indonesia. Remote Sens. 2011, 3, 1957–1982. [Google Scholar] [CrossRef]
- Jang, J.-D.; Payan, V.; Viau, A.A.; Devost, A. The Use of Airborne Lidar for Orchard Tree Inventory. Int. J. Remote Sens. 2008, 29, 1767–1780. [Google Scholar] [CrossRef]
- Mahoney, C.; Hopkinson, C.; Kljun, N.; Van Gorsel, E. Estimating Canopy Gap Fraction Using ICESat GLAS within Australian Forest Ecosystems. Remote Sens. 2017, 9, 59. [Google Scholar] [CrossRef]
- Murgoitio, J.; Shrestha, R.; Glenn, N.; Spaete, L. Airborne LiDAR and Terrestrial Laser Scanning Derived Vegetation Obstruction Factors for Visibility Models. Trans. GIS 2014, 18, 147–160. [Google Scholar] [CrossRef]
- Pourrahmati, M.R.; Baghdadi, N.N.; Darvishsefat, A.A.; Namiranian, M.; Fayad, I.; Bailly, J.-S.; Gond, V. Capability of GLAS/ICESat Data to Estimate Forest Canopy Height and Volume in Mountainous Forests of Iran. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 5246–5261. [Google Scholar] [CrossRef]
- Magruder, L.; Neumann, T.; Kurtz, N. The Ice, Cloud and Land Elevation Satellite-2 (ICESat-2): Mission Status, Science Results and Outlook. 2021. Available online: https://ui.adsabs.harvard.edu/abs/2021EGUGA..23.8967M/abstract (accessed on 20 November 2024).
- Herzfeld, U.C.; Trantow, T.M.; Harding, D.; Dabney, P.W. Surface-Height Determination of Crevassed Glaciers—Mathematical Principles of an Autoadaptive Density-Dimension Algorithm and Validation Using ICESat-2 Simulator (SIMPL) Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1874–1896. [Google Scholar] [CrossRef]
- Zhang, J.; Kerekes, J. An Adaptive Density-Based Model for Extracting Surface Returns From Photon-Counting Laser Altimeter Data. IEEE Geosci. Remote Sens. Lett. 2015, 12, 726–730. [Google Scholar] [CrossRef]
- Febriana, N.L.; Sitanggang, I.S. Outlier Detection on Hotspot Data in Riau Province Using OPTICS Algorithm. IOP Conf. Ser. Earth Environ. Sci. 2017, 58, 012004. [Google Scholar] [CrossRef]
- Pan, J.; Gao, F.; Wang, J.; Zhang, J.; Liu, Q.; Deng, Y. A Main Direction-Based Noise Removal Algorithm for ICESat-2 Photon-Counting LiDAR Data. J. Geod. 2024, 98, 80. [Google Scholar] [CrossRef]
- Popescu, S.C.; Zhou, T.; Nelson, R.; Neuenschwander, A.; Sheridan, R.; Narine, L.; Walsh, K.M. Photon Counting LiDAR: An Adaptive Ground and Canopy Height Retrieval Algorithm for ICESat-2 Data. Remote Sens. Environ. 2018, 208, 154–170. [Google Scholar] [CrossRef]
- Yang, X.; Wang, C.; Nie, S.; Xi, X.; Hu, Z.; Qin, H. Application and Validation of a Model for Terrain Slope Estimation Using Space-Borne LiDAR Waveform Data. Remote Sens. 2018, 10, 1691. [Google Scholar] [CrossRef]
- Chen, B.; Pang, Y.; Li, Z.; Lu, H.; Liu, L.; North, P.R.J.; Rosette, J.A.B. Ground and Top of Canopy Extraction From Photon-Counting LiDAR Data Using Local Outlier Factor With Ellipse Searching Area. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1447–1451. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, Q.; Su, Y.; Xue, B. Improved Progressive TIN Densification Filtering Algorithm for Airborne LiDAR Data in Forested Areas. ISPRS J. Photogramm. Remote Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef]
- Guo, Y.; Zhong, L.; Min, L.; Wang, J.; Wu, Y.; Chen, K.; Wei, K.; Rao, C. Adaptive Optics Based on Machine Learning: A Review. Opto-Electron. Adv. 2022, 5, 200082. [Google Scholar] [CrossRef]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN Revisited, Revisited. ACM Trans. Database Syst. 2017, 42, 1–21. [Google Scholar] [CrossRef]
- Hahsler, M.; Piekenbrock, M.; Doran, D. Dbscan: Fast Density-Based Clustering with R. J. Stat. Softw. 2019, 91, 1–30. [Google Scholar] [CrossRef]
- Geelhood, K.; Colameco, D.; Bales, M.; Corson, J.; Kyriazidis, L. FAST-1.0 Software Release Document; U.S. Department of Energy: Richland, WA, USA, 2020.
- Kopsinis, Y.; McLaughlin, S. Development of EMD-Based Denoising Methods Inspired by Wavelet Thresholding. IEEE Trans. Signal Process. 2009, 57, 1351–1362. [Google Scholar] [CrossRef]
- Li, D.; Xu, L.; Li, X.; Ma, L. Full-Waveform LiDAR Signal Filtering Based on Empirical Mode Decomposition Method. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; pp. 3399–3402. [Google Scholar]
- Zhang, Y.; Ma, X.; Hua, D.; Cui, Y.; Sui, L. An EMD-Based Denoising Method for Lidar Signal. In Proceedings of the 2010 3rd International Congress on Image and Signal Processing, Yantai, China, 16–18 October 2010; pp. 4016–4019. [Google Scholar]
- Beland, M.; Parker, G.; Sparrow, B.; Harding, D.; Chasmer, L.; Phinn, S.; Antonarakis, A.; Strahler, A. On Promoting the Use of Lidar Systems in Forest Ecosystem Research. For. Ecol. Manag. 2019, 450, 117484. [Google Scholar] [CrossRef]
- Matasci, G.; Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W.; Zald, H.S.J. Large-Area Mapping of Canadian Boreal Forest Cover, Height, Biomass and Other Structural Attributes Using Landsat Composites and Lidar Plots. Remote Sens. Environ. 2018, 209, 90–106. [Google Scholar] [CrossRef]
- Liu, A.; Cheng, X.; Chen, Z. Performance Evaluation of GEDI and ICESat-2 Laser Altimeter Data for Terrain and Canopy Height Retrievals. Remote Sens. Environ. 2021, 264, 112571. [Google Scholar] [CrossRef]



| Terrain | Hilly | Plain | |||||
|---|---|---|---|---|---|---|---|
| True | False | Total | True | False | Total | ||
| Original | Points | 343 | 122 | 465 | 273 | 86 | 359 |
| Accuracy (%) | 73.76 | 26.24 | 100.00 | 76.04 | 23.96 | 100.00 | |
| Improve | Points | 386 | 79 | 465 | 313 | 46 | 359 |
| Accuracy (%) | 83.01 | 16.99 | 100.00 | 87.19 | 12.81 | 100.00 | |
| Original | Improve | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Slope (°) | DEM | DSM | CHM | DEM | DSM | CHM | ||||
| RMSE(m) | R2 | PA(%) | RMSE(m) | R2 | PA(%) | |||||
| 0–2 | 0.89 | 6.10 | 5.90 | 0.98 | 74.45 | 0.8 | 2.81 | 3.02 | 0.99 | 86.92 |
| 2–6 | 1.45 | 6.59 | 6.13 | 0.97 | 73.85 | 1.04 | 3.41 | 3.20 | 0.98 | 86.35 |
| 6–15 | 3.35 | 6.65 | 6.03 | 0.97 | 73.60 | 0.98 | 4.00 | 4.01 | 0.98 | 82.44 |
| 15–25 | 3.39 | 5.96 | 6.10 | 0.97 | 74.15 | 1.52 | 3.53 | 3.73 | 0.98 | 84.19 |
| >25 | 2.30 | 5.22 | 5.37 | 0.98 | 78.66 | 1.41 | 4.95 | 5.16 | 0.98 | 79.49 |
| total | 2.70 | 6.30 | 6.03 | 0.97 | 74.94 | 1.19 | 3.76 | 3.83 | 0.98 | 84.48 |
| Original (RMSE (m)) | Improve (RMSE (m)) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cover (%) | DEM | DSM | CHM | DEM | DSM | CHM | ||||
| RMSE(m) | R2 | PA(%) | RMSE(m) | R2 | PA(%) | |||||
| 0–0.2 | 1.03 | 0.72 | ||||||||
| 0.2–0.4 | 1.19 | 5.73 | 5.35 | 0.98 | 78.68 | 1.01 | 3.19 | 3.92 | 0.98 | 84.38 |
| 0.4–0.6 | 2.15 | 5.08 | 4.75 | 0.98 | 80.70 | 0.81 | 3.56 | 4.03 | 0.98 | 83.63 |
| 0.6–0.8 | 2.98 | 7.31 | 6.89 | 0.97 | 71.46 | 1.16 | 3.66 | 3.36 | 0.98 | 86.08 |
| 0.8–1.0 | 3.12 | 6.31 | 6.05 | 0.98 | 74.33 | 1.36 | 3.84 | 3.84 | 0.98 | 83.71 |
| total | 2.7 | 6.3 | 6.03 | 0.97 | 74.94 | 1.19 | 3.76 | 3.83 | 0.98 | 84.48 |
| Conifer | Broadleaf | |||||
|---|---|---|---|---|---|---|
| DEM | DSM | CHM | DEM | DSM | CHM | |
| RMSE(m) | 0.95 | 3.05 | 2.89 | 1.28 | 3.49 | 3.45 |
| R2 | 0.98 | 0.99 | 0.98 | 0.98 | 0.99 | 0.98 |
| PA(%) | 95.35 | 85.08 | 85.86 | 93.78 | 83.04 | 83.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Yu, Y.; Li, M.; Yang, X.; Dong, H.; Guan, X. Estimation of Forest Canopy Height Using ATLAS Data Based on Improved Optics and EEMD Algorithms. Remote Sens. 2025, 17, 941. https://doi.org/10.3390/rs17050941
Wang G, Yu Y, Li M, Yang X, Dong H, Guan X. Estimation of Forest Canopy Height Using ATLAS Data Based on Improved Optics and EEMD Algorithms. Remote Sensing. 2025; 17(5):941. https://doi.org/10.3390/rs17050941
Chicago/Turabian StyleWang, Guanran, Ying Yu, Mingze Li, Xiguang Yang, Hanyuan Dong, and Xuebing Guan. 2025. "Estimation of Forest Canopy Height Using ATLAS Data Based on Improved Optics and EEMD Algorithms" Remote Sensing 17, no. 5: 941. https://doi.org/10.3390/rs17050941
APA StyleWang, G., Yu, Y., Li, M., Yang, X., Dong, H., & Guan, X. (2025). Estimation of Forest Canopy Height Using ATLAS Data Based on Improved Optics and EEMD Algorithms. Remote Sensing, 17(5), 941. https://doi.org/10.3390/rs17050941








