Reconstructing Evapotranspiration in British Columbia Since 1850 Using Publicly Available Tree-Ring Plots and Climate Data
Abstract
1. Introduction
2. Methods
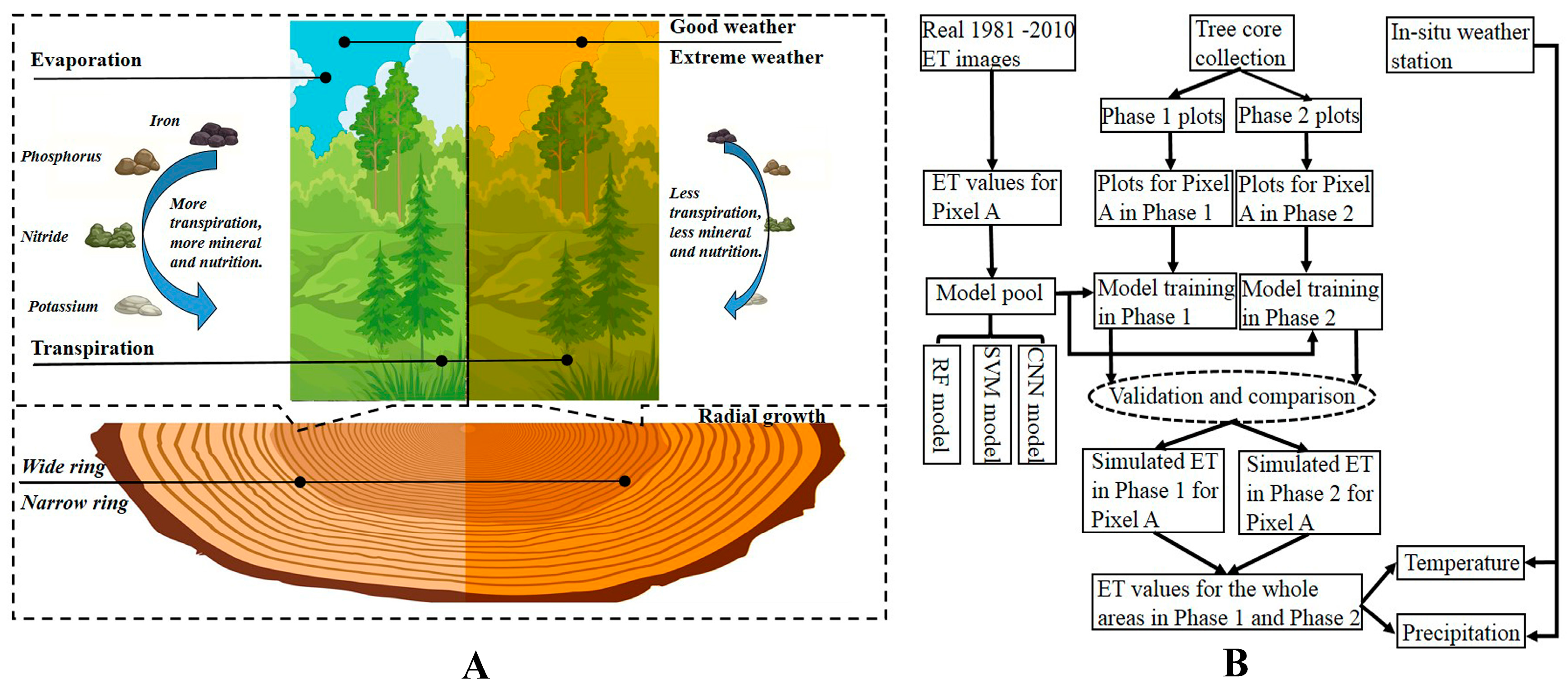
2.1. Study Areas and Data Collection
2.2. Tree-Ring ET Model
2.3. Regression Model Selection and Validation
2.4. Exploring the Relationship Between the ET and Climate Factors
3. Results
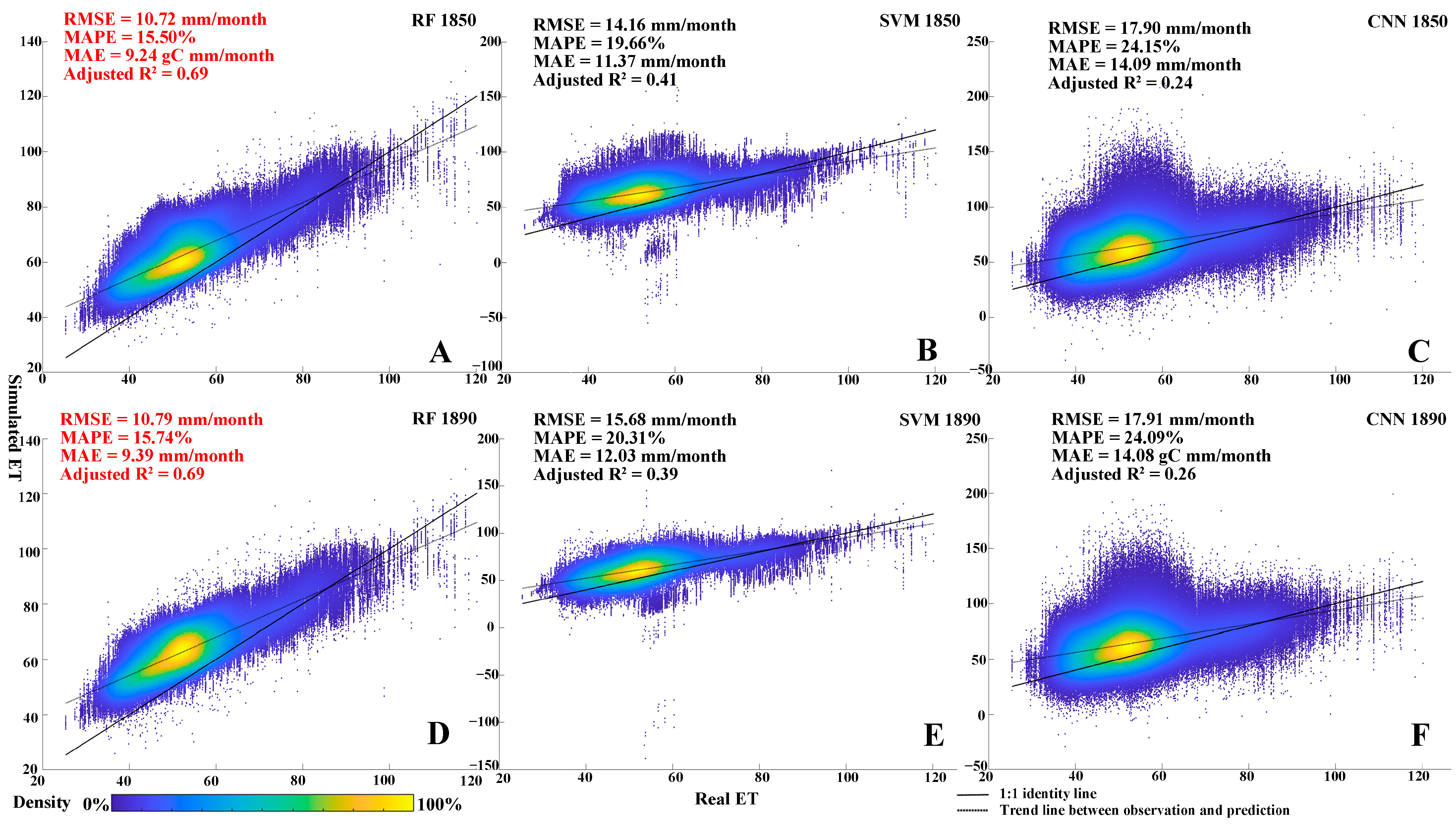
3.1. Model Performances
3.2. Spatiotemporal Change in ET
3.3. ET and Climate Factors in the Three Ecodomains
4. Discussion
4.1. RF Model Is the Best Model Among the Three
4.2. ET Increase from 1850 to 2010
4.3. Regional Effects on the ET in the Three Ecodomains
4.4. Limitation and Future Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| ID | ITRDB Plot Name | Species | Period 1850–1889 or Period 1890–1981 | Lat | Lon | ITRDB DOI |
|---|---|---|---|---|---|---|
| 1 | wa137 | PIPO | Period 1890–1981 | 48.7800 | −120.2700 | https://doi.org/10.25921/x9g7-8z46 |
| 2 | wa138 | PIPO | Period 1890–1981 | 48.1800 | −120.2600 | https://doi.org/10.25921/8xmk-5s78 |
| 3 | wa139 | PIPO | Period 1890–1981 | 48.5100 | −118.7500 | https://doi.org/10.25921/k6rt-kb84 |
| 4 | wa140 | PIPO | Period 1890–1981 | 48.5900 | −119.1400 | https://doi.org/10.25921/y0kg-f958 |
| 5 | wa141 | PIPO | Period 1890–1981 | 48.6000 | −119.7000 | https://doi.org/10.25921/ytpk-jj18 |
| 6 | wa143 | TSME | Period 1890–1981 | 48.8607 | −121.6850 | https://doi.org/10.25921/bxk6-be53 |
| 7 | wa145 | TSME | Period 1890–1981 | 48.5048 | −121.2088 | https://doi.org/10.25921/h1nx-5503 |
| 8 | wa146 | TSME | Period 1890–1981 | 47.8444 | −121.0359 | https://doi.org/10.25921/h0qc-1372 |
| 9 | wa148 | TSME | Period 1890–1981 | 48.6798 | −121.3227 | https://doi.org/10.25921/jz4r-sm15 |
| 10 | wa149 | PSME | Period 1890–1981 | 48.5880 | −123.1970 | https://doi.org/10.25921/1frg-zk64 |
| 11 | wa150 | CANO | Period 1890–1981 | 48.8150 | −121.9281 | https://doi.org/10.25921/j01a-m794 |
| 12 | wa151 | CANO | Period 1890–1981 | 48.0708 | −121.8103 | https://doi.org/10.25921/ybdk-x158 |
| 13 | wa152 | CANO | Period 1890–1981 | 48.8119 | −122.0361 | https://doi.org/10.25921/pf2c-qw03 |
| 14 | wa153 | TSME | Period 1890–1981 | 48.7979 | −121.8739 | https://doi.org/10.25921/5w1w-qd73 |
| 15 | wa154 | LALY | Period 1890–1981 | 48.1608 | −120.3522 | https://doi.org/10.25921/znf2-hk61 |
| 16 | wa161 | THPL | Period 1890–1981 | 48.7676 | −117.0609 | https://doi.org/10.25921/7rpk-ec27 |
| 17 | ak131 | TSME | Period 1890–1981 | 58.3833 | −134.4333 | https://doi.org/10.25921/qnyc-ex43 |
| 18 | ak150 | TSME | Period 1890–1981 | 58.7400 | −135.9800 | https://doi.org/10.25921/xwfv-gf55 |
| 19 | ak192 | CHNO | Period 1890–1981 | 58.6300 | −134.9310 | https://doi.org/10.25921/87db-m027 |
| 20 | ak193 | CHNO | Period 1890–1981 | 58.6580 | −134.9640 | https://doi.org/10.25921/cznb-x933 |
| 21 | ak195 | CHNO | Period 1890–1981 | 58.4120 | −134.5250 | https://doi.org/10.25921/9dzn-gd10 |
| 22 | ak197 | CHNO | Period 1890–1981 | 56.8320 | −133.5840 | https://doi.org/10.25921/hj2w-ev37 |
| 23 | ak198 | PICO | Period 1890–1981 | 58.4410 | −135.6090 | https://doi.org/10.25921/gna9-m858 |
| 24 | ak209 | TSME | Period 1890–1981 | 58.7400 | −135.9800 | https://doi.org/10.25921/zqx9-3t97 |
| 25 | cana590 | PCGL | Period 1890–1981 | 60.7600 | −135.7400 | https://doi.org/10.25921/wqs2-sf82 |
| 26 | cana591 | PICO | Period 1890–1981 | 60.7600 | −135.7400 | https://doi.org/10.25921/9yz1-2q87 |
| 27 | cana490 | TSME | Period 1890–1981 | 52.2800 | −126.9000 | https://doi.org/10.25921/vn0c-7h28 |
| 28 | cana469 | TSME | Period 1890–1981 | 52.2800 | −126.8900 | https://doi.org/10.25921/ze1d-4312 |
| 29 | can675 | TSME | Period 1890–1981 | 52.2900 | −126.8900 | https://doi.org/10.25921/f6ak-yk37 |
| 30 | cana476 | TSME | Period 1890–1981 | 52.2200 | −126.3400 | https://doi.org/10.25921/snpm-sr02 |
| 31 | cana467 | TSME | Period 1890–1981 | 51.2700 | −125.4300 | https://doi.org/10.25921/7tna-ek16 |
| 32 | cana646 | TSME | Period 1890–1981 | 50.5919 | −123.0172 | https://doi.org/10.25921/rctz-nf70 |
| 33 | cana645 | ABAM | Period 1890–1981 | 50.5919 | −123.0172 | https://doi.org/10.25921/z774-jr28 |
| 34 | cana641 | TSME | Period 1890–1981 | 50.3580 | −122.4875 | https://doi.org/10.25921/24rp-df66 |
| 35 | cana468 | TSME | Period 1890–1981 | 50.3500 | −122.4800 | https://doi.org/10.25921/8k3r-bs88 |
| 36 | can674 | TSME | Period 1890–1981 | 50.3500 | −122.4800 | https://doi.org/10.25921/24rp-df66 |
| 37 | can673 | TSME | Period 1890–1981 | 49.1600 | −121.6300 | https://doi.org/10.25921/gcj6-nk39 |
| 38 | cana557 | PCMA | Period 1890–1981 | 61.3080 | −121.2990 | https://doi.org/10.25921/pjfz-jw90 |
| 39 | cana643 | PIPO | Period 1890–1981 | 50.5364 | −121.2763 | https://doi.org/10.25921/k0q5-fd38 |
| 40 | can679 | PIPO | Period 1890–1981 | 50.5400 | −121.2700 | https://doi.org/10.25921/t0zq-j160 |
| 41 | can678 | PCEN | Period 1890–1981 | 50.8100 | −118.9700 | https://doi.org/10.25921/axw7-1j58 |
| 42 | can677 | PCEN | Period 1890–1981 | 51.1700 | −118.1300 | https://doi.org/10.25921/ymyd-k033 |
| 43 | can717 | PCEN | Period 1890–1981 | 49.5872 | −117.4003 | https://doi.org/10.25921/16g7-w724 |
| 44 | cana647 | PCEN | Period 1890–1981 | 52.2230 | −117.1955 | https://doi.org/10.25921/5ms4-ym52 |
| 45 | can676 | PCEN | Period 1890–1981 | 51.7100 | −116.5100 | https://doi.org/10.25921/4731-ge67 |
| 46 | cana581 | PCEN | Period 1890–1981 | 50.6100 | −115.1200 | https://doi.org/10.25921/n1jk-f831 |
| 47 | cana529 | PIAL | Period 1890–1981 | 49.7700 | −114.5300 | https://doi.org/10.25921/17r9-sf87 |
| 48 | cana528 | LALY | Period 1890–1981 | 49.3100 | −114.4300 | https://doi.org/10.25921/j0qn-qq37 |
| 49 | cana566 | PSME | Period 1890–1981 | 49.8900 | −114.3000 | https://doi.org/10.25921/z637-rn38 |
| 50 | cana583 | PSME | Period 1890–1981 | 49.8900 | −114.1800 | https://doi.org/10.25921/dp7t-w436 |
| 51 | cana464 | ABLA | Both | 50.5900 | −123.5900 | https://doi.org/10.25921/y1dm-7r82 |
| 52 | cana611 | PSME | Both | 50.8530 | −120.5200 | https://doi.org/10.25921/xn24-th08 |
| 53 | cana644 | PIPO | Both | 50.5478 | −121.2729 | https://doi.org/10.25921/94td-1252 |
| 54 | cana649 | PSME | Both | 54.6485 | −124.4300 | https://doi.org/10.25921/10c9-v582 |

References
- Novák, V.; Novák, V. Evapotranspiration: A component of the water cycle. In Evapotranspiration in the Soil-Plant-Atmosphere System; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–13. [Google Scholar] [CrossRef]
- Lu, Y.; Kueppers, L. Increased heat waves with loss of irrigation in the United States. Environ. Res. Lett. 2015, 10, 064010. [Google Scholar] [CrossRef]
- Ritchie, J.T. Soil water balance and plant water stress. In Understanding Options for Agricultural Production; Springer: Dordrecht, The Netherlands, 1998; pp. 41–54. [Google Scholar] [CrossRef]
- Tan, X.; Liu, M.; Du, N.; Zwiazek, J.J. Ethylene enhances root water transport and aquaporin expression in trembling aspen (Populus tremuloides) exposed to root hypoxia. BMC Plant Biol. 2021, 21, 227. [Google Scholar] [CrossRef] [PubMed]
- Tanner, W.; Beevers, H. Transpiration, a prerequisite for long-distance transport of minerals in plants? Proc. Natl. Acad. Sci. USA 2001, 98, 9443–9447. [Google Scholar] [CrossRef] [PubMed]
- Glenn, E.P.; Huete, A.R.; Nagler, P.L.; Hirschboeck, K.K.; Brown, P. Integrating remote sensing and ground methods to estimate evapotranspiration. Crit. Rev. Plant Sci. 2007, 26, 139–168. [Google Scholar] [CrossRef]
- Alfieri, J.G.; Kustas, W.P.; Anderson, M.C. A Brief Overview of Approaches for Measuring Evapotranspiration. Agroclimatol. Link. Agric. Clim. 2020, 60, 109–127. [Google Scholar] [CrossRef]
- Zhang, Y.; Qin, H.; Zhang, J.; Hu, Y. An in-situ measurement method of evapotranspiration from typical LID facilities based on the three-temperature model. J. Hydrol. 2020, 588, 125105. [Google Scholar] [CrossRef]
- Mao, Y.; Wang, K. Comparison of evapotranspiration estimates based on the surface water balance, modified Pen-man-Monteith model, and reanalysis data sets for continental China. J. Geophys. Res. Atmos. 2017, 122, 3228–3244. [Google Scholar] [CrossRef]
- Elnashar, A.; Wang, L.; Wu, B.; Zhu, W.; Zeng, H. Synthesis of global actual evapotranspiration from 1982 to 2019. Earth Syst. Sci. Data 2021, 13, 447–480. [Google Scholar] [CrossRef]
- Senay, G.B.; Leake, S.; Nagler, P.L.; Artan, G.; Dickinson, J.; Cordova, J.T.; Glenn, E.P. Estimating basin scale evapotranspiration (ET) by water balance and remote sensing methods. Hydrol. Process. 2011, 25, 4037–4049. [Google Scholar] [CrossRef]
- Talsma, C.J.; Good, S.P.; Jimenez, C.; Martens, B.; Fisher, J.B.; Miralles, D.G.; McCabe, M.F.; Purdy, A.J. Partitioning of evapotranspiration in remote sensing-based models. Agric. For. Meteorol. 2018, 260, 131–143. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, Y.; Su, B.; Wang, A.; Tao, H.; Zhai, J.; Kundzewicz, Z.W.; Jiang, T. Choice of potential evapotranspiration formulas influences drought assessment: A case study in China. Atmos. Res. 2020, 242, 104979. [Google Scholar] [CrossRef]
- Cabral-Alemán, C.; Villanueva-Díaz, J.; Quiñonez-Barraza, G.; Gómez-Guerrero, A.; Arreola-Ávila, J.G. Reconstruction of the standardized precipitation-evapotranspiration index for the Western Region of Durango State, Mexico. Forests 2022, 13, 1233. [Google Scholar] [CrossRef]
- Li, H.; Thapa, I.; Speer, J.H. Fine-scale NDVI reconstruction back to 1906 from tree-rings in the greater Yellowstone ecosystem. Forests 2021, 12, 1324. [Google Scholar] [CrossRef]
- Li, H.; Speer, J.H.; Malubeni, C.C.; Wilson, E. Reconstructing a Fine Resolution Landscape of Annual Gross Primary Product (1895–2013) with Tree-Ring Indices. Remote Sens. 2024, 16, 3744. [Google Scholar] [CrossRef]
- D’Andrea, G.; Šimůnek, V.; Castellaneta, M.; Vacek, Z.; Vacek, S.; Pericolo, O.; Zito, R.G.; Ripullone, F. Mismatch between Annual Tree-Ring Width Growth and NDVI Index in Norway Spruce Stands of Central Europe. Forests 2022, 13, 1417. [Google Scholar] [CrossRef]
- Gilani, H.R.; Innes, J.L. The state of British Columbia’s forests: A global comparison. Forests 2020, 11, 316. [Google Scholar] [CrossRef]
- Demarchi, D.A. An Introduction to the Ecoregions of British Columbia; Wildlife Branch, Ministry of Environment, Lands and Parks: Victoria, BC, USA, 1996. [Google Scholar]
- Richard, L.H.; Harold, C.F. User’s Manual for Program ARSTAN. Tree-Ring Chronologies of Western North America: California, Eastern Oregon and Northern Great Basin; University of Arizona Press: Tucson, AZ, USA, 1986; Available online: https://books.google.ca/books/about/Tree_ring_Chronologies_of_Western_North.html?id=iLwbHwAACAAJ&redir_esc=y (accessed on 5 January 2025).
- Speer, J.H. Fundamentals of Tree-Ring Research; University of Arizona Press: Tucson, AZ, USA, 2010. [Google Scholar]
- Government of Canada, Natural Resources Canada, Canada Centre for Remote Sensing. 2010 Land Cover of Canada. Natural Resources Canada, Federal Geospatial Platform. 2023. Available online: https://www.cec.org/north-american-environmental-atlas/land-cover-2010-landsat-30m/ (accessed on 5 January 2025).
- Liu, H.; Xiao, P.; Zhang, X.; Chen, S.; Wang, Y.; Wang, W. Winter snow cover influences growing-season vegetation productivity non-uniformly in the Northern Hemisphere. Commun. Earth Environ. 2023, 4, 487. [Google Scholar] [CrossRef]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, L.; Zhang, Y.; Chen, C.P. A SVM controller for the stable walking of biped robots based on small sample sizes. Appl. Soft Comput. 2016, 38, 738–753. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, D.; Wan, K.; Huang, W.; Chen, N. Estimation and Spatiotemporal Analysis of Surface Evaporation in the Yangtze River Basin from 2010 to 2019. Remote Sens. 2023, 16, 57. [Google Scholar] [CrossRef]
- Liang, M.; Zhang, L.; Wu, S.; Zhu, Y.; Dai, Z.; Wang, Y.; Qi, J.; Chen, Y.; Du, Z. A high-resolution land surface temperature downscaling method based on geographically weighted neural network regression. Remote Sens. 2023, 15, 1740. [Google Scholar] [CrossRef]
- Li, H.; Thapa, I.; Xu, S.; Yang, P. Mapping the Normalized Difference Vegetation Index for the Contiguous US Since 1850 Using 391 Tree-Ring Plots. Remote Sens. 2024, 16, 3973. [Google Scholar] [CrossRef]
- Spiess, A.N.; Neumeyer, N. An evaluation of R2 as an inadequate measure for nonlinear models in pharmacological and biochemical research: A Monte Carlo approach. BMC Pharmacol. 2010, 10, 6. [Google Scholar] [CrossRef] [PubMed]
- Shahinfar, S.; Meek, P.; Falzon, G. “How many images do I need?” Understanding how sample size per class affects deep learning model performance metrics for balanced designs in autonomous wildlife monitoring. Ecol. Inform. 2020, 57, 101085. [Google Scholar] [CrossRef]
- Matykiewicz, P.; Pestian, J. Effect of small sample size on text categorization with support vector machines. In BioNLP: Proceedings of the 2012 Workshop on Biomedical Natural Language Processing; Association for Computational Linguistics: Montréal, QC, Canada, 2012; pp. 193–201. [Google Scholar]
- Webb, G.I.; Zheng, Z. Multistrategy ensemble learning: Reducing error by combining ensemble learning techniques. IEEE Trans. Knowl. Data Eng. 2004, 16, 980–991. [Google Scholar] [CrossRef]
- Shinker, J.J. Visualizing spatial heterogeneity of western US climate variability. Earth Interact. 2010, 14, 1–15. [Google Scholar] [CrossRef]
- Zhang, Y.; He, T.; Liang, S.; Zhao, Z. A framework for estimating actual evapotranspiration through spatial heterogeneity-based machine learning approaches. Agric. Water Manag. 2023, 289, 108499. [Google Scholar] [CrossRef]
- McVicar, T.R.; Van Niel, T.G.; Li, L.; Hutchinson, M.F.; Mu, X.; Liu, Z. Spatially distributing monthly reference evapotranspiration and pan evaporation considering topographic influences. J. Hydrol. 2007, 338, 196–220. [Google Scholar] [CrossRef]
- Kosatsky, T.; Henderson, S.B.; Pollock, S.L. Shifts in mortality during a hot weather event in Vancouver, British Columbia: Rapid assessment with case-only analysis. Am. J. Public Health 2012, 102, 2367–2371. [Google Scholar] [CrossRef]
- Long-term Change in Air Temperature in B.C. (1900–2013) (July 2015). Available online: https://www2.gov.bc.ca/gov/content/environment/research-monitoring-reporting/reporting/environmental-reporting-bc/climate-change-indicators?keyword=2016 (accessed on 5 January 2025).
- Lee, M.J.; McLean, K.E.; Kuo, M.; Richardson, G.R.; Henderson, S.B. Chronic diseases associated with mortality in British Columbia, Canada during the 2021 western North America extreme heat event. GeoHealth 2023, 7, e2022GH000729. [Google Scholar] [CrossRef]
- Lo, Y.H.; Blanco, J.A.; Seely, B.; Welham, C.; Kimmins, J.H. Relationships between climate and tree radial growth in interior British Columbia, Canada. For. Ecol. Manag. 2010, 259, 932–942. [Google Scholar] [CrossRef]
- Xu, Z.; Shimizu, H.; Ito, S.; Yagasaki, Y.; Zou, C.; Zhou, G.; Zheng, Y. Effects of elevated CO2, warming and precipitation change on plant growth, photosynthesis and peroxidation in dominant species from North China grassland. Planta 2014, 239, 421–435. [Google Scholar] [CrossRef]
- Hui, D.; Yu, C.L.; Deng, Q.; Dzantor, E.K.; Zhou, S.; Dennis, S.; Luo, Y. Effects of precipitation changes on switchgrass photosynthesis, growth, and biomass: A mesocosm experiment. PLoS ONE 2018, 13, e0192555. [Google Scholar] [CrossRef] [PubMed]
- Baribault, T.W.; Kobe, R.K.; Finley, A.O. Tropical tree growth is correlated with soil phosphorus, potassium, and calcium, though not for legumes. Ecol. Monogr. 2012, 82, 189–203. [Google Scholar] [CrossRef]
- Bearup, L.A.; Maxwell, R.M.; Clow, D.W.; McCray, J.E. Hydrological effects of forest transpiration loss in bark beetle-impacted watersheds. Nat. Clim. Change 2014, 4, 481–486. [Google Scholar] [CrossRef]
- Erbeli, F.; He, K.; Cheek, C.; Rice, M.; Qian, X. Exploring the machine learning paradigm in determining risk for reading disability. Sci. Stud. Read. 2023, 27, 5–20. [Google Scholar] [CrossRef]
- Halabaku, E.; Bytyçi, E. Overfitting in Machine Learning: A Comparative Analysis of Decision Trees and Random Forests. Intell. Autom. Soft Comput. 2024, 39, 5–20. [Google Scholar] [CrossRef]
- Creasman, P.P.; Bannister, B.; Towner, R.H.; Dean, J.S.; Leavitt, S.W. Reflections on the foundation, persistence, and growth of the Laboratory of Tree-Ring Research, circa 1930–1960. Tree-Ring Res. 2012, 68, 81–89. [Google Scholar] [CrossRef]
- Guiterman, C.H.; Gille, E.; Shepherd, E.; McNeill, S.; Payne, C.R.; Morrill, C. The international tree-ring Data Bank at fifty: Status of stewardship for future scientific discovery. Tree-Ring Res. 2024, 80, 13–18. [Google Scholar] [CrossRef]
- Niccoli, F.; Pacheco-Solana, A.; Delzon, S.; Kabala, J.P.; Asgharinia, S.; Castaldi, S.; Valentini, R.; Battipaglia, G. Effects of wildfire on growth, transpiration and hydraulic properties of Pinus pinaster Aiton forest. Dendrochronologia 2023, 79, 126086. [Google Scholar] [CrossRef]
- Szatniewska, J.; Zavadilova, I.; Nezval, O.; Krejza, J.; Petrik, P.; Čater, M.; Stojanović, M. Species-specific growth and transpiration response to changing environmental conditions in floodplain forest. For. Ecol. Manag. 2022, 516, 120248. [Google Scholar] [CrossRef]


| Order | Training Set (23/24) | Validation Year (1) |
|---|---|---|
| Fold 1 | 1987–2010 | 1985 |
| Fold 2 | 1982–1986, 1993–2010 | 1990 |
| Fold 3 | 1982–1992, 1999–2010 | 1995 |
| Fold 4 | 1982–1998, 2005–2010 | 2000 |
| Fold 5 | 1982–2004 | 2005 |
| Phases | Methods | Adjusted R2 | RMSE | MAPE | MAE |
|---|---|---|---|---|---|
| 1850–1889 | RF | 0.69 | 10.72 | 0.15 | 9.24 |
| SVM | 0.41 | 14.16 | 0.20 | 11.37 | |
| CNN | 0.24 | 17.90 | 0.24 | 14.09 | |
| 1890–1981 | RF | 0.69 | 10.79 | 0.16 | 9.39 |
| SVM | 0.39 | 15.68 | 0.20 | 12.03 | |
| CNN | 0.26 | 17.91 | 0.24 | 14.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Rex, J. Reconstructing Evapotranspiration in British Columbia Since 1850 Using Publicly Available Tree-Ring Plots and Climate Data. Remote Sens. 2025, 17, 930. https://doi.org/10.3390/rs17050930
Li H, Rex J. Reconstructing Evapotranspiration in British Columbia Since 1850 Using Publicly Available Tree-Ring Plots and Climate Data. Remote Sensing. 2025; 17(5):930. https://doi.org/10.3390/rs17050930
Chicago/Turabian StyleLi, Hang, and John Rex. 2025. "Reconstructing Evapotranspiration in British Columbia Since 1850 Using Publicly Available Tree-Ring Plots and Climate Data" Remote Sensing 17, no. 5: 930. https://doi.org/10.3390/rs17050930
APA StyleLi, H., & Rex, J. (2025). Reconstructing Evapotranspiration in British Columbia Since 1850 Using Publicly Available Tree-Ring Plots and Climate Data. Remote Sensing, 17(5), 930. https://doi.org/10.3390/rs17050930







