A 3D Blur Suppression Method for High-Resolution and Wide-Swath Blurred Images Based on Estimating and Eliminating Defocused Point Clouds
Abstract
1. Introduction
- Range de-ambiguity is carried out in 3D-space. By taking advantage of the characteristic that range ambiguity will cause further defocusing in the height direction, focused targets are selected, and the defocused point clouds are estimated and eliminated by using the focused targets to achieve range de-ambiguity.
- The phase errors existing in the process of estimating the defocused point clouds are analyzed. Part of these errors is introduced by the registration offset in the near-area and far-area images, and the other part is introduced during the transformation process between the near-area and far-area targets. Moreover, these errors have been corrected.
2. Methods
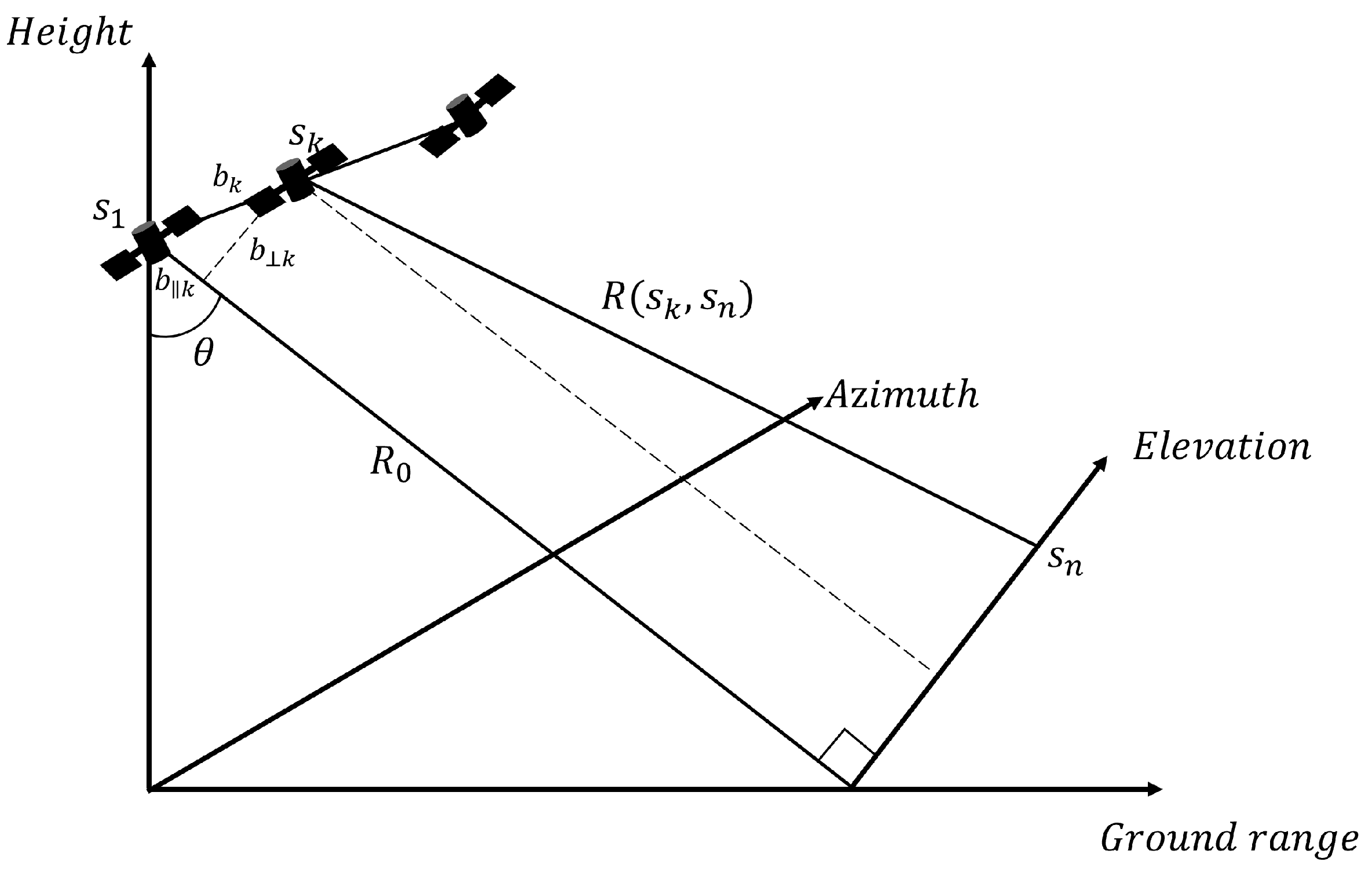
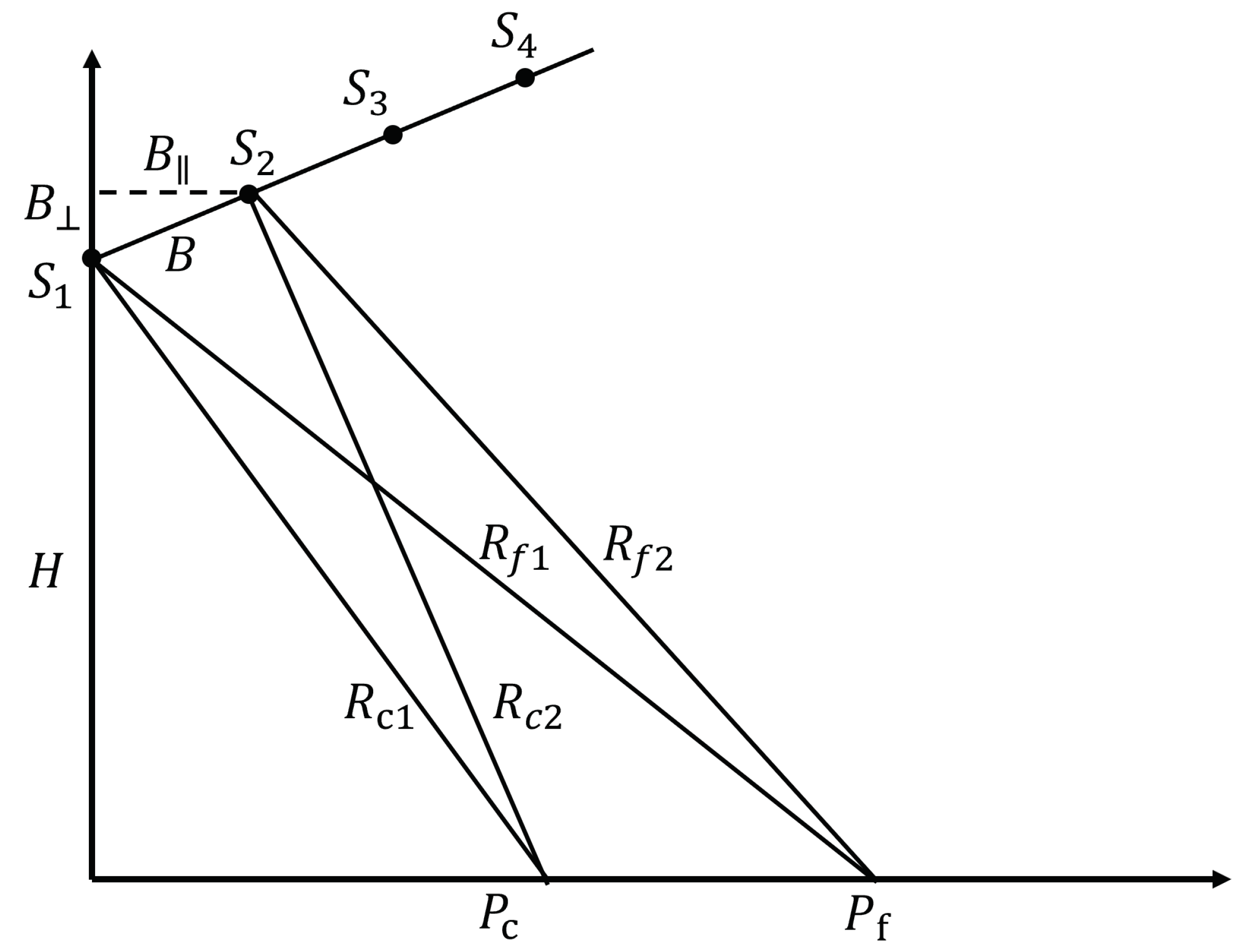
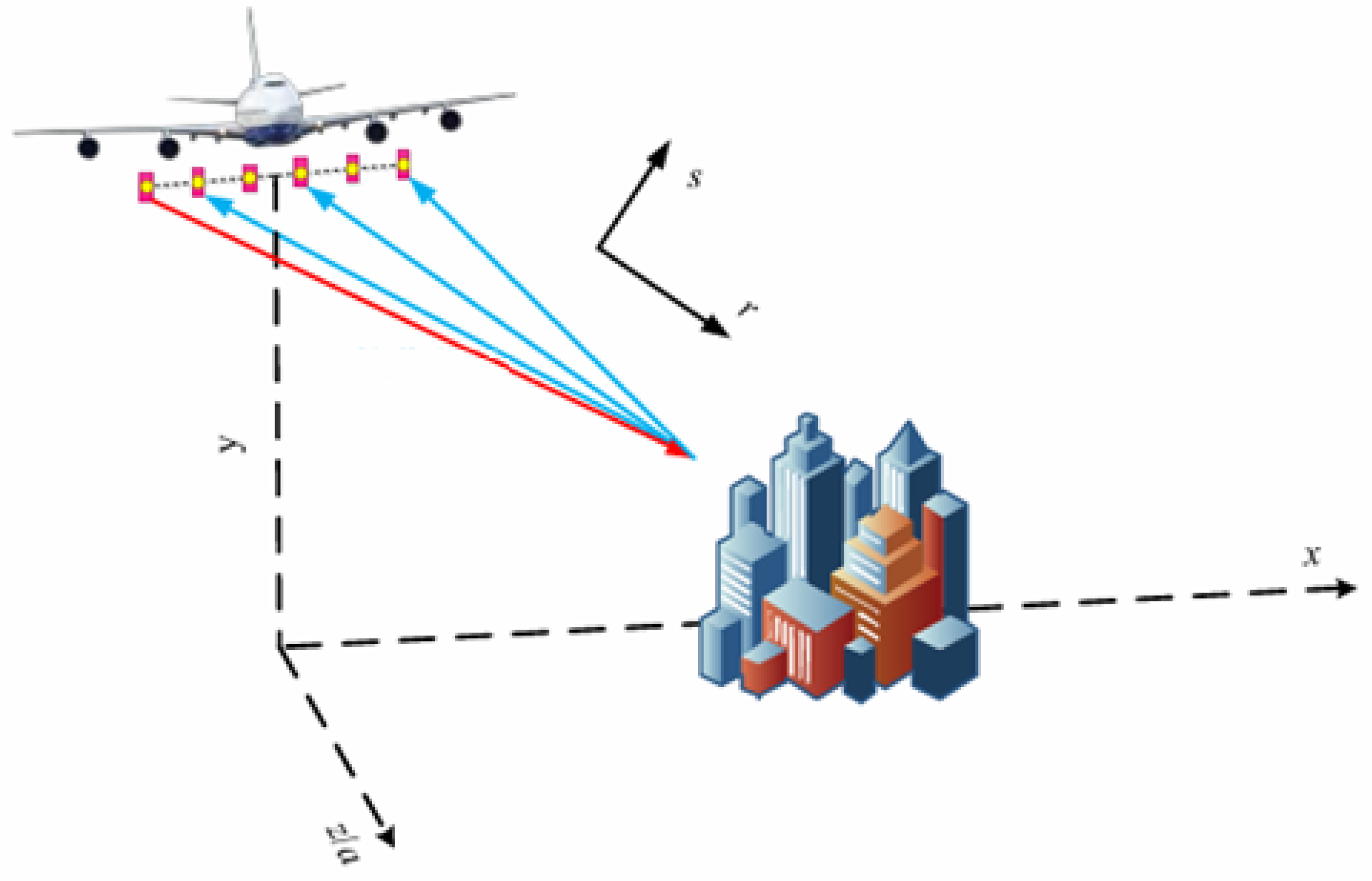
2.1. 3D-Imaging Principle of Distributed SAR System
2.2. 3D Blur Suppression Method
2.3. Calculation of Defocused Point Clouds
- Inverse Fourier Transform (IFT) in the height direction
- 2.
- Azimuth Defocusing
- 3.
- Range Offset and Sinc Defocusing
- 4.
- Phase Error Compensation
- 5.
- Fourier Transform (FT) in the channel direction
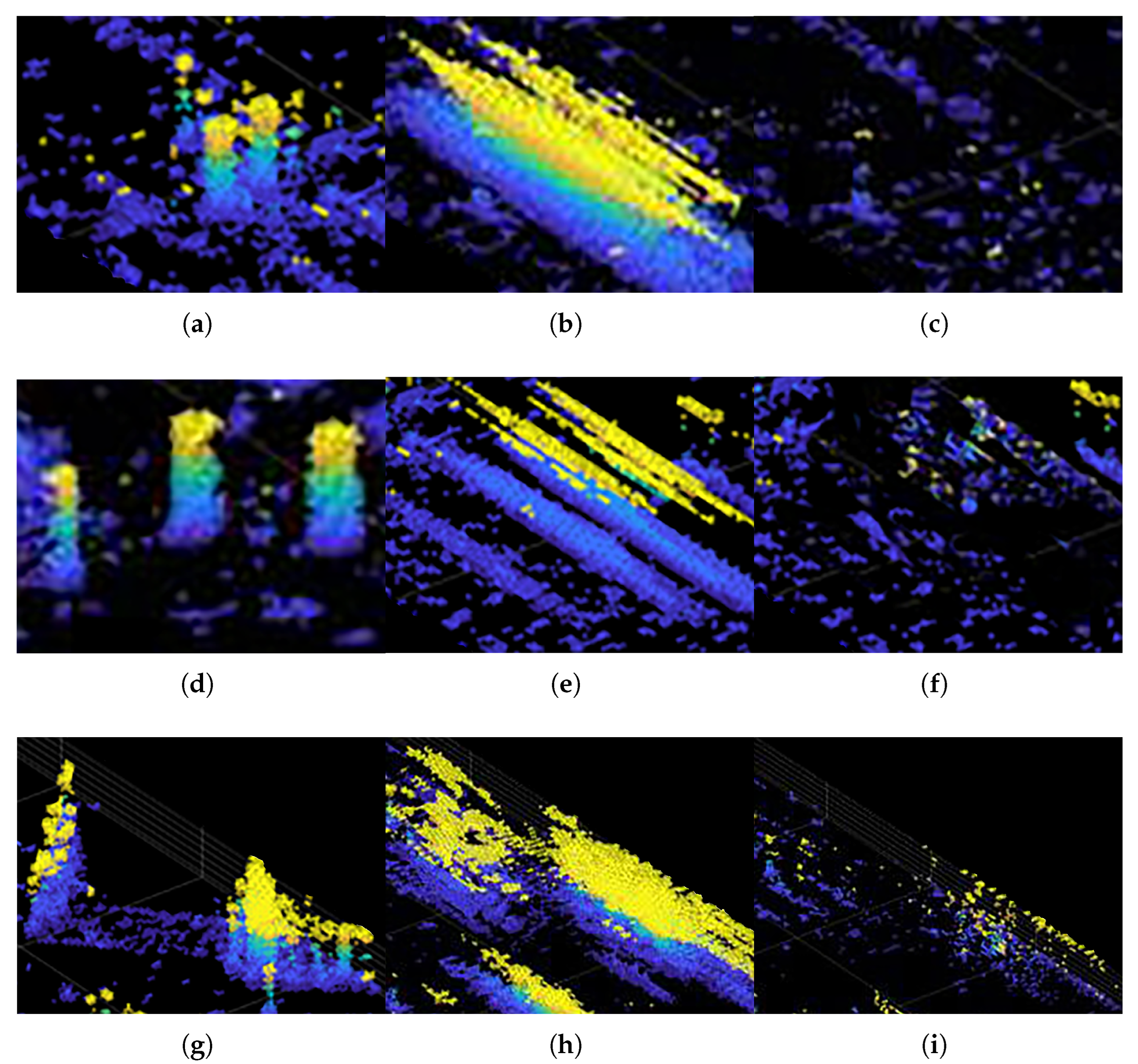
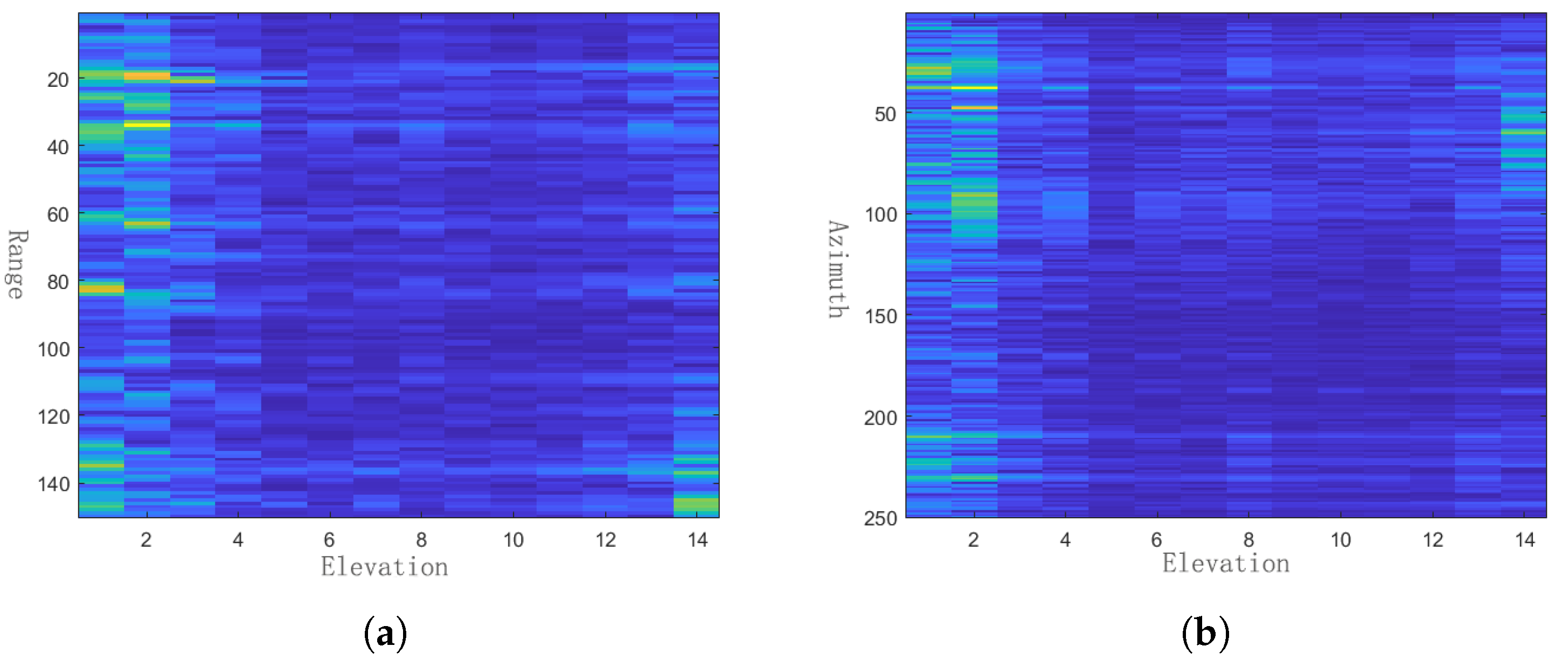
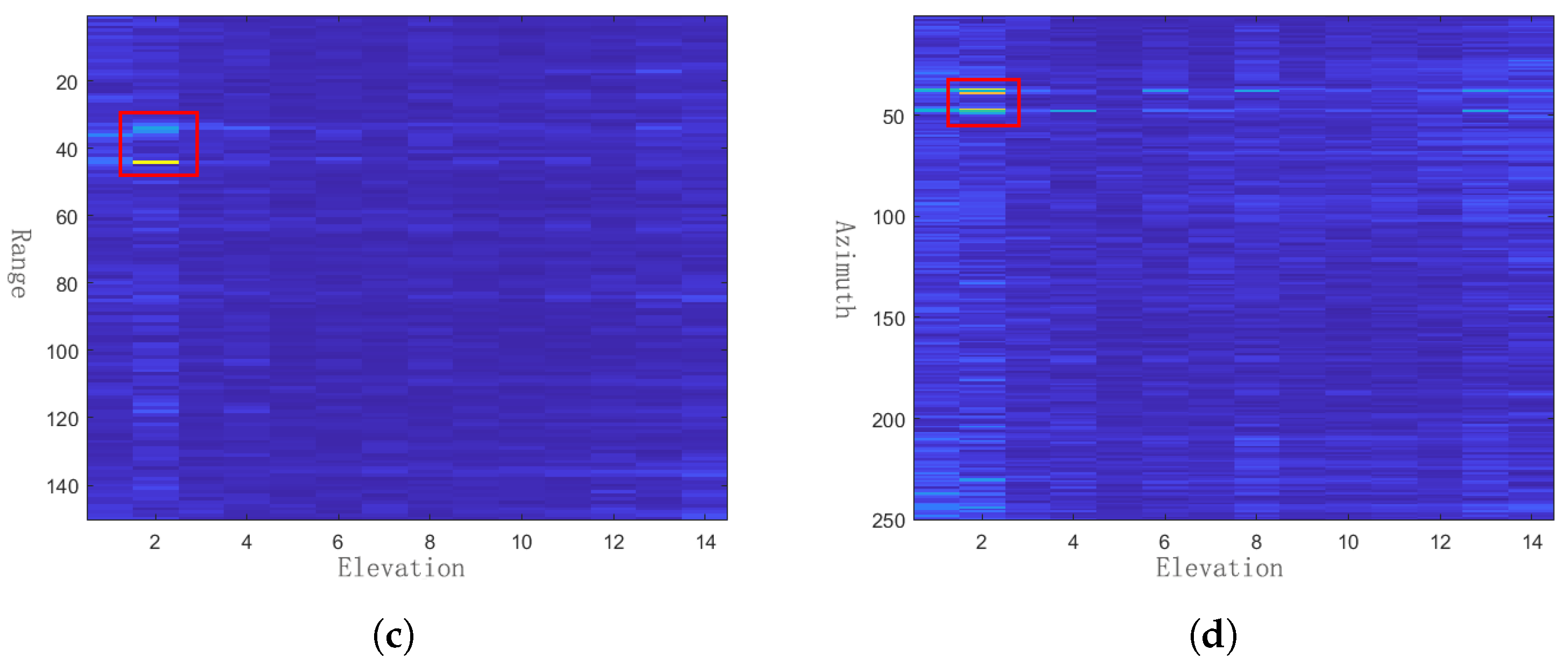
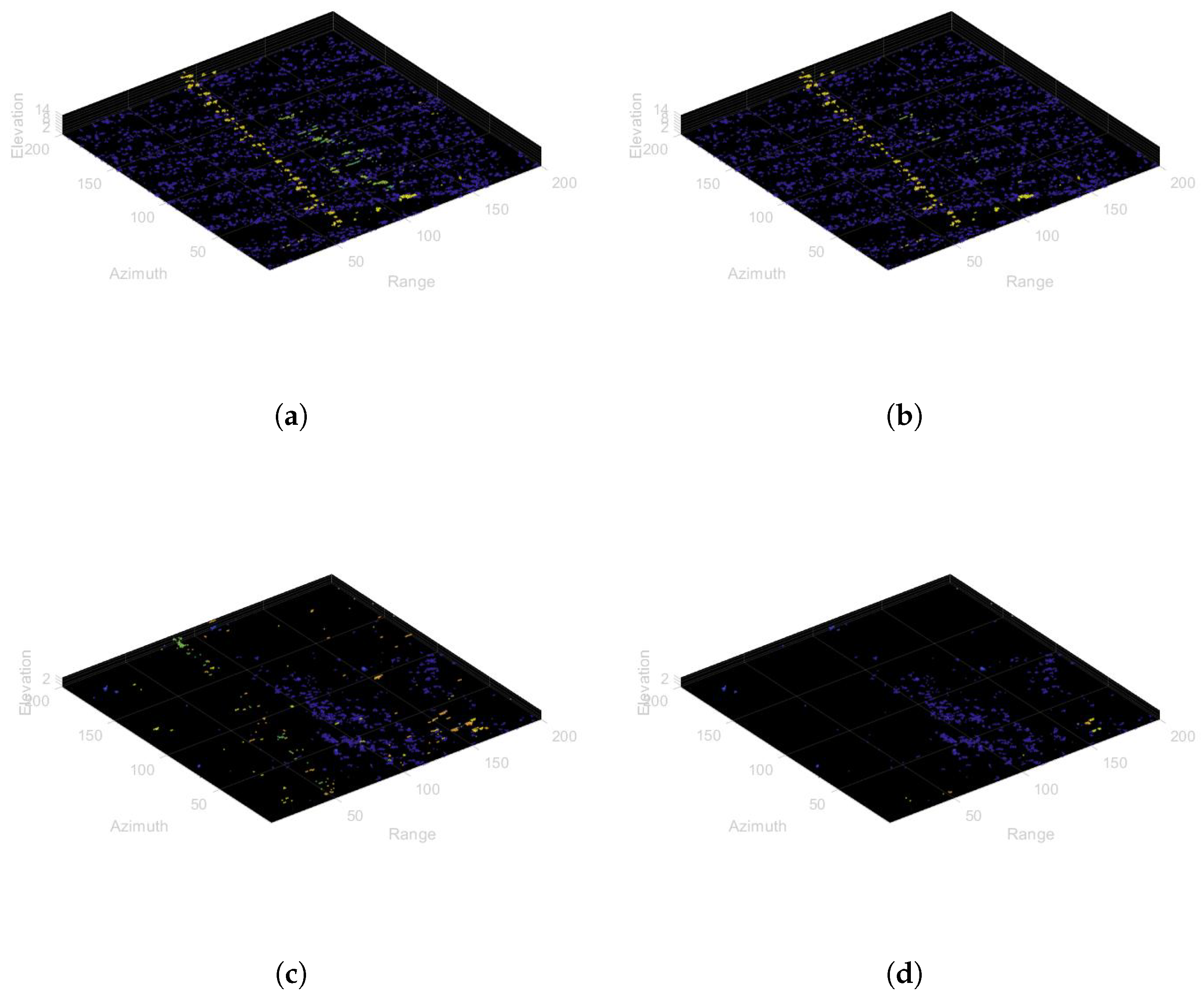
3. Experiments and Results
3.1. Study Area and Data
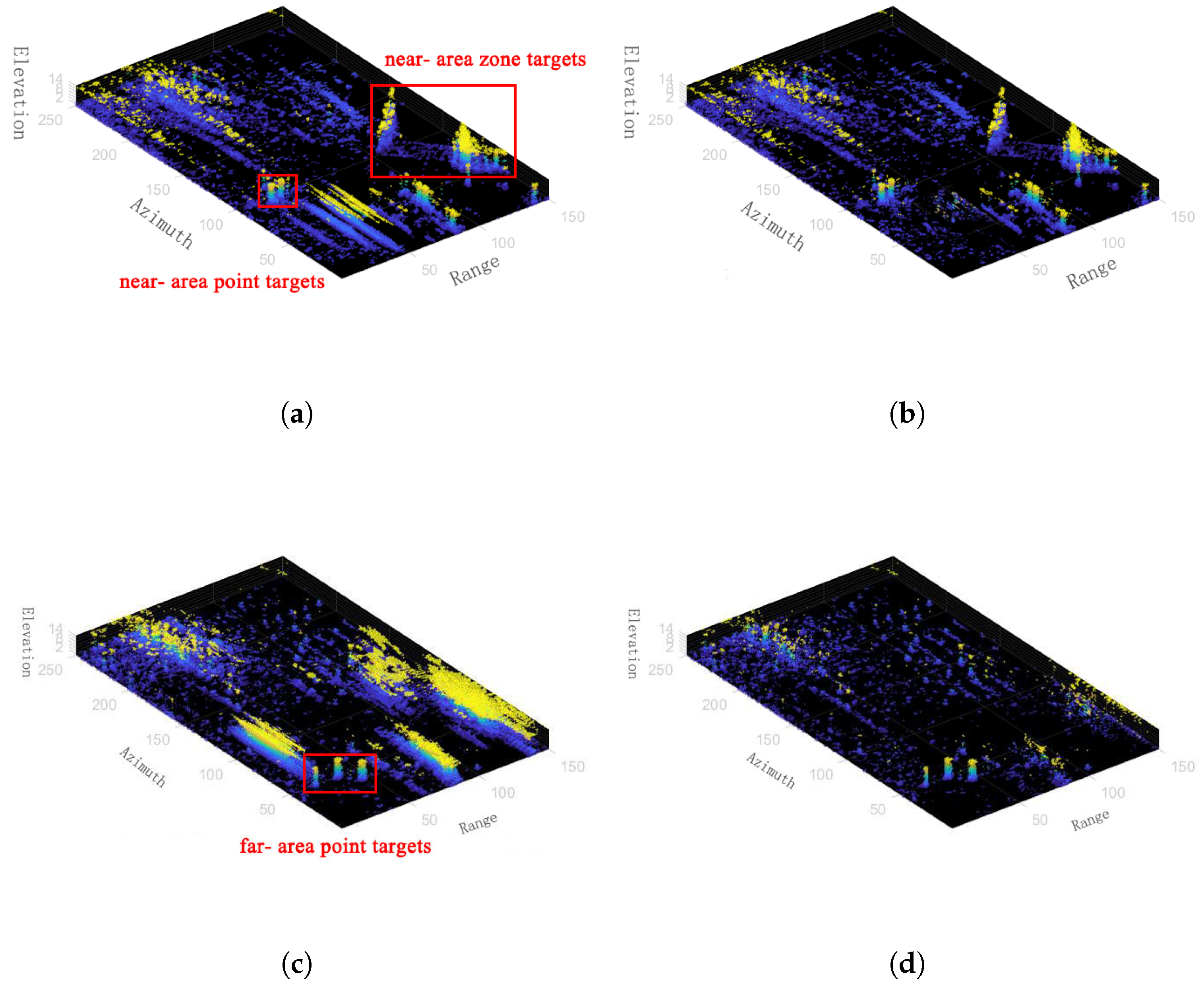
3.2. Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Goodman, N.; Lin, S.C.; Rajakrishna, D.; Stiles, J. Processing of multiple-receiver spaceborne arrays for wide-area SAR. IEEE Trans. Geosci. Remote Sens. 2002, 40, 841–852. [Google Scholar] [CrossRef]
- Das, A.; Cobb, R.G.; Stallard, M. Techsat 21—A revolutionary concept in distributed space based sensing. In Proceedings of the AIAA Defense and Civil Space Programs Conference and Exhibit, Huntsville, AL, USA, 28–30 October 1998. [Google Scholar] [CrossRef]
- Martin, M.; Stallard, M. Distributed satellite missions and technologies—The TechSat 21 program. In Proceedings of the Space Technology Conference and Exposition, Albuquerque, NM, USA, 28–30 September 1999. [Google Scholar] [CrossRef]
- Jilla, C.; Miller, D. A Multiobjective, Multidisciplinary Design Optimization Methodology for the Conceptual Design of Distributed Satellite Systems. In Proceedings of the 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, GA, USA, 4–6 September 2002. [Google Scholar] [CrossRef]
- Burns, R.; McLaughlin, C.; Leitner, J.; Martin, M. TechSat 21: Formation design, control, and simulation. In Proceedings of the 2000 IEEE Aerospace Conference, Big Sky, MT, USA, 18–25 March 2000. [Google Scholar] [CrossRef]
- Girard, R.; Séguin, G. The RADARSAT-2 & 3 interferometric mission. In Proceedings of the 2002 9th International Symposium on Antenna Technology and Applied Electromagnetics, St. Hubert, QC, Canada, 31 July–2 August 2002; pp. 1–4. [Google Scholar]
- Lee, P.; James, K. The RADARSAT-2/3 topographic mission. In Proceedings of the IEEE 2001 International Geoscience and Remote Sensing Symposium, Scanning the Present and Resolving the Future, Sydney, NSW, Australia, 9–13 July 2001; Proceedings (Cat. No.01CH37217). IEEE: New York, NY, USA, 2001; Volume 1, pp. 499–501. [Google Scholar] [CrossRef]
- Cote, S.; Lapointe, M.; De Lisle, D.; Arsenault, E.; Wierus, M. The RADARSAT Constellation: Mission Overview and Status. In Proceedings of the EUSAR 2021, 13th European Conference on Synthetic Aperture Radar, Online, 29 March–1 April 2021; pp. 1–5. [Google Scholar]
- Moro, M.; Chini, M.; Saroli, M.; Atzori, S.; Stramondo, S.; Salvi, S. Analysis of large, seismically induced, gravitational deformations imaged by high-resolution COSMO-SkyMed synthetic aperture radar. Ann. Biol. Clin. 2011, 39, 527–530. [Google Scholar] [CrossRef]
- Massonnet, D. Capabilities and limitations of the interferometric cartwheel. IEEE Trans. Geosci. Remote Sens. 2001, 39, 506–520. [Google Scholar] [CrossRef]
- Massonnet, D. The interferometric cartwheel: A constellation of passive satellites to produce radar images to be coherently combined. Int. J. Remote Sens. 2001, 22, 2413–2430. [Google Scholar] [CrossRef]
- Romeiser, R. On the suitability of a TerraSAR-L Interferometric Cartwheel for ocean current measurements. In Proceedings of the IGARSS 2004—2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; Volume 5, pp. 3345–3348. [Google Scholar] [CrossRef]
- Mittermayer, J.; Krieger, G.; Moreira, A.; Wendler, M. Interferometric performance estimation for the interferometric Cartwheel in combination with a transmitting SAR-satellite. In Proceedings of the IEEE 2001 International Geoscience and Remote Sensing Symposium, Scanning the Present and Resolving the Future, Sydney, NSW, Australia, 9–13 July 2001; Proceedings (Cat. No.01CH37217). IEEE: New York, NY, USA, 2001; Volume 7, pp. 2955–2957. [Google Scholar] [CrossRef]
- Ebner, H.; Riegger, S.; Hajnsek, I.; Hounam, D.; Krieger, G.; Moreira, A.; Werner, M. Single-Pass SAR Interferometry with a Tandem TerraSAR-X Configuration. In Proceedings of the EUSAR 2004, Ulm, Germany, 25–27 May 2004; VDE/ITG, Ed.; VDE: San Jose, CA, USA, 2004; Volumes 1 and 2, p. 53. [Google Scholar]
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. TanDEM-X: A Satellite Formation for High-Resolution SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3317–3341. [Google Scholar] [CrossRef]
- Fiedler, H.; Krieger, G.; Werner, M.; Reiniger, K.; Eineder, M.; D’Amico, S.; Diedrich, E.; Wickler, M. The TanDEM-X Mission Design and Data Acquisition Plan. In Proceedings of the European Conference on Synthetic Aperture Radar (EUSAR), Dresden, Germany, 16–18 May 2006; VDE, Ed.; VDE: San Jose, CA, USA, 2006; p. 4. [Google Scholar]
- Sanfourche, J.P. ‘SAR-lupe’, an important German initiative. Air Space Eur. 2000, 2, 26–27. [Google Scholar] [CrossRef]
- Mou, J.; Wang, Y.; Fu, X.; Guo, S.; Lu, J.; Yang, R.; Ma, X.; Hong, J. Initial Results of Geometric Calibration of Interferometric Cartwheel SAR HT-1. In Proceedings of the IGARSS 2024—2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; pp. 8886–8890. [Google Scholar] [CrossRef]
- Callaghan, G.D.; Longstaff, I.D. Wide-swath space-borne SAR using a quad-element array. IEE Proc.—Radar Sonar Navig. 1999, 146, 159–165. [Google Scholar] [CrossRef]
- Bordoni, F.; Younis, M.; Varona, E.M.; Gebert, N.; Krieger, G. Performance Investigation on Scan-On-Receive and Adaptive Digital Beam-Forming for High-Resolution Wide-Swath Synthetic Aperture Radar. In Proceedings of the International ITG Workshop of Smart Antennas, Berlin, Germany, 16–18 February 2009; EURASIP, Ed.; Informationstechnische Gesellschaft im VDE, ITG: San Jose, CA, USA, 2009; pp. 114–121. [Google Scholar]
- Gebert, N.; Krieger, G.; Moreira, A. Digital Beamforming on Receive: Techniques and Optimization Strategies for High-Resolution Wide-Swath SAR Imaging. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 564–592. [Google Scholar] [CrossRef]
- Suess, M.; Grafmueller, B.; Zahn, R. A novel high resolution, wide swath SAR system. In Proceedings of the IEEE 2001 International Geoscience and Remote Sensing Symposium, Scanning the Present and Resolving the Future, Sydney, NSW, Australia, 9–13 July 2001; Proceedings (Cat. No.01CH37217). Volume 3, pp. 1013–1015. [Google Scholar] [CrossRef]
- Makhoul Varona, E. Adaptive Digital Beam-Forming for High-Resolution Wide-Swath Synthetic Aperture Radar. Ph.D. Thesis, UPC, Escola Tècnica Superior d’Enginyeria de Telecomunicació de Barcelona, Departament de Teoria del Senyal i Comunicacions, Barcelona, Spain, 2009. [Google Scholar]
- Liu, B.; He, Y. Improved DBF Algorithm for Multichannel High-Resolution Wide-Swath SAR. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1209–1225. [Google Scholar] [CrossRef]
- Xie, H.; Gao, Y.; Dang, X.; Tan, X.; Li, S.; Chang, X. A robust DBF method for Spaceborne SAR. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Ye, S.; Yang, T.; Li, W. A Novel Algorithm for Spacebome SAR DBF Based on Sparse Spatial Spectrum Estimation. In Proceedings of the 2018 China International SAR Symposium (CISS), Shanghai, China, 10–12 October 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, F.; Tian, Y.; Chen, L.; Wang, R.; Wu, Y. High-Resolution and Wide-Swath 3D Imaging for Urban Areas Based on Distributed Spaceborne SAR. Remote Sens. 2023, 15, 3938. [Google Scholar] [CrossRef]
- Wang, W.Q. Range-Angle Dependent Transmit Beampattern Synthesis for Linear Frequency Diverse Arrays. IEEE Trans. Antennas Propag. 2013, 61, 4073–4081. [Google Scholar] [CrossRef]
- Xu, J.; Liao, G.; Zhu, S. Receive beamforming of frequency diverse array radar systems. In Proceedings of the 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), Beijing, China, 16–23 August 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Sammartino, P.F.; Baker, C.J.; Griffiths, H.D. Frequency Diverse MIMO Techniques for Radar. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 201–222. [Google Scholar] [CrossRef]
- Wang, W.Q.; So, H.C.; Shao, H. Nonuniform Frequency Diverse Array for Range-Angle Imaging of Targets. IEEE Sens. J. 2014, 14, 2469–2476. [Google Scholar] [CrossRef]
- Wei, J.; Li, Y.; Sun, Z. A Range Ambiguity Resolution Method for High-Resolution and Wide-Swath SAR Imaging Based on Continuous Pulse Coding. In Proceedings of the 2021 CIE International Conference on Radar (Radar), Hainan, China, 15–19 December 2021; pp. 211–214. [Google Scholar] [CrossRef]
- Wen, X.; Qiu, X.; Han, B.; Ding, C.; Lei, B.; Chen, Q. A Range Ambiguity Suppression Processing Method for Spaceborne SAR with Up and Down Chirp Modulation. Sensors 2018, 18, 1454. [Google Scholar] [CrossRef] [PubMed]
- Chang, S.; Deng, Y.; Zhang, Y.; Zhao, Q.; Wang, R.; Zhang, K. An Advanced Scheme for Range Ambiguity Suppression of Spaceborne SAR Based on Blind Source Separation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5230112. [Google Scholar] [CrossRef]
- Chang, S.; Deng, Y.; Zhang, Y.; Zhao, Q.; Wang, R.; Jia, X. An Advanced Scheme for Range Ambiguity Suppression of Spaceborne SAR Based on Cocktail Party Effect. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 2075–2078. [Google Scholar] [CrossRef]
- Budillon, A.; Evangelista, A.; Schirinzi, G. Three-Dimensional SAR Focusing From Multipass Signals Using Compressive Sampling. IEEE Trans. Geosci. Remote Sens. 2011, 49, 488–499. [Google Scholar] [CrossRef]










| Parameter | Value |
|---|---|
| Center frequency | 10 GHz |
| Flight height | 5 km |
| Bandwidth | 500 MHz |
| Baseline length | 2.0 m |
| Baseline interval | 0.2 m |
| The horizontal inclination of the baseline | 0° |
| Central incidence angle | 35° |
| Near Area | Far Area |
|---|---|
| 87.2% | 92.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhang, F.; Chen, L.; Jiang, T. A 3D Blur Suppression Method for High-Resolution and Wide-Swath Blurred Images Based on Estimating and Eliminating Defocused Point Clouds. Remote Sens. 2025, 17, 928. https://doi.org/10.3390/rs17050928
Liu Y, Zhang F, Chen L, Jiang T. A 3D Blur Suppression Method for High-Resolution and Wide-Swath Blurred Images Based on Estimating and Eliminating Defocused Point Clouds. Remote Sensing. 2025; 17(5):928. https://doi.org/10.3390/rs17050928
Chicago/Turabian StyleLiu, Yuling, Fubo Zhang, Longyong Chen, and Tao Jiang. 2025. "A 3D Blur Suppression Method for High-Resolution and Wide-Swath Blurred Images Based on Estimating and Eliminating Defocused Point Clouds" Remote Sensing 17, no. 5: 928. https://doi.org/10.3390/rs17050928
APA StyleLiu, Y., Zhang, F., Chen, L., & Jiang, T. (2025). A 3D Blur Suppression Method for High-Resolution and Wide-Swath Blurred Images Based on Estimating and Eliminating Defocused Point Clouds. Remote Sensing, 17(5), 928. https://doi.org/10.3390/rs17050928






