Influences of Global Warming and Upwelling on the Acidification in the Beaufort Sea
Abstract
1. Introduction
2. Materials and Methods
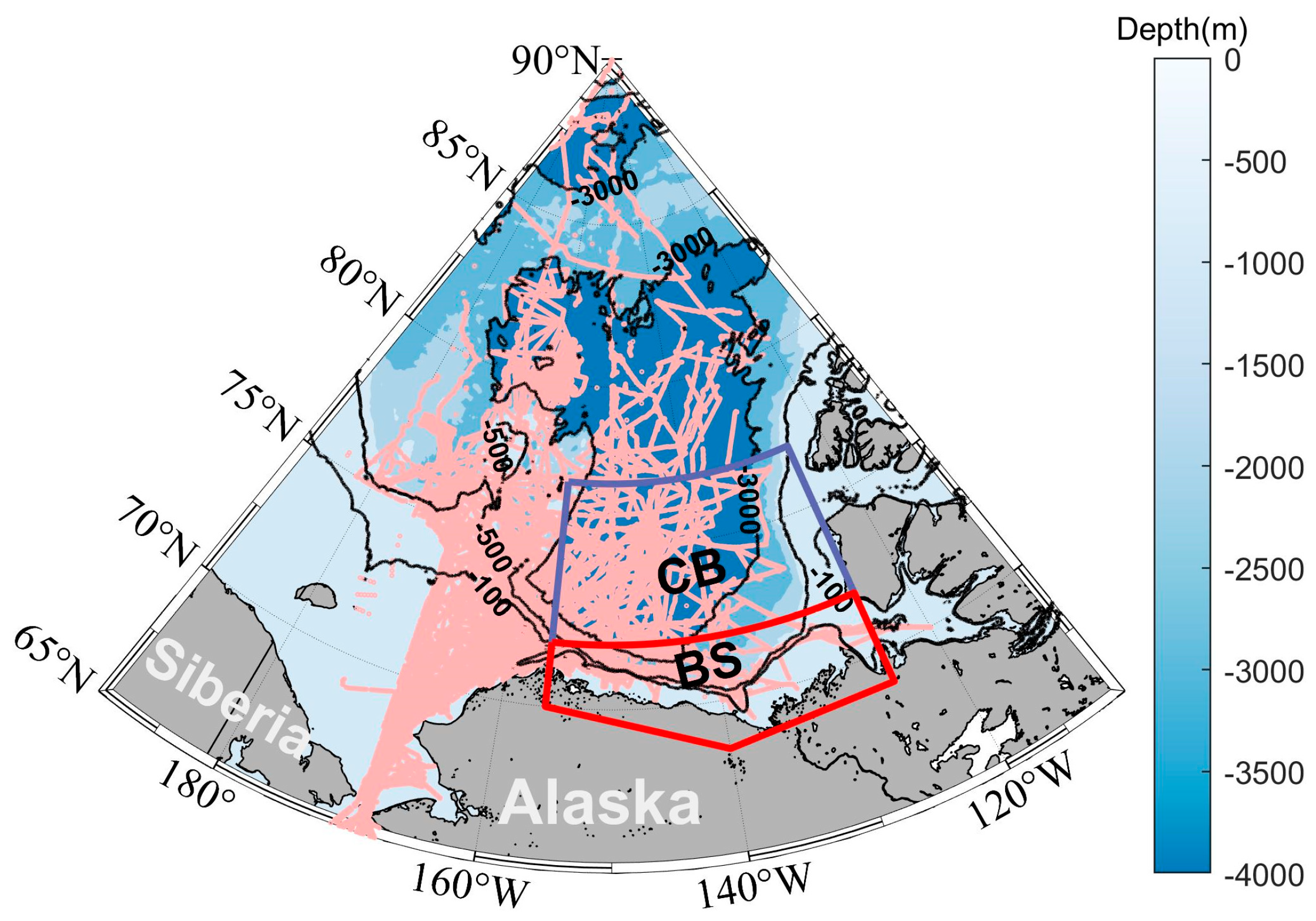
2.1. The RASM and Study Area
2.2. NSIDC Sea Ice Data, In Situ Observations and JRA-55 Reanalysis Data
2.3. EPV and Multiple Linear Regression Calculations
3. Results
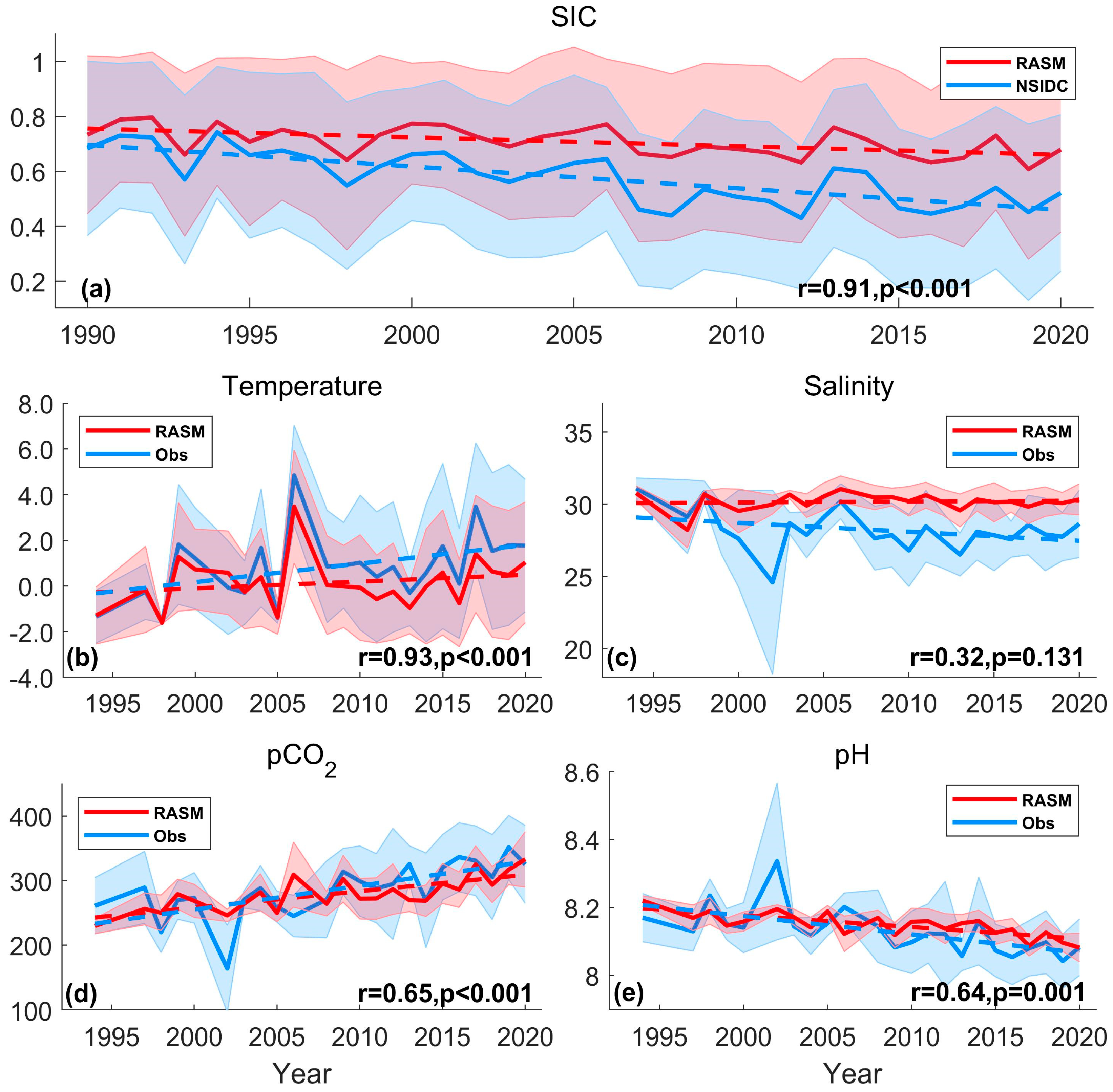
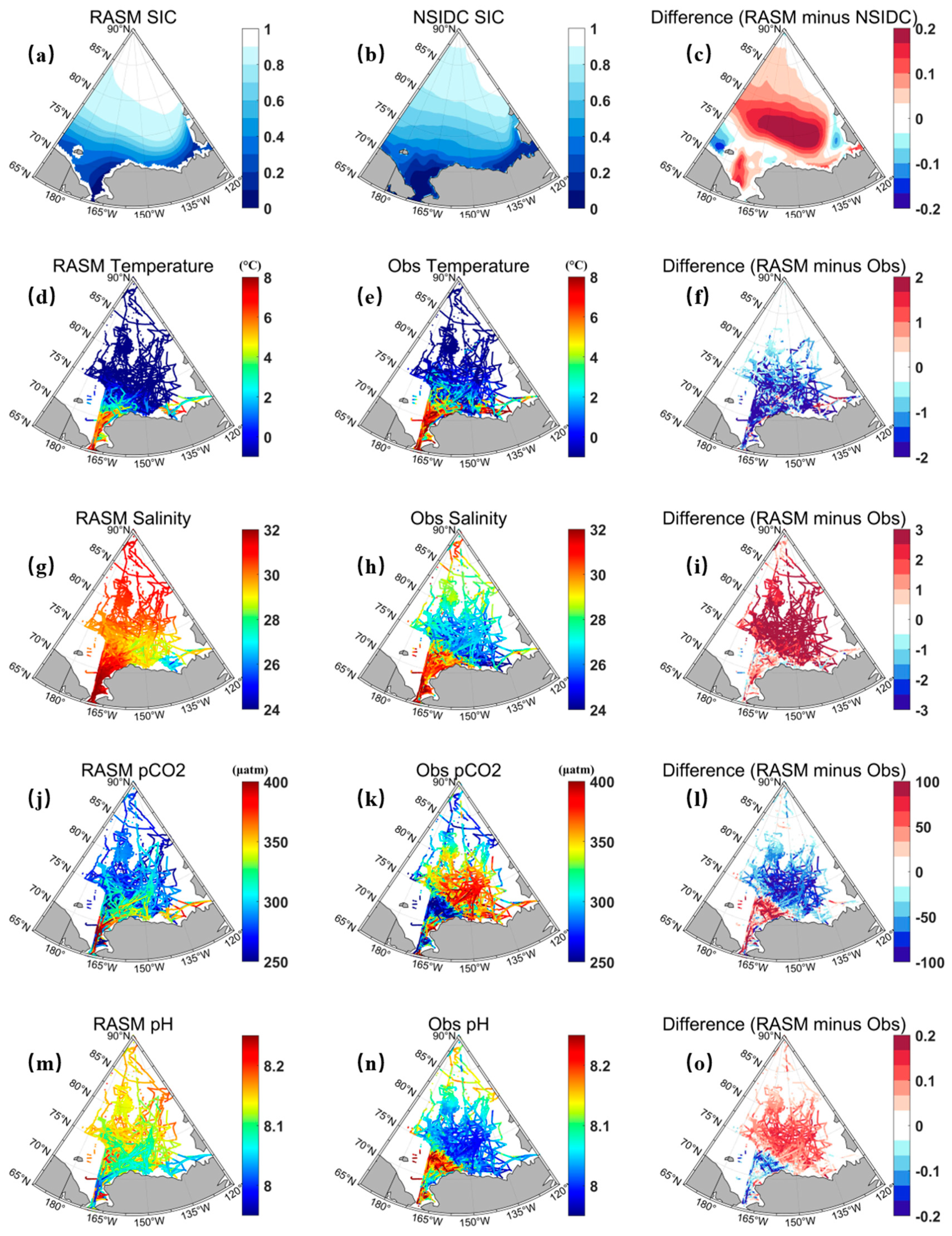
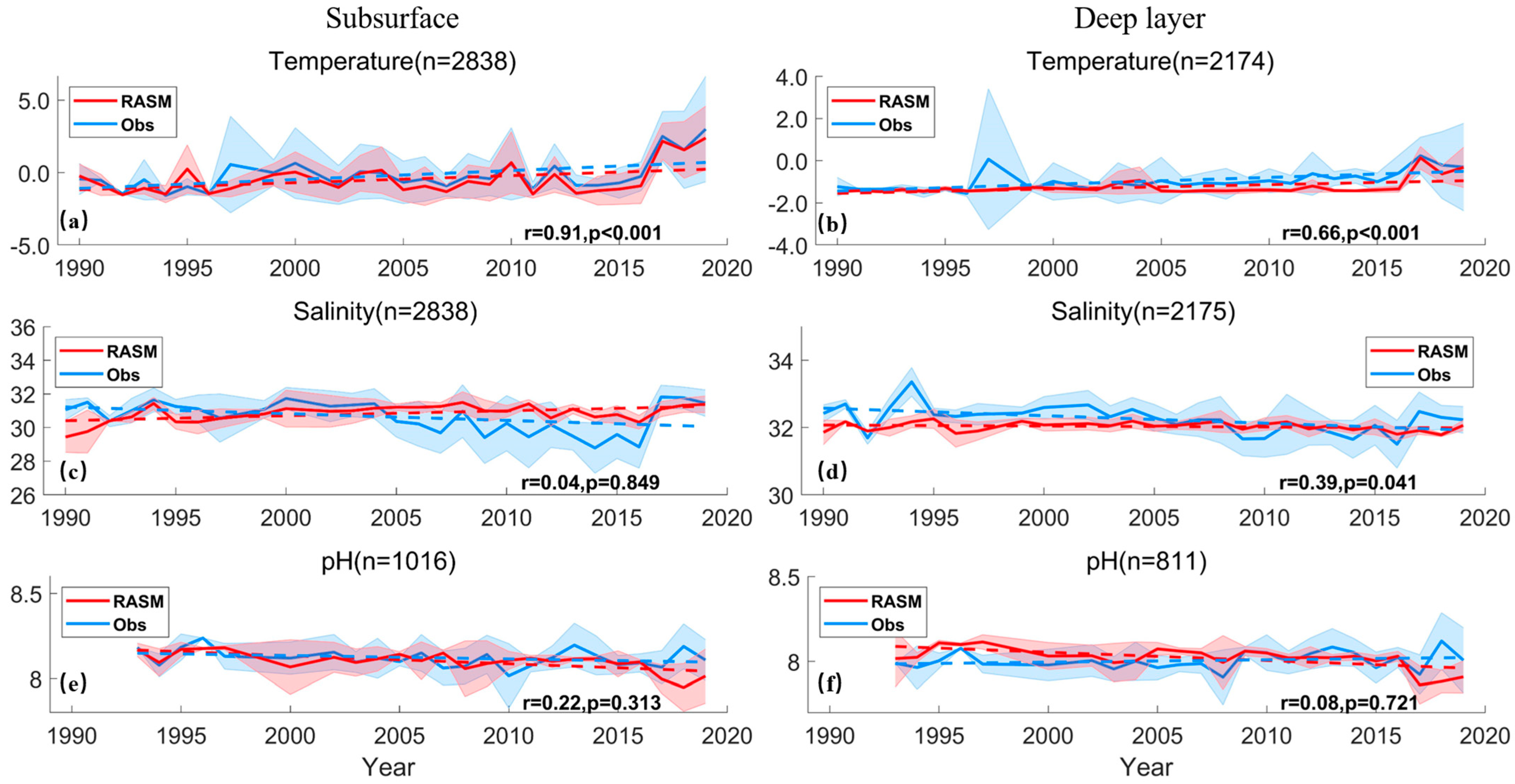
3.1. Model Validation
3.2. Long-Term Trends of Changes in the BS
3.3. Interannual Variation in Ph in the BS
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Budget, G.C. Global Carbon Budget 2023; Global Carbon Budget: Exeter, UK, 2023. [Google Scholar]
- Sabine, C.L.; Feely, R.A.; Gruber, N.; Key, R.M.; Lee, K.; Bullister, J.L.; Wanninkhof, R.; Wong, C.S.; Wallace, D.W.R.; Tilbrook, B.; et al. The Oceanic Sink for Anthropogenic CO2. Science 2004, 305, 367–371. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, T.; Sutherland, S.C.; Wanninkhof, R.; Sweeney, C.; Feely, R.A.; Chipman, D.W.; Hales, B.; Friederich, G.; Chavez, F.; Sabine, C.; et al. Climatological Mean and Decadal Change in Surface Ocean pCO2, and Net Sea–Air CO2 Flux over the Global Oceans. Deep Sea Res. Part II 2009, 56, 554–577. [Google Scholar] [CrossRef]
- Cai, W.-J.; Chen, L.; Chen, B.; Gao, Z.; Lee, S.H.; Chen, J.; Pierrot, D.; Sullivan, K.; Wang, Y.; Hu, X.; et al. Decrease in the CO2 Uptake Capacity in an Ice-Free Arctic Ocean Basin. Science 2010, 329, 556–559. [Google Scholar] [CrossRef] [PubMed]
- Orr, J.C.; Fabry, V.J.; Aumont, O.; Bopp, L.; Doney, S.C.; Feely, R.A.; Gnanadesikan, A.; Gruber, N.; Ishida, A.; Joos, F. Anthropogenic Ocean Acidification over the Twenty-First Century and Its Impact on Calcifying Organisms. Nature 2005, 437, 681–686. [Google Scholar] [CrossRef]
- Yamamoto−Kawai, M.; McLaughlin, F.A.; Carmack, E.C.; Nishino, S.; Shimada, K. Aragonite Undersaturation in the Arctic Ocean: Effects of Ocean Acidification and Sea Ice Melt. Science 2009, 326, 1098–1100. [Google Scholar] [CrossRef]
- Feely, R.A.; Sabine, C.L.; Lee, K.; Berelson, W.; Kleypas, J.; Fabry, V.J.; Millero, F.J. Impact of Anthropogenic CO2 on the CaCO3 System in the Oceans. Science 2004, 305, 362–366. [Google Scholar] [CrossRef]
- Walsh, J.E. Climate of the Arctic Marine Environment. Ecol. Appl. 2008, 18, S3–S22. [Google Scholar] [CrossRef]
- Yasunaka, S.; Siswanto, E.; Olsen, A.; Hoppema, M.; Watanabe, E.; Fransson, A.; Chierici, M.; Murata, A.; Lauvset, S.K.; Wanninkhof, R. Arctic Ocean CO2 Uptake: An Improved Multiyear Estimate of the Air–Sea CO2 Flux Incorporating Chlorophyll a Concentrations. Biogeosciences 2018, 15, 1643–1661. [Google Scholar] [CrossRef]
- Takahashi, T.; Sutherland, S.C.; Chipman, D.W.; Goddard, J.G.; Ho, C.; Newberger, T.; Sweeney, C.; Munro, D.R. Climatological Distributions of pH, pCO2, Total CO2, Alkalinity, and CaCO3 Saturation in the Global Surface Ocean, and Temporal Changes at Selected Locations. Mar. Chem. 2014, 164, 95–125. [Google Scholar] [CrossRef]
- Qi, D.; Ouyang, Z.; Chen, L.; Wu, Y.; Lei, R.; Chen, B.; Feely, R.A.; Anderson, L.G.; Zhong, W.; Lin, H.; et al. Climate Change Drives Rapid Decadal Acidification in the Arctic Ocean from 1994 to 2020. Science 2022, 377, 1544–1550. [Google Scholar] [CrossRef]
- Duffey, A.; Mallett, R.; Irvine, P.J.; Tsamados, M.; Stroeve, J. ESD Ideas: Arctic Amplification’s Contribution to Breaches of the Paris Agreement. Earth Syst. Dyn. 2023, 14, 1165–1169. [Google Scholar] [CrossRef]
- Peng, G.; Matthews, J.L.; Yu, J.T. Sensitivity Analysis of Arctic Sea Ice Extent Trends and Statistical Projections Using Satellite Data. Remote Sens. 2018, 10, 230. [Google Scholar] [CrossRef]
- Else, B.G.T.; Papakyriakou, T.N.; Galley, R.J.; Mucci, A.; Gosselin, M.; Miller, L.A.; Shadwick, E.H.; Thomas, H. Annual Cycles of p CO2sw in the Southeastern Beaufort Sea: New Understandings of Air-sea CO2 Exchange in Arctic Polynya Regions. J. Geophys. Res. 2012, 117, C00G13. [Google Scholar] [CrossRef]
- Wang, H.; Lin, P.; Pickart, R.S.; Cross, J.N. Summer Surface CO2 Dynamics on the Bering Sea and Eastern Chukchi Sea Shelves From 1989 to 2019. JGR Ocean. 2022, 127, e2021JC017424. [Google Scholar] [CrossRef]
- Lewis, K.M.; Van Dijken, G.L.; Arrigo, K.R. Changes in Phytoplankton Concentration Now Drive Increased Arctic Ocean Primary Production. Science 2020, 369, 198–202. [Google Scholar] [CrossRef]
- Tu, Z.; Le, C.; Bai, Y.; Jiang, Z.; Wu, Y.; Ouyang, Z.; Cai, W.; Qi, D. Increase in CO2 Uptake Capacity in the Arctic Chukchi Sea During Summer Revealed by Satellite-Based Estimation. Geophys. Res. Lett. 2021, 48, e2021GL093844. [Google Scholar] [CrossRef]
- Hufford, G.L. On Apparent Upwelling in the Southern Beaufort Sea. J. Geophys. Res. 1974, 79, 1305–1306. [Google Scholar] [CrossRef]
- Else, B.G.T.; Galley, R.J.; Papakyriakou, T.N.; Miller, L.A.; Mucci, A.; Barber, D. Sea Surface p CO2 Cycles and CO2 Fluxes at Landfast Sea Ice Edges in Amundsen Gulf, Canada. J. Geophys. Res. 2012, 117, C007901. [Google Scholar] [CrossRef]
- Tremblay, J.-É.; Bélanger, S.; Barber, D.G.; Asplin, M.; Martin, J.; Darnis, G.; Fortier, L.; Gratton, Y.; Link, H.; Archambault, P.; et al. Climate Forcing Multiplies Biological Productivity in the Coastal Arctic Ocean: Upwelling and productivity in the arctic. Geophys. Res. Lett. 2011, 38, L18604. [Google Scholar] [CrossRef]
- Fabry, V.J.; McClintock, J.B.; Mathis, J.T.; Grebmeier, J.M. Ocean Acidification at High Latitudes: The Bellwether. Oceanography 2009, 22, 160–171. [Google Scholar] [CrossRef]
- Kroeker, K.J.; Kordas, R.L.; Crim, R.N.; Singh, G.G. Meta-analysis Reveals Negative yet Variable Effects of Ocean Acidification on Marine Organisms. Ecol. Lett. 2010, 13, 1419–1434. [Google Scholar] [CrossRef] [PubMed]
- Harvey, B.P.; Gwynn−Jones, D.; Moore, P.J. Meta-analysis Reveals Complex Marine Biological Responses to the Interactive Effects of Ocean Acidification and Warming. Ecol. Evol. 2013, 3, 1016–1030. [Google Scholar] [CrossRef] [PubMed]
- Kroeker, K.J.; Kordas, R.L.; Crim, R.; Hendriks, I.E.; Ramajo, L.; Singh, G.S.; Duarte, C.M.; Gattuso, J. Impacts of Ocean Acidification on Marine Organisms: Quantifying Sensitivities and Interaction with Warming. Glob. Change Biol. 2013, 19, 1884–1896. [Google Scholar] [CrossRef]
- Bates, N.R.; Astor, Y.M.; Church, M.J.; Currie, K.; Dore, J.E.; González−Dávila, M.; Lorenzoni, L.; Muller−Karger, F.; Olafsson, J.; Santana−Casiano, J.M. A Time-Series View of Changing Surface Ocean Chemistry Due to Ocean Uptake of Anthropogenic CO2 and Ocean Acidification. Oceanography 2014, 27, 126–141. [Google Scholar] [CrossRef]
- Yamamoto, A.; Kawamiya, M.; Ishida, A.; Yamanaka, Y.; Watanabe, S. Impact of Rapid Sea-Ice Reduction in the Arctic Ocean on the Rate of Ocean Acidification. Biogeosciences 2012, 9, 2365–2375. [Google Scholar] [CrossRef]
- Terhaar, J.; Torres, O.; Bourgeois, T.; Kwiatkowski, L. Arctic Ocean Acidification over the 21st Century Co-Driven by Anthropogenic Carbon Increases and Freshening in the CMIP6 Model Ensemble. Biogeosciences 2021, 18, 2221–2240. [Google Scholar] [CrossRef]
- Ouyang, Z.; Qi, D.; Chen, L.; Takahashi, T.; Zhong, W.; DeGrandpre, M.D.; Chen, B.; Gao, Z.; Nishino, S.; Murata, A.; et al. Sea-Ice Loss Amplifies Summertime Decadal CO2 Increase in the Western Arctic Ocean. Nat. Clim. Change 2020, 10, 678–684. [Google Scholar] [CrossRef]
- Meneghello, G.; Marshall, J.; Timmermans, M.-L.; Scott, J. Observations of Seasonal Upwelling and Downwelling in the Beaufort Sea Mediated by Sea Ice. J. Phys. Oceanogr. 2018, 48, 795–805. [Google Scholar] [CrossRef]
- Ma, B.; Steele, M.; Lee, C.M. Ekman Circulation in the A Rctic O Cean: Beyond the B Eaufort G Yre. JGR Ocean. 2017, 122, 3358–3374. [Google Scholar] [CrossRef]
- Xu, A.; Jin, M.; Wu, Y.; Qi, D. Response of Nutrients and Primary Production to High Wind and Upwelling-Favorable Wind in the Arctic Ocean: A Modeling Perspective. Front. Mar. Sci. 2023, 10, 1065006. [Google Scholar] [CrossRef]
- Mathis, J.T.; Pickart, R.S.; Byrne, R.H.; McNeil, C.L.; Moore, G.W.K.; Juranek, L.W.; Liu, X.; Ma, J.; Easley, R.A.; Elliot, M.M.; et al. Storm-induced Upwelling of High p CO2 Waters onto the Continental Shelf of the Western Arctic Ocean and Implications for Carbonate Mineral Saturation States. Geophys. Res. Lett. 2012, 39, L07606. [Google Scholar] [CrossRef]
- Mol, J.; Thomas, H.; Myers, P.G.; Hu, X.; Mucci, A. Inorganic Carbon Fluxes on the Mackenzie Shelf of the Beaufort Sea. Biogeosciences 2018, 15, 1011–1027. [Google Scholar] [CrossRef]
- Peralta−Ferriz, C.; Woodgate, R.A. Seasonal and Interannual Variability of Pan-Arctic Surface Mixed Layer Properties from 1979 to 2012 from Hydrographic Data, and the Dominance of Stratification for Multiyear Mixed Layer Depth Shoaling. Prog. Oceanogr. 2015, 134, 19–53. [Google Scholar] [CrossRef]
- Jin, M.; Deal, C.; Maslowski, W.; Matrai, P.; Roberts, A.; Osinski, R.; Lee, Y.J.; Frants, M.; Elliott, S.; Jeffery, N.; et al. Effects of Model Resolution and Ocean Mixing on Forced Ice-Ocean Physical and Biogeochemical Simulations Using Global and Regional System Models. JGR Ocean. 2018, 123, 358–377. [Google Scholar] [CrossRef]
- Jin, M.; Popova, E.E.; Zhang, J.; Ji, R.; Pendleton, D.; Varpe, Ø.; Yool, A.; Lee, Y.J. Ecosystem Model Intercomparison of Under-ice and Total Primary Production in the A Rctic O Cean. JGR Ocean. 2016, 121, 934–948. [Google Scholar] [CrossRef]
- Steele, M.; Morley, R.; Ermold, W. PHC: A Global Ocean Hydrography with a High-Quality Arctic Ocean. J. Clim. 2001, 14, 2079–2087. [Google Scholar] [CrossRef]
- Harada, Y.; Kamahori, H.; Kobayashi, C.; Endo, H.; Kobayashi, S.; Ota, Y.; Onoda, H.; Onogi, K.; Miyaoka, K.; Takahashi, K. The JRA-55 Reanalysis: Representation of Atmospheric Circulation and Climate Variability. J. Meteorol. Soc. Japan. Ser. II 2016, 94, 269–302. [Google Scholar] [CrossRef]
- Moore, J.K.; Doney, S.C.; Lindsay, K. Upper Ocean Ecosystem Dynamics and Iron Cycling in a Global Three-dimensional Model. Glob. Biogeochem. Cycles 2004, 18, GB4028. [Google Scholar] [CrossRef]
- DiGirolamo, N.; Parkinson, C.L.; Cavalieri, D.J.; Gloersen, P.; Zwally, H.J. Sea Ice Concentrations from Nimbus-7 SMMR and DMSP SSM/I-SSMIS Passive Microwave Data, Version 2; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2022. [Google Scholar]
- Olsen, A.; Key, R.M.; Van Heuven, S.; Lauvset, S.K.; Velo, A.; Lin, X.; Schirnick, C.; Kozyr, A.; Tanhua, T.; Hoppema, M. The Global Ocean Data Analysis Project Version 2 (GLODAPv2)—An Internally Consistent Data Product for the World Ocean. Earth Syst. Sci. Data 2016, 8, 297–323. [Google Scholar] [CrossRef]
- Key, R.M.; Olsen, A.; van Heuven, S.; Lauvset, S.K.; Velo, A.; Lin, X.; Schirnick, C.; Kozyr, A.; Tanhua, T.; Hoppema, M. Global Ocean Data Analysis Project, Version 2 (GLODAPv2). Ornl/Cdiac-162 Ndp-093. 2015. Available online: https://glodap.info/index.php/data-access/ (accessed on 3 June 2024).
- Kobayashi, C.; Iwasaki, T. Brewer-Dobson Circulation Diagnosed from JRA-55. JGR Atmos. 2016, 121, 1493–1510. [Google Scholar] [CrossRef]
- Yang, J. The Seasonal Variability of the Arctic Ocean Ekman Transport and Its Role in the Mixed Layer Heat and Salt Fluxes. J. Clim. 2006, 19, 5366–5387. [Google Scholar] [CrossRef]
- Zhong, W.; Steele, M.; Zhang, J.; Zhao, J. Greater Role of Geostrophic Currents in Ekman Dynamics in the Western Arctic Ocean as a Mechanism for Beaufort Gyre Stabilization. JGR Ocean. 2018, 123, 149–165. [Google Scholar] [CrossRef]
- McPhee, M.G. An Analysis of Pack Ice Drift in Summer. In Sea Ice Processes Models; Pritchard, R., Ed.; University of Washington Press: Seattle, WA, USA, 1980; pp. 62–75. [Google Scholar]
- Lee, K.; Wanninkhof, R.; Feely, R.A.; Millero, F.J.; Peng, T. Global Relationships of Total Inorganic Carbon with Temperature and Nitrate in Surface Seawater. Glob. Biogeochem. Cycles 2000, 14, 979–994. [Google Scholar] [CrossRef]
- Bozec, Y.; Thomas, H.; Schiettecatte, L.-S.; Borges, A.V.; Elkalay, K.; De Baar, H.J.W. Assessment of the Processes Controlling the Seasonal Variations of Dissolved Inorganic Carbon in the North Sea. Limnol. Oceanogr. 2006, 51, 2746–2762. [Google Scholar] [CrossRef]
- Lee, K.; Tong, L.T.; Millero, F.J.; Sabine, C.L.; Dickson, A.G.; Goyet, C.; Park, G.; Wanninkhof, R.; Feely, R.A.; Key, R.M. Global Relationships of Total Alkalinity with Salinity and Temperature in Surface Waters of the World’s Oceans. Geophys. Res. Lett. 2006, 33, L19605. [Google Scholar] [CrossRef]
- Carter, B.R.; Feely, R.A.; Williams, N.L.; Dickson, A.G.; Fong, M.B.; Takeshita, Y. Updated Methods for Global Locally Interpolated Estimation of Alkalinity, pH, and Nitrate. Limnol. Ocean. Methods 2018, 16, 119–131. [Google Scholar] [CrossRef]
- Li, B.; Watanabe, Y.W.; Yamaguchi, A. Spatiotemporal Distribution of Seawater pH in the North Pacific Subpolar Region by Using the Parameterization Technique. JGR Ocean. 2016, 121, 3435–3449. [Google Scholar] [CrossRef]
- Williams, N.L.; Juranek, L.W.; Johnson, K.S.; Feely, R.A.; Riser, S.C.; Talley, L.D.; Russell, J.L.; Sarmiento, J.L.; Wanninkhof, R. Empirical Algorithms to Estimate Water Column pH in the Southern Ocean. Geophys. Res. Lett. 2016, 43, 3415–3422. [Google Scholar] [CrossRef]
- Hauri, C.; Irving, B.; Dupont, S.; Pagés, R.; Hauser, D.D.; Danielson, S.L. Insights into Carbonate Environmental Conditions in the Chukchi Sea. Biogeosciences 2024, 21, 1135–1159. [Google Scholar] [CrossRef]
- Dewey, S.; Morison, J.; Kwok, R.; Dickinson, S.; Morison, D.; Andersen, R. Arctic Ice-Ocean Coupling and Gyre Equilibration Observed with Remote Sensing. Geophys. Res. Lett. 2018, 45, 1499–1508. [Google Scholar] [CrossRef]
- Zhang, J.; Steele, M.; Runciman, K.; Dewey, S.; Morison, J.; Lee, C.; Rainville, L.; Cole, S.; Krishfield, R.; Timmermans, M.-L.; et al. The Beaufort Gyre Intensification and Stabilization: A Model-Observation Synthesis: Beaufort gyre stabilization. J. Geophys. Res. Ocean. 2016, 121, 7933–7952. [Google Scholar] [CrossRef]
- Timmermans, M.-L.; Toole, J.M. The Arctic Ocean’s Beaufort Gyre. Annu. Rev. Mar. Sci. 2023, 15, 223–248. [Google Scholar] [CrossRef] [PubMed]
- Qi, D.; Chen, B.; Chen, L.; Lin, H.; Gao, Z.; Sun, H.; Zhang, Y.; Sun, X.; Cai, W. Coastal Acidification Induced by Biogeochemical Processes Driven by Sea-Ice Melt in the Western Arctic Ocean. Polar Sci. 2020, 23, 100504. [Google Scholar] [CrossRef]
- Laney, S.R.; Krishfield, R.A.; Toole, J.M. The Euphotic Zone under Arctic Ocean Sea Ice: Vertical Extents and Seasonal Trends. Limnol. Oceanogr. 2017, 62, 1910–1934. [Google Scholar] [CrossRef]
- Zhong, W.; Steele, M.; Zhang, J.; Cole, S.T. Circulation of Pacific Winter Water in the Western Arctic Ocean. JGR Ocean. 2019, 124, 863–881. [Google Scholar] [CrossRef]
- Guo, L.; Macdonald, R.W. Source and Transport of Terrigenous Organic Matter in the Upper Yukon River: Evidence from Isotope (d13C, D14C, and d15N) Composition of Dissolved, Colloidal, and Particulate Phases. Glob. Biogeochem. Cycles 2006, 20, 1–12. [Google Scholar] [CrossRef]
- Cai, W.-J.; Hu, X.; Huang, W.-J.; Murrell, M.C.; Lehrter, J.C.; Lohrenz, S.E.; Chou, W.-C.; Zhai, W.; Hollibaugh, J.T.; Wang, Y. Acidification of Subsurface Coastal Waters Enhanced by Eutrophication. Nat. Geosci. 2011, 4, 766–770. [Google Scholar] [CrossRef]

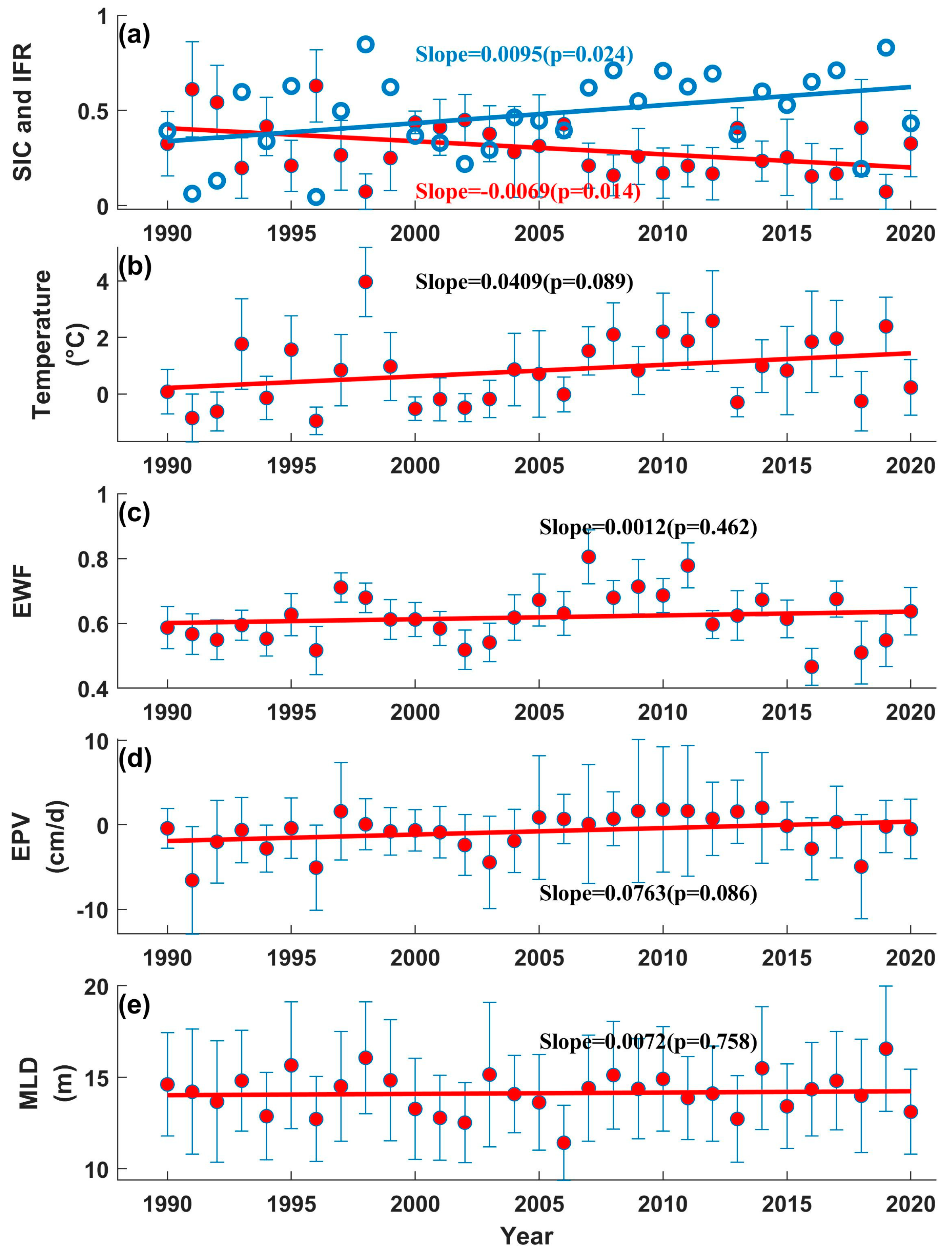
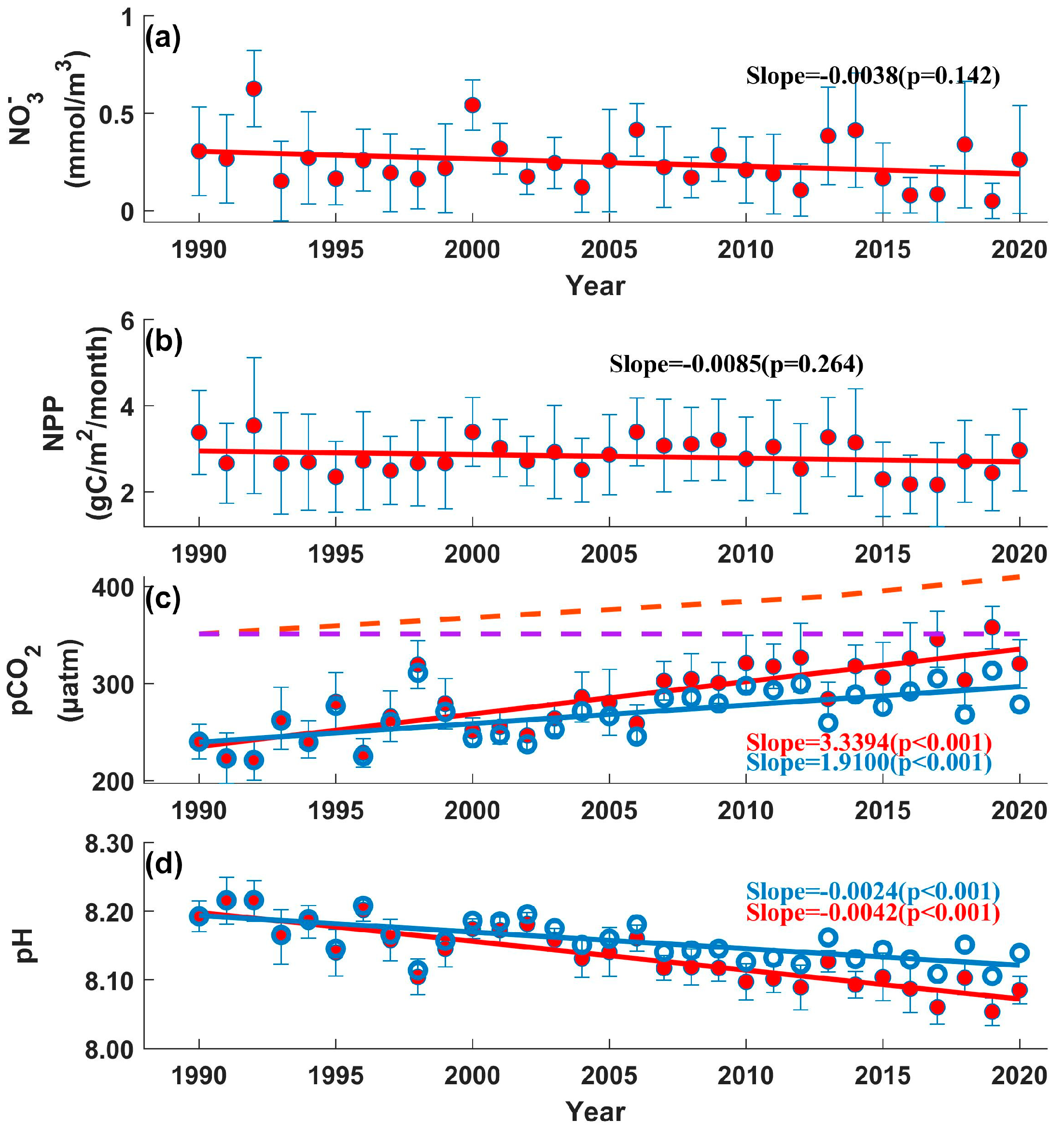
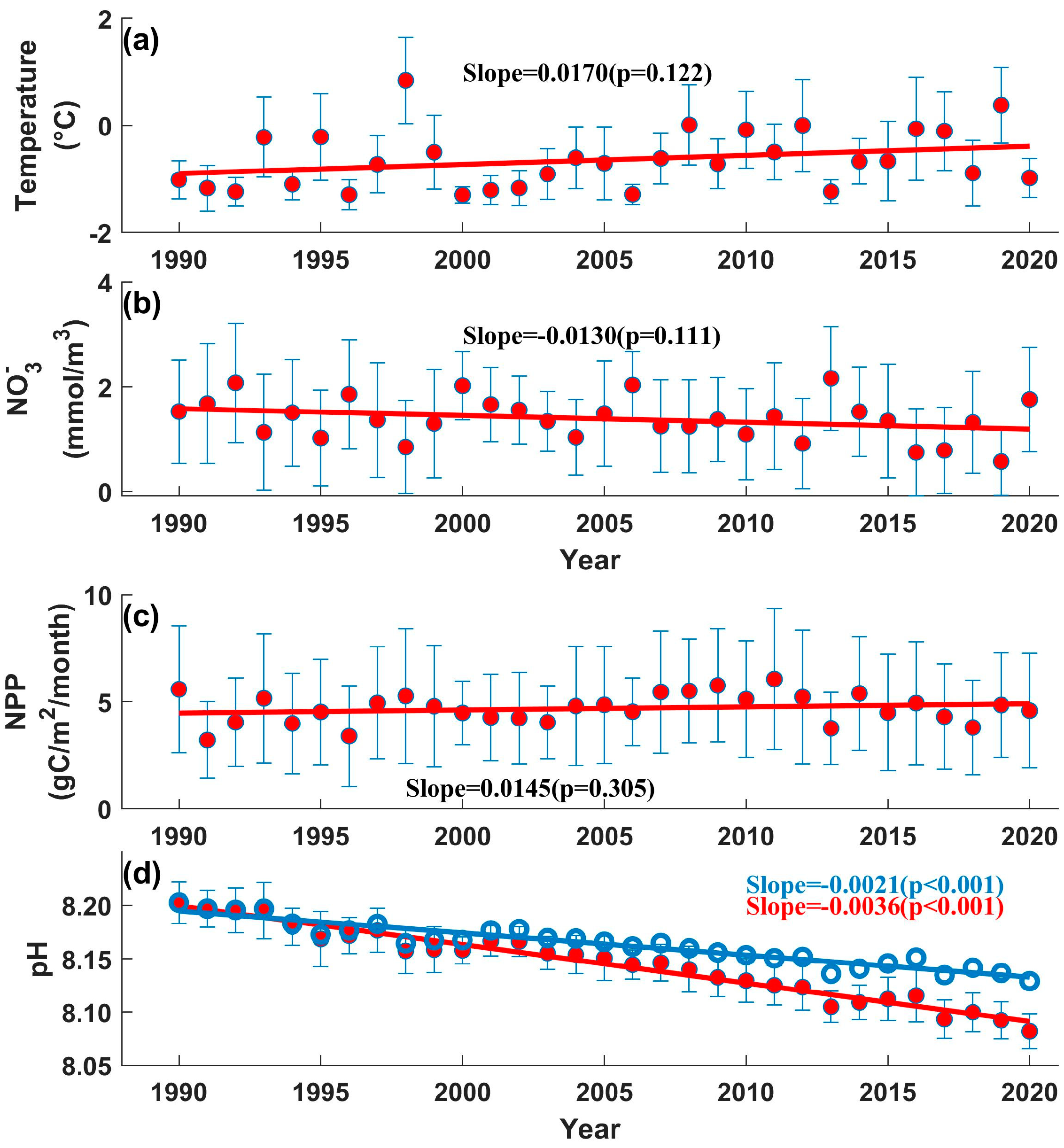
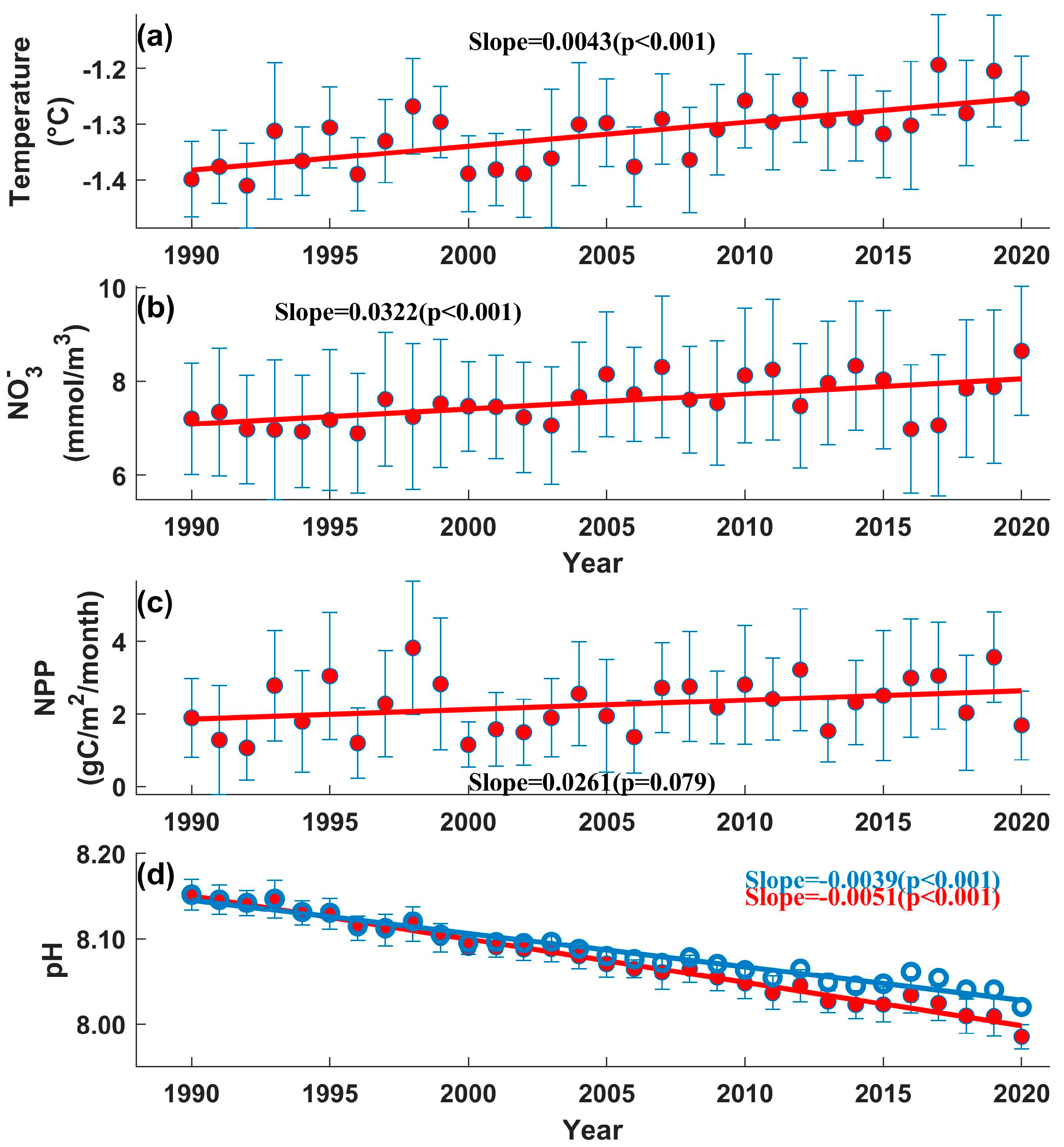

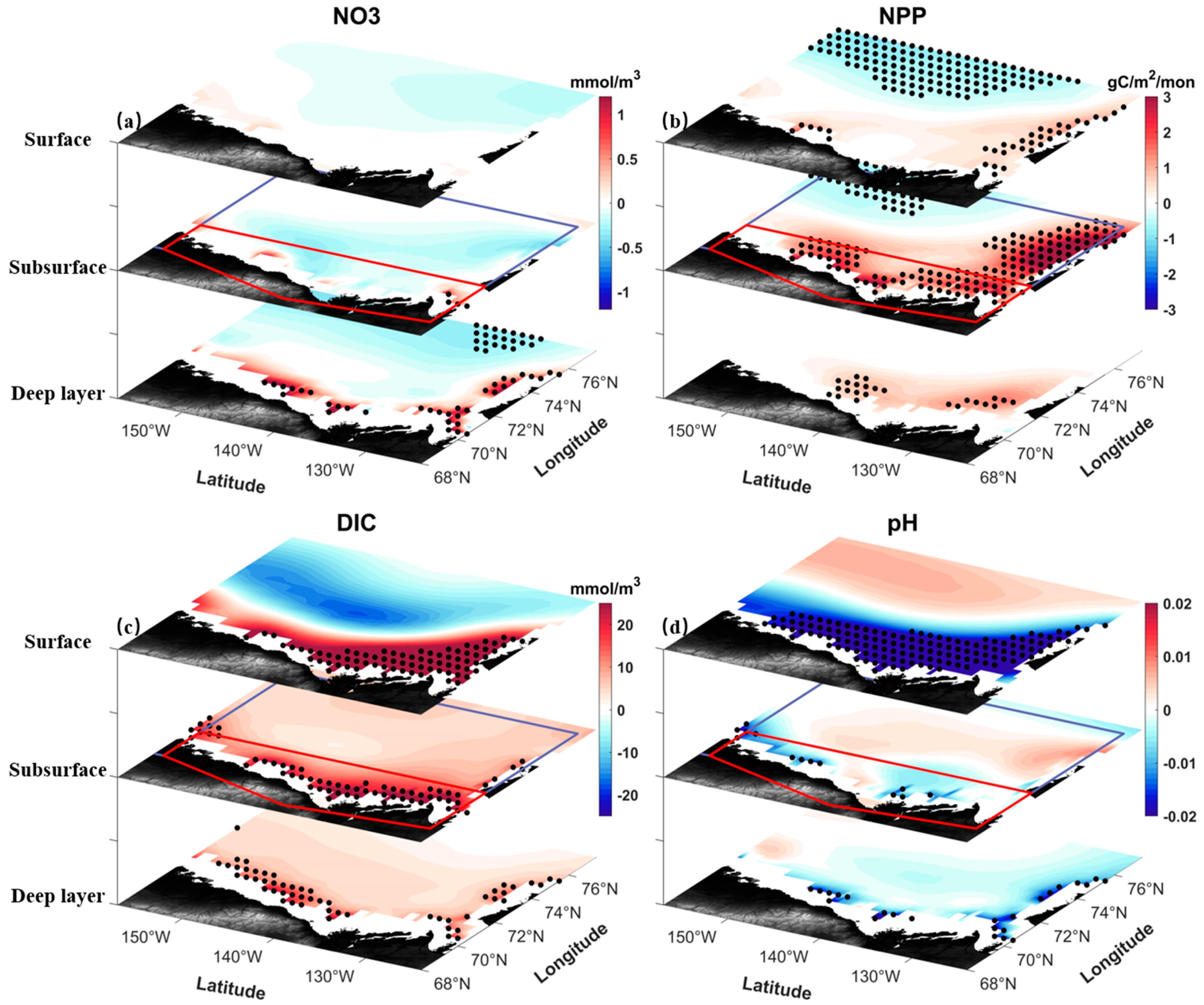
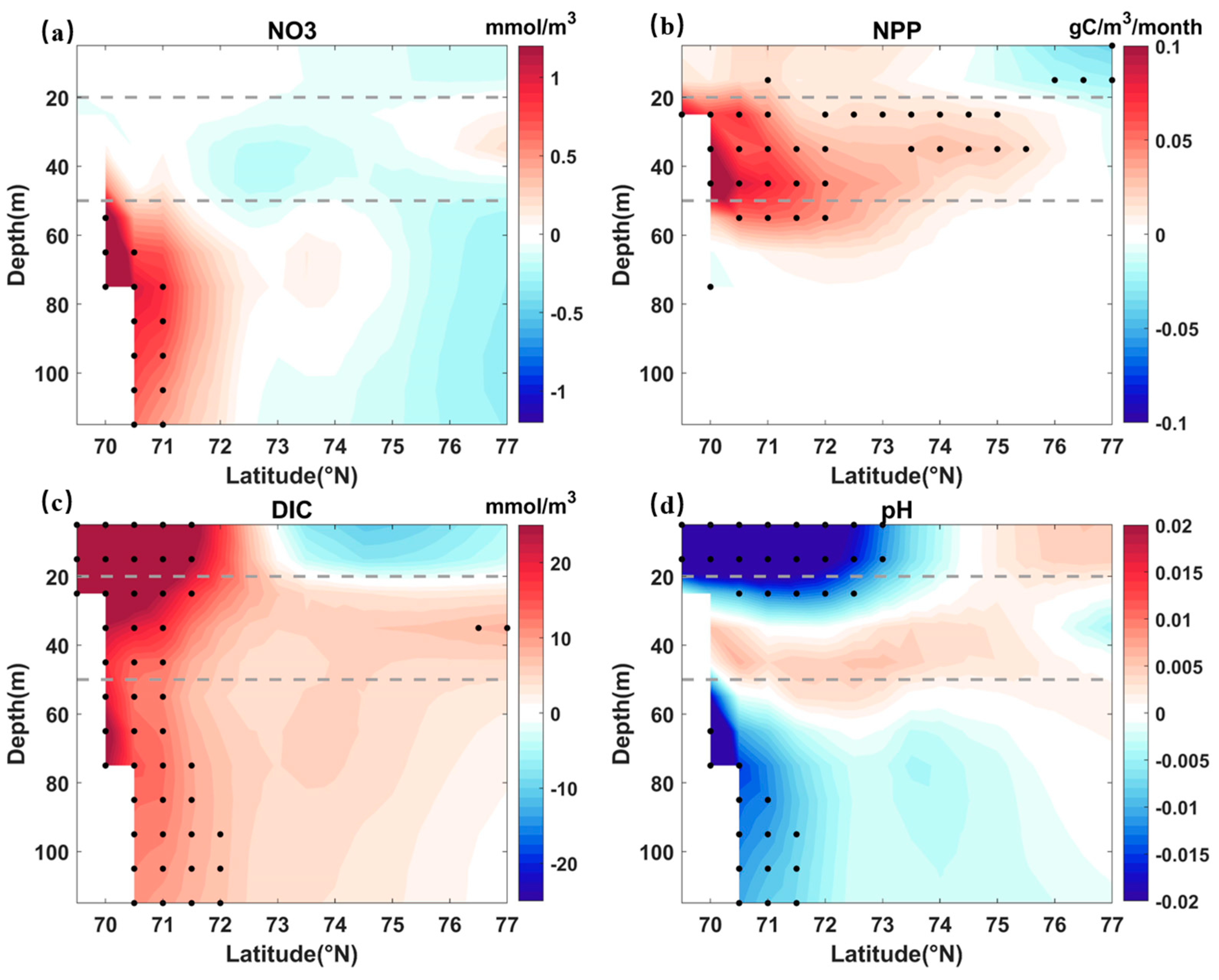
| Layer | AtmCO2 (Case C) | SIC (Case C) | EPV (Case C) | NPP (Case C) | MLD (Case C) | SIC (Case S) | EPV (Case S) | NPP (Case S) | MLD (Case S) |
|---|---|---|---|---|---|---|---|---|---|
| Surface | −0.668 −77.1% | 0.346 20.7% | −0.087 | 0.084 | −0.112 −2.2% | 0.883 100% | −0.040 | 0.117 | 0.076 |
| Subsurface | −0.956 −94.4% | −0.010 | −0.176 −3.2% | 0.154 2.4% | −0.067 | 0.990 69.6% | −0.291 | 0.654 30.4% | 0.357 |
| Deep layer | −1.006 −97.6% | −0.169 | −0.158 −2.4% | −0.025 | 0.018 | 1.442 | 0.193 | 0.707 | 0.458 |
| Layer | SIC (Case C) | EPV (Case C) | NPP (Case C) | MLD (Case C) | SIC (Case S) | EPV (Case S) | NPP (Case S) | MLD (Case S) |
|---|---|---|---|---|---|---|---|---|
| Surface | 0.606 78.0% | −0.113 | 0.180 6.9% | −0.266 −15.1% | 0.662 91.1% | −0.130 | 0.155 | −0.207 −8.9% |
| Subsurface | −0.005 | −0.660 −35.7% | 0.886 64.3% | −0.458 | 0.057 | −0.756 −46.1% | 0.818 53.9% | −0.298 |
| Deep layer | −0.757 | −0.623 −100% | 0.215 | −0.101 | −0.677 | −0.672 −100% | 0.075 | 0.028 |
| Difference | Subsurface Layer | Deep Layer |
|---|---|---|
| NO3 (mmol/m3) | 0.01 | 0.64 |
| NPP (gC/m2/month) | 1.53 | 0.43 |
| DIC (mmol/m3) | 18.5 | 11.2 |
| pH | −0.0035 | −0.0094 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, M.; Chen, Z.; Lin, X.; Li, C.; Qi, D. Influences of Global Warming and Upwelling on the Acidification in the Beaufort Sea. Remote Sens. 2025, 17, 866. https://doi.org/10.3390/rs17050866
Jin M, Chen Z, Lin X, Li C, Qi D. Influences of Global Warming and Upwelling on the Acidification in the Beaufort Sea. Remote Sensing. 2025; 17(5):866. https://doi.org/10.3390/rs17050866
Chicago/Turabian StyleJin, Meibing, Zijie Chen, Xia Lin, Chenglong Li, and Di Qi. 2025. "Influences of Global Warming and Upwelling on the Acidification in the Beaufort Sea" Remote Sensing 17, no. 5: 866. https://doi.org/10.3390/rs17050866
APA StyleJin, M., Chen, Z., Lin, X., Li, C., & Qi, D. (2025). Influences of Global Warming and Upwelling on the Acidification in the Beaufort Sea. Remote Sensing, 17(5), 866. https://doi.org/10.3390/rs17050866







