An Adaptive Constant Acceleration Model for Maneuvering Target Tracking
Abstract
1. Introduction
2. CS Modeling
3. ACA Model
4. Tracking Precision Analysis
5. Simulations and Results
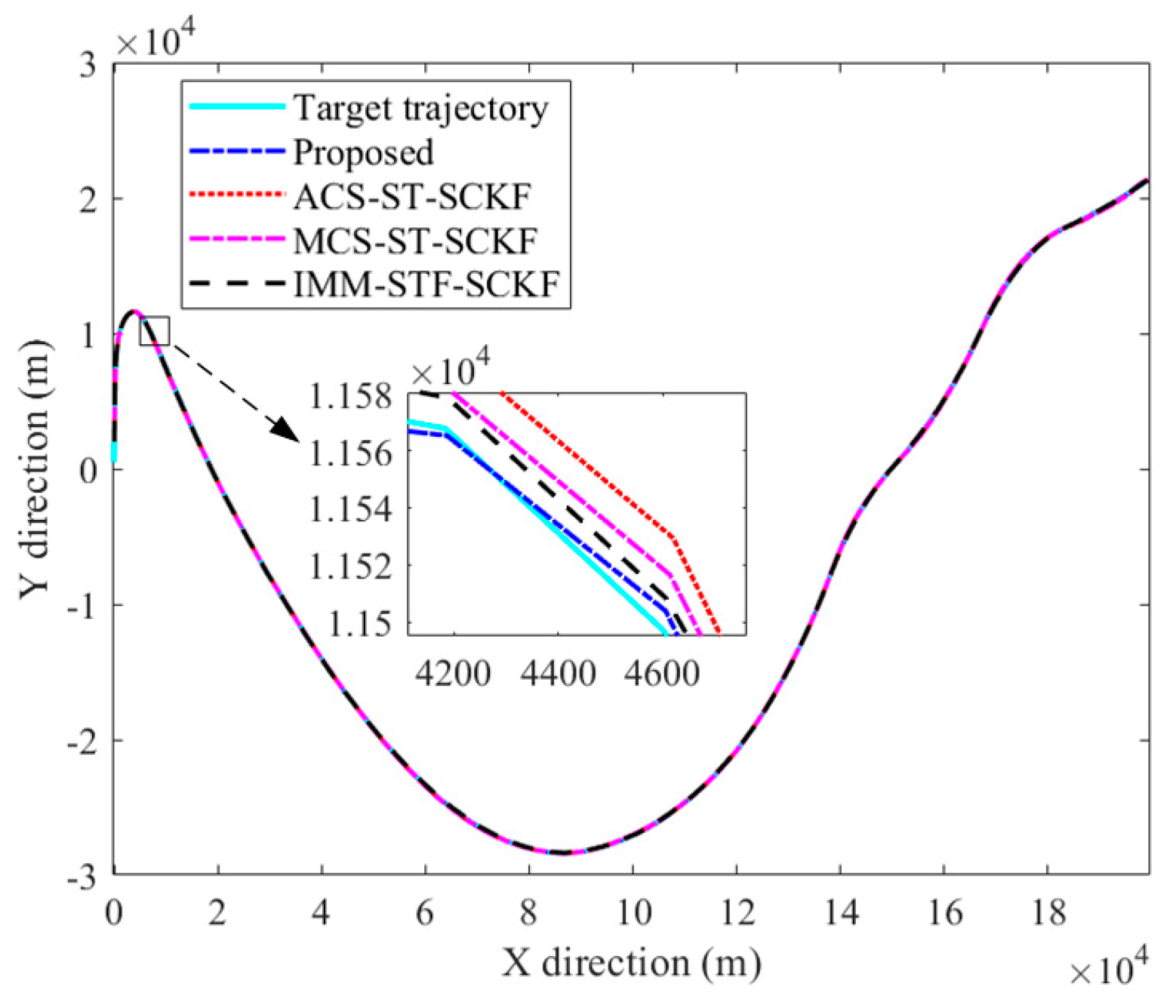
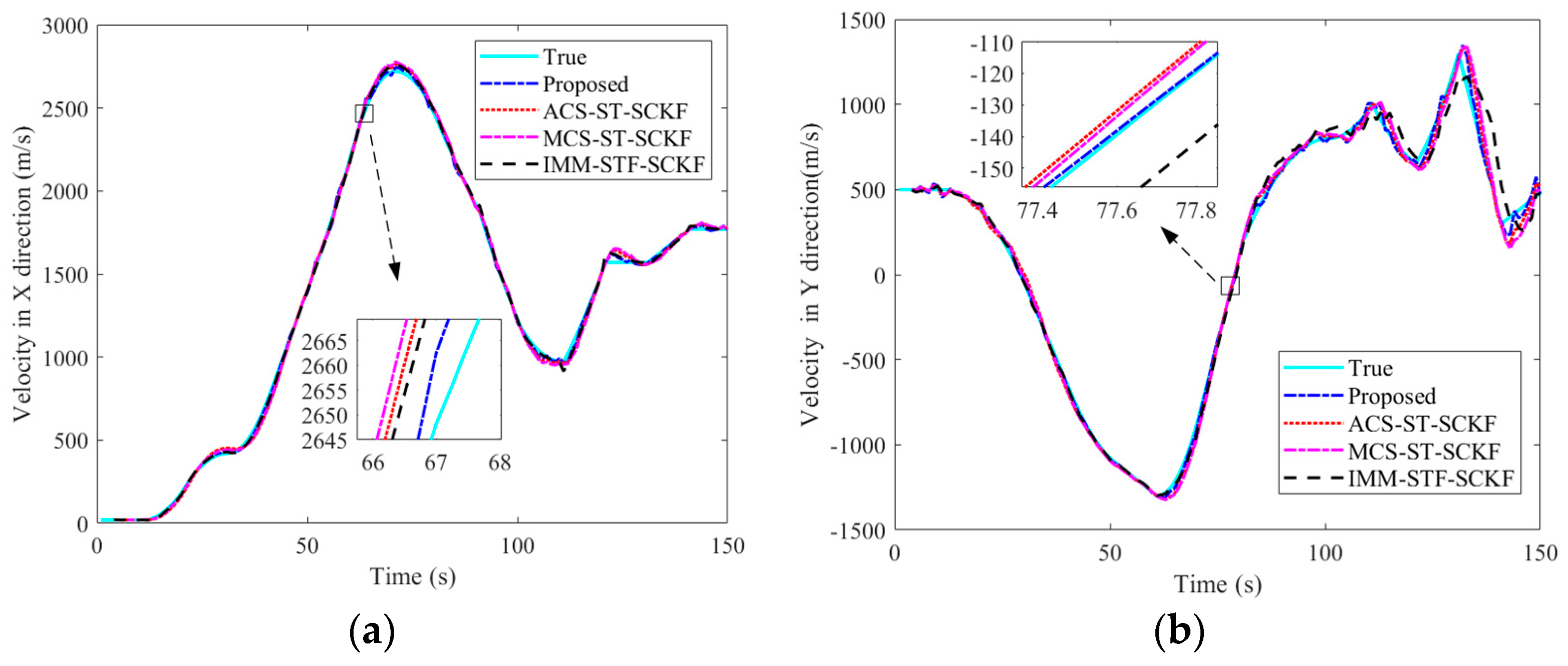
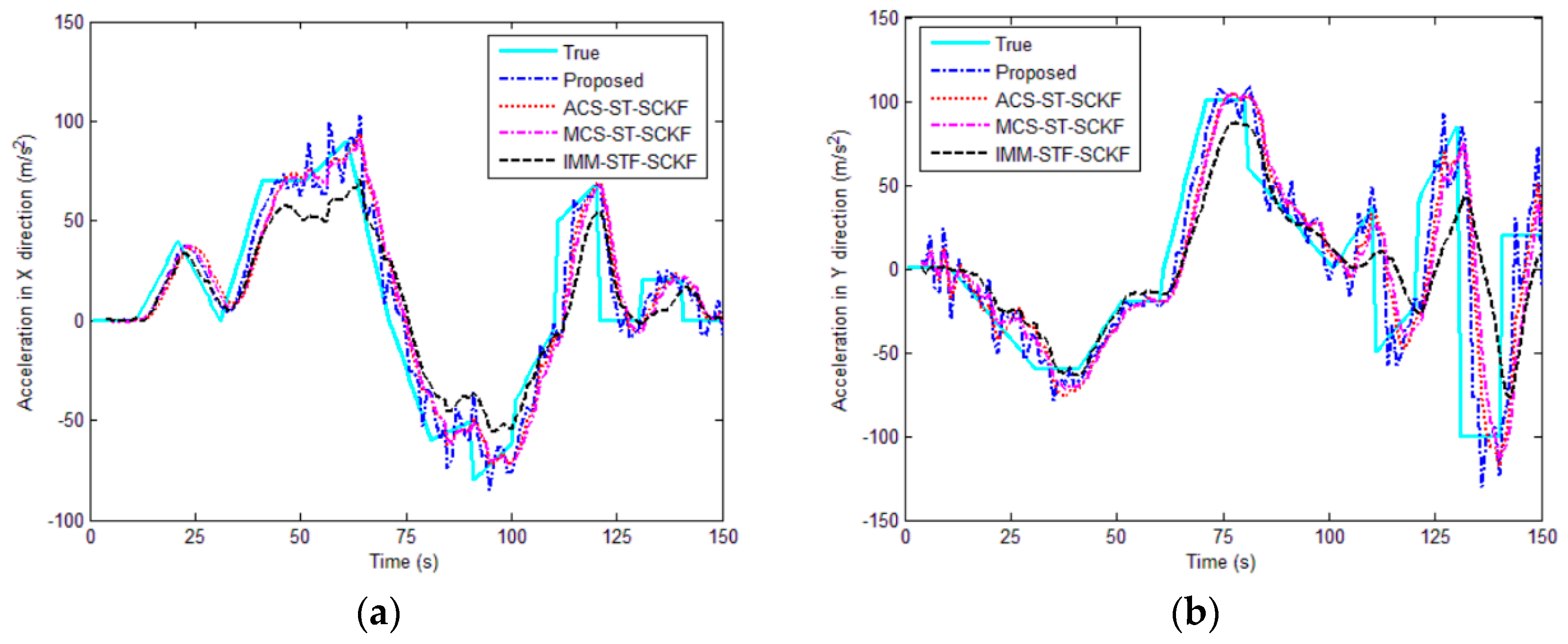
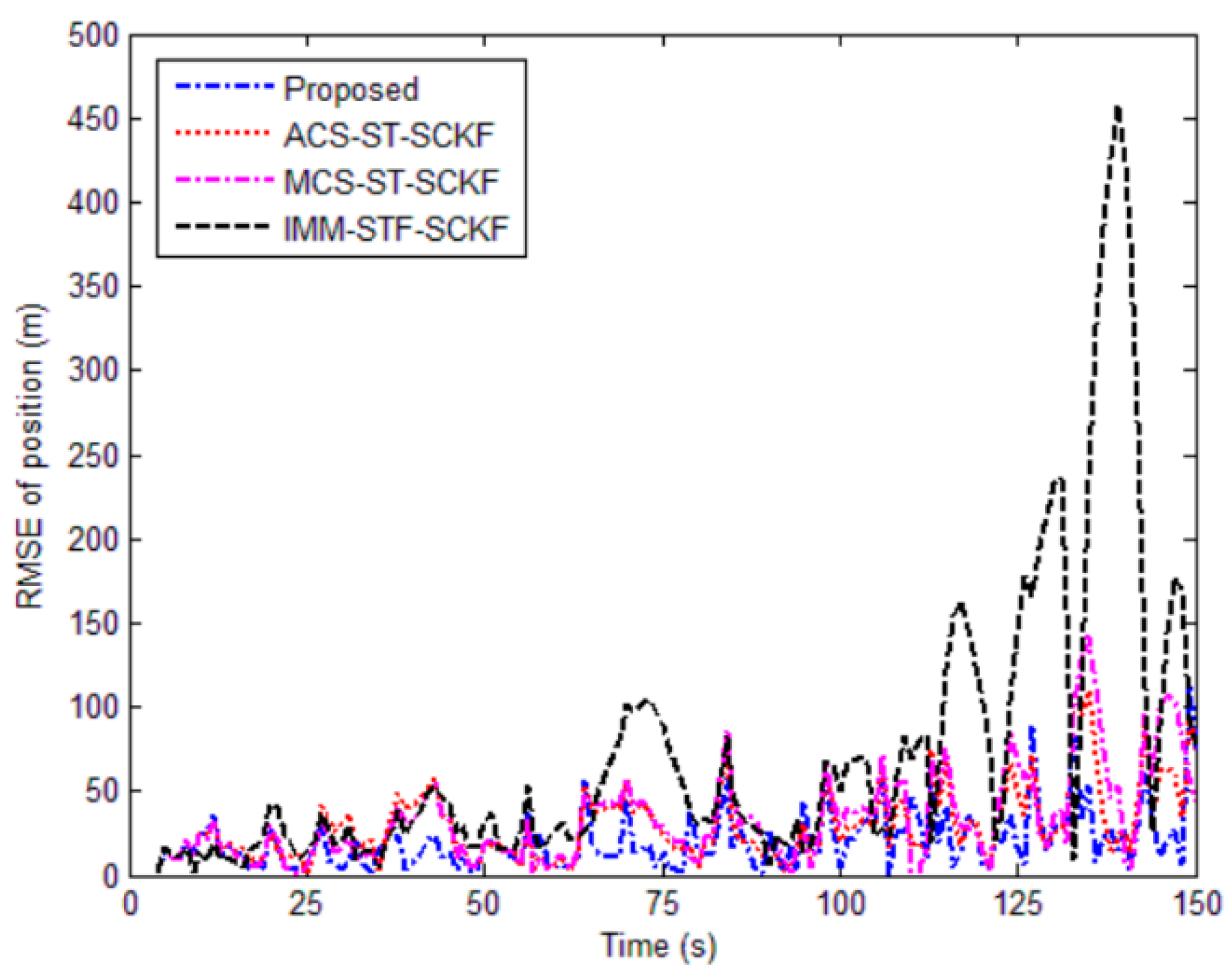
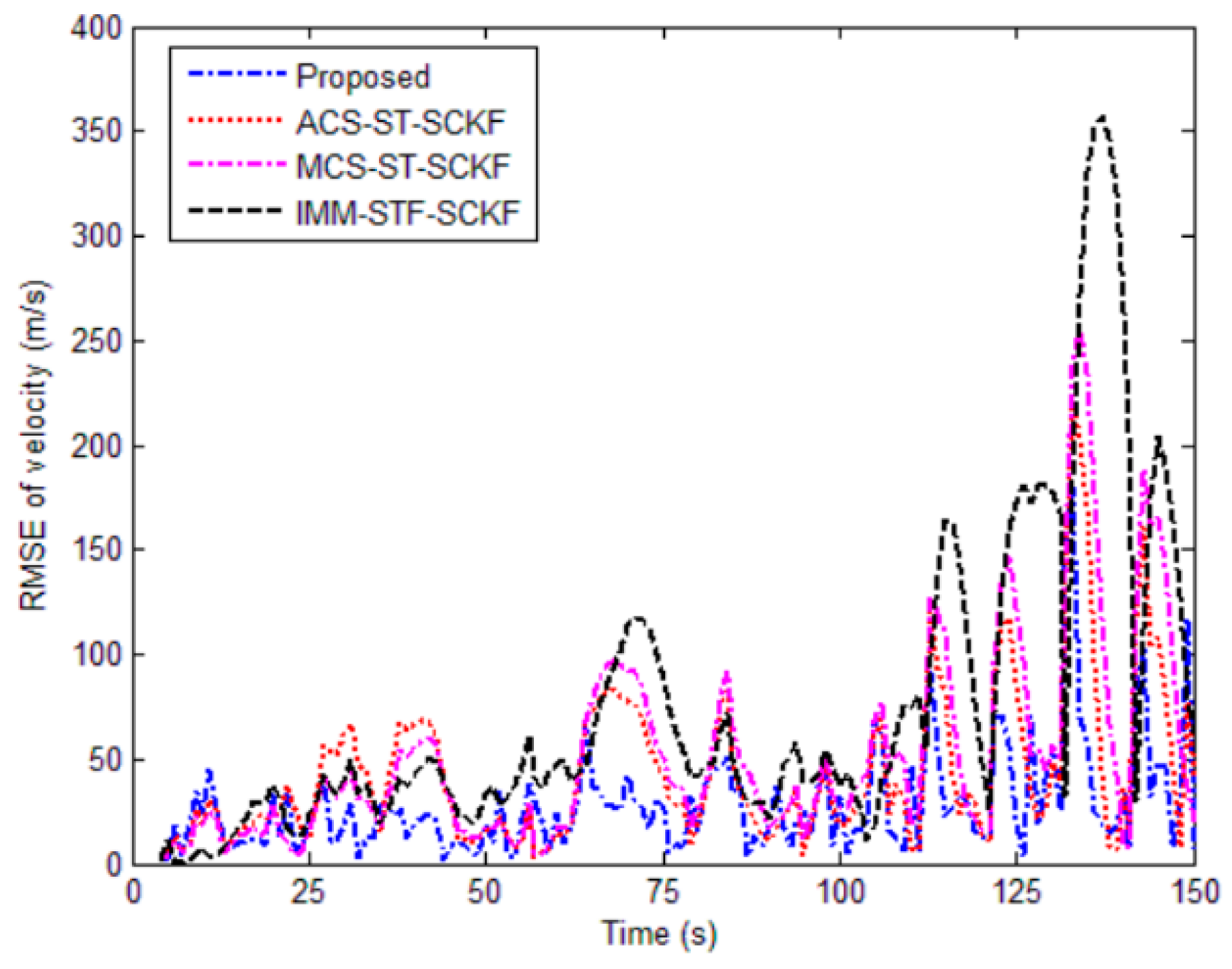
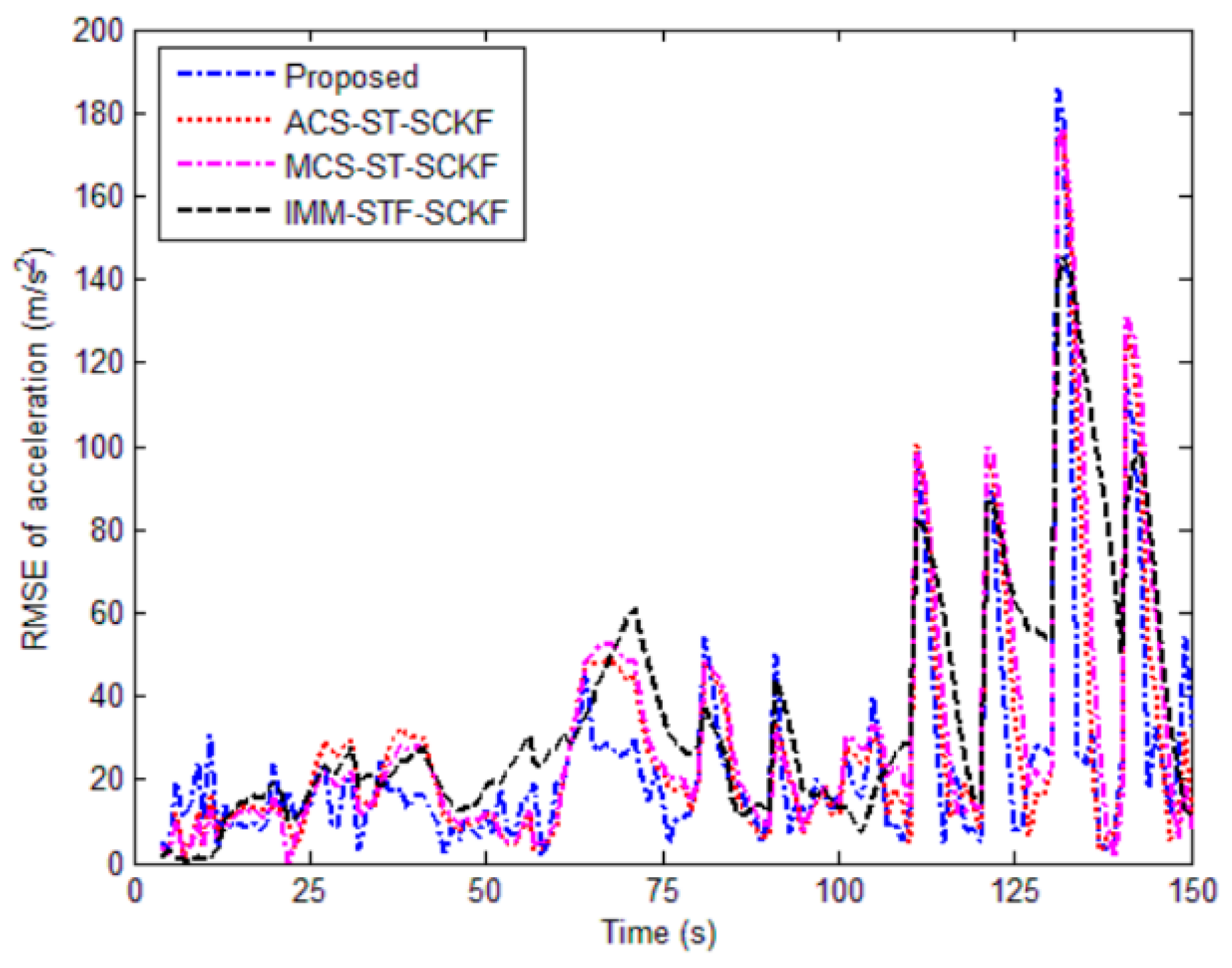
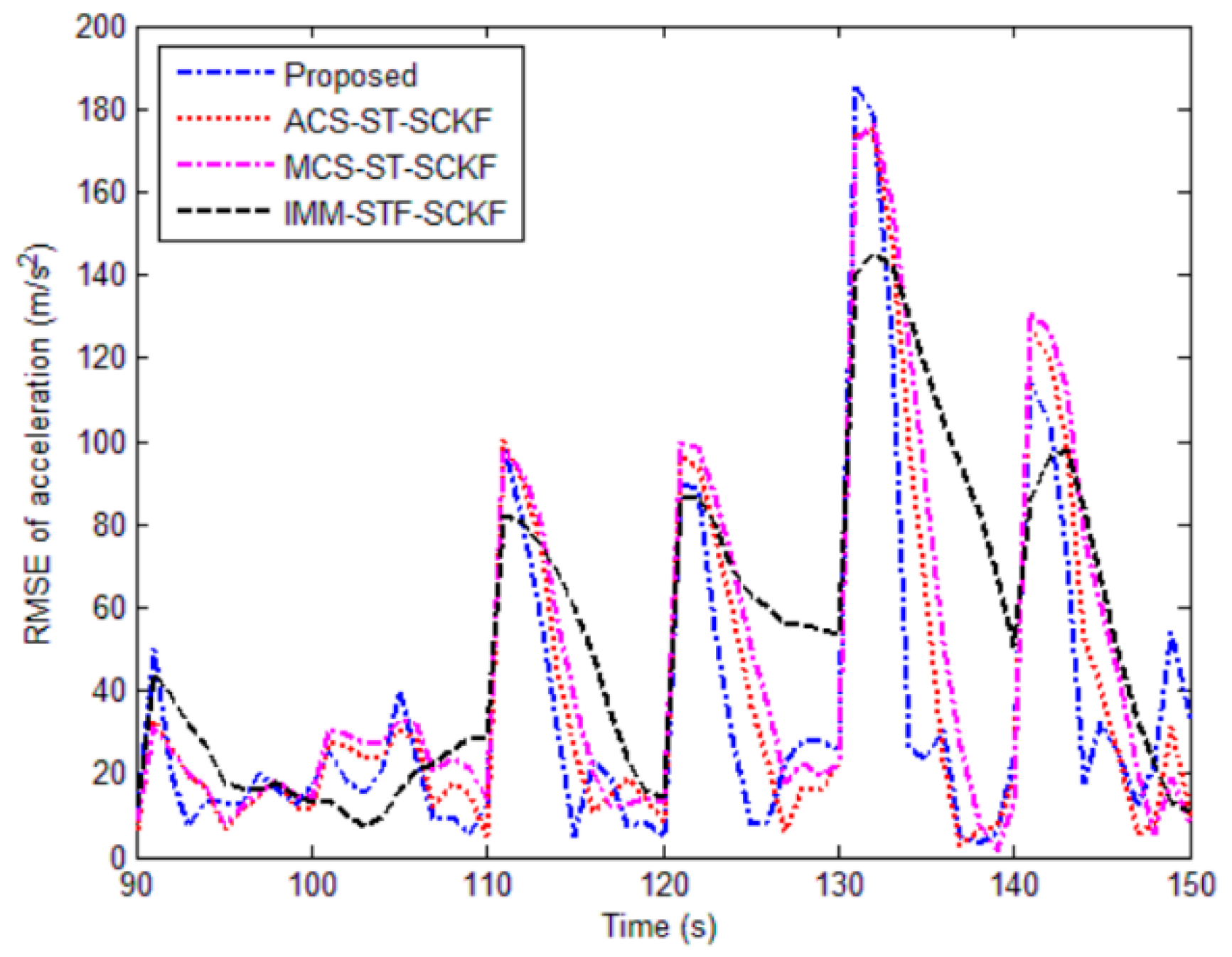
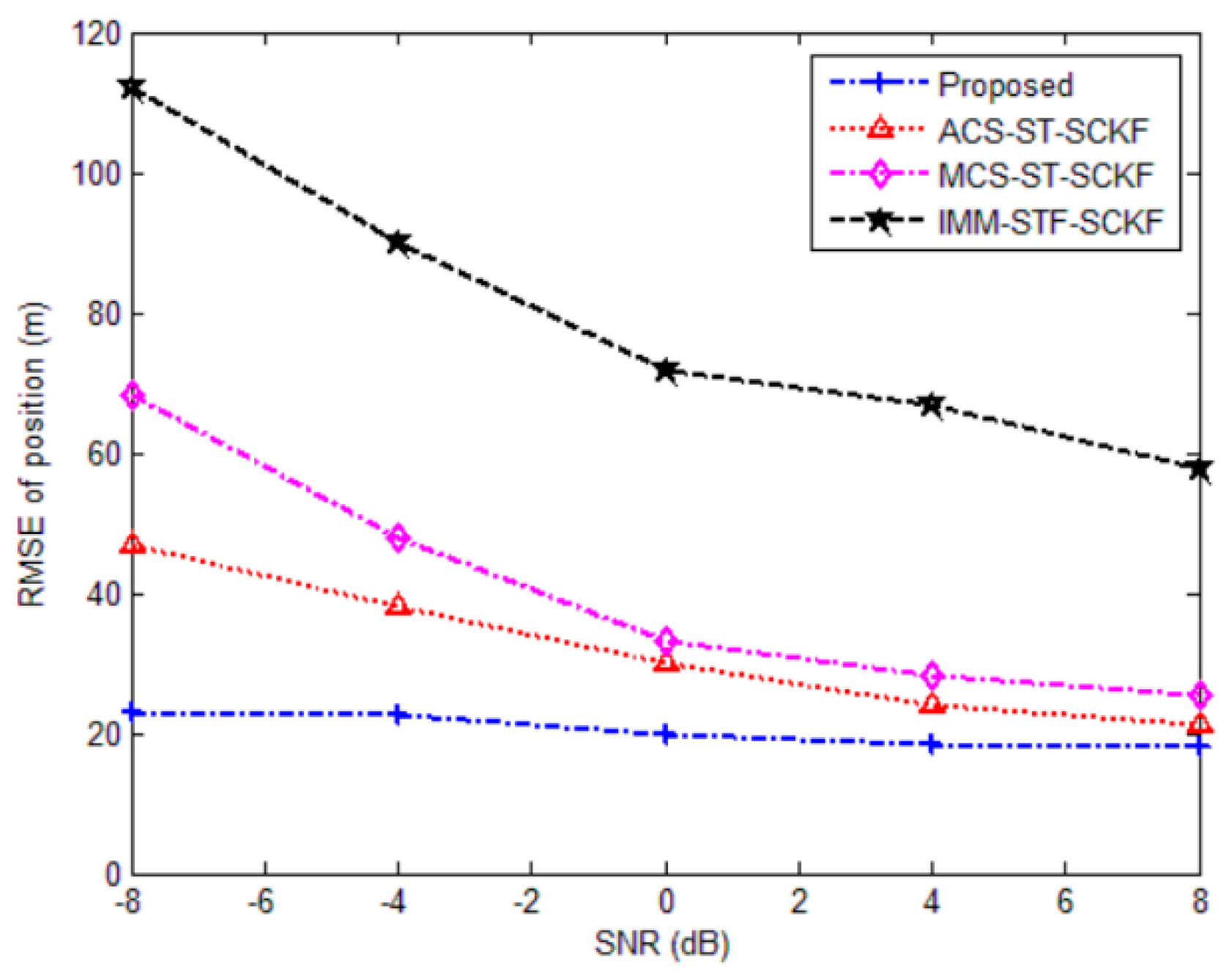
5.1. Simulation
5.2. Computational Complexity
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking. Part I: Dynamic models. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1333–1363. [Google Scholar]
- Singer, R.A. Estimating optimal tracking filter performance for manned maneuvering targets. IEEE Trans. Aerosp. Electron. Syst. 1970, 6, 473–483. [Google Scholar] [CrossRef]
- Zhou, H.; Kumar, K.S.P. A ‘current’ statistical model and adaptive algorithm for estimating maneuvering targets. AIAA J. Guid. 1984, 7, 596–602. [Google Scholar] [CrossRef]
- Kishore, M.; Pravas, R.M. A Jerk model for tracking highly maneuvering targets. IEEE Trans. Aerosp. Electron. Syst. 1997, 3, 1094–1105. [Google Scholar]
- Zhang, H.; Xie, J.; Ge, J.; Lu, W.; Liu, B. Strong tracking SCKF based on adaptive CS model for manoeuvring aircraft tracking. IET Radar Sonar Navig. 2018, 12, 742–749. [Google Scholar] [CrossRef]
- Zhang, H.; Xie, J.; Ge, J.; Lu, W.; Zong, B. Adaptive strong tracking square-root cubature Kalman filter for maneuvering aircraft tracking. IEEE Access 2018, 6, 10052–10061. [Google Scholar] [CrossRef]
- Liu, W.; Li, Y.; Cui, L. Adaptive strong tracking algorithm for maneuvering targets based on current statistical model. Syst. Eng. Electron. 2011, 33, 1937–1940. [Google Scholar]
- Yang, Y.; Fan, X.; Zhuo, Z. AFAKF for manoeuvring target tracking based on current statistical model. IET Sci. Meas. Technol. 2016, 10, 637–643. [Google Scholar] [CrossRef]
- Wang, M.; Wang, H. An adaptive attitude algorithm based on a current statistical model for maneuvering acceleration. Chin. J. Aeronaut. 2017, 30, 426–433. [Google Scholar] [CrossRef]
- Chen, L.; Gong, X.; Shi, H.; Yang, J. Maneuvering frequency adaptive algorithm of maneuvering target tracking. In Proceedings of the Fourth International Conference on Intelligent Control and Information Processing, Beijing, China, 9–11 June 2013; pp. 455–458. [Google Scholar]
- Zhu, D.; Chen, K.; Gen, W. A new adaptive filtering algorithm based on the current statistical model. In Proceedings of the Fifth International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2013; pp. 3–6. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K.; Durrant-Whyte, H.F. A new method for the nonlinear transformation of means and covariances in filters and estimators. IEEE Trans. Autom. Control 2000, 45, 477–482. [Google Scholar] [CrossRef]
- Jia, B.; Xin, M.; Cheng, Y. Sparse-grid quadrature nonlinear filtering. Automatica 2012, 48, 327–341. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Jazwinski, H. Filtering for nonlinear dynamic systems. IEEE Trans. Autom. Control 1996, 11, 765–766. [Google Scholar] [CrossRef]
- Zhou, D.H.; Sun, Y.X.; Xi, Y.G.; Zhang, Z.J. Extension of friedland’s separate bias estimation to randomly time-varying bias of nonlinear systems. IEEE Trans. Autom. Control 1993, 38, 1270–1273. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, X.; Zeng, L.; Dai, S.; Zhang, M.; Lian, F. Filtering in Triplet Markov Chain Model in the Presence of Non-Gaussian Noise with Application to Target Tracking. Remote Sens. 2023, 15, 5543. [Google Scholar] [CrossRef]
- Shan, C.; Zhou, W.; Jiang, Z.; Shan, H. A new Gaussian approximate filter with colored non-stationary heavy-tailed measurement noise. Digit. Signal Process. 2022, 122, 103358. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Li, N.; Wu, Z.; Chambers, J.A. A Novel Robust Student’s t-Based Kalman Filter. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1545–1554. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Shi, P.; Wu, Z.; Qian, J.; Chambers, J.A. Robust Kalman Filters Based on Gaussian Scale Mixture Distributions With Application to Target Tracking. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 2082–2096. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Shi, P.; Chambers, J. Variational Adaptive Kalman Filter With Gaussian-Inverse-Wishart Mixture Distribution. IEEE Trans. Autom. Control 2021, 66, 1786–1793. [Google Scholar] [CrossRef]
- Xue, C.; Huang, Y.; Zhu, F.; Zhang, Y.; Chambers, J.A. An Outlier-Robust Kalman Filter With Adaptive Selection of Elliptically Contoured Distributions. IEEE Trans. Signal Process. 2022, 70, 994–1009. [Google Scholar] [CrossRef]
- Zhu, F.; Huang, Y.; Xue, C.; Mihaylova, L.; Chambers, J. A Sliding Window Variational Outlier-Robust Kalman Filter Based on Student’s t-Noise Modeling. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4835–4849. [Google Scholar] [CrossRef]
- Pan, Q.; Liang, Y.; Yang, F.; Cheng, Y. Modern Aircraft Tracking and Information Fusion, 1st ed.; National Defense Industry Press: Beijing, China, 2009. [Google Scholar]
- Han, B.; Huang, H.; Lei, L.; Huang, C.; Zhang, Z. An Improved IMM Algorithm Based on STSRCKF for Maneuvering Target Tracking. IEEE Access 2019, 7, 57795–57804. [Google Scholar] [CrossRef]
- Wang, L.; Zhan, R.; Liu, S.; Zhang, J.; Zhuang, Z. Joint tracking and classification of multiple extended targets via the PHD filter and star-convex RHM. Digit. Signal Prog. 2021, 111, 102961. [Google Scholar] [CrossRef]
- Ding, L.; Xu, X.; Cao, Y.; Zhai, G.; Yang, F.; Qian, L. Detection and tracking of infrared small target by jointly using SSD and pipeline filter. Digit. Signal Prog. 2021, 110, 102949. [Google Scholar] [CrossRef]
- Luo, Q.; Gao, Z.; Xie, C. Improved GM-PHD filter based on threshold separation clusterer for space-based starry-sky background weak point target tracking. Digit. Signal Prog. 2020, 103, 102766. [Google Scholar] [CrossRef]
| Parameters | Description |
|---|---|
| state transition matrix | |
| acceleration input matrix | |
| input acceleration mean | |
| nonlinear transformation | |
| process noise, , i.e., the Gaussian distribution with zero mean and covariance | |
| symmetric matrices of fixed form | |
| maneuvering frequency | |
| measurement noise, |
| Maneuver Description | Time (s) |
|---|---|
| Steady state | 0~10, 130~140, 140~150 |
| Weak maneuver | 50~60, 60~70, 70~80, 80~90, 90~100, 100~110, 110~120, 120~130 |
| Continuous maneuver | 0~50 |
| Abrupt maneuver | 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140 |
| Algorithms | Mean Error (ME) | Mean Runtime (s) | ||
|---|---|---|---|---|
| Position (m) | Velocity (m/s) | Acceleration (m/s2) | ||
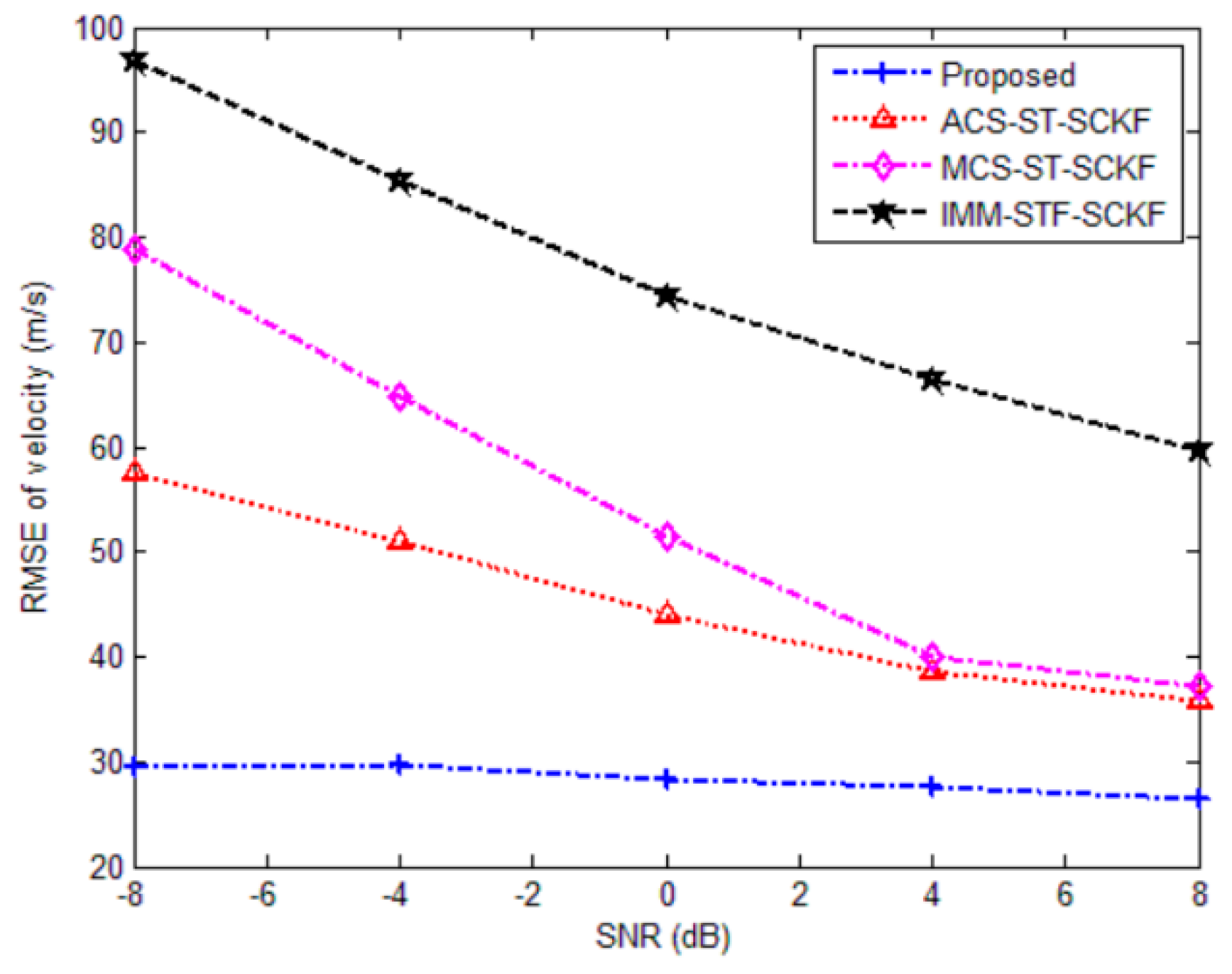
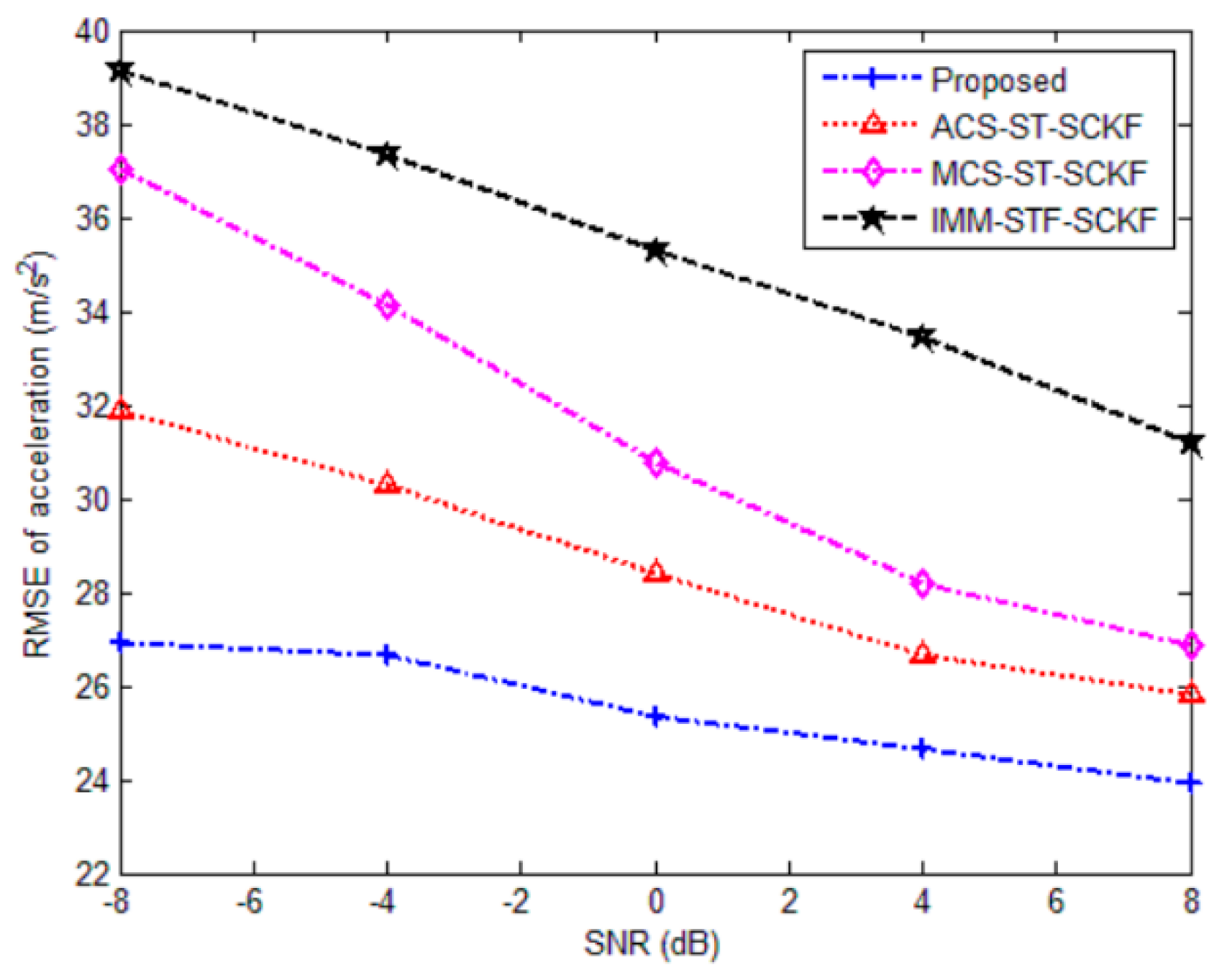
| Proposed | 19.8865 | 28.3562 | 25.3383 | 0.0460 |
| ACS-ST-SCKF | 29.9112 | 44.0516 | 28.3746 | 0.0588 |
| MCS-ST-SCKF | 33.1428 | 51.4056 | 30.7385 | 0.0596 |
| IMM- STF-SCKF | 71.6874 | 74.4300 | 35.2635 | 0.1154 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Xie, J.; Zhai, H.; Li, Z.; Feng, W. An Adaptive Constant Acceleration Model for Maneuvering Target Tracking. Remote Sens. 2025, 17, 850. https://doi.org/10.3390/rs17050850
Huang J, Xie J, Zhai H, Li Z, Feng W. An Adaptive Constant Acceleration Model for Maneuvering Target Tracking. Remote Sensing. 2025; 17(5):850. https://doi.org/10.3390/rs17050850
Chicago/Turabian StyleHuang, Jieyu, Junwei Xie, Haolong Zhai, Zhengjie Li, and Weike Feng. 2025. "An Adaptive Constant Acceleration Model for Maneuvering Target Tracking" Remote Sensing 17, no. 5: 850. https://doi.org/10.3390/rs17050850
APA StyleHuang, J., Xie, J., Zhai, H., Li, Z., & Feng, W. (2025). An Adaptive Constant Acceleration Model for Maneuvering Target Tracking. Remote Sensing, 17(5), 850. https://doi.org/10.3390/rs17050850






