Abstract
Seven extreme marine heatwave (MHW) events that occurred in the central–eastern tropical Pacific over the past four decades are divided into high-(MHW#1 and #2), moderate-(MHW#3–5), and low-predictive (MHW#6 and #7) categories based on the accuracy of the 30–60d forecast by the Nanjing University of Information Science and Technology Climate Forecast System (NUIST CFS1.1). By focusing on high- and low-predictive MHWs, we found that metrics indicative of strong and severe warming (S > 2 and S > 3, where S is MHW severity index) pose greater challenges for accurate forecasting, with the biggest disparity observed for S > 2. All events are intertwined with the El Niño–Southern Oscillation (ENSO), yet a robust ENSO forecast does not guarantee a good MHW forecast. Heat budget analysis within the surface mixed layer during the rapid warming periods revealed that the moderate and severe warming in MHW#1, #2, #6 are primarily caused by heat convergence due to advection (Adv), whereas MHW#7 is mainly driven by air–sea heat flux into the sea surface (Q). The NUIST CFS1.1 model better captures Adv than Q. High-predictive events exhibit a greater contribution from Adv, especially the zonal component associated with the zonal gradient of sea surface temperature anomalies, which may explain their higher sub-seasonal forecast skills.
1. Introduction
Marine heatwaves (MHWs) are defined as prolonged discrete anomalously extreme warm water events, characterized by the sea surface temperature (SST) typically exceeding the 90th, 95th, or 98th percentile of a fixed baseline period [1]. MHWs can have devastating and long-term impacts on ecosystems as well as political and socio-economic systems [2,3,4,5,6]. Amidst the ongoing global warming trends, MHWs have been observed with increasing frequency, intensity, spatial extent, and annual duration [7,8,9,10,11]. Hence, a better understanding of the spatiotemporal features, underlying dynamic drivers of MHWs, and improving prediction skills of MHWs at a longer time lead is of increasing importance [12,13,14].
The drivers and mechanisms of MHWs are intricate and multifarious, ranging from local oceanic and atmospheric processes to remote processes via teleconnections [15,16,17,18], which are briefly described as follows:
- (i)
- Local oceanic processes that contribute to MHWs encompass enhanced horizontal heat advection [19], weakened boundary currents [20], and favorable mesoscale eddies [21,22]. Notably, horizontal upper ocean heat convergence is often responsible for the start of most MHWs [23]. The warm water forcing via anomalous ocean circulation was the predominant oceanic pattern during MHWs [21]. Furthermore, persistent MHWs are more intense and frequent in tropical eastern and western boundary currents [16,22,24].
- (ii)
- Numerous prominent and impactful MHWs have been linked to atmospheric forcing, which brings anomalously strong heat fluxes from the atmosphere into the ocean. Examples include the 2012 MHW in the Northwest Atlantic [25], the 2015/16 summer MHW around tropical Australia [26], the 2017–2018 Tasman Sea MHW [27], the 2019–2020 Northeast Pacific MHW [28], and the 2020 Great Barrier Reef and Coral Sea MHW [12]. Notably, air–sea heat fluxes drove the majority of MHWs in the Tasman Sea from 1993 to 2021 [29,30]. These events tend to occur during summer or in tropical regions, particularly in the eastern South Pacific [23,26,31,32,33].
- (iii)
- Climate variations also play a pivotal role in modulating the occurrence of MHWs. It is noteworthy that the El Niño-Southern Oscillation (ENSO), the largest global driver of MHWs, can amplify the intensity, duration, and spatial extent of MHWs on interannual and shorter timescales [34,35]. Two-thirds of recorded MHWs occurring in the tropical Pacific are associated with El Niño events. Warm SSTs in the eastern equatorial Pacific and anomalous changes in the Indian Ocean Dipole (IOD) during El Niño could further facilitate MHW occurrence [22,36]. On longer timescales, the Pacific Decadal Oscillation has been found to modulate the frequency and intensity of El Niño events, thereby influencing the tropical MHWs [37].
Recent research indicates that developing forecast models excel at resolving the physical nonlinearities of the system and demonstrate robust forecast skills for MHWs at seasonal timescales [38,39,40,41,42]. However, sub-seasonal forecasting remains a bottleneck in seamless forecast systems and necessitates further advancements. Given its significance for improved marine management and decision making, sub-seasonal MHW forecasting is gaining prominence [14,29,43]. For example, in [12], the researchers found that the ACCESS-S1 prediction system could capture the area extent and intensity of MHWs during their development phase up to 1–2 weeks in advance, but underestimated the spatial extent and failed to predict their termination. Moreover, based on the NUIST CFS1.1 model (latest version of the Nanjing University of Information Science and Technology Climate Forecast System) [44,45,46,47,48], the sub-seasonal forecast skill evaluation of seven extreme MHWs in the central and eastern tropical Pacific indicates that the index, which is defined as the spatial integral of SST anomalies over area with largest contiguous MHW with moderate warming that intersects the region (hereinafter referred to as IS>1), is predictable at sub-seasonal timescales. While the model struggles to capture indices related to extreme warming and the onset date of MHW [49]. Nevertheless, MHW forecasts exhibit skillful performance on seasonal to annual timescales, particularly in tropical oceans. Specifically, the forecast skill for MHWs over the tropical Pacific Ocean remains high at lead times of 1–24 months [50].
Based on the seven extreme MHWs selected in the central–eastern tropical Pacific [48], this study verifies the sub-seasonal forecast skills across these MHW events and then explores the probable cause of the variation in forecast skills. Focusing on the MHWs, especially with the best and worst sub-seasonal forecast skills, we investigate both the tropical background SST during MHW occurrence and the local processes within the mixed layer during the rapid warming period of MHW event, and then we endeavor to ascertain the primary factors contributing to the disparities in sub-seasonal forecast accuracy among the selected MHWs using the NUIST CFS1.1 model. Section 2 outlines the data and methods. Section 3 commences with a thorough analysis of the spatiotemporal characteristics of moderate, strong, and severe warming, contrasting the MHWs with best and worst sub-seasonal forecast skills. Then, we examine the prediction skills of ENSO to uncover its potential influence on the sub-seasonal predictability of extreme MHWs. Finally, we evaluate the relative significance of local oceanic and atmospheric processes in driving MHWs with varying prediction skills via a heat budget analysis within the surface mixed layer. The results of this study are anticipated to shed light on the physical mechanisms crucial for enhancing the sub-seasonal forecasting capabilities of extreme MHWs in the central–eastern tropical Pacific region.
2. Materials and Methods
The daily National Oceanic and Atmospheric Administration (NOAA, in Washington, DC, USA) Optimum Interpolation Sea Surface Temperature V2 data (NOAA OISSTV2, hereinafter referred to as OISST) are used as the observational data of the sea surface temperature (SST) to calculate the metrics of MHW, as shown in Table 1. This is based on in situ data received through the Global Telecommunication System and satellite-derived SST from the Advanced Very High-Resolution Radiometer (AVHRR), and then interpolated to a high spatial resolution of 0.25° (https://psl.noaa.gov/data/gridded/data.noaa.oisst.v2.highres.html, accessed on 21 February 2025) [51,52,53,54].

Table 1.
Metrics of MHW.
Additionally, variables included in Equations (5)–(9), such as SST, net downward heat flux (Qnet), mixed layer depth (h), meridional velocity (v), and zonal velocity (u), are derived from Ocean Reanalysis System 5 global ocean reanalysis monthly mean data (ORAS5), prepared by the European Centre (in the Bracknell, UK) for Medium-Range Weather Forecasts (https://cds.climate.copernicus.eu/datasets/reanalysis-oras5?tab=overview, accessed on 21 February 2025). ORAS5, renowned for its high resolution in tropical regions and its consistency with OISST, is deemed reliable for quantifying the contribution of individual terms in the heat budget equation [55,56,57]. Consequently, both OISST and ORAS5 data are interpolated to a 1.125° × 1.125° grid to align with the resolution of the NUIST CFS1.1 model outputs. The relatively low spatial resolution guarantees the model forecasting efficiency but may limit the accuracy of MHW selection and estimation to some degree. The global model simulations forced by higher-resolution reanalysis could reproduce more realistic results in the frequency and duration of global MHWs [58].
The sub-seasonal forecasted SST is derived from the NUIST CFS1.1 model, which incorporates sophisticated nudging coefficients for SST and atmospheric variables, along with intricate model coupling schemes addressing the influence of surface ocean currents on wind stress calculations [48,49,59]. There are three SST nudging coefficients and two sets of atmosphere nudging coefficients for divergence, vorticity, temperature, and surface pressure in the initialization and three model coupling schemes for the effects of surface ocean currents on the wind stress calculation. These nudging coefficients refine the initial conditions every few hours, ensuring a robust initialization process [45,46,48,49]. The forecasts are initialized on the first day of every month in each year and run out to 2 months, with ensemble mean forecasts from 18 members, spanning 30–60 days in advance, combined to construct continuous daily SST time series for each grid point. This approach facilitates the calculation of SST climatology and the 90th percentile SST over the period 1983–2012. The sub-seasonal forecast variables included in Equations (5)–(9), such as SST, net downward heat flux (Qnet), mixed layer depth (h), meridional velocity (v), and zonal velocity (u), are derived from the NUIST CFS1.1 model’s monthly outputs. Similarly, the forecasts are also initialized on the first day of every month in each year and run out to 2 months, with 18 members, and the monthly forecasts are constructed into continuous monthly time series for variables for each grid point.
2.1. Metrics of MHW Events
The observed MHW severity index (S) is calculated as follows:
where is the long-term daily mean SST on the dth day of the year at location i, is the 90th SST on the dth day of the year at location i. A moving 11-day window is used to provide a robust 90th SST estimate [1,38,60]. Note that the and in this study are derived from the period 1983–2012, in order to maintain consistency with previous studies [49,53]. An MHW event according to the observed MHW severity index is commonly divided into four categories: moderate (1 < S ≤ 2), strong (2 < S ≤ 3), severe (3 < S ≤ 4), and extreme (4 < S ≤ 5), which are abbreviated as S > 1, S > 2, S > 3, and S > 4, respectively [53,60]. By scrutinizing various indices commonly employed to detect MHWs [49,53], scientists found that the combined temporal evolutions of IS>1, IS>2, and IS>3 indices (shown in Table 1) best capture the moderate warming processes. These indices exhibit similar characteristics to the proportion of grid points reaching the standard of S > 1, S > 2, and S > 3 (PS>1, PS>2, and PS>3 index, shown in Table 1), respectively, during MHW events. Furthermore, DS>1, DS>2, and DS>3 indices (shown in Table 1) are selected to illustrate the spatial characteristics of each MHW event by quantifying the total days that each grid point meets the moderate, strong, and severe warming standard in the region. Thus, nine metrics are selected to comprehensively characterize the spatiotemporal features of MHWs, as detailed in Table 1. Notably, extreme MHWs exhibit significant spatial variability and rarely surpass the S > 4 threshold [49], and S > 4 metrics are excluded from this study. To evaluate the forecast performance of NUIST CFS1.1 model, we employ the anomaly correlation coefficient (ACC) and root mean square error (RMSE) for the selected metrics, and the temporal correlation coefficient (TCC) and ACC for Niño indices [61,62]. The calculations of ACC, TCC, and RMSE are given by Equations (2)–(4).
where is the averaged regional forecast time series of a specific index in the period from one month before the observed start date to one month after the end date of MHWs, and represents the observed time series in the same period. Moreover, and mean the temporal average of and , respectively.
2.2. Upper-Ocean Temperature Budget Analysis
Drawing inspiration from previous studies [24,63], we conduct a heat budget analysis to pinpoint the dominant processes contributing to anomalous SSTs and hence to the occurrence of MHWs. The heat budget equation, averaged from the sea surface to a fixed depth h, is formulated as follows [64,65,66,67,68]:
where
Based on the monthly climatology data from 1983–2012 derived from the ORAS5 and NUIST CFS1.1 models, the tendency of the sea surface temperature anomaly () is calculated using the central difference method in the left-hand side of the equation with time (t). The right-hand side of the equation consists of three terms: (i) the diabatic heating term (Q) measuring the net downward heat flux anomaly () scaled by the density of seawater (), the specific heat content of seawater (), and the mixed layer depth anomaly (), wherein () and () are the departure from the climatology field of () and (h) from 1983 to 2012; (ii) the advection term (Adv) measuring the convergence of heat in the sea surface due to the horizontal velocity and the SST gradient, and (iii) a residual term that includes the additional physical processes not explicitly accounted for here including vertical advection, entrainment, and mixing [22,36,54]. Given the negligible impact of the residual term (three orders of magnitude smaller than the other terms), it is disregarded in our analysis [68,69,70]. Since we are concerned about the temperature changes at sea surface, the mixed layer depth is defined as the depth where the average sea water density exceeds the near-surface density by 0.01 kgm−3. Furthermore, the advection term (Adv) is decomposed into the zonal (Adv-u) and meridional (Adv-v) components, each further segmented into climatological mean advection of SST anomalies ( and ), anomalous advection of climatological mean SST ( and ), and anomalous advection of SST anomalies ( and ), respectively. Here, represents the climatological SST from 1983 to 2012.
3. Results
To evaluate the sub-seasonal forecast skills across the seven extreme MHWs that occurred in the central–eastern tropical Pacific, the anomaly correlation coefficient (hereinafter referred to as ACC) and root mean square errors (hereinafter referred to as RMSE) are computed for the time series of PS>1, IS>1, PS>2, IS>2, PS>3, and IS>3 metrics (see Table 1) in the period from 30 days before the onset of MHW to 30 days after the end of each MHW event. Displayed in Figure 1 are the ACCs and RMSEs for each category of warming (i.e., S > 1, S > 2, S > 3) and their averages over all categories. If the symbol that represents an MHW event is located in the top-left corner, it signifies that the MHW has an above-average ACC and a below-average RMSE, indicating better forecast skills. Oppositely, the symbols in the bottom-right corner indicate MHWs with poorer forecast skills. From Figure 1d, it is evident that the symbols representing various metrics of MHW#1 and #2 are located in the top-left corner, with ACC values above the average of 0.39 and RMSE values below the average of 1.02. This indicates that, in terms of the average of all categories of warming, these two events exhibit the highest forecast skill among the studied cases. On the contrary, the symbols which represent MHW#6 and #7 located in the bottom-right corner, and metrics mostly have negative ACCs and higher RMSEs skills. Similar conclusions are found in metrics corresponding to S > 1, S > 2, and S > 3, respectively (Figure 1a–c), except that PS>1 in MHW#1 and S > 3 metrics in MHW#2 have ACC skills slightly lower than the averaged ACC (0.29). Note that in MHW#1, the parameter PS>3 and IS>3 are best forecasted, which have ACC skills above 0.7 and RMSE skills below 0.9. Generally speaking, MHW#1 and #2 are the best forecasted and categorized as high-predictive MHWs, MHW#6 and #7 are the worst forecasted and categorized as low-predictive MHWs, and the remaining (MHW#3~5) are categorized as moderate-predictive MHWs (as listed in Table 2). In order to further explore what causes the diversity of the sub-seasonal forecast skill of MHWs, we focus on the MHWs that are especially high-predictive (MHW#1–2) and low-predictive (MHW#6–7) according to the NUIST CFS1.1 model for further investigation and comparison.
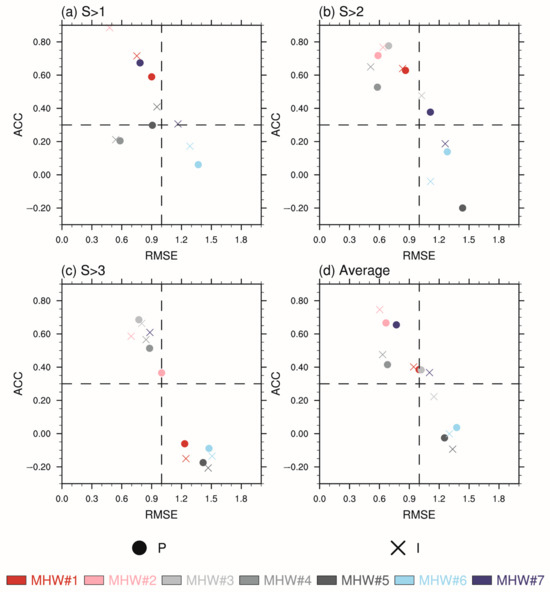
Figure 1.
The anomaly correlation coefficient (ACC) and root mean square error (RMSE) skill of metrics corresponding to (a) S > 1 (PS>1 and IS>1, units: % and °CM km2), (b) S > 2 (PS>2 and IS>2, units: % and °CM km2), (c) S > 3 (PS>3 and IS>3, units: % and °CM km2), and (d) their averages based on the ensemble mean forecasts of the NUIST CFS1.1 model averaged in the period from 30 days before the onset to 30 days after the end of each MHW event. The red, pink, light gray, dark gray, black, light blue and blue dots represent the P parameter in MHW#1–7, respectively. The sign “×” with the above colors represents the I parameter in MHW#1–7. The black dashed lines represent the average ACCs and RMSEs for S > 1, S > 2, S > 3, and all metrics in MHW#1~7, respectively. If the symbol that represents an MHW event is located in the top-left corner, it signifies that MHW has an above-average ACC and a below-average RMSE, indicating better forecast skills. Oppositely, the symbols in the bottom-right corner indicate MHWs with poorer forecast skills.

Table 2.
The characteristics of seven extreme MHWs occurred in the central–eastern tropical Pacific, including the MHW period and their connection with El Niño. The symbol “√” here indicates that the MHW event is under the corresponding background shown in the table, while the symbol “×” means on the contrary.
3.1. Main Features of Metrics in MHWs: High-Predictive vs. Low-Predictive
Both high-predictive events occurred during the eastern-type super El Niño periods (i.e., the winters of 2015/2016 and 1982/1983), primarily within the key area of El Niño region (Table 2). The MHW#1 lasts for 260 days and is characterized by large-scale moderate and strong warming. In particular, the proportion of the region experiencing moderate warming (PS>1) is up to 90% and the proportion with strong warming (PS>2) is up to 30% (Figure 2c,e). Additionally, the S index, averaged over all grid points where the occurring MHW remained above 1, indicate moderate to strong warming in the MHW#1 region (Figure 2b). The key metrics, including IS>1, PS>2, and IS>2, exhibit an upward trend from September to December 2015 (Figure 2d–f), with the proportion and intensity with extreme warming (PS>3 and IS>3) peaking during this period (Figure 2g,h). The MHW#2 event, which lasts for 167 days, shows similar observational features to MHW#1, except that there is a secondary surge in PS>2, IS>2, PS>3, and IS>3 from January to March in 1983, which is most pronounced in PS>3 and IS>3 (Figure 3).
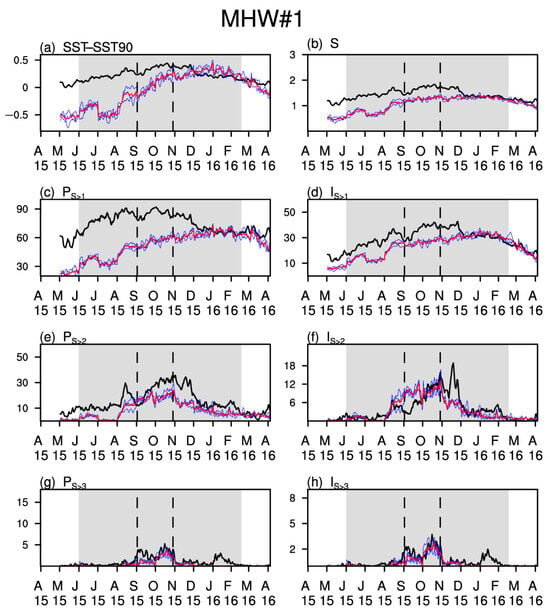
Figure 2.
The time series of MHW metrics including (a) the difference between the regional average SST and 90th SST (units: °C), (b) the regional mean S index, and metrics (c) PS>1 (units: %), (d) IS>1 (units: °CM km2), (e) PS>2 (units: %), (f) IS>2 (units: °CM km2), (g) PS>3 (units: %), and (h) IS>3 (units: °CM km2), which are derived from observations (black bold curves) and 30–60 d forecasts (red curves represent the ensemble mean forecasts, and blue curves represent forecasts of members with different nudging coefficient in SST) by the NUIST CFS1.1 model during the period around the MHW#1 event. The period of observed MHW event is marked by gray rectangular. The rapid warming period, featured by distinct upward trends in IS>1 and IS>2, along with the inclusion of the IS>3 peak, is visually identified and demarcated by the space between two black dashed lines. Corresponding indicators. The occurrence region of the corresponding MHW event is shown in Figure A1.
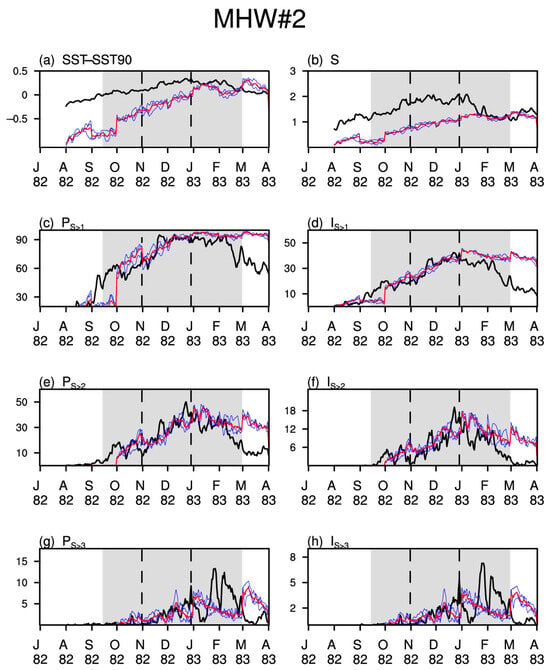
Figure 3.
As in Figure 2, the time series of MHW metrics including (a) the difference between the regional average SST and 90th SST (units: °C), (b) the regional mean S index, and metrics (c) PS>1 (units: %), (d) IS>1 (units: °CM km2), (e) PS>2 (units: %), (f) IS>2 (units: °CM km2), (g) PS>3 (units: %), and (h) IS>3 (units: °CM km2), which are derived from observations (black bold curves) and 30–60 d forecasts (red curves represent the ensemble mean forecasts, and blue curves represent forecasts of members with different nudging coefficient in SST) by the NUIST CFS1.1 model during the period but for the event MHW#2.
The 30–60 forecasts generated by the NUIST CFS1.1 model accurately capture the upward and downward trends of the above-mentioned MHW metrics during MHW#1 and #2, especially for PS>2, IS>2, PS>3, and IS>3 during MHW#1 (Figure 2e–h). However, the model underestimates the regional mean SST-SST90 (the difference between the regional average SST and 90th SST) and parameters S, PS>1, IS>1, and PS>2 in MHW#1 (Figure 2a–e). Additionally, although the forecasts show a second peak in March for the PS>3 and IS>3 metrics, they are significantly delayed compared to observations, thus the model fails to predict their second surge within the observed period of MHW#2 (Figure 3g,h).
For comparison, two low-predictive MHW events, MHW#6 and MHW#7, are also analyzed. MHW#6 and MHW#7 last for 97 and 170 days, respectively (Table 2). They are located at the periphery and within the domain region of mega ENSO [71]. MHW#6 occurs during the 2015/2016 super El Niño winter, outside the key area of El Niño but within the region of the mega ENSO. It displays distinct features compared to the high-predictive events. The positive regional mean SST-SST90s values are smaller than those from the other three MHW events. The observed magnitudes of IS>1, IS>2, and IS>3 are approximately one order smaller (Figure 4d,f,h), accompanied by significantly shorter-term fluctuations, particularly in PS>1, PS>2 and S (Figure 4b,c,e). MHW#6 exhibits two distinct warming phases, respectively, peaking in November–December 2015 and January–February 2016, with the latter exhibiting stronger warming and reaching maximum values for all metrics related to S > 2 (Figure 4e,f). The forecasts underestimated SST-SST90 and all metrics during the second warming phase, with PS>3 and IS>3 largely absent (Figure 4g,h), indicating the model’s inability to replicate severe warming trends during these low-predictive events.
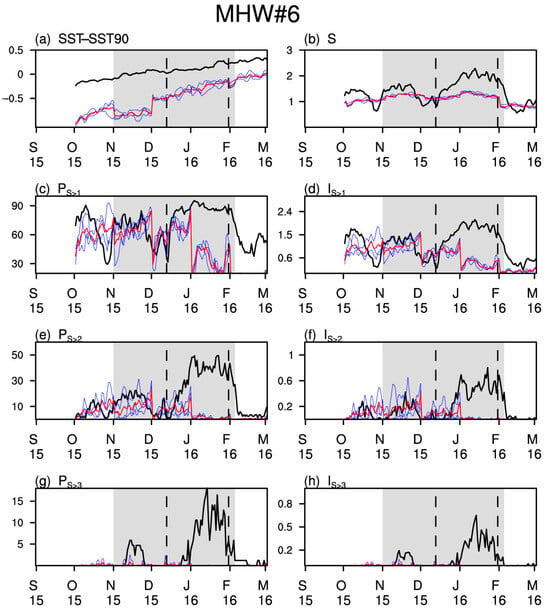
Figure 4.
As in Figure 2, the time series of MHW metrics including (a) the difference between the regional average SST and 90th SST (units: °C), (b) the regional mean S index, and metrics (c) PS>1 (units: %), (d) IS>1 (units: °CM km2), (e) PS>2 (units: %), (f) IS>2 (units: °CM km2), (g) PS>3 (units: %), and (h) IS>3 (units: °CM km2), which are derived from observations (black bold curves) and 30–60 d fore-casts (red curves represent the ensemble mean forecasts, and blue curves represent forecasts of members with different nudging coefficient in SST) by the NUIST CFS1.1 model during the period but for the event MHW#6.
Similar to MHW#1 and #6, the MHW#7 event is related to the super El Niño in 2015/2016 winter but primarily occurs in spring and summer, post-El Niño. Notably, MHW#7 is located within the domain region of mega ENSO. MHW#7 shares many similarities with MHW#6, except for weaker SST-SST90 and S values, which are mostly smaller than 0.5 °C and 1.5 °C, respectively (Figure 5a,b). However, the observed IS>1 and IS>2 magnitudes are larger (Figure 5d,f) and there are more pronounced short-term fluctuations in all metrics except S and SST-SST90 (Figure 5). The model underestimates the peaks of IS>1, IS>2, and IS>3 and introduces time shifts exceeding two months for all metrics except S, indicating poor forecasts of moderate, strong, and severe warming trends during MHW#7.
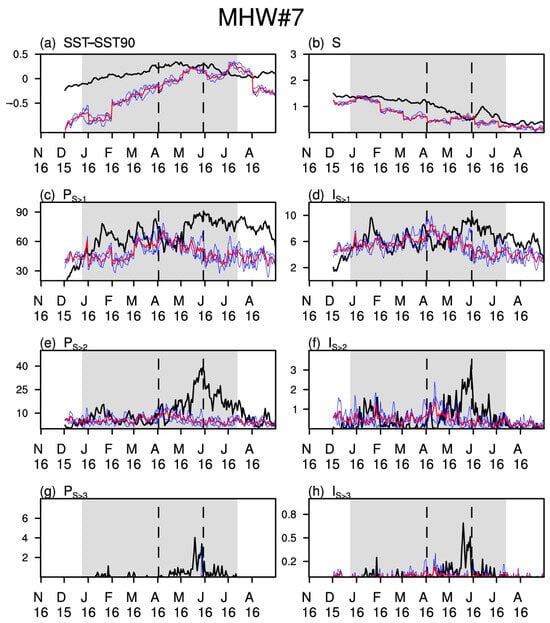
Figure 5.
As in Figure 2, the time series of MHW metrics including (a) the difference between the regional average SST and 90th SST (units: °C), (b) the regional mean S index, and metrics (c) PS>1 (units: %), (d) IS>1 (units: °CM km2), (e) PS>2 (units: %), (f) IS>2 (units: °CM km2), (g) PS>3 (units: %), and (h) IS>3 (units: °CM km2), which are derived from observations (black bold curves) and 30–60 d fore-casts (red curves represent the ensemble mean forecasts, and blue curves represent forecasts of members with different nudging coefficient in SST) by the NUIST CFS1.1 model during the period but for the event MHW#7.
In Figure 6, we present the spatial distribution of the observed warming, measured by parameter DS>1, DS>2, and DS>3, which represent the total days meeting the criteria for moderate, strong, and severe warming at each grid point, respectively. For MHW#1, DS>1 exceeds 150 days in most of the occurring region, peaking near the equator with more than 250 days (Figure 6a). This indicates prolonged and widespread moderate warming. During MHW#2 and #7 events, DS>1 also reaches its maximum near the equator, exceeding 150 days (Figure 6d,j). In contrast, for MHW#6, DS>1 is only about 50 days (Figure 6g). A similar spatial distribution can be observed for DS>2 and DS>3, except that in MHW#1, the maximum values of DS>2 and DS>3 are located on the southeast and east sides of the region (Figure 6a–c).
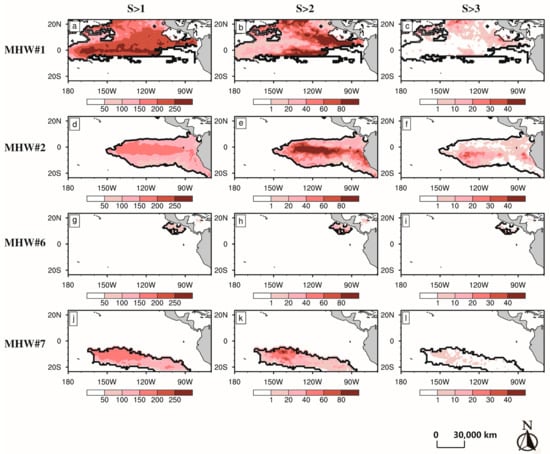
Figure 6.
The spatial distribution of DS>1, DS>2, and DS>3 (units: days) derived from observations for MHW#1 (a–c), MHW#2 (d–f), MHW#6 (g–i), and MHW#7 (j–l), respectively. The black contour lines show the spatial extent of the occurrence of MHW#1, #2, #6, and #7, which is selected based on the maximum yearly mean SSTA from 1983 to 2020, strictly following Lin et al. [49].
Upon inspecting the forecasted spatial distribution of the metrics DS>1, DS>2, and DS>3 as shown in Figure 7, we found that the 30–60d forecasts accurately capture the magnitudes of DS>1 in all four MHW events but struggle to replicate DS>2 and DS>3 in MHW#6–7 (Figure 7). Specifically, in MHW#1 and MHW#2, the forecast overestimates DS>1 primarily along the southeastern fringe and underestimates it in the northeast for MHW#2 (Figure 7a,d). However, in MHW#6 and MHW#7, the underestimation extends to the west and the entire region, respectively (Figure 7g,j). Despite the general consistency between forecasts and observations for DS>1, notable discrepancies emerge for DS>2 and DS>3. The forecasted DS>2 exaggerates values mainly on the southeast edge in MHW#1 and the eastern part in MHW#2, with a significant spatial mismatch, particularly in MHW#2 (Figure 7b,e). Furthermore, substantial negative differences are observed north of 5°N in MHW#1 and west of 105°W in MHW#2. For MHW#6 and MHW#7, the forecasts completely miss DS>2 signatures (Figure 7h,k). Similarly, the forecasts have difficulty capturing both magnitudes and distribution of the DS>3 in MHW#1–2 and MHW#6–7 (Figure 7c,f,i,l). Specifically, there are localized overestimations near the equator in MHW#1 and #2 (Figure 7c,f) but a complete absence in MHW#6 and #7 (Figure 7i,l). These findings underscore the superior performance of NUIST CFS1.1 in predicting moderate warming (S > 1) metrics compared to stronger warming (S > 2 and S > 3), particularly at the lead time of 30–60-day. This further supports the previous statement made in [50].
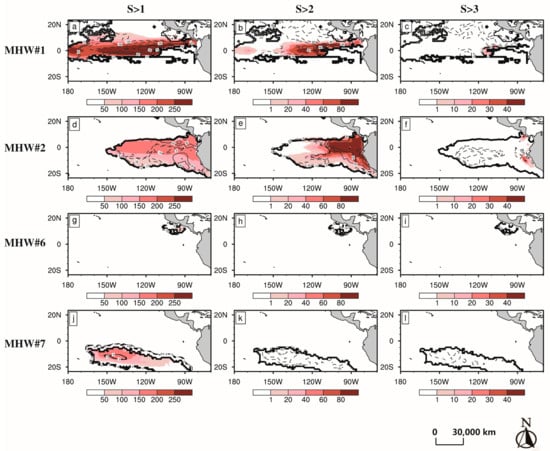
Figure 7.
As in Figure 6, but from NUIST CFS1.1 forecasts. The positive and negative values of forecast-minus-observation differences are depicted by the black solid and black dashed contours for MHW#1 (a–c), MHW#2 (d–f), MHW#6 (g–i), and MHW#7 (j–l), respectively. The black contour lines show the spatial extent of the occurrence of MHW#1, #2, #6, and #7.
By combining the forecasts of various metrics, it becomes evident that the NUIST CFS1.1 model faces greater challenges in accurately capturing metrics that indicate strong and severe warming. Notably, these strong warming metrics play a crucial role in distinguishing the sub-seasonal forecast capabilities between high- and low-predictive MHW events.
3.2. Influencing Factors of Sub-Seasonal Forecast Skills of Extreme MHWs: Tropical Background SST and Process in the Mixed Layer Heat Budget
In this section, we delve into the tropical background SST from 30 days before the onset of MHW to 30 days after the end of MHW as well as the local mixed-layer processes during the rapid warming period, which are pivotal drivers of MHWs. By comparing high- and low-predictive events, our objective is to identify the potential factors that influence the sub-seasonal forecast skill of extreme MHWs by the NUIST CFS1.1 model.
3.2.1. ENSO Forcing
All four MHWs occurred during a super El Niño. Prior studies have emphasized enhanced predictability of longer-duration MHWs in the eastern Pacific [14,54]. Additionally, forecasts initialized during boreal spring or during active ENSO phases tend to be more skillful, with notable improvements in central–eastern Pacific seasonal forecasts [71]. Compared to traditional ENSO indices, “mega ENSO” captures a broader range of SST variability [72]. In our study, MHW#1–2 occurred within the key area of ENSO, and MHW#6–7 occurred at the periphery and within the domain region of mega ENSO. Thus, we first examine whether ENSO forcing exhibits distinct forecast skill disparities between high- and low-predictive MHW events. To do this, we select the Niño 3.4 index, Eastern type El Niño index (NiñoEP index), and mega ENSO index for further evaluation [72,73,74,75]. The ACC and RMSE for ENSO indices are calculated based on the observed and forecast time series in the period from 30 days before the onset to 30 days after the end of each MHW event.
From Figure 8a, we find that at the lead time of 30–60 days, the model accurately forecasts the Niño indices in both high- and low-predictive MHWs, because the temporal correlation coefficients (hereinafter referred to as TCCs) [61,62] have skills all above 0.9. The Niño indices in MHW#1, #2, and #7 exhibit mostly positive ACCs above 0.3, with MHW#7 yielding the highest ACC skill (Figure 8b). However, in MHW#6, the ACCs have negative skills, potentially due to the model’s failure to capture the sub-seasonal variability of the Nino indices, especially the Niño 3.4 index. This inconsistency between the forecast skill of the ENSO as the SST background and forecast skill of MHW events highlights that a good ENSO forecast does not necessarily lead to a good MHW forecast. The discrepancy in the sub-seasonal forecast skills of ENSO and MHW events may be attributed to the relatively shorter timescales of MHWs and their focus on the extreme warming anomalies, in contrast to the broader and more prolonged nature of ENSO. Nevertheless, for high-predictive cases that are located within the key area of ENSO, the ACC skills of Niño indices are higher for MHW#1 compared to MHW#2, consistent with those for these two MHW events, confirming the role of ENSO in the forecast skills of MHWs if they are located in the key area of ENSO [14,38,56,71].
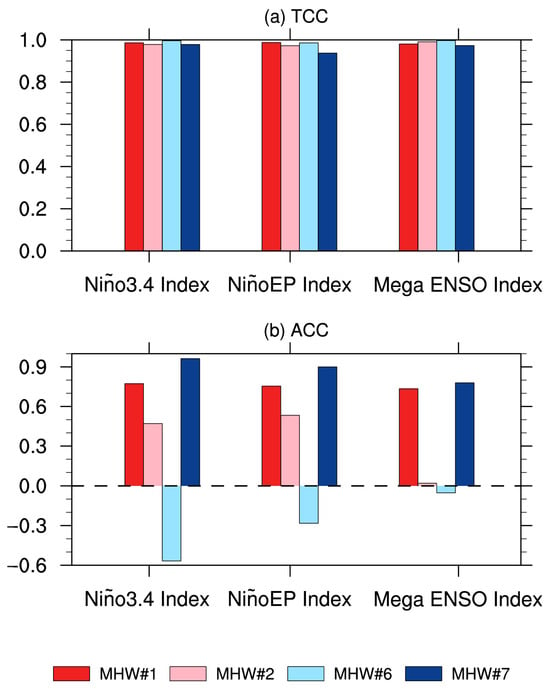
Figure 8.
The (a) temporal correlation coefficient (TCC) and (b) ACC of Niño 3.4, NiñoEP and mega ENSO index between the observations and forecasts at lead times of 30–60 days for the period from 30 days before the onset of MHW to 30 days after the end of MHW.
3.2.2. Ocean Mixed-Layer Heat Budget
We next focus on the rapid warming periods of MHWs and perform a heat budget analysis within the surface mixed layer to investigate the local processes responsible for MHW formation. These periods are selected because the intensity metrics, including IS>1 and IS>2, increase remarkably to their peaks, and the peak of IS>3 is also included in these periods. Thereby, a positively large value of SSTA tendency term is ensured. For high- and low-predictive MHWs, the rapid warming periods, as demarcated by the space between two black dashed lines in Figure 2, Figure 3, Figure 4 and Figure 5, are identified as from 2 September to 29 October 2015 for MHW#1, 1 November to 30 December 1982 for MHW#2, 12 December 2015 to 30 January 2016 for MHW#6, and 11 April to 30 May 2016 for MHW#7. To simplify, when calculating the terms in Equation (5) from monthly data, the rapid warming periods are approximated as September to November 2015 for MHW#1, November to January 1982 for MHW#2, December 2015 to February 2016 for MHW#6, and April to June 2016 for MHW#7.
In addition, the heat budget analysis is limited to the grid points that meet the MHW criteria of moderate, strong, and severe warming (i.e., S > 1, S > 2, and S > 3) for at least one day during the identified rapid warming periods. The spatial distributions of these grid points closely resemble the high values of DS>1, DS>2, and DS>3, especially in MHW#1, #6, and #7 (cp. Figure A1 and Figure 6).
On this basis, we calculate the contribution rates of Q and Adv to SST’ tendency terms during the rapid warming periods, specifically for regions experiencing moderate (S > 1), strong (S > 2), and severe (S > 3) warming. This is derived by averaging the and at all grid points where S > 1, S > 2, and S > 3 are reached during these periods, respectively.
The contribution rates of Q and Adv to the SST tendency term during the rapid warming periods for moderate warming (S > 1) and strong warming (S > 2) are shown in Figure 9a,b, respectively. Notably, exhibits consistently positive values or Adv term makes substantial contributions to warming during MHW#1, #2, and #6, whereas is largely negative or the Q term largely contributes negatively. An exception is found in MHW#7. This suggests that the intensified horizontal heat convergence at sea surface is the primary driver of moderate and strong warming in MHW#1, #2, and #6, whereas in MHW#7, the strengthened air–sea heat fluxes from the atmosphere into the ocean are responsible. For the severe warming (S > 3), Adv’s positive contributions persist across all MHW events except MHW#2 (Figure 9c), where insufficient grids reach S > 3 and therefore not considered. It emerges that Adv predominantly governs moderate, strong, and severe warming in MHW#1–2 and MHW#6, except in MHW#7, where Q drives moderate and strong warming. This aligns with the prior research consensus that horizontal heat convergence is the main driver of MHW onset in 78% of global MHWs [23,76]. Notably, within the specific domains where MHW#1–2 and MHW#6–7 have been observed, these studies have highlighted that the contribution of Adv significantly surpasses that of Q in the warming process, with numerous grid points even exhibiting a negative contribution from Q.
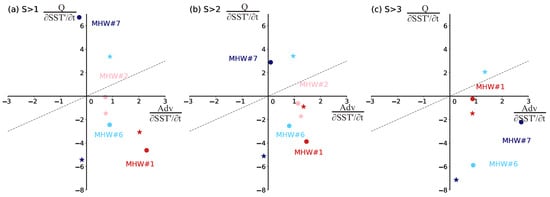
Figure 9.
The contribution rates of Q and Adv to the SST’ tendency ( and ) in the equation corresponding to the grids where MHW occurrences meet the criteria for (a) moderate warming (S > 1), (b) strong warming (S > 2), and (c) severe warming (S > 3) in MHW#1, #2, #6 and #7, respectively. The red, pink, light blue, and blue dots represent observations from MHW#1, #2, #6 and #7, respectively. The stars of the same colors represent the corresponding ensemble mean forecasts in MHW#1, #2, #6 and #7. The gray dashed line represents the line y = x. Since the percentage of grid points experiencing severe warming in MHW#2 is less than 5% of the total region, MHW#2 is excluded in panel (c).
An inspection on the contribution rates derived from 30 to 60 d forecasts by NUIST CFS1.1 model yields that for S > 1 grids, both Q and Adv contributions closely match observations in MHW#1 and #2 but diverge significantly in MHW#6 and #7, with Q’s forecasted contributions even opposing observations. Similar discrepancies persist across S > 2 and S > 3 grids in Figure 9b,c, except for S > 3 grids in MHW#7, where Adv’s contribution is severely underestimated. Therefore, from MHW#1, #2, #6 to #7, the forecast error in Q and Adv contributions escalates, consistent with the sub-seasonal forecast skill of these extreme MHWs. Notably, Adv’s forecast errors are consistently smaller than Q’s, suggesting that the 30–60d forecasts better capture the horizontal advection processes compared to the heat flux processes. Moreover, it is likely that the two high-predictive events are forecasted most accurately due to the higher contribution from the Adv. When diabatic processes dominate in the SST rapid warming, sub-seasonal forecast skill for MHW events may decline, as exemplified by MHW#7. Therefore, enhancing the model’s ability to capture and forecast Q might be crucial for improving sub-seasonal forecasts of extreme MHWs. This further suggests that in order to capture the air–sea heat flux (Q) contributions accurately, the NUIST CFS1.1 model’s radiation and boundary layer parameterization schemes are in urgent need for improvement. It is worth noting that according to previous studies, the MHWs are often dominated by air–sea heat flux in the South China Sea and most of the tropics where the upper ocean layer is shallow (e.g., the tropical Atlantic Ocean and Indonesian Seas), and extreme MHW events tend to be related to a shallower mixed layer depths under 36 m [10,38,76,77,78]. Therefore, the challenges in accurately forecasting shallow mixed layer depths, and consequently the Q term, could hinder advancements in MHW sub-seasonal forecasts.
Further analysis of Adv’s components reveals the contribution rates of Adv-u (zonal advection) and Adv-v (meridional advection) to the SST’ tendency ( and ), as shown in Figure 10. For grids with S > 1 and S > 2 (indicating moderate and strong warming), both Adv-u and Adv-v contribute positively and similarly in MHW#1, #2, and #6, suggesting their significance in these warming categories. In high-predictive events (MHW#1 and #2), the contribute rate of Adv-v slightly exceeds that of Adv-u. In other words, the contribution rate of Adv-v is approximately 30% higher than that of Adv-u in MHW#1, and the contribution rate of Adv-v exceeds that of Adv-u by more than 66% in MHW#2. However, for grids with S > 3 (indicating severe warming), equals in MHW#1 but surpasses it in low-predictive events (MHW#6 and #7). When Adv-u and Adv-v are further divided according to Equations (8) and (9) for grids with S > 1 and S > 2, it appears that the climatological mean meridional advection of SST anomalies () dominates the Adv term in MHW#1 and #2 (Table 3 and Table 4), whereas climatological mean zonal advection of SST anomalies () prevails in MHW#6. Therefore, the primary distinction in Adv between high- and low-predictive MHW events lies in the meridional or zonal advection of SST anomaly.
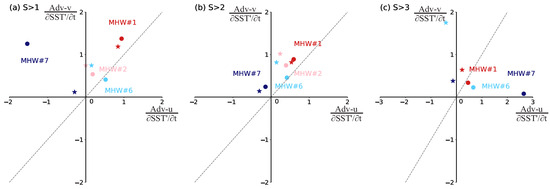
Figure 10.
As in Figure 9, but for the contribution rates of Adv-u and Adv-v to SST’ tendency ( and ) which meet the criteria for (a) moderate warming (S > 1), (b) strong warming (S > 2), and (c) severe warming (S > 3) in MHW#1, #2, #6 and #7, respectively. The red, pink, light blue, and blue dots represent observations from MHW#1, #2, #6 and #7, respectively. The stars of the same colors represent the corresponding ensemble mean forecasts in MHW#1, #2, #6 and #7. The gray dashed line represents the line y = x. MHW#2 is excluded in panel (c), as in Figure 9c.

Table 3.
The contribution rate of each term in Adv-u and Adv-v to SST’ tendency in the equation corresponding to the grids with moderate warming (S > 1) in the rapid warming period of MHW#1–2 and #6–7, in which the Adv term makes the dominant contribution, and the main contribution items are highlighted in bold.

Table 4.
As in Table 3, but for the strong warming, and the main contribution items are highlighted in bold.
The forecasts presented in Figure 10 show that for grids with S > 1 and S > 2, the forecasted values of and have the smallest error in MHW#1, followed by MHW#2 and MHW#6, with the largest errors observed in MHW#7. For grids with S > 3, the forecasted value of has the opposite sign and a larger error in MHW#6–7, especially in MHW#7. This suggests that the 30–60d forecast skills of severe warming might be more limited by Adv-u than by Adv-v.
Table 3 and Table 4 confirm that the meridional terms and their positive contributions to SST’ tendency are accurately forecasted in the meridional advection-dominated MHW events (MHW#1 and #2), but zonal terms are often incorrectly signed or underestimated in the zonal advection-dominated event (MHW#6). The severe warming forecasts (Table 5) also demonstrate a robust capture of , but remain challenging to grasp for low-predictive events. Emphasizing the accurate forecasts of zonal advection of SST anomalies is paramount for enhancing sub-seasonal MHW forecasts, given its pivotal role in mixed layer temperature balance, particularly in the Equatorial Pacific [79,80,81,82,83]. Furthermore, the zonal component of Adv in MHW#1–2, particularly its association with the zonal advection of SST anomalies, is well captured, which may explain their higher sub-seasonal forecast skills.

Table 5.
The contribution rate of each term in Adv-u and Adv-v to SST’ tendency in the equation corresponding to the grids with severe warming (S > 3) in the rapid warming period of MHW#1 and #6–7, in which the Adv term makes the dominant contribution, and the main contribution items are highlighted in bold.
4. Discussion
4.1. Spatial-Temporal Analysis of Extreme Marine Heatwave (MHW) Events That Occurred in the Central–Eastern Tropical Pacific
Marine heatwaves (MHWs) are defined as prolonged discrete anomalously extreme warm water events, which could lead to devastating and long-term impacts on ecosystems as well as political and socio-economic systems [2,3,4,5,6]. Especially, MHWs occurring in the tropical central–eastern tropical Pacific have relatively longer duration and stronger intensity, they are more extreme and harmful [4,9].
Based on the seven extreme MHWs that occurred in the central–eastern tropical Pacific in the period from 1983 to 2020, we further classify them into high-predictive (MHW#1 and #2), moderate-predictive (MHW#3–5), and low-predictive (MHW#6 and #7) categories. To evaluate the key features of these events, we select specific metrics including the proportion of the region experiencing moderate, strong, and severe warming (PS>1, PS>2, PS>3, respectively, where S is the MHW severity index), and the spatial integrals of SST anomalies with largest contiguous MHW (IS>1, IS>2, IS>3). These metrics are further used to calculate the anomaly correlation coefficient (ACC) and root mean square error (RMSE) skills for each MHW event in the sub-seasonal forecasts made by the Nanjing University of Information Science and Technology Climate Forecast System (NUIST CFS1.1). Notably, the metrics in MHW#1–2 mostly have ACC skills above 0.39 and RMSEs below 1.02, while MHW#6 and #7 show mostly negative ACCs and higher RMSEs. There is obvious disparity in the sub-seasonal forecast skill of MHWs between high- (MHW#1–2) and low-predictive MHWs (MHW#6–7). Thus, we then focus our further exploration on these four MHW events to investigate the underlying causes of this variation in forecast skills.
First, the temporal evolutions of various MHW metrics are systematically evaluated, including PS>1, PS>2, PS>3, IS>1, IS>2, IS>3, and the MHW severity index (S), and the spatial distribution of total days of grid-level warming (DS>1, DS>2, DS>3). It seems that high-predictive MHWs exhibit large-scale moderate and strong warming, with the model adept at capturing the temporal trends of all MHW metrics. In contrast, low-predictive MHWs display more pronounced short-term fluctuations. The NUIST CFS1.1 model performs well in capturing metrics related to S > 1 and even S > 2 in high-predictive events but struggles with metrics related to S > 2 and S > 3 in low-predictive MHWs, indicating that metrics indicative of strong and severe warming (S > 2 and S > 3) pose greater challenges for accurate forecasting compared to those associated with moderate warming (S > 1). Notably, the most pronounced disparity in the sub-seasonal forecast skills is observed between high- and low-predictive MHWs for S > 2 metrics.
4.2. Influencing Factors of Sub-Seasonal Forecast Skills of Extreme MHWs: Tropical Background SST
The drivers and mechanisms of MHWs are intricate and multifarious, ranging from local oceanic and atmospheric processes to remote processes via teleconnections [15,16,17,18], wherein climate variations play a pivotal role in modulating the occurrence of MHWs. It is noteworthy that the El Niño–Southern Oscillation (ENSO), the largest global driver of MHWs, can amplify the intensity, duration, and spatial extent of MHWs on interannual and shorter timescales [34,35]. The seven extreme MHWs mostly occur in the period and key area of ENSO; two-thirds of recorded MHWs occurring in the tropical Pacific are associated with El Niño events [16]. Despite the fact that all high-predictive (MHW#1 and #2) and low-predictive (MHW#6 and #7) MHWs are related to ENSO, an assessment of the 30–60 day forecast skills of Niño indices reveals inconsistencies with the forecast skills of MHW, suggesting that a good ENSO does not necessarily translate into a well-forecasted MHW, indicating that other factors beyond ENSO may play a significant role in the accuracy of MHW forecasts.
4.3. Influencing Factors of Sub-Seasonal Forecast Skills of Extreme MHWs: Process in the Mixed Layer Heat Budget
The heat budget analysis in the surface mixed layer in the rapid warming periods of MHWs further yields the role of the convergence of heat in the sea mixed layer due to advection (Adv) and the air–sea heat flux into the sea surface (Q) in each MHW event [49,52]. Results show that the moderate and strong warming (S > 1 and S > 2) observed in MHW#1, #2, and #6 are primarily driven by Adv, whereas in MHW#7, it is dominated by Q. Notably, even for the extreme warming (S > 3), Adv contributes positively to MHW#7, highlighting its persistent significance. It highlights the pivotal roles of heat convergence within this layer, which aligns with the prior research consensus that horizontal heat convergence is the main driver of MHW onset in 78% of global MHWs [23,75]. It is further found that Adv consistently exhibits smaller forecast errors in influencing sea surface temperature anomaly (SST’) tendencies across all warming categories (from S > 1 to S > 3) compared to Q, suggesting a better capture of horizontal advection processes than diabatic processes by the model. Moreover, for the two high-predictive events (MHW#1 and #2), the warmings are mainly contributed from the Adv and thus their higher forecast skills might be due to the higher contribution from the more predictable Adv. Furthermore, enhancing the model’s ability to capture and forecast Q might be crucial for improving sub-seasonal forecasts of extreme MHWs. It is worth noting that according to previous studies, the MHWs are often dominated by air–sea heat flux in the South China Sea and most of the tropics where the upper ocean layer is shallow (e.g., the tropical Atlantic Ocean and Indonesian Seas), and extreme MHW events tend to be related to a shallower mixed layer depths under 36 m [10,23,76,78]. Therefore, the challenges in accurately forecasting shallow mixed layer depths, and consequently the Q term, could hinder advancements in MHW sub-seasonal forecasts. To better capture the Q, improvements in model’s radiation and boundary layer parameterization might be helpful.
Further dissecting the advection component into its zonal (Adv-u) and meridional (Adv-v) reveals that an accurate representation of Adv-u, particularly the component associated with the zonal advection of SST’, holds the potential to significantly enhance sub-seasonal forecasting capabilities for MHWs. This underscores the importance of refining the models’ ability to capture the intricate dynamics of horizontal heat convergence, particularly along the zonal direction, for improving MHW predictions, particularly in the Equatorial Pacific [79,80,81,82,83].
4.4. Limitations and Future Outlook
In this paper, we focus on the seven extreme MHWs identified during the warmest year in specific regions of the central–eastern tropical Pacific and further evaluate the factors influencing the disparity in sub-seasonal forecast skill through comparing high- and low-predictive MHWs. There are some potential uncertainties in the results of this study. First, the conclusion of this paper needs to be validated using a larger number of MHW events with broader definitions [1,38] across typical regions of interest (e.g., the north and south coasts of the central–eastern tropical Pacific, the coasts of Mexico and Peru), and this research is in progress. Second, although the established credibility of monthly ORAS5 data supports our study in facilitating heat budget analyses within the surface mixed layer [67,84,85,86]. We highlight the importance of future endeavors leveraging daily datasets to strengthen the conclusions and propel advancements in the predictability of these devastating climatic phenomena.
5. Conclusions
Based on the sub-seasonal forecast skill of seven extreme marine heatwave (MHW) events that occurred in the central–eastern tropical Pacific in the period from 1983 to 2020, we divide them into high- (MHW#1 and #2), moderate- (MHW#3–5), and low-predictive (MHW#6 and #7) categories. To evaluate the key features of these events, we select specific metrics, respectively, indicative of moderate, strong and severe warming (S > 1, S > 2 and S > 3, where S is the MHW severity index). Notably, there is obvious disparity in the sub-seasonal forecast skill of MHWs between high- and low-predictive MHWs. Focusing on the high- and low-predictive MHWs, results show that the S > 2 and S > 3 metrics, especially S > 2 metrics, pose greater challenges for accurate forecasting by Nanjing University of Information Science and Technology Climate Forecast System (NUIST CFS1.1). Although these four MHWs are related to the El Niño–Southern Oscillation (ENSO), a good ENSO does not necessarily translate into a well-forecasted MHW. The analysis of the heat budget in the surface mixed layer during the rapid warming periods of MHWs highlights the pivotal roles of heat convergence within this layer. It seems that the moderate and strong warming observed in MHW#1, #2, and #6 is primarily driven by Adv, whereas in MHW#7, it is dominated by Q. Notably, even for the extreme warming (S > 3), Adv contributes positively to MHW#7, highlighting its persistent significance. Moreover, the model better captures horizontal advection processes than diabatic processes. Thus, the higher forecast skills in MHW#1 and #2 might be due to the higher contribution from the more predictable Adv. With further dissection of Adv, it seems that an accurate representation of the component associated with the zonal advection, holds the potential to significantly enhance sub-seasonal forecasting capabilities for MHWs. This underscores the importance of refining models’ ability to capture the intricate dynamics of horizontal heat convergence, particularly along the zonal direction, for improving MHW predictions.
Author Contributions
Conceptualization, C.L., L.L. and Y.Y.; methodology, L.L.; software, J.W.; validation, C.L., L.L. and Y.Y.; formal analysis, L.L.; investigation, L.L. and Y.Y.; resources, L.L.; data curation, J.W.; writing—original draft preparation, L.L.; writing—review and editing, C.L., L.L. and Y.Y.; visualization, C.L., L.L. and Y.Y.; supervision, J.L. and G.L.; project administration, C.L. and Y.Y.; funding acquisition, L.L., Y.Y. and J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (42088101, 41330425, 42005020), National Key Research and Development Program of China (2019YFC1510201), and the Project Funded by the Priority Academic Program Development of Jiangsu Province, and Postgraduate Research & Practice Innovation Program of Jiangsu Province (KYCX23_1300).
Data Availability Statement
Data are openly available from the National Oceanic Atmospheric Administration Optimum Interpolation Sea Surface Temperature V2 data (OISST V2) [9,52,53,54,55] (https://psl.noaa.gov/data/gridded/data.noaa.oisst.v2.highres.html, accessed on 21 February 2025) and the Ocean Reanalysis System 5 global ocean reanalysis monthly mean data (ORAS5) prepared by European Centre for Medium-Range Weather Forecasts [56,57,58] (https://cds.climate.copernicus.eu/datasets/reanalysis-oras5?tab=overview, accessed on 21 February 2025). The numerical calculations of NUIST CFS1.1 model in this study are conducted in the High-Performance Computing Center of Nanjing University of Information Science and Technology [49,51,87,88,89,90].
Acknowledgments
We acknowledge the National Oceanic Atmospheric Administration for providing NOAA OISST V2 High Resolution Datasets, the European Centre for providing ORAS5 monthly mean data, the High-Performance Computing Center of Nanjing University of Information Science and Technology for providing NUIST CFS1.1 model data.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
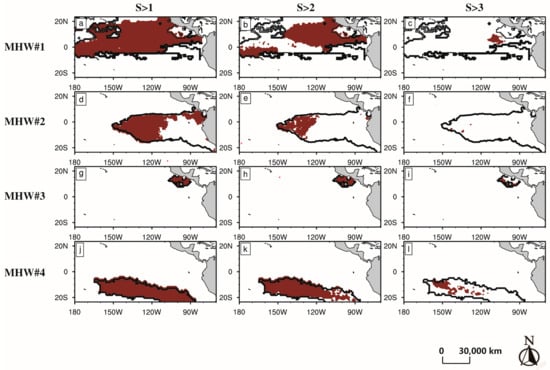
Figure A1.
The spatial distribution of grids reaching the standard of moderate, strong, and severe warming (i.e., S > 1, S > 2, and S > 3) during the rapid warming period for MHW#1 (a–c), MHW#2 (d–f), MHW#6 (g–i), and MHW#7 (j–l), respectively.
References
- Hobday, A.J.; Alexander, L.V.; Perkins, S.E.; Smale, D.A.; Straub, S.C.; Oliver, E.C.J.; Benthuysen, J.A.; Burrows, M.T.; Donat, M.G.; Feng, M.; et al. A hierarchical approach to defining marine heatwaves. Prog. Oceanogr. 2016, 141, 227–238. [Google Scholar] [CrossRef]
- Wernberg, T.; Bennett, S.; Babcock, R.C.; de Bettignies, T.; Cure, K.; Depczynski, M.; Dufois, F.; Fromont, J.; Fulton, C.J.; Hovey, R.K.; et al. Climate-driven regime shift of a temperate marine ecosystem. Science 2016, 353, 169–172. [Google Scholar] [CrossRef] [PubMed]
- Cavole, L.M.; Demko, A.M.; Diner, R.E.; Giddings, A.; Koester, I.; Pagniello, C.M.; Paulsen, M.L.; Ramirez-Valdez, A.; Schwenck, S.M.; Yen, N.K.; et al. Biological impacts of the 2013–2015 warm-water anomaly in the Northeast Pacific: Winners, losers, and the future. Oceanography 2016, 29, 273–285. [Google Scholar] [CrossRef]
- Oliver, E.C.J.; Donat, M.G.; Burrows, M.T.; Moore, P.J.; Smale, D.A.; Alexander, L.V.; Benthuysen, J.A.; Feng, M.; Gupta, A.S.; Hobday, A.J.; et al. Longer and more frequent marine heatwaves over the past century. Nat. Commun. 2018, 9, 1324. [Google Scholar] [CrossRef] [PubMed]
- Ummenhofer, C.C.; Meehl, G.A. Extreme weather and climate events with ecological relevance: A review. Philos. Trans. R. Soc. B Biol. Sci. 2017, 372, 20160135. [Google Scholar] [CrossRef] [PubMed]
- Frölicher, T.L.; Laufkötter, C. Emerging risks from marine heat waves. Nat. Commun. 2018, 9, 650. [Google Scholar] [CrossRef] [PubMed]
- Gan, R.; Liu, Q.; Huang, G.; Hu, K.; Li, X. Greenhouse warming and internal variability increase extreme and central Pacific El Niño frequency since 1980. Nat. Commun. 2023, 14, 394. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wu, R.; Dai, P.; Cai, R.; Tan, H. Diverse marine heatwave intensity trends in the marginal seas of China. Theor. Appl. Clim. 2024, 155, 5237–5250. [Google Scholar] [CrossRef]
- Scannell, H.A.; Johnson, G.C.; Thompson, L.; Lyman, J.M.; Riser, S.C. Subsurface evolution and persistence of marine heatwaves in the Northeast Pacific. Geophys. Res. Lett. 2020, 47, e2020GL090548. [Google Scholar] [CrossRef]
- Tan, H.-J.; Cai, R.-S.; Wu, R.-G. Summer marine heatwaves in the South China Sea: Trend, variability and possible causes. Adv. Clim. Change Res. 2022, 13, 323–332. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, F.; Zhu, J.; Chen, X. Observed Frequent Occurrences of Marine Heatwaves in Most Ocean Regions during the Last Two Decades. Adv. Atmos. Sci. 2022, 39, 1579–1587. [Google Scholar] [CrossRef]
- Benthuysen, J.A.; Smith, G.A.; Spillman, C.M.; Steinberg, C.R. Subseasonal prediction of the 2020 Great Barrier Reef and Coral Sea marine heatwave. Environ. Res. Lett. 2021, 16, 124050. [Google Scholar] [CrossRef]
- Hu, S.; Li, S.; Zhang, Y.; Guan, C.; Du, Y.; Feng, M.; Ando, K.; Wang, F.; Schiller, A.; Hu, D. Observed strong subsurface marine heatwaves in the tropical western Pacific Ocean. Environ. Res. Lett. 2021, 16, 104024. [Google Scholar] [CrossRef]
- Jacox, M.G.; Alexander, M.A.; Amaya, D.; Becker, E.; Bograd, S.J.; Brodie, S.; Hazen, E.L.; Buil, M.P.; Tommasi, D. Global seasonal forecasts of marine heatwaves. Nature 2022, 604, 486–490. [Google Scholar] [CrossRef]
- Holbrook, N.J.; Gupta, A.S.; Oliver, E.C.J.; Hobday, A.J.; Benthuysen, J.A.; Scannell, H.A.; Smale, D.A.; Wernberg, T. Keeping pace with marine heatwaves. Nat. Rev. Earth Environ. 2020, 1, 482–493. [Google Scholar] [CrossRef]
- Oliver, E.C.; Benthuysen, J.A.; Darmaraki, S.; Donat, M.G.; Hobday, A.J.; Holbrook, N.J.; Schlegel, R.W.; Gupta, A.S. Marine heatwaves. Annu. Rev. Mar. Sci. 2021, 13, 313–342. [Google Scholar] [CrossRef] [PubMed]
- Vogt, L.; Burger, F.A.; Griffies, S.M.; Frölicher, T.L. Local drivers of marine heatwaves: A global analysis with an earth system model. Front. Clim. 2022, 4, 847995. [Google Scholar] [CrossRef]
- Song, S.-Y.; Yeh, S.-W.; Kim, H.; Holbrook, N.J. Arctic warming contributes to increase in Northeast Pacific marine heatwave days over the past decades. Commun. Earth Environ. 2023, 4, 25. [Google Scholar] [CrossRef]
- Oliver, E.C.J.; Benthuysen, J.A.; Bindoff, N.L.; Hobday, A.J.; Holbrook, N.J.; Mundy, C.N.; Perkins-Kirkpatrick, S.E. The unprecedented 2015/16 Tasman Sea marine heatwave. Nat. Commun. 2017, 8, 16101. [Google Scholar] [CrossRef]
- Benthuysen, J.; Feng, M.; Zhong, L. Spatial patterns of warming off Western Australia during the 2011 Ningaloo Niño: Quantifying impacts of remote and local forcing. Cont. Shelf Res. 2014, 91, 232–246. [Google Scholar] [CrossRef]
- Schlegel, R.W.; Oliver, E.C.J.; Perkins-Kirkpatrick, S.; Kruger, A.; Smit, A.J. Smit. Predominant atmospheric and oceanic patterns during coastal marine heatwaves. Front. Mar. Sci. 2017, 4, 323. [Google Scholar] [CrossRef]
- Holbrook, N.J.; Scannell, H.A.; Gupta, A.S.; Benthuysen, J.A.; Feng, M.; Oliver, E.C.J.; Alexander, L.V.; Burrows, M.T.; Donat, M.G.; Hobday, A.J.; et al. A global assessment of marine heatwaves and their drivers. Nat. Commun. 2019, 10, 2624. [Google Scholar] [CrossRef] [PubMed]
- Marin, M.; Feng, M.; Bindoff, N.L.; Phillips, H.E. Local drivers of extreme upper ocean marine heatwaves assessed using a global ocean circulation model. Front. Clim. 2022, 4, 788390. [Google Scholar] [CrossRef]
- Elzahaby, Y.; Schaeffer, A.; Roughan, M.; Delaux, S. Oceanic circulation drives the deepest and longest marine heatwaves in the East Australian Current system. Geophys. Res. Lett. 2021, 48, e2021GL094785. [Google Scholar] [CrossRef]
- Chen, K.; Gawarkiewicz, G.G.; Lentz, S.J.; Bane, J.M. Diagnosing the warming of the Northeastern U.S. Coastal Ocean in 2012: A linkage between the atmospheric jet stream variability and ocean response. J. Geophys. Res. Oceans 2014, 119, 218–227. [Google Scholar] [CrossRef]
- Benthuysen, J.A.; Oliver, E.C.J.; Feng, M.; Marshall, A.G. Extreme marine warming across tropical Australia during austral summer 2015–2016. J. Geophys. Res. Oceans 2018, 123, 1301–1326. [Google Scholar] [CrossRef]
- Perkins-Kirkpatrick, S.E.; King, A.D.; Cougnon, E.; Grose, M.R.; Oliver, E.C.J.; Holbrook, N.; Lewis, S.C.; Pourasghar, F. The role of natural variability and anthropogenic climate change in the 2017/18 Tasman Sea marine heatwave. Bull. Am. Meteorol. Soc. 2019, 100, S105–S110. [Google Scholar] [CrossRef]
- Chen, Z.; Shi, J.; Liu, Q.; Chen, H.; Li, C. A persistent and intense marine heatwave in the Northeast Pacific during 2019–2020. Geophys. Res. Lett. 2021, 48, e2021GL093239. [Google Scholar] [CrossRef]
- Gregory, C.H.; Holbrook, N.J.; Marshall, A.G.; Spillman, C.M. Atmospheric Drivers of Tasman Sea Marine Heatwaves. J. Clim. 2023, 36, 5197–5214. [Google Scholar] [CrossRef]
- Li, Z.; Holbrook, N.J.; Zhang, X.; Oliver, E.C.J.; Cougnon, E.A. Remote forcing of Tasman Sea marine heatwaves. J. Clim. 2020, 33, 5337–5354. [Google Scholar] [CrossRef]
- Echevin, V.; Colas, F.; Espinoza-Morriberon, D.; Vasquez, L.; Anculle, T.; Gutierrez, D. Forcings and evolution of the 2017 coastal El Niño off Northern Peru and Ecuador. Front. Mar. Sci. 2018, 5, 367. [Google Scholar] [CrossRef]
- Schlegel, R.W.; Oliver, E.C.J.; Chen, K. Drivers of marine heatwaves in the Northwest Atlantic: The role of air–sea interaction during onset and decline. Front. Mar. Sci. 2021, 8, 627970. [Google Scholar] [CrossRef]
- Carrasco, D.; Pizarro, O.; Jacques-Coper, M.; Narváez, D.A. Main drivers of marine heat waves in the eastern South Pacific. Front. Mar. Sci. 2023, 10, 1129276. [Google Scholar] [CrossRef]
- Barriopedro, D.; García-Herrera, R.; Ordóñez, C.; Miralles, D.G.; Salcedo-Sanz, S. Heat waves: Physical understanding and scientific challenges. Rev. Geophys. 2023, 61, e2022RG000780. [Google Scholar] [CrossRef]
- Misra, R.; Sérazin, G.; Meissner, K.J.; Gupta, A.S. Projected changes to Australian marine heatwaves. Geophys. Res. Lett. 2021, 48, e2020GL091323. [Google Scholar] [CrossRef]
- Jacox, M.G. Marine heatwaves in a changing climate. Nature 2019, 571, 485–487. [Google Scholar] [CrossRef]
- Di Lorenzo, E.; Mantua, N. Multi-year persistence of the 2014/15 North Pacific marine heatwave. Nat. Clim. Change 2016, 6, 1042–1047. [Google Scholar] [CrossRef]
- Hobday, A.J.; Spillman, C.M.; Eveson, J.P.; Hartog, J.R. Seasonal forecasting for decision support in marine fisheries and aquaculture. Fish. Oceanogr. 2016, 25, 45–56. [Google Scholar] [CrossRef]
- Jacox, M.G.; Alexander, M.A.; Stock, C.A.; Hervieux, G. On the skill of seasonal sea surface temperature forecasts in the California Current System and its connection to ENSO variability. Clim. Dyn. 2019, 53, 7519–7533. [Google Scholar] [CrossRef]
- Jacox, M.G.; Tommasi, D.; Alexander, M.A.; Hervieux, G.; Stock, C.A. Predicting the evolution of the 2014–2016 California Current System marine heatwave from an ensemble of coupled global climate forecasts. Front. Mar. Sci. 2019, 6, 497. [Google Scholar] [CrossRef]
- Giamalaki, K.; Beaulieu, C.; Prochaska, J.X. Assessing predictability of marine heatwaves with random forests. Geophys. Res. Lett. 2022, 49, e2022GL099069. [Google Scholar] [CrossRef]
- de Boisséson, E.; Balmaseda, M.A. Predictability of marine heatwaves: Assessment based on the ECMWF seasonal forecast system. Ocean Sci. 2024, 20, 265–278. [Google Scholar] [CrossRef]
- Gupta, A.S.; Ryan, S.; Hernaman, V. Advances in marine heatwave interactions. Front. Clim. 2023, 5, 1177781. [Google Scholar] [CrossRef]
- Luo, J.-J.; Masson, S.; Behera, S.; Yamagata, T. Experimental forecasts of the Indian Ocean dipole using a coupled OAGCM. J. Clim. 2007, 20, 2178–2190. [Google Scholar] [CrossRef]
- Luo, J.; Behera, S.; Masumoto, Y.; Sakuma, H.; Yamagata, T. Successful prediction of the consecutive IOD in 2006 and 2007. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Luo, J.-J.; Masson, S.; Behera, S.K.; Yamagata, T. Extended ENSO predictions using a fully coupled ocean–atmosphere model. J. Clim. 2008, 21, 84–93. [Google Scholar] [CrossRef]
- Peng, K.; Luo, J.-J.; Liu, Y. Prediction of Seasonal Tropical Cyclone Activity in the NUIST-CFS1.0 Forecast System. Adv. Atmos. Sci. 2023, 40, 1309–1325. [Google Scholar] [CrossRef]
- Wu, J.; Li, Y.; Luo, J.J.; Zhang, Y.; Doi, T.; Yamagata, T. Improved MJO prediction using a multi-member subseasonal to seasonal forecast system of NUIST (NUIST CFS 1.1). Preprints 2023, 202307013. [Google Scholar] [CrossRef]
- Lin, L.; Yu, Y.; Lu, C.; Luo, J.; Chen, L.; Ma, J.; Guan, Z.; Wu, J. Are the extreme marine heatwave events in the central-eastern tropical Pacific predictable 30–60 days in advance by NUIST CFS1.1 model? Atmos. Res. 2023, 289, 106744. [Google Scholar] [CrossRef]
- Ma, J.; Xu, H.; Dong, C.; Luo, J.-J. The Forecast Skills and Predictability Sources of Marine Heatwaves in the NUIST-CFS1.0 Hindcasts. Adv. Atmos. Sci. 2024, 41, 1589–1600. [Google Scholar] [CrossRef]
- Gupta, H.; Sil, S. Assessment of GHRSST and OISST Datasets in Identification of Marine Heat-Waves and Heat-Spikes. IEEE Geosci. Remote Sens. 2024, 21, 1501705. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Y.; Wang, F.; Lv, M. Weak Mesoscale Variability in the Optimum Interpolation Sea Surface Temperature (OISST)-AVHRR-Only Version 2 Data before 2007. Remote Sens. 2022, 14, 409. [Google Scholar] [CrossRef]
- Gupta, A.S.; Thomsen, M.; Benthuysen, J.A.; Hobday, A.J.; Oliver, E.; Alexander, L.V.; Burrows, M.T.; Donat, M.G.; Feng, M.; Holbrook, N.J.; et al. Drivers and impacts of the most extreme marine heatwave events. Sci. Rep. 2020, 10, 19359. [Google Scholar] [CrossRef]
- Plecha, S.M.; Soares, P.M.M.; Silva-Fernandes, S.M.; Cabos, W. On the uncertainty of future projections of marine heatwave events in the North Atlantic Ocean. Clim. Dyn. 2021, 56, 2027–2056. [Google Scholar] [CrossRef]
- Zuo, H.; Balmaseda, M.A.; Tietsche, S.; Mogensen, K.; Mayer, M. The ECMWF operational ensemble reanalysis–analysis system for ocean and sea ice: A description of the system and assessment. Ocean Sci. 2019, 15, 779–808. [Google Scholar] [CrossRef]
- de Boisseson, E. Monitoring marine heatwaves in CMEMS ocean analysis systems. In Proceedings of the 22nd EGU General Assembly Conference Abstracts, Online, 4–8 May 2020; p. 19468. [Google Scholar] [CrossRef]
- Li, Z.; Wu, G.; Xu, C.; Zhu, X.-H.; Long, Y. Summer marine heatwaves in the tropical Indian Ocean associated with an unseasonable positive Indian Ocean Dipole event 2012. Front. Mar. Sci. 2024, 11, 1425813. [Google Scholar] [CrossRef]
- Guo, X.; Gao, Y.; Zhang, S.; Wu, L.; Chang, P.; Cai, W.; Zscheischler, J.; Leung, L.R.; Small, J.; Danabasoglu, G.; et al. Threat by marine heatwaves to adaptive large marine ecosystems in an eddy-resolving model. Nat. Clim. Change 2022, 12, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Li, Y.; Luo, J.-J.; Jiang, X. Assessing the Role of Air–Sea Coupling in Predicting Madden–Julian Oscillation with an Atmosphere–Ocean Coupled Model. J. Clim. 2021, 34, 9647–9663. [Google Scholar] [CrossRef]
- Hobday, A.J.; Oliver, E.C.J.; Gupta, A.S.; Benthuysen, J.A.; Burrows, M.T.; Donat, M.G.; Holbrook, N.J.; Moore, P.J.; Thomsen, M.S.; Wernberg, T.; et al. Categorizing and naming marine heatwaves. Oceanography 2018, 31, 162–173. [Google Scholar] [CrossRef]
- Wu, J.; Ren, H.L.; Zhang, S.; Liu, Y.; Liu, X. Evaluation and predictability analysis of seasonal prediction by BCC second-generation climate system model. Chin. J. Atmos. Sci. 2017, 41, 1300–1315. [Google Scholar]
- Liu, L.; Bai, H.; Feng, G.; Gong, Z.; Zhou, B. Evaluation and correction of sub-seasonal dynamic model forecast of precipitation in eastern China. Clim. Dyn. 2023, 61, 4643–4659. [Google Scholar] [CrossRef]
- Stevenson, J.W.; Niiler, P.P. Upper ocean heat budget during the hawaii-to-tahiti shuttle experiment. J. Phys. Oceanogr. 1983, 13, 1894–1907. [Google Scholar] [CrossRef]
- Jin, D.; Guan, Z.; Huo, L.; Wang, X. Possible impacts of spring sea surface temperature anomalies over South Indian Ocean on summer rainfall in Guangdong-Guangxi region of China. Clim. Dyn. 2017, 49, 3075–3090. [Google Scholar] [CrossRef]
- Foltz, G.R.; Grodsky, S.A.; Carton, J.A.; McPhaden, M.J. Seasonal mixed layer heat budget of the tropical Atlantic Ocean. J. Geophys. Res. Oceans 2003, 108. [Google Scholar] [CrossRef]
- Du, Y.; Qu, T.; Meyers, G.; Masumoto, Y.; Sasaki, H. Seasonal heat budget in the mixed layer of the southeastern tropical Indian Ocean in a high-resolution ocean general circulation model. J. Geophys. Res. Oceans 2005, 110. [Google Scholar] [CrossRef]
- Haijun, Y.; Qinyu, L.; Xujing, J. On the upper oceanic heat budget in the south china sea:Annual cycle. Adv. Atmos. Sci. 1999, 16, 619–629. [Google Scholar] [CrossRef]
- Zhu, J.; Yu, Y.; Guan, Z.; Wang, X. Dominant coupling mode of SST in maritime continental region and East Asian summer monsoon circulation. J. Geophys. Res.-Atmos. 2022, 127, e2022JD036739. [Google Scholar] [CrossRef]
- Swenson, M.S.; Hansen, D.V. Tropical Pacific Ocean mixed layer heat budget: The Pacific cold tongue. J. Phys. Oceanogr. 1999, 29, 69–81. [Google Scholar] [CrossRef]
- Peter, A.; Le Hénaff, M.; du Penhoat, Y.; Menkes, C.E.; Marin, F.; Vialard, J.; Caniaux, G.; Lazar, A. A model study of the seasonal mixed layer heat budget in the equatorial Atlantic. J. Geophys. Res. Oceans 2006, 111. [Google Scholar] [CrossRef]
- Jacox, M.G.; Alexander, M.A.; Siedlecki, S.; Chen, K.; Kwon, Y.-O.; Brodie, S.; Ortiz, I.; Tommasi, D.; Widlansky, M.J.; Barrie, D.; et al. Seasonal-to-interannual prediction of North American coastal marine ecosystems: Forecast methods, mechanisms of predictability, and priority developments. Prog. Oceanogr. 2020, 183, 102307. [Google Scholar] [CrossRef]
- Wang, B.; Liu, J.; Kim, H.-J.; Webster, P.J.; Yim, S.-Y.; Xiang, B. Northern Hemisphere summer monsoon intensified by mega-ElNiño/Southern Oscillation and Atlantic multidecadal oscillation. Proc. Natl. Acad. Sci. USA 2013, 110, 5347–5352. [Google Scholar] [CrossRef] [PubMed]
- China Meteorological Administration. El Niño/La Niña Event Discrimination Method: QX/T 370; China Standard Press: Beijing, China, 2017. [Google Scholar]
- Ren, H.-L.; Jin, F.-F. Niño indices for two types of ENSO. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Zhan, R.; Wang, Y.; Zhao, J. Intensified Mega-ENSO has increased the proportion of intense tropical cyclones over the western Northwest Pacific since the late 1970s. Geophys. Res. Lett. 2017, 44, 11–959. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, Y.; Feng, M.; Hobday, A.J. Vertical structures of marine heatwaves. Nat. Commun. 2023, 14, 6483. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Roughan, M.; Hemming, M. Interactions between cold cyclonic eddies and a western boundary current modulate marine heatwaves. Commun. Earth Environ. 2023, 4, 380. [Google Scholar] [CrossRef]
- Köhn, E.E.; Vogt, M.; Münnich, M.; Gruber, N. On the vertical structure and propagation of marine heatwaves in the Eastern Pacific. J. Geophys. Res.-Oceans 2024, 129, e2023JC020063. [Google Scholar] [CrossRef]
- Johnson, E.S.; Mc Phaden, M.J. Structure of intraseasonal Kelvin waves in the equatorial Pacific Ocean. J. Phys. Oceanogr. 1993, 23, 608–625. [Google Scholar] [CrossRef]
- Kessler, W.S.; McPhaden, M.J.; Weickmann, K.M. Forcing of intraseasonal Kelvin waves in the equatorial Pacific. J. Geophys. Res. Oceans 1995, 100, 10613–10631. [Google Scholar] [CrossRef]
- Wang, W.; McPhaden, M.J. The surface-layer heat balance in the equatorial Pacific Ocean. Part II: Interannual variability. J. Phys. Oceanogr. 2000, 30, 2989–3008. [Google Scholar] [CrossRef]
- Zhang, C. Intraseasonal perturbations in sea surface temperatures of the equatorial eastern Pacific and their association with the Madden–Julian oscillation. J. Clim. 2001, 14, 1309–1322. [Google Scholar] [CrossRef]
- McPhaden, M.J. Mixed layer temperature balance on intraseasonal timescales in the equatorial Pacific Ocean. J. Clim. 2002, 15, 2632–2647. [Google Scholar] [CrossRef]
- Amaya, D.J.; Alexander, M.A.; Scott, J.D.; Jacox, M.G. An evaluation of high-resolution ocean reanalyses in the California current system. Prog. Oceanogr. 2023, 210, 102951. [Google Scholar] [CrossRef]
- Schmeisser, L.; Bond, N.A.; Siedlecki, S.A.; Ackerman, T.P. The role of clouds and surface heat fluxes in the maintenance of the 2013–2016 Northeast Pacific marine heatwave. J. Geophys. Res. Atmos. 2019, 124, 10772–10783. [Google Scholar] [CrossRef]
- de Souza, J.M.A.C.; Couto, P.; Soutelino, R.; Roughan, M. Evaluation of four global ocean reanalysis products for New Zealand waters–A guide for regional ocean modelling. N. Z. J. Mar. Freshw. Res. 2021, 55, 132–155. [Google Scholar] [CrossRef]
- Asfaw, T.G.; Luo, J.-J. Seasonal Prediction of Summer Precipitation over East Africa Using NUIST-CFS1.0. Adv. Atmos. Sci. 2022, 39, 355–372. [Google Scholar] [CrossRef]
- Ma, J.; Xu, H.; Luo, J.; Chen, S. Impact of tropical Atlantic SST anomaly on ENSO in the NUIST-CFS1.0 Hindcasts. Int. J. Climatol. 2022, 42, 6055–6071. [Google Scholar] [CrossRef]
- Tang, S.; Luo, J.-J.; He, J.; Wu, J.; Zhou, Y.; Ying, W. Toward understanding the extreme floods over Yangtze River valley in June–July 2020: Role of Tropical Oceans. Adv. Atmos. Sci. 2021, 38, 2023–2039. [Google Scholar] [CrossRef]
- Ying, W.; Yan, H.; Luo, J.-J. Seasonal predictions of summer precipitation in the middle-lower reaches of the Yangtze River with global and regional models based on NUIST-CFS1.0. Adv. Atmos. Sci. 2022, 39, 1561–1578. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).