Progress in Atmospheric Density Inversion Based on LEO Satellites and Preliminary Experiments for SWARM-A
Abstract
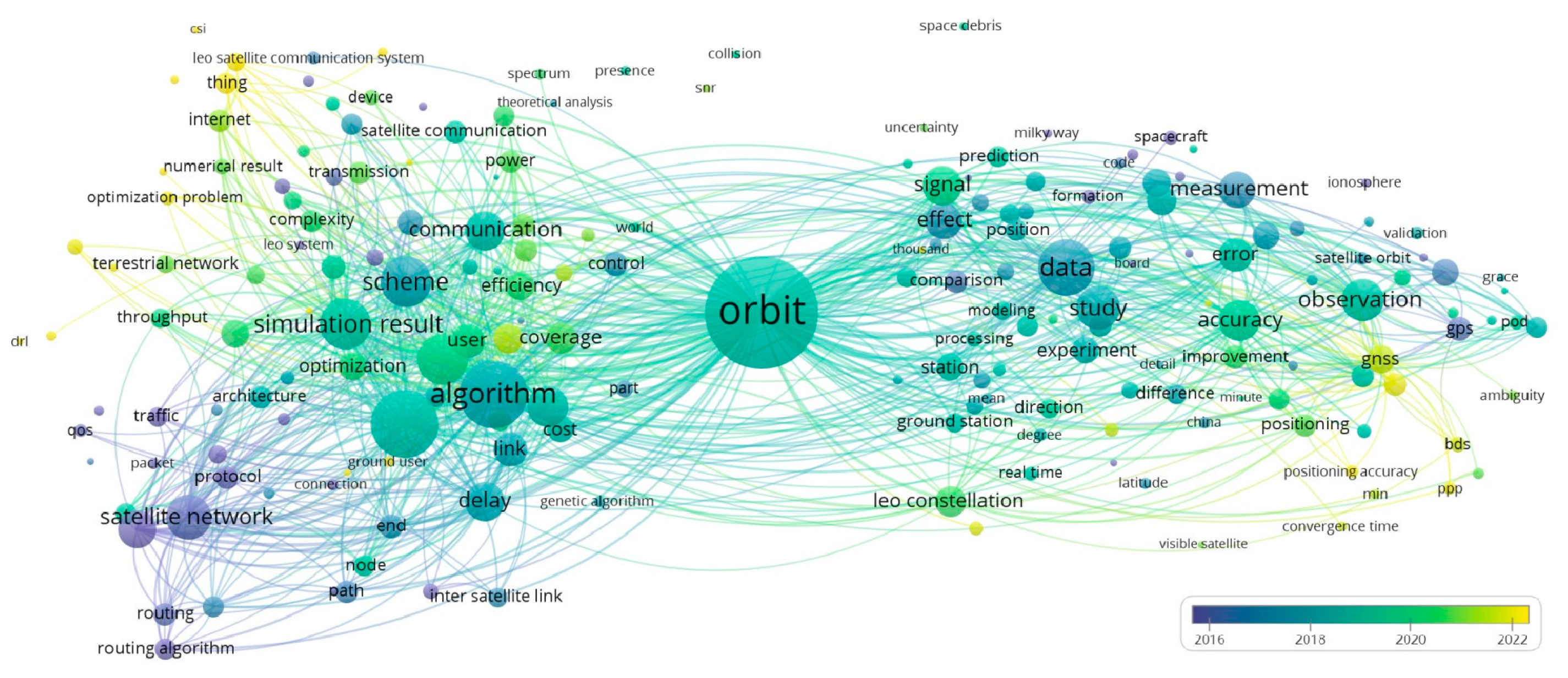
1. Introduction
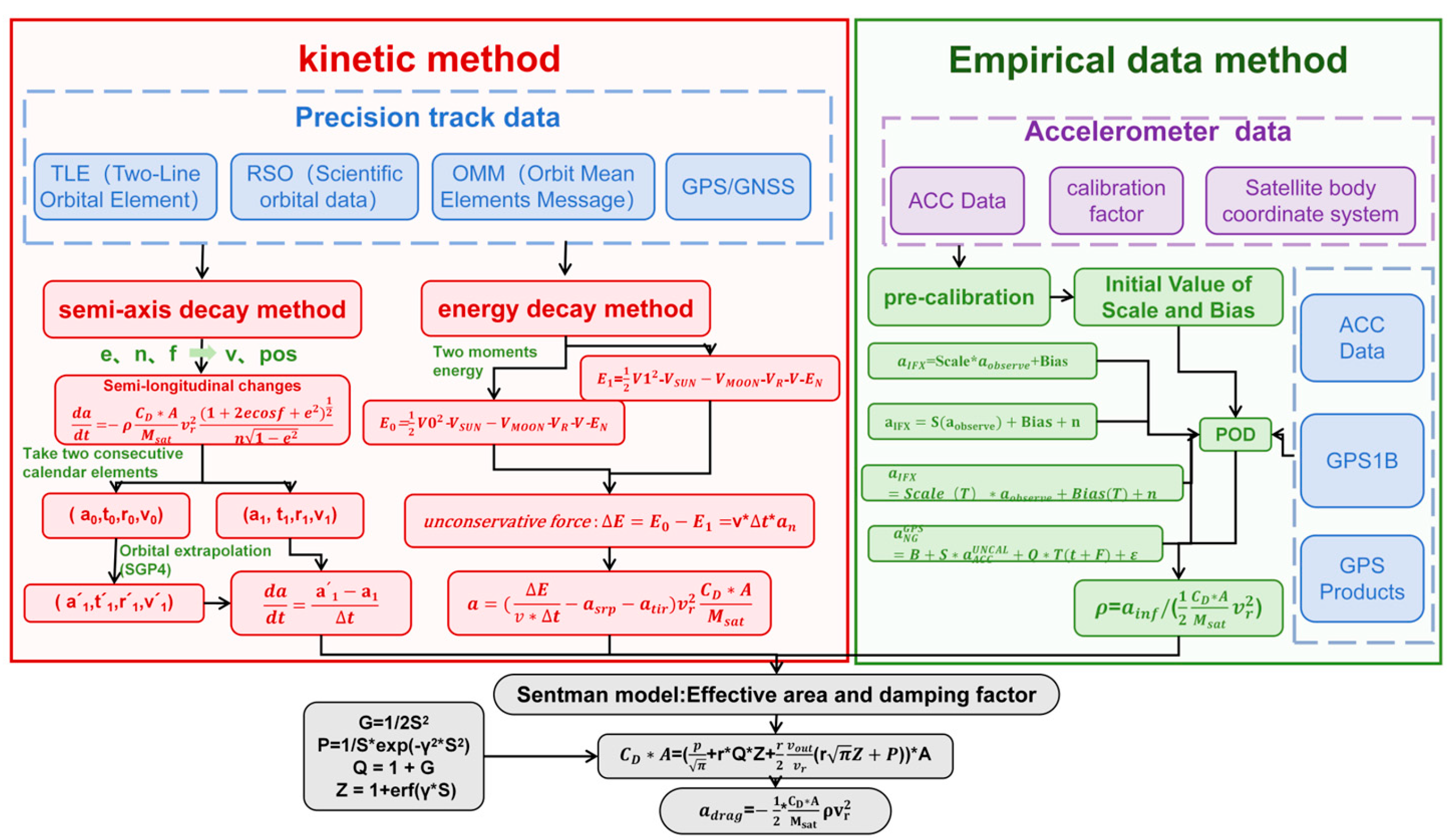
2. Methods of Atmospheric Density Inversion for Low Earth Orbit Satellites
2.1. Calculation of Atmospheric Drag Force
2.2. Product of Atmospheric Damping Coefficient and Effective Area
2.3. Comparison of Three Inversion Methods
3. Progress in Atmospheric Density Inversion for Low Earth Orbit Satellites
3.1. Advances in Atmospheric Density Inversion Using Orbital Data
3.2. Advances in Accelerometer Inversion
4. The Preliminary Experiment of Atmospheric Density Inversion for SWARM-A
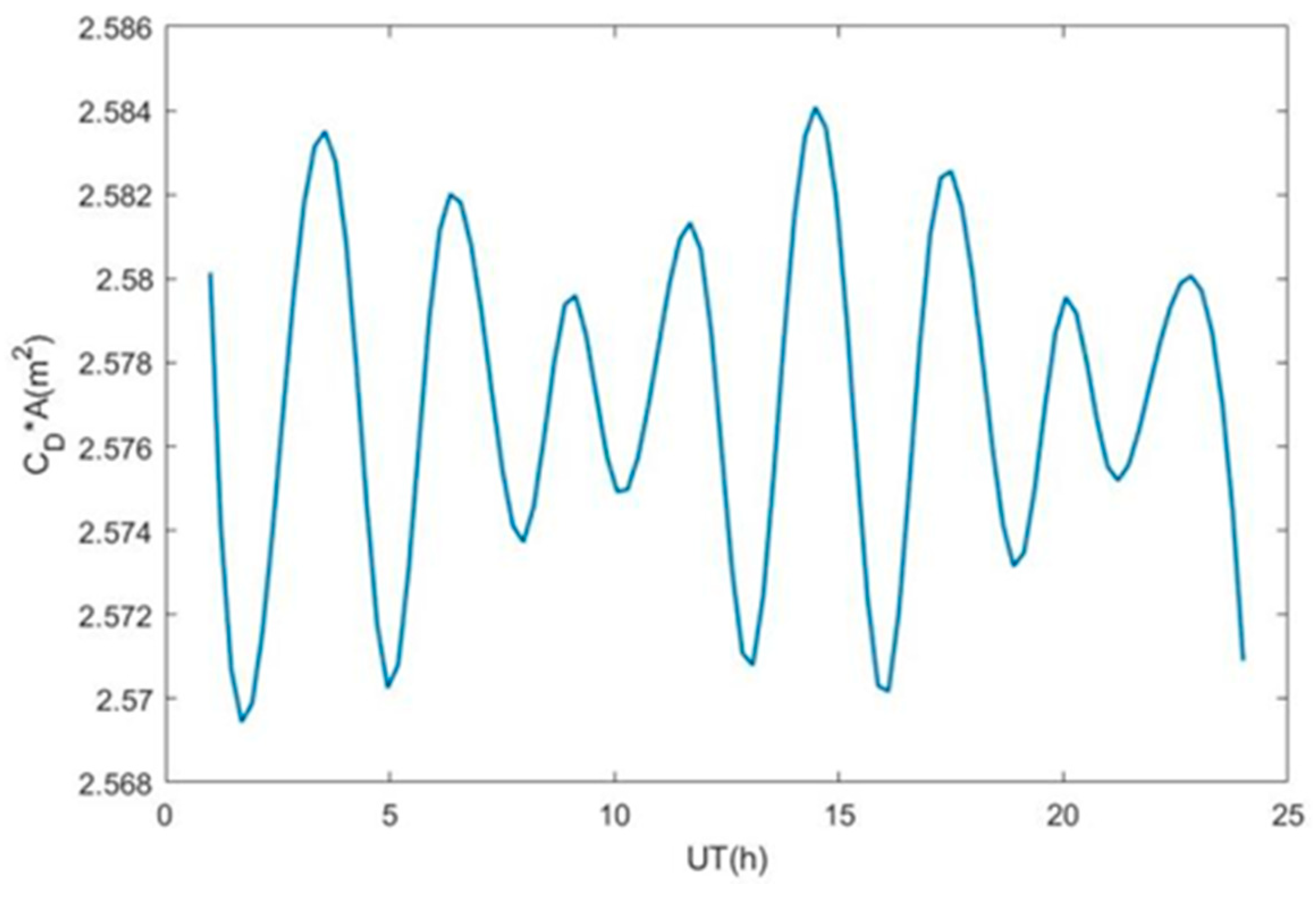
4.1. Product of Atmospheric Damping Factor and Cross-Section
4.2. Inversion of SWARM-A Atmospheric Density by Semi-Long-Axis Decay Method
4.2.1. SWARM-A Precision Orbital Data Processing
4.2.2. Orbital Extrapolation Calculations
4.3. Accelerometer Inversion of SWARM-A Atmospheric Density
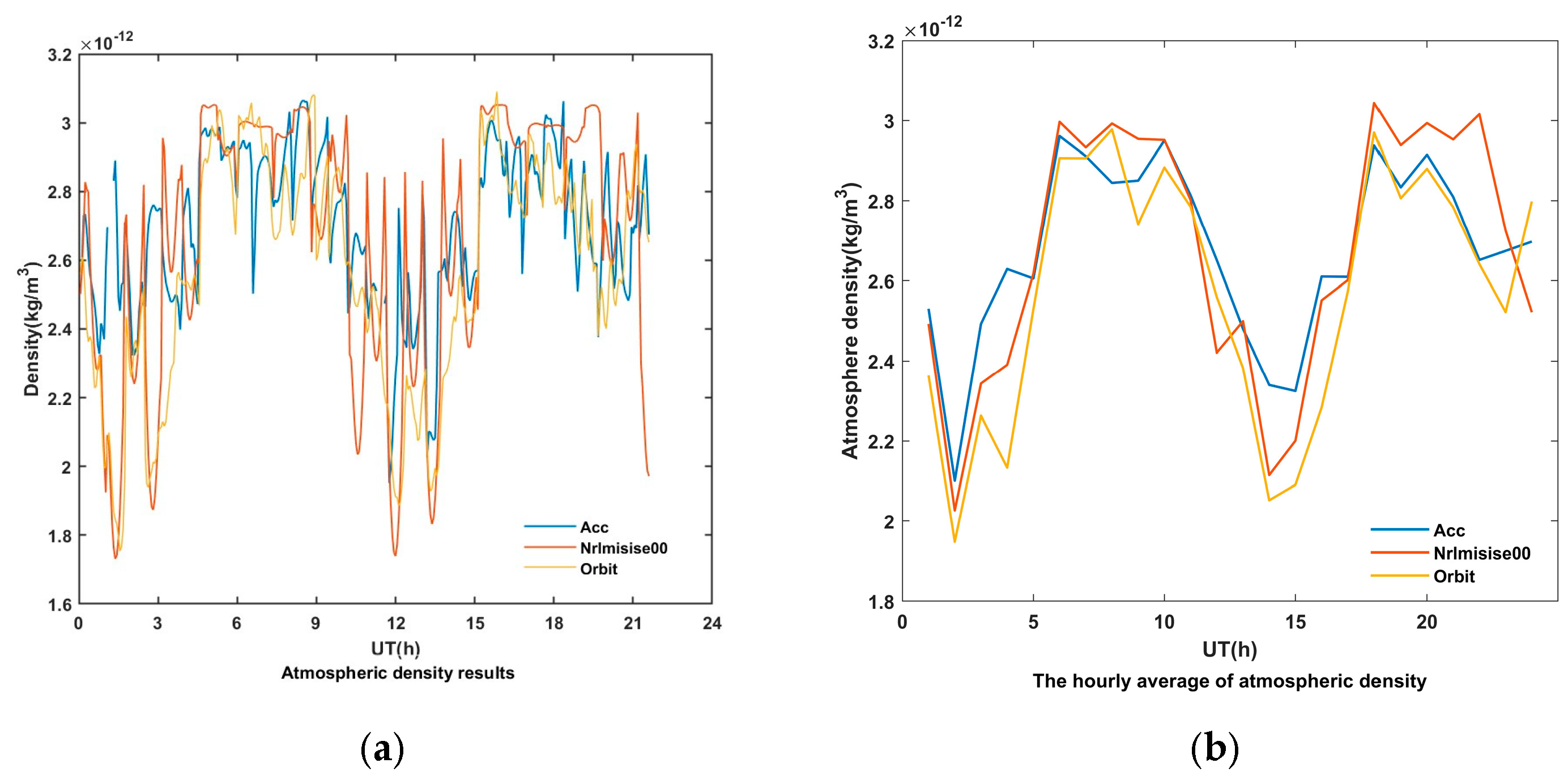
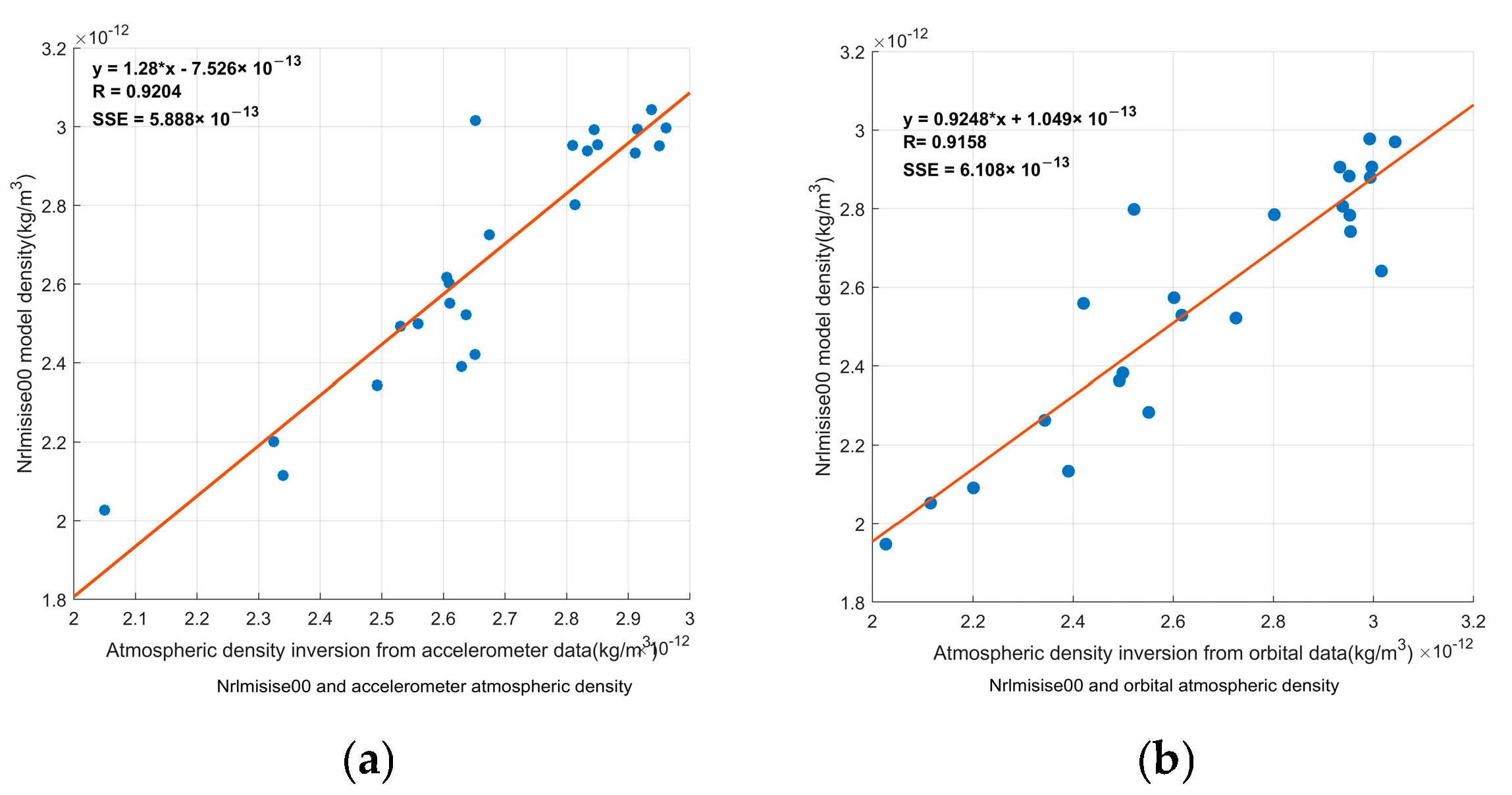
4.4. Inversion Results and Comparative Validation
5. Conclusions
Funding
Conflicts of Interest
References
- McDowell, J.C. The edge of space: Revisiting the Karman Line. Acta Astronaut. 2018, 151, 668–677. [Google Scholar] [CrossRef]
- Inter-Agency Space Debris Coordination Committee. IADC Space Debris Mitigation Guidelines; Central Research Institute of Machine Building: Koroylev, Russia, 2007; pp. 1–10. [Google Scholar]
- Su, Y.; Liu, Y.; Zhou, Y.; Yuan, J.; Cao, H.; Shi, J. Broadband LEO satellite communications: Architectures and key technologies. IEEE Wirel. Commun. 2019, 26, 55–61. [Google Scholar] [CrossRef]
- Horne, E.; Shafi, S.; Burke, J.; Prettitore, Z. SpaceX Report; Federal Aviation Administration: Washington, DC, USA. Available online: https://professordunagan.com/wp-content/uploads/2021/03/SpaceX-Report.pdf (accessed on 20 January 2025).
- SpaceX 2019. Application for Fixed Satellite Service by Space Exploration Holdings. LLC, Technical Report, SAT-MOD-20190830-00087. Available online: https://fcc.report/IBFS/SAT-MOD-20190830-00087/1877764.pdf (accessed on 20 January 2025).
- Henri, Y. The OneWeb satellite system. In Handbook of Small Satellites: Technology, Design, Manufacture, Applications, Economics and Regulation; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 1091–1100. [Google Scholar]
- Osoro, O.B.; Oughton, E.J.; Wilson, A.R.; Rao, A. Sustainability assessment of Low Earth Orbit (LEO) satellite broadband mega-constellations. arXiv 2023, arXiv:2309.02338. [Google Scholar]
- Zhi, H.; Jiang, X.; Wang, J. Multicolour photometry of LEO mega-constellations Starlink and OneWeb. Mon. Not. R. Astron. Soc. 2024, 530, 5006–5015. [Google Scholar] [CrossRef]
- Radtke, J.; Kebschull, C.; Stoll, E. Interactions of the space debris environment with mega constellations—Using the example of the OneWeb constellation. Acta Astronaut. 2017, 131, 55–68. [Google Scholar] [CrossRef]
- Burns, A.G.; Solomon, S.C.; Qian, L.; Wang, W.; Emery, B.A.; Wiltberger, M.; Weimer, D.R. The effects of corotating interaction region/high speed stream storms on the thermosphere and ionosphere during the last solar minimum. J. Atmos. Sol.-Terr. Phys. 2012, 83, 79–87. [Google Scholar] [CrossRef]
- Kavanagh, L.D., Jr.; Schardt, A.W.; Roelof, E.C. Solar wind and solar energetic particles: Properties and interactions. Rev. Geophys. 1970, 8, 389–460. [Google Scholar] [CrossRef]
- Zhang, Y.; Bocquet, M.; Mallet, V.; Seigneur, C.; Baklanov, A. Real-time air quality forecasting, part II: State of the science, current research needs, and future prospects. Atmos. Environ. 2012, 60, 656–676. [Google Scholar] [CrossRef]
- Yu, H.; Pang, Y.; Chen, B.; Feng, X.; Wang, B.; Zhao, Y. Simulation of orbital decay of LEO satellites due to atmospheric drag during magnetic storms. In Proceedings of the 2022 IEEE International Conference on Unmanned Systems (ICUS), Guangzhou, China, 28–30 October 2022; pp. 1179–1184. [Google Scholar] [CrossRef]
- Calabia, A.; Jin, S.; Tenzer, R. A new GPS-based calibration of GRACE accelerometers using the arc-to-chord threshold uncovered sinusoidal disturbing signal. Aerosp. Sci. Technol. 2015, 45, 265–271. [Google Scholar] [CrossRef]
- Calabia, A.; Jin, S. Thermospheric density estimation and responses to the March 2013 geomagnetic storm from GRACE GPS-determined precise orbits. J. Atmos. Sol.-Terr. Phys. 2017, 154, 167–179. [Google Scholar] [CrossRef]
- Lundin, R.; Lammer, H.; Ribas, I. Planetary magnetic fields and solar forcing: Implications for atmospheric evolution. Space Sci. Rev. 2007, 129, 245–278. [Google Scholar] [CrossRef]
- Champion KS, W.; Marcos, F.A. The triaxial—Accelerometer system on Atmosphere Explorer. Radio. Sci. 1973, 8, 297–303. [Google Scholar] [CrossRef]
- Doornbos, E. Thermospheric Density and Wind Determination from Satellite Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- March, G.; Visser, T.; Visser, P.; Doornbos, E.N. CHAMP and GOCE thermospheric wind characterization with improved gas-surface interactions modeling. Adv. Space Res. 2019, 64, 1225–1242. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Dang, T.; Lei, J.; Wang, W.; Zhang, B.; Burns, A.; Le, H.; Wu, Q.; Ruan, H.; Dou, X.; Wan, W. Global responses of the coupled thermosphere and ionosphere system to the August 2017 Great American Solar Eclipse. J. Geophys. Res. Space Phys. 2018, 123, 7040–7050. [Google Scholar] [CrossRef]
- Lei, J.; Burns, A.G.; Thayer, J.P.; Wang, W.; Mlynczak, M.G.; Hunt, L.A.; Dou, X.; Sutton, E. Overcooling in the upper thermosphere during the recovery phase of the 2003 October storms. J. Geophys. Res. Space Phys. 2012, 117. [Google Scholar] [CrossRef]
- Emmert, J.T. Thermospheric mass density: A review. Adv. Space Res. 2015, 56, 773–824. [Google Scholar] [CrossRef]
- Celiberto, R.; Armenise, I.; Cacciatore, M.; Capitelli, M.; Esposito, F.; Gamallo, P.; Janev, R.K.; Laganà, A.; Laporta, V.; Laricchiuta, A. Atomic and molecular data for spacecraft re-entry plasmas. Plasma Sources Sci. Technol. 2016, 25, 033004. [Google Scholar] [CrossRef]
- Van Leeuwen, P.J. Particle filtering in geophysical systems. Mon. Weather Rev. 2009, 137, 4089–4114. [Google Scholar] [CrossRef]
- Sentman, L.H. Free Molecule Flow Theory and Its Application to the Determination of Aerodynamic Forces; Lockheed Missiles & Space Company: Sunnyvale, CA, USA, 1961. [Google Scholar]
- Moe, K.; Moe, M.M. Gas–surface interactions and satellite drag coefficients. Planet. Space Sci. 2005, 53, 793–801. [Google Scholar] [CrossRef]
- Vallado, D.A. Fundamentals of Astrodynamics and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Curtis, H.D. Orbital Mechanics for Engineering Students: Revised Reprint; Butterworth-Heinemann: Oxford, UK, 2020. [Google Scholar]
- Sang, J.; Smith, C.; Zhang, K. Towards accurate atmospheric mass density determination using precise positional information of space objects. Adv. Space Res. 2012, 49, 1088–1096. [Google Scholar] [CrossRef]
- Gerlach, C.; Sneeuw, N.; Visser, P.; Švehla, D. CHAMP gravity field recovery using the energy balance approach. Adv. Geosci. 2003, 1, 73–80. [Google Scholar] [CrossRef]
- Jekeli, C. The determination of gravitational potential differences from satellite-to-satellite tracking. Celest. Mech. Dyn. Astron. 1999, 75, 85–101. [Google Scholar] [CrossRef]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. An earth gravitational model to degree 2160: EGm2008. In Proceedings of the 2008 General Assembly of the European Geosciences Union, Vienna, Austria, 13–18 April 2008. [Google Scholar]
- Förste, C.; Schwintzer, P.; Reigber, C. Format Description: The CHAMP Data Format; CH-GFZ-FD-001; 2002. Available online: https://gfzpublic.gfz-potsdam.de/rest/items/item_18184_5/component/file_309987/content (accessed on 20 January 2025).
- Miao, J.; Ren, T.; Gong, J.; Liu, S.; Li, Z. Atmospheric density inversion based on high-precision GPS observation data from satellites. J. Geophys. 2016, 59, 3566–3572. (In Chinese) [Google Scholar]
- Li, R.X.; Lei, J.H.; Wang, X.J.; Dou, X.K.; Jin, S.G. Thermospheric mass density derived from CHAMP satellite precise orbit determination data based on energy balance method. Sci. China Earth Sci. 2017, 60, 1495–1506. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Wang, B. Application of the hp-adaptive pseudospectral method in spacecraft orbit pursuit-evasion game. Adv. Space Res. 2024, 73, 1597–1610. [Google Scholar] [CrossRef]
- Li, R.; Lei, J.; Wang, X.; Dou, X.; Jin, S. Using the energy attenuation method to invert the density of the thermosphere atmosphere using CHAMP satellite precise orbit data Chinese Science. Earth Sci. 2017, 47, 13. (In Chinese) [Google Scholar]
- Bruinsma, S.; Tamagnan, D.; Biancale, R. Atmospheric densities derived from CHAMP/STAR accelerometer observations. Planet. Space Sci. 2004, 52, 297–312. [Google Scholar] [CrossRef]
- Floberghagen, R.; Fehringer, M.; Lamarre, D.; Muzi, D.; Frommknecht, B.; Steiger, C.; da Costa, A. Mission design, operation, and exploitation of the gravity field and steady-state ocean circulation explorer mission. J. Geod. 2011, 85, 749–758. [Google Scholar] [CrossRef]
- Livadiotti, S.; Crisp, N.H.; Roberts, P.C.E.; Worrall, S.D.; Oiko, V.T.A.; Edmondson, S.; Haigh, S.J.; Huyton, C.; Smith, K.L.; Sinpetru, L.A.; et al. A review of gas-surface interaction models for orbital aerodynamics applications. Prog. Aerosp. Sci. 2020, 119, 100675. [Google Scholar] [CrossRef]
- Drinkwater, M.R.; Haagmans, R.; Muzi, D.; Muzi, D. The GOCE gravity mission: ESA’s first core Earth explorer. In Proceedings of the 3rd international GOCE user workshop, Noordwijk, Frascati, Italy, 6–8 November 2006; European Space Agency: Noordwijk, The Netherlands, 2006; pp. 6–8. [Google Scholar]
- Reigber, C.; Lühr, H.; Schwintzer, P.; Wickert, J. Earth Observation with CHAMP. Results from Three Years; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- van den IJssel, J.; Doornbos, E.; Iorfida, E.; March, G.; Siemes, C.; Montenbruck, O. Thermosphere densities derived from Swarm GPS observations. Adv. Space Res. 2020, 65, 1758–1771. [Google Scholar] [CrossRef]
- Wickert, J.; Reigber, C.; Beyerle, G.; König, R.; Marquardt, C.; Schmidt, T.; Grunwaldt, L.; Galas, R.; Meehan, T.K.; Melbourne, W.G.; et al. Atmosphere sounding by GPS radio occultation: First results from CHAMP. Geophys. Res. Lett. 2001, 28, 3263–3266. [Google Scholar] [CrossRef]
- Perosanz, F.; Biancale, R.; Lemoine, J.M.; Vales, N.; Loyer, S.; Bruinsma, S. Evaluation of the CHAMP Accelerometer on Two Years of Mission; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar] [CrossRef]
- Yin, L.; Wang, L.; Zheng, W.; Ge, L.; Tian, J.; Liu, Y.; Yang, B.; Liu, S. Evaluation of empirical atmospheric models using Swarm-C satellite data. Atmosphere 2022, 13, 294. [Google Scholar] [CrossRef]
- Hajj, G.A.; Ao, C.O.; Iijima, B.A.; Kuang, D.; Kursinski, E.R.; Mannucci, A.J.; Meehan, T.K.; Romans, L.J.; de la Torre Juarez, M.; Yunck, T.P.; et al. CHAMP and SAC-C atmospheric occultation results and intercomparisons. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Hwang, C.; Tseng, T.P.; Lin, T.; Schreiner, B. Precise orbit determination for the FORMOSAT-3/COSMIC satellite mission using GPS. J. Geod. 2009, 83, 477–489. [Google Scholar] [CrossRef]
- Tang, G.; Li, X.; Cao, J.; Liu, S.; Chen, G.; Man, H.; Zhang, X.; Shi, S.; Sun, J.; Li, Y.; et al. APOD mission status and preliminary results. Sci. China Earth Sci. 2020, 63, 257–266. [Google Scholar] [CrossRef]
- Kennedy, G.M.; Wyatt, M.C. Collisional evolution of irregular satellite swarms: Detectable dust around Solar system and extrasolar planets. Mon. Not. R. Astron. Soc. 2011, 412, 2137–2153. [Google Scholar] [CrossRef]
- Michalak, A. Phenolic compounds and their antioxidant activity in plants growing under heavy metal stress. Pol. J. Environ. Stud. 2006, 15, 523–530. [Google Scholar]
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. J. Geophys. Res. Space Phys. 2002, 107, SIA 15-1–SIA 15-16. [Google Scholar] [CrossRef]

| Method | Sensor Detections | Precision Orbits | Accelerometer Data | |
|---|---|---|---|---|
| Theory | Instrument detection | Semi-long axis attenuation | Conservation of mechanical energy | Acceleration calibration |
| Data | Atmospheric density | Positional velocity | Gravity field model Gravitational potential | Scale, bias, and temperature factors |
| Factors affecting accuracy | Atmospheric environment signal source | Quality and period of orbital data | Model assumptions and parameter | Instrument noise and error |
| Conditions of application | Widespread monitoring | Long-term monitoring and large-scale | Scenes of high-precision inversion | Real-time monitoring and dynamic inversion |
| Launch Time | Satellite Program | Measurement Altitude Range | Products |
|---|---|---|---|
| 2000–2010 | CHAMP | <450 km | AI ME OG GPS |
| 2001–2010 | TIMED | <625 km | Atmospheric data Solar radiation data Thermosphere and ionosphere dynamic process |
| 2002–2017 | GRACE | <480 km | GSM GAA GAB GAC GAD |
| 2006- | COSMIC | <800 km | Atmospheric profile data Weather forecast data |
| 2009–2013 | GOCE | <260 km | VT TEC and ROTI SSTI ANTEX Global gravity field model and grid |
| 2014- | Swarm | <530 km | Core Lithosphere Mantle Oceans Thermosphere |
| 2018- | GRACE-FO | <490 km | Land, water, glaciers, and ocean currents Grace-FO RL-06.1 |
| Panel Name | Panel Size | X | Y | Z |
|---|---|---|---|---|
| Nadir 1 | 1.540 | 0.0 | 0.0 | 1.0 |
| Nadir 2 | 1.400 | −0.19766 | 0.0 | 0.98027 |
| Nadir 3 | 1.600 | −0.13808 | 0.0 | 0.99042 |
| Solar Array +Y | 3.450 | 0.0 | 0.58779 | −0.80902 |
| Solar Array −Y | 3.450 | 0.0 | −0.58779 | −0.8090 |
| Zenith | 0.500 | 0.0 | 0.0 | −1.0 |
| Front | 0.560 | 1.0 | 0.0 | 0.0 |
| Side Wall +Y | 0.753 | 0.0 | 1.0 | 0.0 |
| Side Wall −Y | 0.753 | 0.0 | −1.0 | 0.0 |
| Shear Panel Nadir Front | 0.800 | 1.0 | 0.0 | 0.0 |
| Shear Panel Nadir Back | 0.800 | −1.0 | 0.0 | 0.0 |
| Boom +Y | 0.600 | 0.0 | 1.0 | 0.0 |
| Boom −Y | 0.600 | 0.0 | −1.0 | 0.0 |
| Boom Zenith | 0.600 | −0.23924 | 0.0 | −0.97096 |
| Boom Nadi | 0.600 | 0.22765 | 0.0 | 0.97374 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, X.; Xiao, C.; Song, S.; Wu, M. Progress in Atmospheric Density Inversion Based on LEO Satellites and Preliminary Experiments for SWARM-A. Remote Sens. 2025, 17, 793. https://doi.org/10.3390/rs17050793
Bian X, Xiao C, Song S, Wu M. Progress in Atmospheric Density Inversion Based on LEO Satellites and Preliminary Experiments for SWARM-A. Remote Sensing. 2025; 17(5):793. https://doi.org/10.3390/rs17050793
Chicago/Turabian StyleBian, Xiaoyu, Cunying Xiao, Shuli Song, and Mengjun Wu. 2025. "Progress in Atmospheric Density Inversion Based on LEO Satellites and Preliminary Experiments for SWARM-A" Remote Sensing 17, no. 5: 793. https://doi.org/10.3390/rs17050793
APA StyleBian, X., Xiao, C., Song, S., & Wu, M. (2025). Progress in Atmospheric Density Inversion Based on LEO Satellites and Preliminary Experiments for SWARM-A. Remote Sensing, 17(5), 793. https://doi.org/10.3390/rs17050793








