Contrastive Feature Disentanglement via Physical Priors for Underwater Image Enhancement

Abstract

Underwater image enhancement (UIE) serves as a fundamental preprocessing step in ocean remote sensing applications, encompassing marine life detection, archaeological surveying, and subsea resource exploration. However, UIE encounters substantial technical challenges due to the intricate physics of underwater light propagation and the inherent homogeneity of aquatic environments. Images captured underwater are significantly degraded through wavelength-dependent absorption and scattering processes, resulting in color distortion, contrast degradation, and illumination irregularities. To address these challenges, we propose a contrastive feature disentanglement network (CFD-Net) that systematically addresses underwater image degradation. Our framework employs a multi-stream decomposition architecture with three specialized decoders to disentangle the latent feature space into components associated with degradation and those representing high-quality features. We incorporate hierarchical contrastive learning mechanisms to establish clear relationships between standard and degraded feature spaces, emphasizing intra-layer similarity and inter-layer exclusivity. Through the synergistic utilization of internal feature consistency and cross-component distinctiveness, our framework achieves robust feature extraction without explicit supervision. Compared to existing methods, our approach achieves a 12% higher UIQM score on the EUVP dataset and outperforms other state-of-the-art techniques on various evaluation metrics such as UCIQE, MUSIQ, and NIQE, both quantitatively and qualitatively.

1. Introduction

Underwater optical imaging has evolved into an indispensable modality in contemporary ocean remote sensing, including marine biology research, coral reef monitoring, underwater archaeology, and autonomous underwater vehicle (AUV) navigation [1]. However, the quality of underwater optical images often suffers from degradation due to various degradation factors, such as light scattering, absorption, and color distortion [2,3]. Such degradation mechanisms manifest in compromised visibility, attenuated contrast, and distorted color fidelity, which impede critical tasks like object detection, recognition, and tracking [4,5].

To address these challenges, underwater image enhancement (UIE) techniques aim to restore image clarity and improve visibility. Recent studies [6] highlight the significance of UIE as a preprocessing step for enhancing the performance of vision-based systems in underwater environments. Despite significant progress, existing methods often fail to adequately address the inherent complexities of underwater imaging, particularly when applied to real-world scenarios with diverse environmental conditions.

Compared to in-air image enhancement tasks, such as image denoising [7], dehazing [8], and low-light enhancement [9,10], UIE presents distinctive challenges [2,11,12]. These challenges stem from the unique properties of the underwater environment, including the following: (1) light scattering and absorption: light scattering reduces image clarity, while absorption causes wavelength-dependent color distortions, leading to the predominance of blue and green hues in underwater images; (2) scene homogeneity: the uniformity of underwater scenes, with limited texture and natural contrast, makes it difficult for enhancement algorithms to distinguish between degraded and authentic features; (3) data scarcity: collecting large-scale paired datasets of degraded and clean underwater images is inherently challenging due to the dynamic and unpredictable nature of underwater environments. Most existing datasets rely on synthetic image pairs, which fail to fully capture real-world complexities, worsening the domain shift issue between synthetic and real images.

These inherent challenges have motivated the development of various UIE methodologies, which can be systematically categorized into three main approaches: traditional model-based [13,14,15], deep learning-based [7,8,9,10,16,17,18,19], and physics-guided learning-based methods [11,20,21,22].

Traditional model-based approaches utilize specific mathematical models to simulate the underwater imaging process, relying on prior knowledge for parameter estimation, such as Dark Channel Prior (DCP) [13] and Retinex [14,15]. However, these approaches are often constrained by their inability to adapt to the varied environmental conditions encountered in real-world underwater scenarios.

Deep learning-based methods have significantly advanced image restoration tasks [7,8,9,10]. Such data-driven approaches excel in learning latent features from large datasets and modeling the relationship between degraded and enhanced images. Recent UIE-specific methods [16,17,18,19] have demonstrated promising results, regardless of whether they use paired or unpaired training datasets. However, these methods encounter significant challenges: (1) the domain gap between synthetic and real-world underwater images limits generalization capabilities; (2) the scarcity of paired datasets makes pixel-to-pixel mapping difficult during training; and (3) the black-box nature of deep learning models reduces interpretability, making it harder to trust their outputs in critical applications.

To overcome the limitations associated with paired samples, semisupervised and unsupervised methods have been explored. Generative Adversarial Networks (GANs) [1] and contrastive learning (CL) [18,19] have demonstrated promise by enabling the use of unpaired datasets. However, these approaches often experience instability during training and require physical priors to facilitate cross-domain feature transfer.

Unlike traditional and deep learning-based approaches, physics-guided learning-based methods embed physical priors into neural network architectures, improving interpretability and enhancing generalization. These methods leverage physical information to guide network design [11,20,21] and establish optimal solution boundaries [22]. While promising, these approaches often lack mechanisms to fully leverage unpaired data or to handle the inherent variability of underwater environments.

In this paper, we propose a novel hybrid framework that combines supervised and unsupervised learning paradigms along with physical priors in a unified architecture to overcome the limitations of existing methods. The primary challenge in UIE arises from the difficulty in handling the variability of underwater environments and the lack of paired data for supervised training. While many existing methods either rely on synthetic datasets or do not effectively address real-world variability, our framework uniquely integrates both supervised and unsupervised learning, making it capable of effectively leveraging unpaired data from real-world underwater images.

Our CFD-Net introduces a multi-stream decomposition approach that encodes degraded underwater images into a latent embedding space, separating components, including clean background, transmission maps, and ambient light, into distinct branches. This decomposition helps preserve the physical characteristics of the scene, enabling better alignment with the physical degradation process commonly encountered in underwater environments. By maintaining the realism of each generative component, our method ensures the estimated components are accurate and more reliable for subsequent enhancement. Specifically, we incorporate hierarchical contrastive learning mechanisms within a physics-guided architecture, enabling effective cross-domain feature learning to address the domain gap between synthetic and real-world underwater images. This allows our model to not only learn from synthetic data but also adapt well to the challenging variations of real-world underwater environments. Furthermore, we propose a novel cross-space contrastive loss function, which enhances feature separability within individual spaces and exclusivity between distinct spaces, improving the quality of decomposition and leading to superior image enhancement results.

This is the first approach that employs contrastive learning and physical feature decomposition for UIE, offering a unique perspective on underwater image restoration. By effectively addressing both the challenges of unpaired data and the inherent variability of underwater imaging, our method outperforms existing state-of-the-art techniques in both quantitative and qualitative evaluations. The primary contributions of this work are summarized as follows:

• We propose a novel unsupervised UIE method leveraging contrastive feature decomposition, offering a new perspective for underwater image enhancement.
• We introduce a unique cross-space and content contrastive loss, facilitating the simultaneous exploration of intra-similarity within latent spaces and inter-exclusiveness between feature spaces.
• Comprehensive experiments are conducted to evaluate the proposed method, demonstrating its outstanding performance both quantitatively and qualitatively.

The remainder of this paper is organized as follows: Section 2 discusses related work in UIE. Section 3 details the proposed methodology. Section 4 presents the experimental results and comparisons with state-of-the-art methods. Finally, Section 5 concludes the paper and summarizes key findings.

2. Related Work

2.1. Traditional Methods

Underwater image enhancement predominantly relies on image processing and computer vision techniques. These non-physical methods, distinct from physical or deep learning models, function at the pixel level to enhance visual quality, such as histogram equalization [23], white balancing [24], and Retinex [14]. Ancuti et al. [25] proposed a multi-scale fusion method that combines white balancing with traditional contrast histogram equalization, enhancing the quality of the original image. Hitam et al. [26] introduced a hybrid Contrast Limited Adaptive Histogram Equalization (CLAHE) technique, employing the Euclidean norm to merge outputs from RGB and HSV color models, thereby improving contrast and reducing noise. Additionally, Ren et al. [15] developed the Low-Rank Regularized Retinex Model (LR3M), which combines a low-rank prior with Retinex decomposition to reduce noise in reflection images. While these methods are computationally efficient and easy to implement, they rely heavily on handcrafted priors and often fail to address the physical properties of underwater environments, limiting their effectiveness in complex scenarios.

2.2. Physical Methods

Inspired by the image degradation process, many low-quality restoration methods have been developed [13,27,28,29,30], each reconstructing the degradation process by estimating key parameters like light and transmission. Drawing inspiration from the Dark Channel Prior (DCP) used in dehazing tasks [27], Drews et al. [28] introduced the Underwater DCP (UDCP), which consists of transmission estimation methods tailored for underwater scenarios, primarily focusing on the blue and green channels to account for the rapid attenuation of red light underwater. Similarly, Galdran et al. [29] introduced the Red Channel Prior, which acknowledges the rapid attenuation of red wavelengths in water, thus providing another perspective on underwater image enhancement. Extending this concept, Peng et al. [13] introduced a technique incorporating depth-dependent color transformations for estimating environmental light. This approach enables adaptive color correction within the image formation framework, enhancing image clarity. Lastly, Akkaynak et al. [30] modified the conventional imaging model to address the limitations of standard models designed for atmospheric conditions. Liang et al. [31] introduced the enhancement method CDCR to restore color, detail, and contrast of degraded images. Despite their interpretability and reliance on well-defined mathematical models, physical methods often fail to generalize across diverse underwater environments. They rely on accurate parameter estimation, which is challenging in real-world scenarios with varying light conditions, turbidity levels, and depth variations.

2.3. Learning-Based Methods

Deep learning approaches have significantly advanced underwater image enhancement by overcoming the limitations inherent in traditional methods. Early methods, primarily based on Convolutional Neural Networks (CNNs), concentrated on extracting low-level feature representations for tasks such as color correction and contrast restoration. For example, Wang et al. [32] developed UIE-Net, a CNN-based approach aiming at color correction and dehazing. Similarly, Li et al. [33] introduced UWCNN, which integrates underwater scene priors to synthesize underwater images and reconstruct enhanced outputs without requiring explicit physical parameter estimation.

However, these methods often require large-scale paired datasets of degraded and clean images, which are challenging to obtain in underwater scenarios due to environmental variability and data scarcity. To address this issue, semisupervised and unsupervised learning frameworks have gained prominence in UIE tasks [11,34,35,36]. Notably, Li et al. [34] introduced WaterGAN to generate color-corrected underwater images, while Li et al. [35] adopted the CycleGAN [36] to facilitate unpaired feature domain transfer between degraded and enhanced images, reducing reliance on paired datasets. Chen et al. [11] proposed a generator with embedded physical priors for synthesizing training data and improving real-world underwater image enhancement.

More recently, contrastive learning (CL) has shown significant promise for self-supervised feature representation learning [37,38,39,40], particularly in image enhancement and restoration tasks [18,41,42]. For example, Wu et al. [41] introduced a contrast regularization technique leveraging CL for dehazing tasks. Liu et al. [42] applied a twin adversarial contrastive learning framework for underwater image enhancement. Huang et al. [18] proposed the Semi-UIR model, which integrates unlabeled data using CL to improve underwater image restoration.

Despite these advancements, existing learning-based methods continue to face critical challenges: (1) generative models often fail to fully capture the relationship between factor-related feature distributions and the physical degradation process, leading to suboptimal image restoration; (2) current methods primarily focus on mapping degraded images to clean counterparts but lack mechanisms to enforce independence among decomposed components, such as backgrounds and transmission maps; (3) the domain gap between synthetic and real-world underwater images remains a major barrier to generalization.

To address these limitations, we propose a novel contrastive multi-stream decomposition architecture that leverages physical priors and contrastive learning strategies. By embedding physical knowledge into latent feature spaces and utilizing cross-space contrastive loss functions, our method enhances generalization, improves interpretability, and effectively bridges the domain gap. This approach uniquely integrates the decomposition of degraded components (e.g., clean background, transmission maps, and ambient light layers) with cross-domain feature learning, providing a more robust solution for underwater image enhancement.

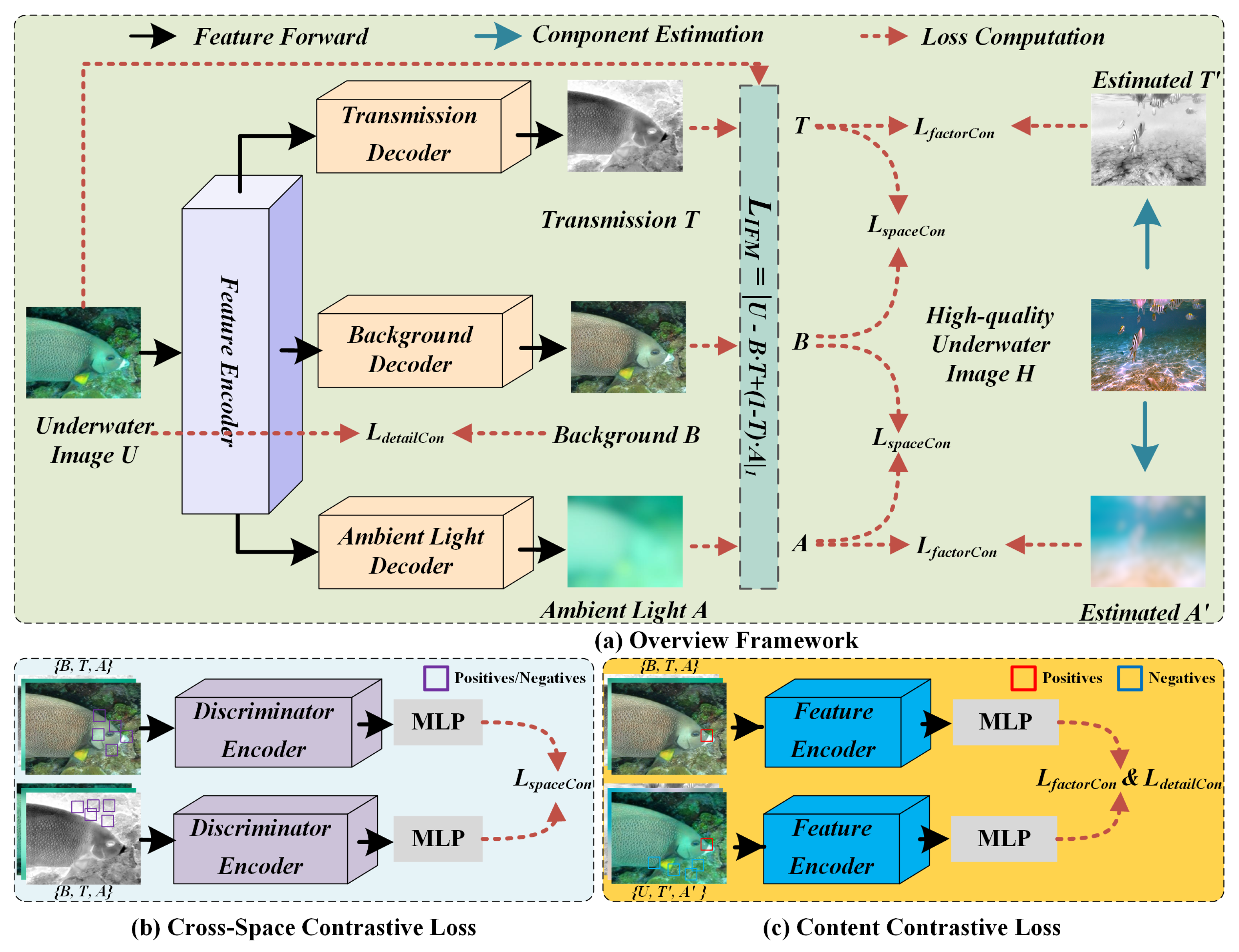
3. Proposed Method

To systematically address the inherent challenges of underwater image enhancement, we propose a physics-guided multi-stream decomposition framework providing theoretical foundations. The proposed framework comprises three key components: (1) a physics-guided image formation model that establishes the theoretical foundation and mathematical formulations; (2) a multi-stream decomposition architecture that disentangles various degradation factors; and (3) a hierarchical contrastive learning mechanism that ensures the distinctiveness of features.

In this section, we first introduce the physics-guided image formation model (Section 3.1), then detail our network architecture (Section 3.2), and, finally, present the learning objectives (Section 3.3).

3.1. Physics-Guided Image Formation Model

The underwater image formation process is governed by wavelength-dependent optical principles that characterize light propagation in aquatic media. For each color channel $c\in \{R,G,B\}$, the formation model is:

$$I^c\left(x\right)=J^c\left(x\right)t^c\left(x\right)+\left(1-t^c\left(x\right)\right)A^c$$

(1)

where $I^c\left(x\right)$ denotes the observed degraded image, $J^c\left(x\right)$ represents the scene radiance, $t^c\left(x\right)$ characterizes the transmission map, and $A^c$ indicates the ambient light. The transmission follows the Beer–Lambert law:

$$t^c\left(x\right)=exp(-{\beta }^{c}d\left(x\right))$$

(2)

where ${\beta }^c$ represents the wavelength-dependent attenuation coefficient for channel c and $d\left(x\right)$ denotes the scene depth at position x. The attenuation coefficients satisfy ${\beta }^R>{\beta }^G>{\beta }^B$, which explains the characteristic blue-green color cast in underwater images.

To facilitate efficient network optimization while preserving physical consistency, we derive a simplified formulation based on two key observations from underwater optics. First, the transmission maps across RGB channels exhibit strong correlation due to the continuous nature of the attenuation spectrum:

$$T\left(x\right)={\mathbb{E}}_c\left[t^c\left(x\right)\right]={\displaystyle \frac{1}{3}}\sum _{c\in \{R,G,B\}}{t}^c\left(x\right)$$

(3)

where $T\left(x\right)$ represents the unified transmission map that captures the average attenuation effect across all channels. Second, the ambient light variation primarily affects intensity rather than spectral distribution:

$$\mathbf{A}={\mathbb{E}}_c\left[{\mathbf{A}}^c\right]+\Delta \mathbf{A}$$

(4)

where $\mathbf{A}$ denotes the mean ambient light intensity and $\Delta \mathbf{A}$ represents the channel-specific intensity variation. These physical insights lead to our simplified formation model:

$$\mathbf{I}=\mathbf{J}·\mathbf{T}+(1-\mathbf{T})·\mathbf{A}$$

(5)

This physically grounded model naturally suggests a feature decomposition strategy where the degraded underwater image can be disentangled into three components: clean background $\mathbf{J}$ representing features free from degradation, transmission map $\mathbf{T}$ capturing depth-dependent attenuation, and ambient light $\mathbf{A}$ encoding global illumination. Such decomposition provides clear guidance for contrastive feature learning—features from different components should be mutually exclusive in the latent space, while features within each component should maintain consistency across varying degradation levels.

Based on this formulation, we design a multi-stream architecture with three specialized decoders: the background decoder (${\mathbf{D}}_{\mathbf{b}}$) estimates clean image $\mathbf{J}$, the transmission decoder (${\mathbf{D}}_{\mathbf{t}}$) computes transmission map $\mathbf{T}$, and the ambient light decoder (${\mathbf{D}}_{\mathbf{a}}$) predicts ambient light $\mathbf{A}$. This physically constrained decomposition framework not only ensures the physical validity of the enhanced results but also provides natural supervision for contrastive feature learning, which will be detailed in the following sections.

3.2. Multi-Stream Decomposition Architecture

Given an unpaired underwater image set $X_U={\left\{\mathbf{U}\right\}}_{i=1}^{N1}$ and its corresponding high-quality reference set $X_H={\left\{\mathbf{H}\right\}}_{i=1}^{N2}$, where $N_1$ and $N_2$ represent the sample sizes, we design a multi-stream architecture guided by the physical image formation model. The framework aims to learn disentangled representations that capture distinct physical properties: background features representing scene content, transmission features encoding depth-dependent attenuation, and ambient light features characterizing global illumination patterns. As illustrated in Figure 1, the framework consists of a shared encoder $\mathbf{E}$ and three specialized decoders $\{{\mathbf{D}}_{\mathbf{b}},{\mathbf{D}}_{\mathbf{t}},{\mathbf{D}}_{\mathbf{a}}\}$.

The feature embedding network: The feature embedding network $\mathbf{E}$ extracts multi-scale features guided by the physics of underwater image formation. Given an input image $\mathbf{U}$, the hierarchical feature extraction process is formulated as:

$$F=\{f_1,f_2,f_3,f_4\}=\mathbf{E}\left(\mathbf{U}\right)$$

(6)

where $f_1$ (1/2 scale) preserves fine-grained details for background reconstruction, $\{f_2,f_3\}$ (1/4, 1/8 scales) capture medium-range context for transmission estimation, and $f_4$ (1/16 scale) encodes global information for ambient light prediction.

Specialized decoders: the framework incorporates three physically motivated decoders, each designed to capture specific aspects of the underwater formation model:

(1) Background decoder ${\mathbf{D}}_{\mathbf{b}}$: following the multiplicative nature of background–transmission interaction in $\mathbf{J}·\mathbf{T}$, the decoder utilizes features at all scales:

$$\mathbf{B}={\mathbf{D}}_{\mathbf{b}}\left(F\right)={\mathbf{D}}_{\mathbf{b}}\left(\{f_1,f_2,f_3,f_4\}\right)$$

(7)

(2) Transmission decoder ${\mathbf{D}}_{\mathbf{t}}$: guided by the spatial continuity of transmission map $T\left(x\right)=exp(-\beta d(x\left)\right)$, the decoder focuses on medium- and high-level features:

$$\mathbf{T}={\mathbf{D}}_{\mathbf{t}}\left(F\right)={\mathbf{D}}_{\mathbf{t}}\left(\{f_2,f_3,f_4\}\right)$$

(8)

(3) Ambient light decoder ${\mathbf{D}}_{\mathbf{a}}$: following the global nature of ambient light $\mathbf{A}={\mathbb{E}}_c\left[{\mathbf{A}}^c\right]$, the decoder exclusively uses global semantic features:

$$\mathbf{A}={\mathbf{D}}_{\mathbf{a}}\left(F\right)={\mathbf{D}}_{\mathbf{a}}\left(\left\{f_4\right\}\right)$$

(9)

where $\mathbf{A}$ represents the estimated ambient light, derived from the deepest feature representations.

The network components leverage proven architectures while incorporating task-specific modifications. The transmission decoder ${\mathbf{D}}_{\mathbf{t}}$ and ambient light decoder ${\mathbf{D}}_{\mathbf{a}}$ adopt U-Net-like structures [43] for effective parameter estimation. The background decoder ${\mathbf{D}}_{\mathbf{b}}$ employs a modified ResNet architecture in [44] enhanced with dual-attention mechanisms:

$${\mathbf{D}}_{\mathbf{b}}\left(f\right)={\mathrm{Conv}}_{1\times 1}(\sum _{i=1}^4{\alpha }_i·{\mathrm{ResBlock}}_b\left(f_i\right))$$

(10)

where ${\alpha }_i$ represents learnable attention weights and ${\mathrm{ResBlock}}_b$ incorporates both spatial and channel attention for comprehensive feature refinement. This physically guided architecture ensures that each component maintains its specific role while enabling efficient feature extraction and enhancement.

3.3. Training Objectives

The training objectives are designed to tackle underwater image enhancement challenges by incorporating physical priors derived from the image formation model (IFM). The IFM provides a mathematical foundation for decomposing an underwater image $\mathbf{U}$ into its constituent components: clean background $\mathbf{B}$, transmission map $\mathbf{T}$, and ambient light $\mathbf{A}$, as formulated in Equation (5). The UIE task is thus formulated as an ill-posed inverse problem of recovering the clean background $\mathbf{B}$ from the degraded observation $\mathbf{U}$ while simultaneously estimating the transmission map $\mathbf{T}$ and ambient light $\mathbf{A}$.

The total loss function combines reconstruction fidelity, physical consistency, and feature learning:

$${\mathcal{L}}_{\mathrm{total}}={\lambda }_{CL}{\mathcal{L}}_{\mathrm{CL}}+{\lambda }_{IFM}{\mathcal{L}}_{\mathrm{IFM}}+{\lambda }_{adv}{\mathcal{L}}_{\mathrm{adv}}$$

(11)

where ${\lambda }_{CL}$, ${\lambda }_{IFM}$, and ${\lambda }_{adv}$ are hyperparameters that balance the contributions of adversarial learning, physical consistency, and contrastive feature learning, respectively.

3.3.1. Hierarchical Contrastive Learning Function

To effectively disentangle underwater image components while preserving their physical relationships, we propose a hierarchical contrastive learning framework that operates at multiple semantic levels. This framework leverages self-supervised learning to optimize feature representations and guide the decomposition process through carefully designed contrastive objectives. The comprehensive contrastive learning objective integrates three complementary components:

$$\begin{array}{c}\hfill {\mathcal{L}}_{\mathrm{CL}}={\mathcal{L}}_{\mathrm{spaceCon}}(\mathbf{B},\mathbf{T},\mathbf{A})+{\mathcal{L}}_{\mathrm{factorCon}}(\mathbf{T},{\mathbf{T}}^{\prime })+{\mathcal{L}}_{\mathrm{factorCon}}(\mathbf{A},{\mathbf{A}}^{\prime })+{\mathcal{L}}_{\mathrm{detailCon}}(\mathbf{B},\mathbf{U})\end{array}$$

(12)

where ${\mathcal{L}}_{\mathrm{spaceCon}}$ enforces inter-component distinctiveness by regulating relationships between background, transmission, and ambient light features, ${\mathcal{L}}_{\mathrm{factorCon}}$ maintains physical consistency by aligning estimated components with their reference counterparts, and ${\mathcal{L}}_{\mathrm{detailCon}}$ ensures structural fidelity by preserving fine-grained image details during enhancement.

The framework implements these specialized contrastive losses to jointly optimize three fundamental aspects of the decomposition. First, intra-component coherence requires features within each component space (background, transmission, ambient light) to maintain high correlation, ensuring consistent physical interpretations through positive sample pairs drawn from the same component space. Second, inter-component separation demands features from different physical components to remain well separated in the latent space, preventing information leakage and ensuring clean decomposition through negative sample pairs across component spaces. Third, structural preservation guarantees that the enhanced outputs faithfully preserve the essential structural information present in the original underwater image while maintaining physical validity through detail-preserving contrastive constraints.

This hierarchical design enables our framework to learn physically meaningful and well-separated representations for each component while maintaining the intrinsic relationships that characterize underwater image formation. The following sections detail the specific formulation and implementation of each contrastive objective.

Degraded factor contrastive learning: To systematically model degradation-related features, the framework implements a physics-guided simulation of the underwater degradation process using unpaired image pairs. Consider a reference underwater image $I_h^c$, where its physical degradation process is characterized by:

$$I_h^c\left(x\right)=J_h^c\left(x\right)T_h^c\left(x\right))+\left(1-T_h^c\left(x\right)\right)A_h^c$$

(13)

where $J_h^c\left(x\right)$ represents the scene radiance, $T_h^c\left(x\right)$ denotes the transmission distribution, and $A_h^c$ characterizes the ambient illumination.

Through the introduction of a degradation coefficient $\alpha \in \left\{0,1\right\}$, the degraded image formation $I_l^c$ is mathematically formulated as:

$$\begin{array}{cc}\hfill I_l^c\left(x\right)& =J_h^c\left(x\right)\left(\alpha T_h^c\left(x\right)\right)+\left(1-\alpha T_h^c\left(x\right)\right)A_h^c\hfill \\ & =J_h^c\left(x\right)T_l^c\left(x\right)+\left(1-T_l^c\left(x\right)\right)A_l^c\hfill \end{array}$$

(14)

As established in Equations (13) and (14), images $I_l^c\left(x\right)$ and $I_h^c\left(x\right)$ share an identical scene radiance $J_h^c\left(x\right)$. The degraded variant $I_l^c\left(x\right)$ exhibits enhanced attenuation characteristics due to the constraint $\alpha T_h^c\left(x\right)<T_h^c\left(x\right)$. Consequently, the estimated transmission map $T_p^c\left(x\right)\in \left\{T\right\}$ and ambient light $A_p^c\left(x\right)\in \left\{A\right\}$ should converge to their respective reference values $T_h^c\left(x\right)$ and $A_h^c\left(x\right)$.

To achieve this objective, the framework defines contrastive objectives for the transmission map $\mathbf{T}$ and ambient light $\mathbf{A}$ estimation:

$$P_t\left(T\right)={\mathcal{L}}_{\mathrm{factorCon}}(T_h^c\left(x\right),T_p^c\left(x\right))$$

(15)

$$P_a\left(A\right)={\mathcal{L}}_{\mathrm{factorCon}}(A_h^c\left(x\right),A_p^c\left(x\right))$$

(16)

The framework implements a patch-based contrastive learning strategy where spatially corresponding patches within each decomposed component constitute positive pairs, while non-corresponding patches serve as negative samples. For a degraded input image $\mathbf{U}$, the framework extracts feature representations $\mathbf{T}$ and $\mathbf{A}$, with their high-quality counterparts denoted as ${\mathbf{T}}^{\prime }$ and ${\mathbf{A}}^{\prime }$. Feature embeddings are computed through specialized Residual encoder $E_{res}$ and multi-layer perceptron $MLP$, yielding representations $v_{A_i}=MLP\left(E_{res}\left(P_{A_i}\right)\right)$, $v_{A_i^{\prime }}=MLP\left(E_{res}\left(P_{A_i^{\prime }}\right)\right)$, $v_{T_i}=MLP\left(E_{res}\left(P_{T_i}\right)\right)$, and $v_{T_i^{\prime }}=MLP\left(E_{res}\left(P_{T_i^{\prime }}\right)\right)$.

The factor-aware contrastive loss is formulated as:

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\mathrm{factorCon}}=& \sum _{i=1}^N{\displaystyle \frac{exp\left(v_{A_i^{\prime }}·v_{A_i}/\tau \right)}{exp\left(v_{A_i^{\prime }}·v_{A_i}/\tau \right)+{\sum }_{j=1}^{N}exp\left(v_{A_j^{\prime }}·v_{A_i}/\tau \right)}}+\hfill \\ \hfill & \sum _{i=1}^N{\displaystyle \frac{exp\left(v_{T_i^{\prime }}·v_{T_i}/\tau \right)}{exp\left(v_{T_i^{\prime }}·v_{T_i}/\tau \right)+{\sum }_{j=1}^{N}exp\left(v_{T_j^{\prime }}·v_{T_i}/\tau \right)}}\hfill \end{array}$$

(17)

where N denotes the number of negative samples and $\tau$ represents the temperature coefficient. This formulation ensures that corresponding patches (e.g., $P_{A_i}$ and $P_{T_i}$) exhibit stronger feature correlations with their high-quality counterparts $P_{A_i^{\prime }}$ and $P_{T_i^{\prime }}$ compared to randomly sampled negative patches, thereby promoting consistent feature learning for transmission and ambient light estimation.

Detail preservation contrastive learning: The structural and perceptual consistency between the enhanced image $\mathbf{B}$ and the observed image $\mathbf{U}$ is systematically enforced through a detail-preserving contrastive mechanism. Spatially corresponding patches from $\mathbf{B}$ and $\mathbf{U}$ are designated as positive pairs to maintain local structural fidelity, while non-corresponding patches serve as negative samples. The feature extraction process utilizes the encoder $E_{res}$, yielding patch-level representations $v_{U_i}=MLP\left(E_{res}\left(P_{U_i}\right)\right)$ and $v_{B_i}=MLP\left(E_{res}\left(P_{B_i}\right)\right)$. The detail preservation contrastive loss is formulated as:

$${\mathcal{L}}_{\mathrm{detailCon}}=\sum _{i=1}^N{\displaystyle \frac{exp\left(v_{U_i}·v_{B_i}/\tau \right)}{exp\left(v_{U_i}·v_{B_i}/\tau \right)+{\sum }_{j=1}^{N}exp\left(v_{U_j}·v_{B_i}/\tau \right)}}$$

(18)

Inter-component contrastive learning: The framework integrates cross-space contrastive learning to articulate relationships between decomposed components, thereby facilitating more refined decomposition. The clean image $\mathbf{B}$, transmission map $\mathbf{T}$, and ambient light $\mathbf{A}$ exhibit distinct physical characteristics: $\mathbf{T}$ encodes scene depth and attenuation information, $\mathbf{A}$ captures global illumination patterns, and $\mathbf{B}$ preserves intrinsic scene structure and texture.

To model these inter-component relationships, we propose a cross-space contrastive loss that regulates the integration among components. The loss function is formulated as:

$${\mathcal{L}}_{\mathrm{spaceCon}}=-{\displaystyle \frac{1}{N_X}}\sum _{k=1}^{N_X}\sum _{i=1}^{N_X}{\displaystyle \frac{exp\left(f_{X_i}·f_{X_k}/\tau \right)}{{\sum }_{j=1}^{N_Y}exp\left(f_{X_i}·f_{Y_j}/\tau \right)}}-{\displaystyle \frac{1}{N_Y}}\sum _{m=1}^{N_Y}\sum _{j=1}^{N_Y}{\displaystyle \frac{exp\left(f_{Y_j}·f_{Y_m}/\tau \right)}{{\sum }_{i=1}^{N_X}exp\left(f_{Y_j}·f_{X_i}/\tau \right)}}$$

(19)

where $X,Y\in \{B,T,A\}$ and $N_X$ and $N_Y$ denote the cardinalities of positive and negative sample sets, respectively. The feature vectors $f_{X_i}$ and $f_{Y_i}$ are extracted using discriminator encoder $E_{dis}$, which captures component-specific characteristics. The temperature parameter $\tau$ modulates the sensitivity of the similarity metric, following the principles established in [37].

This cross-space contrastive mechanism maximizes intra-component feature similarity while promoting inter-component feature distinctiveness, thereby ensuring effective separation of the physical components in the learned feature space. The selection of positive and negative samples is guided by non-local patch similarity to ensure meaningful contrastive relationships.

The complete contrastive learning objective integrates component-specific constraints:

$${\mathcal{L}}_{CL}={\mathcal{L}}_{factorCon}+{\mathcal{L}}_{spaceCon}+{\mathcal{L}}_{detailCon}$$

(20)

where each term enforces specific aspects of the physical decomposition model while maintaining feature distinctiveness through carefully selected positive and negative samples.

Sampling strategy: The effectiveness of contrastive learning relies on clear distinctions between positive and negative samples while maintaining intra-class similarity. Unlike conventional CL approaches that employ data augmentation [37], we propose a physics-guided sampling strategy based on local patch similarity:

$$Distance\left(p_i,p_{i_R}\right)={∥p_i-p_{i_{\mathsf{\Omega }}}∥}^2$$

(21)

where $p_i$ denotes the query patch and $p_{i_{\mathsf{\Omega }}}$ represents candidate patches within support set $\mathsf{\Omega }$. Patches with the lowest distance values form positive pairs, while those with the highest values constitute negative pairs.

For detail preservation (${\mathcal{L}}_{detailCon}$), positive pairs are selected from spatially corresponding regions between enhanced background $\mathbf{B}$ and input image $\mathbf{U}$, which maintain consistent structural details. The factor consistency objective (${\mathcal{L}}_{factorCon}$) forms positive pairs between estimated components $\left(\mathbf{T},\mathbf{A}\right)$ and their high-quality references $\left({\mathbf{T}}^{\prime },{\mathbf{A}}^{\prime }\right)$, considering depth-dependent attenuation for transmission and illumination consistency for ambient light. For component distinctiveness (${\mathcal{L}}_{spaceCon}$), positive pairs are selected within each component space, while negative pairs are sampled across different components to maximize feature distinctiveness.

This physics-guided sampling strategy ensures both reliable feature learning through intra-component consistency and effective decomposition through inter-component distinctiveness, while maintaining computational efficiency through local patch-based selection.

3.3.2. Information Formulation Supervised Function

The decomposition framework leverages physical priors to guide the separation of an underwater image $\mathbf{U}$ into its constituent components: background $\mathbf{B}$, transmission map $\mathbf{T}$, and ambient light $\mathbf{A}$. These physics-based constraints ensure both the stability and the physical validity of the decomposition process. The estimated components $\left(\mathbf{T},\mathbf{A}\right)$ provide gradient supervision through an L1-based reconstruction loss:

$${\mathcal{L}}_{IFM}={\left|\mathbf{U}-(\mathbf{B}·\mathbf{T}+(1-\mathbf{T})·\mathbf{A})\right|}_1$$

(22)

The L1 norm is specifically chosen over alternative metrics (e.g., L2) for its superior characteristics in preserving fine-grained details and robustness to outliers—properties crucial for high-fidelity image restoration. This constraint enforces the decomposed components to adhere to the physical degradation process defined by the IFM, guaranteeing physically consistent outputs from the decoders $({\mathbf{D}}_{\mathbf{b}},{\mathbf{D}}_{\mathbf{t}},{\mathbf{D}}_{\mathbf{a}})$.

3.3.3. Adversarial Learning Function

The adversarial learning framework optimizes decoder ${\mathbf{D}}_{\mathbf{b}}$ to synthesize clean background images $\mathbf{B}$ that accurately emulate the characteristics of natural underwater scenes. This is achieved through an adversarial discriminator $\mathbf{Dis}$ that learns to differentiate between authentic and synthesized backgrounds. The corresponding adversarial loss is formulated as:

$$\begin{array}{c}\hfill {\mathcal{L}}_{adv}({\mathbf{D}}_{\mathbf{b}},\mathbf{Dis})={\mathbb{E}}_{\mathbf{B}\sim P_{bg}\left(\mathbf{B}\right)}[log\mathbf{Dis}\left(\mathbf{B}\right)]+{\mathbb{E}}_{\mathbf{U}\sim P_{uw}\left(\mathbf{U}\right)}\left[log\left(1-\mathbf{Dis}\left({\mathbf{D}}_{\mathbf{b}}\left(\mathbf{U}\right)\right)\right)\right]\end{array}$$

(23)

where $P_{bg}\left(\mathbf{B}\right)$ characterizes the probability distribution of authentic background images in the target domain and $P_{uw}\left(\mathbf{U}\right)$ represents the distribution of underwater observations in the source domain. Through iterative optimization, the decoder ${\mathbf{D}}_{\mathbf{b}}$ learns to minimize this objective, thereby generating perceptually realistic and physically plausible background images.

For transmission and ambient light components, we extend this adversarial learning strategy with specialized formulations ${\mathcal{L}}_{adv}({\mathbf{D}}_{\mathbf{t}},\mathbf{Dis})$ and ${\mathcal{L}}_{adv}({\mathbf{D}}_{\mathbf{a}},\mathbf{Dis})$, respectively. Specifically, the transmission decoder ${\mathbf{D}}_{\mathbf{t}}$ employs local attention mechanisms to capture spatially varying degradation patterns, as the transmission map exhibits pixel-wise variations in projection rates. Conversely, the ambient light decoder ${\mathbf{D}}_{\mathbf{a}}$ adopts a global representation approach, reflecting the scene-level nature of ambient illumination. For initialization, the transmission map $\mathbf{T}$ utilizes a second-order Laplacian filter to extract edge-based degradation cues, while the ambient light $\mathbf{A}$ leverages the dark channel prior.

Hence, the whole adversarial learning framework is formulated as:

$${\mathcal{L}}_{adv}={\mathcal{L}}_{adv}({\mathbf{D}}_{\mathbf{b}},\mathbf{Dis})+{\mathcal{L}}_{adv}({\mathbf{D}}_{\mathbf{t}},\mathbf{Dis})+{\mathcal{L}}_{adv}({\mathbf{D}}_{\mathbf{a}},\mathbf{Dis})$$

(24)

4. Experiments

4.1. Implementation Details

Network structure: The feature extraction backbone for ${\mathcal{L}}_{crossSpace}$ is specifically engineered to optimize inter-component feature discrimination through a hierarchical representation learning scheme. The framework implements a classification-based architecture similar to PatchGAN [45], incorporating a discriminator–generator structure (illustrated in Figure 1b). This design enables ${\mathcal{L}}_{crossSpace}$ to effectively capture discriminative semantic features necessary for component classification.

For ${\mathcal{L}}_{detailCon}$ and ${\mathcal{L}}_{factorCon}$ objectives, the feature extraction mechanism emphasizes local patch-level consistency between decomposed components and their corresponding observations. The framework employs ResNet [46] as the backbone feature extractor, followed by a two-layer multilayer perceptron (MLP) with 256 hidden units for feature embedding (detailed in Figure 1c). The sampling parameters are empirically set as $N=256$ for negative samples, $N_X=8$ for positive samples, and $N_Y=256$ for cross-space negative samples.

Training details: Our method employs a three-phase training protocol to ensure stable convergence and accurate component decomposition: (1) background initialization: the background decoder is optimized using ${\mathcal{L}}_{detailCon}$, ${\mathcal{L}}_{adv}$, and ${\mathcal{L}}_{IFM}$ for 10 epochs while keeping other components fixed; (2) degradation component learning: the transmission and ambient light decoders are jointly trained for 20 epochs using ${\mathcal{L}}_{factorCon}$ and auxiliary losses, with the background decoder parameters frozen; (3) joint optimization: all components are collectively refined for 170 epochs using ${\mathcal{L}}_{spaceCon}$ and the complete loss function set, enabling comprehensive feature interaction. The optimization framework adopts the momentum contrast mechanism from MOCO [40], with momentum coefficient 0.99 and temperature parameter 0.77. The implementation utilizes the PyTorch 1.9.0 framework [47] on NVIDIA RTX 4090 GPUs. The Adam optimizer [48] is employed with initial learning rate 1 ×${10}^{-4}$, which is decreased by a factor of 0.1 after 100 epochs. Training proceeds for 200 epochs with mini-batch size 4 and input resolution $256\times 256$. The loss weights are configured as ${\lambda }_{adv}=1$, ${\lambda }_{IFM}=0.5$, and ${\lambda }_{CL}=0.1$.

4.2. Datasets

The experimental dataset comprises 2000 unpaired unlabeled samples and 2000 paired images with referenced clean labels, ensuring comprehensive coverage of diverse underwater scenarios. The unlabeled images are randomly sampled from the EUVP [1]. Additionally, 2000 labeled images are selected from the LSUI dataset [49], which ensures diversity in real underwater scenes, water types, lighting conditions, and target categories. Pseudo labels (i.e., estimated T′ and A′) are generated for training by processing all labeled and unlabeled high-quality underwater images using widely adopted underwater transmission and ambient light estimation methods [50]; the details can be seen on the right side of Figure 1a. The testing set consists of four commonly used datasets, UIEB [51], EUVP [1], RUIE [52], and SUIM [17], frequently employed in underwater image enhancement (UIE) research.

4.3. Quantitative and Quantitative Comparison

The performance evaluation of the proposed framework encompasses both quantitative metrics and qualitative visual evaluation, benchmarking against state-of-the-art underwater image enhancement methods. The comparative analysis includes two traditional methods (GDCP [13] and MMLE [53]) and five learning-based approaches (WaterNet [51], FUINE [1], CWR [19], SEMUIR [18], and HUPE [54]). For fair comparison, all learning-based methods are retrained using the proposed training dataset.

Visual quality assessment: The qualitative evaluation examines enhancement performance across four diverse datasets, encompassing various underwater scenes and degradation patterns. As illustrated in Figure 2, existing methods often exhibit inconsistent enhancement results, resulting in over-smoothing artifacts and color distortions at both global and local scales. For instance, WaterNet [51] introduces artifacts along high-frequency edges, while FUINE [1] and CWR [19] demonstrate limitations in color fidelity and detail preservation under challenging conditions.

The challenge of maintaining color fidelity while correcting hue distortions is particularly significant in unpaired learning frameworks. SEMUIR [18] addresses this through using estimated illumination maps as auxiliary inputs, showing improved color correction particularly for foreground objects (e.g., red and blue fish in the 11th and 12th rows of Figure 2). The proposed framework achieves superior color restoration by integrating physical underwater image formation principles into the network architecture, thereby resulting in more natural and vibrant color distributions compared to methods relying solely on unpaired training data.

Quantitative performance analysis: The quantitative evaluation employs four widely used non-reference metrics, each targeting different dimensions of underwater image degradation. UIQM [55] evaluates three key aspects, colorfulness, sharpness, and contrast, addressing common underwater image issues. UCIQE [56] quantifies color casts and low contrast, which are typical challenges in underwater imaging. MUSIQ [57] uses a multi-scale transformer architecture to assess structural fidelity and texture preservation across frequency bands. And NIQE [58] models natural scene statistics (NSSs) in the wavelet domain to detect artificial artifacts, with lower scores indicating higher naturalness. Although these metrics are heuristic and domain-specific, they cover important facets of underwater image quality: UIQM/UCIQE focus on the unique challenges of color distortions and turbidity, while MUSIQ/NIQE contribute to texture preservation and naturalness. As evidenced in

Table 1. Comprehensive evaluation of compared methods (quality metrics and computational efficiency) on benchmarks in terms of UIQM [55], UCIQE [56], MUSIQ [57], and NIQE [58] across RUIE [52], SUIM [17], EVUP [1], and UIEB [51] datasets. The ↑ indicates higher values are better, while ↓ indicates lower values are better. Best results are in bold and second-best results are underlined.

Method	UIQM ↑				UCIQE ↑				MUSIQ ↑				NIQE ↓				Efficiency
	RUIE	SUIM	EVUP	UIEB	RUIE	SUIM	EVUP	UIEB	RUIE	SUIM	EVUP	UIEB	RUIE	SUIM	EVUP	UIEB	FLOPs (G)	Time (ms)
Original	2.294	2.027	2.254	1.677	0.523	0.597	0.543	0.533	33.874	60.855	43.678	41.697	5.062	3.957	4.976	6.905	-	-
GDCP [13]	2.738	1.970	2.337	1.899	0.608	0.678	0.638	0.624	32.671	58.897	40.886	51.002	4.738	3.885	4.697	5.190	-	173.8
MMLE [53]	2.871	2.137	2.337	1.953	0.567	0.612	0.638	0.580	36.510	62.704	40.886	40.345	4.859	4.045	4.697	4.845	-	91.7
WaterNet [51]	3.168	2.644	3.077	2.317	0.568	0.607	0.597	0.581	30.289	60.280	42.402	40.006	4.755	4.007	4.420	5.702	571.8	40.6
FUINE [1]	3.145	2.557	2.944	2.867	0.538	0.610	0.572	0.552	28.726	60.158	38.110	46.827	4.906	3.611	5.106	5.299	81.91	2.9
CWR [19]	3.154	2.847	3.008	2.459	0.583	0.637	0.618	0.607	25.310	58.915	37.854	30.131	4.730	4.058	4.744	5.338	338.9	20.8
SEMUIR [18]	3.063	2.502	2.957	2.164	0.554	0.636	0.599	0.570	32.446	62.272	47.882	42.460	4.633	3.439	4.352	5.697	105.6	43.4
HUPE [54]	3.000	2.481	2.779	2.198	0.550	0.637	0.602	0.582	29.766	54.57	38.817	35.559	4.598	4.148	5.136	7.771	87.5	50.2
Ours	3.227	3.117	3.116	2.793	0.558	0.620	0.600	0.569	34.398	61.348	47.175	39.412	3.922	2.863	3.639	3.938	147.5	19.3

FLOPs: float operations; time: 4090 GPU latency; “-”: non-deep methods.

, our method achieves optimal balance across these orthogonal dimensions.

Our CFD-Net consistently outperforms existing methods in UIQM and NIQE metrics across all datasets while maintaining competitive performance in UCIQE and MUSIQ. While GDCP [13] demonstrates superior performance in UCIQE and SEMUIR [18] achieves high scores in MUSIQ, our method exhibits balanced performance across all metrics, effectively improving both contrast enhancement and semantic feature preservation. This comprehensive enhancement capability is attributed to the synergistic integration of decomposed generative branches and multi-scale contrastive learning mechanisms.

Figure 3a–d present the channel-wise color distribution analysis of compared methods across different datasets. The results demonstrate that the proposed method consistently achieves more balanced and natural color distributions, particularly evident in the red channel where underwater degradation is most severe. Additionally, Figure 4 provides statistical analysis of color characteristics across all methods in the EVUP dataset, utilizing mean, standard deviation, median, and color range metrics to comprehensively evaluate enhancement quality. Our method achieves balanced mean values ($\mu$ = 0.497, 0.642, 0.590) with stable standard deviations ($\sigma$ = 0.207, 0.195, 0.196) across RGB channels, showing a notable 66.1% improvement in red channel mean intensity compared to original images ($\mu$ = 0.299, 0.592, 0.555) while maintaining more consistent color distributions than competing methods such as GDCP ($\sigma$ = 0.296, 0.301, 0.292). These quantitative results validate the effectiveness of our method in addressing the characteristic color distortion in underwater imagery while preserving natural color appearances.

Comprehensive performance evaluation: To evaluate computational efficiency, we compare the FLOPs and inference time of various methods. All experiments are performed on an NVIDIA RTX 4090 GPU using $512\times 512$ input images and a batch size of 1. Inference time is averaged over 100 forward passes to ensure consistency.

As shown in Table 1, our method achieves an inference time of 19.3 ms, making it the 2nd fastest among all methods. While FUINE achieves the fastest time (2.9 ms), it sacrifices quality, particularly in NIQE (5.106 vs. 3.922). Compared to CWR (20.8 ms) and WaterNet (40.6 ms), our model offers superior speed without compromising enhancement performance. Regarding computational cost, our method operates at 147.5 G FLOPs, significantly lower than WaterNet (571.8 G) and CWR (338.9 G). Although our approach has a higher FLOP count than FUINE (81.91 G) and HUPE (87.5 G), it strikes a favorable balance between efficiency and quality. This makes it particularly suitable for real-time underwater vision applications, especially in resource-constrained environments.

4.4. Ablation Study

To comprehensively evaluate the contributions of different components, we conduct ablation experiments on the UIEB dataset using four complementary quality metrics. We categorize the losses into three groups: (1) physics-consistency losses ($L_{IFM}$), (2) feature contrastive losses ($L_{detailCon}$, $L_{spaceCon}$, $L_{factorCon}$), and (3) adversarial loss ($L_{adv}$). The relative performance drop, denoted as $\Delta$, is computed as follows:

$$\Delta ={\displaystyle \frac{M_{\mathrm{full}}-M_{\mathrm{ablated}}}{M_{\mathrm{full}}}}\times 100\%$$

(25)

where $M_{\mathrm{full}}$ denotes the metric value of the full model and $M_{\mathrm{ablated}}$ represents the value when specific components are removed.

As shown in

Table 2. Component-wise ablation analysis on UIEB dataset (updated). The ↑ indicates higher values are better, while ↓ indicates lower values are better. Best results are in bold.

Category	Components	UIQM ↑	$\mathbf{\Delta }$ UIQM	UCIQE ↑	$\mathbf{\Delta }$ UCIQE	MUSIQ ↑	$\mathbf{\Delta }$ MUSIQ	NIQE ↓	$\mathbf{\Delta }$ NIQE
Physical only	$L_{IFM}$	1.667	−40.3%	0.572	−1.2%	39.476	−4.7%	4.107	−9.9%
Feature contrastive	+$L_{detailCon}$	2.506	−10.3%	0.522	−8.3%	38.912	−6.0%	4.246	−13.6%
	+$L_{spaceCon}$	2.301	−17.6%	0.551	−3.2%	39.102	−5.6%	4.102	−9.7%
	+$L_{factorCon}$	2.410	−13.7%	0.563	−1.1%	39.875	−3.7%	3.980	−6.5%
Adversarial	+$L_{adv}$	2.155	−22.8%	0.548	−3.7%	40.213	−2.9%	3.890	−4.1%
Full	All	2.793	-	0.569	-	41.412	-	3.738	-

$\Delta$: Relative drop versus full model.

, the physics-only baseline achieves moderate performance (UIQM = 1.667) and provides moderate enhancement quality, confirming the necessity of physical modeling. However, removing contrastive learning drastically reduces performance (e.g., UIQM ↓ 40.3%), indicating that feature-level constraints are critical for enhancement quality. Among the contrastive losses, $L_{detailCon}$ contributes the most to texture enhancement, improving UIQM by 50.3% (1.667 → 2.506), $L_{spaceCon}$ mainly enhances color balance, increasing UCIQE by 7.2%, and $L_{factorCon}$ improves perceptual quality and denoising, reducing NIQE from 4.107 to 3.980. The adversarial loss alone ($L_{adv}$) achieves reasonable enhancement, but its full effect emerges when combined with physical and contrastive constraints. Notably, the full model achieves the best balance between all metrics, demonstrating the complementary interactions between loss categories. These results confirm that feature contrastive learning is the most crucial factor for underwater image enhancement, while adversarial learning provides additional refinement, particularly in perceptual quality (MUSIQ ↑ 41.412 vs. 40.213).

Figure 5 illustrates the impact of individual components on visual results. Initially, the $L_{IFM}$ function restores the contour information but results in some color and contrast loss. The addition of $L_{detailCon}$ enhances fine-grained details, notably the printed text. When $L_{spaceCon}$ and $L_{factorCon}$ are introduced, color vibrancy improves, but some noise artifacts are also present. The adversarial loss ($L_{adv}$) enhances color fidelity and texture preservation, especially in low-light scenarios. The integration of all components yields the best overall performance in terms of clarity, detail retention, and contrast.

4.5. Evaluation on Other Applications

To demonstrate the practical utility of the proposed framework, we evaluate its performance on downstream high-level computer vision tasks. Specifically, we assess the impact of image enhancement on underwater semantic segmentation performance using the SUIM dataset [17]. The evaluation compares the segmentation accuracy using original underwater images, images enhanced by competing methods, and those processed by our framework.

The segmentation results are illustrated in Figure 6, with quantitative evaluation metrics presented in

Table 3. Pixel Accuracy (PA), Mean Pixel Accuracy (mPA), and Mean Intersection over Union (mIoU) comparison on SUIM dataset. The ↑ indicates higher values are better. Best results are in bold and second-best results are underlined.

	GDCP	MMLE	WaterNet	FUNIE	CWR	SEMUIR	HUPE	Ours
PA ↑	0.812	0.805	0.655	0.806	0.800	0.816	0.826	0.830
MPA ↑	0.301	0.304	0.261	0.297	0.300	0.304	0.312	0.319
mIoU ↑	0.267	0.268	0.200	0.264	0.268	0.273	0.284	0.284

. The proposed framework achieves superior performance across all evaluation metrics, attaining a PA of 0.830, mPA of 0.319, and mIoU of 0.284. These results represent significant improvements compared to both traditional methods (GDCP [13], MMLE [53]) and learning-based approaches (WaterNet [51], FUINE [1], CWR [19], SEMUIR [18], and HUPE [54]). The enhanced performance on semantic segmentation demonstrates the capability of our framework to recover discriminative features that benefit high-level computer vision tasks.

5. Conclusions

Our CFD-Net integrates decomposed feature representation with physical priors, which combines underwater image enhancement techniques with unsupervised learning algorithms, effectively addressing the challenges posed by degradation processes and refined feature representations. Through extensive experiments, we demonstrate that CFD-Net consistently outperforms state-of-the-art methods in both image enhancement and high-level downstream tasks, such as semantic segmentation. The integration of physical priors and innovative learning mechanisms allows our framework to recover vibrant, natural colors and significantly improve segmentation accuracy. Future work will explore the extension of this approach to multi-frame sequences and videos, where temporal information and multi-view perspectives could provide additional cues for enhanced underwater image restoration.