Anomaly-Aware Tropical Cyclone Track Prediction Using Multi-Scale Generative Adversarial Networks
Abstract
1. Introduction
- We develop a novel multi-source prediction model that synergistically integrates satellite imagery, wind speed, geopotential height, and vorticity data for TC tracking, achieving high-precision tracking for both over-ocean and over-land TC trajectories.
- Our model is able to detect and predict automatically beyond the International Best Track Archive for Climate Stewardship (IBTrACS) dataset by accurately tracing post-TC locations until dissipation, covering the full life cycle of landfalling TCs and enabling the overland TC-associated impact analysis.
- Unlike other TC forecasting systems that discard abnormal satellite imagery, our approach successfully processes and utilizes these challenging imagery by leveraging a multi-scale generative adversarial network (GAN) framework integrated with an advanced center localization algorithm.
2. Data and Methodology
2.1. Dataset
2.2. Model
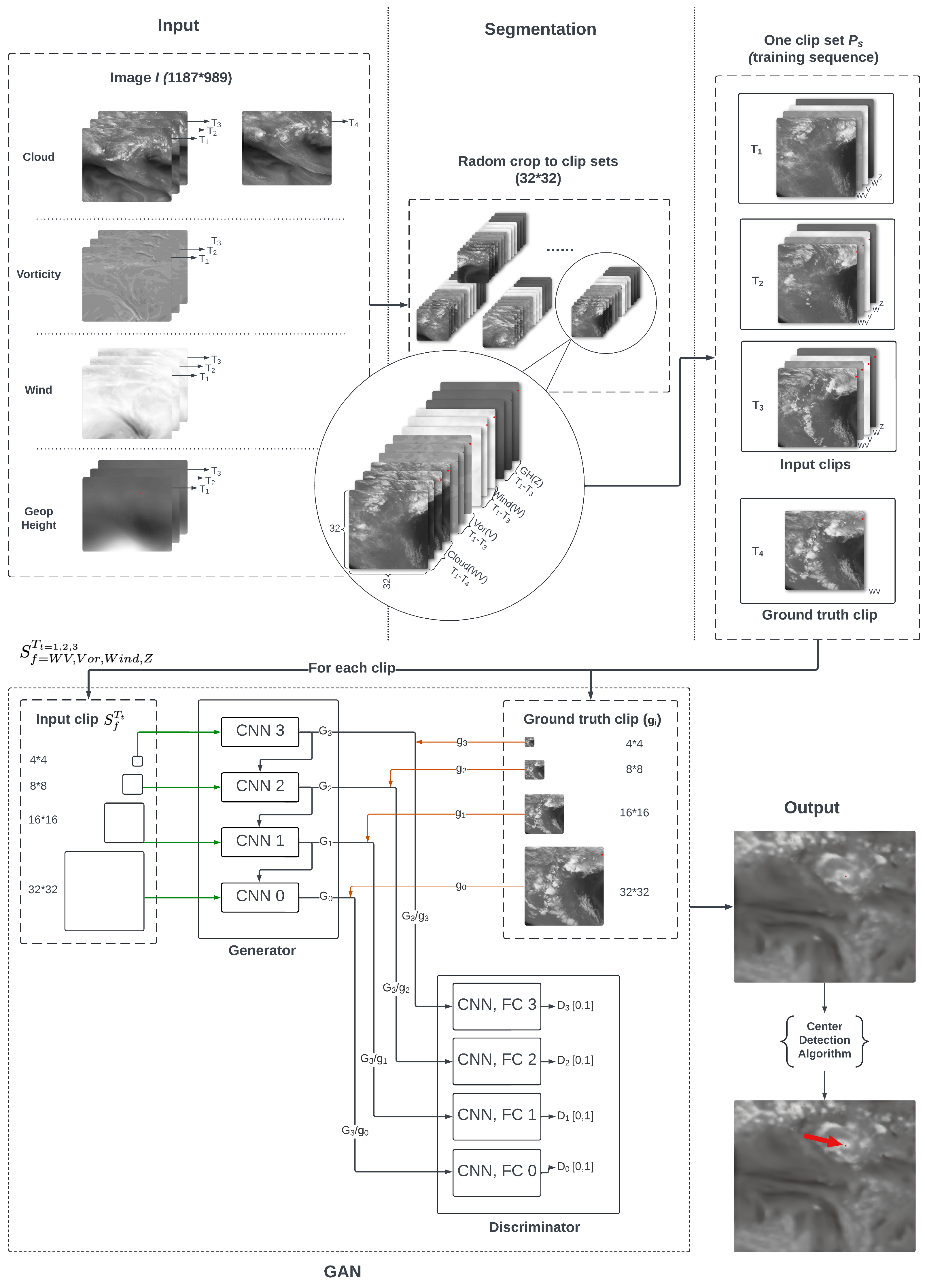
2.2.1. Input Data and Segmentation Algorithm
| Algorithm 1 Segmentation algorithm for TCs prediction. |
| Require:
TCs images I at different time steps , where for , ; for , Require: Number of feature subsets , where Ensure: Preprocessed image clips with included
|
2.2.2. Multi-Scale GAN
2.2.3. Center Detection Algorithm
| Algorithm 2 Center detection algorithm. |
| Require:
Image I, Previous Center (optional) Ensure: Coordinates of the detected red point
|
2.3. Model Performance Evaluation
3. Results
3.1. Model Performance over Ocean and Land, Best Track and Extended Track and Its Robustness
3.2. Model Performance for TCs with Abnormal Satellite Imagery
3.3. Case Study
4. Discussion
4.1. Accuracy over Land and in the Extended Tracks
4.2. Challenges with Rapid TC Movement and Complex Trajectories
4.3. Segmentation Algorithm
4.4. Handling Abnormal Satellite Image
4.5. Model Output Cloud Image
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, S.; Toumi, R. More tropical cyclones are striking coasts with major intensities at landfall. Sci. Rep. 2022, 12, 5236. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Zhang, W.; Wang, X. Machine learning in tropical cyclone forecast modeling: A review. Atmosphere 2020, 11, 676. [Google Scholar] [CrossRef]
- Klotzbach, P.; Blake, E.; Camp, J.; Caron, L.P.; Chan, J.C.; Kang, N.Y.; Kuleshov, Y.; Lee, S.M.; Murakami, H.; Saunders, M.; et al. Seasonal tropical cyclone forecasting. Trop. Cyclone Res. Rev. 2019, 8, 134–149. [Google Scholar] [CrossRef]
- Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge University Press: Cambridge, UK, 2003; Volume 341. [Google Scholar]
- Roy, C.; Kovordányi, R. Tropical cyclone track forecasting techniques―A review. Atmos. Res. 2012, 104, 40–69. [Google Scholar] [CrossRef]
- Long, T.; Fu, J.; Tong, B.; Chan, P.; He, Y. Identification of tropical cyclone centre based on satellite images via deep learning techniques. Int. J. Climatol. 2022, 42, 10373–10386. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, J.; Huang, H.; Wang, X. A review on the application of machine learning methods in tropical cyclone forecasting. Front. Earth Sci. 2022, 10, 902596. [Google Scholar] [CrossRef]
- Wimmers, A.; Velden, C.; Cossuth, J.H. Using deep learning to estimate tropical cyclone intensity from satellite passive microwave imagery. Mon. Weather Rev. 2019, 147, 2261–2282. [Google Scholar] [CrossRef]
- Zhang, C.J.; Wang, X.J.; Ma, L.M.; Lu, X.Q. Tropical cyclone intensity classification and estimation using infrared satellite images with deep learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2070–2086. [Google Scholar] [CrossRef]
- Rüttgers, M.; Jeon, S.; Lee, S.; You, D. Prediction of typhoon track and intensity using a generative adversarial network with observational and meteorological data. IEEE Access 2022, 10, 48434–48446. [Google Scholar] [CrossRef]
- Gan, S.; Fu, J.; Zhao, G.; Chan, P.; He, Y. Short-term prediction of tropical cyclone track and intensity via four mainstream deep learning techniques. J. Wind Eng. Ind. Aerodyn. 2024, 244, 105633. [Google Scholar] [CrossRef]
- Dorffner, G. Neural networks for time series processing. Neural Netw. World 1996, 6, 447–468. [Google Scholar]
- Hochreiter, S. Long Short-term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Alemany, S.; Beltran, J.; Perez, A.; Ganzfried, S. Predicting hurricane trajectories using a recurrent neural network. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January 2019–1 February 2019; Volume 33, pp. 468–475. [Google Scholar]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Wang, C.; Xu, Q.; Li, X.; Cheng, Y. CNN-based tropical cyclone track forecasting from satellite infrared images. In Proceedings of the IGARSS 2020–2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 5811–5814. [Google Scholar]
- Tong, B.; Wang, X.; Fu, J.; Chan, P.; He, Y. Short-term prediction of the intensity and track of tropical cyclone via ConvLSTM model. J. Wind Eng. Ind. Aerodyn. 2022, 226, 105026. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Advances in Neural Information Processing Systems, Proceedings of the NIPS’14: Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; MIT Press: Cambridge, MA, USA, 2014; Volume 27. [Google Scholar]
- Rüttgers, M.; Lee, S.; Jeon, S.; You, D. Prediction of a typhoon track using a generative adversarial network and satellite images. Sci. Rep. 2019, 9, 6057. [Google Scholar] [CrossRef]
- Huang, C.; Bai, C.; Chan, S.; Zhang, J.; Wu, Y. MGTCF: Multi-generator tropical cyclone forecasting with heterogeneous meteorological data. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 5096–5104. [Google Scholar]
- Vaswani, A. Attention is all you need. In Advances in Neural Information Processing Systems, Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017. [Google Scholar]
- Bi, K.; Xie, L.; Zhang, H.; Chen, X.; Gu, X.; Tian, Q. Accurate medium-range global weather forecasting with 3D neural networks. Nature 2023, 619, 533–538. [Google Scholar] [CrossRef]
- Lian, J.; Dong, P.; Zhang, Y.; Pan, J.; Liu, K. A novel data-driven tropical cyclone track prediction model based on CNN and GRU with multi-dimensional feature selection. IEEE Access 2020, 8, 97114–97128. [Google Scholar] [CrossRef]
- Moradi Kordmahalleh, M.; Gorji Sefidmazgi, M.; Homaifar, A. A sparse recurrent neural network for trajectory prediction of atlantic hurricanes. In Proceedings of the Genetic and Evolutionary Computation Conference, Denver, CO, USA, 20–24 July 2016; pp. 957–964. [Google Scholar]
- Takaya, Y.; Caron, L.P.; Blake, E.; Bonnardot, F.; Bruneau, N.; Camp, J.; Chan, J.; Gregory, P.; Jones, J.J.; Kang, N.; et al. Recent advances in seasonal and multi-annual tropical cyclone forecasting. Trop. Cyclone Res. Rev. 2023, 12, 182–199. [Google Scholar] [CrossRef]
- Bi, K.; Xie, L.; Zhang, H.; Chen, X.; Gu, X.; Tian, Q. Pangu-weather: A 3d high-resolution model for fast and accurate global weather forecast. arXiv 2022, arXiv:2211.02556. [Google Scholar]
- Olander, T.L.; Velden, C.S. The advanced Dvorak technique (ADT) for estimating tropical cyclone intensity: Update and new capabilities. Weather Forecast. 2019, 34, 905–922. [Google Scholar] [CrossRef]
- Shen, H.; Li, X.; Cheng, Q.; Zeng, C.; Yang, G.; Li, H.; Zhang, L. Missing information reconstruction of remote sensing data: A technical review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 61–85. [Google Scholar] [CrossRef]
- Wang, P.; Bayram, B.; Sertel, E. A comprehensive review on deep learning based remote sensing image super-resolution methods. Earth-Sci. Rev. 2022, 232, 104110. [Google Scholar] [CrossRef]
- Shen, H.; Wu, J.; Cheng, Q.; Aihemaiti, M.; Zhang, C.; Li, Z. A spatiotemporal fusion based cloud removal method for remote sensing images with land cover changes. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 862–874. [Google Scholar] [CrossRef]
- Guillemot, C.; Le Meur, O. Image inpainting: Overview and recent advances. IEEE Signal Process. Mag. 2013, 31, 127–144. [Google Scholar] [CrossRef]
- Tang, Z.; Amatulli, G.; Pellikka, P.K.; Heiskanen, J. Spectral temporal information for missing data reconstruction (stimdr) of landsat reflectance time series. Remote Sens. 2021, 14, 172. [Google Scholar] [CrossRef]
- Liu, W.; Jiang, Y.; Wang, J.; Zhang, G.; Li, D.; Song, H.; Yang, Y.; Huang, X.; Li, X. Global and Local Dual Fusion Network for Large-Ratio Cloud Occlusion Missing Information Reconstruction of a High-Resolution Remote Sensing Image. IEEE Geosci. Remote Sens. Lett. 2024, 21, 5001705. [Google Scholar] [CrossRef]
- Xu, H.; Tang, X.; Ai, B.; Gao, X.; Yang, F.; Wen, Z. Missing data reconstruction in VHR images based on progressive structure prediction and texture generation. ISPRS J. Photogramm. Remote Sens. 2021, 171, 266–277. [Google Scholar] [CrossRef]
- Long, C.; Li, X.; Jing, Y.; Shen, H. Bishift networks for thick cloud removal with multitemporal remote sensing images. Int. J. Intell. Syst. 2023, 2023, 9953198. [Google Scholar] [CrossRef]
- Li, Y.; Wei, F.; Zhang, Y.; Chen, W.; Ma, J. HS2P: Hierarchical spectral and structure-preserving fusion network for multimodal remote sensing image cloud and shadow removal. Inf. Fusion 2023, 94, 215–228. [Google Scholar] [CrossRef]
- Deng, D.; Ritchie, E. Tropical cyclone rainfall enhancement following landfalling over Australia-Part III. In Proceedings of the American Geophysical Union Fall Meeting 2023, San Francisco, CA, USA, 11–15 December 2023; Volume 2023, p. A54F-06. [Google Scholar]
- Deng, D. A Physical-based Semi-Automatic Algorithm for Post-Tropical Cyclone Identification and Tracking in Australia. Remote Sens. 2025, 17, 539. [Google Scholar] [CrossRef]
- Deng, D.; Ritchie, E. Tropical cyclone rainfall enhancement following landfalling over Australia. In Proceedings of the Australian Meteorological and Oceanographic Society Annual Conference 2024, Canberra, ACT, Australia, 5–9 February 2024. [Google Scholar]
- Chan, K.T. Are global tropical cyclones moving slower in a warming climate? Environ. Res. Lett. 2019, 14, 104015. [Google Scholar] [CrossRef]








| TC ID | Surface | Track | All | ||
|---|---|---|---|---|---|
| Ocean | Land | Best | Extended | ||
| 199634S609129-NICHOLAS | 36 | 23 | 55 | 4 | 59 |
| 199636S515137-RACHEL | 46 | 67 | 101 | 12 | 113 |
| 199705S351142-ITA | 46 | 23 | 35 | 12 | 47 |
| 199833S31120-BILLY | 40 | 23 | 47 | 6 | 53 |
| 199934S42123-JOHN | 30 | 14 | 55 | 3 | 58 |
| 200010S509127-ROSITA | 44 | 14 | 55 | 3 | 58 |
| 200104S541442-WYLVIA | 12 | 19 | 55 | 3 | 58 |
| 200405S518125-MONTY | 35 | 52 | 81 | 7 | 88 |
| 200706S214119-JACOB | 76 | 20 | 55 | 6 | 61 |
| 201035S13152-TASHA | 11 | 17 | 21 | 7 | 28 |
| 201102S81380-YASI | 45 | 32 | 69 | 11 | 80 |
| 201209S112118-HEIDI | 53 | 44 | 79 | 8 | 87 |
| 201303S251126-RUSTY | 50 | 101 | 105 | 7 | 112 |
| 201403S14124-NOT_NAMED | 25 | 112 | 105 | 32 | 137 |
| Type | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2015–2020 | ||
|---|---|---|---|---|---|---|---|---|---|
| All | Ave.Er | 47.2 | 45.6 | 36.6 | 37.8 | 40.8 | 39.2 | 41.0 | |
| hlstd | 41.4 | 51.1 | 38.2 | 48.2 | 29.1 | 42.9 | 42.8 | ||
| Surface | Ocean | Ave.Er | 38.5 | 40.7 | 36.7 | 38.3 | 37.7 | 31.1 | 37.8 |
| std | 40.1 | 47.9 | 35.9 | 43.8 | 27.7 | 44.2 | 39.8 | ||
| Land | Ave.Er | 49.4 | 67.4 | 41.9 | 41.5 | 41.7 | 42.8 | 47.5 | |
| std | 42.7 | 50.9 | 42.9 | 60.0 | 32.7 | 42.1 | 47.0 | ||
| Track | Best | Ave.Er | 31.5 | 30.8 | 31.0 | 33.5 | 37.0 | 24.6 | 32.0 |
| std | 26.4 | 30.3 | 30.7 | 45.2 | 27.1 | 17.7 | 33.0 | ||
| Extended | Ave.Er | 82.5 | 90.9 | 76.2 | 70.0 | 57.6 | 74.2 | 78.4 | |
| std | 58.1 | 56.0 | 49.4 | 52.6 | 41.5 | 60.9 | 55.3 | ||
| TC ID | Surface | Track | All | ||
|---|---|---|---|---|---|
| Ocean | Land | Best | Extended | ||
| 2015045S12145-LAM | 18.1 | 47.2 | 24.7 | 63.1 | 38.6 |
| 2015047S15152-MARCIA | 39.7 | 36.7 | 35.5 | 45.2 | 37.6 |
| 2015068S12151-NATHAN | 62.7 | 88.6 | 30.4 | 120.9 | 40.6 |
| 2015068S14113-OLWYN | 67.6 | 105.0 | 67.9 | 104.4 | 62.6 |
| 2015117S12115-QUANG | 38.7 | 68.9 | 21.9 | 132.5 | 56.0 |
| 2015355S16136-NOT_NAMED | NaN | 57.6 | 33.4 | 81.8 | 47.6 |
| 2016027S13119-STAN | 94.6 | 127.1 | 69.7 | 152.0 | 61.1 |
| 2016074S16137-NOT_NAMED | 24.9 | 41.0 | 23.3 | 60.3 | 32.4 |
| 2016353S11130-NOT_NAMED | 89.5 | 50.3 | 27.8 | 111.9 | 61.0 |
| 2016354S15116-YVETTE | 29.2 | 12.7 | 24.5 | 5.5 | 28.1 |
| 2017026S16127-NOT_NAMED | 30.3 | 27.6 | 29.0 | NaN | 30.2 |
| 2017046S17137-ALFRED | 55.3 | 61.9 | 30.9 | 86.2 | 52.0 |
| 2017060S09139-BLANCHE | 57.6 | 39.9 | 28.7 | 68.8 | 44.1 |
| 2017079S13122-NOT_NAMED | 22.8 | 51.4 | 36.0 | 53.6 | 34.2 |
| 2017081S13152-DEBBIE | 108.7 | 48.6 | 43.6 | 178.9 | 44.4 |
| 2017096S08135-NOT_NAMED | 41.1 | 20.6 | 26.8 | 49.2 | 32.8 |
| 2017360S15124-HILDA | 12.8 | 38.2 | 12.2 | 64.6 | 18.8 |
| 2018007S13129-JOYCE | 31.8 | 28.2 | 23.1 | 45.5 | 26.4 |
| 2018044S10133-KELVIN | 44.5 | 50.8 | 20.1 | 75.2 | 34.3 |
| 2018074S09130-MARCUS | 98.8 | 32.0 | 33.8 | 162.0 | 48.2 |
| 2018079S08137-NORA | 43.5 | 31.7 | 25.9 | 49.3 | 35.8 |
| 2018336S14154-OWEN | 43.5 | 106.6 | 69.9 | 53.6 | 42.8 |
| 2018365S13140-PENNY | 37.7 | 39.4 | 33.1 | 50.2 | 39.3 |
| 2019077S13146-TREVOR | 18.9 | 60.1 | 25.3 | 88.7 | 27.1 |
| 2019132S16159-ANN | 54.0 | 66.6 | 60.3 | NaN | 54.6 |
| 2020006S16121-BLAKE | 21.2 | 35.8 | 22.5 | 47.6 | 32.8 |
| 2020037S17121-DAMIEN | 105.9 | 55.0 | 21.0 | 139.9 | 40.2 |
| 2020055S15139-ESTHER | 24.7 | 55.0 | 28.1 | 78.5 | 44.6 |
| TC ID | Total Points | Abnormal | Absolute Error (km) | |
|---|---|---|---|---|
| [10,19] | Ours | |||
| 2017026S16127-NOT_NAMED | 50 | 49 | 3465.3 | 30.2 |
| 2017079S13122-NOT_NAMED | 48 | 48 | 2012.5 | 34.2 |
| 2017081S13152-DEBBIE | 83 | 83 | 3451.6 | 44.4 |
| 2017096S08135-NOT_NAMED | 83 | 83 | 3713.6 | 32.8 |
| 2018044S10133-KELVIN | 86 | 10 | 623.8 | 34.3 |
| Average | 70 | 55 | 2653.4 | 35.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Deng, D.; Hu, L.; Sun, N. Anomaly-Aware Tropical Cyclone Track Prediction Using Multi-Scale Generative Adversarial Networks. Remote Sens. 2025, 17, 583. https://doi.org/10.3390/rs17040583
Huang H, Deng D, Hu L, Sun N. Anomaly-Aware Tropical Cyclone Track Prediction Using Multi-Scale Generative Adversarial Networks. Remote Sensing. 2025; 17(4):583. https://doi.org/10.3390/rs17040583
Chicago/Turabian StyleHuang, He, Difei Deng, Liang Hu, and Nan Sun. 2025. "Anomaly-Aware Tropical Cyclone Track Prediction Using Multi-Scale Generative Adversarial Networks" Remote Sensing 17, no. 4: 583. https://doi.org/10.3390/rs17040583
APA StyleHuang, H., Deng, D., Hu, L., & Sun, N. (2025). Anomaly-Aware Tropical Cyclone Track Prediction Using Multi-Scale Generative Adversarial Networks. Remote Sensing, 17(4), 583. https://doi.org/10.3390/rs17040583







