WindRAD Scatterometer Quality Control in Rain
Abstract
1. Introduction
2. Data and QC Algorithms
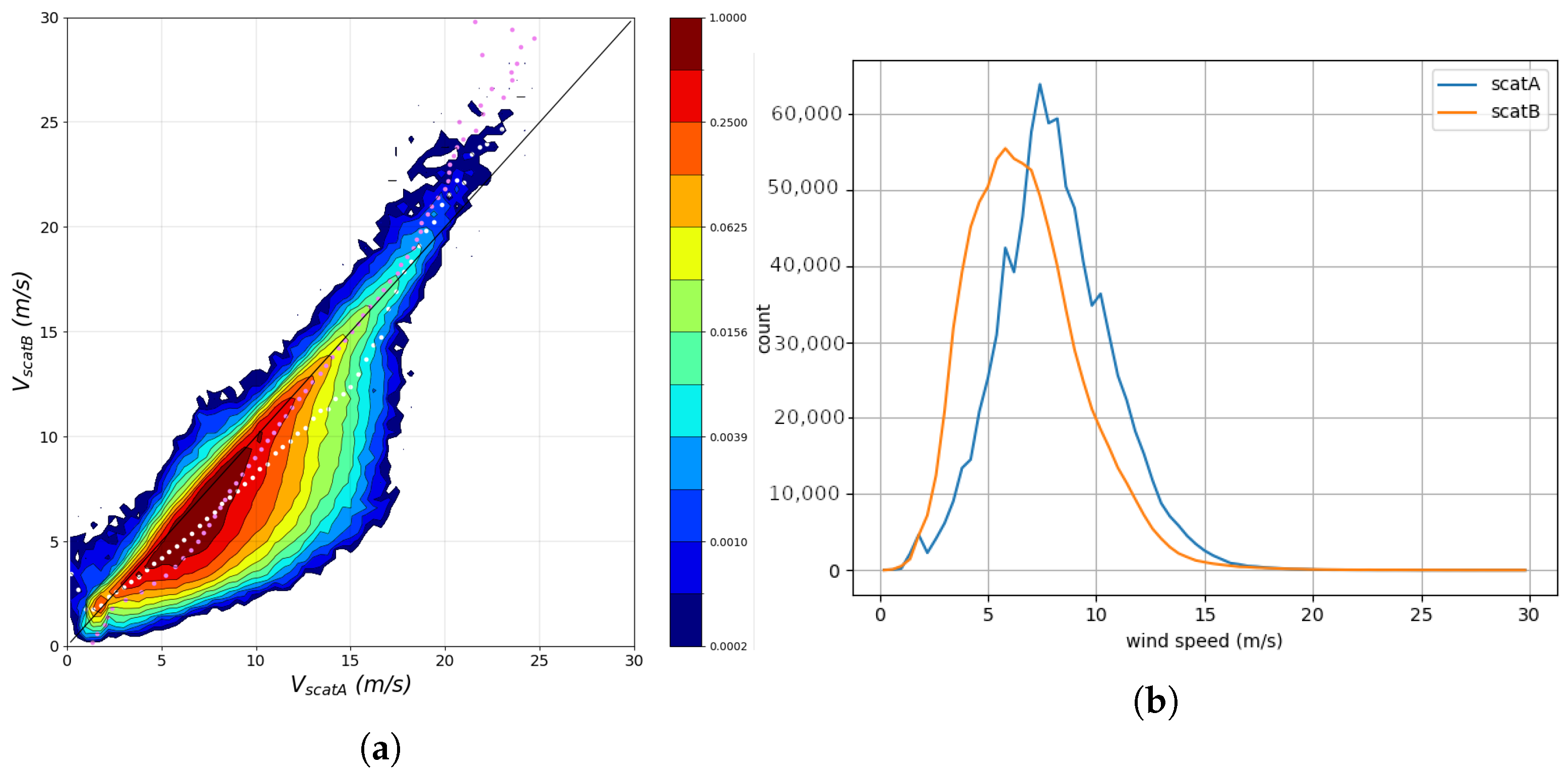
2.1. WindRAD Data
2.2. 3IMERG Precipitation Product
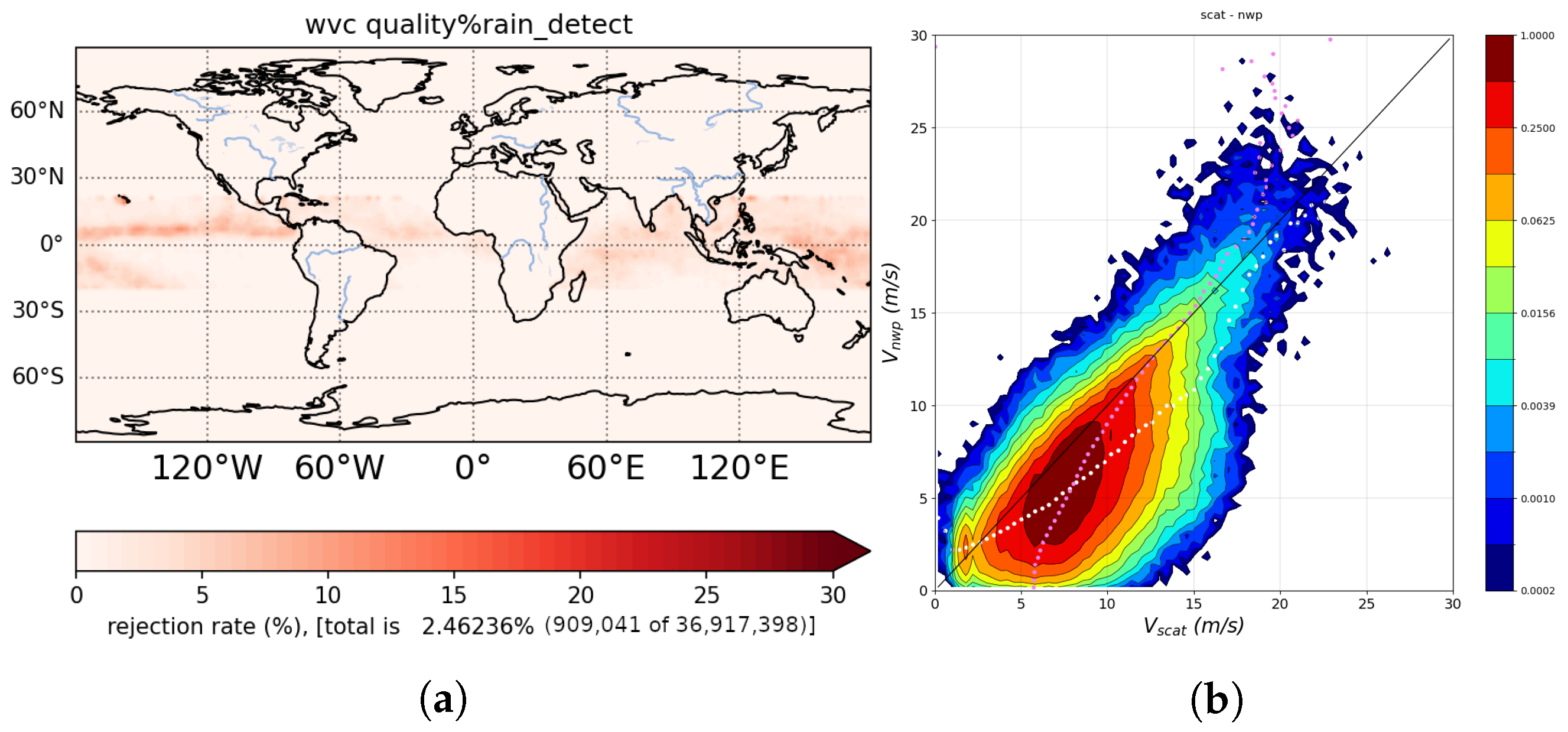
2.3. NWP Wind
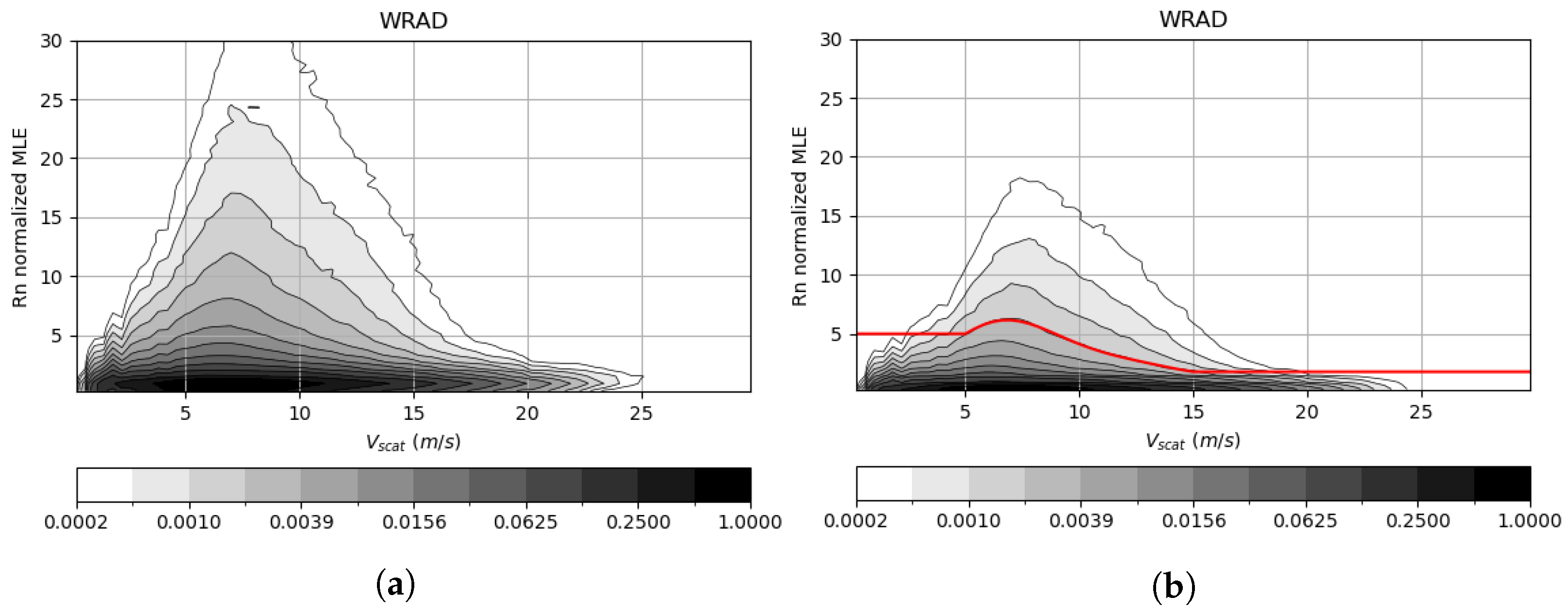
2.4. QC Algorithm
2.5. QC Algorithm and Its Adaption to
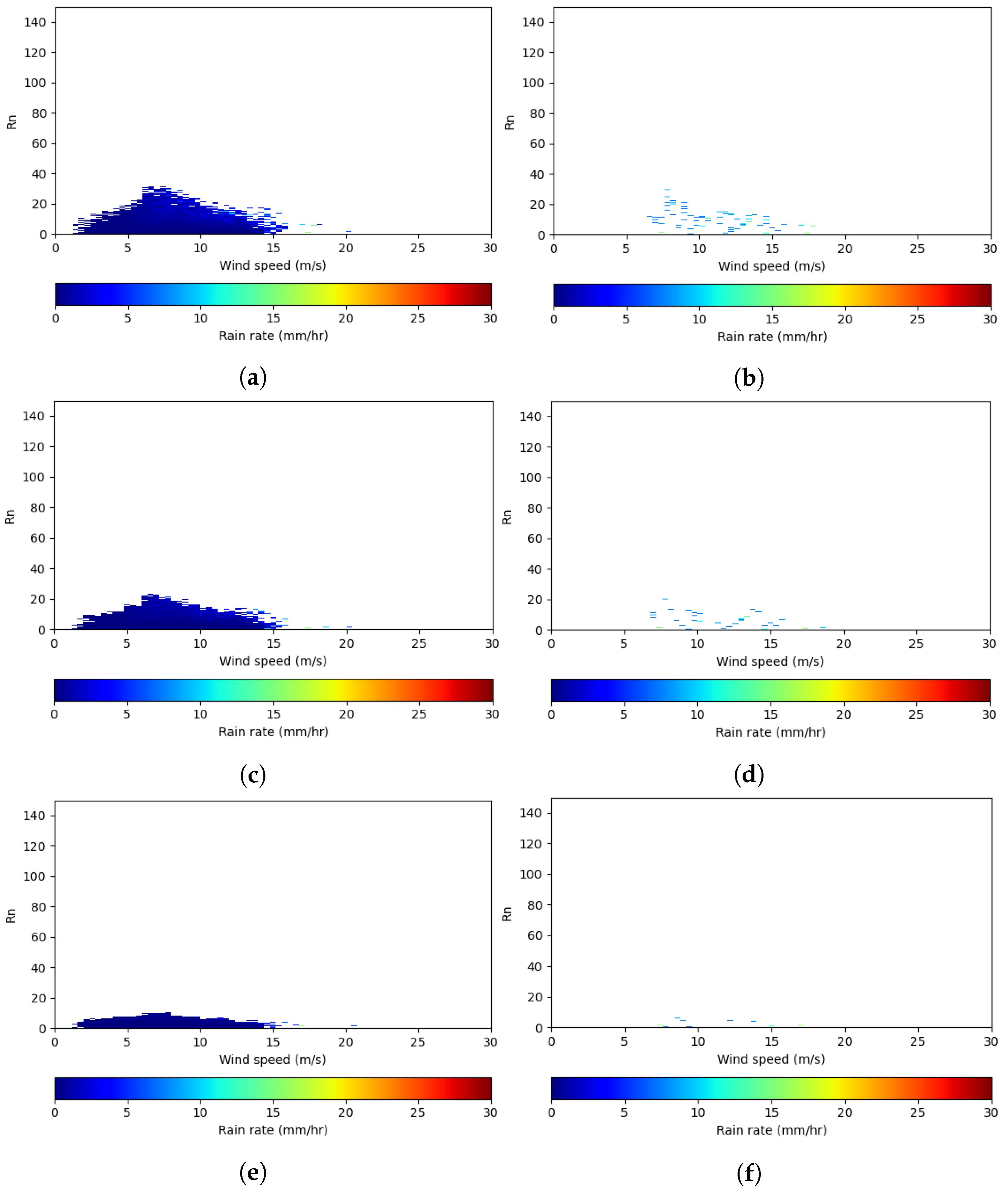
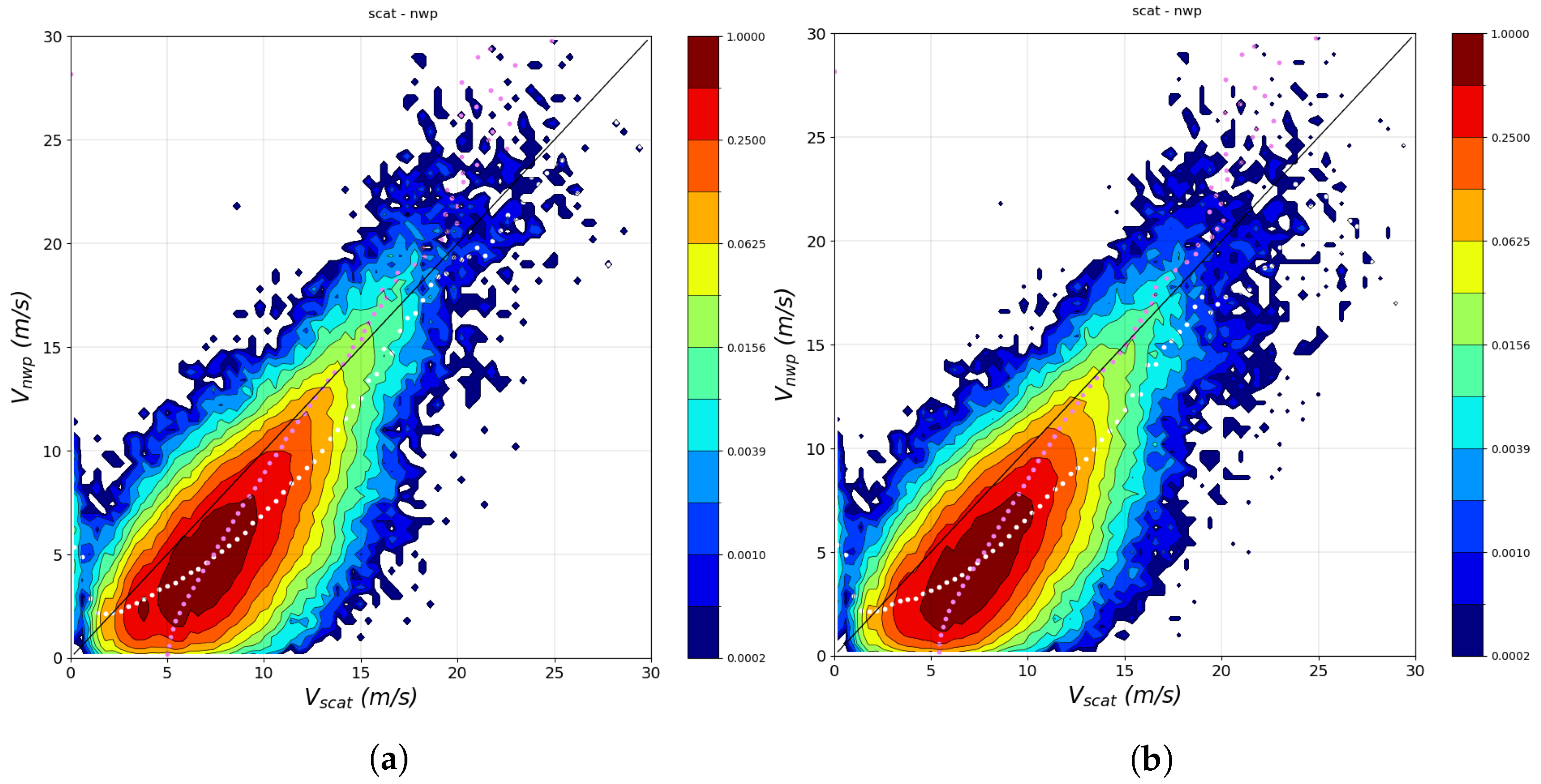
3. Ku-Band and QC Results and Discussion
3.1. QC Evaluation
3.2. QC Evaluation
4. C–Ku Combined and QC Results and Discussion
4.1. Evaluation of the Ku Contribution to in QC
4.2. QC Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ASCAT | Advanced Scatterometer |
| CDF | Cumulative Distribution Function |
| CMA | China Meteorological Administration |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| FY-3E | Fengyun-3E |
| GMF | Geophysical Model Function |
| GPM | Global Precipitation Measurement |
| HOC | Higher-Order Calibration |
| HY | Haiyang |
| KNMI | Royal Netherlands Meteorological Institute |
| MLE | Maximal Likelihood Estimation |
| NASA | National Aeronautics and Space Administration |
| NOCant | NWP Ocean Calibration (as a function of incidence angle and relative antenna angle) |
| NWP | Numerical Weather Prediction |
| OSI SAF | Ocean and Sea Ice Satellite Application Facility |
| Probability Density Function | |
| QC | Quality Control |
| SST | Sea Surface Temperature |
| SDD | Standard Deviation Difference |
| WindRAD | Wind Radar |
| WVC | Wind Vector Cell |
| 2DVAR | 2D Variational Ambiguity Removal |
| 3IMERG | Level-3 Integrated Multi-Satellite Retrievals for GPM |
References
- Jiang, X.; Lin, M.; Liu, J.; Zhang, Y.; Xie, X.; Peng, H.; Zhou, W. The HY-2 satellite and its preliminary assessment. Int. J. Digit. Earth 2012, 5, 266–281. [Google Scholar] [CrossRef]
- Gelsthorpe, R.V.; Schied, E.; Wilson, J.J.W. ASCAT—Metop’s Advanced Scatterometer; ESA Bulletin-European Space Agency: Paris, France, 2000. [Google Scholar]
- Li, Z.; Verhoef, A.; Stoffelen, A.; Shang, J.; Dou, F. First Results from the WindRAD Scatterometer on Board FY-3E: Data Analysis, Calibration and Wind Retrieval Evaluation. Remote Sens. 2023, 15, 2087. [Google Scholar] [CrossRef]
- Li, Z.; Stoffelen, A.; Verhoef, A.; Wang, Z.; Shang, J.; Yin, H. Higher-order calibration on WindRAD (Wind Radar) scatterometer winds. Atmos. Meas. Tech. 2023, 16, 4769–4783. [Google Scholar] [CrossRef]
- Chi, C.Y.; Li, F.K. A comparative study of several wind estimation algorithms for spaceborne scatterometers. IEEE Trans. Geosci. Remote Sens. 1988, 26, 115–121. [Google Scholar] [CrossRef]
- Pierson, W.J. Probabilities and statistics for backscatter estimates obtained by a scatterometer. J. Geophys. Res. 1989, 94, 9743–9759. [Google Scholar] [CrossRef]
- Portabella, M.; Stoffelen, A. Characterization of Residual Information for SeaWinds Quality Control. IEEE Trans. Geosci. Rem. Sens 2002, 40, 2747–2759. [Google Scholar] [CrossRef]
- Cornford, D.; Csató, L.; Evans, D.J.; Opper, M. Bayesian Analysis of the Scatterometer Wind Retrieval Inverse Problem: Some New Approaches. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2004, 66, 609–652. [Google Scholar] [CrossRef]
- Stoffelen, A.; Portabella, M. On Bayesian Scatterometer Wind Inversion. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1523–1533. [Google Scholar] [CrossRef]
- Isaksen, L.; Stoffelen, A. ERS scatterometer wind data impact on ECMWF’s tropical cyclone forecasts. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1885–1892. [Google Scholar] [CrossRef]
- Atlas, R.; Hoffman, R.N.; Leidner, S.M.; Sienkiewicz, J.; Yu, T.W.; Bloom, S.C.; Brin, E.; Ardizzone, J.; Terry, J.; Bungatoand, D.; et al. The Effects of Marine Winds from Scatterometer Data on Weather Analysis and Forecasting. Bull. Amer. Meteor. Soc. 2001, 82, 1965–1990. [Google Scholar] [CrossRef]
- Singh, R.; Kumar, P.; Pal, P.K. Assimilation of oceansat-2-scatterometer-derived surface winds in the weather research and forecasting model. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1015–1021. [Google Scholar] [CrossRef]
- Belmonte Rivas, M.; Stoffelen, A. Characterizing ERA-Interim and ERA5 surface wind biases using ASCAT. Ocean Sci. 2019, 15, 831–852. [Google Scholar] [CrossRef]
- Trindade, A.; Portabella, M.; Stoffelen, A.; Lin, W.; Verhoef, A. ERAstar: A High-Resolution Ocean Forcing Product. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1337–1347. [Google Scholar] [CrossRef]
- Van de Hulst, H.C. Light Scattering by Small Particles; John Wiley and Sons: New York, NY, USA, 1958. [Google Scholar]
- Portabella, M.; Stoffelen, A. Rain Detection and Quality Control of SeaWinds. J. Atmos. Ocean. Technol. 2001, 18, 1171–1183. [Google Scholar] [CrossRef]
- Xu, X.; Stoffelen, A. Improved Rain Screening for Ku-Band Wind Scatterometry. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2494–2503. [Google Scholar] [CrossRef]
- Zhao, K.; Stoffelen, A.; Verspeek, J.; Verhoef, A.; Zhao, C. Bayesian Algorithm for Rain Detection in Ku-Band Scatterometer Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4203416. [Google Scholar] [CrossRef]
- Portabella, M.; Stoffelen, A.; Lin, W.; Turiel, A.; Verhoef, A.; Verspeek, J.; Ballabrera-Poy, J. Rain effects on ASCAT-retrieved winds: Toward an improved quality control. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2495–2506. [Google Scholar] [CrossRef]
- Portabella, M.; Stoffelen, A.; Verhoef, A.; Verspeek, J. A new method for improving scatterometer wind quality control. IEEE Geosci. Remote Sens. Lett. 2012, 9, 579–583. [Google Scholar] [CrossRef]
- Verhoef, A.; Stoffelen, A. ASCAT Wind Validation Report; Royal Netherlands Meteorological Institute: de Bilt, The Netherlands, 2018. [Google Scholar]
- Priftis, G.; Lang, T.J.; Chronis, T. Combining ASCAT and NEXRAD Retrieval Analysis to Explore Wind Features of Mesoscale Oceanic Systems. J. Geophys. Res. Atmos. 2018, 123, 10341–10360. [Google Scholar] [CrossRef]
- Lin, W.; Portabella, M.; Turiel, A.; Stoffelen, A.; Verhoef, A. An improved singularity analysis for ASCAT wind quality control: Application to low winds. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3890–3898. [Google Scholar] [CrossRef]
- Bliven, L.F.; Giovanangeli, J.P. An experimental study of microwave scattering from rain- and wind-roughened seas. Int. J. Remote Sens. 1993, 14, 855–869. [Google Scholar] [CrossRef]
- Craeye, C.; Schlüssel, P. Rainfall on the sea: Surface Renewals and Damping. Bound.-Layer Meteorol. 1998, 89, 349–355. [Google Scholar] [CrossRef]
- Tournadre, J. Impact of rain cell on scatterometer data: 1. Theory and modeling. J. Geophys. Res. 2003, 108, 3225. [Google Scholar] [CrossRef]
- Stoffelen, A.; Anderson, D. Scatterometer data interpretation: Measurement space and inversion. J. Atmos. Ocean. Technol. 1997, 14, 1298–1313. [Google Scholar] [CrossRef]
- Figa, J.; Stoffelen, A. On the assimilation of Ku-band scatterometer winds for weather analysis and forecasting. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1893–1920. [Google Scholar] [CrossRef]
- Li, Z.; Verhoef, A.; Stoffelen, A.; Verhoef, A.; Verhoef, A. CWDP L2A Processor Specification and User Manual; Technical Report; KNMI: de Bilt, The Netherlands, 2019. [Google Scholar]
- Xu, X.; Stoffelen, A.; Lin, W.; Dong, X. Rain False-Alarm-Rate Reduction for CSCAT. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1000805. [Google Scholar] [CrossRef]
- Bolvin, D.T.; Joyce, R.; Nelkin, E.J.; Tan, J.; Braithwaite, D.; Hsu, K.; Kelley, O.A.; Nguyen, P.; Sorooshian, S.; Watters, D.C.; et al. Algorithm Theoretical Basis Document (ATBD) NASA Global Precipitation Measurement (GPM) Integrated Multi-satellitE Retrievals for GPM (IMERG) Version 07.; Technical Report; NASA: Greenbelt, MD, USA, 2023. [Google Scholar]
- De Kloe, J.; Stoffelen, A.; Verhoef, A. Improved Use of Scatterometer Measurements by Using Stress-Equivalent Reference Winds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2340–2347. [Google Scholar] [CrossRef]
- Vogelzang, J.; Stoffelen, A. On the Accuracy and Consistency of Quintuple Collocation Analysis of In Situ, Scatterometer, and NWP Winds. Remote Sens. 2022, 14, 4552. [Google Scholar] [CrossRef]
- Verhoef, A. Algorithm Theoretical Basis Document for the Scatterometer Wind Products; Royal Netherlands Meteorological Institute: de Bilt, The Netherlands, 2024. [Google Scholar]
- Vogelzang, J. Two-Dimensional Variational Ambiguity Removal (2DVAR); Technical Report; KNMI: de Bilt, The Netherlands, 2013. [Google Scholar]
- Verhoef, A.; Stoffelen, A. Advances in Ku-Band Scatterometer Quality Control; Technical Report; Royal Netherlands Meteorological Institute: de Bilt, The Netherlands, 2021. [Google Scholar]








| QC Method | Speed Bias (m/s) | SDD of u (m/s) | SDD of v (m/s) | |
|---|---|---|---|---|
| Rejected winds | 2.312 | 2.34 | 2.38 | |
| 2.491 | 2.39 | 2.44 | ||
| Accepted Winds | 0.113 | 1.15 | 1.19 | |
| 0.096 | 1.13 | 1.17 |
| QC Method | Speed Bias (m/s) | SDD of u (m/s) | SDD of v (m/s) | |
|---|---|---|---|---|
| Rejected winds | 1.469 | 2.99 | 2.42 | |
| 1.466 | 3.09 | 2.53 | ||
| Accepted Winds | 0.367 | 1.34 | 1.29 | |
| 0.362 | 1.32 | 1.28 |
| Compared Against | Speed Bias (m/s) | SDD of u (m/s) | SDD of v (m/s) | |
|---|---|---|---|---|
| Rejected winds | NWP winds | 2.301 | 2.24 | 2.35 |
| C-band (WindRAD) | 1.375 | 2.28 | 2.40 | |
| Accepted Winds | NWP winds | 0.120 | 1.14 | 1.22 |
| C-band (WindRAD) | 0.359 | 1.27 | 1.22 |
| QC Method | Speed Bias (m/s) | SDD of u (m/s) | SDD of v (m/s) | |
|---|---|---|---|---|
| Rejected winds | 2.301 | 2.24 | 2.35 | |
| 2.690 | 2.42 | 2.50 | ||
| Accepted Winds | 0.120 | 1.14 | 1.22 | |
| 0.103 | 1.12 | 1.20 |
| QC Method | Speed Bias (m/s) | SDD of u (m/s) | SDD of v (m/s) | |
|---|---|---|---|---|
| Rejected winds | 1.375 | 2.82 | 2.40 | |
| 1.293 | 2.97 | 2.60 | ||
| Accepted Winds | 0.359 | 1.27 | 1.22 | |
| 0.355 | 1.25 | 1.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Verhoef, A.; Stoffelen, A. WindRAD Scatterometer Quality Control in Rain. Remote Sens. 2025, 17, 560. https://doi.org/10.3390/rs17030560
Li Z, Verhoef A, Stoffelen A. WindRAD Scatterometer Quality Control in Rain. Remote Sensing. 2025; 17(3):560. https://doi.org/10.3390/rs17030560
Chicago/Turabian StyleLi, Zhen, Anton Verhoef, and Ad Stoffelen. 2025. "WindRAD Scatterometer Quality Control in Rain" Remote Sensing 17, no. 3: 560. https://doi.org/10.3390/rs17030560
APA StyleLi, Z., Verhoef, A., & Stoffelen, A. (2025). WindRAD Scatterometer Quality Control in Rain. Remote Sensing, 17(3), 560. https://doi.org/10.3390/rs17030560






