A Comparative Study of Downscaling Methods for Groundwater Based on GRACE Data Using RFR and GWR Models in Jiangsu Province, China
Abstract
1. Introduction
2. Study Area and Datasets
2.1. Study Area
2.2. Research Framework
2.3. Data Source
2.3.1. GRACE Mascon Products
2.3.2. GLDAS Model Products
2.3.3. MODIS Dataset
2.3.4. Temperature and Precipitation Dataset
3. Methods
3.1. Downscaling Method
3.2. Feature Selection
3.3. Random Forest Regression
3.4. Geographically Weighted Regression
3.5. Model Accuracy Evaluation Metrics
4. Results
4.1. Multicollinearity Analysis
4.2. Contribution Analysis of Feature Dataset
4.3. Analysis of Downscaling Results
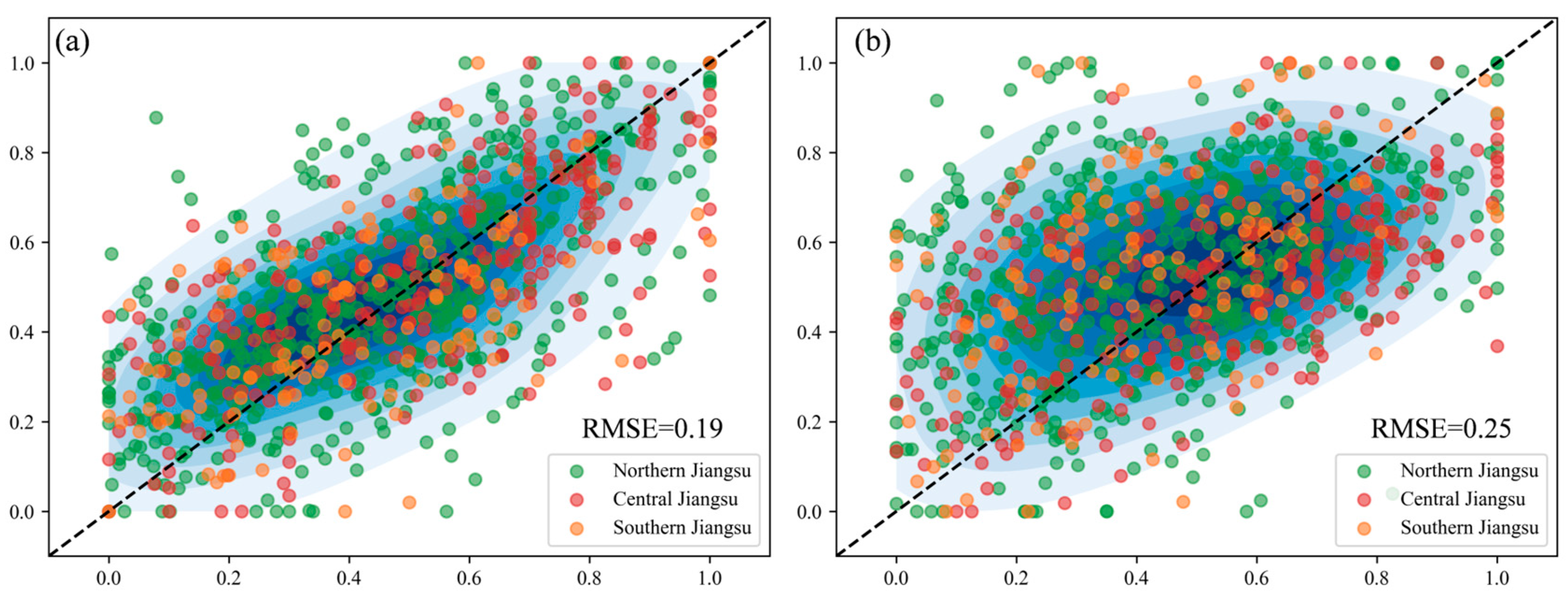
4.3.1. Model Accuracy Validation
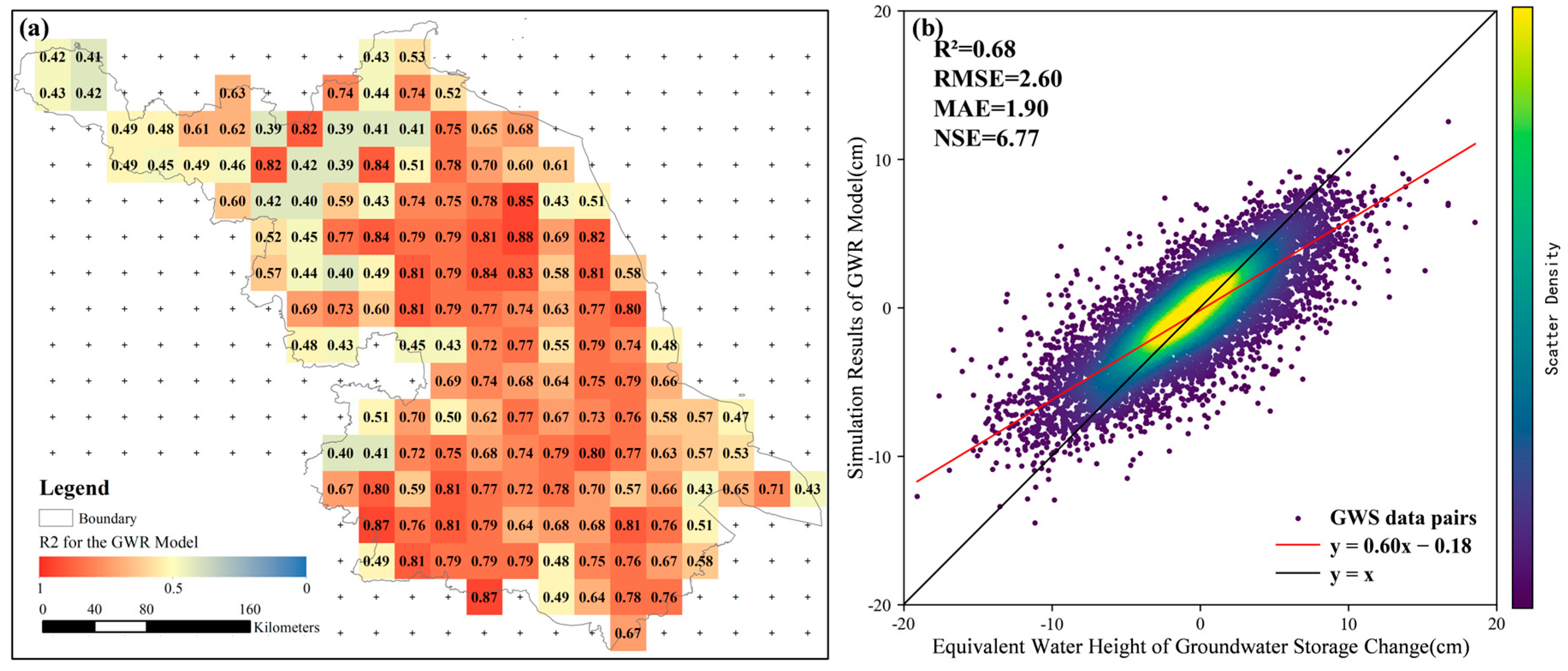
- GWR Model Accuracy Validation
- 2.
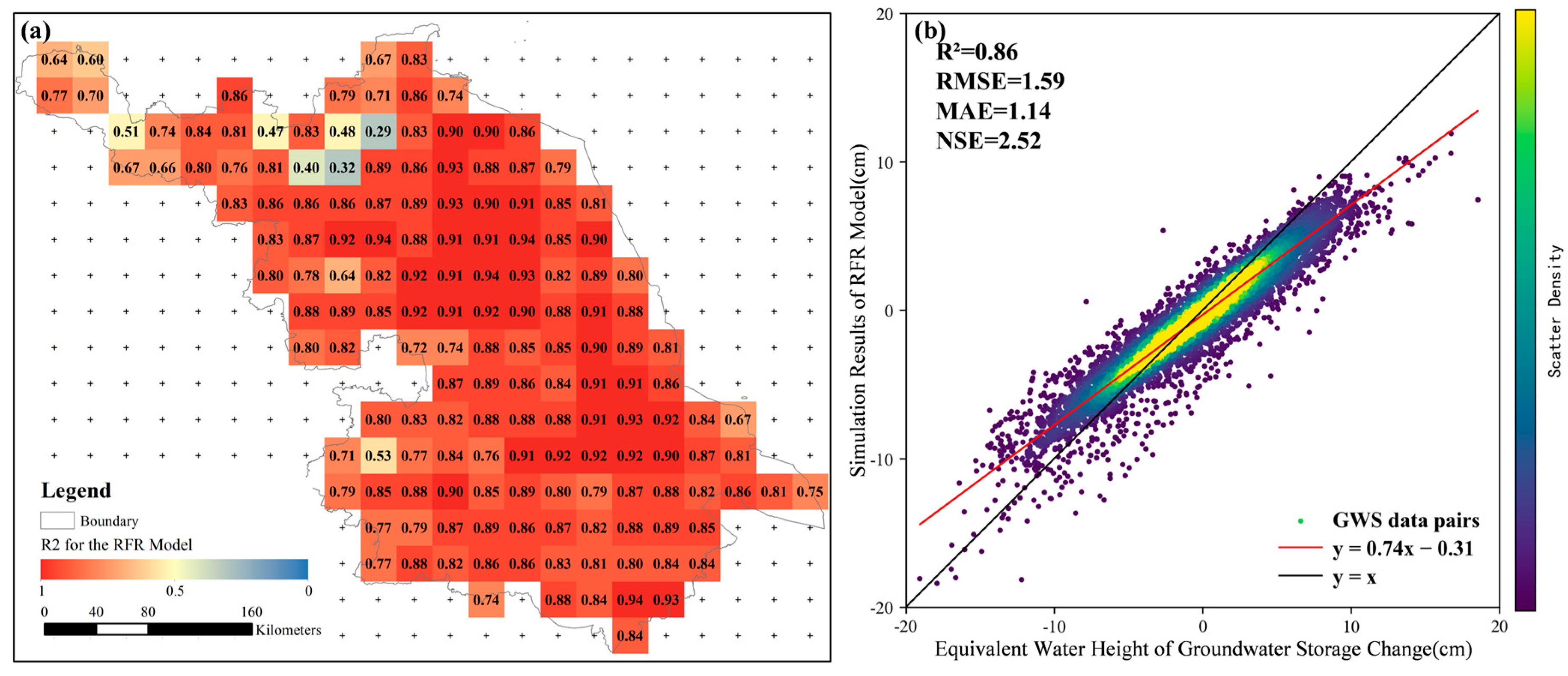
- RFR Model Accuracy Validation
- 3.
- Comparison of RFR and GWR Models
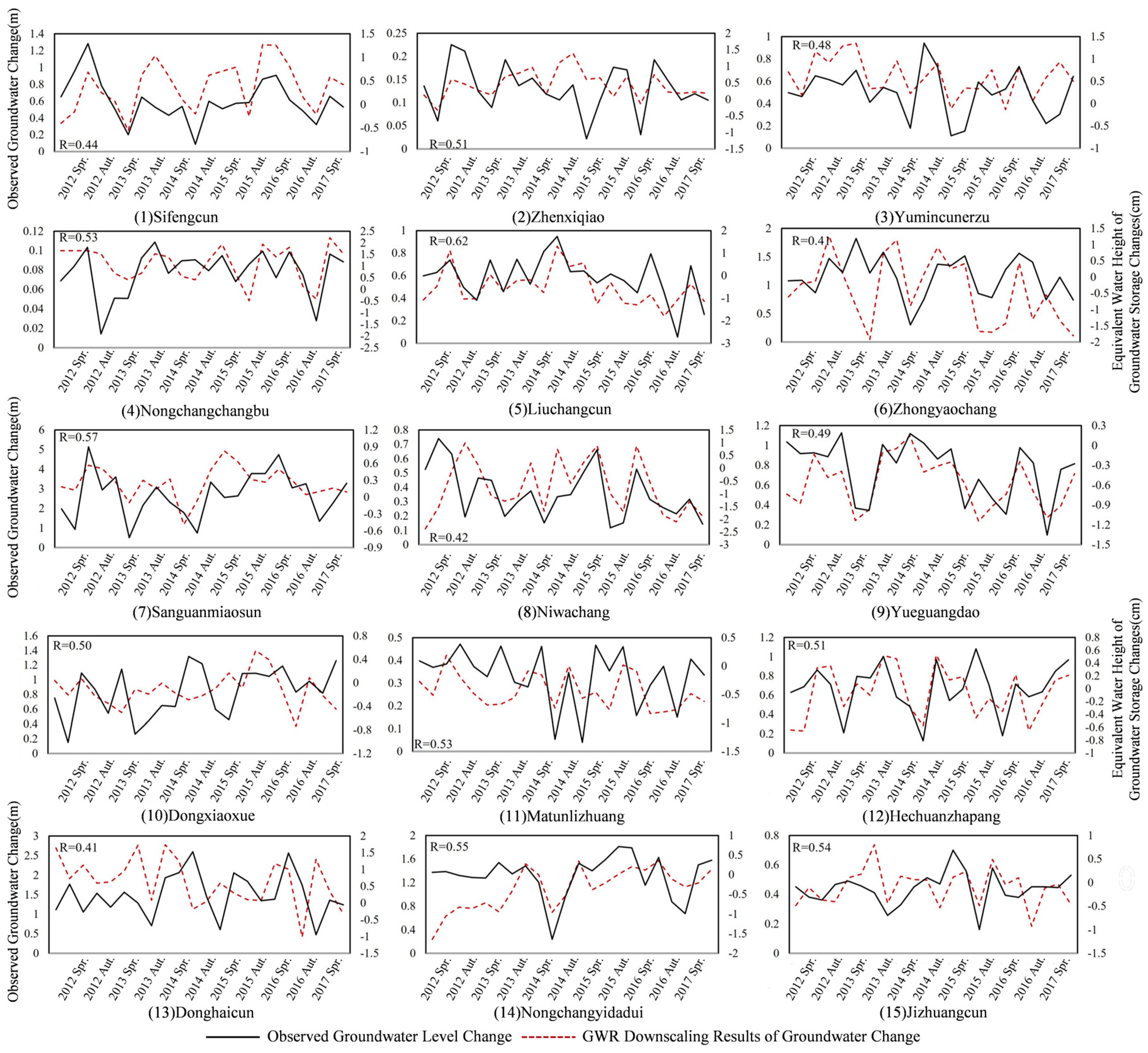
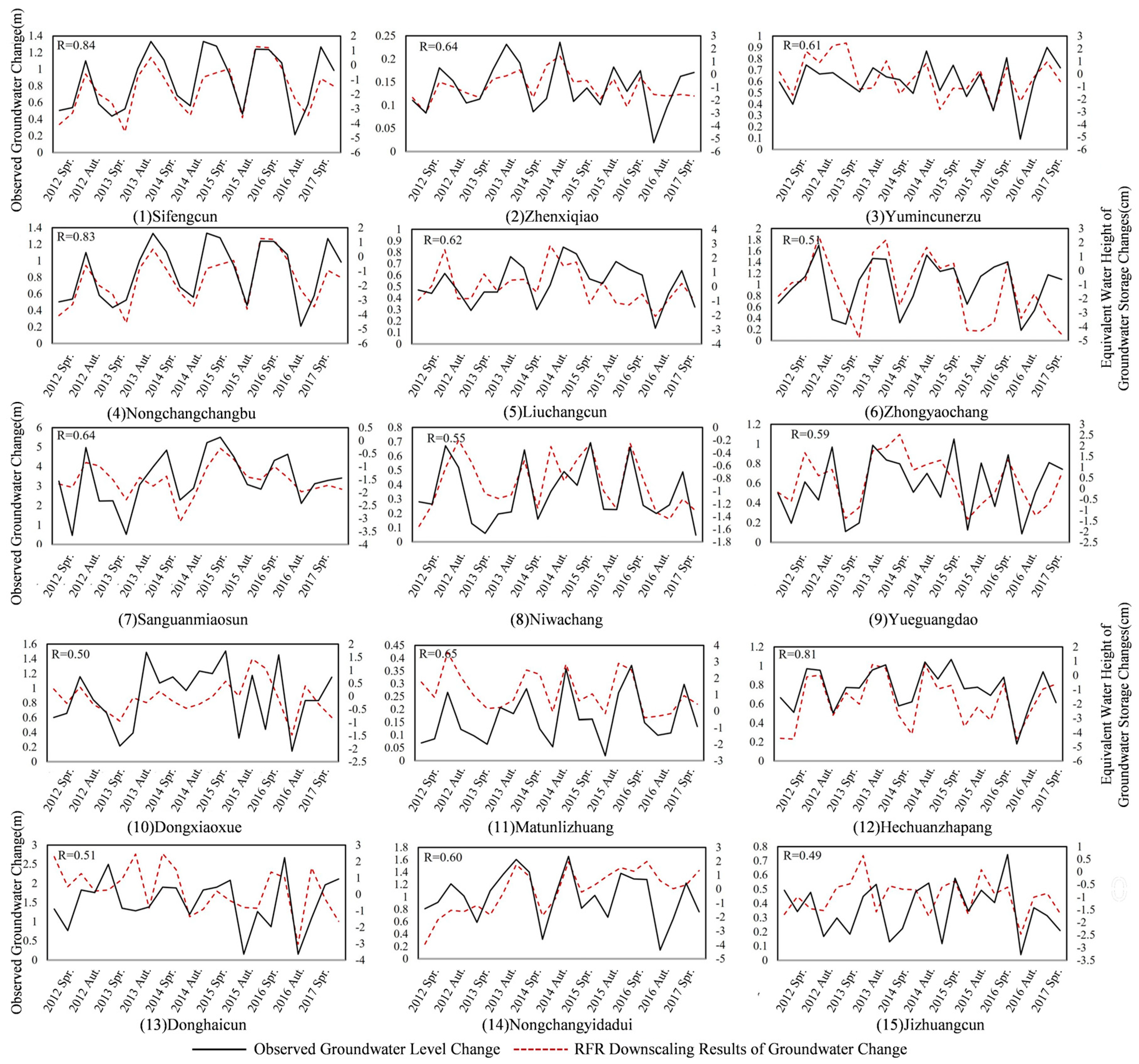
4.3.2. Downscaling Accuracy Validation
- Downscaling validation based on the GWR model
- 2.
- Downscaling validation based on the RFR model
- 3.
- Comparison of RFR and GWR models in downscaling
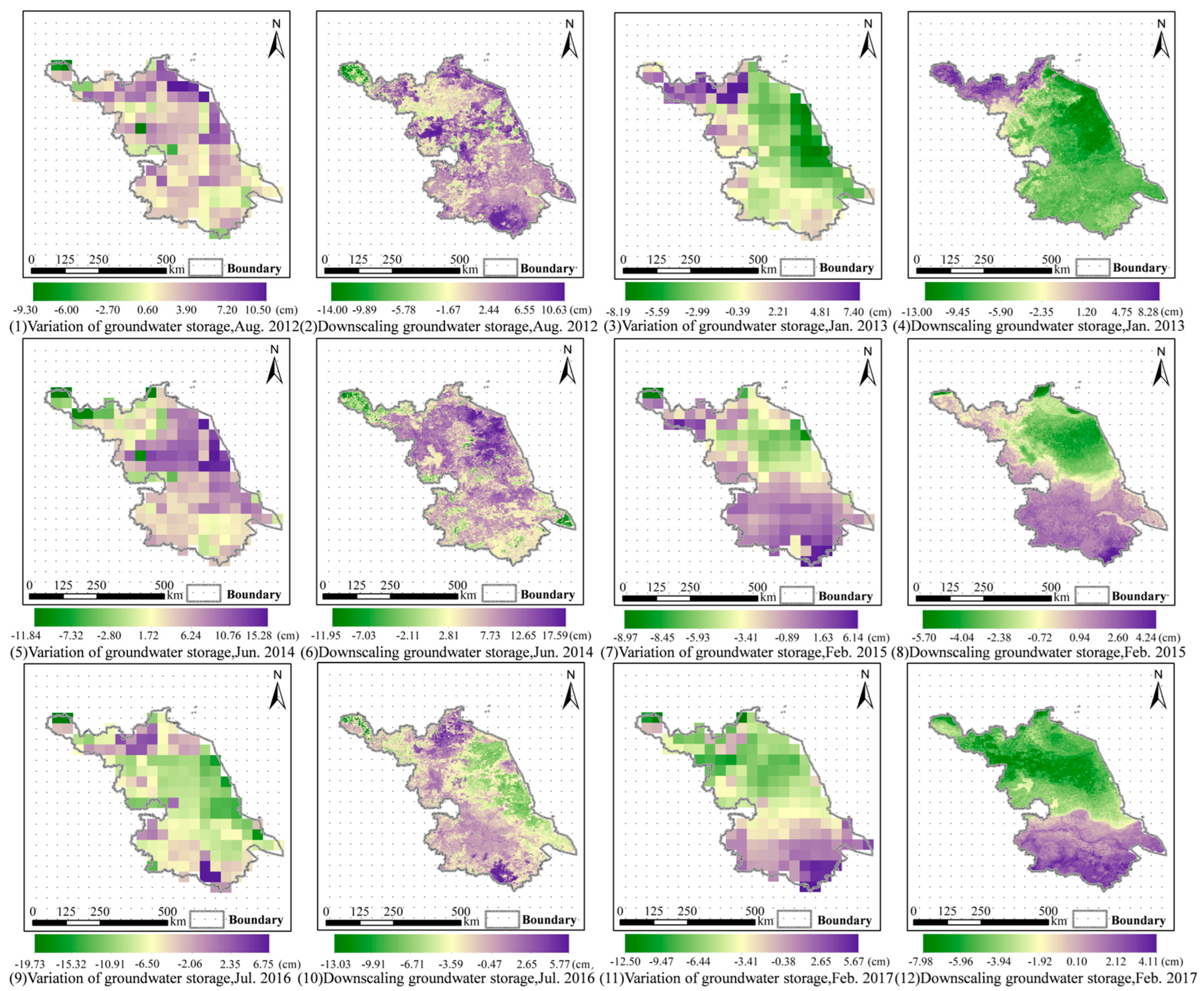
4.4. Spatial Distribution of Groundwater in Jiangsu Province
5. Discussion
5.1. Comparison of GWR and RFR in Downscaling Modeling
5.2. Spatial–Temporal Characteristics of Groundwater Storage of Jiangsu Province
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cuthbert, M.O.; Gleeson, T.; Moosdorf, N.; Befus, K.M.; Schneider, A.; Hartmann, J.; Lehner, B. Global Patterns and Dynamics of Climate–Groundwater Interactions. Nat. Clim. Change 2019, 9, 137–141. [Google Scholar] [CrossRef]
- Famiglietti, J.S. The Global Groundwater Crisis. Nat. Clim. Change 2014, 4, 945–948. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J. Sustainable Utilization of China’s Water Resources. Bull. Chin. Acad. Sci. 2012, 27, 352–358. [Google Scholar] [CrossRef]
- de Graaf, I.E.M.; Gleeson, T.; Rens van Beek, L.P.H.; Sutanudjaja, E.H.; Bierkens, M.F.P. Environmental Flow Limits to Global Groundwater Pumping. Nature 2019, 574, 90–94. [Google Scholar] [CrossRef]
- Wada, Y.; van Beek, L.P.H.; van Kempen, C.M.; Reckman, J.W.T.M.; Vasak, S.; Bierkens, M.F.P. Global Depletion of Groundwater Resources. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Jasechko, S.; Perrone, D. Global Groundwater Wells at Risk of Running Dry. Science 2021, 372, 418–421. [Google Scholar] [CrossRef]
- Chen, Z.; Zang, X.; Ran, J.; Hu, B.; Zhou, B. Terrestrial Water Storage Changes in Pearl River Region Derived from the Latest Release Temporal Gravity Field Models. J. Geod. Geodyn. 2020, 40, 305–310. [Google Scholar] [CrossRef]
- Guo, F.; Sun, Z.; Ren, F.; Wen, Y. Analysis of global water storage variation based on GRACE time-variable gravity during 2003–2013. Prog. Geophys. 2019, 34, 1298–1302. [Google Scholar] [CrossRef]
- Sun, P.; Guo, C.; Wei, D. Estimating Terrestrial Water Storage Variations in Chile with the Effects of Earthquakes Deducted. Hydrol. Sci. J. 2023, 68, 1663–1679. [Google Scholar] [CrossRef]
- Ran, Q.; Pan, Y.; Wang, Y.; Chen, L.; Xu, H. Estimation of annual groundwater exploitation in Haihe River Basin by use of GRACE satellite data. Adv. Sci. Technol. Water Res. 2013, 33. 42–46+67. [Google Scholar] [CrossRef]
- Tu, M.; Liu, Z.; He, C.; Ren, Q.; Lu, W. Research progress of groundwater storage changes monitoring in China based on GRACE satellite data. Adv. Earth Sci. 2020, 35, 643–656. [Google Scholar] [CrossRef]
- Sarkar, T.; Karunakalage, A.; Kannaujiya, S.; Chaganti, C. Quantification of Groundwater Storage Variation in Himalayan & Peninsular River Basins Correlating with Land Deformation Effects Observed at Different Indian Cities. Contrib. Geophys. Geod. 2022, 52, 1–52. [Google Scholar] [CrossRef]
- Jasechko, S.; Seybold, H.; Perrone, D.; Fan, Y.; Shamsudduha, M.; Taylor, R.G.; Fallatah, O.; Kirchner, J.W. Rapid Groundwater Decline and Some Cases of Recovery in Aquifers Globally. Nature 2024, 625, 715–721. [Google Scholar] [CrossRef]
- Rana, S.K.; Chamoli, A. GRACE-Derived Groundwater Variability and Its Resilience in North India: Impact of Climatic and Socioeconomic Factors. Hydrol. Sci. J. 2024, 69, 2159–2171. [Google Scholar] [CrossRef]
- Yoshe, A.K. Water Availability Identification from GRACE Dataset and GLDAS Hydrological Model over Data-Scarce River Basins of Ethiopia. Hydrol. Sci. J. 2024, 69, 721–745. [Google Scholar] [CrossRef]
- Cho, Y. Analysis of Terrestrial Water Storage Variations in South Korea Using GRACE Satellite and GLDAS Data in Google Earth Engine. Hydrol. Sci. J. 2024, 69, 1032–1045. [Google Scholar] [CrossRef]
- Su, H.; Zhang, G.; Zhang, D.; Yin, W.; Meng, X. Improving the spatial resolution of GRACE satellites based on high-resolution hydrological simulations. Bull. Surv. Mapp. 2022, 8, 41–47. [Google Scholar] [CrossRef]
- Atkinson, P.M. Downscaling in Remote Sensing. Int. J. Appl. Earth Obs. Geoinf. 2013, 22, 106–114. [Google Scholar] [CrossRef]
- Shokri, A.; Walker, J.P.; van Dijk, A.I.J.M.; Pauwels, V.R.N. On the Use of Adaptive Ensemble Kalman Filtering to Mitigate Error Misspecifications in GRACE Data Assimilation. Water Resour. Res. 2019, 55, 7622–7637. [Google Scholar] [CrossRef]
- Zaitchik, B.F.; Rodell, M.; Reichle, R.H. Assimilation of GRACE Terrestrial Water Storage Data into a Land Surface Model: Results for the Mississippi River Basin. J. Hydrometeorol. 2008, 9, 535–548. [Google Scholar] [CrossRef]
- Shokri, A.; Walker, J.P.; van Dijk, A.I.J.M.; Pauwels, V.R.N. Performance of Different Ensemble Kalman Filter Structures to Assimilate GRACE Terrestrial Water Storage Estimates Into a High-Resolution Hydrological Model: A Synthetic Study. Water Resour. Res. 2018, 54, 8931–8951. [Google Scholar] [CrossRef]
- Zhang, M.; Hu, L. Research Progress on Statistical Downscaling Method. South-North Water Transf. Water Sci. Technol. 2013, 11, 118–122. [Google Scholar]
- Tourian, M.J.; Saemian, P.; Ferreira, V.G.; Sneeuw, N.; Frappart, F.; Papa, F. A Copula-Supported Bayesian Framework for Spatial Downscaling of GRACE-Derived Terrestrial Water Storage Flux. Remote Sens. Environ. 2023, 295, 113685. [Google Scholar] [CrossRef]
- Yazdian, H.; Salmani-Dehaghi, N.; Alijanian, M. A Spatially Promoted SVM Model for GRACE Downscaling: Using Ground and Satellite-Based Datasets. J. Hydrol. 2023, 626, 130214. [Google Scholar] [CrossRef]
- Sahour, H.; Sultan, M.; Vazifedan, M.; Abdelmohsen, K.; Karki, S.; Yellich, J.; Gebremichael, E.; Alshehri, F.; Elbayoumi, T. Statistical Applications to Downscale GRACE-Derived Terrestrial Water Storage Data and to Fill Temporal Gaps. Remote Sens. 2020, 12, 533. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, K.; Wang, M. Downscaling Groundwater Storage Data in China to a 1-Km Resolution Using Machine Learning Methods. Remote Sens. 2021, 13, 523. [Google Scholar] [CrossRef]
- Kalu, I.; Ndehedehe, C.E.; Ferreira, V.G.; Janardhanan, S.; Currell, M.; Crosbie, R.S.; Kennard, M.J. Remote Sensing Estimation of Shallow and Deep Aquifer Response to Precipitation-Based Recharge Through Downscaling. Water Resour. Res. 2024, 60, e2024WR037360. [Google Scholar] [CrossRef]
- Ali, S.; Khorrami, B.; Jehanzaib, M.; Tariq, A.; Ajmal, M.; Arshad, A.; Shafeeque, M.; Dilawar, A.; Basit, I.; Zhang, L.; et al. Spatial Downscaling of GRACE Data Based on XGBoost Model for Improved Understanding of Hydrological Droughts in the Indus Basin Irrigation System (IBIS). Remote Sens. 2023, 15, 873. [Google Scholar] [CrossRef]
- Kalu, I.; Ndehedehe, C.E.; Ferreira, V.G.; Kennard, M.J. Machine Learning Assessment of Hydrological Model Performance under Localized Water Storage Changes through Downscaling. J. Hydrol. 2024, 628, 130597. [Google Scholar] [CrossRef]
- Wang, Y.; Li, C.; Cui, Y.; Cui, Y.; Xu, Y.; Hora, T.; Zaveri, E.; Rodella, A.-S.; Bai, L.; Long, D. Spatial Downscaling of GRACE-Derived Groundwater Storage Changes across Diverse Climates and Human Interventions with Random Forests. J. Hydrol. 2024, 640, 131708. [Google Scholar] [CrossRef]
- Huang, S.; Duan, G.; He, J. Groundwater storage downscaling in the Hai River Basin based on the GWR model. Hydrop. Energy Sci. 2023, 41, 39–42+30. [Google Scholar] [CrossRef]
- Chen, Z.; Zheng, W.; Yin, W.; Li, X.; Zhang, G.; Zhang, J. Improving the Spatial Resolution of GRACE-Derived Terrestrial Water Storage Changes in Small Areas Using the Machine Learning Spatial Downscaling Method. Remote Sens. 2021, 13, 4760. [Google Scholar] [CrossRef]
- Janowicz, K.; Gao, S.; McKenzie, G.; Hu, Y.; Bhaduri, B. GeoAI: Spatially Explicit Artificial Intelligence Techniques for Geographic Knowledge Discovery and Beyond. Int. J. Geogr. Inf. Sci. 2020, 34, 625–636. [Google Scholar] [CrossRef]
- Jiangsu Provincial Water Resources Department. Jiangsu Province Water Resources Bulletin-2023; China Water & Power Press: Beijing, China, 2024. [Google Scholar]
- Wu, A. Annual Report on Groundwater Levels Monitoring of Geological Environment in China-2012; China Land Press: Beijing, China, 2013. [Google Scholar]
- Wu, A. Annual Report on Groundwater Levels Monitoring of Geological Environment in China-2013; China Land Press: Beijing, China, 2014. [Google Scholar]
- Wu, A. Annual Report on Groundwater Levels Monitoring of Geological Environment in China-2014; China Land Press: Beijing, China, 2016. [Google Scholar]
- Wu, A. Annual Report on Groundwater Levels Monitoring of Geological Environment in China-2015; China Land Press: Beijing, China, 2017. [Google Scholar]
- Peng, S. 1-Km Monthly Mean Temperature Dataset for China (1901–2021); National Tibetan Plateau/Third Pole Environment Data Center (TPDC): Beijing, China, 2019. [Google Scholar] [CrossRef]
- Qu, L.; Zhu, Q.; Zhu, C.; Zhang, J. Monthly Precipitation Data Set with 1 Km Resolution in China from 1960 to 2020. Sci. Data Bank 2022. [Google Scholar] [CrossRef]
- Peng, S.; Ding, Y.; Liu, W.; Li, Z. 1 Km Monthly Temperature and Precipitation Dataset for China from 1901 to 2017. Earth Syst. Sci. Data 2019, 11, 1931–1946. [Google Scholar] [CrossRef]
- Jin, S.; Feng, G. Large-Scale Variations of Global Groundwater from Satellite Gravimetry and Hydrological Models, 2002–2012. Glob. Planet. Change 2013, 106, 20–30. [Google Scholar] [CrossRef]
- Long, D.; Yang, W.; Sun, Z.; Cui, Y.; Zhang, C.; Cui, Y. GRACE satellite-based estimation of groundwater storage changes and water balance analysis for the Haihe River Basin. J. Hydraul. Eng. 2023, 54, 255–267. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, S.; Charlton, M.E. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Salmerón, R.; García, C.B.; García, J. Variance Inflation Factor and Condition Number in Multiple Linear Regression. J. Stat. Comput. Simul. 2018, 88, 2365–2384. [Google Scholar] [CrossRef]
- Foody, G.M. Geographical Weighting as a Further Refinement to Regression Modelling: An Example Focused on the NDVI–Rainfall Relationship. Remote Sens. Environ. 2003, 88, 283–293. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, Y.; Gu, C.; Wei, B. Land cover classification based on random forest and feature optimism in the Southeast Qinghai-Tibet Plateau. Sci. Geogr. Sin. 2023, 43, 388–397. [Google Scholar] [CrossRef]
- Li, M. Downscaling of GRACE-Derived Groundwater Storage Changes Based on Hierarchical Clustering and Non-Linear Regression Model. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2021. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.; Woo, W. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. In Proceedings of the Advances in Neural Information Processing Systems 28 (NIPS 2015), Montreal, QC, Canada, 7–12 December 2015; Cortes, C., Lawrence, N.D., Lee, D.D., Sugiyama, M., Garnett, R., Eds.; Neural Information Processing Systems (nips): La Jolla, CA, USA, 2015; Volume 28. [Google Scholar]
- Sun, L.; Guo, J.; Zhu, Y.; Chen, S. Feature Selection Using Stacking Integration and Partial Exploration Bayesian Optimization. J. Shanxi Univ. (Nat. Sci.) 2024, 47, 93–102. [Google Scholar] [CrossRef]
- Ali, S.; Ran, J.; Luan, Y.; Khorrami, B.; Yun, X.; Tangdamrongsub, N. The GWR Model-Based Regional Downscaling of GRACE/GRACE-FO Derived Groundwater Storage to Investigate Local-Scale Variations in the North China Plain. Sci. Total Environ. 2024, 908, 168239. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Wu, C.; Wang, L.; Gonsamo, A.; Shen, Y.; Niu, Z. A New Satellite-Based Monthly Precipitation Downscaling Algorithm with Non-Stationary Relationship between Precipitation and Land Surface Characteristics. Remote Sens. Environ. 2015, 162, 119–140. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, X.; Tian, Y.; Lin, J.; Wang, D. Analysis of temporal and spatial variation characteristics and driving factors of vegetation CUE in typical basin entering the sea in Beibu Gulf. Bull. Surv. Mapp. 2023, 8, 1–6. [Google Scholar] [CrossRef]
- Bradley, P.E.; Keller, S.; Weinmann, M. Unsupervised Feature Selection Based on Ultrametricity and Sparse Training Data: A Case Study for the Classification of High-Dimensional Hyperspectral Data. Remote Sens. 2018, 10, 1564. [Google Scholar] [CrossRef]
- Yang, X.; Li, D. Precipitation Variation Characteristics and Arid Climate Division in China. J. Arid Meteorol. 2008, 26, 17–24. [Google Scholar]
- Cheng, C.; Wen, C.; Hai-xia, Z. Spatial Matching Pattern between Industrial Space and Ecological Protection in Areas along the Yangtze River in Jiangsu Province. Geogr. Res. 2011, 30, 269–277. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, X.; Wang, L. Spatial Distribution and Source Analysis of Heavy Metals in Soils Influenced by Industrial Enterprise Distribution: Case Study in Jiangsu Province. Sci. Total Environ. 2020, 710, 134953. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhang, X.; Wu, Q.; Li, H. The Coordination About Quality and Scale of Urbanization: Case Study of Jiangsu Province. Sci. Geogr. Sin. 2013, 33, 16–22. [Google Scholar] [CrossRef]
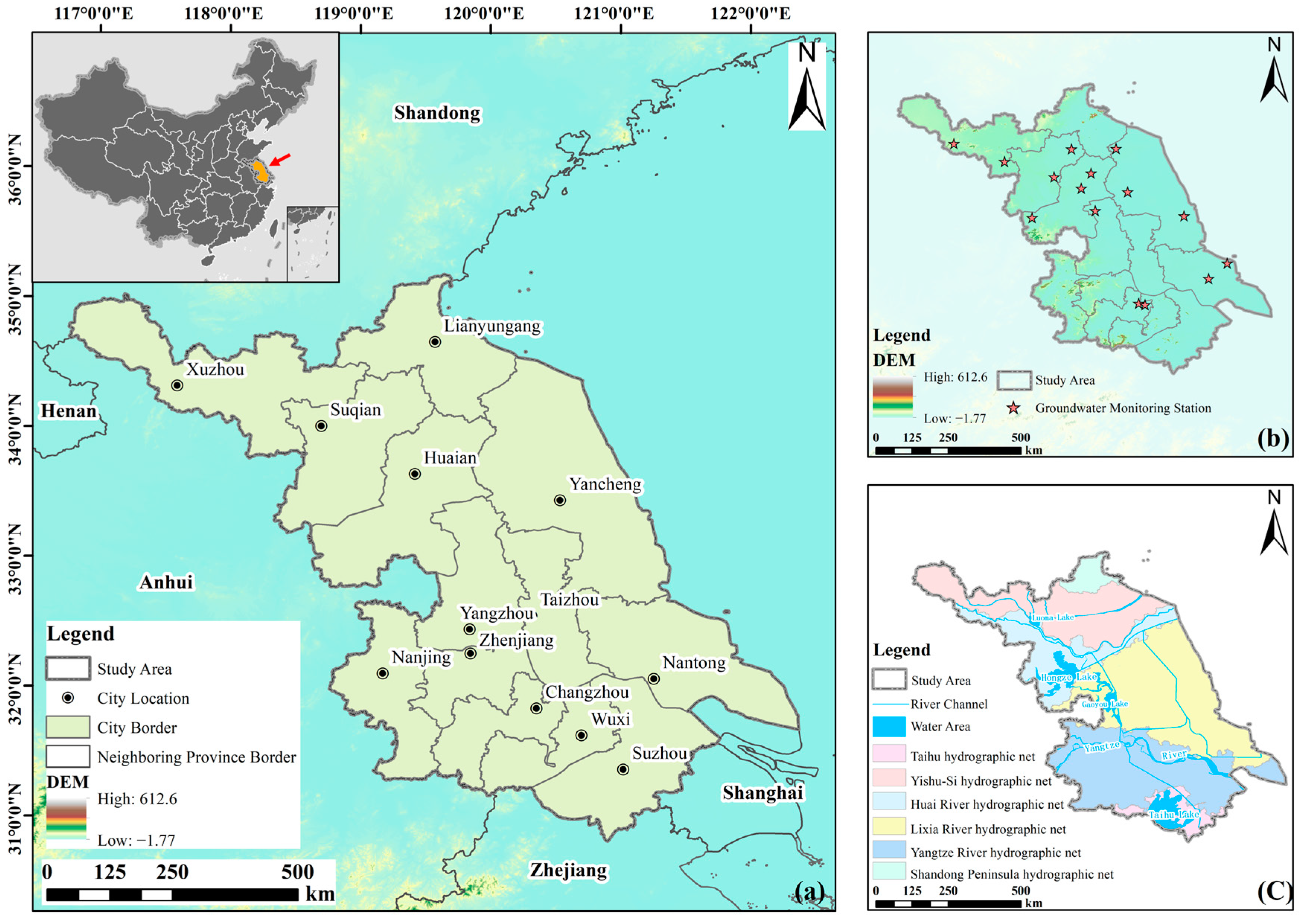
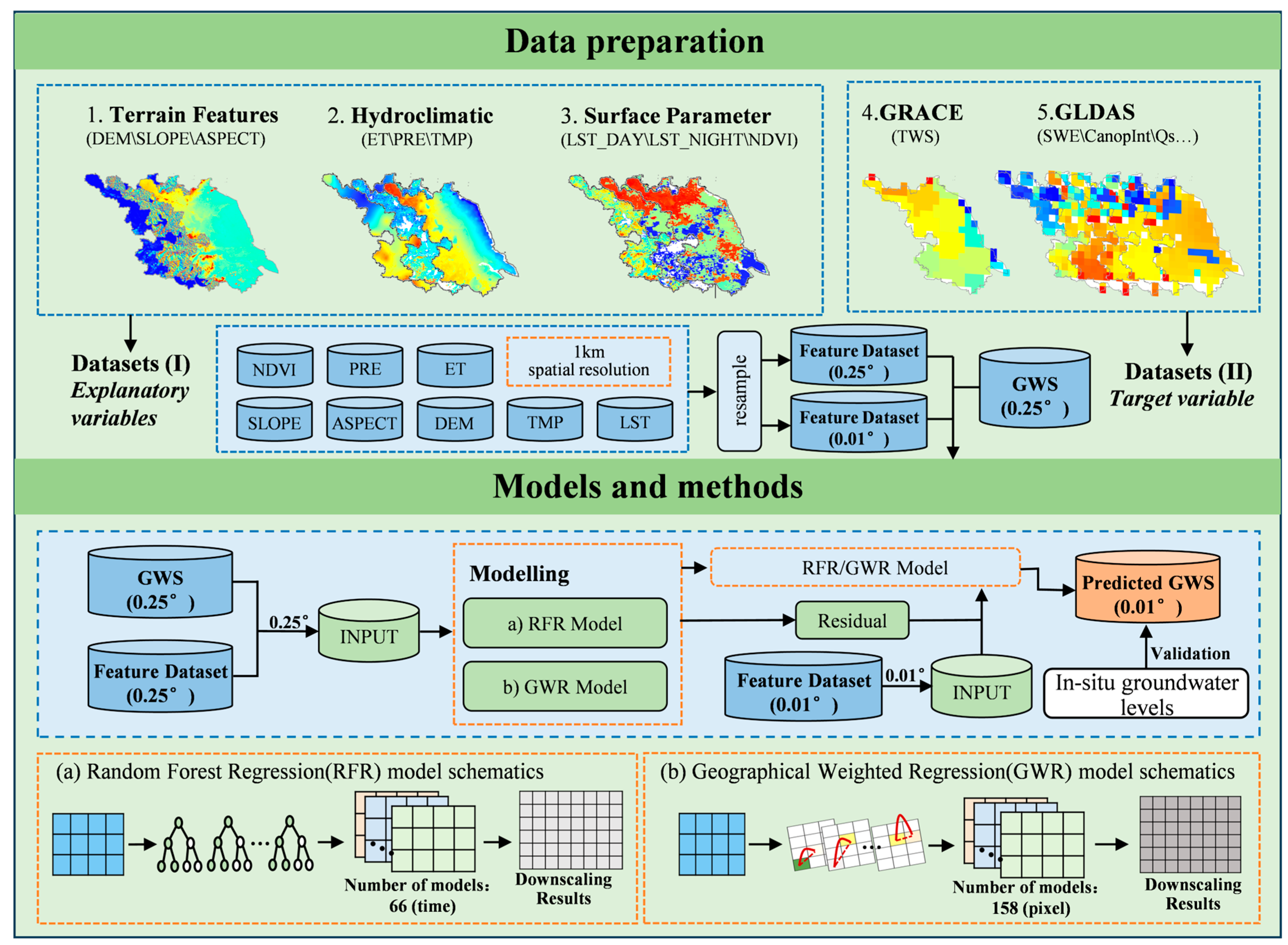






| Dataset | Variable Name | Spatial (Temporal) Resolution | Source |
|---|---|---|---|
| GRACE Mascon (CSR RL06M) | Terrestrial Water Storage (TWS) | 0.25° (monthly) | https://www2.csr.utexas.edu/grace (accessed on 16 September 2023) |
| GLDAS Noah v2.1 | Soil moisture (SM) | 0.25° (monthly) | https://disc.gsfc.nasa.gov/datasets/ (accessed on 28 August 2023) |
| Snow depth water equivalent (SWE_inst) | 0.25° (monthly) | ||
| Plant canopy surface water (CanopInt_inst) | 0.25° (monthly) | ||
| Storm surface runoff (QS_acc) | 0.25° (monthly) | ||
| TPDC Temperature and precipitation dataset | Precipitation (Pre) | 1 km (monthly) | https://data.tpdc.ac.cn/ (accessed on 19 December 2023) |
| Temperature (Tmp) | 1 km (monthly) | ||
| MODIS 13A3 | Normalized Difference Vegetation Index (NDVI) | 1 km (8 days) | https://search.earthdata.nasa.gov (accessed on 20 August 2023) |
| MODIS 16A2 | Evapotranspiration (ET) | 1 km (8 days) | |
| MODIS 11A2 | Land Surface Temperature (LST) | 1 km (8 days) | |
| Groundwater level dataset | Ground observations | Stations (monthly) | Annual Report on Groundwater Levels Monitoring of Geological Environment in China |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Zhong, Y.; Zhang, X.; Maimaitituersun, A.; Ju, X. A Comparative Study of Downscaling Methods for Groundwater Based on GRACE Data Using RFR and GWR Models in Jiangsu Province, China. Remote Sens. 2025, 17, 493. https://doi.org/10.3390/rs17030493
Yang R, Zhong Y, Zhang X, Maimaitituersun A, Ju X. A Comparative Study of Downscaling Methods for Groundwater Based on GRACE Data Using RFR and GWR Models in Jiangsu Province, China. Remote Sensing. 2025; 17(3):493. https://doi.org/10.3390/rs17030493
Chicago/Turabian StyleYang, Rihui, Yuqing Zhong, Xiaoxiang Zhang, Aizemaitijiang Maimaitituersun, and Xiaohan Ju. 2025. "A Comparative Study of Downscaling Methods for Groundwater Based on GRACE Data Using RFR and GWR Models in Jiangsu Province, China" Remote Sensing 17, no. 3: 493. https://doi.org/10.3390/rs17030493
APA StyleYang, R., Zhong, Y., Zhang, X., Maimaitituersun, A., & Ju, X. (2025). A Comparative Study of Downscaling Methods for Groundwater Based on GRACE Data Using RFR and GWR Models in Jiangsu Province, China. Remote Sensing, 17(3), 493. https://doi.org/10.3390/rs17030493






