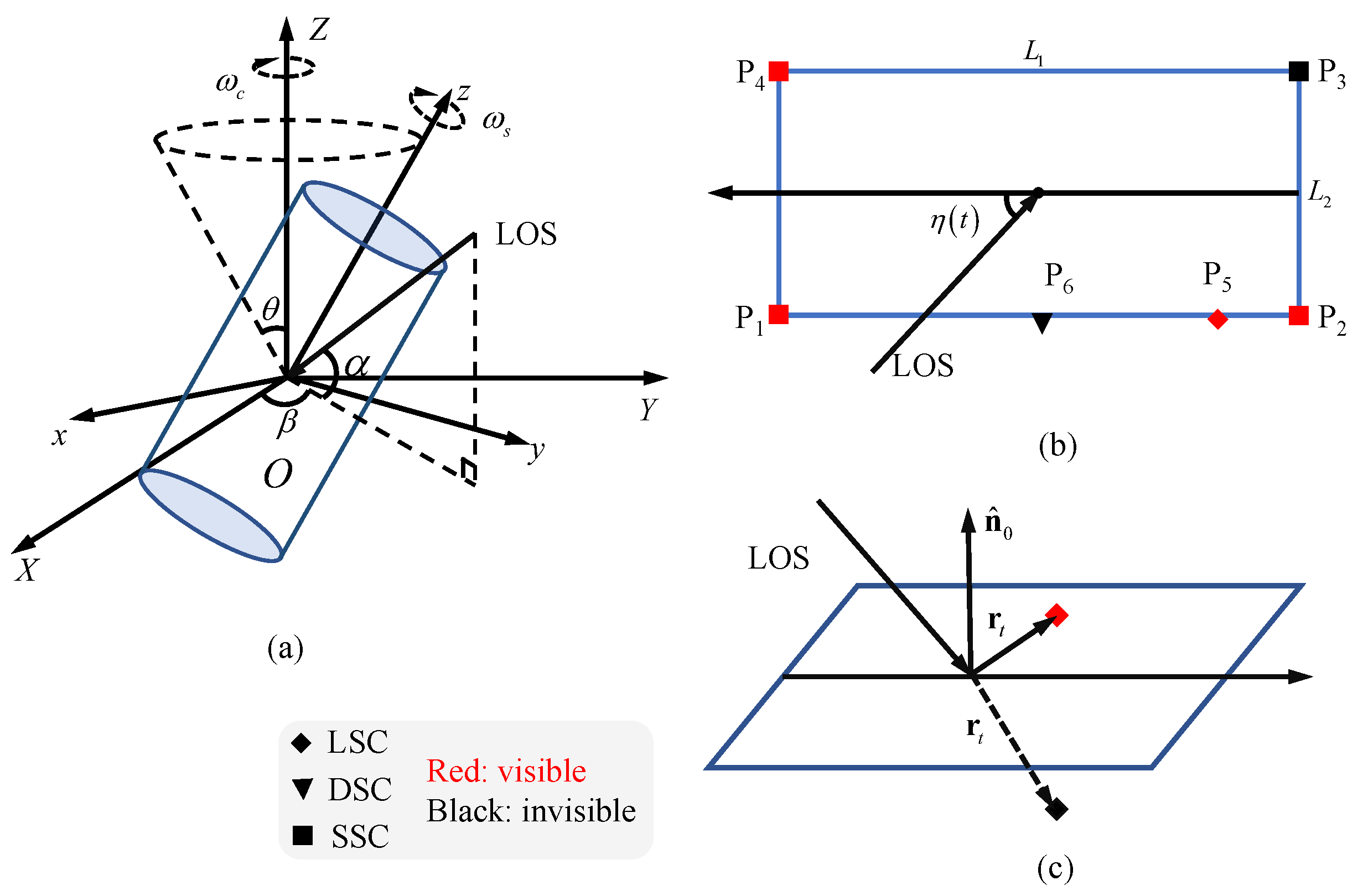
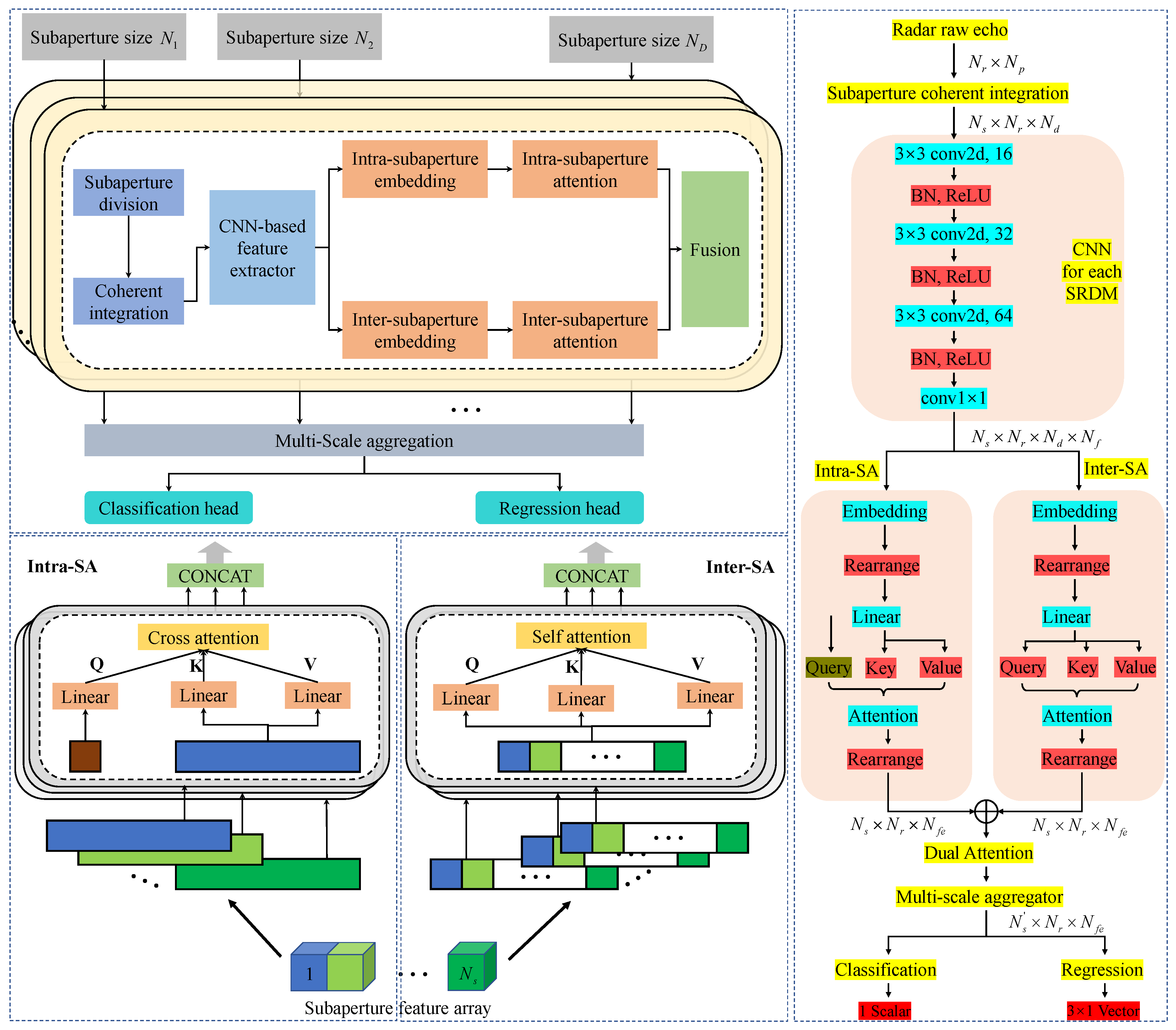
1. Introduction
In recent years, the rapid advancement in space technology has led to a significant increase in the number of various space objects, including satellites, space debris, and spacecrafts [
1,
2,
3]. Among these, cylindrical targets, as a common structural form, have seen a notable rise in prevalence. The motion status of these objects in orbit directly impacts the safe operation of spacecraft and the efficient utilization of space resources. Consequently, timely and accurate detection of space targets, along with the estimation of their motion parameters, has become an essential prerequisite for ensuring the smooth progress of space activities.
Radar technology, with its high-precision velocity and range measurement capabilities and all-weather, all-time operational characteristics, has garnered significant attention in the field of space situational awareness. However, space targets are typically distant and small [
4], leading to extremely low signal-to-noise ratios (SNRs) in the echoes, which significantly reduce the detection probability for traditional methods. A common approach to addressing this issue is long-time integration along the slow-time dimension, enhancing the SNR and thereby improving detection performance. Nevertheless, the high maneuverability of space targets or their rotational motion presents new challenges for effective signal integration. Specifically, high maneuverability can lead to signal energy dispersion across the range–Doppler unit (ARDU), which results in a low integration efficiency. Additionally, fluctuations in the amplitude and phase of scattering center echo, caused by micromotion, lead to signal decoherence and further hinder integration efficiency. To tackle these challenges, researchers continue to explore signal processing techniques and algorithms to promote deeper applications and developments of radar technology in space detection [
5].
In previous research, long-time coherent integration techniques have primarily been categorized into two main types. The first type focuses on parameter search, which can effectively enhance integration performance under low-SNR conditions but is associated with relatively high computational complexity. Perry et al. [
6] proposed the Keystone Transform (KT) algorithm, which decouples the relationship between range frequency and slow time through scaling transform. This technique effectively corrects first-order range migration caused by target velocity. Expanding on this, Su et al. [
7] introduced the dechirp process to estimate target acceleration and compensate for phase discrepancies, eliminating first-order Doppler frequency migration. Li et al. [
8] employed the fractional Fourier transform to not only remove Doppler frequency migration but also achieve coherent energy integration of the target. Additionally, Huang et al. [
9] applied three-dimensional matched filtering in the range frequency and slow-time domain following KT, successfully decoupling range and slow time while correcting third-order range migration and compensating for Doppler frequency migration. However, KT processing often relies on interpolation, inevitably introducing interpolation loss and increasing computational load. In contrast, the Radon Fourier Transform (RFT), proposed by Xu et al. [
10], achieves coherent integration for targets with first-order range migration through a joint search of range and velocity. Xu et al. demonstrated that, in a Gaussian white noise background, RFT serves as an optimal detector capable of maximum likelihood estimation [
11]. Later, Xu et al. [
12] further developed the generalized Radon Fourier transform (GRFT) algorithm, which, through multi-dimensional parameter search, constructs a matched filter to compensate for phase discrepancies in the extracted echo sequence. However, RFT integration outputs may be affected by blind speed sidelobes, increasing the false alarm rate (FAR) in target detection, while the multi-dimensional parameter search significantly raises GRFT’s computational costs. Building on these foundations, numerous KT and RFT variants have been proposed [
13,
14,
15,
16,
17,
18] in efforts to balance their respective advantages and limitations, thereby adapting these methods to different practical application scenarios.
Another approach is based on non-parametric search, which circumvents the search process by directly manipulating the correlation of the echo, thereby effectively reducing computational load, which makes it challenging to achieve the coherent integration of target echo energy in low-SNR environments. Zheng et al. [
19] introduced the scaled inverse Fourier transform (SCIFT), which first uses frequency-domain autocorrelation to convert the echo into the range frequency and slow-time delay domain, followed by SCIFT to accumulate target energy. Niu et al. [
20] proposed a fast algorithm based on the frequency domain, further optimizing computational efficiency. Additionally, Li et al. [
21] applied sequence-reversing Transformation (SRT) along the slow-time dimension to achieve temporal correlation, correcting for range migration and enhancing energy integration. Zhang et al. [
22] achieved energy integration and parameter estimation by computing the time-domain cross-correlation of adjacent echoes, which also significantly reduces computational complexity. Moreover, to achieve long-time coherent integration for targets with high-order motion parameters, researchers have combined parametric and non-parametric search techniques to correct the range migration of different orders. For example, Huang et al. [
23] first applied KT to correct first-order range migration, then used the second-order Wigner–Ville distribution transform to estimate target acceleration and compensate for Doppler frequency migration. Zhang et al. [
24] employed second-order KT (SKT) to correct second-order range migration and computed the symmetric instantaneous autocorrelation function of the corrected echo to address range and Doppler frequency migration. Li et al. [
25] successively corrected third-, first-, and second-order range migration using time-reversal transformation and SKT, ultimately performing coherent integration with the Lv distribution. However, when the target contains multiple scattering centers and exhibits micromotion, the echo becomes highly complex [
26]. In this case, the motion of each scattering center can no longer be accurately described by simple low-order polynomials. The application of higher-order motion models sharply increases the number of parameters, making parameter search methods impractical. Furthermore, during autocorrelation operations, multiple scattering centers tend to produce cross-terms, which degrade integration performance.
Recently, radar moving target detection (MTD) methods based on deep learning have gained popularity. Wang et al. [
27] was one of the first to analyze the potential applications of deep neural networks (DNNs) in radar target detection (RTD), designing a detector based on DNNs and comparing it with traditional detectors. Jiang et al. [
28] proposed a multi-task model based on convolutional neural networks (CNN), which leverages both time and frequency information to detect and localize targets in a multi-dimensional space of range, velocity, azimuth, and elevation. Wang et al. [
29] introduced a dual-head CNN with one head for binary classification to determine target presence and another for estimating target offset, incorporating a non-maximum suppression mechanism at the network output to effectively reduce FAR. Subsequently, Tian et al. [
30] proposed a fully convolutional network for rapid detection across the whole range-Doppler map and achieved accuracy comparable to the previous methods. The methods mentioned above typically assume a simple point target model. Extracting micromotion features remains a significant challenge in RTD. Su et al. [
31] used time-frequency images as inputs to a CNN for detecting maritime targets under varying sea states. Research on targets with micromotion has predominantly focused on small unmanned aerial vehicles (UAVs). Sun et al. [
32] introduced an LSTM-based detection, classification, and localization method for small UAVs utilizing micro-Doppler signatures (mDSs), but traditional methods were still used for feature extraction. In the case of highly maneuverable space targets, translational and micromotion information are coupled within the Doppler domain and are difficult to separate. Yang et al. [
33] developed a UAV detection method based on the Transformer architecture. They first designed a complex encoder specifically for range-pulse echo data and employed the Transformer to extract both Doppler shift and mDSs simultaneously, achieving improved detection performance and measurement accuracy.
In space target detection, the signals of micromotion targets exhibit significant non-uniformity and sparsity in both intensity and spatial distribution, posing challenges for traditional feature extraction methods. The attention mechanism in Transformer effectively addresses this issue by adaptively focusing on key feature regions and allocating more computational resources to prominent scattering center signals, thereby enhancing the efficiency and accuracy of feature extraction. Furthermore, target echoes exhibit long temporal dependencies, which traditional recurrent neural network methods struggle to model due to gradient vanishing issues and low computational efficiency. In contrast, the Transformer, which does not rely on a recursive structure, offers the capability to efficiently process long sequences and enables superior modeling of the dynamic temporal variations in target echo signals [
34].
In this paper, we proposed a novel end-to-end approach called multi-scale subaperture coherent integration Transformer (MsSCIFormer) for detecting and estimating the parameters of cylindrical space targets (CSTs). The core of this method lies in the precise modeling of the scattering centers of CSTs, from which accurate signal models are derived. Furthermore, we designed a multi-scale subaperture processing module that segments the long-time echo along the slow-time dimension into multiple subapertures of varying scales and performs coherent integration within each. This strategy not only significantly enhances the SNR but also effectively mitigates the ARDU of scattering center energies. Building on this, a CNN-based feature extractor was introduced to perform deep feature extraction from each subaperture range-Doppler map (SRDM). Subsequently, a Transformer with a dual-attention mechanism was employed to process these feature arrays, efficiently fusing spatial and temporal characteristics of the target’s scattering centers. By aggregating multi-scale fused features, we utilized classification and regression heads to achieve precise target detection and accurate motion parameter estimation. The proposed method offers several key advantages:
- (1)
The detailed modeling of scattering centers and the accurate derivation of signal models provide a solid foundation for subsequent processing, improving both target detection and parameter estimation accuracy.
- (2)
The design of the multi-scale subaperture processing module addresses the ARDU of scattering centers while preserving the mDS and enhancing the robustness and applicability of the method.
- (3)
The combination of CNN feature extraction and the Transformer’s dual-attention mechanism deeply integrates spatial and temporal features of scattering centers and, through multi-scale feature aggregation, significantly boosts overall detection and estimation performance.
The rest of this paper is organized as follows. In
Section 2, we conduct an in-depth analysis of the scattering center variation patterns of a typical micromotion cylindrical space target and provide precise signal modeling.
Section 3 offers a comprehensive overview of the MsSCIFormer architecture. In
Section 4, the performance of MsSCIFormer is validated through a series of simulation experiments, including comparative analysis, ablation studies and robustness analysis. Finally, a summary and conclusion are presented in
Section 5.
4. Experimental Evaluation
4.1. Experimental Setup
Experimental data. A widely accepted view in evaluating the effectiveness of deep learning models across various application scenarios is that their success largely depends on an efficient training process and access to abundant, high-quality data resources. However, due to the dynamic and unpredictable nature of the space environment, acquiring extensive real radar data to support the training of deep learning models is highly challenging. Therefore, this study employs simulation techniques to generate a substantial amount of labeled radar complex data. By accurately modeling the physical characteristics of radar systems and the electromagnetic scattering behavior of space targets, as discussed in
Section 2, highly realistic radar echo data can be produced. These data contain authentic parameter information of the targets, such as initial range, initial velocity, acceleration and scattering properties, thereby ensuring both the practicality and representativeness of the simulated data.
In this study, the detailed parameter configurations of the simulated dataset are provided in
Table 2. Specifically, a narrowband S-band pulsed radar system was selected as the research foundation, with a carrier frequency set at 3
and a bandwidth of 10
. The pulse repetition frequency was set to 100
, while the sampling frequency was configured to be twice the bandwidth to ensure adequate signal sampling. Based on these parameters, the radar system’s range resolution is derived to be 7.5
, with a maximum unambiguous velocity of 5
. For the micromotion CST, a set of specific physical parameters and dynamic characteristics were predefined. The cylinder length was assumed to be 6
, with a base diameter of 3
. In terms of micromotion, the CST was configured to undergo precession with an angle of
, with spin and precession periods set to 2
and 4
, respectively. These configurations were designed to simulate the complex dynamic behavior that CSTs may exhibit in real-world scenarios. Notably, MsSCIFormer effectively models the spatial and temporal dynamics of target scattering center signals, ensuring that the structure and micromotion parameters of the CST do not affect the network’s performance.
To comprehensively evaluate the accuracy of MsSCIFormer in residual translational motion parameter regression, a uniform distribution strategy was adopted when constructing the dataset to select the target’s translational motion parameters. The initial range, velocity, and acceleration were sampled within the intervals of , and , respectively. Considering the computational cost, the range-pulse echo samples were generated with 1024 pulses and 32 range cells, defining a detection window of 240 in the range dimension. To comprehensively evaluate system performance, different noise environments were simulated by setting the SNR range from to , with increments of 3 ; we generated 5000 samples for each SNR. Considering the condition of target absence, the final simulated dataset consisted of 60,000 samples, with allocated for model training and the remaining reserved for testing.
Experimental metrics. In the evaluation section, we systematically applied various performance metrics to comprehensively and accurately assess the effectiveness of the MsSCIFormer. Specifically, we focused on two widely recognized evaluation criteria in RTD: detection probability and FAR. Within this framework, samples containing targets were defined as positive samples, while those without targets were considered negative samples. Additionally, algorithm predictions indicating the presence of a target were labeled as true, and predictions indicating the absence of a target were labeled as false. Based on this classification, four distinct cases were identified:
samples that contain a target and are correctly detected (true positives),
samples that contain a target but are missed (false negatives),
samples that do not contain a target and are correctly classified (true negatives), and
samples that do not contain a target but are incorrectly detected as containing one (false positives). Using these definitions, detection probability and FAR can be expressed as follows:
In addition, given the focus of this algorithm on accurately estimating target translational motion parameters, measurement error was introduced as another key evaluation metric. Specifically, measurement errors assess the algorithm’s accuracy in estimating residual translational motion parameters, including range, velocity, and acceleration. The errors were quantified using the absolute errors, as shown in Equations (
24)–(
26).
where
,
and
represent the estimated residual range, velocity, and acceleration, respectively;
,
and
denote the corresponding ground truths. By quantifying these errors, we can more precisely evaluate the performance of the MsSCIFormer in complex dynamic environments, especially when dealing with targets whose actual trajectories deviate from the guidance track. These error metrics provide a direct quantitative measure of the robustness and accuracy of the network.
Implementation Details. In the experimental setup of this paper, the batch size was set to 16 to balance memory efficiency and data throughput during the model training process. The MsSCIFormer model was optimized using the Adam optimizer, with the learning rate set to be . The model was implemented in PyTorch version 2.1.2 and trained for 40 epochs on an NVIDIA RTX 3090 GPU. The GPU is manufactured by NVIDIA Corporation, which is based in Santa Clara, CA, USA. A key component of the MsSCIFormer model is the multi-scale subaperture processing block, which includes five varying scales, namely .
4.2. Comparison Experiments
To demonstrate the superiority of the proposed algorithm, this section presents a comparative analysis of five previous RTD algorithms. In particular, two traditional algorithms were selected: the MTD, the SRT and the GRFT. Since deep learning-based detection algorithms lack constant FAR characteristics, the detection thresholds for traditional algorithms in this study were determined using Monte Carlo simulations based on preset FAR. The MTD method performs a Fourier transform along the slow-time dimension of echo data but overlooks the ARDU effects of target scattering centers. SRT applied time-reversed echo flipping along the slow-time dimension to achieve temporal correlation, only correcting for the first-order range migration and enhancing energy accumulation. GRFT, on the other hand, performs an ergodic search for translational parameters; however, for CSTs with multiple scattering centers and micromotions, the phase variation of the scattering centers becomes complex, making effective compensation challenging.
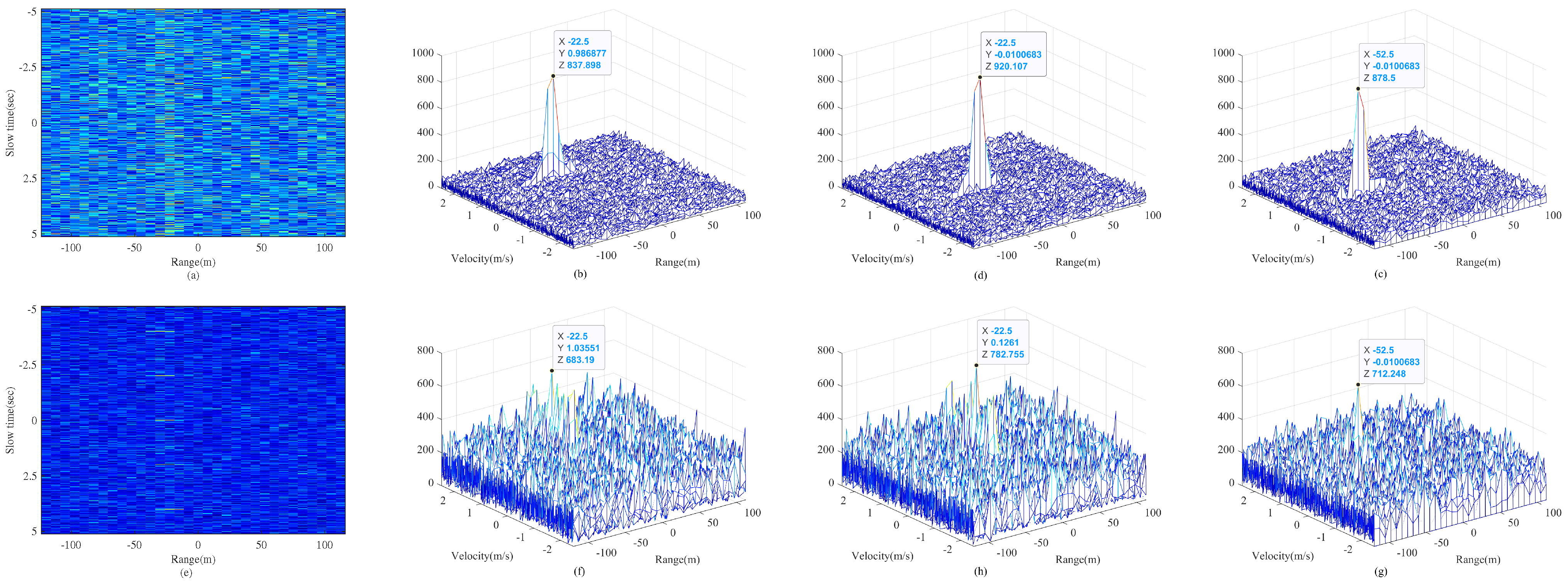
Figure 6 illustrates the coherent integration results under low-SNR conditions (
) for point targets and CSTs with precession. Specifically,
Figure 6b–d shows that all traditional algorithms effectively achieve energy integration for point targets. However, for CSTs, as shown in
Figure 6f–h, their integration performance deteriorates significantly.
For scenarios involving CSTs with complex motion models, deep convolutional networks can autonomously learn and extract data features, enabling end-to-end target detection and parameter estimation. To facilitate comparison, three deep learning-based algorithms were selected for this study. The first is an RTD network based on DNN proposed by Wang [
27], which includes only a binary classification head. The second is a multi-task model based on CNN proposed by Jiang [
28], which outputs target range, velocity, azimuth, and elevation in addition to detection. The third is the EchoFormer proposed by Yang [
33], which is designed for complex data and leverages a Transformer architecture to fully utilize mDS information for target detection and parameter estimation. All the above algorithms were reproduced by us, maintaining the primary network structures. However, for consistency and comparability, task heads were modified or added as needed.
For traditional algorithms, the FAR was set to match that of MsSCIFormer, namely
, and the MTD did not account for the estimation of acceleration parameters. It is worth noting that RTD methods based on deep learning often exhibit relatively high FAR [
41,
42,
43,
44]. However, performing track association on the initial measurements has been shown to effectively eliminate false detections, and improve overall detection reliability [
45].
Table 3 provides a detailed comparison of the detection performance of different methods on the dataset used in this study. The table reveals that traditional algorithms exhibit poor detection performance and especially low parameter estimation accuracy, primarily due to the significant impact of ARDU effects. Even when the SNR is high, the micromotion still causes deviation in the measurement of velocity, which accounts for the large errors in the regression of residual velocity. The algorithms proposed by Wang [
27] and Jiang [
28] rely solely on basic convolutional networks for feature extraction, failing to effectively leverage the mDS of the targets. This limitation results in low detection probabilities accompanied by higher FAR. In contrast, the EchoFormer [
33], which incorporates both phase information and mDS, demonstrates significantly improved performance. Building upon these advancements, the proposed MsSCIFormer algorithm further enhances detection probability and parameter estimation accuracy while effectively reducing the FAR.
To evaluate the performance of the proposed algorithm under low SNR conditions, a comparative analysis was conducted between Jiang’s method, EchoFormer, and MsSCIFormer. Each method was trained and tested on three datasets with SNR ranges of
∼
dB,
∼
dB, and
∼
dB, respectively. The experimental results are summarized in
Table 4. The results indicate that detection performance deteriorates for all three methods as the SNR decreases to varying extents. Jiang’s method experienced the most significant decline, with the detection probability dropping to 69.68% and the FAR increasing to 15.9% on the
∼
dB dataset. Additionally, its regression error showed a substantial increase. In comparison, EchoFormer exhibited less pronounced degradation in both classification and regression tasks. However, MsSCIFormer demonstrated superior robustness, achieving a detection probability of 89.23% on the
∼
dB dataset while maintaining a low FAR. Its regression errors remained stable across all three low-SNR datasets. This superior performance can be attributed to the dual-attention mechanism, which enhances the extraction of both spatial and temporal features of scattering centers.
4.3. Ablation Experiments
To better understand the impact of each component in the MsSCIFormer model on overall algorithm performance, we conducted ablation experiments focusing on multi-scale subaperture coherent integration (MsSCI), Intra-SA, and Inter-SA.
Table 5 lists the results of the ablation experiments.
First, a baseline model without MsSCI was constructed, employing a single-scale subaperture segmentation strategy in its workflow. This baseline model was designed to evaluate the effectiveness of the MsSCI module. Further, subaperture segmentations with scales of 16, 32, and 64 were implemented, categorized as fine, medium, and coarse subapertures, respectively, to comprehensively assess the potential impact of different subaperture scales on network performance. A comparative analysis of the single-scale model and the complete MsSCIFormer model revealed that incorporating MsSCI not only ensured regression accuracy but also significantly improved target detection probability and reduced the FAR. Performance analysis across different subaperture scales demonstrated that coarser-scale subaperture segmentation enhanced binary classification performance, while finer-scale segmentation provided significant advantages in the precise regression of range and velocity parameters.
Subsequently, the specific impact of Intra-SA and Inter-SA mechanisms on model performance was investigated in detail. To this end, three variant models were constructed: two with each attention mechanism removed and one with both attention mechanisms removed. The experimental results demonstrated that models lacking the two attention mechanisms exhibited significantly lower classification accuracy and regression precision. The model incorporating only the Intra-SA effectively enhanced the ability to capture the spatial distribution features of scattering centers, thereby improving the regression accuracy of range and velocity parameters. However, due to the lack of efficient handling of global contextual information, this model struggled to utilize long-time data effectively, resulting in a significantly lower detection probability and a higher FAR compared to the complete MsSCIFormer model. In contrast, the model incorporating only the Inter-SA significantly improved global comprehension and generalization by promoting information exchange across subapertures, leading to excellent performance in classification tasks. However, due to insufficient focus on intra-subaperture features, this model exhibited slightly reduced localization performance when dealing with targets containing multiple complex scattering centers.
Furthermore, the performance of the models was systematically evaluated under varying SNR conditions, as shown in
Figure 7. Specifically,
Figure 7a highlights the superior performance of the complete MsSCIFormer network, with an overall detection probability consistently above
and rapidly increasing to
when the SNR exceeds
. In contrast, the model employing a single-scale dual-attention Transformer exhibits a performance degradation of approximately
compared to the multi-scale structure. Notably, network models lacking attention mechanisms show a significant decline in performance. Further comparative analysis reveals that Inter-SA contributes more to performance enhancement than Intra-SA, aligning with prior findings.
Figure 7b–d demonstrates the robustness of MsSCIFormer in regression accuracy across varying SNR levels, providing strong evidence of its ability to accurately detect targets.
Above all, the ablation experiments not only validated the necessity of each key component in the MsSCIFormer model but also provided a deeper understanding of how these components work synergistically to enhance the overall algorithm performance. Specifically, the MsSCI improved the model’s adaptability to complex scenarios; the Intra-SA enhanced the precision of local feature extraction, and the Inter-SA facilitated the integration and utilization of global information.
4.4. Robustness Experiments
(1) Multi-scale sets: The ablation experiments have clearly demonstrated the positive impact of the MsSCI module on the network performance. This section aims to further assess the specific effects of different multi-scale sets on the network performance. To this end, a full-scale set containing 8 subaperture sizes, denoted as
, was defined. First, we focused on the influence of multi-scale sets with varying sizes. The MsSCIFormer model was configured with different multi-scale sets, denoted as
, where
i represents the size of the set, and underwent a training and evaluation process. To eliminate potential bias from varying subaperture sizes, a consistent selection strategy was followed when choosing scales from
: the smallest
i values were selected to form the multi-scale set for configuring MsSCIFormer. Additionally, we evaluated the performance of multi-scale sets of the same size (in this case,
) but with different elements, namely
,
,
, and
. The experimental results are detailed in
Table 6.
When comparing the performance of MsSCIFormer with multi-scale sets of different sizes, we found that, as the size increases, the detection probability gradually increases, the FAR decreases, and the regression errors for motion parameters continue to shrink. In addition, the performance improvement begins to saturate after the size reaches 6, the detection probability increases by less than , and the FAR and regression errors barely decrease with further increases in the size of multi-scale sets. Given that computational complexity increases with the number of scales, the size being 5 or 6 is considered a reasonable choice, as it ensures good performance while controlling computational cost. Furthermore, we compared network performance with multi-scale sets of the same size. In these four cases, consisted of the smallest four subaperture values, consisted of the largest four, and the others were selected with intervals from the full set. The results showed that the network configured with exhibited the best regression performance, while the network with achieved the best classification performance. Networks using sets and provided a better trade-off between classification and regression tasks. Overall, the network performance showed minimal fluctuation, and MsSCIFormer demonstrated robust performance with multi-scale sets of the same size.
(2) Incomplete observations: As delineated in
Section 2, the constraint of limited radar resources frequently results in incomplete observations, which impede the acquisition of comprehensive spatial distribution and temporal evolution characteristics of target scattering centers. To rigorously assess the performance of MsSCIFormer under such incomplete observation scenarios, we meticulously simulated three additional datasets with degrees of incompleteness of
,
, and
, respectively. Together with the original complete dataset, these constituted four experimental conditions for both training and evaluation. The experimental results, presented in
Table 7, also include TFCs of the targets under different levels of completeness.
A comprehensive analysis of the results revealed a clear trend: the availability of more observational information positively correlates with enhanced detection performance. Specifically, the network achieved optimal performance under complete observations. In comparison to scenarios with and incompleteness, the detection probability decreased by and , respectively, while the FAR increased by and . Additionally, a slight decline in regression accuracy was observed. Notably, a significant deterioration in performance was evident when the degree of incompleteness reached . Compared to complete observations, the detection probability dropped substantially by , the FAR rose by , and the estimation errors for target motion parameters increased by , and , respectively. These findings suggest that when the degree of incomplete observations is less than , the decline in detection performance of the network is relatively modest. In such cases, MsSCIFormer demonstrates a certain level of robustness to the completeness of observational data. In practical applications, this implies a potential trade-off between network performance and radar resource allocation, allowing for flexible decision-making based on specific requirements and constraints.