A Fast Collaborative Representation Algorithm Based on Extended Multi-Attribute Profiles for Hyperspectral Anomaly Detection
Highlights
- We use the Extended Multi-Attribute Profile (EMAP) method to extract feature attributes of hyperspectral images, and then replace the sliding dual-window model in collaborative representation with the K-Means clustering algorithm to achieve both higher anomaly detection accuracy and faster detection speed.
- We experiment on four real hyperspectral datasets and a synthetic dataset, showing that the EMAPKCRD algorithm achieves the highest AUC value among all compared algorithms. Compared with the traditional CRD and its variant RCRD, it not only improves detection accuracy but also shortens the detection time.
- We address “ignoring spatial features” and “high computational cost” in traditional hyperspectral anomaly detection: EMAP extracts spatial features to enhance anomaly–background distinguishability, and K-means-based background reconstruction reduces complexity, enabling practical engineering applications.
- We offer a superior technical solution for hyperspectral anomaly detection, whose stable performance in complex scenarios supports “high accuracy and efficiency” demands in military reconnaissance, environmental monitoring, and precision agriculture, with practical application value.
Abstract
1. Introduction
- We utilize EMAP extraction to derive spatial features from HSIs, integrating these with the spatial information inherent in the images to preprocess the hyperspectral data and enhance detection performance.
- For background reconstruction, we advocate the use of the k-means clustering algorithm post-spatial feature extraction to select representative points for reconstructing background pixels, thereby further augmenting the accuracy of anomaly detection.
- The reconstructed background matrix, derived from the aforementioned two steps, will serve as the input for the CRD algorithm, facilitating more rapid and accurate anomaly detection results.
2. Related Work
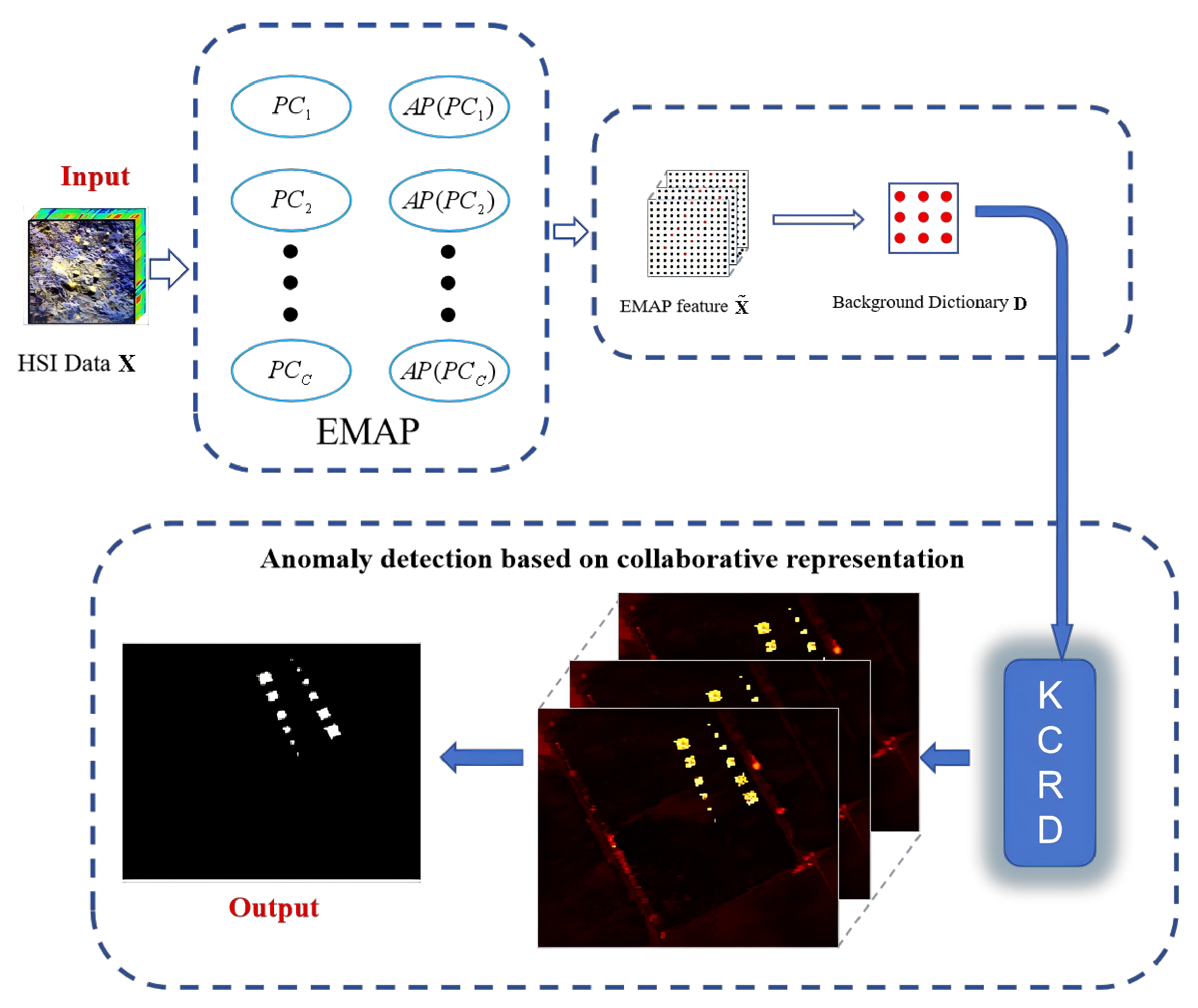
3. The Proposed EMAPKCRD Method
3.1. Extended Multi-Attribute Profiles
| Algorithm 1 EMAP |
|
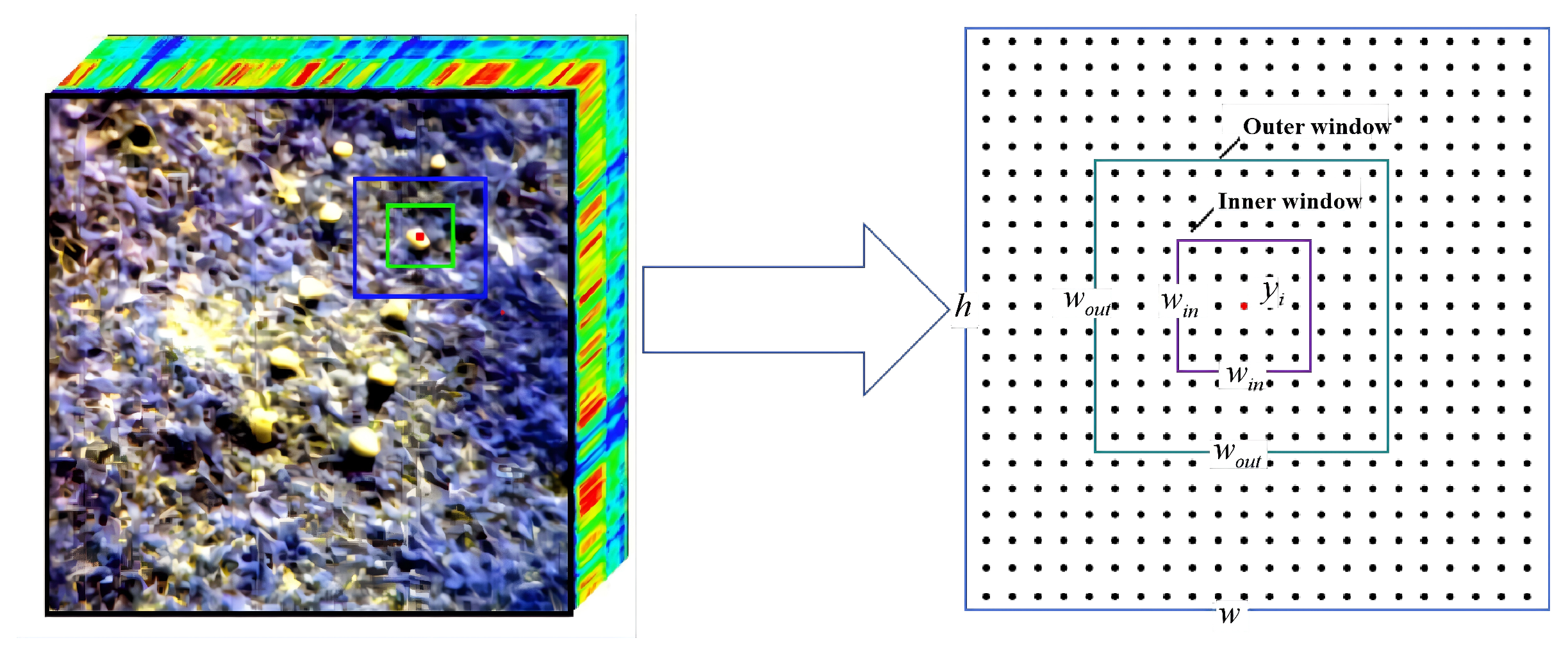
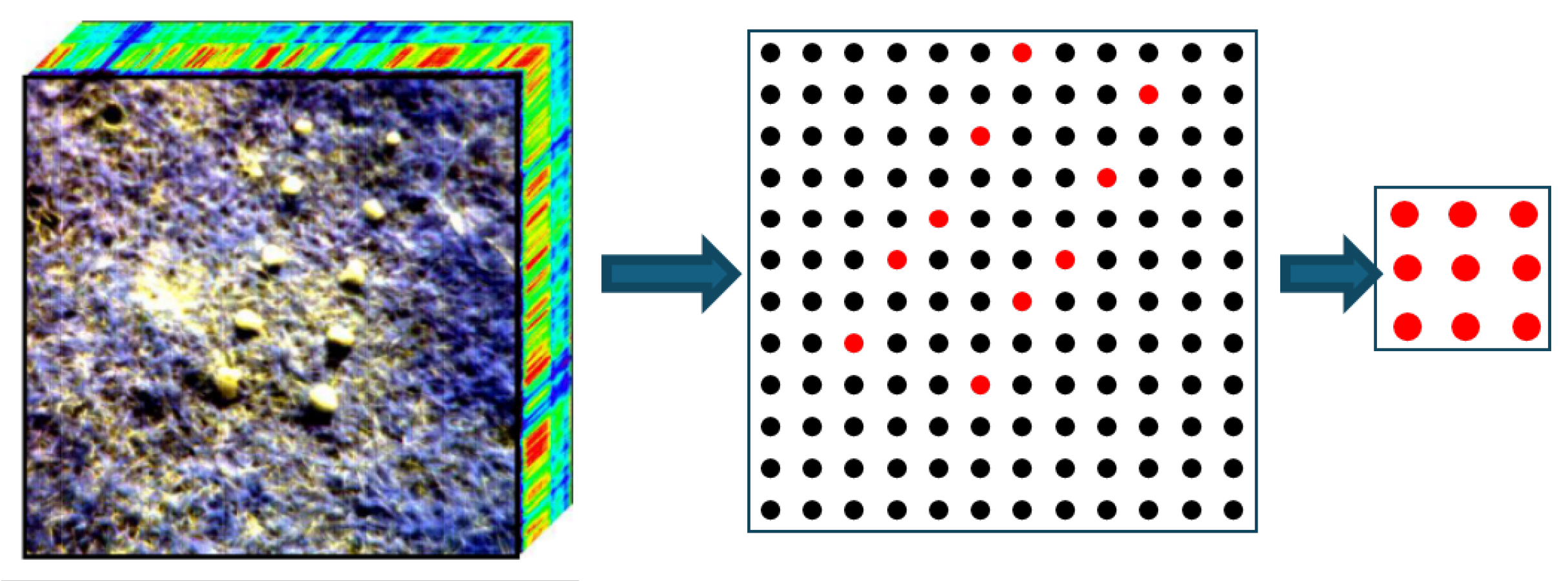
3.2. Window Reconstruction Model Based on K-Means Clustering
| Algorithm 2 K-means Clustering |
|
3.3. EMAPKCRD
| Algorithm 3 EMAPKCRD |
|
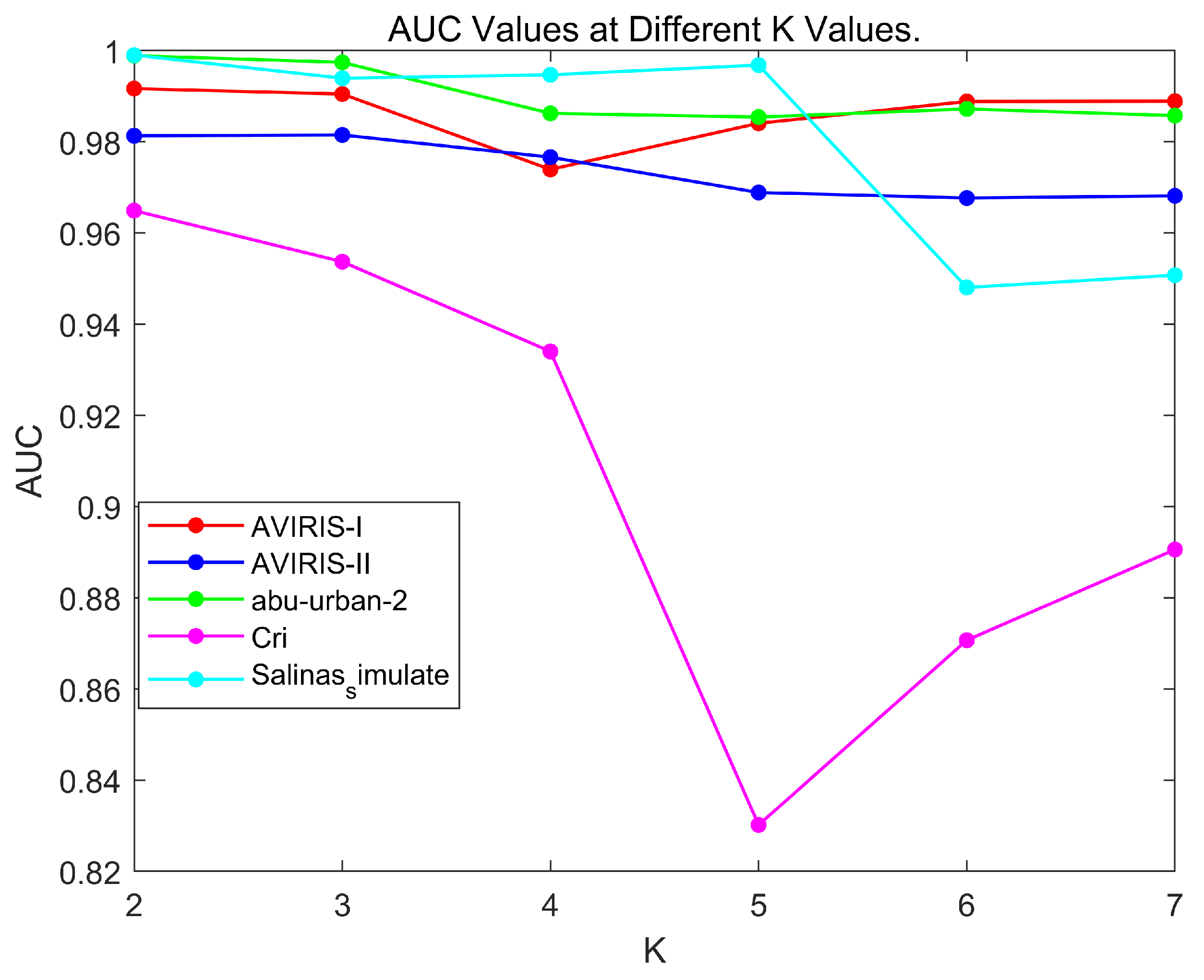
4. Experiments and Results
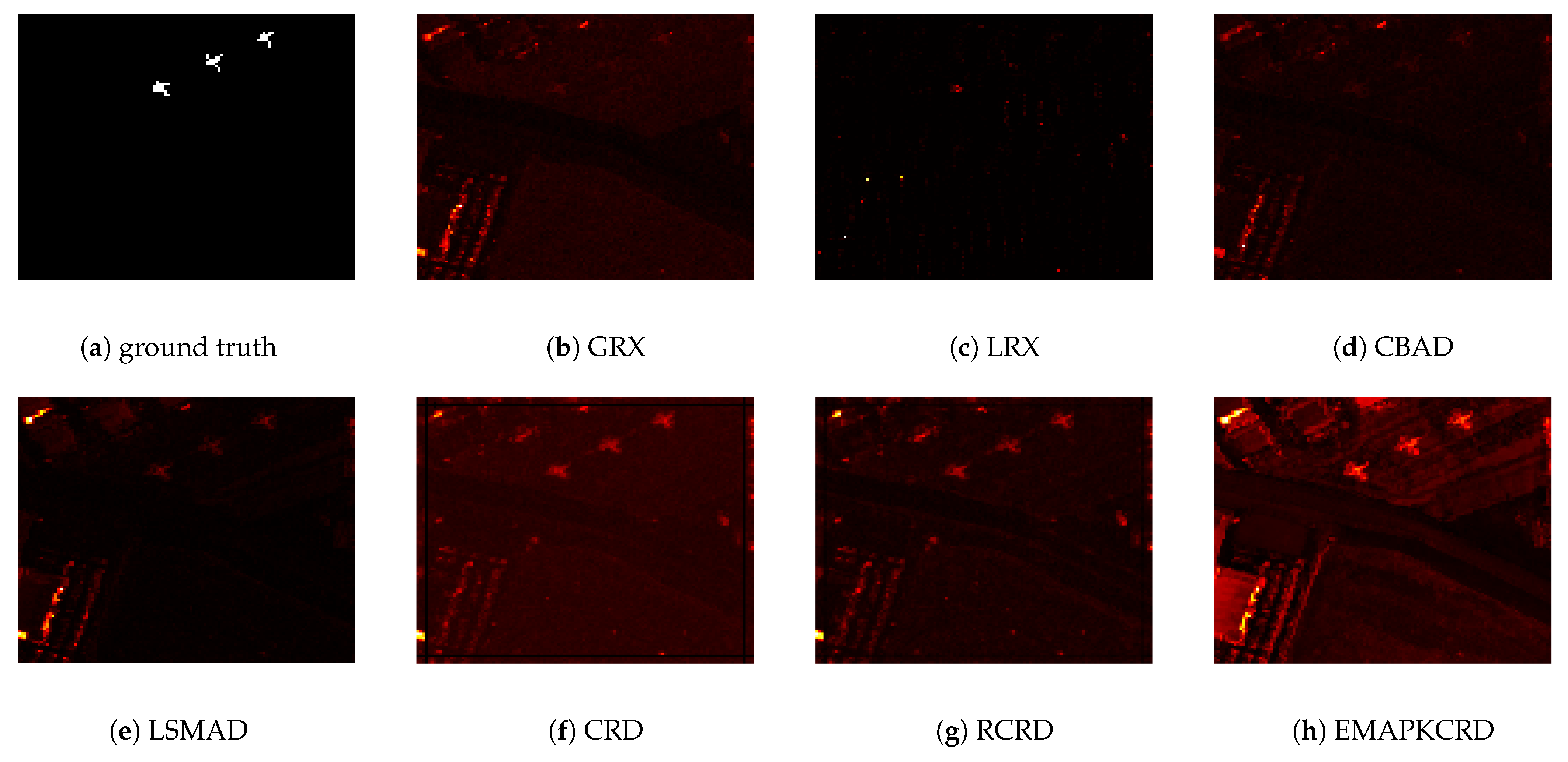
- AVIRIS-I dataset: As depicted in the accompanying figure, it provides a comprehensive visual representation of the spectral reflectance properties of the agricultural field under study. In the case of (a) and (f), the data was collected using the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) instrument stationed at the San Diego, California, USA facility. The visual representation of the scene spans a resolution of 400 pixels in both width and height, and is composed of 224 distinct spectral bands, each corresponding to a unique wavelength range that stretches from 370 nanometers to 2510 nanometers. As referenced in [7], the AVIRIS-I dataset occupies a specific region within the image, located at the upper-left quadrant, and spans 120 pixels by 120 pixels. Following the elimination of bands associated with water absorption, reduced signal-to-noise ratios, and suboptimal quality, a total of 189 distinct spectral components were retained during the experimental analysis. In this region, a cluster of three distinct planes each containing 58 pixels appears to be associated with anomalous data points.
- abu-urban-2 dataset: The Abu-urban-2 dataset is a high-resolution urban landscape map derived from the ABU collection, comprising 210 spectral bands. This instrument operates across a broad spectral range, spanning from 400 nanometers to 2500 nanometers, and achieves a resolution of 10 nanometers in terms of wavelength. The Abu-urban-2 dataset is composed of a 100 × 100 pixel resolution and spans a total of 207 distinct spectral bands, which are used for multispectral analysis. According to [40] various vehicles in the map are considered abnormal pixels and should be detected. The false color image and ground truth image of the abu-urban-2 dataset are shown in Figure 4c and Figure 4h, respectively.
- Cri dataset: This dataset was obtained from the Nuance Cri hyperspectral sensor and obtained from [7]. It has a size of 400 × 400 pixels and contains 46 spectral bands with a wavelength range of 650 to 1100 nm. In this image, rocks composed of 2216 pixels were identified as abnormal pixels and should be detected. The false color map and ground truth map of this dataset are shown in the Figure 4d,i.
- Salinas simulation dataset [11]: This dataset is a simulated dataset. Firstly, a binary mask image M with pixel sizes of 150 and 126 is constructed by generating six square matrices. Then, a region of the same size as the binary mask image M cut out from the Salinas scene datatset is used to construct the synthesized image . In this image, 12 blocks with side lengths ranging from 1 to 6 pixels in opposite order are considered abnormal.Based on the real images of the Salinas scene scene, setting the parameter to 14, the final simulated dataset’s false color image and ground truth image are shown in Figure 4e,j.
4.1. Evaluation Methods
4.2. Compared Methods
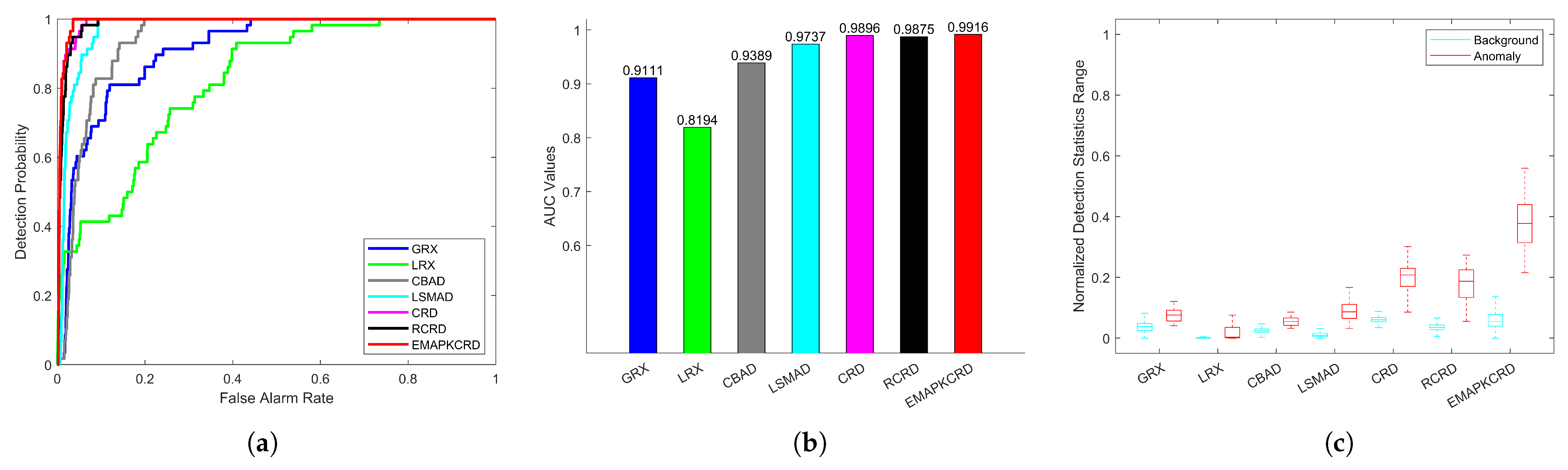
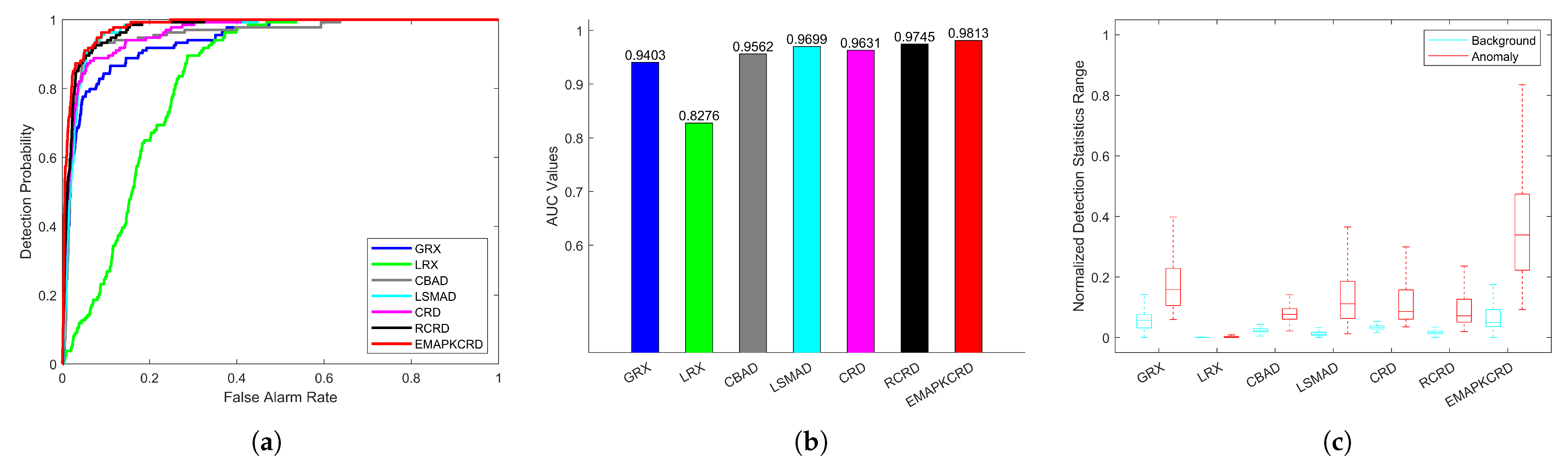
- GRX: Global RX detector. This algorithm models the background using the entire image. Although the method is simple and efficient, it only produces good results for some images with relatively simple topological structures.
- LRX: Local RX algorithm, using a dual window model to capture local areas for modeling, can protect background pixels from interference when testing abnormal pixels. However, the choice of window size has brought poor robustness to LRX.
- CBAD: Clustering-based anomaly detection algorithm. This method clusters background pixels and then uses the RX method for anomaly detection, which can obtain satisfying results, but lacks consideration for the weight of each category.
- LSMAD: Low rank and sparse matrix factorization-based anomaly detection. This method uses the background part after data decomposition to estimate the background, and then performs RX anomaly detection. It can improve the robustness of the algorithm.
- CRD: Collaborative Representation based Anomaly Detection (CRD) Algorithm. This method assumes that each background pixel can be approximately represented linearly by its surrounding pixels. However, due to its sliding dual window strategy, the algorithm has a high complexity and longer detection time in actual detection.
- RCRD: A hyperspectral image anomaly detector based on fast recursive collaborative representation. This method constructs two elementary transformation matrices based on the position of pixels, and uses matrix inversion lemma to derive a recursive update method to improve the detection speed of the detector.
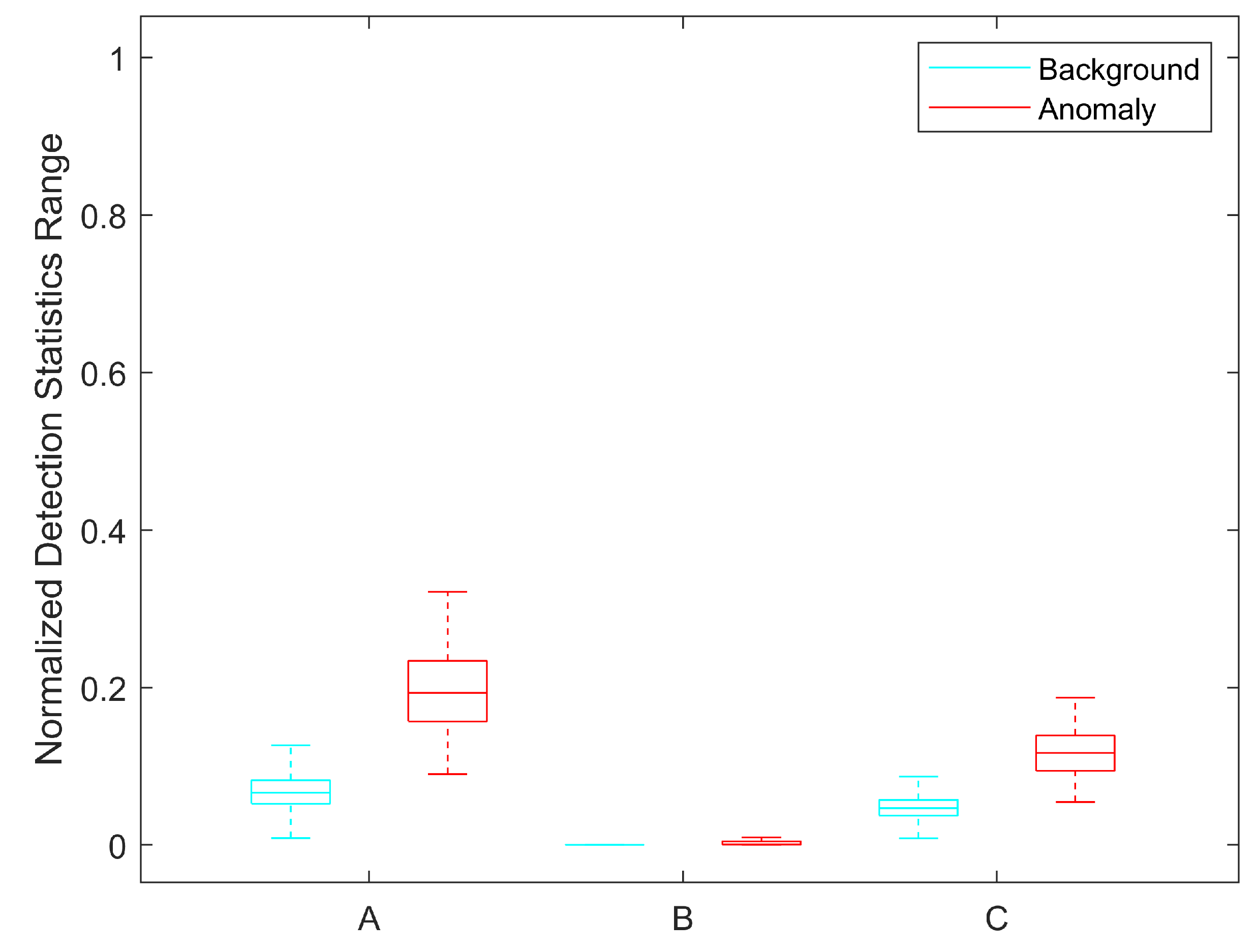
4.3. Detection Result
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shen, X.; Bao, W.; Liang, H.; Zhang, X.; Ma, X. Grouped Collaborative Representation for Hyperspectral Image Classification Using a Two-Phase Strategy. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Dong, S.; Feng, W.; Long, Y.; Bao, W.; Li, K.; Dauphin, G.; Quan, Y. Hyperspectral Image Classification Method Based on Data Expansion and Consistency Regularization with Small Samples. IEEE Geosci. Remote Sens. Lett. 2025, 22, 1–5. [Google Scholar] [CrossRef]
- Li, S.; Zhang, K.; Duan, P.; Kang, X. Hyperspectral Anomaly Detection with Kernel Isolation Forest. IEEE Trans. Geosci. Remote. Sens. 2020, 58, 319–329. [Google Scholar] [CrossRef]
- Patel, N.K.; Patnaik, C.; Dutta, S.; Shekh, A.M.; Dave, A.J. Study of crop growth parameters using Airborne Imaging Spectrometer data. Int. J. Remote Sens. 2001, 22, 2401–2411. [Google Scholar] [CrossRef]
- Shaw, G.; Manolakis, D. Signal processing for hyperspectral image exploitation. IEEE Signal Process. Mag. 2002, 19, 12–16. [Google Scholar] [CrossRef]
- Du, B.; Zhang, L. Random-Selection-Based Anomaly Detector for Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1578–1589. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.; Li, J.; Plaza, A.; Wei, Z. Anomaly Detection in Hyperspectral Images Based on Low-Rank and Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1990–2000. [Google Scholar] [CrossRef]
- Huyan, N.; Zhang, X.; Zhou, H. Hyperspectral Anomaly Detection via Background and Potential Anomaly Dictionaries Construction. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2263–2276. [Google Scholar] [CrossRef]
- Cai, W.; Ning, X.; Zhou, G.; Bai, X.; Jiang, Y.; Li, W.; Qian, P. A Novel Hyperspectral Image Classification Model Using Bole Convolution with Three-Directions Attention Mechanism: Small sample and Unbalanced Learning. IEEE Trans. Geosci. Remote. Sens. 2022, 61, 5500917. [Google Scholar] [CrossRef]
- Cai, W.; Wei, Z. Remote Sensing Image Classification Based on a Cross-Attention Mechanism and Graph Convolution. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- He, F.; Yan, S.; Ding, Y.; Sun, Z.; Zhao, J.; Hu, H.; Zhu, Y. Recursive RX with Extended Multi-Attribute Profiles for Hyperspectral Anomaly Detection. Remote Sens. 2023, 15, 589. [Google Scholar] [CrossRef]
- Chu, Y.; Wang, Z.; Peng, J.; Ding, W.; Cao, H. Fuzzy Triple Contrastive Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2025, 63, 1–17. [Google Scholar] [CrossRef]
- Cao, Z.; Chen, S.; Li, J. Enhancing Hyperspectral Image Classification in Small Sample Settings Using Conditional Denoising Diffusion Implicit Model. IEEE Signal Process. Lett. 2025, 32, 2479–2483. [Google Scholar] [CrossRef]
- Wei, Y.; Niu, C.; Wang, H.; Liu, D. The Hyperspectral Image Clustering Based on Spatial Information and Spectral Clustering. In Proceedings of the 2019 IEEE 4th International Conference on Signal and Image Processing (ICSIP), Wuxi, China, 19–21 July 2019; pp. 127–131. [Google Scholar]
- Mei, Z.; Yin, Z. Self-Supervised Learning of Discriminative Spatial–Spectral Features for Hyperspectral Images Clustering. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Chi, J.; Shen, X.; Yu, H.; Shang, X.; Chanussot, J.; Shi, Y. Robust Linear Unmixing for Hyperspectral Remote Sensing Imagery Based on Enhanced Constraint of Classification. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 1628–1631. [Google Scholar]
- Chen, J.; Li, J.; Gamba, P. A Multi-Tasks Autoencoder Hyperspectral Unmixing Model with Information Gain Based On Graph Network. In Proceedings of the Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Athens, Greece, 31 October–2 November 2023; pp. 1–5. [Google Scholar]
- Xiao, Z. Hyperspectral Image Denoising Based on Low-Rank Matrix Decomposition Image Prior. In Proceedings of the 2024 6th International Conference on Electronics and Communication, Network and Computer Technology (ECNCT), Guangzhou, China, 19–21 July 2024; pp. 56–59. [Google Scholar]
- Lin, P.; Jiang, X.; Sun, L. Hyperspectral Image Denoising Via Cosine Transform-Based Tensor Subspace Representation. In Proceedings of the 2023 13th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing, Athens, Greece, 31 October–2 November 2023; pp. 1–5. [Google Scholar]
- Ma, H.; Wang, Y.; Jiang, L.; Song, M.; Yu, C.; Zhao, E. Multi-Scale Fusion Maximum Entropy Subspace Clustering for Hyperspectral Band Selection. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 779–782. [Google Scholar]
- Francis, J.; Shanthini, K.S.; George, S.N.; George, S. A Tensor Non-Convex Low Rank and Sparse Constrained Band Selection Scheme for Clustering of Hyperspectral Paper Data. In Proceedings of the 2022 12th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Rome, Italy, 13–16 September 2022; pp. 1–5. [Google Scholar]
- Liang, C.; Chen, Z. A Self-Supervised Hierarchical Clustering Network For Multiple Change Detection In Multitemporal Hyper-spectral Images. In Proceedings of the 2022 12th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Rome, Italy, 13–16 September 2022; pp. 1–4. [Google Scholar]
- Shammi, S.A.; Du, Q. Hyperspectral Image Change Detection Using Deep Learning and Band Expansion. In Proceedings of the 2022 12th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Rome, Italy, 13–16 September 2022; pp. 1–5. [Google Scholar]
- Han, X.; Wei, Y.; Zhang, H.; Xu, Q.; Sun, W. Tuning to Real for Single-Spectrum Hyperspectral Target Detection. In Proceedings of the 2023 13th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Athens, Greece, 31 October–2 November 2023; pp. 1–5. [Google Scholar]
- Li, G.; Hao, H.; Wu, L.; Liu, B. Current Situation of Denoising And Target Detection In Hyperspectral Images. In Proceedings of the 2022 3rd International Conference on Geology, Mapping and Remote Sensing (ICGMRS), Zhoushan, China, 22–24 April 2022; pp. 555–559. [Google Scholar]
- Wang, Y.; Sun, J.; Xu, Y.; Wei, Z.; Zheng, S.; Wu, Z. Fast Processing of Massive Hyperspectral Image Anomaly Detection Based on Cloud-Edge Collaboration. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 14644–14657. [Google Scholar] [CrossRef]
- Wang, Y.; Li, W.; Gui, Y.; Xie, H.; Zhang, L. A Generalized Non-Convex Surrogated Framework for Anomaly Detection on Blurred Hyperspectral Images. IEEE Trans. Image Process. 2025, 34, 3108–3122. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Tao, X.; Paoletti, M.E.; Haut, J.M.; Pastor-Vargas, R.; Plaza, A. Deep Unrolling Network with Active Dictionary Learning for Hyperspectral Anomaly Detection. In Proceedings of the 2023 13th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Athens, Greece, 31 October–2 November 2023; pp. 1–5. [Google Scholar]
- Reed, I.S.; Yu, X. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1760–1770. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, Y.; Qi, B.; Wang, J. Global and Local Real-Time Anomaly Detectors for Hyperspectral Remote Sensing Imagery. Remote Sens. 2015, 7, 3966–3985. [Google Scholar] [CrossRef]
- Molero, J.M.; Garzn, E.M.; Garca, I.; Plaza, A. Analysis and optimizations of global and local versions of the RX algorithm for anomaly detection in hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 801–814. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, B.; Ran, Q.; Gao, L.; Li, J.; Plaza, A. Weighted-RXD and Linear Filter-Based RXD: Improving Background Statistics Estimation for Anomaly Detection in Hyperspectral Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2351–2366. [Google Scholar] [CrossRef]
- Tang, L.; Song, Y.; Li, J.; Li, Q.; Li, R.; Li, R.; Chen, J. Hyperspectral Anomaly Detection with CNN-Based VAE and RX Algorithm. In Proceedings of the 2024 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Bali, Indonesia, 19–22 August 2024; pp. 1–5. [Google Scholar]
- Li, J.; Zhang, H.; Zhang, L.; Ma, L. Hyperspectral Anomaly Detection by the Use of Background Joint Sparse Representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2523–2533. [Google Scholar] [CrossRef]
- Ma, N.; Peng, Y.; Wang, S. A Fast Recursive Collaboration Representation Anomaly Detector for Hyperspectral Image. IEEE Geosci. Remote Sens. Lett. 2019, 16, 588–592. [Google Scholar] [CrossRef]
- Wang, R.; Feng, W.; Zhang, Q. Ensemble and Random Collaborative Representation-Based Anomaly Detector for Hyperspectral Imagery. Signal Process. 2023, 204, 108835. [Google Scholar]
- Pesarest, M.; Benediktsson, J.A. A new approach for the morphological segmentation of high-resolution satellite imagery. IEEE Trans. Geosci. Remote Sens. 2002, 39, 309–320. [Google Scholar] [CrossRef]
- Mura, M.D.; Benediktsson, J.A.; Waske, B.; Bruzzone, L. Morphological Attribute Profiles for the Analysis of Very High Resolution Images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3747–3762. [Google Scholar] [CrossRef]
- Xia, J.; Mura, M.D.; Chanussot, J.; Du, P.; He, X. Random Subspace Ensembles for Hyperspectral Image Classification with Extended Morphological Attribute Profiles. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4768–4786. [Google Scholar] [CrossRef]
- Kang, X.; Zhang, X.; Li, S.; Li, K.; Li, J. Hyperspectral Anomaly Detection with Attribute and Edge-Preserving Filters. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5600–5611. [Google Scholar] [CrossRef]
- Manolakis, D.; Marden, D.; Shaw, G.A. Hyperspectral image processing for automatic target detection applications. Linc. Lab. J. 2003, 14, 79–116. [Google Scholar]





| Dataset | CRD | RCRD | EMAPKCRD |
|---|---|---|---|
| AVIRIS-I | 8.6520 | 7.6974 | 0.6768 |
| AVIRIS-II | 6.0194 | 5.2538 | 0.3962 |
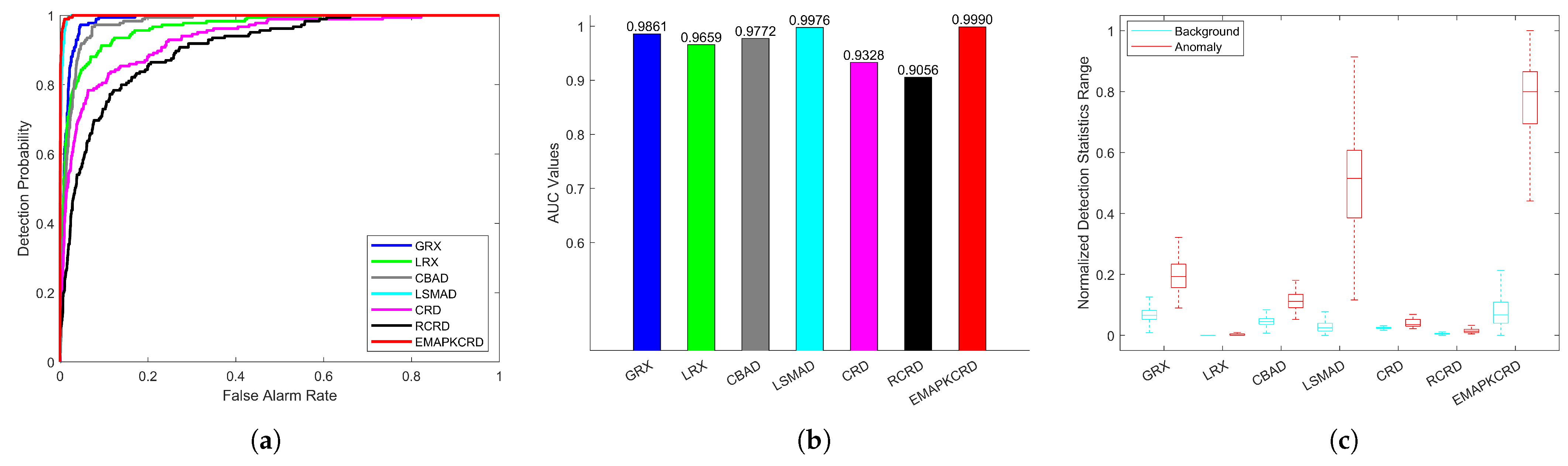
| Salinas-simulate | 11.5895 | 10.3151 | 3.0305 |
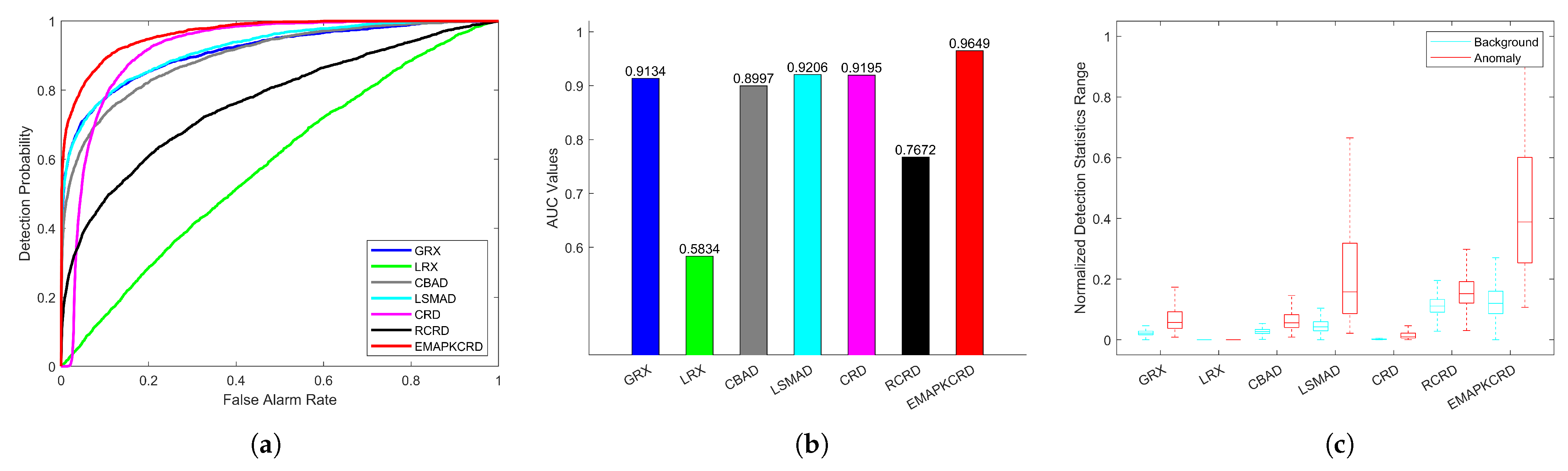
| Cri | 80.0832 | 62.0249 | 22.7172 |
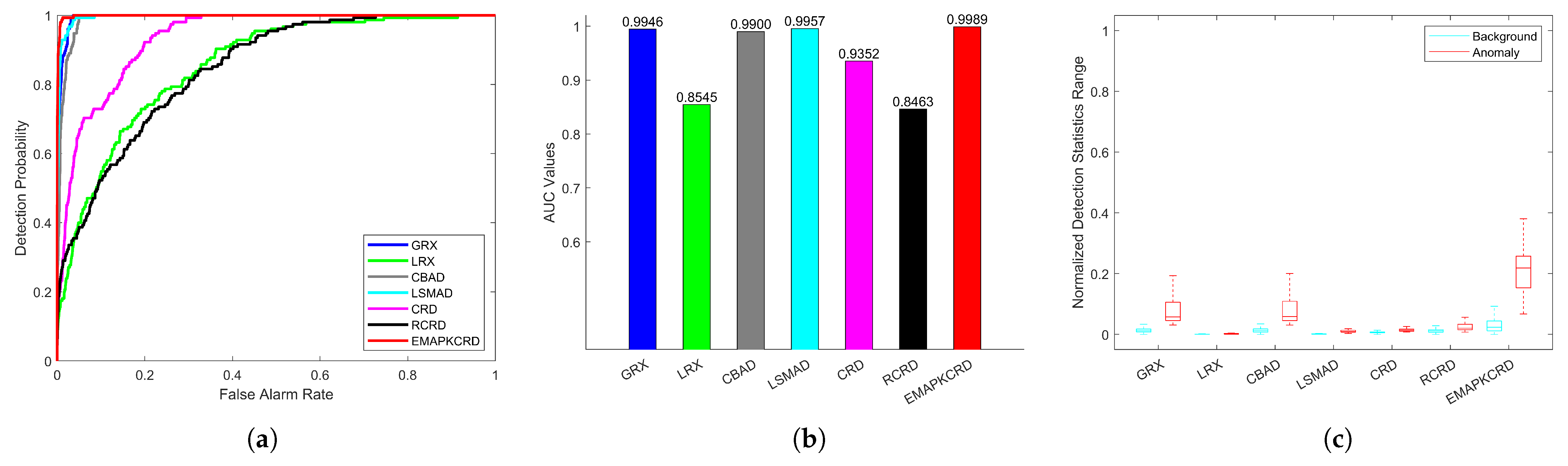
| abu-urban-2 | 6.3766 | 5.8111 | 0.7924 |
| Dataset | CRD | RCRD | EMAPKCRD |
|---|---|---|---|
| AVIRIS-I | 0.9896 | 0.9875 | 0.9916 |
| AVIRIS-II | 0.9631 | 0.9745 | 0.9813 |
| Salinas-simulate | 0.9328 | 0.9056 | 0.9990 |
| Cri | 0.9195 | 0.7672 | 0.9649 |
| abu-urban-2 | 0.9352 | 0.8463 | 0.9989 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, F.; Fan, S.; Hu, H.; Zhao, J.; Dong, J.; Jia, W. A Fast Collaborative Representation Algorithm Based on Extended Multi-Attribute Profiles for Hyperspectral Anomaly Detection. Remote Sens. 2025, 17, 3857. https://doi.org/10.3390/rs17233857
He F, Fan S, Hu H, Zhao J, Dong J, Jia W. A Fast Collaborative Representation Algorithm Based on Extended Multi-Attribute Profiles for Hyperspectral Anomaly Detection. Remote Sensing. 2025; 17(23):3857. https://doi.org/10.3390/rs17233857
Chicago/Turabian StyleHe, Fang, Shuanghao Fan, Haojie Hu, Jianwei Zhao, Jiaxin Dong, and Weimin Jia. 2025. "A Fast Collaborative Representation Algorithm Based on Extended Multi-Attribute Profiles for Hyperspectral Anomaly Detection" Remote Sensing 17, no. 23: 3857. https://doi.org/10.3390/rs17233857
APA StyleHe, F., Fan, S., Hu, H., Zhao, J., Dong, J., & Jia, W. (2025). A Fast Collaborative Representation Algorithm Based on Extended Multi-Attribute Profiles for Hyperspectral Anomaly Detection. Remote Sensing, 17(23), 3857. https://doi.org/10.3390/rs17233857






