A High-Fidelity Star Map Simulation Method for Airborne All-Time Three-FOV Star Sensor Under Dynamic Conditions
Highlights
- A comprehensive star map simulation method for airborne All-Time Three-FOV star sensors is proposed, integrating coordinate transformation, energy transfer, and image degradation models.
- The method offers a reliable technical basis for optimizing the design and assessing the performance of airborne All-Time Three-FOV star sensors under dynamic conditions.
- It enables the validation of star centroid extraction and identification algorithms under controlled disturbance scenarios, reducing dependency on costly and time-consuming real-world stargazing experiments.
Abstract
1. Introduction
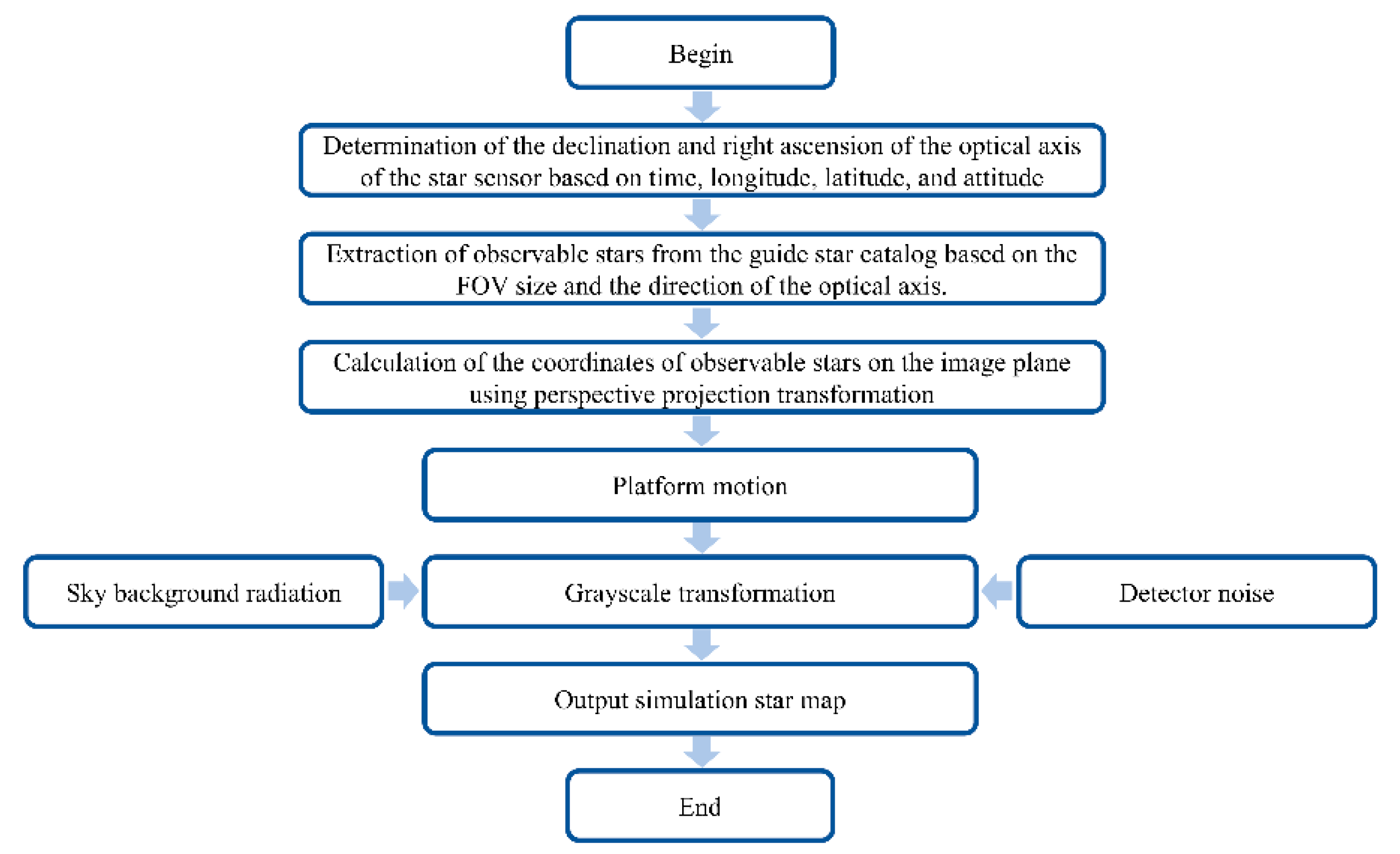
2. The Fundamental Workflow of Star Map Simulation
2.1. Coordinate Transformation
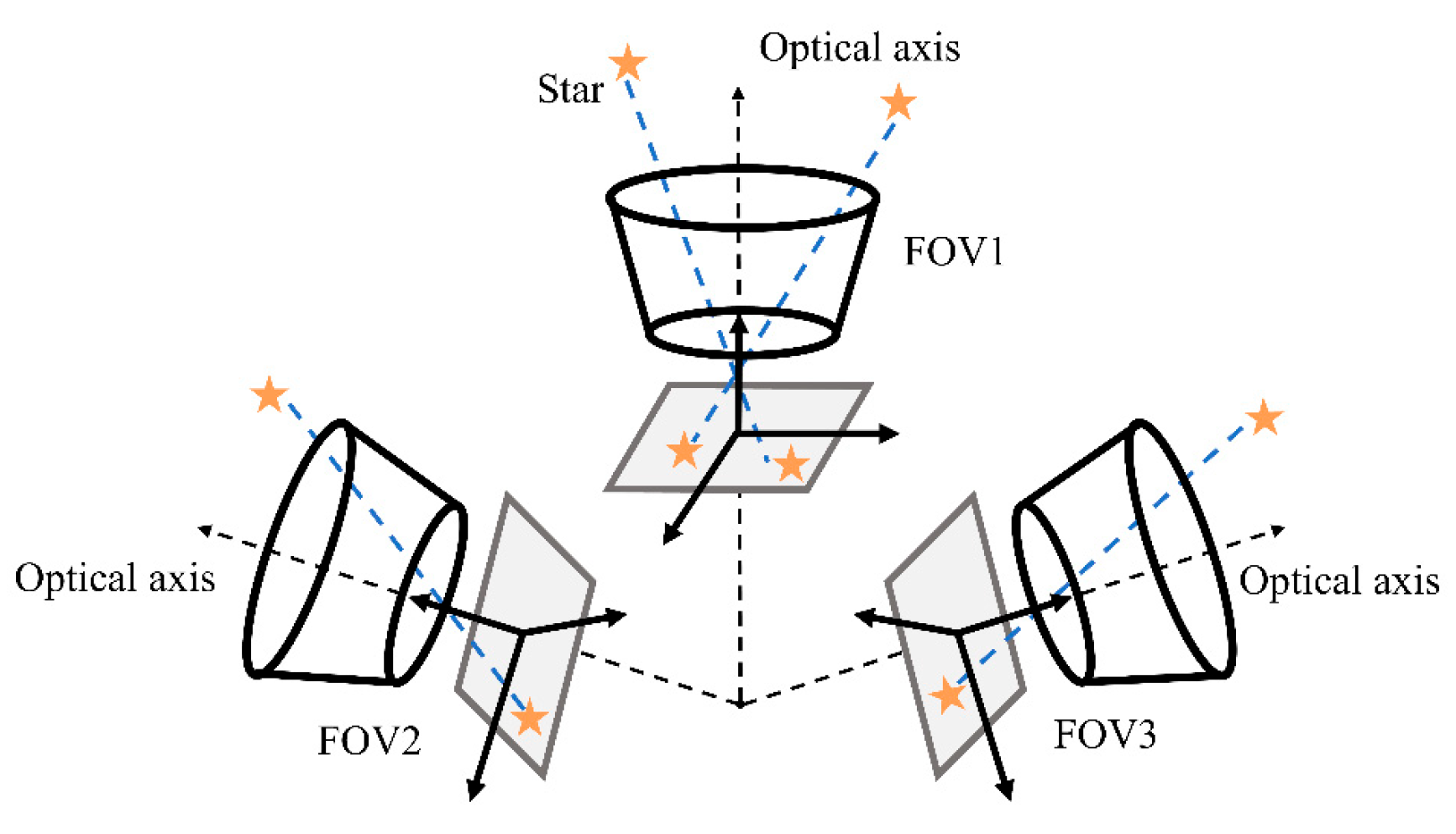
2.1.1. Coordinate System Definition
2.1.2. Extraction of Observable Stars
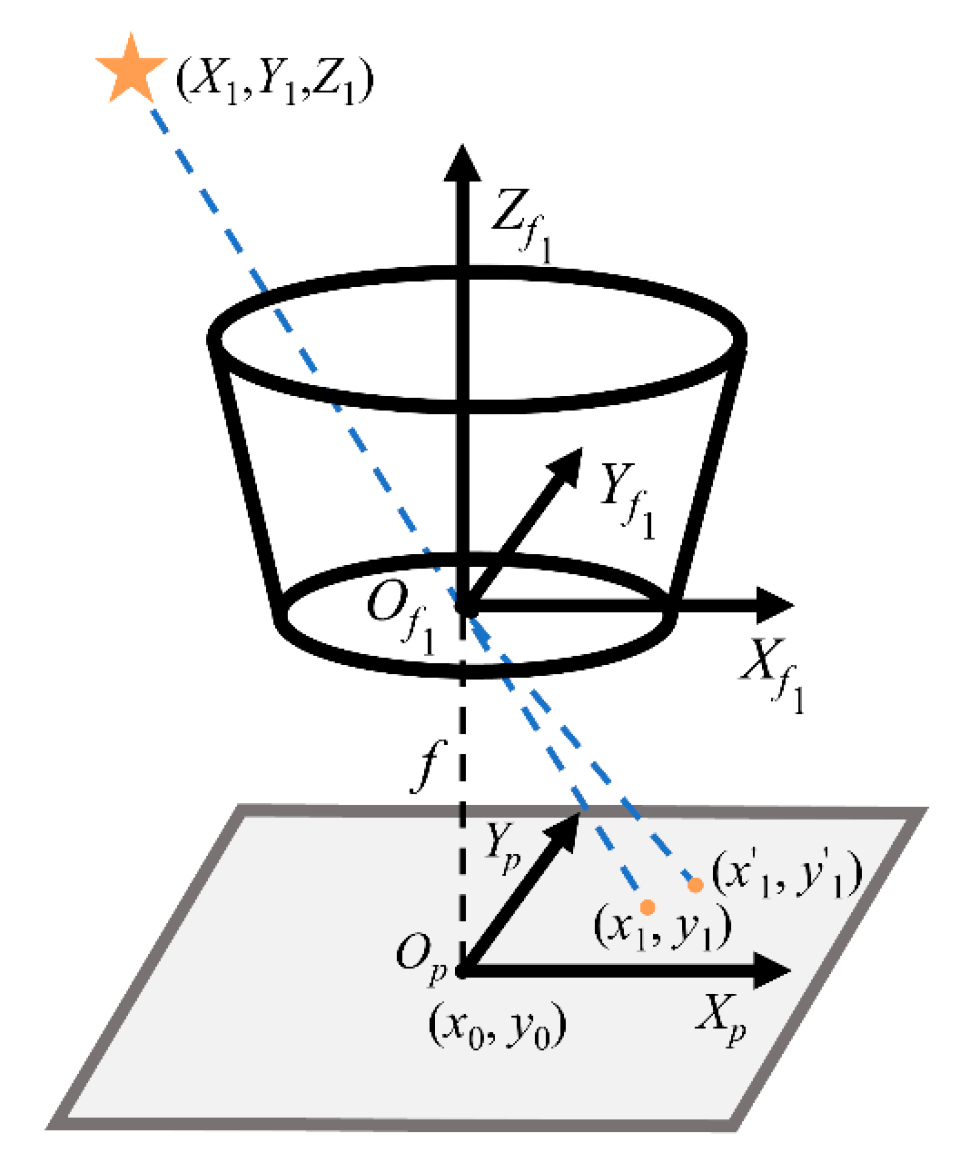
2.1.3. Transformation from Celestial to Image Coordinate Systems
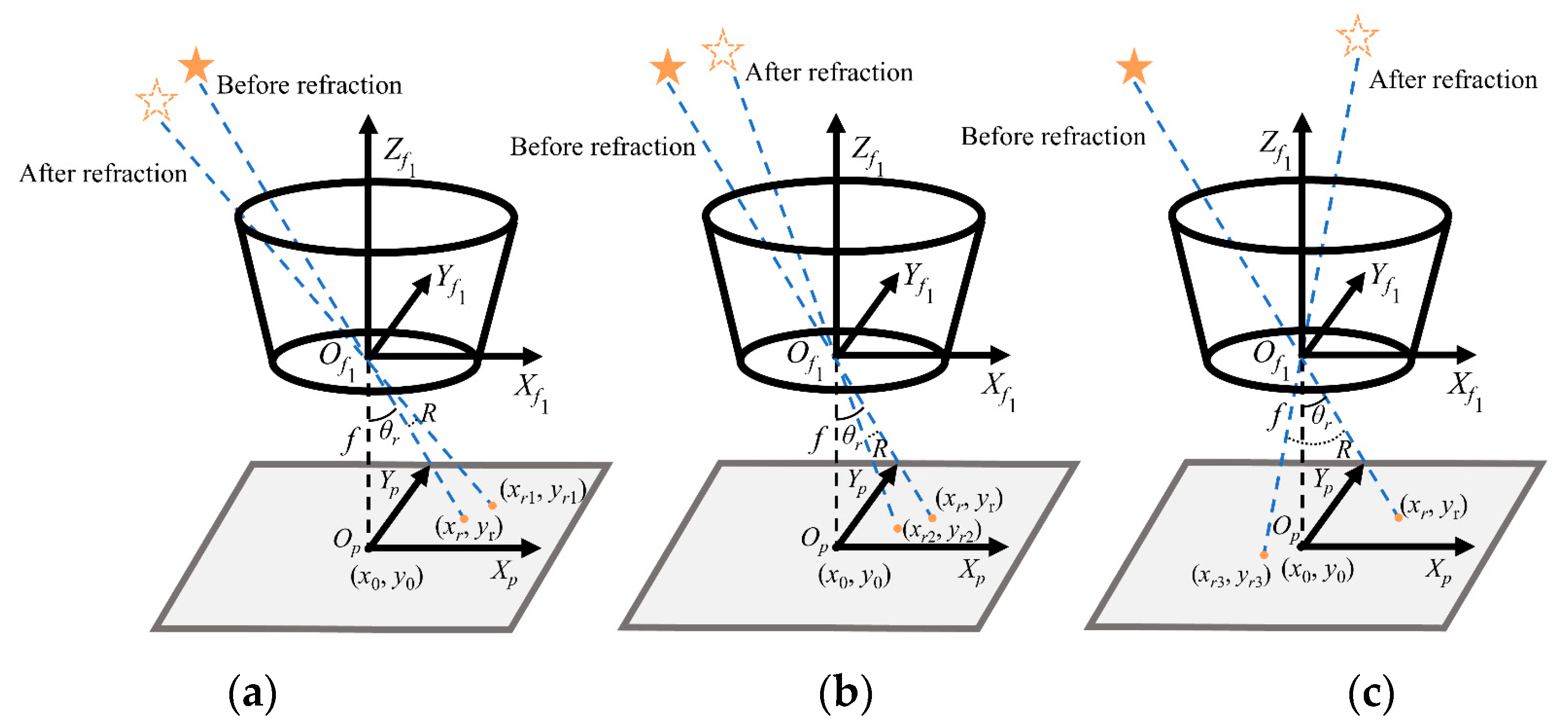
2.1.4. Impact of Atmospheric Refraction on Stellar Imaging
2.2. Star Imaging Model Under Dynamic Conditions
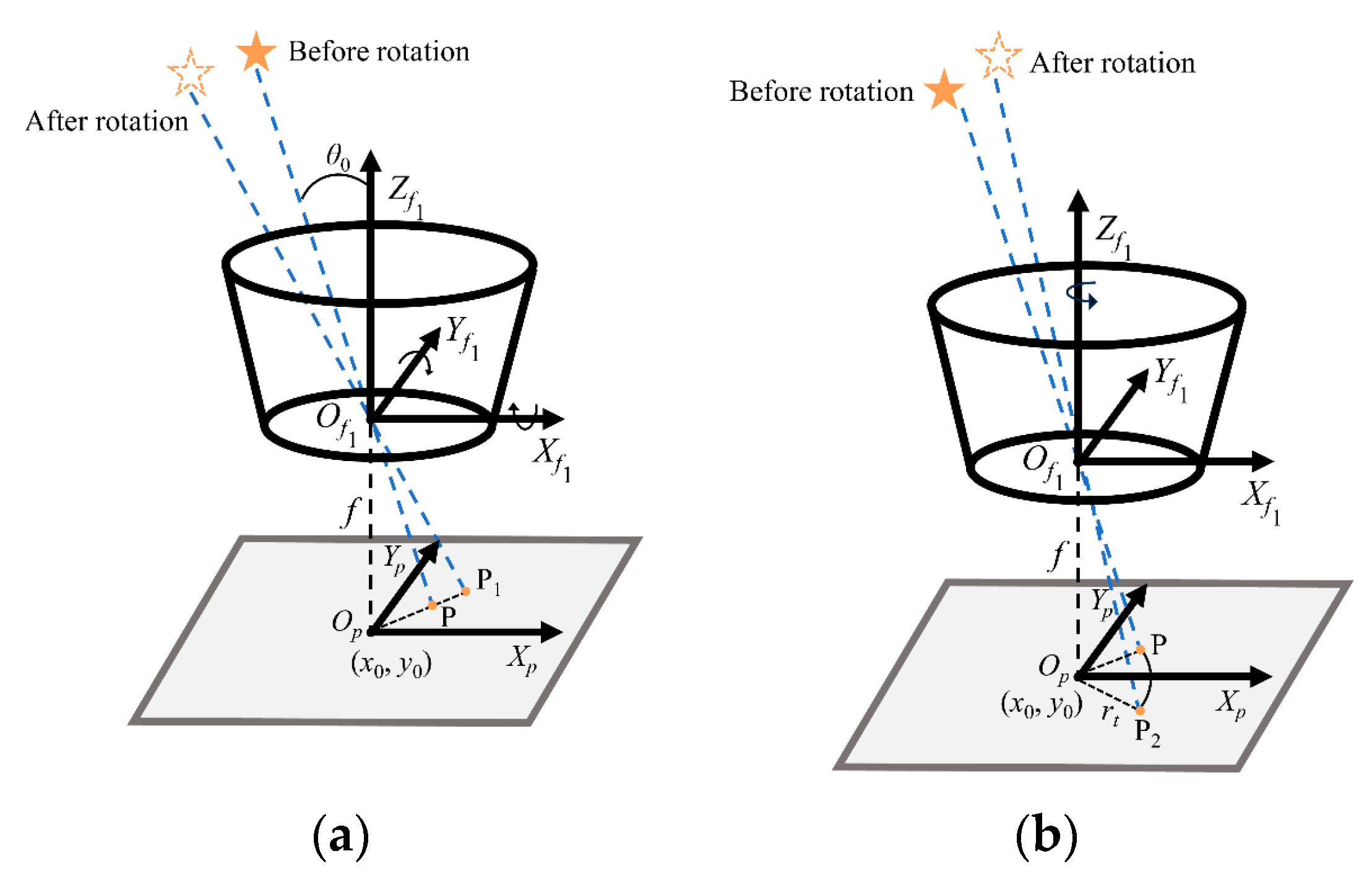
2.2.1. Rotation of the Airborne Platform About an Arbitrary Axis
- Non-optical axes component contribution: The angular velocities ωx and ωy induce linear displacement of the star spot, as illustrated in Figure 5a. At time t, the displacement components along the image coordinate system axes Xp and Yp, denoted Lx1(t) and Ly1(t) respectively, are given by:
- 2.
- Optical-axis component contribution: The angular velocity ωz induces circumferential motion of the star spot about point Op. At time t, the corresponding arc length Lz(t) is given by:
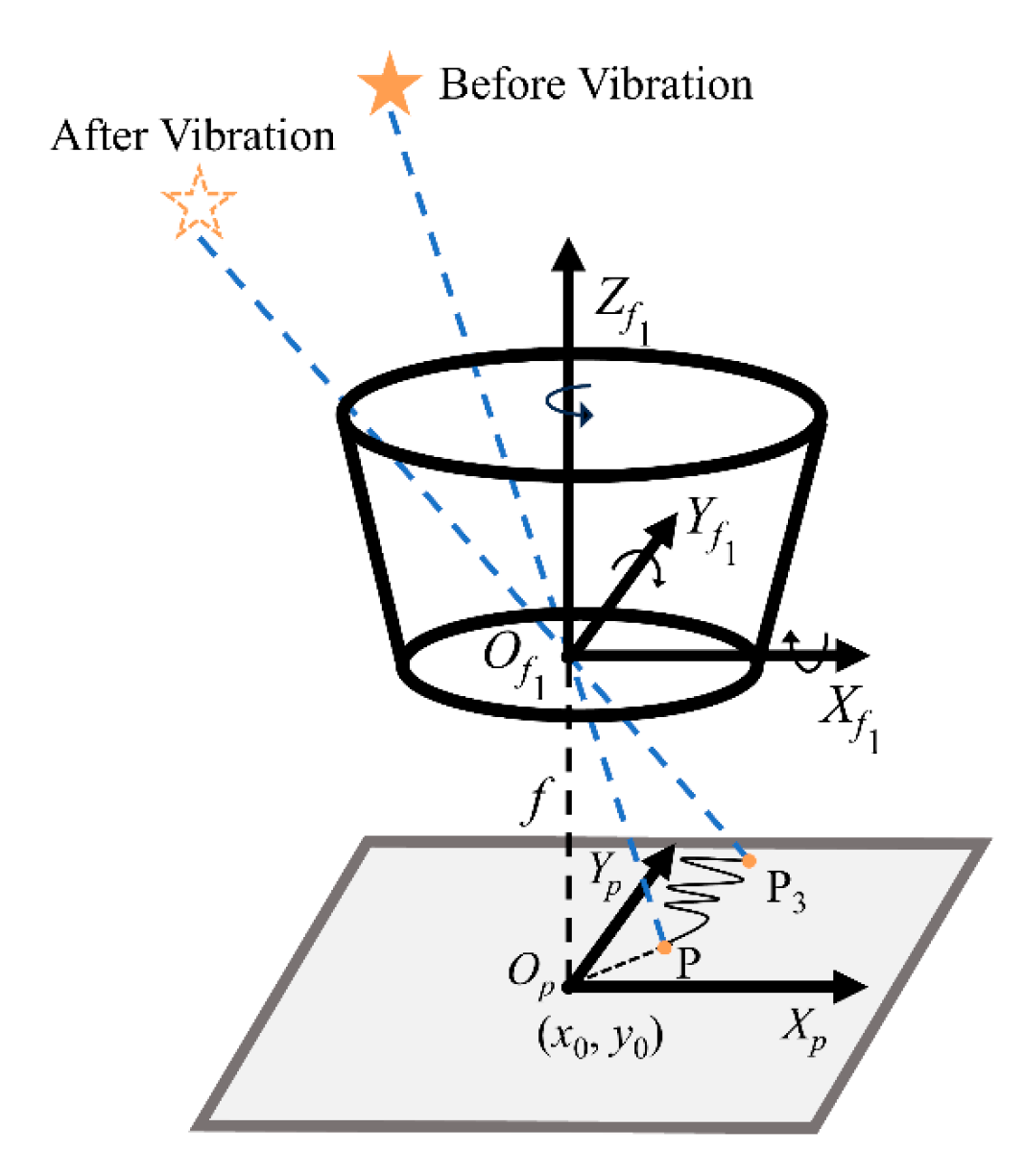
2.2.2. Angular Vibration of the Airborne Platform About an Arbitrary Axis
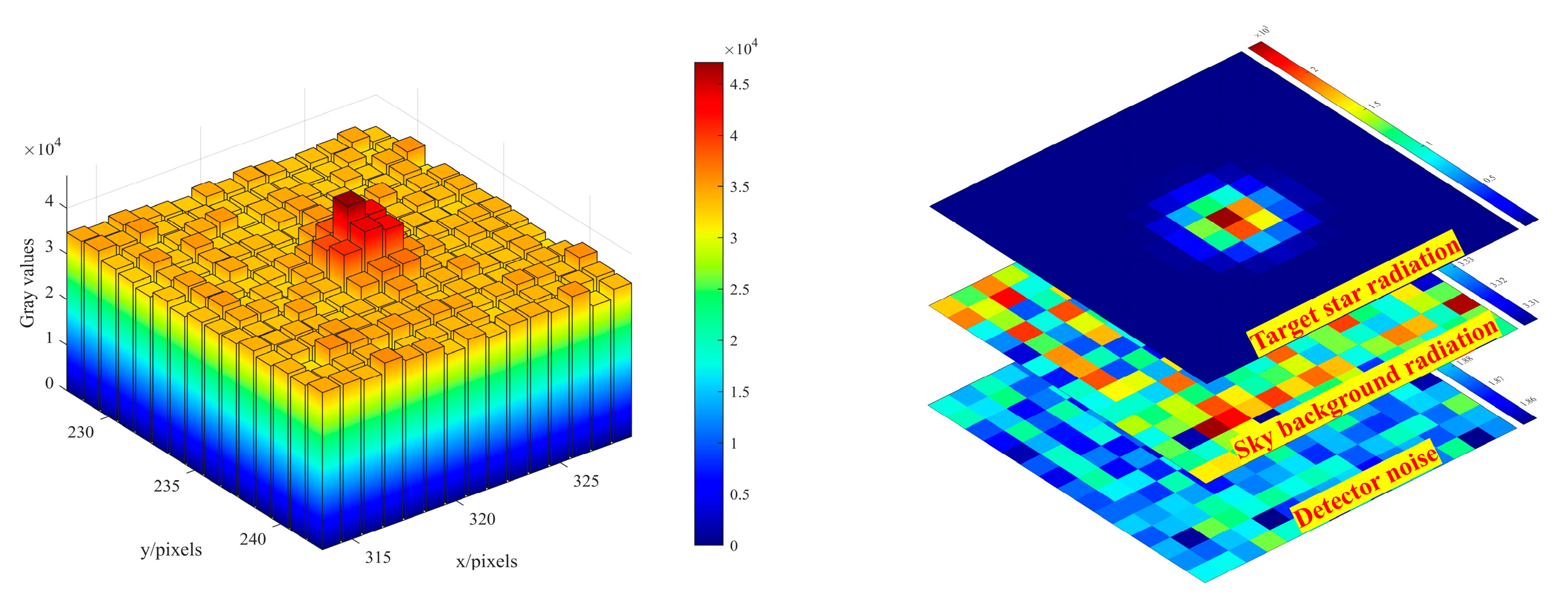
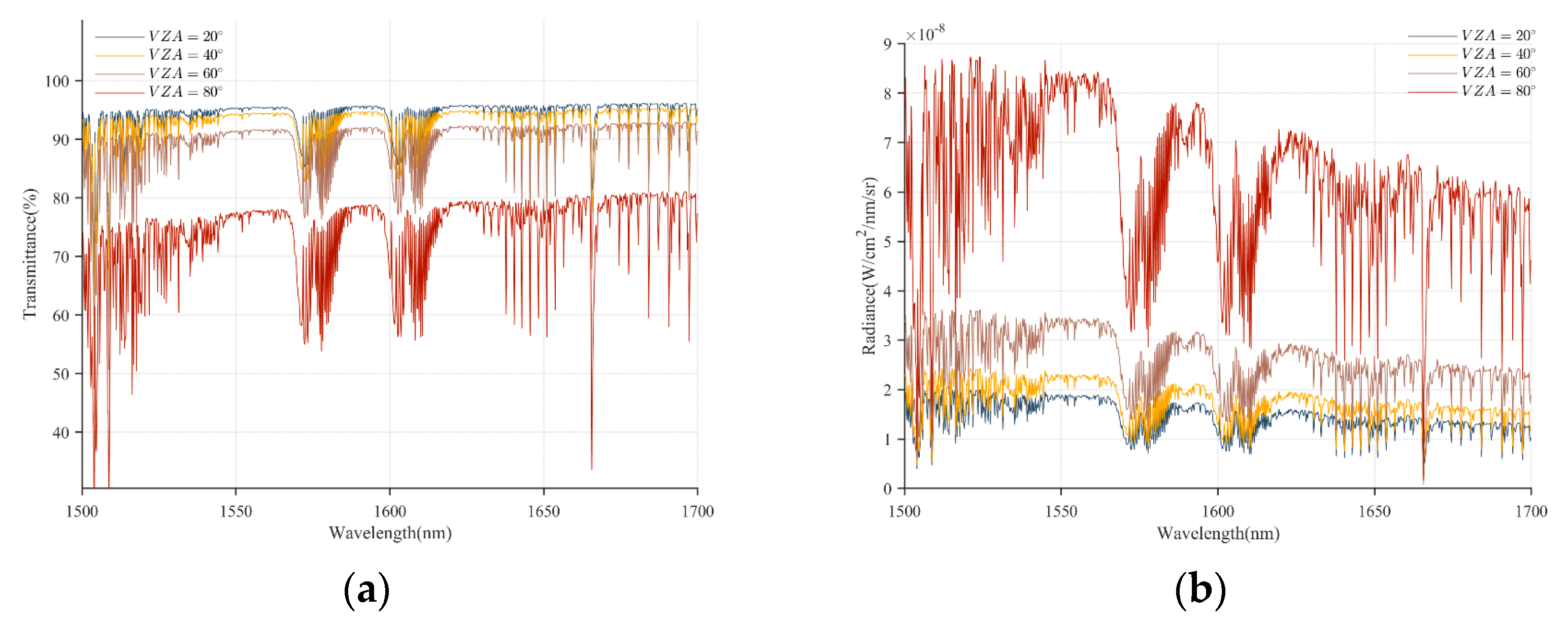
2.3. Energy Modeling of Star Map
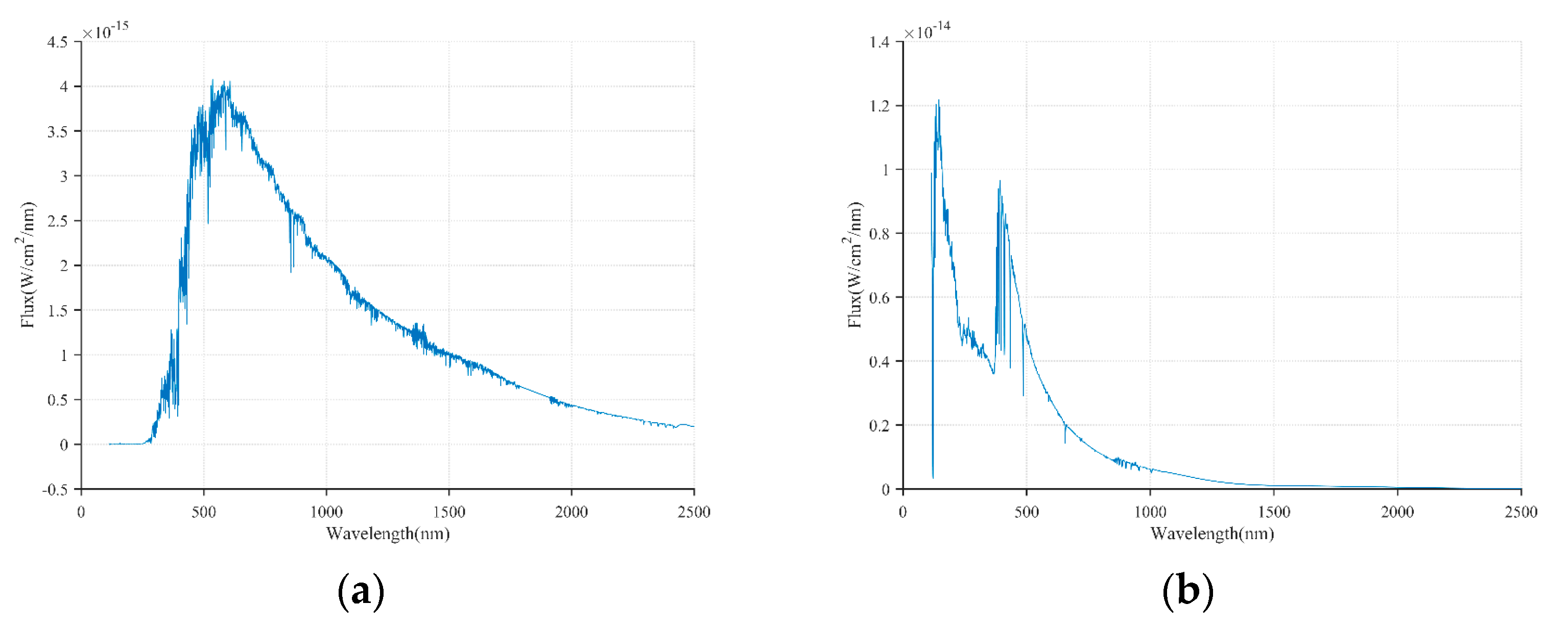
2.3.1. Stellar Radiation Model
2.3.2. Sky Background Radiation Model
2.3.3. Detector Noise Model
2.4. Stellar Energy Distribution
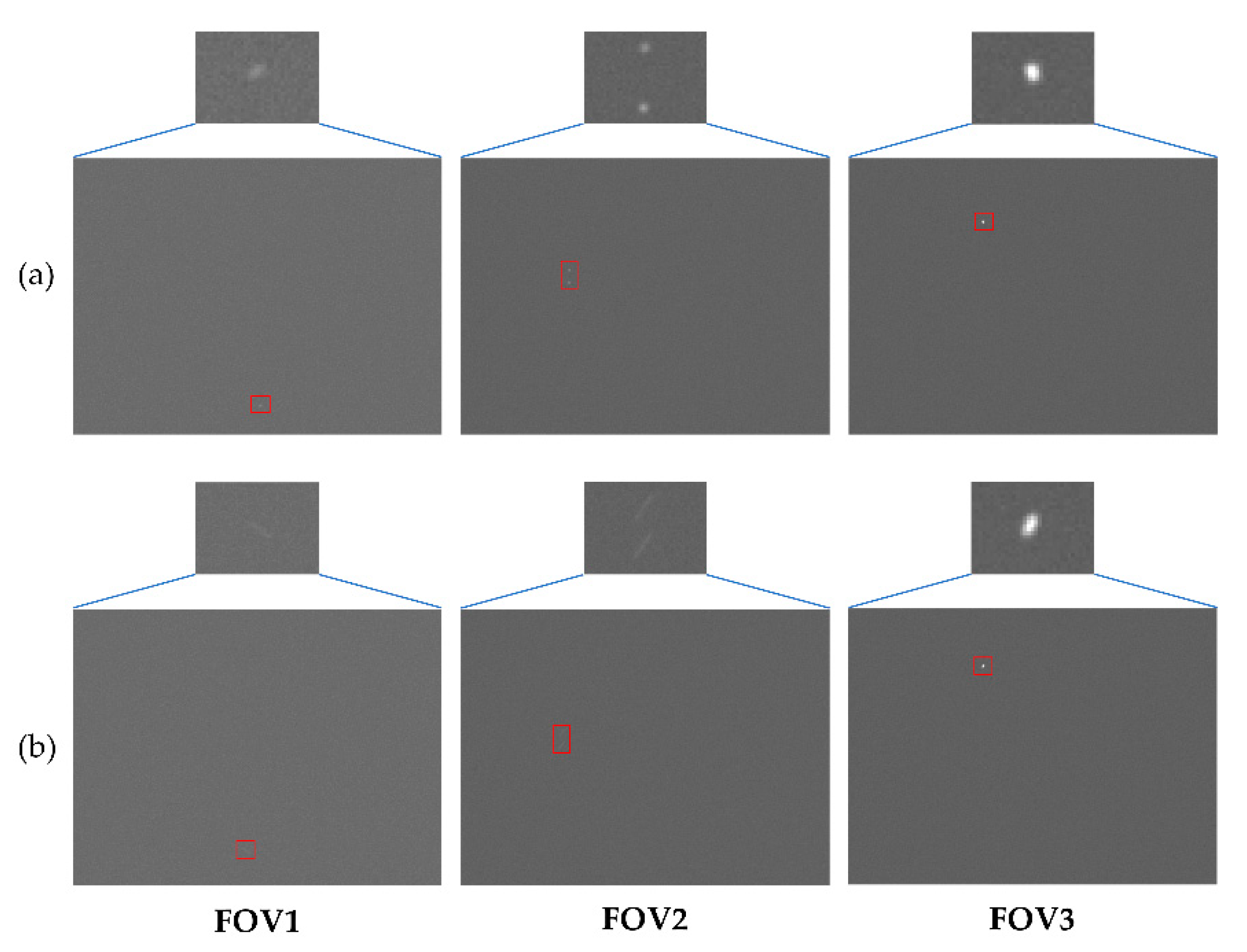
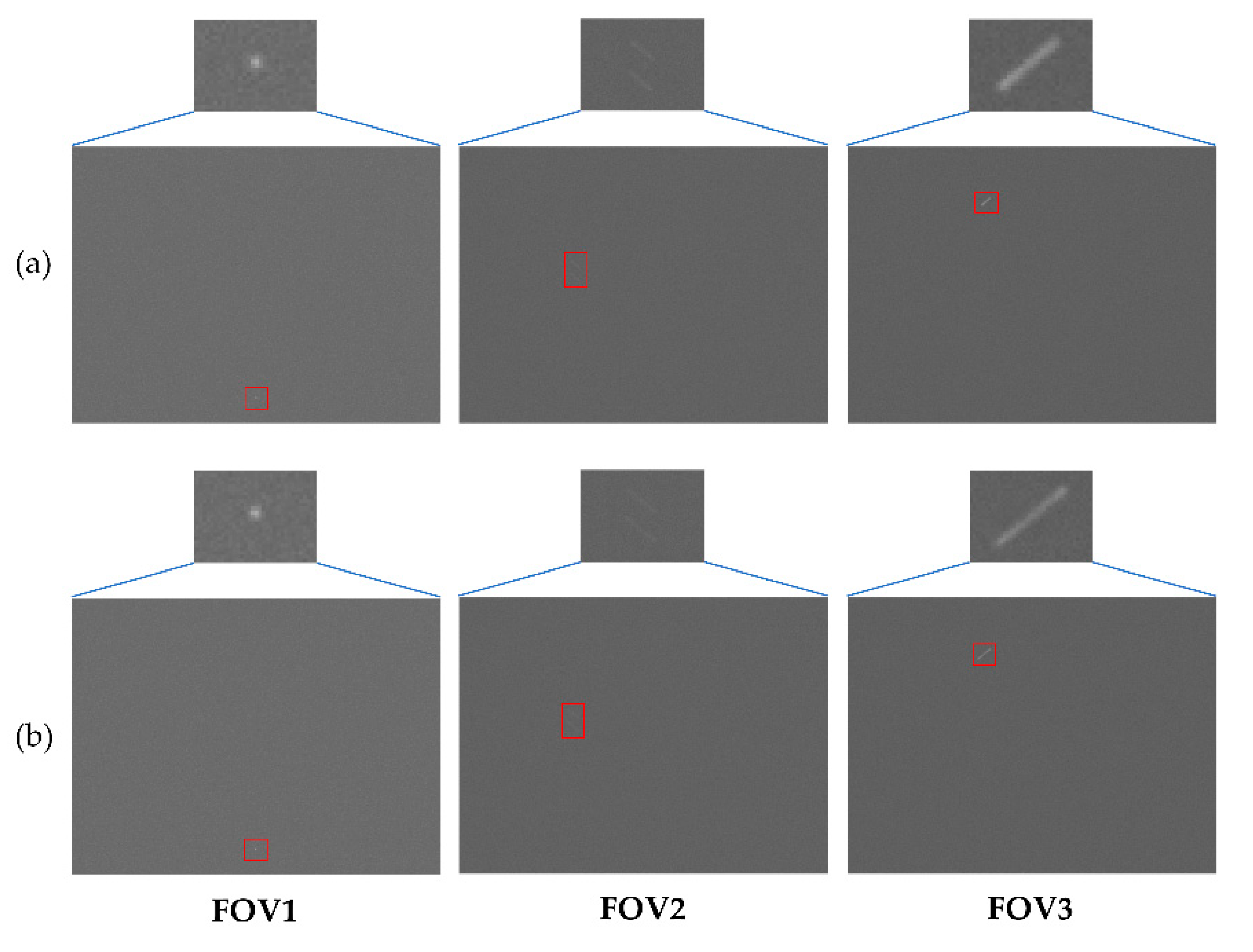
3. Star Map Simulation and Validation
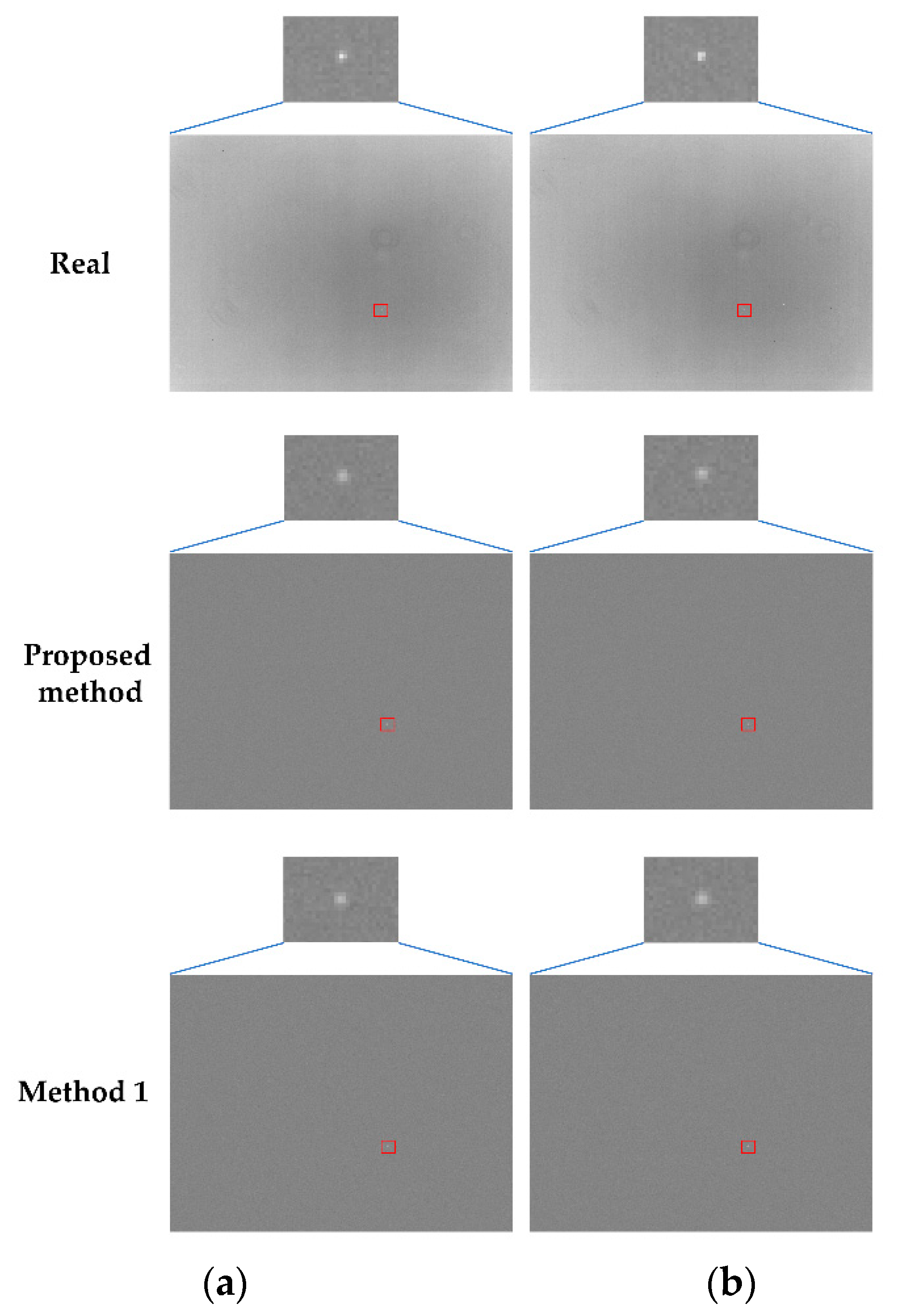
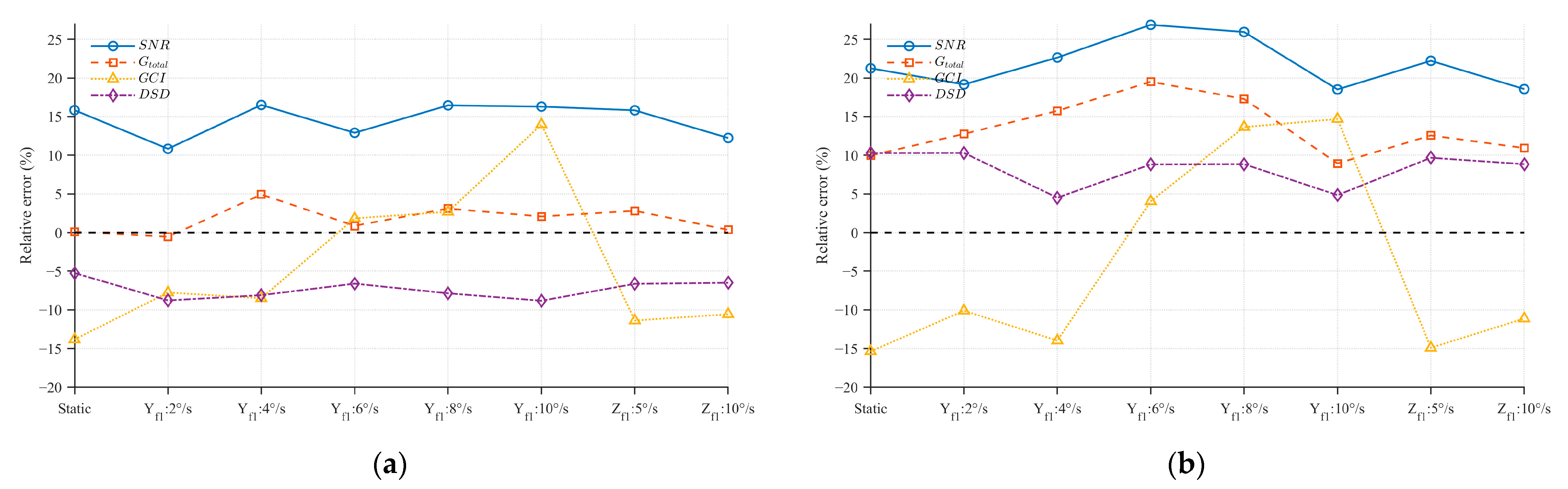
3.1. Evaluation Metrics
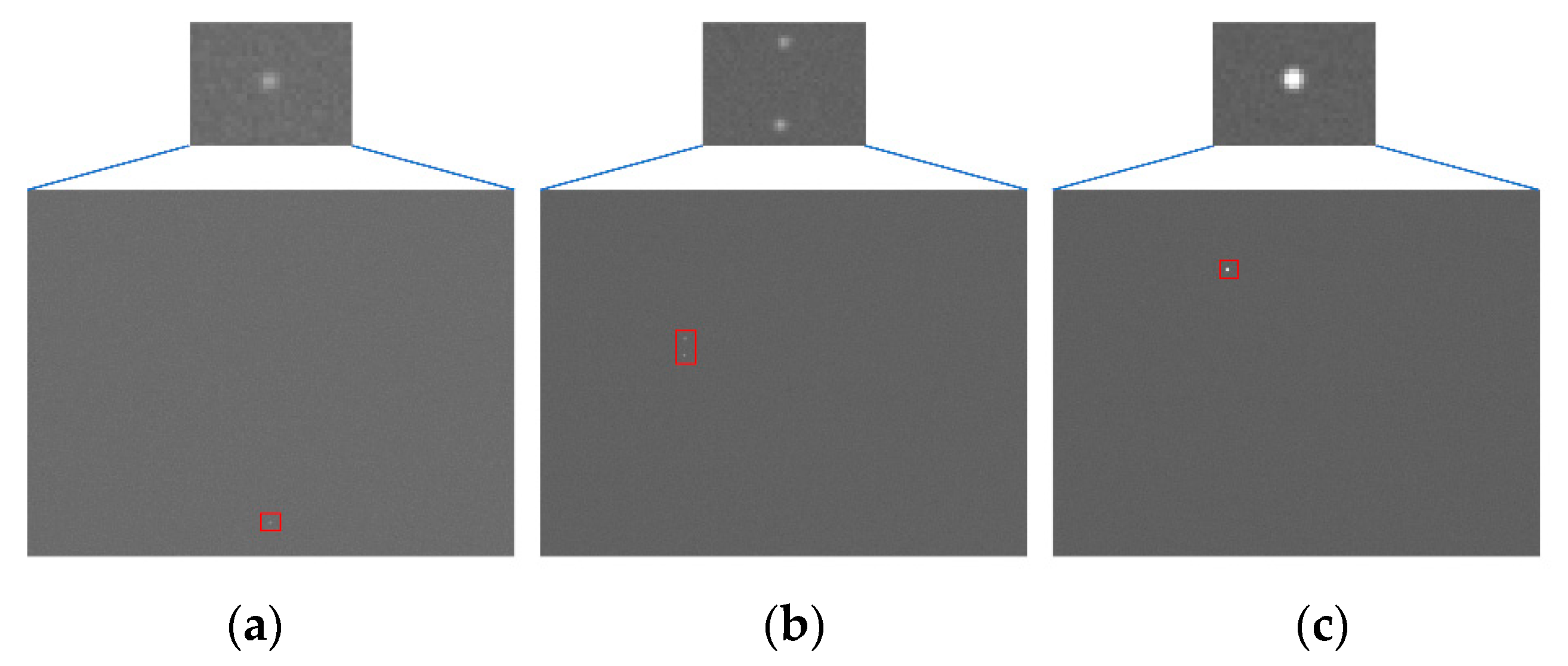
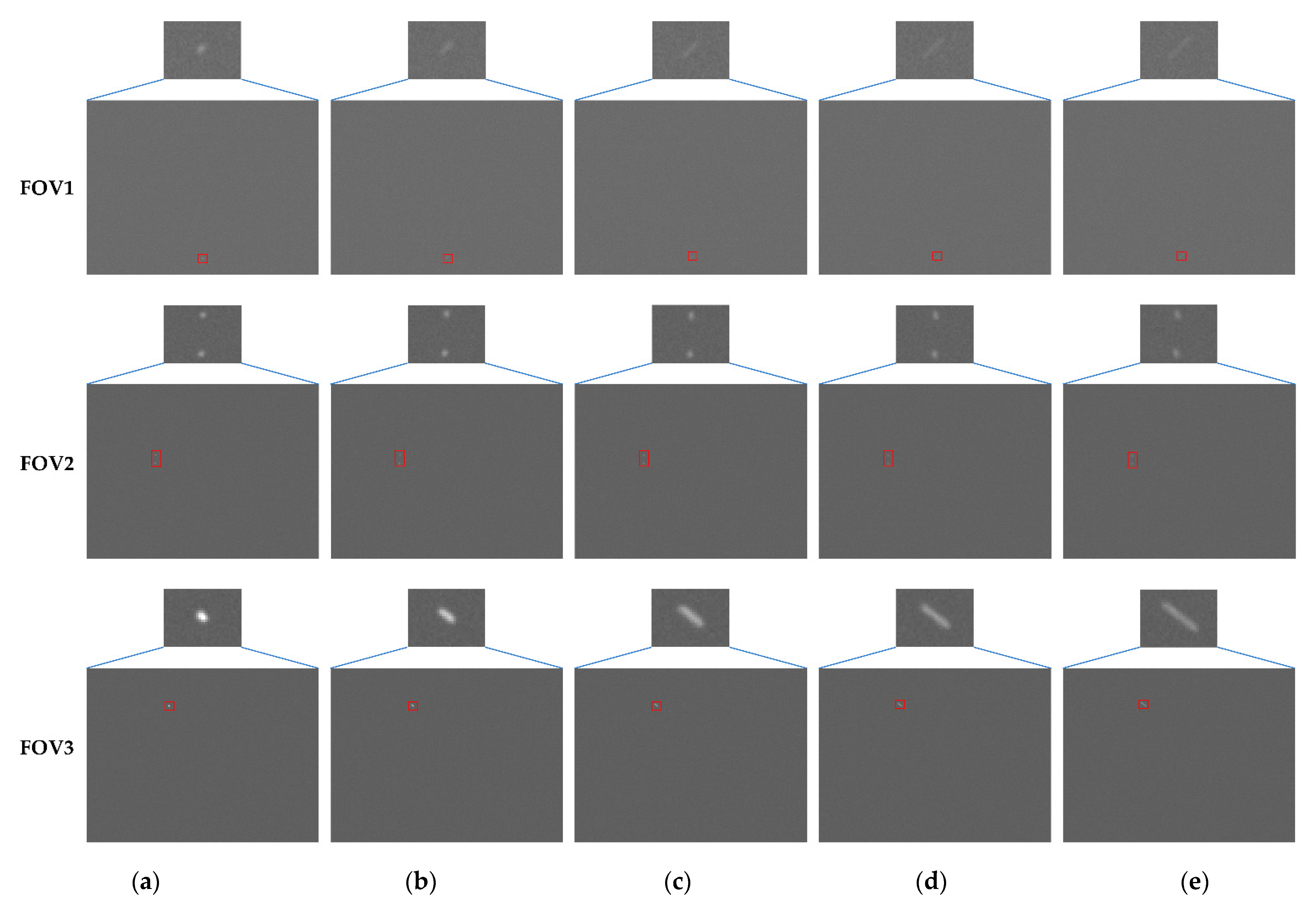
3.2. Simulation Results
- Motion parameters of the airborne platform, including the angular velocity and angular vibration amplitude coefficient;
- FOV installation parameters, specifically the pointing deviation between each FOV’s optical axis and the rotation/vibration axis.
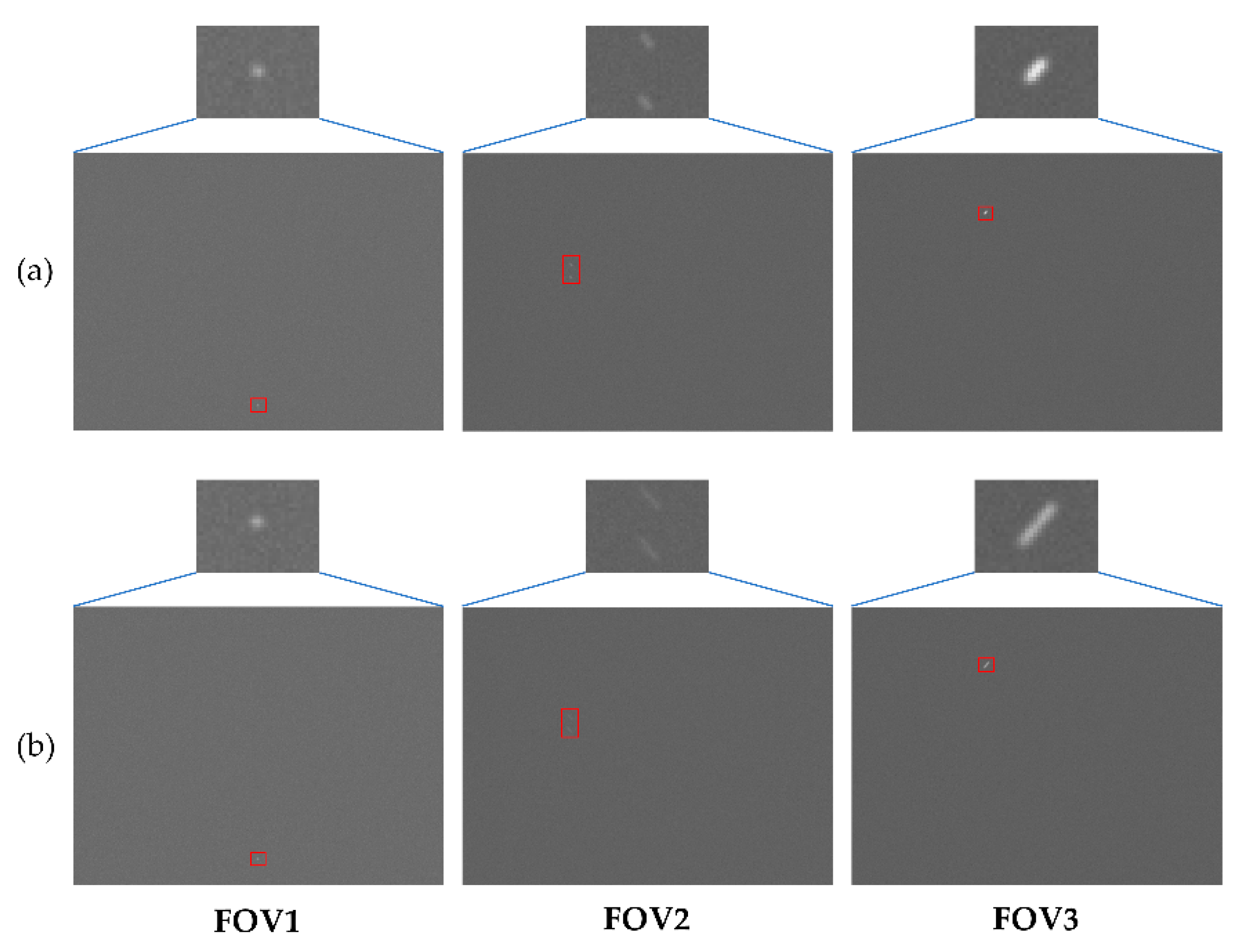
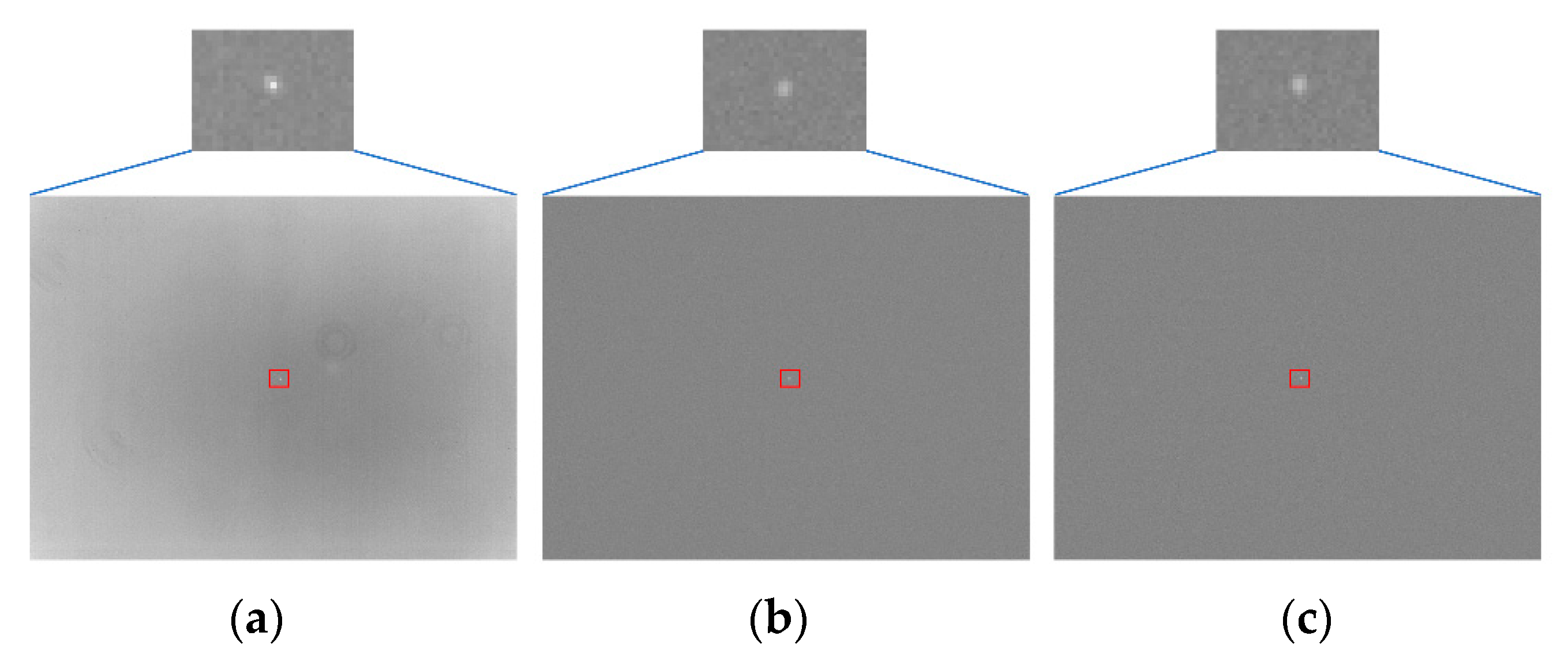
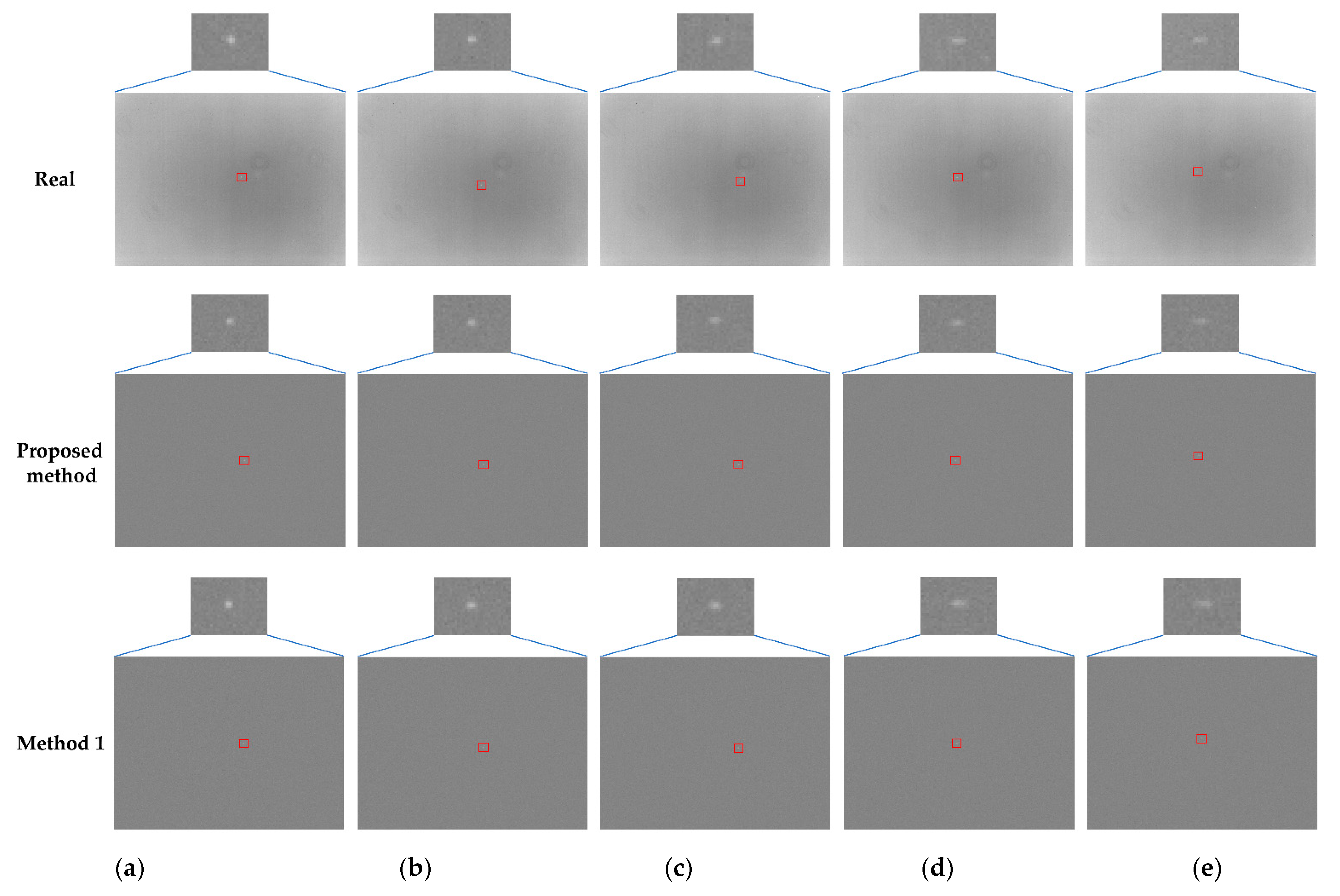
3.3. Experimental Verification
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.; Zhou, X.; Wang, X.; Tian, H. Survey of technology status and development of all-time star sensors in near-earth space. Hangkong Xuebao 2020, 41, 13–25. [Google Scholar]
- Lu, X.; Li, C.; Li, X.; Sun, D.; Xia, M. Current Situation and Development Trends of Starlight Navigation Technology. Aerosp. Control Appl. 2017, 43, 1–8. [Google Scholar]
- Huang, H.; Chen, C.; Guan, B.; Tan, Z.; Shang, Y.; Li, Z.; Yu, Q. Ridge estimation-based vision and laser ranging fusion localization method for UAVs. Appl. Opt. 2025, 64, 1352–1361. [Google Scholar] [CrossRef]
- Liu, Z.; Liang, S.; Guan, B.; Tan, D.; Shang, Y.; Yu, Q. Collimator-assisted high-precision calibration method for event cameras. Opt. Lett. 2025, 50, 4254–4257. [Google Scholar] [CrossRef] [PubMed]
- Liebe, C.C. Accuracy performance of star trackers-a tutorial. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 587–599. [Google Scholar] [CrossRef]
- Li, J.; Wang, G.; Wei, X. Generation of guide star catalog for star trackers. IEEE Sens. J. 2018, 18, 4592–4601. [Google Scholar] [CrossRef]
- Dai, Y.; Shi, C.; Ben, L.; Zhu, H.; Zhang, R.; Wu, S.; Shan, S.; Xu, Y.; Zhou, W. Star Identification Algorithm Based on Dynamic Distance Ratio Matching. Remote Sens. 2024, 17, 62. [Google Scholar] [CrossRef]
- Ma, L.; Zhu, D.; Sun, C.; Dai, D.; Wang, X.; Qin, S. Three-axis attitude accuracy of better than 5 arcseconds obtained for the star sensor in a long-term on-ship dynamic experiment. Appl. Opt. 2018, 57, 9589–9595. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Cao, Q.; Fu, Z.; Xu, T.; Duan, R.; Yang, X. Multi-Centroid Extraction Method for High-Dynamic Star Sensors Based on Projection Distribution of Star Trail. Remote Sens. 2025, 17, 266. [Google Scholar] [CrossRef]
- Feng, J.; Wang, H.C.; Cui, Y.H.; Li, Y.D.; Guo, Q.; Wen, L.; Fu, J. Effects of gamma radiation on the performance of star sensors for star map recognition. Radiat. Phys. Chem. 2023, 203, 110607. [Google Scholar] [CrossRef]
- Fang, L.; Liu, E.; Zhang, H.; Wei, X.; Cheng, X.; Liao, Z.; Zhao, R. Optical imaging system for an all-time star sensor based on field of view gated technology. Appl. Opt. 2022, 61, 5859–5868. [Google Scholar] [CrossRef]
- Liao, Z.; Dong, Z.; Wang, H.; Mao, X.; Wang, B.; Wu, S.; Zang, Y.; Lu, Y. Analysis of flow field aero-optical effects on the imaging by near-earth space all-time short-wave infrared star sensors. IEEE Sens. J. 2022, 22, 15044–15053. [Google Scholar] [CrossRef]
- Rex, M.; Chapin, E.; Devlin, M.J.; Gundersen, J.; Klein, J.; Pascale, E.; Wiebe, D. BLAST autonomous daytime star cameras. In Ground-Based and Airborne Instrumentation for Astronomy; SPIE: Orlando, FL, USA, 2006; pp. 1093–1100. [Google Scholar]
- Liu, B.; Zhu, W.; Zhang, T.; Yang, L.; Guo, J. Determination of ship attitude based on dual star sensors. Opt. Precis. Eng. 2014, 22, 569–575. [Google Scholar] [CrossRef]
- Lei, H.; Li, B.; Wei, Q.; Yue, Y.; Ding, X.; Liang, K.; Chen, L.; Yang, H.; Zhang, W.; Hu, X. Inertial information based star detection for airborne star sensor. Opt. Laser Technol. 2023, 162, 109325. [Google Scholar] [CrossRef]
- Yuan, J.; Wu, J.; Kang, G. High-Precision Centroid Localization Algorithm for Star Sensor Under Strong Straylight Condition. Remote Sens. 2025, 17, 1108. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, H.; Gao, X.; Fang, L.; Lu, K.; Zhao, R. Generation of guide star catalog for the all-time three-FOV star sensor applied on airborne platforms. J. Opt. Soc. Am. A 2025, 42, 151–164. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Xu, Q.; Wang, H.; Lyu, H.; Li, K. Guide star selection for the three-FOV daytime star sensor. Sensors 2019, 19, 1457. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Yang, J. Simulation technology of airborne star sensor imaging. Optoelectron. Technol. 2010, 30, 192–198. [Google Scholar]
- Zhao, M.; Liu, Y.; Tao, Z.; He, Y. One method on star image simulation of airborne astronomical navigation. Optoelectron. Technol. 2008, 28, 184–188. [Google Scholar]
- Li, Z.; Liang, B.; Zhang, T.; Zhu, H. Image simulation for airborne star tracker under strong background radiance. In Proceedings of the 2012 IEEE International Conference on Computer Science and Automation Engineering (CSAE), Zhangjiajie, China, 25–27 May 2012; pp. 644–648. [Google Scholar]
- Wang, H.; Wang, B.; Gao, Y.; Wu, S. Near-earth space star map simulation method of short-wave infrared star sensor. Infrared Phys. Technol. 2022, 127, 104436. [Google Scholar] [CrossRef]
- Zheng, X.; Shen, J.; Wei, Z.; Wang, H. Star map simulation and platform influence of airborne star sensor based on J-band data of 2MASS catalog. Infrared Phys. Technol. 2020, 111, 103541. [Google Scholar] [CrossRef]
- Wei, E.; Chang, L.; Yang, H. Transformation between ICRS and ITRS based on SOFA. J. Geomat. 2012, 37, 31–33. [Google Scholar]
- Men, T.; Shi, J.; Xu, R.; Liu, C.; Wen, C. Correction method of atmospheric refraction based on the low elevation infrared measurement. Infrared Laser Eng. 2016, 45, 0117004. [Google Scholar] [CrossRef]
- Xiaojuan, W.; Xinlong, W. Multiple blur of star image and the restoration under dynamic conditions. Acta Astronaut. 2011, 68, 1903–1913. [Google Scholar] [CrossRef]
- Huang, B.; Ma, J.; Tian, J. Research on simulation of vibration blurred star images. Comput. Digital Eng. 2012, 40, 90–92. [Google Scholar]
- Pickles, A. A stellar spectral flux library: 1150–25000 Å. Publ. Astron. Soc. Pac. 1998, 110, 863. [Google Scholar] [CrossRef]
- Lu, R.; Wu, Y. Estimation of stellar instrument magnitudes using synthetic photometry. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; pp. 1–7. [Google Scholar]
- Wang, W.; Zhang, G.; Wei, X. Modeling analysis and experimental verification for all-time star sensor. Infrared Laser Eng. 2019, 48, 1113001. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, W.; Lin, H.; Wang, X. Parameter Estimation of Gaussian Gray Diffusion Model of Static lmage Spot. Acta Opt. Sin. 2012, 32, 323004. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| FOV/° | 1.96 × 1.96 |
| Focal length/mm | 298 |
| Optics aperture/mm | 100 |
| Transmittance | 90% |
| g1/mm−2 | 2.31 × 10−5 |
| Parameter | Value |
|---|---|
| Array format/pixels | 640 × 512 |
| Pixel pitch/μm | 20 |
| Wavelength range/μm | 1.3–1.7 |
| Quantum efficiency | 80% |
| Dark current/fA | 30 |
| Condition Type | Motion Parameters | FOV | SNR | Gtotal | GCI | DSD |
|---|---|---|---|---|---|---|
| Static Baseline | - | FOV1 | 34.5/ 39.9, 47.6/ 158.6 | 75,847/ 79,915, 95,281/ 310,800 | 68.1%/ 64.0%, 70.6%/ 60.4% | 8.9/ 8.1, 8.2/ 5.8 |
| FOV2 | ||||||
| FOV3 | ||||||
| Non- Optical Axis Rotation | Xf1: −2°/s Yf1: 2°/s | FOV1 | 27.0/ 38.0, 42.0/ 144.3 | 59,439/ 75,751, 83,599/ 283,100 | 51.8%/ 63.3%, 62.9%/ 48.0% | 11.0/ 9.2, 9.5/ 7.0 |
| FOV2 | ||||||
| FOV3 | ||||||
| Xf1: −4°/s Yf1: 4°/s | FOV1 | 15.0/ 36.6, 39.7/ 95.1 | 33,262/ 73,369, 79,498/ 187,055 | 33.7%/ 55.3%, 57.1%/ 38.3% | 13.2/ 10.1, 10.3/ 9.2 | |
| FOV2 | ||||||
| FOV3 | ||||||
| Xf1: −6°/s Yf1: 6°/s | FOV1 | 10.3/ 34.3, 34.0/ 70.0 | 22,855/ 68,539, 68,000/ 137,232 | 32.0%/ 53.7%, 52.0%/ 32.5% | 17.1/ 11.0, 11.4/ 13.2 | |
| FOV2 | ||||||
| FOV3 | ||||||
| Xf1: −8°/s Yf1: 8°/s | FOV1 | 9.3/ 31.0, 31.2/ 53.8 | 20,460/ 62,090, 62,471/ 105,696 | 31.0%/ 52.6%, 50.1%/ 31.8% | 20.3/ 11.9, 11.9/ 16.4 | |
| FOV2 | ||||||
| FOV3 | ||||||
| Xf1: −10°/s Yf1: 10°/s | FOV1 | 7.3/ 25.9, 27.9/ 39.2 | 16,102/ 51,830, 55,710/ 77,154 | 27.7%/ 45.5%, 44.5%/ 29.0% | 22.9/ 12.7, 13.1/ 19.7 | |
| FOV2 | ||||||
| FOV3 | ||||||
| Optical Axis Rotation | Zf1: 5°/s | FOV1 | 34.4/ 20.7, 24.1/ 121.7 | 75,562/ 41,574, 48,273/ 239,275 | 66.0%/ 38.7%, 40.0%/ 41.1% | 10.1/ 13.1, 14.9/ 8.4 |
| FOV2 | ||||||
| FOV3 | ||||||
| Zf1: 10°/s | FOV1 | 33.4/ 12.5, 13.5/ 66.1 | 73,678/ 24,971, 26,978/ 130,187 | 61.6%/ 36.0%, 37.1%/ 37.9% | 11.0/ 18.2, 18.5/ 11.6 | |
| FOV2 | ||||||
| FOV3 | ||||||
| Non- Optical Axis Angular Vibration | Xf1: 5 × 105 Yf1: 5 × 105 | FOV1 | 24.3/ 34.0, 44.5/ 145.6 | 53,596/ 68,401, 89,398/ 285,175 | 46.2%/ 59.1%, 64.9%/ 49.4% | 12.0/ 10.8, 11.1/ 7.1 |
| FOV2 | ||||||
| FOV3 | ||||||
| Xf1: 106 Yf1: 106 | FOV1 | 7.5/ 9.8, 10.1/ 140.3 | 16,551/ 19,672, 20,638/ 275,581 | 36.1%/ 35.5%, 34.9%/ 47.6% | 24.0/ 25.2, 24.9/ 8.0 | |
| FOV2 | ||||||
| FOV3 | ||||||
| Optical Axis Angular Vibration | Zf1: 5 × 106 | FOV1 | 34.4/ 10.4, 8.7/ 44.5 | 76,062/ 20,827, 17,363/ 87,411 | 64.5%/ 41.4%, 34.9%/ 35.7% | 10.1/ 31.1, 32.0/ 28.3 |
| FOV2 | ||||||
| FOV3 | ||||||
| Zf1: 107 | FOV1 | 32.2/ 6.7, 5.3/ 29.9 | 70,925/ 13,542, 10,658/ 58,787 | 59.0%/ 33.0%, 26.4%/ 34.7% | 11.3/ 36.9, 38.4/ 40.6 | |
| FOV2 | ||||||
| FOV3 |
| Condition Type | Motion Parameters | SNR[R/Sp/S1] 1 | Gtotal[R/Sp/S1] | GCI[R/Sp/S1] | DSD[R/Sp/S1] |
|---|---|---|---|---|---|
| Static Baseline | - | 24.0/27.8/29.1 | 74,680/74,746/82,123 | 78.1%/67.3%/66.1% | 10.11/9.58/11.15 |
| Non-Optical Axis Rotation | Yf1: 2°/s | 24.0/26.6/28.6 | 71,623/71,233/80,764 | 68.2%/62.9%/61.3% | 11.84/10.80/13.06 |
| Yf1: 4°/s | 21.2/24.7/26.0 | 63,629/66,760/73,645 | 69.4%/63.5%/59.7% | 13.32/12.24/13.92 | |
| Yf1: 6°/s | 18.6/21.0/23.6 | 55,726/56,217/66,604 | 54.5%/55.5%/56.7% | 14.52/13.56/15.80 | |
| Yf1: 8°/s | 15.8/18.4/19.9 | 47,994/49,480/56,288 | 44.7%/45.9%/50.8% | 16.39/15.10/17.84 | |
| Yf1: 10°/s | 13.5/15.7/16.0 | 41,564/42,429/45,280 | 42.9%/48.9%/49.2% | 17.57/16.02/18.42 | |
| Optical Axis Rotation | Zf1: 5°/s | 23.4/27.1/28.6 | 71,379/73,385/80,346 | 73.8%/65.4%/62.8% | 10.85/10.13/11.90 |
| Zf1: 10°/s | 23.7/26.6/28.1 | 71,335/71,583/79,134 | 71.9%/64.3%/63.9% | 11.53/10.78/12.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Zhang, H.; Fang, L.; Gao, X.; Lu, K.; Sun, W.; Zhao, R. A High-Fidelity Star Map Simulation Method for Airborne All-Time Three-FOV Star Sensor Under Dynamic Conditions. Remote Sens. 2025, 17, 3853. https://doi.org/10.3390/rs17233853
Zhou J, Zhang H, Fang L, Gao X, Lu K, Sun W, Zhao R. A High-Fidelity Star Map Simulation Method for Airborne All-Time Three-FOV Star Sensor Under Dynamic Conditions. Remote Sensing. 2025; 17(23):3853. https://doi.org/10.3390/rs17233853
Chicago/Turabian StyleZhou, Jingsong, Hui Zhang, Liang Fang, Xiaodong Gao, Kaili Lu, Wei Sun, and Rujin Zhao. 2025. "A High-Fidelity Star Map Simulation Method for Airborne All-Time Three-FOV Star Sensor Under Dynamic Conditions" Remote Sensing 17, no. 23: 3853. https://doi.org/10.3390/rs17233853
APA StyleZhou, J., Zhang, H., Fang, L., Gao, X., Lu, K., Sun, W., & Zhao, R. (2025). A High-Fidelity Star Map Simulation Method for Airborne All-Time Three-FOV Star Sensor Under Dynamic Conditions. Remote Sensing, 17(23), 3853. https://doi.org/10.3390/rs17233853






