Investigation of Physics-Informed Methods for Improving Sea Surface Height Prediction Based on Neural Networks in the South China Sea

Highlights

What are the main findings?

• The proposed Physics-Informed methods improve the prediction accuracy of the SimVPv2 model by 13% (RMSE decrease from 0.0198 m to 0.0173 m).
• Incorporating the land mask information into the inputs is implied and proved to be a simple yet effective way to enhance the AI model (especially the PredRNNv2) performance on the oceanic data.
• Seasonal/spatial analyses and a case study investigate how the geostrophic constraint improves model performance by connecting with the physical oceanography.

What are the implications of the main findings?

• This study demonstrates that integrating a latitude-weighted geostrophic constraint enhances both physical consistency and prediction accuracy in data-driven ocean models.
• To the best of our knowledge, the issue of artifacts in AI models caused by land points in oceanic data is first proposed here, and we provide a simple yet effective solution.
• The limitation of directly concatenating heterogeneous oceanic data as inputs for AI models is also first revealed here, as far as we know.

Abstract

Sea surface height (SSH) derived from satellite altimetry is essential for oceanographic research and marine monitoring. Although artificial intelligence (AI) models show considerable potential in forecasting, their application in oceanography remains constrained by several limitations. To address these challenges, we propose a set of physics-informed methods to improve SSH prediction based on neural networks in the South China Sea (SCS). The key strategies include: (1) incorporating land mask information to mitigate artifacts induced by the presence of land in marine data; (2) introducing a geostrophic constraint into the loss function; and applying latitude-dependent weighting to this constraint to account for the breakdown of geostrophic balance near the equator. On the test dataset, the physics-informed SimVPv2 (Phys-SV) model achieves an RMSE of 0.0173 m, a 13% improvement over the baseline SimVPv2 (Base-SV). The PredRNNv2 (PR) model also benefits significantly from the inclusion of land mask input, with RMSE reduced by 12% (from 0.0280 m to 0.0246 m). To the best of our knowledge, this study is the first to identify the artifact issue in AI models caused by land points in ocean data and to reveal the limitations of directly concatenating heterogeneous oceanic variables as model inputs.

1. Introduction

As a critical indicator of mesoscale oceanic dynamical processes, sea surface height (SSH) is routinely used to map mesoscale circulation features [1,2] and quantify mesoscale eddy dynamics [3,4], which contributes to oceanic mass transport comparable in magnitude to that of the large-scale wind- and thermohaline-driven circulation [5]. Given this scientific importance, the ability to accurately forecast SSH is of critical operational and engineering significance. Timely and reliable SSH forecasts provide the basis for deriving surface currents, which are essential for a wide range of maritime activities. In the offshore energy sector, precise knowledge of future current and eddy locations is indispensable for the safe execution of sensitive operations, such as the installation and maintenance of oil rigs and offshore wind turbines [6]. Therefore, developing models that can deliver high-accuracy SSH forecasts is a key objective in modern operational oceanography.

Approaches to forecasting SSH can be broadly categorized into three groups: numerical models, statistical methods, and data-driven deep learning models. Numerical models, such as the Hybrid Coordinate Ocean Model (HYCOM) [7] and Regional Ocean Model System (ROMS) [8,9], have been applied to forecast SSH for a long time. The numerical models solve fundamental hydrodynamic equations to simulate oceanic states and are physically comprehensive. But they require complex parameterization of sub-grid-scale processes, and the accuracy is highly sensitive to initial and boundary conditions—limitations, which have motivated the search for alternative approaches. Statistical methods, such as autoregressive models, offer a computationally cheaper alternative but are often based on linear assumptions, limiting their ability to capture the complex, non-linear dynamics inherent in ocean systems [10].

The rapid development of artificial intelligence (AI) has revolutionized spatiotemporal forecasting in oceanography, with deep learning models emerging as particularly powerful tools. These data-driven approaches have demonstrated remarkable success across various oceanographic applications. Convolutional neural networks (CNNs) have proven effective for El Niño-Southern Oscillation (ENSO) prediction [11], while the integration of multivariate empirical orthogonal function (MEOF) analysis with one-dimensional convolutional long short-term memory (Conv1D-LSTM) networks has shown promising results for multi-variable sea surface forecasting [12]. Innovative adaptations of vision Transformers (ViT) with self-attention mechanisms have enabled three-dimensional multivariate modeling for enhanced ENSO prediction [13].

Despite these advances, fundamental limitations persist in purely data-driven approaches. The inherent “black box” nature of these models raises concerns about physical consistency in their predictions [14], particularly when extrapolating beyond the temporal scope of training data or processing noisy observational inputs. This limitation has motivated the development of Physics-Informed Neural Networks (PINNs), which embed physical laws into the learning process through penalty terms that quantify violations of governing equations [15]. The PINN framework has shown considerable promise across various oceanographic applications, including tropical cyclone field reconstruction [16], three-dimensional thermohaline modeling in the tropical Pacific [17], and improved air–sea flux parameterizations [18].

Among the fundamental principles of ocean dynamics, the geostrophic balance provides a robust first-order approximation for large-scale, low-frequency ocean circulation. This balance, which describes an equilibrium between the Coriolis force and the pressure gradient force, is known to govern the circulation in many regions of the world’s oceans [3]. The SCS is one such region, where the large-scale circulation is predominantly in geostrophic balance [19,20]. A key practical advantage of using a geostrophic constraint is its elegance and efficiency: it relates the sea level gradient to the velocity field, meaning the constraint can be formulated using only SSH data, without requiring external variables like wind forcing or in situ velocity measurements.

Although numerous studies have explored the use of AI models for forecasting SSH [21,22,23,24], few have integrated these models with physical laws. To our knowledge, only one study has incorporated the geostrophic constraint into an AI framework to predict sea surface currents [25]. As such, the potential of PINNs for SSH forecasting remains largely untapped.

In this study, we proposed physics-informed methods to enhance the AI model’s accuracy for ten-day SSH forecasting in the SCS. A latitude-weighted geostrophic constraint is embedded into the loss function, along with the incorporation of mask information, to further enhance model performance. Our primary objective is to demonstrate that this physics-informed approaches improve both forecast accuracy and physical consistency compared to a purely data-driven baseline. In addition to extensive experiments validating the model’s improvement, we conduct a comprehensive analysis of its performance across different seasons, forecast lead times, and bathymetric regimes. A case study also provides a concrete example of how the physics-informed methods impact the forecasting SSH field. The analyses aim to quantify the benefits and limitations of applying the geostrophic constraint in this dynamically complex region.

2. Data and Methods

2.1. Data

This study employs daily mean absolute dynamic topography data—defined as the sea surface height above the geoid and hereafter referred to as SSH—obtained from the Copernicus Marine Environment Monitoring Service (CMEMS). The dataset has a spatial resolution of 1/8° × 1/8° and incorporates multi-satellite altimeter observations. It has undergone tidal correction and mean dynamic topography processing to ensure data quality. Besides, the 1/4° × 1/4° daily (averaged per 6 h) ERA5 wind data obtained from Copernicus Climate Change Service (C3S) is utilized after being interpolated into 1/8° × 1/8° during the analyses.

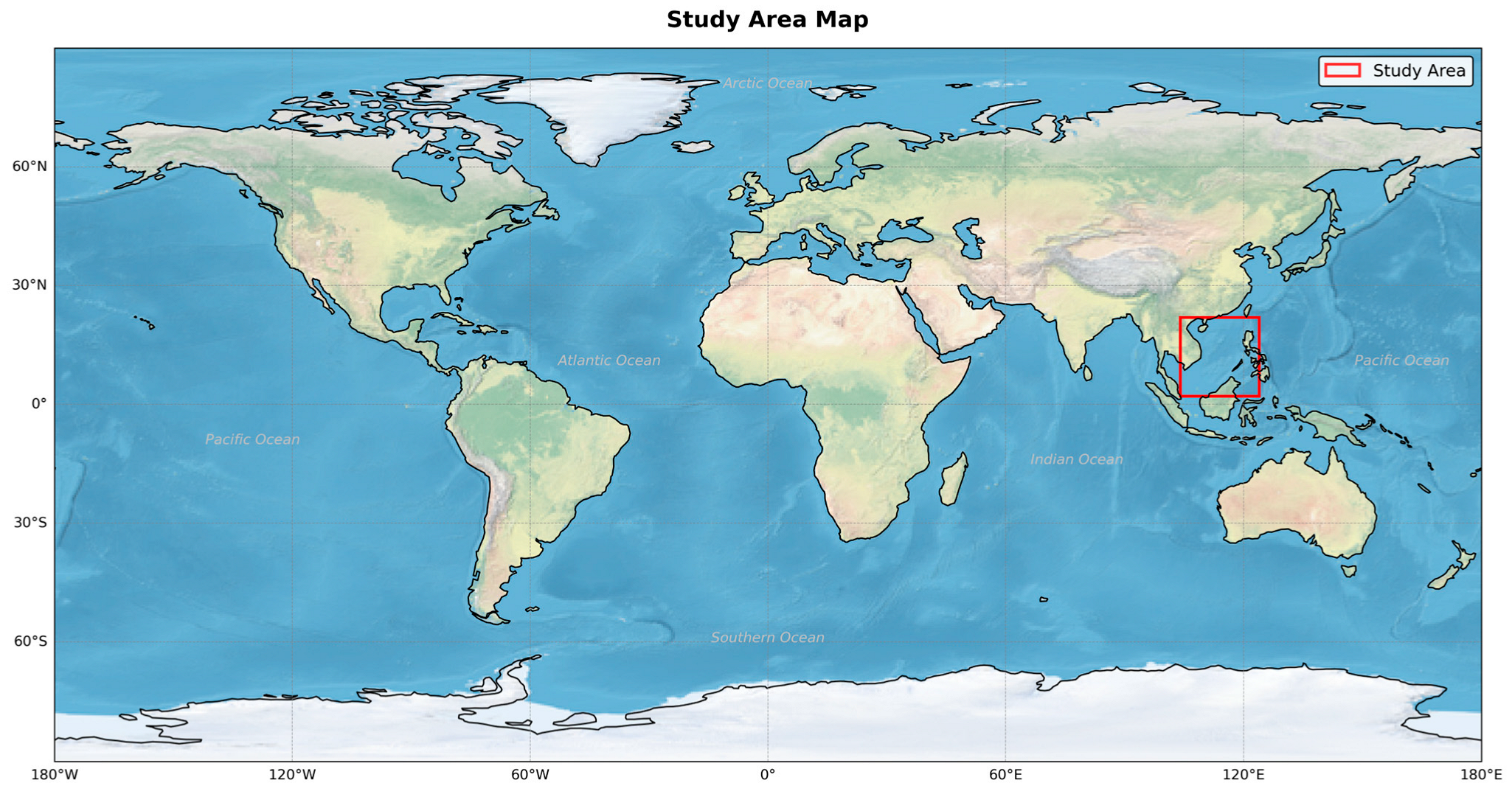
As shown in Figure 1, the study domain (2°N–22°N, 104°E–124°E) encompasses the SCS basin and adjacent Luzon Strait, corresponding to a 160 × 160 grid. This region captures critical dynamical features, including the Kuroshio intrusion through the Luzon Strait, which significantly modulates SCS circulation patterns [26] and consequently influences SSH variability across the basin. The dataset covers the period from 1 January 1993 to 13 June 2024 and is divided into three subsets: a training set (1993–2021), a validation set (2022), and a test set (2023–13 June 2024). The validation set is used for hyperparameter tuning and monitoring the training process, while the test set serves as an independent dataset to evaluate the model’s predictive performance. Notably, 2022 was a La Niña year, whereas 2023 transitioned to an El Niño year. Previous studies have demonstrated that ENSO signals can influence SCS circulation and SSH variability through processes such as the Luzon Strait water exchange [27]. This interannual variability introduces additional challenges for model predictions but provides a more rigorous assessment of the model’s generalization capability.

2.2. Model Structure

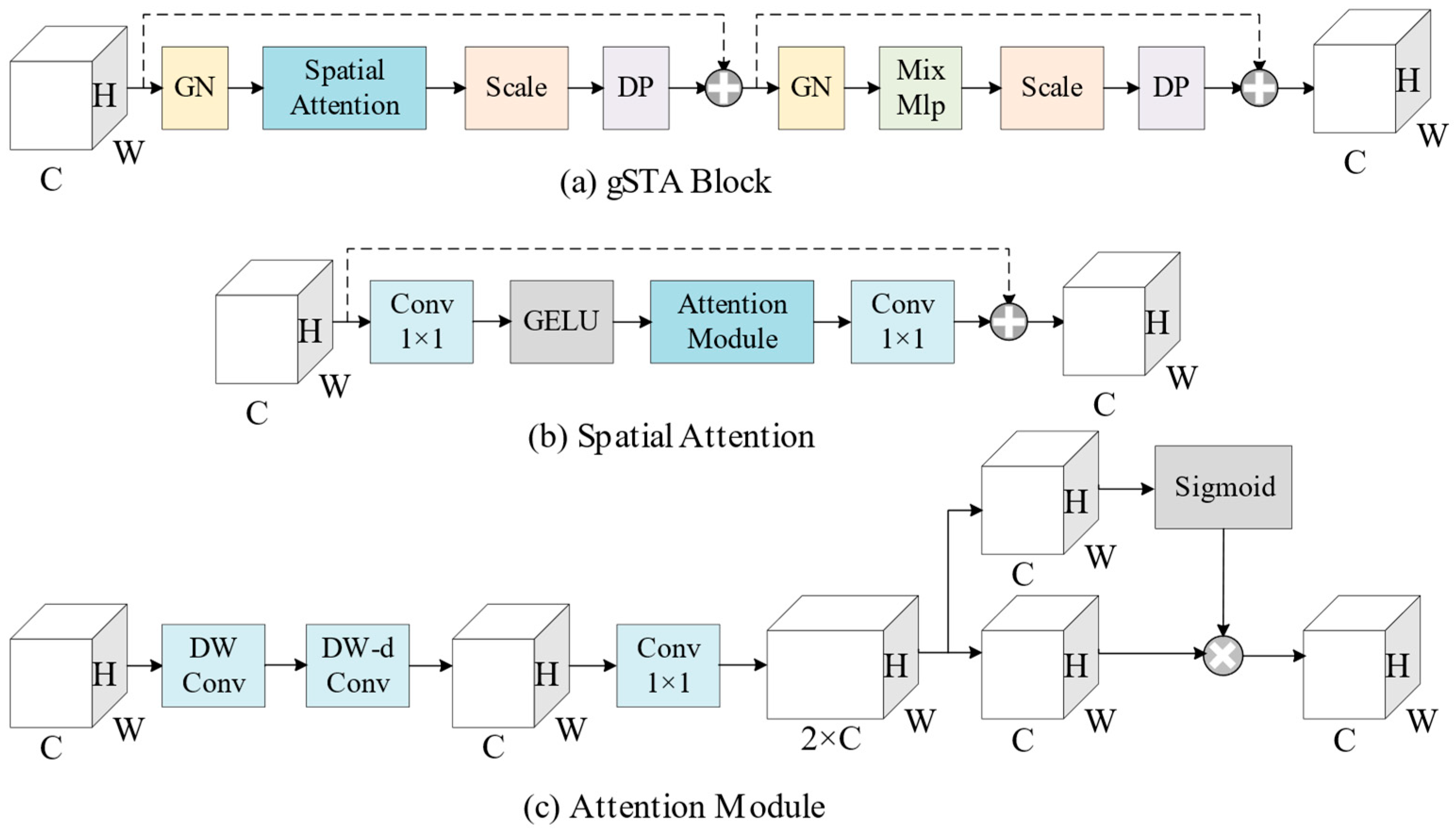
The SimVPv2 model employed in this study is a purely convolutional architecture that efficiently captures spatiotemporal coupling relationships through a gated spatiotemporal attention (gSTA) mechanism. Compared to conventional spatiotemporal prediction models (e.g., ConvLSTM [28], PredRNN [29]), SimVPv2 demonstrates superior performance in terms of structural simplicity, computational efficiency, and prediction accuracy, showing exceptional performance on multiple benchmark datasets [30]. These characteristics make it particularly suitable for modeling complex oceanographic data.

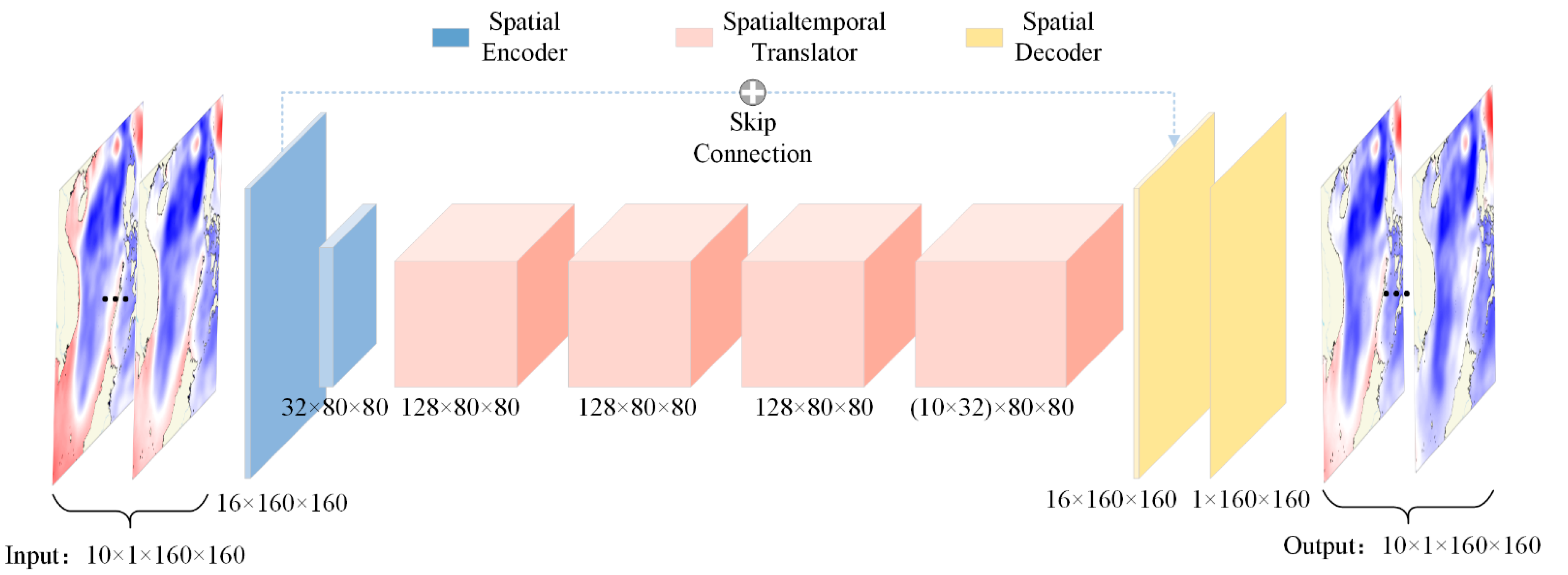
Designed for sequential prediction of two-dimensional spatial variables, the SimVPv2 architecture consists of three primary components: (1) Spatial Encoder, (2) Spatiotemporal Translator, and (3) Spatial Decoder. Similar to U-Net, the model incorporates skip connections between the initial encoder layers and final decoder layers to preserve original features. Figure 2 illustrates the overall structure of SimVPv2, and the more concrete structure is given in Appendix A.

For an input tensor of dimensions $\left(B,T,C,H,W\right)$, where B denotes batch size (the number of samples to proceed), T denotes days of inputs, C denotes the number of channels, H denotes image height, and W denotes image width, the model first flattens the temporal dimension into the batch dimension $\left(B\times T,C,H,W\right)$. After spatial encoding, the tensor $\left(B\times T,C,H^f,W^f\right)$ undergoes channel-temporal folding to $\left(B,T\times C,W^f,W^f\right)$, where $H^f=H/2^{N_s}$ and $W^f=W/2^{N_s}$. The translator’s operations on this restructured tensor enable simultaneous learning of spatial and temporal relationships through depthwise spatial attention and channel-wise convolutions.

As shown in Figure 2, we adopt a 10-day sequence of SSH fields as inputs to predict the subsequent 10-day SSH fields, corresponding to inputs and outputs dimensions of (10, 1, 160, 160). Given the relatively low spatial resolution (160 × 160), we minimize information loss during downsampling and upsampling by limiting the encoder layers (Ns) to 2, performing only one downsampling and one upsampling operation. Within the attention module, we employ dilated convolutions with a dilation rate of 2 (skipping every other grid point) and an effective kernel size of 21 to capture broader spatial dependencies.

2.3. Strategies

2.3.1. Geostrophic Constraint in SSH Prediction

In physical oceanography, the geostrophic balance is a fundamental dynamical approximation in which the Coriolis force is balanced by the horizontal pressure gradient force. Owing to its clear physical meaning and relatively simple mathematical form, it is widely used to estimate large-scale oceanic currents from sea surface height (SSH) observations.

Under the f-plane approximation, where the Coriolis parameter is assumed constant, the geostrophic balance can be expressed as:

$$f{u}_g=-g{\displaystyle \frac{\partial \mathsf{\zeta }}{\partial y}},$$

(1)

$$f{v}_g=g{\displaystyle \frac{\partial \mathsf{\zeta }}{\partial x}},$$

(2)

where ($u_g,v_g$) are the zonal and meridional components of the geostrophic velocity, g is the gravitational acceleration (taken as 9.81 m/s⁻²), ζ represents the sea surface height (SSH), and f is the Coriolis parameter, defined as:

$$f=2\mathsf{\Omega }sin\left(\mathsf{\varphi }\right),$$

(3)

Here, Ω is the Earth’s angular velocity (taken as 7.2921 × 10⁻⁵ rad/s), and ϕ is the latitude.

Solving Equations (1) and (2) for the velocity components yields:

$$u_g=-{\displaystyle \frac{g}{f}}{\displaystyle \frac{\partial \mathsf{\zeta }}{\partial y}},$$

(4)

$$v_g={\displaystyle \frac{g}{f}}{\displaystyle \frac{\partial \mathsf{\zeta }}{\partial x}},$$

(5)

In the training of our SSH prediction model, both the inputs and outputs are exclusively SSH fields. The primary loss function is the Mean Squared Error (MSE) between the predicted and target SSH:

$$los{s}_{SSH}=MSE\left({\mathsf{\zeta }}_{pred},{\mathsf{\zeta }}_{target}\right),$$

(6)

Here, ${\zeta }_{pred},{\zeta }_{target}$ denote the predicted SSH and the target SSH from the training dataset for the corresponding date, respectively. The MSE is calculated as:

$$MSE\left(x,y\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(x_i-y_i\right)}^2,$$

(7)

where N is the total number of valid data points (excluding the land grids). Through exclusively calculating the loss of valid data points, we aim to eliminate the interference in model training caused by artifacts from land points.

To incorporate the geostrophic balance into the model’s loss function, a geostrophic constraint loss is introduced. First, the SSH spatial gradient fields of predictions and targets are computed using a Sobel operator. Subsequently, the geostrophic velocity components ($u_{pred},v_{pred},u_{target},v_{target}$) are derived from the SSH spatial gradient fields as described in Equations (4) and (5). The calculated geostrophic velocities are divided by the standard deviation from CMEMS geostrophic velocity data (from 1993 to 2021) and multiplied by that from CMEMS SSH data (from 1993 to 2021)—a step intended to align the dimension of the computed geostrophic velocities with that of SSH, so that the magnitude of the loss terms is balanced and each of the loss terms would not be dominant solely because its larger magnitude. Finally, the MSE between the predicted and target geostrophic velocities forms the geostrophic loss term:

$$los{s}_u=MSE\left(u_{pred}/{\mathsf{\sigma }}_u\cdot {\mathsf{\sigma }}_{SSH},u_{target}/{\mathsf{\sigma }}_u\cdot {\mathsf{\sigma }}_{SSH}\right),$$

(8)

$$los{s}_v=MSE\left(v_{pred}/{\mathsf{\sigma }}_v\cdot {\mathsf{\sigma }}_{SSH},v_{target}/{\sigma }_v\cdot {\sigma }_{SSH}\right),$$

(9)

$$los{s}_{geo}=loss\_u+loss\_v,$$

(10)

The total loss function for training the model is a linear combination of the SSH prediction loss and the geostrophic velocity loss:

$$los{s}_{total}=los{s}_{SSH}+\mathsf{\lambda }los{s}_{geo},$$

(11)

where λ is the geostrophic constraint coefficient. A larger value of λ imposes a stronger geostrophic constraint, whereas a smaller value signifies a weaker constraint.

2.3.2. Latitude-Weighted Loss

The geostrophic constraint in our model is based on the geostrophic velocity equations (Equations (4) and (5)). A direct application of these equations is problematic at low latitudes, as the Coriolis parameter f in the denominator approaches zero, leading to an over-amplification of the geostrophic loss term where the geostrophic balance is inherently weak. This can introduce significant errors into the model training process.

To mitigate this issue, we introduce a latitude-dependent weighting factor, w(ϕ), designed to smoothly suppress the geostrophic constraint in equatorial regions. The weight is calculated using the following square-rooted sigmoid function:

$$w\left(\mathsf{\varphi }\right)={\displaystyle \frac{1}{\sqrt{\left(1+e^{-k\left(\mathsf{\varphi }-{\mathsf{\varphi }}_0\right)}\right)}}},$$

(12)

The factor $w\left(\mathsf{\varphi }\right)$ is applied in the loss function as below:

$$los{s}_{geo\left(weighted\right)}=los{s}_{geo}\cdot w\left(\varphi \right),$$

(13)

According to Lagerloef et al. [31], the geostrophic approximation under the f-plane assumption is generally valid at latitudes higher than approximately 5°N. Based on this guidance, we introduce a latitude-dependent weighting scheme to gradually apply the geostrophic constraint with increasing latitude. Specifically, we define a sigmoid-shaped weight function with parameters ${\mathsf{\varphi }}_0=7°$ and k = 2, such that the weight transitions smoothly from nearly 0 south of 5°N to nearly 1 north of 10°N.

2.3.3. Mask-Informed Inputs

In the application of deep learning models, particularly convolutional neural networks, to oceanographic data, a significant challenge is the prevalence of NaN (Not a Number) values, which often correspond to land grids in marine datasets. A common practice is to replace these NaN values with zeros. However, this approach is suboptimal, as simply zero-filling may mislead the convolutional model during feature extraction, given that such models rely on sliding kernels across the grid to capture meaningful spatial patterns. Another method involves interpolation, which fills the land grids using values derived from surrounding ocean data. While interpolation may offer better performance than simply assigning zeros to land grids, it still introduces misleading information to the model: originally, information-free land areas are now filled with artificially imputed values, which do not correspond to any real physical processes and may still distort feature learning.

For instance, in SSH prediction tasks, shallow network layers could misinterpret zero-filled or interpolated land grids as authentic SSH values, thereby propagating erroneous information to deeper layers. To address this issue, we propose a simple yet effective method: concatenating a binary mask that identifies valid grids—a tensor of ones and zeros with the same spatial dimensions as the inputs, but with a single channel—to the inputs along the channel dimension. This operation transforms the inputs shape from (B, T, C, H, W) to (B, T, C+1, H, W) for the SimVPv2 model, while for the PredRNNv2 model, the mask is concatenated with not only with the first inputs, but also the outputs of last step (which is also the inputs of the current step) at each time step, thereby explicitly informing the model about the presence of invalid grid cells in a straightforward yet effective manner.

3. Results

3.1. Impact of the Geostrophic Constraint Coefficient

To determine the optimal weighting for the geostrophic constraint, we conducted a series of experiments in which the model was trained under varying values of the geostrophic constraint coefficient, denoted as. In order to mitigate the effects of randomness and enhance the robustness of the results, each experiment was repeated five times under identical hyperparameter settings except for the random seed. The performance of each configuration was evaluated on the test dataset, and the results were averaged across the five runs to ensure a more reliable and statistically meaningful comparison.

Figure 3 illustrates the relationship between model performance and λ, using the RMSE and the averaged Point-to-point Correlation Coefficient (PCC) as evaluation metrics. And PCC is computed as below:

$$PCC={\displaystyle \frac{{\sum }_{\mathrm{i}=1}^{\mathrm{N}}\left(x_i-{\overline{x}}_i\right)\left(y_i-{\overline{y}}_i\right)}{\sqrt{{\sum }_{\mathrm{i}=1}^{\mathrm{N}}{\left(x_i-{\overline{x}}_i\right)}^2{\sum }_{\mathrm{i}=1}^{\mathrm{N}}{\left(y_i-{\overline{y}}_i\right)}^2}}}$$

(14)

where N denotes the total number of valid data points (excluding the land points).

For each value of λ, the mean values are derived from five independent models, which were trained under identical configurations differing only in their random seeds. The 95% confidence intervals (CIs) are calculated using the Bootstrap method (as detailed in Appendix B). The Base-SV model denotes the SimVPv2 baseline trained without any of the proposed strategies.

As λ increases from zero, the RMSE initially decreases and the PCC increases, indicating improved performance. Optimal performance is achieved at λ = 0.7, after which the model’s accuracy degrades. Therefore, the term Phys-SV hereafter refers specifically to the model trained at this optimal value (λ = 0.7).

Given that the geostrophic loss was normalized, the coefficient λ can be interpreted as the relative importance of the geostrophic loss. The degradation in performance for λ > 0.7 suggests that the geostrophic constraint should serve as a supplementary component of the loss function. This phenomenon can be mainly attributed to the presence of ageostrophic dynamics. Forcing the model to adhere too strictly to geostrophy by increasing λ penalizes the data-driven model for learning the ageostrophic dynamics.

3.2. Ablation Study

In the Section 2, we introduced three strategies aimed at enhancing model performance. As demonstrated in Figure 3, integrating all three leads to notable improvement. However, the individual contribution of each strategy had not been evaluated. To assess their respective effectiveness, we conducted a series of ablation studies in which one strategy was omitted at a time.

As shown in Figure 4, the removal of any of the three strategies results in an increase in RMSE and a decrease in PCC. Among them, abandoning the geostrophic constraint has the most pronounced effect. These results confirm that all three strategies contribute to improving the performance of the Phys-SV, and that the geostrophic constraint plays an especially critical role, which is probably because the dominance of geostrophic dynamics in the SCS makes the geostrophic constraint an effective regularizer for the model.

4. Analysis of Results

From the experiments above, it can be observed that the fluctuations caused by randomness during the training process are considerable. To minimize the impact of such randomness, all random seeds were fixed to 42 and cuDNN’s (Nvida’s CUDA Deep Neural Network library) deterministic algorithms were enabled throughout the training of the subsequent models. This ensures that models trained under the same hyperparameters are strictly identical, except for those trained with geostrophic constraint loss. Due to its additional computational steps, this loss introduces new uncertainties. Nevertheless, as

Table 1. Independent replicate experiments using the same random seeds.

Model	RMSE (m)
	Trial 1	Trial 2	Trial 3	Mean	Standard Deviation
Base-SV	0.019768	0.019768	0.019768	0.019768	0
Base-SV + MI	0.019329	0.019329	0.019329	0.019329	0
Base-SV + GC	0.017899	0.017921	0.018242	0.018021	0.000157
Phys-SV	0.017309	0.017316	0.017286	0.017304	0.000013
Base-PR	0.027973	0.027973	0.027973	0.027973	0
Base-PR + MI	0.024610	0.024610	0.024610	0.024610	0
Base-PR + GC	0.033604	0.033604	0.033604	0.033604	0
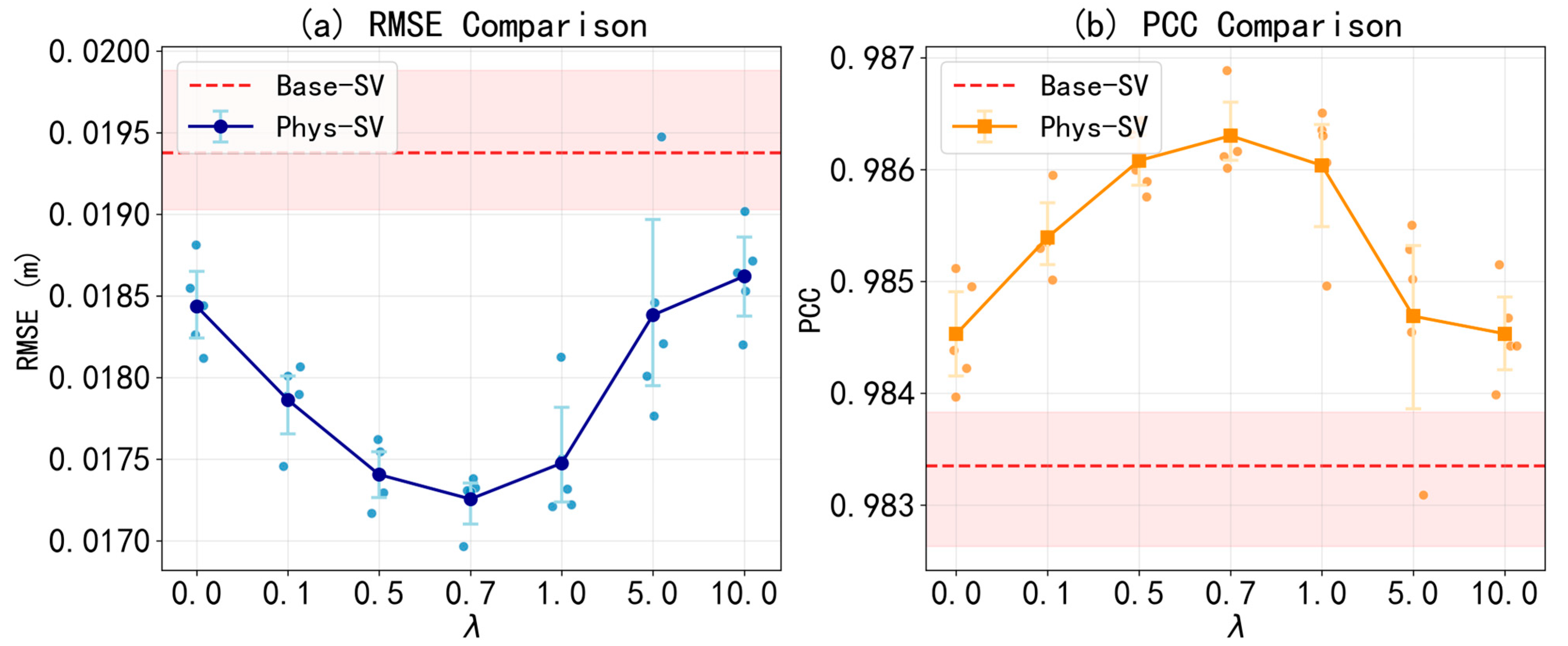
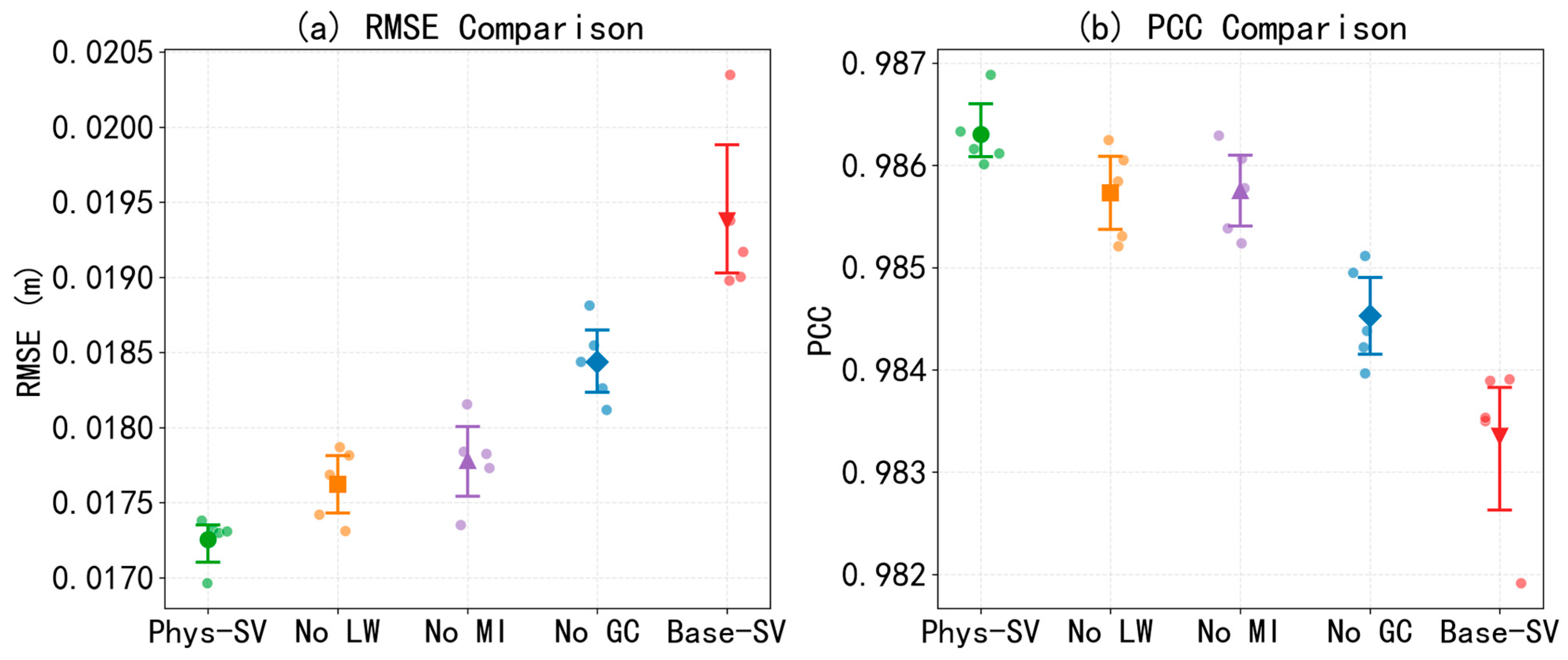
Phys-PR	0.028282	0.028282	0.028282	0.028282	0

demonstrates, despite not being entirely identical, the use of fixed random seeds and cuDNN’s deterministic algorithms still results in highly consistent outputs across repeated trials under identical hyperparameters. Across three independent trials, the RMSE values exhibit minimal deviation, remaining within 1.6% of the mean RMSE. Based on this high consistency, we selected one of the three runs as the representative instance of the Phys-SV for all subsequent analyses.

As shown in Table 1, we have also trained the PR model using the proposed methods to explore their generalizability. To ensure a fair comparison, we adjusted the hyperparameter configurations to make the two models similar in scale of parameters. (SV: 3,273,809 parameters, PR: 3,340,288 parameters). It is important to note that the PR model exhibits significantly different characteristics compared to the SV model. Firstly, the PR model is much more sensitive to data normalization than the SV model, even when the inputs are solely SSH. Consequently, we trained the PR model using normalized SSH data. Secondly, land masks are integrated into the PR model at every time step, as it is an autoregressive model. Thirdly, while the GC method improves the performance of the SV model, it diminishes that of the PR model. Conversely, the MI method significantly enhances the performance of the PR model, but only marginally for the SV model.

It is the difference in model structure that we think makes the MI method boost the PR more significantly, and demonstrates an appealing prospect to apply the mask-informed method to the autoregressive model. As for the SV, it may be better to concatenate the mask not only into the original inputs, and the reformative practice remains unexplored. Regarding the degradation of PR’s performance caused by the GC, we supposethe reason may be that the PR requires a larger scale of parameters to achieve overfitting, where the GC, acting as a penalty term, could enhance the performance.

4.1. Comparative Performance Analysis

To further evaluate the effectiveness of the physics-informed approaches, the performance at different lead times of the Phys-SV and Mask-PR (Base-PR + MI) was compared against other models: Base-SV, Base-PR and Persistence. Persistence, which assumes the future state is identical to the current state (ζ(t+1) = ζ(t)), is a benchmark comparison and forecast reference widely accepted in oceanic science [32], and serves as a simple baseline for forecast skill here.

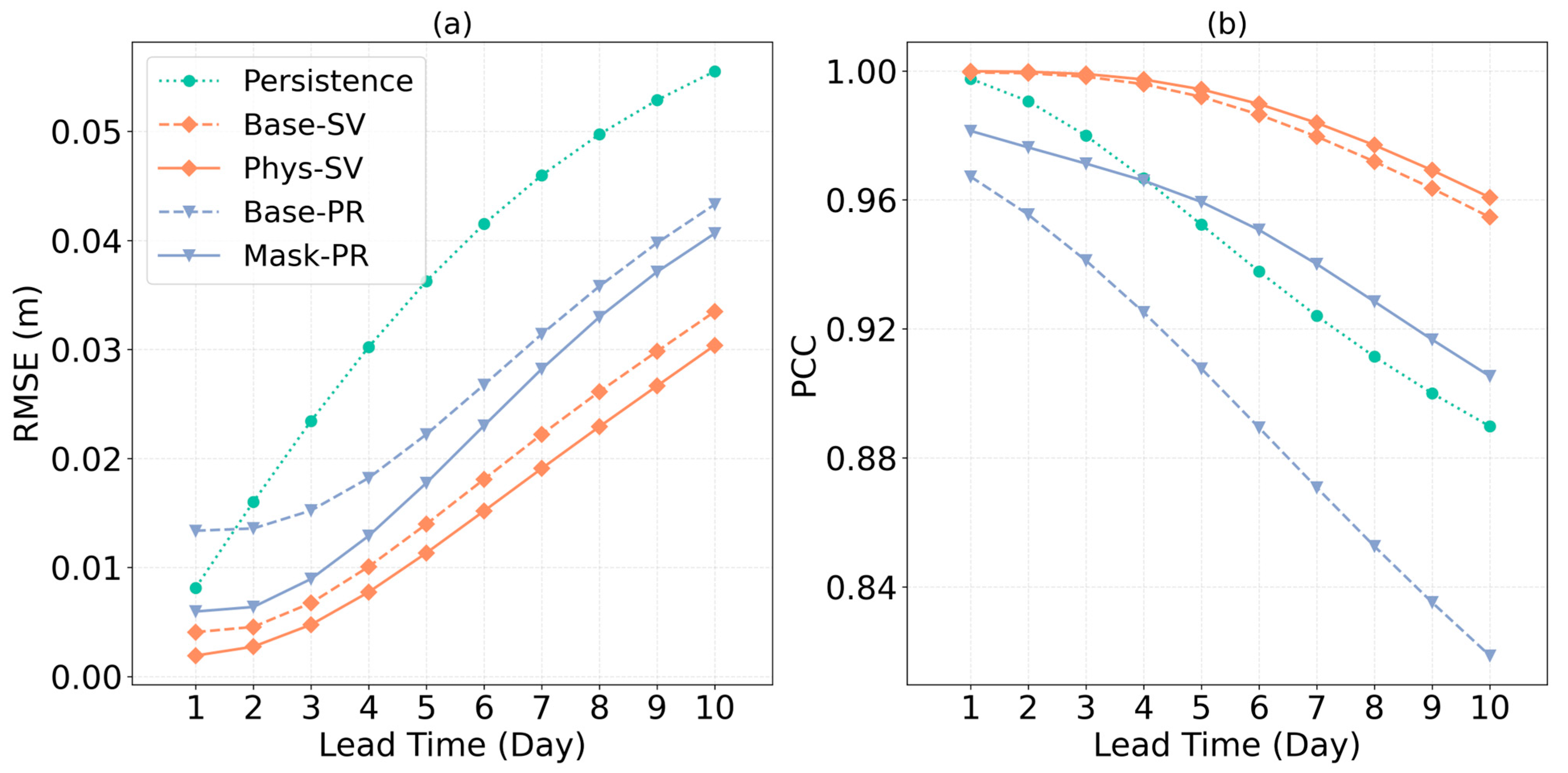
As shown in Figure 5, both the Phys-SV and Mask Base-SV outperform Base models. For the PR, the MI method significantly enhances its performance, especially in PCC. The introduction of MI effectively slows down the rate of PCC degradation, indicating that mask information helps the PR cope with the accumulated errors due to the artifacts introduced by the land points during its autoregressive process.

Moreover, for the SV models, they both exhibit greater performance than the PR models, and the Physics-Informed methods enhance the performance of the SV in a comparably average way, exhibiting lower RMSE and higher PCC across all lead times. However, the magnitude of this improvement is modest, which is likely attributable to the challenges of applying the geostrophic constraint over a domain that includes extensive low-latitude and inshore areas where the geostrophic balance is weak. Although the latitude-weighting scheme was implemented to mitigate this, it may introduce discontinuities in the loss function that can complicate the training process, thereby limiting the full potential benefit of the physical constraint.

4.2. Seasonal Variation in Prediction Accuracy

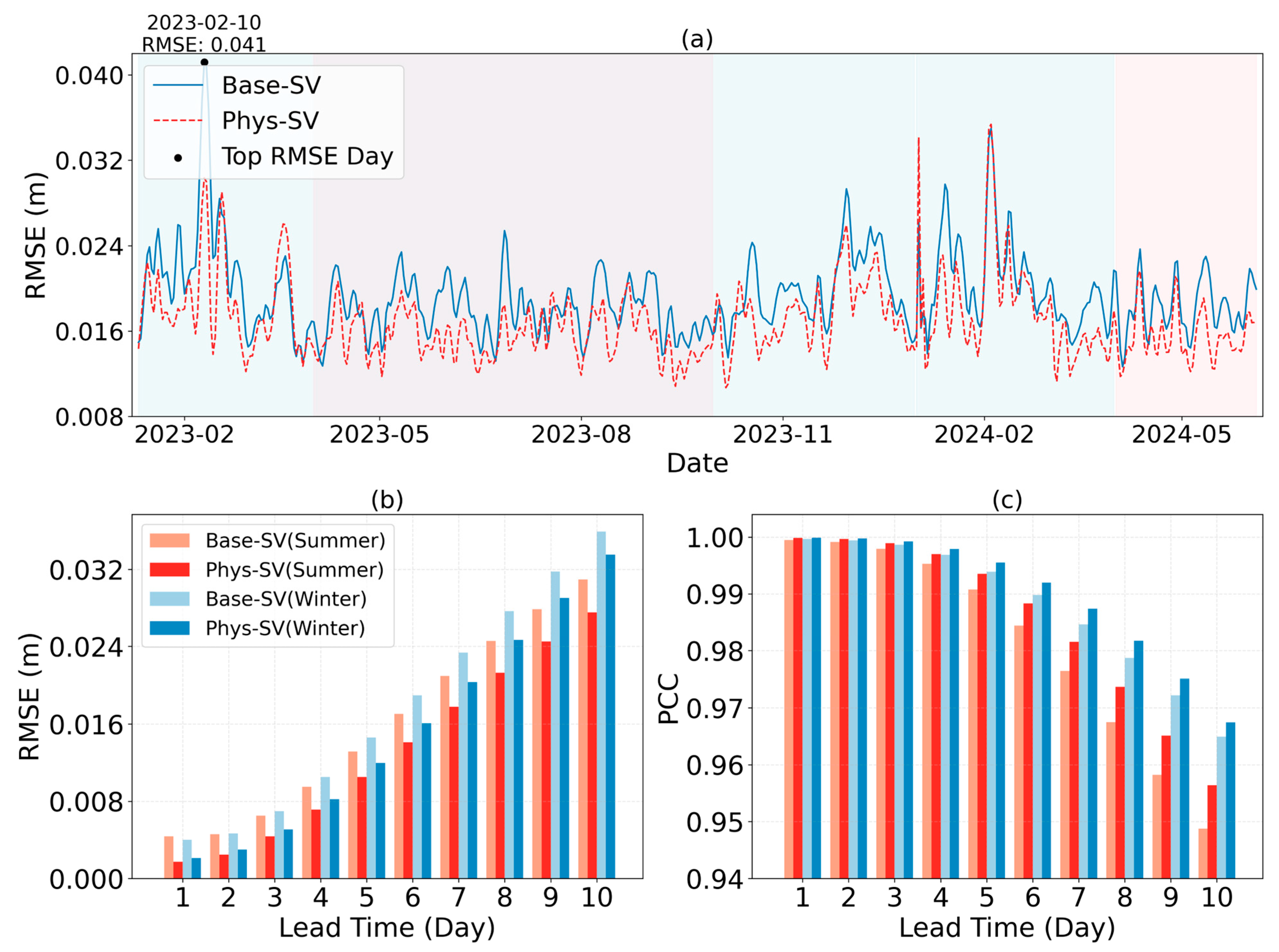
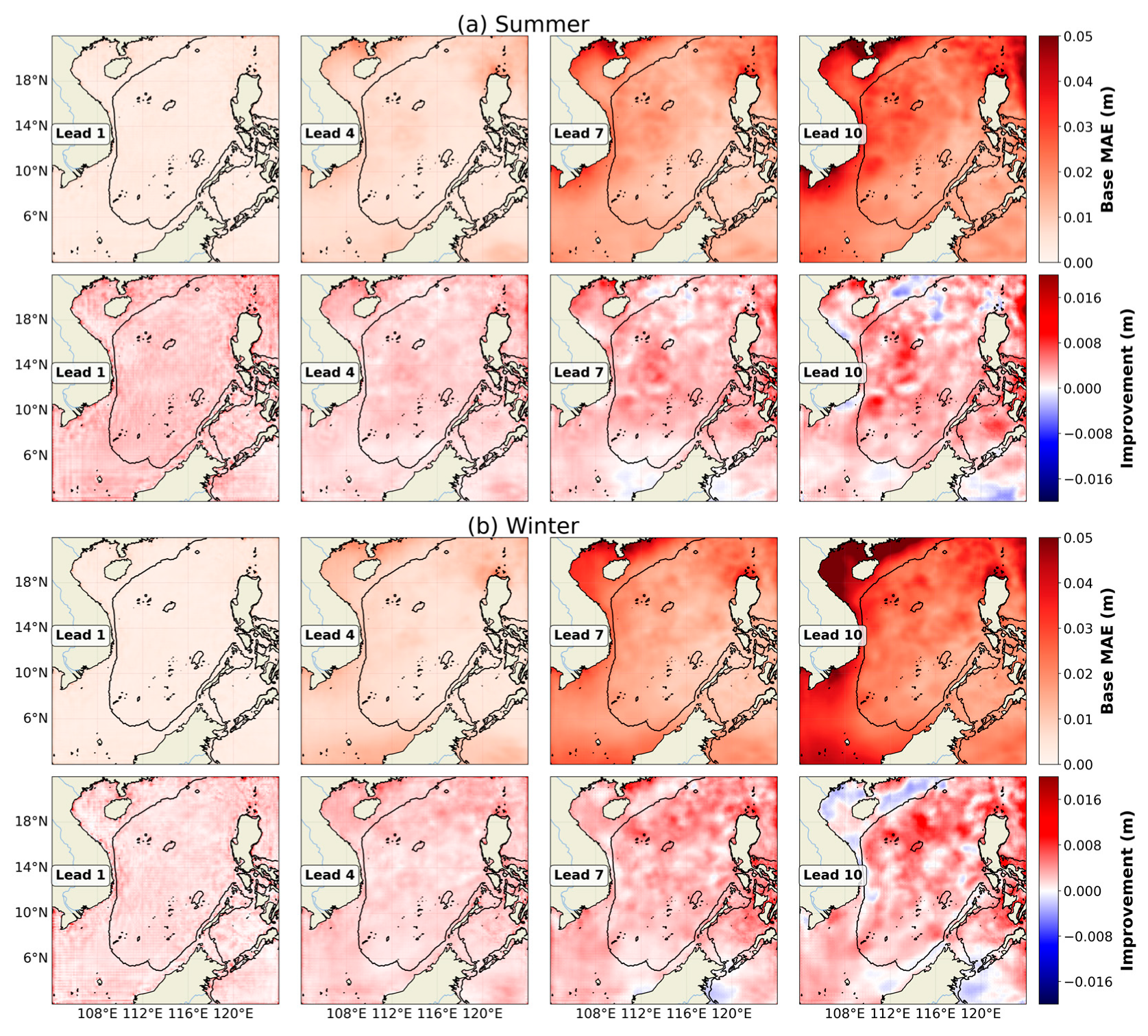
The predictive performance of both the Base-SV and the Phys-SV exhibits a distinct seasonal cycle, as illustrated in the time series of forecast errors in Figure 6. For this analysis, the error metric for any given start date represents the average performance over the subsequent ten-day forecast period. Figure 6 clearly indicates that for both models, the RMSE and the PCC are both systematically lower during the summer months (April–September, red shading) compared to the winter months (October–March, blue shading).

We hypothesize that this seasonal difference in forecast skill is primarily driven by the inherent seasonal variability of the SSH field itself. To investigate this, we quantified the temporal and spatial variability of SSH for each season in the test dataset. Mean Temporal variability, denoted as ${\overline{\mathsf{\sigma }}}_T$, is defined as the spatial average of the standard deviation calculated over time at each grid point. It measures the typical magnitude of temporal fluctuations within the SSH field. Mean Spatial Variability, denoted as ${\overline{\mathsf{\sigma }}}_S$, is defined as the standard deviation of the time-averaged SSH field. It represents the magnitude of spatial fluctuations within the time-averaged SSH field.

As summarized in

Table 2. Seasonal statistics of SSH variability and the PCC between ${\mathsf{\sigma }}_{\mathit{T}}$ and mean absolute error (MAE) of the Base-SV prediction.

Season	${\overline{\mathsf{\sigma }}}_{\mathit{S}}$ (m)	${\overline{\mathsf{\sigma }}}_{\mathit{T}}$ (m)	PCC (100%)
Summer	0.0741	0.0545	0.52
Winter	0.0954	0.0697	0.58

, both the mean temporal and spatial variability are significantly lower in summer than in winter. This indicates that the SSH field is generally more quiescent and spatially smoother during the summer. To directly link this variability to prediction error, we computed the PCC between the temporal variability (${\mathsf{\sigma }}_T$) and the mean absolute error (MAE) of the Base-SV prediction. The analysis revealed statistically significant positive correlations in both summer (PCC = 0.52) and winter (PCC = 0.58), with confidence levels exceeding 99.9%. This confirms that locations with greater temporal variability are inherently more difficult to predict, and that the higher overall variability in winter is a key driver of the observed seasonal degradation in RMSE.

Considering that RMSE and PCC describe different aspects of the prediction performance (the absolute accuracy and spatial correlation, respectively), and that the ${\overline{\mathsf{\sigma }}}_T$ and ${\overline{\mathsf{\sigma }}}_S$ are both higher in winter, the seemingly counterintuitive phenomenon whereby both RMSE and PCC are higher in winter can be explained as below: while higher-magnitude variations in the SSH field in winter makes it harder to predict precisely for the model, the more significant variation make it easier for the model to capture the variation mode of the SSH field than in summer, which accounts for why the PCC of prediction is higher in winter.

4.3. Spatial Distribution of Forecast Error

The previous section established that the overall forecast error is lower in summer and that the performance improvement of the Phys-SV is also season-dependent. To further investigate these patterns, we analyze the spatial distribution of the mean absolute error (MAE) for both the Base-SV model and the Phys-SV, as shown in Figure 7 and Figure 8.

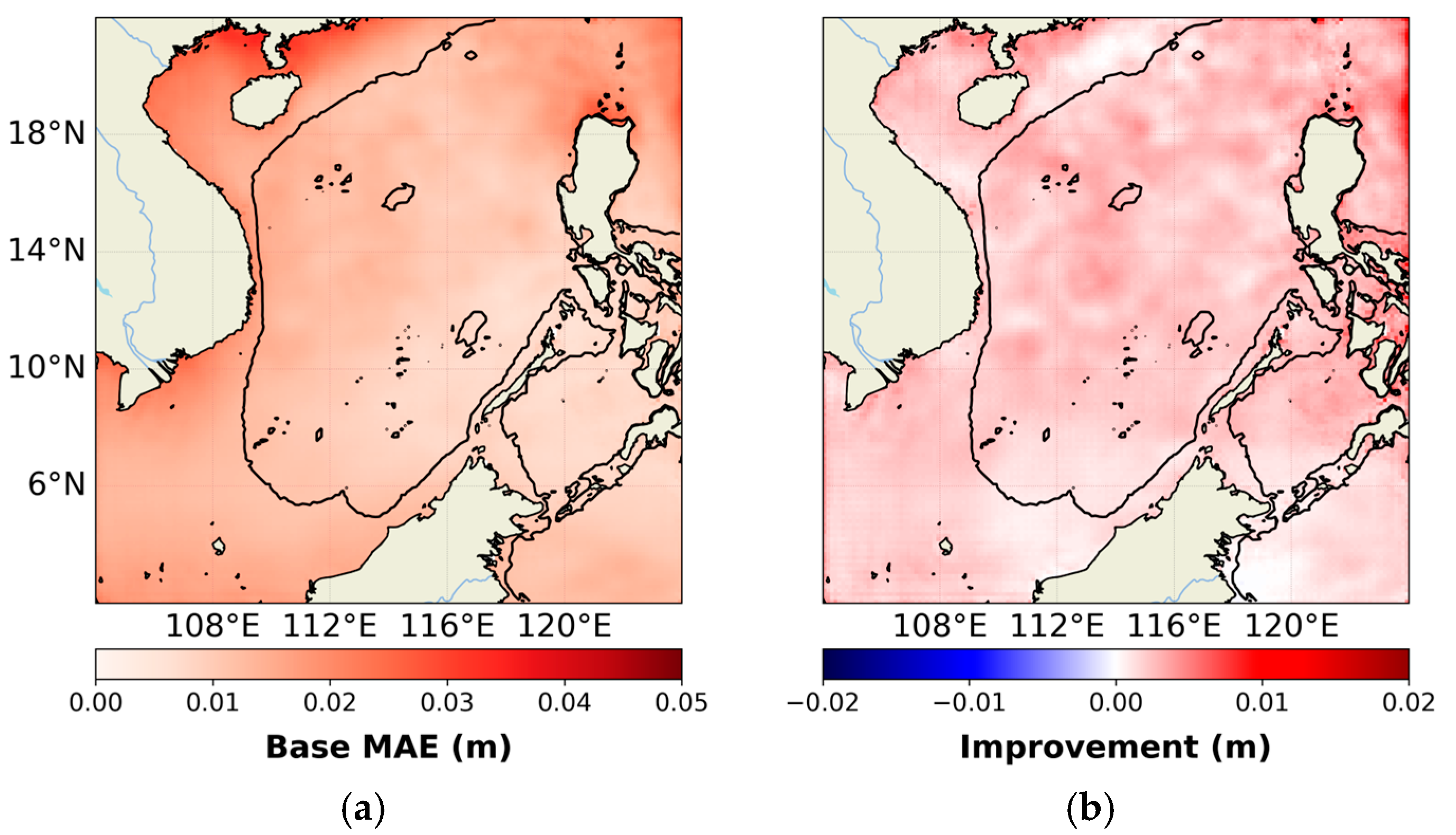
Figure 7 illustrates that the MAE of the Base-SV model is not uniformly distributed, with elevated errors concentrated in dynamically active regions, including the coastal waters off Vietnam, the Beibu Gulf (also known as the Gulf of Tonkin), the Guangdong coast, the area east of the Luzon Strait, and the Sunda Shelf.

Further analysis of Figure 8 reveals that the MAE of the Base-SV model is initially relatively uniform but becomes increasingly heterogeneous as lead time increases. This inhomogeneity also exhibits seasonal variations. For example, at a lead time of 10 days, the MAE is notably higher during winter along the Vietnamese coast, the Guangdong coast, the Beibu Gulf, and the Sunda Shelf. This pattern is consistent with the winter intensification of monsoon-driven circulation features, such as the Vietnam Coastal Current and the Natuna Eddy, which are associated with stronger nonlinear dynamics [33].

In addition to seasonal variations, another prominent characteristic of the forecast error is the strong influence of bathymetry. High-error regions are predominantly located in shallow coastal and shelf waters. To quantify this, we divided the domain into shelf areas (<200 m) and deep-basin regions (DB; defined as areas with water depth exceeding 200 m). As summarized in

Table 3. RMSE (m) for the whole domain (WD) and deep-basin areas (DB, depth > 200 m).

Model	Scope	Full Year	Summer	Winter
Base-SV	WD	0.0198	0.0185	0.0210
	DB	0.0172	0.0169	0.0172
Phys-SV	WD	0.0173	0.0159	0.0188
	DB	0.0145	0.0142	0.0149

, the RMSE for the Base-SV model in the DB region is 0.0172 m, which is 13% lower than the full-domain RMSE of 0.0198 m. This discrepancy can be attributed to two main factors: (1) the reduced accuracy of satellite altimetry data in coastal zones [34], and (2) the presence of complex nearshore dynamical processes—such as coastal currents, shelf waves, tides, and upwelling—which are often nonlinear, high-frequency, and not fully resolved by the model [35].

Moreover, the seasonal differences in the models’ prediction RMSE are mainly concentrated in the shallow water area. For the Base-SV, the seasonal RMSE differences are 0.0025 m in WD and only 0.0003 m in DB. For the Phys-SV, 0.0029 m in WD and 0.0007 m in DB. This phenomenon may be closely linked to the dynamic effects of the winter monsoon in the South China Sea [36]. The specific mechanisms include the following two aspects: First, the winter monsoon is stronger and exhibits higher variability, which tends to induce more frequent and intense coastal jets, enhancing nonlinear effects in the flow and thereby increasing simulation challenges for the models. Second, the prevailing northeasterly winds in winter drive the transport and accumulation of surface water toward the western coastal areas of the South China Sea via Ekman transport, leading to a significant rise in sea surface height. This process not only alters the regional dynamic structure but may also amplify pressure gradients and flow variability, further increasing forecasting uncertainties.

4.4. Impact of the Geostrophic Constraint

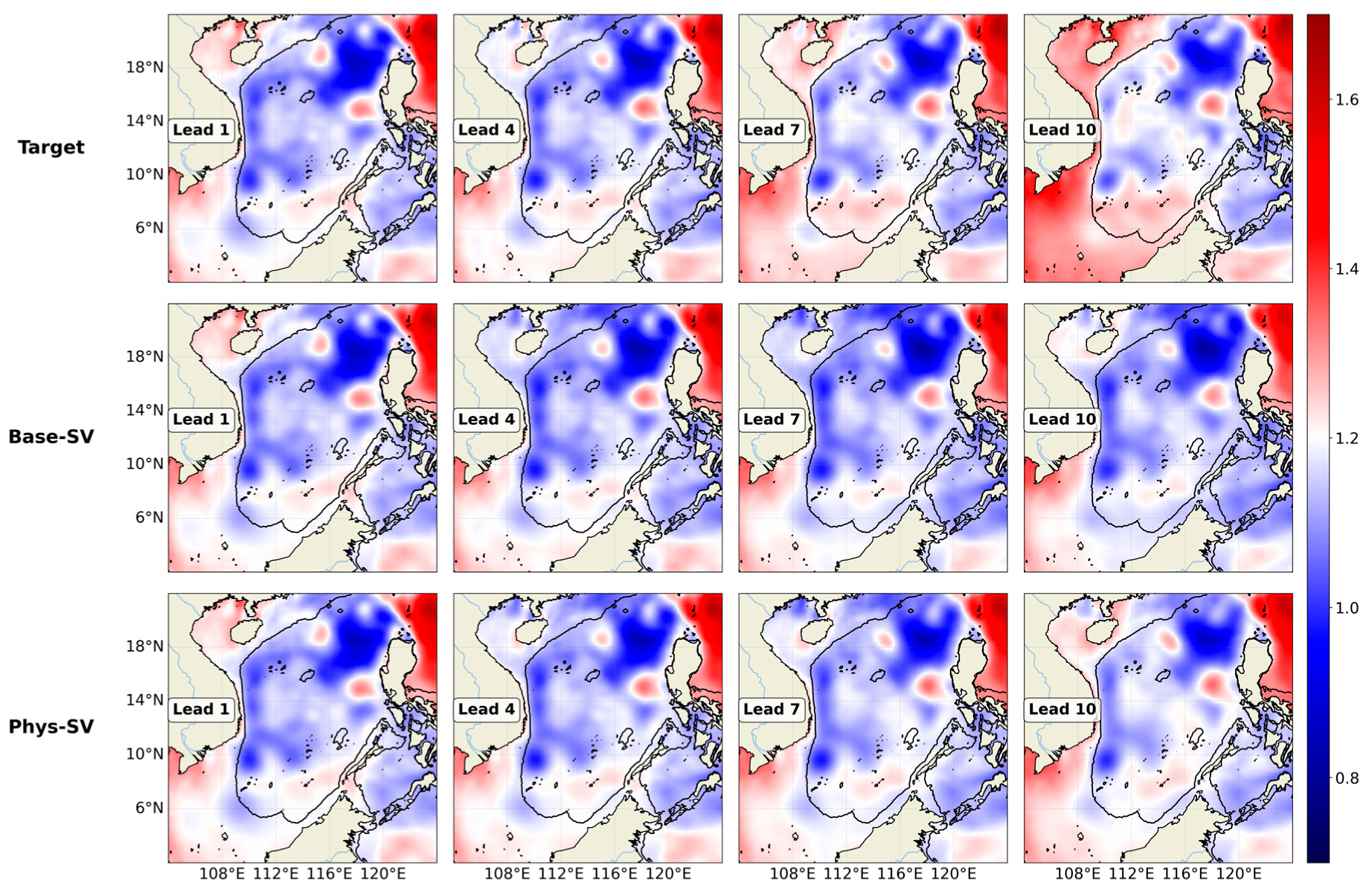
The application of the geostrophic constraint also leads to significant spatial variation in forecast performance. As indicated in Table 3, the improvement achieved by the Phys-SV over the Base-SV model is more pronounced in the DB region, where the RMSE is reduced by 16%, compared to a 12% reduction in the whole domain (WD).

Figure 7 shows that the Phys-SV improves forecast accuracy across most of the study areas. One of the most substantial improvements occurs east of the Luzon Strait. This result aligns with previous studies suggesting that the Kuroshio transport through the strait is primarily governed by geostrophic dynamics [37], confirming that the integration of this physical constraint enhances model performance in regions where the underlying assumption is most valid.

The effect of the geostrophic constraint also varies with forecast lead time (Figure 8). At a one-day lead time, the Phys-SV provides relatively uniform improvement across the domain. However, as the lead time extends to 7 and 10 days, the spatial distribution of improvements becomes more heterogeneous. While performance gains intensify in regions where geostrophic balance dominates—such as east of the Luzon Strait and the central deep basin—some areas near the land boundary show limited improvement or even increased error. This may be related to complex nonlinear effects induced by boundary dynamics, which warrant further investigation.

4.5. Case Study

To examine the specific impact of the geostrophic constraint on the prediction, we selected the day with the most notable RMSE—10 February 2023, as indicated in Figure 6a—for a case study. As Figure 9 illustrates, this is a typical western boundary current (WBC) strengthening process. From lead 1 to lead 10, the SSH rose markedly to west of the 200 m isobath, a phenomenon primarily driven by the intraseasonal strengthening of northeasterly winds, as demonstrated in previous research [36]. Additionally, the anticyclonic eddy in the northeastern SCS exhibited variability during the forecast period, likely influenced by a combination of wind effects and Kuroshio intrusion [38].

A comparison of model predictions reveals that although both Base-SV and Phys-SV underestimate the SSH rise in the western boundary, the output from Phys-SV aligns more closely with the target data. Furthermore, Phys-SV more accurately represents the evolution of the anticyclonic eddy in the northeastern SCS than Base-SV, both in terms of spatial structure and intensity.

In this case, the RMSE of the Phys-SV model is 0.0303 m, compared to 0.0412 m for the Base-SV model, representing a 26% reduction in RMSE. Moreover, the RMSE values of both models in this case are higher than those on the entire test dataset, which we attribute primarily to the high magnitude and rapid variation in wind during this period.

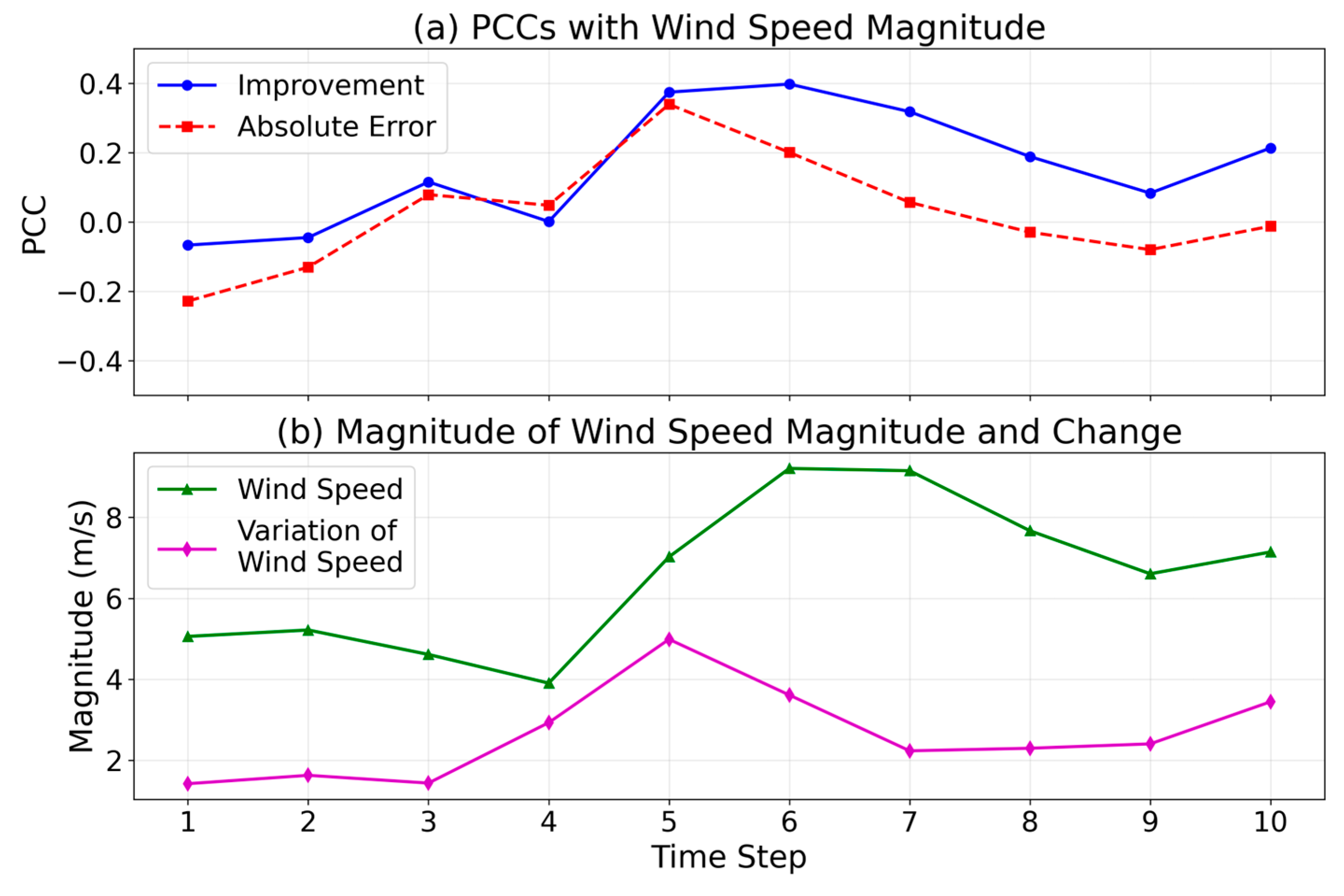
To verify this hypothesis, we computed the Pearson correlation coefficient (PCC) between the absolute error of Base-SV and wind speed magnitude (denoted as PCC-E), as well as the PCC between the improvement by Phys-SV and wind speed magnitude (denoted as PCC-I), at each time step. As shown in Figure 10, the PCC-E curve closely resembles the curve of the magnitude of wind speed variation (MVW), and similarly, the PCC-I curve aligns with the magnitude of wind speed (MW). We further calculated the correlation coefficients (CCs) between PCC-E and MVW, and between PCC-I and MW. Both pairs exhibit statistically significant correlations: CC = 0.85 (p = 0.002) for PCC-E and MVW, and CC = 0.92 (p = 0.0002) for PCC-I and MW.

The strong correlation between PCC-E and MVW suggests that under high wind variability, the prediction errors of the Base-SV model increase with wind speed. Similarly, the high correlation between PCC-I and MW indicates that the performance improvement of Phys-SV over Base-SV becomes more pronounced as wind speed intensifies.

The former result underscores the substantial influence of wind on SSH prediction and highlights a key limitation in existing approaches: the absence of wind data as input. To address this, we incorporated normalized interpolated ERA5 wind data together with normalized SSH as inputs to the Base-SV model and retrained it under the same configuration. However, the resulting test RMSE was 0.0207 m, higher than the 0.0198 m achieved without wind data. This suggests that the model struggled to effectively integrate the two distinct types of data, pointing to the need for further work on multimodal data alignment to enable more efficient information fusion.

The latter result indicates that, in this case, a higher wind magnitude is associated with a greater improvement. This is likely because the GC—a form of gradient loss function—guides the Phys-SV model to become more sensitive to gradient variations, thereby enhancing its capacity to capture the underlying patterns of SSH gradients, which are strongly influenced by wind forcing.

5. Conclusions

In this study, we developed physics-informed methods, including latitude-weighted geostrophic constraints (GCs) and mask-informed inputs (MIs), to enhance SSH forecasting in the South China Sea. For MI, we utilize mask information as input to reduce artifacts caused by the processing of extensive land points in oceanographic datasets using AI models. As for GC, we integrated a latitude-weighted geostrophic constraint into the loss function by minimizing the difference between predicted and target geostrophic currents, which are derived from SSH gradients. The latitude weights address the diminished validity of geostrophic balance near the equator by applying smaller weights to the geostrophic loss in that region. We tested the effect of the physics-informed methods on two mainstream spatiotemporal prediction models: SimVPv2 (SV) and PredRNNv2 (PR). The results indicate that GC primarily enhances SV’s performance, while it worsens PR’s performance; MI improves the performance of both models, with significant benefits for PR and marginal improvements for SV.

We investigated the influence of seasonality on model performance. Both the Base-SV and Phys-SV models demonstrated higher forecast accuracy during summer compared to winter. Correlation analysis between the MAE of the Base-SV prediction and the temporal variability of the SSH field confirmed that regions with higher temporal variability are inherently more challenging to predict. Consequently, the increased temporal variability of SSH during winter is identified as a significant factor contributing to seasonal degradation in forecast accuracy.

The bathymetric effects were also examined. Both models demonstrated significantly lower RMSE in deep basin areas (DB, with depths greater than 200 m) compared to the entire domain. Furthermore, the seasonal performance discrepancies of the models are found to exist primarily in shallow water areas, and the performance advantage of Phys-SV over Base-SV is more pronounced in DB. These findings emphasize the role of topographic features in influencing prediction errors and in modulating the effectiveness of physical constraints, highlighting the necessity of incorporating the bathymetric context into the design of future models.

Overall, this study confirms the feasibility and value of embedding the physics-informed methods into deep learning frameworks for SSH forecasting. Phys-SV improves prediction skill while enhancing interpretability by aligning with physical ocean dynamics. Mask-PR demonstrates the significance of informing the AI model of the land masks to mitigate the artifact inputs into the model. This work demonstrates a promising direction for integrating physical knowledge with data-driven modeling in ocean prediction.

As the case study illustrates, wind variation significantly contributes to prediction errors. Therefore, integrating wind data into the model is expected to enhance SSH predictions. Nevertheless, the poorer outcomes from attempts to combine wind data with SSH as inputs for the SV model underscore the need for exploring improved methods to incorporate heterogeneous oceanic data into AI models, which is our future research direction.

Moreover, considering the inherent limitations and finite scope of applicability of the geostrophic approximation itself, the incorporation of broader physical constraints is recommended for future oceanic AI models to further enhance their predictive performance and physical consistency.