Evaluating Terrestrial Water Storage, Fluxes, and Drivers in the Pearl River Basin from Downscaled GRACE/GFO and Hydrometeorological Data
Highlights
- A joint inversion approach fuses GRACE/GFO observations with WGHM outputs to produce a high-resolution TWSA dataset for the Pearl River Basin (PRB).
- The downscaled product outperforms WGHM, capturing seasonal and interannual variations in water storage and fluxes.
- The downscaled TWSA enables basin-scale monitoring in the PRB, capturing seasonal accumulation, interannual shifts, and major extremes (e.g., the 2021 drought and wet-season floods) to improve risk assessment and water management.
- Coupling the product with XGBoost–SHAP could provide quantitative attribution of drivers (precipitation, runoff, evapotranspiration, vegetation), supporting process interpretation, forecasting, and decision-making.
Abstract
1. Introduction
2. Data
2.1. Downscaling GRACE/GFO-Derived TWSA
2.2. WaterGap Global Hydrological Model Outputs
2.3. Hydrometeorological Data
2.4. Climate Indices
2.5. Auxiliary Data
3. Methodology
3.1. Water Balance Equation
3.2. Performance Metrics
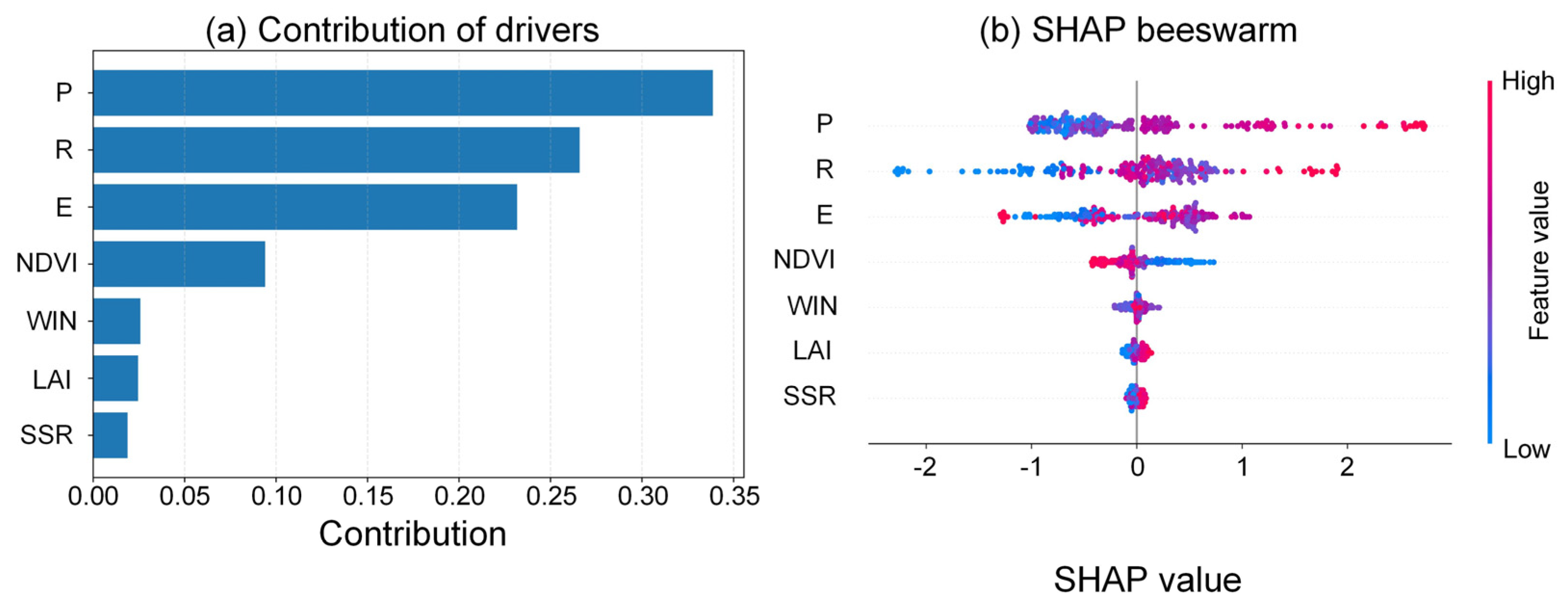
3.3. Quantifying Drivers of TWSA
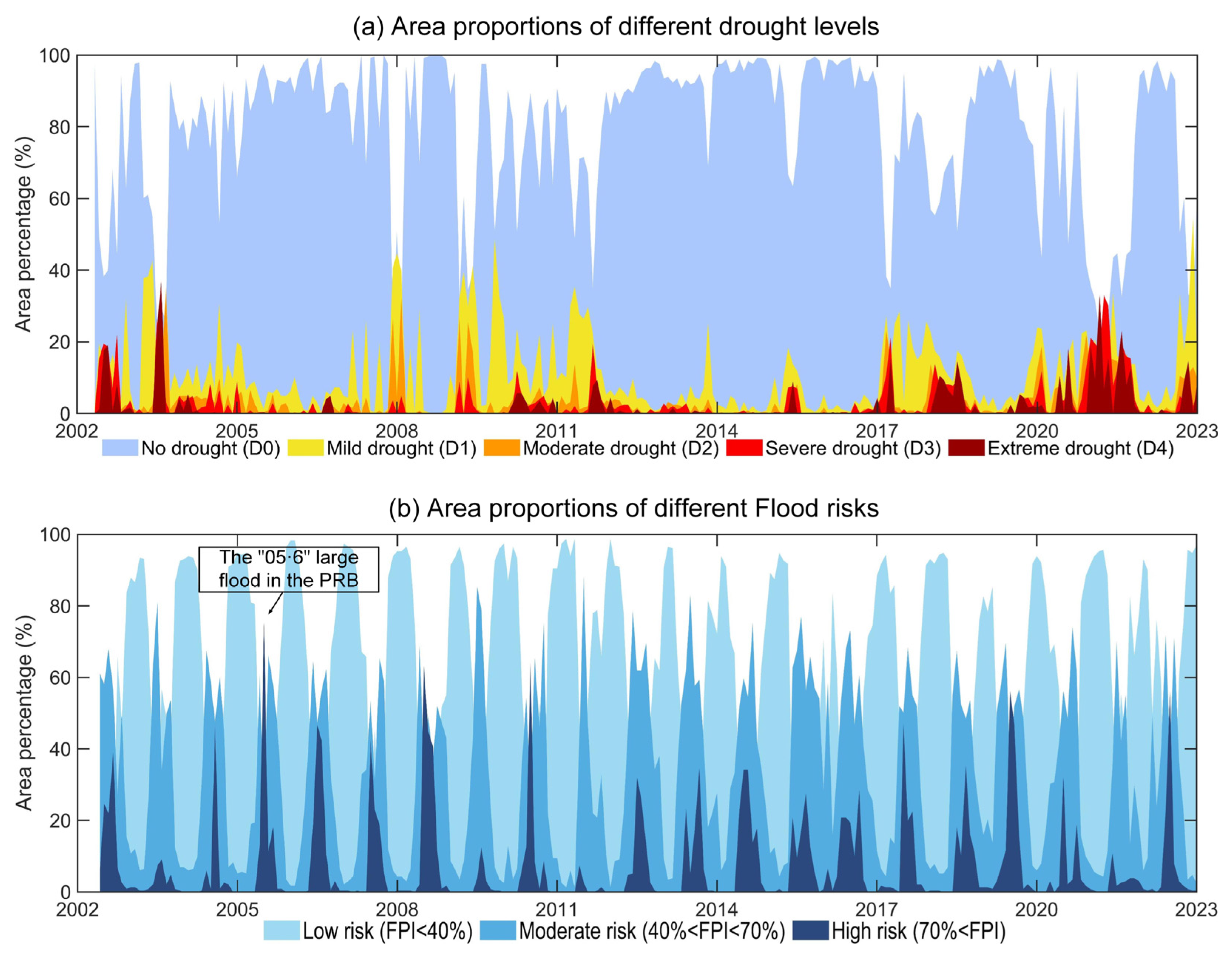
3.4. Drought Severity Index
3.5. Flood Potential Index
4. Results
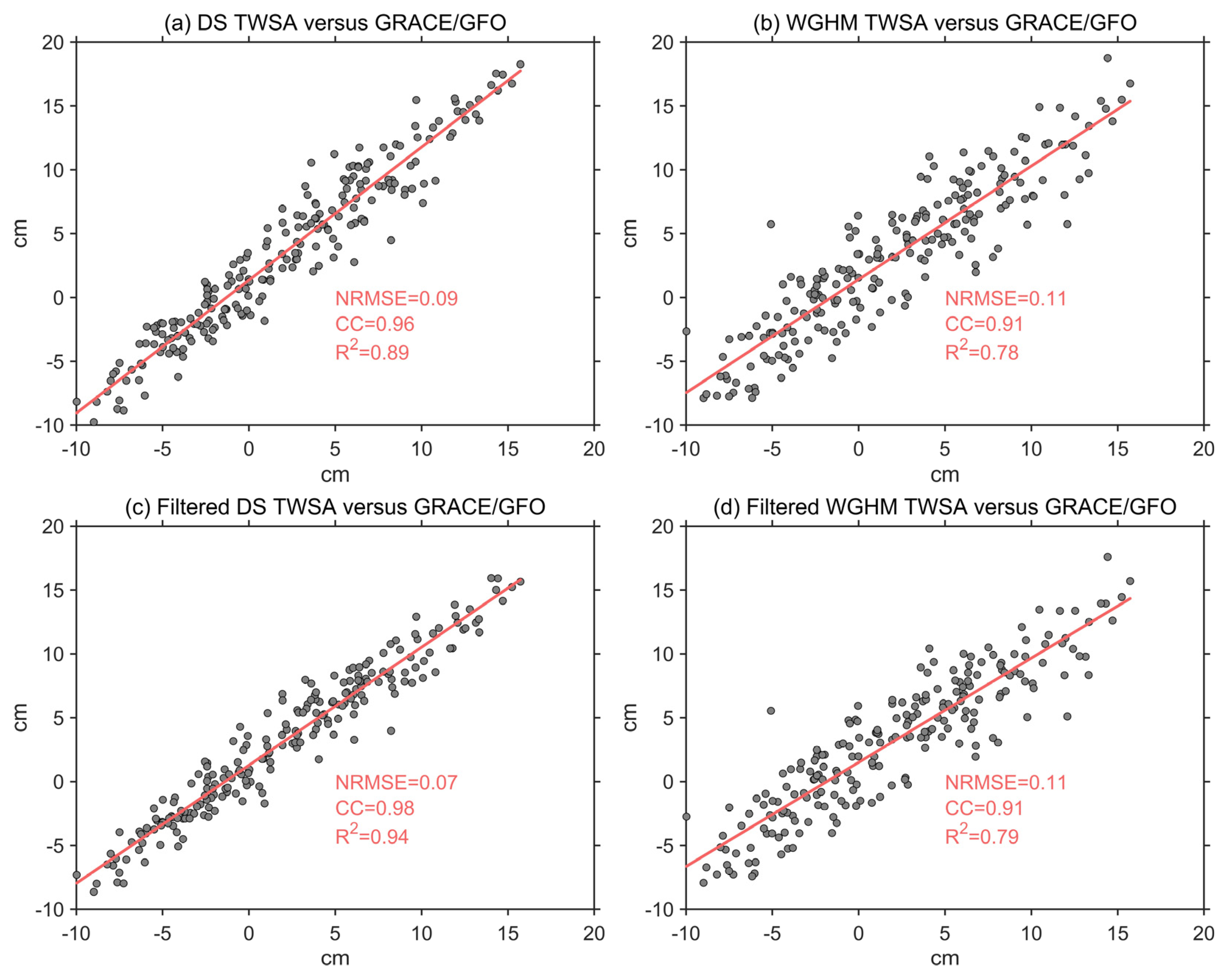
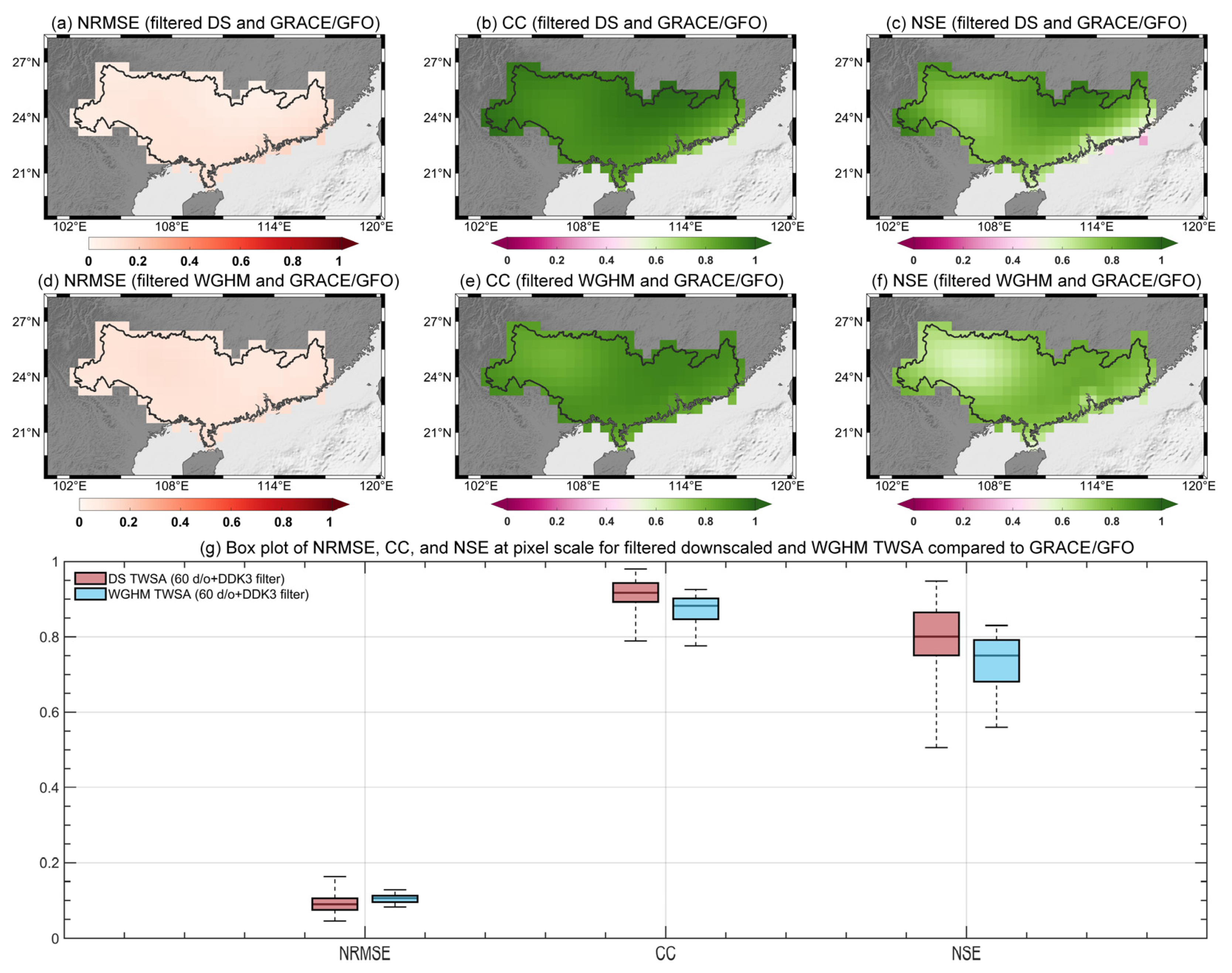
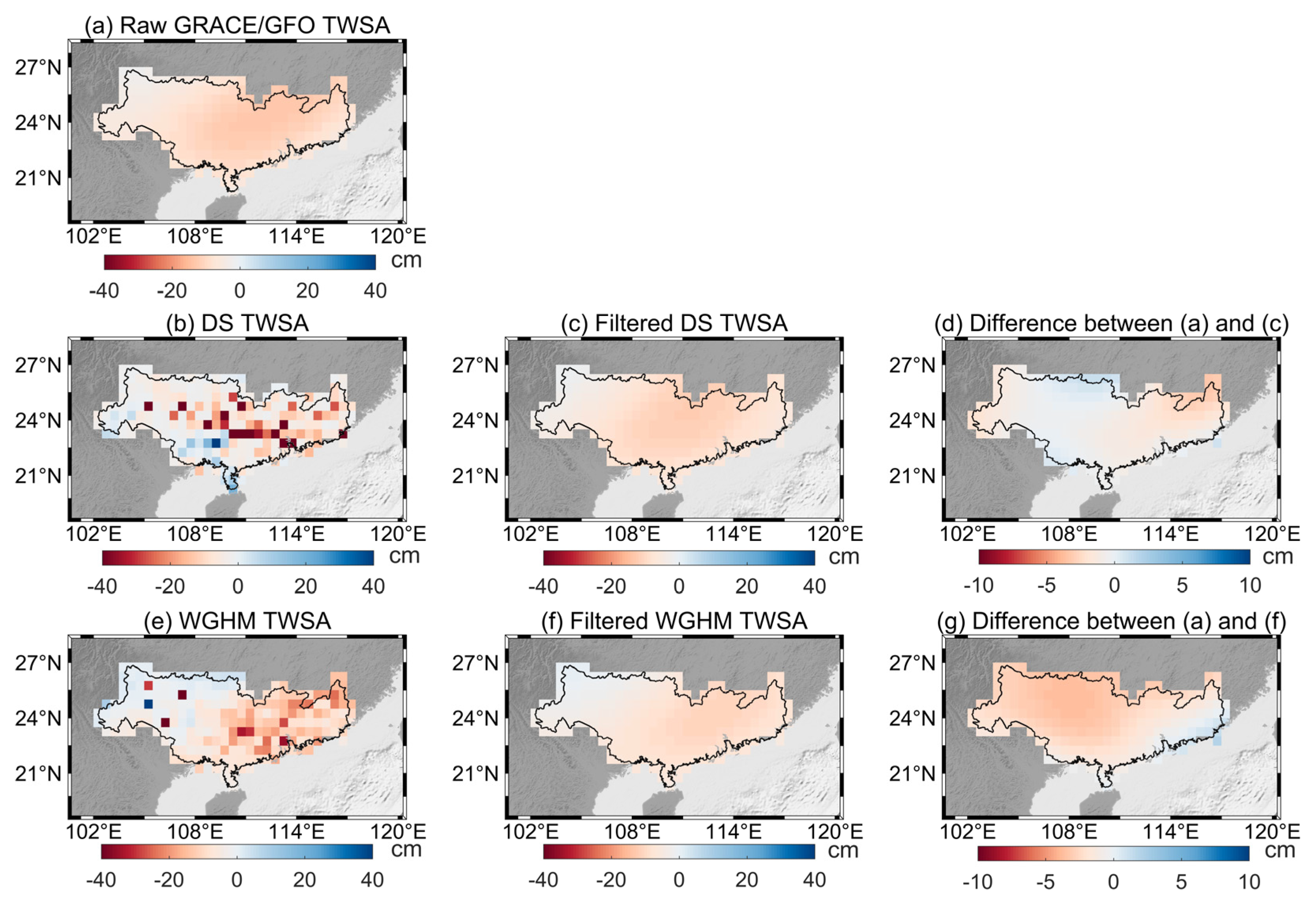
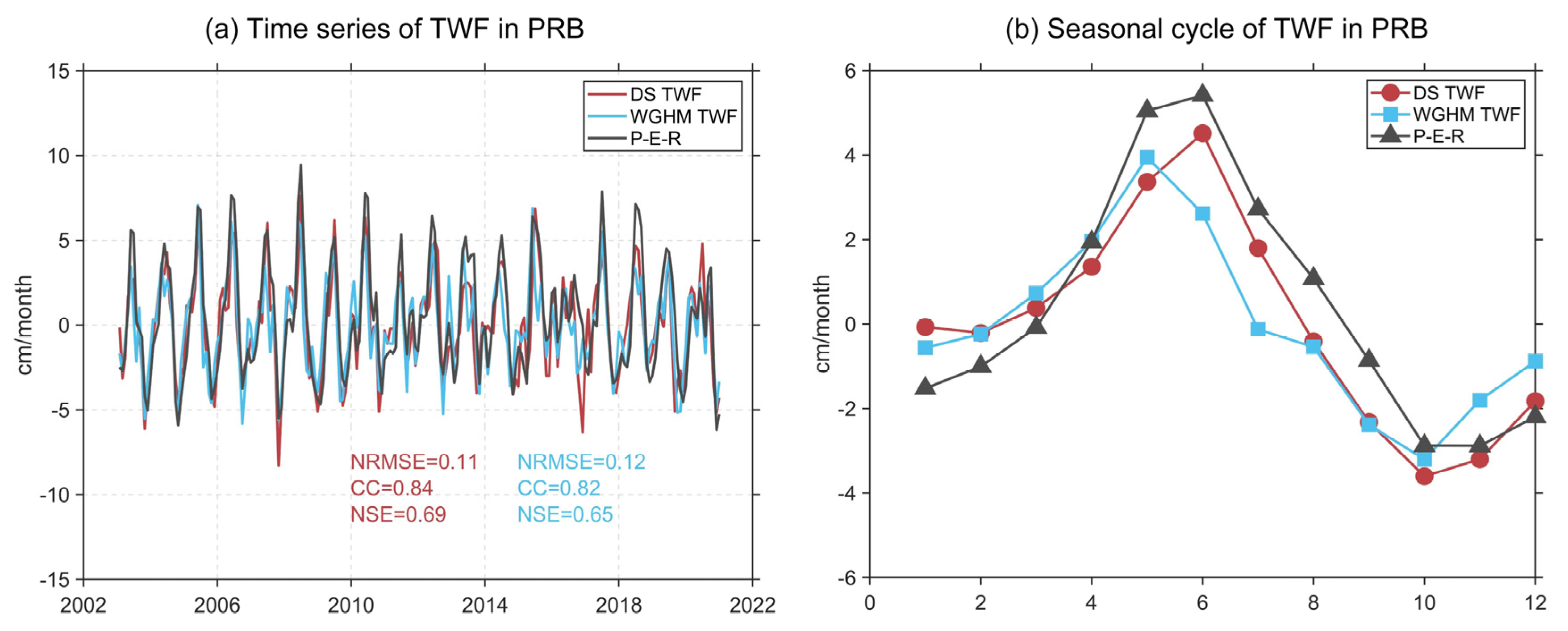
4.1. Performance of Downscaled TWSA
4.1.1. Basin-Averaged Comparison
4.1.2. Pixel-Level Comparison at GRACE/GFO Resolution
4.1.3. Comparison of Water Fluxes
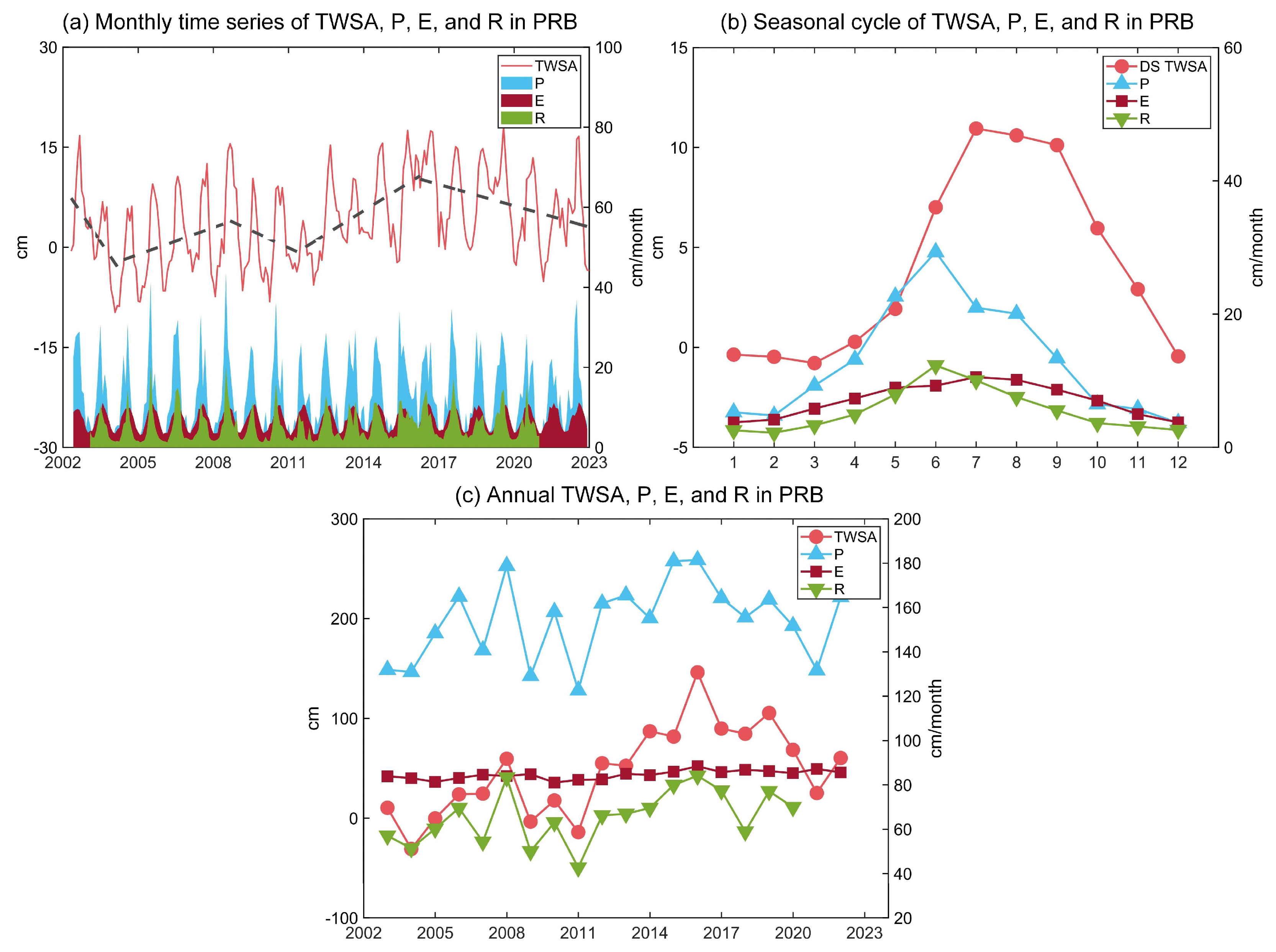
4.2. TWSA and Water Balance Components in the PRB
4.3. Drivers of TWSA in the PRB
4.4. Characteristics of Hydrological Droughts and Floods in PRB
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ou, H.; Cai, S.; Fan, W.; Qiu, J.; Mu, X.; Zhou, T.; Yang, X.; Picco, L. Sustaining the Pearl River: A Critical Review of Changes in Fluvial Geomorphological Processes and the Driving Forces in the Pearl River Basin. Water 2024, 16, 1001. [Google Scholar] [CrossRef]
- Ouyang, R.; Liu, W.; Fu, G.; Liu, C.; Hu, L.; Wang, H. Linkages between ENSO/PDO signals and precipitation, streamflow in China during the last 100 years. Hydrol. Earth Syst. Sci. 2014, 18, 3651–3661. [Google Scholar] [CrossRef]
- Niu, J. Precipitation in the Pearl River basin, South China: Scaling, regional patterns, and influence of large-scale climate anomalies. Stoch. Environ. Res. Risk Assess. 2013, 27, 1253–1268. [Google Scholar] [CrossRef]
- Huang, Z.; Jiao, J.J.; Luo, X.; Pan, Y.; Jin, T. Drought and Flood Characterization and Connection to Climate Variability in the Pearl River Basin in Southern China Using Long-Term GRACE and Reanalysis Data. J. Clim. 2021, 34, 2053–2078. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.-Y.; Zhang, Z. Observed changes of drought/wetness episodes in the Pearl River basin, China, using the standardized precipitation index and aridity index. Theor. Appl. Climatol. 2009, 98, 89–99. [Google Scholar] [CrossRef]
- Qiu, J.; Cao, B.; Park, E.; Yang, X.; Zhang, W.; Tarolli, P. Flood Monitoring in Rural Areas of the Pearl River Basin (China) Using Sentinel-1 SAR. Remote Sens. 2021, 13, 1384. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, H.; Chen, W.; Huang, G. Urbanization and climate change impacts on future flood risk in the Pearl River Delta under shared socioeconomic pathways. Sci. Total Environ. 2021, 762, 143144. [Google Scholar] [CrossRef]
- Sun, A.Y.; Scanlon, B.R.; AghaKouchak, A.; Zhang, Z. Using GRACE Satellite Gravimetry for Assessing Large-Scale Hydrologic Extremes. Remote Sens. 2017, 9, 1287. [Google Scholar] [CrossRef]
- Reager, J.T.; Famiglietti, J.S. Global terrestrial water storage capacity and flood potential using GRACE. Geophys. Res. Lett. 2009, 36, L23402. [Google Scholar] [CrossRef]
- Zhao, M.; Geruo, A.; Velicogna, I.; Kimball, J.S. Satellite Observations of Regional Drought Severity in the Continental United States Using GRACE-Based Terrestrial Water Storage Changes. J. Clim. 2017, 30, 6297–6308. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Rateb, A.; Anyamba, A.; Kebede, S.; MacDonald, A.M.; Shamsudduha, M.; Small, J.; Sun, A.; Taylor, R.G.; Xie, H. Linkages between GRACE water storage, hydrologic extremes, and climate teleconnections in major African aquifers. Environ. Res. Lett. 2022, 17, 014046. [Google Scholar] [CrossRef]
- Neves, M.C. Links Between Extremes in GRACE TWS and Climate Patterns Across Iberia. Water 2025, 17, 1108. [Google Scholar] [CrossRef]
- Huang, Z.; Yeh, P.J.F.; Pan, Y.; Jiao, J.J.; Gong, H.; Li, X.; Güntner, A.; Zhu, Y.; Zhang, C.; Zheng, L. Detection of large-scale groundwater storage variability over the karstic regions in Southwest China. J. Hydrol. 2019, 569, 409–422. [Google Scholar] [CrossRef]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P. Contributions of GRACE to understanding climate change. Nat. Clim. Change 2019, 9, 358–369. [Google Scholar] [CrossRef]
- Rodell, M.; Li, B. Changing intensity of hydroclimatic extreme events revealed by GRACE and GRACE-FO. Nat. Water 2023, 1, 241–248. [Google Scholar] [CrossRef]
- Xiong, Y.; Feng, W.; Chen, J.; Shen, Y.; Bai, H.; Jiang, Z.; Zhong, M. Refined GRACE/GFO-Derived Terrestrial Water Storage Anomaly in Middle East Recovered by ICA-Based Forward Modeling Approach. Water Resour. Res. 2025, 61, e2024WR039837. [Google Scholar] [CrossRef]
- Vishwakarma, B.D.; Devaraju, B.; Sneeuw, N. What Is the Spatial Resolution of grace Satellite Products for Hydrology? Remote Sens. 2018, 10, 852. [Google Scholar] [CrossRef]
- Pail, R.; Bingham, R.; Braitenberg, C.; Dobslaw, H.; Eicker, A.; Güntner, A.; Horwath, M.; Ivins, E.; Longuevergne, L.; Panet, I.; et al. Science and User Needs for Observing Global Mass Transport to Understand Global Change and to Benefit Society. Surv. Geophys. 2015, 36, 743–772. [Google Scholar] [CrossRef]
- Xiong, Y.; Feng, W.; Bai, H.; Chen, W.; Jiang, Z.; Zhong, M. High-Resolution Terrestrial Water Storage Anomalies and Components in China From GRACE/GFO via Joint Inversion Downscaling. Water Resour. Res. 2025, 61, e2024WR038996. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Sun, A.Y.; Müller Schmied, H.; Van Beek, L.P.; Wiese, D.N.; Wada, Y.; Long, D.; Reedy, R.C. Global models underestimate large decadal declining and rising water storage trends relative to GRACE satellite data. Proc. Natl. Acad. Sci. USA 2018, 115, E1080–E1089. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Rateb, A.; Sun, A.; Wiese, D.; Save, H.; Beaudoing, H.; Lo, M.H.; Müller-Schmied, H.; Döll, P.; et al. Tracking Seasonal Fluctuations in Land Water Storage Using Global Models and GRACE Satellites. Geophys. Res. Lett. 2019, 46, 5254–5264. [Google Scholar] [CrossRef]
- Eicker, A.; Schumacher, M.; Kusche, J.; Döll, P.; Schmied, H.M. Calibration/Data Assimilation Approach for Integrating GRACE Data into the WaterGAP Global Hydrology Model (WGHM) Using an Ensemble Kalman Filter: First Results. Surv. Geophys. 2014, 35, 1285–1309. [Google Scholar] [CrossRef]
- Li, B.; Rodell, M.; Kumar, S.; Beaudoing, H.K.; Getirana, A.; Zaitchik, B.F.; de Goncalves, L.G.; Cossetin, C.; Bhanja, S.; Mukherjee, A.; et al. Global GRACE Data Assimilation for Groundwater and Drought Monitoring: Advances and Challenges. Water Resour. Res. 2019, 55, 7564–7586. [Google Scholar] [CrossRef]
- Gerdener, H.; Kusche, J.; Schulze, K.; Döll, P.; Klos, A. The global land water storage data set release 2 (GLWS2.0) derived via assimilating GRACE and GRACE-FO data into a global hydrological model. J. Geod. 2023, 97, 73. [Google Scholar] [CrossRef]
- Yang, F.; Schumacher, M.; Retegui-Schiettekatte, L.; van Dijk, A.I.J.M.; Forootan, E. PyGLDA: A fine-scale Python-based Global Land Data Assimilation system for integrating satellite gravity data into hydrological models. Geosci. Model Dev. Discuss. 2024, 18, 6195–6217. [Google Scholar] [CrossRef]
- Gou, J.; Soja, B. Global high-resolution total water storage anomalies from self-supervised data assimilation using deep learning algorithms. Nat. Water 2024, 2, 139–150. [Google Scholar] [CrossRef]
- Vishwakarma, B.D.; Zhang, J.; Sneeuw, N. Downscaling GRACE total water storage change using partial least squares regression. Sci. Data 2021, 8, 95. [Google Scholar] [CrossRef]
- Agarwal, V.; Akyilmaz, O.; Shum, C.K.; Feng, W.; Yang, T.-Y.; Forootan, E.; Syed, T.H.; Haritashya, U.K.; Uz, M. Machine learning based downscaling of GRACE-estimated groundwater in Central Valley, California. Sci. Total Environ. 2023, 865, 161138. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S.; Wiese, D.N.; Reager, J.T.; Beaudoing, H.K.; Landerer, F.W.; Lo, M.H. Emerging trends in global freshwater availability. Nature 2018, 557, 651–659. [Google Scholar] [CrossRef]
- Trautmann, T.; Koirala, S.; Carvalhais, N.; Güntner, A.; Jung, M. The importance of vegetation in understanding terrestrial water storage variations. Hydrol. Earth Syst. Sci. 2022, 26, 1089–1109. [Google Scholar] [CrossRef]
- Yi, S.; Sun, W.; Feng, W.; Chen, J. Anthropogenic and climate-driven water depletion in Asia. Geophys. Res. Lett. 2016, 43, 9061–9069. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, C.; Gong, H.; Yeh, P.J.-F.; Shen, Y.; Guo, Y.; Huang, Z.; Li, X. Detection of human-induced evapotranspiration using GRACE satellite observations in the Haihe River basin of China. Geophys. Res. Lett. 2017, 44, 190–199. [Google Scholar] [CrossRef]
- Humphrey, V.; Gudmundsson, L. GRACE-REC: A reconstruction of climate-driven water storage changes over the last century. Earth Syst. Sci. Data 2019, 11, 1153–1170. [Google Scholar] [CrossRef]
- Li, D.; Pan, M.; Cong, Z.; Zhang, L.; Wood, E. Vegetation control on water and energy balance within the Budyko framework. Water Resour. Res. 2013, 49, 969–976. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef]
- Fan, Y.; Miguez-Macho, G.; Jobbágy, E.G.; Jackson, R.B.; Otero-Casal, C. Hydrologic regulation of plant rooting depth. Proc. Natl. Acad. Sci. USA 2017, 114, 10572–10577. [Google Scholar] [CrossRef]
- Fan, C.; Song, C.; Liu, K.; Ke, L.; Xue, B.; Chen, T.; Fu, C.; Cheng, J. Century-Scale Reconstruction of Water Storage Changes of the Largest Lake in the Inner Mongolia Plateau Using a Machine Learning Approach. Water Resour. Res. 2021, 57, e2020WR028831. [Google Scholar] [CrossRef]
- Ding, K.; Zhao, X.; Cheng, J.; Yu, Y.; Luo, Y.; Couchot, J.; Zheng, K.; Lin, Y.; Wang, Y. GRACE/ML-based analysis of the spatiotemporal variations of groundwater storage in Africa. J. Hydrol. 2025, 647, 132336. [Google Scholar] [CrossRef]
- Landerer, F. Monthly Estimates of Degree-1 (Geocenter) Gravity Coefficients, Generated from GRACE (04-2002–06/2017) and GRACE-FO (06/2018 onward) RL06.1 Solutions. GRACE Technical Note 13, The GRACE Project, NASA Jet Propulsion Laboratory. 2019. Available online: https://podaac.jpl.nasa.gov/gravity/grace-documentation#Level2Documentation/TN-13_GEOC_JPL_RL0601.txt (accessed on 23 November 2025).
- Sun, Y.; Riva, R.; Ditmar, P. Optimizing estimates of annual variations and trends in geocenter motion and J2 from a combination of GRACE data and geophysical models. J. Geophys. Res. Solid Earth 2016, 121, 8352–8370. [Google Scholar] [CrossRef]
- Loomis, B.D.; Rachlin, K.E.; Wiese, D.N.; Landerer, F.W.; Luthcke, S.B. Replacing GRACE/GRACE-FO With Satellite Laser Ranging: Impacts on Antarctic Ice Sheet Mass Change. Geophys. Res. Lett. 2020, 47, e2019GL085488. [Google Scholar] [CrossRef]
- Peltier, W.R.; Argus, D.F.; Drummond, R. Comment on “An Assessment of the ICE-6G_C (VM5a) Glacial Isostatic Adjustment Model” by Purcell et al. J. Geophys. Res. Solid Earth 2018, 123, 2019–2028. [Google Scholar] [CrossRef]
- Kusche, J. Approximate decorrelation and non-isotropic smoothing of time-variable GRACE-type gravity field models. J. Geod. 2007, 81, 733–749. [Google Scholar] [CrossRef]
- Kusche, J.; Schmidt, R.; Petrovic, S.; Rietbroek, R. Decorrelated GRACE time-variable gravity solutions by GFZ, and their validation using a hydrological model. J. Geod. 2009, 83, 903–913. [Google Scholar] [CrossRef]
- Yang, F.; Luo, Z.; Zhou, H.; Kusche, J. On study of the Earth topography correction for the GRACE surface mass estimation. J. Geod. 2022, 96, 95. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Müller Schmied, H.; Cáceres, D.; Eisner, S.; Flörke, M.; Herbert, C.; Niemann, C.; Peiris, T.A.; Popat, E.; Portmann, F.T.; Reinecke, R. The global water resources and use model WaterGAP v2. 2d: Model description and evaluation. Geosci. Model Dev. 2021, 14, 1037–1079. [Google Scholar] [CrossRef]
- Wu, J.; Gao, X.; Giorgi, F.; Chen, D. Changes of effective temperature and cold/hot days in late decades over China based on a high resolution gridded observation dataset. Int. J. Climatol. 2017, 37, 788–800. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Bai, H.; Ming, Z.; Zhong, Y.; Zhong, M.; Kong, D.; Ji, B. Evaluation of evapotranspiration for exorheic basins in China using an improved estimate of terrestrial water storage change. J. Hydrol. 2022, 610, 127885. [Google Scholar] [CrossRef]
- Li, S.; Wu, L.; Yang, Y.; Geng, T.; Cai, W.; Gan, B.; Chen, Z.; Jing, Z.; Wang, G.; Ma, X. The Pacific Decadal Oscillation less predictable under greenhouse warming. Nat. Clim. Change 2020, 10, 30–34. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service. ERA5-Land Monthly Averaged Data from 1950 to Present; Copernicus Climate Change Service (C3S) Climate Data Store (CDS): Reading, UK, 2019. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Uncertainty in evapotranspiration from land surface modeling, remote sensing, and GRACE satellites. Water Resour. Res. 2014, 50, 1131–1151. [Google Scholar] [CrossRef]
- Landerer, F.W.; Dickey, J.O.; Güntner, A. Terrestrial water budget of the Eurasian pan-Arctic from GRACE satellite measurements during 2003–2009. J. Geophys. Res. Atmos. 2010, 115, D23115. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar]
- Xie, J.; Xu, Y.-P.; Yu, H.; Huang, Y.; Guo, Y. Monitoring the extreme flood events in the Yangtze River basin based on GRACE and GRACE-FO satellite data. Hydrol. Earth Syst. Sci. 2022, 26, 5933–5954. [Google Scholar] [CrossRef]
- Boergens, E.; Kvas, A.; Eicker, A.; Dobslaw, H.; Schawohl, L.; Dahle, C.; Murböck, M.; Flechtner, F. Uncertainties of GRACE-Based Terrestrial Water Storage Anomalies for Arbitrary Averaging Regions. J. Geophys. Res. Solid Earth 2022, 127, e2021JB022081. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, W.; Geng, X.; Jin, F.-F. Recent Shift in the State of the Western Pacific Subtropical High due to ENSO Change. J. Clim. 2020, 33, 229–241. [Google Scholar] [CrossRef]
- Huang, H.; Feng, G.; Cao, Y.; Feng, G.; Dai, Z.; Tian, P.; Wei, J.; Cai, X. Simulation and Driving Factor Analysis of Satellite-Observed Terrestrial Water Storage Anomaly in the Pearl River Basin Using Deep Learning. Remote Sens. 2023, 15, 3983. [Google Scholar] [CrossRef]
- Luo, Z.; Yao, C.; Li, Q.; Huang, Z. Terrestrial water storage changes over the Pearl River Basin from GRACE and connections with Pacific climate variability. Geod. Geodyn. 2016, 7, 171–179. [Google Scholar] [CrossRef]
- Liu, K.; Li, X.; Wang, S.; Zhou, G. Past and future adverse response of terrestrial water storages to increased vegetation growth in drylands. npj Clim. Atmos. Sci. 2023, 6, 113. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48, W04531. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Global analysis of approaches for deriving total water storage changes from GRACE satellites. Water Resour. Res. 2015, 51, 2574–2594. [Google Scholar] [CrossRef]
- Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
- Loomis, B.D.; Luthcke, S.B.; Sabaka, T.J. Regularization and error characterization of GRACE mascons. J. Geod. 2019, 93, 1381–1398. [Google Scholar] [CrossRef] [PubMed]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Sheffield, J.; Ferguson, C.R.; Troy, T.J.; Wood, E.F.; McCabe, M.F. Closing the terrestrial water budget from satellite remote sensing. Geophys. Res. Lett. 2009, 36, L07403. [Google Scholar] [CrossRef]
- Aas, K.; Jullum, M.; Løland, A. Explaining individual predictions when features are dependent: More accurate approximations to Shapley values. Artif. Intell. 2021, 298, 103502. [Google Scholar] [CrossRef]
- Daras, I.; March, G.; Pail, R.; Hughes, C.W.; Braitenberg, C.; Güntner, A.; Eicker, A.; Wouters, B.; Heller-Kaikov, B.; Pivetta, T.; et al. Mass-change And Geosciences International Constellation (MAGIC) expected impact on science and applications. Geophys. J. Int. 2023, 236, 1288–1308. [Google Scholar] [CrossRef]
- Bender, P.L.; Conklin, J.W.; Wiese, D.N. Short-Period Mass Variations and the Next Generation Gravity Mission. J. Geophys. Res. Solid Earth 2025, 130, e2024JB030290. [Google Scholar] [CrossRef]
- Luo, J.; Ai, L.; Ai, Y.; An, Z.; Bai, W.; Bai, Y.; Bao, J.; Cao, B.; Chang, W.; Chen, C.; et al. A brief introduction to the TianQin project. Acta Sci. Nat. Univ. Sunyatseni 2023, 60, 1–19. [Google Scholar]
- Xiao, Y.; Yang, Y.; Pan, Z.; Liu, X.; Sun, Z. Performance and application of the Chinese satellite-to-satellite tracking gravimetry system. Chin. Sci. Bull 2023, 68, 2655–2664. [Google Scholar] [CrossRef]

| Drought Category | Description | DSI Value |
|---|---|---|
| D0 | No drought | ≥−0.79 |
| D1 | Mild drought | −0.8 to −1.29 |
| D2 | Moderate drought | −1.3 to −1.59 |
| D3 | Severe drought | −1.6 to −1.99 |
| D4 | Extreme drought | ≤−2.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, Y.; Liang, J.; Feng, W. Evaluating Terrestrial Water Storage, Fluxes, and Drivers in the Pearl River Basin from Downscaled GRACE/GFO and Hydrometeorological Data. Remote Sens. 2025, 17, 3816. https://doi.org/10.3390/rs17233816
Xiong Y, Liang J, Feng W. Evaluating Terrestrial Water Storage, Fluxes, and Drivers in the Pearl River Basin from Downscaled GRACE/GFO and Hydrometeorological Data. Remote Sensing. 2025; 17(23):3816. https://doi.org/10.3390/rs17233816
Chicago/Turabian StyleXiong, Yuhao, Jincheng Liang, and Wei Feng. 2025. "Evaluating Terrestrial Water Storage, Fluxes, and Drivers in the Pearl River Basin from Downscaled GRACE/GFO and Hydrometeorological Data" Remote Sensing 17, no. 23: 3816. https://doi.org/10.3390/rs17233816
APA StyleXiong, Y., Liang, J., & Feng, W. (2025). Evaluating Terrestrial Water Storage, Fluxes, and Drivers in the Pearl River Basin from Downscaled GRACE/GFO and Hydrometeorological Data. Remote Sensing, 17(23), 3816. https://doi.org/10.3390/rs17233816





