ASROT: A Novel Resampling Algorithm to Balance Training Datasets for Classification of Minor Crops in High-Elevation Regions
Highlights
- Imbalanced training data result from insufficient samples of rare classes and typically lead to the limited accuracy of crop classification.
- The adaptive synthetic and repeat oversampling technique (ASROT) was proposed to balance training datasets for accurate classification of multiple crops.
- ASROT simultaneously increases the classification accuracy of major and minor crops.
- The classification of minor crops was improved by up to 30% balancing training datasets.
Abstract
1. Introduction
2. Materials
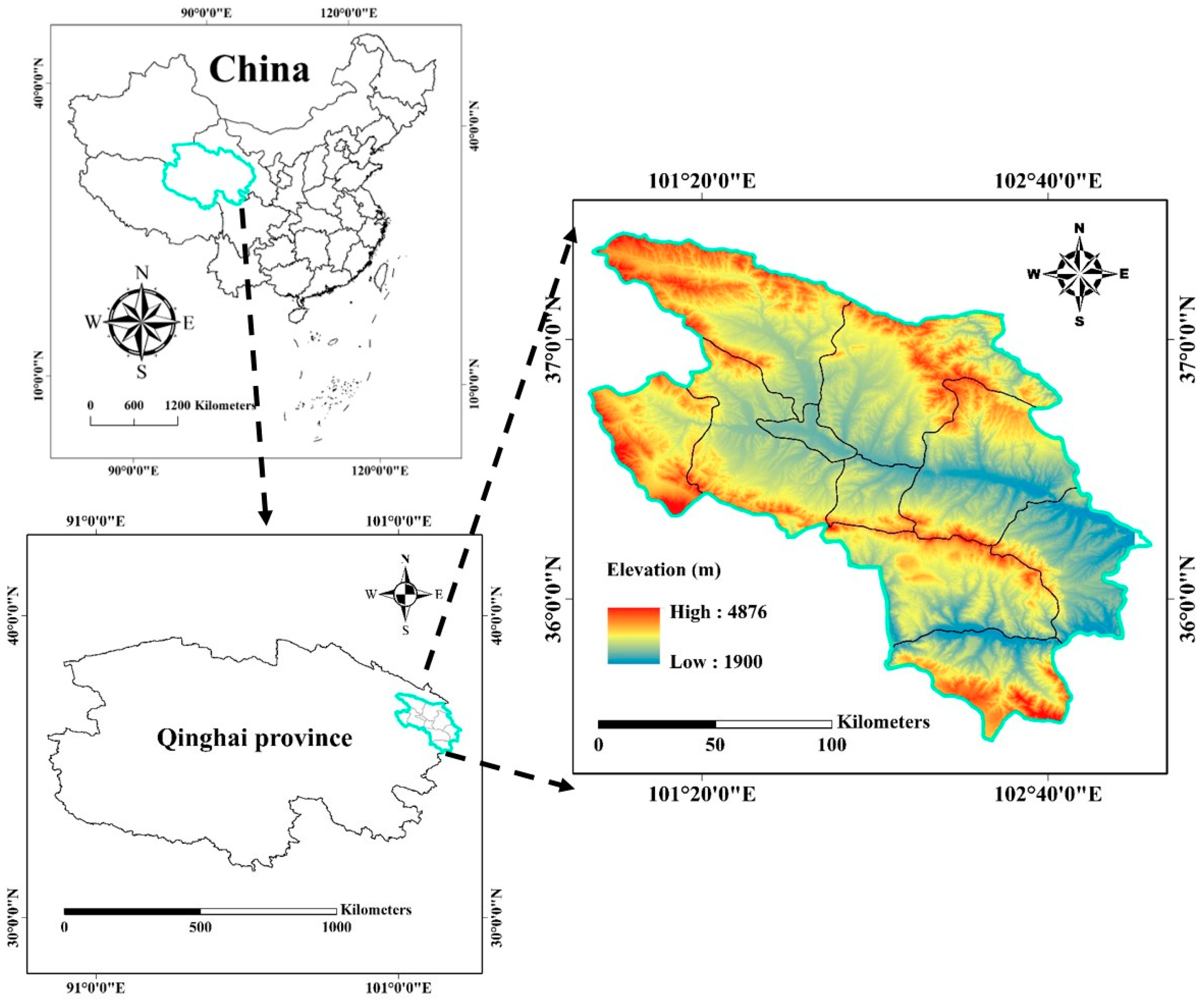
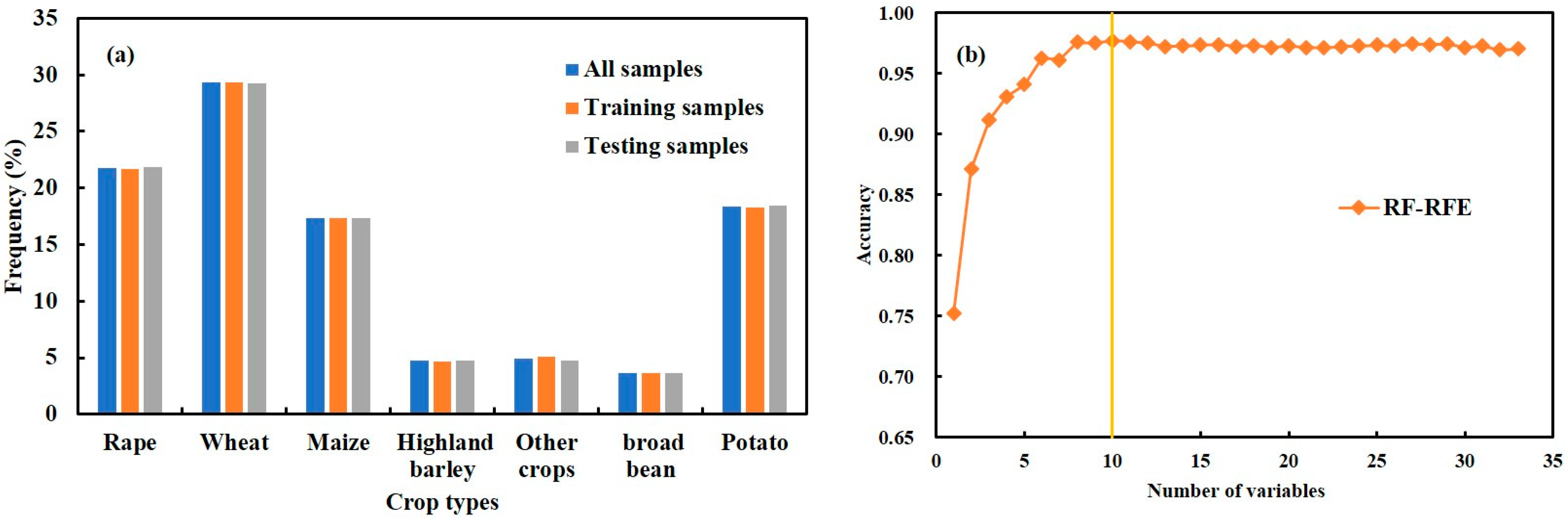
2.1. Study Area and Field Survey
2.2. Acquisition and Pre-Processing of Imagery and Other Digital Data
2.3. Generation of Reference Data for Training and Accuracy Evaluation
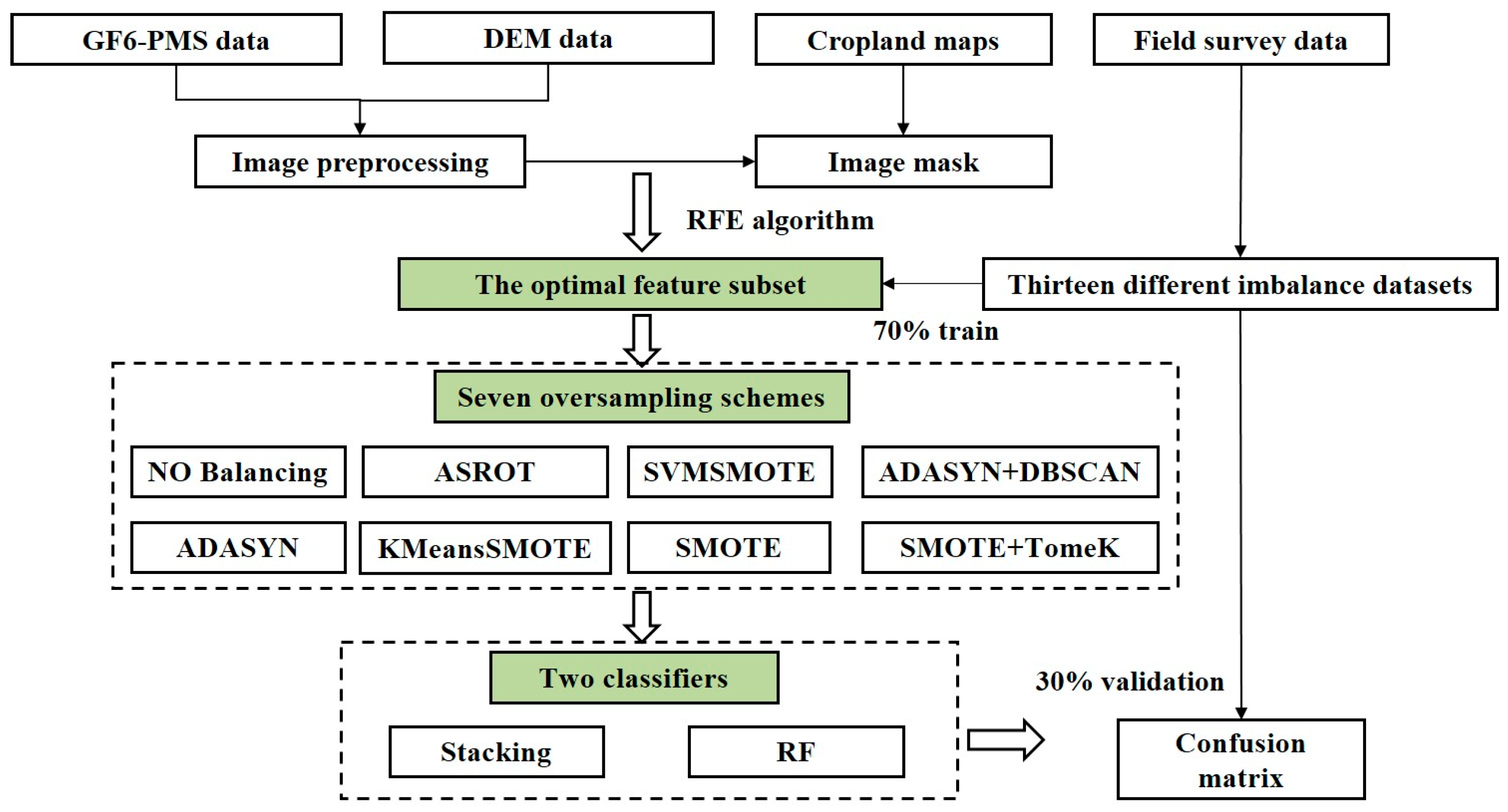
3. Methods
3.1. Feature Space Creation
3.2. Resampling Algorithms
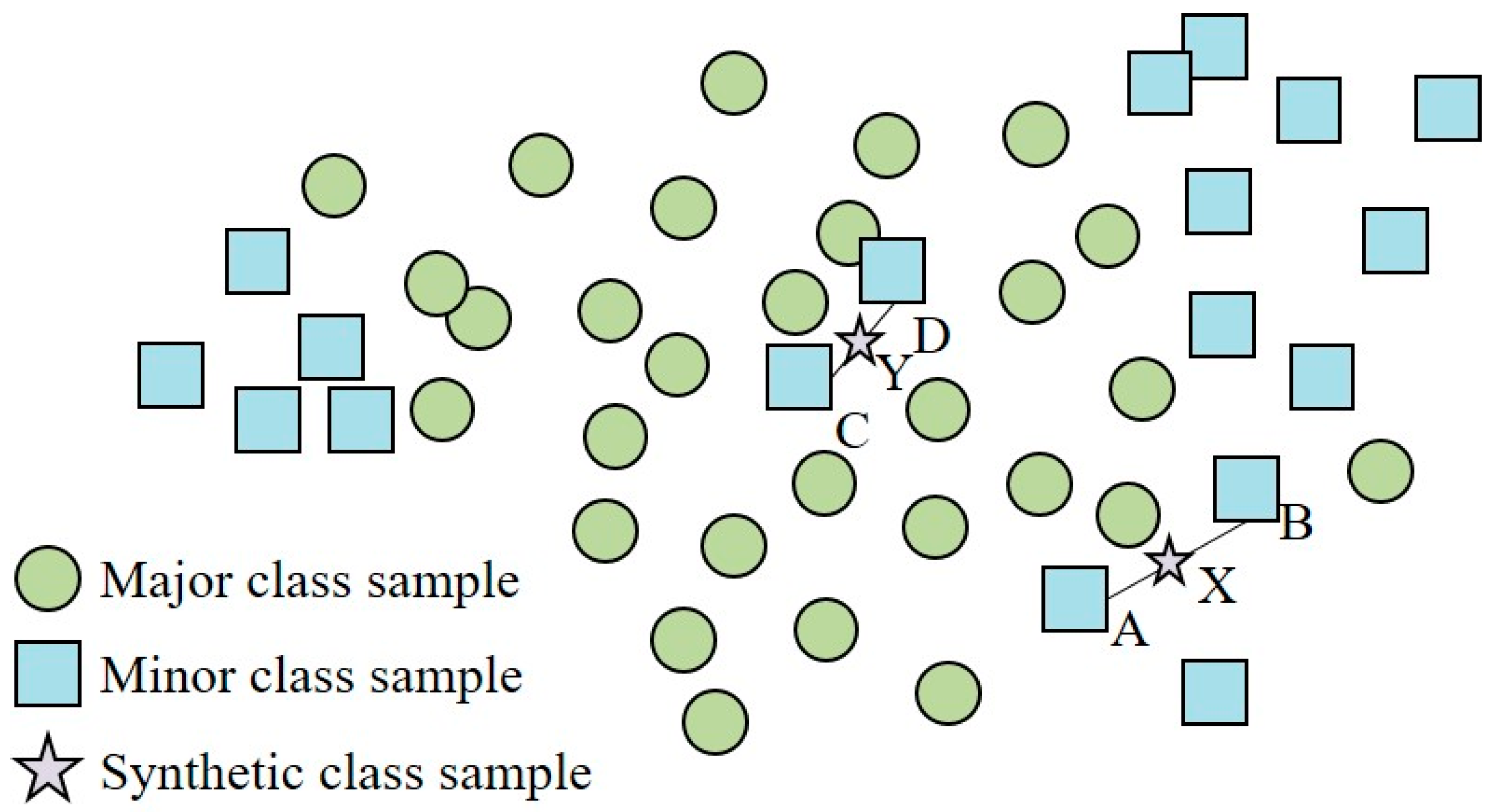
3.2.1. Adaptive Synthetic Sampling (ADASYN)
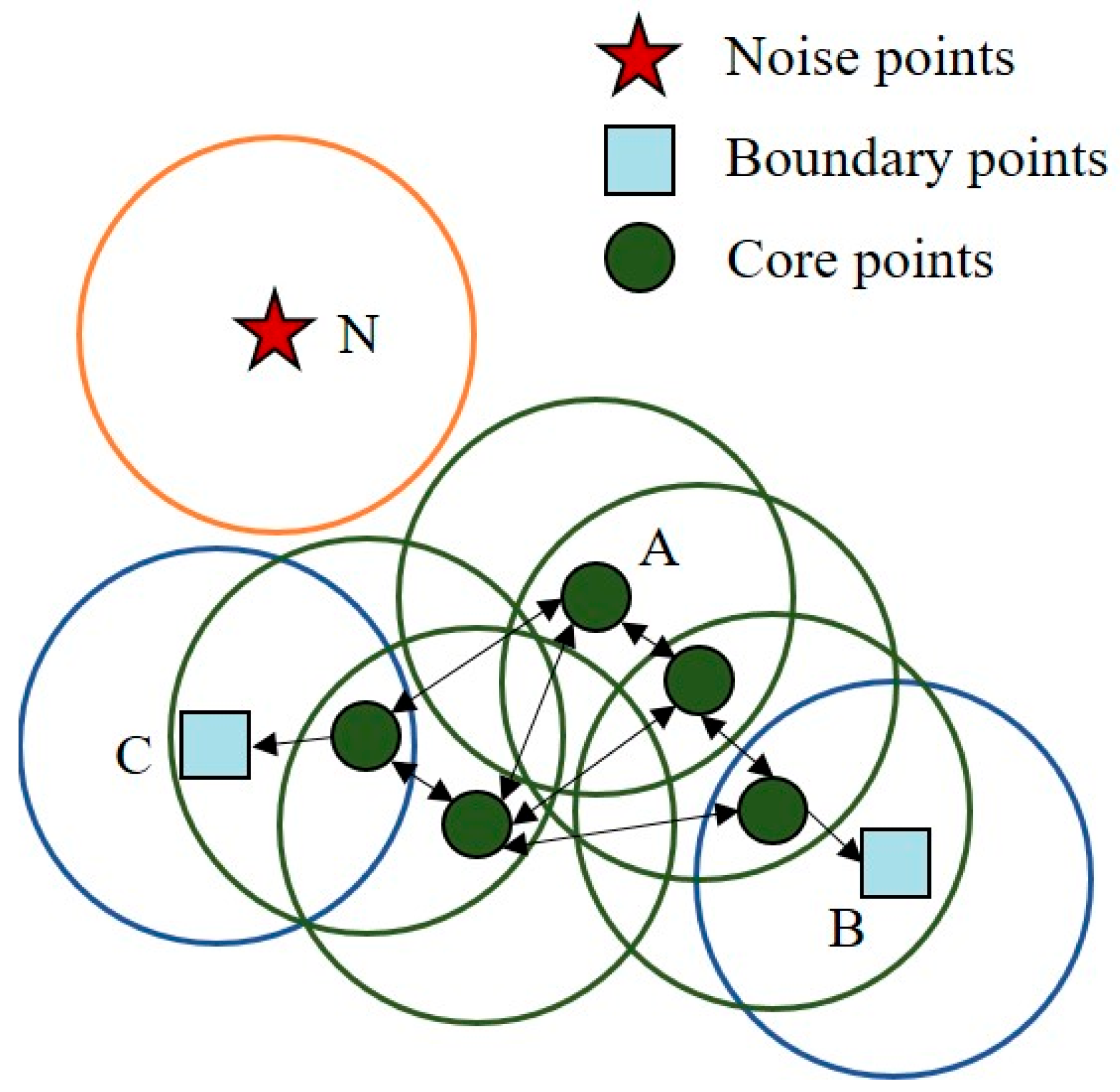
3.2.2. Density Based Spatial Clustering of Applications with Noise (DBSCAN)
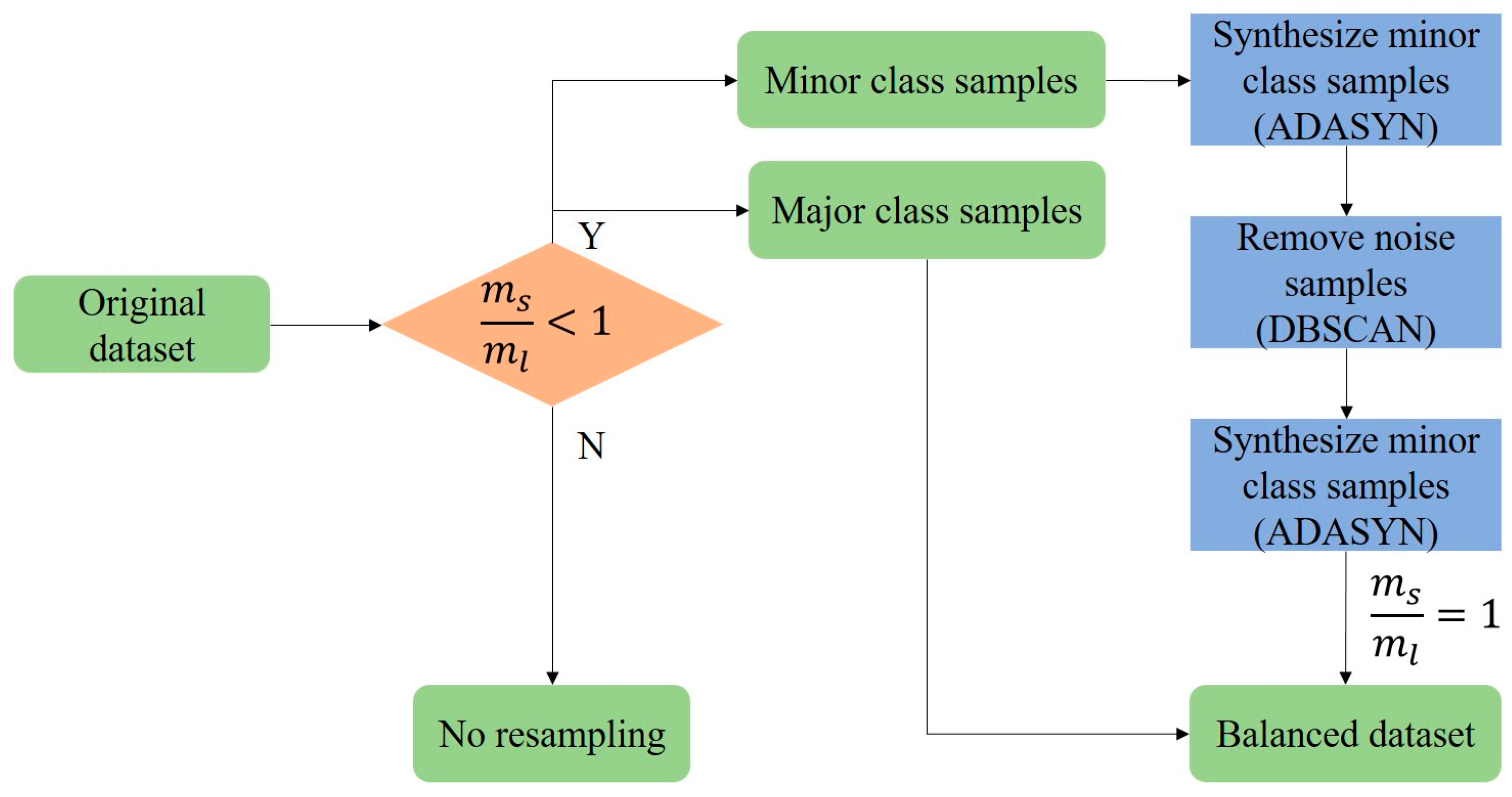
3.2.3. Adaptive Synthetic and Repeat Oversampling Technique (ASROT)
3.2.4. Other Resampling Algorithms
3.3. Classification Models
3.4. Accuracy Assessment and Statistical Analysis
3.5. Application of ASROT Algorithm for Crop Mapping
4. Results
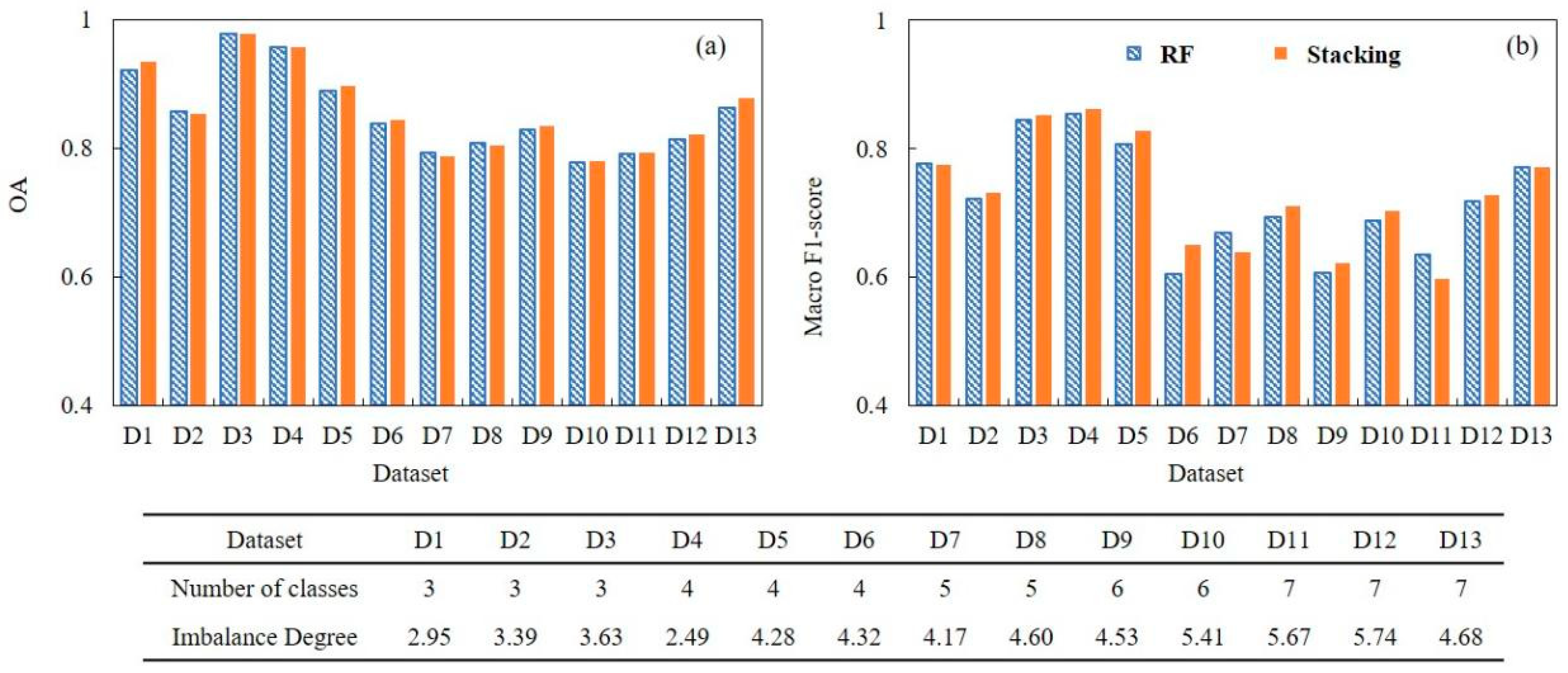
4.1. Effect of Imbalanced Dataset on Classification Performance
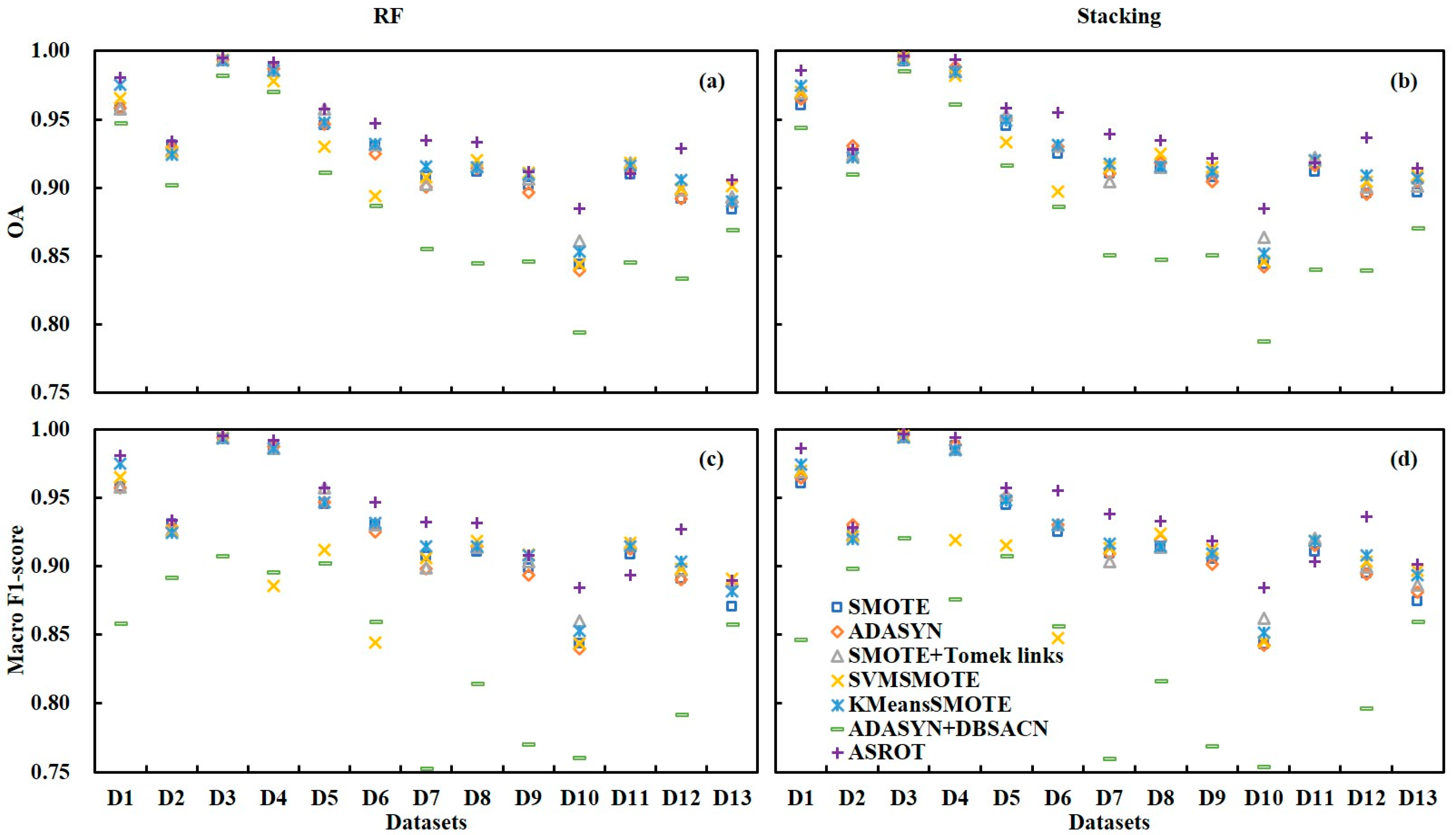
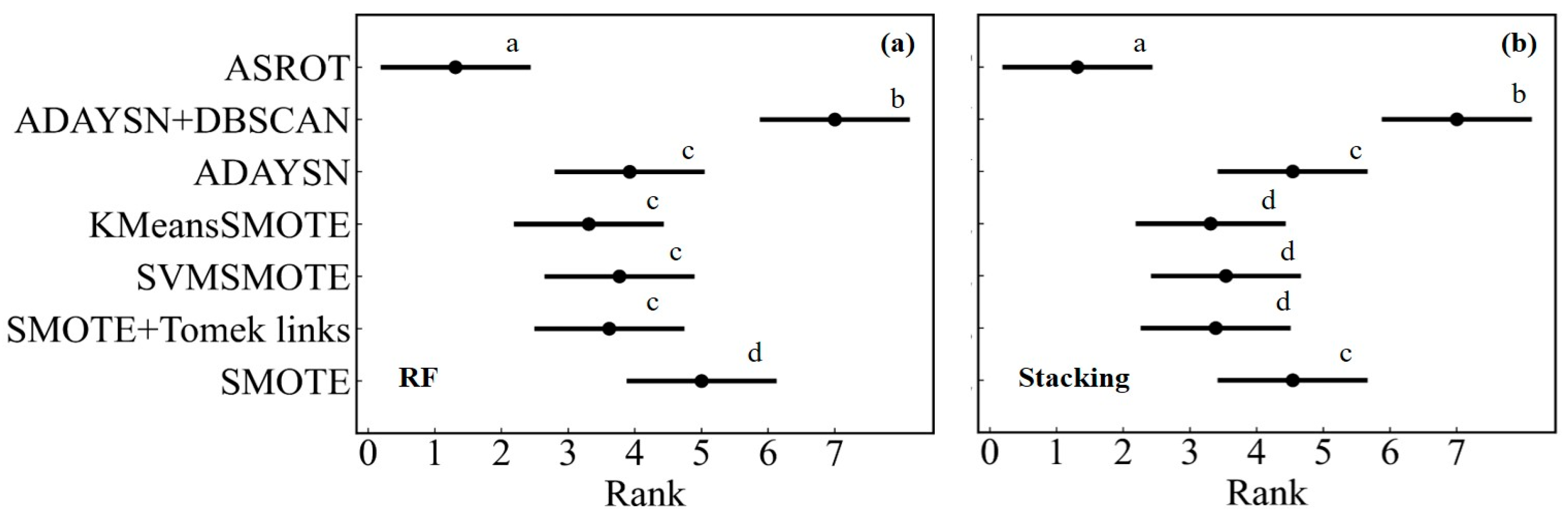
4.2. Comparison of Classification Accuracies of the Different Resampling Algorithms
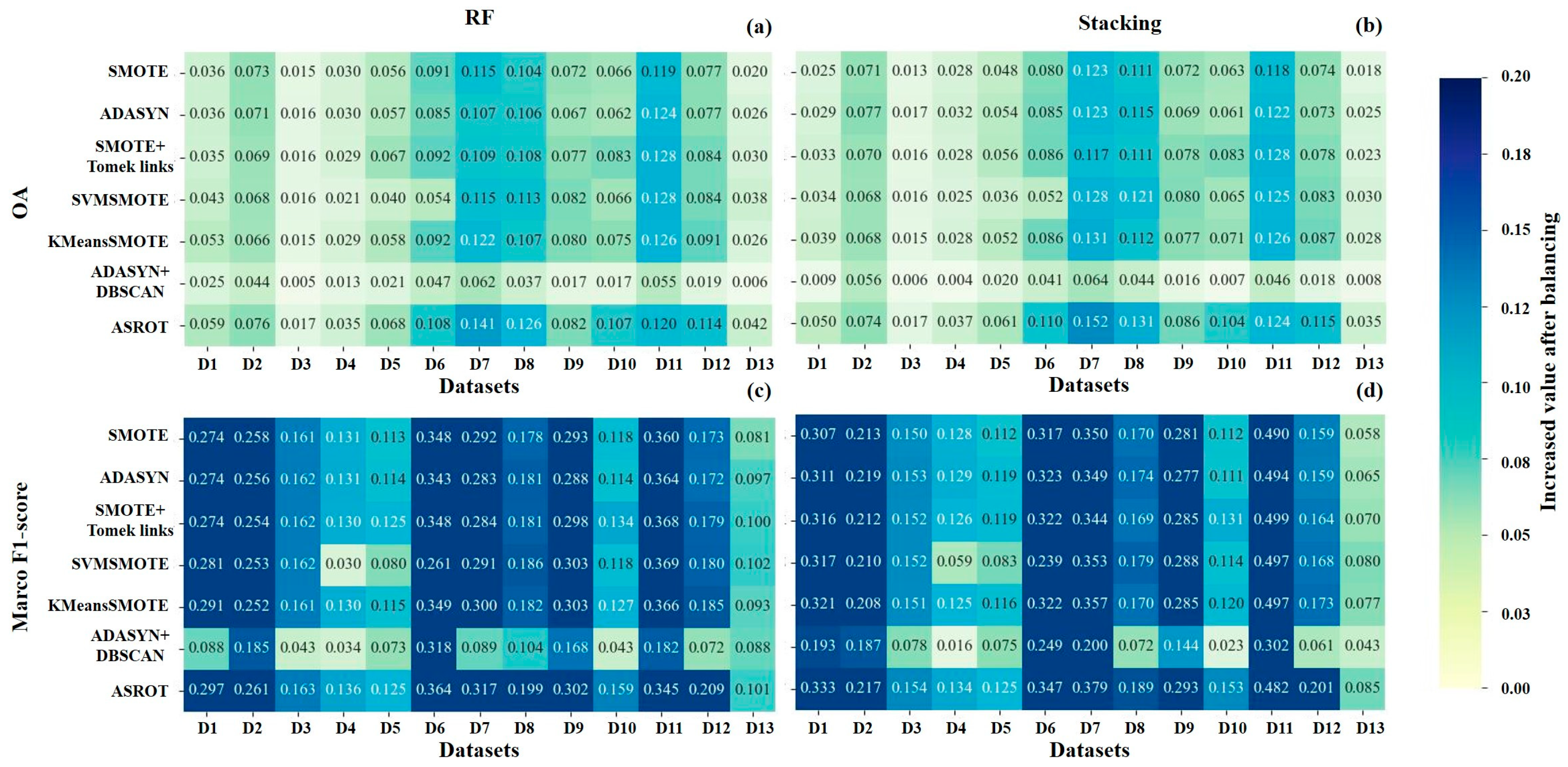
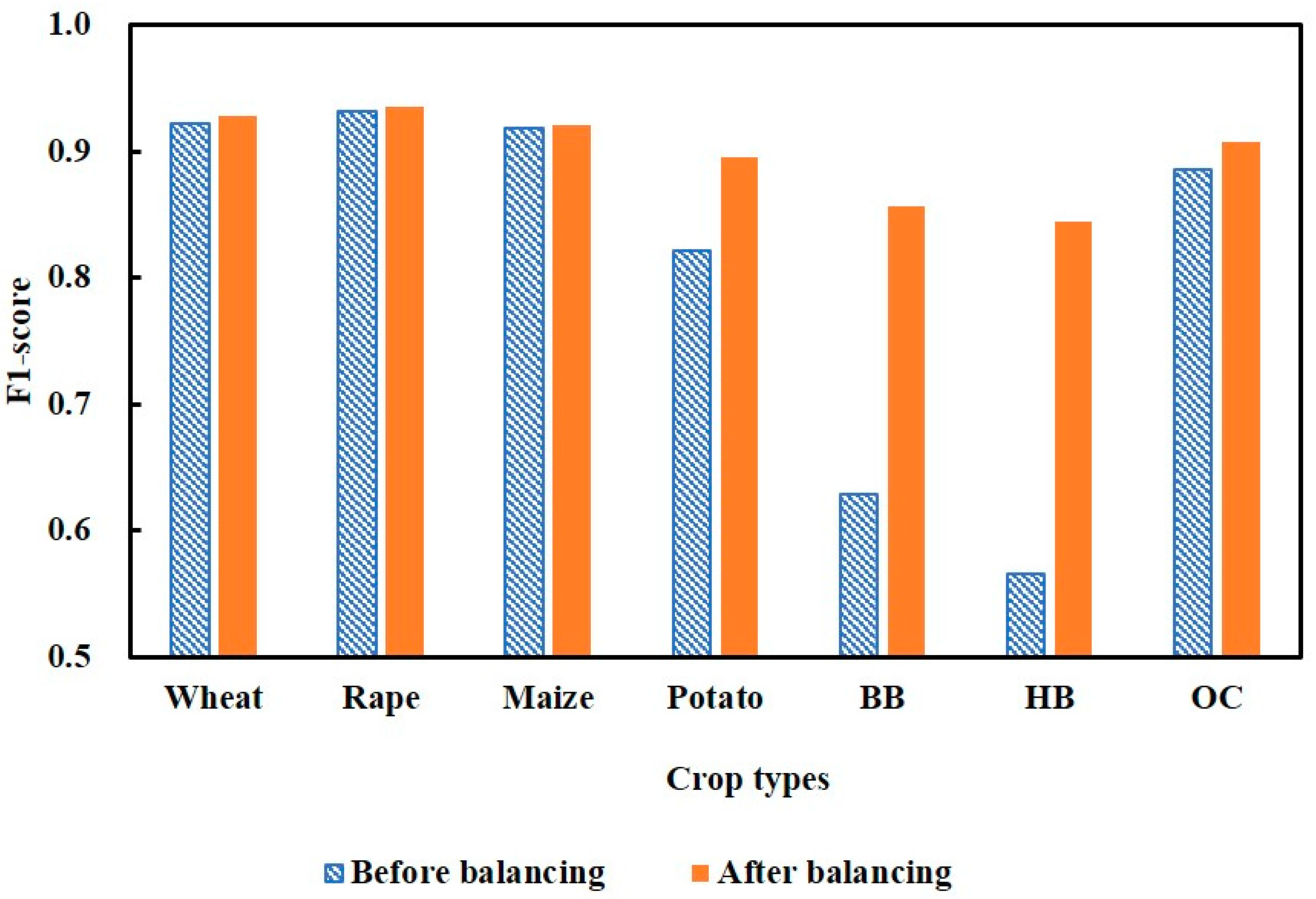
4.3. Improvements in Classification Accuracy Following Application of the ASROT Algorithm
5. Discussion
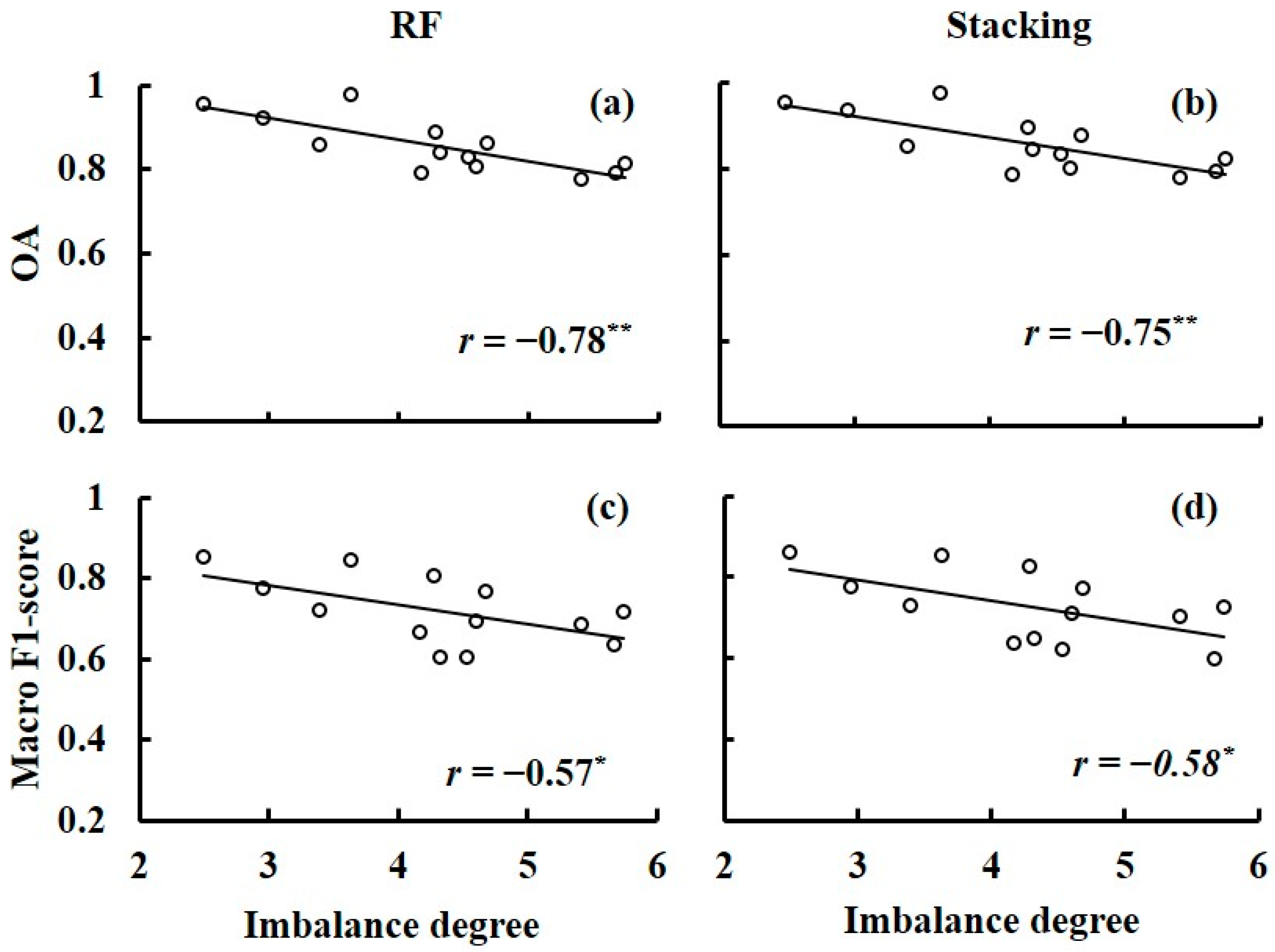
5.1. Effect of Sample Imbalance on the ML-Based Crop Classification
5.2. Importance of the Choice Resampling Algorithm for Crop Classification of Complex Scenes
5.3. Potential of ASROT Algorithm to Improve Classification Accuracy of Minor Crops
5.4. Effect of Interaction Between the Spectral Distortion and Texture Features of Panchromatic Fusion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fritz, S.; See, L.; Bayas, J.C.L.; Waldner, F.; Jacques, D.; Becker-Reshef, I.; Whitcraft, A.; Baruth, B.; Bonifacio, R.; Crutchfield, J. A comparison of global agricultural monitoring systems and current gaps. Agric. Syst. 2019, 168, 258–272. [Google Scholar] [CrossRef]
- Lobell, D.B.; Thau, D.; Seifert, C.; Engle, E.; Little, B. A scalable satellite-based crop yield mapper. Remote Sens. Environ. 2015, 164, 324–333. [Google Scholar] [CrossRef]
- Vanino, S.; Nino, P.; De Michele, C.; Bolognesi, S.F.; D’Urso, G.; Di Bene, C.; Pennelli, B.; Vuolo, F.; Farina, R.; Pulighe, G. Capability of Sentinel-2 data for estimating maximum evapotranspiration and irrigation requirements for tomato crop in Central Italy. Remote Sens. Environ. 2018, 215, 452–470. [Google Scholar] [CrossRef]
- Waldner, F.; Chen, Y.; Lawes, R.; Hochman, Z. Needle in a haystack: Mapping rare and infrequent crops using satellite imagery and data balancing methods. Remote Sens. Environ. 2019, 233, 111375. [Google Scholar] [CrossRef]
- Cai, J.; Luo, J.; Wang, S.; Yang, S. Feature selection in machine learning: A new perspective. Neurocomputing 2018, 300, 70–79. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- Ramezan, C.A.; Warner, T.A.; Maxwell, A.E.; Price, B.S. Effects of training set size on supervised machine-learning land-cover classification of large-area high-resolution remotely sensed data. Remote Sens. 2021, 13, 368. [Google Scholar] [CrossRef]
- Xiao, Y.; Huang, J.; Weng, W.; Huang, R.; Shao, Q.; Zhou, C.; Li, S. Class imbalance: A crucial factor affecting the performance of tea plantations mapping by machine learning. Int. J. Appl. Earth Obs. Geoinf. 2024, 129, 103849. [Google Scholar] [CrossRef]
- Foody, G.M.; Mathur, A. The use of small training sets containing mixed pixels for accurate hard image classification: Training on mixed spectral responses for classification by a SVM. Remote Sens. Environ. 2006, 103, 179–189. [Google Scholar] [CrossRef]
- Ma, Z.; Li, W.; Warner, T.A.; He, C.; Wang, X.; Zhang, Y.; Guo, C.; Cheng, T.; Zhu, Y.; Cao, W. A framework combined stacking ensemble algorithm to classify crop in complex agricultural landscape of high altitude regions with Gaofen-6 imagery and elevation data. Int. J. Appl. Earth Obs. Geoinf. 2023, 122, 103386. [Google Scholar] [CrossRef]
- Khoury, C.K.; Bjorkman, A.D.; Dempewolf, H.; Ramirez-Villegas, J.; Guarino, L.; Jarvis, A.; Rieseberg, L.H.; Struik, P.C. Increasing homogeneity in global food supplies and the implications for food security. Proc. Natl. Acad. Sci. USA 2014, 111, 4001–4006. [Google Scholar] [CrossRef]
- Prati, R.C.; Batista, G.E.; Silva, D.F. Class imbalance revisited: A new experimental setup to assess the performance of treatment methods. Knowl. Inf. Syst. 2015, 45, 247–270. [Google Scholar] [CrossRef]
- Johnson, J.M.; Khoshgoftaar, T.M. Survey on deep learning with class imbalance. J. Big Data 2019, 6, 27. [Google Scholar] [CrossRef]
- LemaÃŽtre, G.; Nogueira, F.; Aridas, C.K. Imbalanced-learn: A python toolbox to tackle the curse of imbalanced datasets in machine learning. J. Mach. Learn. Res. 2017, 18, 1–5. [Google Scholar]
- He, H.; Garcia, E.A. Learning from imbalanced data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar] [CrossRef]
- Cheng, R.; Zhang, L.; Wu, S.; Xu, S.; Gao, S.; Yu, H. Probability density machine: A new solution of class imbalance learning. Sci. Program. 2021, 2021, 7555587. [Google Scholar] [CrossRef]
- Liu, J. Importance-SMOTE: A synthetic minority oversampling method for noisy imbalanced data. Soft Comput. 2022, 26, 1141–1163. [Google Scholar] [CrossRef]
- Dubey, H.; Pudi, V. Class based weighted k-nearest neighbor over imbalance dataset. In Advances in Knowledge Discovery and Data Mining, Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Gold Coast, Australia, 14–17 April 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 305–316. [Google Scholar]
- Elreedy, D.; Atiya, A.F. A comprehensive analysis of synthetic minority oversampling technique (SMOTE) for handling class imbalance. Inf. Sci. 2019, 505, 32–64. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Ebrahimy, H.; Mirbagheri, B.; Matkan, A.A.; Azadbakht, M. Effectiveness of the integration of data balancing techniques and tree-based ensemble machine learning algorithms for spatially-explicit land cover accuracy prediction. Remote Sens. Appl. Soc. Environ. 2022, 27, 100785. [Google Scholar] [CrossRef]
- Han, L.; Yang, G.; Yang, X.; Song, X.; Xu, B.; Li, Z.; Wu, J.; Yang, H.; Wu, J. An explainable XGBoost model improved by SMOTE-ENN technique for maize lodging detection based on multi-source unmanned aerial vehicle images. Comput. Electron. Agric. 2022, 194, 106804. [Google Scholar] [CrossRef]
- Fernández, A.; Garcia, S.; Herrera, F.; Chawla, N.V. SMOTE for learning from imbalanced data: Progress and challenges, marking the 15-year anniversary. J. Artif. Intell. Res. 2018, 61, 863–905. [Google Scholar] [CrossRef]
- García, V.; Sánchez, J.S.; Mollineda, R.A. Classification of high dimensional and imbalanced hyperspectral imagery data. In Pattern Recognition and Image Analysis, Proceedings of the Iberian Conference on Pattern Recognition and Image Analysis, Las Palmas de Gran Canaria, Spain, 8–10 June 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 644–651. [Google Scholar]
- Douzas, G.; Bacao, F.; Last, F. Improving imbalanced learning through a heuristic oversampling method based on k-means and SMOTE. Inf. Sci. 2018, 465, 1–20. [Google Scholar] [CrossRef]
- Bache, K.; Lichman, M. UCI Machine Learning Repository; School of Information and Computer Science, University of California: Irvine, CA, USA, 2013. [Google Scholar]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar]
- Arafa, A.; El-Fishawy, N.; Badawy, M.; Radad, M. RN-SMOTE: Reduced Noise SMOTE based on DBSCAN for enhancing imbalanced data classification. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 5059–5074. [Google Scholar] [CrossRef]
- Ijaz, M.F.; Alfian, G.; Syafrudin, M.; Rhee, J. Hybrid prediction model for type 2 diabetes and hypertension using DBSCAN-based outlier detection, synthetic minority over sampling technique (SMOTE), and random forest. Appl. Sci. 2018, 8, 1325. [Google Scholar] [CrossRef]
- Asniar; Maulidevi, N.U.; Surendro, K. SMOTE-LOF for noise identification in imbalanced data classification. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 3413–3423. [Google Scholar] [CrossRef]
- Sanguanmak, Y.; Hanskunatai, A. DBSM: The combination of DBSCAN and SMOTE for imbalanced data classification. In Proceedings of the 2016 13th International Joint Conference on Computer Science and Software Engineering (JCSSE), Khon Kaen, Thailand, 13–15 July 2016; pp. 1–5. [Google Scholar]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the KDD-96, Munich, Germany, 12–15 August 1996; pp. 226–231. [Google Scholar]
- Puri, A.; Kumar Gupta, M. Improved hybrid bag-boost ensemble with K-means-SMOTE–ENN technique for handling noisy class imbalanced data. Comput. J. 2022, 65, 124–138. [Google Scholar] [CrossRef]
- Kim, J.; Lee, H.; Ko, Y.M. Constrained density-based spatial clustering of applications with noise (DBSCAN) using hyperparameter optimization. Knowl.-Based Syst. 2024, 303, 112436. [Google Scholar] [CrossRef]
- Qian, J.; Wang, Y.; Zhou, Y.H.X. MDBSCAN: A multi-density DBSCAN based on relative density. Neurocomputing 2024, 576, 127329. [Google Scholar] [CrossRef]
- Li, D.; Wang, M.; Jiang, J. China’s high-resolution optical remote sensing satellites and their mapping applications. Geo-Spat. Inf. Sci. 2021, 24, 85–94. [Google Scholar] [CrossRef]
- Felde, G.W.; Anderson, G.P.; Cooley, T.W.; Matthew, M.W.; Berk, A.; Lee, J. Analysis of Hyperion data with the FLAASH atmospheric correction algorithm. In Proceedings of the IGARSS 2003. 2003 IEEE International Geoscience and Remote Sensing Symposium, Proceedings (IEEE Cat. No. 03CH37477), Toulouse, France, 21–25 July 2003; pp. 90–92. [Google Scholar]
- Sun, W.; Chen, B.; Messinger, D.W. Nearest-neighbor diffusion-based pan-sharpening algorithm for spectral images. Opt. Eng. 2014, 53, 013107. [Google Scholar] [CrossRef]
- Ortigosa-Hernández, J.; Inza, I.; Lozano, J.A. Measuring the class-imbalance extent of multi-class problems. Pattern Recognit. Lett. 2017, 98, 32–38. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Pullanagari, R.R.; Kereszturi, G.; Yule, I. Integrating airborne hyperspectral, topographic, and soil data for estimating pasture quality using recursive feature elimination with random forest regression. Remote Sens. 2018, 10, 1117. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Haralick, R.M. Statistical and structural approaches to texture. Proc. IEEE 1979, 67, 786–804. [Google Scholar] [CrossRef]
- Sesnie, S.E.; Gessler, P.E.; Finegan, B.; Thessler, S. Integrating Landsat TM and SRTM-DEM derived variables with decision trees for habitat classification and change detection in complex neotropical environments. Remote Sens. Environ. 2008, 112, 2145–2159. [Google Scholar] [CrossRef]
- Gameng, H.A.; Gerardo, B.B.; Medina, R.P. Modified adaptive synthetic SMOTE to improve classification performance in imbalanced datasets. In Proceedings of the 2019 IEEE 6th International Conference on Engineering Technologies and Applied Sciences (ICETAS), Kuala Lumpur, Malaysia, 20–21 December 2019; pp. 1–5. [Google Scholar]
- Ram, A.; Jalal, S.; Jalal, A.S.; Kumar, M. A density based algorithm for discovering density varied clusters in large spatial databases. Int. J. Comput. Appl. 2010, 3, 1–4. [Google Scholar] [CrossRef]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN revisited, revisited: Why and how you should (still) use DBSCAN. ACM Trans. Database Syst. (TODS) 2017, 42, 1–21. [Google Scholar] [CrossRef]
- Huang, F.; Zhu, Q.; Zhou, J.; Tao, J.; Zhou, X.; Jin, D.; Tan, X.; Wang, L. Research on the parallelization of the DBSCAN clustering algorithm for spatial data mining based on the spark platform. Remote Sens. 2017, 9, 1301. [Google Scholar] [CrossRef]
- Marqués, A.I.; García, V.; Sánchez, J.S. On the suitability of resampling techniques for the class imbalance problem in credit scoring. J. Oper. Res. Soc. 2013, 64, 1060–1070. [Google Scholar] [CrossRef]
- Matharaarachchi, S.; Domaratzki, M.; Muthukumarana, S. Enhancing SMOTE for imbalanced data with abnormal minority instances. Mach. Learn. Appl. 2024, 18, 100597. [Google Scholar] [CrossRef]
- Blagus, R.; Lusa, L. SMOTE for high-dimensional class-imbalanced data. BMC Bioinform. 2013, 14, 106. [Google Scholar] [CrossRef]
- Nguyen, H.M.; Cooper, E.W.; Kamei, K. Borderline over-sampling for imbalanced data classification. Int. J. Knowl. Eng. Soft Data Paradig. 2011, 3, 4–21. [Google Scholar] [CrossRef]
- Batista, G.E.; Prati, R.C.; Monard, M.C. A study of the behavior of several methods for balancing machine learning training data. ACM SIGKDD Explor. Newsl. 2004, 6, 20–29. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Frazier, R.J.; Coops, N.C.; Wulder, M.A.; Kennedy, R. Characterization of aboveground biomass in an unmanaged boreal forest using Landsat temporal segmentation metrics. ISPRS J. Photogramm. Remote Sens. 2014, 92, 137–146. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, Y.; Pu, R.; Zhang, Z. Mapping Robinia pseudoacacia forest health conditions by using combined spectral, spatial, and textural information extracted from IKONOS imagery and random forest classifier. Remote Sens. 2015, 7, 9020–9044. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Luo, X.; Sun, J.; Wang, L.; Wang, W.; Zhao, W.; Wu, J.; Wang, J.-H.; Zhang, Z. Short-term wind speed forecasting via stacked extreme learning machine with generalized correntropy. IEEE Trans. Ind. Inform. 2018, 14, 4963–4971. [Google Scholar] [CrossRef]
- Xia, T.; He, Z.; Cai, Z.; Wang, C.; Wang, W.; Wang, J.; Hu, Q.; Song, Q. Exploring the potential of Chinese GF-6 images for crop mapping in regions with complex agricultural landscapes. Int. J. Appl. Earth Obs. Geoinf. 2022, 107, 102702. [Google Scholar] [CrossRef]
- Mohammadi, S.; Belgiu, M.; Stein, A. A source-free unsupervised domain adaptation method for cross-regional and cross-time crop mapping from satellite image time series. Remote Sens. Environ. 2024, 314, 114385. [Google Scholar] [CrossRef]
- Demšar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Wang, S.; Chen, W.; Xie, S.M.; Azzari, G.; Lobell, D.B. Weakly supervised deep learning for segmentation of remote sensing imagery. Remote Sens. 2020, 12, 207. [Google Scholar] [CrossRef]
- Buda, M.; Maki, A.; Mazurowski, M.A. A systematic study of the class imbalance problem in convolutional neural networks. Neural Netw. 2018, 106, 249–259. [Google Scholar] [CrossRef] [PubMed]
- Chabalala, Y.; Adam, E.; Ali, K.A. Exploring the effect of balanced and imbalanced multi-class distribution data and sampling techniques on fruit-tree crop classification using different machine learning classifiers. Geomatics 2023, 3, 70–92. [Google Scholar] [CrossRef]
- Shumilo, L.; Okhrimenko, A.; Kussul, N.; Drozd, S.; Shkalikov, O. Generative adversarial network augmentation for solving the training data imbalance problem in crop classification. Remote Sens. Lett. 2023, 14, 1129–1138. [Google Scholar] [CrossRef]
- Özdemir, A.; Polat, K.; Alhudhaif, A. Classification of imbalanced hyperspectral images using SMOTE-based deep learning methods. Expert Syst. Appl. 2021, 178, 114986. [Google Scholar] [CrossRef]
- Barati, S.; Rayegani, B.; Saati, M.; Sharifi, A.; Nasri, M. Comparison the accuracies of different spectral indices for estimation of vegetation cover fraction in sparse vegetated areas. Egypt. J. Remote Sens. Space Sci. 2011, 14, 49–56. [Google Scholar] [CrossRef]
- Sáez, J.A.; Luengo, J.; Stefanowski, J.; Herrera, F. SMOTE–IPF: Addressing the noisy and borderline examples problem in imbalanced classification by a re-sampling method with filtering. Inf. Sci. 2015, 291, 184–203. [Google Scholar] [CrossRef]
- Feng, W.; Bao, W. Weight-based rotation forest for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2167–2171. [Google Scholar] [CrossRef]
- Waldner, F.; Lambert, M.-J.; Li, W.; Weiss, M.; Demarez, V.; Morin, D.; Marais-Sicre, C.; Hagolle, O.; Baret, F.; Defourny, P. Land cover and crop type classification along the season based on biophysical variables retrieved from multi-sensor high-resolution time series. Remote Sens. 2015, 7, 10400–10424. [Google Scholar] [CrossRef]
- Zhu, X.; Pan, Y.; Zhang, J.; Wang, S.; Gu, X. The effects of training samples on the wheat planting area measure accuracy in tm scale (i): The accuracy response of different classifiers to training samples. J. Remote Sens. 2007, 11, 826. [Google Scholar] [CrossRef]
- Ma, W.; Jia, W.; Su, P.; Feng, X.; Liu, F.; Wang, J.a. Mapping Highland Barley on the Qinghai–Tibet Combing Landsat OLI Data and Object-Oriented Classification Method. Land 2021, 10, 1022. [Google Scholar] [CrossRef]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Jain, A.K.; Duin, R.P.W.; Mao, J. Statistical pattern recognition: A review. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 4–37. [Google Scholar] [CrossRef]
- Gärtner, P.; Förster, M.; Kleinschmit, B. The benefit of synthetically generated RapidEye and Landsat 8 data fusion time series for riparian forest disturbance monitoring. Remote Sens. Environ. 2016, 177, 237–247. [Google Scholar] [CrossRef]
- Chen, Y.; Li, C.; Ghamisi, P.; Jia, X.; Gu, Y. Deep Fusion of Remote Sensing Data for Accurate Classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1253–1257. [Google Scholar] [CrossRef]
- Ghassemian, H. A review of remote sensing image fusion methods. Inf. Fusion 2016, 32, 75–89. [Google Scholar] [CrossRef]
- Rokni, K. Investigating the impact of Pan Sharpening on the accuracy of land cover mapping in Landsat OLI imagery. Geod. Cartogr. 2023, 49, 12–18. [Google Scholar] [CrossRef]

| Bands | Name | Wavelength Range (nm) | Spatial Resolution (m) |
|---|---|---|---|
| P | Panchromatic | 450–900 | 2 |
| B1 | Blue | 450–520 | 8 |
| B2 | Green | 520–600 | |
| B3 | Red | 630–690 | |
| B4 | NIR | 760–900 |
| Dataset | Crops | Class Allocations | Total Samples (Pixels) | Imbalance Degree |
|---|---|---|---|---|
| 1 | 3 | Wheath–Rape–Maizel | 3000 | 2.95 |
| 2 | 3 | Wheath–Maizei–HBl | 4000 | 3.39 |
| 3 | 3 | Rapev–HBl–BBl | 5500 | 3.63 |
| 4 | 4 | Wheath–Rapel–Potatol–HBl | 3250 | 2.49 |
| 5 | 4 | Rapeh–Maizei–Potatoi–HBl | 5250 | 4.28 |
| 6 | 4 | Wheatv–Maizeh–HBi–BBl | 9000 | 4.32 |
| 7 | 5 | Wheati–Rapei–Potatol–BBl–Och | 5500 | 4.17 |
| 8 | 5 | Wheath–Rapel–HBh–Bbi–Ocv | 11,500 | 4.60 |
| 9 | 6 | Wheatl–Rapel–Maizeh–HBh–BBh–Ocl | 8250 | 4.53 |
| 10 | 6 | Wheati–Rapeh–Maizei–Potatoh–Bbi–Oci | 10,000 | 5.41 |
| 11 | 7 | Wheatv–Rapeh–Maizei–Potatoi–HBl–BBl–Och | 13,000 | 5.67 |
| 12 | 7 | Wheati–Rapei–Maizeh–Potatoh–HBv–BBv–Oci | 18,750 | 5.74 |
| 13 | 7 | Wheat–Rape–Maize–Potato–HB–BB–OC | 186,381 | 4.68 |
| Type of Feature | Features Selected |
|---|---|
| Spectral bands | Green (B2), Red (B3), NIR (B4) |
| Vegetation indices | GNDVI = (B4 − B2)/(B4 + B2), TVI = 0.5 * [120 * (B4 − B2) − 200 * (B3 − B2)], |
| Texture features | B1_Mean, B2_Mean, B3_Mean, B4_Mean |
| Topographic features | Elevation |
| Class | Before Balancing Dataset | After Balancing Dataset | ||||
|---|---|---|---|---|---|---|
| UA | PA | F1-score | UA | PA | F1-score | |
| Wheat | 92.12% | 92.27% | 92.19% | 92.55% | 92.99% | 92.77% |
| Rape | 93.81% | 92.39% | 93.09% | 91.92% | 95.11% | 93.49% |
| Maize | 92.17% | 91.43% | 91.80% | 91.83% | 92.41% | 92.12% |
| Potato | 87.18% | 77.72% | 82.18% | 89.51% | 89.41% | 89.46% |
| BB | 57.95% | 68.67% | 62.86% | 87.02% | 84.32% | 85.65% |
| HB | 50.41% | 64.58% | 56.62% | 83.99% | 84.65% | 84.32% |
| Other | 87.35% | 89.81% | 88.56% | 88.80% | 92.79% | 90.75% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Zhu, J.; Li, T.; Ma, Z.; Warner, T.A.; Zheng, H.; Jiang, C.; Cheng, T.; Tian, Y.; Zhu, Y.; et al. ASROT: A Novel Resampling Algorithm to Balance Training Datasets for Classification of Minor Crops in High-Elevation Regions. Remote Sens. 2025, 17, 3814. https://doi.org/10.3390/rs17233814
Li W, Zhu J, Li T, Ma Z, Warner TA, Zheng H, Jiang C, Cheng T, Tian Y, Zhu Y, et al. ASROT: A Novel Resampling Algorithm to Balance Training Datasets for Classification of Minor Crops in High-Elevation Regions. Remote Sensing. 2025; 17(23):3814. https://doi.org/10.3390/rs17233814
Chicago/Turabian StyleLi, Wei, Jie Zhu, Tongjie Li, Zhiyuan Ma, Timothy A. Warner, Hengbiao Zheng, Chongya Jiang, Tao Cheng, Yongchao Tian, Yan Zhu, and et al. 2025. "ASROT: A Novel Resampling Algorithm to Balance Training Datasets for Classification of Minor Crops in High-Elevation Regions" Remote Sensing 17, no. 23: 3814. https://doi.org/10.3390/rs17233814
APA StyleLi, W., Zhu, J., Li, T., Ma, Z., Warner, T. A., Zheng, H., Jiang, C., Cheng, T., Tian, Y., Zhu, Y., Cao, W., & Yao, X. (2025). ASROT: A Novel Resampling Algorithm to Balance Training Datasets for Classification of Minor Crops in High-Elevation Regions. Remote Sensing, 17(23), 3814. https://doi.org/10.3390/rs17233814








