A Novel Framework Based on Data Fusion and Machine Learning for Upscaling Evapotranspiration from Flux Towers to the Regional Scale
Highlights
- An integrated framework was developed that combines multi-source data fusion (MODIS, Landsat, and CLDAS), a footprint model, and machine learning to upscale evapotranspiration from site to field scale, successfully achieving daily seamless 30 m ET estimation.
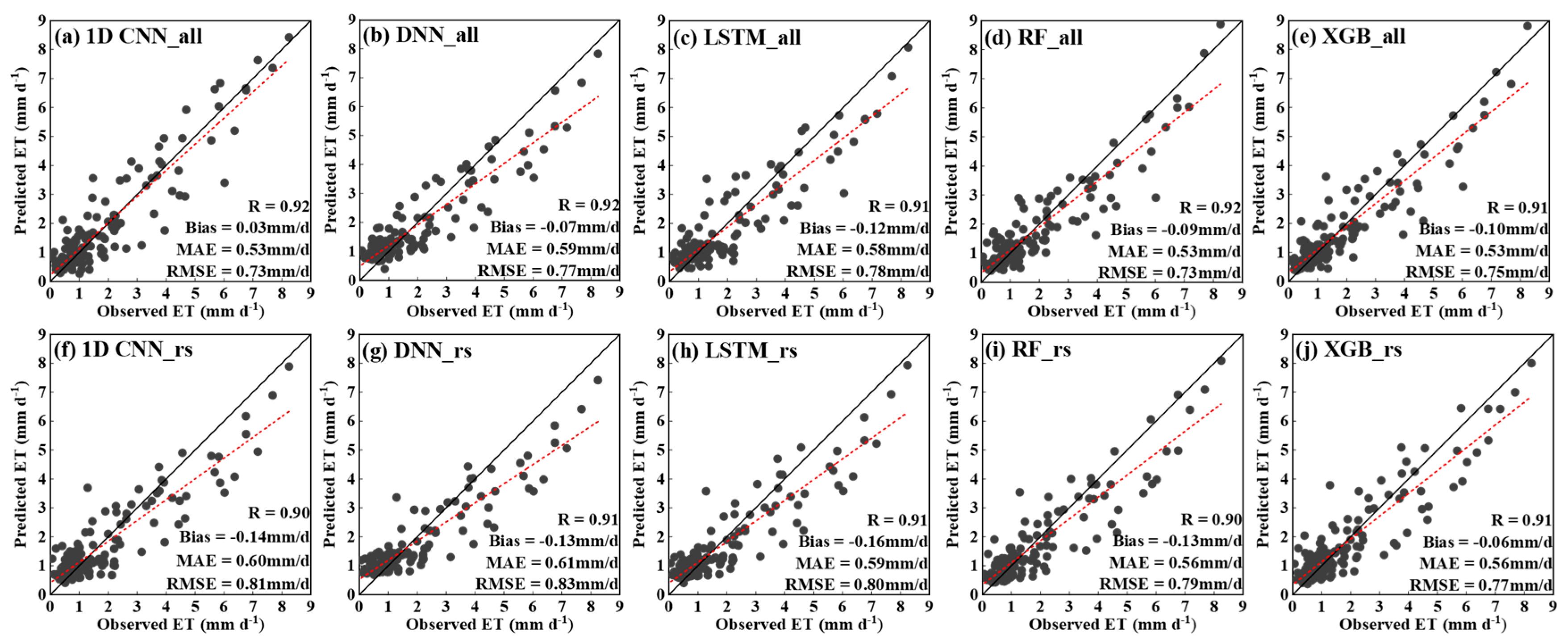
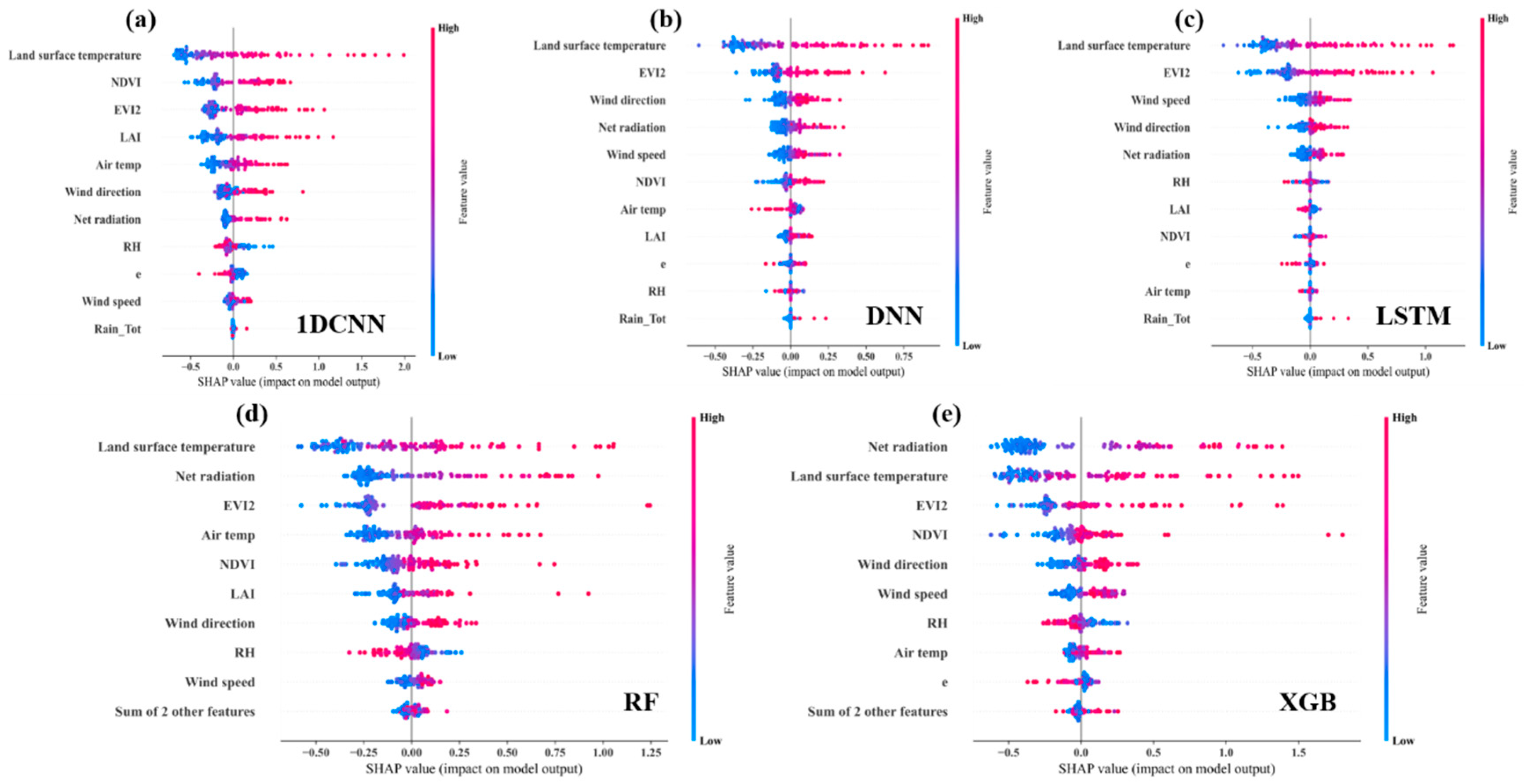
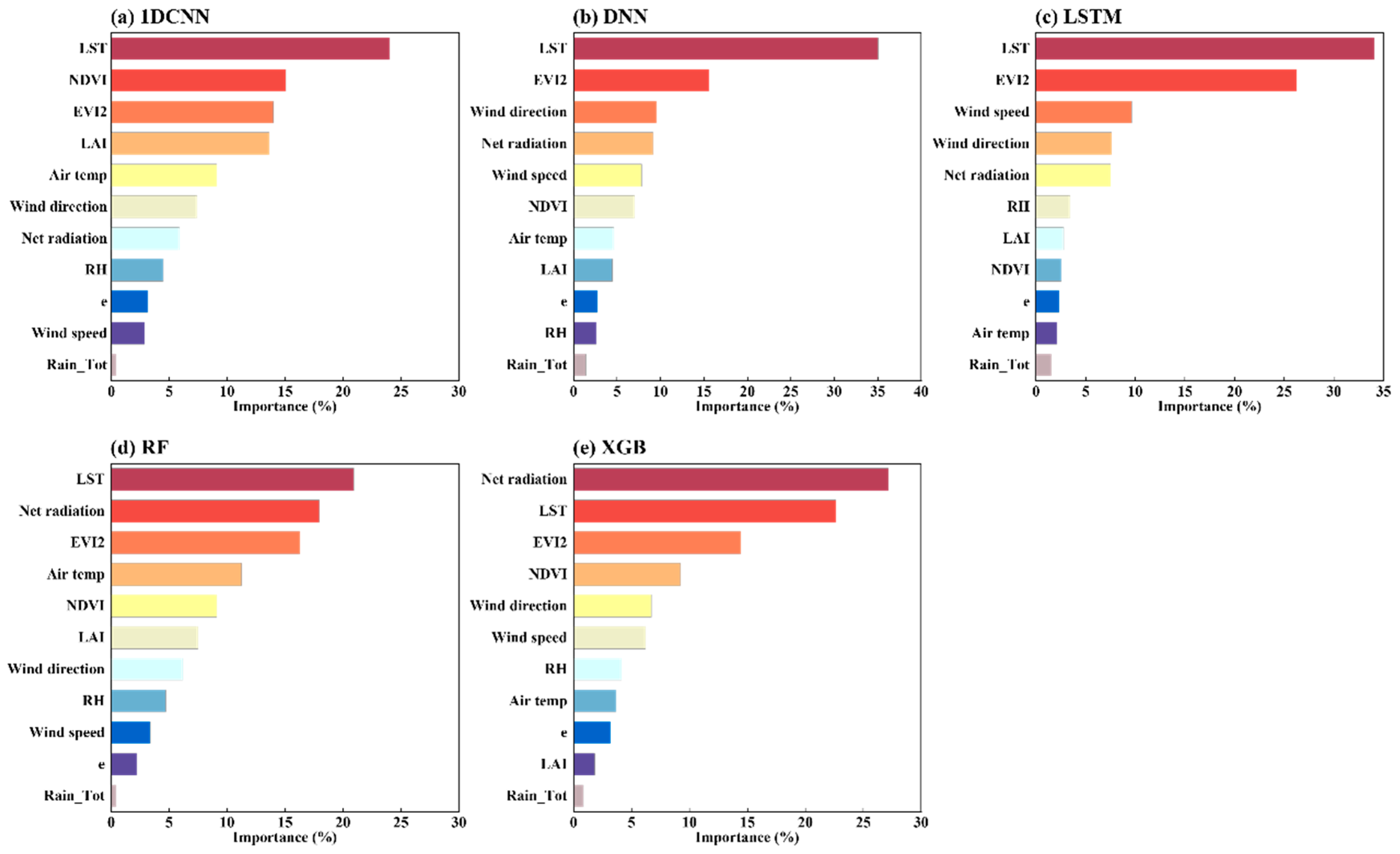
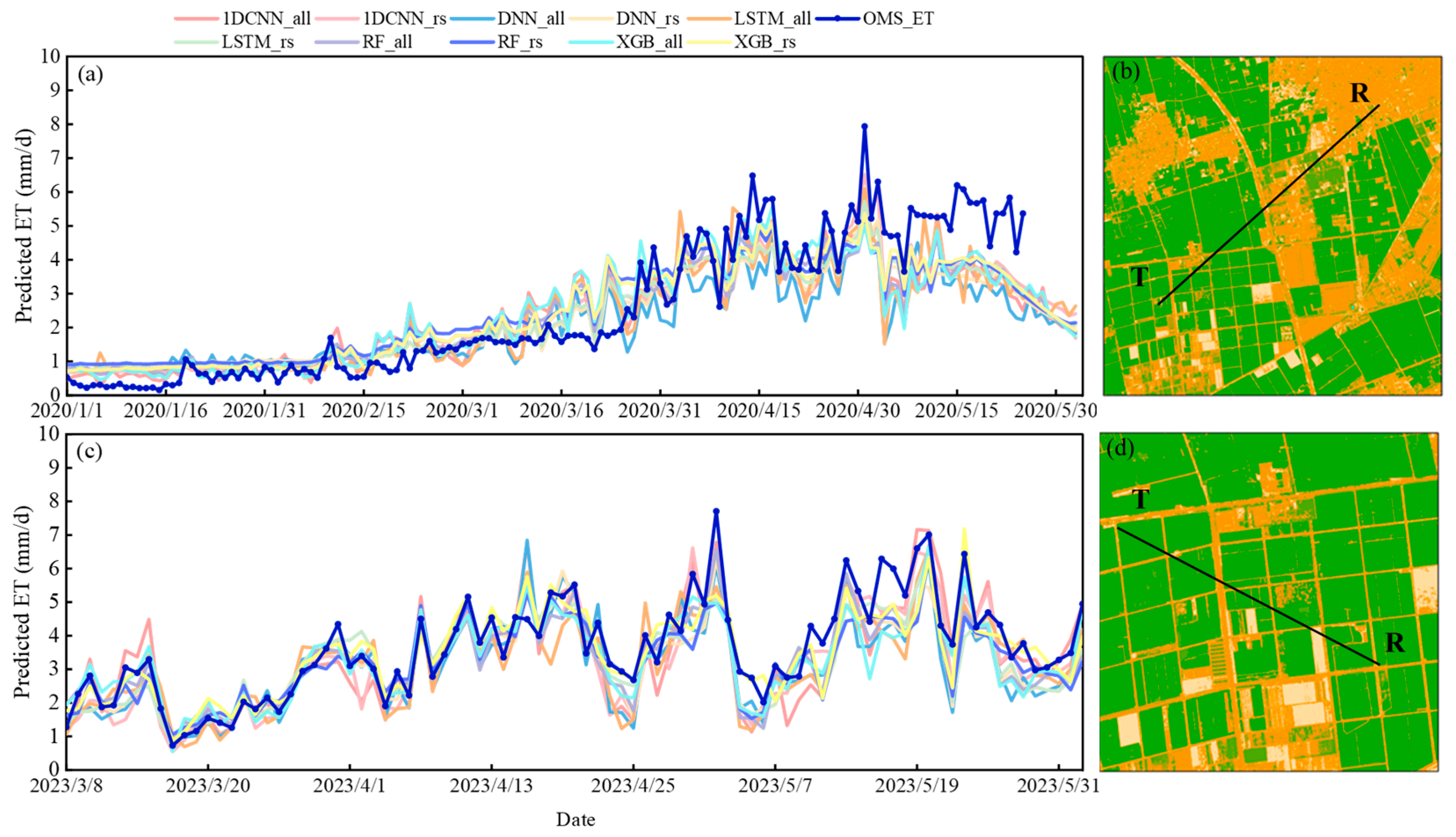
- The 1D CNN model using both remote sensing and meteorological data performed best in homogeneous croplands (R = 0.90, RMSE = 0.66 mm/d), while the model using only remote sensing data achieved superior accuracy in heterogeneous urban–agricultural areas (R = 0.93, RMSE = 0.88 mm/d). SHAP analysis indicated that LST and EVI2 were the most influential drivers of ET.
- By integrating multi-source remote sensing and reanalysis data, the framework enables accurate daily seamless 30 m estimation of LST and vegetation indices, effectively bridging the gap between remote sensing observations and flux measurements and providing strong support for the application of upscaling methods at the field scale.
- By generating high-spatiotemporal-resolution evapotranspiration maps, the framework offers a practical tool for precision water resource management in heterogeneous landscapes.
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Collection and Preprocessing
2.2.1. Eddy Covariance System
2.2.2. Optical-Microwave Scintillometer System
2.2.3. Meteorological Data
2.2.4. Remote Sensing and Reanalysis Data
2.3. Data Processing Procedure
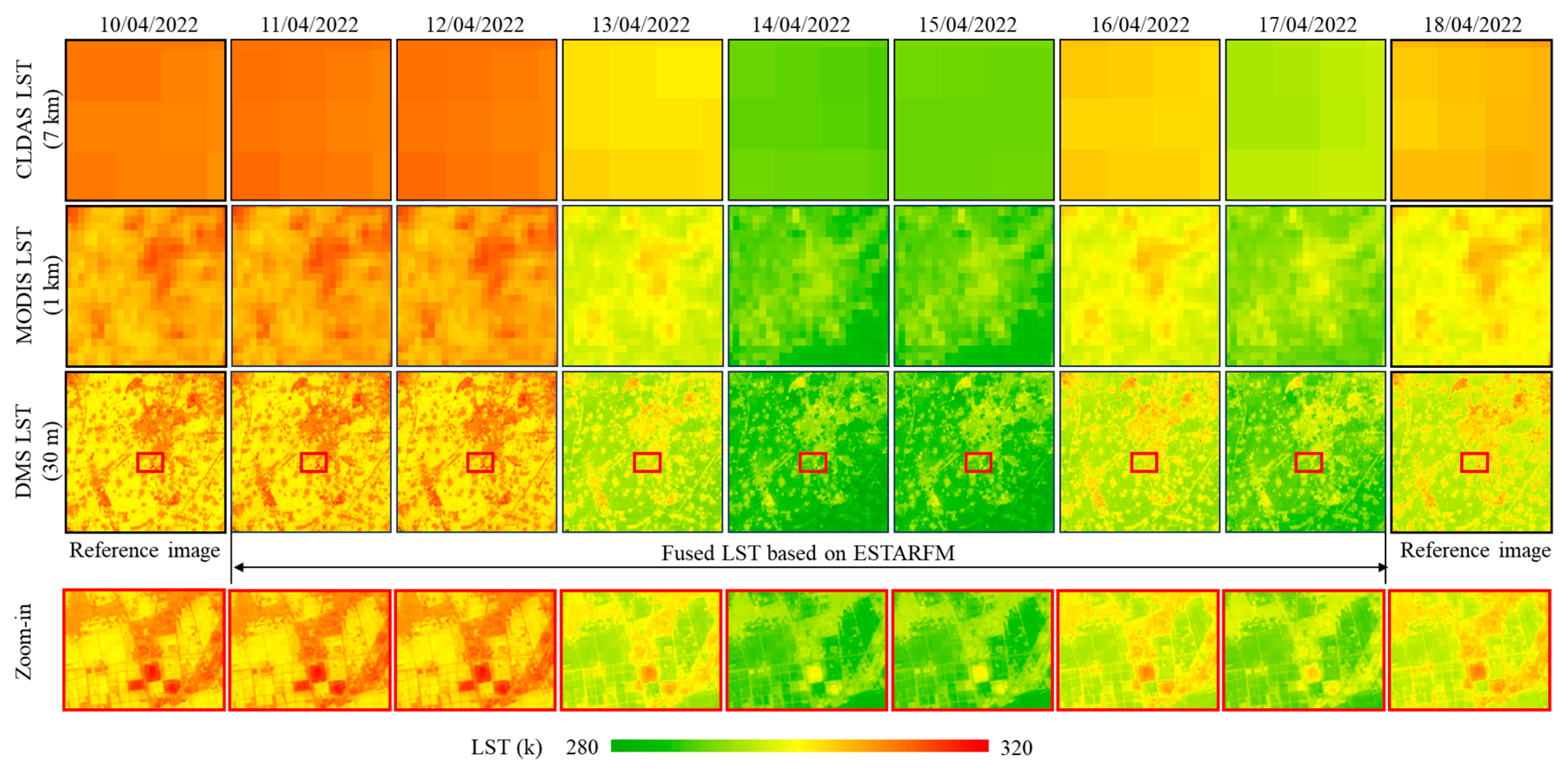
2.3.1. Generation of Daily 30 m Vegetation Indices and LST
2.3.2. Footprint Computation
2.3.3. ET Modeling
2.3.4. Model Interpretability and Importance Analysis
2.3.5. Statistical Metrics
3. Results
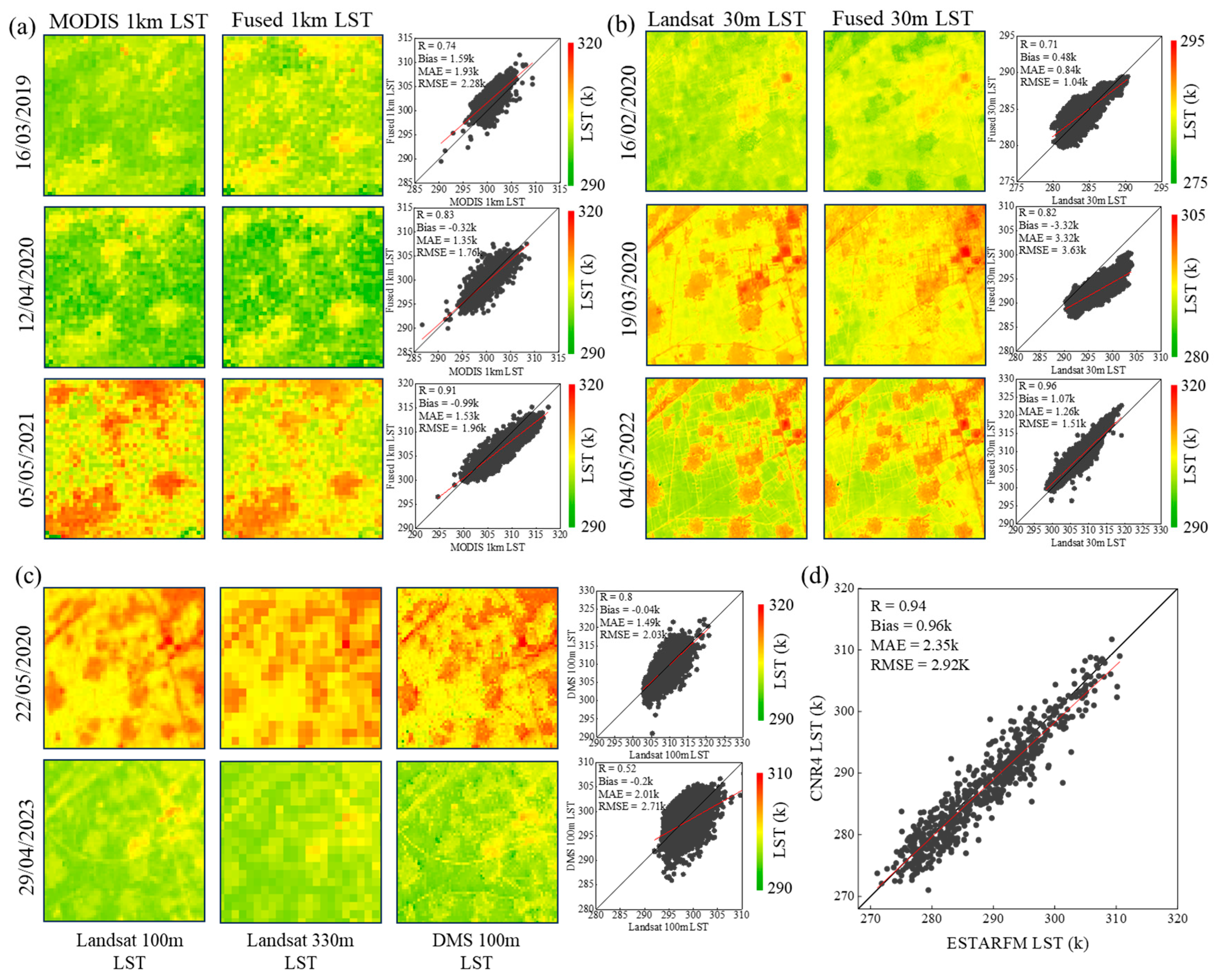
3.1. Performance of Daily LST and Vegetation Indices
3.2. Model Performance on the Test Set
3.3. Global Interpretability of the Model
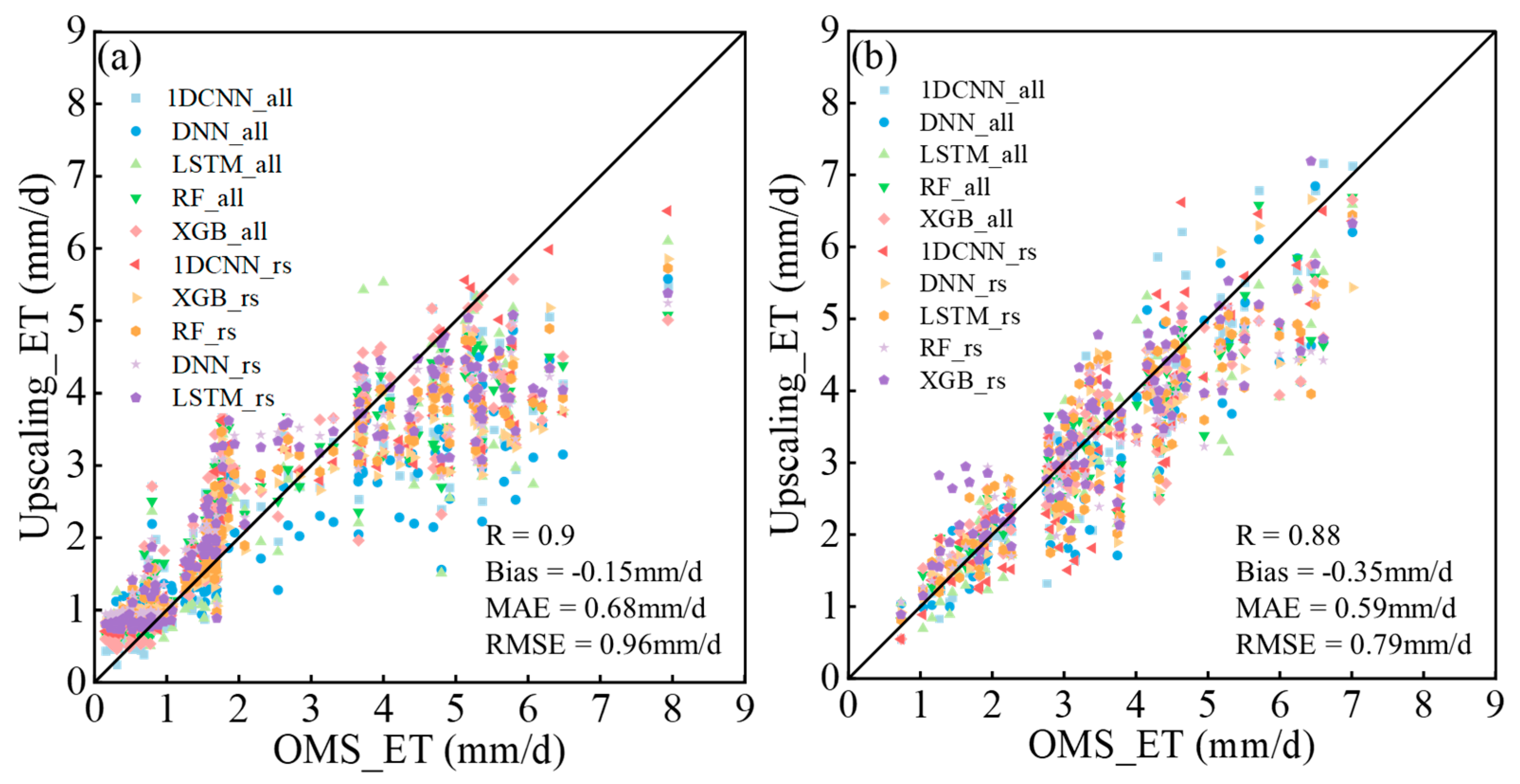
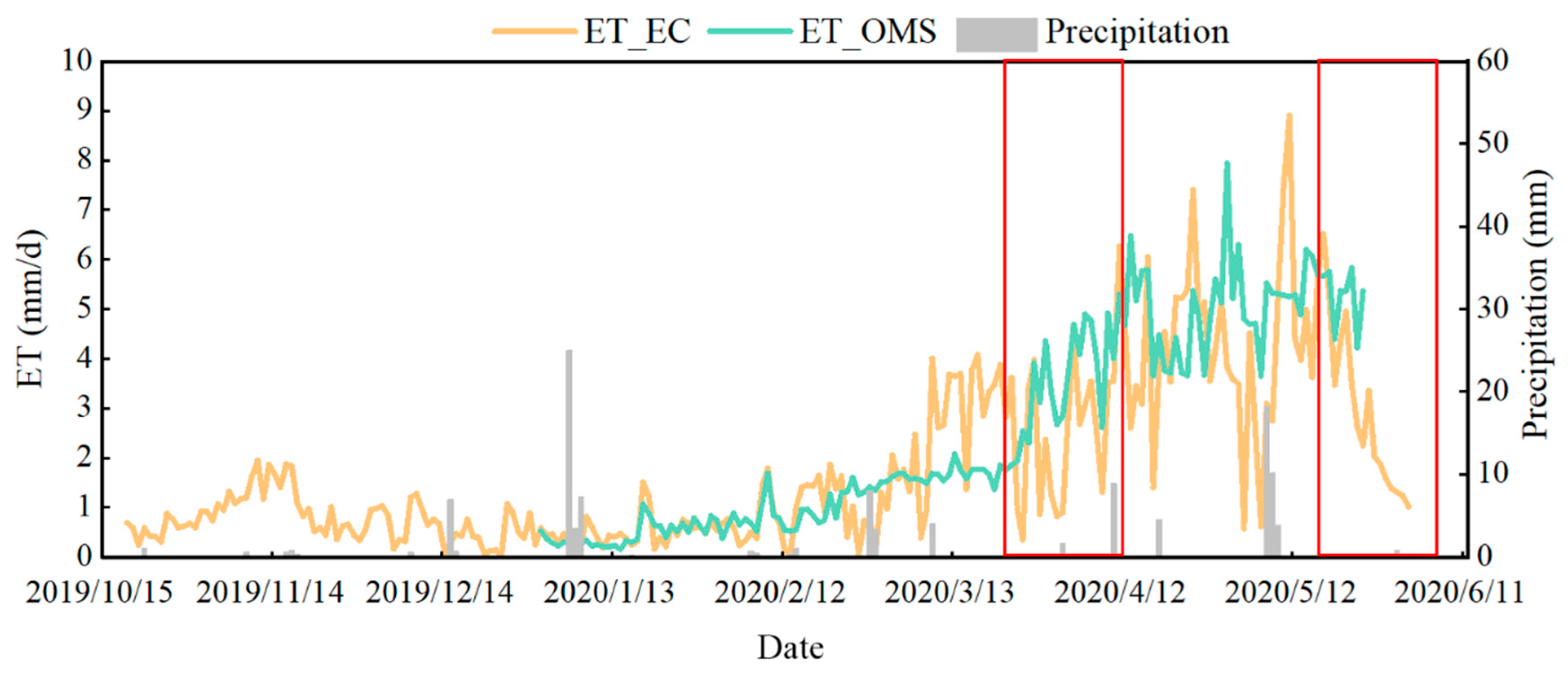
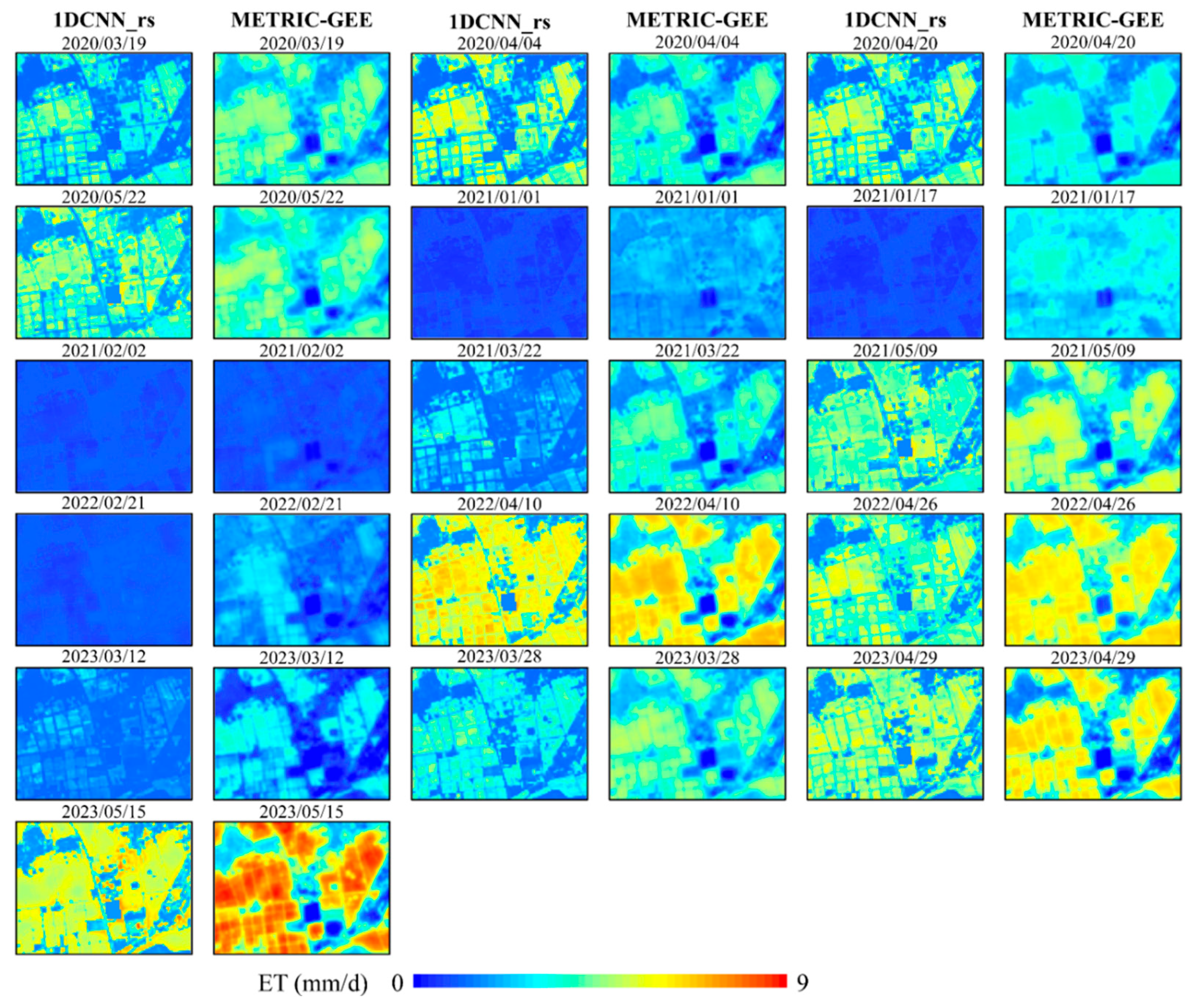
3.4. Direct Comparison of Upscaling_ET with OMS
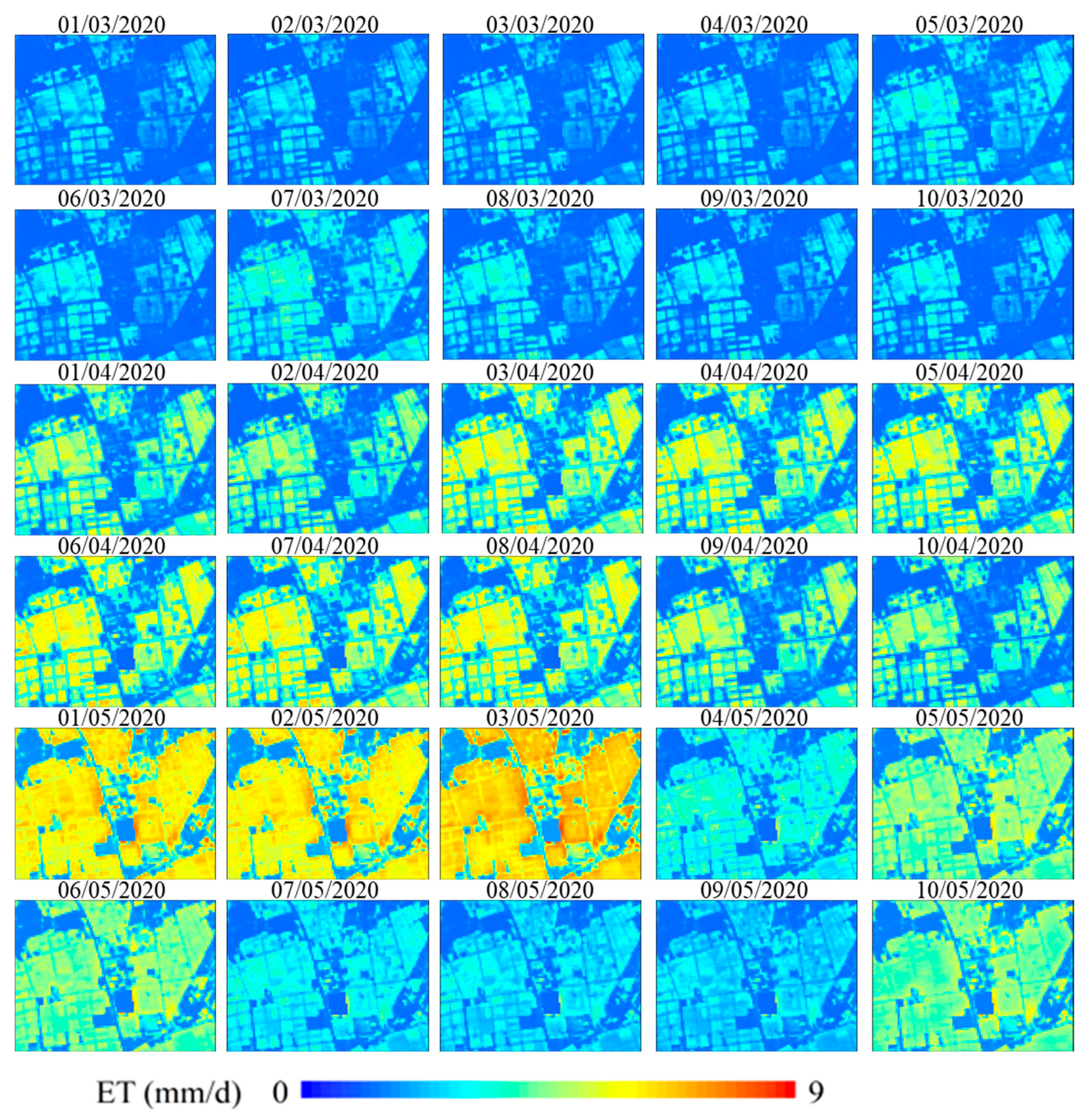
3.5. Spatiotemporal Variations in Upscaling_ET
4. Discussion
4.1. Performance of the Proposed Framework
4.2. Comparison of Upscaling_ET with Existing 30 m Resolution Products
4.3. Uncertainty and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ET | Evapotranspiration |
| CLDAS | China Land Data Assimilation System |
| LST | Land Surface Temperature |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| OMS | Optical-Microwave Scintillometers |
| EC | Eddy Covariance Systems |
| Upscaling_ET | Upscaled ET Results |
| SHAP | SHapley Additive exPlanations |
| 1D CNN | One-Dimensional Convolutional Neural Network |
| SVM | Support Vector Machine |
| RF | Random Forest |
| DMS | Data Mining Sharpening |
| DNN | Deep Neural Network |
| LSTM | Long Short-Term Memory |
| XGB | eXtreme Gradient Boosting |
| ESTARFM | Enhanced Spatial and Temporal Adaptive Reflectance Fusion Model |
| GF-SG | Gap-Filling and Savitzky–Golay filtering |
| NDVI | Normalized Difference Vegetation Index |
| EVI2 | Two Band Enhanced Vegetation Index |
| LAI | Leaf Area Index |
| R | Pearson correlation coefficient |
| R2 | Coefficient of Determination |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
| SEBAL | The Surface Energy Balance Algorithm for Land |
| SEBS | Surface Energy Balance System |
| TSEB | Two Source Energy Balance |
| METRIC | Mapping ET at high Resolution with Internalized Calibration |
| EEflux | Earth Engine Evapotranspiration Flux |
| ECOSTRESS | ECOsystem Spaceborne Thermal Radiometer Experiment on Space Station |
References
- Holmes, T.R.H.; Hain, C.R.; Crow, W.T.; Anderson, M.C.; Kustas, W.P. Microwave Implementation of Two-Source Energy Balance Approach for Estimating Evapotranspiration. Hydrol. Earth Syst. Sci. 2018, 22, 1351–1369. [Google Scholar] [CrossRef]
- Narasimhan, B.; Srinivasan, R. Development and Evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for Agricultural Drought Monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Feng, J.; Wang, W.; Xu, F.; Wang, S. Evaluating the Ability of Deep Learning on Actual Daily Evapotranspiration Estimation over the Heterogeneous Surfaces. Agric. Water Manag. 2024, 291, 108627. [Google Scholar] [CrossRef]
- Hirschi, M.; Michel, D.; Lehner, I.; Seneviratne, S.I. A Site-Level Comparison of Lysimeter and Eddy Covariance Flux Measurements of Evapotranspiration. Hydrol. Earth Syst. Sci. 2017, 21, 1809–1825. [Google Scholar] [CrossRef]
- Shi, T.-T.; Guan, D.-X.; Wu, J.-B.; Wang, A.-Z.; Jin, C.-J.; Han, S.-J. Comparison of Methods for Estimating Evapotranspiration Rate of Dry Forest Canopy: Eddy Covariance, Bowen Ratio Energy Balance, and Penman-Monteith Equation. J. Geophys. Res. Atmos. 2008, 113, D19. [Google Scholar] [CrossRef]
- Xu, F.; Wang, W.; Huang, C.; Wang, J.; Ren, Z.; Feng, J.; Dong, L.; Zhang, Y.; Kang, J. Turbulent Fluxes at Kilometer Scale Determined by Optical-Microwave Scintillometry in a Heterogeneous Oasis Cropland of the Heihe River Basin. Agric. For. Meteorol. 2023, 339, 109544. [Google Scholar] [CrossRef]
- Allen, R.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.; Bastiaanssen, W.G.M.; Kramber, W.J.; Lorite, I.; Robison, C. Satellite-Based Energy Balance for Mapping Evapotranspiration With Internalized Calibration (METRIC)—Applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Chen, J.; Dafflon, B.; Tran, A.P.; Falco, N.; Hubbard, S.S. A Deep Learning Hybrid Predictive Modeling (HPM) Approach for Estimating Evapotranspiration and Ecosystem Respiration. Hydrol. Earth Syst. Sci. 2021, 25, 6041–6066. [Google Scholar] [CrossRef]
- Mallick, K.; Boegh, E.; Trebs, I.; Alfieri, J.G.; Kustas, W.P.; Prueger, J.H.; Niyogi, D.; Das, N.; Drewry, D.T.; Hoffmann, L.; et al. Reintroducing Radiometric Surface Temperature into the Penman-Monteith Formulation. Water Resour. Res. 2015, 51, 6214–6243. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for Estimation of Turbulent Heat Fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Elfarkh, J.; Simonneaux, V.; Jarlan, L.; Ezzahar, J.; Boulet, G.; Chakir, A.; Er-Raki, S. Evapotranspiration Estimates in a Traditional Irrigated Area in Semi-Arid Mediterranean. Comparison of Four Remote Sensing-Based Models. Agric. Water Manag. 2022, 270, 107728. [Google Scholar] [CrossRef]
- Holwerda, F.; Bruijnzeel, L.A.; Scatena, F.N.; Vugts, H.F.; Meesters, A.G.C.A. Wet Canopy Evaporation from a Puerto Rican Lower Montane Rain Forest: The Importance of Realistically Estimated Aerodynamic Conductance. J. Hydrol. 2012, 414–415, 1–15. [Google Scholar] [CrossRef]
- Noilhan, J.; Calvet, J.-C. Mesoscale Land–Atmosphere Models and Usefulness of Microwave Remote-Sensing Data. In Passive Microwave Remote Sensing of Land—Atmosphere Interactions; CRC Press: Boca Raton, FL, USA, 1995; ISBN 978-1-00-342406-2. [Google Scholar]
- Sun, J.; Takle, E.S.; Acevedo, O.C. Understanding Physical Processes Represented by the Monin–Obukhov Bulk Formula for Momentum Transfer. Bound. Layer Meteorol. 2020, 177, 69–95. [Google Scholar] [CrossRef]
- van Dijk, A.I.; Gash, J.H.; van Gorsel, E.; Blanken, P.D.; Cescatti, A.; Emmel, C.; Gielen, B.; Harman, I.N.; Kiely, G.; Merbold, L.; et al. Rainfall Interception and the Coupled Surface Water and Energy Balance. Agric. For. Meteorol. 2015, 214–215, 402–415. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Diak, G.R.; Kustas, W.P.; Mecikalski, J.R. A Two-Source Time-Integrated Model for Estimating Surface Fluxes Using Thermal Infrared Remote Sensing. Remote Sens. Environ. 1997, 60, 195–216. [Google Scholar] [CrossRef]
- Anderson, M.; Norman, J.; Kustas, W.; Houborg, R.; Starks, P.; Agam, N. A Thermal-Based Remote Sensing Technique for Routine Mapping of Land-Surface Carbon, Water and Energy Fluxes from Field to Regional Scales. Remote Sens. Environ. 2008, 112, 4227–4241. [Google Scholar] [CrossRef]
- Boulet, G.; Mougenot, B.; Lhomme, J.-P.; Fanise, P.; Lili-Chabaane, Z.; Olioso, A.; Bahir, M.; Rivalland, V.; Jarlan, L.; Merlin, O.; et al. The SPARSE Model for the Prediction of Water Stress and Evapotranspiration Components from Thermal Infra-Red Data and Its Evaluation over Irrigated and Rainfed Wheat. Hydrol. Earth Syst. Sci. 2015, 19, 4653–4672. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source Approach for Estimating Soil and Vegetation Energy Fluxes in Observations of Directional Radiometric Surface Temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Gokool, S.; Riddell, E.; Jarmain, C.; Chetty, K.; Feig, G.; Thenga, H. Evaluating the Accuracy of Satellite-Derived Evapotranspiration Estimates Acquired during Conditions of Water Stress. Int. J. Remote Sens. 2019, 41, 704–724. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Yan, G.; Zhang, X. A Review of Current Methodologies for Regional Evapotranspiration Estimation from Remotely Sensed Data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef]
- Li, X.; Pang, Z.; Xue, F.; Ding, J.; Wang, J.; Xu, T.; Xu, Z.; Ma, Y.; Zhang, Y.; Shi, J. Analysis of Spatial and Temporal Variations in Evapotranspiration and Its Driving Factors Based on Multi-Source Remote Sensing Data: A Case Study of the Heihe River Basin. Remote Sens. 2024, 16, 2696. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P.; Li, Z.-L. How Sensitive Is SEBAL to Changes in Input Variables, Domain Size and Satellite Sensor? J. Geophys. Res. Atmos. 2011, 116, D21. [Google Scholar] [CrossRef]
- Jung, M.; Koirala, S.; Weber, U.; Ichii, K.; Gans, F.; Camps-Valls, G.; Papale, D.; Schwalm, C.; Tramontana, G.; Reichstein, M. The FLUXCOM Ensemble of Global Land-Atmosphere Energy Fluxes. Sci. Data 2019, 6, 74. [Google Scholar] [CrossRef]
- Xiao, J.; Chen, J.; Davis, K.J.; Reichstein, M. Advances in Upscaling of Eddy Covariance Measurements of Carbon and Water Fluxes. J. Geophys. Res. Biogeosci. 2012, 117, G1. [Google Scholar] [CrossRef]
- Yang, F.; White, M.A.; Michaelis, A.R.; Ichii, K.; Hashimoto, H.; Votava, P.; Zhu, A.-X.; Nemani, R.R. Prediction of Continental-Scale Evapotranspiration by Combining MODIS and AmeriFlux Data Through Support Vector Machine. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3452–3461. [Google Scholar] [CrossRef]
- Zhang, C.; Brodylo, D.; Rahman, M.; Rahman, M.A.; Douglas, T.A.; Comas, X. Using an Object-Based Machine Learning Ensemble Approach to Upscale Evapotranspiration Measured from Eddy Covariance Towers in a Subtropical Wetland. Sci. Total Environ. 2022, 831, 154969. [Google Scholar] [CrossRef] [PubMed]
- Bodesheim, P.; Jung, M.; Gans, F.; Mahecha, M.D.; Reichstein, M. Upscaled Diurnal Cycles of Land–Atmosphere Fluxes: A New Global Half-Hourly Data Product. Earth Syst. Sci. Data 2018, 10, 1327–1365. [Google Scholar] [CrossRef]
- Shang, K.; Yao, Y.; Liang, S.; Zhang, Y.; Fisher, J.B.; Chen, J.; Liu, S.; Xu, Z.; Zhang, Y.; Jia, K.; et al. DNN-MET: A Deep Neural Networks Method to Integrate Satellite-Derived Evapotranspiration Products, Eddy Covariance Observations and Ancillary Information. Agric. For. Meteorol. 2021, 308–309, 108582. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.; Li, H.; Ma, Y.; Wang, J.; Zhang, Y.; Xu, Z.; Xu, T.; Song, L.; Yang, X.; et al. Intercomparison of Six Upscaling Evapotranspiration Methods: From Site to the Satellite Pixel. J. Geophys. Res. Atmos. 2018, 123, 6777–6803. [Google Scholar] [CrossRef]
- Tramontana, G.; Jung, M.; Schwalm, C.R.; Ichii, K.; Camps-Valls, G.; Ráduly, B.; Reichstein, M.; Arain, M.A.; Cescatti, A.; Kiely, G.; et al. Predicting Carbon Dioxide and Energy Fluxes across Global FLUXNET Sites with Regression Algorithms. Biogeosciences 2016, 13, 4291–4313. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; de Jeu, R.; et al. Recent Decline in the Global Land Evapotranspiration Trend Due to Limited Moisture Supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef]
- Pang, X.; Lei, H.; Cong, Z.; Yang, H.; Duan, L.; Yang, D. Long Term Variation of Evapotranspiration and Water Balance Based on Upscaling Eddy Covariance Observations over the Temperate Semi-Arid Grassland of China. Agric. For. Meteorol. 2021, 308–309, 108566. [Google Scholar] [CrossRef]
- Xu, T.; Guo, Z.; Liu, S.; He, X.; Meng, Y.; Xu, Z.; Xia, Y.; Xiao, J.; Zhang, Y.; Ma, Y.; et al. Evaluating Different Machine Learning Methods for Upscaling Evapotranspiration from Flux Towers to the Regional Scale. J. Geophys. Res. Atmos. 2018, 123, 8674–8690. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, S.; Song, L.; Xu, Z.; Liu, Y.; Xu, T.; Zhu, Z. Estimation of Daily Evapotranspiration and Irrigation Water Efficiency at a Landsat-like Scale for an Arid Irrigation Area Using Multi-Source Remote Sensing Data. Remote Sens. Environ. 2018, 216, 715–734. [Google Scholar] [CrossRef]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of Flux Measurements for Density Effects Due to Heat and Water Vapour Transfer. Q. J. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Mauder, M.; Foken, T. Documentation and Instruction Manual of the Eddy-Covariance Software Package TK3. In Arbeitsergebnisse, Universität Bayreuth, Abt. Mikrometeorologie; University of Bayreuth: Bayreuth, Germany, 2015; Volume 62, p. 62. ISSN 1614-8916. [Google Scholar]
- Falge, E.; Baldocchi, D.; Olson, R.; Anthoni, P.; Aubinet, M.; Bernhofer, C.; Burba, G.; Ceulemans, R.; Clement, R.; Dolman, H.; et al. Gap Filling Strategies for Long Term Energy Flux Data Sets. Agric. For. Meteorol. 2001, 107, 71–77. [Google Scholar] [CrossRef]
- Wang, T.; Ochs, G.R.; Clifford, S.F. A Saturation-Resistant Optical Scintillometer to Measure Cn2+. J. Opt. Soc. Am. JOSA 1978, 68, 334–338. [Google Scholar] [CrossRef]
- Ward, H.C.; Evans, J.G.; Hartogensis, O.K.; Moene, A.F.; De Bruin, H.A.R.; Grimmond, C.S.B. A Critical Revision of the Estimation of the Latent Heat Flux from Two-wavelength Scintillometry. Q. J. R. Meteorol. Soc. 2013, 139, 1912–1922. [Google Scholar] [CrossRef]
- Lüdi, A.; Beyrich, F.; Mätzler, C. Determination of the Turbulent Temperature–Humidity Correlation from Scintillometric Measurements. Bound. Layer Meteorol. 2005, 117, 525–550. [Google Scholar] [CrossRef]
- Wyngaard, J.C.; Clifford, S.F. Estimating Momentum, Heat and Moisture Fluxes from Structure Parameters. J. Atmos. Sci. 1978, 35, 1204–1211. [Google Scholar] [CrossRef]
- Andreas, E.L. Estimating Cn2 over Snow and Sea Ice from Meteorological Data. J. Opt. Soc. Am. A JOSAA 1988, 5, 481–495. [Google Scholar] [CrossRef]
- Kleissl, J.; Hong, S.-H.; Hendrickx, J.M.H. New Mexico Scintillometer Network: Supporting Remote Sensing and Hydrologic and Meteorological Models. Bull. Am. Meteorol. Soc. 2009, 90, 207–218. [Google Scholar] [CrossRef]
- Kleissl, J.; Hartogensis, O.K.; Gomez, J.D. Test of Scintillometer Saturation Correction Methods Using Field Experimental Data. Bound. Layer Meteorol. 2010, 137, 493–507. [Google Scholar] [CrossRef]
- Zhang, C.; Comas, X.; Brodylo, D. A Remote Sensing Technique to Upscale Methane Emission Flux in a Subtropical Peatland. J. Geophys. Res. Biogeosci. 2020, 125, e2020JG006002. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Shi, C.; Xie, Z.; Qian, H.; Liang, M.; Yang, X. China Land Soil Moisture EnKF Data Assimilation Based on Satellite Remote Sensing Data. Sci. China Earth Sci. 2011, 54, 1430–1440. [Google Scholar] [CrossRef]
- Sun, S.; Shi, C.; Liang, X.; Han, S.; Jiang, Z.; Zhang, T. Assessment of Ground Temperature Simulation in China by Different Land Surface Models Based on Station Observations. J. Appl. Meteorol. Sci. 2017, 28, 737–749. [Google Scholar] [CrossRef]
- Chen, Y.; Cao, R.; Chen, J.; Liu, L.; Matsushita, B. A Practical Approach to Reconstruct High-Quality Landsat NDVI Time-Series Data by Gap Filling and the Savitzky–Golay Filter. ISPRS J. Photogramm. Remote Sens. 2021, 180, 174–190. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A Simple Method for Reconstructing a High-Quality NDVI Time-Series Data Set Based on the Savitzky–Golay Filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Steven, M.D.; Malthus, T.J.; Baret, F.; Xu, H.; Chopping, M.J. Intercalibration of Vegetation Indices from Different Sensor Systems. Remote Sens. Environ. 2003, 88, 412–422. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.; Kim, Y.; Didan, K. 2-Band Enhanced Vegetation Index without a Blue Band and Its Application to AVHRR Data. Proc. SPIE Int. Soc. Opt. Eng. 2007, 6679, 667905. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.; Yang, X.; Ma, Y.; He, X.; Xu, Z.; Xu, T.; Song, L.; Zhang, Y.; Hu, X.; et al. Upscaling Evapotranspiration from a Single-Site to Satellite Pixel Scale. Remote Sens. 2021, 13, 4072. [Google Scholar] [CrossRef]
- Wang, D.; Yu, T.; Liu, Y.; Gu, X.; Mi, X.; Shi, S.; Ma, M.; Chen, X.; Zhang, Y.; Liu, Q.; et al. Estimating Daily Actual Evapotranspiration at a Landsat-Like Scale Utilizing Simulated and Remote Sensing Surface Temperature. Remote Sens. 2021, 13, 225. [Google Scholar] [CrossRef]
- Wang, S.; Wang, C.; Zhang, C.; Xue, J.; Wang, P.; Wang, X.; Wang, W.; Zhang, X.; Li, W.; Huang, G.; et al. A Classification-Based Spatiotemporal Adaptive Fusion Model for the Evaluation of Remotely Sensed Evapotranspiration in Heterogeneous Irrigated Agricultural Area. Remote Sens. Environ. 2022, 273, 112962. [Google Scholar] [CrossRef]
- Long, D.; Yan, L.; Bai, L.; Zhang, C.; Li, X.; Lei, H.; Yang, H.; Tian, F.; Zeng, C.; Meng, X.; et al. Generation of MODIS-like Land Surface Temperatures under All-Weather Conditions Based on a Data Fusion Approach. Remote Sens. Environ. 2020, 246, 111863. [Google Scholar] [CrossRef]
- Gao, F.; Kustas, W.P.; Anderson, M.C. A Data Mining Approach for Sharpening Thermal Satellite Imagery over Land. Remote Sens. 2012, 4, 3287–3319. [Google Scholar] [CrossRef]
- Anderson, M.C.; Yang, Y.; Xue, J.; Knipper, K.R.; Yang, Y.; Gao, F.; Hain, C.R.; Kustas, W.P.; Cawse-Nicholson, K.; Hulley, G.; et al. Interoperability of ECOSTRESS and Landsat for Mapping Evapotranspiration Time Series at Sub-Field Scales. Remote Sens. Environ. 2021, 252, 112189. [Google Scholar] [CrossRef]
- Xue, J.; Anderson, M.C.; Gao, F.; Hain, C.; Knipper, K.R.; Yang, Y.; Kustas, W.P.; Yang, Y.; Bambach, N.; McElrone, A.J.; et al. Improving the Spatiotemporal Resolution of Remotely Sensed ET Information for Water Management through Landsat, Sentinel-2, ECOSTRESS and VIIRS Data Fusion. Irrig. Sci. 2022, 40, 609–634. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Li, S.; Wang, J.; Chen, Z. Estimation of Evapotranspiration from the People’s Victory Irrigation District Based on the Data Mining Sharpener Model. Agronomy 2023, 13, 3082. [Google Scholar] [CrossRef]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A Simple Two-Dimensional Parameterisation for Flux Footprint Prediction (FFP). Geosci. Model Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Wang, W.Z.; Jia, Z.Z.; Zhu, M.J.; Bai, J.; Wang, J.M. A Comparison of Eddy-Covariance and Large Aperture Scintillometer Measurements with Respect to the Energy Balance Closure Problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef]
- Kormann, R.; Meixner, F.X. An Analytical Footprint Model For Non-Neutral Stratification. Bound. Layer Meteorol. 2001, 99, 207–224. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z.; Song, L.; Zhao, Q.; Ge, Y.; Xu, T.; Ma, Y.; Zhu, Z.; Jia, Z.; Zhang, F. Upscaling Evapotranspiration Measurements from Multi-Site to the Satellite Pixel Scale over Heterogeneous Land Surfaces. Agric. For. Meteorol. 2016, 230–231, 97–113. [Google Scholar] [CrossRef]
- Amani, S.; Shafizadeh-Moghadam, H. A Review of Machine Learning Models and Influential Factors for Estimating Evapotranspiration Using Remote Sensing and Ground-Based Data. Agric. Water Manag. 2023, 284, 108324. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Abowarda, A.; Bai, L.; Zhang, C.; Long, D.; Li, X.; Huang, Q.; Sun, Z. Generating Surface Soil Moisture at 30 m Spatial Resolution Using Both Data Fusion and Machine Learning toward Better Water Resources Management at the Field Scale. Remote Sens. Environ. 2021, 255, 112301. [Google Scholar] [CrossRef]
- Vulova, S.; Meier, F.; Rocha, A.D.; Quanz, J.; Nouri, H.; Kleinschmit, B. Modeling Urban Evapotranspiration Using Remote Sensing, Flux Footprints, and Artificial Intelligence. Sci. Total Environ. 2021, 786, 147293. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, L.B.; da Cunha, F.F. New Approach to Estimate Daily Reference Evapotranspiration Based on Hourly Temperature and Relative Humidity Using Machine Learning and Deep Learning. Agric. Water Manag. 2020, 234, 106113. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Kiranyaz. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Kumar, M.; Raghuwanshi, N.S.; Singh, R.; Wallender, W.W.; Pruitt, W.O. Estimating Evapotranspiration Using Artificial Neural Network. Irrig. Drain. Eng. 2002, 128, 224–233. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D Convolutional Neural Networks and Applications: A Survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Vennerød, C.B.; Kjærran, A.; Bugge, E.S. Long Short-Term Memory RNN. arXiv 2021, arXiv:2105.06756. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Babaeian, E.; Paheding, S.; Siddique, N.; Devabhaktuni, V.K.; Tuller, M. Short- and Mid-Term Forecasts of Actual Evapotranspiration with Deep Learning. J. Hydrol. 2022, 612, 128078. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, L.; Zhu, G.; Cheng, C.; He, J.; Traore, S.; Singh, V.P. Exploring Interpretable and Non-Interpretable Machine Learning Models for Estimating Winter Wheat Evapotranspiration Using Particle Swarm Optimization with Limited Climatic Data. Comput. Electron. Agric. 2023, 212, 108140. [Google Scholar] [CrossRef]
- Shapley, L.S. 17. A Value for n-Person Games. In Contributions to the Theory of Games, Volume II; Kuhn, H.W., Tucker, A.W., Eds.; Princeton University Press: Princeton, NJ, USA, 2016; pp. 307–318. ISBN 978-1-4008-8197-0. [Google Scholar]
- Hu, X.; Shi, L.; Lin, G. The Data-Driven Solution of Energy Imbalance-Induced Structural Error in Evapotranspiration Models. J. Hydrol. 2021, 597, 126205. [Google Scholar] [CrossRef]
- Štrumbelj, E.; Kononenko, I. Explaining Prediction Models and Individual Predictions with Feature Contributions. Knowl. Inf. Syst. 2014, 41, 647–665. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Cao, R.; Xu, Z.; Chen, Y.; Chen, J.; Shen, M. Reconstructing High-Spatiotemporal-Resolution (30 m and 8-Days) NDVI Time-Series Data for the Qinghai–Tibetan Plateau from 2000–2020. Remote Sens. 2022, 14, 3648. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, H.; Niu, X.; Shao, W.; Yang, Y. Comparative Analysis and Comprehensive Trade-Off of Four Spatiotemporal Fusion Models for NDVI Generation. Remote Sens. 2022, 14, 5996. [Google Scholar] [CrossRef]
- Kotthaus, S.; Grimmond, S. Energy Exchange in a Dense Urban Environment—Part II: Impact of Spatial Heterogeneity of the Surface. Urban Clim. 2013, 10, 281–307. [Google Scholar] [CrossRef]
- Guzinski, R.; Nieto, H.; Sánchez, J.M.; López-Urrea, R.; Boujnah, D.M.; Boulet, G. Utility of Copernicus-Based Inputs for Actual Evapotranspiration Modeling in Support of Sustainable Water Use in Agriculture. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 11466–11484. [Google Scholar] [CrossRef]
- Guzinski, R.; Nieto, H.; Sánchez, R.; Sánchez-Tomás, J.; Jomaa, I.; Roupsard, O.; López-Urrea, R. Improving Field-Scale Crop Actual Evapotranspiration Monitoring with Sentinel-3, Sentinel-2, and Landsat Data Fusion. Int. J. Appl. Earth Obs. Geoinf. 2023, 125, 103587. [Google Scholar] [CrossRef]
- Ma, Z.; Wu, B.; Yan, N.; Zhu, W.; Xu, J. Coupling Water and Carbon Processes to Estimate Field-Scale Maize Evapotranspiration with Sentinel-2 Data. Agric. For. Meteorol. 2021, 306, 108421. [Google Scholar] [CrossRef]
- Awada, H.; Di Prima, S.; Sirca, C.; Giadrossich, F.; Marras, S.; Spano, D.; Pirastru, M. A Remote Sensing and Modeling Integrated Approach for Constructing Continuous Time Series of Daily Actual Evapotranspiration. Agric. Water Manag. 2022, 260, 107320. [Google Scholar] [CrossRef]
- Lu, X.; Zhuang, Q. Evaluating Evapotranspiration and Water-Use Efficiency of Terrestrial Ecosystems in the Conterminous United States Using MODIS and AmeriFlux Data. Remote Sens. Environ. 2010, 114, 1924–1939. [Google Scholar] [CrossRef]
- Li, X.; He, Y.; Zeng, Z.; Lian, X.; Wang, X.; Du, M.; Jia, G.; Li, Y.; Ma, Y.; Tang, Y.; et al. Spatiotemporal Pattern of Terrestrial Evapotranspiration in China during the Past Thirty Years. Agric. For. Meteorol. 2018, 259, 131–140. [Google Scholar] [CrossRef]
- Zhang, L.; Xiao, J.; Zheng, Y.; Li, S.; Zhou, Y. Increased Carbon Uptake and Water Use Efficiency in Global Semi-Arid Ecosystems. Environ. Res. Lett. 2020, 15, 034022. [Google Scholar] [CrossRef]
- Kadam, S.A.; Stöckle, C.O.; Liu, M.; Gao, Z.; Russell, E.S. Suitability of Earth Engine Evaporation Flux (EEFlux) Estimation of Evapotranspiration in Rainfed Crops. Remote Sens. 2021, 13, 3884. [Google Scholar] [CrossRef]
- Foken, T. The Energy Balance Closure Problem: An Overview. Ecol. Appl. 2008, 18, 1351–1367. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting Eddy-Covariance Flux Underestimates over a Grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
- Finnigan, J.J.; Clement, R.; Malhi, Y.; Leuning, R.; Cleugh, H.A. A Re-Evaluation of Long-Term Flux Measurement Techniques Part I: Averaging and Coordinate Rotation. Bound. Layer Meteorol. 2003, 107, 1–48. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K.; et al. MERRA: NASA’s Modern-Era Retrospective Analysis for Research and Applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Zhao, M.; Running, S.W.; Nemani, R.R. Sensitivity of Moderate Resolution Imaging Spectroradiometer (MODIS) Terrestrial Primary Production to the Accuracy of Meteorological Reanalyses. J. Geophys. Res. Biogeosci. 2006, 111, G1. [Google Scholar] [CrossRef]
- Wei, J.; Sun, J.; Liu, S.; Song, L.; Ma, Y.; Xu, Z.; Xu, T.; Zhou, J.; Wang, Z.; Peng, Z.; et al. A Robust Framework for Improving Fine-Scale Evapotranspiration Estimation From UAV-Based Multispectral and Thermal Images. IEEE Trans. Geosci. Remote Sens. 2025, 63, 4417615. [Google Scholar] [CrossRef]
- Zhou, Z.-H.; Feng, J. Deep Forest: Towards An Alternative to Deep Neural Networks. Natl. Sci. Rev. 2017, 6, 3553–3559. [Google Scholar]
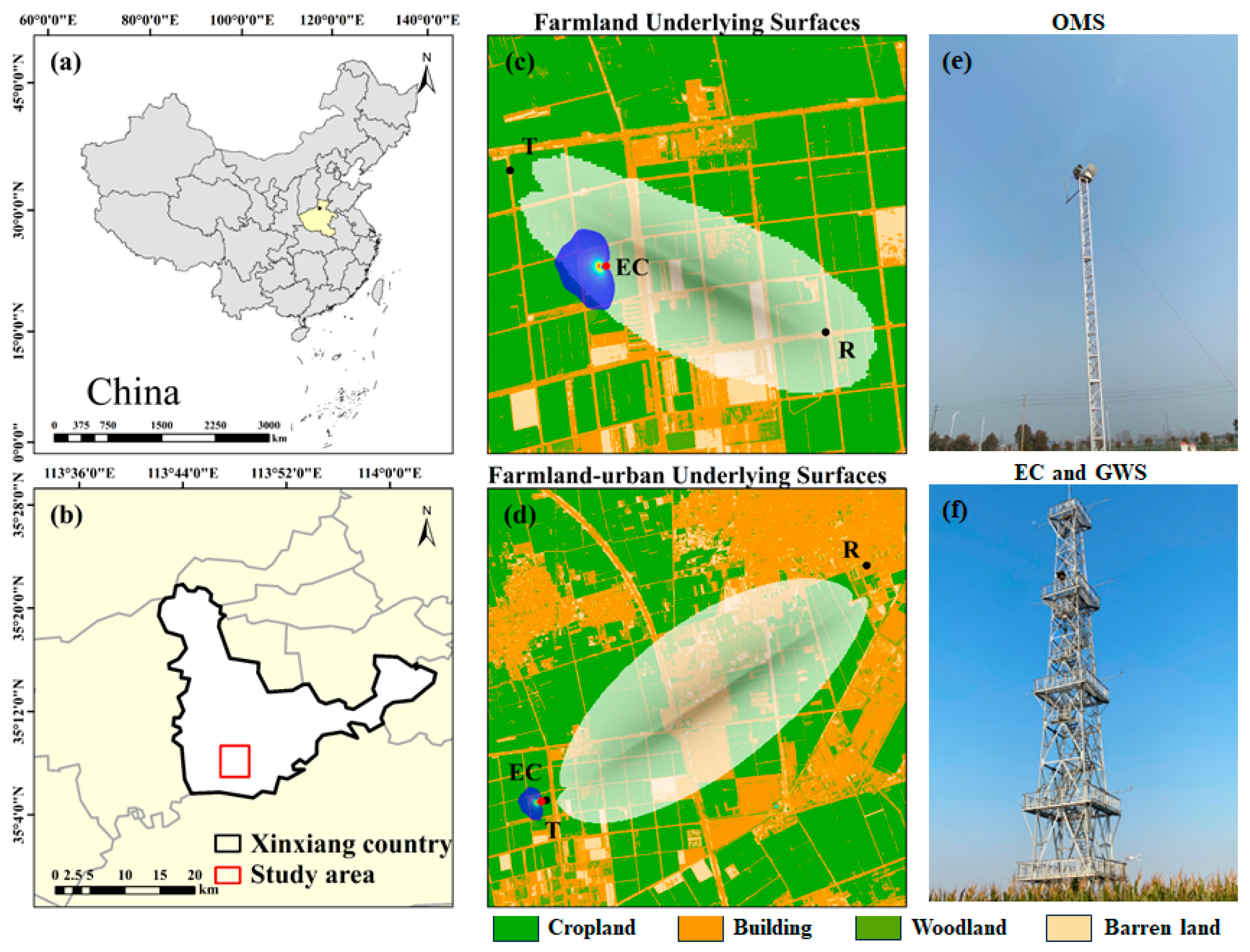
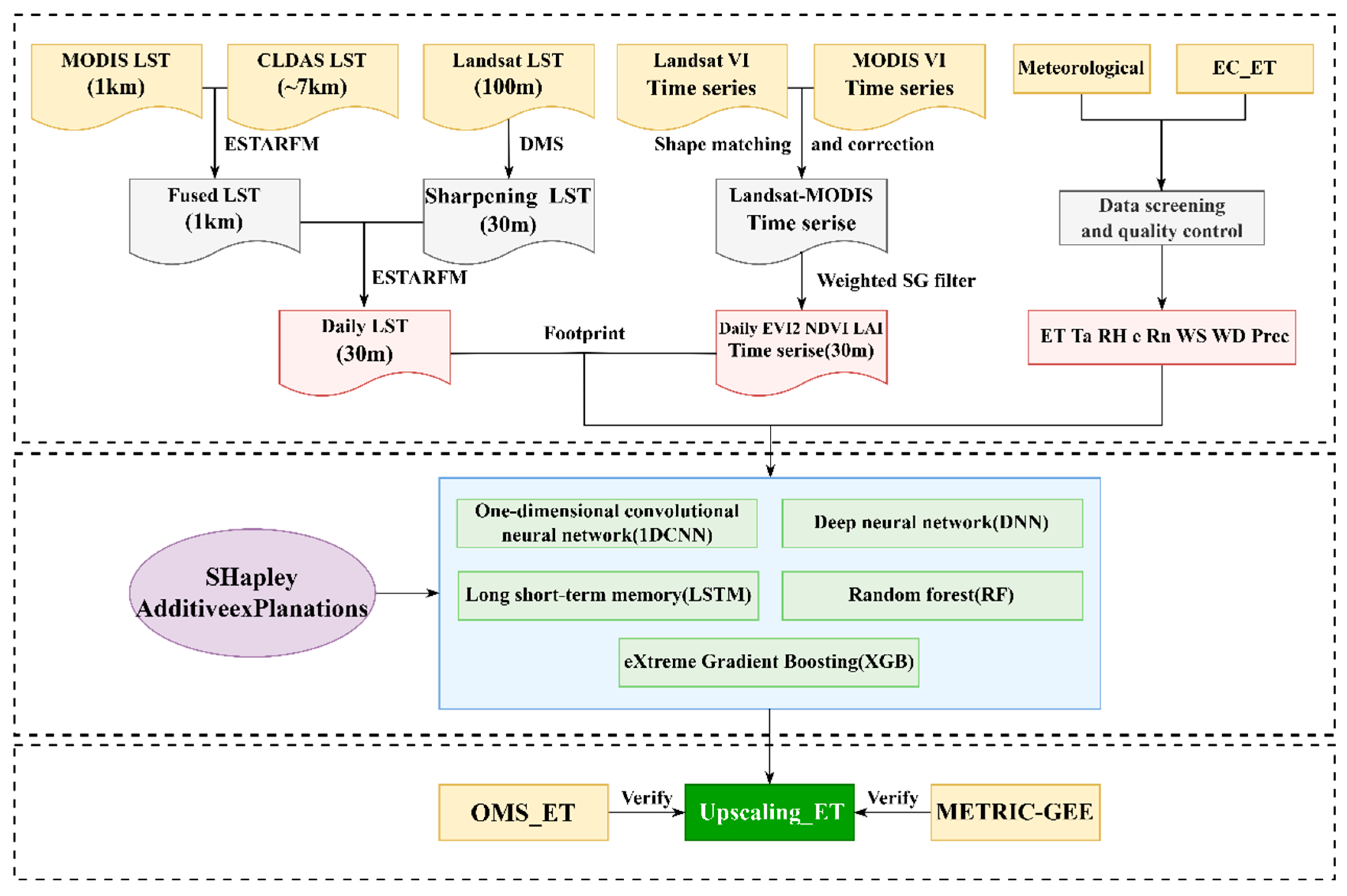
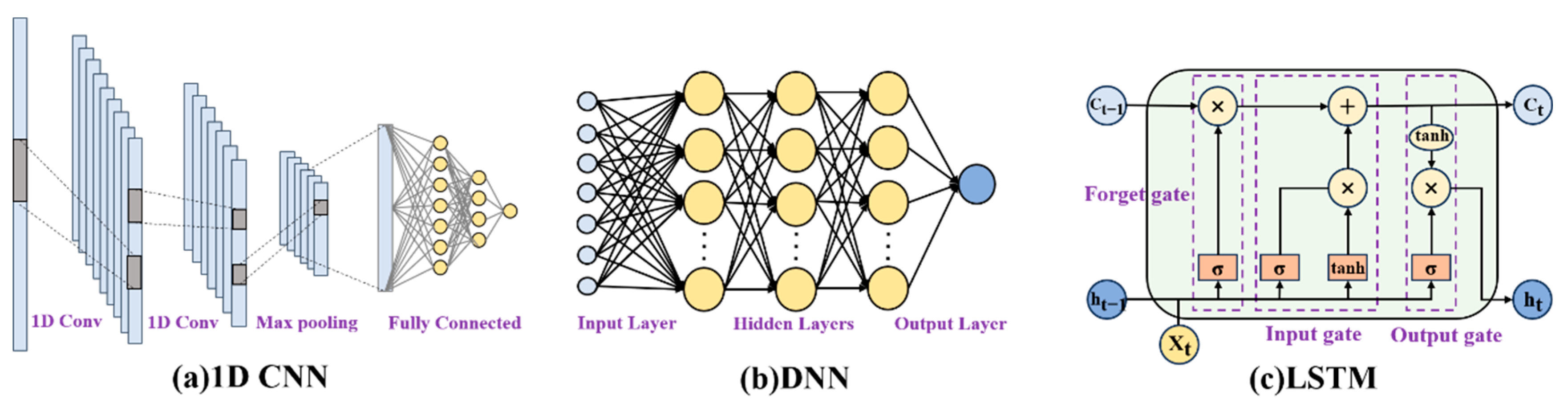
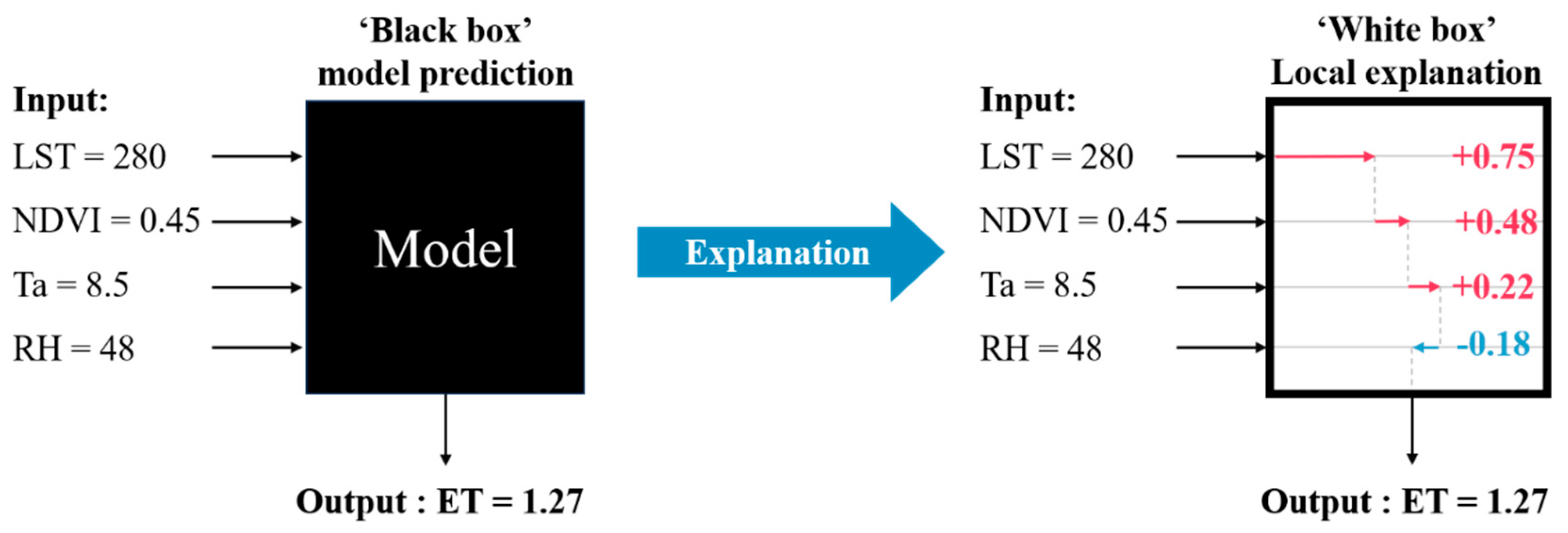

| Observation Item | Sensor | Observation Height (m) | Location |
|---|---|---|---|
| EC | CSAT3&EC155 | 4.5 | 35°8′12″N, 113°45′48″E |
| Sensible and latent flux | |||
| OMS (2019) | LAS Mk II&RPG-MWSC-160 | Transmitter 34 | 35°9′10.4″N, 113°48′3.5″E |
| Sensible and latent flux | Receiver 40 | 35°8′12″N, 113°45′48″E | |
| OMS (2023) | LAS Mk II&RPG-MWSC-160 | Transmitter 9 | 35°08′22″N, 113°45′35″E |
| Sensible and latent flux | Receiver 9 | 35°08′01″N, 113°46′11″E | |
| wind speed | 010C-1 | 3/5/10/20/30/40 | |
| wind direction | 020C-2 | 3/5/10/20/30/40 | |
| Air temperature and humidity | HMP155A | 3/5/10/20/30/40 | |
| four-component radiation | CNR4 | 4 | 35°8′12″N, 113°45′48″E |
| infrared temperature | SI-111 | 4.5 | |
| Soil heat flux | HFP01 | −0.15/−0.35/−0.55/−0.75/−0.95/−1.15 | |
| Precipitation | TE525MM | 10 | |
| Soil temperature | 109 | −0.15/−0.35/−0.55/−0.75/−0.95/−1.15 | |
| Soil water content | CS616 | −0.15/−0.35/−0.55/−0.75/−0.95/−1.15 |
| Methods/Observation | Urban-Agricultural Mixed Surface (2019) | Farmland Surface (2023) | ||||||
|---|---|---|---|---|---|---|---|---|
| R | Bias | MAE | RMSE | R | Bias | MAE | RMSE | |
| 1DCNN_all | 0.89 | −0.19 | 0.75 | 1.03 | 0.90 | −0.14 | 0.46 | 0.66 |
| 1DCNN_rs | 0.93 | −0.14 | 0.66 | 0.88 | 0.91 | −0.34 | 0.56 | 0.72 |
| DNN_all | 0.89 | −0.41 | 0.88 | 1.18 | 0.87 | −0.50 | 0.58 | 0.76 |
| DNN_rs | 0.94 | −0.25 | 0.70 | 0.96 | 0.89 | −0.41 | 0.59 | 0.75 |
| LSTM_all | 0.88 | −0.23 | 0.73 | 1.03 | 0.86 | −0.43 | 0.56 | 0.74 |
| LSTM_rs | 0.94 | −0.19 | 0.66 | 0.90 | 0.86 | −0.36 | 0.62 | 0.78 |
| RF_all | 0.91 | −0.12 | 0.70 | 0.95 | 0.90 | −0.35 | 0.48 | 0.68 |
| RF_rs | 0.91 | 0.01 | 0.77 | 0.97 | 0.87 | −0.37 | 0.56 | 0.75 |
| XGB_all | 0.88 | −0.05 | 0.72 | 1.00 | 0.88 | −0.33 | 0.52 | 0.70 |
| XGB_rs | 0.92 | −0.05 | 0.68 | 0.90 | 0.88 | −0.25 | 0.55 | 0.70 |
| ET_EC | 0.77 | −0.25 | 0.96 | 1.35 | - | - | - | - |
| Algorithm Type | Study Area | Description of Input Variables | Temporal and Spatial Resolution | RMSE | Verify | Reference |
|---|---|---|---|---|---|---|
| SVM | 25 AmeriFlux sites | LST, EVI, SWR, LC | 8 days, 8 km | 0.62 mm/d | EC | [27] |
| ANN | 28 AmeriFlux sites | LST, NDVI, NDWI, LAI, PAR, Ta, Ws, LC | daily, 4 km | 0.07–0.2 mm/d | EC | [90] |
| SVM | 13 flux towers temperate semi-arid grassland of China | NDVI, Srad, Rn, P30, RH, Ws, LST. | 8 days, 1 km | 0.50 mm/d (typical steppe) 0.35 mm/d (sandy grassland) | EC | [34] |
| MTE | 36 flux towers | Ta, Rs, RH, Prec, NDVI | monthly, 0.1° | 0.5 mm/d | EC | [91] |
| Regression-tree ensemble | 79 FLUXNET | Prec, Ta, NDVI, PAR | 15 days, 8 km | 0.72 mm/d | EC | [92] |
| ANN, Cubist, DBN, RF, SVM | 36 flux towers Heihe River Basin | Ta, Rs, RH, P30, LAI | daily, 1 km | 0.65–0.99 mm/d (RF) | LAS | [35] |
| ANN, RF, DBN | 11 flux towers Heihe River Basin | Rn, LST, NDVI, FVC | daily, 30 m | 0.27–0.77 mm/d | LAS | [31] |
| DNN | 19 EC flux towers | LC, topography, climate, sampling locations, MOD16, ET-SEMI, ET-JPL, ET-MS, ET-HF, GLEAM, ETMonitor, EB-ET | daily, 0.01° | 0.37 mm/d | EC | [30] |
| EA, ANN, SVM | 13 flux towers wetland ecosystems | LST, Emissivity, LAI, FPAR, EVI, Prec | 32 days, 1 km | 0.27–0.44 mm/d (EA) | EC | [28] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, P.; Han, Q.; Li, S.; Liu, H.; Li, C.; Ma, Y.; Wang, J. A Novel Framework Based on Data Fusion and Machine Learning for Upscaling Evapotranspiration from Flux Towers to the Regional Scale. Remote Sens. 2025, 17, 3813. https://doi.org/10.3390/rs17233813
Zhu P, Han Q, Li S, Liu H, Li C, Ma Y, Wang J. A Novel Framework Based on Data Fusion and Machine Learning for Upscaling Evapotranspiration from Flux Towers to the Regional Scale. Remote Sensing. 2025; 17(23):3813. https://doi.org/10.3390/rs17233813
Chicago/Turabian StyleZhu, Pengyuan, Qisheng Han, Shenglin Li, Hao Liu, Caixia Li, Yanchuan Ma, and Jinglei Wang. 2025. "A Novel Framework Based on Data Fusion and Machine Learning for Upscaling Evapotranspiration from Flux Towers to the Regional Scale" Remote Sensing 17, no. 23: 3813. https://doi.org/10.3390/rs17233813
APA StyleZhu, P., Han, Q., Li, S., Liu, H., Li, C., Ma, Y., & Wang, J. (2025). A Novel Framework Based on Data Fusion and Machine Learning for Upscaling Evapotranspiration from Flux Towers to the Regional Scale. Remote Sensing, 17(23), 3813. https://doi.org/10.3390/rs17233813








