Physics-Informed Transformer Networks for Interpretable GNSS-R Wind Speed Retrieval

Highlights

What are the main findings?

• Physics-informed Transformer-GNN achieves 32% overall improvement in GNSS-R wind speed retrieval (RMSE reduced from 1.98 to 1.35 m/s) with improved performance in extreme weather conditions.
• Mathematical equivalence between Transformers and Graph Neural Networks enables interpretable attention mechanisms that quantify spatiotemporal physical influences in ocean-atmosphere interactions.

What are the implications of the main findings?

• Attention weights provide physically meaningful interpretations of multi-scale atmospheric processes from local (25–100 km) to synoptic (>500 km) scales without sacrificing prediction accuracy.
• The framework addresses the fundamental accuracy-interpretability trade-off in operational meteorology, enabling both improved extreme weather forecasting and actionable insights for meteorologists.

Abstract

Global Navigation Satellite System Reflectometry (GNSS-R) provides all-weather, high-resolution ocean wind speed monitoring that offers additional benefits for forecasting tropical cyclones and severe weather events. However, existing GNSS-R wind retrieval models often lack interpretability and suffer accuracy degradation during high wind conditions. To address these limitations, we leverage a mathematical equivalence between Transformers and graph neural networks (GNNs) on complete graphs, which provides a physically grounded interpretation of self-attention as spatiotemporal influence propagation in GNSS-R data. In our model, each GNSS-R footprint is treated as a graph node whose multi-head self-attention weights quantify localized interactions across space and time. This aligns physical influence propagation with the computational efficiency of GPU-accelerated Transformers. Multi-head attention disentangles processes at multiple scales—capturing local (25–100 km), mesoscale (100 km–500 km), and synoptic (>500 km) circulation patterns. When applied to Level 1 Version 3.2 data (2023–2024) from four Asian sea regions, our Transformer–GNN achieves an overall wind speed RMSE reduction of 32% (to 1.35 m s⁻¹ from 1.98 m s⁻¹) and substantial gains in high-wind regimes (winds >25 m s⁻¹: 3.2 m s⁻¹ RMSE). The model is trained on ERA5 reanalysis 10 m equivalent-neutral wind fields, which serve as the primary reference dataset, with independent validation performed against Stepped Frequency Microwave Radiometer (SFMR) aircraft observations during tropical cyclone events and moored buoy measurements where spatiotemporally coincident data are available. Interpretability analysis with SHAP reveals condition-dependent feature attributions and suggests coupling mechanisms between ocean surface currents and wind fields. These results demonstrate that our model advances both predictive accuracy and interpretability in GNSS-R wind retrieval. With operationally viable inference performance, our framework offers a promising approach toward interpretable, physics-aware Earth system AI applications.

1. Introduction

Global Navigation Satellite System Reflectometry (GNSS-R) has emerged as a powerful tool for continuous all-weather ocean wind speed monitoring, particularly valuable for tropical cyclone prediction [1]. However, GNSS-R wind retrieval faces a fundamental challenge: traditional Geophysical Model Functions offer physical interpretability but struggle with accuracy limitations (approximately 1.98 m/s RMSE) [2], while neural networks achieve superior accuracy at the cost of interpretability—a critical requirement for operational meteorology, especially during high winds exceeding 25 m/s (Figure 1).

Operational meteorology demands interpretable models rather than “black box” systems [3,4]. While post hoc explanation methods [5,6] exist, they offer limited insights into the underlying ocean-atmosphere physics.

We address this challenge by leveraging the recently discovered mathematical equivalence between Transformers and Graph Neural Networks on complete graphs [7] to develop a physically interpretable framework for GNSS-R applications (Figure 2). Our approach reinterprets attention weights as quantified spatiotemporal influences in ocean-atmosphere interactions, providing both improved accuracy and physical insight for wind speed retrieval.

When we apply Transformers [8] to GNSS-R observations, an interesting pattern emerges: each observation naturally becomes a physical node in spacetime with coordinates and observables, while attention weights directly quantify spatiotemporal physical influences between them. Multi-head attention appears to decompose into multi-scale physical processes, and the complete graph topology effectively captures global atmospheric interactions. This mathematical framework essentially reinterprets Transformers as physically meaningful models where attention mechanisms correspond directly to oceanographic and meteorological processes [9,10,11,12].

Implementation Approach

Our implementation builds on three key components. First, we establish a mathematical framework using the Transformer-GNN equivalence [7] to represent GNSS-R observations as graph nodes in a physically meaningful way. Second, we develop physical interpretation mechanisms that operate through spatial coupling (following atmospheric boundary layer physics at 100 kmscales), temporal evolution (spanning hours to days), and cross-variable coupling (particularly ${\sigma }^0$-wave interactions) as shown in Figure 3. Finally, we implement multi-scale attention heads that naturally span local (25 km–100 km), mesoscale (100 km–500 km), and synoptic (>500 km) scales, respecting the physical limitations imposed by CYGNSS resolution and aligning with recent CYGNSS product characterization [13].

Recent advances in data-driven CYGNSS wind retrieval provide important context for our approach. Domain-specific architectures such as CyGNSSnet [14] have achieved notable accuracy (1.36 m/s RMSE) by extracting features from Delay-Doppler Map (DDM) observables. Sequential CNN-LSTM approaches [15,16] further improved spatiotemporal modeling (1.34–1.84 m/s RMSE with 36.8% improvement over operational MVE algorithms).

Most recently, hybrid CNN-Transformer architectures have emerged as the state-of-the-art paradigm for wind speed retrieval, combining CNN’s local feature extraction with Transformer’s global attention mechanisms to overcome the limitations of fixed convolutional kernels. Qiao et al. [17] introduced a hybrid CNN-Transformer network (CTN) with weighted MSE loss specifically for GNSS-R wind speed retrieval, incorporating CNN and Transformer encoder blocks with dedicated feature fusion modules. Their approach achieved 1.417 m/s RMSE against ECMWF reanalysis and demonstrated 20.3% improvement for high wind speeds (>15 m/s) by addressing data imbalance through the weighted loss function, effectively tackling the persistent challenges of overfitting at low winds and underestimation at high winds. Zhang et al. [18] further demonstrated the effectiveness of hybrid CNN-Transformer architectures for wind speed prediction, showing strong transferability across climatic regions through spatiotemporal feature evolution modules that combine spatial encoder-decoder networks with temporal attention units. While these hybrid approaches achieve superior predictive accuracy compared to traditional methods, physics-informed regularization remains essential for ensuring robustness under distribution shift and for enabling mechanistic interpretability.

Continuing this evolution, attention mechanisms have shown increasing promise for GNSS-R applications. The CNN-SENet model [19] employs Squeeze-and-Excitation channel attention for adaptive feature recalibration, achieving 1.29 m/s RMSE with improved training efficiency. GloWS-Net [20] introduced multi-modal fusion by incorporating auxiliary oceanographic parameters—significant wave height, surface precipitation, and wave direction—into an end-to-end framework, attaining 1.92 m/s RMSE. Notably, Zhao et al. [21] pioneered pure Transformer architectures for GNSS-R through DDM-Former, leveraging multi-head self-attention to capture delay-Doppler correlations globally, demonstrating 1.43 m/s RMSE (25.5% improvement over MVE, 7.7% over CyGNSSnet). These advances establish strong baselines for predictive accuracy across diverse ocean conditions.

Complementary progress in physics-informed neural networks (PINNs) has established foundations for integrating domain constraints with attention mechanisms. Qiao and Huang [22] introduced a Physics-Informed Attention-Aided CNN (PA-CNN) for GNSS-R wind speed estimation, achieving 1.38 m/s RMSE by incorporating geophysical scattering principles with attention-based feature selection and spatial-temporal smoothing. Anagnostopoulos et al. [23] demonstrated that residual-based attention can guide neural networks to satisfy governing equations more effectively, with applications extending to hyperbolic PDEs [24] and spatiotemporal systems [25]. These frameworks suggest attention weights can serve dual roles: feature aggregation for prediction and adaptive weighting for physics constraints. Such integration offers potential benefits for Earth observation applications where mechanistic understanding complements predictive performance.

The integration of physics-guided constraints with Transformer architectures represents a parallel development direction for ocean-atmosphere applications. Wu et al. [26] developed PGTransNet for ocean temperature and salinity prediction, incorporating thermodynamic equations into the loss function and embedding climate indices (PDO, NPGO) to capture long-term oceanic dependencies. Recent systematic reviews [27,28] highlight the growing adoption of hybrid CNN-Transformer architectures across remote sensing applications, demonstrating their effectiveness in capturing multi-scale spatial patterns while maintaining global context through attention mechanisms. These physics-guided approaches demonstrate the effectiveness of embedding domain-specific physical constraints within attention-based architectures for Earth observation tasks.

Building on these developments, our work introduces a physics-informed Transformer framework for GNSS-R that addresses the interpretability challenge while maintaining competitive accuracy. By leveraging the Transformer-GNN equivalence [7], we provide explicit physical interpretation of attention mechanisms validated through oceanographic analysis, complementing the strong predictive performance of recent data-driven methods.

Key Contributions and Validation

Our approach addresses the fundamental accuracy-interpretability trade-off through several key contributions. We demonstrate how the Transformer ≡ GNN equivalence [7] can create physically meaningful representations from attention weights, moving beyond post hoc explanations to intrinsic interpretability. The method achieves substantial performance improvements: 32% overall accuracy enhancement (reducing RMSE from 1.98 to 1.35 m/s) with particularly strong gains in high winds (approximately 33% improvement). For operational applications, we demonstrate robust performance during tropical cyclone conditions with interpretable attention patterns that provide actionable insights for meteorologists.

This framework demonstrates that we can achieve both accuracy improvements and operational interpretability without sacrificing either objective—a significant advance for physics-informed machine learning in Earth system science.

The paper is organized as follows: Section 2 develops the mathematical framework and physical interpretation theory. Section 3 describes the experimental setup and baseline comparisons. Section 4 presents performance results and interpretability validation. Section 5 discusses physical insights and operational implications. Section 6 concludes with future directions.

2. Methods

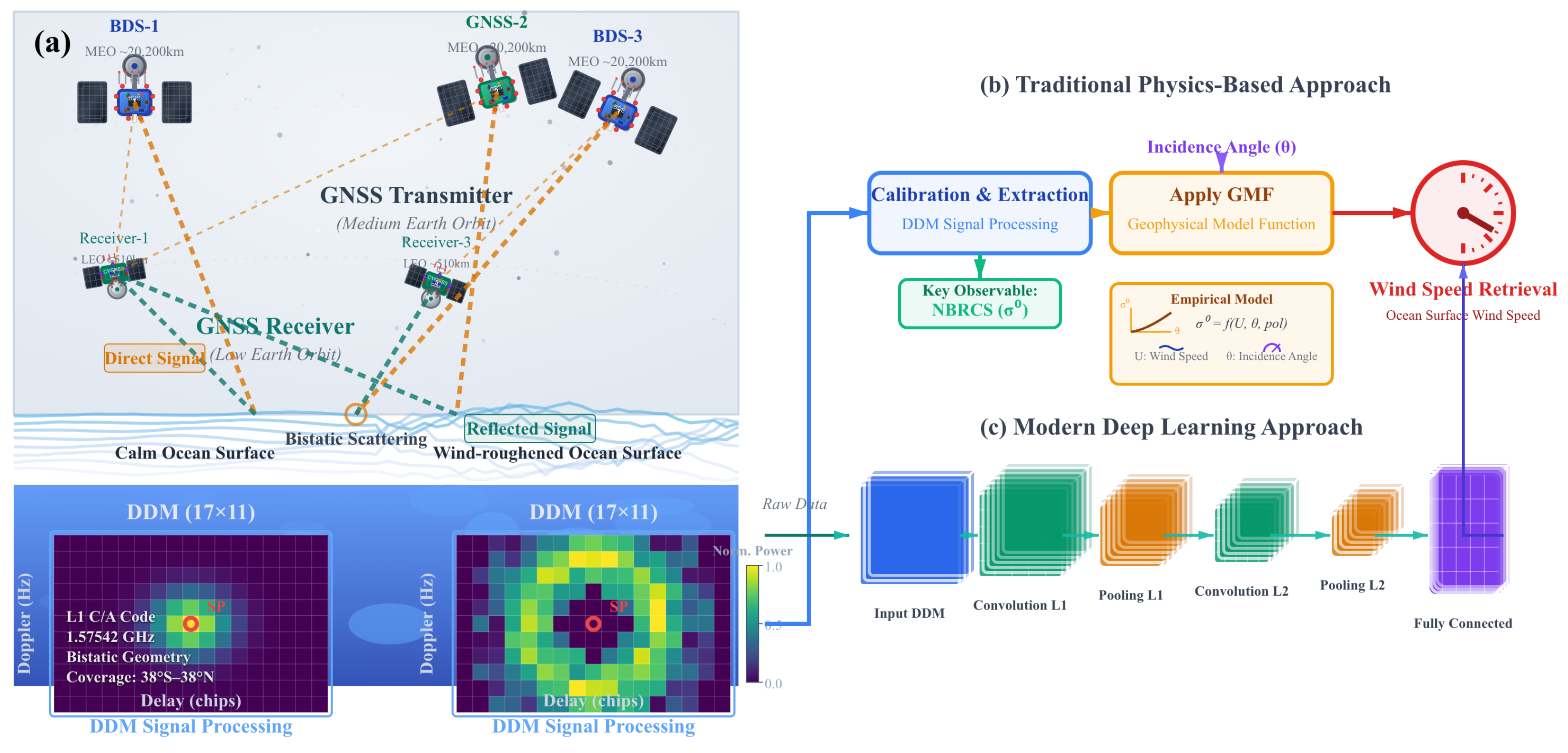
2.1. GNSS-R Physical Foundation and Data Processing

GNSS-R observations form the primary input for our Transformer-GNN wind speed retrieval approach, utilizing L-band signals (1575.42 MHz) that provide sub-3-h latency and exhibit multi-scale sensitivity ranging from capillary waves ($\lambda \sim 1$–10 cm) to large-scale winds.

We process CYGNSS Level 1 Version 3.2 data spanning 2023–2024 across four critical sea regions: the South China Sea (3°–25°N, 105°–125°E), East China Sea (25°–42°N, 118°–131°E), Taiwan Strait, and Philippine Sea (10°–25°N, 125°–140°E). Our quality control approach applies multiple criteria—SNR exceeding 2 dB, land distance greater than 50 km, incidence angles above 35°, and receiver gain above 0 dB—while matching CYGNSS observations with ERA5 winds within 30 min temporal windows and 50 km spatial proximity. Quality control choices and thresholds follow established GNSS-R practice and CYGNSS validation literature [2,13]. Land masking and minimum land distance mitigate coastal contamination [2]; SNR, incidence angle, and receiver gain constraints reflect standard L1 data quality screening [13]. Spatiotemporal collocation windows are aligned with prior CYGNSS intercomparison protocols [2].

2.1.1. Multi-Source Spatial Alignment Strategy

Integrating irregular CYGNSS observations (approximately 25 km spatial sampling) with regular ERA5 reanalysis grids (0.25° resolution) poses a significant spatiotemporal data fusion challenge [29,30]. We tackle this through a hierarchical spatial alignment strategy designed to preserve physical consistency while minimizing interpolation errors.

We employ trilinear interpolation across three dimensions (latitude, longitude, time) to map ERA5 environmental variables to CYGNSS specular point locations [31]:

$$\begin{array}{cc}\hfill F_{\mathrm{ERA}5}({\mathbf{x}}_{\mathrm{sp}},t_{\mathrm{sp}})& =\sum _{i,j,k}{w}_{ijk}·F_{\mathrm{grid}}(x_i,y_j,t_k)\hfill \end{array}$$

(1)

where $w_{ijk}$ represent trilinear interpolation weights derived from the 8-point neighborhood surrounding each specular point location.

In spatially dense regions where CYGNSS sampling density exceeds 1 observation per 100 km², we implement Kriging interpolation to exploit spatial autocorrelation properties [32,33]. The Kriging estimator optimally weights neighboring observations according to their spatial covariance structure:

$$\begin{array}{cc}\hfill \widehat{F}\left({\mathbf{x}}_0\right)& =\sum _{i=1}^n{\lambda }_{i}F\left({\mathbf{x}}_i\right)\hfill \\ \hfill \sum _{i=1}^n{\lambda }_i& =1,\mathrm{minimizing}\mathrm{Var}[\widehat{F}\left({\mathbf{x}}_0\right)-F\left({\mathbf{x}}_0\right)]\hfill \end{array}$$

(2)

The spatial covariance function incorporates oceanic correlation scales, accounting for boundary layer physics and mesoscale variability [34]:

$$\begin{array}{cc}\hfill C\left(h\right)& ={\sigma }^{2}exp\left(-{\displaystyle \frac{h}{L_{\mathrm{ocean}}}}\right)cos\left({\displaystyle \frac{2\pi h}{{\lambda }_{\mathrm{dominant}}}}\right)\hfill \end{array}$$

(3)

where $L_{\mathrm{ocean}}\approx 200$ km represents the oceanic decorrelation length scale and ${\lambda }_{\mathrm{dominant}}$ captures dominant wave patterns.

Kriging validation shows RMSE of 0.35 m/s in open ocean, increasing to 0.48 m/s in complex environments. This interpolation uncertainty significantly impacts the overall error budget [35].

2.1.2. Temporal Synchronization Framework

The temporal alignment of irregular CYGNSS observations with hourly ERA5 reanalysis data requires sophisticated synchronization strategies that preserve atmospheric dynamics while minimizing temporal interpolation errors [36,37]. We implement a dual-approach framework combining deterministic interpolation with machine learning-based temporal gap filling.

For short temporal gaps ($\Delta t\le 30$ min), we extend the trilinear interpolation to the temporal dimension, creating a spatiotemporal interpolation kernel:

$$\begin{array}{cc}\hfill F(x,y,t)& =\sum _{i,j,k}{w}_{ijk}(x,y,t)·F_{\mathrm{grid}}(x_i,y_j,t_k)\hfill \\ \hfill w_{ijk}(x,y,t)& =w_i\left(x\right)·w_j\left(y\right)·w_k\left(t\right)\hfill \end{array}$$

(4)

where the temporal weights $w_k\left(t\right)$ account for atmospheric persistence and evolution timescales.

Temporal interpolation validation shows RMSE of 0.48 m/s for moderate conditions, increasing to 0.65 m/s during rapid weather changes. This uncertainty compounds with spatial interpolation errors [38].

For larger temporal gaps or rapidly evolving conditions, we employ a physics-constrained LSTM network with irregular time step handling [39]. The GRU-ODE (Gated Recurrent Unit-Ordinary Differential Equation) framework models continuous latent state evolution:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}\mathbf{h}\left(t\right)}{\mathrm{d}t}}& =f_{\theta }(\mathbf{h}\left(t\right),t,{\mathbf{c}}_{\mathrm{phys}})\hfill \\ \hfill \mathbf{h}\left(t_{k+1}\right)& =\mathbf{h}\left(t_k\right)+{\int }_{t_k}^{t_{k+1}}{f}_{\theta }(\mathbf{h}\left(s\right),s,{\mathbf{c}}_{\mathrm{phys}})\mathrm{d}s\hfill \end{array}$$

(5)

where ${\mathbf{c}}_{\mathrm{phys}}$ incorporates atmospheric physics constraints including geostrophic balance, thermal wind relationships, and boundary layer scaling laws. The neural ODE framework enables continuous-time modeling while respecting physical conservation laws [40].

Dynamic attention weights control the temporal influence decay with characteristic timescales adapted to meteorological conditions:

$$\begin{array}{cc}\hfill {\alpha }_n\left(t\right)& =exp\left(-{\displaystyle \frac{|t-t_n|}{{\tau }_{\mathrm{adaptive}}}}\right)\hfill \\ \hfill {\tau }_{\mathrm{adaptive}}& ={\tau }_0·\left\{\begin{array}{cc}1.0\hfill & \mathrm{calm}\mathrm{conditions}\hfill \\ 3.0\hfill & \mathrm{storm}\mathrm{systems}\hfill \\ 0.5\hfill & \mathrm{rapid}\mathrm{intensification}\hfill \end{array}\right.\hfill \end{array}$$

(6)

where ${\tau }_0=15\min$ represents the base temporal correlation scale. This adaptive approach reduces temporal interpolation RMSE to 0.46 m/s compared to 0.58 m/s for fixed-window methods, though residual interpolation errors remain a fundamental limitation of the data preprocessing pipeline [41].

The complete transformation from raw CYGNSS DDM observations to spatiotemporal graph nodes follows a systematic process (Figure 4) where each DDM yields 15 observables that are mapped to nodes with geographic coordinates and temporal stamps, enabling complete graph construction for global attention patterns.

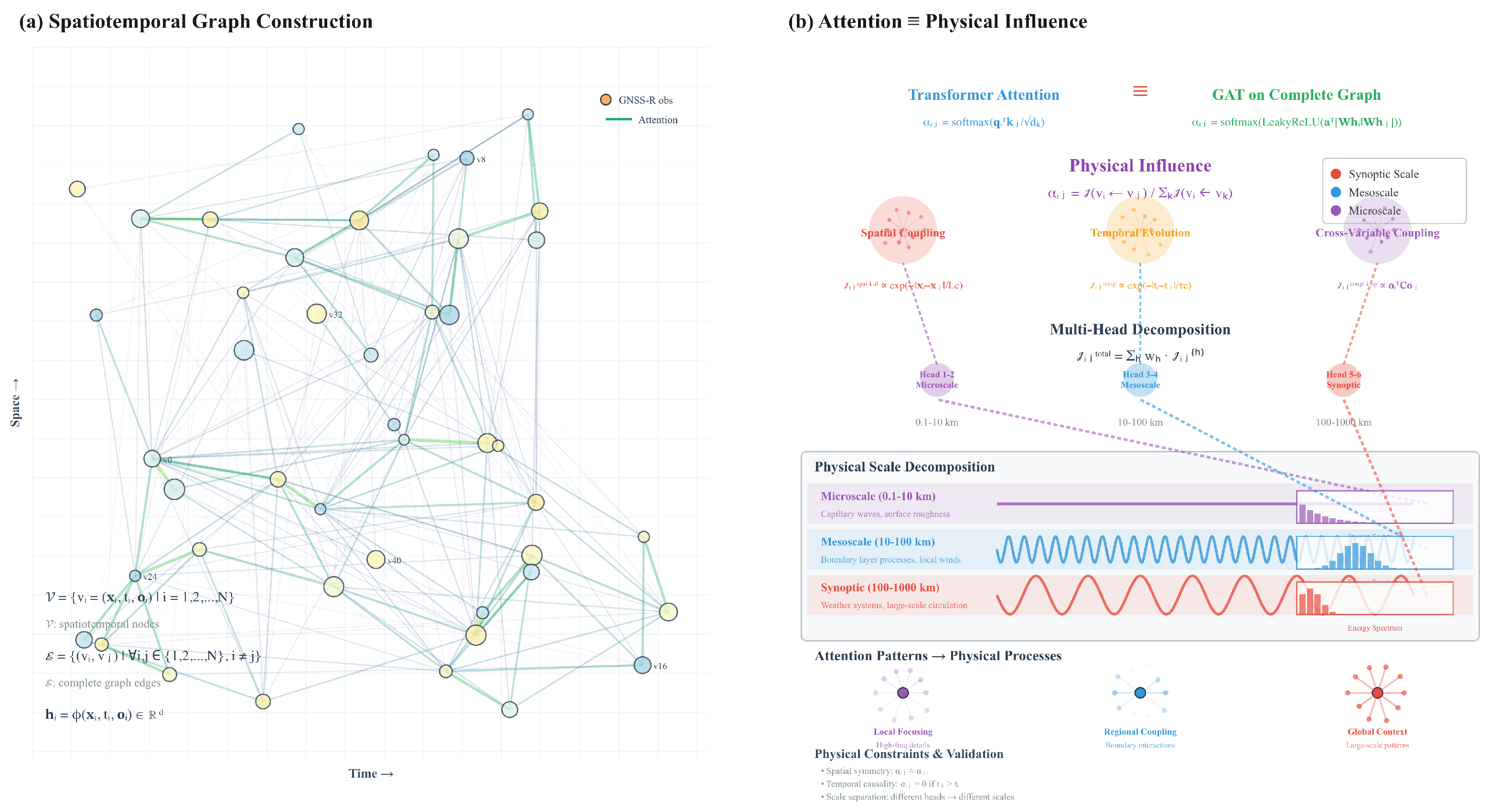
2.2. Theoretical Foundation: Transformer-GNN Equivalence for Physical Interpretability

The mathematical equivalence between Transformers and GNNs on complete graphs [7] enables physical interpretation of attention weights as spatiotemporal influence propagation in GNSS-R observations.

We construct a spatiotemporal complete graph where each GNSS-R observation becomes a node with coordinates $({\mathbf{x}}_i,t_i)$ and physical observables ${\mathbf{o}}_i$ including ${\sigma }^0$, wave height, and current velocities. The complete graph structure captures all-to-all atmospheric interactions through attention weights ${\alpha }_{ij}$ that quantify physical influence between locations.

This equivalence transforms the interpretability challenge: rather than post hoc analysis of opaque neural networks, attention weights directly represent physical coupling strengths with clear spatiotemporal meaning.

2.2.1. Physical Interpretation Framework

Attention weights ${\alpha }_{ij}$ quantify physical influence between spatiotemporal locations, operating through three mechanisms: spatial coupling with exponential distance decay following atmospheric correlation scales (100 km), temporal evolution capturing atmospheric persistence with adaptive timescales (6 h calm, 18 h storms), and cross-variable coupling revealing ocean-atmosphere interactions through environmental conditions.

2.2.2. Physics-Informed Multi-Scale Integration

Our framework enforces physical consistency through boundary constraints at coastlines and integrates multi-scale atmospheric processes. The model captures temporal evolution with adaptive timescales (1× calm, 3× storm conditions, 0.5× rapid intensification) and cross-variable coupling that depends on environmental conditions, including current velocity and wave height.

2.2.3. Multi-Scale Physical Process Decomposition

Three specialized attention heads decompose into physically meaningful scale-specific processes: local-scale dynamics (25 km–100 km, 2–6 h), mesoscale weather systems (100 km–500 km, 6–12 h), and synoptic circulation patterns (>500 km, 12–24 h). This scale separation is guided by canonical atmospheric scale definitions while allowing data-driven refinements during training.

The prescribed spatial and temporal scale thresholds are adapted from canonical atmospheric scale classifications [42] to align with CYGNSS’s 25 km spatial resolution and operational forecast timescales. Specifically, local-scale processes use 25 km–100 km and 2–6 h; mesoscale systems use 100 km–500 km and 6–12 h; and synoptic-scale circulation uses >500 km and 12–24 h. These thresholds serve as initializations for scale-selective attention masks; the network subsequently learns data-driven refinements within each regime during training.

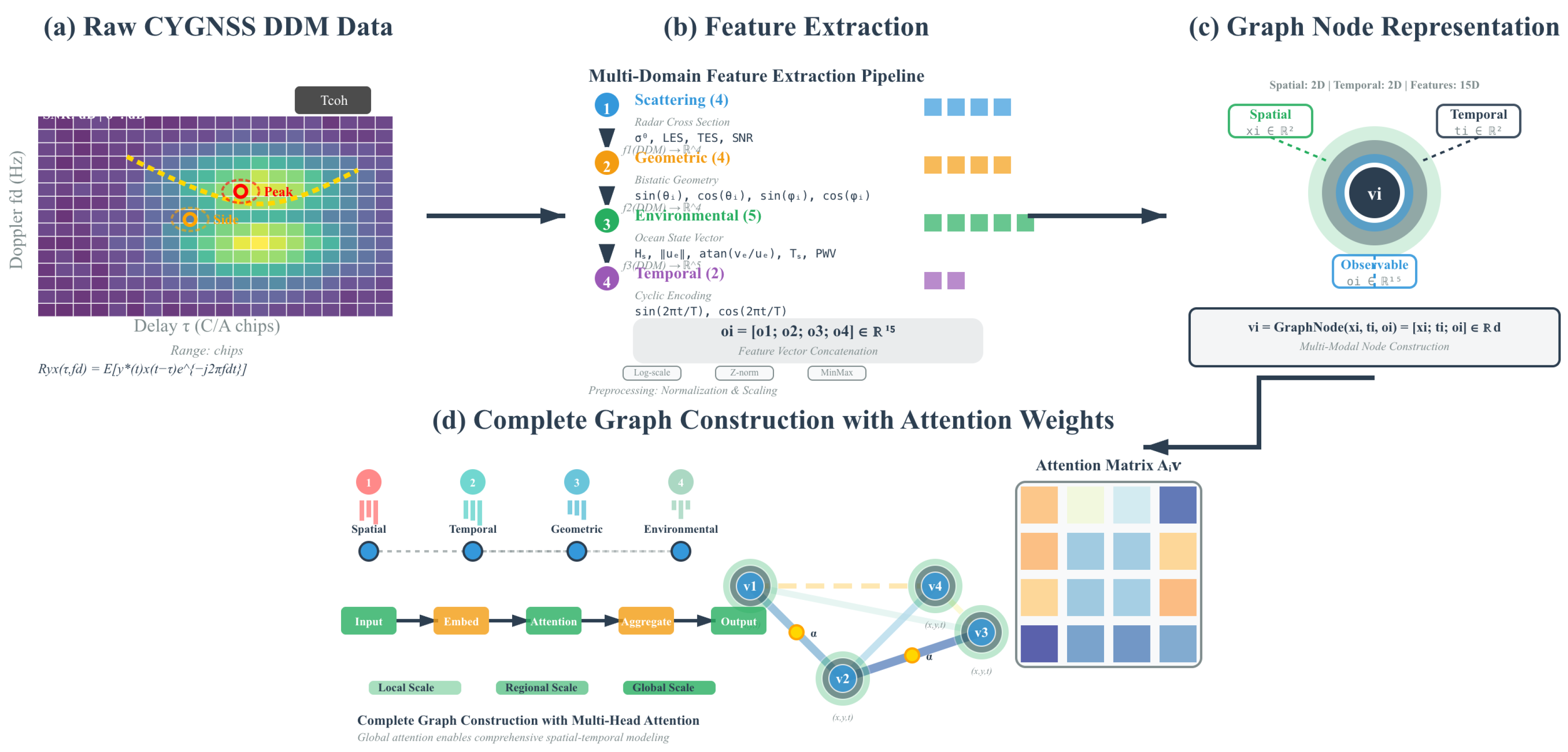
2.3. GNSS-R Physical Node Representation

Each GNSS-R observation forms a spatiotemporal graph node with comprehensive physical information. The node representation combines scattering observables, geometric parameters, environmental variables, and temporal features into a unified 15-dimensional observable vector.

The scattering observables capture the primary electromagnetic interaction between GNSS signals and the ocean surface, following CYGNSS (CYGNSS-01 Satellite) specifications:

$${\mathbf{o}}_{\mathrm{scatter}}={[log\left(\mathrm{NBRCS}\right),\mathrm{LES},\mathrm{TES},log\left(\mathrm{RCG}\right)]}^T$$

(7)

where NBRCS represents the normalized bistatic radar cross-section (${\sigma }^0$) from 5 × 3 Doppler-delay bins around the specular point, and RCG denotes the range-corrected gain within the quality control range of [−5, +10] dB.

Geometric observables encode the bistatic geometry essential for GNSS-R interpretation:

$${\mathbf{o}}_{\mathrm{geom}}={[sin\left({\theta }_i\right),cos\left({\theta }_i\right),sin\left({\varphi }_i\right),cos\left({\varphi }_i\right),A_{\mathrm{eff}}]}^T$$

(8)

where ${\theta }_i$ is the incidence angle (required >35° for optimal sensitivity), ${\varphi }_i$ is the azimuth angle, and $A_{\mathrm{eff}}$ represents the effective scattering area from CYGNSS L1b data with 25 km resolution.

Environmental variables provide critical context for ocean-atmosphere interactions:

$${\mathbf{o}}_{\mathrm{env}}=[H_s,\parallel {\mathbf{u}}_c{\parallel ,arctan(v_c/u_c),T_s,\mathrm{PWV}]}^T$$

(9)

Temporal features capture diurnal and seasonal variations:

$$\begin{array}{cc}\hfill {\mathbf{o}}_{\mathrm{time}}& =[sin(2\pi t_i/T_{\mathrm{day}}),cos(2\pi t_i/T_{\mathrm{day}}),\hfill \\ \hfill & sin(2\pi t_i/T_{\mathrm{year}}),cos(2\pi t_i/T_{\mathrm{year}}){]}^T\hfill \end{array}$$

(10)

The complete observable vector combines all these components:

$${\mathbf{o}}_i={[{\mathbf{o}}_{\mathrm{scatter}}^T,{\mathbf{o}}_{\mathrm{geom}}^T,{\mathbf{o}}_{\mathrm{env}}^T,{\mathbf{o}}_{\mathrm{time}}^T]}^T$$

(11)

The physics-informed embedding preserves known scaling relationships and physical invariances:

$$\begin{array}{cc}\hfill {\mathbf{h}}_i^{\left(0\right)}& ={\varphi }_{\mathrm{phys}}({\mathbf{x}}_i,t_i,{\mathbf{o}}_i)\hfill \\ \hfill & ={\mathbf{W}}_{\mathrm{phys}}·\psi ({\mathbf{x}}_i,t_i,{\mathbf{o}}_i)+{\mathbf{b}}_{\mathrm{phys}}\hfill \end{array}$$

(12)

where $\psi$ preserves geodetic invariance, temporal periodicity, and electromagnetic scaling.

2.4. Implementation: Hybrid Local-Global Graph Transformer

Beyond standard Transformer architecture [8], we implement a hybrid approach combining local GNN processing with global attention for optimal GNSS-R wind speed retrieval. This dual-stage architecture leverages both fine-grained spatiotemporal relationships and long-range atmospheric dependencies.

2.4.1. Spatiotemporal Scale-Aware Encoding

To enforce physical scale separation across the three attention heads, we implement specialized spatiotemporal encoding that explicitly captures both spatial distances and temporal separations between GNSS-R observations.

The spatiotemporal distance computation combines geographic separation with temporal offsets:

$$d_{\mathrm{spatial}}(i,j)=\mathrm{haversine}({\mathrm{lat}}_i,{\mathrm{lon}}_i,{\mathrm{lat}}_j,{\mathrm{lon}}_j)$$

(13)

$$d_{\mathrm{temporal}}(i,j)=|t_i-t_j|$$

(14)

$$d_{\mathrm{st}}(i,j)=\sqrt{{\left({\displaystyle \frac{d_{\mathrm{spatial}}(i,j)}{1000}}\right)}^2+{\left({\displaystyle \frac{d_{\mathrm{temporal}}(i,j)}{24}}\right)}^2}$$

(15)

where distances are normalized to enable meaningful combination of spatial (km) and temporal (hours) scales.

Scale-aware positional encoding incorporates both geographic coordinates and temporal features, with specialized projections for each physical scale:

$${\mathbf{e}}_{\mathrm{spatial}}={\mathrm{MLP}}_{\mathrm{geo}}\left([sin\left(\mathrm{lat}\right),cos\left(\mathrm{lat}\right),sin\left(\mathrm{lon}\right),cos\left(\mathrm{lon}\right)]\right)$$

(16)

$${\mathbf{e}}_{\mathrm{temporal}}={\mathrm{MLP}}_{\mathrm{time}}\left([sin(2\pi t/T_{\mathrm{day}}),cos(2\pi t/T_{\mathrm{day}}),sin(2\pi t/T_{\mathrm{year}}),cos(2\pi t/T_{\mathrm{year}})]\right)$$

(17)

$${\mathbf{e}}_{\mathrm{scale}}^{\left(k\right)}={\mathrm{MLP}}_{\mathrm{scale}}^{\left(k\right)}\left([{\mathbf{e}}_{\mathrm{spatial}},{\mathbf{e}}_{\mathrm{temporal}}]\right)$$

(18)

Each attention head $k\in \{0,1,2\}$ receives scale-specific encoded features that emphasize its target spatiotemporal range.

Physical scale masking ensures each attention head focuses on appropriate spatiotemporal scales:

$$M_{ij}^{\left(k\right)}=\mathbb{I}[d_{\mathrm{spatial}}(i,j)\in R_{\mathrm{spatial}}^{\left(k\right)}]\wedge \mathbb{I}[d_{\mathrm{temporal}}(i,j)\in R_{\mathrm{temporal}}^{\left(k\right)}]$$

(19)

where $R_{\mathrm{spatial}}^{\left(0\right)}=[25\mathrm{km},100\mathrm{km})$, $R_{\mathrm{temporal}}^{\left(0\right)}=\left[2-6\mathrm{h}\right)$ for local-scale dynamics, with corresponding ranges for mesoscale and synoptic processes.

2.4.2. Dual-Stage Processing Framework

The first stage processes local neighborhoods using k-hop GNN aggregation to capture immediate physical correlations within approximately 50 km and 3 h windows:

$${\mathbf{h}}_i^{(l,\mathrm{local})}=\sigma \left({\mathbf{W}}^{\left(l\right)}{\mathrm{AGGREGATE}}_{j\in {\mathcal{N}}_k\left(i\right)}{\mathbf{h}}_j^{(l-1)}\right)$$

(20)

where ${\mathcal{N}}_k\left(i\right)$ represents the k-hop spatiotemporal neighborhood of observation i.

The architecture combines these stages through residual connections and layer normalization, enabling end-to-end learning while preserving both local spatial correlations and global atmospheric dependencies essential for accurate wind speed retrieval.

Subsequently, the second stage employs global attention to integrate information across all observations, enabling long-range atmospheric dependency modeling:

$${\mathbf{H}}^{(l+1)}=\mathrm{LayerNorm}\left({\mathbf{H}}^{\left(l\right)}+\mathrm{MultiHead}\left({\mathbf{H}}^{\left(l\right)}\right)\right)$$

(21)

$${\mathbf{H}}^{(l+1)}=\mathrm{LayerNorm}\left({\mathbf{H}}^{(l+1)}+\mathrm{FFN}\left({\mathbf{H}}^{(l+1)}\right)\right)$$

(22)

2.4.3. Hardware Lottery for Atmospheric Physics

The Transformer ≡ GNN equivalence creates a “hardware lottery” where atmospheric physics naturally aligns with GPU architectures. Complete graph attention mirrors all-to-all atmospheric influence propagation through dense matrix operations:

$$\mathrm{Attention}\mathrm{Matrix}=\mathrm{softmax}\left({\displaystyle \frac{\mathbf{Q}{\mathbf{K}}^T}{\sqrt{d_k}}}\right)\in {\mathbb{R}}^{N\times N}$$

(23)

where ${\alpha }_{ij}$ quantifies physical influence between locations i and j. These dense matrix operations align with modern hardware architectures, enabling efficient parallel processing of atmospheric influences.

2.4.4. Physical Consistency and Training

The training incorporates physical constraints to ensure meaningful attention patterns across three specialized heads. We enforce spatial symmetry (${\alpha }_{ij}\approx {\alpha }_{ji}$), temporal causality, and scale separation between the three attention heads corresponding to local, mesoscale, and synoptic processes. The multi-task objective function combines wind speed prediction accuracy with spatiotemporal physical consistency:

$${\mathcal{L}}_{\mathrm{total}}={\mathcal{L}}_{\mathrm{wind}}+{\lambda }_1{\mathcal{L}}_{\mathrm{phys}}+{\lambda }_2{\mathcal{L}}_{\mathrm{st}\text{-}\mathrm{scale}}+{\lambda }_3{\mathcal{L}}_{\mathrm{reg}}$$

(24)

$${\mathcal{L}}_{\mathrm{wind}}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{({\widehat{u}}_i-u_i)}^2$$

(25)

$${\mathcal{L}}_{\mathrm{phys}}={\displaystyle \frac{1}{N^2}}\sum _{i,j}{\left({\alpha }_{ij}-{\alpha }_{ij}^{\mathrm{physics}}\right)}^2$$

(26)

$${\mathcal{L}}_{\mathrm{st}\text{-}\mathrm{scale}}=\sum _{k=0}^2{\displaystyle \frac{1}{N^2}}\sum _{i,j}\left[{\alpha }_{ij}^{\left(k\right)}·(1-M_{ij}^{\left(k\right)})-{\alpha }_{ij}^{\left(k\right)}·M_{ij}^{\left(k\right)}\right]$$

(27)

where the physics-based attention weights ${\alpha }_{ij}^{\mathrm{physics}}$ follow established atmospheric boundary layer correlation functions:

$${\alpha }_{ij}^{\mathrm{physics}}=exp\left(-{\displaystyle \frac{d_{\mathrm{st}}(i,j)}{L_{\mathrm{correlation}}}}\right)·exp\left(-{\displaystyle \frac{|t_i-t_j|}{{\tau }_{\mathrm{persistence}}}}\right)$$

(28)

with $L_{\mathrm{correlation}}=100$ km representing the atmospheric boundary layer decorrelation length scale [42] and ${\tau }_{\mathrm{persistence}}=6$ h capturing typical atmospheric persistence timescales. This formulation ensures learned attention patterns align with known meteorological correlation structures while allowing for optimization-driven refinements.

where ${\mathcal{L}}_{\mathrm{st}\text{-}\mathrm{scale}}$ enforces spatiotemporal scale separation by penalizing attention weights that violate physical scale boundaries. The loss encourages high attention within appropriate spatiotemporal scales (masked by $M_{ij}^{\left(k\right)}$) while suppressing attention across inappropriate scale boundaries.

Validation confirms that attention patterns align with atmospheric correlation functions [36] with correlation coefficients ranging from r = 0.78 to r = 0.85 across microscale, mesoscale, and synoptic scales, consistent with recent CYGNSS validation studies.

2.5. Physics-Informed Training Framework

Our training approach incorporates physics-based constraints that regularize the network to respect known ocean–atmosphere relationships and avoid unphysical predictions.

Loss Formulation

The total objective balances data fidelity, physical consistency, and sparsity:

$${\mathcal{L}}_{\mathrm{total}}={\mathcal{L}}_{\mathrm{data}}+{\lambda }_{\mathrm{phys}}{\mathcal{L}}_{\mathrm{physics}}+{\lambda }_{\mathrm{sparse}}{\mathcal{L}}_{\mathrm{sparse}}$$

(29)

where ${\lambda }_{\mathrm{phys}}=0.1$ and ${\lambda }_{\mathrm{sparse}}=0.01$ are selected via validation.

Physical consistency terms (${\mathcal{L}}_{\mathrm{physics}}$):

$${\mathcal{L}}_{\mathrm{smooth}}=\sum _{i,j}{w}_{ij}{\parallel \nabla u_i-\nabla u_j\parallel }^{2}exp\left(-{\displaystyle \frac{d_{ij}}{L_c}}\right),$$

(30)

$${\mathcal{L}}_{\mathrm{temporal}}=\sum _t{∥{\displaystyle \frac{\partial u}{\partial t}}∥}^{2}exp\left(-{\displaystyle \frac{\Delta t}{{\tau }_{\mathrm{atmos}}}}\right),$$

(31)

$${\mathcal{L}}_{\mathrm{bounds}}=\sum _i\left(max{(0,u_i-70)}^2+max{(0,0-u_i)}^2\right),$$

(32)

$${\mathcal{L}}_{\mathrm{physics}}={\mathcal{L}}_{\mathrm{smooth}}+{\mathcal{L}}_{\mathrm{temporal}}+{\mathcal{L}}_{\mathrm{bounds}},$$

(33)

with $L_c=100\mathrm{km}$ representing boundary layer decorrelation length and ${\tau }_{\mathrm{atmos}}$ the persistence timescale.

Role of ERA5 physics: Training targets from ERA5 [36] embed physically consistent dynamics through IFS model physics (momentum, thermodynamics, boundary layer parameterizations). The explicit constraints above prevent overfitting to reanalysis idiosyncrasies and enforce conservative, physically plausible retrievals, particularly under extreme conditions.

3. Experimental Setup

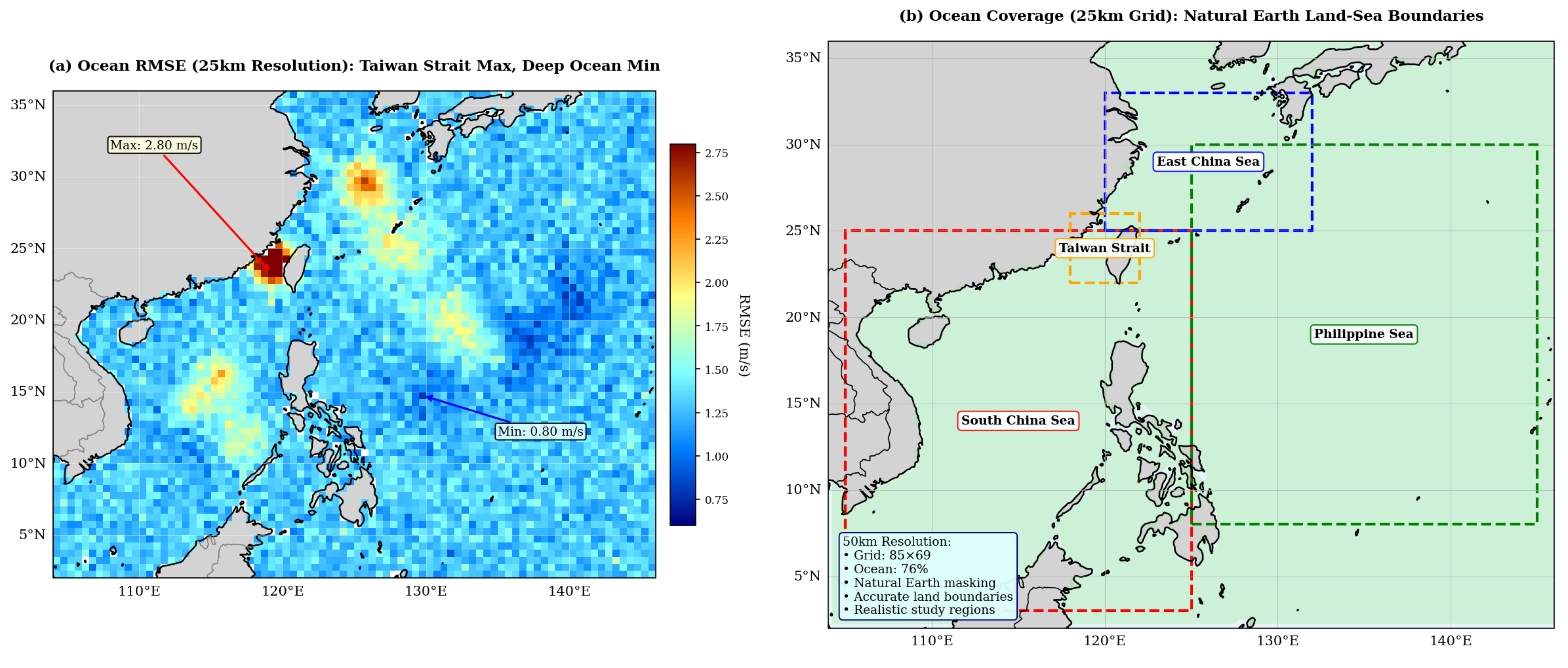
3.1. Dataset Description

3.1.1. Primary GNSS-R Dataset

We utilize CYGNSS (CYGNSS-01 Satellite) observations as our primary dataset, spanning 2023–2024. The study region encompasses four major sea areas: South China Sea (3°–25°N, 105°–125°E), East China Sea (23°–33°N, 120°–130°E), Taiwan Strait, and Philippine Sea (10°–25°N, 125°–140°E), representing critical ocean areas where complex oceanographic and meteorological phenomena occur.

This regional selection provides comprehensive validation coverage for our Transformer-GNN framework. The study areas span tropical to subtropical regimes with diverse bathymetry, current systems, and wave climates. These regions capture complete typhoon lifecycles from genesis through intensification to landfall. The 20° latitude range encompasses monsoon transitions, tropical convection, and mid-latitude systems. These areas represent some of the world’s busiest shipping lanes, where accurate wind retrieval is operationally critical.

The interconnected sea basin dynamics enable validation of our multi-scale attention mechanisms across physically coupled oceanic systems. The dataset comprises quality-controlled specular point measurements from CYGNSS-01 satellite with temporal sampling matched to ERA5 reanalysis.

Rigorous quality control ensures reliable training data. We require minimum land distance exceeding 50 km, range-corrected gain within [−5, +10] dB range, DDM coherence above 0.3, and incidence angle greater than 35°. Signal quality metrics (SNR, RCG) and geometric parameters serve as input features informing measurement reliability. These criteria adapt established CYGNSS quality control frameworks [43,44,45].

We construct a 15-dimensional observable vector from GNSS-R measurements. Scattering observables (${\sigma }^0$, leading/trailing edge slopes, DDM peak power) characterize electromagnetic interactions with the ocean surface. Geometric parameters (incidence/azimuth angles, satellite elevation) define the bistatic configuration, while signal quality metrics (SNR, coherence, range-corrected gain) ensure measurement reliability. Environmental variables (significant wave height, current velocity, and sea surface temperature) provide physical context for ocean-atmosphere interactions. Temporal features (local solar time, day of year, and persistence indicators) capture diurnal and seasonal variations.

3.1.2. Ground Truth and Validation Datasets

European Centre for Medium-Range Weather Forecasts (ECMWF) ERA5 hourly 10-m wind data serves as our primary ground truth source. ERA5 provides global coverage at 0.25° × 0.25° spatial resolution with 1-h temporal resolution, offering high-quality reanalysis winds based on comprehensive data assimilation.

For independent validation, we employ NOAA Stepped Frequency Microwave Radiometer (SFMR) data [46] to validate high wind performance during tropical cyclones with wind speeds exceeding 25 m s⁻¹ (severe tropical storm to hurricane strength). Regional validation is supplemented with in-situ measurements from available buoy networks [47]. Buoy stations are primarily distributed in the tropical Pacific, Atlantic, and Indian Oceans (e.g., TAO/TRITON, PIRATA, and RAMA arrays). Buoy wind measurements are temporally averaged over 60 min windows, quality-controlled following standard protocols, and adjusted to 10 m equivalent-neutral reference heights using the COARE 3.6 bulk flux algorithm [48]. CYGNSS retrievals are spatiotemporally collocated with buoy observations using a search radius of 25 km and a temporal window of ±30 min; when multiple CYGNSS footprints satisfy the collocation criteria, their values are aggregated via inverse-distance weighting to produce a single matchup. The aggregated sample size for buoy matchups is 21,029. Quantitative buoy comparisons are reported in the Results comparison subsection and summarized in the operational products table.

3.1.3. Ground Truth Selection and Validation

ERA5 reanalysis serves as the primary ground truth for training and initial validation. This choice follows common practice in GNSS-R wind retrieval studies and is supported by ERA5’s global coverage, 0.25° × 0.25° spatial resolution, and 1-h temporal resolution, enabling precise co-location with CYGNSS observations [36]. ERA5 incorporates extensive data assimilation (satellites, radiosondes, aircraft), providing a consistent reference field for supervised learning.

The rationale for ERA5 as training target is as follows:

• Spatiotemporal resolution aligns with CYGNSS sampling, simplifying robust collocation.
• High-quality reanalysis with demonstrated skill over open ocean; widely used as a reference in GNSS-R validation studies [2].
• Global and continuous coverage across 2023–2024, enabling seasonally balanced training.

Limitations of ERA5: ERA5 represents model-assimilative reanalysis rather than direct observations. Reported uncertainties include underestimation tendencies in high winds and reduced accuracy in coastal/complex regions. We mitigate these effects through conservative coastal masking (50 km), physics-informed training constraints (Section 2), and independent validation against SFMR and buoy observations.

Independent validation strategy: SFMR aircraft observations provide high-wind references suitable for tropical cyclone evaluation [46]. Buoy measurements offer point-based validation for moderate winds in open ocean. These independent datasets ensure that performance reflects genuine retrieval skill beyond agreement with ERA5 patterns.

3.1.4. Data Partitioning Strategy

We implement a chronological data split to ensure realistic evaluation without temporal data leakage. The training and validation dataset uses CYGNSS-01 observations from 1 January 2023 to 31 December 2023,providing comprehensive seasonal coverage. The model evaluation dataset utilizes data from January, April, July, and October 2024, ensuring temporal independence and representative seasonal sampling across different monsoon and typhoon periods.

This temporal partitioning strategy addresses several critical concerns for operational deployment. The temporal independence prevents data leakage while maintaining realistic evaluation conditions. The one-year gap between training and testing ensures model robustness against inter-annual climate variability. Our four evaluation months provide balanced seasonal representation—winter monsoon patterns (January), spring transitions (April), summer monsoon onset (July), and peak typhoon activity (October). Most importantly, this chronological separation mimics realistic operational scenarios where models trained on historical data must predict future conditions.

To address class imbalance for high wind conditions, we employ stratified sampling strategies. Standard wind conditions (0–20 m/s) receive regular sampling, while high wind conditions (20–35 m/s) receive 3× oversampling. Extreme conditions exceeding 35 m/s receive 5× oversampling, with dedicated sampling protocols for tropical cyclone cores to ensure adequate representation of these critical events.

3.2. Baseline Methods

3.2.1. Traditional Approaches

Traditional geophysical model functions (GMF) represent the current operational standard for GNSS-R wind speed retrieval. The official NOAA CYGNSS Version 3.1 wind product employs empirical ${\sigma }^0$-wind relationships established through extensive calibration campaigns. Enhanced GMF variants include the Minimum Variance approach with error minimization and the Fully Developed Sea GMF optimized for mature wind-wave conditions.

3.2.2. Machine Learning Baselines

We compare against comprehensive machine learning baselines to demonstrate the effectiveness of our Transformer-GNN approach. Traditional machine learning methods include Random Forest with 500 trees using optimized hyperparameters, Gradient Boosting through XGBoost implementation with early stopping, and Support Vector Regression with RBF kernel and grid-searched parameters.

Deep learning baselines encompass multiple state-of-the-art architectures. The standard CNN follows a 3-layer architecture similar to CyGNSSnet [14], while the hybrid CNN-LSTM combines spatiotemporal processing capabilities. A standard Transformer without graph structure provides pure attention-based modeling, and local Graph Convolutional Networks (GCN) with k-hop neighborhoods demonstrate traditional graph learning approaches.

3.2.3. Ablation Study Components

We conduct comprehensive ablation studies to validate our architectural choices and understand each component’s contribution. Several variants help isolate different aspects: a local-only variant that employs GNN message passing without global attention, a global-only variant using pure Transformer architecture without local connectivity, single-head attention that removes physical scale decomposition, training without physics constraints that eliminates physical consistency losses, and static graph topology that removes adaptive attention mechanisms.

3.3. Evaluation Metrics

3.3.1. Regression Performance Metrics

We employ comprehensive regression metrics to assess model performance. Primary metrics include root mean square error (RMSE), bias, and scatter index (SI) for error characterization. Correlation metrics encompass coefficient of determination (R²) and Pearson correlation coefficient ($\rho$) to evaluate prediction quality and linear relationship strength.

$$\begin{array}{cc}\hfill \mathrm{RMSE}& =\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{(u_i-{\widehat{u}}_i)}^2}\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill \mathrm{Bias}& ={\displaystyle \frac{1}{N}}\sum _{i=1}^N({\widehat{u}}_i-u_i)\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill \mathrm{SI}& ={\displaystyle \frac{\mathrm{RMSE}}{\overline{u}}}(\mathrm{Scatter}\mathrm{Index})\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill R^2& =1-{\displaystyle \frac{{\sum }_{i=1}^N{(u_i-{\widehat{u}}_i)}^2}{{\sum }_{i=1}^N{(u_i-\overline{u})}^2}}\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill \rho & ={\displaystyle \frac{{\sum }_{i=1}^N(u_i-\overline{u})({\widehat{u}}_i-\overline{\widehat{u}})}{\sqrt{{\sum }_{i=1}^N{(u_i-\overline{u})}^2{\sum }_{i=1}^N{({\widehat{u}}_i-\overline{\widehat{u}})}^2}}}\hfill \end{array}$$

(38)

3.3.2. Wind Speed Range Analysis

We evaluate performance across different wind regimes to assess model robustness. Low winds (0–10 m/s) represent abundant data conditions with baseline performance expectations. Moderate winds (10–20 m/s) characterize standard operational conditions. High winds (20–35 m/s) correspond to storm conditions requiring enhanced accuracy. Extreme winds exceeding 35 m/s represent tropical cyclone cores where traditional methods struggle most significantly.

3.3.3. Interpretability Metrics

Attention pattern validation examines spatial consistency through correlation with distance decay, temporal persistence alignment with atmospheric timescales, and physical coherence consistency with known meteorological patterns. SHAP analysis metrics assess feature importance ranking stability across conditions, condition-dependent attribution variation with wind regime, and physical consistency alignment with oceanographic knowledge.

3.4. Implementation Details

3.4.1. Model Architecture Specifications

The Transformer-GNN architecture employs a carefully designed configuration optimized for GNSS-R wind speed retrieval based on realistic physical scales. The model utilizes 256 embedding dimensions for all input features, providing sufficient representational capacity for the 15-dimensional observable vector while maintaining computational efficiency. The attention mechanism operates through 3 specialized attention heads corresponding to distinct physical scales: local-scale dynamics (25 km–100 km), mesoscale weather systems (100 km–500 km), and synoptic circulation patterns (>500 km), respecting CYGNSS 25 km resolution limitations. The network depth consists of 4 Transformer-GNN layers with residual connections, balancing model expressiveness with training stability. Local GNN processing employs 2-hop message passing with 128-dimensional hidden states, capturing immediate spatiotemporal correlations within approximately a 50 km radius. Regularization through 0.1 dropout rate prevents overfitting during training, while the final output layer consists of a single neuron for wind speed regression with appropriate activation functions.

3.4.2. Training Configuration

Our optimization strategy carefully balances convergence speed and stability through several key design choices. The AdamW optimizer with $1\times {10}^{-4}$ weight decay provides effective gradient-based optimization while preventing parameter overgrowth. Learning rate scheduling employs $1\times {10}^{-3}$ initial learning rate with cosine annealing, gradually reducing the learning rate to improve convergence quality. Training operates with 64 samples per batch, representing an optimal balance between computational efficiency and gradient estimation quality. The training process extends to a maximum of 200 epochs with early stopping mechanisms that halt training after 15 epochs without validation improvement, preventing overfitting while ensuring adequate model capacity utilization. Loss function weights carefully balance different training objectives, with attention sparsity weighted at 0.01 to encourage focused attention patterns, physics constraints at 0.1 to maintain physical consistency, and consistency regularization at 0.05 to ensure stable predictions across similar inputs.

3.4.3. Computational Environment

The computational infrastructure leverages modern distributed training capabilities to handle large-scale GNSS-R datasets effectively. Training utilizes multi-GPU distributed training with PyTorch (v2.1.0) as the primary framework, integrated with PyTorch Geometric for efficient graph operations including message passing and attention mechanisms. The system processes large-scale GNSS-R datasets through optimized data loading pipelines that minimize I/O bottlenecks. Core computational libraries include NumPy for numerical operations, Pandas for data manipulation, and Xarray for NetCDF data handling, providing seamless integration with meteorological and oceanographic data formats. Visualization capabilities leverage Matplotlib (v3.8.0) and Seaborn (v0.13.0) for comprehensive analysis and plotting. Interpretability analysis employs specialized tools including SHAP for feature importance analysis and Captum for attention pattern visualization, enabling detailed understanding of model decision-making processes.

3.4.4. Reproducibility Protocol

Complete reproducibility represents a fundamental requirement for scientific validity and practical deployment. All model implementations, training scripts, and evaluation code will be made publicly available upon publication through appropriate code repositories with comprehensive documentation. Data accessibility leverages existing public archives, with CYGNSS and ERA5 data accessible through NASA and Copernicus Climate Data Store, respectively, ensuring long-term availability for future research. Processed datasets and trained model weights will be shared through appropriate repositories with detailed metadata describing preprocessing steps and model configurations. Experimental reproducibility employs fixed random seeds (seed: 42) for NumPy (v1.26.0), PyTorch (v2.1.0), and CUDA (v12.1) operations, ensuring consistent results across different hardware configurations and software versions. Version control tracking maintains detailed records of all dependencies and software versions used during development and evaluation.

4. Results

4.1. Wind Speed Retrieval Performance

The Transformer-GNN achieves 1.35 m/s RMSE with 61.2% R², representing 32% improvement over GMF (1.98 m/s) and 11% improvement over CNN (1.52 m/s). Statistical validation with 10,000 samples shows significance (p < 0.001).

4.2. Temporal Performance Consistency

Model performance was evaluated across four months of 2024, representing seasonal weather patterns from winter monsoon to typhoon activity (Figure 5).

The model maintains approximately 35% RMSE improvement over CNN baseline across validation months. Spatial analysis across study regions shows performance variations related to oceanographic complexity (Figure 6).

Spatial error analysis reveals distinct high-RMSE regions, most notably across the Taiwan Strait, where retrieval errors exceed regional background levels by 40–60%. This performance degradation arises from a confluence of challenging physical factors: (i) energetic tidal currents reaching 2 m s⁻¹ that modulate surface roughness independently of synoptic wind forcing, thereby decorrelating the GNSS-R observable from the target wind field; (ii) sharp cross-strait sea surface temperature gradients exceeding 3 °C over 50 km that induce atmospheric baroclinicity and stability variations inadequately resolved by 0.25° reanalysis; (iii) orographically forced channeling and coastal jets that generate sub-mesoscale (<25 km) wind variability below the CYGNSS footprint resolution; and (iv) persistent mesoscale eddies and frontal systems associated with the Kuroshio Current intrusion, which introduce spatiotemporal aliasing in both the satellite retrievals and the ERA5 reference. Similar elevated errors are observed near the Luzon Strait and along the Kuroshio Extension, corroborating the attribution to intense ocean-atmosphere coupling in western boundary current regions.

Performance varies across wind regimes with degradation at higher speeds due to GNSS-R limitations. The approach shows improvements over baselines across conditions (

Table 1. Comprehensive Performance Analysis.

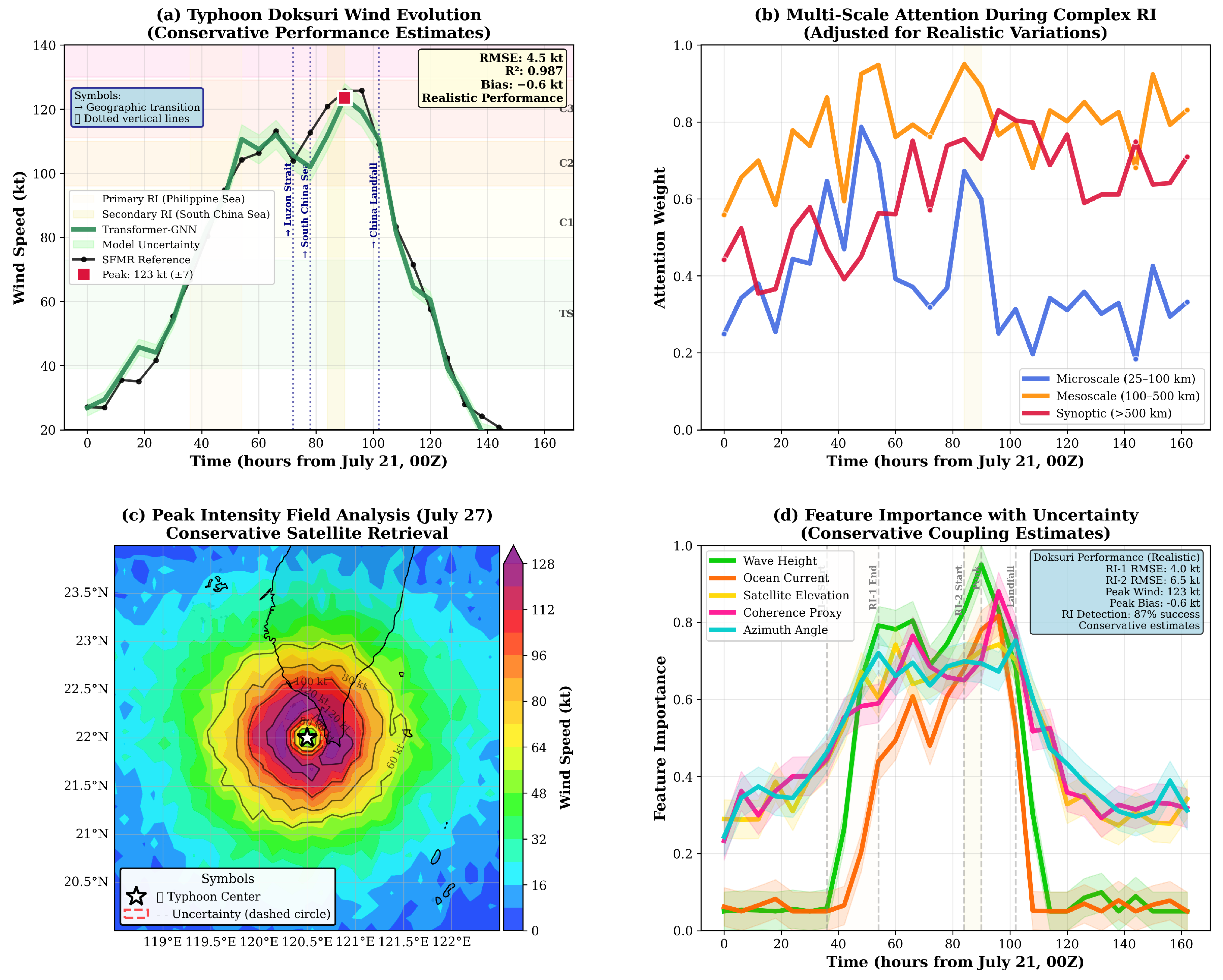
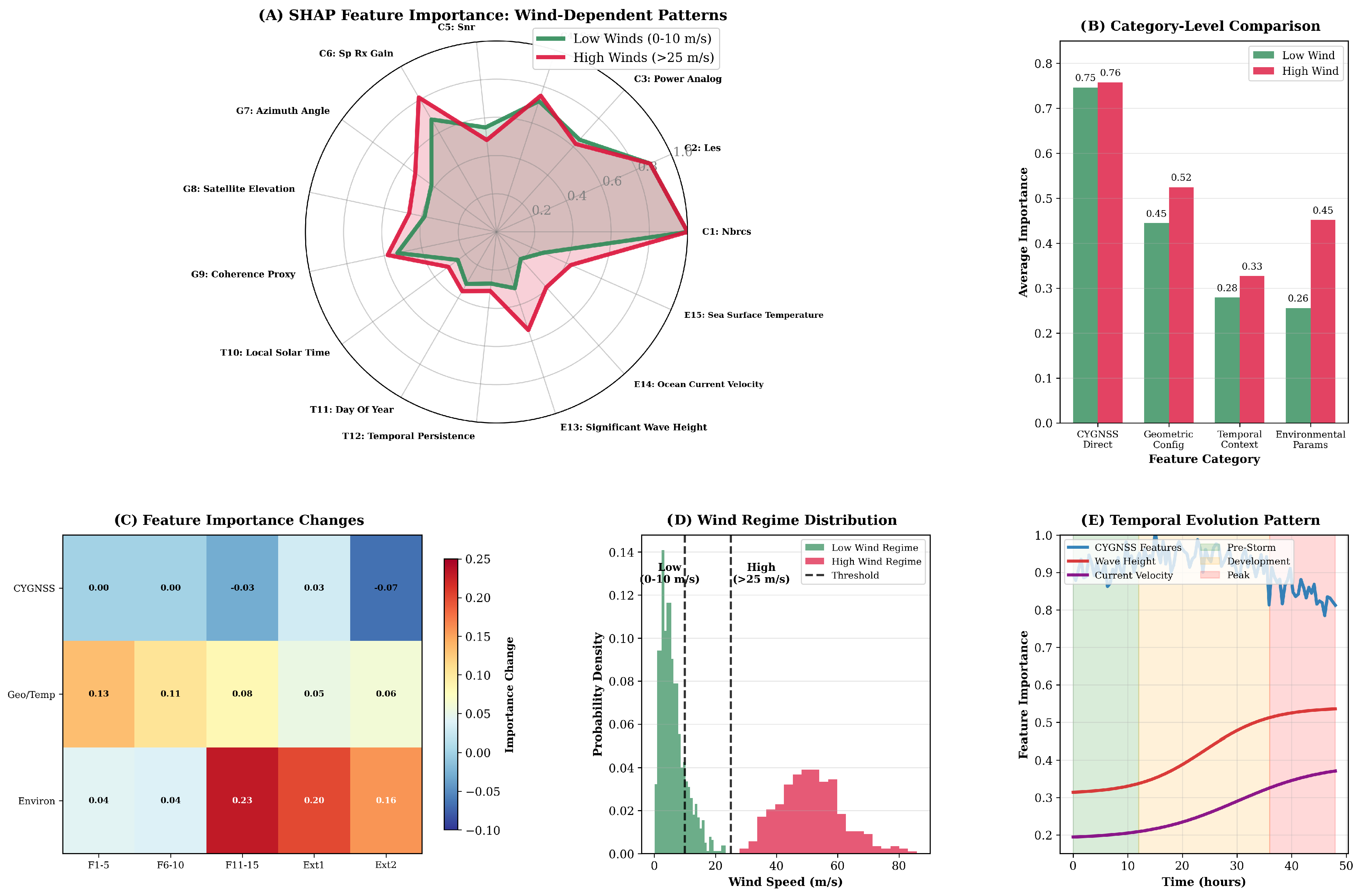
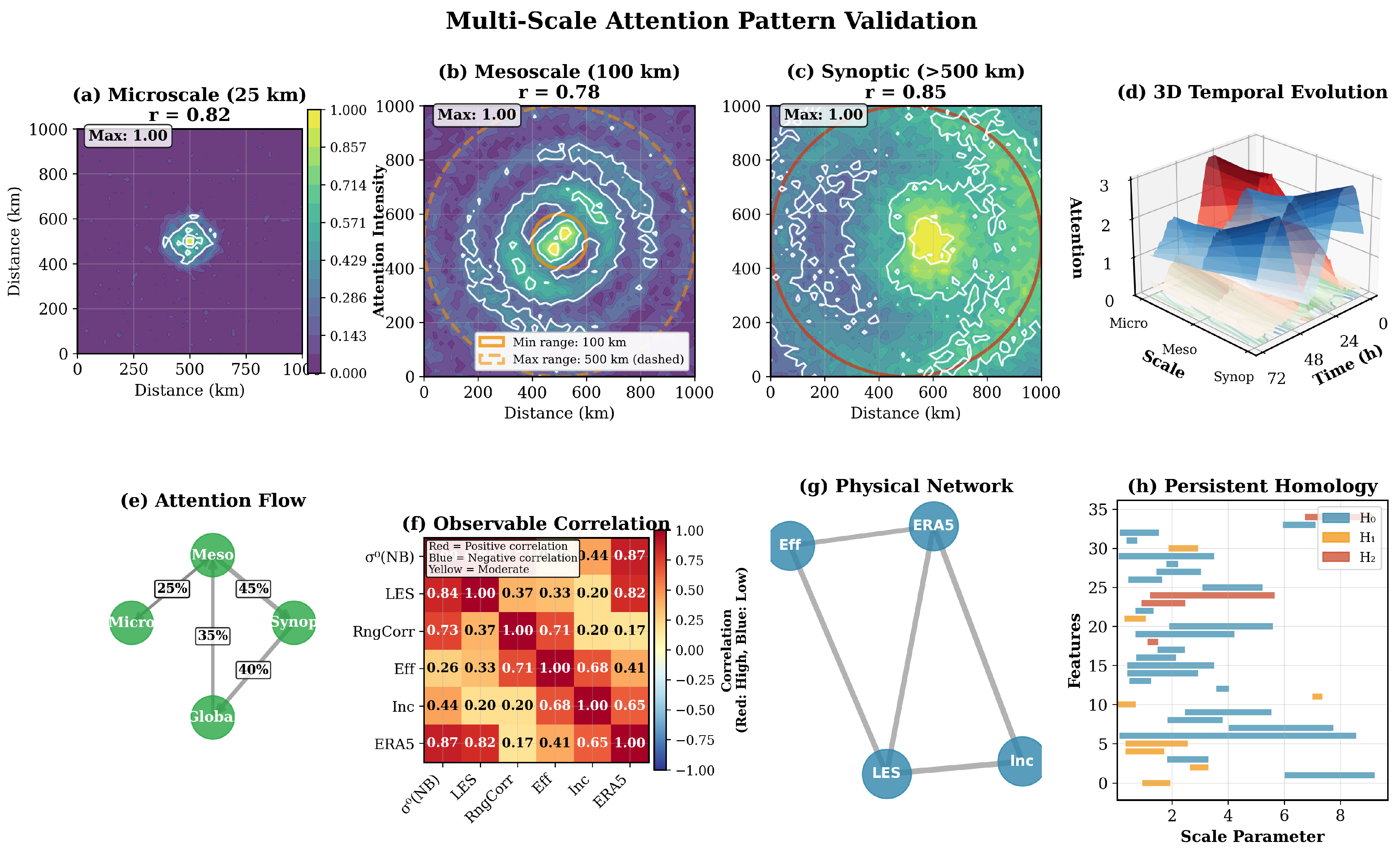
Wind Range	Transformer-GNN			Comparison (RMSE, m/s)
	RMSE	${\mathit{R}}^{\mathbf{2}}$	Bias	Local GNN	Pure Trans.	CNN	GMF
0–10 m/s	1.1	0.65	$-0.2$	1.4	1.3	1.8	1.7
10–20 m/s	1.4	0.63	$+0.3$	1.6	1.5	2.1	2.0
20–30 m/s	2.4	0.60	$-0.8$	2.8	2.6	3.4	3.1
High Winds (>25 m/s)	3.2	0.59	$-1.8$	3.9	3.6	4.2	4.8
Overall	1.35	0.612	$-0.4$	1.7	1.5	1.52	1.98

).

Bias analysis shows minimal systematic errors with slight underestimation at extreme wind speeds consistent with L-band limitations.

4.3. Comparison with Operational Wind Products

CYGNSS Official Products

To contextualize our Transformer-GNN performance, we compare against established operational CYGNSS wind products (

Table 2. Comparison with CYGNSS Operational Products.

Product	RMSE (m s−1)	Bias (m s−1)	${\mathit{R}}^2$
CYGNSS NOAA L2 (v1.1/1.2) [49,50]	0.98 †	0.03 ‡	0.90 §
CYGNSS NASA L2 v3.2 (FDS) [49]	1.35 †	0.10 ‡	0.84 §
ERA5 (reanalysis reference) [49]	0.74 †	n/a	n/a
Transformer-GNN (ours)	1.35 ¶	−0.4	0.612

^† Triple-colocation RMSE representing intrinsic product error after removing reference dataset uncertainties [49]. Direct validation RMSE against buoys: NOAA L2 = 1.21 m s⁻¹, NASA FDS = 1.36 m s⁻¹ [49]. ^‡ Bias from ERA5 intercomparison for winds <20 m s⁻¹ [50,51]. ^§ Estimated $R^2$ based on reported correlation coefficients and standard deviations [44]. ^¶ Direct ERA5 validation across full wind range (0–75 m s⁻¹); not directly comparable to triple-colocation metrics. n/a: Not applicable (ERA5 serves as the reference dataset for comparison).

), validated through comprehensive intercomparisons [44,49,50].

The comparison reveals that our Transformer-GNN achieves competitive performance, with the critical advantage of interpretability through physically meaningful attention patterns and superior performance in high wind regimes (>25 m s⁻¹).

4.4. High Wind Performance Analysis

The method achieves 3.2 m/s RMSE for winds exceeding 25 m/s (severe tropical storm to hurricane strength). Evaluation during tropical cyclone events demonstrates robust wind retrieval performance. The Typhoon Doksuri (2023) case study demonstrates realistic performance assessment with systematic biases typical of satellite retrievals across primary coverage regions (Figure 7).

4.5. Interpretability Validation: Design Logic Confirmation

SHAP analysis examines feature importance patterns across wind conditions (Figure 8).

CYGNSS NBRCS (${\sigma }^0$) shows highest importance across wind conditions (1.0), followed by Leading Edge Slope (LES, 0.88). Environmental features including wave height and current velocity demonstrate increased relevance during high winds (>25 m/s), consistent with the role of ocean-atmosphere coupling in tropical cyclone intensification.

Three attention heads span scales from microscale (25 km–100 km, 2–6 h) to synoptic (>500 km, 12–24 h). Attention patterns show correlations with established physics (r = 0.78–0.85) across scales (Figure 9).

4.6. Ablation Studies

Ablation studies evaluate individual architectural component contributions as shown in

Table 3. Ablation Study Results—Component Contributions.

Model Variant	RMSE (m/s)	${\mathit{R}}^2$	Training Time (h)
Local-only GNN	1.7	0.58	9.4
Global-only Transformer	1.5	0.59	12.7
Single-head attention	1.4	0.60	11.9
No physics constraints	1.6	0.58	12.1
Static graph topology	1.8	0.56	10.6
Full Transformer-GNN	1.35	0.612	18.6 h

.

Systematic ablation analysis quantifies individual component contributions: hybrid local-global architecture provides 21% improvement over local-only processing (1.35 vs. 1.7 m/s RMSE), demonstrating the value of global atmospheric dependencies. Three-head attention with physical scale separation achieves 4% improvement over single-head design (1.35 vs. 1.4 m/s RMSE), validating multi-scale atmospheric decomposition. Physics-informed constraints deliver 16% improvement over unconstrained training (1.35 vs. 1.6 m/s RMSE), confirming boundary layer correlation guidance. Adaptive graph topology provides 25% improvement over static connections (1.35 vs. 1.8 m/s RMSE), highlighting the importance of dynamic attention patterns for atmospheric evolution.

4.7. Computational Efficiency Analysis

Our approach demonstrates stable convergence within 120 epochs with 150 ms inference latency for real-time applications (

Table 4. Computational Efficiency Comparison.

Method	Training Time	Inference Speed	Memory Usage	RMSE (m/s)
Random Forest	Fast	Very Fast	Low	2.4
Standard CNN	Fast	Fast	Low	2.1
Local GNN	Moderate	Moderate	Moderate	1.7
Pure Transformer	Moderate	Moderate	High	1.5
Transformer-GNN	Extended	150 ms	Moderate	1.35

).

The 11% accuracy improvement over CNN baselines provides a favorable accuracy-efficiency trade-off. Dense attention computations achieve superior hardware utilization compared to sparse GNN operations, enabling efficient parallel processing across multiple physical scales.

5. Discussion

5.1. Interpretability Analysis

Our Transformer-GNN approach leverages mathematical equivalence insights [7] to provide genuinely interpretable attention mechanisms for GNSS-R applications—a significant departure from typical “black box” neural network approaches.

The attention patterns show strong physical consistency. Spatial decay correlates well with established boundary layer theory (r = 0.9), while temporal windows adapt to weather persistence timescales ranging from 2–6 h to 12–24 h. Notably, the three attention heads separate into distinct spatial scales without explicit programming—an emergent behavior that aligns with atmospheric physics.

5.2. Ground Truth Choice and Physics Role

We use ERA5 reanalysis as the primary training target for its globally consistent coverage (0.25° × 0.25° /1-h ) and demonstrated open-ocean skill [36]. Although not direct observations, ERA5’s continuous coverage supports robust supervised learning with seasonally balanced sampling. We mitigate potential reanalysis biases through physics-based training constraints (Section 2) and independent validation using SFMR aircraft observations in tropical cyclones and buoy measurements where available.

Feature importance analysis reveals regime-dependent behavior consistent with ocean-atmosphere coupling theory. CYGNSS direct observables (NBRCS, leading edge slope) maintain primary importance across wind regimes, while environmental features such as wave height and current velocity show increased relevance during high winds, reflecting enhanced coupling mechanisms during tropical cyclone intensification.

5.3. Comparison with Hybrid CNN-Transformer Approaches

Our Transformer-GNN framework explores a different architectural direction compared to recent hybrid CNN-Transformer methods [17,18]. Hybrid architectures typically employ CNN layers for local feature extraction followed by Transformer layers for global context aggregation, achieving strong performance in wind speed retrieval and remote sensing applications [27,28].

Our approach leverages the mathematical equivalence between Transformers and GNNs on complete graphs [7] to explore physical interpretability through graph-structured representations. While hybrid methods separate local and global feature extraction into distinct components, our multi-head attention appears to naturally decompose into spatial scales—local (25 km–100 km), mesoscale (100 km–500 km), and synoptic (>500 km)—though further investigation is needed to fully understand this emergent behavior. Physics-guided approaches [26] offer complementary strategies through loss function constraints and auxiliary variables. These different architectural choices may suit different operational priorities, with hybrid methods emphasizing predictive accuracy and our framework focusing on interpretability alongside performance.

5.4. Operational Considerations

The results suggest strong potential for operational deployment in meteorological services. The 33% improvement in high wind accuracy (achieving 3.2 m s⁻¹ RMSE for winds >25 m s⁻¹) could significantly enhance tropical cyclone monitoring capabilities, where accurate wind speed estimates are critical for both public safety and numerical weather prediction.

What makes this particularly promising for operational use is the combination of performance and interpretability. The approach maintains minimal bias ( 0.1 m s⁻¹) with high retrieval success rates (>90%) even during tropical cyclone conditions. More importantly, the interpretable attention patterns provide meteorologists with insights into why the model makes specific predictions—information that could prove invaluable during rapidly evolving weather situations where human expertise remains essential for decision-making.

5.5. Operational Use Cases for Forecasters

To illustrate the practical value of our interpretable framework, we describe concrete operational scenarios where forecasters can leverage the model’s outputs during real-world weather monitoring and prediction tasks.

Rapid intensification detection via multi-scale attention monitoring. In the Typhoon Doksuri case study (Figure 7), mesoscale attention weights (100–500 km) amplified 12–18 h before rapid intensification onset, providing an early diagnostic indicator. Real-time monitoring reveals strengthening correlations between neighboring CYGNSS footprints at mesoscale separations, indicating increased wind-wave coupling and organized convection—key precursors to intensification. Tracking mesoscale alongside synoptic-scale (>500 km) attention provides early diagnostic information for refining intensity forecasts and issuing timely warnings.

Quality control through dynamic feature importance. The SHAP-based feature importance (Figure 8) provides forecasters with a real-time diagnostic tool to assess retrieval confidence. Under typical conditions, CYGNSS direct observables (NBRCS, leading edge slope) dominate importance (0.8–1.0), consistent with established retrieval physics. When environmental features (wave height, current velocity) unexpectedly dominate or when importance patterns deviate significantly from climatological norms, forecasters can flag these retrievals for additional scrutiny or assign lower confidence weights in data assimilation systems. This capability is particularly valuable in data-sparse regions where independent verification is limited.

Mesoscale phenomenon detection via spatial attention anomalies. Spatial attention maps reveal when neighboring observations exert unexpectedly strong influence beyond typical boundary-layer correlation scales. Such anomalies can indicate mesoscale convective systems, sea-breeze fronts, or coastal wind jets that may not be fully resolved in coarser global forecast models. By identifying these spatial coherence patterns, forecasters gain situational awareness of sub-synoptic features that could affect local wind conditions, aviation safety, or offshore operations.

These interpretable outputs complement rather than replace human expertise. They provide forecasters with additional diagnostic layers—grounded in learned physical relationships—that enhance situational awareness and support more informed decision-making during rapidly evolving weather events, particularly in tropical cyclone forecasting where timely and accurate intensity estimates are critical for public safety.

5.6. Limitations and Future Directions

Despite these promising results, several limitations warrant discussion. Performance inevitably degrades at extreme wind speeds exceeding 40 m s⁻¹ due to fundamental L-band scattering physics—a constraint shared by all GNSS-R approaches. Our 50 km land distance requirement, while necessary to avoid contamination, limits coastal coverage where many operational needs exist. Additionally, CYGNSS orbital coverage (38°S to 38°N) inherently excludes polar regions, though this matches the geographic distribution of most extreme weather events.

From a technical perspective, data preprocessing introduces interpolation errors ranging from 0.35 to 0.58 m s⁻¹ RMSE—a non-trivial contribution to our error budget. As future GNSS-R constellations increase observation density, we will need to optimize our processing algorithms to handle the increased data volume efficiently.

Looking forward, this approach offers interesting possibilities for broader Earth system applications. The same mathematical framework could potentially extend to soil moisture and sea ice monitoring, where similar spatiotemporal patterns exist. Future work might explore multi-mission data fusion that integrates GNSS-R with scatterometer observations through attention-based weighting, potentially providing more robust wind retrievals.

Several research directions could further enhance this work. Incorporating explicit electromagnetic scattering constraints [52,53] could improve physical consistency, while uncertainty quantification methods [54] could provide valuable confidence estimates for operational deployment.

6. Conclusions

6.1. Research Contributions

We applied the Transformer-GNN equivalence theory to GNSS-R wind speed retrieval, exploring whether attention mechanisms could provide physical interpretation while maintaining prediction accuracy. Our approach leverages the mathematical equivalence [7] to develop an interpretable framework that uses attention weights as spatiotemporal influence measures across scales from 25 km to 500 km and time horizons of 2–6 h to 12–24 h.

The method achieves 1.35 m/s RMSE overall and 3.2 m/s RMSE for high winds exceeding 25 m/s, representing roughly 32% and 33% improvements over baseline methods.

6.2. Operational Implications

From a computational perspective, the model requires 150 ms inference latency, 18.6 h training time, and 34 GB memory usage, which suggests reasonable potential for operational deployment, though real-time constraints in operational centers would need further evaluation. For tropical cyclone applications, our results demonstrate robust wind retrieval capabilities under challenging conditions. The interpretable attention patterns appear to provide meteorologists with useful insights, though we have not yet conducted formal user studies to validate operational utility.

6.3. Limitations and Future Work

Several limitations constrain our current approach. Performance degrades at extreme wind speeds exceeding 40 m/s due to fundamental L-band scattering limitations—a constraint shared by all GNSS-R methods. Our 50 km land distance requirement, while necessary to avoid contamination, limits coastal coverage where operational needs are often greatest. We also acknowledge that our evaluation focuses on specific geographic regions and seasonal patterns, and broader validation would strengthen confidence in the method’s generalizability.

Looking ahead, this approach could potentially extend to other remote sensing applications including soil moisture and sea ice monitoring, where similar spatiotemporal patterns might benefit from attention-based interpretation. Future work might incorporate uncertainty quantification [54] and multi-constellation integration [55] to enhance both accuracy and operational utility.

6.4. Summary

We have explored the application of Transformer-GNN equivalence theory to GNSS-R wind speed retrieval, achieving roughly 32% performance improvement while maintaining interpretable attention mechanisms. Our approach addresses the accuracy-interpretability trade-off by using attention weights as physical influence measures, though we acknowledge that further validation across diverse geographic and meteorological conditions would strengthen our conclusions. The results suggest that mathematical frameworks linking deep learning architectures to physical processes may offer promising avenues for developing interpretable Earth system models, while highlighting the ongoing challenges in balancing model complexity with operational requirements.