Assessment of Multiple Satellite Precipitation Products over Italy

Highlights

What are the main findings?

• The study compared five satellite precipitation products (CHIRPS, GPM, HSAF, PDIRNOW, and SM2RAIN) against ground-based SCIA-ISPRA data across Italy using daily, seasonal, and annual scales.
• GPM emerged as the most balanced and reliable product overall, while PDIRNOW and SM2RAIN showed high detection but frequent overestimations; CHIRPS performed conservatively, and HSAF exhibited lower reliability in colder seasons.

What is the implication of the main finding?

• The results highlight that no single satellite dataset performs best across all contexts—dataset choice should depend on specific applications, such as flood forecasting or drought monitoring.
• The findings support the adoption of multi-product or hybrid approaches to enhance precipitation monitoring accuracy in complex terrains like Italy.

Abstract

Accurate rainfall estimation remains a critical challenge in hydrology, particularly in Italy, where complex topography and uneven rain-gauge distribution introduce major uncertainties. To address this gap, this study assessed five widely used satellite precipitation products, CHIRPS, GPM, HSAF, PDIRNOW, and SM2RAIN, against the high-resolution SCIA-ISPRA ground dataset. These products were selected because they represent distinct retrieval approaches (infrared–station hybrid, microwave integration, geostationary blending, neural-network infrared, and soil–moisture inversion) and offer diverse temporal and spatial resolutions suitable for both research and operational monitoring. The evaluation, conducted at daily, seasonal, and annual scales using categorical, continuous, and extreme-event indices, revealed that no single product performs optimally across all metrics. GPM achieved the most balanced and reliable performance overall, whereas PDIRNOW and SM2RAIN provided strong detection but frequent overestimation. CHIRPS yielded conservative estimates with few false alarms, while HSAF was less consistent, especially during winter. The results underscore that product suitability depends on the intended application: detection-oriented systems like PDIRNOW are preferable for flood forecasting, whereas conservative datasets like CHIRPS better support drought monitoring. Overall, integrating multiple products or adopting hybrid approaches is recommended to enhance precipitation assessment accuracy over complex Mediterranean terrains.

1. Introduction

Precipitation plays a crucial role in the atmospheric system by driving the hydrological cycle, regulating the energy balance, and exhibiting significant temporal and spatial variability that shapes regional climate patterns [1]. Accurate precipitation measurements are essential for applications in agriculture, hydrology, and natural disaster assessments [2]. However, the global uneven distribution of weather stations results in data scarcity and greater uncertainty in multidisciplinary studies [3]. While traditional gauge-based observations provide precise point measurements, their effectiveness is limited in areas with complex terrain and sparse station networks [4]. To overcome these limitations, satellite-based precipitation products (SPPs) leverage infrared and microwave sensors to estimate precipitation on a gridded scale, offering broader coverage despite inherent uncertainties [5]. These products have become indispensable in water resource management [6], drought monitoring [7], and flood forecasting [8], serving as a crucial alternative in regions with limited or irregularly distributed rain gauges. In recent years, the use of SPPs has expanded significantly, both as standalone datasets and in combination with gauge observations, for various sector-specific applications [9]. Currently, several globally recognized satellite-based rainfall products are available [10], such as the Integrated Multi-satellitE Retrievals for GPM (IMERG), developed within the framework of the Global Precipitation Measurement (GPM) mission; the H05B product, developed by the Hydrology Satellite Application Facility (HSAF) of EUMETSAT; and the PERSIANN family of products (Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks), including PDIRNOW. These products help mitigate the challenges of precipitation studies across different temporal and spatial scales [11]. However, SPPs are often subject to uncertainties due to various factors, including the indirect relationship between satellite measurements and actual precipitation, the limited spatial and temporal resolution of onboard sensors, and inaccuracies in rainfall detection algorithms [12]. These challenges can significantly affect the accuracy of precipitation estimates, particularly in regions with complex climates and topography [13]. As a result, assessing the uncertainty of these products is essential for hydro-meteorological applications, enabling end-users to better understand their strengths and limitations [14,15].

Numerous studies have been conducted to validate satellite-based precipitation estimates using ground-based observations. One notable example is the work carried out within the International Precipitation Working Group (IPWG), established in 2001 to coordinate efforts aimed at enhancing satellite retrieval algorithms [16]. These previous studies generally developed frameworks to assess satellite-based precipitation products (SPPs) using multiple categorical and continuous performance indicators on a global scale [17]. Commonly used categorical indicators include, e.g., Probability of Detection (POD), False Alarm Ratio (FAR), Peirce Skill Score (PSS), and Critical Success Index (CSI), while continuous indicators often include Root Mean Square Error (RMSE), Correlation Coefficients (CC), Kling–Gupta Efficiency (KGE), and Percentage Bias (PBIAS) for comparing the performance of SPPs and reanalysis precipitation products (RPPs). As an example, Satgé et al. [18] evaluated 23 SPPs across West Africa using KGE. In Asia, Wang et al. [19] examined the suitability of European Centre for Medium-Range Weather Forecasts (ECMWF) Re-Analysis Interim (ERA-Interim), Japanese 55-year Reanalysis (JRA-55), and National Center for Atmospheric Research Reanalysis Project 1 (NCAR-1) for the Tibetan Plateau in China, employing CC, PBIAS, RMSE, and Mean Absolute Error (MAE), and found varying performance among the datasets. Similarly, Dandridge et al. [20] assessed two global precipitation products (GPPs) in the Lower Mekong River Basin in Southeast Asia using MAE, CC, RMSE, and BIAS. Sharma et al. [21], by means of CC and RMSE, assessed the accuracy of the Integrated Multi-satellitE Retrievals for GPM algorithm’s Early (GPM IMERG Early), and Final run (GPM IMERG Final), the Global Satellite Mapping of Precipitation with Moving Vector with Kalman filter (GSMaP-MVK), and the Gauge-Adjusted Global Satellite Mapping of Precipitation (GSMaP-Gauge), in capturing spatial and temporal variation in precipitation in the Nepalese Himalaya.

As regards the Mediterranean basin, a region particularly sensitive to climate and specifically to precipitation changes, the reliability of satellite-based rainfall products is especially crucial in Italy, where the interplay of complex topography and coastal regions is expected to have a significant impact on the accuracy of rainfall retrievals. Ciabatta et al. [22,23] evaluated the performance of three satellite-based precipitation products across Italy at a daily timescale: the Tropical Rainfall Measuring Mission (TRMM) Multi-satellite Precipitation Analysis (TMPA), the H05 product of HSAF, and the Soil Moisture to Rainfall from Scatterometer (SM2RAIN) estimates. The results showed lower correlations for SM2RAIN over mountainous regions and for TMPA and HSAF in coastal areas. In southern Italy, Lo Conti et al. [24] analyzed four satellite-based precipitation products over Sicily, including the TMPA product and other products from the PERSIANN family, reporting daily correlation coefficients with ground observations ranging from 0.3 to 0.7. Chiaravalloti et al. [25] investigated the performance of the IMERG, the SM2RAIN and a product combining SM2RAIN and IMERG in the Calabria region (southern Italy) evidencing a significant improvement in the performance given by the combination of IMERG and SM2RAIN according to both the continuous and categorical scores.

In Vietnam, Gummadi [26] evaluated five widely used operational satellite rainfall estimates and found that the Climate Hazards Group InfraRed Precipitation with Station data (CHIRPS) products significantly outperformed CPC, CMORPH, and GSMaP. CHIRPS showed higher skill, lower bias, stronger correlation with observed data, and lower mean absolute error and root mean square error. Finally, in Saudi Arabia [27], a rigorous comparative analysis was conducted from 2017 to 2022, contrasting PDIRNOW with rain gauge data, revealing that PDIRNOW slightly underestimates light precipitation but significantly underestimates heavy precipitation.

In this context, the aim of this paper is to appraise the ability of several satellite-based products to estimate the precipitation at different temporal scales, and to evaluate their accuracy in order to gain a deeper understanding of each product’s strengths and weaknesses and to exploit them effectively for the complex Italian territory. With these aims, the paper presents a comprehensive evaluation of five satellite-based precipitation products, including CHIRPS, GPM, HSAF, PDIRNOW and SM2RAIN at daily, monthly, and annual time scales over Italy by means of a comparison, using multiple metrics, with measured precipitation data extracted from the SCIA-ISPRA dataset. The five satellite precipitation products were selected to provide a comprehensive and methodologically diverse representation of the principal retrieval approaches currently available for global and regional precipitation estimation. Moreover, these products were chosen because together they encompass a broad spectrum of spatial resolutions (0.04–0.1°), temporal frequencies (15 min to daily), and latencies (near-real-time to 3.5 months), thereby offering complementary strengths. This diversity allows for a balanced evaluation of satellite precipitation capabilities under Italy’s complex topography and climate regimes. The selected datasets are also widely used, validated, and accessible, ensuring reproducibility and comparability with previous regional and global validation studies.

2. Study Area and Data

2.1. Case Study

The Mediterranean basin is a region of significant geopolitical and environmental importance, serving as a crossroads between Europe, Asia, and Africa. Encompassing 21 coastal nations, this area is characterized by diverse climatic influences due to its complex geography [28]. Among these countries, Italy stands out from a climatological perspective due to its elongated shape, spanning over ten degrees of latitude, its central position in the western Mediterranean, and its varied topography, which includes extensive mountain ranges [29]. In fact, Italy is located in southern Europe, extending approximately from 35°29′N to 47°06′N latitude and 6°37′E to 18°31′E longitude. The country stretches about 1200 km from the Alps in the north to the central Mediterranean Sea in the south, covering an area of roughly 301,340 km². Italy’s climate is shaped by these geographical features, resulting in warm, dry summers (with average temperatures exceeding 22 °C) and moderately wet winters, typical of a Mediterranean climate. According to the Köppen–Geiger [30] classification, the country exhibits two predominant climatic groups: a temperate/mesothermal climate covering the peninsular and insular regions, and a continental/microthermal climate dominating the northern and northeastern areas.

2.2. Observed Gridded Dataset

The SCIA-ISPRA dataset, developed by the Italian Environmental Protection Agency (ISPRA), provides a comprehensive collection of gridded observational precipitation data with a horizontal resolution of 10 km (Figure 1).

Data collection and verification were carried out through SCIA, the National System for the collection, processing, and dissemination of climate data, a digital platform developed by the Institute for Environmental Protection and Research in collaboration with the national and regional meteorological monitoring networks of the National System for Environmental Protection [31]. This dataset is derived from the interpolation of a large number of daily rain gauge measurements. In particular, to interpolate precipitation data onto a regular grid, a kriging algorithm has been employed, following standard geostatistical principles [32]. The variogram parameters are empirically optimized based on the physical properties of the precipitation variable and the average density of measurement stations [31]. However, the reliability of the data may vary depending on the density of available gauges in different years [33].

2.3. Precipitation Satellite-Based Products

Table 1. Main characteristics of the satellite-based precipitation products.

Product	Spatial Resolution	Temporal Resolution	Data Latency	Spatial Coverage	Description
GPM	0.1° × 0.1° (~10 km)	30 min, daily, monthly	~3.5 months	60°N–60°S (global)	Multi-sensor, gauge-adjusted precipitation estimates from the GPM constellation; optimized for research accuracy.
CHIRPS	0.05° (~5 km)	Daily, 5-day, monthly	~2–3 weeks	50°S–50°N (quasi-global)	Infrared–station blended rainfall product using Cold Cloud Duration (CCD) and in situ data for bias correction.
HSAF05B	3–8 km	15-min Updates (3–24 h integrations)	~15 min after synoptic hours	Europe, North Africa, Middle East	GEO–LEO blended product from EUMETSAT HSAF program for operational hydrological monitoring.
PDIRNOW	0.04° (~4 km)	30 min	15–60 min	60°N–60°S (quasi-global)	Near-real-time PERSIANN algorithm integrating IR and PMW data for improved detection of extreme and orographic rainfall.
SM2RAIN	0.1° × 0.1° (~10 km)	Daily	2–5 days	Global (land only)	Rainfall inferred from ASCAT soil moisture using SM2RAIN algorithm; suitable for data-sparse regions.

shows the main characteristics of the satellite-based precipitation products evaluated in this study, including spatial and temporal resolution, data latency, and spatial coverage.

2.3.1. GPM

The GPM mission, which succeeds the TRMM, is an international collaboration involving around 10 satellite systems aimed at providing global precipitation estimates. The IMERG datasets are among the essential data outputs of the GPM mission. IMERG dataset plays a critical role in delivering valuable precipitation information for both scientific research and operational applications [34].

The IMERG framework offers three distinct types of precipitation products that serve various monitoring and analytical purposes. The IMERG Early product becomes accessible within four hours after satellite measurements are captured. This rapid availability makes it particularly suitable for real-time applications, such as the assessment and monitoring of extreme hydrological events. IMERG Late, on the other hand, becomes available approximately 14 h after the satellite observations are made. Although it introduces a slightly longer delay compared to IMERG Early, this product remains useful for near-real-time monitoring tasks, offering more refined data while still being timely enough for various practical uses [35]. IMERG Final differs significantly from the other two products as it requires a substantially longer processing period, typically around 3.5 months, before being released. The additional time is necessary to incorporate monthly datasets from the Global Precipitation Climatology Centre (GPCC), resulting in a product that is generally more accurate and reliable. Due to its enhanced precision and dependability, IMERG Final was the primary dataset used in this research [34].

This study is based on Version 7 of the IMERG Final product, given its superior accuracy and comprehensive data integration.

2.3.2. CHIRPS

CHIRPS is a high-resolution precipitation dataset developed to enhance climate monitoring and drought assessment. Its innovative approach combines satellite-derived infrared Cold Cloud Duration (CCD) data with ground-based station measurements, offering detailed and reliable precipitation estimates. This hybrid method reduces errors commonly associated with datasets that rely solely on satellite or station data [36]. The dataset covers the period from 1981 to the present and provides near-global precipitation data between latitudes 50°S and 50°N. It features a spatial resolution of 0.05 degrees, equivalent to approximately 5.3 km [36]. Such a fine resolution, combined with continuous updates, makes CHIRPS highly suitable for monitoring long-term precipitation trends and anomalies, as well as conducting operational analyses in near real time [36]. A key strength of CHIRPS lies in its bias-correction method, which integrates high-quality station data to enhance the precision of satellite-derived estimates. This feature is particularly important in areas with complex terrain or limited observational infrastructure [36]. As a versatile dataset, CHIRPS has become a critical tool for applications such as agricultural risk assessments, drought monitoring, flood modeling, and research on precipitation variability in the context of climate change [36].

2.3.3. HSAF

HSAF is an integral part of the distributed application ground segment of the EUMETSAT [37]. This ground segment consists of the Central Application Facilities located at EUMETSAT Headquarters and a network of eight Satellite Application Facilities (SAFs), which are managed by EUMETSAT Member States. The SAFs are dedicated to developing and operating satellite-derived data services that cater to the needs of specific user communities. The main objectives of HSAF are to generate and deliver satellite-based products from both current and future satellites, ensuring that these products meet the spatial and temporal resolution requirements of operational hydrology. This includes the generation, centralization, archiving, and dissemination of a range of products, such as precipitation data in various forms (liquid, solid, rate, and accumulated), soil moisture information at different scales and depths (surface and root zone), and snow-related parameters, including detection, coverage, melting conditions, and water equivalent. In addition to providing these products, HSAF is committed to perform independent validation of their effectiveness, particularly for applications related to flood, landslide, and avalanche management, as well as water resource evaluation. This validation process includes activities such as downscaling and upscaling of observed and predicted fields to the basin level, merging satellite-based measurements with data from radar and rain gauge networks, and assimilating satellite-derived products into hydrological models. The impact of these satellite products on hydrological applications is also assessed. In this study, the focus is on the H05B P-AC-SEVIRI product (HSAF05B), which combines frequent precipitation measurements derived from blending LEO microwave-based precipitation rate data and GEO IR imagery. The product cycle consists of four different time-integrated products, which provide data for 3, 6, 12, and 24-h periods, updated every three hours on a rolling basis. The resolution of the products varies across the full disk, with a finer resolution of 3 km near the sub-satellite point and an average resolution of 8 km over Europe, depending on the SEVIRI instrument’s instantaneous field of view (IFOV). Data is made available with a timeliness of 15 min after synoptic hours (00, 03, 06, 09, 12, 15, 18, and 21 UTC).

2.3.4. SM2RAIN

SM2RAIN-ASCAT is a newly developed global precipitation product derived from ASCAT satellite soil moisture data using the SM2RAIN algorithm [38,39]. The dataset provides precipitation estimates (in mm/day) on a regular grid with 0.1-degree resolution, covering the entire globe. It represents the accumulated precipitation between 00:00 and 23:59 UTC for each specified day. The SM2RAIN algorithm was applied to ASCAT soil moisture data [40] for the period from January 2007 to December 2022 (16 years), in version 2.1.2n (SM2RAIN212N).

By capitalizing on the known relationship between soil moisture and precipitation, SM2RAIN enables accurate precipitation monitoring over large areas and contributes to a better understanding of hydrological processes and climate dynamics. The product supports various applications, including hydrological modeling, drought monitoring, and water resource management. It is especially valuable in regions where conventional precipitation data collection is limited, as it provides near-real-time observations that can be used to improve climate and weather forecasting models. The SM2RAIN212N dataset also aids in the assessment of soil moisture, making it a useful tool for tracking soil conditions and their impact on agriculture. Additionally, this product enhances the accuracy of flood prediction models and water resource management by providing more reliable precipitation estimates. As such, SM2RAIN212N has become an important tool for researchers, meteorologists, and policy makers involved in water management and climate adaptation strategies [39].

2.3.5. PDIRNOW

The PERSIANN algorithm, developed in 1997 [41,42], was designed to offer high-resolution quantitative precipitation estimates using artificial neural networks (ANNs). Over the years, this algorithm evolved, producing the PERSIANN-CDR dataset, a global, daily precipitation product spanning more than 36 years. However, the original PERSIANN product had a 2-day latency, which limited its real-time application in flood modeling. To address this, the PERSIANN-CCS version was introduced, utilizing cloud-type models based on infrared (IR) data, offering short-latency (15 min–1 h) estimates with a higher spatial resolution of 0.04°. However, the lack of passive microwave (PMW) data resulted in a decreased accuracy for extreme precipitation events. To improve upon this, the PDIR (PERSIANN Dynamic Infrared-Rain Rate) algorithm was developed, which integrates PMW data to better estimate extreme and orographic precipitation, enhancing real-time applications [43]. The PDIRNOW dataset, based on this algorithm, employs a refined temperature threshold (263 K instead of 273 K) and includes additional bias correction using IMERG Merged PMW precipitation data, providing quasi-global coverage and high-resolution precipitation estimates for applications like flood modelling [44].

3. Methodology

The comparison between satellite-based datasets and the observed dataset spans the period from 2000 to 2021. However, it is important to note that the temporal coverage of the satellite datasets varies (Figure 2). Some satellites, for instance, have a shorter temporal range, depending on their launch date and mission duration. In particular, CHIRPS, GPM, PDIRNOW datasets provide complete coverage over the entire study period (2000–2021), whereas SM2RAIN212N and HSAF05B show substantial data gaps, especially before 2006 and 2014, respectively, with data availability progressively improving thereafter.

This difference in time periods was addressed by aligning each satellite’s available data to a common comparison period. Additionally, the satellite datasets have different spatial resolutions. While some satellites provide finer spatial detail, others offer coarser resolution data. To ensure consistency across all datasets, the spatial data from the satellites were resampled to match the grid of the ISPRA (Italian Institute for Environmental Protection and Research) observed dataset, which has a resolution of 10 km × 10 km and represents the coarsest resolution among the considered products. The resampling was performed using an area-weighted averaging approach, in which the value assigned to each 10 km grid cell corresponds to the mean of all finer-resolution cells overlapping it, weighted by their fractional area of intersection. This method preserves the areal mean precipitation during the aggregation process and allowed for a uniform comparison of satellite and observed data across the same spatial scale.

In terms of temporal resolution, the satellite datasets typically offer varying temporal scales. To make the datasets comparable, an aggregation process was applied to some of the satellite data, converting them into a daily time step. This adaptation ensured that all satellite datasets aligned with the daily temporal resolution of the observed dataset, facilitating a consistent and fair comparison across the entire period of study.

3.1. Daily Performance

The analysis of daily precipitation focused on evaluating the satellite’s ability to detect precipitation events on a day-to-day basis. To achieve this, the dataset was divided into two temporal subsets: annual and seasonal, allowing for a more granular comparison of model performance across different timeframes. A binary classification system was employed for this evaluation, categorizing each day into one of two outcomes: the occurrence of a precipitation event (“yes”) or its absence (“no”).

The evaluation process utilized a 2 × 2 contingency table (

Table 2. Contingency table.

Forecasted Precipitation	Observed Precipitation
	>0 mm/day	=0 mm/day
>0 mm/day	Hit (H)	False Alarm (F)
=0 mm/day	Miss (M)	Correct negatives (C)

), which systematically recorded the frequencies of predicted and actual outcomes across these two categories. The table identifies four possible cases: Hits (H), where a precipitation event occurs as predicted; Misses (M), where an event occurs but is not predicted; False Alarms (F), where an event is predicted but does not occur; and Correct Negatives (C), where no event occurs, and none is predicted.

3.1.1. Success Ratio (SR)

The Success Ratio (SR) measures the proportion of correctly predicted events (Hits) out of all predicted events. A higher SR indicates fewer false alarms. It is calculated as:

$$SR={\displaystyle \frac{H}{H+F}},$$

(1)

in which H is the number of hits (events correctly predicted) and F is the number of false alarms (events predicted but not observed).

An SR value of 1 indicates no false alarms, while lower values indicate an increasing number of false positives.

3.1.2. Probability of Detection (POD)

The Probability of Detection (POD) quantifies the proportion of observed events correctly identified by the model. This metric focuses on the model’s ability to capture actual events and is calculated as:

$$POD={\displaystyle \frac{H}{H+M}},$$

(2)

with M number of misses (events observed but not predicted).

A POD value of 1 indicates that all observed events were successfully detected, while lower values suggest missed events.

3.1.3. Bias

The Bias score compares the total number of predicted events to the total number of observed events, providing insight into whether the model overestimates or underestimates precipitation occurrence. It is expressed as:

$$Bias={\displaystyle \frac{H+F}{H+M}},$$

(3)

Bias > 1 indicates overprediction (too many events forecasted), Bias < 1 indicates underprediction (too few events forecasted) and Bias = 1 represents perfect agreement in the number of predicted and observed events, though not necessarily in their exact timing.

3.1.4. Critical Success Index (CSI)

The Critical Success Index (CSI) evaluates the overall skill of the model by considering Hits, Misses, and False Alarms. It is a measure of the proportion of correct predictions relative to all events (both observed and predicted) and is calculated as:

$$CSI={\displaystyle \frac{H}{H+M+F}},$$

(4)

The CSI ranges from 0 to 1, with higher values indicating better overall performance. Unlike SR or POD, CSI penalizes both missed events and false alarms equally.

3.1.5. Performance Diagram

The evaluation of the statistical scores (SR, POD, Bias, and CSI) was visualized using a performance diagram [45], providing a clear and intuitive representation of their interrelationships.

In detail, by combining all these elements, the performance diagram serves as a powerful visual tool for identifying the strengths and weaknesses of satellites in detecting and predicting precipitation events across different statistical metrics.

Specifically, in the diagram, the POD is plotted on the y-axis to represent the model’s ability to identify observed events, while the SR, expressed as 1−false alarm rate, is plotted on the x-axis to indicate the precision of the predictions. The Bias is illustrated as diagonal dashed lines radiating outward from the origin, with the labels for bias values displayed at the end of each line. A perfect bias score of 1 is represented by the diagonal line passing through the origin. Additionally, the CSI is shown as solid, curved contours that connect the top of the diagram to its right-hand side. Higher CSI values, indicative of better overall performance, are positioned closer to the upper part of the plot.

The performance diagram also incorporates sampling uncertainty, visualized with crosshairs, and, where available, reference forecasts for sample frequency.

3.2. Annual and Seasonal Assessments

To evaluate the annual and seasonal performance of the models against observed data, the Taylor diagrams are used to offer a concise and informative graphical representation of their statistical performance. In particular, Taylor diagrams provide a comprehensive visualization of model performance by considering multiple statistical parameters simultaneously. These parameters typically include correlation coefficient (R), centered root mean square difference (CRMSD), and standard deviation ratio (SDR). The R quantifies the linear relationship between model predictions and observed data, with values closer to 1 indicating better agreement.

$$\mathrm{R}={\displaystyle \frac{\frac{1}{N}{\sum }_{n=1}^N\left({sat}_n-\overline{\left(sat\right)}\right)\left(ob{s}_n-\overline{\left(obs\right)}\right)}{{\sigma }_{sat}{\sigma }_{obs}}},$$

(5)

in which $N$ is the number of data points, ${sat}_n$ is the model value at point n, $\overline{sat}$ is the mean of model values, $ob{s}_n$ is the observed value at point n, $\overline{obs}$ is the mean of observed values, ${\sigma }_{sat}$ is the standard deviation of model values and ${\sigma }_{obs}$ is the standard deviation of observed values.

The CRMSD is the mean square error between adjusted model and observed values and measures the absolute difference between model and observed data, adjusted for bias, providing insights into both accuracy and precision.

$$\mathrm{C}\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{D}={\displaystyle \frac{1}{N}}{\sum }_{n=1}^N{\left[\left({sat}_n-\overline{sat}\right)-\left(ob{s}_n-\overline{obs}\right)\right]}^2,$$

(6)

The SDR assesses the ratio of the standard deviation of model data to that of observed data, indicating whether the model captures the variability present in the observed data.

$${\mathsf{\sigma }}_{sat}^2={\displaystyle \frac{1}{N}}{\sum }_{n=1}^N{\left({sat}_n-\overline{mdl}\right)}^2,$$

(7)

$${\mathsf{\sigma }}_{obs}^2={\displaystyle \frac{1}{N}}{\sum }_{n=1}^N{\left(ob{s}_n-\overline{obs}\right)}^2,$$

(8)

with ${\sigma }_{sat}^2$ variance of model values and ${\sigma }_{obs}^2$ variance of observed values.

Together, these parameters offer a holistic assessment of model performance, aiding in the comparison and selection of climate models.

3.3. Extreme Index

The extreme indices [46] used in this study were developed by the ETCCDI experts, who are part of the WMO, to analyze long-term precipitation data. These indices can also be used to monitor and assess global extreme climate changes. This paper focuses on the R95pTOT, R99pTOT and Rx5day. In particular, R95pTOT and R99pTOT indices represent the total amount of precipitation accumulated from events exceeding the 95th and 99th percentiles of daily precipitation, respectively. These metrics are crucial for characterizing high-intensity precipitation events and capturing the contribution of extreme events to total precipitation. The selection of R95pTOT and R99pTOT is particularly relevant in the context of climate extremes, as changes in these indices may indicate shifts in the frequency and magnitude of extreme precipitation events, which can have significant socio-economic and environmental consequences, such as flooding and erosion. Rx5day, on the other hand, measures the highest consecutive five-day precipitation total within a given period. This index is widely used to assess the severity and potential impact of prolonged heavy precipitation events. The rationale for including Rx5day in this analysis is its ability to capture the cumulative effect of precipitation over multiple days, which is often more closely related to flood risks and agricultural impacts compared to single-day extremes.

3.4. Satellite Ranking Based Methodology

In this study, to ensure an objective and reproducible comparison among satellite precipitation products, the ranking of various satellites in detection precipitation was achieved through a structured evaluation using several key statistical metrics, followed by normalization and the computation of a Composite Score (CS) obtained combining three key statistical metrics: root mean square error (RMSE), R, and SDR. RMSE was chosen as the ranking metric instead of the CRMSD used in the Taylor diagram because it captures both bias and deviations, providing a comprehensive measure of the total predictive error. In contrast, the CRMSD in the Taylor diagram primarily focuses on error variability while overlooking bias. By incorporating RMSE into the scoring system, all sources of error are accounted in the ranking, making it a more robust and reliable metric for comparing satellite datasets.

3.4.1. Normalization of Metrics

With this approach, each metric was processed to ensure comparability and to maintain a common interpretation, where values closer to 1 indicate better model performance. In particular, the RMSE was normalized (RMSE′) to a unitless scale and transformed as, so that lower errors resulted in higher scores.

$${RMSE}^{\prime }=1-{\displaystyle \frac{RMSE-{RMSE}_{min}}{{RMSE}_{max}-{RMSE}_{min}}},$$

(9)

Similarly, R′ was included in its standard normalized form, where values close to 1 indicate a strong agreement between model predictions and observations.

$$R^{\prime }={\displaystyle \frac{R-R_{min}}{R_{max}-R_{min}}},$$

(10)

To assess the satellites’ ability to reproduce the observed variability the SDR has been incorporated. Ideally, this ratio should be equal to 1, meaning the model captures the same level of variability as the observations. However, if the ratio is greater than 1, the model overestimates variability, while if it is less than 1, it underestimates it. To ensure that this metric aligns with the others in terms of scale and interpretation, the following transformation has been applied:

$${SDR}^{\prime }=1-\left|{\displaystyle \frac{{\sigma }_{satellite}}{{\sigma }_{observed}}}-1\right|,$$

(11)

Finally, to rank the performance of different satellites, a CS approach was employed. This method integrates the normalized metrics (RMSE′, SDR′, and R′) into a single score by assigning weights to each metric. The weights were systematically varied to explore the influence of different evaluation priorities. For example, if accuracy in precipitation estimation is deemed more critical, the RMSE weight could be set higher. On the other hand, if the main objective is to emphasize the satellite’s ability to replicate the variability observed in the data or to capture the relationship between observed and satellite precipitation, then greater weight should be assigned to the SDR′ or the R′.

3.4.2. Weight Generation and Composite Score Computation

To combine the three normalized metrics, a grid-based weighting scheme was implemented. All possible weight combinations, using a step of 0.01, were systematically generated under the constraint:

$$w_{rmse}+w_{{sdr}^{\prime }}+w_{R^{\prime }}=1$$

(12)

where $w_{rmse},w_{{sdr}^{\prime }},w_{R^{\prime }}\in \left[0,1\right]$.

This procedure produced 5151 valid weight combinations, uniformly covering the full space of trade-offs among the three metrics while ensuring their total always equaled 1. This constraint ensures that the contribution of all metrics remains balanced within a single evaluation framework. The composite performance for each satellite was then calculated as:

$$CS=w_{rmse}·{RMSE}^{\prime }+w_{sd}·{SDR}^{\prime }+w_{R^{\prime }}·R^{\prime },$$

(13)

where $w_{rmse},w_{{sdr}^{\prime }},w_{R^{\prime }}\in \left[0,1\right]$ and $w_{rmse}+w_{{sdr}^{\prime }}+w_{R^{\prime }}=1$.

For each weight combination, the composite score was calculated for all satellites products, and the rankings were generated by ordering satellites based on their scores in descending order.

3.4.3. Ranking and Robustness Analysis

To ensure robust evaluation, the mean composite score and the 5th and 95th percentiles were computed for each satellite across all weight combinations. This provided a measure of the sensitivity of the rankings to variations in the weighting scheme. Finally, the satellites were ranked based on their mean composite scores, with lower-ranked satellites reflecting lower overall performance. This ranking approach highlights the flexibility of the weighting framework in adapting to different evaluation priorities while maintaining fairness in the comparison of satellite datasets. This approach ensured that satellites were ranked according to a balanced evaluation, considering multiple facets of their performance, including their error magnitude, variability reproduction, and the strength of their correlation with observed data. In other words, this methodology provides a thorough, objective way to rank satellites based on their precipitation evaluation performance, considering the key aspects of accuracy, variability, and explanatory power, and taking into account the uncertainties introduced by varying weight combinations. Through this comprehensive approach, the best-performing satellite for precipitation estimation can be identified with greater confidence.

4. Results and Discussion

4.1. Comparison Among the Different Products

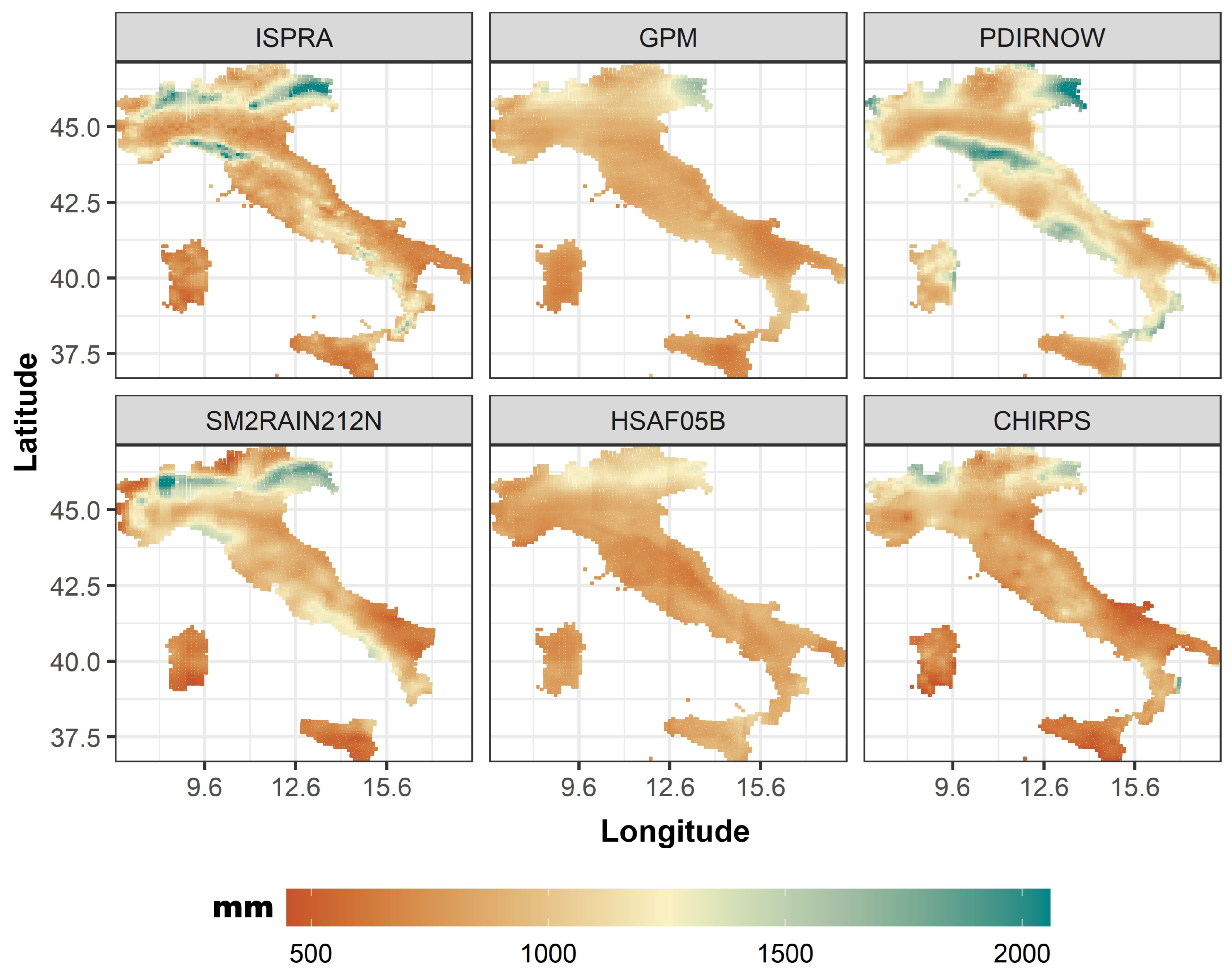
The ISPRA map shows a typical precipitation pattern in Italy, with high precipitation in the north, especially over the Alps and northern Apennines (dark green-blue shades), moderate precipitation in central regions, and lower precipitation in southern Italy and coastal areas (orange shades) (Figure 3).

As regards the SPPs, the GPM tends to smooth out spatial variability compared to ISPRA. In fact, it underestimates precipitation over the Alps and Apennines (missing dark green zones) and shows a more uniform distribution with less contrast between wet and dry areas. Several studies have highlighted the limitations of GPM precipitation products over complex terrain, such as the Alps and Apennines, where steep topographic gradients and frequent orographic precipitation pose significant challenges to satellite-based retrieval algorithms. Satellite sensors, PMW instruments, tend to underestimate precipitation in these regions because they struggle to detect low-level orographic enhancement and shallow convective systems, which often lack strong ice-scattering signatures [47]. The presence of snow-covered ground can further interfere with PMW retrievals, reducing detection efficiency [47]. In the Italian context, Adirosi et al. [48] found that GPM-DPR retrievals underestimate both rainfall and microphysical parameters compared with ground-based disdrometer measurements, particularly over complex terrain, suggesting that the satellite algorithms’ parameterizations may not fully capture natural precipitation variability. Beyond sensor limitations, algorithmic aspects also play a role. Derin et al. [49] showed that IMERG tends to underestimate precipitation in high-elevation regions globally, and that gauge-based corrections only partially mitigate these biases. Moreover, IMERG’s morphing algorithm relies on motion vectors derived from vertically integrated variables such as total column water vapor (TQV), which may be less effective in high-elevation areas where the atmospheric column is thinner and TQV values are lower. Additionally, the performance of GPM products differs between land and ocean surfaces, with generally better agreement over the oceans due to more homogeneous surface emissivity and the absence of orographic effects. This contrast, also noted in the East Asian Summer Monsoon region [50], supports the interpretation that surface heterogeneity and microphysical variability, especially aerosol-induced changes in drop size distributions, affect GPM’s retrieval accuracy over land and mountainous regions.

The PDIRNOW better captures high precipitation zones in northern Italy, especially over the Alps. However, it may slightly overestimate precipitation in some mountainous areas (intense greens) and shows stronger gradients but potentially over-enhanced precipitation patterns in some coastal/mountain regions. The behavior of PDIR-NOW over mountainous areas is highly variable, showing both underestimation and overestimation depending on the geographic and climatic context. As an example, underestimation has been reported in Saudi Arabia [27,51], linked to the IR sensor’s difficulty in detecting warm, shallow orographic clouds, while overestimation has been observed in arid mountainous regions such as the Qinghai–Tibetan Plateau [52] and sub-Saharan Morocco [53], likely due to sub-cloud evaporation or cold non-precipitating clouds. These patterns can be partly explained by the approach used to generate PDIR-NOW, which is based on the fusion of IR-based rain-rate estimates with episodic PMW corrections. This method can accentuate orographic and coastal gradients and, when PMW snapshots are limited, lead to slight positive biases in mountains, consistent with our maps and prior descriptions of PDIR/PDIR-NOW behavior. The SM2RAIN212N closely follows the spatial structure of ISPRA, with good representation of northern and central precipitation peaks. It captures the Alpine ridge and Apennines well, including high precipitation zones. Anyway, there are some overestimation in the far north, but overall, it provides a realistic and detailed distribution. Because SM2RAIN derives rainfall from soil–moisture changes, its estimates can be influenced by topography (through infiltration and runoff) and by the “memory” of antecedent soil moisture. These effects may smooth or displace precipitation signals relative to daily rain maps and can occasionally lead to overestimation in regions with persistently wet soils, such as Northern Italy. While this study did not specifically investigate these mechanisms, previous studies have highlighted them [38,39] and they should be considered as a factor to be taken into account when interpreting the results obtained. The HSAF05B shows a muted precipitation pattern, underestimating high precipitation regions in the north. It seems to be less detailed in representing orographic precipitation and the distribution appears overly smooth and fails to reflect localized precipitation extremes. Finally, the CHIRPS performs quite well in replicating the north–south gradient. Moreover, it captures the general precipitation distribution accurately, with moderate detail in the north. Furthermore, it may slightly underestimate peaks in extreme precipitation zones but offers a balanced performance overall.

Table 3. Strengths and weaknesses of the SCIA-ISPRA gridded dataset and the selected SPPs.

Dataset	Strengths	Weaknesses
ISPRA	High-resolution, observed reference	—
GPM	Smooth, stable coverage	Underestimates orographic precipitation, less spatial contrast
PDIRNOW	Captures extremes well	Possible overestimation in mountain/coastal areas
SM2RAIN212N	Very close to ISPRA, good spatial structure	Slight overestimation in north
HSAF05B	Conservative estimate	Poor orographic detail, underestimates variability
CHIRPS	Balanced, good spatial match to ISPRA	Slight underestimation of extremes

shows the strengths and weaknesses of the SCIA-ISPRA gridded dataset and the selected SPPs. Next sections describe the results of the validation between ground-based and satellite-derived data. Standard scatter plots were not used because a large proportion of the dataset consists of zero-precipitation values masking meaningful variability and weaken correlation patterns. Instead, the categorical performance has been evaluated through the contingency matrix (Table 2), which quantifies hits, misses, and false alarms, and complemented this with statistical indicators and Taylor diagrams. This combination offers a more robust and interpretable assessment of agreement between satellite-derived and ground-based precipitation under conditions dominated by zero or low rainfall.

4.2. Ability of the SPPs to Replicate Observed Daily Precipitation

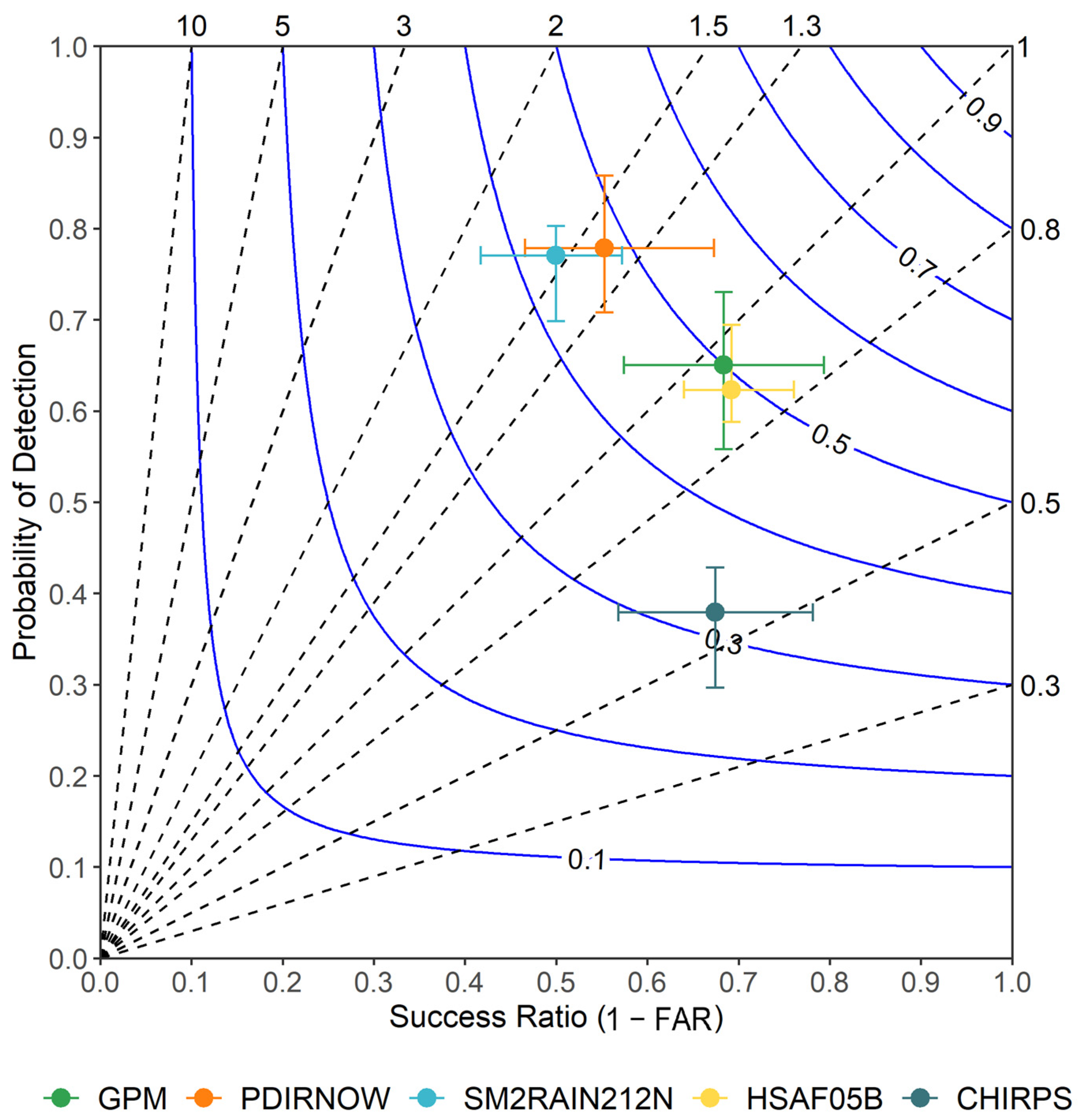
For the analysis of daily precipitation, the dataset was divided into two temporal subsets: annual and seasonal. Figure 4 shows the performance diagram evaluating the annual-scale ability of the five satellite precipitation products to detect precipitation events over Italy. The diagram combines the Probability of Detection (POD) and the Success Ratio (1 − FAR), with curved blue lines representing the Threat Score (TS) and dashed black lines indicating Bias. As a result, the PDIRNOW exhibits the best detection capability, with a high POD about 0.8 and a Success Ratio about 0.5. It lies in a high-skill region of the diagram, although the Bias > 1 suggests some degree of overestimation. The GPM shows the most balanced performance among all datasets. With both POD and Success Ratio around 0.65, and a Bias close to 1, it provides a reliable trade-off between missed detections and false alarms. Its location on higher CSI contours (about 0.5) confirms strong overall performance. The HSAF05B performs similarly to GPM but with slightly lower POD. It also displays greater uncertainty, indicated by wider error bars, which suggests that its reliability may vary depending on time or region. SM2RAIN212N has the highest POD (about 0.8) but a low Success Ratio (about 0.4), meaning it detects most events but frequently produce false alarms. This high false alarm rate (Bias > 2) reduces its practical utility, as reflected by a lower CSI. Finally, the CHIRPS presents the lowest POD (~0.35) but a relatively high Success Ratio (~0.7), showing that it avoids false alarms but misses many events (Bias < 1). This underprediction makes it less suitable for applications requiring high detection sensitivity. In summary, the ideal detection system would lie near the top-right corner (with POD and Success Ratio = 1), which none of the current datasets achieve, highlighting the challenge of balancing detection and false alarms. Among the evaluated datasets, PDIRNOW and GPM demonstrate the highest overall skill, making them suitable choices for precipitation event detection in operational and research settings. Anyway, bias remains a key factor. Datasets with high detection often come with higher false alarms (e.g., SM2RAIN212N), while those with fewer false alarms tend to miss more events (e.g., CHIRPS). Users must consider this trade-off depending on their specific application (e.g., flood forecasting vs. drought monitoring). Error bars suggest variability in performance, potentially linked to spatial or temporal inconsistencies, emphasizing the need for localized validation or hybrid approaches.

As regards the seasonal subset (Figure 5), in Autumn PDIRNOW performs best, with high POD (about 0.8) and moderate Success Ratio (about 0.6), suggesting strong event detection with some overprediction (Bias > 1). The GPM also performs well, slightly lower in POD but better balanced between detection and false alarms. CHIRPS has the lowest POD (about 0.35) but maintains a relatively high Success Ratio, showing its tendency to underdetect but rarely raise false alarms. The SM2RAIN212N shows the usual pattern of high POD and low Success Ratio, indicating frequent overestimations. The HSAF05B lies close to GPM in performance but shows wider error bars. In spring, most datasets (GPM, PDIRNOW, HSAF05B) show better balance than in Autumn, clustering around CSI contours of about 0.5–0.6. The SM2RAIN212N still overpredicts (high POD, low Success Ratio). The CHIRPS again underdetects, with similar placement as in Autumn. The GPM is particularly strong in this season, offering a near-optimal mix of POD and Success Ratio (Bias ≈ 1). Performance is generally strongest in summer, with several datasets approaching the top-right quadrant, indicative of high skill. GPM, HSAF05B, and PDIRNOW all show good balance close to the 0.6–0.7 CSI contours. The CHIRPS still underdetects, but with slightly improved POD compared to other seasons and the SM2RAIN212N continues its trend with a notably high POD and lower reliability. Finally, in winter performance deteriorates across all datasets, with most showing lower POD and Success Ratios. The PDIRNOW maintains high POD but with a steep drop in Success Ratio (about 0.4), reflecting many false alarms. The CHIRPS and HSAF05B struggle significantly, with lower PODs and large uncertainties. The GPM experiences a noticeable drop in POD compared to other seasons, although it still remains fairly balanced.

Seasonal variability is clear, with summer and spring showing the best overall detection skill, while winter tends to challenge all datasets. The GPM stands out for its consistently balanced performance across all seasons, often located near the optimal region with a near-unity Bias. The PDIRNOW consistently achieves high POD, making it valuable for applications where missing an event is costlier than issuing a false alarm. The SM2RAIN212N performs well in detecting events but tends to overestimate occurrences, which might limit its utility where precision is crucial. The CHIRPS performs the most conservatively, with low false alarms but many missed detections, more suited to applications that can tolerate underestimation (e.g., drought monitoring). The HSAF05B is variable in performance and displays relatively high uncertainty, especially in precipitation seasons. Overall, GPM and PDIRNOW are the most reliable performers across seasons, with summer being the most favorable season for precipitation detection by all datasets. However, careful dataset selection should consider the specific season and the tolerance for false alarms vs. missed detections.

The evaluation of satellite-based precipitation products in this study offers a nuanced understanding of their performance in detecting daily precipitation events across various temporal scales. By analyzing metrics such as POD, Success Ratio, and Bias, the study provides insights into the strengths and limitations of each product, contributing to the broader discourse on satellite precipitation estimation. Results obtained for the PDIRNOW product aligns with observations in other regions; for instance, a study over Saudi Arabia reported a POD of 0.73 for PDIRNOW, with a high FAR of 0.80 and a CSI of 0.18, underscoring the product’s proclivity for false alarms despite its detection capabilities [27]. The GPM product demonstrates a balanced performance, indicating a reliable trade-off between missed detections and false alarms. Such balance is crucial for applications requiring consistent performance across varying conditions. Similarly, the HSAF05B product performs comparably to GPM but exhibits greater uncertainty, suggesting variability in reliability depending on temporal or regional factors [26]. The SM2RAIN212N indicates its effectiveness in detecting precipitation events. However, it is characterized by a high rate of false alarms that is consistent with findings in other studies, where similar products have shown limitations in precision due to overestimation tendencies [38]. As regards the CHIRPS, it indicates a conservative approach that minimizes false alarms but may miss many events. This underprediction characteristic has been noted in various regions; for example, in Vietnam, CHIRPS displayed a POD as low as 45% in certain areas, reflecting challenges in detecting all precipitation events. However, its high Success Ratio makes it suitable for applications where false alarms are particularly detrimental [26]. Comparing results of this study with studies from different regions underscores the importance of localized validation. For instance, in Sub-Saharan Morocco, PDIR exhibited low detection capacity with median POD and CSI not exceeding 0.4, and high FAR values reaching up to 1, highlighting the influence of regional climatic conditions on product performance [53]. Similarly, in East and Southern Africa, CHIRPS showed varying performance, with better detection in regions with higher precipitation and challenges in arid areas [54].

4.3. Ability of the SPPs to Replicate Observed Precipitation at Annual and Seasonal Scale

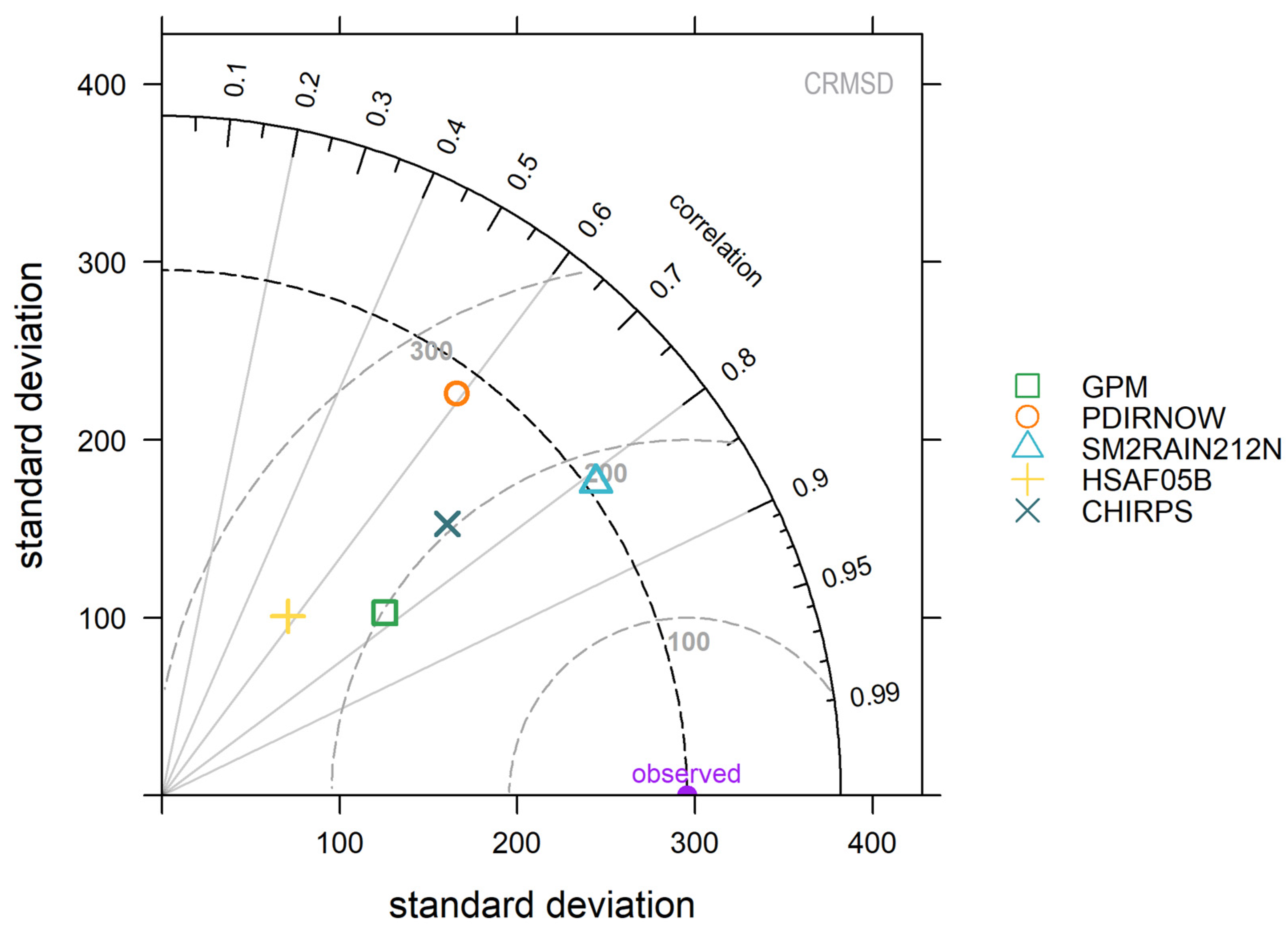
As regards the annual subset, the SM2RAIN212N resulted the closest to the observed point in terms of correlation, standard deviation, and RMS error (Figure 6). In fact, a correlation of about 0.8 indicates a good agreement in temporal patterns and a standard deviation nearly matching that of the observed data suggests accurate representation of variability, exhibiting the best overall performance among all evaluated datasets. The CHIRPS also shows a moderate correlation (about 0.75) and moderate standard deviation, making it a reliable dataset, slightly underestimating the variability if compared to observed values. The low RMS error indicates that it captures the overall pattern well. The GPM shows good correlation (about 0.80), but underestimates standard deviation, suggesting it captures the pattern but not the full variability. The relatively low standard deviation observed in GPM precipitation estimates at the annual scale may reflect a smoothing effect associated with the characteristics of the multi-source fusion algorithm and known limitations of the GPM radar’s sensor, including multiple scattering (MS) and non-uniform beam filling (NUBF) [55,56]. These factors can lead to a slight underestimation of the most intense precipitation events and reduced variability, as observed in our study. Moreover, its position closer to the origin than the observed value indicates less variability in precipitation estimates. The PDIRNOW exhibits a relatively high standard deviation, even overestimating the observed variability. Lower correlation (about 0.6) indicates it struggles to track the timing or pattern of precipitation events and higher RMS error, reflecting less accurate precipitation estimations. The HSAF05B shows the lowest correlation (less than 0.6) among the datasets. Moreover, it underestimates variability and has high RMS error. In general, datasets vary significantly in their ability to replicate observed precipitation with CHIRPS and SM2RAIN212N that resulted the most promising for annual precipitation analysis. On the contrary, caution should be exercised with PDIRNOW and HSAF05B, as their low correlation and error metrics suggest limited reliability for precise analysis.

At seasonal scale, in autumn, the CHIRPS, the GPM and the SM2RAIN212N show the highest correlation (above 0.8), indicating good temporal agreement with observed data. CHIRPS slightly underestimates variability, but maintains a low RMS error, making it one of the most reliable datasets (Figure 7). At the same time, the PDIRNOW and the HSAF05B overestimate variability and have lower correlation, suggesting weaker performance in this season. In spring, all datasets cluster more closely around the observed point indicate better overall performance. In particular, the SM2RAIN212N again shows high correlation and balanced variability, maintaining consistent quality. The CHIRPS and the GPM perform well, with moderate to high correlation and relatively low RMS error. The PDIRNOW slightly overestimates variability but still shows decent correlation. Finally, the HSAF05B has the lowest correlation, suggesting weaker representation of precipitation dynamics. Summer shows generally consistent performance across all datasets. CHIRPS, PDIRNOW and GPM are closest to the observed values. HSAF05B and SM2RAIN212N display greater spread, suggesting more pronounced differences in capturing rainfall during this season.

In winter, the GPM and SM2RAIN212N perform consistently with moderate to high correlation and lower RMS error. The HSAF05B underperforms with low correlation and high RMS error, as seen in other seasons. In summary, at the seasonal scale, the performance of precipitation datasets varies notably across seasons, with certain products demonstrating greater consistency and reliability. CHIRPS, GPM, and SM2RAIN212N emerge as the most reliable datasets overall, particularly in autumn and spring, where they exhibit high correlations (above 0.8) and relatively low RMS errors, indicating strong temporal agreement with observed data and adequate representation of variability. CHIRPS consistently provides a balanced performance, with slightly underestimated variability but high correlation, especially in the cooler seasons. SM2RAIN212N stands out for its robust correlation across all seasons, although it tends to diverge in terms of standard deviation during summer, highlighting the complexity of capturing convective precipitation events typical of that season. GPM shows moderate to good performance, especially in spring and winter, though it tends to smooth out spatial and temporal variability. On the other hand, PDIRNOW and especially HSAF05B show weaker performance across most seasons. PDIRNOW tends to overestimate variability, while HSAF05B consistently suffers from low correlation and high RMS errors, suggesting limitations in representing both the timing and magnitude of seasonal precipitation.

The evaluation of SPPs presented in this study provides a comprehensive assessment of their performance at both annual and seasonal scales in our study region. The superior performance of SM2RAIN212N across most metrics and temporal scales confirms the potential of soil moisture-based precipitation retrieval techniques, especially in regions with limited ground-based observations. This result is consistent with the findings of Brocca et al. [38], who demonstrated the effectiveness of SM2RAIN products in capturing precipitation variability in data-scarce environments, particularly over Australia, Spain, South and North Africa, India, China, the Eastern part of South America, and the central part of the United States. Similarly, CHIRPS performed reliably throughout the year, especially in autumn and spring, supporting the conclusions by Dinku et al. [57], who highlighted CHIRPS’s utility across East Africa. This aligns with earlier studies by Toté et al. [58], which validated CHIRPS in Mozambique, suggesting that its combination of satellite imagery with in situ station data offers a well-balanced representation of precipitation. The GPM dataset displayed generally good temporal agreement but consistently underestimated standard deviation, suggesting a smoothing of precipitation extremes. This pattern is consistent with the limitations noted by Tang et al. [59], who observed similar trends in Mainland China. Unlike previous studies focused solely on specific seasons or annual averages, results of this study highlight that even the best-performing datasets exhibit seasonal sensitivity, particularly evident in summer, where convective events pose substantial challenges. The performance drop during this season, especially for SM2RAIN212N and GPM, is indicative of the complexity in capturing short-lived, high-intensity precipitation events, which remain a challenge for satellite remote sensing globally [60].

4.4. Ability of the SPPs to Replicate Extreme Precipitation Indices

As regards the R95tot, that is the annual total of very wet days (>95th percentile determined from the reference dataset), the GPM is the closest to the observed point (purple), indicating the best match in both standard deviation and correlation (Figure 8). The CHIRPS and the SM2RAIN212N show low correlation (<0.5) but slightly lower variability than observed. HSAF05B also aligns fairly well but has slightly higher variability. The PDIRNOW clearly overestimates variability and shows very low correlation (<0.1), the weakest performance for this index. Concerning the R99tot, indicating the annual total of extremely wet days (>99th percentile), all datasets perform slightly worse here, reflecting the challenge of capturing extreme events. In particular, all the datasets show low correlation. In particular, the GPM and the HSAF05B are close in standard deviation, the CHIRPS and the SM2RAIN212N underestimate variability and the PDIRNOW again overestimates variability and performs poorly in correlation. Finally, for the maximum 5-day precipitation amount (Rx5d) almost all the datasets form a tight cluster near the observed point, except for the PDIRNOW that, once again, greatly overestimates the standard deviation and has poor correlation. This indicates that PDIRNOW amplifies intense precipitation clusters. As a result, the GPM is the most consistently reliable dataset across all indices, the CHIRPS and the SM2RAIN212N tend to underestimate precipitation variability, especially for extremes, the HSAF05B shows moderate performance, and the PDIRNOW has the poorest performance overall.

These findings are consistent with similar validation studies conducted in diverse climatological and topographic settings. For instance, Goodarzi et al. [61] analyzed SPPs over Iran and also found that the GPM IMERG product provided a superior performance in detecting heavy precipitation events compared to other datasets. In East Africa, Dinku et al. [57] found CHIRPS to be among the best-performing SPPs also in detecting precipitation extremes, but acknowledged its tendency to smooth out intense convective events, particularly at sub-seasonal scales.

4.5. Comparison of Satellite Rainfall Detection Accuracy Using the Critical Success Index

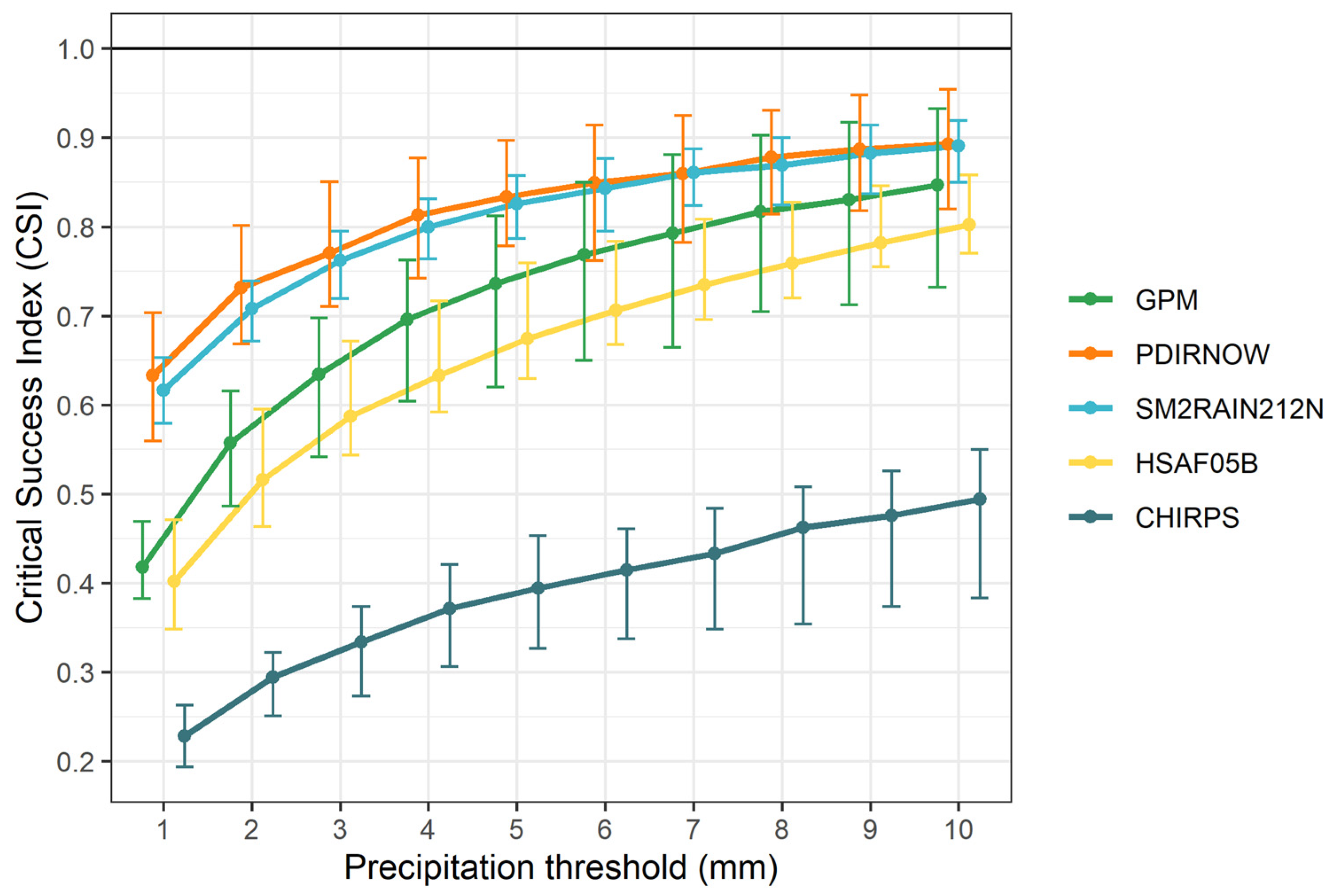
The Critical Success Index (CSI) was evaluated across precipitation thresholds ranging from 1 mm to 10 mm for the different satellite-based precipitation products (Figure 9). Results show that PDIRNOW and SM2RAIN212N consistently achieve the highest CSI scores, exceeding 0.8 for thresholds greater than 5 mm and approaching values close to 0.9 at the upper end of the range. These products demonstrate not only higher detection skill but also greater stability, as reflected by narrower uncertainty ranges. Confidence intervals, represented by the 5th and 95th percentiles, indicate that the differences between the best-performing datasets and the others are statistically significant across almost all thresholds. GPM exhibits moderate performance, with CSI values increasing steadily with the precipitation threshold and reaching approximately 0.8 at 10 mm, though remaining systematically lower than PDIRNOW and SM2RAIN212N. HSAF05B shows lower CSI values, maintaining a performance gap of approximately 0.1 compared to GPM across all thresholds. In contrast, CHIRPS presents the lowest CSI scores, starting below 0.3 at 1 mm and not exceeding 0.5 even at the highest thresholds, combined with visibly wider uncertainty ranges. This suggests a lower reliability in detecting precipitation events. Overall, the analysis highlights that PDIRNOW and SM2RAIN212N provide the most accurate and robust detection across varying precipitation intensities, whereas CHIRPS appears less suitable for operational or research applications requiring high detection reliability. Comparative analyses with studies from diverse geographical regions further confirm these findings. For instance, in Ethiopia, Degefu et al. [62] assessed the performance of various precipitation products during different rainy seasons. Their findings indicated that while products like GPM/IMERG achieved high CSI scores (up to 1.0) during certain seasons, the performance varied significantly across regions and seasons, highlighting the challenges in achieving consistent detection accuracy. Similarly, in Ghana, Agyekum et al. [63] compared GPM and ERA5 products against a dense rain gauge network during a severe flooding event. GPM outperformed ERA5 with CSI values ranging from 0.56 to 0.64 across different sectors, yet these scores were still below the levels achieved by PDIRNOW and SM2RAIN212N in this study. Finally, in Iran, a comprehensive evaluation by Macharia et al. [64] of four high-resolution satellite precipitation products revealed that while certain products performed adequately in specific regions, none consistently achieved high CSI scores across all areas, emphasizing the need for region-specific calibration and validation.

4.6. Satellite Composite Performance Ranking

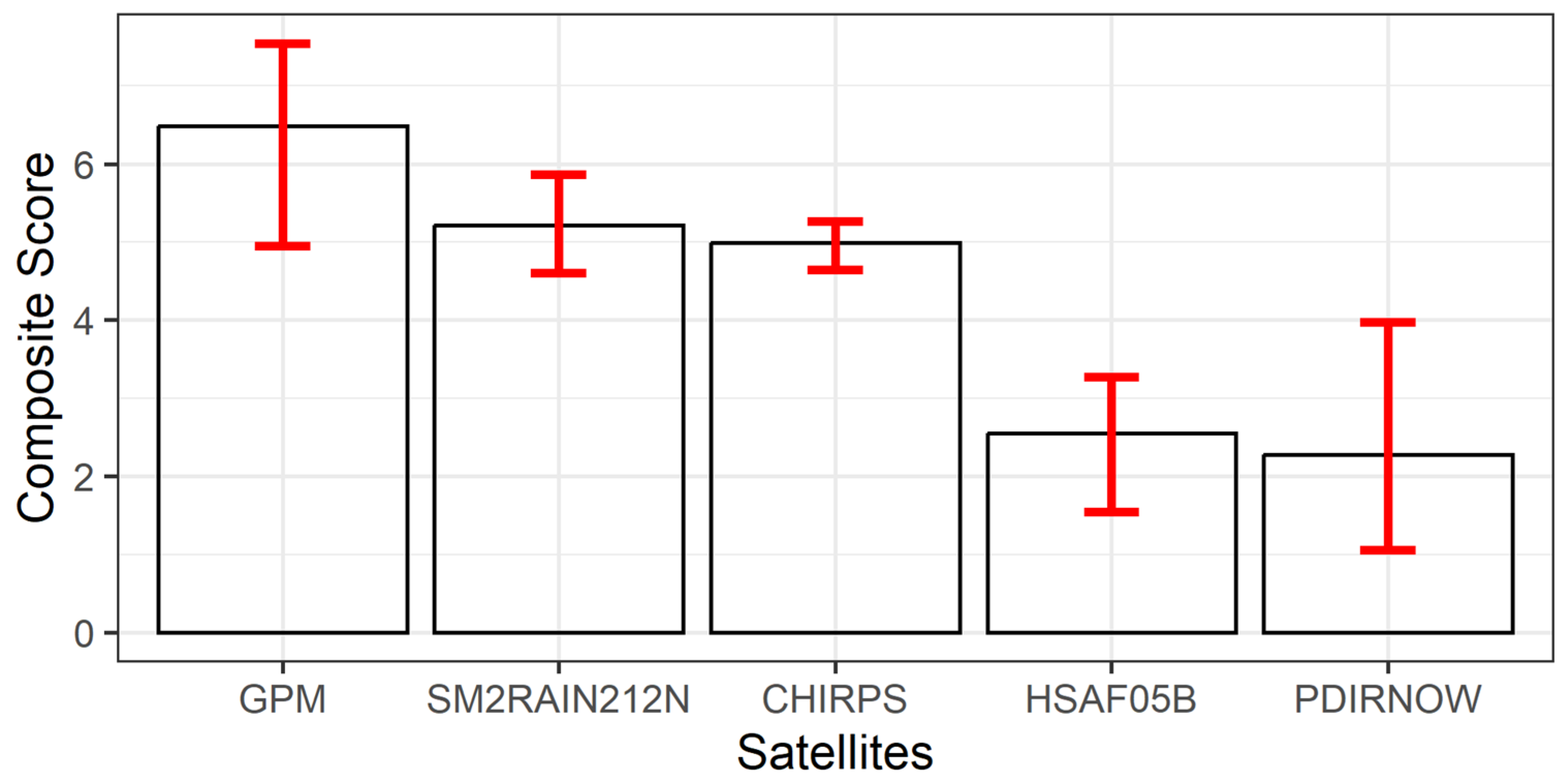
The satellite ranking based on the CS shows that GPM achieved the highest mean composite score (Figure 10). However, it also displayed a relatively large uncertainty range between the 5th and 95th percentiles, indicating some sensitivity to the weighting of the evaluation metrics. SM2RAIN212N ranked second with a slightly lower mean score than GPM but showed a narrower uncertainty interval, suggesting more stable performance across different weighting combinations. CHIRPS followed closely with a comparable mean score but with slightly higher uncertainty compared to SM2RAIN212N.

HSAF05B and PDIRNOW obtained the lowest composite scores. HSAF05B performed marginally better than PDIRNOW and exhibited a smaller uncertainty range, indicating consistently low performance regardless of the weighting scheme. PDIRNOW showed both a low mean score and a wide uncertainty interval, reflecting higher sensitivity to changes in the metric prioritization.

Overall, GPM and SM2RAIN212N demonstrated the best performance among the evaluated satellite products, while HSAF05B and PDIRNOW consistently ranked lower across the different weighting scenarios.

4.7. Data Latency and Product Uncertainties

To provide a clear overview of the characteristics and limitations of the analyzed products, this section focuses on data latency and its implications for operational and research applications. Selecting an appropriate SPP for a given purpose inherently involves a trade-off between data latency and retrieval accuracy. The five products analyzed in this study exhibit distinct features that influence their suitability for operational or research-oriented use.

As summarized in Table 1, the latency of these SPPs varies considerably, ranging from near real-time (NRT) availability to climatological time scales. Products with the lowest latency, such as HSAF05B and PDIRNOW, which provide data 15–60 min after observation, are particularly suitable for operational applications and hydrological early warning systems (it should be noted that HSAF05B was discontinued in January 2023 and replaced by the HSAF61B product, available since July 2020, which remains classified as NRT, although with a slightly higher latency of about 30 min). SM2RAIN212N, with a latency of 2–5 days, belongs to the quasi–real-time category and is appropriate for short-term hydrological monitoring and water resource management. While slower than the NRT products, it still allows timely assessment of rainfall events and their hydrological impacts. In contrast, CHIRPS and GPM have considerably higher latencies (about 2–3 weeks and 3.5 months, respectively), which limits their use in real-time operations. However, these products are well suited for post-event analyses, drought monitoring, and climatological studies, where accuracy is prioritized over immediacy.

Latency differences are closely linked to the intrinsic uncertainties of each product, which directly affect their performance and operational applicability. PDIRNOW and SM2RAIN212N demonstrate strong detection capabilities but tend to overestimate rainfall intensity, potentially leading to false alarms. Previous studies have also noted that SM2RAIN212N may underestimate peak rainfall and occasionally produce spurious precipitation events. Despite these limitations, their near- and quasi–real-time availability makes them valuable tools for flood forecasting and rapid hydrological response. CHIRPS, by contrast, exhibits more conservative behavior, generally underestimating intense precipitation events while providing stable and reliable estimates over longer time scales, making it particularly suitable for drought monitoring and climatological analysis. HSAF05B shows a pronounced seasonal bias, with lower reliability during colder months, reflecting the known limitations of infrared-based algorithms in distinguishing between precipitating and non-precipitating clouds at low temperatures. Finally, GPM emerges as the most balanced and accurate product overall; however, its high latency restricts its use to research and climatological validation rather than operational applications.

In summary, these results emphasize that the choice of an SPP should carefully balance timeliness and accuracy according to the intended application. By explicitly considering both the inherent uncertainties of each product and its data latency, users and future applications can make informed decisions about which product best meets their operational or research needs.

5. Conclusions

This study assessed the performance of several SPPs in reproducing observed daily precipitation, annual and seasonal precipitation patterns, and extreme precipitation indices over the study region. Results demonstrate that while no single dataset excels across all metrics, some products offer more consistent and reliable performance than others depending on the application and season.

The GPM emerged as the most balanced and reliable product overall, particularly for applications requiring a compromise between event detection and accuracy. PDIRNOW showed high detection ability but suffered from overestimation and higher false alarm rates. SM2RAIN212N demonstrated strong detection and temporal correlation but often overestimated variability. CHIRPS displayed conservative detection patterns with low false alarms but missed numerous events, while HSAF05B showed lower reliability and higher uncertainty, especially in precipitation seasons.

The key findings can be summarized as follows:

• Daily Precipitation Detection: GPM offered the best balance between detection, false alarms, and bias, performing consistently across seasons. PDIRNOW had the highest detection but also high false alarms, favoring detection-focused applications. SM2RAIN212N overpredicted events, while CHIRPS was conservative, with fewer false alarms but more missed detections. HSAF05B resembled GPM but showed less reliability due to greater variability.
• Annual and Seasonal Precipitation Replication: SM2RAIN212N showed the highest annual correlation and closely matched precipitation variability. CHIRPS followed with good performance and low RMS error despite slight underestimation. GPM performed well but underestimated summer variability, while PDIRNOW and HSAF05B showed poor correlation and higher errors, especially in winter.
• Seasonal Performance: Dataset performance was highest in spring and summer, with closer alignment to observed metrics. GPM, CHIRPS, and SM2RAIN212N performed well in autumn, while winter showed the weakest results overall. GPM stood out for its consistent seasonal performance and near-unity Bias.
• Extreme Precipitation Indices: GPM best captured R95tot, showing strong agreement with observed data. All datasets struggled with R99tot, reflecting challenges in detecting extreme precipitation. Most performed well on Rx5d, though PDIRNOW overestimated variability and showed poor correlation.

Overall, the findings highlighted the importance of selecting SPPs based on the specific requirements of the intended application, including seasonality and tolerance for false detections. In particular, the variability in performance across datasets and metrics underscores the need for multi-product approaches or hybrid solutions. Moreover, a critical aspect for the adoption of these products in operational contexts is their latency. Products such as PDIRNOW and HSAF05B provide data in near real-time (minutes), making them essential for early warning systems and flood forecasting. Conversely, CHIRPS and GPM exhibit latencies of weeks or months and are thus more suitable for climatological and research studies. Users should be aware that selecting a low-latency, operationally focused product versus a high accuracy, research-oriented product represents a fundamental trade-off. Future applications could benefit from integrating low-latency, detection-oriented products with higher accuracy datasets through calibration or fusion approaches to mitigate the intrinsic uncertainties of each estimate.