GRADE: A Generalization Robustness Assessment via Distributional Evaluation for Remote Sensing Object Detection
Highlights
- We propose the GRADE (Generalization Robustness Assessment via Distributional Evaluation) framework, an evaluation paradigm that systematically links model performance degradation (the effect) to quantifiable data distribution shifts (the cause), moving beyond traditional “black-box” metrics like mAP.
- The framework introduces hierarchical divergence metrics (Scene-level Fréchet Inception Distance (FID) and Instance-level FID) to create an adaptively weighted Generalization Score (GS) that demonstrates high fidelity to empirical model rankings across diverse remote sensing datasets.
- The GRADE framework provides an analytical tool that allows researchers to attribute generalization failure to specific sources (e.g., failure to adapt to new background contexts vs. novel object appearances), guiding targeted model improvement.
- This work establishes a standardized and interpretable protocol for comparing the cross-domain robustness of object detectors, enabling fairer and more reliable model selection for real-world deployment scenarios.
Abstract
1. Introduction
- A Principled Framework for Generalization Assessment: We propose the GRADE framework, a novel paradigm that moves beyond conventional i.i.d. evaluation protocols by explicitly integrating distributional divergence analysis with performance degradation modeling. This protocol provides granular, analytical insights into why a model’s performance declines, not just by how much, attributing failure to specific types of domain shift.
- Hierarchical Distributional Divergence Metrics: We introduce Scene-level and Instance-level FID as specialized metrics to characterize and disentangle distribution shifts at distinct semantic levels (context vs. object). These metrics are integrated with performance measures into an adaptively weighted Generalization Score (GS) that facilitates a fine-grained, interpretable assessment of model vulnerabilities.
- Standardized and Empirically Validated Paradigm: We establish a standardized and reproducible evaluation pipeline and rigorously validate it across multiple public benchmarks and state-of-the-art models. Our extensive empirical results demonstrate that the framework maintains high consistency and stability, providing a reliable and transferable methodology for assessing and comparing cross-domain robustness in a fair and insightful manner.
2. Related Work
2.1. Remote Sensing Object Detection
2.2. Quantifying Data Distribution Differences
2.3. Generalization Evaluation of Object Detection Models
3. Methodology
3.1. The GRADE Framework: A Principled Overview
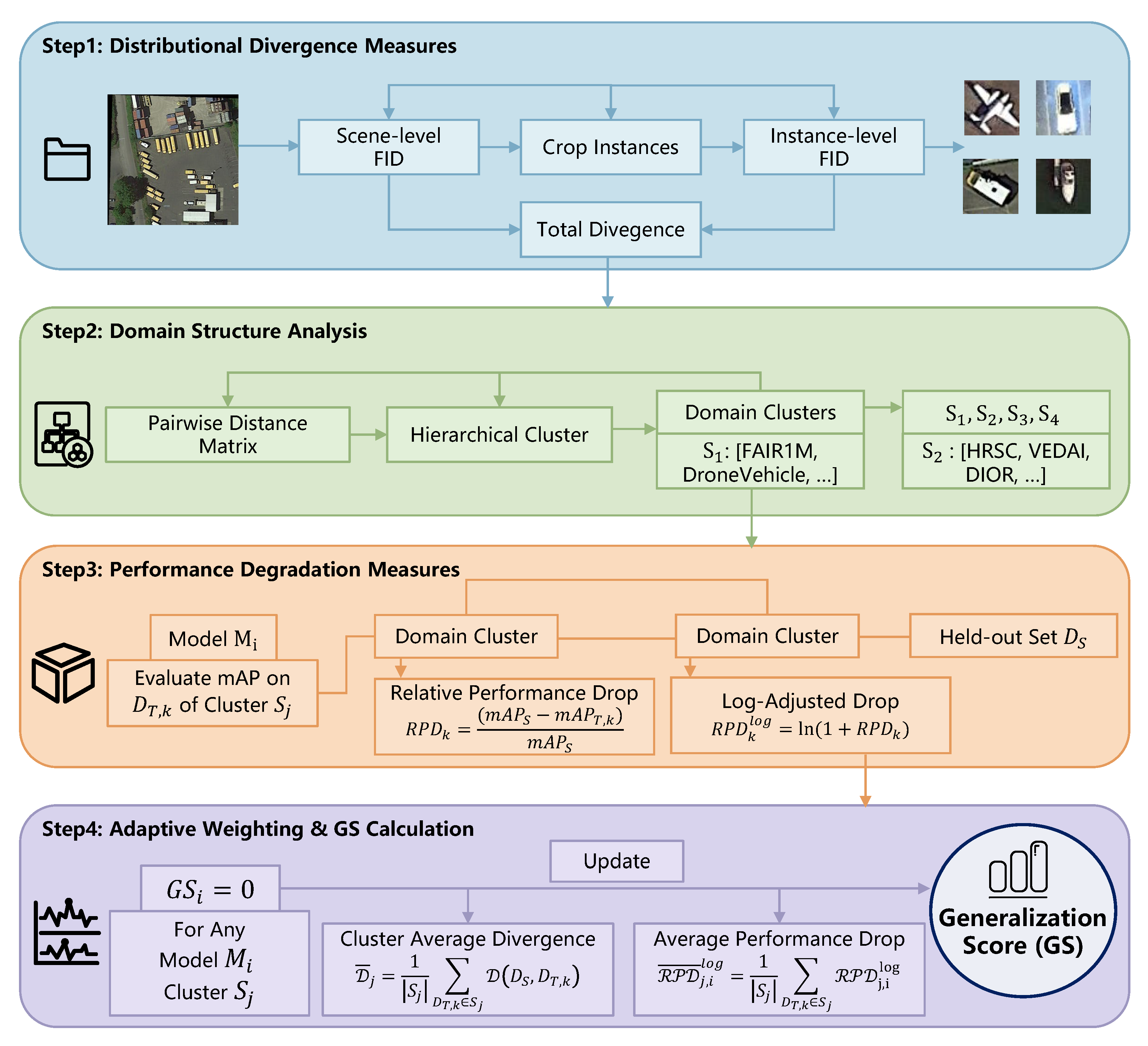
3.2. Distributional Divergence Measures
| Algorithm 1 GRADE: Generalization Robustness Assessment Framework |
|
3.2.1. Theoretical Foundation and In-Depth Formulation of FID
- Term 1: Squared Euclidean Distance between Mean Vectors (): This term quantifies the dissimilarity in the “center of mass” of the two feature distributions. It captures systematic, global shifts that affect the entire dataset. In remote sensing, a large value for this term might signify a bulk translation of the feature manifold due to a change in overall scene brightness (e.g., different sun angles or sensor exposure), a consistent color cast from seasonal variation (e.g., lush green summer landscapes vs. arid brown winter ones), or a fundamental difference in predominant land cover (e.g., urban vs. agricultural). It effectively measures the difference in the average feature activations across all samples.
- Term 2: Trace of the Covariance Discrepancy: This more intricate term measures the difference in the internal structure, or “shape”, of the feature distributions as captured by their covariance matrices and . It can be geometrically interpreted as the work required to optimally transform one distribution’s covariance ellipsoid into the other’s through scaling and rotation of its principal axes. A large value here indicates nuanced structural shifts, which can be further decomposed:
- –
- Difference in Variance (related to and ): The trace of a covariance matrix represents the total variance across all feature dimensions, which serves as a proxy for feature diversity or heterogeneity. For instance, a dataset spanning multiple continents and weather conditions will naturally exhibit higher total variance than a dataset from a single geographical region under clear skies. This term captures such differences in diversity.
- –
- Difference in Correlation (Off-diagonal elements and matrix product): The term is a matrix geometric mean that elegantly handles the interaction between the two covariance structures. It penalizes misalignment in the principal axes of variation, capturing changes in how features co-vary. For example, in a port dataset, features corresponding to ships might consistently co-occur with features for docks. If a target dataset consists of ships in the open sea, this correlation structure would be broken. This term is highly sensitive to such subtle but crucial changes in feature relationships.
3.2.2. Hierarchical FID Metrics for Diagnostic Insight
- Scene-level FID (): This metric is computed using feature vectors extracted from entire, uncropped images. It is therefore designed to measure shifts in the ambient visual domain. This global measure is highly sensitive to changes in background context (e.g., urban vs. rural, desert vs. forest), atmospheric conditions (e.g., clear, hazy, cloudy), global illumination models (e.g., time of day, shadows), and sensor-specific characteristics or artifacts. A high value strongly suggests that a model’s performance degradation may arise from its inability to adapt to novel environmental contexts.
- Instance-level FID (): In contrast, this metric focuses exclusively on the objects of interest by isolating them from their contextual background. To compute it, we first use the ground-truth bounding boxes to crop tight patches around each object. Features are then extracted only from these cropped patches. By design, quantifies the divergence in object-centric attributes. This includes fine-grained intra-class variations (e.g., different models of aircraft), object texture and material properties, object scale distribution, common occlusion patterns, and aspect ratios. A high value indicates that the model’s failure is likely attributable to an inability to recognize novel object appearances, even if the background context remains familiar.
3.3. Generalization Score (GS) Formulation
3.3.1. Relative Performance Drop ()
3.3.2. Adaptive Weighting and Final Score Formulation
- As , the weights approach a uniform distribution (), effectively resulting in a simple average of performance drops across clusters. This represents a “risk-neutral” evaluation.
- As , the softmax function approaches an argmax, placing almost all weight () on the single most divergent cluster and ignoring all others. This corresponds to a “worst-case” or “risk-averse” evaluation.
4. Experiments
4.1. Evaluation Models and Datasets
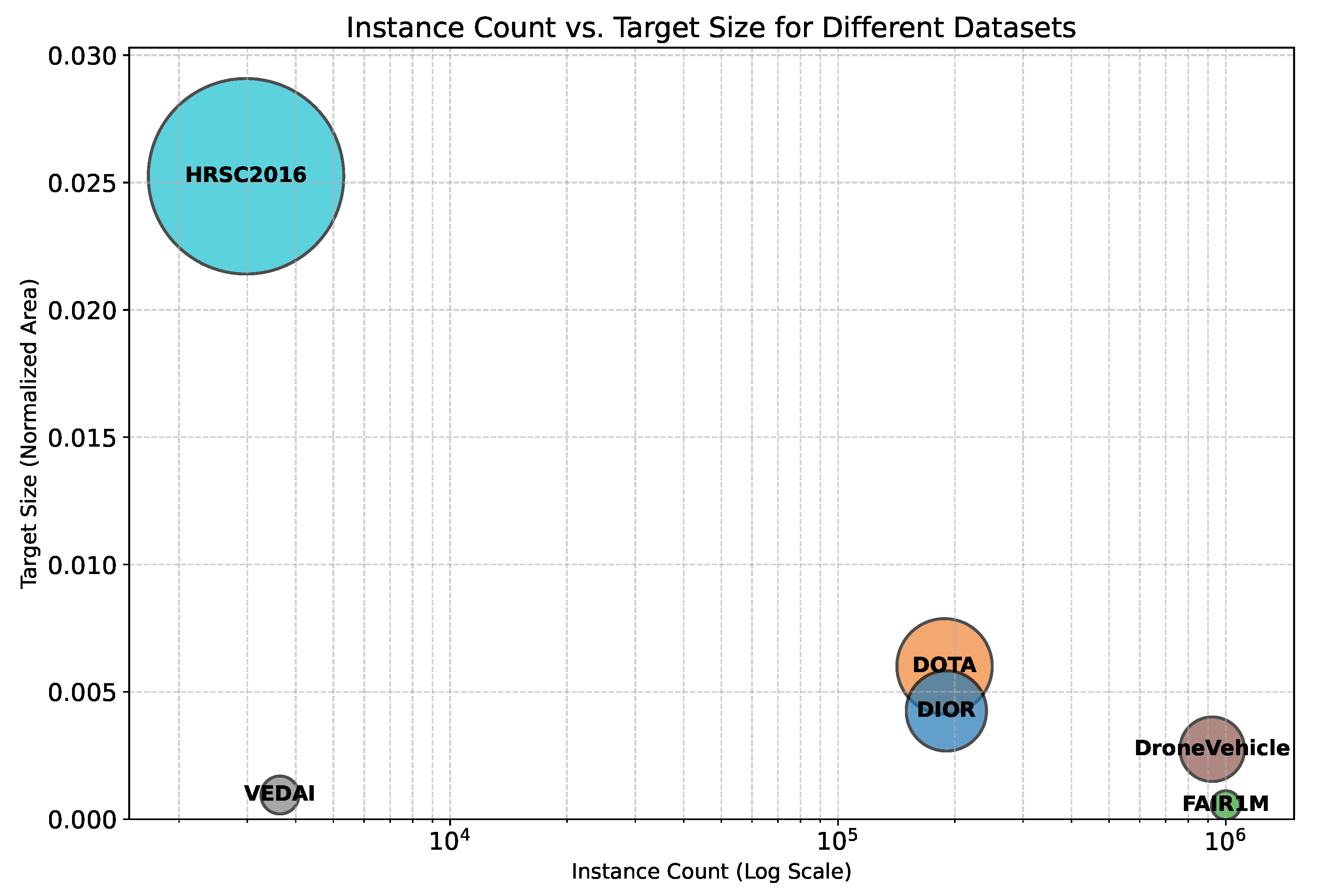
4.2. Dataset Clustering and Visualization Analysis
4.3. Generalization Experiment Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dai, Y.; Zou, M.; Li, Y.; Li, X.; Ni, K.; Yang, J. DenoDet: Attention as Deformable Multisubspace Feature Denoising for Target Detection in SAR Images. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 4729–4743. [Google Scholar] [CrossRef]
- Pang, D.; Shan, T.; Ma, Y.; Ma, P.; Hu, T.; Tao, R. LRTA-SP: Low-Rank Tensor Approximation with Saliency Prior for Small Target Detection in Infrared Videos. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 2644–2658. [Google Scholar] [CrossRef]
- Ni, K.; Yuan, C.; Zheng, Z.; Wang, P. SAR Image Time Series for Land Cover Mapping via Sparse Local–Global Temporal Transformer Network. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 12581–12597. [Google Scholar] [CrossRef]
- Zhao, Z.; Wen, Z.; Xue, C.; Cui, Z.; Hou, X.; Zhu, H.; Mu, Y.; Liu, Z.; Xia, Z.; Liu, X. Improved Clutter Suppression and Detection of Moving Target with a Fully Polarimetric Radar. Remote Sens. 2025, 17, 2975. [Google Scholar] [CrossRef]
- Ringwald, T.; Stiefelhagen, R. Adaptiope: A Modern Benchmark for Unsupervised Domain Adaptation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 5–9 January 2021; pp. 101–110. [Google Scholar]
- Hou, F.; Zhang, Y.; Dong, J.; Fan, J. End-to-End Model Enabled GPR Hyperbolic Keypoint Detection for Automatic Localization of Underground Targets. Remote Sens. 2025, 17, 2791. [Google Scholar] [CrossRef]
- Liu, Y.; Zou, Y.; Qiao, R.; Liu, F.; Lee, M.L.; Hsu, W. Cross-Domain Feature Augmentation for Domain Generalization. In Proceedings of the Thirty-Third International Joint Conference on Artificial Intelligence (IJCAI), Macao, China, 3–9 August 2024; pp. 1146–1154. [Google Scholar]
- Xia, G.; Bai, X.; Ding, J.; Zhu, Z.; Belongie, S.; Luo, J. DOTA: A Large-Scale Dataset for Object Detection in Aerial Images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Sun, X.; Wang, P.; Yan, Z.; Xu, F.; Wang, R.; Diao, W.; Chen, J.; Li, J.; Feng, Y.; Xu, T.; et al. FAIR1M: A Benchmark Dataset for Fine-grained Object Recognition in High-Resolution Remote Sensing Imagery. ISPRS J. Photogramm. Remote Sens. 2022, 184, 116–130. [Google Scholar] [CrossRef]
- Sun, Y.; Cao, B.; Zhu, P.; Hu, Q. Drone-based RGB-infrared Cross-Modality Vehicle Detection via Uncertainty-aware Learning. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 6700–6713. [Google Scholar] [CrossRef]
- Al-Emadi, S.A.; Yang, Y.; Ofli, F. Benchmarking Object Detectors under Real-World Distribution Shifts in Satellite Imagery. In Proceedings of the Computer Vision and Pattern Recognition Conference (CVPR), Nashville, TN, USA, 11–15 June 2025; pp. 8299–8309. [Google Scholar]
- He, T.; Sun, K.; Duan, Y.; Cui, W.; Wang, Z.; Gao, S.; Yao, Y.; Chen, Z. ViTrans: Inter-Frame Alignment Enhancement for Moving Vehicle Detection in Satellite Videos with Stabilization Offsets. Remote Sens. 2025, 17, 2973. [Google Scholar] [CrossRef]
- Li, D.; Yang, Y.; Song, Y.; Hospedales, T. Deeper, Broader and Artier Domain Generalization. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Koh, P.W.; Sagawa, S.; Marklund, H.; Xie, S.M.; Zhang, M.; Balsubramani, A.; Hu, W.; Yasunaga, M.; Phillips, R.L.; Gao, I.; et al. WILDS: A Benchmark of In-the-Wild Distribution Shifts. In Proceedings of the International Conference on Machine Learning (ICML), Virtual Event, 18–24 July 2021; pp. 5637–5664. [Google Scholar]
- Mao, X.; Chen, Y.; Zhu, Y.; Chen, D.; Su, H.; Zhang, R.; Xue, H. COCO-O: A Benchmark for Object Detectors under Natural Distribution Shifts. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023; pp. 6339–6350. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Cai, Z.; Vasconcelos, N. Cascade R-CNN: Delving into High Quality Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 6154–6162. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.-Y.; Berg, A.C. SSD: Single Shot Multibox Detector. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 21–37. [Google Scholar]
- Zhang, Z.; Lu, X.; Cao, G.; Yang, Y.; Jiao, L.; Liu, F. ViT-YOLO: Transformer-based YOLO for Object Detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 2799–2808. [Google Scholar]
- Sapkota, R.; Cheppally, R.H.; Sharda, A.; Karkee, M. YOLO26: Key Architectural Enhancements and Performance Benchmarking for Real-Time Object Detection. arXiv 2025, arXiv:2509.25164. [Google Scholar] [CrossRef]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-End Object Detection with Transformers. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 213–229. [Google Scholar]
- Li, F.; Zhang, H.; Liu, S.; Guo, J.; Ni, L.M.; Zhang, L. DN-DETR: Accelerate DETR Training by Introducing Query Denoising. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 13619–13627. [Google Scholar]
- Chen, Y.; Liu, B.; Yuan, Y. PR-Deformable DETR: DETR for Remote Sensing Object Detection. IEEE Geosci. Remote Sens. Lett. 2024, 21, 2506105. [Google Scholar] [CrossRef]
- Zhang, S.; Song, F.; Liu, X.; Hao, X.; Liu, Y.; Lei, T.; Jiang, P. Text Semantic Fusion Relation Graph Reasoning for Few-Shot Object Detection on Remote Sensing Images. Remote Sens. 2023, 15, 1187. [Google Scholar] [CrossRef]
- Yao, L.; Han, J.; Liang, X.; Xu, D.; Zhang, W.; Li, Z.; Xu, H. DetCLIPv2: Scalable Open-Vocabulary Object Detection Pre-Training via Word-Region Alignment. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 23497–23506. [Google Scholar]
- Liu, S.; Zeng, Z.; Ren, T.; Li, F.; Zhang, H.; Yang, J.; Jiang, Q.; Li, C.; Yang, J.; Su, H.; et al. Grounding DINO: Marrying DINO with Grounded Pre-Training for Open-Set Object Detection. In Proceedings of the European Conference on Computer Vision (ECCV), Milan, Italy, 29 September –4 October 2024; pp. 38–55. [Google Scholar]
- Van Erven, T.; Harremos, P. Rényi Divergence and Kullback-Leibler Divergence. IEEE Trans. Inf. Theory 2014, 60, 3797–3820. [Google Scholar] [CrossRef]
- Li, C.; Chang, W.; Cheng, Y.; Yang, Y.; Poczos, B. MMD GAN: Towards Deeper Understanding of Moment Matching Network. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–9 December 2017; Volume 60, pp. 1–11. [Google Scholar]
- YU, Y.; Zhang, W.; Deng, Y. Frechet Inception Distance (FID) for Evaluating GANs. China Univ. Min. Technol. Beijing Grad. Sch. 2021, 3, 1–7. [Google Scholar]
- Cai, X.; Lai, Q.; Wang, Y.; Wang, W.; Sun, Z.; Yao, Y. Poly Kernel Inception Network for Remote Sensing Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024. [Google Scholar]
- Michaelis, C.; Mitzkus, B.; Geirhos, R.; Rusak, E.; Bringmann, O.; Ecker, A.S.; Bethge, M.; Brendel, W. Benchmarking Robustness in Object Detection: Autonomous Driving When Winter is Coming. arXiv 2019, arXiv:1907.07484. [Google Scholar]
- Han, J.; Ding, J.; Xue, N.; Xia, G. ReDet: A Rotation-Equivariant Detector for Aerial Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021. [Google Scholar]
- Ding, J.; Xue, N.; Long, Y.; Xia, G.; Lu, Q. Learning ROI Transformer for Oriented Object Detection in Aerial Images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Li, W.; Chen, Y.; Hu, K.; Zhu, J. Oriented RepPoints for Aerial Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022. [Google Scholar]
- Pu, C.; Yu, J.; Su, W.; Liu, T. Rotated R-CNN: A Two-Stage Object Detection Method Adapted To Oriented Bounding Boxes. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 27–30 October 2024. [Google Scholar]
- Liu, Y.; Sun, X.; Shao, W.; Yuan, Y. S2ANet: Combining Local Spectral and Spatial Point Grouping for Point Cloud Processing. Virtual Real. Intell. Hardw. 2024, 6, 267–279. [Google Scholar] [CrossRef]
- Yang, X.; Yan, J.; Feng, Z.; He, T. R3Det: Refined Single-Stage Detector with Feature Refinement for Rotating Object. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021. [Google Scholar]
- Wan, G.; Cheng, G.; Meng, L.; Han, J. Object detection in optical remote sensing images: A survey and a new benchmark. ISPRS J. Photogramm. Remote. Sens. 2020, 159, 296–307. [Google Scholar] [CrossRef]
- Liu, Z.; Yuan, L.; Weng, L.; Yang, Y. A High Resolution Optical Satellite Image Dataset for Ship Recognition and Some New Baselines. In Proceedings of the International Conference on Pattern Recognition Applications and Methods (CPRAM), Porto, Portugal, 24–26 February 2017. [Google Scholar]
- Razakarivony, S.; Jurie, F. Vehicle detection in aerial imagery: A small target detection benchmark. J. Vis. Commun. Image Represent. 2016, 34, 187–203. [Google Scholar] [CrossRef]



| Model | RGI (Pseudo-GT) | RGI Rank | GS (Ours) | GS Rank |
|---|---|---|---|---|
| ReDet | 2.1357 | 1 | 0.5286 | 1 |
| RoITrans | 1.5937 | 2 | 0.5771 | 2 |
| Oriented RCNN | 1.4872 | 3 | 0.5842 | 3 |
| S2ANet | 1.4560 | 4 | 0.5988 | 4 |
| R3Det | 1.3310 | 5 | 0.6192 | 5 |
| Oriented RepPoints | 1.3192 | 6 | 0.6256 | 6 |
| Model | RGI (Pseudo-GT) | RGI Rank | GS (Ours) | GS Rank |
|---|---|---|---|---|
| ReDet | 2.4104 | 1 | 0.5002 | 1 |
| S2ANet | 2.0007 | 2 | 0.5274 | 2 |
| R3Det | 1.8764 | 3 | 0.5400 | 3 |
| Oriented RepPoints | 1.8729 | 4 | 0.5401 | 4 |
| Oriented RCNN | 1.7675 | 5 | 0.5422 | 5 |
| RoITrans | 1.5960 | 6 | 0.5624 | 6 |
| Model | RGI (Pseudo-GT) | RGI Rank | GS (Ours) | GS Rank |
|---|---|---|---|---|
| ReDet | 1.8576 | 1 | 0.5884 | 1 |
| RoITrans | 1.3516 | 2 | 0.6425 | 2 |
| Oriented RCNN | 1.2030 | 3 | 0.6532 | 3 |
| S2ANet | 1.2000 | 4 | 0.6601 | 4 |
| R3Det | 1.1460 | 5 | 0.6655 | 5 |
| Oriented RepPoints | 1.1009 | 6 | 0.6822 | 6 |
| Model | RGI (Pseudo-GT) | RGI Rank | GS (Ours) | GS Rank |
|---|---|---|---|---|
| ReDet | 2.1323 | 1 | 0.5600 | 1 |
| S2ANet | 1.7477 | 2 | 0.5864 | 2 |
| R3Det | 1.6914 | 3 | 0.5887 | 3 |
| Oriented RepPoints | 1.6546 | 4 | 0.5967 | 4 |
| Oriented RCNN | 1.4803 | 5 | 0.6112 | 5 |
| RoITrans | 1.3539 | 6 | 0.6277 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Zhang, Y.; Bai, B.; Yu, X.; Shu, X.; Dai, Y. GRADE: A Generalization Robustness Assessment via Distributional Evaluation for Remote Sensing Object Detection. Remote Sens. 2025, 17, 3771. https://doi.org/10.3390/rs17223771
Wang D, Zhang Y, Bai B, Yu X, Shu X, Dai Y. GRADE: A Generalization Robustness Assessment via Distributional Evaluation for Remote Sensing Object Detection. Remote Sensing. 2025; 17(22):3771. https://doi.org/10.3390/rs17223771
Chicago/Turabian StyleWang, Decheng, Yi Zhang, Baocun Bai, Xiao Yu, Xiangbo Shu, and Yimian Dai. 2025. "GRADE: A Generalization Robustness Assessment via Distributional Evaluation for Remote Sensing Object Detection" Remote Sensing 17, no. 22: 3771. https://doi.org/10.3390/rs17223771
APA StyleWang, D., Zhang, Y., Bai, B., Yu, X., Shu, X., & Dai, Y. (2025). GRADE: A Generalization Robustness Assessment via Distributional Evaluation for Remote Sensing Object Detection. Remote Sensing, 17(22), 3771. https://doi.org/10.3390/rs17223771








