An Imaging Method for Marine Targets in Corner Reflector Jamming Scenario Based on Time–Frequency Analysis and Modified Clean Technique
Abstract
1. Introduction
- (1)
- This manuscript establishes motion models for two types of targets in the scenario: rigid ship targets and non-rigid corner reflector arrays. It derives the expression for the residual Doppler caused by motion and analyzes the Doppler distribution characteristics of the two types of targets. The conclusion drawn is that the Doppler parameters of the ship target are linearly correlated with the three-dimensional coordinates, whereas the Doppler parameters of the corner reflector array are related to the fluctuating motion of each corner reflector, with the parameter distribution being approximately random, and there is an occurrence of intersecting Doppler trajectories.
- (2)
- This manuscript proposes a marine target imaging method based on time–frequency analysis and the modified Clean technique, which is capable of unified imaging processing for ship targets and corner reflector arrays in jamming scenarios. Existing Clean-type unified imaging algorithms do not consider the different scattering point densities and Doppler parameter distribution characteristics of the two types of targets in the scene, offering the potential for computational complexity reduction and encountering challenges with inaccurate signal amplitude reconstruction. The proposed method designs a component extraction method based on STFT filtering, which can extract all clustered scattering points on a ship at once, reducing the computational load. A distortion correction method based on FrFT filtering and azimuth interpolation is designed to improve the reconstruction accuracy of the component with intersecting Doppler histories in the corner reflector array. Additionally, addressing the issue of poor robustness in the iterative termination conditions of existing Clean algorithms, this manuscript uses the spectral kurtosis of the residual signal as the termination condition, which offers better noise resistance.
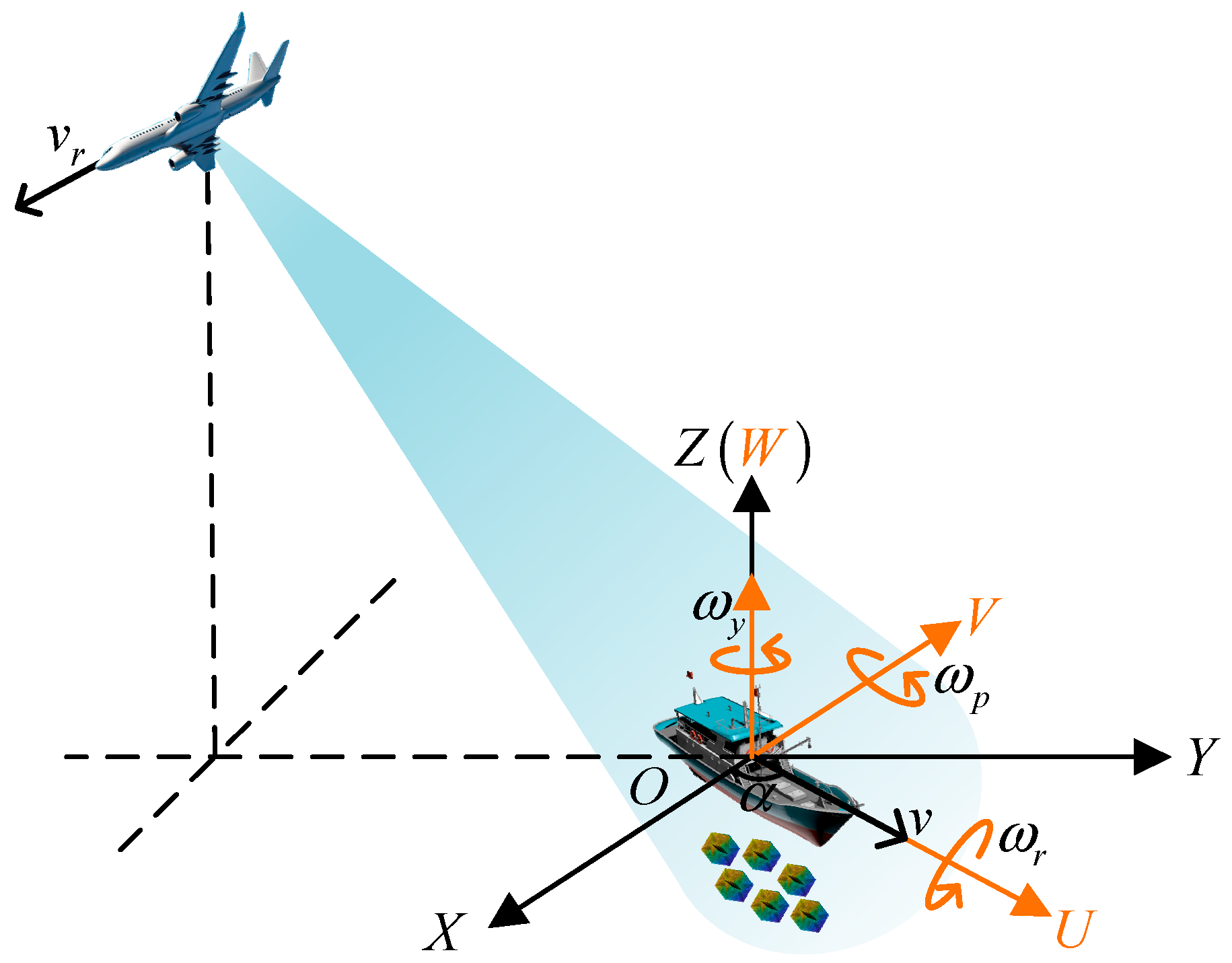
2. Motion Models and Signal Model
2.1. Motion Model of Ship
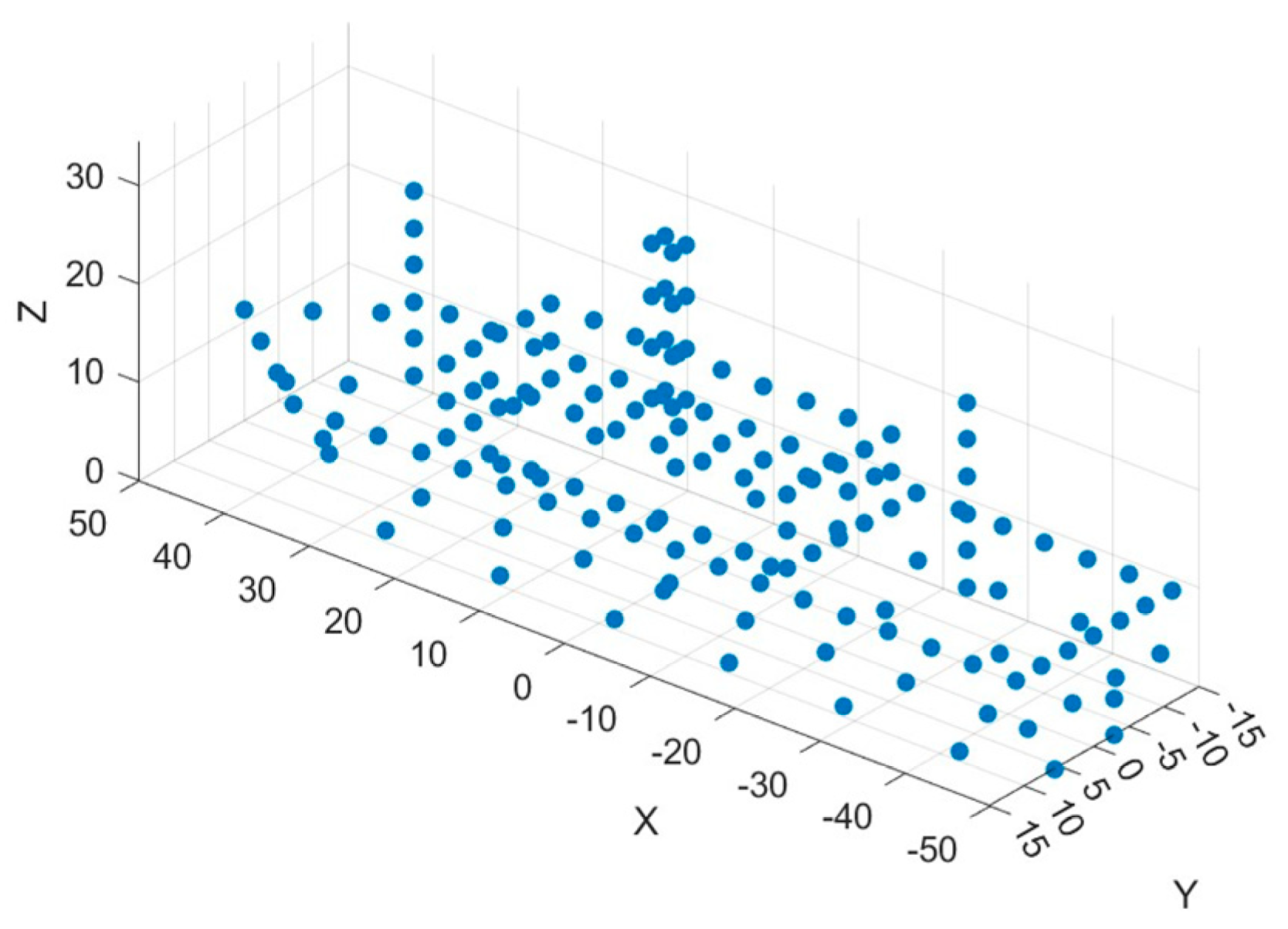
2.2. Motion Model of Corner Reflector Array
2.3. Signal Model
3. Analysis of the Residual Doppler Characteristics
3.1. Analysis of the Residual Doppler of a Ship
3.2. Analysis of the Residual Doppler of Corner Reflector Array
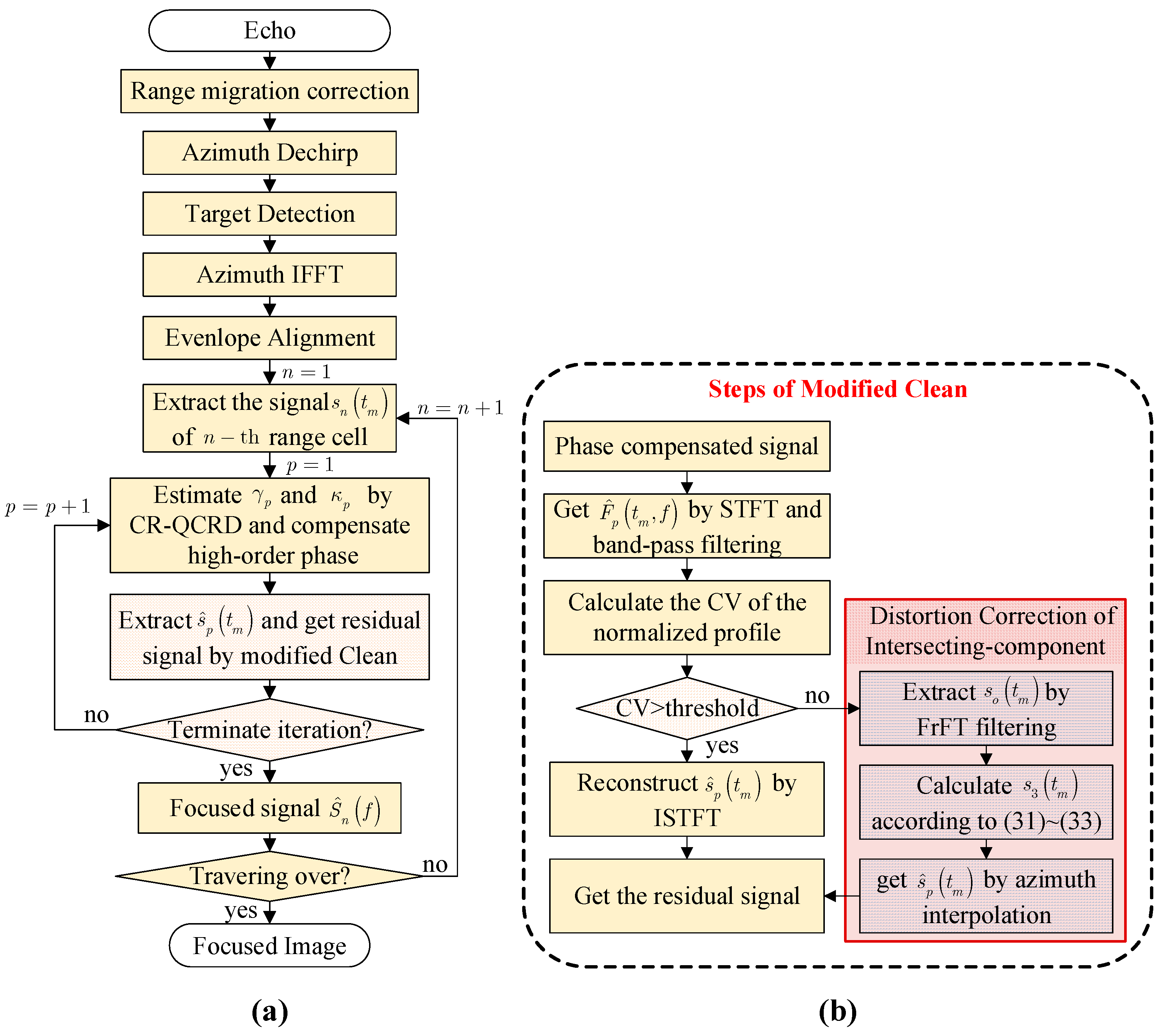
4. Proposed Algorithm
4.1. Parameter Estimation and Phase Compensation
4.2. Modified Clean Technique
4.3. Iteration Termination Condition
4.4. Computational Complexity
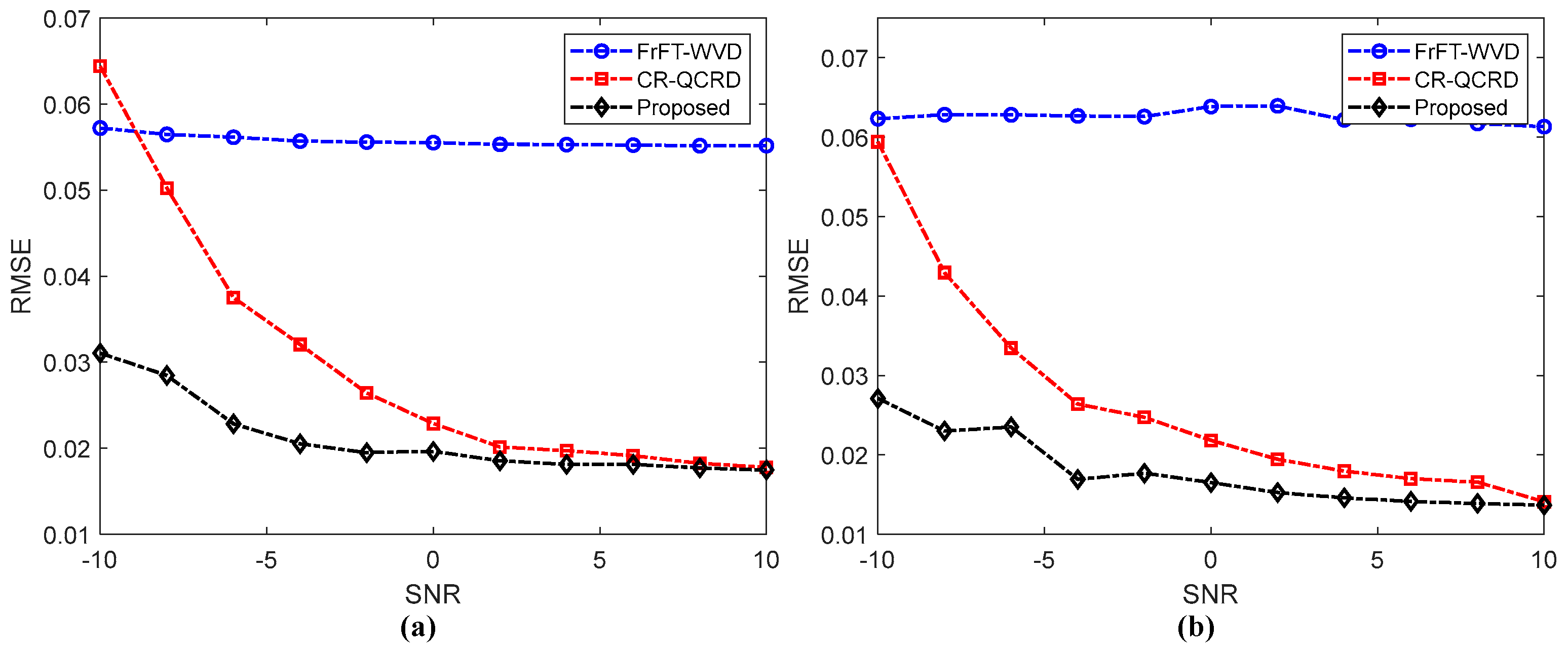
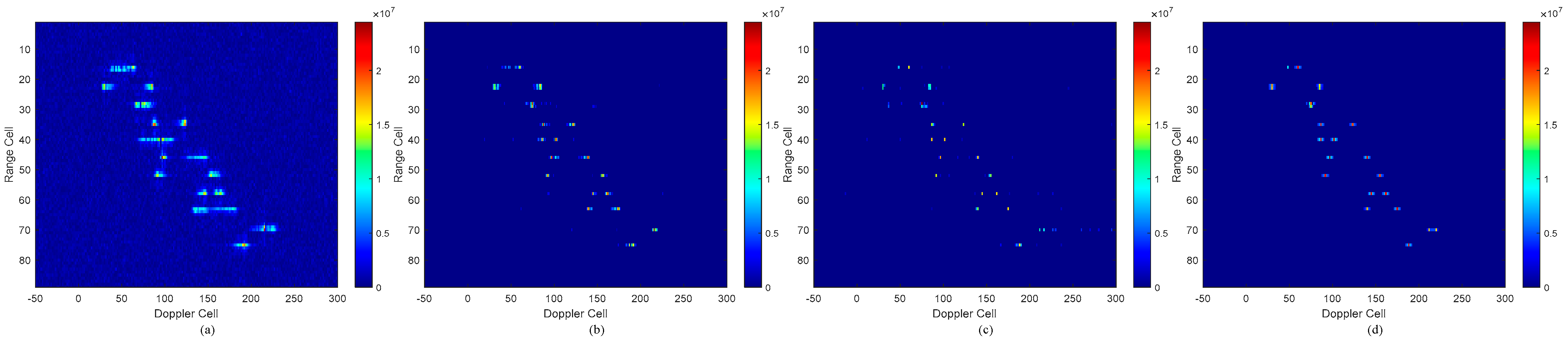
5. Simulation
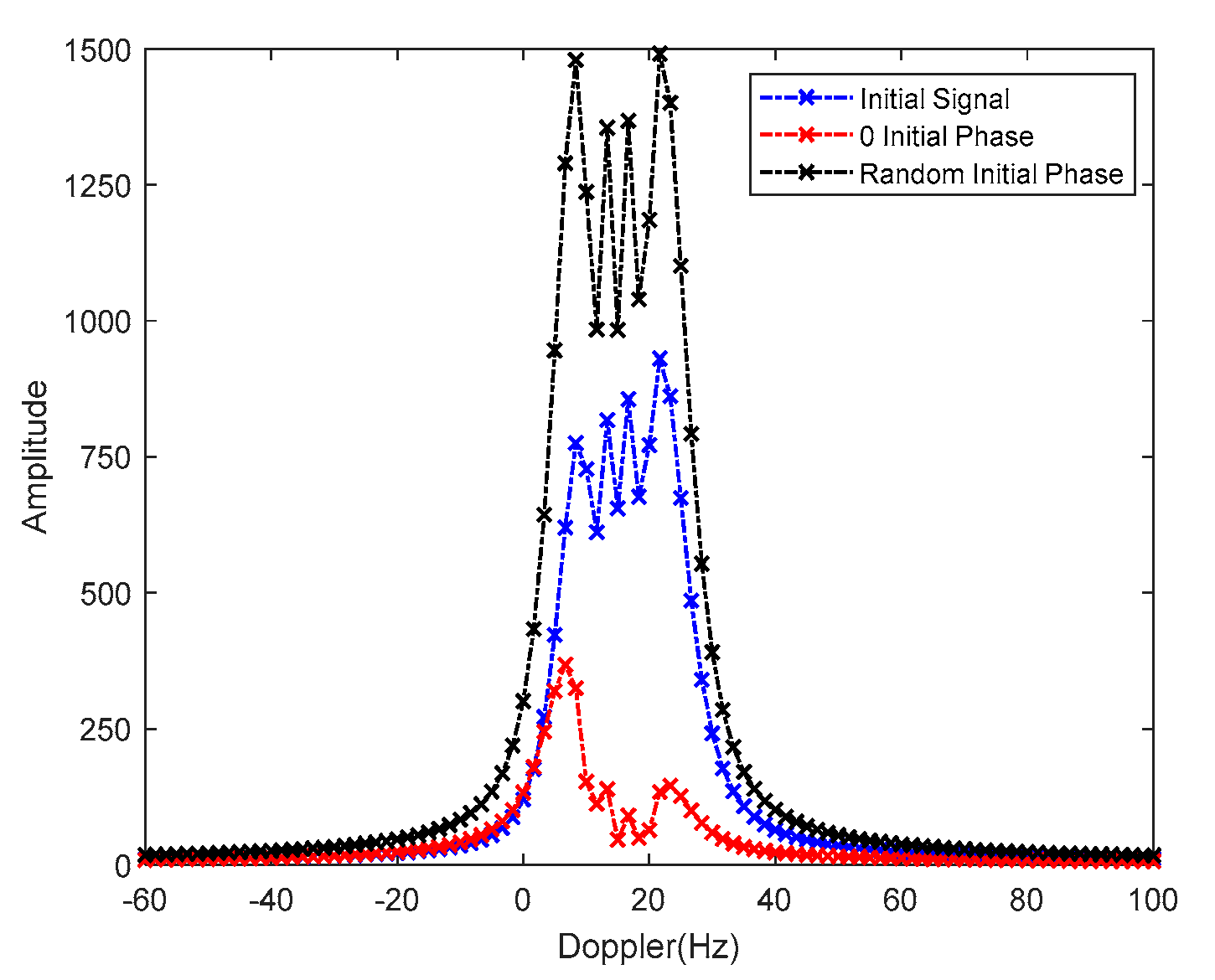
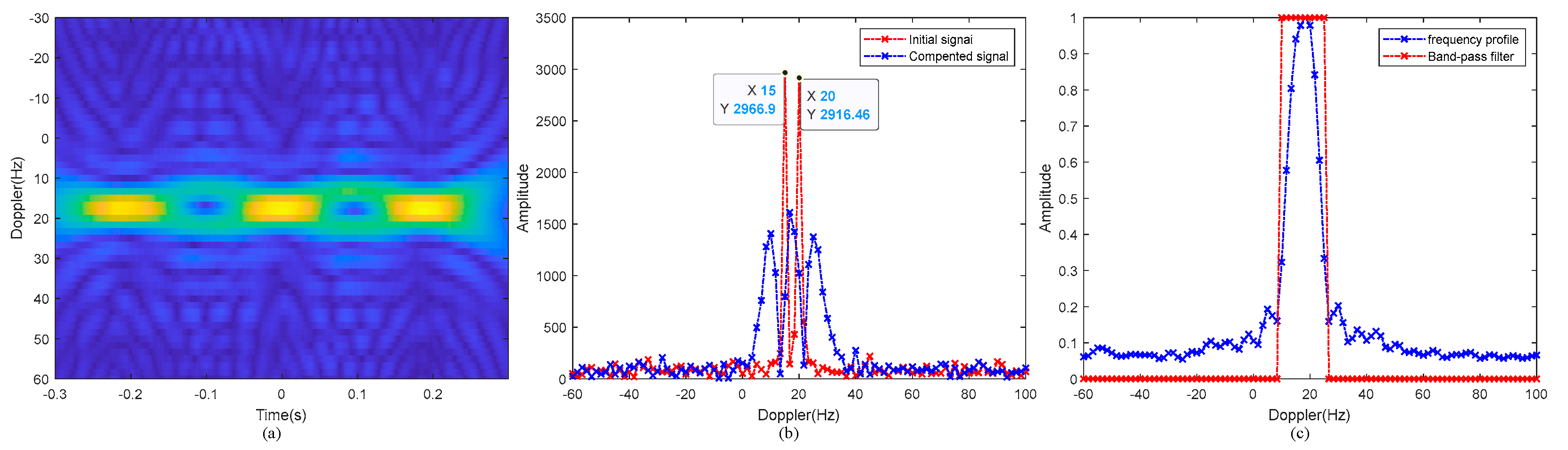
5.1. Simulation for the Multicomponent AM-CPS Signal
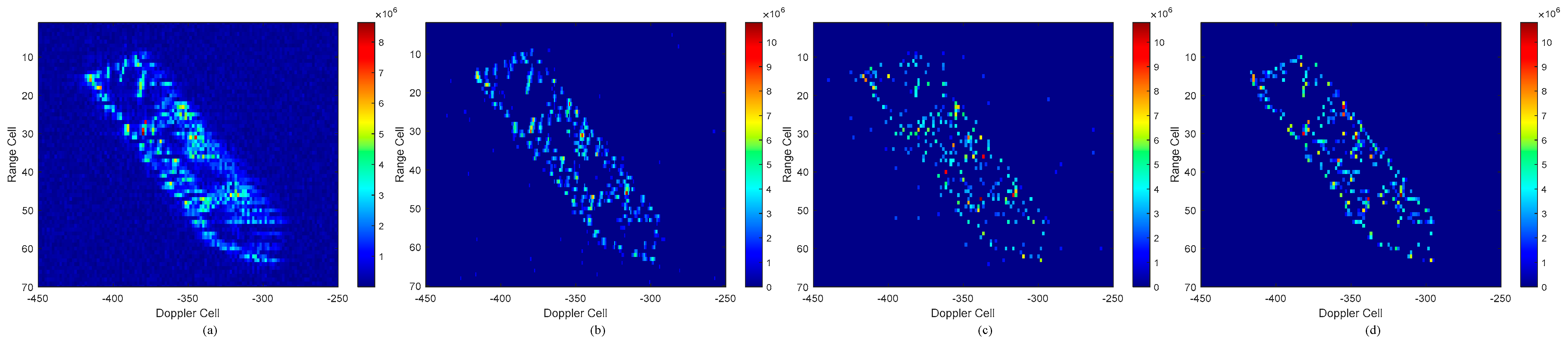
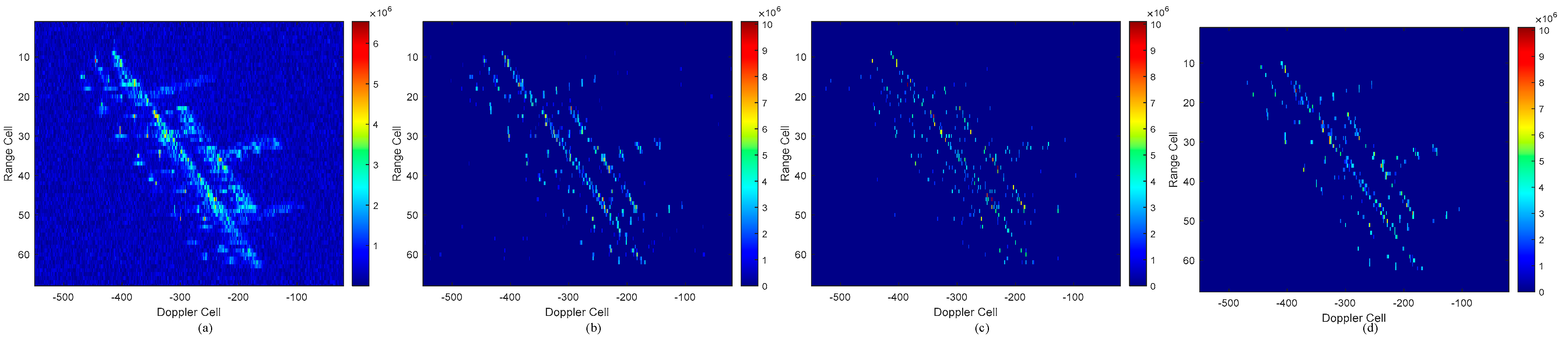
5.2. Simulation for Marine Targets in the Scenario
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cerutti-Maori, D.; Klare, J.; Brenner, A.R.; Ende, J.H.G. Wide-area traffic monitoring with the SAR/GMTI system PAMIR. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3019–3030. [Google Scholar] [CrossRef]
- Renga, A.; Graziano, M.D.; Moccia, A. Segmentation of marine SAR images by sublook analysis and application to sea traffic monitoring. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1463–1477. [Google Scholar] [CrossRef]
- Gao, G.; Wang, X.; Lai, T. Detection of moving ships based on a combination of magnitude and phase in along-track interferometric SAR—Part II: Statistical modeling and CFAR detection. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3582–3599. [Google Scholar] [CrossRef]
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar: Systems and Signal Processing, 1st ed.; Wiley-Interscience: New York, NY, USA, 1991. [Google Scholar]
- Moreira, A.; Prats-Iraola, P. A tutorial on synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data; Artech House: London, UK, 2005; Volume 1, pp. 108–110. [Google Scholar]
- Liu, W.; Li, H.; Zhang, J.; Sun, G.C.; Bian, H.; Xiang, J.; Xing, M. On the Role of Scene Coordinate System in Focusing of GEO SAR Data with Fast Time-Domain Algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2024, 18, 2355–2369. [Google Scholar] [CrossRef]
- Ferrer, P.J.; López-Martínez, C.; Aguasca, A.; Pipia, L.; González-Arbesú, J.M.; Fabregas, X.; Romeu, J. Transpolarizing trihedral corner reflector characterization using a GB-SAR system. IEEE Geosci. Remote Sens. Lett. 2011, 8, 774–778. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, L.; Zhang, X. A study on equipment developments and operational using of ship born gas-filled anti-missile multi-cornerreflector. Def. Technol. Rev. 2018, 39, 74–77. [Google Scholar]
- Luo, Y.; Guo, L.; Zuo, Y.; Liu, W. Time-domain scattering characteristics and jamming effectiveness in corner reflectors. IEEE Access. 2020, 9, 15696–15707. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, Y. Analysis of electromagnetic scattering characteristic for new type icosahedrons triangular trihedral corner reflectors. Command Control Simul. 2018, 40, 133–137. [Google Scholar]
- Li, H.; Chen, S.; Wang, X. Study on characterization of sea corner reflectors in polarimetric rotation domain. Syst. Eng. Electron. 2022, 44, 2065–2073. [Google Scholar]
- Li, H.; Chen, S. Electromagnetic scattering characteristics and radar identification of sea corner reflectors: Advances and prospects. J. Radars 2023, 12, 738–761. [Google Scholar]
- Li, H.; Cui, X.; Li, M.; Chen, S. Characterization of corner reflector array in joint space-time-polarization domain. IET Int. Radar Conf. 2023, 2023, 1328–1332. [Google Scholar] [CrossRef]
- Xie, Y.; Xing, M.; Gao, Y.; Wu, Z.; Sun, G.; Guo, L. Attributed Scattering Center Extraction Method for Microwave Photonic Signals Using DSM-PMM-Regularized Optimization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Zhang, J.; Xing, M.; Xie, Y. A Feature Fusion Framework for SAR Target Recognition Based on Electromagnetic Scattering Features and Deep CNN Features. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2174–2187. [Google Scholar] [CrossRef]
- Duan, D.; Shen, Y.; Wu, Z.; Ou, J. Identification of sea corner reflector array based on spatial morphological features. Fourth Int. Conf. Signal Process. Comput. Sci. 2023, 12970, 382–390. [Google Scholar]
- He, Y.; Yang, H.; He, H.; Yin, J.; Yang, J. A ship discrimination method based on high-frequency electromagnetic theory. Remote Sens. 2022, 14, 3893. [Google Scholar] [CrossRef]
- Doerry, A.W. Ship Dynamics for Maritime ISAR Imaging; Sandia National Laboratories (SNL): Albuquerque, NM, USA; Livermore, CA, USA, 2008. [Google Scholar]
- Schwarz, U.J. Mathematical-statistical description of the iterative beam removing technique (method CLEAN). Astron. Astrophys. 1978, 65, 345. [Google Scholar]
- Tsao, J.; Steinberg, B.D. Reduction of sidelobe and speckle artifacts in microwave imaging: The CLEAN technique. IEEE Trans. Antennas Propag. 1988, 36, 543–556. [Google Scholar] [CrossRef]
- Martorella, M.; Acito, N.; Berizzi, F. Statistical Clean technique for ISAR imaging. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3552–3560. [Google Scholar] [CrossRef]
- Li, X.; Kong, L.; Cui, G.; Yi, W. CLEAN-based coherent integration method for high-speed multi-targets detection. IET Radar Sonar Navig. 2016, 10, 1671–1682. [Google Scholar] [CrossRef]
- Chen, V.C.; Qian, S. Joint time-frequency transform for radar range-Doppler imaging. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 486–499. [Google Scholar] [CrossRef]
- Berizzi, F.; Mese, E.D.; Diani, M.; Martorella, M. High-resolution ISAR imaging of maneuvering targets by means of the range instantaneous Doppler technique: Modeling and performance analysis. IEEE Trans. Image Process. 2001, 10, 1880–1890. [Google Scholar] [CrossRef] [PubMed]
- Xia, X.G.; Wang, G.; Chen, V.C. Quantitative SNR analysis for ISAR imaging using joint time-frequency analysis-Short time Fourier transform. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 649–659. [Google Scholar] [CrossRef]
- Auger, F.; Flandrin, P. Improving the readability of time-frequency and time-scale representations by the reassignment method. IEEE Trans. Signal Process. 1995, 43, 1068–1089. [Google Scholar] [CrossRef]
- Hopgood, J.R.; Rayner, P.J.W. Single channel nonstationary stochastic signal separation using linear time-varying filters. IEEE Trans. Signal Process. 2003, 51, 1739–1752. [Google Scholar] [CrossRef]
- Brevdo, E.; Fučkar, N.S.; Thakur, G. The Synchrosqueezing algorithm: A robust analysis tool for signals with time-varying spectrum. Signal Process. 2011, 93, 1079–1094. [Google Scholar]
- Wang, X.; Dai, Y.; Song, S.; Jin, T.; Huang, X. Deep Learning-Based Enhanced ISAR-RID Imaging Method. Remote Sens. 2023, 15, 5166. [Google Scholar] [CrossRef]
- Xing, M.; Wu, R.; Li, Y.; Bao, Z. New ISAR imaging algorithm based on modified Wigner-Ville distribution. IET Radar Sonar Navig. 2008, 3, 70–80. [Google Scholar] [CrossRef]
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.; Ma, J.; Zhang, X. A Fast SAR Imaging Method for Ground Moving Target Using a Second-Order WVD Transform. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1940–1956. [Google Scholar] [CrossRef]
- Bai, X.; Tao, R.; Wang, Z.; Wang, Y. ISAR imaging of a ship target based on parameter estimation of multicomponent quadratic frequency-modulated signals. IEEE Trans. Geosci. Remote Sens. 2013, 52, 1418–1429. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.; Tao, R.; Bai, X. Adaptive viterbi-based range-instantaneous Doppler algorithm for ISAR imaging of ship target at sea. IEEE J. Ocean. Eng. 2014, 40, 417–425. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, X.; Zhang, Q. Rotation parameters estimation and cross-range scaling research for range instantaneous Doppler ISAR images. IEEE Sens. J. 2020, 20, 7010–7020. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, X.; Qing, Y.; Xiao, Y.; An, H. Hybrid SAR-ISAR Image Formation via Joint FrFT-WVD Processing for BFSAR Ship Target High-Resolution Imaging. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Lv, X.; Xing, M.; Wan, C.; Zhang, S. ISAR imaging of maneuvering targets based on the range centroid Doppler technique. IEEE Trans. Image Process. 2010, 19, 141–153. [Google Scholar]
- Lv, X.; Bi, G.; Wan, C.; Xing, M. Lv’s distribution: Principle, implementation, properties, performance. IEEE Trans. Signal Process. 2011, 59, 3576–3591. [Google Scholar] [CrossRef]
- Ding, Z.; Zhang, T.; Li, Y.; Li, G.; Dong, X.; Zeng, T.; Meng, K. A Ship ISAR Imaging Algorithm Based on Generalized Radon-Fourier Transform With Low SNR. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6385–6396. [Google Scholar] [CrossRef]
- Wang, J.; Leng, X.; Sun, Z.; Zhang, X.; Ji, K. Fast and accurate refocusing for moving ships in SAR imagery based on FrFT. Remote Sens. 2023, 15, 3656. [Google Scholar] [CrossRef]
- O’Shea, P. Improving polynomial phase parameter estimation by using nonuniformly spaced signal sample method. IEEE Trans. Signal Process. 2012, 60, 3405–3414. [Google Scholar] [CrossRef]
- Wu, L.; Wei, X.; Yang, D.; Wang, H.; Li, X. ISAR imaging of targets with complex motion based on discrete chirp Fourier transform for cubic chirps. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4201–4212. [Google Scholar] [CrossRef]
- Zheng, J.; Su, T.; Zhu, W.; Zhang, L.; Liu, Z.; Liu, Q. ISAR imaging of nonuniformly rotating target based on a fast parameter estimation algorithm of cubic phase signal. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4727–4740. [Google Scholar] [CrossRef]
- Huang, P.; Xia, X.; Zhan, M.; Liu, X.; Liao, G.; Jiang, X. ISAR imaging of a maneuvering target based on parameter estimation of multicomponent cubic phase signals. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–18. [Google Scholar] [CrossRef]
- Yang, S.; Li, S.; Fan, H.; Liu, Y. High-resolution ISAR imaging of maneuvering targets based on azimuth adaptive partitioning and compensation function estimation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Zheng, J.; Su, T.; Zhang, L.; Zhu, W.; Liu, Q. ISAR Imaging of Targets With Complex Motion Based on the Chirp Rate-Quadratic Chirp Rate Distribution. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7276–7289. [Google Scholar] [CrossRef]
- Elfouhaily, T.; Chapron, B.; Katsaros, K. A unified directional spectrum for long and short wind-driven waves. J. Geophys. Res. Ocean. 1997, 102, 15781–15796. [Google Scholar] [CrossRef]
- Plant, W.J. The Ocean Wave Height Variance Spectrum: Wavenumber Peak versus Frequency Peak. J. Phys. Oceanogr. 2009, 39, 2382–2383. [Google Scholar] [CrossRef]
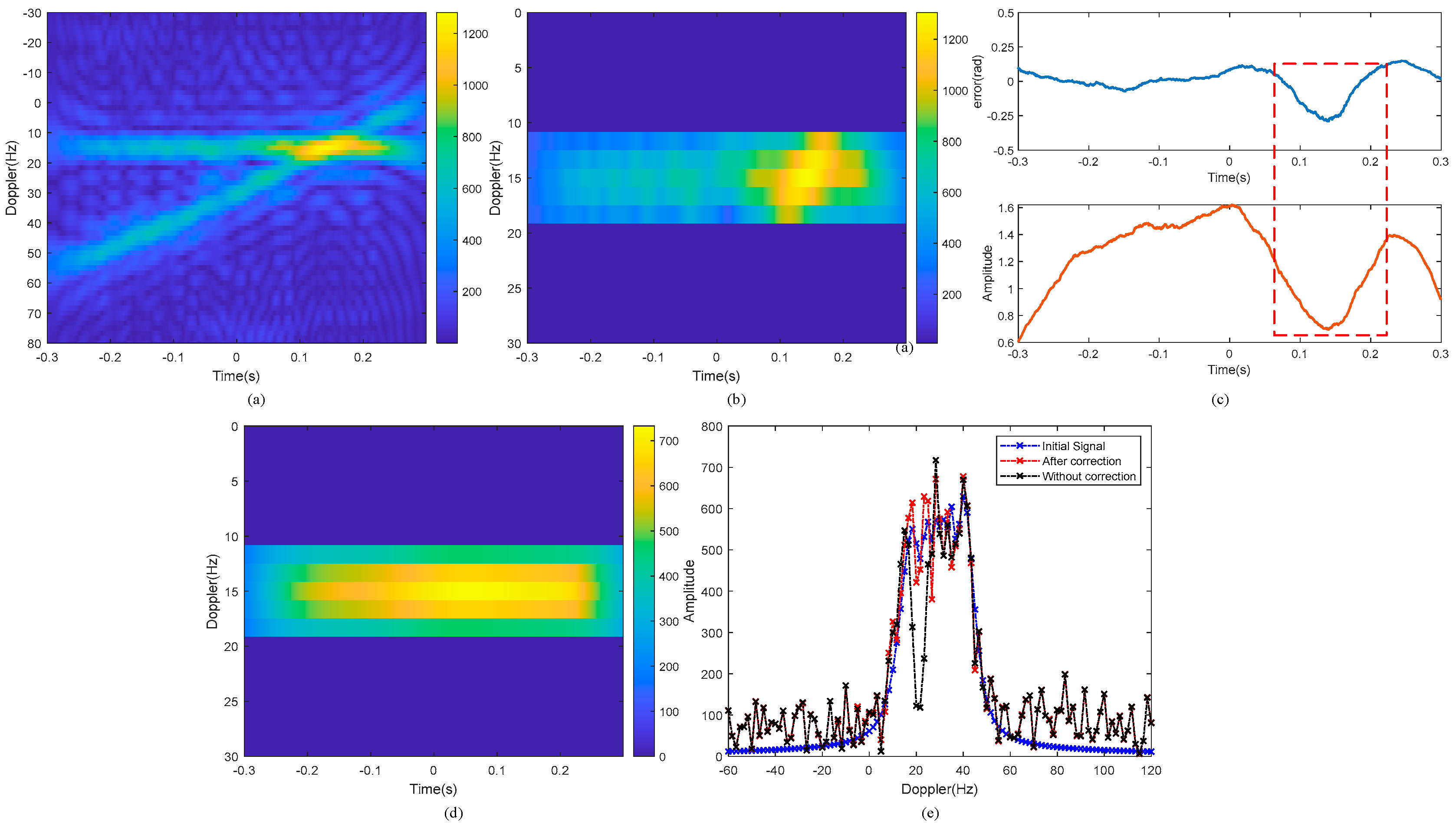
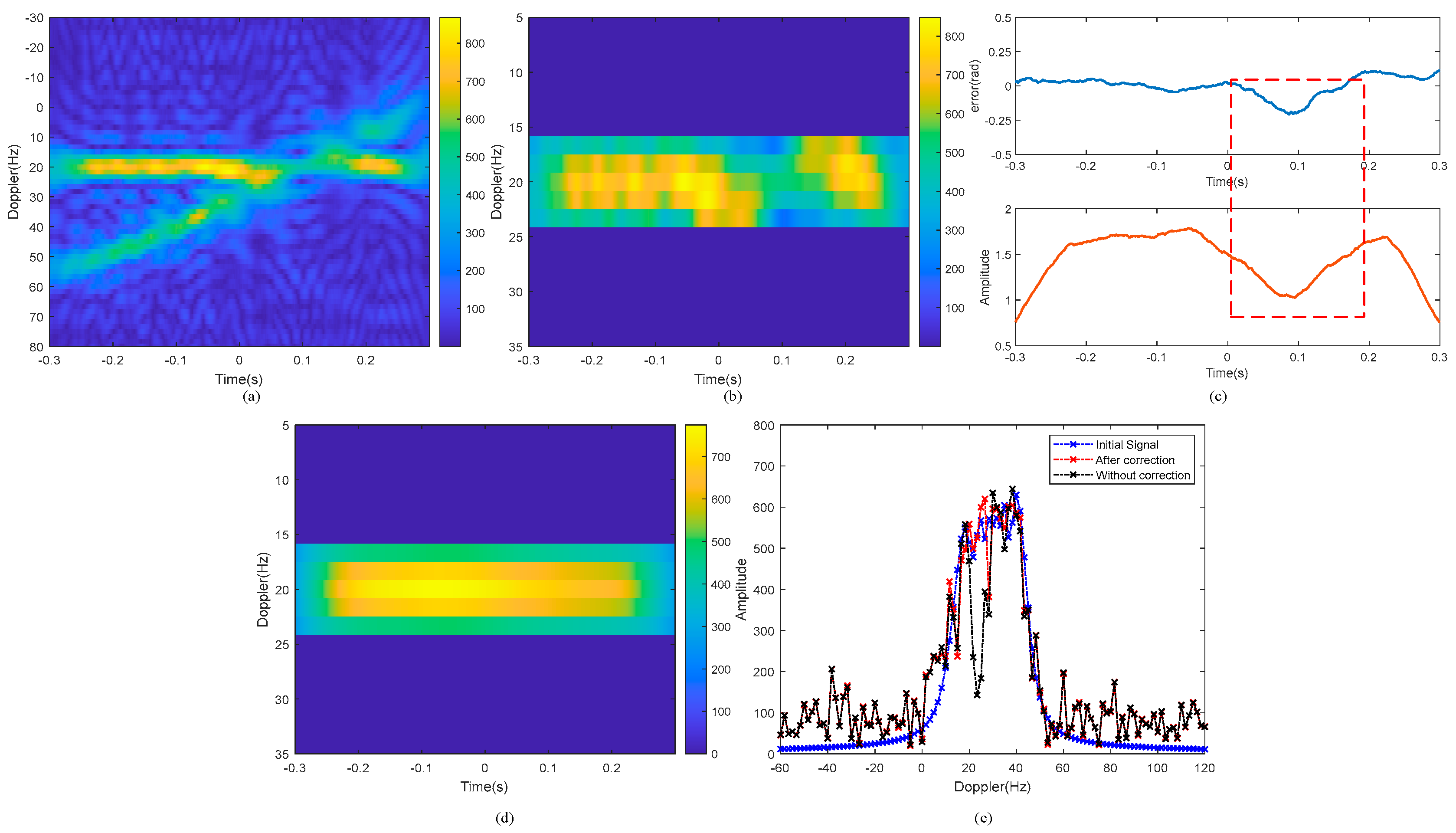
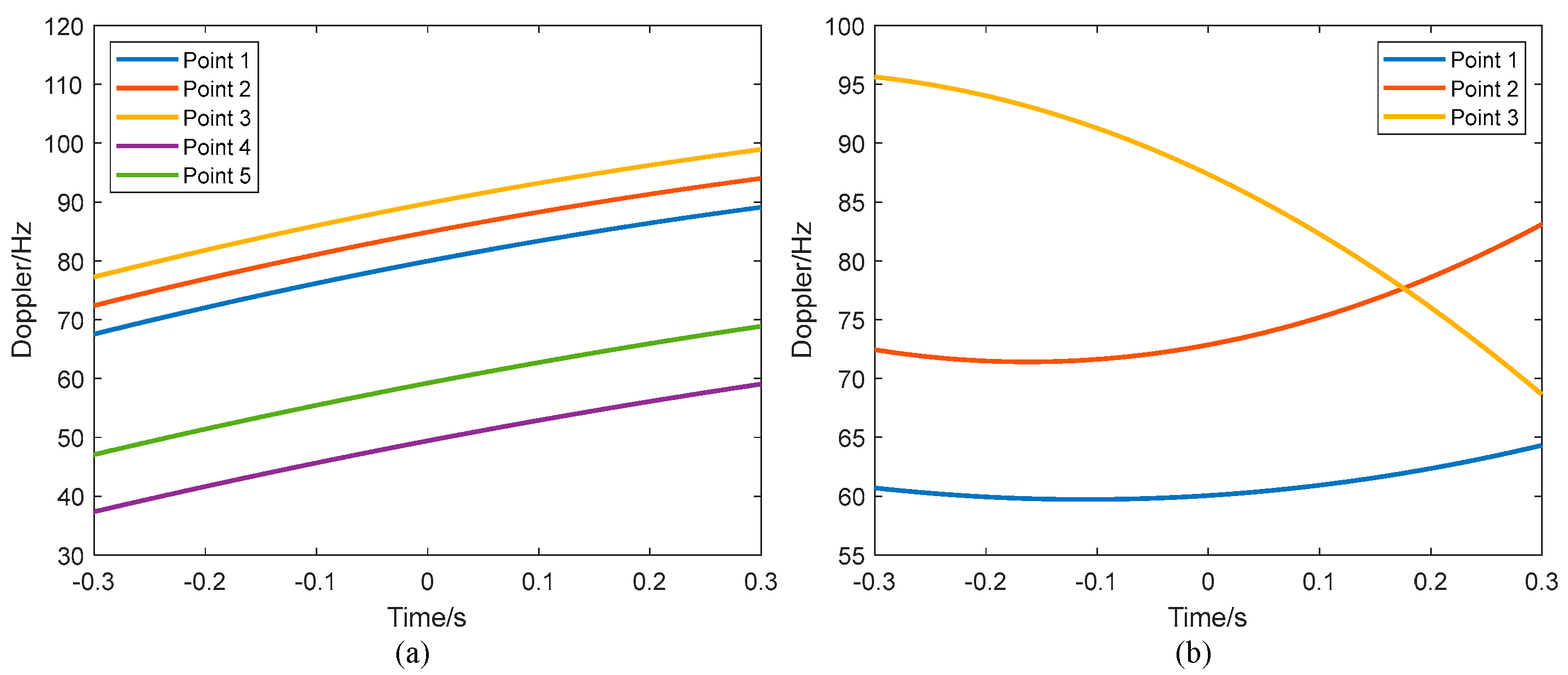
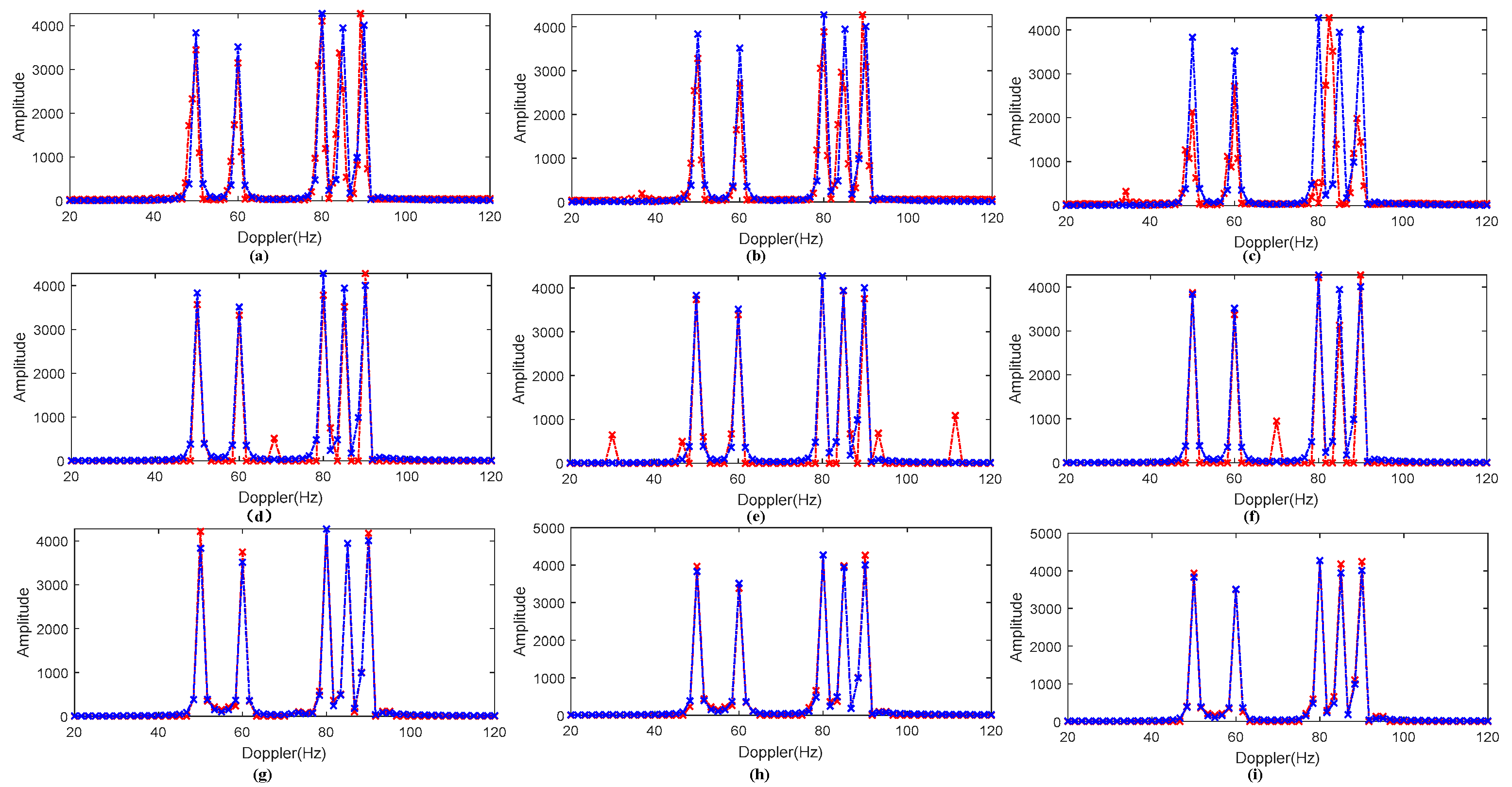



| Component () | (Hz) | (Hz/s) | (Hz/s2) | |
|---|---|---|---|---|
| 1 | 15 | 40 | 20 | |
| 2 | 20 | 43 | 22 | |
| 3 | 30 | −60 | −40 |
| Component () | (Hz) | (Hz/s) | (Hz/s2) | |
|---|---|---|---|---|
| 1 | 2.75 | 79.97 | 35.91 | −18.25 |
| 2 | 2.45 | 85.88 | 36.01 | −18.53 |
| 3 | 2.68 | 89.79 | 36.10 | −18.81 |
| 4 | 2.49 | 50.00 | 36.17 | −13.34 |
| 5 | 2.29 | 60.00 | 36.35 | −19.90 |
| Component () | (Hz) | (Hz/s) | (Hz/s2) | |
|---|---|---|---|---|
| 1 | 5.45 | 50.00 | 6.03 | 27.29 |
| 2 | 5.47 | 72.87 | 17.76 | 54.53 |
| 3 | 5.62 | 80.00 | −44.96 | −58.05 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Bandwidth | 80 MHZ | Pulse width | 20 μs |
| Sampling frequency | 100 MHZ | Pulse repetition frequency | 3000 Hz |
| Wavelength | 3 cm | Center range | 10 Km |
| Sea State | Roll Amplitude | Roll Period | Pitch Amplitude | Pitch Period | Yaw Amplitude | Yaw Period | Wind Speed |
|---|---|---|---|---|---|---|---|
| 3 | 0.0524 rad | 9.76 s | 0.008 rad | 5.66 s | 0.010 rad | 11.6 s | 5 m/s |
| 5 | 0.3351 rad | 12.2 s | 0.0297 rad | 6.7 s | 0.0332 rad | 14.2 s | 11 m/s |
| Characteristic | Ship | Corner Reflector |
|---|---|---|
| Maximum cluster size | 45 | 5 |
| Average correlation coefficient | 0.84 | 0.37 |
| Characteristic | Ship | Corner Reflector |
|---|---|---|
| Maximum cluster size | 21 | 4 |
| Average correlation coefficient | 0.52 | 0.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Liu, W.; Gao, Y.; Cui, L.; Chen, Q.; Fu, J.; Xing, M. An Imaging Method for Marine Targets in Corner Reflector Jamming Scenario Based on Time–Frequency Analysis and Modified Clean Technique. Remote Sens. 2025, 17, 310. https://doi.org/10.3390/rs17020310
Chen C, Liu W, Gao Y, Cui L, Chen Q, Fu J, Xing M. An Imaging Method for Marine Targets in Corner Reflector Jamming Scenario Based on Time–Frequency Analysis and Modified Clean Technique. Remote Sensing. 2025; 17(2):310. https://doi.org/10.3390/rs17020310
Chicago/Turabian StyleChen, Changhong, Wenkang Liu, Yuexin Gao, Lei Cui, Quan Chen, Jixiang Fu, and Mengdao Xing. 2025. "An Imaging Method for Marine Targets in Corner Reflector Jamming Scenario Based on Time–Frequency Analysis and Modified Clean Technique" Remote Sensing 17, no. 2: 310. https://doi.org/10.3390/rs17020310
APA StyleChen, C., Liu, W., Gao, Y., Cui, L., Chen, Q., Fu, J., & Xing, M. (2025). An Imaging Method for Marine Targets in Corner Reflector Jamming Scenario Based on Time–Frequency Analysis and Modified Clean Technique. Remote Sensing, 17(2), 310. https://doi.org/10.3390/rs17020310








