Three-Dimensional Reconstruction of Space Targets Utilizing Joint Optical-and-ISAR Co-Location Observation
Abstract
1. Introduction
- Accurate theoretical models for image offset correction and spatial offset correction: The OC-V3R-OI method starts from the imaging mechanism, and derives detailed analytical expressions for image offset correction and spatial offset correction. This facilitates more accurate 3-D reconstruction and provides substantial support for other situational awareness tasks in this scenario.
- Independence with regard to the prior motion information: The OC-V3R-OI method is independent of the prior motion information, and the corresponding model attitude at each imaging frame can be given during the observation time. This capability makes the OC-V3R-OI method suitable for targets with unknown motion types and enhances its applicability.
- Accurate voxel trimming mechanism: To increase the robustness of the OC-V3R-OI method, the VTM-GL method was deliberately designed to enable the voxel trimming mechanism to dynamically remove and add voxels, thereby ensuring high reconstruction accuracy and optimizing the utilization of available information.
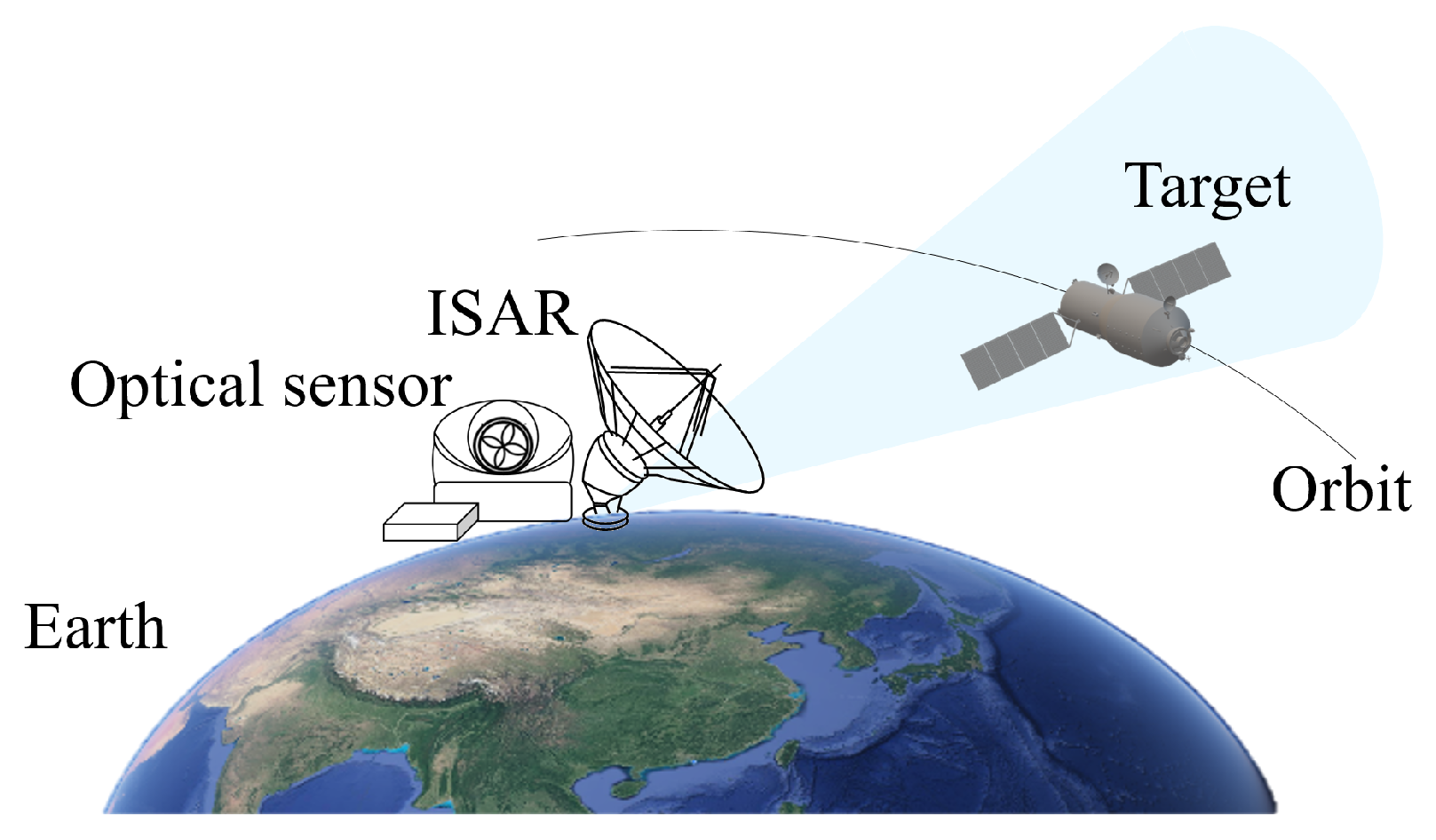
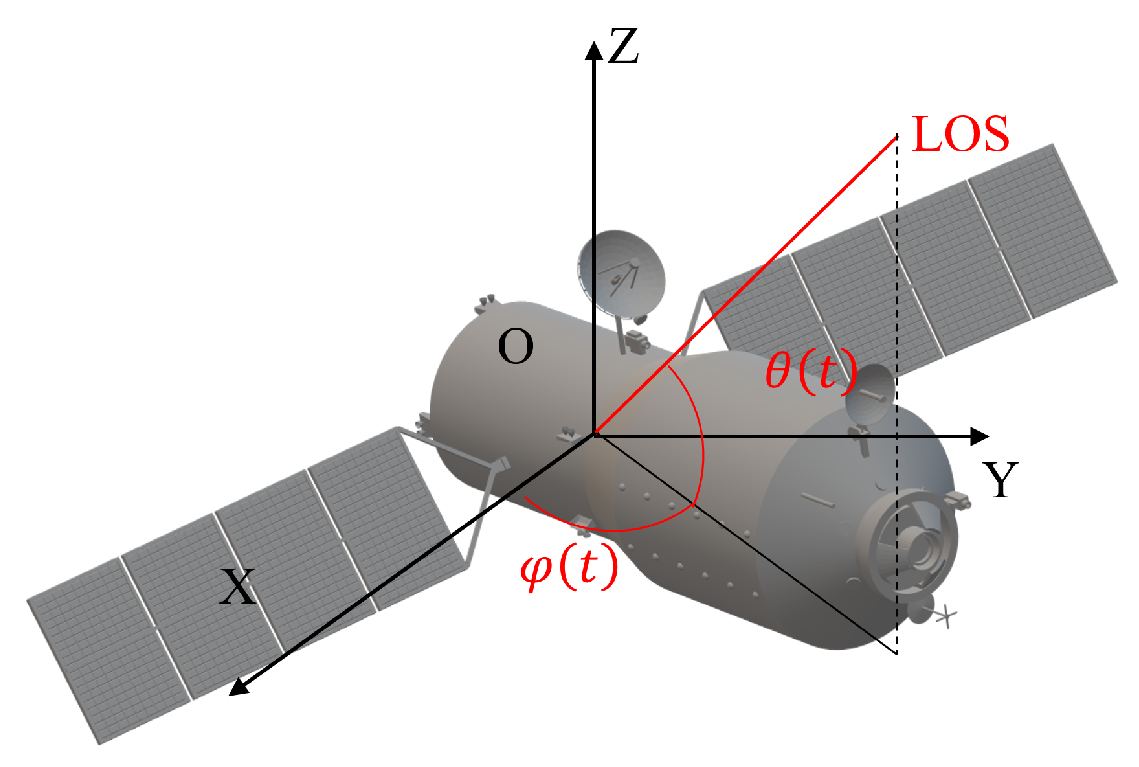
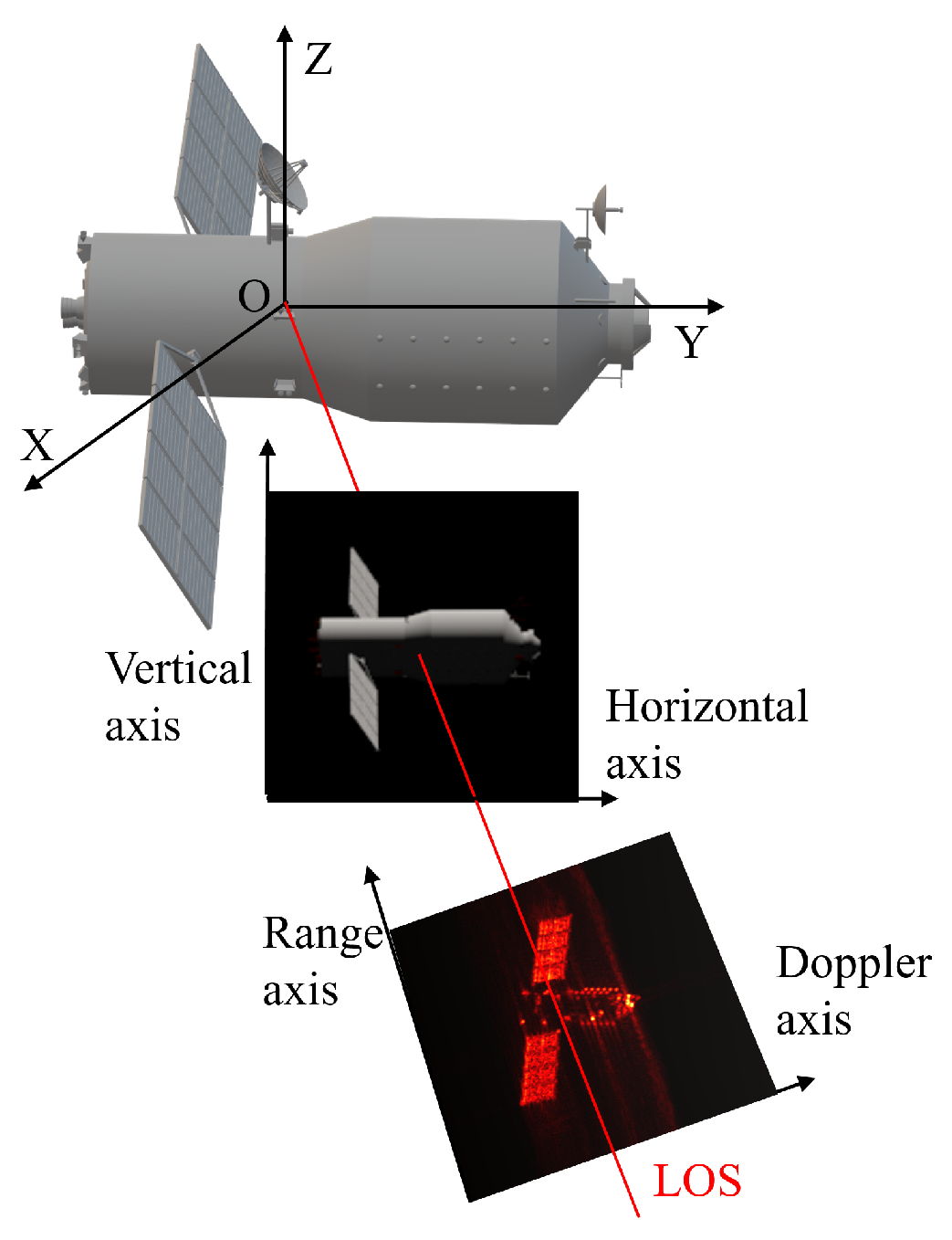
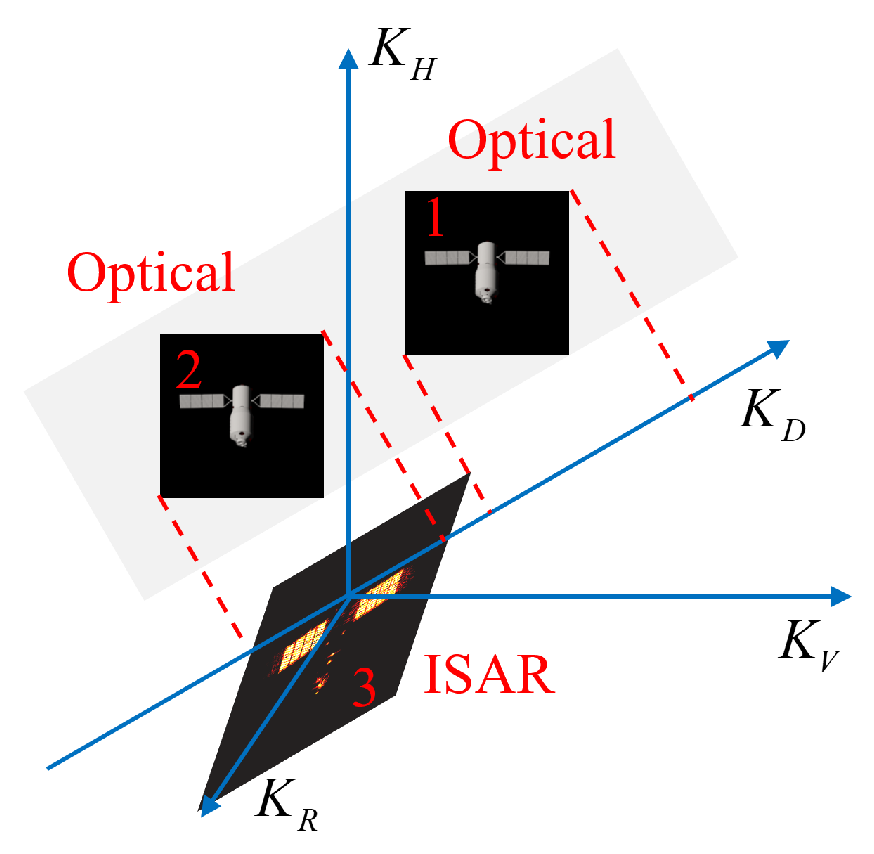
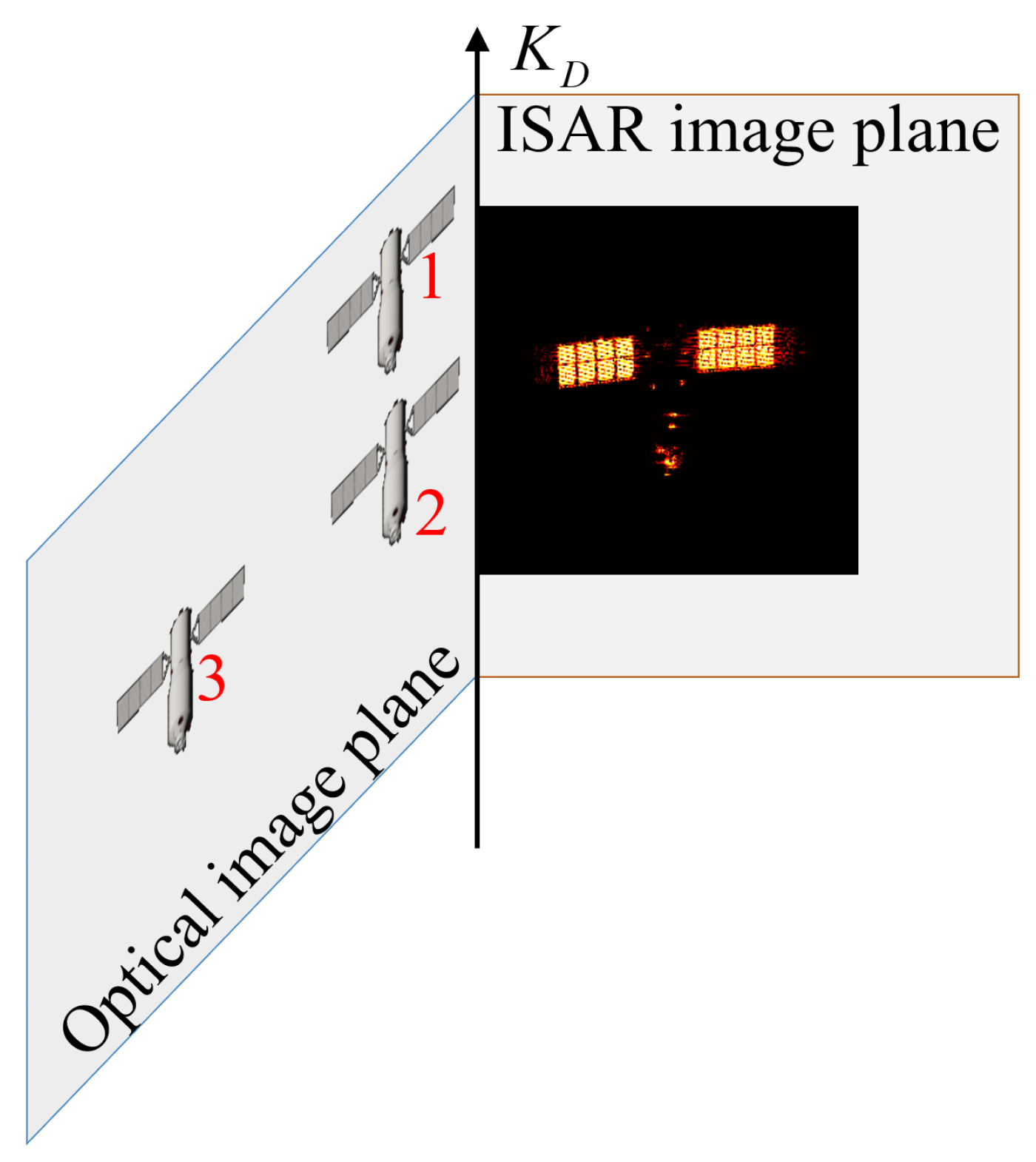
2. Principals of Optical-and-ISAR Co-Location System
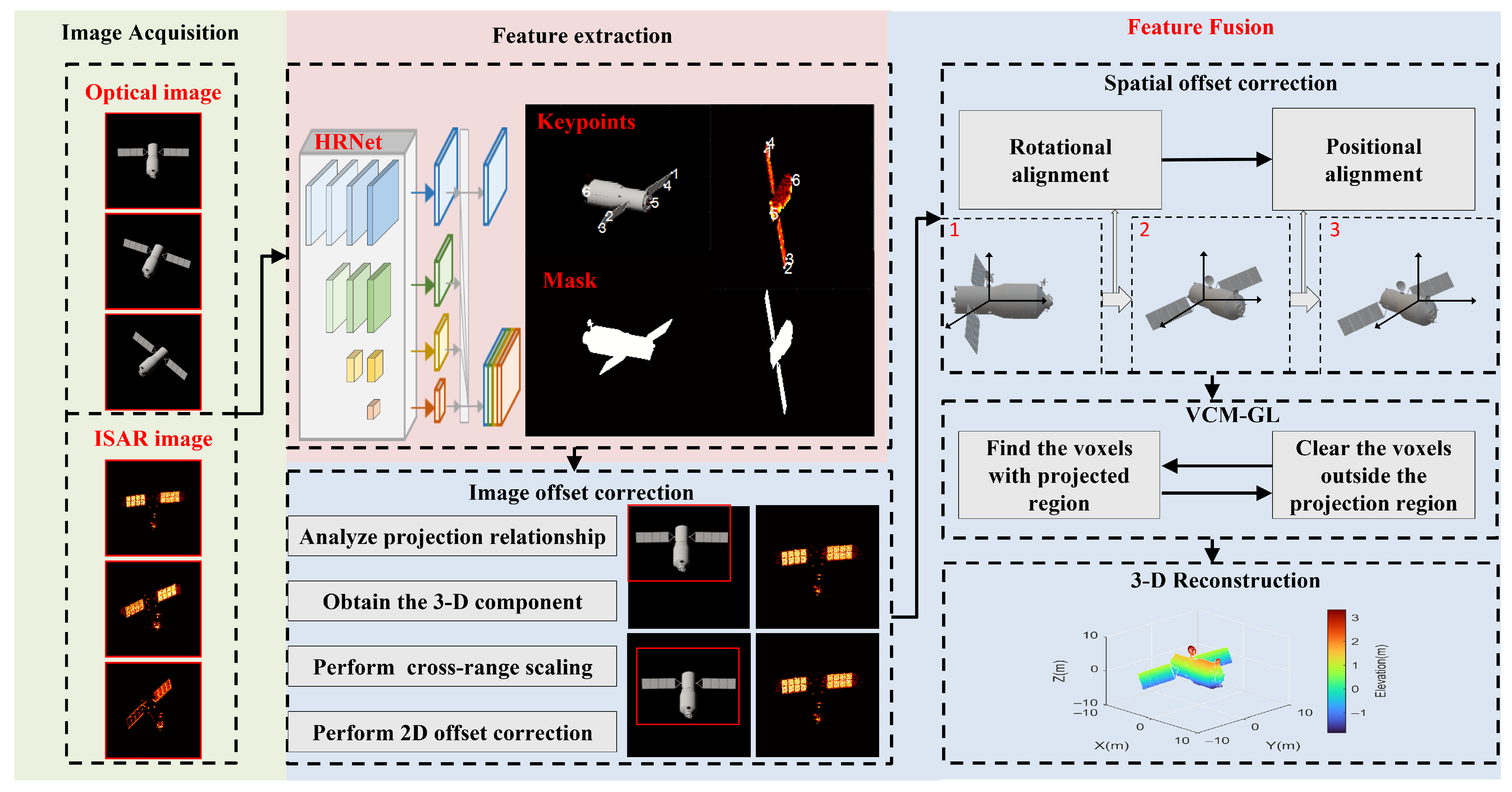
3. Methodology
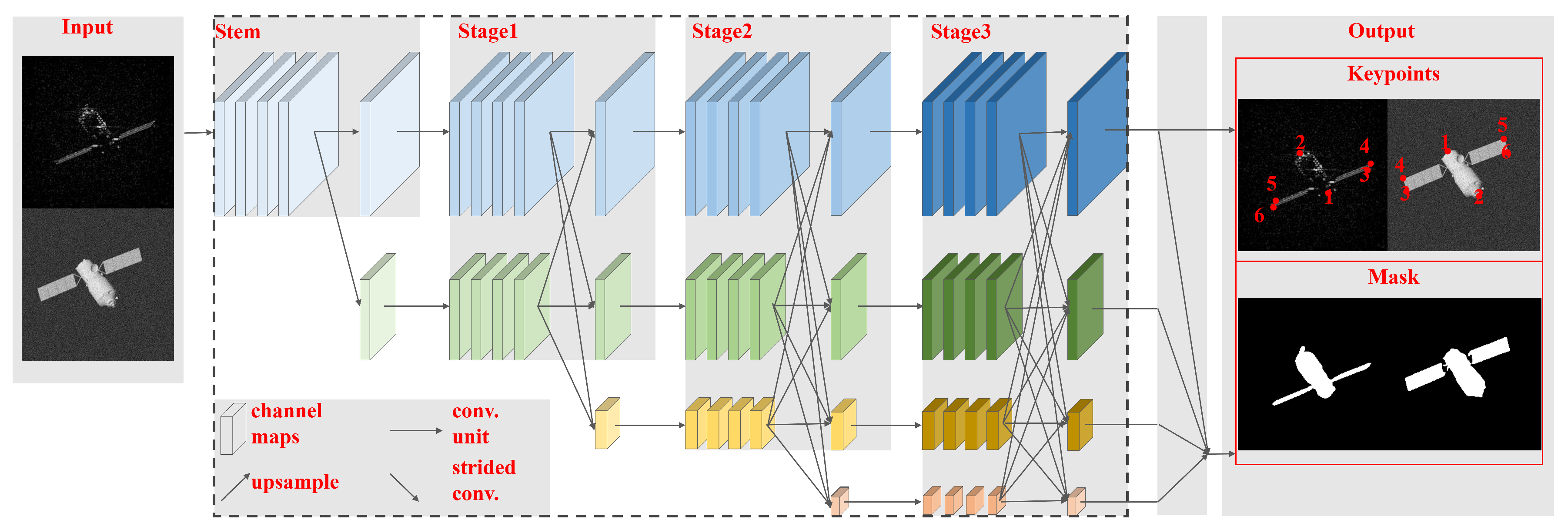
3.1. Feature Extraction
3.2. Image Offset Correction
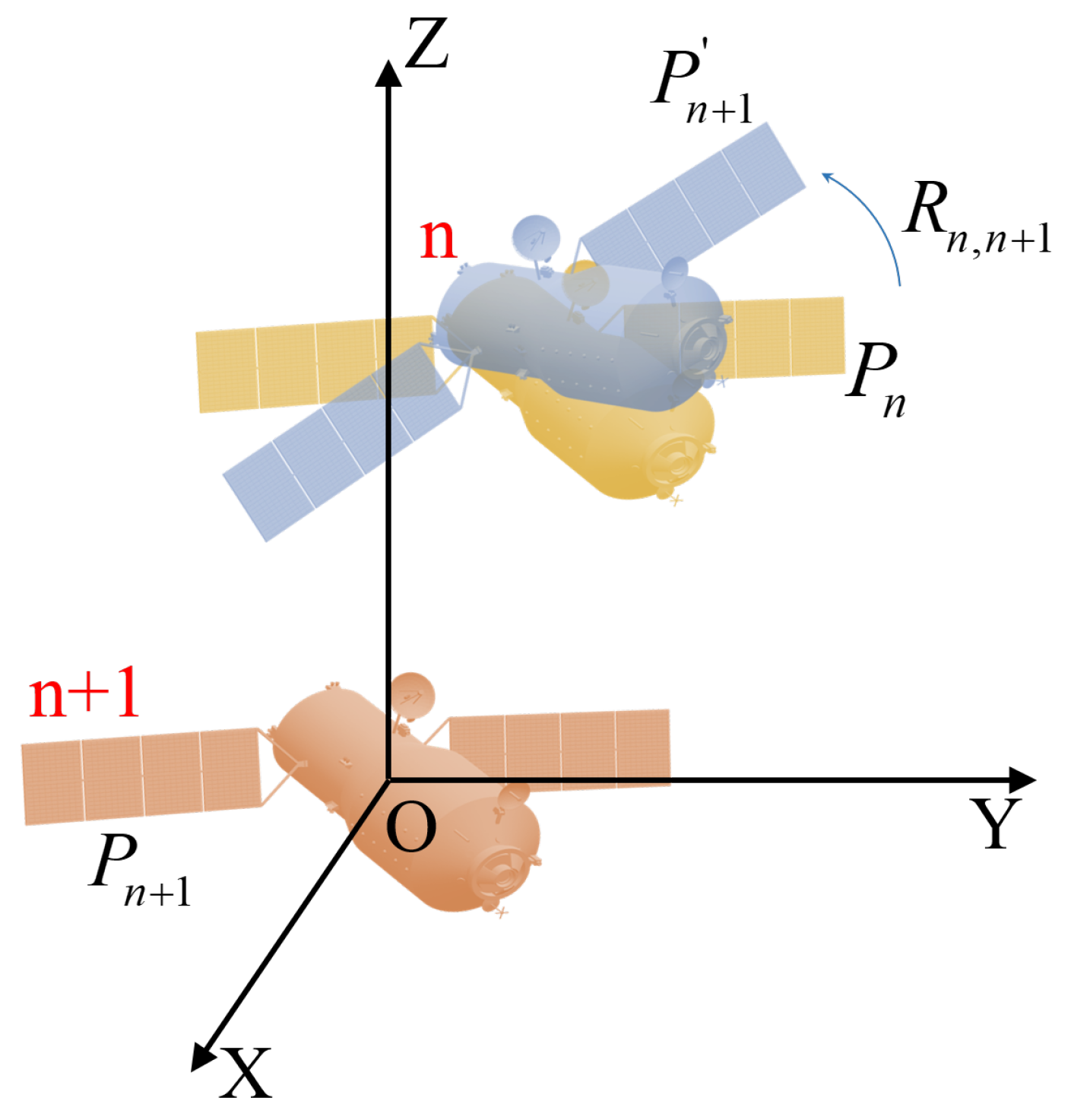
3.3. Spatial Offset Correction
3.4. Voxel Trimming Mechanism Based on Growth Learning
4. Algorithm Summation and Computation Complexity Analysis
| Algorithm 1: The process of three-dimensional reconstruction. |
|
5. Experiments
5.1. Data Description
5.2. Performance Evaluation Metrics
5.3. Analyses
5.3.1. Effectiveness Analysis
5.3.2. Performance Analysis
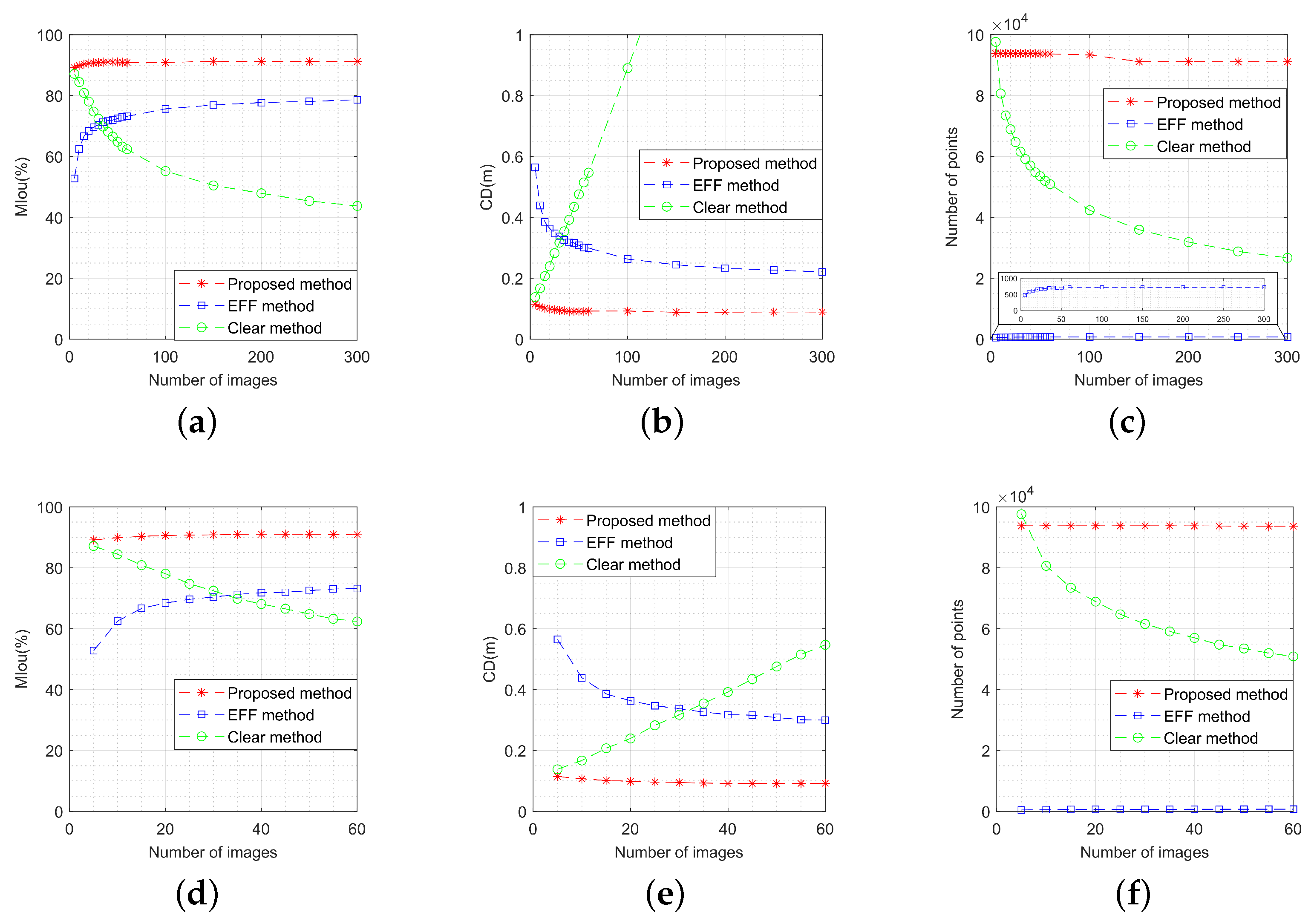
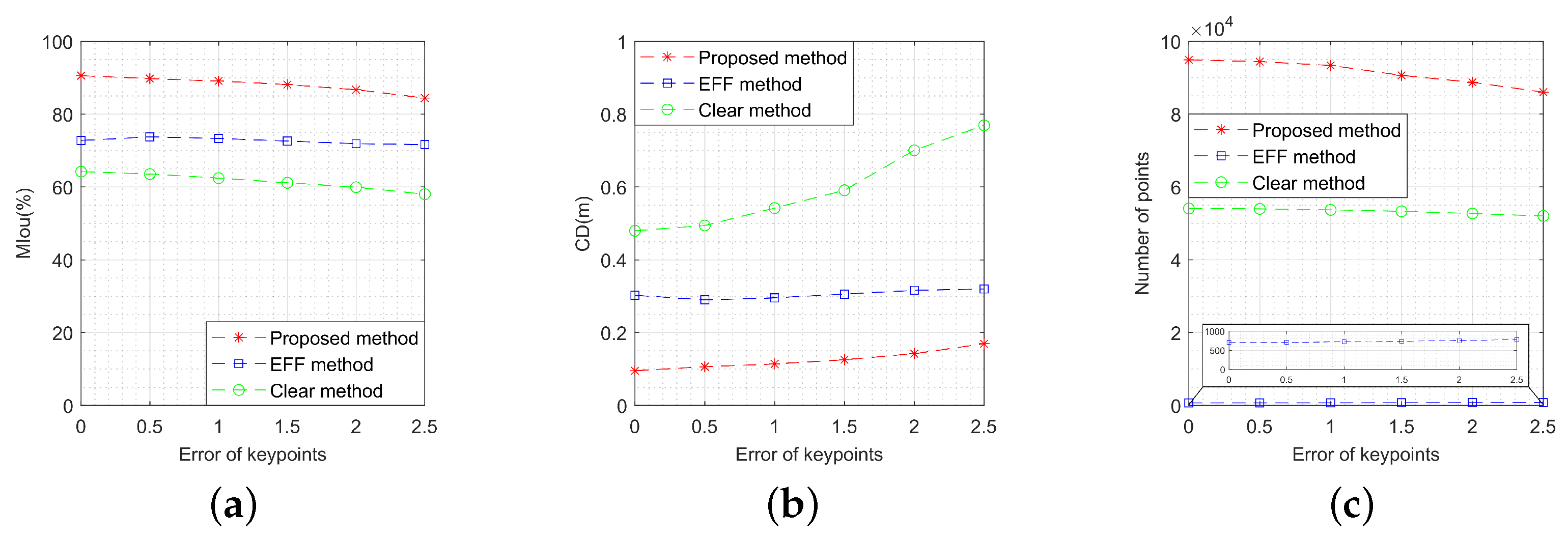
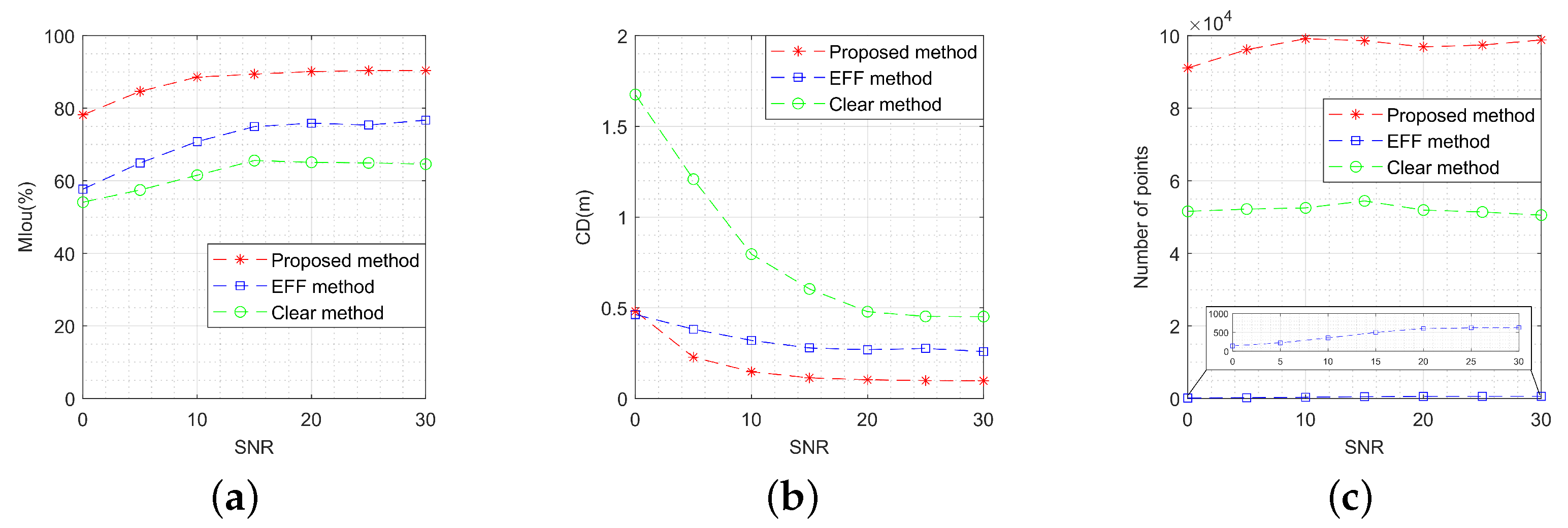
5.3.3. Comparison Analysis
- Target motion characteristics: The OC-V3R-OI method and EFF method exhibit superior performance in handling dynamic targets, maintaining high-quality reconstruction even under rapid motion. Both the clear method and the unaligned method struggle to adapt to such scenarios, resulting in reduced performance in moving target reconstruction.
- Target structural features: The voxel-based representation enhances the OC-V3R-OI method, clear method, and unaligned method in terms of information retention. In contrast, the sparsity of the EFF method may lead to the loss of critical information in certain applications, particularly when complex target structures are involved.
- Imaging quantity conditions: Both the OC-V3R-OI method and EFF method are adaptable to varying image quantities, effectively integrating image features to maintain reconstruction accuracy. The clear method, however, provides only basic reconstruction when data are sparse, and may not meet the precision requirements in high-demand applications. The unaligned method, on the other hand, suffers from cumulative errors as the number of images increases, making it unsuitable for scenarios with larger image datasets.
- Imaging quality conditions: The OC-V3R-OI method, clear method, and unaligned method all leverage the features of mask images directly, fully exploiting the advantages of deep networks in processing low-signal-to-noise-ratio images. The EFF method, however, is more affected by noise, resulting in sparser reconstructions that fail to meet accuracy requirements, particularly in challenging imaging conditions.
6. Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ISAR | inverse synthetic aperture radar |
| 2-D | two-dimensional |
| 3-D | three-dimensional |
| 6D-ICP | six degree iterative closest point |
| InISAR | interferometric inverse synthetic aperture radar |
| LOS | line of sight |
| PSO | particle swarm optimization |
| EFF | extended factorization framework |
| COS | co-location observation system |
| VTM-GL | voxel trimming mechanism based on growth learning |
| CPI | coherent processing interval |
| MCS | measurement coordinate system |
| OCS | orbital coordinate system |
References
- Pi, Y.; Li, X.; Yang, B. Global Iterative Geometric Calibration of a Linear Optical Satellite Based on Sparse GCPs. IEEE Trans. Geosci. Remote Sens. 2020, 58, 436–446. [Google Scholar] [CrossRef]
- Gong, R.; Wang, L.; Wu, B.; Zhang, G.; Zhu, D. Optimal Space-Borne ISAR Imaging of Space Objects with Co-Maximization of Doppler Spread and Spacecraft Component Area. Remote Sens. 2024, 16, 1037. [Google Scholar] [CrossRef]
- Liu, X.w.; Zhang, Q.; Jiang, L.; Liang, J.; Chen, Y.j. Reconstruction of Three-Dimensional Images Based on Estimation of Spinning Target Parameters in Radar Network. Remote Sens. 2018, 10, 1997. [Google Scholar] [CrossRef]
- Shao, S.; Liu, H.; Yan, J. Integration of Imaging and Recognition for Marine Targets in Fast-Changing Attitudes With Multistation Wideband Radars. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 1692–1710. [Google Scholar] [CrossRef]
- Chen, S.Y.; Hsu, K.H.; Kuo, T.H. Hyperspectral Target Detection-Based 2-D–3-D Parallel Convolutional Neural Networks for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 9451–9469. [Google Scholar] [CrossRef]
- Chen, W.; Chen, H.; Yang, S. 3D Point Cloud Fusion Method Based on EMD Auto-Evolution and Local Parametric Network. Remote Sens. 2024, 16, 4219. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, Z.; Zhou, F.; Shi, X. A New 3-D Geometry Reconstruction Method of Space Target Utilizing the Scatterer Energy Accumulation of ISAR Image Sequence. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8345–8357. [Google Scholar] [CrossRef]
- Kucharski, D.; Kirchner, G.; Koidl, F.; Fan, C.; Carman, R.; Moore, C.; Dmytrotsa, A.; Ploner, M.; Bianco, G.; Medvedskij, M.; et al. Attitude and Spin Period of Space Debris Envisat Measured by Satellite Laser Ranging. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7651–7657. [Google Scholar] [CrossRef]
- Koshkin, N.; Korobeynikova, E.; Shakun, L.; Strakhova, S.; Tang, Z. Remote Sensing of the EnviSat and Cbers-2B satellites rotation around the centre of mass by photometry. Adv. Space Res. 2016, 58, 358–371. [Google Scholar] [CrossRef]
- Pittet, J.N.; Šilha, J.; Schildknecht, T. Spin motion determination of the Envisat satellite through laser ranging measurements from a single pass measured by a single station. Adv. Space Res. 2018, 61, 1121–1131. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, Q.; Jiang, Z. 3D Reconstruction of Space Objects from Multi-Views by a Visible Sensor. Sensors 2017, 17, 1689. [Google Scholar] [CrossRef]
- Wang, K.; Liu, H.; Guo, B.; Gao, Y. A 6D-ICP approach for 3D reconstruction and motion estimate of unknown and non-cooperative target. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 6366–6370. [Google Scholar] [CrossRef]
- Wang, G.; Xia, X.g.; Chen, V. Three-dimensional ISAR imaging of maneuvering targets using three receivers. IEEE Trans. Image Process. 2001, 10, 436–447. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Lin, Y.; Teng, F.; Feng, S.; Hong, W. Holographic SAR Volumetric Imaging Strategy for 3-D Imaging With Single-Pass Circular InSAR Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Luo, Y.; Deng, Y.; Xiang, W.; Zhang, H.; Yang, C.; Wang, L. Radargrammetric 3D Imaging through Composite Registration Method Using Multi-Aspect Synthetic Aperture Radar Imagery. Remote Sens. 2024, 16, 523. [Google Scholar] [CrossRef]
- Yang, X.; Sheng, W.; Xie, A.; Zhang, R. Rotational Motion Compensation for ISAR Imaging Based on Minimizing the Residual Norm. Remote Sens. 2024, 16, 3629. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, F.; Bai, X.R.; Tao, M.L.; Zhang, Z.J. Joint Cross-Range Scaling and 3D Geometry Reconstruction of ISAR Targets Based on Factorization Method. IEEE Trans. Image Process. 2016, 25, 1740–1750. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Wang, J.; Su, J.; Luo, H. Spatial Feature-Based ISAR Image Registration for Space Targets. Remote Sens. 2024, 16, 3625. [Google Scholar] [CrossRef]
- Gu, X.; Yang, X.; Liu, H.; Yang, D. Adaptive Granularity-Fused Keypoint Detection for 6D Pose Estimation of Space Targets. Remote Sens. 2024, 16, 4138. [Google Scholar] [CrossRef]
- Niedfeldt, P.C.; Ingersoll, K.; Beard, R.W. Comparison and Analysis of Recursive-RANSAC for Multiple Target Tracking. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 461–476. [Google Scholar] [CrossRef]
- Xu, D.; Bie, B.; Sun, G.C.; Xing, M.; Pascazio, V. ISAR Image Matching and Three-Dimensional Scattering Imaging Based on Extracted Dominant Scatterers. Remote Sens. 2020, 12, 2699. [Google Scholar] [CrossRef]
- Morita, T.; Kanade, T. A sequential factorization method for recovering shape and motion from image streams. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 858–867. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, F.; Bai, X.; Paisley, J.; Ji, H. A Modified EM Algorithm for ISAR Scatterer Trajectory Matrix Completion. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3953–3962. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, L.; Du, R.; Zhou, F. Three-Dimensional Geometry Reconstruction Method for Slowly Rotating Space Targets Utilizing ISAR Image Sequence. Remote Sens. 2022, 14, 1144. [Google Scholar] [CrossRef]
- Zhou, Z.; Jin, X.; Liu, L.; Zhou, F. Three-Dimensional Geometry Reconstruction Method from Multi-View ISAR Images Utilizing Deep Learning. Remote Sens. 2023, 15, 1882. [Google Scholar] [CrossRef]
- Liu, A.; Zhang, S.; Zhang, C.; Zhi, S.; Li, X. RaNeRF: Neural 3-D Reconstruction of Space Targets From ISAR Image Sequences. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, L.; Cao, Y.; Huang, Y. Optical-and-Radar Image Fusion for Dynamic Estimation of Spin Satellites. IEEE Trans. Image Process. 2020, 29, 2963–2976. [Google Scholar] [CrossRef]
- Du, R.; Liu, L.; Bai, X.; Zhou, Z.; Zhou, F. Instantaneous Attitude Estimation of Spacecraft Utilizing Joint Optical-and-ISAR Observation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, L.; Xing, C.; Xie, P.; Cao, Y. Target Three-Dimensional Reconstruction From the Multi-View Radar Image Sequence. IEEE Access 2019, 7, 36722–36735. [Google Scholar] [CrossRef]
- Long, B.; Tang, P.; Wang, F.; Jin, Y.Q. 3-D Reconstruction of Space Target Based on Silhouettes Fused ISAR–Optical Images. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–19. [Google Scholar] [CrossRef]
- Zhou, W.; Liu, L.; Du, R.; Yang, Y.; Zhou, F. A novel 3-D geometry reconstruction method of space target based on joint optical-and-ISAR observation. In Proceedings of the IET International Radar Conference (IRC 2023), Chongqing, China, 3–5 December 2023; Volume 2023, pp. 3231–3236. [Google Scholar] [CrossRef]
- Liu, X.W.; Zhang, Q.; Luo, Y.; Lu, X.; Dong, C. Radar Network Time Scheduling for Multi-Target ISAR Task With Game Theory and Multiagent Reinforcement Learning. IEEE Sens. J. 2021, 21, 4462–4473. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Q.; Luo, Y.; Liu, X.; Ni, J.; Su, L. Joint Optimization of Time and Aperture Resource Allocation Strategy for Multi-Target ISAR Imaging in Radar Sensor Network. IEEE Sens. J. 2021, 21, 19570–19581. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Song, M.; Huang, P.; Xing, M. Noise Robust High-Speed Motion Compensation for ISAR Imaging Based on Parametric Minimum Entropy Optimization. Remote Sens. 2022, 14, 2178. [Google Scholar] [CrossRef]
- Liu, Y.; Yi, D.; Wang, Z. Coordinate transformation methods from the inertial system to the centroid orbit system. Aerosp. Control 2007, 25, 4–8. [Google Scholar]
- Ramalingam, S.; Sturm, P. A Unifying Model for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1309–1319. [Google Scholar] [CrossRef]
- Ning, Q.; Wang, H.; Yan, Z.; Wang, Z.; Lu, Y. A Fast and Robust Range Alignment Method for ISAR Imaging Based on a Deep Learning Network and Regional Multi-Scale Minimum Entropy Method. Remote Sens. 2024, 16, 3677. [Google Scholar] [CrossRef]
- Liu, C.; Luo, Y.; Yu, Z. A Robust Translational Motion Compensation Method for Moving Target ISAR Imaging Based on Phase Difference-Lv’s Distribution and Auto-Cross-Correlation Algorithm. Remote Sens. 2024, 16, 3554. [Google Scholar] [CrossRef]
- Zhao, S.; Luo, Y.; Zhang, T.; Guo, W.; Zhang, Z. A domain specific knowledge extraction transformer method for multisource satellite-borne SAR images ship detection. ISPRS J. Photogramm. Remote Sens. 2023, 198, 16–29. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Z.; Liang, Y.; Persello, C.; Sun, B.; He, G.; Ma, L. RSPS-SAM: A Remote Sensing Image Panoptic Segmentation Method Based on SAM. Remote Sens. 2024, 16, 4002. [Google Scholar] [CrossRef]
- Wang, J.; Sun, K.; Cheng, T.; Jiang, B.; Deng, C.; Zhao, Y.; Liu, D.; Mu, Y.; Tan, M.; Wang, X.; et al. Deep High-Resolution Representation Learning for Visual Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3349–3364. [Google Scholar] [CrossRef]
- Franceschetti, G.; Iodice, A.; Riccio, D. A canonical problem in electromagnetic backscattering from buildings. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1787–1801. [Google Scholar] [CrossRef]
- Boag, A. A fast physical optics (FPO) algorithm for high frequency scattering. IEEE Trans. Antennas Propag. 2004, 52, 197–204. [Google Scholar] [CrossRef]
- Auer, S.; Hinz, S.; Bamler, R. Ray-Tracing Simulation Techniques for Understanding High-Resolution SAR Images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1445–1456. [Google Scholar] [CrossRef]
- Kulpa, K.S.; Samczyński, P.; Malanowski, M.; Gromek, A.; Gromek, D.; Gwarek, W.; Salski, B.; Tański, G. An Advanced SAR Simulator of Three-Dimensional Structures Combining Geometrical Optics and Full-Wave Electromagnetic Methods. IEEE Trans. Geosci. Remote Sens. 2014, 52, 776–784. [Google Scholar] [CrossRef]
- Fan, H.; Su, H.; Guibas, L. A Point Set Generation Network for 3D Object Reconstruction from a Single Image. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2463–2471. [Google Scholar] [CrossRef]

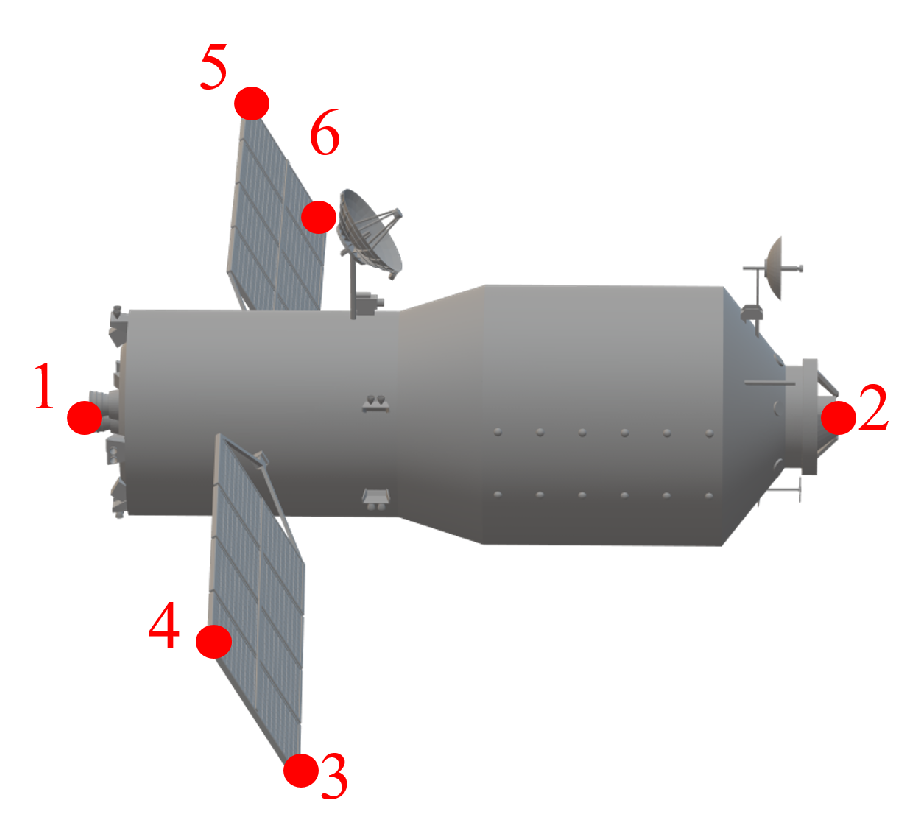





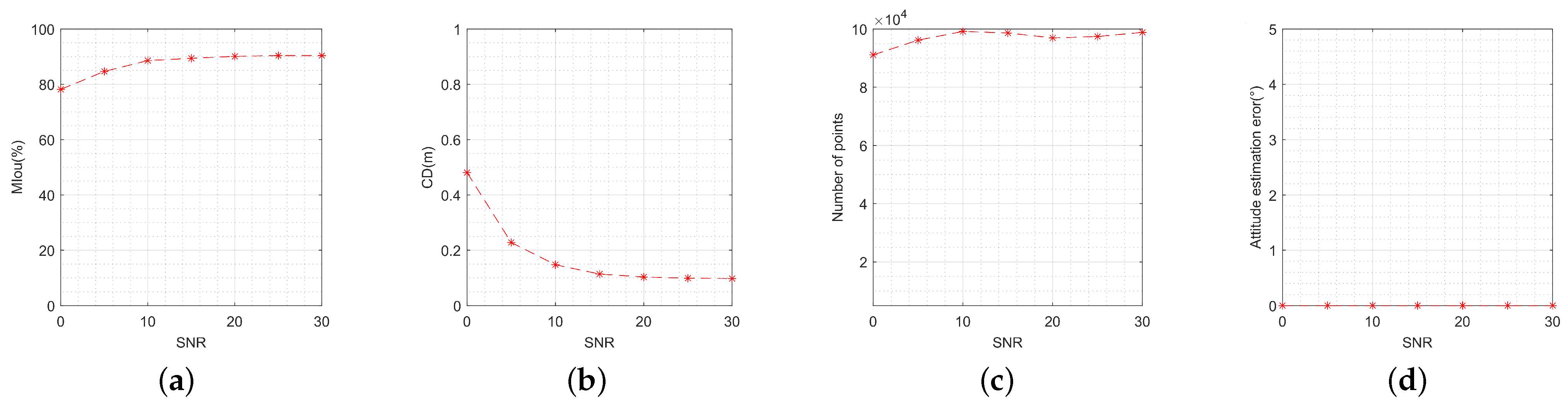






| Type of Movement | MIou (%) | CD (m) | Number of Points | Attitude Estimation Error (°) |
|---|---|---|---|---|
| The triaxially stabilized target | 88.83 | 0.1180 | 107,127 | 0.7555 |
| The chaotic motion target | 91.85 | 0.0848 | 107,644 | 0.7213 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Liu, L.; Du, R.; Wang, Z.; Shang, R.; Zhou, F. Three-Dimensional Reconstruction of Space Targets Utilizing Joint Optical-and-ISAR Co-Location Observation. Remote Sens. 2025, 17, 287. https://doi.org/10.3390/rs17020287
Zhou W, Liu L, Du R, Wang Z, Shang R, Zhou F. Three-Dimensional Reconstruction of Space Targets Utilizing Joint Optical-and-ISAR Co-Location Observation. Remote Sensing. 2025; 17(2):287. https://doi.org/10.3390/rs17020287
Chicago/Turabian StyleZhou, Wanting, Lei Liu, Rongzhen Du, Ze Wang, Ronghua Shang, and Feng Zhou. 2025. "Three-Dimensional Reconstruction of Space Targets Utilizing Joint Optical-and-ISAR Co-Location Observation" Remote Sensing 17, no. 2: 287. https://doi.org/10.3390/rs17020287
APA StyleZhou, W., Liu, L., Du, R., Wang, Z., Shang, R., & Zhou, F. (2025). Three-Dimensional Reconstruction of Space Targets Utilizing Joint Optical-and-ISAR Co-Location Observation. Remote Sensing, 17(2), 287. https://doi.org/10.3390/rs17020287









