3D Seismic Attribute Conditioning Using Multiscale Sheet-Enhancing Filtering
Abstract
1. Introduction
- (1)
- Compatibility: The effectiveness of AMHSF reflies solely on the assumption that interpretative features conform to sheet-like structures. Thus, our AMHSF can effectively filter and enhance any sheet-like structure information within attribute images.
- (2)
- Accuracy: As a typical filter, AMHSF accurately isolates sheet-like structures from non-sheet-like ones in a non-iterative and deterministic manner, as long as the underlying assumption of sheet-like behavior is valid.
- (3)
- No Requirement for Additional Data: AMHSF does not necessitate any supplementary data (e.g., strike and dip information) beyond the coherence images, which further contributes to the precision of the filtering.
- (4)
- Simplicity of Implementation: AMHSF involves only three key stages with two post-processing stages, making it straightforward to implement.
- (1)
- AMHSF enables the precise isolation of relevant sheet-like features, such as faults and fractures, from noise-contaminated attribute images. To the best of our knowledge, we are among the first to introduce the sheet-like assumption and the corresponding AMHSF in seismic attribute analysis for the purpose of attribute conditioning in coherence images.
- (2)
- A major innovation of our proposed AMHSF is the development of a novel enhancement function specifically designed to highlight sheet-like structures in coherence images. This function is fundamentally different from the enhancement functions typically used in vascular structure enhancement.
2. Materials and Methods
2.1. Methods
2.1.1. Preliminaries
2.1.2. Proposed Methods
- (1)
- (2)
- (3)
- Blob-like Structures: Blob-like features are typically indicative of noise. The following equation serves to differentiate blob-like structures from other types [43]:
- (4)
- Noisy Structures: In this case, random noise is found in a structureless state, which is represented by half the maximum Frobenius norm [43]:
2.2. Implementation
| Algorithm 1 AMHSF |
| Require: , , , , . |
Ensure: .
|
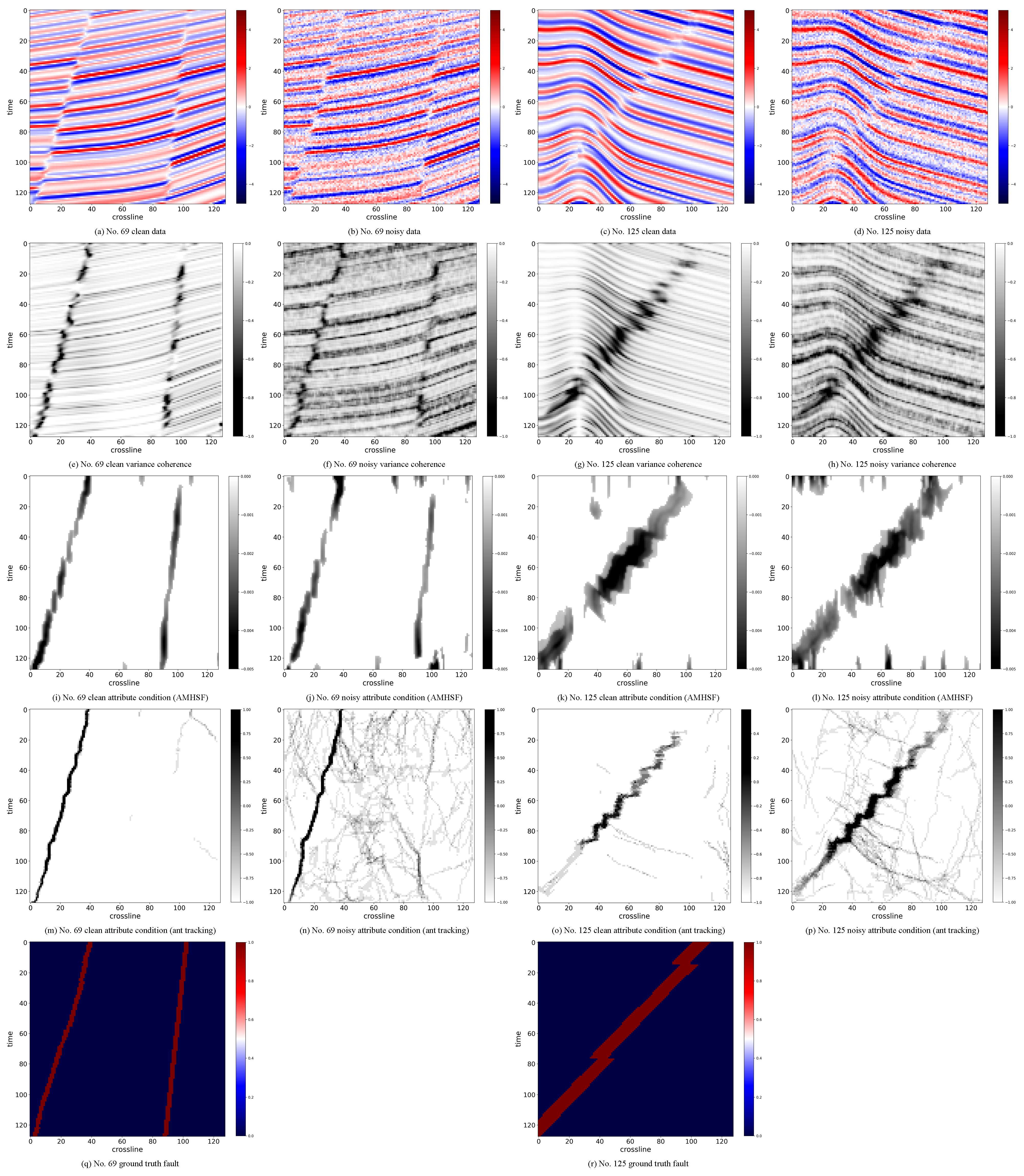
2.3. Data and Data Processing
3. Results
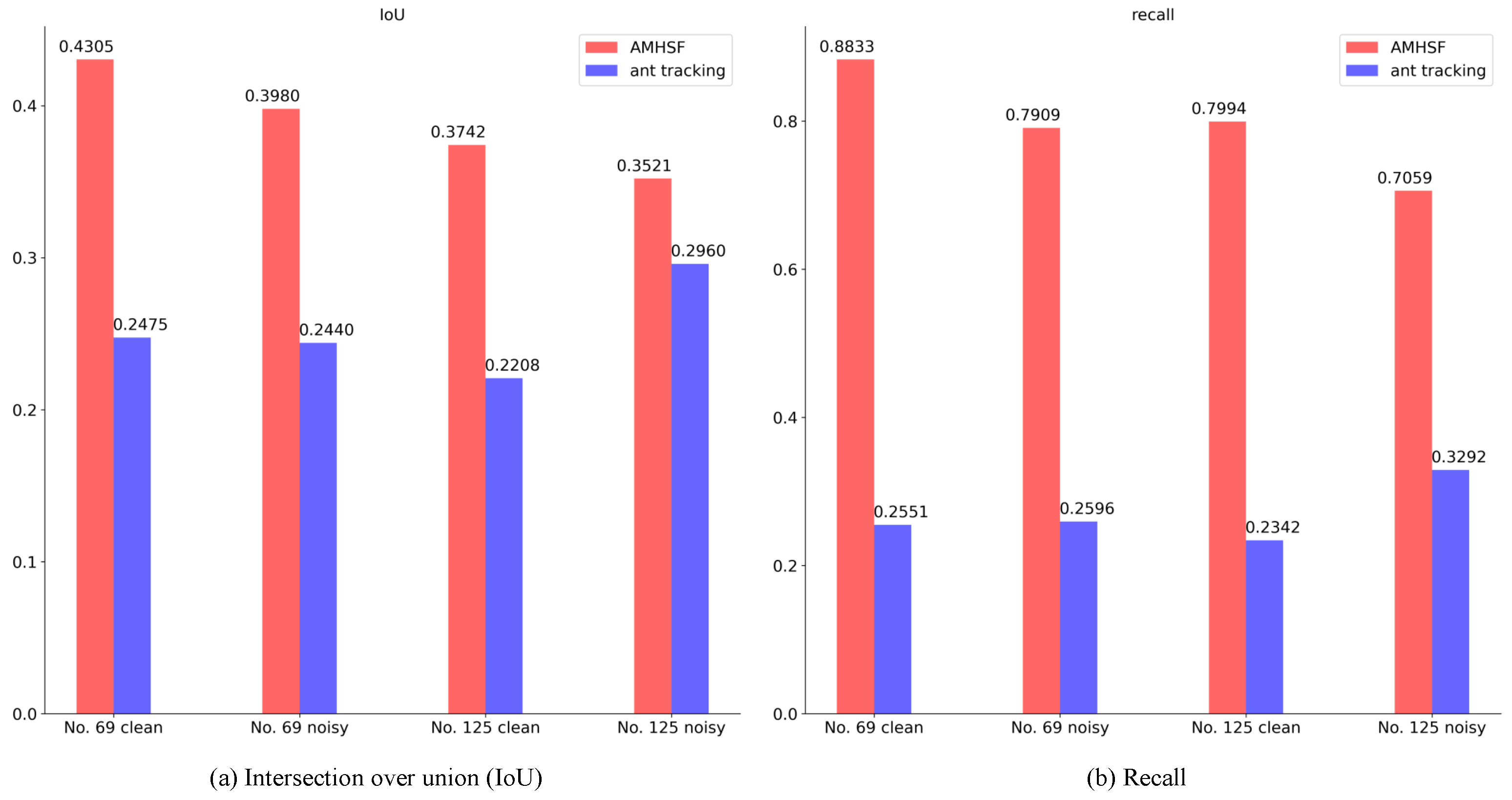
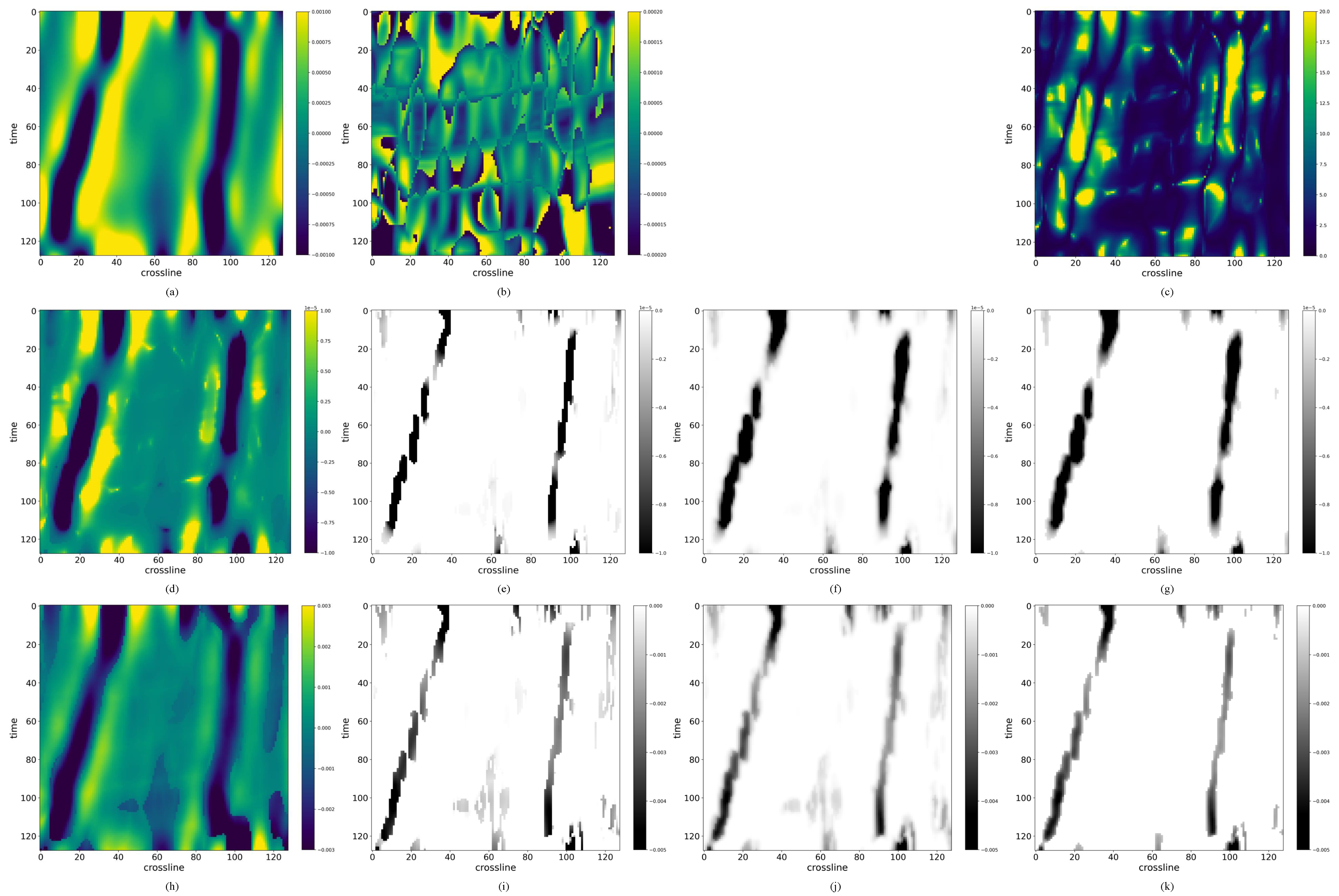
3.1. Experimental Results with the Synthetic 3D Dataset
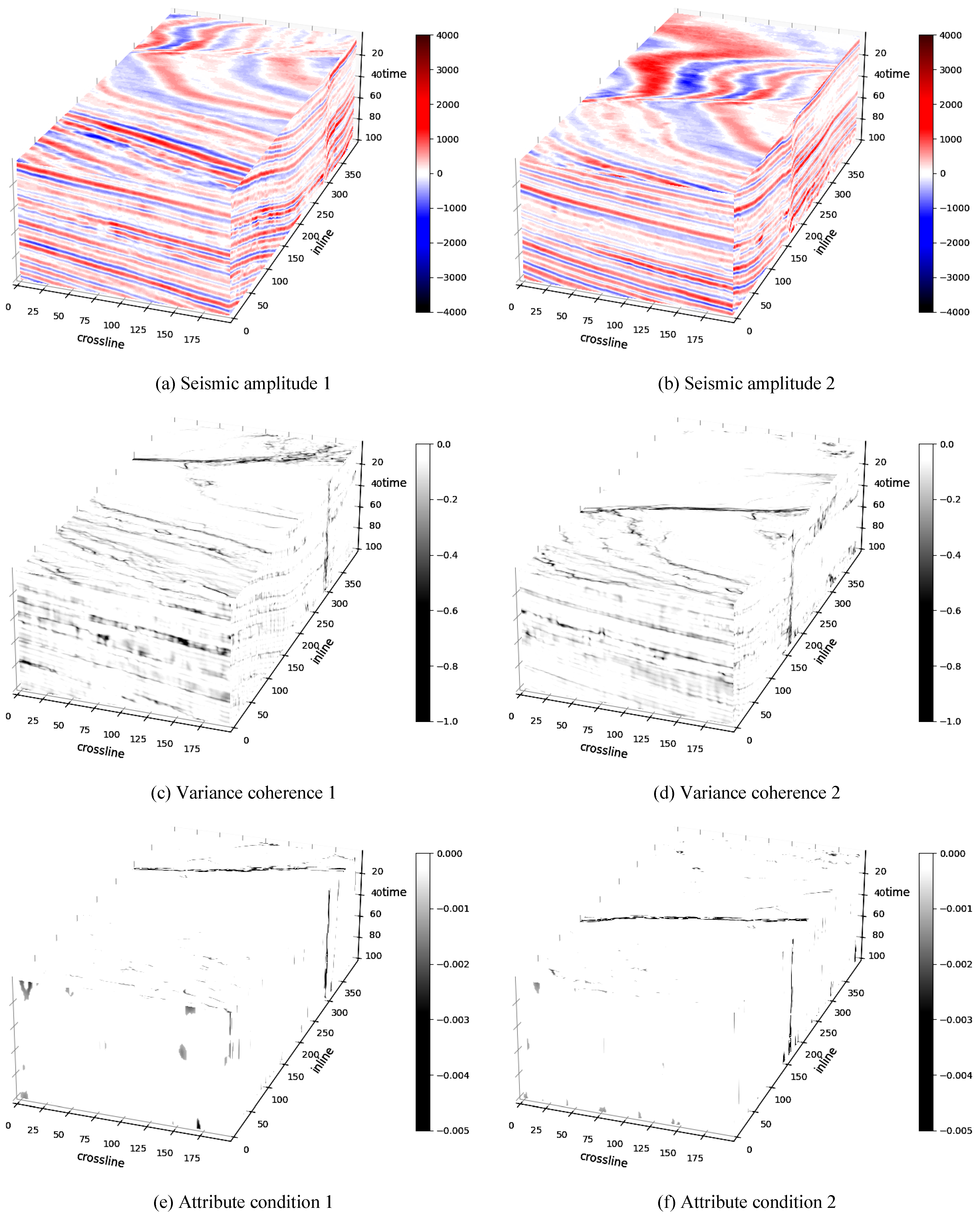
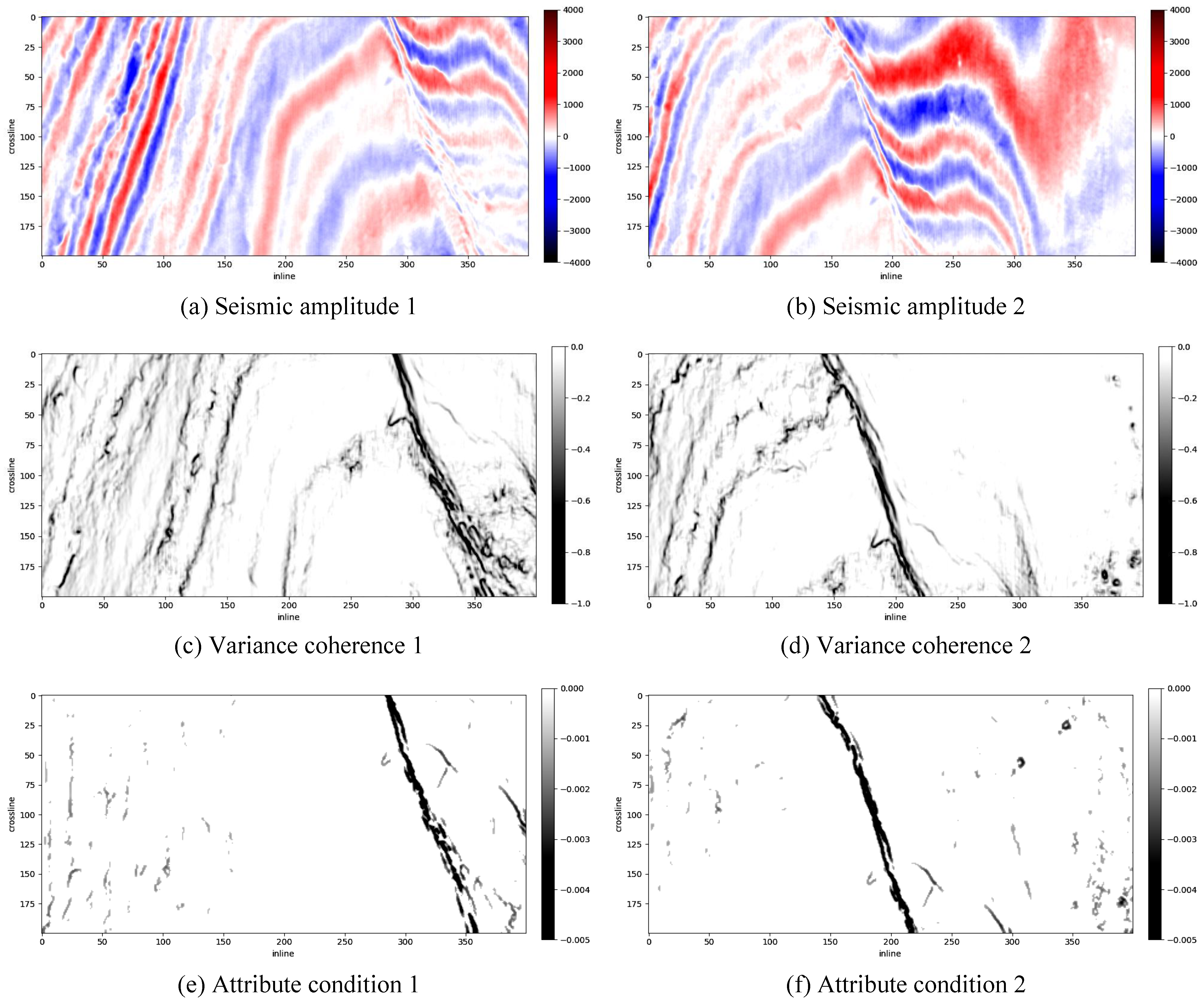
3.2. Experimental Results Using Opunake-3D
3.3. Experimental Results Using Parihaka-3D
4. Discussion
- (1)
- Our proposed method is constructed on the fundamental assumption that seismic data exhibit sheet-like structures. This assumption is satisfied in the majority of cases of faults, as verified in [35]. While it can be readily observed that most features conform to sheet-like structures, a more comprehensive theoretical or experimental investigation is necessary to fully validate this assumption and ensure accurate attribute conditioning. When this sheet-like assumption is not satisfied, our AMHSF will also fail, which is a characteristic of modeling-based methods and a significant drawback.
- (2)
- Our proposed method is sensitive to the selection of parameters. Since the sheetness measure is designed to be maximal at the scale corresponding to the radius of the sheet-like structures, the sheetness index peaks near the center of these features and approaches zero outside. Therefore, to achieve optimal attribute conditioning, the scale parameters must be carefully adjusted throughout the experiment to ensure effective filtering of sheet-like structures, Also, the removal threshold requires fine-tuning, as this parameter directly impacts the suppression of unwanted artifacts in the resulting attribute images. As previously discussed, an excessively high threshold may degrade conditioning performance, while a threshold set too low may result in an excess of artifacts in the final output.
- (3)
- The smoothing ability of AMHSF is limited for various features, leading to difficulties in achieving continuous feature planes as [33,35]. Despite the application of smoothing for post-processing, the final results still exhibit discontinuities. However, as demonstrated in Figure 5, the attribute conditioning of the raw results is already highly effective, with faults being easily identifiable. It is highly probable that applying more advanced smoothing algorithms could lead to improved post-processing outcomes. Therefore, further exploration of smoothing techniques and their impact on the final results presents a promising direction for future work. However, still, attribute conditioning is only an intermediate step of fault detection. A more effective application may be the utilizing of our AMHSF as a pre-processing step for fault detection tasks, such as ant tracking [33], to yield more promising results.
- (4)
- According to other Hessian-based methods [55], the artifacts in AMHSF results may represent theoretical corner cases. As a modeling-based approach, AMHSF shares a common limitation inherent to such methods: the theoretical framework cannot encompass all possible scenarios. Although AHMSF is specifically designed for sheet-like structures, it is inevitably influenced by other non-sheet-like structures that exhibit properties similar to sheet-like structures within our method.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MHF | multiscale Hessian-based filtering |
| AMHF | anisotropic multiscale Hessian-based filtering |
| AMHSF | anisotropic multiscale Hessian-based sheet-enhancing filtering |
References
- Hesthammer, J.; Fossen, H. Research article: The influence of seismic noise in structural interpretation of seismic attribute maps. First Break 1997, 15. [Google Scholar] [CrossRef]
- Won, J.; Shin, J.; Ha, J.; Jun, H. Study on the seismic random noise attenuation for the seismic Attribute analysis. Econ. Environ. Geol. 2024, 57, 51–71. [Google Scholar] [CrossRef]
- Wen, Y.; Qian, F.; Guo, W.; Zong, J.; Peng, D.; Chen, K.; Hu, G. VSP Upgoing and Downgoing Wavefield Separation: A Hybrid Model-Data Driven Approach. IEEE Trans. Geosci. Remote Sens. 2025; in press. [Google Scholar]
- Wu, X.; Liang, L.; Shi, Y.; Fomel, S. FaultSeg3D: Using synthetic data sets to train an end-to-end convolutional neural network for 3D seismic fault segmentation. Geophysics 2019, 84, IM35–IM45. [Google Scholar] [CrossRef]
- Lin, T.; Ha, T.; Marfurt, K.J.; Deal, K.L. Quantifying the significance of coherence anomalies. Interpretation 2016, 4, T205–T213. [Google Scholar] [CrossRef]
- Bahorich, M.; Farmer, S. 3-D seismic discontinuity for faults and stratigraphic features: The coherence cube. Lead. Edge 1995, 14, 1053–1058. [Google Scholar] [CrossRef]
- Marfurt, K.J.; Kirlin, R.L.; Farmer, S.L.; Bahorich, M.S. 3-D seismic attributes using a semblance-based coherency algorithm. Geophysics 1998, 63, 1150–1165. [Google Scholar] [CrossRef]
- Huo, Z.; Liu, X.; Wang, X.; Chen, W. An efficient Eigenstructure-Based coherence measure via dimensionality reduction. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1711–1715. [Google Scholar] [CrossRef]
- Sun, F.; Zhang, B. A generalized coherence algorithm based on kernel correlation. IEEE Geosci. Remote Sens. Lett. 2020, 17, 2040–2044. [Google Scholar] [CrossRef]
- Yang, L.; Gao, J.; Liu, N.; Yang, T.; Jiang, X. A coherence algorithm for 3-D seismic data analysis based on the mutual information. IEEE Geosci. Remote Sens. Lett. 2019, 16, 967–971. [Google Scholar] [CrossRef]
- Marfurt, K.J.; Sudhaker, V.; Gersztenkorn, A.; Crawford, K.D.; Nissen, S.E. Coherency calculations in the presence of structural dip. Geophysics 1999, 64, 104–111. [Google Scholar] [CrossRef]
- Yan, B.; Yuan, S.; Wang, S.; OuYang, Y.; Wang, T.; Shi, P. Improved eigenvalue-based coherence algorithm with dip scanning. Geophysics 2016, 82, V95–V103. [Google Scholar] [CrossRef]
- Rande, T.; Pedersen, S.I.; Sønneland, L. Automatic extraction of fault surfaces from three-dimensional seismic data. In SEG Technical Program Expanded Abstracts 2001; Society of Exploration Geophysicists: Houston, TX, USA, 2001; pp. 551–554. [Google Scholar] [CrossRef]
- Van Bemmel, P.P.; Pepper, R.E. Seismic Signal Processing Method and Apparatus for Generating a Cube of Variance Values. U.S. Patent 6,151,555, 19 August 1999. [Google Scholar]
- Randen, T.; Monsen, E.; Signer, C.; Abrahamsen, A.; Hansen, J.O.; Sæter, T.; Schlaf, J. Three-dimensional texture attributes for seismic data analysis. In SEG Technical Program Expanded Abstracts 2000; Society of Exploration Geophysicists: Houston, TX, USA, 2000; pp. 668–671. [Google Scholar] [CrossRef]
- Bakker, P. Image Structure Analysis for Seismic Interpretation. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2002. [Google Scholar]
- Mahadik, R.; Singh, G.; Routray, A. Multispectral coherence analysis for better fault visualization in seismic data. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Wu, X. Directional structure-tensor-based coherence to detect seismic faults and channels. Geophysics 2017, 82, A13–A17. [Google Scholar] [CrossRef]
- Wang, X.; Chen, W.; Zhu, Z. Robust seismic volumetric dip estimation combining structure tensor and multiwindow technology. IEEE Trans. Geosci. Remote Sens. 2019, 57, 395–405. [Google Scholar] [CrossRef]
- Roberts, A. Curvature attributes and their application to 3D interpreted horizons. First Break 2001, 19, 85–100. [Google Scholar] [CrossRef]
- Al-Dossary, S.; Marfurt, K.J. 3D volumetric multispectral estimates of reflector curvature and rotation. Geophysics 2006, 71, P41–P51. [Google Scholar] [CrossRef]
- Ao, Y.; Lu, W.; Jiang, B.; Monkam, P. Seismic structural curvature volume extraction with convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7370–7384. [Google Scholar] [CrossRef]
- Gao, D. Integrating 3D seismic curvature and curvature gradient attributes for fracture characterization: Methodologies and interpretational implications. Geophysics 2013, 78, O21–O31. [Google Scholar] [CrossRef]
- Klein, P.; Richard, L.; James, H. 3D curvature attributes: A new approach for seismic interpretation. First Break 2008, 26. [Google Scholar] [CrossRef]
- Qi, X.; Marfurt, K. Volumetric aberrancy to map subtle faults and flexures. Interpretation 2018, 6, T349–T365. [Google Scholar] [CrossRef]
- Lyu, B.; Qi, J.; Li, F.; Marfurt, K.J. Multispectral aberrancy. In SEG Technical Program Expanded Abstracts 2020; Society of Exploration Geophysicists: Houston, TX, USA, 2020; pp. 1120–1124. [Google Scholar] [CrossRef]
- Hale, D. Methods to compute fault images, extract fault surfaces, and estimate fault throws from 3D seismic images. Geophysics 2013, 78, O33–O43. [Google Scholar] [CrossRef]
- Qi, J.; Lyu, B.; AlAli, A.; Machado, G.; Hu, Y.; Marfurt, K. Image processing of seismic attributes for automatic fault extraction. Geophysics 2019, 84, O25–O37. [Google Scholar] [CrossRef]
- Neff, D.B.; Grismore, J.R.; Lucas, W.A. Automated Seismic Fault Detection and Picking. U.S. Patent 6,018,498, 2 September 1998. [Google Scholar]
- Cohen, I.; Coult, N.; Vassiliou, A.A. Detection and extraction of fault surfaces in 3D seismic data. Geophysics 2006, 71, P21–P27. [Google Scholar] [CrossRef]
- Wu, X.; Hale, D. 3D seismic image processing for faults. Geophysics 2016, 81, IM1–IM11. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, Z. Methods to enhance seismic faults and construct fault surfaces. Comput. Geosci. 2017, 107, 37–48. [Google Scholar] [CrossRef]
- Pedersen, S.I.; Randen, T.; Sønneland, L.; Steen, Ø. Automatic fault extraction using artificial ants. In SEG Technical Program Expanded Abstracts 2002; Society of Exploration Geophysicists: Houston, TX, USA, 2002; pp. 512–515. [Google Scholar] [CrossRef]
- Han, J.; Gu, B.; Zhu, G.; Liu, Z. High-Precision Depth Domain Migration Method in Imaging of 3D Seismic Data in Coalfield. Remote Sens. 2022, 14, 2850. [Google Scholar] [CrossRef]
- Wu, X.; Fomel, S. Automatic fault interpretation with optimal surface voting. Geophysics 2018, 83, O67–O82. [Google Scholar] [CrossRef]
- Huang, L.; Dong, X.; Clee, T.E. A scalable deep learning platform for identifying geologic features from seismic attributes. Lead. Edge 2017, 36, 249–256. [Google Scholar] [CrossRef]
- Xiong, W.; Ji, X.; Ma, Y.; Wang, Y.; AlBinHassan, N.M.; Ali, M.N.; Luo, Y. Seismic fault detection with convolutional neural network. Geophysics 2018, 83, O97–O103. [Google Scholar] [CrossRef]
- Hu, G.; Hu, Z.; Liu, J.; Cheng, F.; Peng, D. Seismic fault interpretation using Deep Learning-Based Semantic Segmentation Method. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Wang, Z.; Li, B.; Liu, N.; Wu, B.; Zhu, X. Distilling knowledge from an ensemble of convolutional neural networks for seismic fault detection. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Pochet, A.; Diniz, P.H.B.; Lopes, H.; Gattass, M. Seismic fault detection using convolutional neural networks trained on synthetic poststacked amplitude maps. IEEE Geosci. Remote Sens. Lett. 2018, 16, 352–356. [Google Scholar] [CrossRef]
- Tang, Z.; Wu, B.; Wu, W.; Ma, D. Fault Detection via 2.5D Transformer U-Net with Seismic Data Pre-Processing. Remote Sens. 2023, 15, 1039. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, R.; Ma, J. Improving Seismic Fault Recognition with Self-Supervised Pre-Training: A Study of 3D Transformer-Based with Multi-Scale Decoding and Fusion. Remote Sens. 2024, 16, 922. [Google Scholar] [CrossRef]
- Frangi, A.F.; Niessen, W.J.; Vincken, K.L.; Viergever, M.A. Multiscale vessel enhancement filtering. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention, Cambridge, MA, USA, 11–33 October 1998. [Google Scholar]
- Annunziata, R.; Garzelli, A.; Ballerini, L.; Mecocci, A.; Trucco, E. Leveraging multiscale Hessian-Based enhancement with a novel exudate inpainting technique for retinal vessel segmentation. IEEE J. Biomed. Health Inform. 2015, 20, 1129–1138. [Google Scholar] [CrossRef]
- Jerman, T.; Pernus, F.; Likar, B.; Spiclin, Z. Enhancement of vascular structures in 3D and 2D angiographic images. IEEE Trans. Med. Imaging 2016, 35, 2107–2118. [Google Scholar] [CrossRef]
- Descoteaux, M.; Audette, M.; Chinzei, K.; Siddiqi, K. Bone enhancement filtering: Application to sinus bone segmentation and simulation of pituitary surgery. Comput. Aided Surg. 2006, 11, 247–255. [Google Scholar] [CrossRef]
- Geusebroek, J.; Smeulders, A.W.M.; Van De Weijer, J. Fast anisotropic gauss filtering. IEEE Trans. Image Process. 2003, 12, 938–943. [Google Scholar] [CrossRef]
- Nie, S.; Yu, J.; Chen, P.; Wang, Y.; Zhang, J.Q. A Hessian plate filter and shape feature-based approach to automatically localizing the NT VOI of 3D ultrasound data. Comput. Assist. Surg. 2016, 21 (Suppl. S1), 83–91. [Google Scholar] [CrossRef][Green Version]
- Voorn, M.; Exner, U.; Rath, A. Multiscale Hessian fracture filtering for the enhancement and segmentation of narrow fractures in 3D image data. Comput. Geosci. 2013, 57, 44–53. [Google Scholar] [CrossRef]
- Sato, Y.; Westin, C.; Bhalerao, A.; Nakajima, S.; Shiraga, N.; Tamura, S.; Kikinis, R. Tissue classification based on 3D local intensity structures for volume rendering. IEEE Trans. Vis. Comput. Graph. 2000, 6, 160–180. [Google Scholar] [CrossRef]
- Charalampidis, D. Recursive implementation of the Gaussian filter using truncated cosine functions. IEEE Trans. Signal Process. 2016, 64, 3554–3565. [Google Scholar] [CrossRef]
- Hale, D. Recursive Gaussian filters. Tech. Rep. CWP-546, Center for Wave Phenomena, Colorado School of Mines, Golden. Colorado. 2006. Available online: https://cwp.mines.edu/wp-content/uploads/sites/112/2018/09/cwp546.pdf (accessed on 4 December 2024).
- Kopp, J. Efficient numerical diagonalization of hermitian 3 × 3 matrices. Int. J. Mod. Phys. C 2008, 19, 523–548. [Google Scholar] [CrossRef]
- Weickert, J. Anisotropic Diffusion in Image Processing; Teubner: Stuttgart, Germany, 1998. [Google Scholar]
- Vignati, A.; Giannini, V.; Bert, A.; Borrelli, P.; De Luca, M.; Martincich, L.; Sardanelli, F.; Regge, D. A fully automatic multiscale 3-Dimensional Hessian-Based algorithm for vessel detection in breast DCE-MRI. Investig. Radiol. 2012, 47, 705–710. [Google Scholar] [CrossRef]
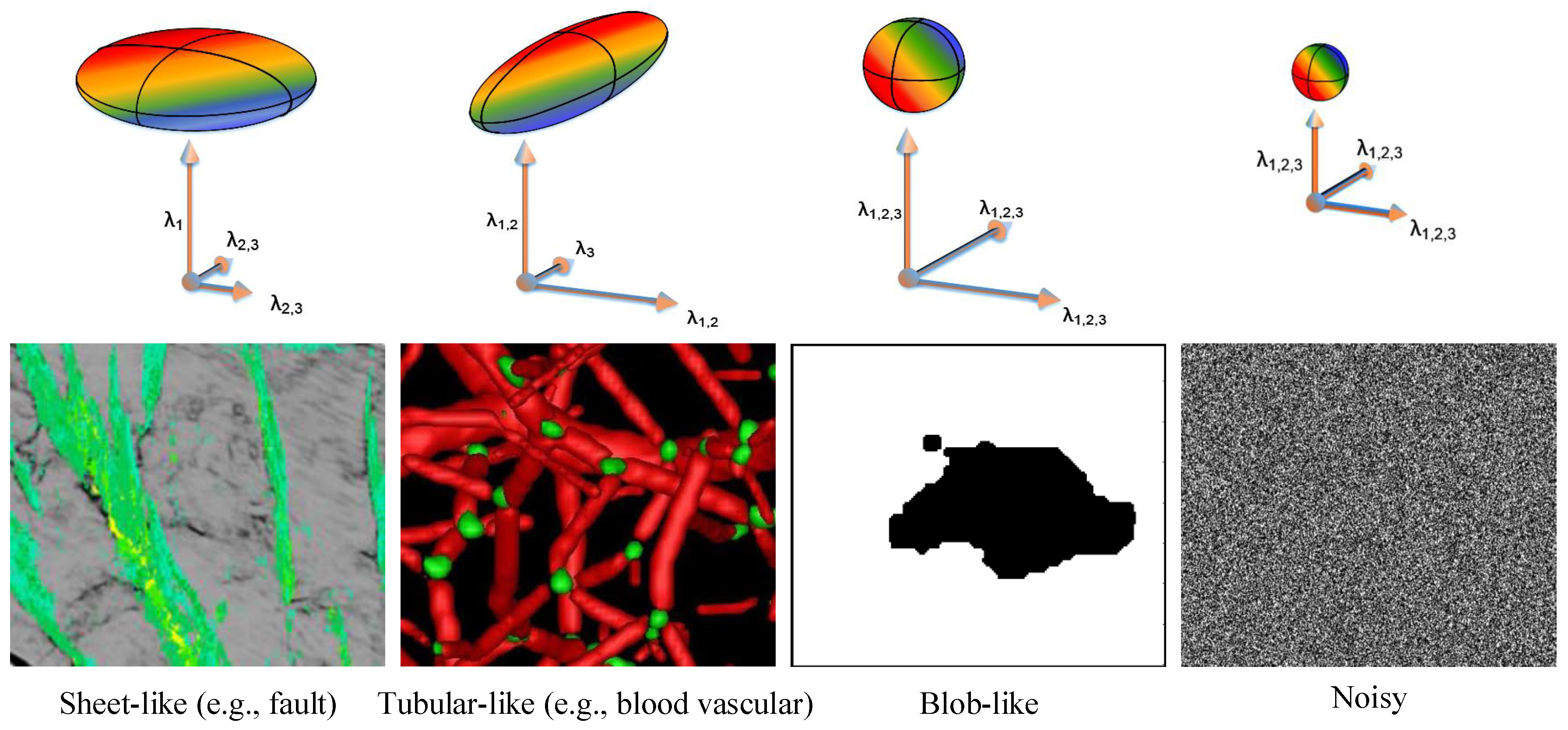



| Structure Type | * | * | * |
|---|---|---|---|
| Sheet-like, bright | Low | Low | High negative |
| Sheet-like, dark | Low | Low | High positive |
| Tubular-like, bright | Low | High negative | High negative |
| Tubular-like, dark | Low | High positive | High positive |
| Blob-like, bright | High negative | High negative | High negative |
| Blob-like, dark | High positive | High positive | High positive |
| Noisy | Low | Low | Low |
| Dataset | ||||
|---|---|---|---|---|
| Synthetic | 0.0:0.4:8.0 * | 0.0:0.4:8.0 | 0.0:0.15:3.0 | |
| Opunake-3D | 0.0:0.2:4.0 | 0.0:0.2:4.0 | 4.0:0.2:8.0 | |
| Parihaka-3D | 0.0:0.1:4.0 | 0.0:0.1:4.0 | 2.0:0.1:6.0 |
| Figure 5a * | 0.0:0.4:8.0 | 0.0:0.4:8.0 | 0.0:0.15:3.0 | 0.0015 |
| Figure 5b * | 0.0:0.4:8.0 | 0.0:0.4:8.0 | 0.0:0.15:3.0 | 0.0015 |
| Figure 5c | 4.0:0.4:12.0 | 0.0:0.4:8.0 | 0.0:0.15:3.0 | 0.0015 |
| Figure 5d | 4.0:0.4:12.0 | 0.0:0.4:8.0 | 0.0:0.15:3.0 | 0.0015 |
| Figure 5e | 0.0:0.4:8.0 | 4.0:0.4:12.0 | 0.0:0.15:3.0 | 0.0015 |
| Figure 5f | 0.0:0.4:8.0 | 4.0:0.4:12.0 | 0.0:0.15:3.0 | 0.0015 |
| Figure 5g | 0.0:0.4:8.0 | 0.0:0.4:8.0 | 0.0:0.05:1.0 | 0.0015 |
| Figure 5h | 0.0:0.4:8.0 | 0.0:0.4:8.0 | 0.0:0.05:1.0 | 0.0015 |
| Figure 5i | 0.0:0.4:8.0 | 0.0:0.4:8.0 | 0.0:0.15:3.0 | 0.0005 |
| Figure 5j | 0.0:0.4:8.0 | 0.0:0.4:8.0 | 0.0:0.15:3.0 | 0.0005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, T.; Yue, Y.; Chen, T.; Qian, F. 3D Seismic Attribute Conditioning Using Multiscale Sheet-Enhancing Filtering. Remote Sens. 2025, 17, 278. https://doi.org/10.3390/rs17020278
Zhao T, Yue Y, Chen T, Qian F. 3D Seismic Attribute Conditioning Using Multiscale Sheet-Enhancing Filtering. Remote Sensing. 2025; 17(2):278. https://doi.org/10.3390/rs17020278
Chicago/Turabian StyleZhao, Taiyin, Yuehua Yue, Tian Chen, and Feng Qian. 2025. "3D Seismic Attribute Conditioning Using Multiscale Sheet-Enhancing Filtering" Remote Sensing 17, no. 2: 278. https://doi.org/10.3390/rs17020278
APA StyleZhao, T., Yue, Y., Chen, T., & Qian, F. (2025). 3D Seismic Attribute Conditioning Using Multiscale Sheet-Enhancing Filtering. Remote Sensing, 17(2), 278. https://doi.org/10.3390/rs17020278






