Projected Spatiotemporal Evolution of Urban Form Using the SLEUTH Model with Urban Master Plan Scenarios
Abstract
1. Introduction
2. Materials and Methods
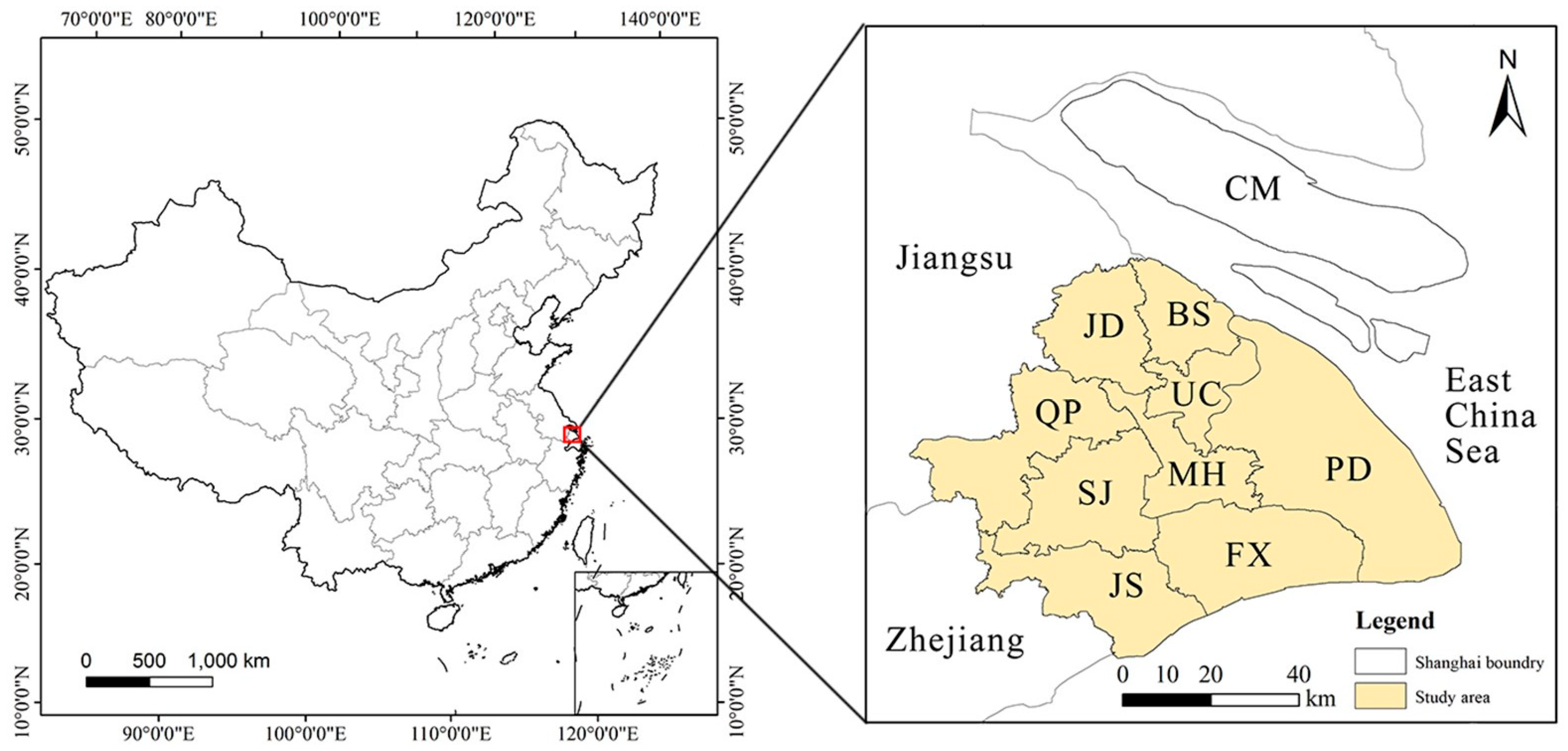
2.1. Study Area
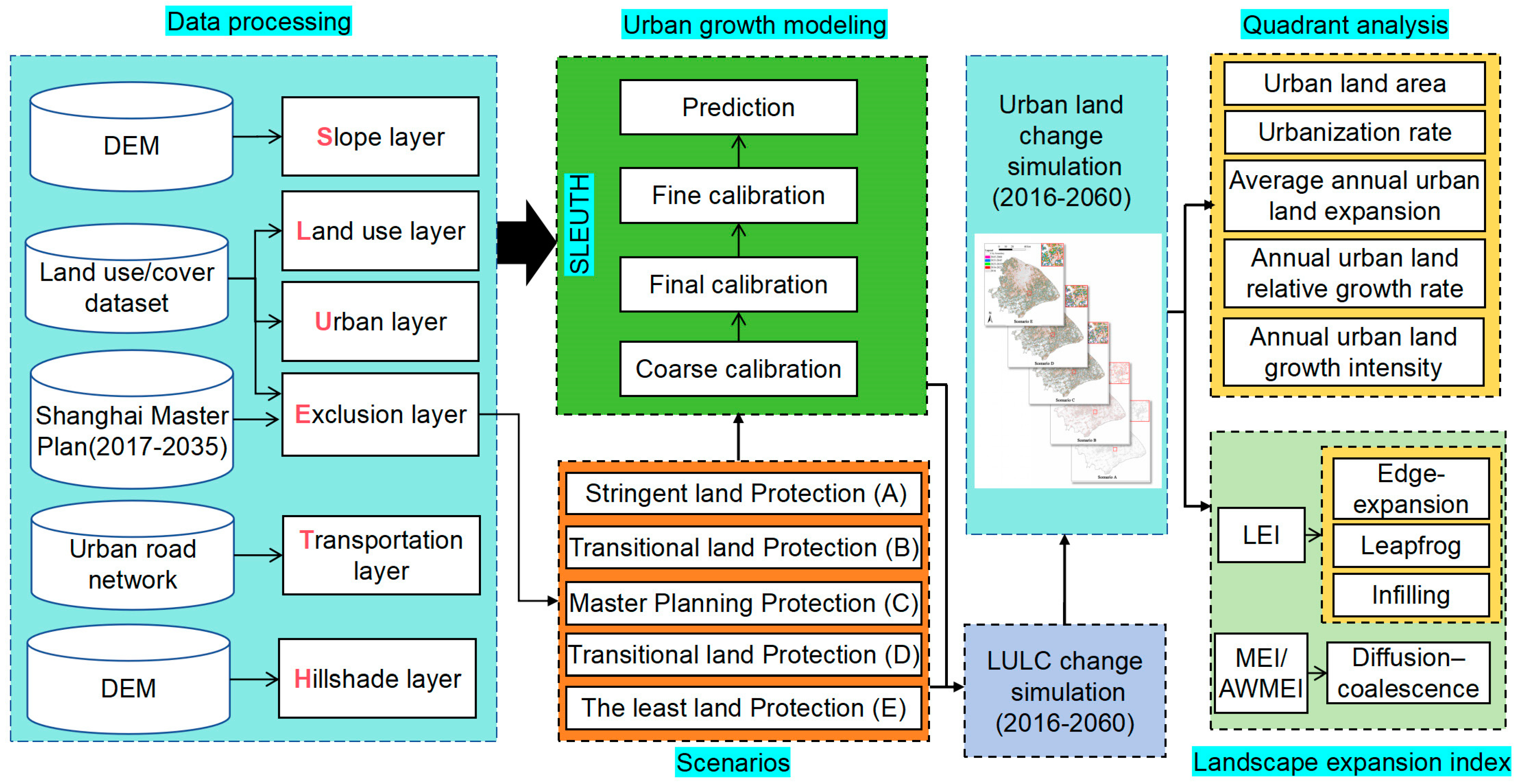
2.2. Research Framework
2.3. The SLEUTH Model
2.3.1. Input Dataset of the SLEUTH Model
2.3.2. Scenario Settings for the SLEUTH Model
2.3.3. SLEUTH Model Calibration and Parameter Determination
2.4. Accuracy Assessment for the Projected LULC Results
2.5. Quantification of the Spatiotemporal Dynamics of Urban Growth
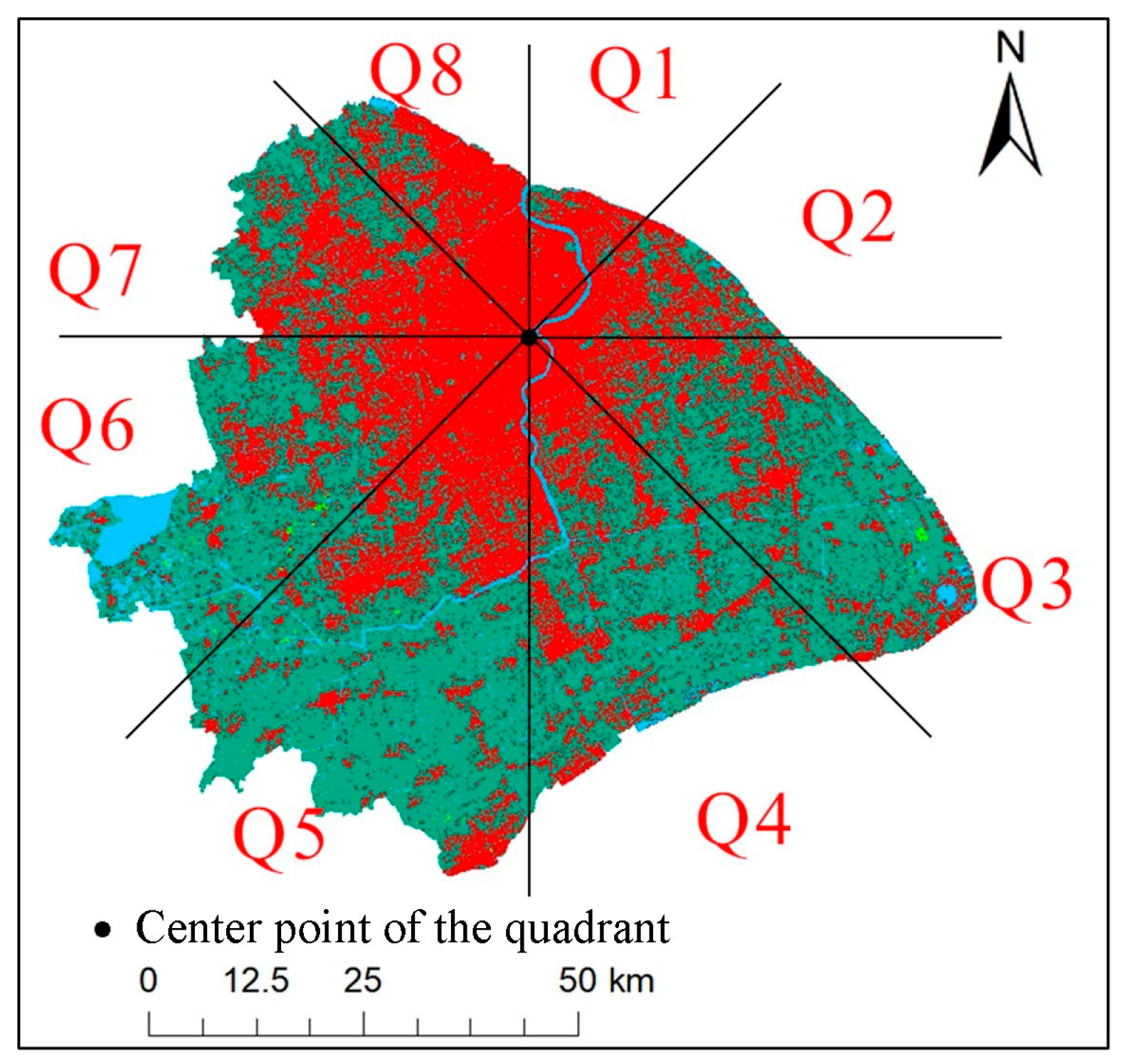
2.6. Quantification of the Changes in Urban Form
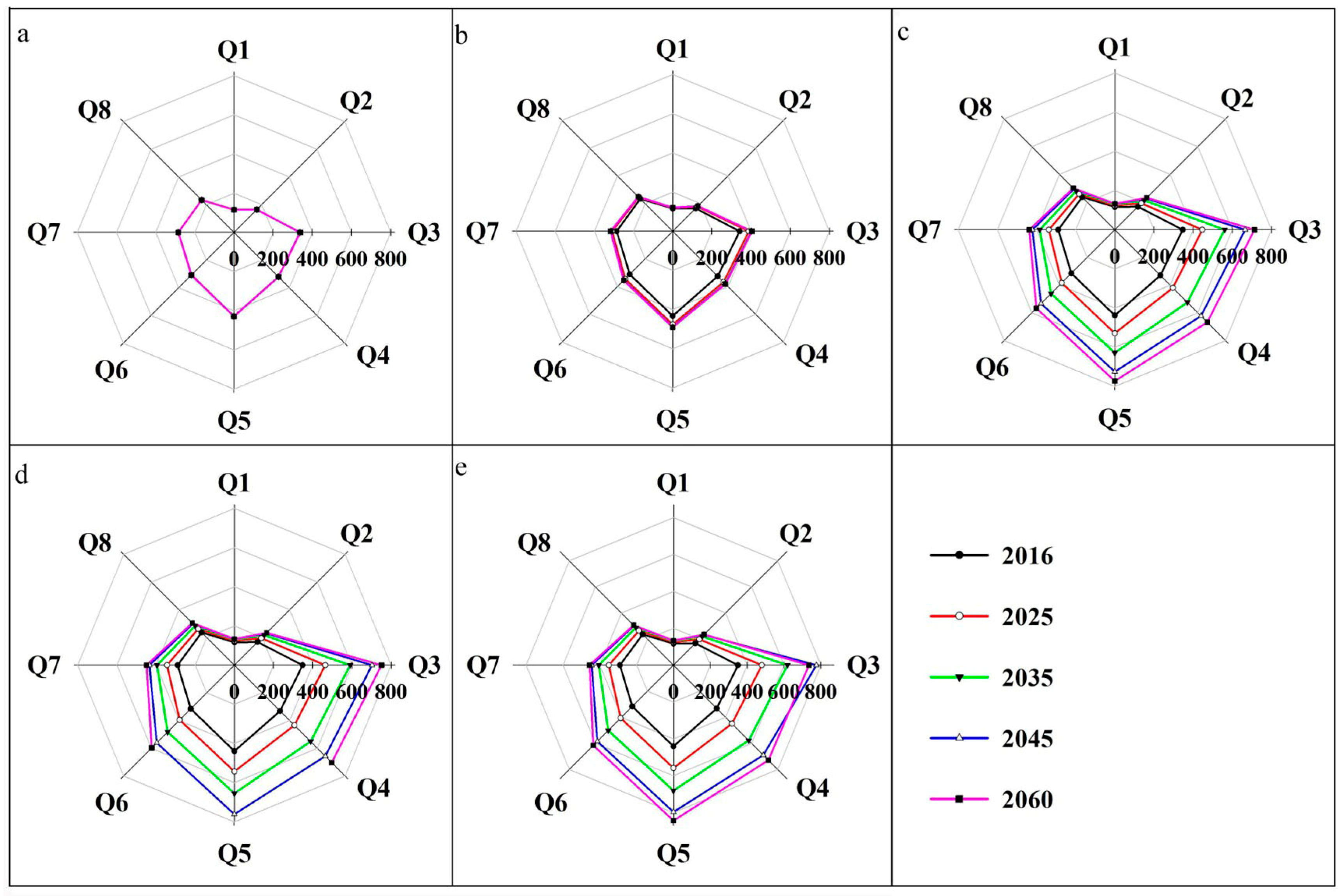
3. Results
3.1. Spatiotemporal Dynamics of the Projected Urban Land
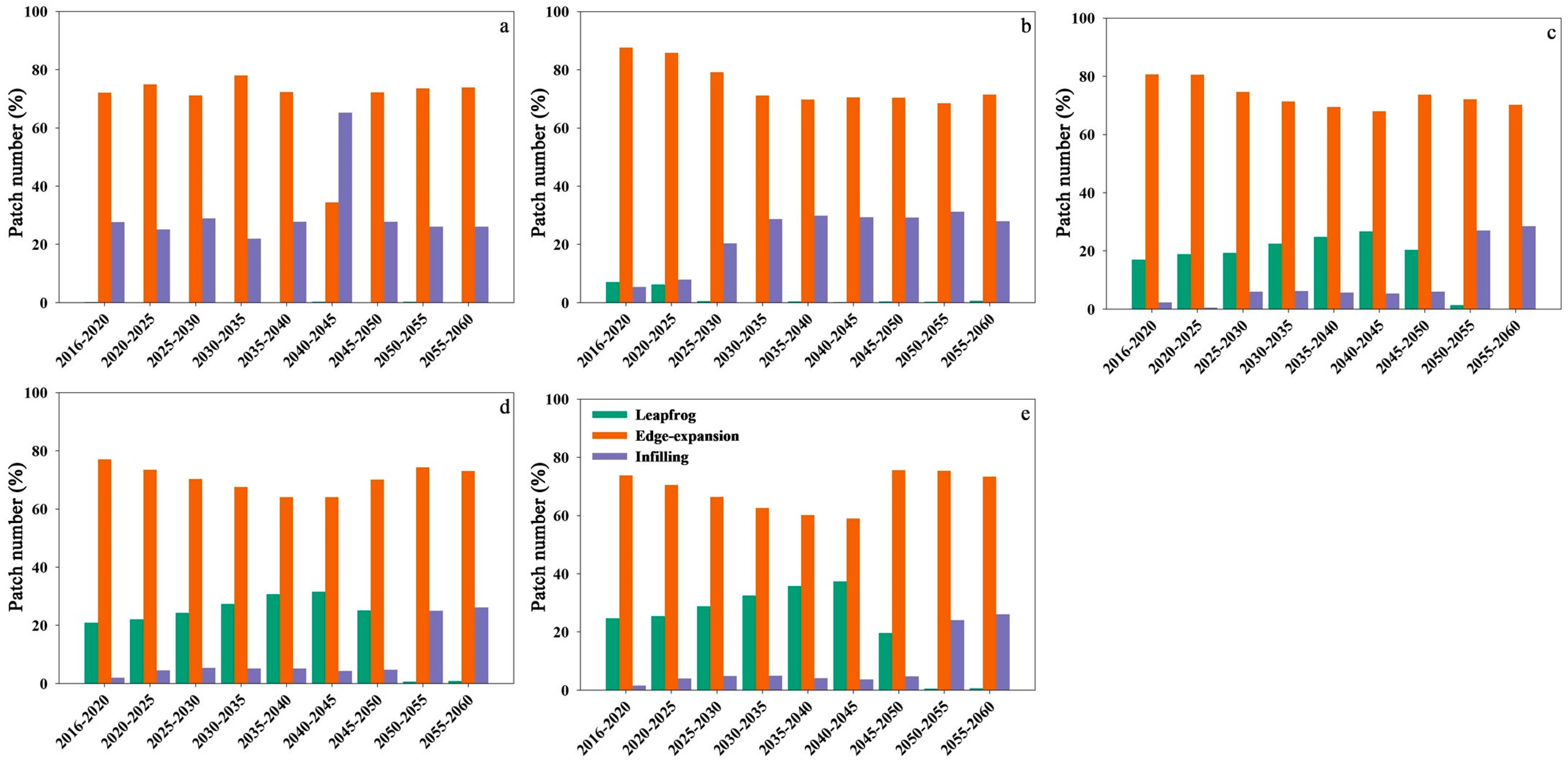
3.2. Spatiotemporal Patterns of Projected Urban Growth
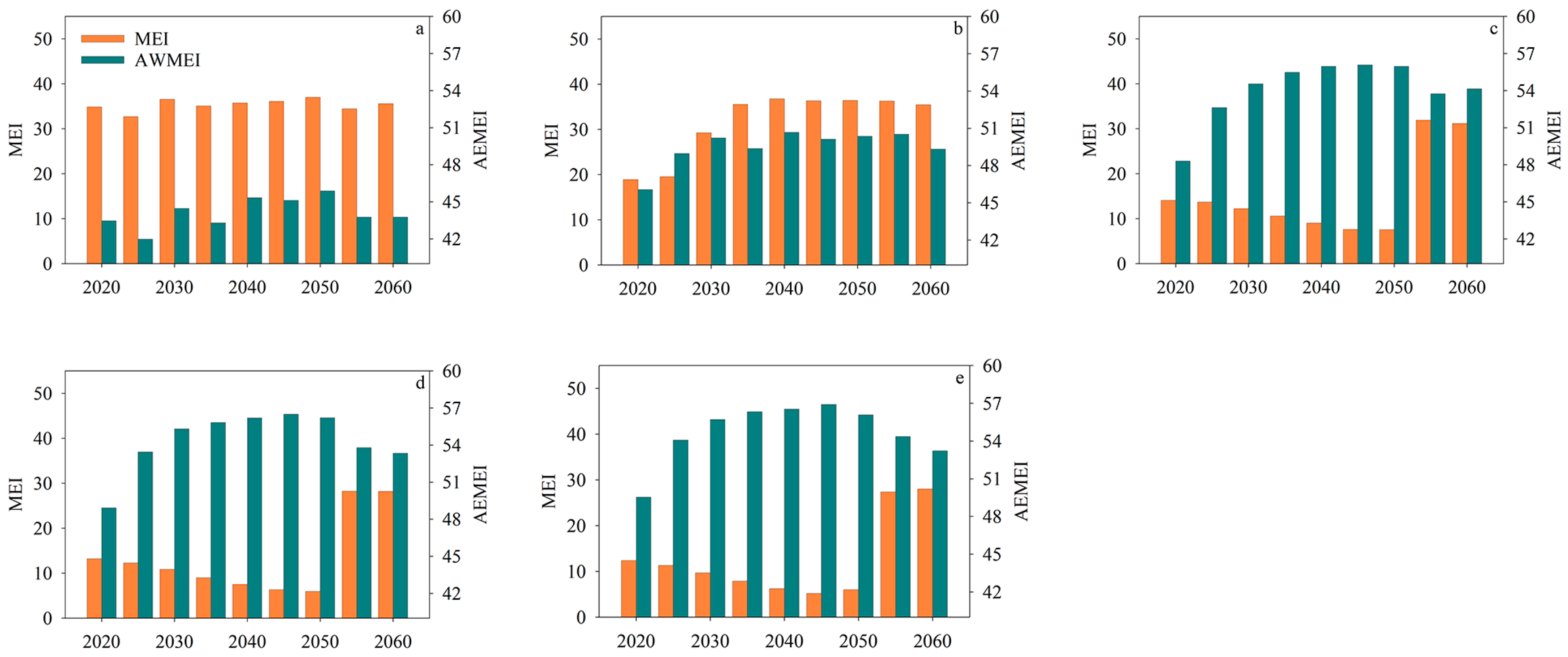
3.3. Characteristics of Urban Form Changes
4. Discussion
4.1. The Patterns of Urban Land Growth
4.2. Characteristics of the Spatiotemporal Changes in Urban Growth
4.3. The Evolution of the Urban Form
4.4. Limitations and Implications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- United Nations (UN). World Urbanization Prospects 2018; United Nations (UN): New York, NY, USA, 2019. [Google Scholar]
- Wentz, E.A.; York, A.M.; Alberti, M.; Conrow, L.; Fischer, H.; Inostroza, L.; Jantz, C.; Pickett, S.T.A.; Seto, K.C.; Taubenböck, H. Six fundamental aspects for conceptualizing multidimensional urban form: A spatial mapping perspective. Landsc. Urban Plan. 2018, 179, 55–62. [Google Scholar] [CrossRef]
- Cai, Z.; Demuzere, M.; Tang, Y.; Wan, Y. The characteristic and transformation of 3D urban morphology in three Chinese mega-cities. Cities 2022, 131, 103988. [Google Scholar] [CrossRef]
- Krueger, E.H.; Constantino, S.M.; Centeno, M.A.; Elmqvist, T.; Weber, E.U.; Levin, S.A. Governing sustainable transformations of urban social-ecological-technological systems. npj Urban Sustain. 2022, 2, 10. [Google Scholar] [CrossRef]
- He, X.; Zhou, Y. Urban spatial growth and driving mechanisms under different urban morphologies: An empirical analysis of 287 Chinese cities. Landsc. Urban Plan. 2024, 248, 105096. [Google Scholar] [CrossRef]
- Wu, C.; Li, C.; Ouyang, L.; Xiao, H.; Wu, J.; Zhuang, M.; Bi, X.; Li, J.; Wang, C.; Song, C.; et al. Spatiotemporal evolution of urbanization and its implications to urban planning of the megacity, Shanghai, China. Landsc. Ecol. 2023, 38, 1105–1124. [Google Scholar] [CrossRef]
- Liu, Y.; He, Q.; Tan, R.; Liu, Y.; Yin, C. Modeling different urban growth patterns based on the evolution of urban form: A case study from Huangpi, Central China. Appl. Geogr. 2016, 66, 109–118. [Google Scholar] [CrossRef]
- Wang, Q.; Guan, Q.; Lin, J.; Luo, H.; Tan, Z.; Ma, Y. Simulating land use/land cover change in an arid region with the coupling models. Ecol. Indic. 2021, 122, 107231. [Google Scholar] [CrossRef]
- Shafizadeh-Moghadam, H.; Asghari, A.; Tayyebi, A.; Taleai, M. Coupling machine learning, tree-based and statistical models with cellular automata to simulate urban growth. Comput. Environ. Urban Syst. 2017, 64, 297–308. [Google Scholar] [CrossRef]
- Yeh, A.G.O.; Li, X.; Xia, C. Cellular Automata Modeling for Urban and Regional Planning. In Urban Informatics; Shi, W., Goodchild, M.F., Batty, M., Kwan, M.-P., Zhang, A., Eds.; Springer: Singapore, 2021; pp. 865–883. [Google Scholar]
- Clarke, K.C.; Hoppen, S.; Gaydos, L. A self-modifying cellular automaton model of historical urbanization in the San Francisco Bay area. Environ. Plan. B Plan. Des. 1997, 24, 247–261. [Google Scholar] [CrossRef]
- Zhou, Y.; Varquez, A.C.G.; Kanda, M. High-resolution global urban growth projection based on multiple applications of the SLEUTH urban growth model. Sci. Data 2019, 6, 34. [Google Scholar] [CrossRef]
- Liu, D.; Clarke, K.C.; Chen, N. Integrating spatial nonstationarity into SLEUTH for urban growth modeling: A case study in the Wuhan metropolitan area. Comput. Environ. Urban Syst. 2020, 84, 101545. [Google Scholar] [CrossRef]
- Dietzel, C.; Clarke, K. The effect of disaggregating land use categories in cellular automata during model calibration and forecasting. Comput. Environ. Urban Syst. 2006, 30, 78–101. [Google Scholar] [CrossRef]
- Varquez, A.C.G.; Dong, S.; Hanaoka, S.; Kanda, M. Evaluating future railway-induced urban growth of twelve cities using multiple SLEUTH models with open-source geospatial inputs. Sustain. Cities Soc. 2023, 91, 104442. [Google Scholar] [CrossRef]
- Cui, L.; Shi, J. Urbanization and its environmental effects in Shanghai, China. Urban Clim. 2012, 2, 1–15. [Google Scholar] [CrossRef]
- Zheng, K.; Xu, X.; Zhang, X.; Liu, L. Spatial-temporal characteristics and future prediction of urban expansion in Shanghai. J. Geo-Inf. Sci. 2012, 14, 490–496. [Google Scholar] [CrossRef]
- Chandan, M.C.; Nimish, G.; Bharath, H.A. Analysing spatial patterns and trend of future urban expansion using SLEUTH. Spat. Inf. Res. 2020, 28, 11–23. [Google Scholar] [CrossRef]
- Liang, Y.; Liu, L. Spatiotemporal Dynamics of Rapid Urban Growth on the Loess Plateau from 1995 to 2050. J. Resour. Ecol. 2023, 14, 567–580. [Google Scholar] [CrossRef]
- Gao, L.; Tao, F.; Liu, R.; Wang, Z.; Leng, H.; Zhou, T. Multi-scenario simulation and ecological risk analysis of land use based on the PLUS model: A case study of Nanjing. Sustain. Cities Soc. 2022, 85, 104055. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J.; Xiong, N.; Sun, L.; Xu, J. Impacts of Land Use Changes on Net Primary Productivity in Urban Agglomerations under Multi-Scenarios Simulation. Remote Sens. 2022, 14, 1755. [Google Scholar] [CrossRef]
- Akyol Alay, M.; Tunçay, H.E.; Clarke, K.C. SLEUTH modeling informed by landscape ecology principles: Case study using scenario-based planning in Sariyer, Istanbul, Turkey. J. Urban Plan. Dev. 2021, 147, 05021043. [Google Scholar] [CrossRef]
- Li, F.; Wang, L.; Chen, Z.; Clarke, K.C.; Li, M.; Jiang, P. Extending the SLEUTH model to integrate habitat quality into urban growth simulation. J. Environ. Manag. 2018, 217, 486–498. [Google Scholar] [CrossRef] [PubMed]
- Choudhury, U.; Kanga, S.; Singh, S.K.; Kumar, A.; Meraj, G.; Kumar, P.; Singh, S. Projecting Urban Expansion by Analyzing Growth Patterns and Sustainable Planning Strategies—A Case Study of Kamrup Metropolitan, Assam, North-East India. Earth 2024, 5, 169–194. [Google Scholar] [CrossRef]
- Rao, Y.; Dai, J.; Dai, D.; He, Q.; Wang, H. Effect of Compactness of Urban Growth on Regional Landscape Ecological Security. Land 2021, 10, 848. [Google Scholar] [CrossRef]
- He, Q.; He, W.; Song, Y.; Wu, J.; Yin, C.; Mou, Y. The impact of urban growth patterns on urban vitality in newly built-up areas based on an association rules analysis using geographical ‘big data’. Land Use Policy 2018, 78, 726–738. [Google Scholar] [CrossRef]
- Li, C.; Li, J.; Wu, J. Quantifying the speed, growth modes, and landscape pattern changes of urbanization: A hierarchical patch dynamics approach. Landsc. Ecol. 2013, 28, 1875–1888. [Google Scholar] [CrossRef]
- Liu, X.; Li, X.; Chen, Y.; Tan, Z.; Li, S.; Ai, B. A new landscape index for quantifying urban expansion using multi-temporal remotely sensed data. Landsc. Ecol. 2010, 25, 671–682. [Google Scholar] [CrossRef]
- Wu, J.; Wu, C.; Zhang, Q.; Zhuang, M.; Xiao, H.; Wu, H.; Ouyang, L.; Liu, Y.; Meng, C.; Song, C.; et al. Spatiotemporal Evolution of Urban Agglomeration and Its Impact on Landscape Patterns in the Pearl River Delta, China. Remote Sens. 2023, 15, 2520. [Google Scholar] [CrossRef]
- He, Q.; Song, Y.; Liu, Y.; Yin, C. Diffusion or coalescence? Urban growth pattern and change in 363 Chinese cities from 1995 to 2015. Sustain. Cities Soc. 2017, 35, 729–739. [Google Scholar] [CrossRef]
- Chakraborty, S.; Maity, I.; Dadashpoor, H.; Novotnẏ, J.; Banerji, S. Building in or out? Examining urban expansion patterns and land use efficiency across the global sample of 466 cities with million+ inhabitants. Habitat Int. 2022, 120, 102503. [Google Scholar] [CrossRef]
- Rybski, D.; Li, Y.; Born, S.; Kropp, J.P. Modeling urban morphology by unifying diffusion-limited aggregation and stochastic gravitation. Findings 2021. [Google Scholar] [CrossRef]
- Jatayu, A.; Saizen, I.; Rustiadi, E.; Pribadi, D.O.; Juanda, B. Urban Form Dynamics and Modelling towards Sustainable Hinterland Development in North Cianjur, Jakarta–Bandung Mega-Urban Region. Sustainability 2022, 14, 907. [Google Scholar] [CrossRef]
- Haselsteiner, E.; Smetschka, B.; Remesch, A.; Gaube, V. Time-Use Patterns and Sustainable Urban Form: A Case Study to Explore Potential Links. Sustainability 2015, 7, 8022–8050. [Google Scholar] [CrossRef]
- Peng, W.; Wang, G.; Zhou, J.; Zhao, J.; Yang, C. Studies on the temporal and spatial variations of urban expansion in Chengdu, western China, from 1978 to 2010. Sustain. Cities Soc. 2015, 17, 141–150. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y.; Li, Y.; Du, G. Quantifying spatio-temporal patterns of urban expansion in Beijing during 1985–2013 with rural-urban development transformation. Land Use Policy 2018, 74, 220–230. [Google Scholar] [CrossRef]
- Miles, L.S.; Carlen, E.J.; Winchell, K.M.; Johnson, M.T.J. Urban evolution comes into its own: Emerging themes and future directions of a burgeoning field. Evol. Appl. 2021, 14, 3–11. [Google Scholar] [CrossRef]
- Monteiro, J.; Sousa, N.; Coutinho-Rodrigues, J.; Natividade-Jesus, E. Challenges Ahead for Sustainable Cities: An Urban Form and Transport System Review. Energies 2024, 17, 409. [Google Scholar] [CrossRef]
- Woldesemayat, E.M.; Genovese, P.V. Monitoring Urban Expansion and Urban Green Spaces Change in Addis Ababa: Directional and Zonal Analysis Integrated with Landscape Expansion Index. Forests 2021, 12, 389. [Google Scholar] [CrossRef]
- Wang, S.; Luo, X. The evolution of government behaviors and urban expansion in Shanghai. Land Use Policy 2022, 114, 105973. [Google Scholar] [CrossRef]
- Gao, C.; Feng, Y.; Wang, R.; Lei, Z.; Chen, S.; Tang, X.; Xi, M. 50-Year Urban Expansion Patterns in Shanghai: Analysis Using Impervious Surface Data and Simulation Models. Land 2023, 12, 2065. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Song, Y.; Wang, H. GIS-based analysis of spatial characteristics of watercourse and its water pollution in Shanghai City. China Environ. Sci. 2004, 24, 632–635, (In Chinese with English abstract). [Google Scholar]
- Li, J.; Li, C.; Zhu, F.; Song, C.; Wu, J. Spatiotemporal pattern of urbanization in Shanghai, China between 1989 and 2005. Landsc. Ecol. 2013, 28, 1545–1565. [Google Scholar] [CrossRef]
- SMBS (Shanghai Municipal Bureau of Statistics). Shanghai Statistical Yearbook 2023; SMBS: Shanghai, China, 2023.
- SMBS (Shanghai Municipal Bureau of Statistics). Shanghai Statistical Yearbook 2022; SMBS: Shanghai, China, 2022.
- Silva, E.A.; Clarke, K.C. Calibration of the SLEUTH urban growth model for Lisbon and Porto, Portugal. Comput. Environ. Urban Syst. 2002, 26, 525–552. [Google Scholar] [CrossRef]
- Yang, J.; Huang, X. The 30 m annual land cover dataset and its dynamics in China from 1990 to 2019. Earth Syst. Sci. Data 2021, 13, 3907–3925. [Google Scholar] [CrossRef]
- Li, J.; Song, C.; Cao, L.; Zhu, F.; Meng, X.; Wu, J. Impacts of landscape structure on surface urban heat islands: A case study of Shanghai, China. Remote Sens. Environ. 2011, 115, 3249–3263. [Google Scholar] [CrossRef]
- Xiang, W.; Clarke, K.C. The use of scenarios in land-use planning. Environ. Plan. B Plan. Des. 2003, 30, 885–909. [Google Scholar] [CrossRef]
- Jantz, C.A.; Goetz, S.J.; Shelley, M.K. Using the SLEUTH urban growth model to simulate the impacts of future policy scenarios on urban land use in the Baltimore-Washington metropolitan area. Environ. Plan. B Plan. Des. 2004, 31, 251–271. [Google Scholar] [CrossRef]
- SMPG (Shanghai Municipal People’s Government). Shanghai Urban Master Plan (2017–2035); SMPG: Shanghai, China, 2018.
- Pontius, R.G.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Xu, X.; Min, X. Quantifying spatiotemporal patterns of urban expansion in China using remote sensing data. Cities 2013, 35, 104–113. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Z.; Li, P.; Zhang, Y.; Liu, H.; Pan, J. Impacts and Projections of Land Use and Demographic Changes on Ecosystem Services: A Case Study in the Guanzhong Region, China. Sustainability 2022, 14, 3003. [Google Scholar] [CrossRef]
- Kii, M. Projecting future populations of urban agglomerations around the world and through the 21st century. npj Urban Sustain. 2021, 1, 10. [Google Scholar] [CrossRef]
- Li, X.; Gong, P. Urban growth models: Progress and perspective. Sci. Bull. 2016, 61, 1637–1650. [Google Scholar] [CrossRef]
- Xi, F.; Hu, Y.; He, H.; Shi, T.; Bu, R.; Wu, X.; Zhu, J. Urban planning based on SLEUTH model in Shenyang-Fushun metropolitan area. J. Univ. Chin. Acad. Sci. 2009, 26, 765–773. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X. Applying SLEUTH for simulating urban expansion of Hangzhou. In Proceedings of the Second International Conference on Earth Observation for Global Changes, Chengdu, China, 25–29 May 2009; pp. 42–49. [Google Scholar]
- Liu, X.; Sun, R.; Yang, Q.; Su, G.; Qi, W. Simulating urban expansion using an improved SLEUTH model. J. Appl. Remote Sens. 2012, 6, 061709. [Google Scholar] [CrossRef]
- Hua, L.; Tang, L.; Cui, S.; Yin, K. Simulating urban growth using the SLEUTH model in a coastal peri-urban district in China. Sustainability 2014, 6, 3899–3914. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, D.; Zhou, Y.; Zhang, X.; Shi, R.; Chen, M. Simulation of land use/cover change in Shanghai based on SLEUTH model. In Proceedings of the Remote Sensing and Modeling of Ecosystems for Sustainability XV, San Diego, CA, USA, 22 August 2018; pp. 208–216. [Google Scholar]
- Zhang, Q.; Ban, Y.; Liu, J.; Hu, Y. Simulation and analysis of urban growth scenarios for the Greater Shanghai Area, China. Comput. Environ. Urban Syst. 2011, 35, 126–139. [Google Scholar] [CrossRef]
- Zhou, L.; Dang, X.; Sun, Q.; Wang, S. Multi-scenario simulation of urban land change in Shanghai by random forest and CA-Markov model. Sustain. Cities Soc. 2020, 55, 102045. [Google Scholar] [CrossRef]
- Yue, W.; Fan, P.; Wei, Y.D.; Qi, J. Economic development, urban expansion, and sustainable development in Shanghai. Stoch. Environ. Res. Risk Assess. 2014, 28, 783–799. [Google Scholar] [CrossRef]
- Yin, J.; Yin, Z.; Zhong, H.; Xu, S.; Hu, X.; Wang, J.; Wu, J. Monitoring urban expansion and land use/land cover changes of Shanghai metropolitan area during the transitional economy (1979–2009) in China. Environ. Monit. Assess. 2011, 177, 609–621. [Google Scholar] [CrossRef]
- Hu, Y.n.; Connor, D.S.; Stuhlmacher, M.; Peng, J.; Turner Ii, B.L. More urbanization, more polarization: Evidence from two decades of urban expansion in China. npj Urban Sustain. 2024, 4, 33. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, R. Remote sensing monitoring and driving force analysis of urban expansion in Guangzhou City, China. Habitat Int. 2010, 34, 228–235. [Google Scholar] [CrossRef]
- Fei, W.; Zhao, S. Urban land expansion in China’s six megacities from 1978 to 2015. Sci. Total Environ. 2019, 664, 60–71. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Ling, Y.; Zhu, A.X.; Zeng, H.; Song, J.; Zhu, Y.; Qian, L. Incorporation of spatial anisotropy in urban expansion modelling with cellular automata. Int. J. Geogr. Inf. Sci. 2022, 36, 86–113. [Google Scholar] [CrossRef]
- Schneider, A.; Woodcock, C.E. Compact, dispersed, fragmented, extensive? A comparison of urban growth in twenty-five global cities using remotely sensed data, pattern metrics and census information. Urban Stud. 2008, 45, 659–692. [Google Scholar] [CrossRef]
- Deng, H.; Zhang, K.; Wang, F.; Dang, A. Compact or disperse? Evolution patterns and coupling of urban land expansion and population distribution evolution of major cities in China, 1998–2018. Habitat Int. 2021, 108, 102324. [Google Scholar] [CrossRef]
- Lin, B.; Meyers, J.; Barnett, G. Understanding the potential loss and inequities of green space distribution with urban densification. Urban For. Urban Green. 2015, 14, 952–958. [Google Scholar] [CrossRef]


| Scenarios | Green Land (%) | Water Body (%) | Farmland (%) |
|---|---|---|---|
| A | 100 | 100 | 86 |
| B | 100 | 100 | 51 |
| C | 100 | 100 | 17 |
| D | 63 | 100 | 10 |
| E | 27 | 100 | 4 |
| Finalized Parameters | END |
|---|---|
| DIFFUSION | 4 |
| BREED | 1 |
| SPREAD | 39 |
| SLOPE | 56 |
| ROAD | 24 |
| Year | Scenarios | Allocation Disagreement (%) | Quantity Disagreement (%) | Standard Kappa Coefficient |
|---|---|---|---|---|
| 2016 | A | 8 | 4 | 0.98 |
| B | 8 | 3 | 0.98 | |
| C | 9 | 4 | 0.98 | |
| D | 9 | 5 | 0.95 | |
| E | 8 | 4 | 0.94 | |
| 2017 | A | 11 | 5 | 0.94 |
| B | 12 | 5 | 0.96 | |
| C | 12 | 6 | 0.97 | |
| D | 12 | 7 | 0.94 | |
| E | 13 | 8 | 0.93 | |
| 2018 | A | 10 | 4 | 0.92 |
| B | 11 | 2 | 0.94 | |
| C | 13 | 3 | 0.92 | |
| D | 12 | 9 | 0.92 | |
| E | 13 | 10 | 0.90 | |
| 2019 | A | 11 | 5 | 0.91 |
| B | 10 | 5 | 0.92 | |
| C | 12 | 7 | 0.88 | |
| D | 16 | 6 | 0.88 | |
| E | 15 | 5 | 0.87 | |
| 2020 | A | 15 | 7 | 0.89 |
| B | 15 | 2 | 0.91 | |
| C | 19 | 8 | 0.86 | |
| D | 18 | 9 | 0.86 | |
| E | 20 | 11 | 0.83 |
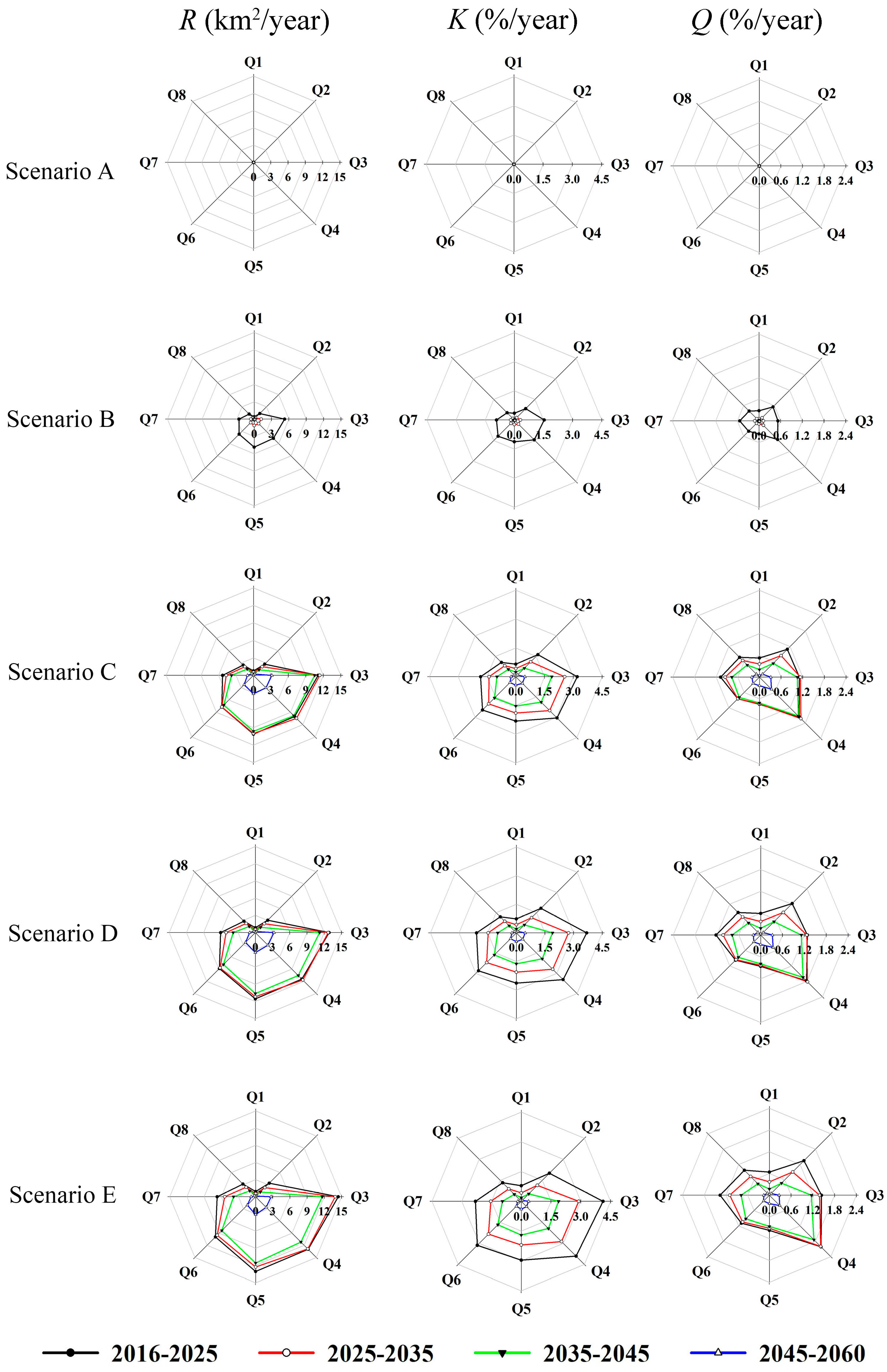
| Indicators | Year | Scenario A | Scenario B | Scenario C | Scenario D | Scenario E |
|---|---|---|---|---|---|---|
| Urban land expansion (R) (km2/year) | 2016–2025 | 0.11 | 14.02 | 49.65 | 55.91 | 61.71 |
| 2025–2035 | 0.10 | 0.67 | 31.99 | 33.77 | 33.35 | |
| 2035–2045 | 0.10 | 0.67 | 0.79 | 0.82 | 0.85 | |
| 2045–2060 | 0.10 | 0.67 | 0.78 | 0.81 | 0.83 | |
| Urban land growth rate (K) (%/year) | 2016–2025 | 0.01 | 0.63 | 2.22 | 2.49 | 2.74 |
| 2025–2035 | 0 | 0.03 | 1.01 | 1.02 | 0.97 | |
| 2035–2045 | 0 | 0.03 | 0.02 | 0.02 | 0.02 | |
| 2045–2060 | 0 | 0.03 | 0.02 | 0.02 | 0.02 | |
| Urban land growth intensity (Q) (%/year) | 2016–2025 | 0.02 | 3.05 | 10.81 | 12.17 | 13.43 |
| 2025–2035 | 0.02 | 0.15 | 6.96 | 7.35 | 7.26 | |
| 2035–2045 | 0.02 | 0.15 | 0.17 | 0.18 | 0.18 | |
| 2045–2060 | 0.02 | 0.15 | 0.17 | 0.18 | 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Wu, C.; Wu, J.; Zhang, Y.; Bi, X.; Wang, M.; Yan, E.; Song, C.; Li, J. Projected Spatiotemporal Evolution of Urban Form Using the SLEUTH Model with Urban Master Plan Scenarios. Remote Sens. 2025, 17, 270. https://doi.org/10.3390/rs17020270
Liu Y, Wu C, Wu J, Zhang Y, Bi X, Wang M, Yan E, Song C, Li J. Projected Spatiotemporal Evolution of Urban Form Using the SLEUTH Model with Urban Master Plan Scenarios. Remote Sensing. 2025; 17(2):270. https://doi.org/10.3390/rs17020270
Chicago/Turabian StyleLiu, Yuhan, Caiyan Wu, Jiong Wu, Yangcen Zhang, Xing Bi, Meng Wang, Enrong Yan, Conghe Song, and Junxiang Li. 2025. "Projected Spatiotemporal Evolution of Urban Form Using the SLEUTH Model with Urban Master Plan Scenarios" Remote Sensing 17, no. 2: 270. https://doi.org/10.3390/rs17020270
APA StyleLiu, Y., Wu, C., Wu, J., Zhang, Y., Bi, X., Wang, M., Yan, E., Song, C., & Li, J. (2025). Projected Spatiotemporal Evolution of Urban Form Using the SLEUTH Model with Urban Master Plan Scenarios. Remote Sensing, 17(2), 270. https://doi.org/10.3390/rs17020270








