Comparison of Single and Ensemble Regression Model Workflows for Estimating Basal Area by Tree Size Class in Pine Forests of Southeastern U.S
Abstract
1. Introduction
2. Materials and Methods
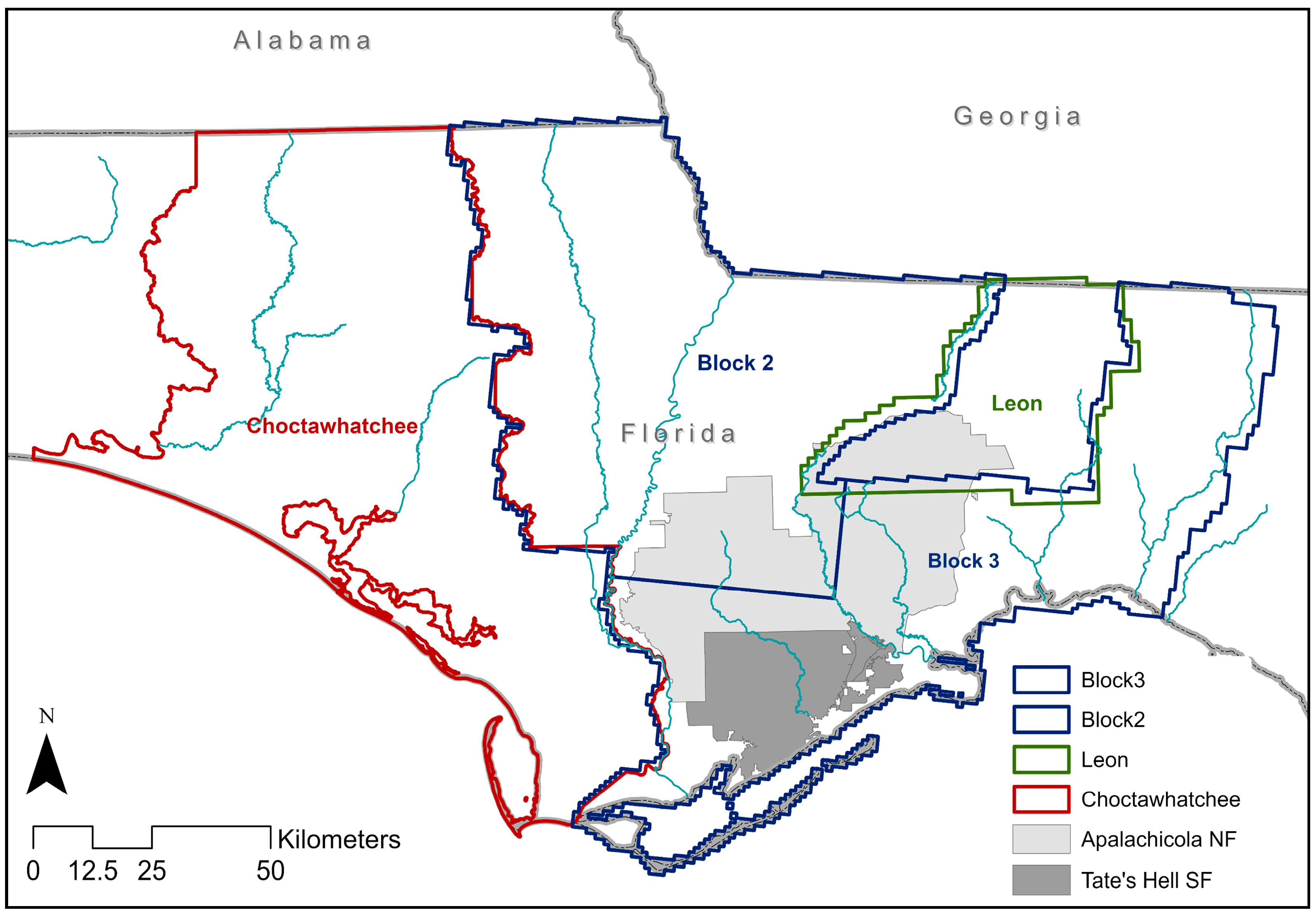
2.1. Study Area
2.2. LiDAR Datasets
LiDAR Processing
2.3. Forest Plots
Processing Forest Plot Data
2.4. Basal Area Modeling by Tree Size
2.4.1. Single Model Selection
2.4.2. Ensemble Linear Model
2.4.3. Ensemble Generalized Additive Model
2.5. Raster Outputs
3. Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| library(rgdal) library(raster) library(rgeos) library(gstat) library(mgcv) library(sf) #Function to create the ensemble linear model createEnsembleLm <- function(frm, df, nmdl = 50, ptrain = 0.75, kfact = 20) { if(!is.data.frame(df)) { stop(“Input ‘df’ is not a data frame.”) } pb <- txtProgressBar(min = 0, max = nmdl, style = 3) mdlV = list(length = nmdl) rmseV = vector(mode = “double”, length = nmdl) rmseT = vector(mode = “double”, length = nmdl) n = round(ptrain * nrow(df)) mdlCnt = 0 while (mdlCnt < nmdl) { sIndex = sample(nrow(df), n) tdf = df[sIndex,] vdf = df[-sIndex,] try({ mdl = lm(frm, data = tdf) pvlV = predict(mdl, newdata = vdf) ovlV = getResponseValueslm(vdf, mdl) t_rmseV = sqrt(mean((pvlV - ovlV)^2)) pvlT = predict(mdl, newdata = tdf) ovlT = getResponseValueslm(tdf, mdl) t_rmseT = sqrt(mean((pvlT - ovlT)^2)) if (t_rmseV <= (t_rmseT * kfact)) { mdlCnt = mdlCnt + 1 setTxtProgressBar(pb,mdlCnt) mdlV[[mdlCnt]] = mdl rmseV[mdlCnt] = t_rmseV rmseT[mdlCnt] = t_rmseT } }, silent = TRUE) if(inherits(mdl, “try-error”)) { stop(“An error occurred while fitting a model in iteration”, mdlCnt) } } return(list(mdlV, rmseV, rmseT)) } # Gets the response values from a linear model given a dataframe # df = dataframe # md = linear model getResponseValueslm <- function(df, md) { return(df[[1]]) } # added to change formula to lm syntax getFormulalm <- function(rVar, pVars, numlp) { if (numlp == 1) { fm <- as.formula(paste(rVar, “ ~ ”, paste(pVars, collapse = “ + ”))) } else { fml <- vector(mode = “list”, length = numlp) for (f in 1:numlp) { fml[[f]] <- as.formula(paste(rVar, “ ~ “, paste(pVars, collapse = “ + “))) } fm <- fml } return(fm) } ## function used to apply the ensemble LM to a raster given a set of input rasters predictEnsembleLm <- function(bLmMdl, df) { m = NULL s = NULL mdls = length(bLmMdl) n = nrow(df) sV = vector(mode = “double”, length = n) s2V = vector(mode = “double”, length = n) for (i in seq(mdls)) { mdl = bLmMdl[[i]] p = predict(mdl, df, type = “response”) sV = sV + p s2V = s2V + p ^ 2 } m = sV/mdls s = sqrt((s2V - ((sV ^ 2)/mdls))/(mdls - 1)) return(cbind(m, s)) } # Set the dataframe dft = Plots_RDCC ## Change the next two lines for different DBH classes, this example is for our model ## of pine_GT_35.56 predVar1 = c(“Pred_Band7”,“Pred_Band17”, “Pred_Band26”,“Pred_Band33”, Pred_Band45”,“Leon_y_n”) #Input the response variable from your dataframe into the quotations frmlm = getFormulalm(“Pine_BAA_DBH_GT_35.56”,predVar1,1) #Create the ensemble LM model and save the model as the elm variable elmOut = createEnsembleLm(frmlm,dft,nmdl = 50,ptrain = 0.75,kfact = 30) elm = elmOut[[1]] #Change the raster brick of predictor variables for each block pred_ras <- brick(“~/Pred_Vars_for_r/Chocta_Pine_DBH_GT_14_preds.tif”) names(pred_ras) = c(“Pred_Band7”,“Pred_Band17”, “Pred_Band26”,”Pred_Band33”, “Pred_Band45”,“Leon_y_n”) # Run the ELM prediction function in parallel # If you are unsure how many cores your computer has run # this function: detectCores() beginCluster(8) system.time({ baaRs = clusterR(pred_ras, predict, args = list(model = elm, fun = predictEnsembleLm, index = 1:2), verbose = TRUE, datatype = “FLT4S”, NAFlag = -9999, progress = ‘text’) }) endCluster() #Save the output rasters #Change the raster output name for each block # baaRs[[1]] is the mean ensemble value raster # baaRs[[2]] is the standard error ensemble value raster writeRaster(baaRs[[1]],filename = “~/EGAM_Outputs/Leon_Pine_BAA_GT_35.56_Mean_lm”,format = “GTiff”) writeRaster(baaRs[[2]], filename = “~/EGAM_Outputs/Leon_Pine_BAA_GT_35.56 _SEE_lm”,format = “GTiff”) |
References
- Coomes, D.A.; Allen, R.B. Effects of size, competition and altitude on tree growth. J. Ecol. 2007, 95, 1084–1097. [Google Scholar] [CrossRef]
- Konôpka, B.; Pajtík, J.; Moravčík, M.; Lukac, M. Biomass partitioning and growth efficiency in four naturally regenerated forest tree species. Basic Appl. Ecol. 2010, 11, 234–243. [Google Scholar] [CrossRef]
- Duchateau, E.; Schneider, R.; Tremblay, S.; Dupont-Leduc, L. Density and diameter distributions of saplings in naturally regenerated and planted coniferous stands in Québec after various approaches of commercial thinning. Ann. For. Sci. 2020, 77, 38. [Google Scholar] [CrossRef]
- Leclère, L.; Lejeune, P.; Bolyn, C.; Latte, N. Estimating Species-Specific Stem Size Distributions of Uneven-Aged Mixed Deciduous Forests Using ALS Data and Neural Networks. Remote Sens. 2022, 14, 1362. [Google Scholar] [CrossRef]
- Nordman, C.; White, R.; Wilson, R.; Ware, C.; Rideout, C.; Pyne, M.; Hunter, C. Rapid Assessment Metrics to Enhance Wildlife Habitat and Biodiversity Within Southern Open Pine Ecosystems; U.S. Fish and Wildlife Service and NatureServe, for the Gulf Coastal Plains and Ozarks Landscape Conservation Cooperative: Tallahassee, FL, USA, 2016; Available online: https://www.natureserve.org/sites/default/files/openpinemetrics-finalreport_12may16.pdf (accessed on 4 November 2024).
- America’s Longleaf. 2014 Longleaf Pine Maintenance Condition Class Definitions. Available online: https://americaslongleaf.org/media/mjroaokz/final-lpc-maintenance-condition-class-metrics-oct-2014-high-res.pdf (accessed on 4 November 2024).
- Garabedian, J.E.; McGaughey, R.J.; Reutebuch, S.E.; Parresol, B.R.; Kilgo, J.C.; Moorman, C.E.; Peterson, M.N. Quantitative analysis of woodpecker habitat using high-resolution airborne LiDAR estimates of forest structure and composition. Remote Sens. Environ. 2014, 145, 68–80. [Google Scholar] [CrossRef]
- Gove, J.H.; Patil, G.P. Modeling the Basa Area-size Distribution of Forest Stands: A Compatible Approach. For. Sci. 1999, 44, 285–297. [Google Scholar]
- Spriggs, R.A.; Coomes, D.A.; Jones, T.A.; Caspersen, J.P.; Vanderwel, M.C. An Alternative Approach to Using LiDAR Remote Sensing Data to Predict Stem Diameter Distributions across a Temperate Forest Landscape. Remote Sens. 2017, 9, 944. [Google Scholar] [CrossRef]
- Coomes, D.A.; Dalponte, M.; Jucker, T.; Asner, G.P.; Banin, L.F.; Burslem, D.; Simon, L.L.; Nilus, R.; Phillips, O.L.; Phua, M.; et al. Area-based vs tree-centric approaches to mapping forest carbon in Southeast Asian forests from airborne laser scanning data. Remote Sens. Environ. 2017, 194, 77–88. [Google Scholar] [CrossRef]
- Fu, L.; Duan, G.; Ye, Q.; Meng, X.; Luo, P.; Sharma, R.P.; Sun, H.; Wand, G.; Liu, Q. Prediction of Individual Tree Diameter Using a Nonlinear Mixed-Effects Modeling Approach and Airborne LiDAR Data. Remote Sens. 2020, 12, 1066. [Google Scholar] [CrossRef]
- Maltamo, M.; Gobakken, T. Predicting Tree Diameter Distributions. In Forestry Applications of Airborne Laser Scanning: Concepts and Case Studies; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Springer Science+Business Media: Dordrecht, The Netherlands, 2014; pp. 177–193. [Google Scholar] [CrossRef]
- Persson, Å.; Holmgren, J.; Söderman, U. Detecting and measuring individual trees using an airborne laser scanner. Photogramm. Eng. Remote Sens. 2002, 68, 357–363. [Google Scholar]
- Vauhkonen, J.; Ene, L.; Gupta, S.; Heinzel, J.; Holmgren, J.; Pitkänen, J.; Solberg, S.; Wang, Y.; Weinacker, H.; Hauglin, K.M.; et al. Comparative testing of single-tree detection algorithms under different types of forest. For. Int. J. For. Res. 2012, 85, 27–40. [Google Scholar] [CrossRef]
- Gobakken, T.; Næsset, E. Estimation of Diameter and Basal Area Distributions in Coniferous Forest by Means of Airborne Laser Scanner Data. Scand. J. For. Res. 2004, 19, 529–542. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, T.; Skidmore, A.K.; Cao, F.; She, G. An improved areas-based approach for estimating plot-level tree DBH from airborne LiDAR data. For. Ecosyst. 2023, 10, 100089. [Google Scholar] [CrossRef]
- Breidenbach, J.; Gläser, C.; Schmidt, M. Estimation of diameter distributions by means of airborne laser scanner data. Can. J. For. Res. 2008, 38, 1611–1620. [Google Scholar] [CrossRef]
- Bollandsås, O.M.; Maltamo, M.; Gobakken, T.; Næsset, E. Comparing parametric and non-parametric modelling of diameter distributions on independent data using airborne laser scanning in a boreal conifer forest. Forestry 2013, 86, 493–501. [Google Scholar] [CrossRef]
- Mauro, F.; Frank, B.; Monleon, V.J.; Temesgen, H.; Ford, K.R. Prediction of diameter distributions and tree-lists in southwestern Oregon using LiDAR and stand-level auxiliary information. Can. J. For. Res. 2019, 49, 775–787. [Google Scholar] [CrossRef]
- Packalén, P.; Maltamo, M. Estimation of species-specific diameter distributions using airborne laser scanning and aerial photographs. Can. J. For. Res. 2008, 38, 1750–1760. [Google Scholar] [CrossRef]
- Maltamo, M.; Eerikäinen, K.; Pitkänen, J.; Hyyppä, J.; Vehmas, M. Estimation of timber volume and stem density based on scanning laser altimetry and expected tree size distribution functions. Remote Sens. Environ. 2004, 90, 319–330. [Google Scholar] [CrossRef]
- Trager, M.D.; Drake, J.B.; Jenkins, A.M.; Petrick, C.J. Mapping and Modeling Ecological Conditions of Longleaf Pine Habitats in the Apalachicola National Forest. For. Ecol. 2018, 116, 304–311. [Google Scholar] [CrossRef]
- Meijer, C.; Grootes, M.; Koma, Z.; Dzigan, Y.; Gonçalves, R.; Andela, B.; van den Oord, G.; Ranguelova, E.; Renaud, N.; Kissling, W. Laserchicken—A tool for distributed feature calculation from massive LiDAR point cloud datasets. SoftwareX 2020, 12, 100626. [Google Scholar] [CrossRef]
- St. Peter, J.; Drake, J.; Medley, P.; Ibeanusi, V. Forest Structural Estimates Derived Using a Practical, Open-Source Lidar-Processing Workflow. Remote Sens. 2021, 13, 4763. [Google Scholar] [CrossRef]
- Hogland, J.; Affleck, D.L.; Anderson, N.; Seielstad, C.; Dobrowski, S.; Graham, J.; Smith, R. Estimating Forest Characteristics for Longleaf Pine. Forests 2020, 11, 426. [Google Scholar] [CrossRef]
- Stein, B.A.; Kutner, L.S.; Adams, J.S. Precious Heritage: The Status of Biodiversity in the United States; Oxford University Press: New York, NY, USA, 2000. [Google Scholar]
- Noss, R.F. The longleaf pine landscape of the Southeast: Almost gone and almost forgotten. Endanger. Species Update 1988, 5, 1–8. [Google Scholar]
- Oswalt, C.; Cooper, J.; Brockway, D.; Brooks, H.; Walker, J.; Connor, K.; Oswalt, S.N.; Conner, R.C. History and Current Condition of Longleaf Pine in the Southern United States; U.S. Department of Agriculture Forest Service, Southern Research Station: Ashville, NC, USA, 2012. [Google Scholar]
- Cooperative Land Cover, Version 3.7. Published November 2023. Available online: https://myfwc.com/research/gis/wildlife/cooperative-land-cover/ (accessed on 18 December 2024).
- United States Geological Survey. 3D Elevation Program. USGS Core Science Systems. Available online: https://www.usgs.gov/core-science-systems/ngp/3dep/what-is-3dep?qt-science_support_page_related_con=0#qt-science_support_page_related_con (accessed on 2 August 2021).
- NOAA Fisheries. OCM Partners 2018 TLCGIS Lidar: Leon County, FL. Available online: https://www.fisheries.noaa.gov/inport/item/60045 (accessed on 25 June 2021).
- NOAA Fisheries. OCM Partners 2018 USGS Lidar: Florida Panhandle. Available online: https://www.fisheries.noaa.gov/inport/item/58298 (accessed on 25 June 2021).
- NOAA Fisheries. OCM Partners 2017 NWFWMD Lidar: Lower Choctawhatchee. Available online: https://www.fisheries.noaa.gov/inport/item/55725 (accessed on 25 June 2021).
- R Core Team. R. A Language and Environment for Statistical Computing. In R Foundation for Statistical Computing; R Core Team: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 25 October 2024).
- Roussel, J.; Auty, D.; Coops, N.; Tompalski, P.; Goodbody, T.; Meador, A.; Bourdon, J.; de Boissieu, F.; Achim, A. lidR: An R package for analysis of Airborne Laser Scanning (ALS) data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Roussel, J.; Auty, D. Airborne LiDAR Data Manipulation and Visualization for Forestry Applications. R Package Version 3.1.4. Available online: https://cran.r-project.org/package=lidR (accessed on 4 November 2024).
- Hogland, J.; Anderson, N.; Affleck, D.L.; St. Peter, J. Using Forest Inventory Data with Landsat 8 Imagery to Map Longleaf Pine Forest Characteristics in Georgia, USA. Remote Sens. 2019, 11, 1803. [Google Scholar] [CrossRef]
- Hogland, J. Rocky Mountain Research Station, RMRS Raster Utility. Available online: https://research.fs.usda.gov/rmrs/products/dataandtools/tools/rmrs-raster-utility (accessed on 4 November 2024).
- Hogland, J. Ensemble Generalized Additive Models (EGAM). Jupyter Notebook. Available online: https://colab.research.google.com/drive/1GnRagruTUCoPJQZSkZ2vMKS9aAKgnhEw?usp=sharing (accessed on 4 November 2024).
- Asner, G.; Mascaro, J. Mapping tropical forest carbon: Calibrating plot estimates to a simple LiDAR metric. Remote Sens. Environ. 2014, 140, 614–624. [Google Scholar] [CrossRef]
- Næsset, E. Effects of different flying altitudes on biophysical stand properties estimated from canopy height and density measured with small-footprint airborne scanning laser. Remote Sens. Environ. 2004, 91, 243–255. [Google Scholar] [CrossRef]
- LaRue, E.A.; Fahey, R.; Fuson, T.L.; Foster, J.R.; Matthes, J.H.; Krause, K.; Hardiman, B.S. Evaluating the sensitivity of forest structural diversity characterization to LiDAR point density. Ecosphere 2022, 13, e4209. [Google Scholar] [CrossRef]
| Predictor Band | Description |
|---|---|
| 1 | Mean of all relative heights |
| 2 | Std. dev of all relative heights |
| 3 | Relative height 95% |
| 4 | Relative height 90% |
| 5 | Relative height 75% |
| 6 | Relative height 50% |
| 7 | Relative height 25% |
| 8 | Relative height 10% |
| 9 | Relative height 5% |
| 10 | Relative density 0.6096 m to 3.048 m (shrubs) |
| 11 | Relative density 3.048 m to 6.096 m (low midstory) |
| 12 | Relative density 6.096 m to 14.935 m (high midstory) |
| 13 | Relative density all returns ≥ 0.6096 m |
| 14 | Relative density all returns ≥ 3.048 m |
| 15 | Relative density all returns ≥ 6.096 m |
| 16 | Relative density all returns ≥ 14.935 m |
| 17 | Canopy cover ≥ 0.6096 m (based only on first returns) |
| 18 | Canopy cover ≥ 3.048 m (based only on first returns) |
| 19 | Canopy cover ≥ 6.096 m (based only on first returns) |
| 20 | Canopy cover ≥ 14.935 m (based only on first returns) |
| 21 | Mean of all relative heights ≥ 0.6096 m |
| 22 | Mean of all relative heights ≥ 3.048 m |
| 23 | Mean of all relative heights ≥ 6.096 m |
| 24 | Mean of all relative heights ≥ 14.935 m |
| All Tree Species | r2 | RMSE | Pine Tree Species | r2 | RMSE |
|---|---|---|---|---|---|
| DBH < 25.4 Single Model | 0.657 | 6.52 | DBH < 25.4 Single Model | 0.657 | 5.25 |
| DBH < 25.4 ELM | 0.516 | 8.27 | DBH < 25.4 ELM | 0.667 | 5.12 |
| DBH < 25.4 EGAM | 0.675 | 6.51 | DBH < 25.4 EGAM | 0.731 | 4.61 |
| DBH 25.4–35.56 Single Model | 0.447 | 4.01 | DBH 25.4–35.56 Single Model | 0.445 | 3.29 |
| DBH 25.4–35.56 ELM | 0.456 | 3.93 | DBH 25.4–35.56 ELM | 0.459 | 3.20 |
| DBH 25.4–35.56 EGAM | 0.514 | 3.72 | DBH 25.4–35.56 EGAM | 0.511 | 3.04 |
| DBH > 35.56 Single Model | 0.709 | 4.37 | DBH > 35.56 Single Model | 0.593 | 4.37 |
| DBH > 35.56 ELM | 0.712 | 4.35 | DBH > 35.56 ELM | 0.606 | 4.26 |
| DBH > 35.56 EGAM | 0.805 | 3.59 | DBH > 35.56 EGAM | 0.623 | 4.16 |
| LiDAR Block and Model | ELM | EGAM | Difference in Multiples |
|---|---|---|---|
| Block3 Pine < 25.4 | 21.8 | 656.6 | 30 |
| Block3 Pine 25.4–35.56 | 19.2 | 538.1 | 28 |
| Block3 Pine > 35.56 | 17.4 | 456.0 | 26 |
| Block2 Pine < 25.4 | 24.3 | 791.6 | 33 |
| Block2 Pine 25.4–35.56 | 17.5 | 606.0 | 35 |
| Block2 Pine > 35.56 | 17.6 | 535.9 | 30 |
| Chocta Pine < 25.4 | 33.5 | 991.7 | 30 |
| Chocta Pine 25.4–35.56 | 30.4 | 752.0 | 25 |
| Chocta Pine > 35.56 | 23.8 | 663.0 | 28 |
| Leon Pine < 25.4 | 6.9 | 229.0 | 33 |
| Leon Pine 25.4–35.56 | 7.3 | 192.3 | 26 |
| Leon Pine > 35.56 | 6.8 | 172.5 | 25 |
| Model | r2 | RMSE |
| All Single Model | 0.726 | 9.84 |
| All ELM | 0.724 | 9.86 |
| All EGAM | 0.791 | 8.63 |
| Pine Single Model | 0.740 | 8.43 |
| Pine ELM | 0.742 | 8.40 |
| Pine EGAM | 0.773 | 7.87 |
| St. Peter, et al., 2021 [24] | r2 | RMSE |
| All Model | 0.777 | 7.67 |
| Pine Model | 0.687 | 5.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
St. Peter, J.; Drake, J.; Medley, P.; Broadbent, E.; Chen, G.; Ibeanusi, V. Comparison of Single and Ensemble Regression Model Workflows for Estimating Basal Area by Tree Size Class in Pine Forests of Southeastern U.S. Remote Sens. 2025, 17, 253. https://doi.org/10.3390/rs17020253
St. Peter J, Drake J, Medley P, Broadbent E, Chen G, Ibeanusi V. Comparison of Single and Ensemble Regression Model Workflows for Estimating Basal Area by Tree Size Class in Pine Forests of Southeastern U.S. Remote Sensing. 2025; 17(2):253. https://doi.org/10.3390/rs17020253
Chicago/Turabian StyleSt. Peter, Joseph, Jason Drake, Paul Medley, Eben Broadbent, Gang Chen, and Victor Ibeanusi. 2025. "Comparison of Single and Ensemble Regression Model Workflows for Estimating Basal Area by Tree Size Class in Pine Forests of Southeastern U.S" Remote Sensing 17, no. 2: 253. https://doi.org/10.3390/rs17020253
APA StyleSt. Peter, J., Drake, J., Medley, P., Broadbent, E., Chen, G., & Ibeanusi, V. (2025). Comparison of Single and Ensemble Regression Model Workflows for Estimating Basal Area by Tree Size Class in Pine Forests of Southeastern U.S. Remote Sensing, 17(2), 253. https://doi.org/10.3390/rs17020253







