Diffractive Neural Network Enabled Spectral Object Detection
Abstract
Highlights
- We proposed an innovative DNN-SOD diffractive neural network architecture that leverages spectral characteristics and field-of-view segmentation to enable direct spectral feature reconstruction and target detection for infrared targets.
- The architecture achieved 84.27% on an infrared target dataset, demonstrating its feasibility for large-scale remote sensing tasks.
- This study presents a new paradigm of applying optical computing to spectral remote sensing target detection, overcoming the limitations of traditional optical computing methods that fail to fully exploit spectral properties of targets and handle large-scale data effectively.
- It provides a novel pathway for integrated sensing-computing information processing in future sky-based remote sensing, highlighting the potential of optical computing inference in real-world applications.
Abstract
1. Introduction
2. Materials and Methods
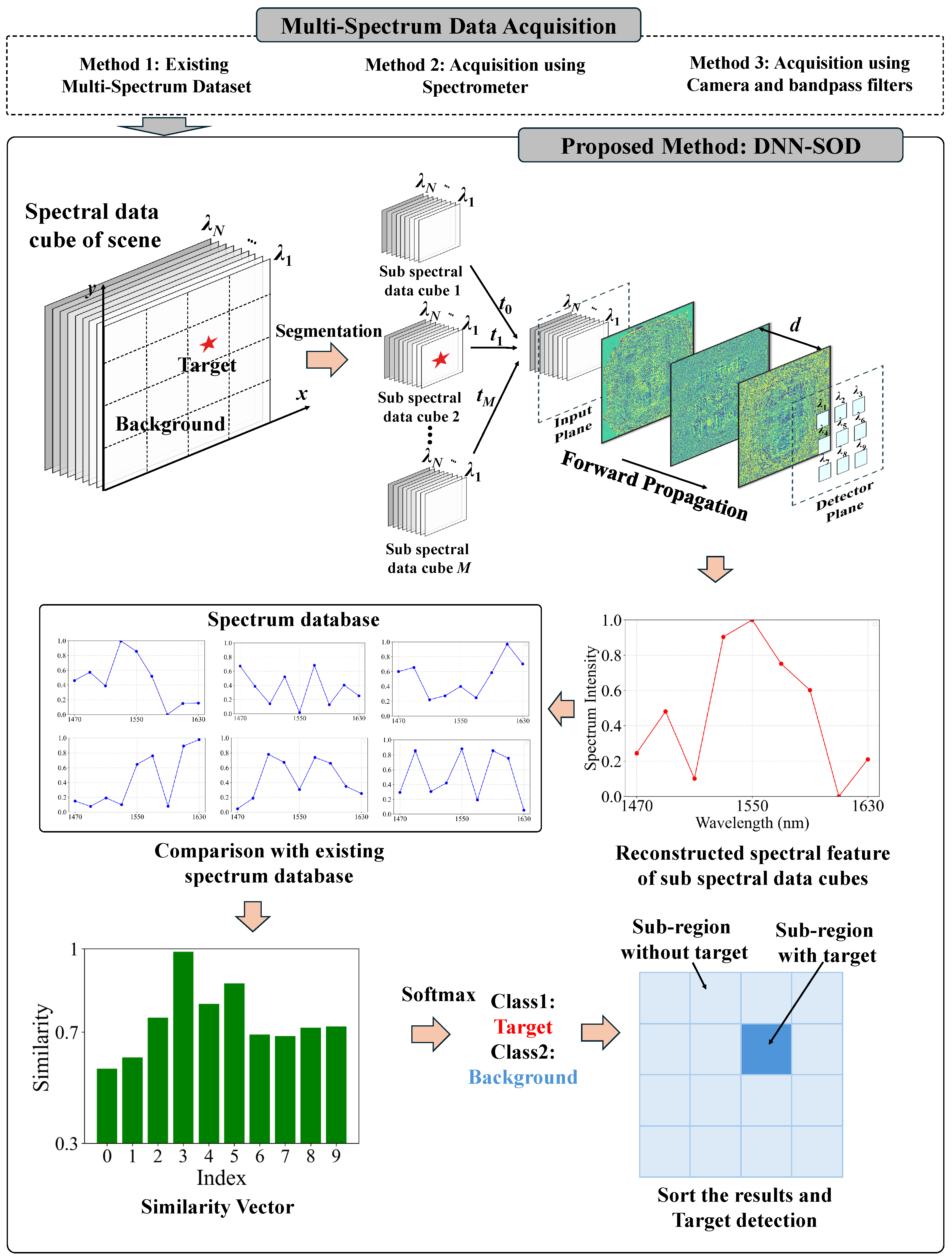
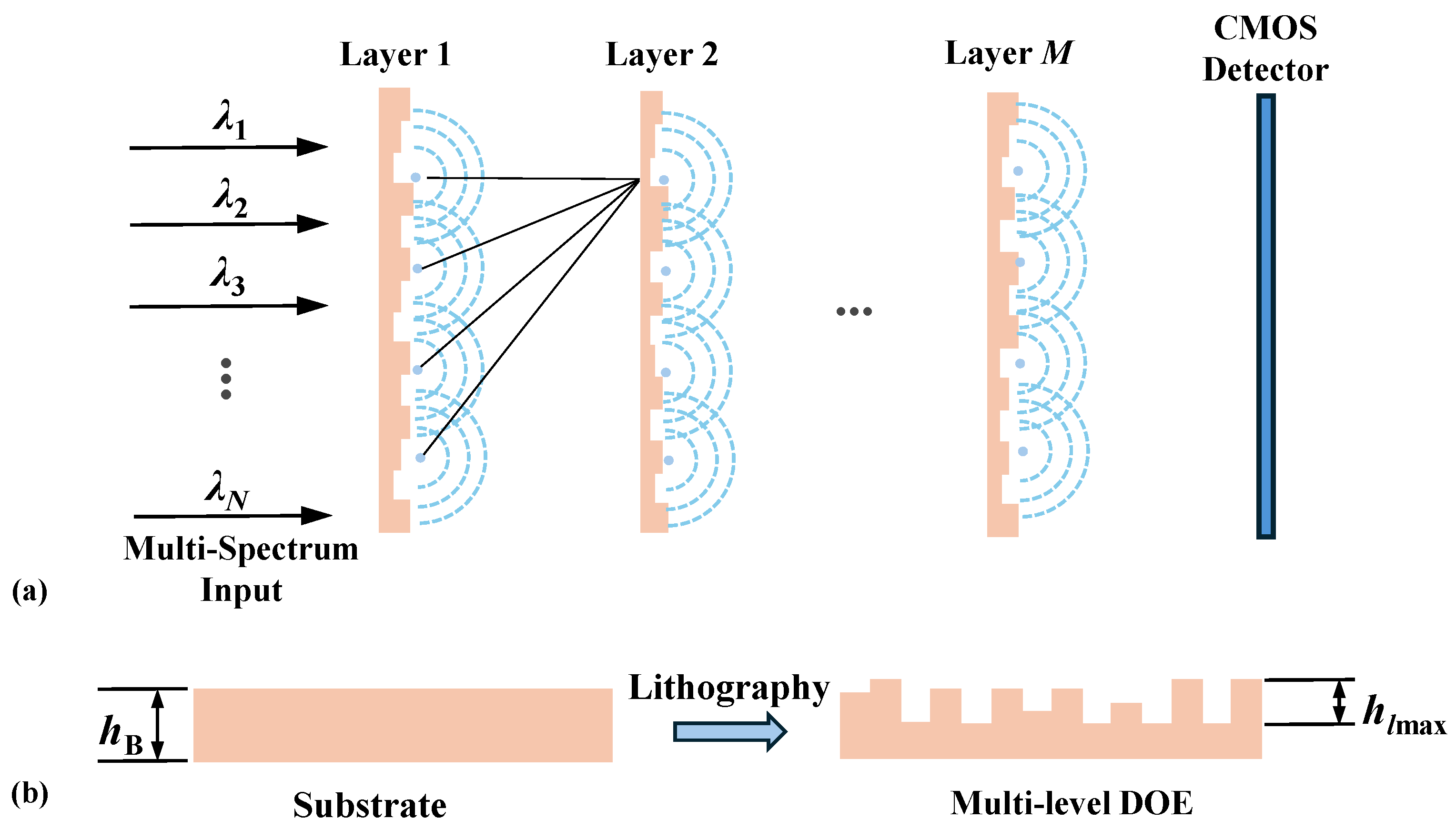
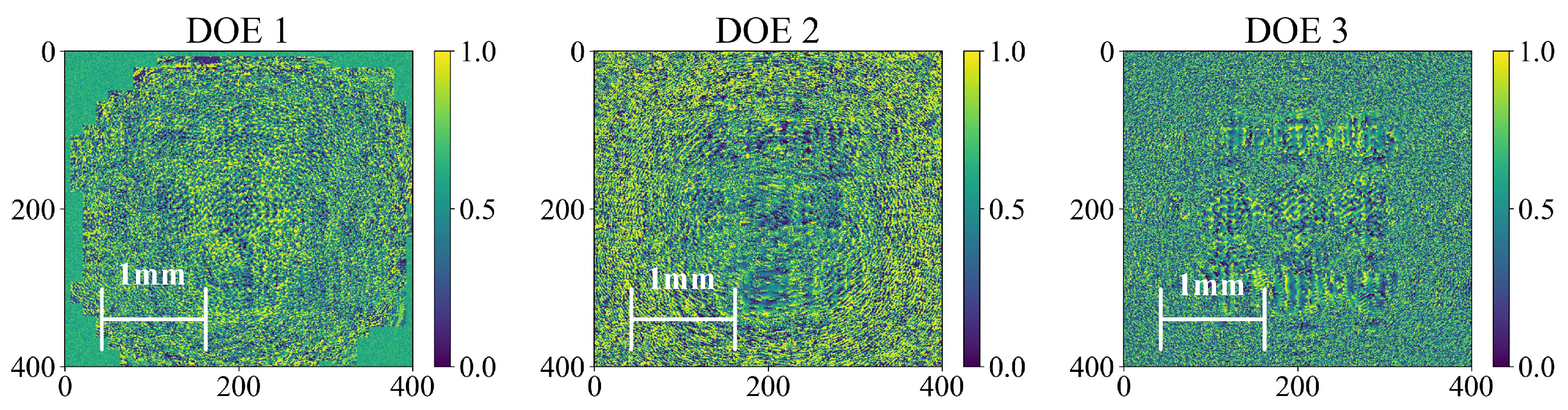
2.1. Architecture of DNN-SOD
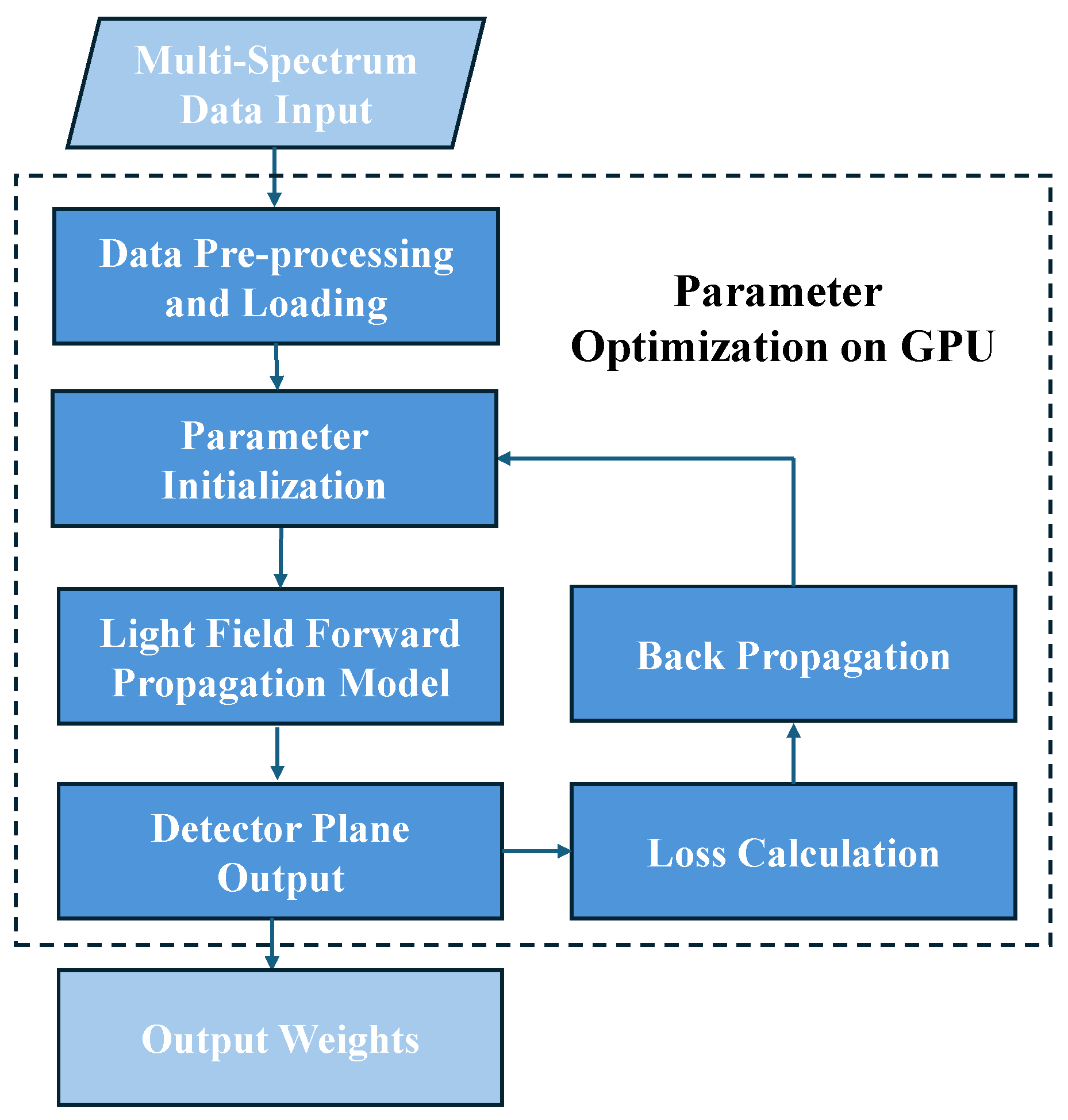
2.2. Forward Propagation Model of DNN-SOD
2.3. Dataset Generation and Training of DNN-SOD
3. Results
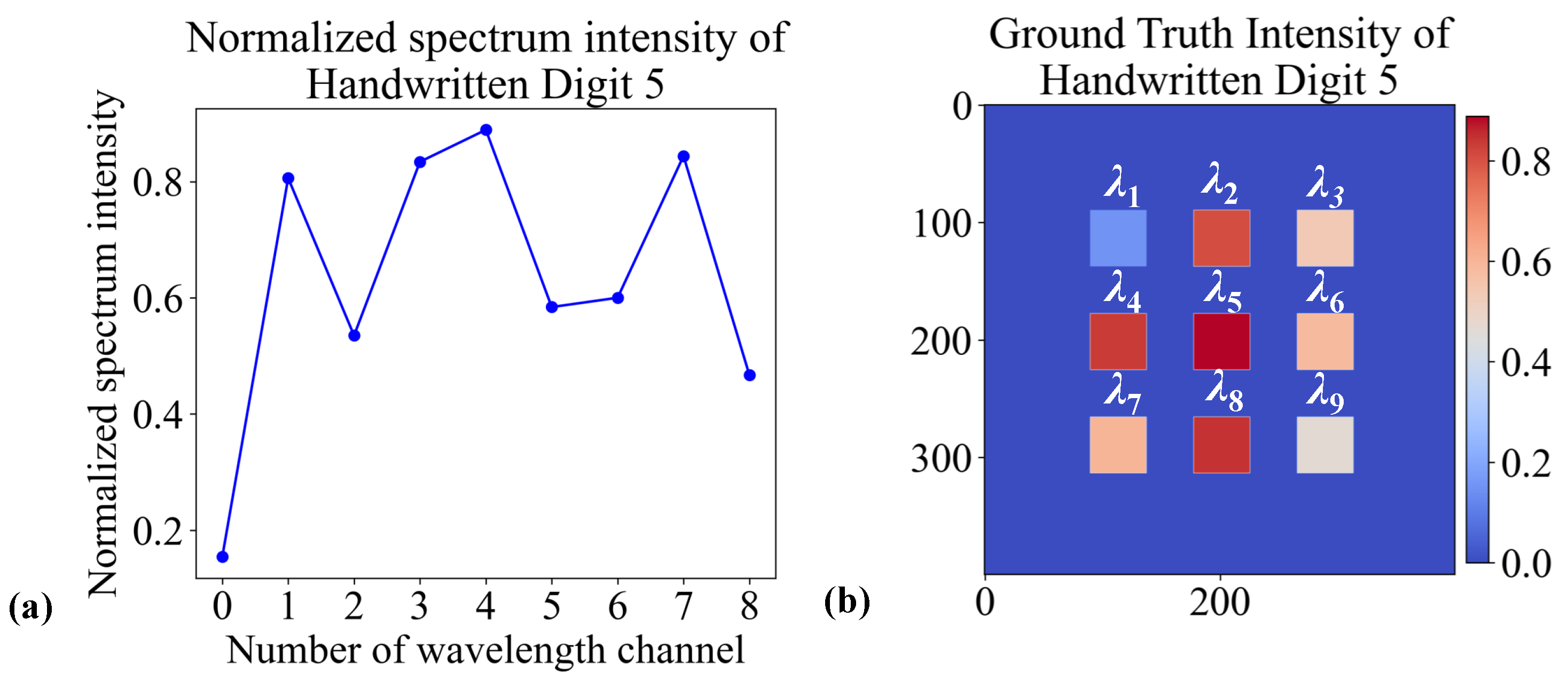
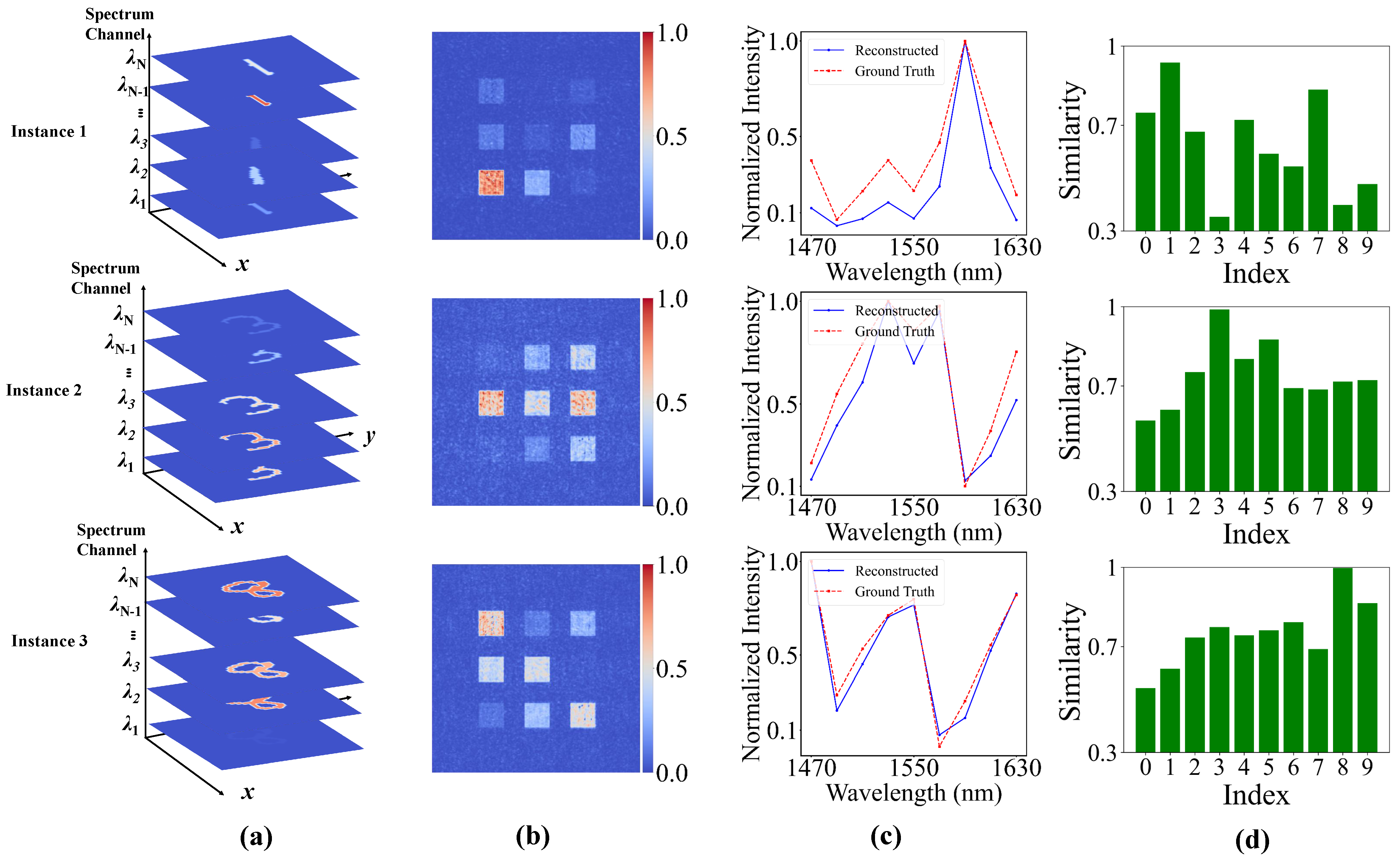
3.1. Preliminary Validation on the Multi-Spectrum MNIST Dataset
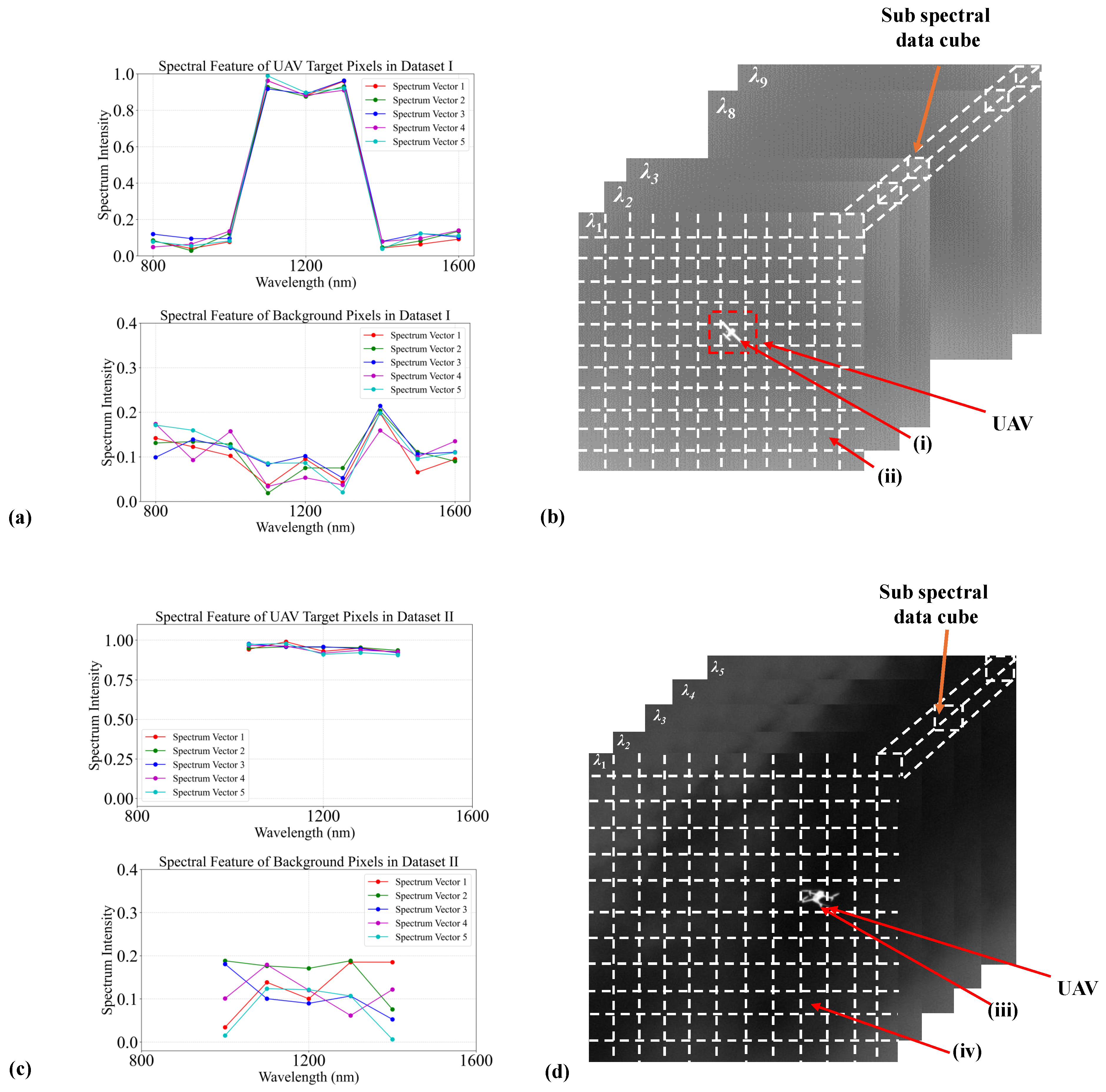
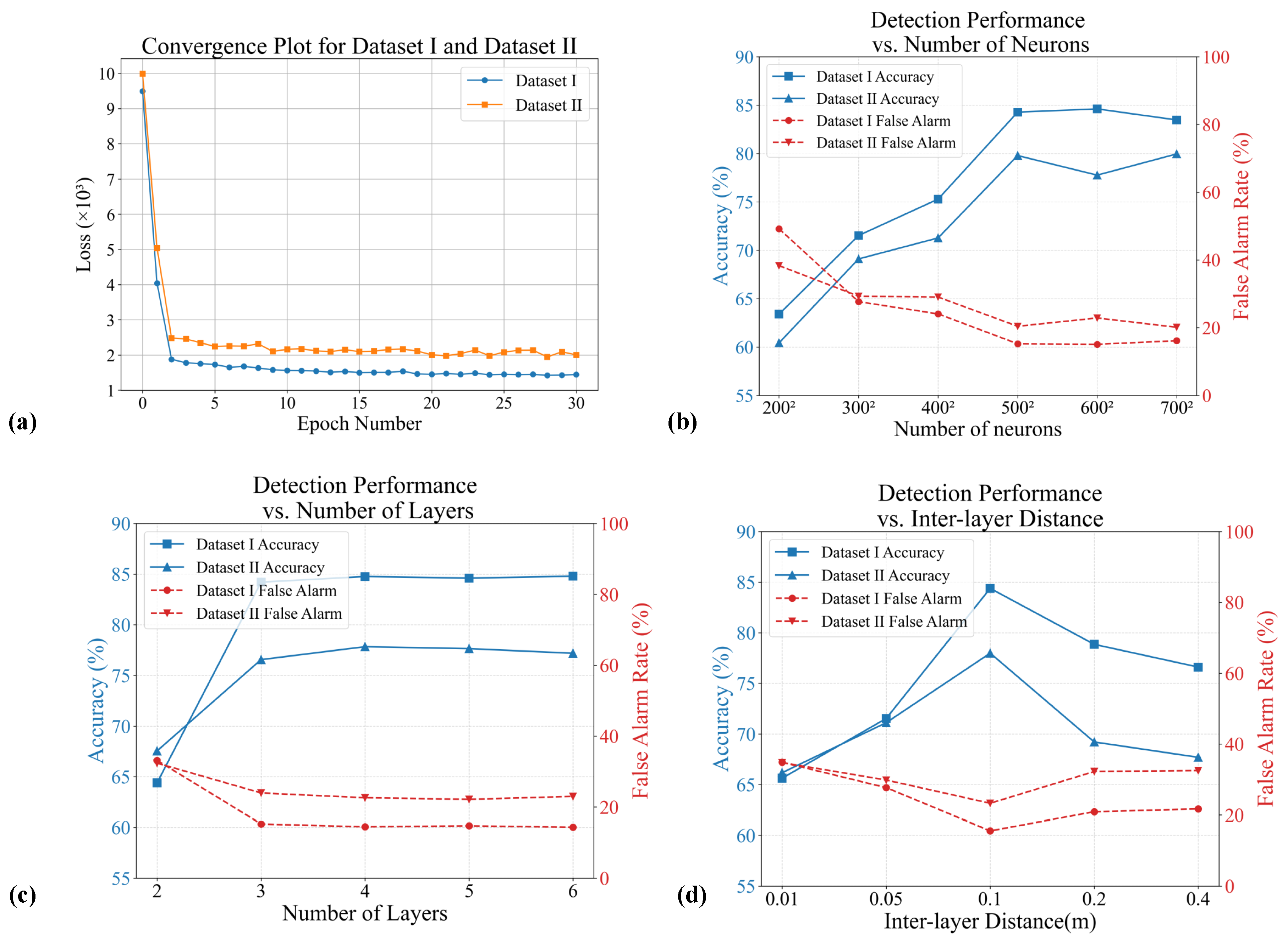
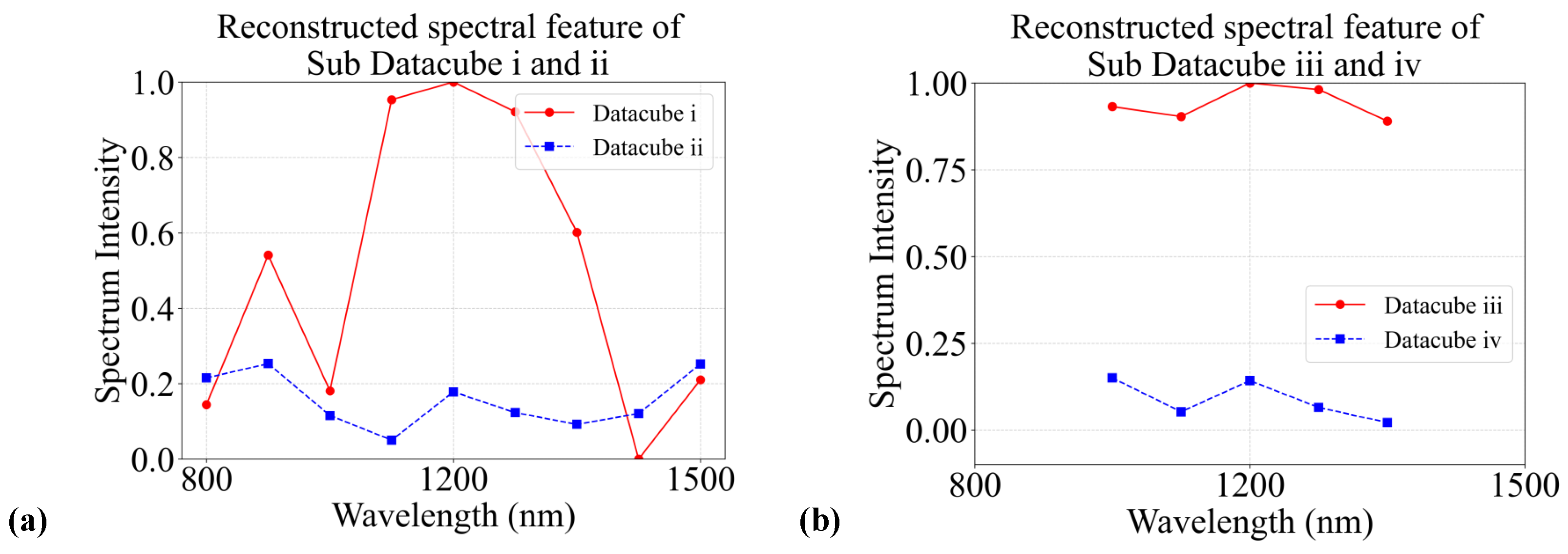
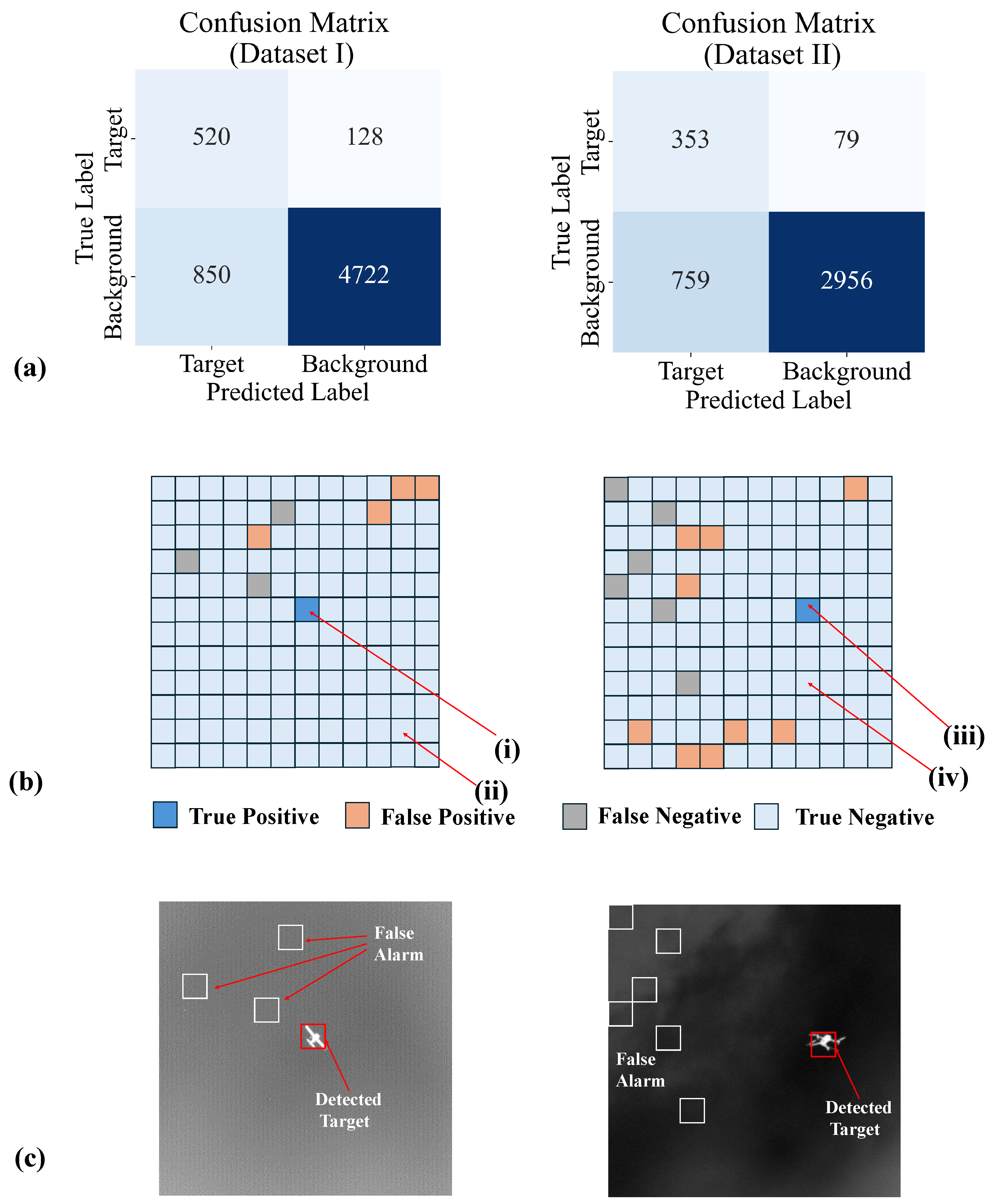
3.2. Validation on Dataset with Infrared Targets
4. Discussion
4.1. Research Implications
4.2. Limitation and Future Perspectives
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.N.; Sun, D.X.; Hu, X.N.; Ye, X.; Li, Y.D.; Liu, S.F.; Cao, K.Q.; Chai, M.Y.; Zhou, W.Y.N.; Zhang, J.; et al. The advanced hyperspectral imager: Aboard China’s GaoFen-5 satellite. IEEE Geosci. Remote Sens. Mag. 2019, 7, 23–32. [Google Scholar] [CrossRef]
- Chen, L.; Letu, H.; Fan, M.; Shang, H.; Tao, J.; Wu, L.; Zhang, Y.; Yu, C.; Gu, J.; Zhang, N.; et al. An introduction to the Chinese high-resolution Earth observation system: Gaofen-1~7 civilian satellites. J. Remote Sens. 2022, 2022, 9769536. [Google Scholar] [CrossRef]
- Deschamps, P.Y.; Bréon, F.M.; Leroy, M.; Podaire, A.; Bricaud, A.; Buriez, J.C.; Seze, G. The POLDER mission: Instrument characteristics and scientific objectives. IEEE Trans. Geosci. Remote Sens. 1994, 32, 598–615. [Google Scholar] [CrossRef]
- Fan, Y.; Huang, W.; Zhu, F.; Liu, X.; Jin, C.; Guo, C.; An, Y.; Kivshar, Y.; Qiu, C.W.; Li, W. Dispersion-assisted high-dimensional photodetector. Nature 2024, 630, 77–83. [Google Scholar] [CrossRef] [PubMed]
- Tiwary, A.R.; Mathew, S.K.; Bayanna, A.R.; Venkatakrishnan, P.; Yadav, R. Imaging spectropolarimeter for the multi-application solar telescope at Udaipur solar observatory: Characterization of polarimeter and preliminary observations. Sol. Phys. 2017, 292, 49. [Google Scholar] [CrossRef]
- Li, B.; Xiao, C.; Wang, L.; Wang, Y.; Lin, Z.; Li, M.; An, W.; Guo, Y. Dense nested attention network for infrared small target detection. IEEE Trans. Image Process. 2022, 32, 1745–1758. [Google Scholar] [CrossRef]
- Xiong, P.; Tong, L.; Zhang, K.; Shen, X.; Battiston, R.; Ouzounov, D.; Iuppa, R.; Crookes, D.; Long, C.; Zhou, H. Towards advancing the earthquake forecasting by machine learning of satellite data. Sci. Total Environ. 2021, 771, 145256. [Google Scholar] [CrossRef]
- Higuchi, A. Toward more integrated utilizations of geostationary satellite data for disaster management and risk mitigation. Remote Sens. 2021, 13, 1553. [Google Scholar] [CrossRef]
- Feldmann, J.; Youngblood, N.; Wright, C.D.; Bhaskaran, H.; Pernice, W.H. All-optical spiking neurosynaptic networks with self-learning capabilities. Nature 2019, 569, 208–214. [Google Scholar] [CrossRef]
- Li, C.; Zhang, X.; Li, J.; Fang, T.; Dong, X. The challenges of modern computing and new opportunities for optics. PhotoniX 2021, 2, 20. [Google Scholar] [CrossRef]
- Shastri, B.J.; Tait, A.N.; Ferreira de Lima, T.; Pernice, W.H.; Bhaskaran, H.; Wright, C.D.; Prucnal, P.R. Photonics for artificial intelligence and neuromorphic computing. Nat. Photonics 2021, 15, 102–114. [Google Scholar] [CrossRef]
- Lin, X.; Rivenson, Y.; Yardimci, N.T.; Veli, M.; Luo, Y.; Jarrahi, M.; Ozcan, A. All-optical machine learning using diffractive deep neural networks. Science 2018, 361, 1004–1008. [Google Scholar] [CrossRef]
- Mengu, D.; Tabassum, A.; Jarrahi, M.; Ozcan, A. Snapshot multispectral imaging using a diffractive optical network. Light Sci. Appl. 2023, 12, 86. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, H.; Li, J.; Xu, T.; Zhao, Z.; Duan, Z.; Gao, S.; Lin, X. Opto-intelligence spectrometer using diffractive neural networks. Nanophotonics 2024, 13, 3883–3893. [Google Scholar] [CrossRef]
- Allington-Smith, J. Basic principles of integral field spectroscopy. New Astron. Rev. 2006, 50, 244–251. [Google Scholar] [CrossRef]
- Wright, G.S.; Rieke, G.H.; Glasse, A.; Ressler, M.; Marín, M.G.; Aguilar, J.; Alberts, S.; Álvarez-Márquez, J.; Argyriou, I.; Banks, K.; et al. The mid-infrared instrument for JWST and its in-flight performance. Publ. Astron. Soc. Pac. 2023, 135, 48003. [Google Scholar] [CrossRef]
- Yu, H.; Huang, Z.; Lamon, S.; Wang, B.; Ding, H.; Lin, J.; Wang, Q.; Luan, H.; Gu, M.; Zhang, Q. All-optical image transportation through a multimode fibre using a miniaturized diffractive neural network on the distal facet. Nat. Photonics 2025, 19, 486–493. [Google Scholar] [CrossRef]
- Suda, R.; Naruse, M.; Horisaki, R. Incoherent computer-generated holography. Opt. Lett. 2022, 47, 3844–3847. [Google Scholar] [CrossRef]
- Rahman, M.S.S.; Yang, X.; Li, J.; Bai, B.; Ozcan, A. Universal linear intensity transformations using spatially incoherent diffractive processors. Light Sci. Appl. 2023, 12, 195. [Google Scholar] [CrossRef]
- Chen, R.; Ma, Y.; Zhang, C.; Xu, W.; Wang, Z.; Sun, S. All-optical perception based on partially coherent optical neural networks. Opt. Express 2025, 33, 1609–1624. [Google Scholar] [CrossRef]
- Filipovich, M.J.; Malyshev, A.; Lvovsky, A. Role of spatial coherence in diffractive optical neural networks. Opt. Express 2024, 32, 22986–22997. [Google Scholar] [CrossRef]
- Hui, B.; Song, Z.; Fan, H.; Zhong, P.; Hu, W.; Zhang, X.; Lin, J.; Su, H.; Jin, W.; Zhang, Y.; et al. A dataset for infrared image dim-small aircraft target detection and tracking under ground/air background. Sci. Data Bank 2019. [Google Scholar] [CrossRef]
- Chen, R.; Ma, Y.; Wang, Z.; Sun, S. Incoherent Optical Neural Networks for Passive and Delay-Free Inference in Natural Light. Photonics 2025, 12, 278. [Google Scholar] [CrossRef]
- Khanam, R.; Hussain, M. YOLOv11: An overview of the key architectural enhancements. arXiv 2024, arXiv:2410.17725. [Google Scholar] [CrossRef]
- Wang, A.; Chen, H.; Liu, L.; Chen, K.; Lin, Z.; Han, J.; Ding, G. YOLOv10: Real-time end-to-end object detection. Adv. Neural Inf. Process. Syst. 2024, 37, 107984–108011. [Google Scholar]
- Wang, J.; Chen, J.; Yu, F.; Chen, R.; Wang, J.; Zhao, Z.; Li, X.; Xing, H.; Li, G.; Chen, X.; et al. Unlocking ultra-high holographic information capacity through nonorthogonal polarization multiplexing. Nat. Commun. 2024, 15, 6284. [Google Scholar] [CrossRef]
- Yang, Y.; Pan, C.; Li, Y.; Yangdong, X.; Wang, P.; Li, Z.A.; Wang, S.; Yu, W.; Liu, G.; Cheng, B.; et al. In-sensor dynamic computing for intelligent machine vision. Nat. Electron. 2024, 7, 225–233. [Google Scholar] [CrossRef]
- Zhou, F.; Chai, Y. Near-sensor and in-sensor computing. Nat. Electron. 2020, 3, 664–671. [Google Scholar] [CrossRef]
- Li, T.; Miao, J.; Fu, X.; Song, B.; Cai, B.; Ge, X.; Zhou, X.; Zhou, P.; Wang, X.; Jariwala, D.; et al. Reconfigurable, non-volatile neuromorphic photovoltaics. Nat. Nanotechnol. 2023, 18, 1303–1310. [Google Scholar] [CrossRef]
- Plastiras, G.; Terzi, M.; Kyrkou, C.; Theocharides, T. Edge intelligence: Challenges and opportunities of near-sensor machine learning applications. In Proceedings of the 2018 IEEE 29th International Conference on Application-Specific Systems, Architectures and Processors (ASAP), Milan, Italy, 10–12 July 2018; pp. 1–7. [Google Scholar]
- Li, J.; Zheng, K.; Li, Z.; Gao, L.; Jia, X. X-Shaped Interactive Autoencoders with Cross-Modality Mutual Learning for Unsupervised Hyperspectral Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5518317. [Google Scholar] [CrossRef]
- Li, J.; Zheng, K.; Liu, W.; Li, Z.; Yu, H.; Ni, L. Model-Guided Coarse-to-Fine Fusion Network for Unsupervised Hyperspectral Image Super-Resolution. IEEE Geosci. Remote Sens. Lett. 2023, 20, 5508605. [Google Scholar] [CrossRef]
- Li, J.; Zheng, K.; Gao, L.; Han, Z.; Li, Z.; Chanussot, J. Enhanced Deep Image Prior for Unsupervised Hyperspectral Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5504218. [Google Scholar] [CrossRef]
- Ma, Q.; Jiang, J.; Liu, X.; Ma, J. Reciprocal transformer for hyperspectral and multispectral image fusion. Inf. Fusion 2024, 104, 102148. [Google Scholar] [CrossRef]


| Incoherent Light Modeling Method | Computational Complexity | Characteristics |
|---|---|---|
| Random phase superposition | High accuracy with rapidly growing cost | |
| Mode decomposition | Suitable for sparse scenes; parallelizable | |
| Convolution-based method | Fastest approach, limited by linearity and shift invariance |
| Bit Number | Quantization Levels | Diffraction Efficiency |
|---|---|---|
| 1 | 2 | 40.5% |
| 2 | 4 | 81.0% |
| 3 | 8 | 95.0% |
| 4 | 16 | 98.7% |
| Dataset | Number of Spectrum Channel | Center Wavelength(nm) | Number of Sub Spectrum Cubes |
|---|---|---|---|
| Dataset I | 9 | 800, 900, 1000, 1100, 1200, 1300, 1400, 1500, 1600 | 31,104 |
| Dataset II | 5 | 1000, 1100, 1200, 1300, 1400 | 20,736 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Chen, R.; Qian, S.; Sun, S. Diffractive Neural Network Enabled Spectral Object Detection. Remote Sens. 2025, 17, 3381. https://doi.org/10.3390/rs17193381
Ma Y, Chen R, Qian S, Sun S. Diffractive Neural Network Enabled Spectral Object Detection. Remote Sensing. 2025; 17(19):3381. https://doi.org/10.3390/rs17193381
Chicago/Turabian StyleMa, Yijun, Rui Chen, Shuaicun Qian, and Shengli Sun. 2025. "Diffractive Neural Network Enabled Spectral Object Detection" Remote Sensing 17, no. 19: 3381. https://doi.org/10.3390/rs17193381
APA StyleMa, Y., Chen, R., Qian, S., & Sun, S. (2025). Diffractive Neural Network Enabled Spectral Object Detection. Remote Sensing, 17(19), 3381. https://doi.org/10.3390/rs17193381





