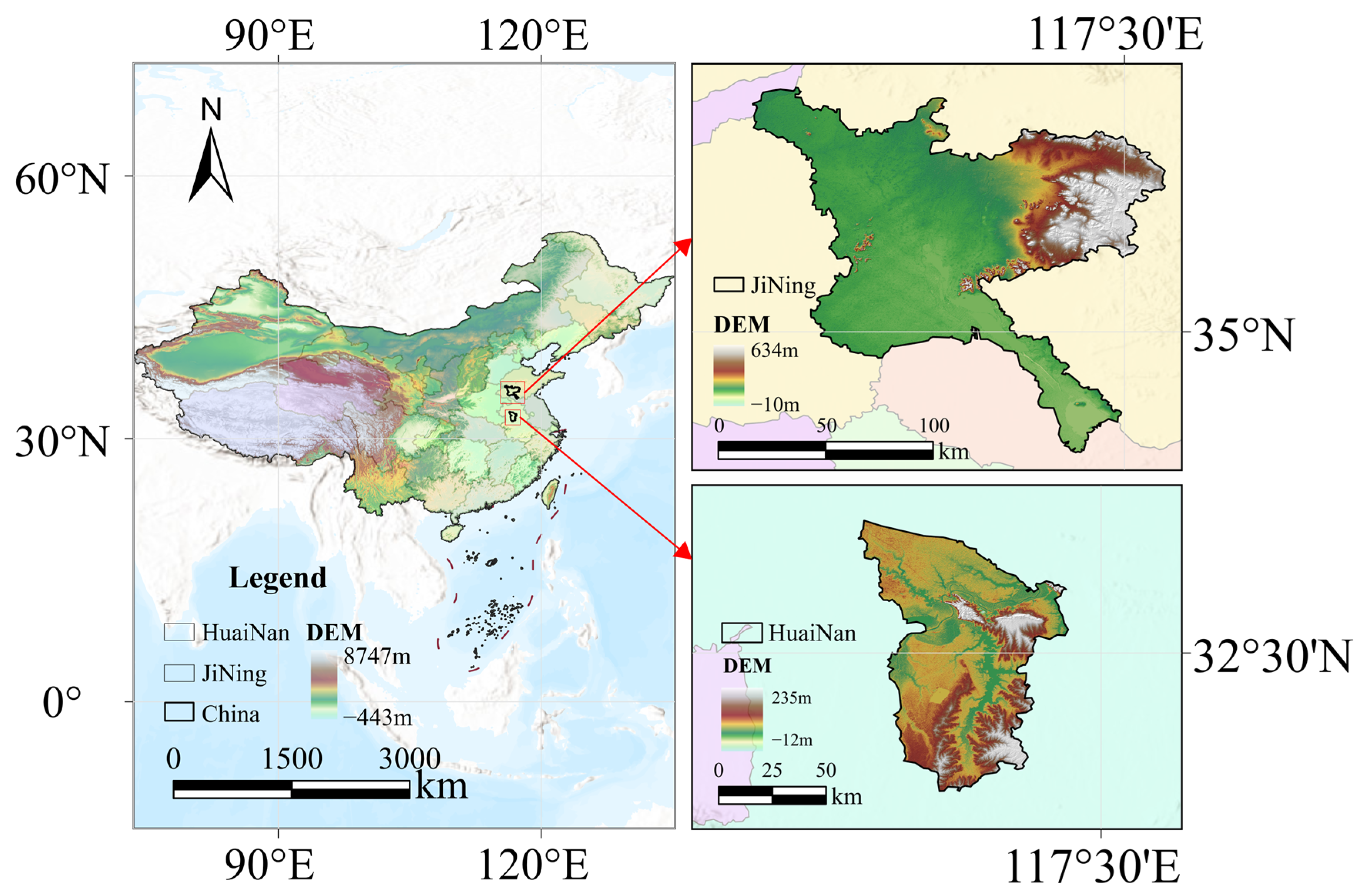
Figure 1.
Location map of the two study areas.
Figure 1.
Location map of the two study areas.
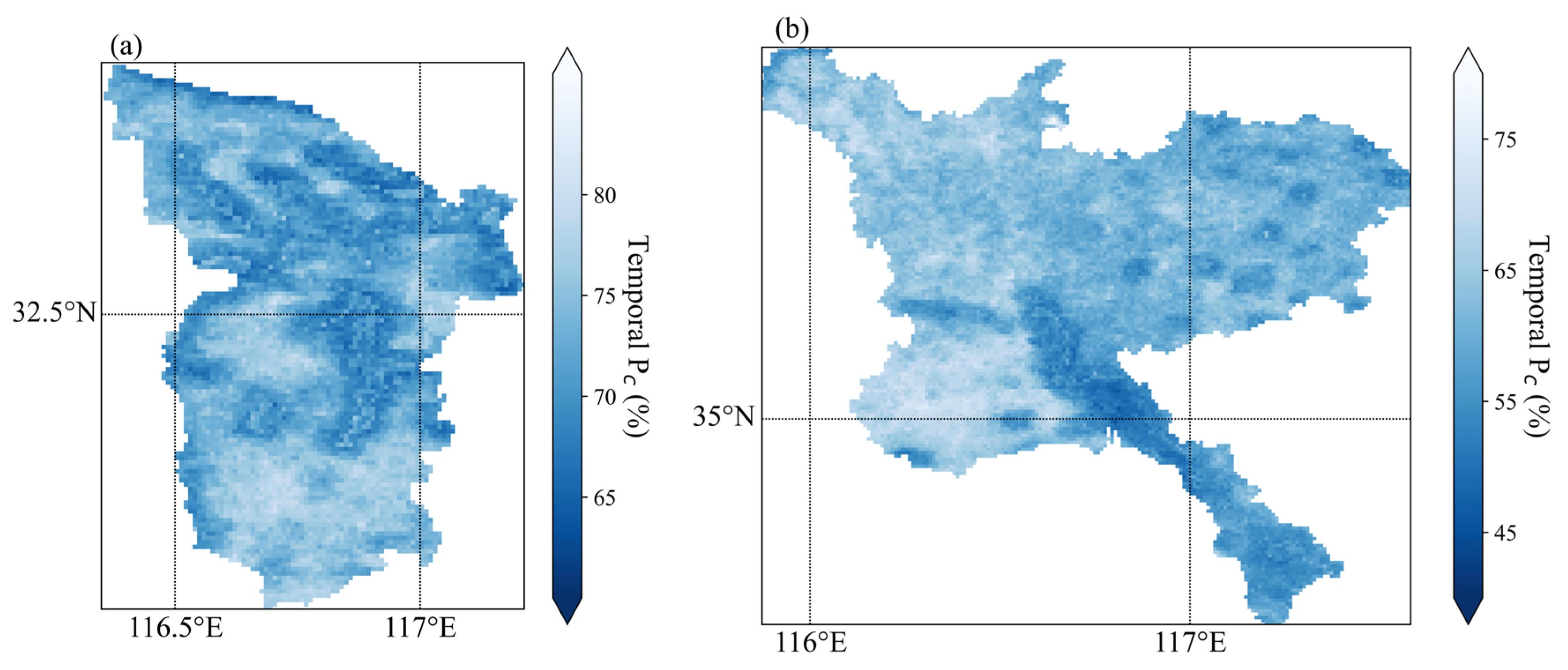
Figure 2.
Monthly average spatial Pc for the two regions in 2018.
Figure 2.
Monthly average spatial Pc for the two regions in 2018.
Figure 3.
Annual temporal Pc in 2018 for Huainan (a) and Jining (b).
Figure 3.
Annual temporal Pc in 2018 for Huainan (a) and Jining (b).
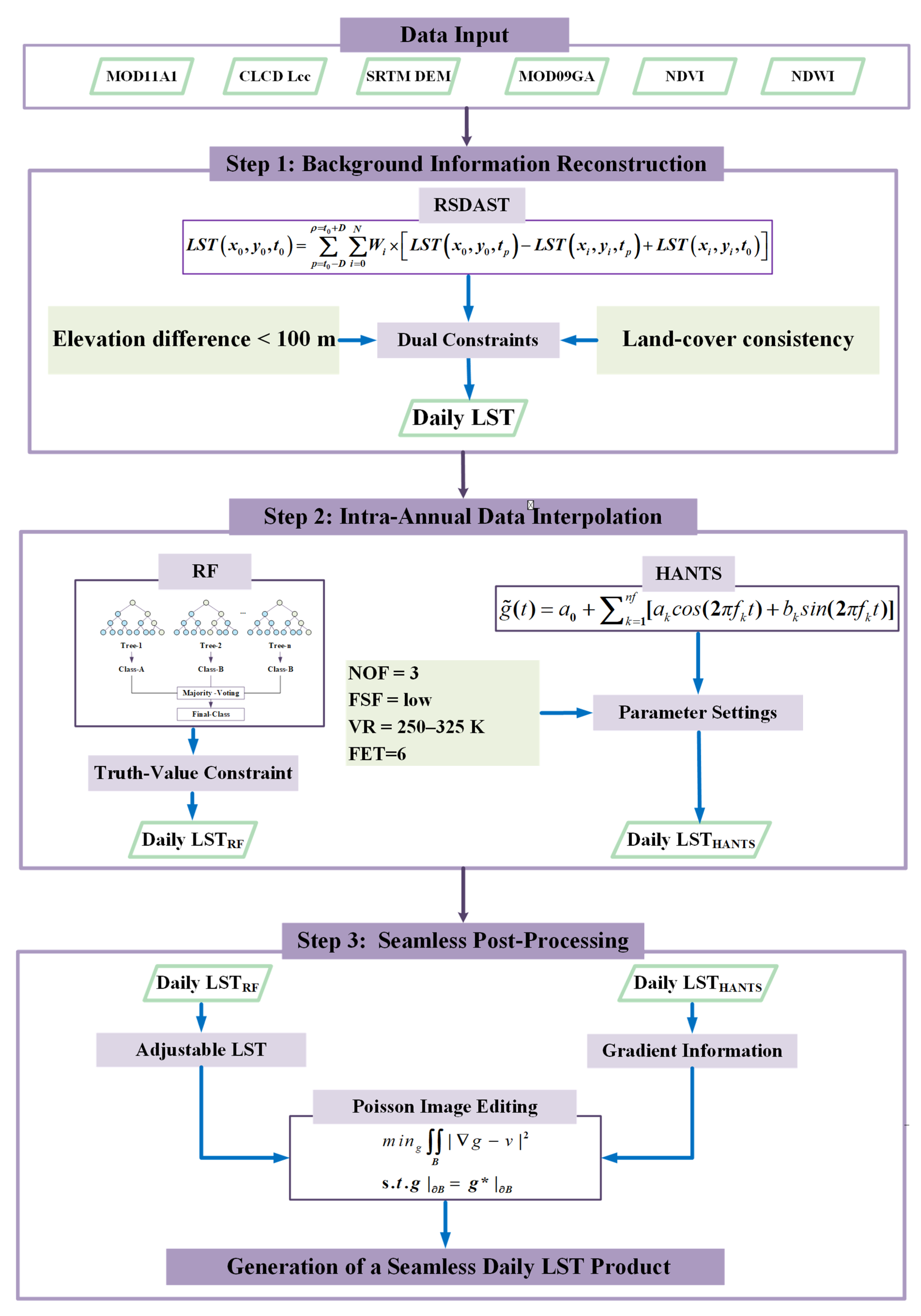
Figure 4.
Technical framework.
Figure 4.
Technical framework.
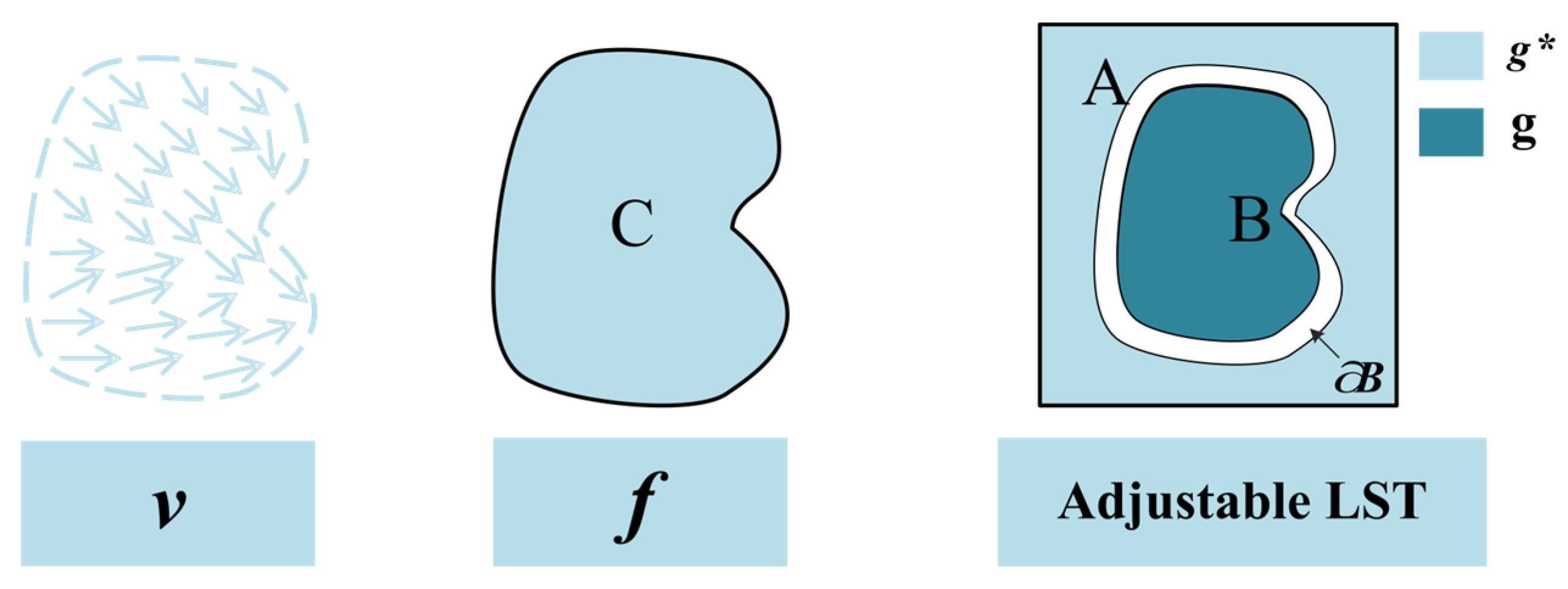
Figure 5.
The typical flowchart of the Poisson equation method.
Figure 5.
The typical flowchart of the Poisson equation method.
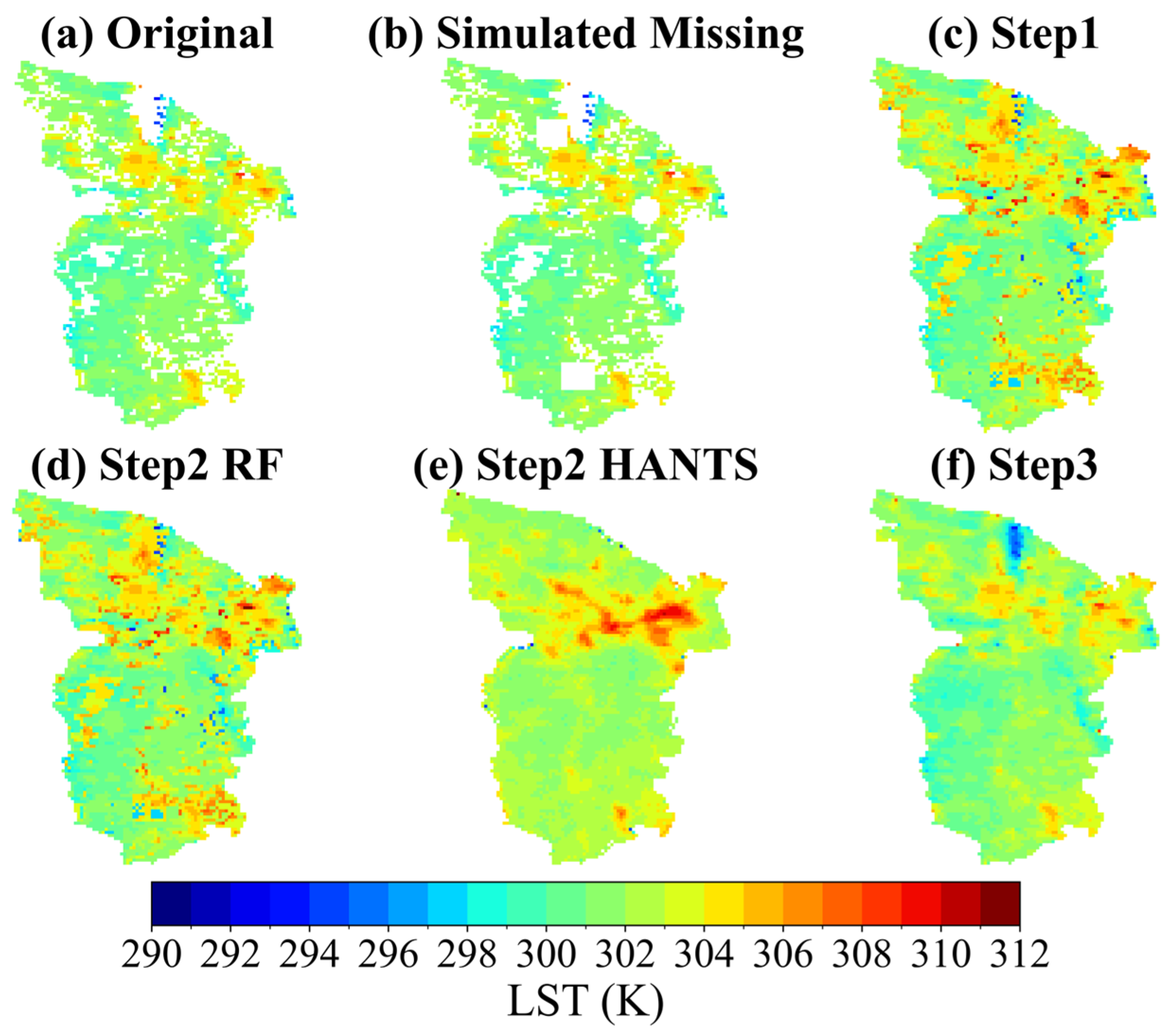
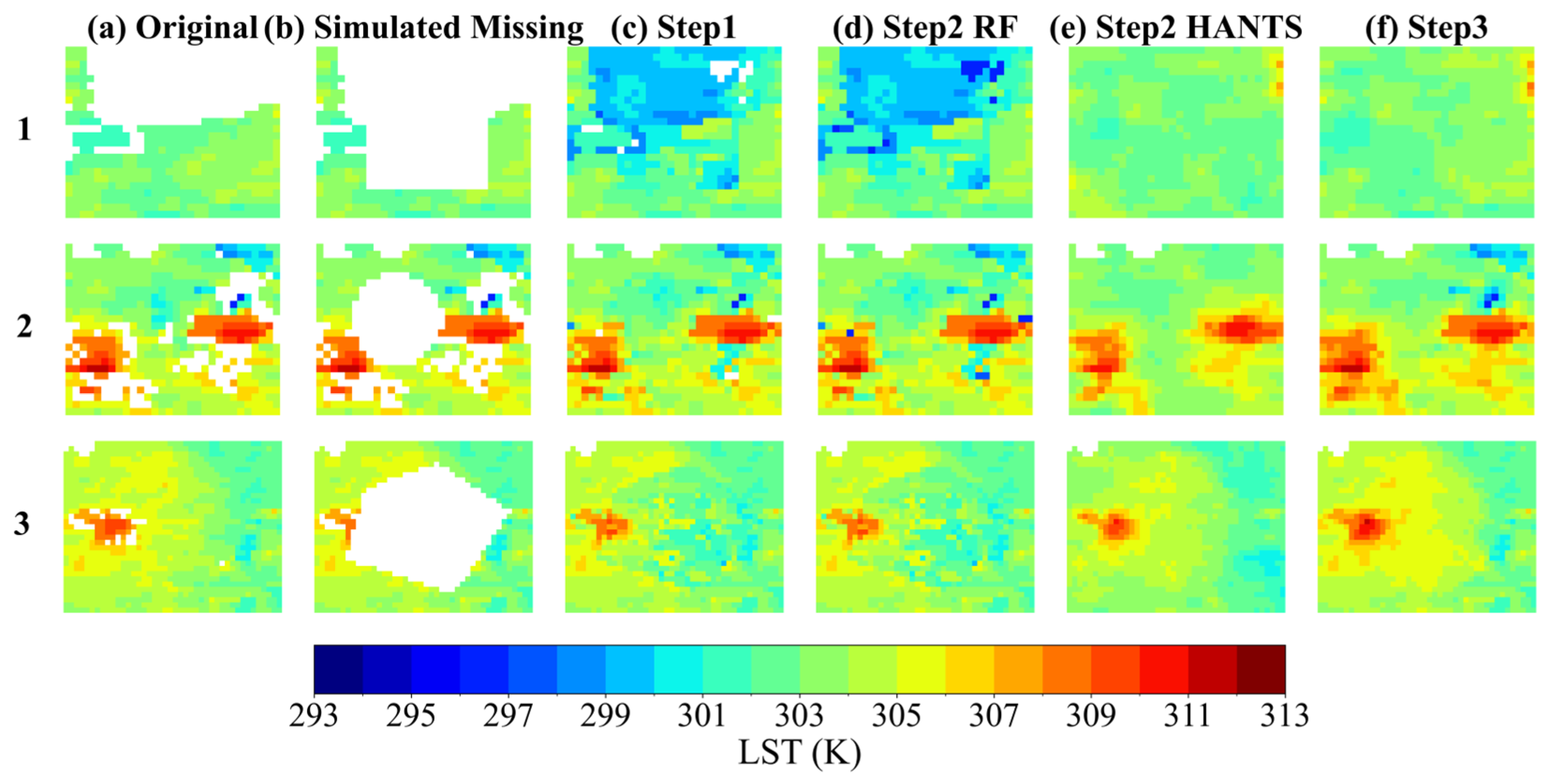
Figure 6.
Reconstructed daily LST for 12 August 2018 (day) in the Huainan region using each step of the integrated method. Simulated missing areas are represented by blank regions in rectangular, circular, and polygonal shapes. (a) Original daily LST; (b) simulated missing daily LST; (c) background-constrained reconstructed daily LST; (d) RF-reconstructed daily LST; (e) HANTS-reconstructed daily LST; (f) Poisson image reconstruction of daily LST.
Figure 6.
Reconstructed daily LST for 12 August 2018 (day) in the Huainan region using each step of the integrated method. Simulated missing areas are represented by blank regions in rectangular, circular, and polygonal shapes. (a) Original daily LST; (b) simulated missing daily LST; (c) background-constrained reconstructed daily LST; (d) RF-reconstructed daily LST; (e) HANTS-reconstructed daily LST; (f) Poisson image reconstruction of daily LST.
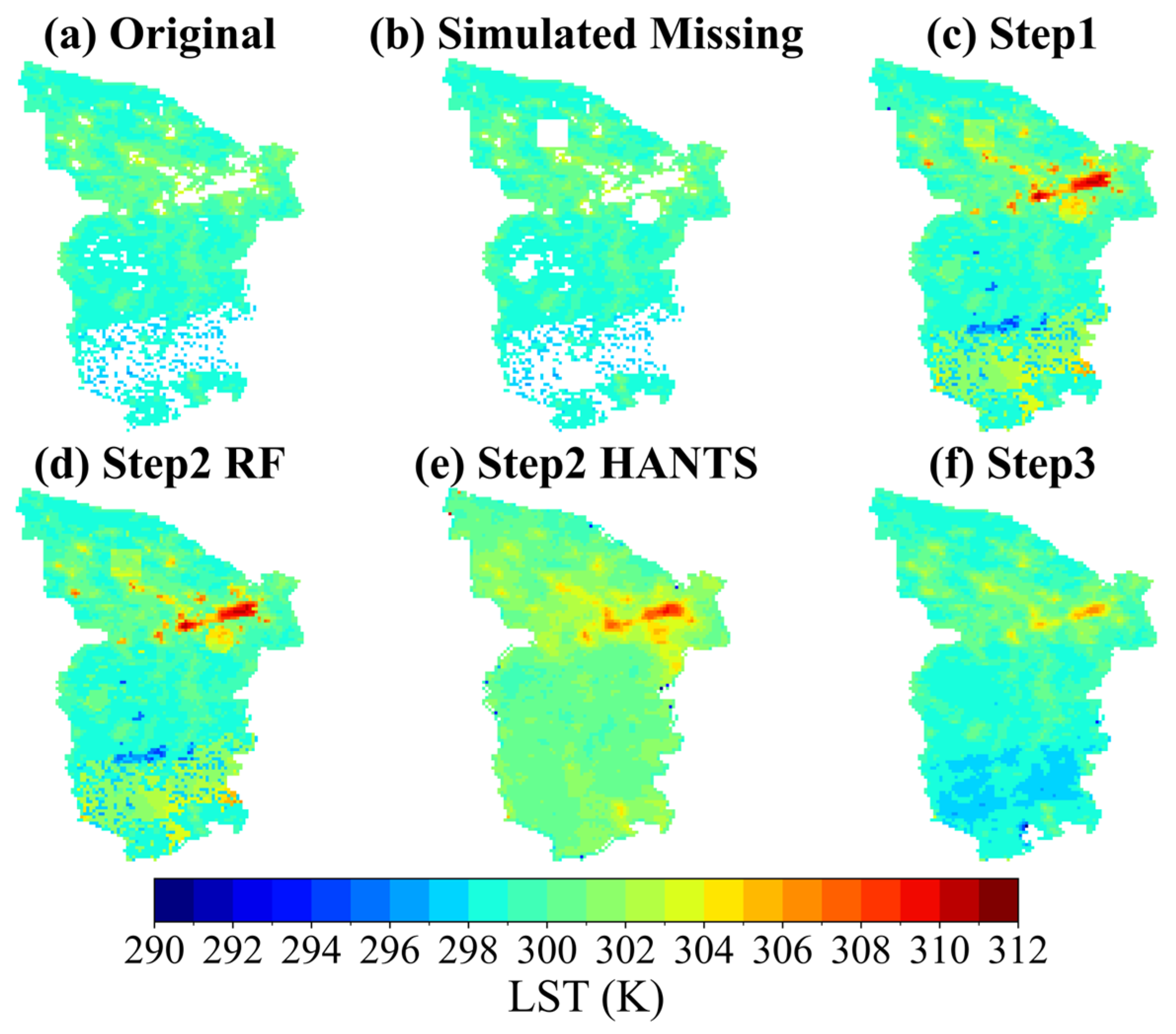
Figure 7.
Reconstructed daily LST for 24 August 2018 (night) in the Huainan region using each step of the integrated method. Simulated missing areas are represented by blank regions in rectangular, circular, and polygonal shapes. (a) Original daily LST; (b) simulated missing daily LST; (c) background-constrained reconstructed daily LST; (d) RF-reconstructed daily LST; (e) HANTS-reconstructed daily LST; (f) Poisson image reconstruction of daily LST.
Figure 7.
Reconstructed daily LST for 24 August 2018 (night) in the Huainan region using each step of the integrated method. Simulated missing areas are represented by blank regions in rectangular, circular, and polygonal shapes. (a) Original daily LST; (b) simulated missing daily LST; (c) background-constrained reconstructed daily LST; (d) RF-reconstructed daily LST; (e) HANTS-reconstructed daily LST; (f) Poisson image reconstruction of daily LST.
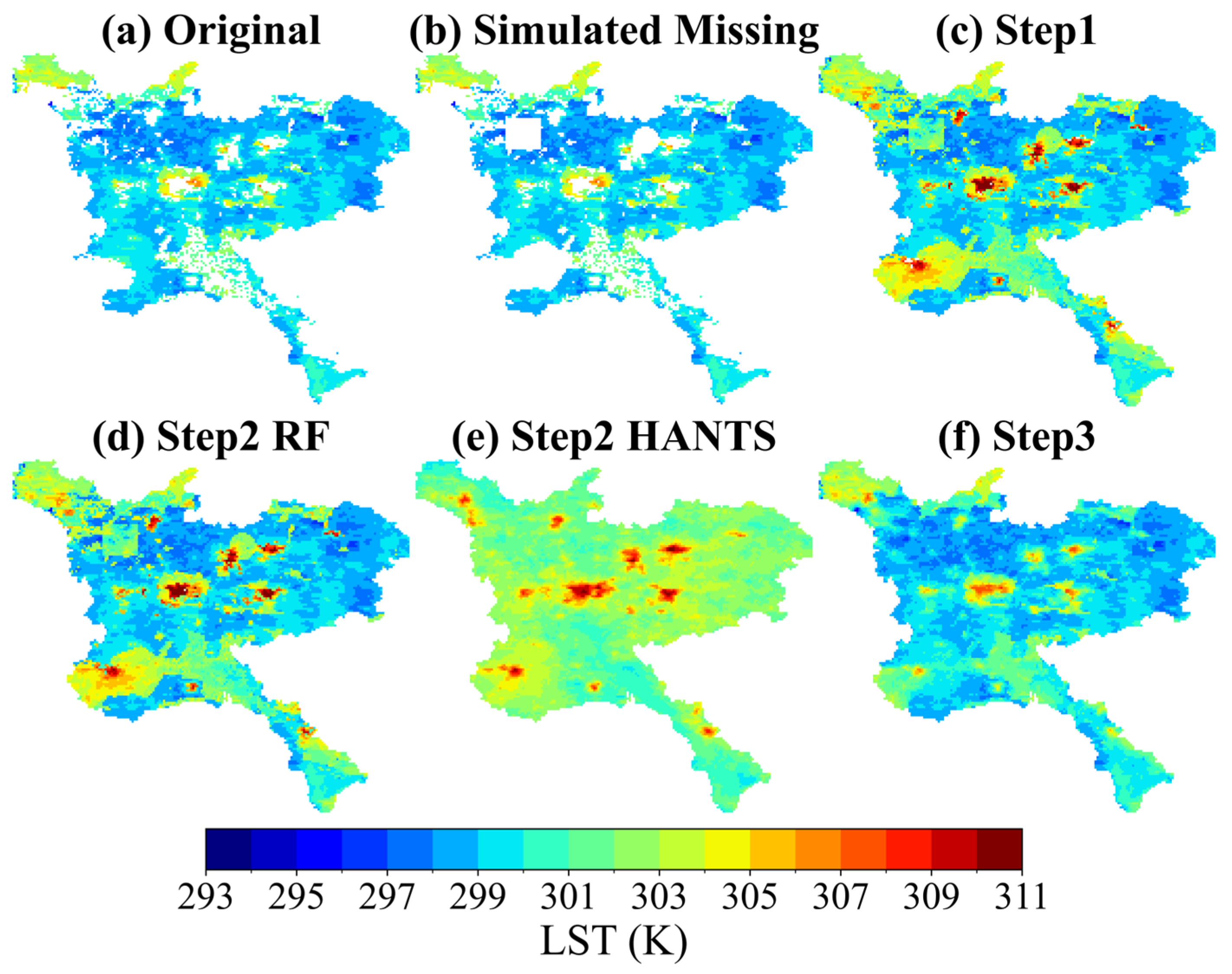
Figure 8.
Reconstructed daily LST for 26 August 2018 (day) in the Jining region using each step of the integrated method. Simulated missing areas are represented by blank regions in rectangular, circular, and polygonal shapes. (a) Original daily LST; (b) simulated missing daily LST; (c) background-constrained reconstructed daily LST; (d) RF-reconstructed daily LST; (e) HANTS-reconstructed daily LST; (f) Poisson image reconstruction of daily LST.
Figure 8.
Reconstructed daily LST for 26 August 2018 (day) in the Jining region using each step of the integrated method. Simulated missing areas are represented by blank regions in rectangular, circular, and polygonal shapes. (a) Original daily LST; (b) simulated missing daily LST; (c) background-constrained reconstructed daily LST; (d) RF-reconstructed daily LST; (e) HANTS-reconstructed daily LST; (f) Poisson image reconstruction of daily LST.
Figure 9.
Reconstructed daily LST for 25 August 2018 (night) in the Jining region using each step of the integrated method. Simulated missing areas are represented by blank regions in rectangular, circular, and polygonal shapes. (a) Original daily LST; (b) simulated missing daily LST; (c) background-constrained reconstructed daily LST; (d) RF-reconstructed daily LST; (e) HANTS-reconstructed daily LST; (f) Poisson image reconstruction of daily LST.
Figure 9.
Reconstructed daily LST for 25 August 2018 (night) in the Jining region using each step of the integrated method. Simulated missing areas are represented by blank regions in rectangular, circular, and polygonal shapes. (a) Original daily LST; (b) simulated missing daily LST; (c) background-constrained reconstructed daily LST; (d) RF-reconstructed daily LST; (e) HANTS-reconstructed daily LST; (f) Poisson image reconstruction of daily LST.
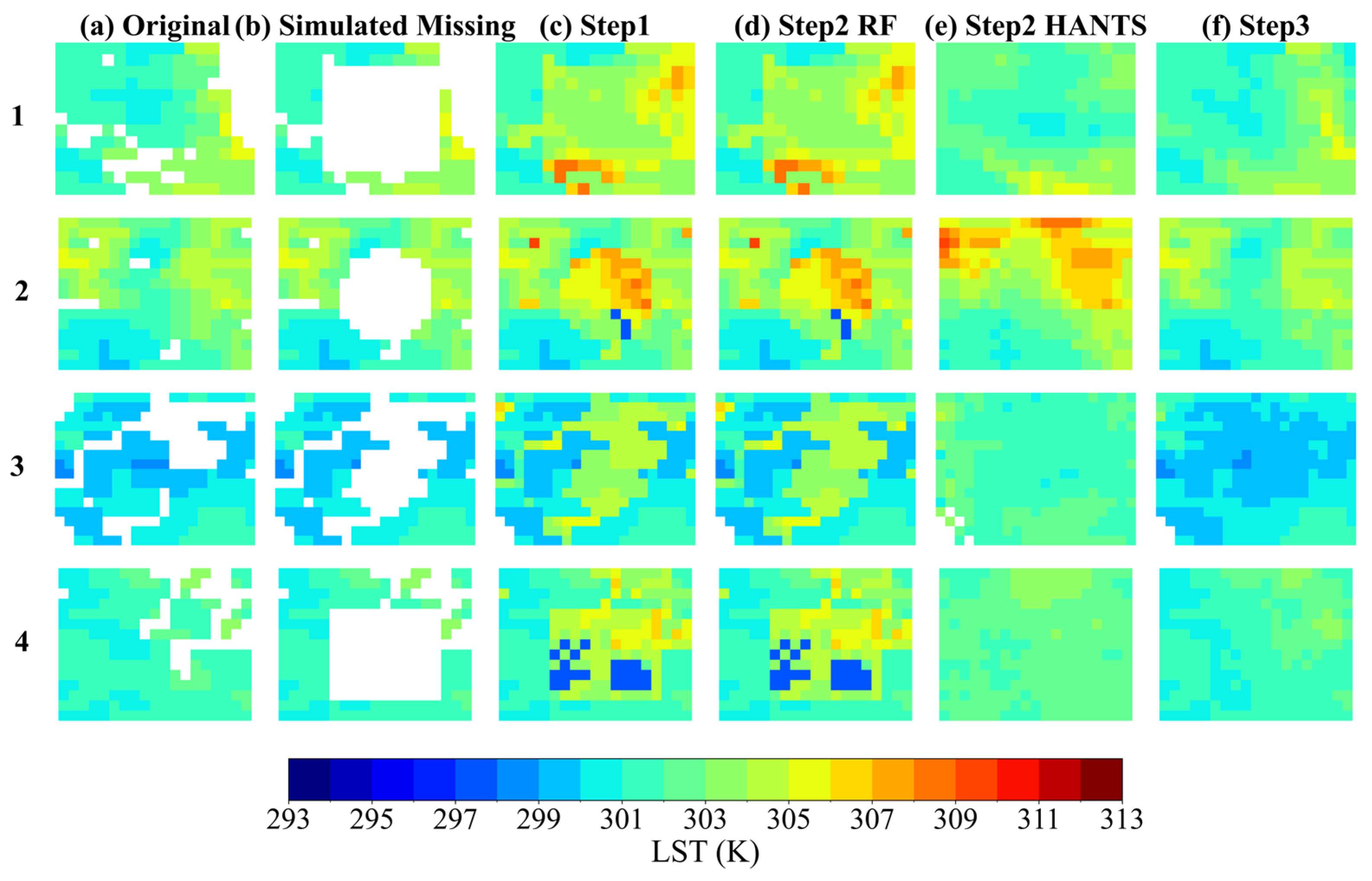
Figure 10.
Zoomed-in views of the first to fourth simulated missing areas in the Huainan region (day, 12 August 2018).
Figure 10.
Zoomed-in views of the first to fourth simulated missing areas in the Huainan region (day, 12 August 2018).
Figure 11.
Zoomed-in views of the first to fourth simulated missing areas in the Huainan region (night, 24 August 2018).
Figure 11.
Zoomed-in views of the first to fourth simulated missing areas in the Huainan region (night, 24 August 2018).
Figure 12.
Zoomed-in views of the first to third simulated missing areas in the Jining region (day, 26 August 2018).
Figure 12.
Zoomed-in views of the first to third simulated missing areas in the Jining region (day, 26 August 2018).
Figure 13.
Zoomed-in views of the first to third simulated missing areas in the Jining region (night, (25 August 2018).
Figure 13.
Zoomed-in views of the first to third simulated missing areas in the Jining region (night, (25 August 2018).
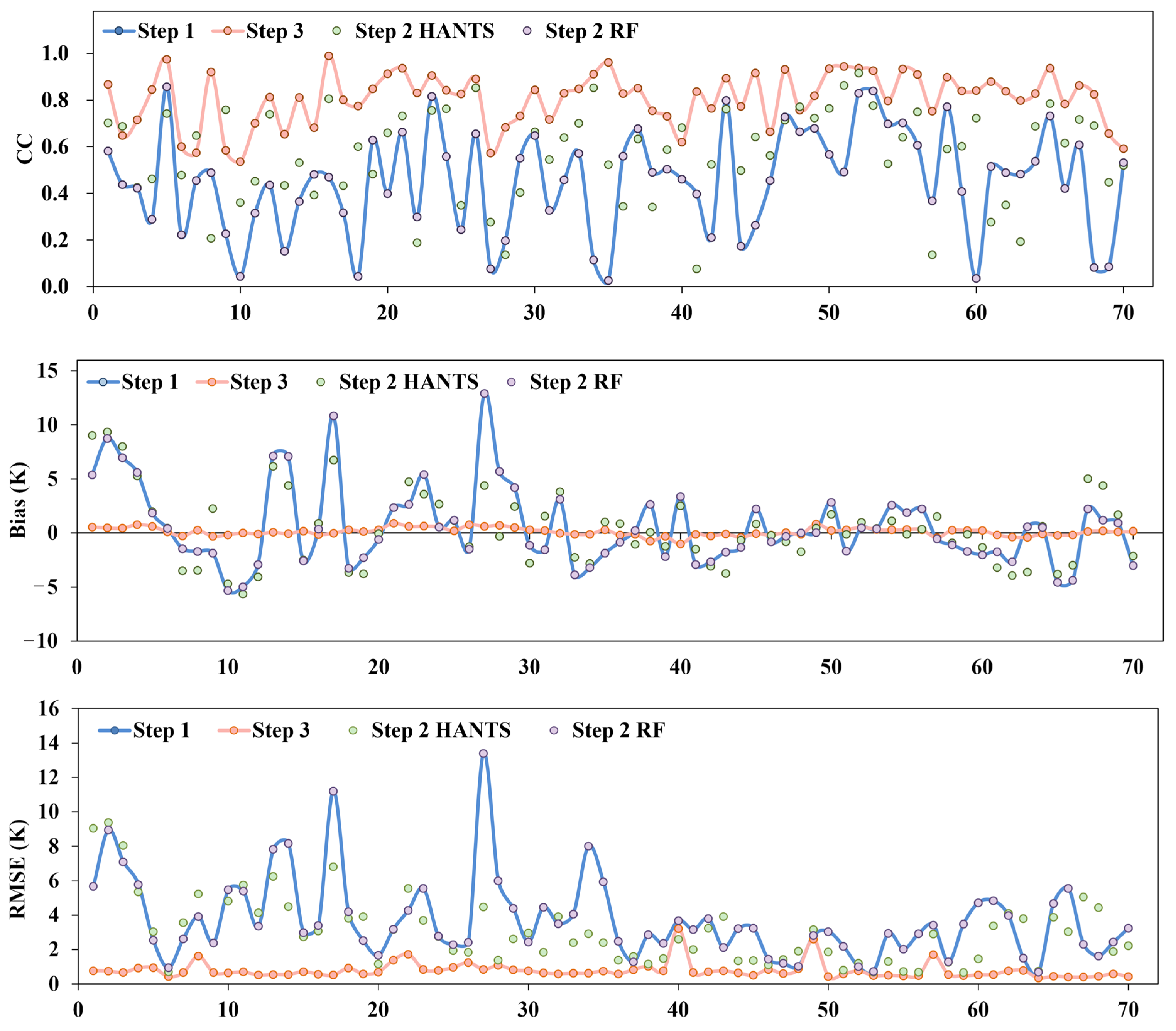
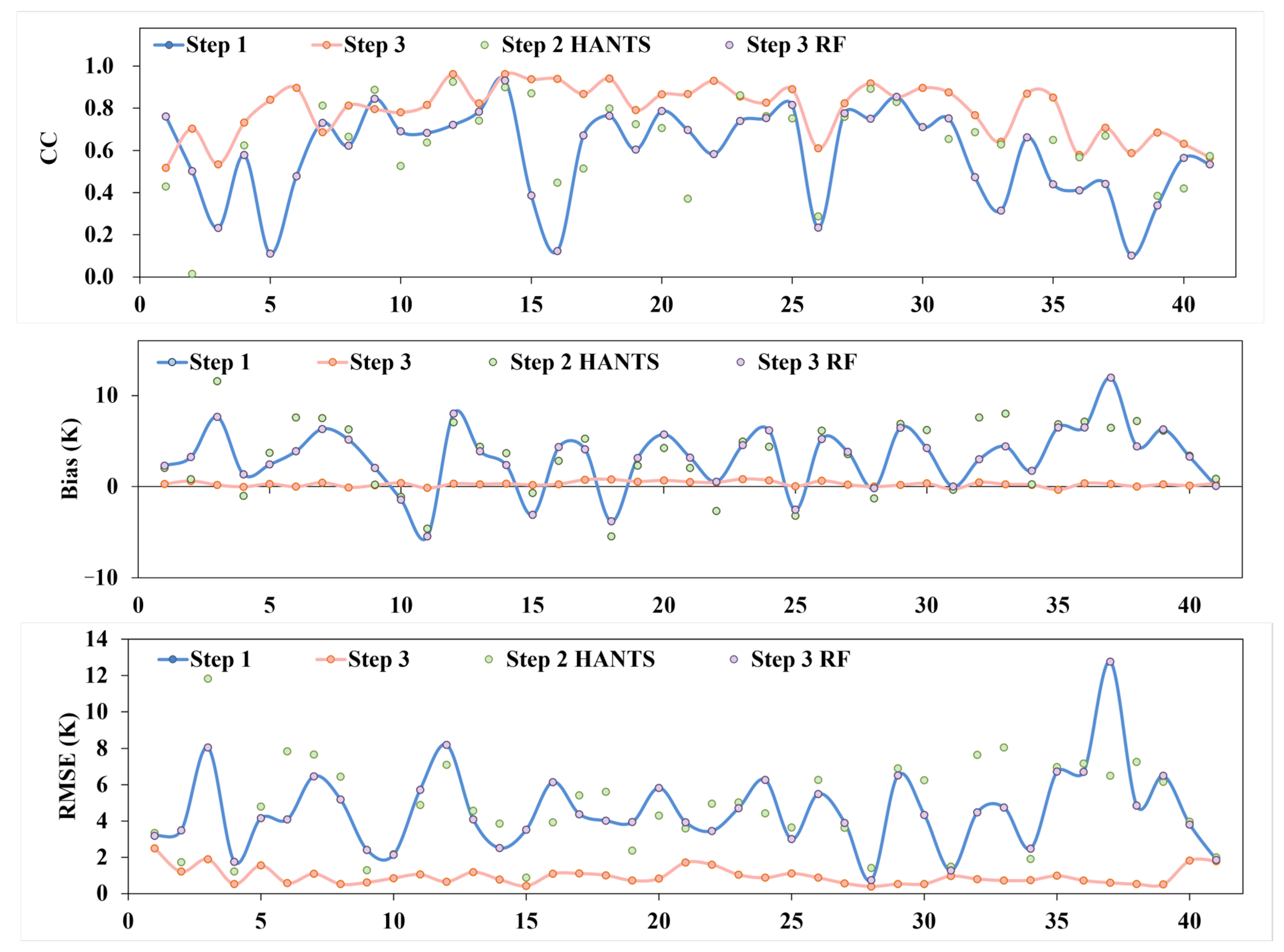
Figure 14.
Temporal comparison of CC, Bias, and RMSE across 71 daytime LST images in the Huainan region, reconstructed using Step 1, Step 2 RF, Step 2 HANTS, and Step 3.
Figure 14.
Temporal comparison of CC, Bias, and RMSE across 71 daytime LST images in the Huainan region, reconstructed using Step 1, Step 2 RF, Step 2 HANTS, and Step 3.
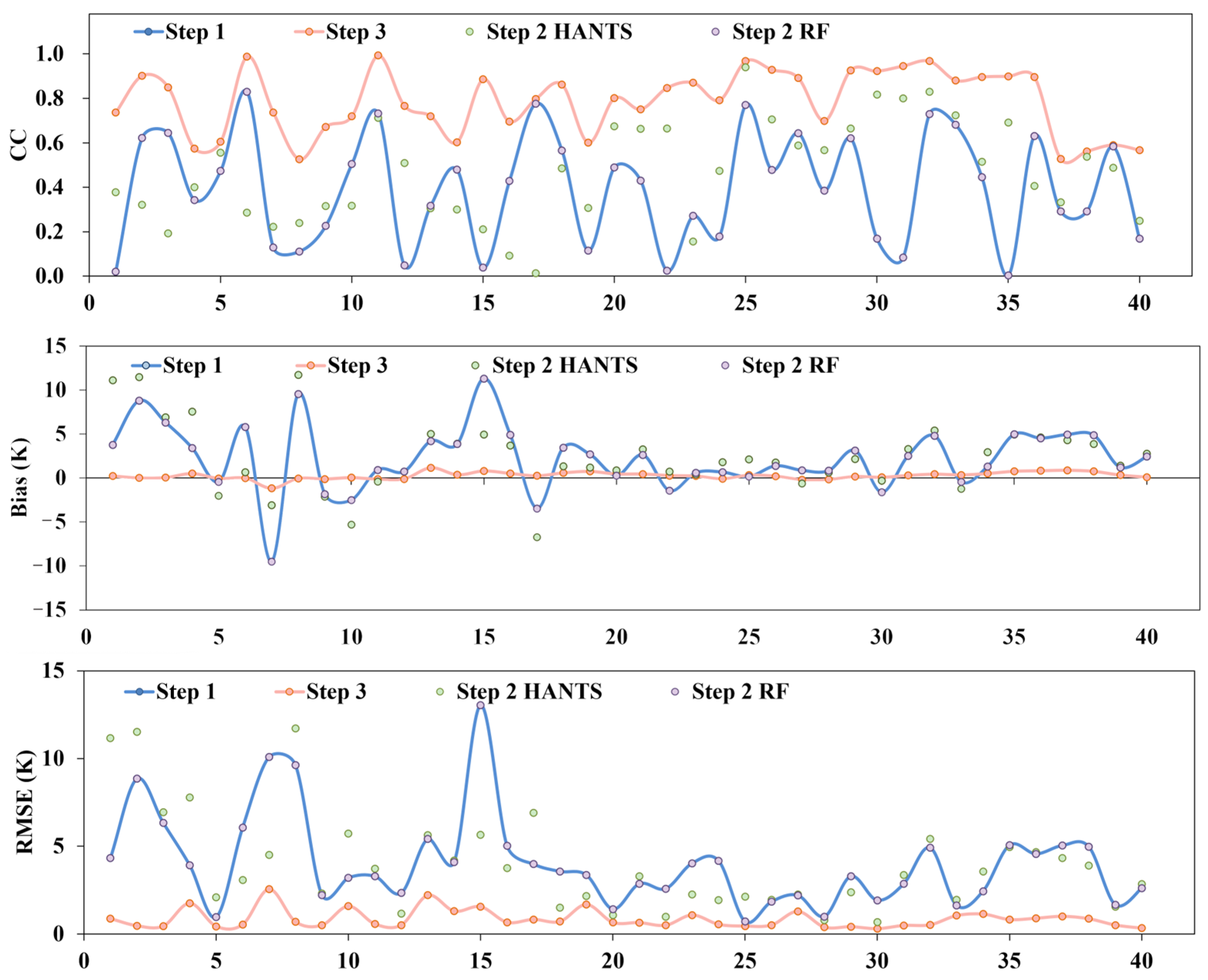
Figure 15.
Temporal comparison of CC, Bias, and RMSE across 40 nighttime LST images in the Huainan region, reconstructed using Step 1, Step 2 RF, Step 2 HANTS, and Step 3.
Figure 15.
Temporal comparison of CC, Bias, and RMSE across 40 nighttime LST images in the Huainan region, reconstructed using Step 1, Step 2 RF, Step 2 HANTS, and Step 3.
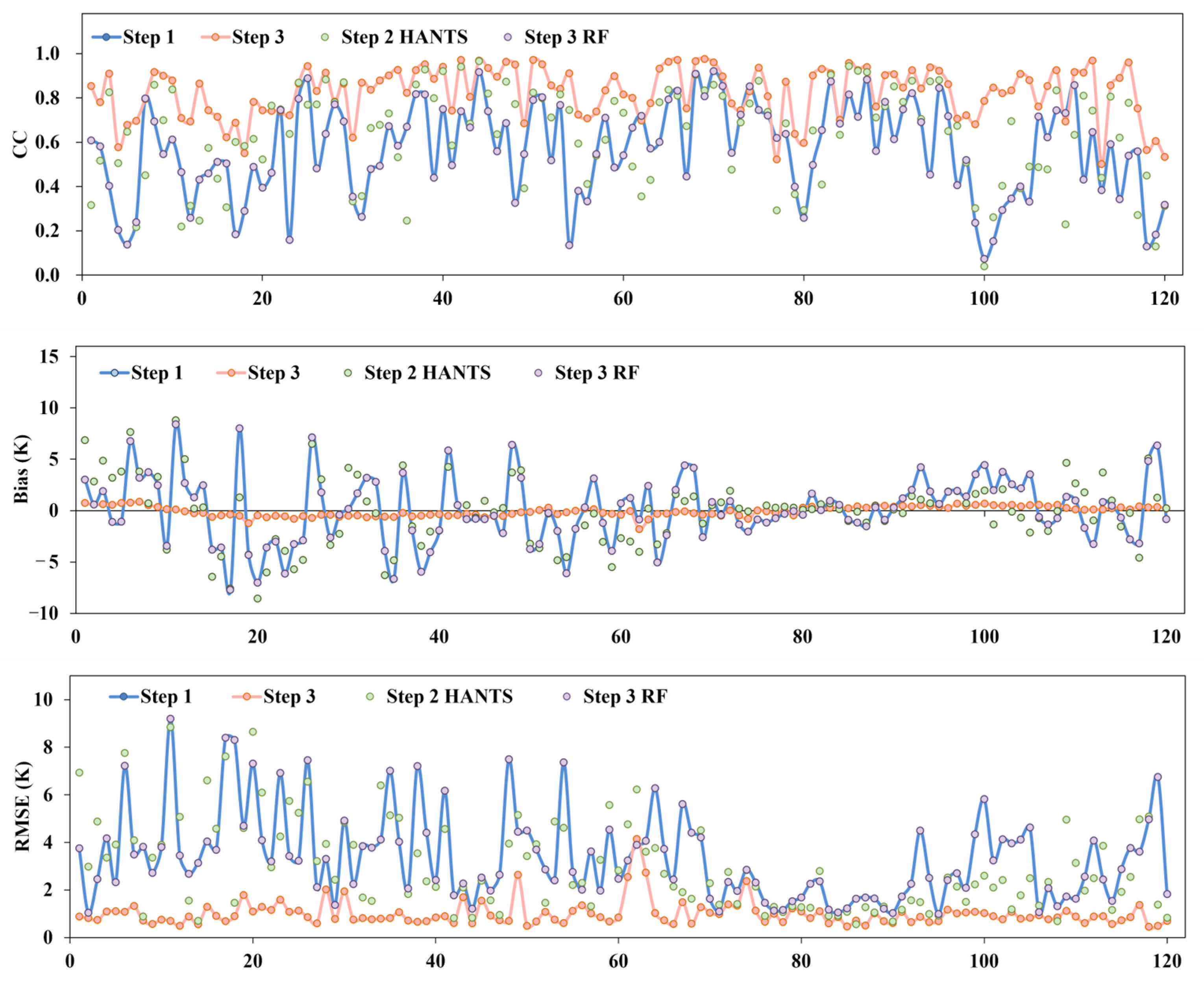
Figure 16.
Temporal comparison of CC, Bias, and RMSE across 121 daytime LST images in the Jining region, reconstructed using Step 1, Step 2 RF, Step 2 HANTS, and Step 3.
Figure 16.
Temporal comparison of CC, Bias, and RMSE across 121 daytime LST images in the Jining region, reconstructed using Step 1, Step 2 RF, Step 2 HANTS, and Step 3.
Figure 17.
Temporal comparison of CC, Bias, and RMSE across 41 nighttime LST images in the Jining region, reconstructed using Step 1, Step 2 RF, Step 2 HANTS, and Step 3.
Figure 17.
Temporal comparison of CC, Bias, and RMSE across 41 nighttime LST images in the Jining region, reconstructed using Step 1, Step 2 RF, Step 2 HANTS, and Step 3.
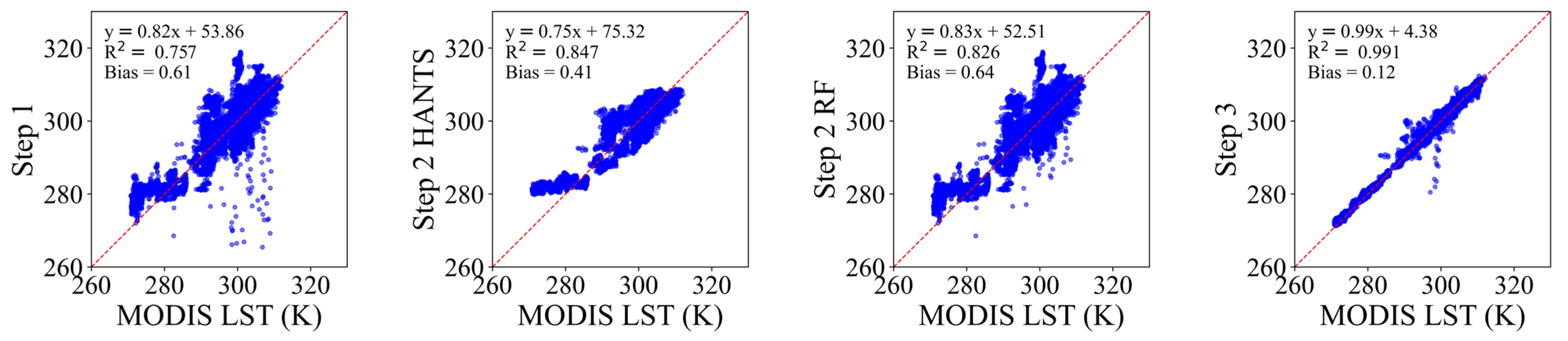
Figure 18.
Scatter plot comparisons between reconstructed and original values of all simulated missing pixels across 71 selected daytime images in the Huainan region (Day). Results are shown for Step 1-reconstructed daily LST, Step 2 HANTS-reconstructed daily LST, Step 2 RF-reconstructed daily LST, and Step 3-reconstructed daily LST. (Note: R denotes the correlation coefficient, i.e., CC).
Figure 18.
Scatter plot comparisons between reconstructed and original values of all simulated missing pixels across 71 selected daytime images in the Huainan region (Day). Results are shown for Step 1-reconstructed daily LST, Step 2 HANTS-reconstructed daily LST, Step 2 RF-reconstructed daily LST, and Step 3-reconstructed daily LST. (Note: R denotes the correlation coefficient, i.e., CC).
Figure 19.
Scatter plot comparisons between reconstructed and original values of all simulated missing pixels across 121 selected daytime images in the Jining region (Day). Results are shown for Step 1-reconstructed daily LST, Step 2 HANTS-reconstructed daily LST, Step 2 RF-reconstructed daily LST, and Step 3-reconstructed daily LST. (Note: R denotes the correlation coefficient, i.e., CC).
Figure 19.
Scatter plot comparisons between reconstructed and original values of all simulated missing pixels across 121 selected daytime images in the Jining region (Day). Results are shown for Step 1-reconstructed daily LST, Step 2 HANTS-reconstructed daily LST, Step 2 RF-reconstructed daily LST, and Step 3-reconstructed daily LST. (Note: R denotes the correlation coefficient, i.e., CC).
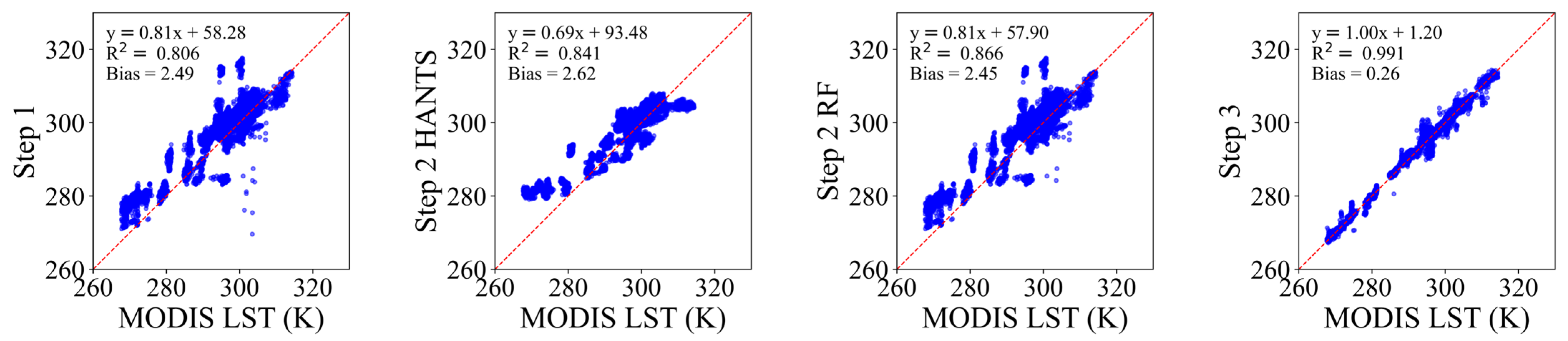
Figure 20.
Scatter plot comparisons between reconstructed and original values of all simulated missing pixels across 40 selected nighttime images in the Huainan region (Night). Results are shown for Step 1-reconstructed daily LST, Step 2 HANTS-reconstructed daily LST, Step 2 RF-reconstructed daily LST, and Step 3-reconstructed daily LST.
Figure 20.
Scatter plot comparisons between reconstructed and original values of all simulated missing pixels across 40 selected nighttime images in the Huainan region (Night). Results are shown for Step 1-reconstructed daily LST, Step 2 HANTS-reconstructed daily LST, Step 2 RF-reconstructed daily LST, and Step 3-reconstructed daily LST.
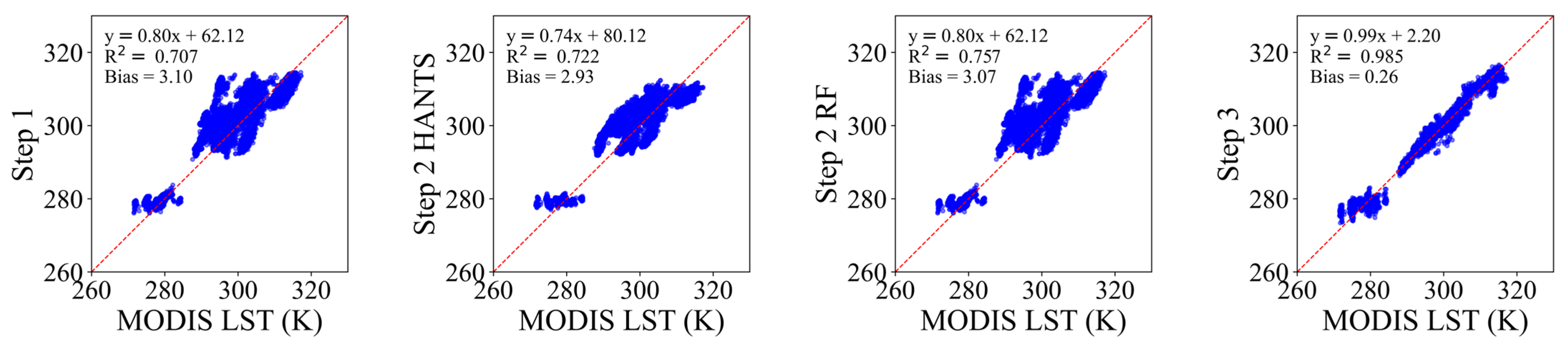
Figure 21.
Scatter plot comparisons between reconstructed and original values of all simulated missing pixels across 41 selected nighttime images in the Jining region (Night). Results are shown for Step 1-reconstructed daily LST, Step 2 HANTS-reconstructed daily LST, Step 2 RF-reconstructed daily LST, and Step 3-reconstructed daily LST.
Figure 21.
Scatter plot comparisons between reconstructed and original values of all simulated missing pixels across 41 selected nighttime images in the Jining region (Night). Results are shown for Step 1-reconstructed daily LST, Step 2 HANTS-reconstructed daily LST, Step 2 RF-reconstructed daily LST, and Step 3-reconstructed daily LST.
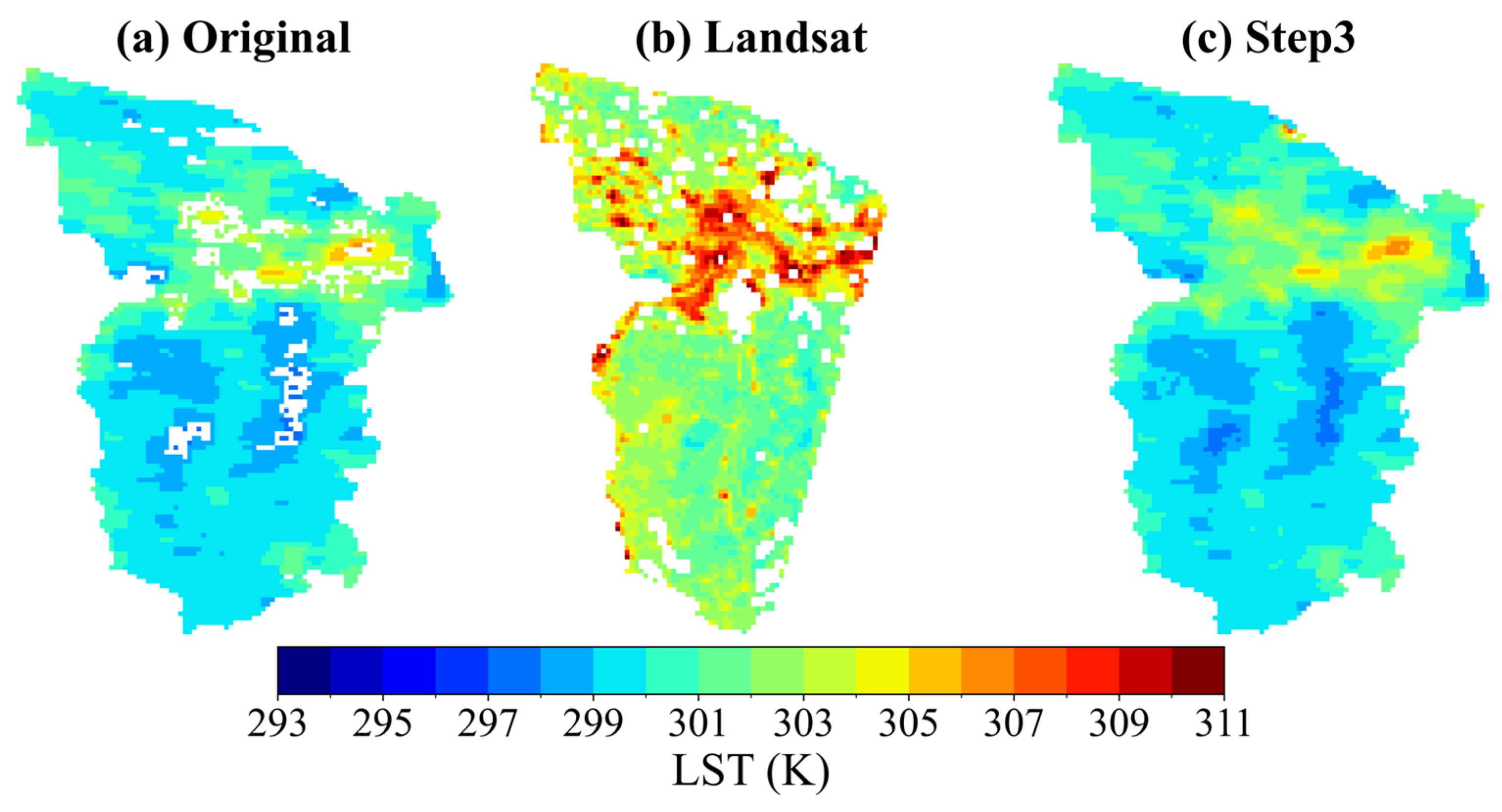
Figure 22.
Spatial comparison between reconstructed daily LST and original MODIS daily LST with Landsat LST for 8 September 2018, in the Huainan region. (a) Original daily LST; (b) Landsat daily LST; (c) Step 3-reconstructed daily LST.
Figure 22.
Spatial comparison between reconstructed daily LST and original MODIS daily LST with Landsat LST for 8 September 2018, in the Huainan region. (a) Original daily LST; (b) Landsat daily LST; (c) Step 3-reconstructed daily LST.
Figure 23.
Spatial comparison between reconstructed daily LST and original MODIS daily LST with Landsat LST for 23 August 2018, in the Jining region. (a) Original daily LST; (b) Landsat daily LST; (c) Step 3-reconstructed daily LST.
Figure 23.
Spatial comparison between reconstructed daily LST and original MODIS daily LST with Landsat LST for 23 August 2018, in the Jining region. (a) Original daily LST; (b) Landsat daily LST; (c) Step 3-reconstructed daily LST.
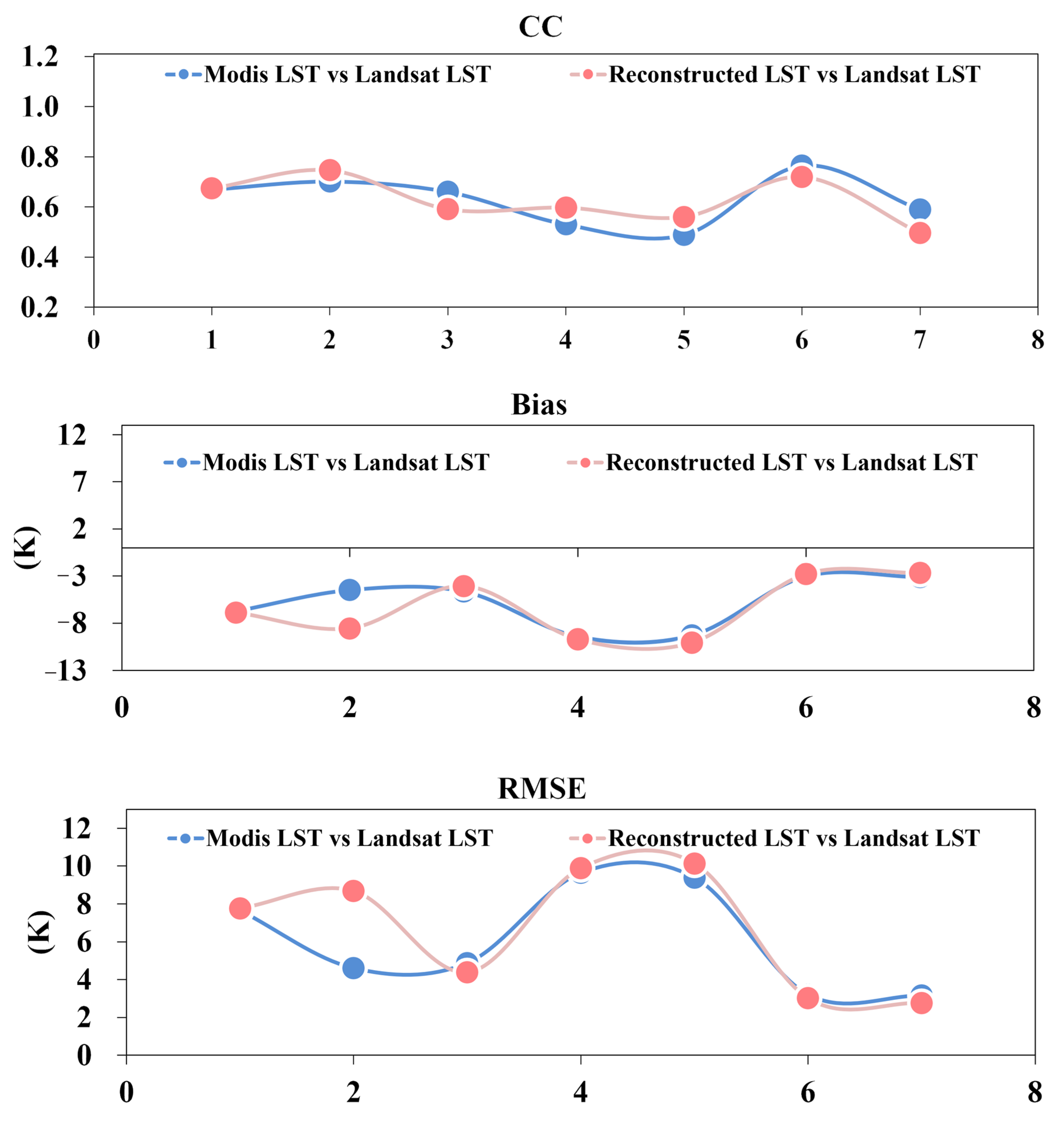
Figure 24.
Comparison curves of three evaluation metrics (CC, Bias, and RMSE) for seven selected daytime images in the Huainan region. Results are shown for both original MODIS LST vs. Landsat LST and Step 3-reconstructed LST vs. Landsat LST.
Figure 24.
Comparison curves of three evaluation metrics (CC, Bias, and RMSE) for seven selected daytime images in the Huainan region. Results are shown for both original MODIS LST vs. Landsat LST and Step 3-reconstructed LST vs. Landsat LST.
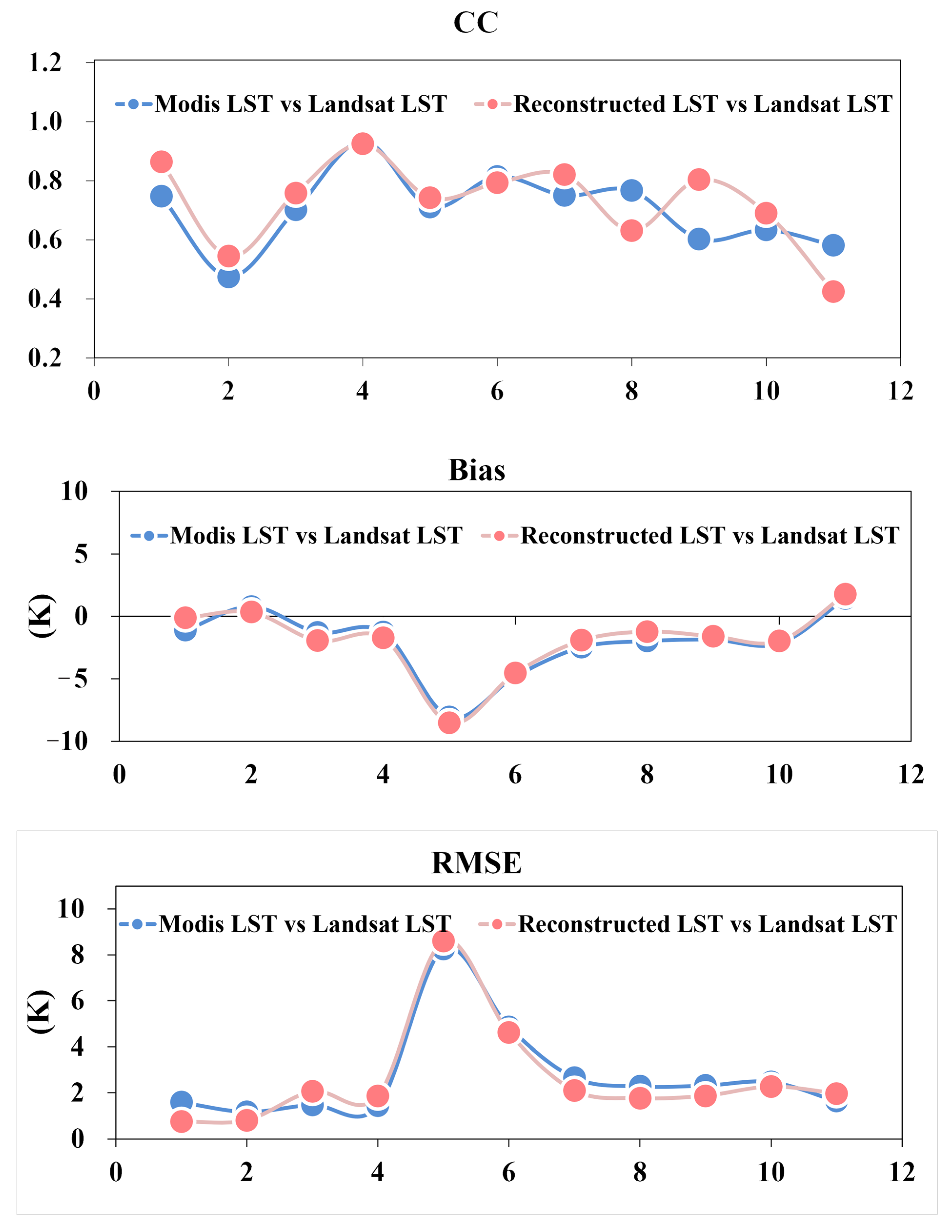
Figure 25.
Comparison curves of three evaluation metrics (CC, Bias, and RMSE) for seven selected daytime images in the Jining region. Results are shown for both original MODIS LST vs. Landsat LST and Step 3 reconstructed LST vs. Landsat LST.
Figure 25.
Comparison curves of three evaluation metrics (CC, Bias, and RMSE) for seven selected daytime images in the Jining region. Results are shown for both original MODIS LST vs. Landsat LST and Step 3 reconstructed LST vs. Landsat LST.
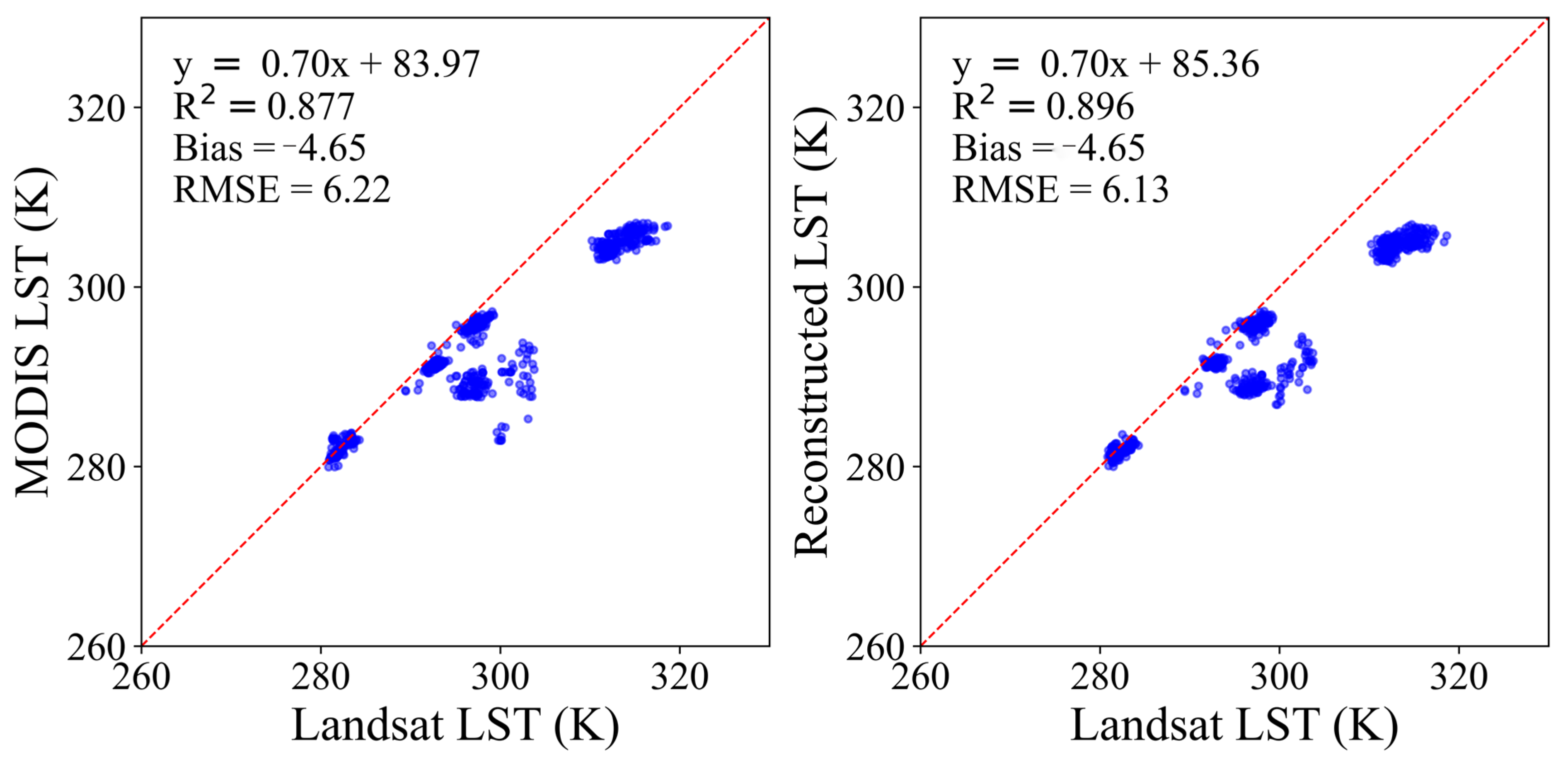
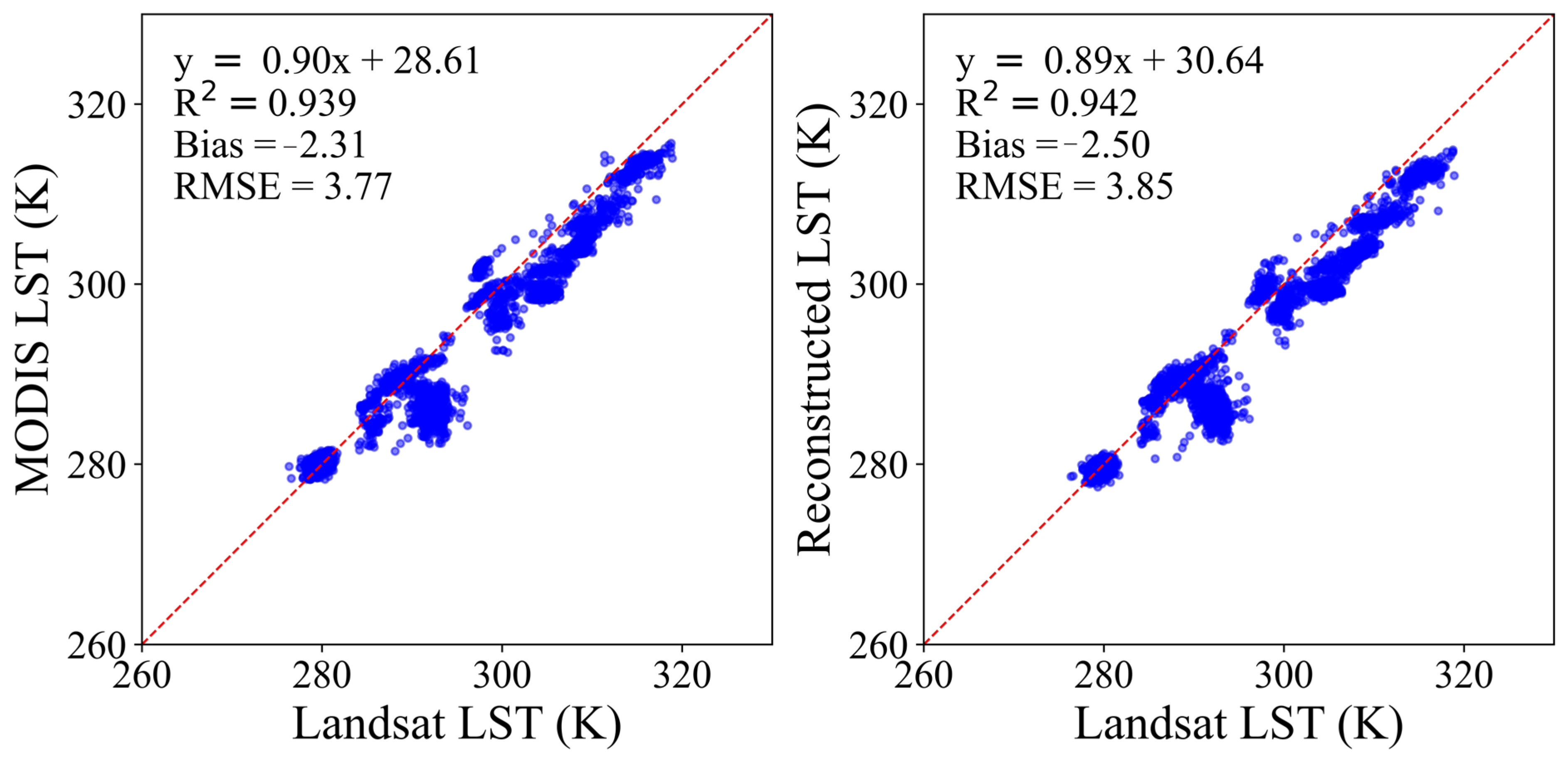
Figure 26.
Scatter plot comparisons between reconstructed and original MODIS LST values and Landsat LST for all simulated missing pixels across seven selected images in the Huainan region.
Figure 26.
Scatter plot comparisons between reconstructed and original MODIS LST values and Landsat LST for all simulated missing pixels across seven selected images in the Huainan region.
Figure 27.
Scatter plot comparisons between reconstructed and original MODIS LST values and Landsat LST for all simulated missing pixels across eleven selected images in the Jining region.
Figure 27.
Scatter plot comparisons between reconstructed and original MODIS LST values and Landsat LST for all simulated missing pixels across eleven selected images in the Jining region.
Table 1.
Data sources.
| Data Source | Temporal Resolution | Spatial Resolution | Time Range | Data Type/Usage |
|---|
| MOD11A1 | Daily | 1 km | 2016–2024 | Land Surface Temperature (day/night), with QC flag |
| MOD09GA | Daily | 50 0m | 2016–2024 | Surface Reflectance (Bands 1–7), with QC flag |
| Landsat LST | 16d | 100 m | 2016–2024 | High-resolution LST for validation |
| CLCD LCC | Year | 30 m | 2016–2024 | Land Cover Classification |
| SRTM DEM | - | 30 m | - | Digital Elevation Model for topographic factors |
Table 2.
Parameter settings of the HANTS algorithm.
Table 2.
Parameter settings of the HANTS algorithm.
| Parameters | Description | Values |
|---|
| NOF | Number of frequencies | 3 |
| SF | The suppression flag indicating whether high or
low values should be rejected during curve fitting | low |
| low | Low threshold | 250 |
| high | High threshold | 325 |
| FET | Fit error tolerance | 6 |
Table 3.
Evaluation metrics for reconstructed daytime LST (12 and 26 August 2018).
Table 3.
Evaluation metrics for reconstructed daytime LST (12 and 26 August 2018).
| Day | HN (12 August 2018) | JN (26 August 2018) |
|---|
| CC | Bias | RMSE | CC | Bias | RMSE |
|---|
| Step 1 | 0.727 | −0.295 | 1.195 | 0.715 | −1.154 | 1.634 |
| Step 2 HANTS | 0.713 | −0.814 | 1.417 | 0.922 | −0.113 | 0.561 |
| Step 2 RF | 0.721 | −0.283 | 1.094 | 0.720 | −1.134 | 1.600 |
| Step 3 | 0.932 | 0.049 | 0.599 | 0.925 | 0.426 | 0.718 |
Table 4.
Evaluation metrics for reconstructed nighttime LST (24 and 25 August 2018).
Table 4.
Evaluation metrics for reconstructed nighttime LST (24 and 25 August 2018).
| Night | HN (24 August 2018) | JN (25 August 2018) |
|---|
| CC | Bias | RMSE | CC | Bias | RMSE |
|---|
| Step 1 | 0.620 | 3.111 | 3.282 | 0.776 | 3.806 | 3.898 |
| Step 2 HANTS | 0.664 | 2.150 | 2.380 | 0.759 | 3.580 | 3.630 |
| Step 2 RF | 0.645 | 3.001 | 2.958 | 0.785 | 3.704 | 3.248 |
| Step 3 | 0.926 | 0.150 | 0.408 | 0.823 | 0.206 | 0.564 |
Table 5.
Statistical evaluation of reconstruction accuracy for missing pixels in selected daytime LST images.
Table 5.
Statistical evaluation of reconstruction accuracy for missing pixels in selected daytime LST images.
| Day | HN (71 Images) | JN (121 Images) |
|---|
| CC | Bias (K) | RMSE (K) | CC | Bias (K) | RMSE (K) |
|---|
| Step 1 | 0.900 | 0.714 | 4.448 | 0.886 | 2.310 | 5.003 |
| Step 2 HANTS | 0.937 | 0.901 | 3.967 | 0.901 | 2.584 | 5.088 |
| Step 2 RF | 0.902 | 0.701 | 4.389 | 0.887 | 2.270 | 5.053 |
| Step 3 | 0.996 | 0.147 | 0.861 | 0.995 | 0.251 | 1.021 |
Table 6.
Overall quantitative evaluation of missing pixel reconstruction in selected nighttime images.
Table 6.
Overall quantitative evaluation of missing pixel reconstruction in selected nighttime images.
| Night | HN (40 Images) | JN (41 Images) |
|---|
| CC | Bias (K) | RMSE (K) | CC | Bias (K) | RMSE (K) |
|---|
| Step 1 | 0.886 | 2.310 | 5.003 | 0.908 | 3.023 | 5.194 |
| Step 2 HANTS | 0.901 | 2.584 | 5.088 | 0.908 | 3.206 | 5.327 |
| Step 2 RF | 0.898 | 2.230 | 4.998 | 0.907 | 3.018 | 5.104 |
| Step 3 | 0.995 | 0.251 | 1.021 | 0.994 | 0.274 | 1.155 |
Table 7.
Quantitative evaluation of MODIS and reconstructed LST against Landsat reference for two selected images.
Table 7.
Quantitative evaluation of MODIS and reconstructed LST against Landsat reference for two selected images.
| * vs. Landsat | HN (8 September 2018) | JN (23 September 2018) |
|---|
| CC | Bias | RMSE | CC | Bias | RMSE |
|---|
| Modis | 0.765 | −3.015 | 3.203 | 0.720 | −2.792 | 3.013 |
| Reconstructed | 0.751 | −2.465 | 2.657 | 0.822 | −1.920 | 2.100 |
Table 8.
Overall quantitative evaluation of missing pixel reconstruction in selected images (36 images in Huainan and 64 in Jining during 2018, with 7 and 11 matched with Landsat, respectively; ~50% match rate).
Table 8.
Overall quantitative evaluation of missing pixel reconstruction in selected images (36 images in Huainan and 64 in Jining during 2018, with 7 and 11 matched with Landsat, respectively; ~50% match rate).
| * vs. Landsat | HN (7 Images) | JN (11 Images) |
|---|
| CC | Bias (K) | RMSE (K) | CC | Bias (K) | RMSE (K) |
|---|
| Modis | 0.867 | −5.988 | 7.159 | 0.981 | −1.828 | 3.052 |
| Reconstructed | 0.846 | −5.950 | 7.275 | 0.984 | −1.677 | 2.978 |