Assessing the Capability of Visible Near-Infrared Reflectance Spectroscopy to Monitor Soil Organic Carbon Changes with Localized Predictive Modeling
Abstract
Highlights
- A localized spectral modelling framework was developed to monitor SOC changes.
- Combining spectral and soil property similarities during local learning improved model performance.
- The developed approach could enable the detection of hotspots that underwent significant SOC loss and gain.
- Localized modelling with VNIR spectroscopy offers strong potential for tracking SOC changes.
Abstract
1. Introduction
2. Materials and Methods
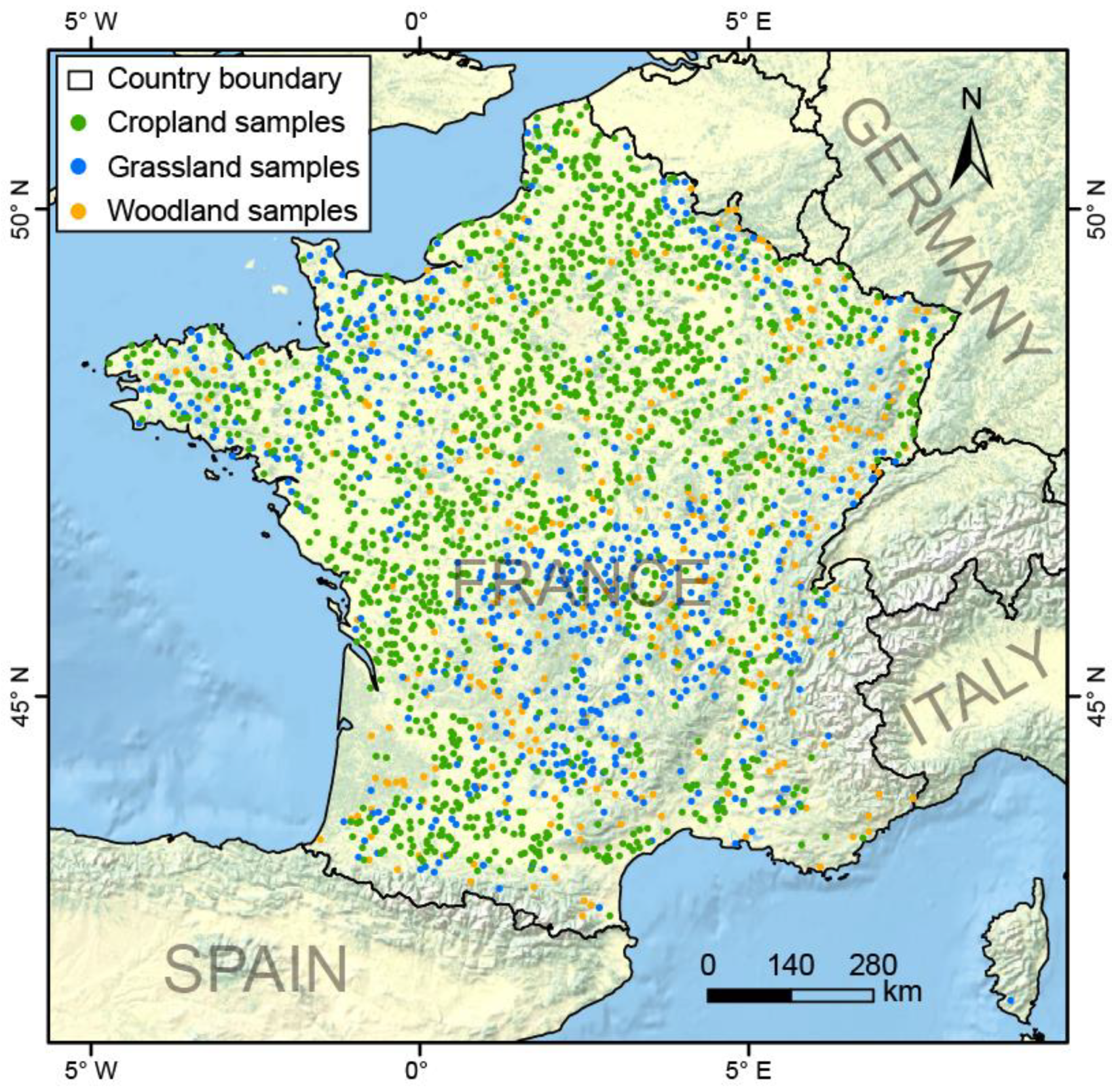
2.1. Test Dataset
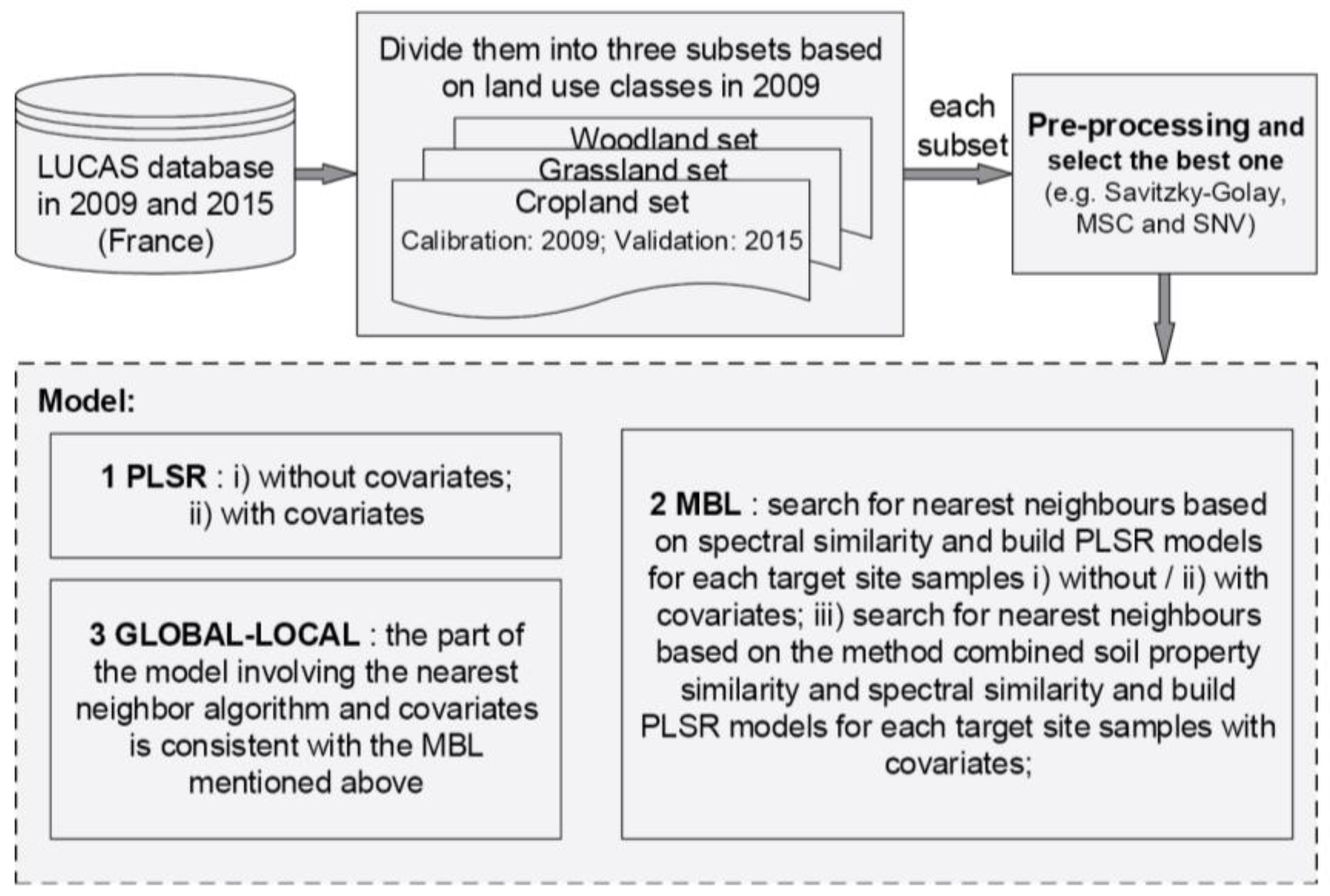
2.2. Spectral Modeling Methodology
2.2.1. Spectral Pre-Processing
2.2.2. MBL Model
2.2.3. GLOBAL-LOCAL Model
2.2.4. Performance Evaluation of Modeling Strategies
2.3. Detection of SOC Changes by Soil Spectroscopy
3. Results
3.1. Temporal Change in SOC Based on Measured Data
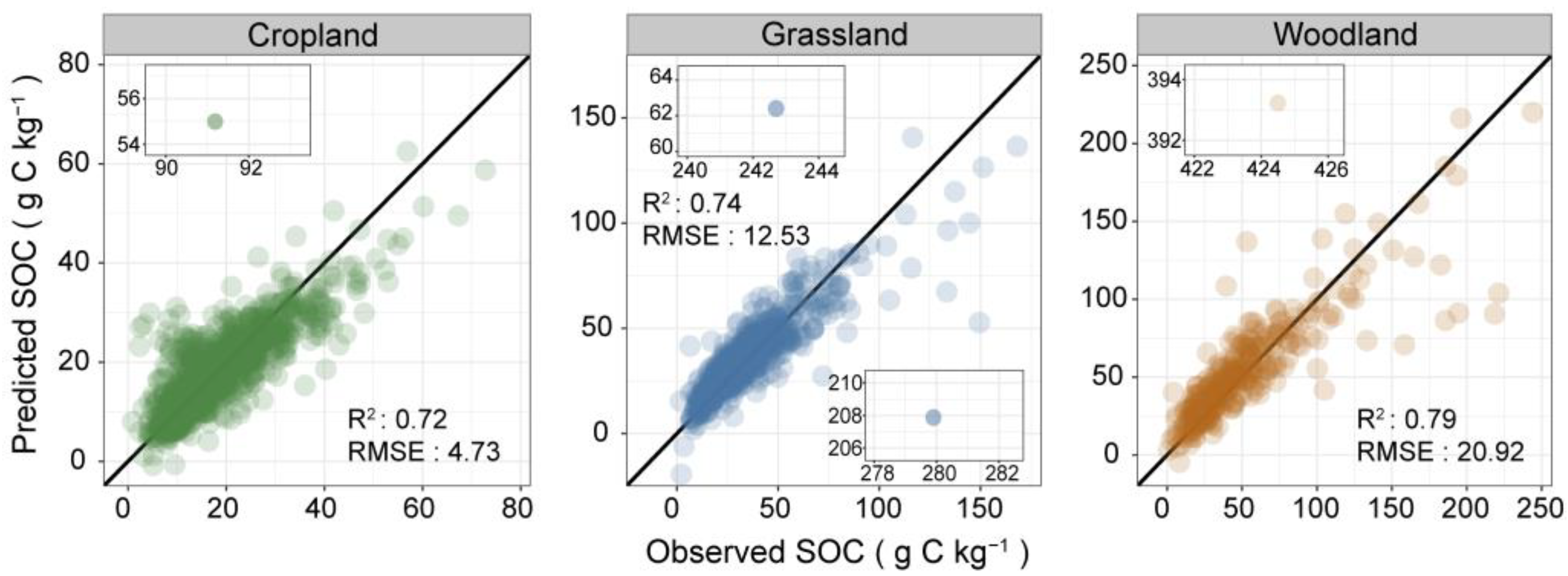
3.2. Performances of Different Modeling Strategies
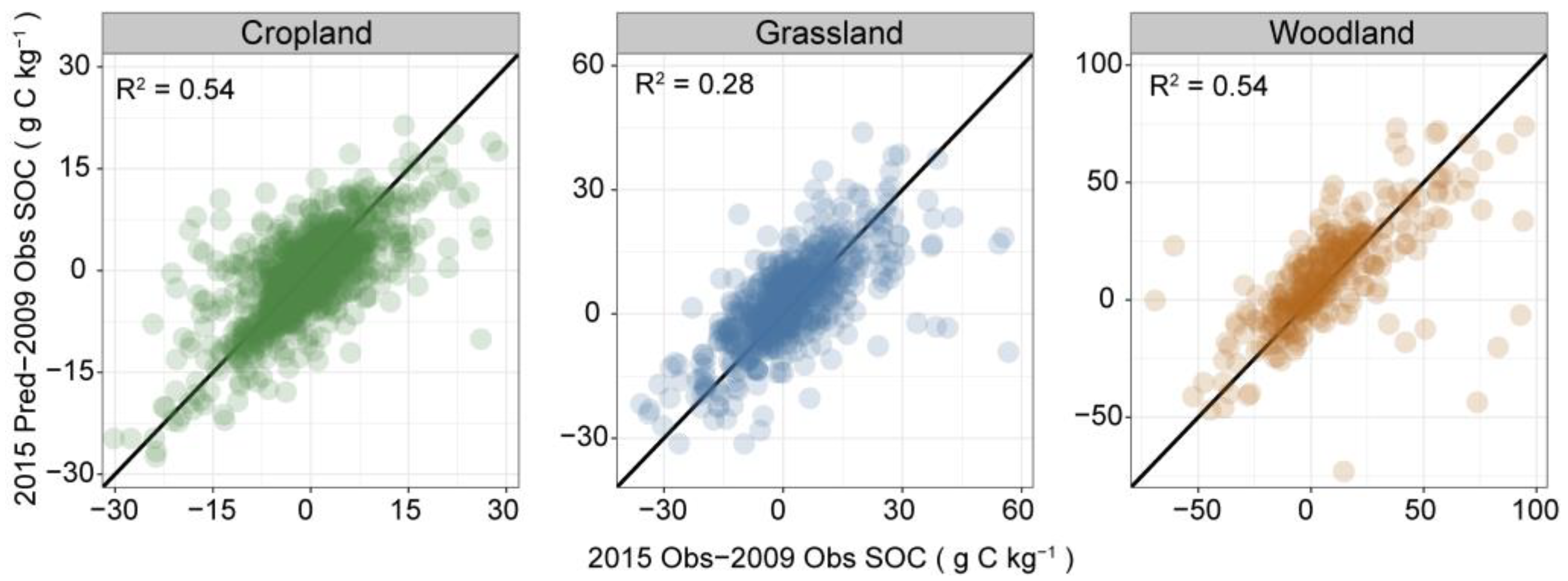
3.3. Evaluation on the Capability of Soil Spectroscopy to Detect SOC Changes
4. Discussion
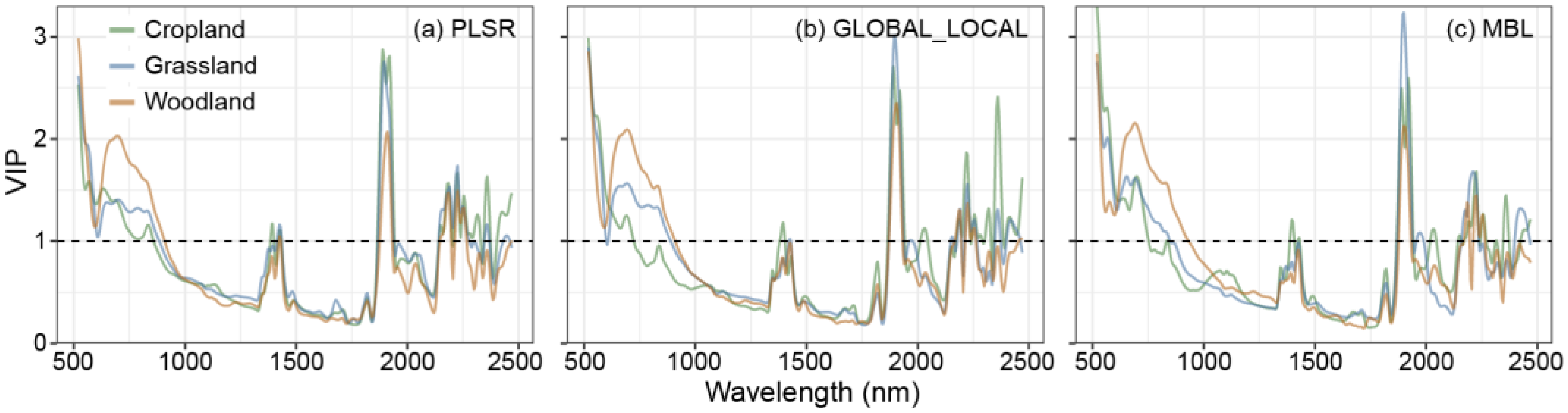
4.1. The Effectiveness of Local Modeling for SOC Spectral Prediction
4.2. The Ability of Soil Spectroscopy to Monitor SOC Changes
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Janzen, H.H. Carbon cycling in earth systems—A soil science perspective. Agric. Ecosyst. Environ. 2004, 104, 399–417. [Google Scholar] [CrossRef]
- Lal, R. Soil carbon sequestration to mitigate climate change. Geoderma 2004, 123, 1–22. [Google Scholar] [CrossRef]
- Lorenz, K.; Lal, R.; Ehlers, K. Soil organic carbon stock as an indicator for monitoring land and soil degradation in relation to United Nations’ Sustainable Development Goals. Land Degrad. Dev. 2019, 30, 824–838. [Google Scholar] [CrossRef]
- Urbina-Salazar, D.; Vaudour, E.; Richer-de-Forges, A.C.; Chen, S.; Martelet, G.; Baghdadi, N.; Arrouays, D. Sentinel-2 and Sentinel-1 Bare Soil Temporal Mosaics of 6-Year Periods for Soil Organic Carbon Content Mapping in Central France. Remote Sens. 2023, 15, 2410. [Google Scholar] [CrossRef]
- Paustian, K.; Lehmann, J.; Ogle, S.; Reay, D.; Robertson, G.P.; Smith, P. Climate-smart soils. Nature 2016, 532, 49–57. [Google Scholar] [CrossRef] [PubMed]
- Moinet, G.Y.K.; Hijbeek, R.; van Vuuren, D.P.; Giller, K.E. Carbon for soils, not soils for carbon. Glob. Change Biol. 2023, 29, 2384–2398. [Google Scholar] [CrossRef]
- Minasny, B.; Malone, B.P.; McBratney, A.B.; Angers, D.A.; Arrouays, D.; Chambers, A.; Chaplot, V.; Chen, Z.-S.; Cheng, K.; Das, B.S.; et al. Soil carbon 4 per mille. Geoderma 2017, 292, 59–86. [Google Scholar] [CrossRef]
- Smith, P.; Soussana, J.-F.; Angers, D.; Schipper, L.; Chenu, C.; Rasse, D.P.; Batjes, N.H.; van Egmond, F.; McNeill, S.; Kuhnert, M.; et al. How to measure, report and verify soil carbon change to realize the potential of soil carbon sequestration for atmospheric greenhouse gas removal. Glob. Change Biol. 2020, 26, 219–241. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Behrens, T.; Ben-Dor, E.; Brown, D.J.; Dematte, J.A.M.; Shepherd, K.D.; Shi, Z.; Stenberg, B.; Stevens, A.; Adamchuk, V.; et al. A global spectral library to characterize the world’s soil. Earth-Sci. Rev. 2016, 155, 198–230. [Google Scholar] [CrossRef]
- Nocita, M.; Stevens, A.; van Wesemael, B.; Brown, D.J.; Shepherd, K.D.; Towett, E.; Vargas, R.; Montanarella, L. Soil spectroscopy: An opportunity to be seized. Glob. Change Biol. 2015, 21, 10–11. [Google Scholar] [CrossRef]
- Kalopesa, E.; Tziolas, N.; Tsakiridis, N.L.; Safanelli, J.L.; Hengl, T.; Sanderman, J. Large-Scale Soil Organic Carbon Estimation via a Multisource Data Fusion Approach. Remote Sens. 2025, 17, 771. [Google Scholar] [CrossRef]
- Li, S.; Shen, X.; Shen, X.; Cheng, J.; Xu, D.; Makar, R.S.; Guo, Y.; Hu, B.; Chen, S.; Hong, Y.; et al. Improving the Accuracy of Soil Classification by Using Vis–NIR, MIR, and Their Spectra Fusion. Remote Sens. 2025, 17, 1524. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Inbar, Y.; Chen, Y. The reflectance spectra of organic matter in the visible near-infrared and short wave infrared region (400–2500 nm) during a controlled decomposition process. Remote Sens. Environ. 1997, 61, 1–15. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Shen, Z.; Ramirez Lopez, L.; Behrens, T.; Shi, Z.; Wetterlind, J.; Sudduth, K.A.; Stenberg, B.; Guerrero, C.; Gholizadeh, A.; et al. An imperative for soil spectroscopic modelling is to think global but fit local with transfer learning. Earth-Sci. Rev. 2024, 254, 104797. [Google Scholar] [CrossRef]
- Deng, F.; Minasny, B.; Knadel, M.; McBratney, A.; Heckrath, G.; Greve, M.H. Using Vis-NIR Spectroscopy for Monitoring Temporal Changes in Soil Organic Carbon. Soil Sci. 2013, 178, 389–399. [Google Scholar] [CrossRef]
- Guerrero, C.; Lorenzetti, R. Use of composite samples and NIR spectroscopy to detect changes in SOC contents. Geoderma 2021, 396, 115069. [Google Scholar] [CrossRef]
- Orgiazzi, A.; Ballabio, C.; Panagos, P.; Jones, A.; Fernández-Ugalde, O. LUCAS Soil, the largest expandable soil dataset for Europe: A review. Eur. J. Soil Sci. 2018, 69, 140–153. [Google Scholar] [CrossRef]
- Shen, Z.; Ramirez-Lopez, L.; Behrens, T.; Cui, L.; Zhang, M.; Walden, L.; Wetterlind, J.; Shi, Z.; Sudduth, K.A.; Baumann, P.; et al. Deep transfer learning of global spectra for local soil carbon monitoring. ISPRS J. Photogramm. Remote Sens. 2022, 188, 190–200. [Google Scholar] [CrossRef]
- Gruszczyński, S.; Gruszczyński, W. Supporting soil and land assessment with machine learning models using the Vis-NIR spectral response. Geoderma 2022, 405, 115451. [Google Scholar] [CrossRef]
- St. Luce, M.; Ziadi, N.; Viscarra Rossel, R.A. GLOBAL-LOCAL: A new approach for local predictions of soil organic carbon content using large soil spectral libraries. Geoderma 2022, 425, 116048. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, Q.L.; Peng, J.; Ji, W.J.; Liu, H.J.; Li, X.; Viscarra Rossel, R.A. Development of a national VNIR soil-spectral library for soil classification and prediction of organic matter concentrations. Sci. China Earth Sci. 2014, 57, 1671–1680. [Google Scholar] [CrossRef]
- Ramirez-Lopez, L.; Behrens, T.; Schmidt, K.; Stevens, A.; Dematte, J.A.M.; Scholten, T. The spectrum-based learner: A new local approach for modeling soil vis-NIR spectra of complex datasets. Geoderma 2013, 195, 268–279. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, S.; Lu, R.; Zhang, X.; Ma, Y.; Shi, Z. Non-linear memory-based learning for predicting soil properties using a regional vis-NIR spectral library. Geoderma 2024, 441, 116752. [Google Scholar] [CrossRef]
- Lobsey, C.R.; Viscarra Rossel, R.A.; Roudier, P.; Hedley, C.B. rs-local data-mines information from spectral libraries to improve local calibrations. Eur. J. Soil Sci. 2017, 68, 840–852. [Google Scholar] [CrossRef]
- Tziolas, N.; Tsakiridis, N.; Ben-Dor, E.; Theocharis, J.; Zalidis, G. A memory-based learning approach utilizing combined spectral sources and geographical proximity for improved VIS-NIR-SWIR soil properties estimation. Geoderma 2019, 340, 11–24. [Google Scholar] [CrossRef]
- Lamichhane, S.; Kumar, L.; Wilson, B. Digital soil mapping algorithms and covariates for soil organic carbon mapping and their implications: A review. Geoderma 2019, 352, 395–413. [Google Scholar] [CrossRef]
- Garosi, Y.; Ayoubi, S.; Nussbaum, M.; Sheklabadi, M. Effects of different sources and spatial resolutions of environmental covariates on predicting soil organic carbon using machine learning in a semi-arid region of Iran. Geoderma Reg. 2022, 29, e00513. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, F.; Wang, D.; Wu, H.; Zhang, G. Improving 3D Digital Soil Mapping Based on Spatialized Lab Soil Spectral Information. Remote Sens. 2023, 15, 5228. [Google Scholar] [CrossRef]
- Stevens, A.; Nocita, M.; Toth, G.; Montanarella, L.; van Wesemael, B. Prediction of Soil Organic Carbon at the European Scale by Visible and Near InfraRed Reflectance Spectroscopy. PLoS ONE 2013, 8, e66409. [Google Scholar] [CrossRef]
- Nocita, M.; Stevens, A.; Toth, G.; Panagos, P.; van Wesemael, B.; Montanarella, L. Prediction of soil organic carbon content by diffuse reflectance spectroscopy using a local partial least square regression approach. Soil Biol. Biochem. 2014, 68, 337–347. [Google Scholar] [CrossRef]
- Sun, Q.; Shi, P. Enhancing proximal and remote sensing of soil organic carbon: A local modelling approach guided by spectral and spatial similarities. Geoderma 2025, 457, 117298. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Peng, Y.; Ben-Dor, E.; Biswas, A.; Chabrillat, S.; Demattê, J.A.M.; Ge, Y.; Gholizadeh, A.; Gomez, C.; Guerrero, C.; Herrick, J.; et al. Spectroscopic solutions for generating new global soil information. Innovation 2025, 6, 100839. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Behrens, T.; Ben-Dor, E.; Chabrillat, S.; Demattê, J.A.M.; Ge, Y.; Gomez, C.; Guerrero, C.; Peng, Y.; Ramirez-Lopez, L.; et al. Diffuse reflectance spectroscopy for estimating soil properties: A technology for the 21st century. Eur. J. Soil Sci. 2022, 73, e13271. [Google Scholar] [CrossRef]
- Ramirez-Lopez, L.; Behrens, T.; Schmidt, K.; Rossel, R.A.V.; Demattê, J.A.M.; Scholten, T. Distance and similarity-search metrics for use with soil vis–NIR spectra. Geoderma 2013, 199, 43–53. [Google Scholar] [CrossRef]
- Sims, N.C.; Newnham, G.J.; England, J.R.; Guerschman, J.; Cox, S.J.D.; Roxburgh, S.H.; Viscarra Rossel, R.A.; Fritz, S.; Wheeler, I. Good Practice Guidance. SDG Indicator 15.3.1, Proportion of Land That Is Degraded over Total Land Area. Version 2.0; United Nations: New York, NY, USA, 2021. [Google Scholar]
- Ma, J.; Shi, P. Remotely sensed inter-field variation in soil organic carbon content as influenced by the cumulative effect of conservation tillage in northeast China. Soil Tillage Res. 2024, 243, 106170. [Google Scholar] [CrossRef]
- Baumann, P.; Helfenstein, A.; Gubler, A.; Keller, A.; Meuli, R.G.; Wächter, D.; Lee, J.; Viscarra Rossel, R.; Six, J. Developing the Swiss mid-infrared soil spectral library for local estimation and monitoring. SOIL 2021, 7, 525–546. [Google Scholar] [CrossRef]
- Safanelli, J.L.; Hengl, T.; Parente, L.L.; Minarik, R.; Bloom, D.E.; Todd-Brown, K.; Gholizadeh, A.; Mendes, W.d.S.; Sanderman, J. Open Soil Spectral Library (OSSL): Building reproducible soil calibration models through open development and community engagement. PLoS ONE 2025, 20, e0296545. [Google Scholar] [CrossRef] [PubMed]
- Shi, P.; Six, J.; Sila, A.; Vanlauwe, B.; Van Oost, K. Towards spatially continuous mapping of soil organic carbon in croplands using multitemporal Sentinel-2 remote sensing. ISPRS J. Photogramm. Remote Sens. 2022, 193, 187–199. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, Y.; Chen, S.; Wang, Y.; Hu, W.; Ye, S.; Song, X.; Liu, F.; Zhao, Y.; Demattê, J.A.M.; et al. Bridging the gap between laboratory VNIR-SWIR spectra and Landsat-8 bare soil composite image for soil organic carbon prediction. Remote Sens. Environ. 2025, 328, 114874. [Google Scholar] [CrossRef]
- Tziolas, N.; Tsakiridis, N.; Heiden, U.; van Wesemael, B. Soil organic carbon mapping utilizing convolutional neural networks and Earth observation data, a case study in Bavaria state Germany. Geoderma 2024, 444, 116867. [Google Scholar] [CrossRef]

| Land Use | Parameter | SOC Change in Percentage | ||
|---|---|---|---|---|
| ≥10% | ≤−10% | −10–10% | ||
| Cropland | Sample size | 430 | 534 | 489 |
| Mean SOC | 21.62 | 13.84 | 16.28 | |
| SD | 10.28 | 6.95 | 7.82 | |
| Grassland | Sample size | 284 | 219 | 168 |
| Mean SOC | 43.69 | 25.97 | 35.74 | |
| SD | 31.12 | 14.19 | 17.17 | |
| Woodland | Sample size | 164 | 100 | 40 |
| Mean SOC | 66.71 | 30.89 | 53.79 | |
| SD | 53.08 | 17.97 | 42.23 | |
| Land Use | Modeling Strategy | RMSE | R2 | RPD | RPIQ |
|---|---|---|---|---|---|
| Cropland | PLSR 1 | 5.67 | 0.60 | 1.58 | 1.78 |
| PLSR 2 | 5.10 | 0.67 | 1.75 | 1.98 | |
| MBL 1 | 5.35 | 0.64 | 1.67 | 1.89 | |
| MBL 2 | 4.87 | 0.70 | 1.83 | 2.07 | |
| MBL 3 | 4.73 | 0.72 | 1.89 | 2.14 | |
| GLOBAL_LOCAL 1 | 5.60 | 0.61 | 1.60 | 1.80 | |
| GLOBAL_LOCAL 2 | 5.10 | 0.67 | 1.75 | 1.98 | |
| GLOBAL_LOCAL 3 | 4.99 | 0.69 | 1.79 | 2.02 | |
| Grassland | PLSR 1 | 16.40 | 0.56 | 1.50 | 1.33 |
| PLSR 2 | 14.40 | 0.66 | 1.71 | 1.52 | |
| MBL 1 | 14.47 | 0.65 | 1.70 | 1.51 | |
| MBL 2 | 12.40 | 0.75 | 1.99 | 1.76 | |
| MBL 3 | 12.53 | 0.74 | 1.97 | 1.74 | |
| GLOBAL_LOCAL 1 | 15.39 | 0.61 | 1.60 | 1.42 | |
| GLOBAL_LOCAL 2 | 13.66 | 0.69 | 1.80 | 1.60 | |
| GLOBAL_LOCAL 3 | 13.55 | 0.70 | 1.82 | 1.61 | |
| Woodland | PLSR 1 | 24.49 | 0.71 | 1.87 | 1.51 |
| PLSR 2 | 22.07 | 0.77 | 2.08 | 1.67 | |
| MBL 1 | 27.78 | 0.63 | 1.65 | 1.33 | |
| MBL 2 | 21.70 | 0.78 | 2.11 | 1.70 | |
| MBL 3 | 20.92 | 0.79 | 2.19 | 1.77 | |
| GLOBAL_LOCAL 1 | 23.90 | 0.73 | 1.92 | 1.55 | |
| GLOBAL_LOCAL 2 | 21.65 | 0.78 | 2.12 | 1.71 | |
| GLOBAL_LOCAL 3 | 21.70 | 0.78 | 2.11 | 1.70 |
| 2009 Land Use Classes | Parameter | Percentage Variation | ||
|---|---|---|---|---|
| ≥10% | ≤−10% | −10–10% | ||
| Cropland | Size | 286 | 377 | 223 |
| Ratio of detection | 66.5% | 70.6% | 45.6% | |
| Grassland | Size | 234 | 121 | 62 |
| Ratio of detection | 82.4% | 55.3% | 36.9% | |
| Woodland | Size | 140 | 58 | 19 |
| Ratio of detection | 85.9% | 58.0% | 47.5% | |
| 2009 Land Use Classes | RMSE | R2 | RPD | RPIQ |
|---|---|---|---|---|
| Grassland | 9.88 | 0.75 | 1.98 | 2.19 |
| Woodland | 18.14 | 0.66 | 1.71 | 1.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, N.; Wang, D.; Cai, H.; Sun, Q.; Shi, P. Assessing the Capability of Visible Near-Infrared Reflectance Spectroscopy to Monitor Soil Organic Carbon Changes with Localized Predictive Modeling. Remote Sens. 2025, 17, 3373. https://doi.org/10.3390/rs17193373
Dong N, Wang D, Cai H, Sun Q, Shi P. Assessing the Capability of Visible Near-Infrared Reflectance Spectroscopy to Monitor Soil Organic Carbon Changes with Localized Predictive Modeling. Remote Sensing. 2025; 17(19):3373. https://doi.org/10.3390/rs17193373
Chicago/Turabian StyleDong, Na, Dongyan Wang, Hongguang Cai, Qi Sun, and Pu Shi. 2025. "Assessing the Capability of Visible Near-Infrared Reflectance Spectroscopy to Monitor Soil Organic Carbon Changes with Localized Predictive Modeling" Remote Sensing 17, no. 19: 3373. https://doi.org/10.3390/rs17193373
APA StyleDong, N., Wang, D., Cai, H., Sun, Q., & Shi, P. (2025). Assessing the Capability of Visible Near-Infrared Reflectance Spectroscopy to Monitor Soil Organic Carbon Changes with Localized Predictive Modeling. Remote Sensing, 17(19), 3373. https://doi.org/10.3390/rs17193373






