Assessing the Sensitivity of Snow Depth Retrieval Algorithms to Inter-Sensor Brightness Temperature Differences
Abstract
Highlights
- We analyzed the sensitivity of seven snow depth retrieval algorithms (Chang, SPD, Foster, AMSR2, WESTDC, FY-3B, and FY-3D) to brightness temperature differences (TBDs) between passive microwave sensors (SSMIS, AMSR2, and MWRI).
- The SPD, WESTDC, FY-3B, and FY-3D algorithms exhibit relatively low sensitivity to TBDs, while the Foster algorithm demonstrates high sensitivity, especially in forested areas.
- Algorithms with low sensitivity to TBDs improve the consistency of multi-sensor snow depth retrievals and lay the foundation for developing more stable retrieval methods in the future.
- These findings contribute to building passive microwave virtual constellations and ensuring reliable long-term snow depth records for climatology and hydrology.
Abstract
1. Introduction
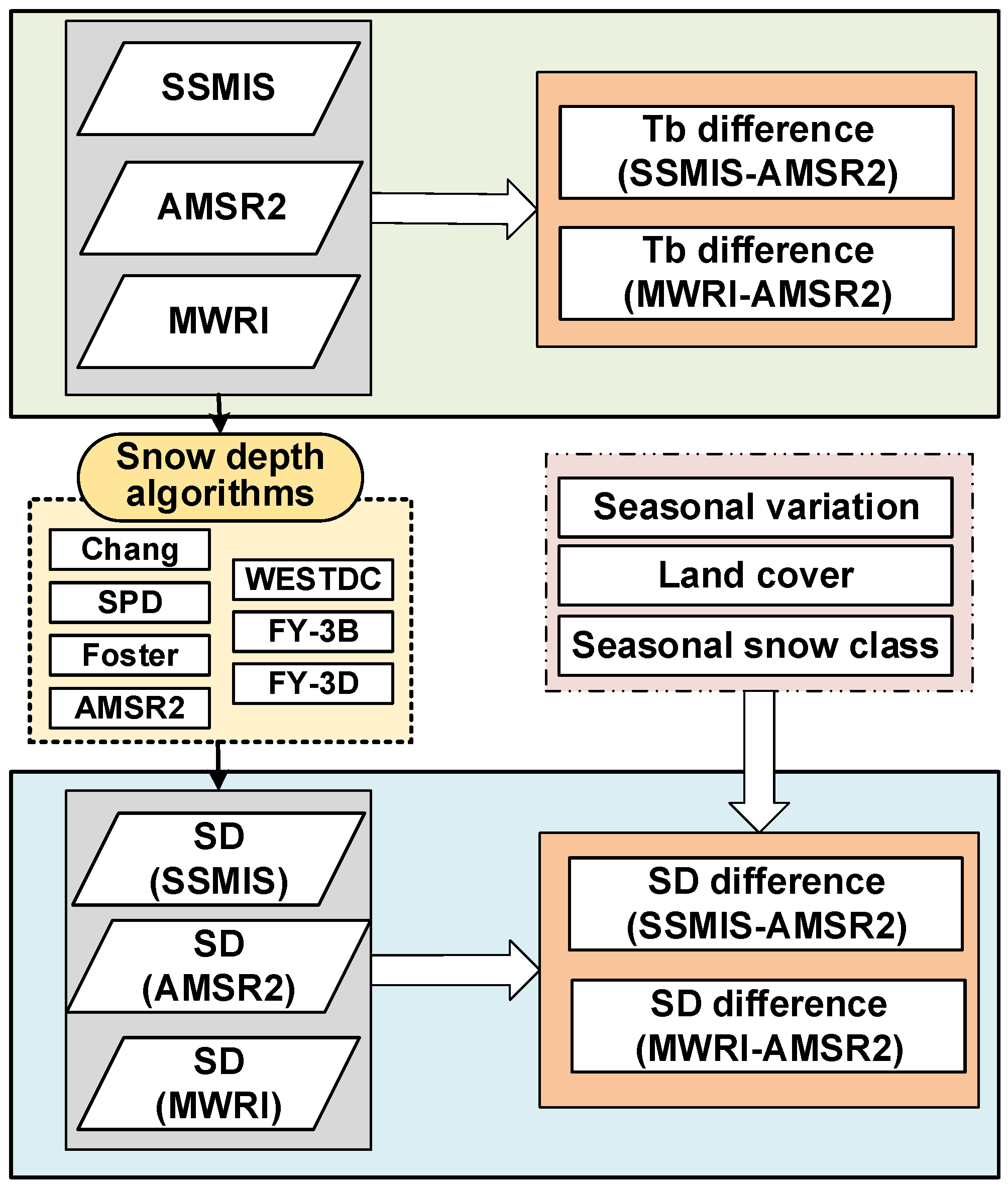
2. Data and Methods
2.1. Data
2.1.1. Passive Microwave Brightness Temperature Data
2.1.2. Auxiliary Data
2.2. Methods
2.2.1. Dry Snow Detection
2.2.2. Snow Depth Retrieval Algorithms
2.2.3. Multi-Sensor Comparison and Sensitivity Assessment
3. Results
3.1. Brightness Temperature Differences Between Sensors
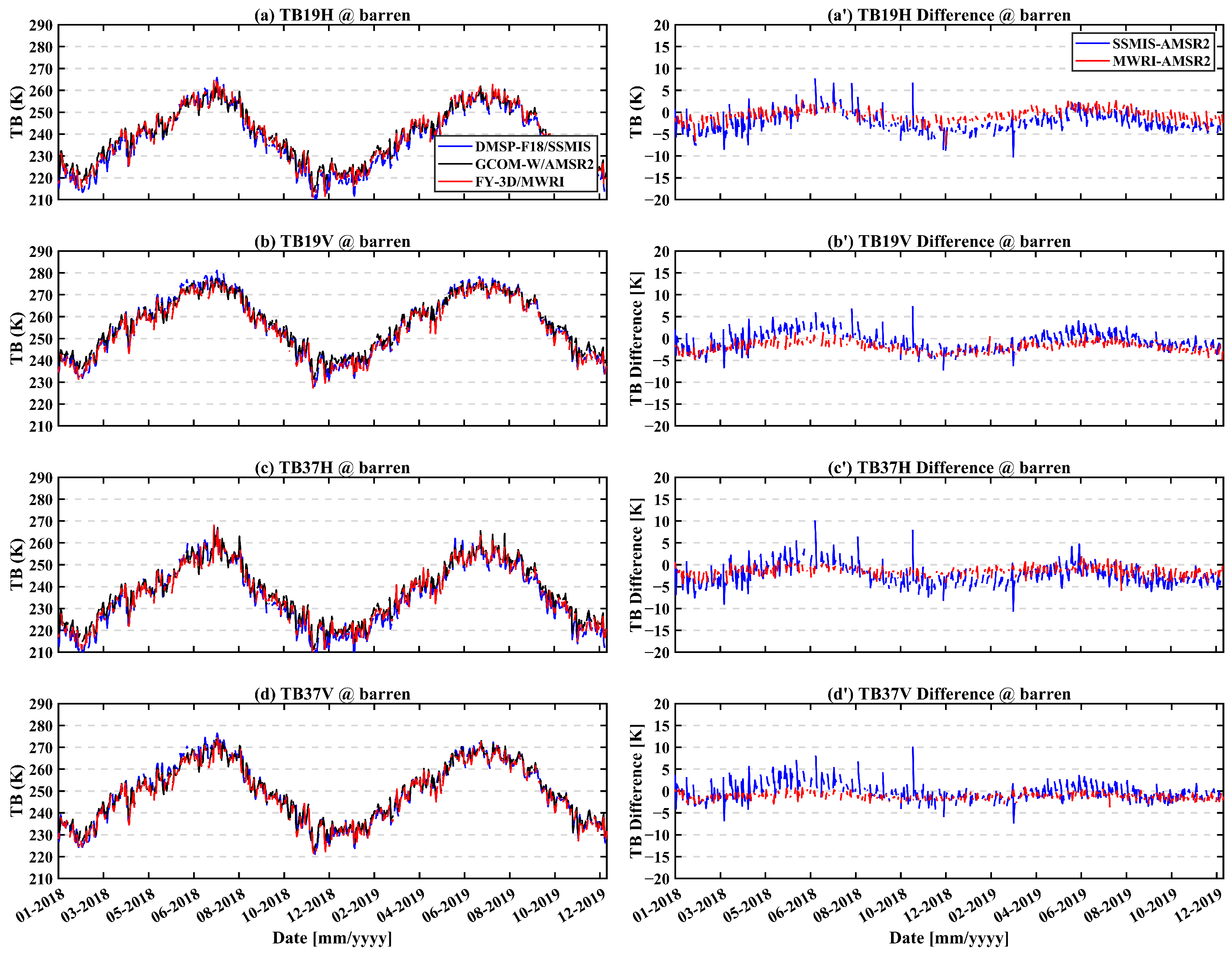
3.1.1. Time Series of Brightness Temperature Differences Between Different Sensors
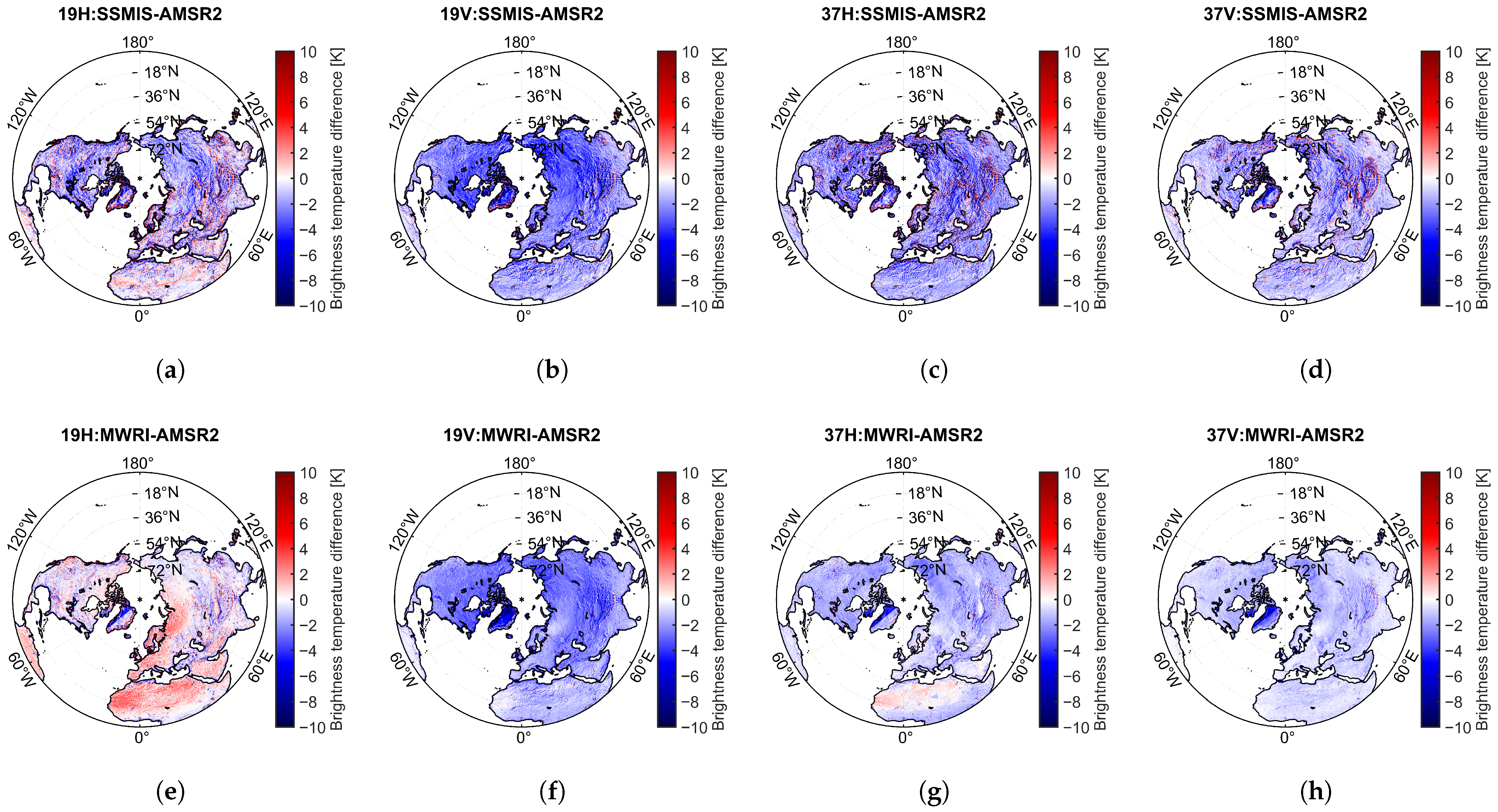
3.1.2. Spatial Distribution of Brightness Temperature Differences Between Sensors in the Northern Hemisphere Land Areas
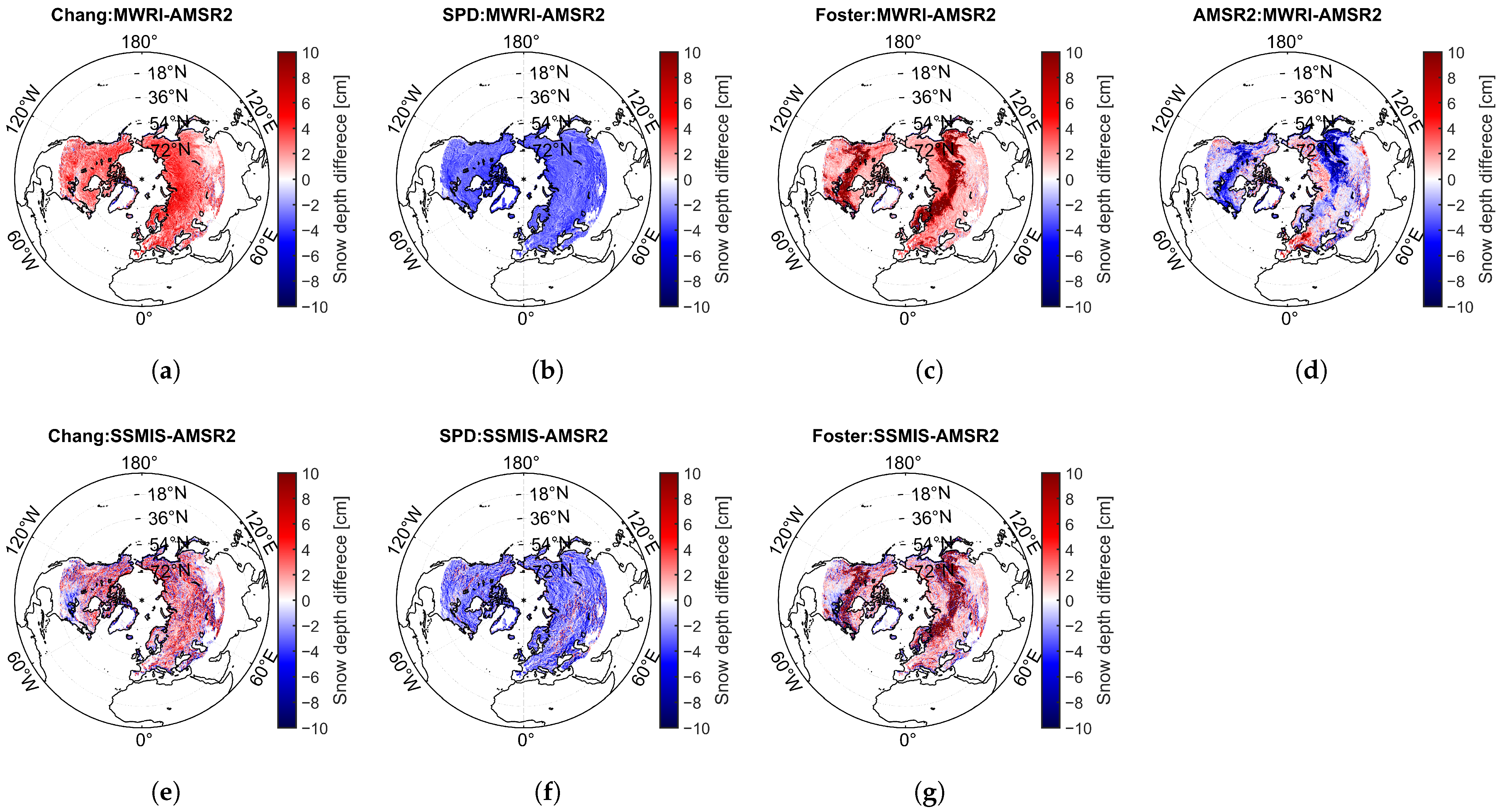
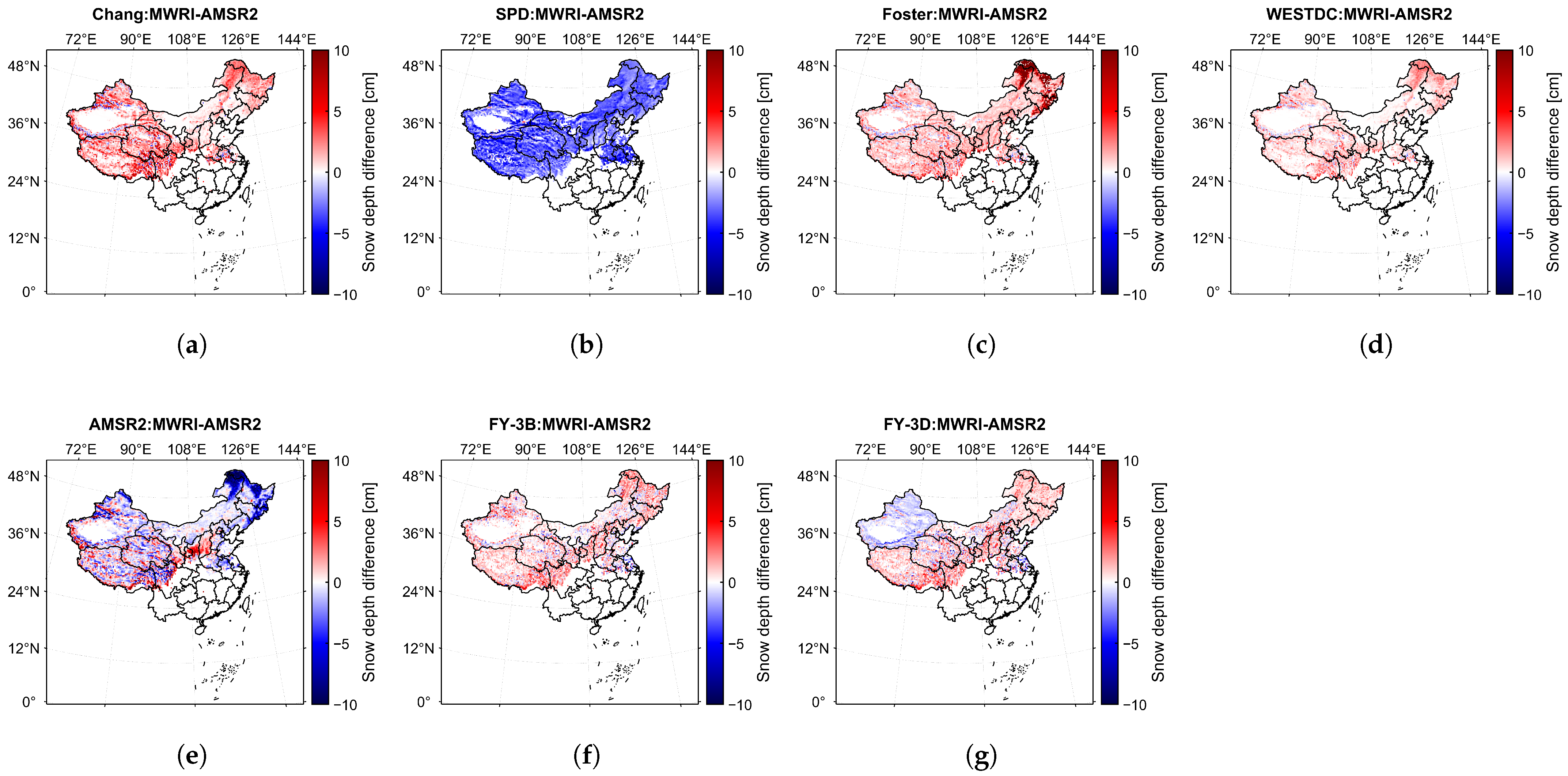
3.2. Sensitivity Analysis of Snow Depth Retrieval Algorithms to Brightness Temperature Differences
3.3. Sensitivity of Snow Depth Retrieval Algorithms to Environmental and Snow Conditions
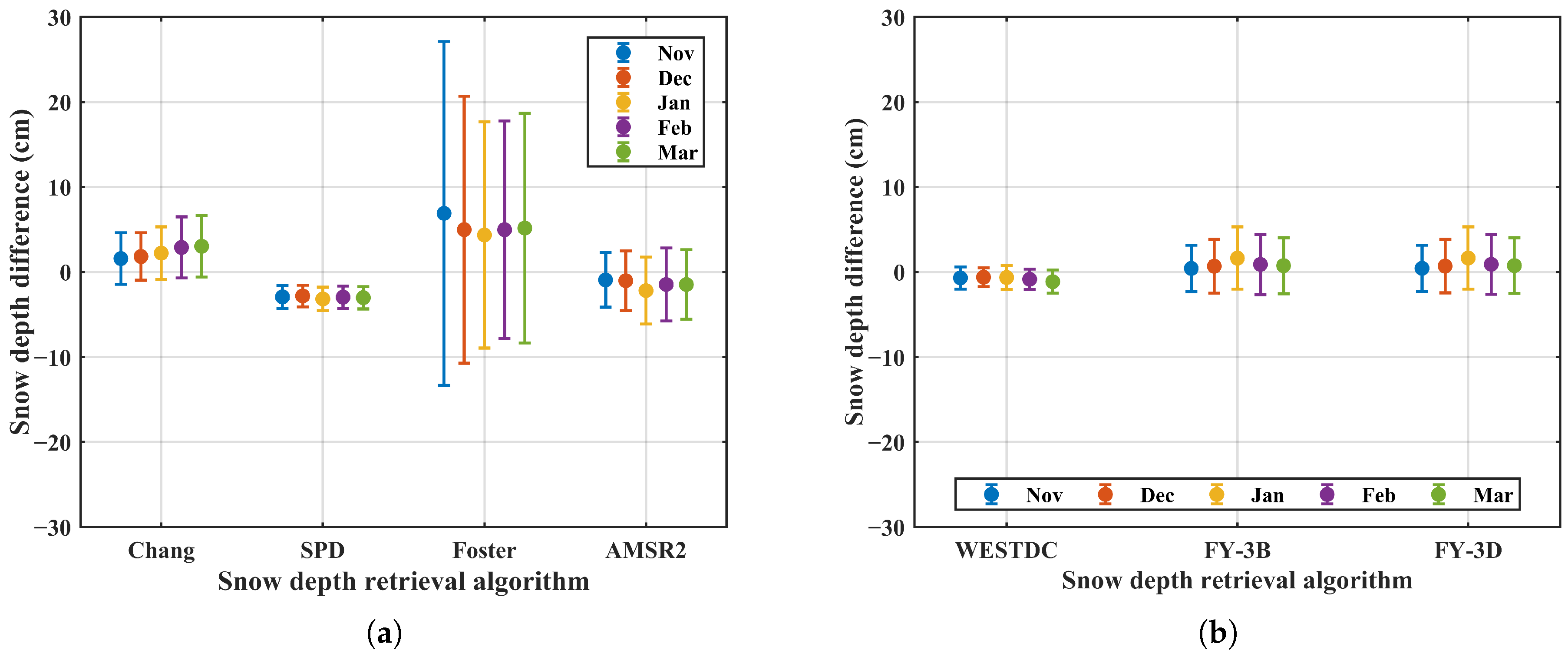
3.3.1. Influence of Seasonal Snow Period on Snow Depth Retrieval Algorithms Sensitivity
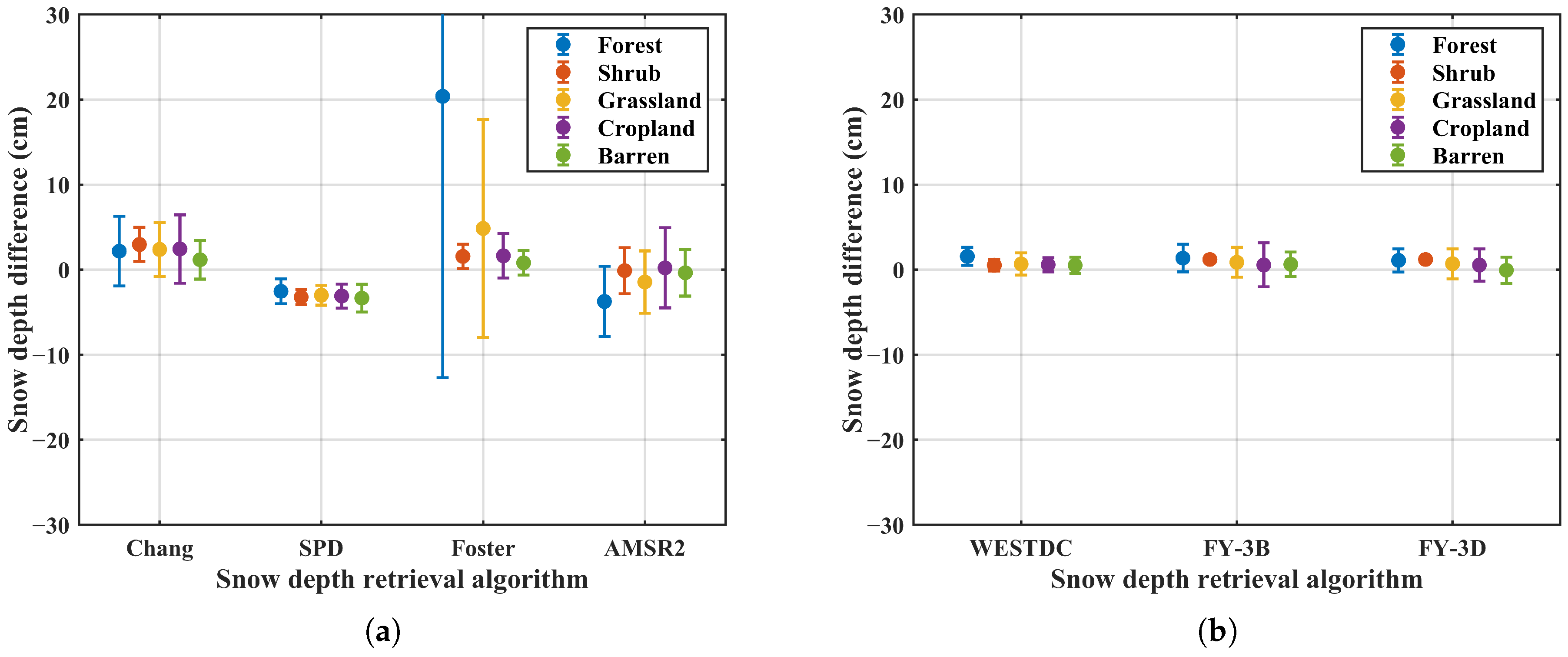
3.3.2. Influence of Land Cover on Snow Depth Retrieval Algorithms Sensitivity
3.3.3. Influence of Seasonal Snow Classification on Snow Depth Retrieval Algorithms Sensitivity
4. Discussion
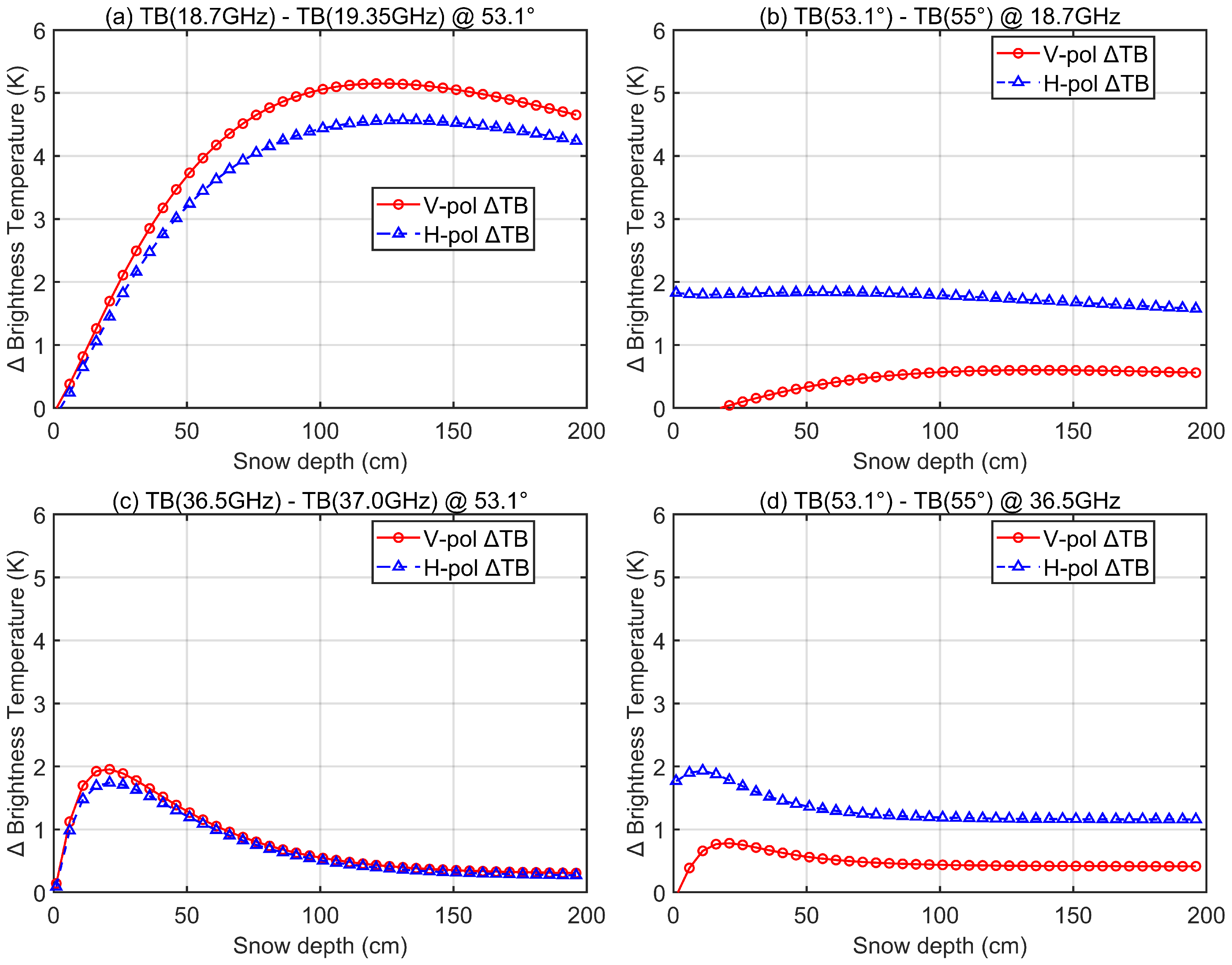
4.1. Influence of Sensor Specification on the Brightness Temperature Difference Across Sensors
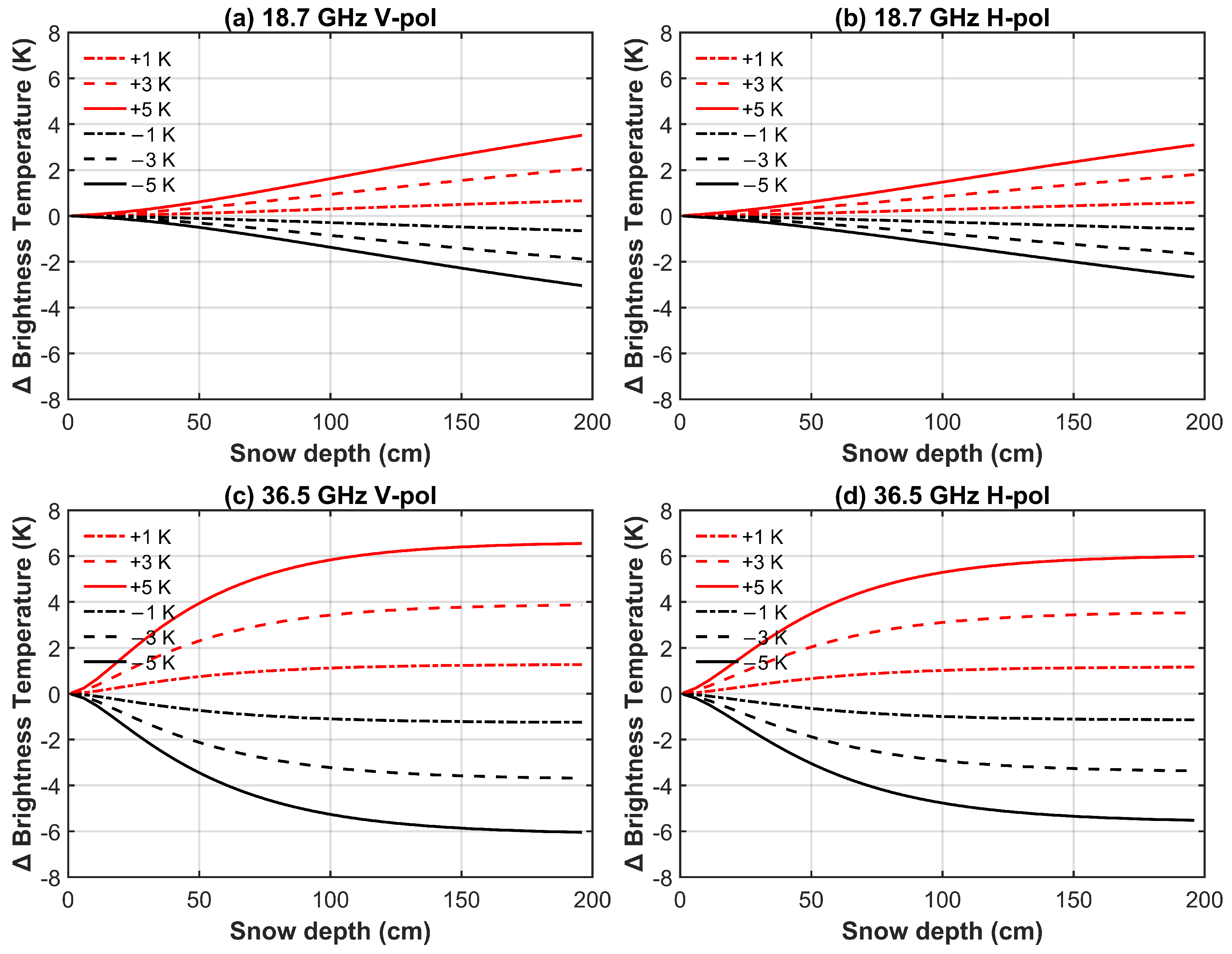
4.2. Influence Factor for Snow Depth Algorithm Sensitivity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, R.; Zhao, H.; Wang, X.; Key, J.; Qu, X.; Hall, A. Controls on Northern Hemisphere snow albedo feedback quantified using satellite Earth observations. Geophys. Res. Lett. 2009, 36, 2009GL040057. [Google Scholar] [CrossRef]
- Flanner, M.G.; Shell, K.M.; Barlage, M.; Perovich, D.K.; Tschudi, M.A. Radiative forcing and albedo feedback from the Northern Hemisphere cryosphere between 1979 and 2008. Nat. Geosci. 2011, 4, 151–155. [Google Scholar] [CrossRef]
- Pulliainen, J.; Luojus, K.; Derksen, C.; Mudryk, L.; Lemmetyinen, J.; Salminen, M.; Ikonen, J.; Takala, M.; Cohen, J.; Smolander, T.; et al. Patterns and trends of Northern Hemisphere snow mass from 1980 to 2018. Nature 2020, 581, 294–298. [Google Scholar] [CrossRef]
- Qin, Y.; Abatzoglou, J.T.; Siebert, S.; Huning, L.S.; AghaKouchak, A.; Mankin, J.S.; Hong, C.; Tong, D.; Davis, S.J.; Mueller, N.D. Agricultural risks from changing snowmelt. Nat. Clim. Change 2020, 10, 459–465. [Google Scholar] [CrossRef]
- Siirila-Woodburn, E.R.; Rhoades, A.M.; Hatchett, B.J.; Huning, L.S.; Szinai, J.; Tague, C.; Nico, P.S.; Feldman, D.R.; Jones, A.D.; Collins, W.D.; et al. A low-to-no snow future and its impacts on water resources in the western united states. Nat. Rev. Earth Environ. 2021, 2, 800–819. [Google Scholar] [CrossRef]
- Sturm, M.; Goldstein, M.A.; Parr, C. Water and life from snow: A trillion dollar science question. Water Resour. Res. 2017, 53, 3534–3544. [Google Scholar] [CrossRef]
- Schöner, W.; Auer, I.; Böhm, R. Long term trend of snow depth at sonnblick (austrian alps) and its relation to climate change. Hydrol. Process. 2009, 23, 1052–1063. [Google Scholar] [CrossRef]
- Reba, M.L.; Marks, D.; Seyfried, M.; Winstral, A.; Kumar, M.; Flerchinger, G. A long-term data set for hydrologic modeling in a snow-dominated mountain catchment. Water Resour. Res. 2011, 47, 2010WR010030. [Google Scholar] [CrossRef]
- Wegmann, M.; Orsolini, Y.; Dutra, E.; Bulygina, O.; Sterin, A.; Brönnimann, S. Eurasian snow depth in long-term climate reanalyses. Cryosphere 2017, 11, 923–935. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, L.; Dai, L.; Pan, J.; Wu, S.; Wang, G. The Consistency of SSM/I vs. SSMIS and the Influence on Snow Cover Detection and Snow Depth Estimation over China. Remote Sens. 2019, 11, 1879. [Google Scholar] [CrossRef]
- Alsweiss, S.O.; Jelenak, Z.; Chang, P.S.; Park, J.D.; Meyers, P. Inter-calibration Results of the Advanced Microwave Scanning Radiometer-2 Over Ocean. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4230–4238. [Google Scholar] [CrossRef]
- Dai, L.; Che, T.; Ding, Y. Inter-Calibrating SMMR, SSM/I and SSMI/S Data to Improve the Consistency of Snow-Depth Products in China. Remote Sens. 2015, 7, 7212–7230. [Google Scholar] [CrossRef]
- Kroodsma, R.A.; McKague, D.S.; Ruf, C.S. Inter-Calibration of Microwave Radiometers Using the Vicarious Cold Calibration Double Difference Method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1006–1013. [Google Scholar] [CrossRef]
- Chander, G.; Hewison, T.J.; Fox, N.; Wu, X.; Xiong, X.; Blackwell, W.J. Overview of Intercalibration of Satellite Instruments. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1056–1080. [Google Scholar] [CrossRef]
- Takala, M.; Luojus, K.; Pulliainen, J.; Derksen, C.; Lemmetyinen, J.; Kärnä, J.P.; Koskinen, J.; Bojkov, B. Estimating northern hemisphere snow water equivalent for climate research through assimilation of space-borne radiometer data and ground-based measurements. Remote Sens. Environ. 2011, 115, 3517–3529. [Google Scholar] [CrossRef]
- Che, T.; Li, X.; Jin, R.; Armstrong, R.; Zhang, T. Snow depth derived from passive microwave remote-sensing data in China. Ann. Glaciol. 2008, 49, 145–154. [Google Scholar] [CrossRef]
- Imaoka, K.; Maeda, T.; Kachi, M.; Kasahara, M.; Ito, N.; Nakagawa, K. Status of AMSR2 instrument on GCOM-W1. In Proceedings of the Earth Observing Missions and Sensors: Development, Implementation, and Characterization II, Kyoto, Japan, 30 October–1 November 2012; SPIE: Bellingham, WA, USA, 2012; Volume 8528, pp. 201–206. [Google Scholar] [CrossRef]
- Berg, W.; Kroodsma, R.; Kummerow, C.; McKague, D. Fundamental Climate Data Records of Microwave Brightness Temperatures. Remote Sens. 2018, 10, 1306. [Google Scholar] [CrossRef]
- Kummerow, C.D.; Berg, W.K.; Kuo, C.P.; NOAA CDR Program. NOAA Climate Data Record (CDR) of SSMI(S) and AMSR2 Microwave Brightness Temperatures, CSU Version 2; NOAA National Centers for Environmental Information (NCEI): Asheville, NC, USA, 2022. [CrossRef]
- Chang, A.; Foster, J.; Hall, D. Nimbus-7 SMMR Derived Global Snow Cover Parameters. Ann. Glaciol. 1987, 9, 39–44. [Google Scholar] [CrossRef]
- Foster, J. Comparison of snow mass estimates from a prototype passive microwave snow algorithm, a revised algorithm and a snow depth climatology. Remote Sens. Environ. 1997, 62, 132–142. [Google Scholar] [CrossRef]
- Aschbacher, J. Land Surface Studies and Atmospheric Effects by Satellite Microwave Radiometry. Ph.D. Thesis, University of Innsbruck, Innsbruck, Austria, 1993; p. 1. [Google Scholar]
- Kelly, R. The AMSR-E Snow Depth Algorithm: Description and Initial Results. J. Remote Sens. Soc. Jpn. 2009, 29, 307–317. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, P.; LiXin, Z.; Hu, Y.; JunTao, Y. Improvement of snow depth retrieval for FY3B-MWRI in China. Sci. China (Earth Sci.) 2014, 57, 1278–1292. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, L.; Wu, S.; Wang, G.; Wang, J.; Liu, X. Development of a Snow Depth Estimation Algorithm over China for the FY-3D/MWRI. Remote Sens. 2019, 11, 977. [Google Scholar] [CrossRef]
- Che, T.; Li, X.; Jin, R.; Huang, C. Assimilating passive microwave remote sensing data into a land surface model to improve the estimation of snow depth. Remote Sens. Environ. 2014, 143, 54–63. [Google Scholar] [CrossRef]
- Jiang, L.; Shi, J.; Tjuatja, S.; Dozier, J.; Chen, K.; Zhang, L. A parameterized multiple-scattering model for microwave emission from dry snow. Remote Sens. Environ. 2007, 111, 357–366. [Google Scholar] [CrossRef]
- Jiang, L.; Shi, J.; Tjuatja, S.; Chen, K.S.; Du, J.; Zhang, L. Estimation of Snow Water Equivalence Using the Polarimetric Scanning Radiometer From the Cold Land Processes Experiments (CLPX03). IEEE Geosci. Remote Sens. Lett. 2011, 8, 359–363. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, T.; Zhong, X.; Shao, W.; Li, X. Support vector regression snow-depth retrieval algorithm using passive microwave remote sensing data. Remote Sens. Environ. 2018, 210, 48–64. [Google Scholar] [CrossRef]
- Bair, E.H.; Abreu Calfa, A.; Rittger, K.; Dozier, J. Using machine learning for real-time estimates of snow water equivalent in the watersheds of Afghanistan. Cryosphere 2018, 12, 1579–1594. [Google Scholar] [CrossRef]
- Yang, J.W.; Jiang, L.M.; Lemmetyinen, J.; Pan, J.M.; Luojus, K.; Takala, M. Improving snow depth estimation by coupling HUT-optimized effective snow grain size parameters with the random forest approach. Remote Sens. Environ. 2021, 264, 112630. [Google Scholar] [CrossRef]
- Pulliainen, J. Mapping of snow water equivalent and snow depth in boreal and sub-arctic zones by assimilating space-borne microwave radiometer data and ground-based observations. Remote Sens. Environ. 2006, 101, 257–269. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, L.; Luojus, K.; Pan, J.; Lemmetyinen, J.; Takala, M.; Wu, S. Snow depth estimation and historical data reconstruction over China based on a random forest machine learning approach. Cryosphere 2020, 14, 1763–1778. [Google Scholar] [CrossRef]
- Tedesco, M.; Jeyaratnam, J. A New Operational Snow Retrieval Algorithm Applied to Historical AMSR-E Brightness Temperatures. Remote Sens. 2016, 8, 1037. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, L.; Zheng, Z.; Pan, J.; Shayiran, A. A new operational northern hemisphere snow water equivalent retrieval algorithm for FY-3F/MWRI-II based on pixel-based regression coefficients. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4302915. [Google Scholar] [CrossRef]
- Du, J.; Kimball, J.; Shi, J.; Jones, L.; Wu, S.; Sun, R.; Yang, H. Inter-calibration of satellite passive microwave land observations from AMSR-E and AMSR2 using overlapping FY3B-MWRI sensor measurements. Remote Sens. 2014, 6, 8594–8616. [Google Scholar] [CrossRef]
- Grody, N.; Basist, A. Global identification of snowcover using SSM/I measurements. IEEE Trans. Geosci. Remote Sens. 1996, 34, 237–249. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, L.; Wu, S.; Hao, S.; Wang, G.; Yang, J. Assessment of methods for passive microwave snow cover mapping using FY-3C/MWRI data in China. Remote Sens. 2018, 10, 524. [Google Scholar] [CrossRef]
- Zschenderlein, L.; Luojus, K.; Takala, M.; Venäläinen, P.; Pulliainen, J. Evaluation of passive microwave dry snow detection algorithms and application to SWE retrieval during seasonal snow accumulation. Remote Sens. Environ. 2023, 288, 113476. [Google Scholar] [CrossRef]
- Derksen, C.; LeDrew, E.; Walker, A.; Goodison, B. Influence of Sensor Overpass Time on Passive Microwave-Derived Snow Cover Parameters. Remote Sens. Environ. 2000, 71, 297–308. [Google Scholar] [CrossRef]
- Kummerow, C.; Duncan, D.; Randel, D.; Brown, P. AMSR-E/AMSR2 Unified Algorithm – Ocean Suite: Algorithm Theoretical Basis Document. National Snow and Ice Data Center (NSIDC): Boulder, CO, USA, 2021. [Google Scholar]
- Li, D.; Zhang, Y.; Feng, X.; Song, K.; Fan, Y.; Xie, J.; Liao, Y. Multichannel radiometer frontend based on bandwidth synthetic technology. IEEE Trans. Microw. Theory Tech. 2017, 65, 632–640. [Google Scholar] [CrossRef]
- Meunier, V.; Löhnert, U.; Kollias, P.; Crewell, S. Biases caused by the instrument bandwidth and beam width on simulated brightness temperature measurements from scanning microwave radiometers. Atmos. Meas. Tech. 2013, 6, 1171–1187. [Google Scholar] [CrossRef]
- Tsang, L.; Pan, J.; Liang, D.; Li, Z.; Cline, D.W.; Tan, Y. Modeling Active Microwave Remote Sensing of Snow Using Dense Media Radiative Transfer (DMRT) Theory With Multiple-Scattering Effects. IEEE Trans. Geosci. Remote Sens. 2007, 45, 990–1004. [Google Scholar] [CrossRef]
- Liang, D.; Xu, X.; Tsang, L.; Andreadis, K.M.; Josberger, E.G. The Effects of Layers in Dry Snow on Its Passive Microwave Emissions Using Dense Media Radiative Transfer Theory Based on the Quasicrystalline Approximation (QCA/DMRT). IEEE Trans. Geosci. Remote Sens. 2008, 46, 3663–3671. [Google Scholar] [CrossRef]
- Lemmetyinen, J.; Derksen, C.; Toose, P.; Proksch, M.; Pulliainen, J.; Kontu, A.; Rautiainen, K.; Seppänen, J.; Hallikainen, M. Simulating seasonally and spatially varying snow cover brightness temperature using HUT snow emission model and retrieval of a microwave effective grain size. Remote Sens. Environ. 2015, 156, 71–95. [Google Scholar] [CrossRef]

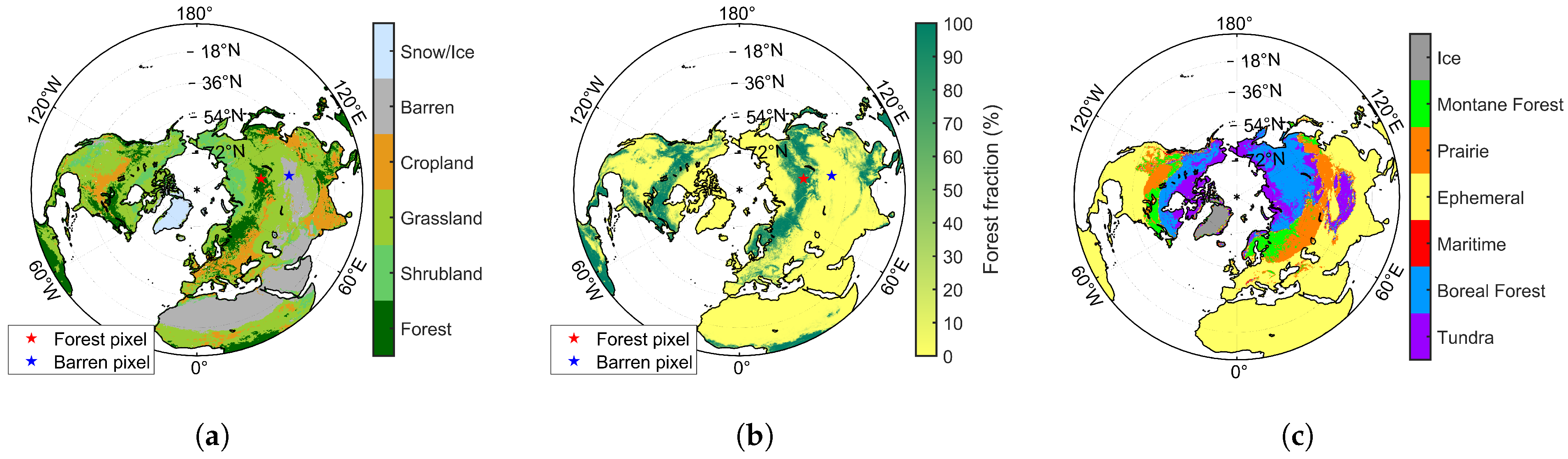




| Satellite Platform | DMSP-F18 | GCOM-W | FY-3D |
|---|---|---|---|
| Sensor | SSMIS | AMSR2 | MWRI-I |
| Time Coverage | 2009–present | 2012–present | 2017–present |
| Overpass Time | A: 18:00 D: 07:00 | A: 13:30 D: 01:30 | A: 13:40 D: 01:40 |
| Channels (GHz): Footprint (km) | 19.3: 70 × 45 22.2: 60 × 40 37.0: 38 × 30 91.7: 16 × 13 | 6.925: 35 × 62 7.3: 35 × 62 10.65: 24 × 42 18.7: 14 × 22 23.8: 15 × 26 36.5: 7 × 12 89: 3 × 5 | 10.65: 51 × 85 18.7: 30 × 50 23.8: 27 × 45 36.5: 18 × 30 89: 9 × 15 |
| Observation Angle | 53.1° | 55° | 53.1° |
| Algorithm | Formula Form | Application Region |
|---|---|---|
| Chang | Global | |
| Foster | Global | |
| SPD | , | |
| Global | ||
| AMSR2 | , | |
| , | ||
| Global | ||
| WESTDC | China | |
| FY-3B | China | |
| FY-3D | In Northeast China: , | |
| In Xinjiang: , | ||
| Other regions: same as FY-3B | China |
| Channel | SSMIS-AMSR2 | MWRI-AMSR2 | ||
|---|---|---|---|---|
| Barren | Forest | Barren | Forest | |
| 19H | −2.26 ± 2.30 | −0.52 ± 3.15 | −0.65 ± 1.46 | 0.35 ± 1.07 |
| 19V | −0.60 ± 2.17 | −1.53 ± 3.03 | −1.94 ± 1.18 | −2.06 ± 0.80 |
| 37H | −2.27 ± 2.46 | −2.28 ± 4.47 | −1.51 ± 1.12 | −1.19 ± 1.35 |
| 37V | −0.20 ± 2.08 | −1.51 ± 3.90 | −1.22 ± 0.77 | −0.59 ± 1.09 |
| Channel | SSMIS-AMSR2 | MWRI-AMSR2 | ||
|---|---|---|---|---|
| Mean (K) | Std (K) | Mean (K) | Std (K) | |
| 19H | −1.60 | 8.46 | −0.85 | 5.76 |
| 19V | −3.78 | 6.19 | −3.90 | 3.64 |
| 37H | −2.66 | 7.34 | −1.89 | 2.56 |
| 37V | −2.16 | 4.82 | −1.95 | 1.95 |
| Algorithm | SSMIS-AMSR2 | MWRI-AMSR2 | ||
|---|---|---|---|---|
| Mean (cm) | Std (cm) | Mean (cm) | Std (cm) | |
| Chang | 0.64 | 4.81 | 2.28 | 3.61 |
| SPD | −2.30 | 2.71 | −3.01 | 1.32 |
| Foster | 2.14 | 15.10 | 5.95 | 16.84 |
| AMSR2 | / | / | −1.40 | 3.97 |
| Algorithm | SSMIS-AMSR2 | MWRI-AMSR2 | ||
|---|---|---|---|---|
| Mean (cm) | Std (cm) | Mean (cm) | Std (cm) | |
| Chang | 0.76 | 3.41 | 1.38 | 2.07 |
| SPD | −2.57 | 2.35 | −3.01 | 1.44 |
| Foster | 2.23 | 11.41 | 3.20 | 11.18 |
| AMSR2 | / | / | −0.60 | 3.20 |
| WESTDC | 0.34 | 1.71 | 0.68 | 1.16 |
| FY-3B | / | / | 0.79 | 1.86 |
| FY-3D | / | / | 0.49 | 1.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Jiang, L.; Cui, H.; Pan, J.; Yang, J.; Wu, M. Assessing the Sensitivity of Snow Depth Retrieval Algorithms to Inter-Sensor Brightness Temperature Differences. Remote Sens. 2025, 17, 3355. https://doi.org/10.3390/rs17193355
Liu G, Jiang L, Cui H, Pan J, Yang J, Wu M. Assessing the Sensitivity of Snow Depth Retrieval Algorithms to Inter-Sensor Brightness Temperature Differences. Remote Sensing. 2025; 17(19):3355. https://doi.org/10.3390/rs17193355
Chicago/Turabian StyleLiu, Guangjin, Lingmei Jiang, Huizhen Cui, Jinmei Pan, Jianwei Yang, and Min Wu. 2025. "Assessing the Sensitivity of Snow Depth Retrieval Algorithms to Inter-Sensor Brightness Temperature Differences" Remote Sensing 17, no. 19: 3355. https://doi.org/10.3390/rs17193355
APA StyleLiu, G., Jiang, L., Cui, H., Pan, J., Yang, J., & Wu, M. (2025). Assessing the Sensitivity of Snow Depth Retrieval Algorithms to Inter-Sensor Brightness Temperature Differences. Remote Sensing, 17(19), 3355. https://doi.org/10.3390/rs17193355






