Comparative Evaluation of SNO and Double Difference Calibration Methods for FY-3D MERSI TIR Bands Using MODIS/Aqua as Reference
Abstract
Highlights
- A systematic comparison of SNO and DD calibration for FY-3D MERSI TIR Bands 24 and 25.
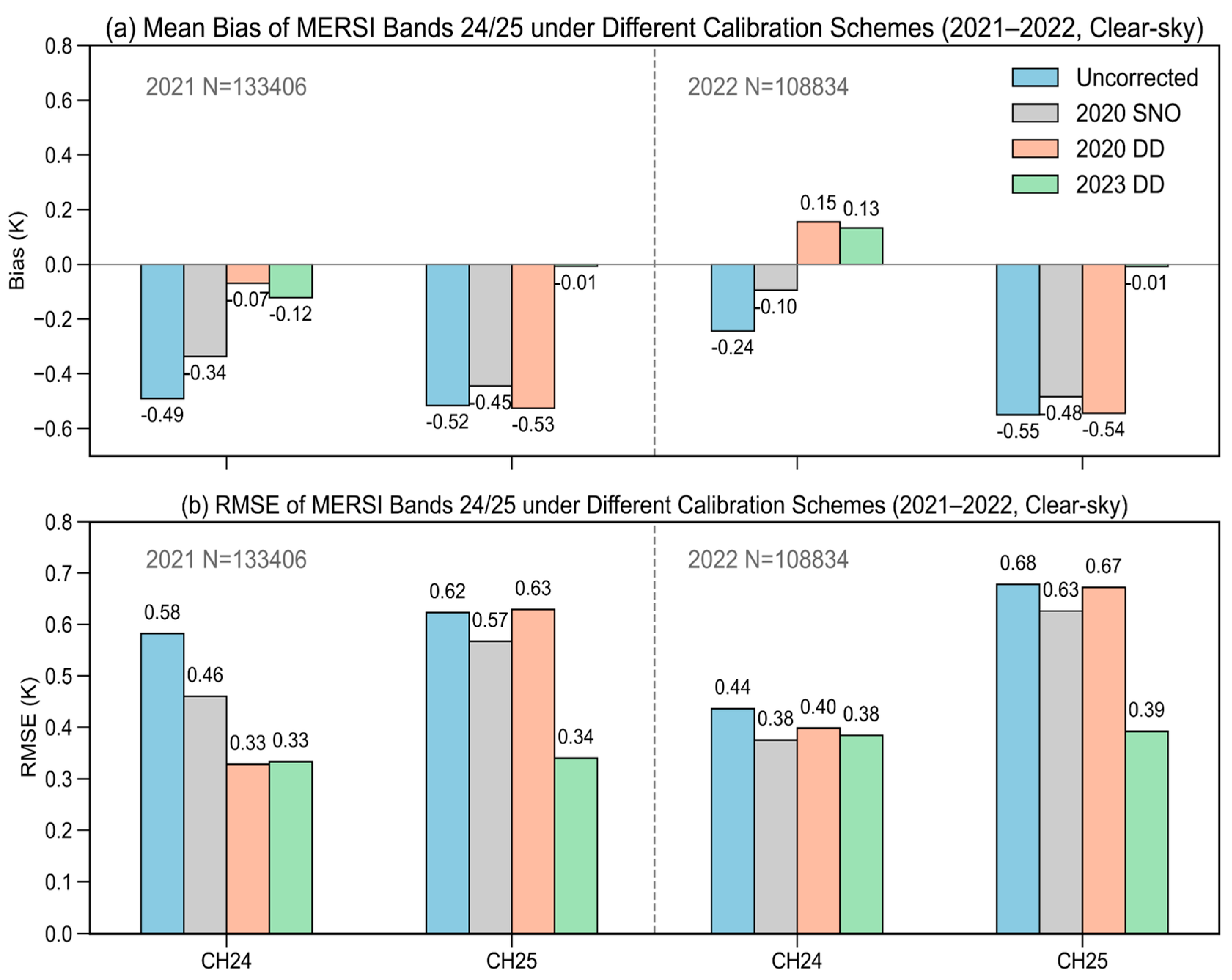
- Double-difference reduces mean bias to ±0.1 K and RMSE to 0.3–0.4 K under clear-sky conditions.
- DD offers higher accuracy and scalability, while SNO provides stability under cloudy scenes.
- These findings support improved cross-sensor calibration and enhance consistency of long-term climate data records.
Abstract
1. Introduction
2. Model and Datasets
2.1. Advanced Radiative Transfer Modeling System (ARMS)
2.2. FY-3D/MERSI and MODIS/Aqua Datasets
2.3. ERA5 Atmospheric Reanalysis Data
2.4. Dataset Overview
3. Methodology
3.1. Calibration Workflow and Validation Framework
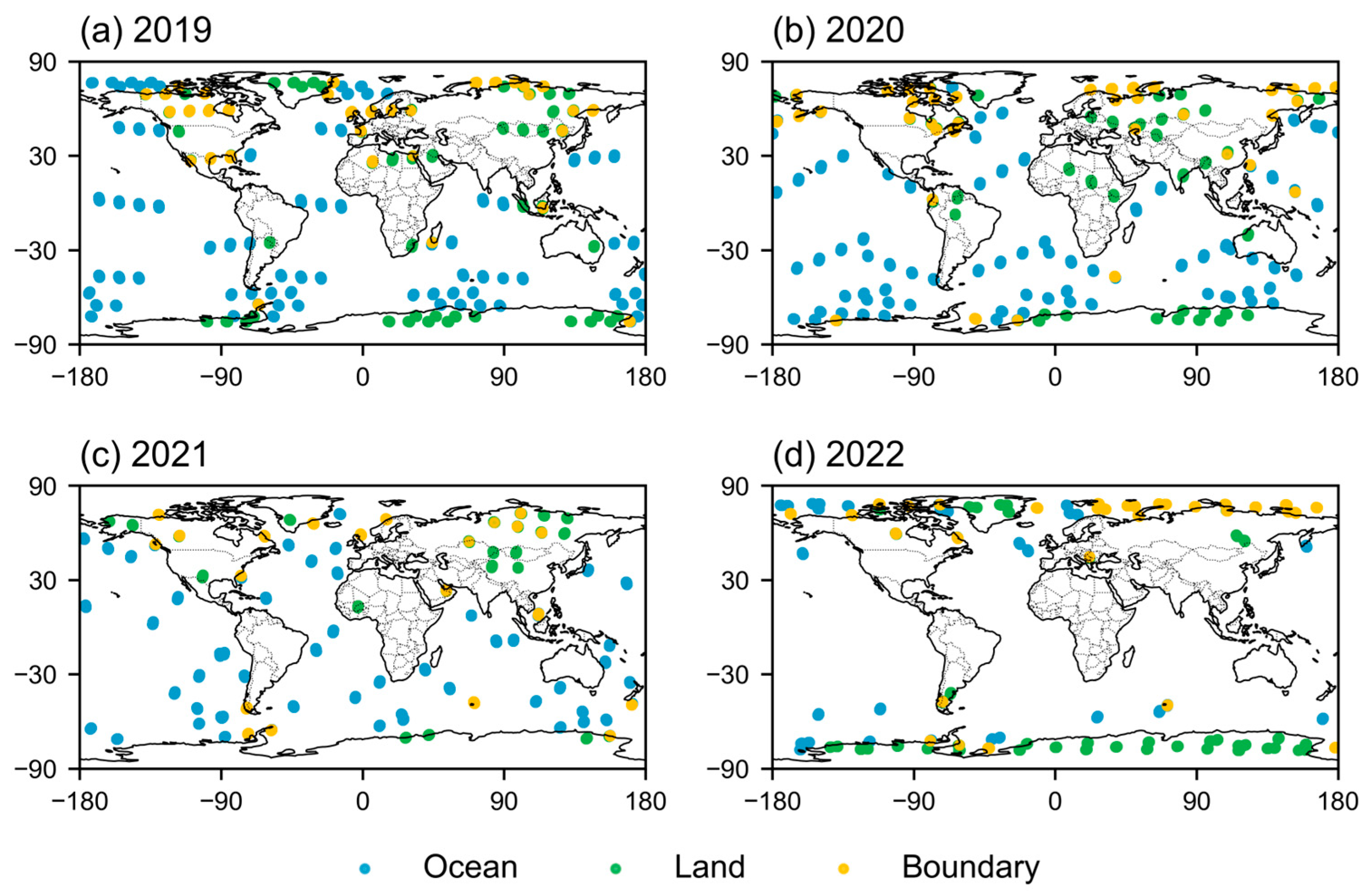
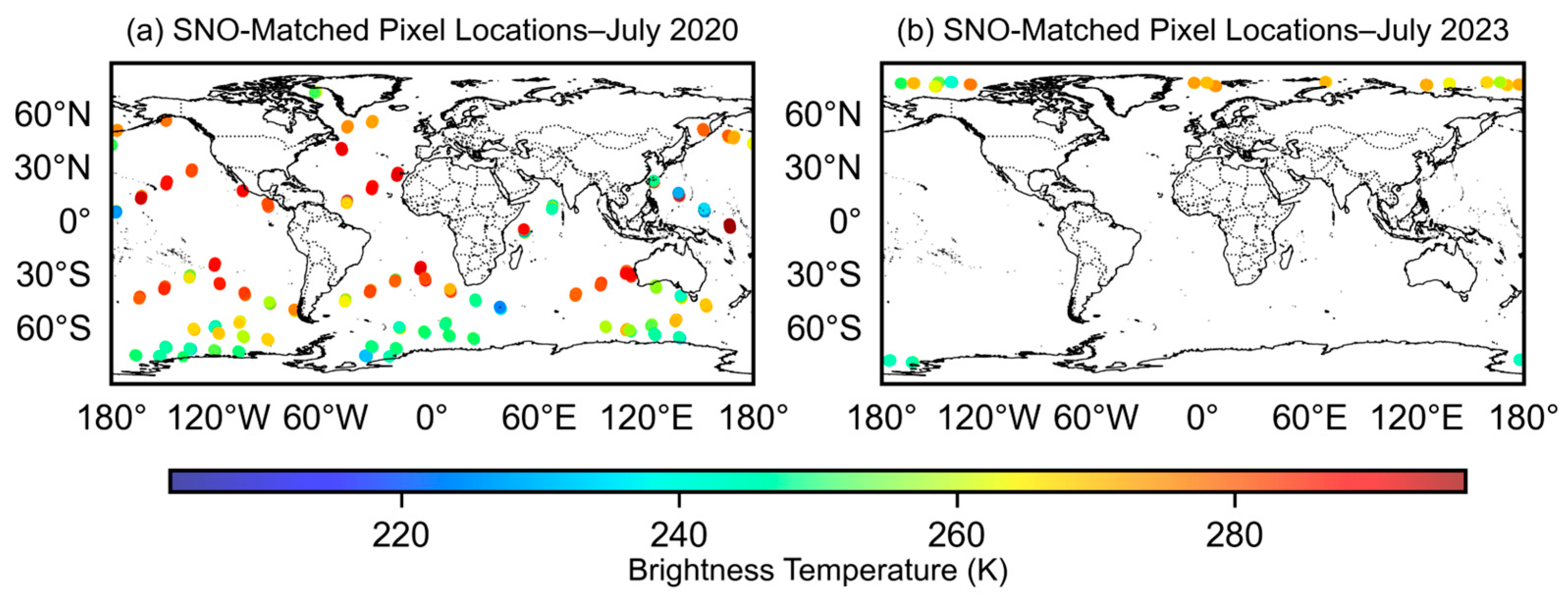
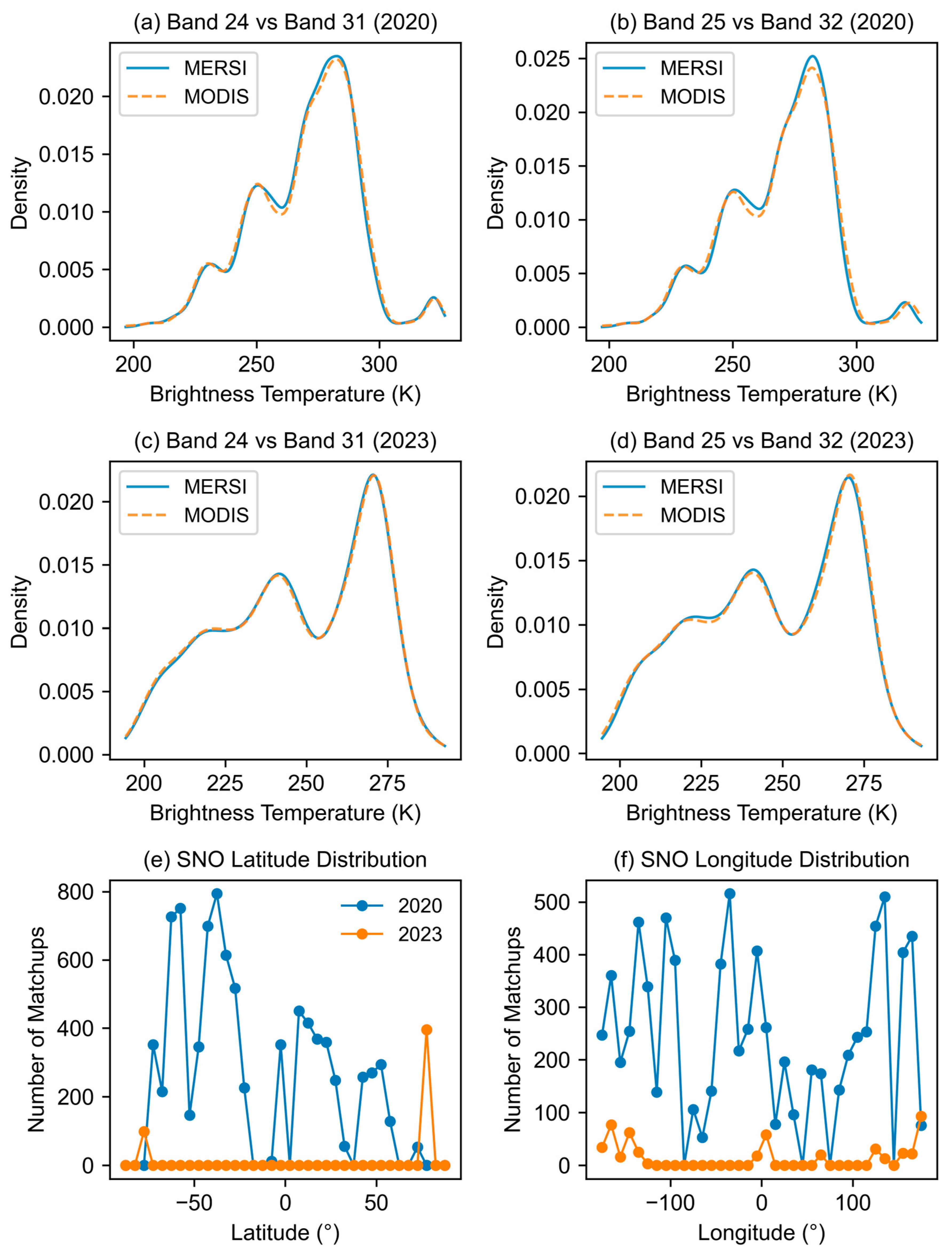
3.2. Simultaneous Nadir Overpass (SNO)-Based Cross-Calibration
- Temporal threshold: within 10 min, to limit the impact of atmospheric thermal variations on brightness temperature consistency;
- Spatial colocation: within 1 km, to reduce errors from surface heterogeneity;
- Zenith angle difference: less than 1°, to suppress the effects of atmospheric path length.
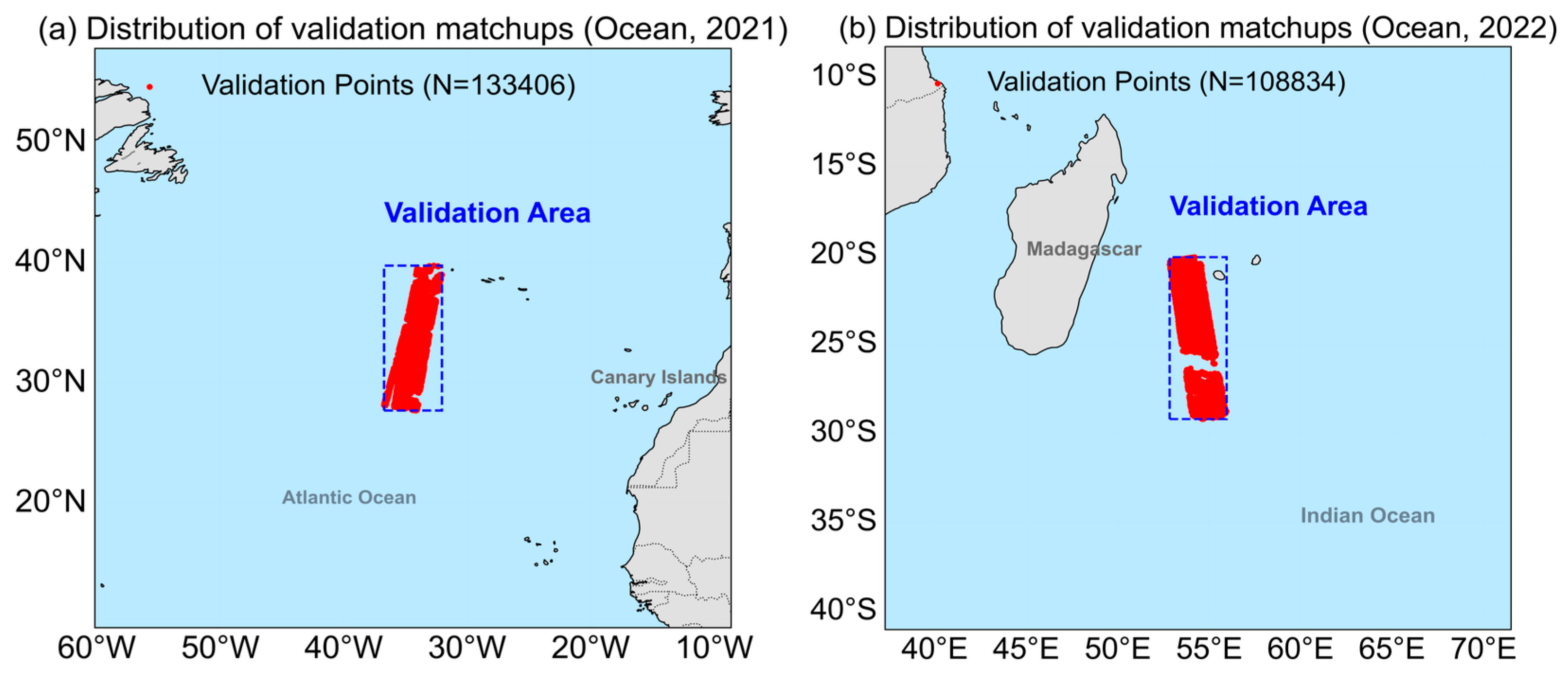
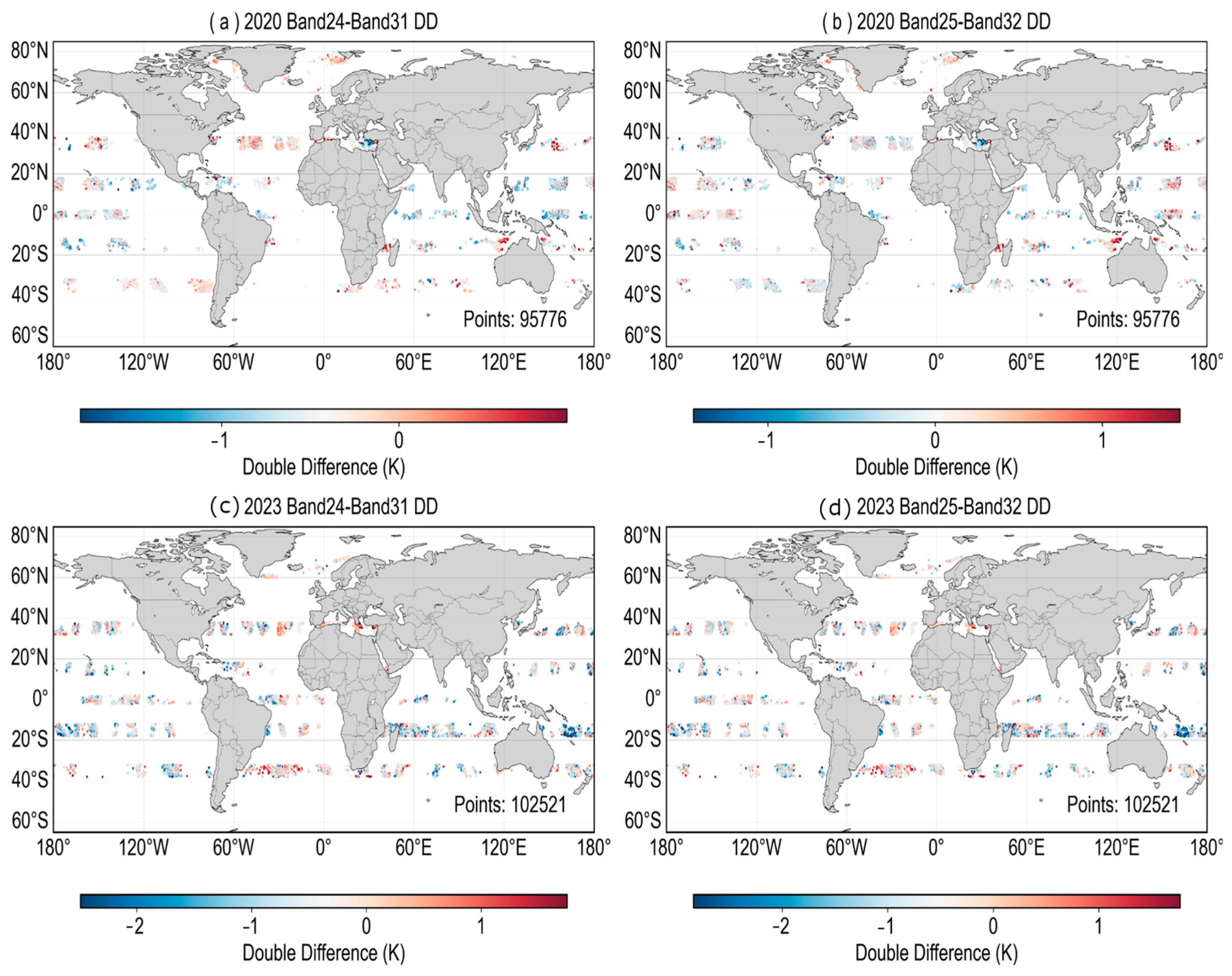
3.3. Double Difference (DD) Cross-Calibration Method
4. Result Analysis
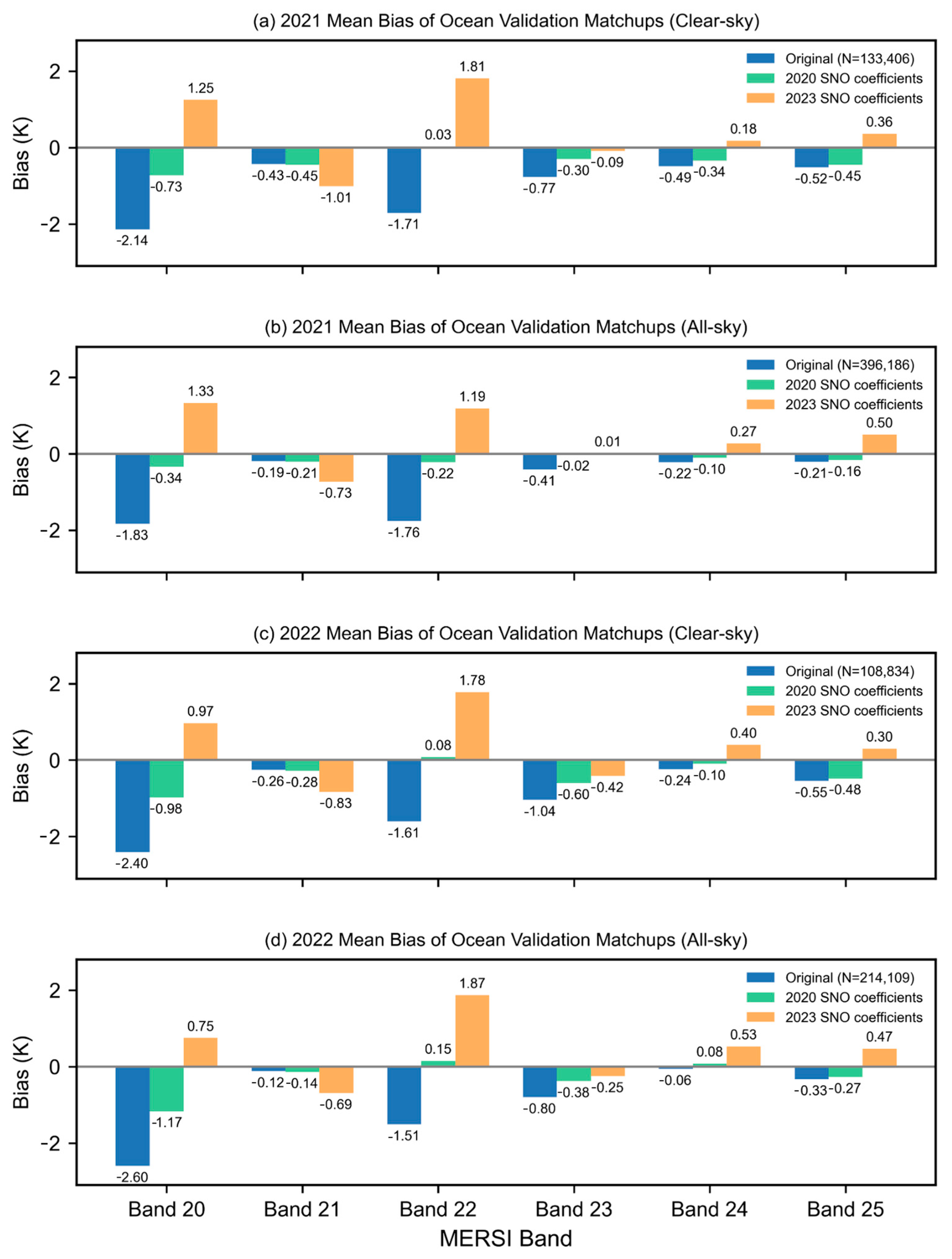
4.1. Calibration Results Using the SNO Method
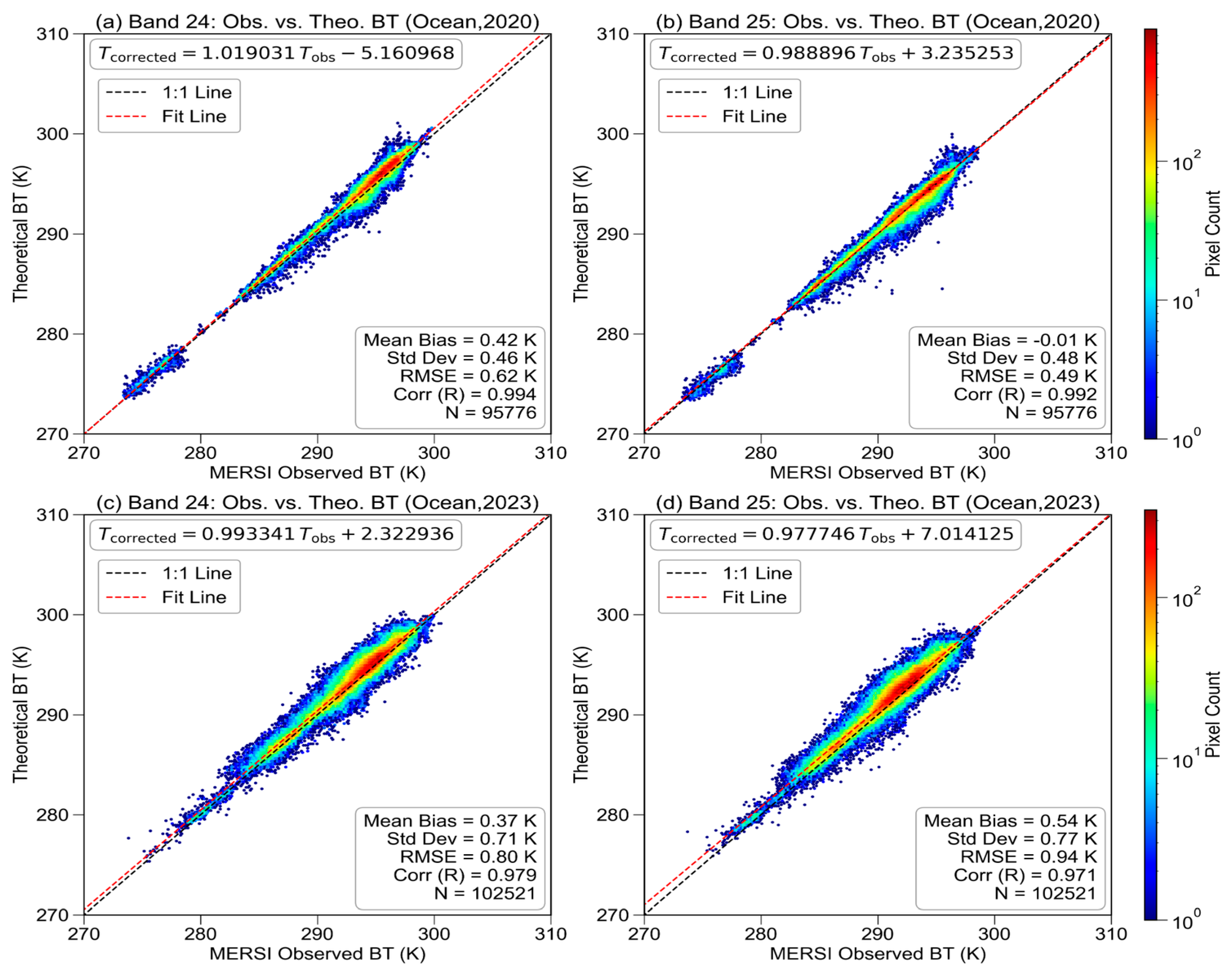
4.2. Double Difference Fitting Analysis Based on ARMS Simulation
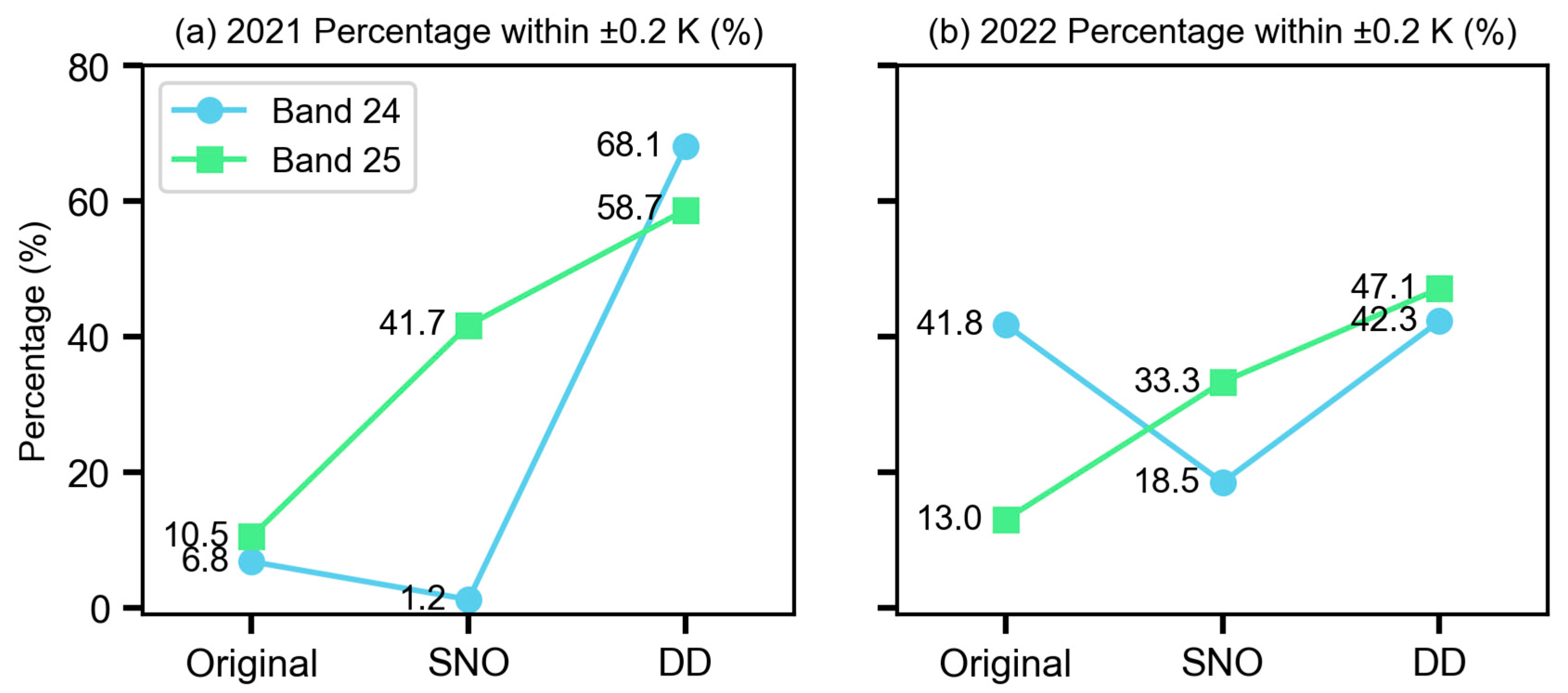
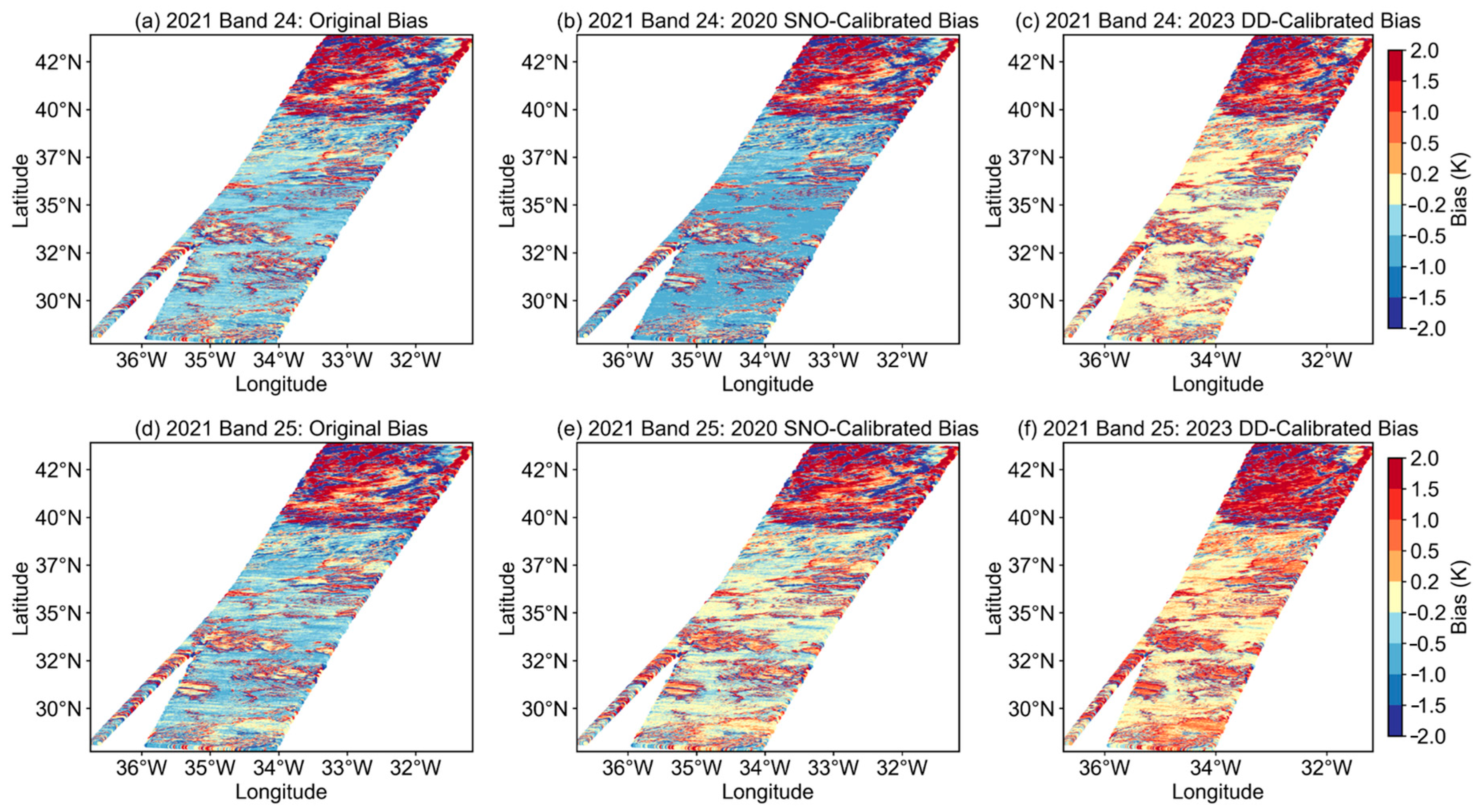
4.3. Comparative Analysis of Calibration Performance: SNO vs. DD Methods
5. Discussion
5.1. Uncertainty Considerations
5.2. Advances and Contributions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FY-3D | Fengyun-3D (Chinese Polar-Orbiting Meteorological Satellite) |
| MERSI | Medium Resolution Spectral Imager |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| SNO | Simultaneous Nadir Overpass |
| DD | Double Difference |
| TIR | Thermal Infrared |
| SRF | Spectral Response Function |
| BT | Brightness Temperature |
| LST | Land Surface Temperature |
| OMB | Observation minus Background (or Simulation) |
| RMSE | Root Mean Square Error |
| ARMS | Advanced Radiative Transfer Modeling System |
| ERA5 | Fifth-Generation ECMWF Atmospheric Reanalysis |
| NASA | National Aeronautics and Space Administration |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| RTM | Radiative Transfer Model |
| NWP | Numerical Weather Prediction |
| GSICS | Global Space-based Inter-Calibration System |
| IASI | Infrared Atmospheric Sounding Interferometer |
| CrIS | Cross-track Infrared Sounder |
References
- Minnis, P.; Nguyen, L.; Doelling, D.R.; Young, D.F.; Miller, W.F.; Kratz, D.P. Rapid calibration of operational and research meteorological satellite imagers. Part II: Comparison of infrared channels. J. Atmos. Oceanic Technol. 2002, 19, 1250–1266. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Li, Z.; Wu, H.; Duan, S.; Zhao, W.; Ren, H.; Liu, X.; Leng, P.; Tang, R.; Ye, X.; Zhu, J.; et al. Satellite remote sensing of global land surface temperature: Definition, methods, products, and applications. Rev. Geophys. 2023, 61, e2022RG000777. [Google Scholar] [CrossRef]
- Giering, R.; Quast, R.; Mittaz, J.P.D.; Hunt, S.E.; Harris, P.M.; Woolliams, E.R.; Merchant, C.J. A novel framework to harmonise satellite data series for climate applications. Remote Sens. 2019, 11, 1002. [Google Scholar] [CrossRef]
- Xiong, X.; Barnes, W. An overview of MODIS radiometric calibration and characterization. Adv. Atmos. Sci. 2006, 23, 69–79. [Google Scholar] [CrossRef]
- Xiong, X.; Chiang, K.; Esposito, J.; Guenther, B.; Barnes, W. MODIS on-orbit calibration and characterization. Metrologia 2003, 40, S89–S92. [Google Scholar] [CrossRef]
- Chander, G.; Hewison, T.J.; Fox, N.; Wu, X.; Xiong, X.; Blackwell, W.J. Overview of intercalibration of satellite instruments. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1056–1080. [Google Scholar] [CrossRef]
- Gil, J.; Rodrigo, J.F.; Salvador, P.; Gómez, D.; Sanz, J.; Casanova, J.L. An empirical radiometric intercomparison methodology based on global simultaneous nadir overpasses applied to Landsat 8 and Sentinel-2. Remote Sens. 2020, 12, 2736. [Google Scholar] [CrossRef]
- Uprety, S.; Cao, C.; Xiong, X.; Blonski, S.; Wu, A.; Shao, X. Radiometric intercomparison between Suomi-NPP VIIRS and Aqua MODIS reflective solar bands using simultaneous nadir overpass in the low latitudes. J. Atmos. Oceanic Technol. 2013, 30, 2720–2736. [Google Scholar] [CrossRef]
- Xu, N.; Chen, L.; Hu, X.; Zhang, L.; Zhang, P. Assessment and correction of on-orbit radiometric calibration for FY-3 VIRR thermal infrared channels. Remote Sens. 2014, 6, 2884–2897. [Google Scholar] [CrossRef]
- Cao, C.; Uprety, S.; Blonski, S. Establishing radiometric consistency among VIIRS, MODIS, and AVHRR using SNO and SNOx methods. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; IEEE: New York, NY, USA; pp. 6928–6931. [Google Scholar]
- Ye, X.; Ren, H.; Liang, Y.; Zhu, J.; Guo, J.; Nie, J.; Zeng, H.; Zhao, Y.; Qian, Y. Cross-calibration of Chinese Gaofen-5 thermal infrared images and its improvement on land surface temperature retrieval. Int. J. Appl. Earth Obs. Geoinf. 2021, 101, 102357. [Google Scholar] [CrossRef]
- Gu, Z.; Chen, L.; Dai, H.; Tian, L.; Hu, X.; Zhang, P. The uncertainty of SNO cross-calibration for satellite infrared channels. Remote Sens. 2023, 15, 3313. [Google Scholar] [CrossRef]
- Gorroño, J.; Banks, A.C.; Fox, N.P.; Underwood, C. Radiometric inter-sensor cross-calibration uncertainty using a traceable high accuracy reference hyperspectral imager. ISPRS J. Photogramm. Remote Sens. 2017, 130, 393–417. [Google Scholar] [CrossRef]
- Kroodsma, R.A.; McKague, D.S.; Ruf, C.S. Inter-calibration of microwave radiometers using the vicarious cold calibration double difference method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1006–1013. [Google Scholar] [CrossRef]
- Zec, J.; Jones, W.; Alsabah, R.; Al-Sabbagh, A. RapidScat cross-calibration using the double difference technique. Remote Sens. 2017, 9, 1160. [Google Scholar] [CrossRef]
- Zhang, Y.-F.; Jiang, G.-M. Intercalibration of FY-3D MWHS-II water vapor absorption channels against S-NPP ATMS channels using the double difference method. In Proceedings of the IGARSS 2024–2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7 July 2024; IEEE: New York, NY, USA; pp. 6255–6258. [Google Scholar]
- Alsweiss, S.O.; Jelenak, Z.; Chang, P.S.; Park, J.D.; Meyers, P. Inter-calibration results of the Advanced Microwave Scanning Radiometer-2 over ocean. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4230–4238. [Google Scholar] [CrossRef]
- Wu, S.; Sun, F.; Gu, S.; Zhang, P. Re-calibration of MWRI onboard FY series satellites. In Proceedings of the IGARSS 2023–2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16 July 2023; IEEE: New York, NY, USA; pp. 4384–4387. [Google Scholar]
- Jiang, G.-M.; Zou, Y.; Chen, H. Assessment and correction of the on-orbit radiometric calibration in FY-3D MERSI-2 thermal infrared channels. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–10. [Google Scholar] [CrossRef]
- Jiang, G.-M.; Xin, Y.-C. Intercalibration of FY-4A AGRI thermal infrared channels against AHI channels using the double difference method. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Zhang, C.; Qi, C.; Yang, T.; Gu, M.; Zhang, P.; Lee, L.; Xie, M.; Hu, X. Evaluation of FY-3E/HIRAS-II radiometric calibration accuracy based on OMB analysis. Remote Sens. 2022, 14, 3222. [Google Scholar] [CrossRef]
- He, X.; Xu, N.; Feng, X.; Hu, X.; Xu, H.; Peng, Y. Assessing radiometric calibration of FY-4A/AGRI thermal infrared channels using CrIS and IASI. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Goldberg, M.; Ohring, G.; Butler, J.; Cao, C.; Datla, R.; Doelling, D.; Gärtner, V.; Hewison, T.; Iacovazzi, B.; Kim, D.; et al. The Global Space-Based Inter-Calibration System. Bull. Am. Meteorol. Soc. 2011, 92, 467–475. [Google Scholar] [CrossRef]
- Hewison, T.J.; Doelling, D.R.; Lukashin, C.; Tobin, D.; John, V.O.; Joro, S.; Bojkov, B. Extending the Global Space-Based Inter-Calibration System (GSICS) to tie satellite radiances to an absolute scale. Remote Sens. 2020, 12, 1782. [Google Scholar] [CrossRef]
- Hewison, T.J.; Wu, X.; Yu, F.; Tahara, Y.; Hu, X.; Kim, D.; Koenig, M. GSICS inter-calibration of infrared channels of geostationary imagers using Metop/IASI. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1160–1170. [Google Scholar] [CrossRef]
- Wang, S.; Yin, X.; Zhou, W.; Bao, Q.; Li, Y.; Kong, J.; He, M. Intercalibration of HY-2B SMR using double difference method based on GPM GMI. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–18. [Google Scholar] [CrossRef]
- Zou, X. Studies of FY-3 observations over the past 10 years: A review. Remote Sens. 2021, 13, 673. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, P.; Gu, S.; Hu, X.; Tang, S.; Yang, L.; Xu, N.; Zhen, Z.; Wang, L.; Wu, Q.; et al. Capability of Fengyun-3D satellite in Earth system observation. J. Meteorol. Res. 2019, 33, 1113–1130. [Google Scholar] [CrossRef]
- Tang, F.; Zhuge, X.; Zeng, M.; Li, X.; Dong, P.; Han, Y. Applications of the Advanced Radiative Transfer Modeling System (ARMS) to characterize the performance of Fengyun–4A/AGRI. Remote Sens. 2021, 13, 3120. [Google Scholar] [CrossRef]
- Yang, J.; Ding, S.; Dong, P.; Bi, L.; Yi, B. Advanced Radiative Transfer Modeling System developed for satellite data assimilation and remote sensing applications. J. Quant. Spectrosc. Radiat. Transf. 2020, 251, 107043. [Google Scholar] [CrossRef]
- Shi, Y.-N.; Yang, J.; Weng, F. Discrete Ordinate Adding Method (DOAM), a new solver for Advanced Radiative Transfer Modeling System (ARMS). Opt. Express 2021, 29, 4700. [Google Scholar] [CrossRef] [PubMed]
- Weng, F.; Yu, X.; Duan, Y.; Yang, J.; Wang, J. Advanced Radiative Transfer Modeling System (ARMS): A new-generation satellite observation operator developed for numerical weather prediction and remote sensing applications. Adv. Atmos. Sci. 2020, 37, 131–136. [Google Scholar] [CrossRef]
- Weng, F. Advances in radiative transfer modeling in support of satellite data assimilation. J. Atmos. Sci. 2007, 64, 3799–3807. [Google Scholar] [CrossRef]
- Peng, W.; Weng, F.; Ye, C. The impact of MERRA-2 and CAMS aerosol reanalysis data on FengYun-4B geostationary interferometric infrared sounder simulations. Remote Sens. 2025, 17, 761. [Google Scholar] [CrossRef]
- Wang, H.; Mao, K.; Mu, F.; Shi, J.; Yang, J.; Li, Z.; Qin, Z. A split window algorithm for retrieving land surface temperature from FY-3D MERSI-2 data. Remote Sens. 2019, 11, 2083. [Google Scholar] [CrossRef]
- Yan, L.; Hu, Y.; Zhang, Y.; Li, X.-M.; Dou, C.; Li, J.; Si, Y.; Zhang, L. Radiometric calibration evaluation for FY-3D MERSI-II thermal infrared channels at Lake Qinghai. Remote Sens. 2021, 13, 466. [Google Scholar] [CrossRef]
- Chen, H.; Meng, X.; Li, L.; Ni, K. Quality assessment of FY-3D/MERSI-II thermal infrared brightness temperature data from the Arctic region: Application to ice surface temperature inversion. Remote Sens. 2022, 14, 6392. [Google Scholar] [CrossRef]
- Xiong, X.; Angal, A.; Chang, T.; Aldoretta, E.; Geng, X.; Link, D.; Sun, J.; Twedt, K.; Wu, A. Aqua MODIS: 20 years of on-orbit calibration and performance. J. Appl. Remote Sens. 2023, 17, 037501. [Google Scholar] [CrossRef]
- Xiong, X.; Chiang, K.; Sun, J.; Barnes, W.L.; Guenther, B.; Salomonson, V.V. NASA EOS Terra and Aqua MODIS on-orbit performance. Adv. Space Res. 2009, 43, 413–422. [Google Scholar] [CrossRef]
- Bell, B.; Hersbach, H.; Simmons, A.; Berrisford, P.; Dahlgren, P.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis: Preliminary extension to 1950. Q. J. R. Meteorol. Soc. 2021, 147, 4186–4227. [Google Scholar] [CrossRef]
- Cao, C.; Weinreb, M.; Xu, H. Predicting simultaneous nadir overpasses among polar-orbiting meteorological satellites for the intersatellite calibration of radiometers. J. Atmos. Oceanic Technol. 2004, 21, 537–542. [Google Scholar] [CrossRef]
- Yang, W.; Meng, H.; Ferraro, R.R.; Chen, Y. Inter-calibration of AMSU-A window channels. Remote Sens. 2020, 12, 2988. [Google Scholar] [CrossRef]
- Wang, L.; Goldberg, M.; Wu, X.; Cao, C.; Iacovazzi, R.A.; Yu, F.; Li, Y. Consistency assessment of Atmospheric Infrared Sounder and Infrared Atmospheric Sounding Interferometer radiances: Double differences versus simultaneous nadir overpasses. J. Geophys. Res. 2011, 116, D11111. [Google Scholar] [CrossRef]
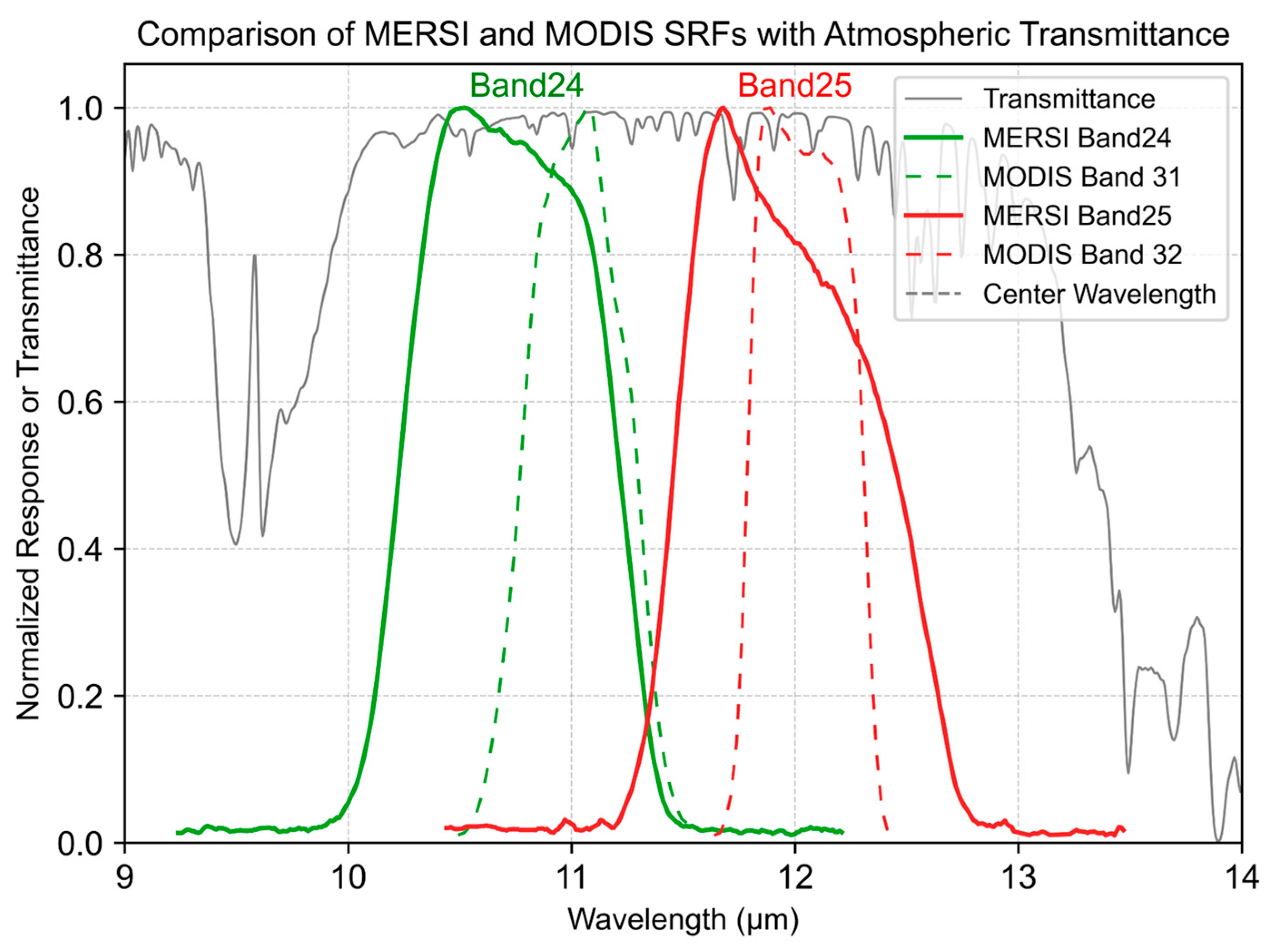











| MERSI Band | Wavelength (µm) | Primary Application | MODIS Band | Wavelength (µm) | Primary Application |
|---|---|---|---|---|---|
| 20 | 3.60–3.90 | Land and cloud temperature | 20 | 3.66–3.84 | Land and cloud temperature |
| 21 | 4.00–4.10 | Fire detection/high-temp anomaly | 23 | 4.02–4.08 | Fire detection/high-temp anomaly |
| 22 | 7.15–7.25 | Atmospheric water vapor | 28 | 7.18–7.48 | Atmospheric water vapor |
| 23 | 8.45–8.65 | Surface emissivity/cloud phase | 29 | 8.40–8.70 | Surface emissivity/cloud phase |
| 24 | 10.60–11.00 | Land and cloud temperature | 31 | 10.78–11.28 | Land and cloud temperature |
| 25 | 11.80–12.20 | Land and cloud temperature | 32 | 11.77–12.27 | Land and cloud temperature |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, S.; Weng, F.; Han, X.; Ye, C. Comparative Evaluation of SNO and Double Difference Calibration Methods for FY-3D MERSI TIR Bands Using MODIS/Aqua as Reference. Remote Sens. 2025, 17, 3353. https://doi.org/10.3390/rs17193353
An S, Weng F, Han X, Ye C. Comparative Evaluation of SNO and Double Difference Calibration Methods for FY-3D MERSI TIR Bands Using MODIS/Aqua as Reference. Remote Sensing. 2025; 17(19):3353. https://doi.org/10.3390/rs17193353
Chicago/Turabian StyleAn, Shufeng, Fuzhong Weng, Xiuzhen Han, and Chengzhi Ye. 2025. "Comparative Evaluation of SNO and Double Difference Calibration Methods for FY-3D MERSI TIR Bands Using MODIS/Aqua as Reference" Remote Sensing 17, no. 19: 3353. https://doi.org/10.3390/rs17193353
APA StyleAn, S., Weng, F., Han, X., & Ye, C. (2025). Comparative Evaluation of SNO and Double Difference Calibration Methods for FY-3D MERSI TIR Bands Using MODIS/Aqua as Reference. Remote Sensing, 17(19), 3353. https://doi.org/10.3390/rs17193353






