Bundled-Images Based Geo-Positioning Method for Satellite Images Without Using Ground Control Points
Abstract
Highlights
- A new bundled-images based geo-positioning method without ground control points.
- A detailed strategy for leveraging a Kalman filter to integrate new image observations with their corresponding historical information.
- Validated with heterogeneous TH-1 and ZY-3 datasets and homologous IKONOS datasets, meeting the mapping demands at the corresponding scale without ground control points.
- Potential for regional and global mapping without using ground control points.
Abstract
1. Introduction
- 1.
- We utilize a Kalman filter to integrate new image observations with their a priori covariance information derived from bundled images. This approach enables efficient image orientation while excluding bundled image point observations.
- 2.
- The historical bundled images can be updated with posterior covariance information to maintain consistent accuracy with the new bundled image.
- 3.
- Without using GCPs, the proposed bundled-images based geo-positioning method meets 1:50,000 mapping standards with heterogeneous TH-1 and ZY-3 datasets and 1:10,000 mapping accuracy requirements with homologous IKONOS datasets.
2. Related Work
2.1. Attitude Error Compensation
2.2. Virtual Control Points Taken as a Substitute for GCPs
2.3. High-Precision Geographic Data Taken as a Substitute for GCPs
3. Methodology
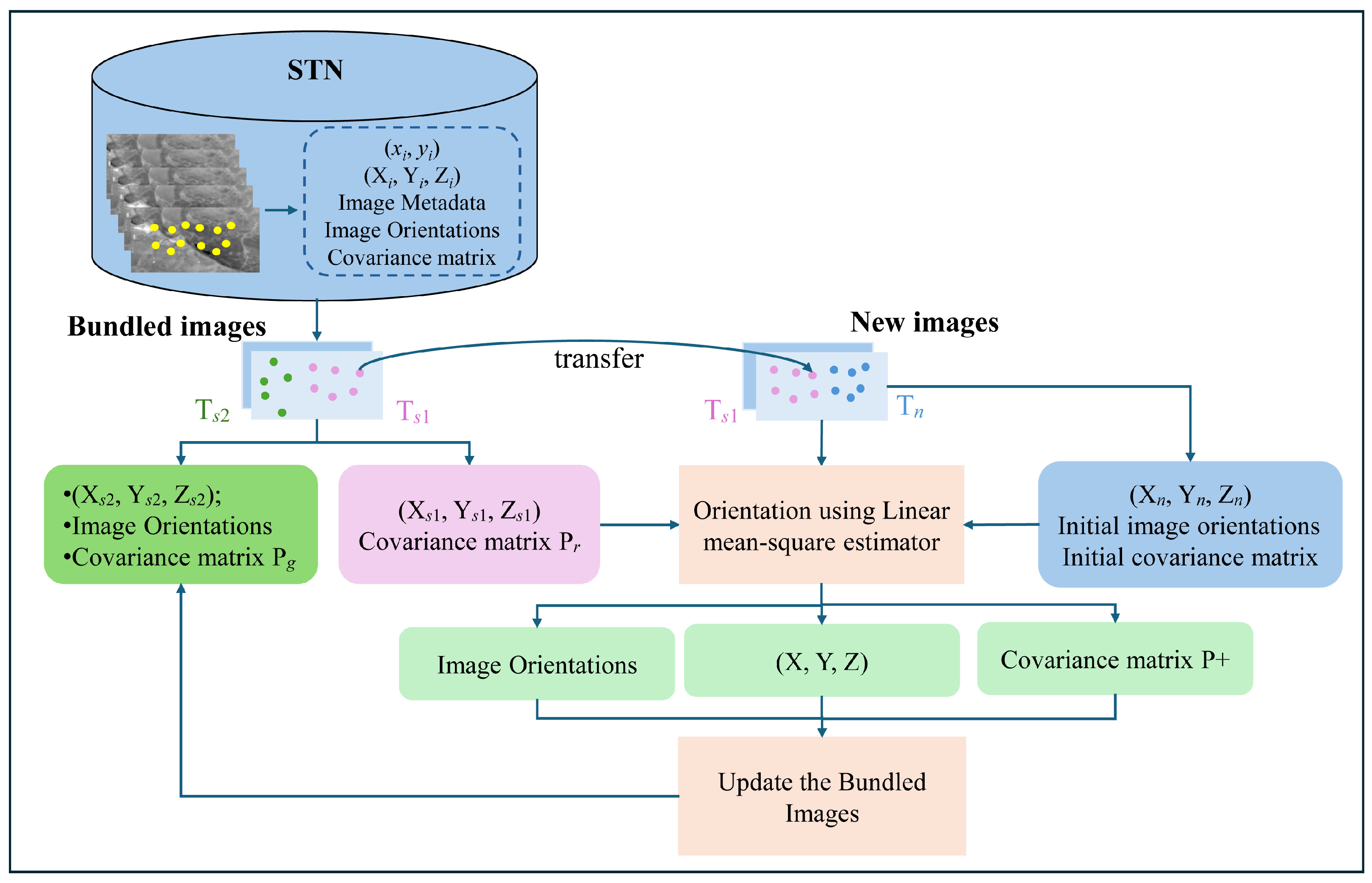
3.1. Overview of the Proposed Merged Method
3.2. The Theoretical Foundations of the Proposed Merged Method
3.2.1. Corresponding Points Acquisition
3.2.2. The Mathematics of RFM
3.2.3. Basic Principles of the Kalman Filter
3.2.4. The Proposed Merged Method
- (1)
- The first step of orientation
- (2)
- The second step of updating
- (3)
- Accuracy assessment
4. Data
4.1. Homologous IKONOS Datasets
4.2. Heterogeneous TH-1 and ZY-3 Datasets
5. Experimental Analysis and Discussion
5.1. Heterogeneous TH-1 and ZY-3 Datasets
5.1.1. Comparative Experiments
5.1.2. Analysis and Discussion
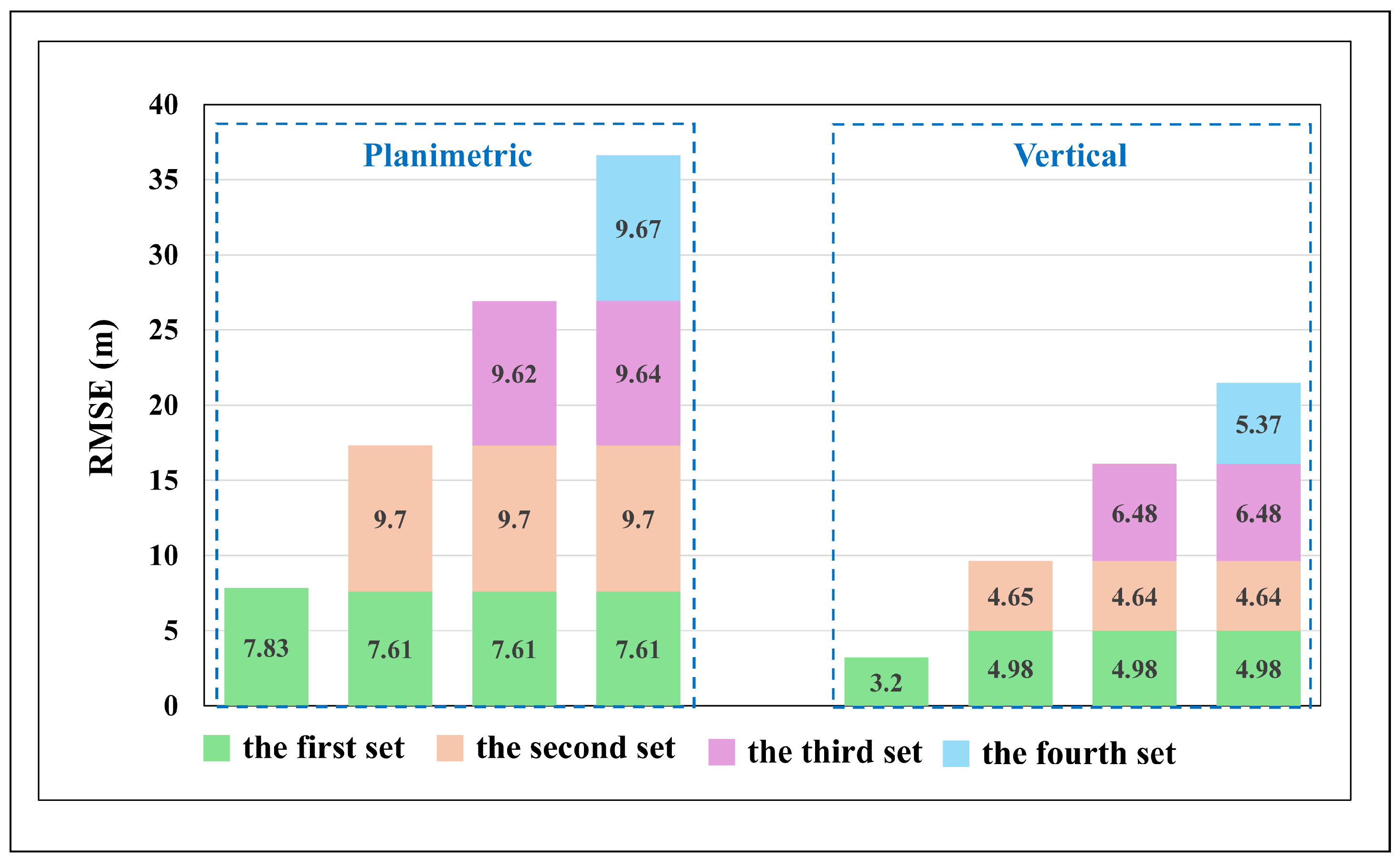
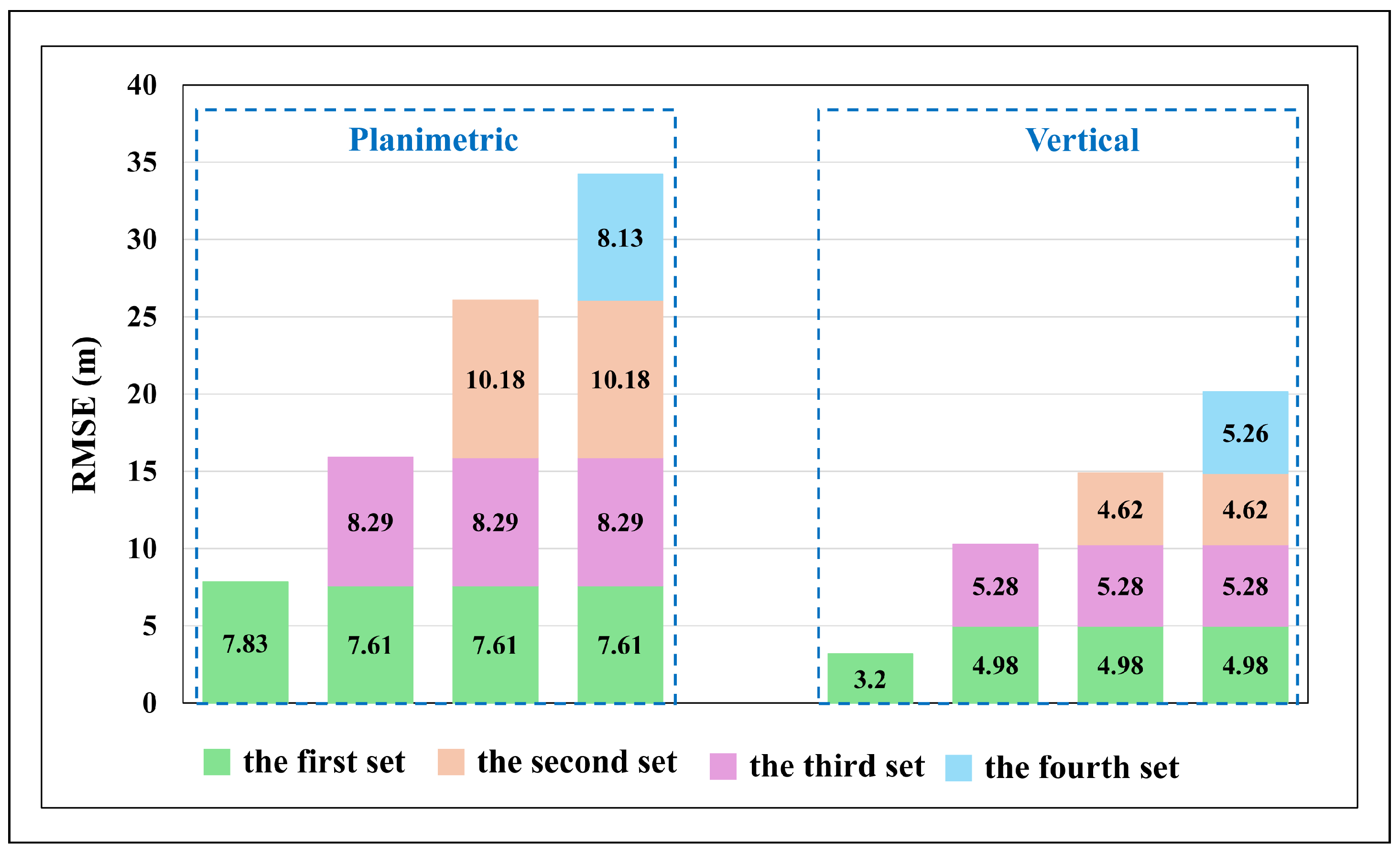
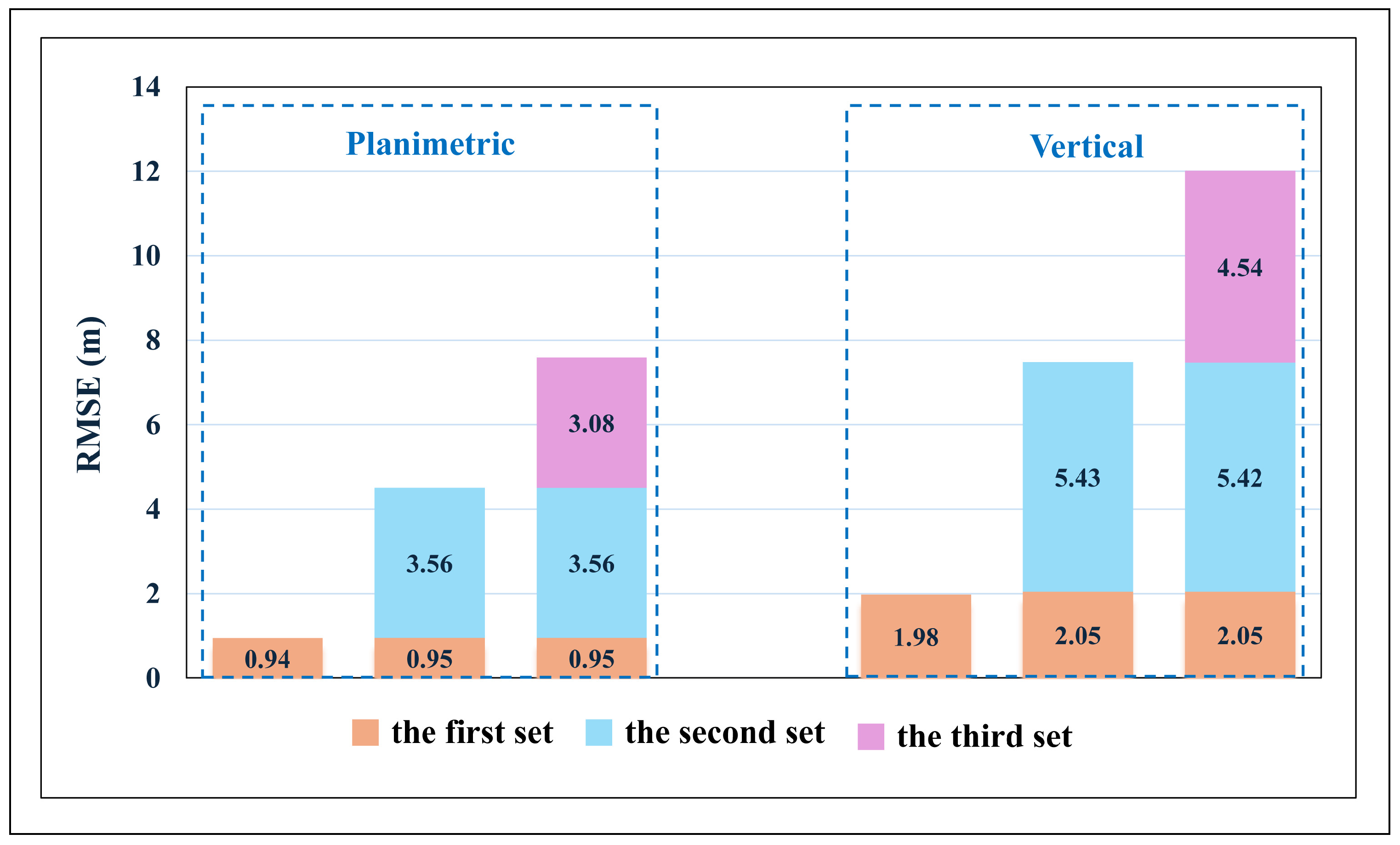
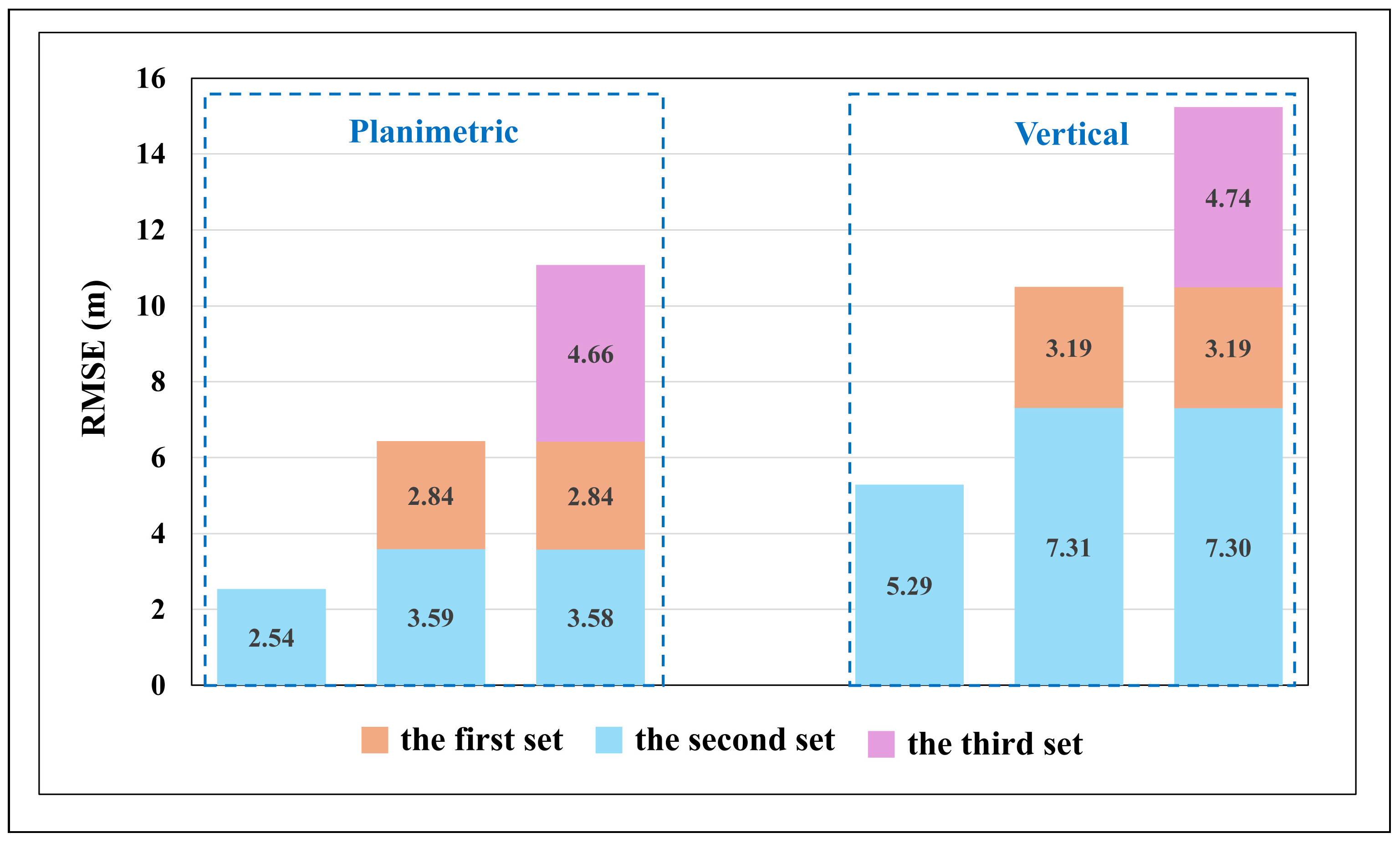
- (1)
- The first experiment with the proposed merged method
- (2)
- The second experiment with the proposed merged method
- (3)
- The second experiment with the proposed merged method
5.2. Homologous IKONOS Datasets
5.2.1. Comparative Experiments
5.2.2. Analysis and Discussion
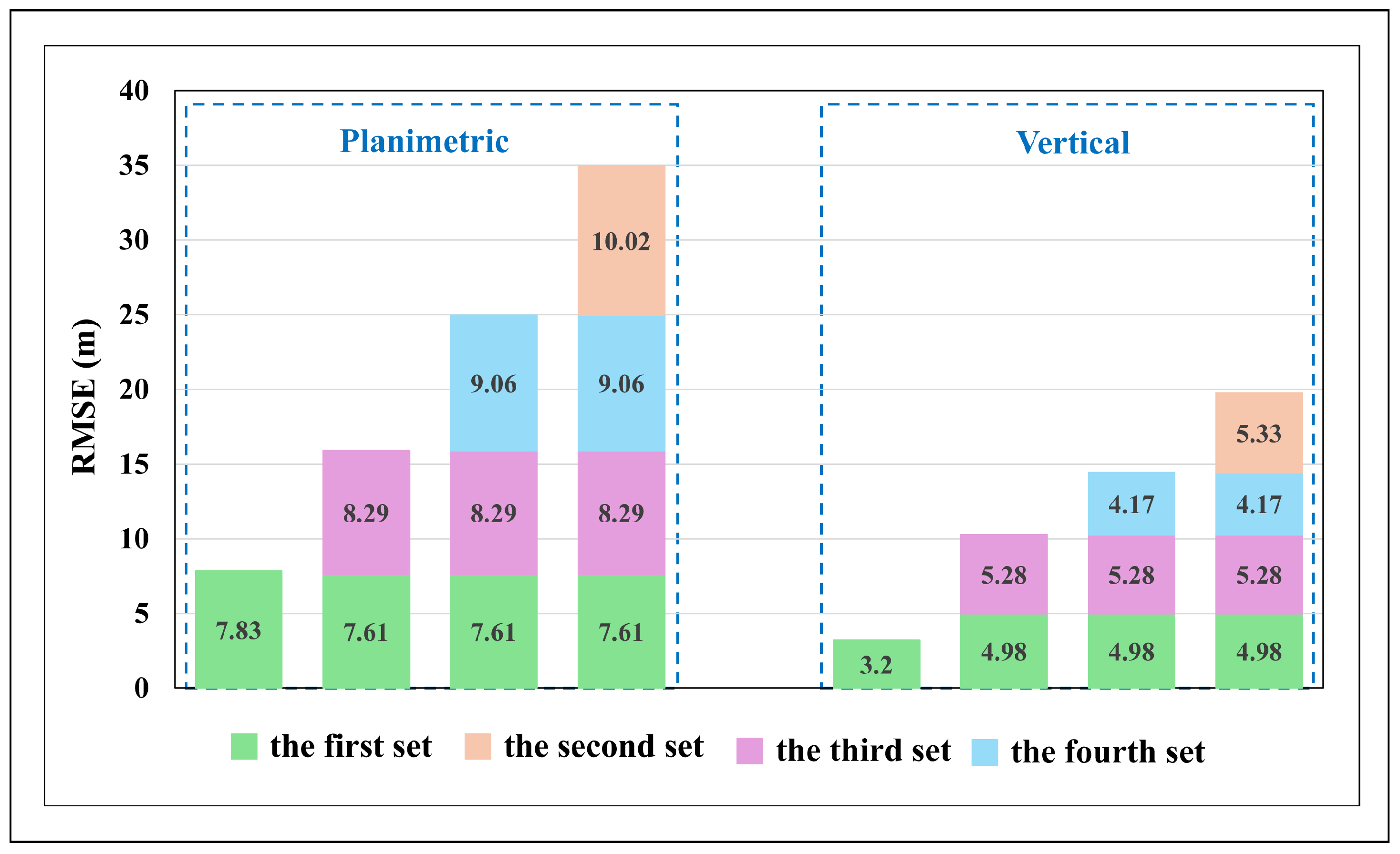
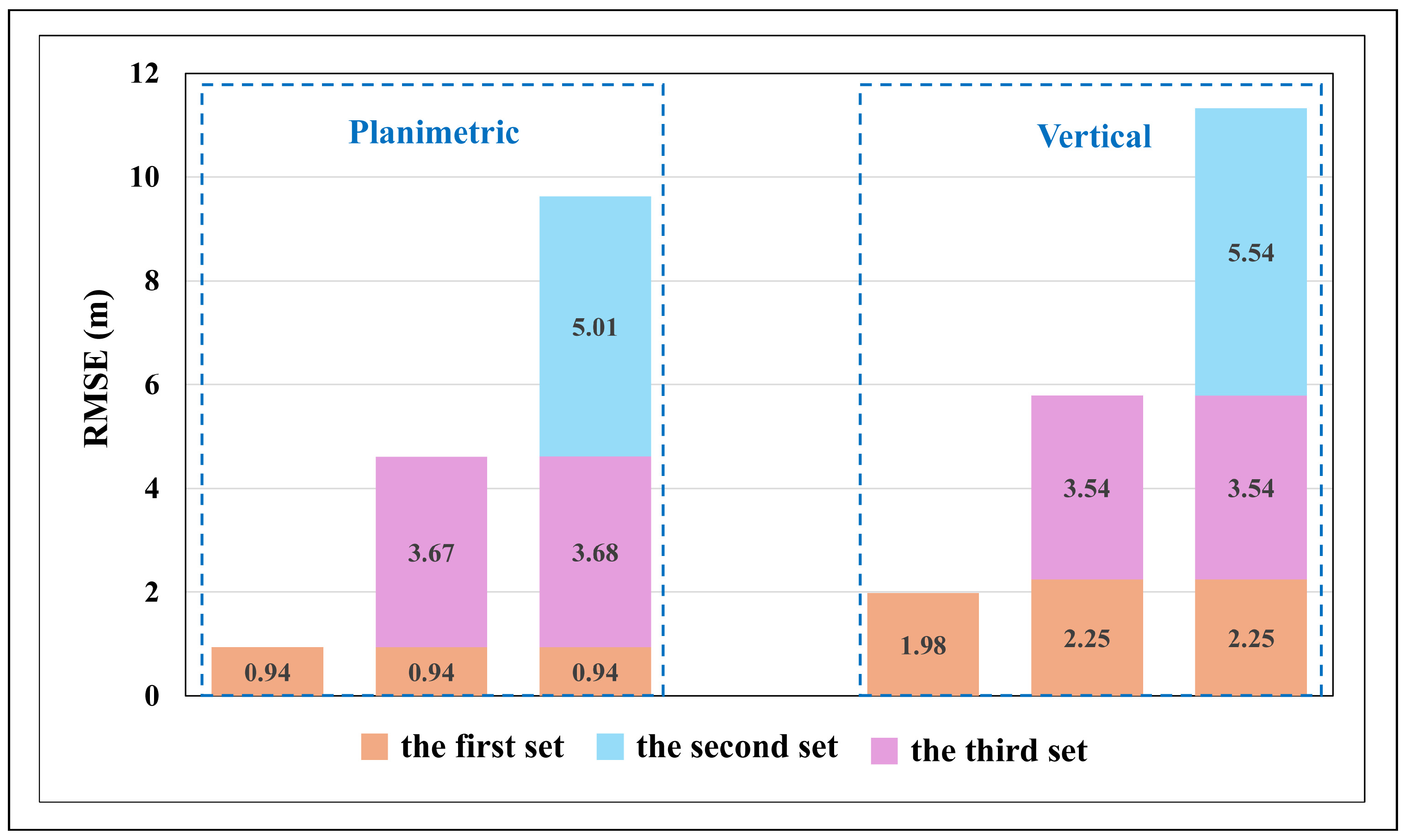
- (1)
- The first experiment with the proposed merged method
- (2)
- The second experiment with the proposed merged method
- (3)
- The third experiment with the proposed merged method
5.3. Computational Performance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tong, X.; Fu, Q.; Liu, S.; Wang, H.; Ye, Z.; Jin, Y.; Chen, P.; Xu, X.; Wang, C.; Liu, S.; et al. Optimal selection of virtual control points with planar constraints for large-scale block adjustment of satellite imagery. Photogramm. Rec. 2020, 35, 487–508. [Google Scholar] [CrossRef]
- Zhang, Z.; Tao, P. An Overview on “Cloud Control” Photogrammetry in Big Data Era. Acta Geod. Cartogr. Sin. 2017, 46, 1238–1248. [Google Scholar]
- Zhong, H.; Duan, Y.; Zhou, Q.; Chen, Q.; Cai, B.; Tao, P.; Zhang, Z. Calibrating an airborne linear-array multi-camera system on the master focal plane with existing bundled images. Geo-Spat. Inf. Sci. 2025, 28, 1141–1159. [Google Scholar] [CrossRef]
- Cao, H.; Tao, P.; Li, H.; Zhang, Z. Using DEM as full controls in block adjustment of satellite imagery. Acta Geod. Cartogr. Sin. 2020, 49, 79–91. [Google Scholar]
- Liu, C.; Tang, X.; Zhang, H.; Li, G.; Wang, X.; Li, F. Geopositioning improvement of ZY-3 satellite imagery integrating GF-7 Laser Altimetry data. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Wang, J.; Wang, R.; Hu, X.; Su, Z. The on-orbit calibration of geometric parameters of the Tian-Hui 1 (TH-1) satellite. ISPRS J. Photogramm. Remote Sens. 2017, 124, 144–151. [Google Scholar] [CrossRef]
- Wang, J.; Wang, R. Efp multi-functional bundle adjustment without ground control points for th-1 satellite. J. Remote Sens. 2012, 16, 112–115. [Google Scholar]
- Wang, R.; Wang, J.; Li, J. Improvement strategy for location accuracy without ground control points of 3rd satellite of TH-1. Acta Geod. Cartogr. Sin. 2019, 48, 671–675. [Google Scholar]
- Zhang, Y.; Zheng, M.; Xiong, X.; Xiong, J. Multistrip bundle block adjustment of zy-3 satellite imagery by rigorous sensor model without ground control point. IEEE Geosci. Remote Sens. Lett. 2015, 12, 865–869. [Google Scholar] [CrossRef]
- Yang, B.; Pi, Y.; Li, X.; Wang, M. Relative geometric refinement of patch images without use of ground control points for the geostationary optical satellite gaofen4. IEEE Trans. Geosci. Remote Sens. 2018, 56, 474–484. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, L.; Xu, B.; Zhang, Y. Method and GCP-independent block adjustment for ZY-3 satellite images. J. Remote Sens. 2019, 23, 205–214. [Google Scholar] [CrossRef]
- Toutin, T.; Schmitt, C.; Wang, H. Impact of no gcp on elevation extraction from worldview stereo data. ISPRS J. Photogramm. Remote Sens. 2012, 72, 73–79. [Google Scholar] [CrossRef]
- Liu, K.; Tao, P.; Tan, K.; Duan, Y.; He, J.; Luo, X. Adaptive re-weighted block adjustment for multi-coverage satellite stereo images without ground control points. IEEE Access 2019, 7, 112120–112130. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Zhang, Z.; Li, X.; Tao, P.; Song, M. Icesat laser points assisted block adjustment for mapping satellite-1 imagery. Acta Geod. Cartogr. Sin. 2018, 47, 359–369. [Google Scholar]
- Zhang, G.; Jiang, B.; Wang, T.; Ye, Y.; Li, X. Combined block adjustment for optical satellite stereo imagery assisted by spaceborne sar and laser altimetry data. Remote Sens. 2021, 13, 3062. [Google Scholar] [CrossRef]
- Wang, M.; Wei, Y.; Pi, Y. Geometric positioning integrating optical satellite stereo imagery and a global database of icesat-2 laser control points: A framework and key technologies. Geo-Spat. Inf. Sci. 2023, 26, 206–217. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, Z.; Tan, M.; Wei, S.; Zhang, G.; Guan, Z.; Han, B. A stable block adjustment method without ground control points using bound constrained optimization. Int. J. Remote Sens. 2022, 43, 4708–4722. [Google Scholar] [CrossRef]
- Pi, Y.; Yang, B. Block adjustment of multispectral images without gcp aided by stereo tlc images for zy-3 satellite. isprs annals of the photogrammetry. Remote Sens. Spat. Inf. Sci. 2020, V-2-2020, 65–72. [Google Scholar] [CrossRef]
- Cheng, C.; Zhang, J.; Huang, G.; Zhang, L.; Yang, J. Combined positioning of TerraSAR-X and SPOT-5 HRS images with RFM considering accuracy information of orientation parameters. Acta Geod. Cartogr. Sin. 2017, 46, 179–187. [Google Scholar]
- Teo, T.; Chen, L.; Liu, C.; Tung, Y.; Wu, W. Dem-aided block adjustment for satellite images with weak convergence geometry. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1907–1918. [Google Scholar] [CrossRef]
- Ma, Z.; Wu, X.; Yan, L.; Xu, Z. Geometric Positioning for Satellite Imagery without Ground Control Points by Exploiting Repeated Observation. Sensors 2017, 17, 240. [Google Scholar] [CrossRef] [PubMed]
- Dolloff, J.; Iiyama, M. Fusion of image block adjustments for the generation of a ground control network. In Proceeding of the 10th International Conference on Information Fusion, Québec, QC, Canada, 9–12 July 2007. [Google Scholar]
- Ma, Z.; Song, W.; Deng, J.; Wang, J.; Cui, C. A rational function model based geo-positioning method for satellite images without using ground control points. Remote Sens. 2018, 10, 182. [Google Scholar] [CrossRef]
- Grodecki, J.; Dial, G. Block adjustment of high-resolution satellite images described by rational polynomials. Photogramm. Eng. Remote Sens. 2003, 69, 59–68. [Google Scholar] [CrossRef]
- ITEK Corporation. Conceptual Design of an Automated Mapping Satellite System (Mapsat); National Technology Information Server: Lexington, KY, USA, 1981. [Google Scholar]
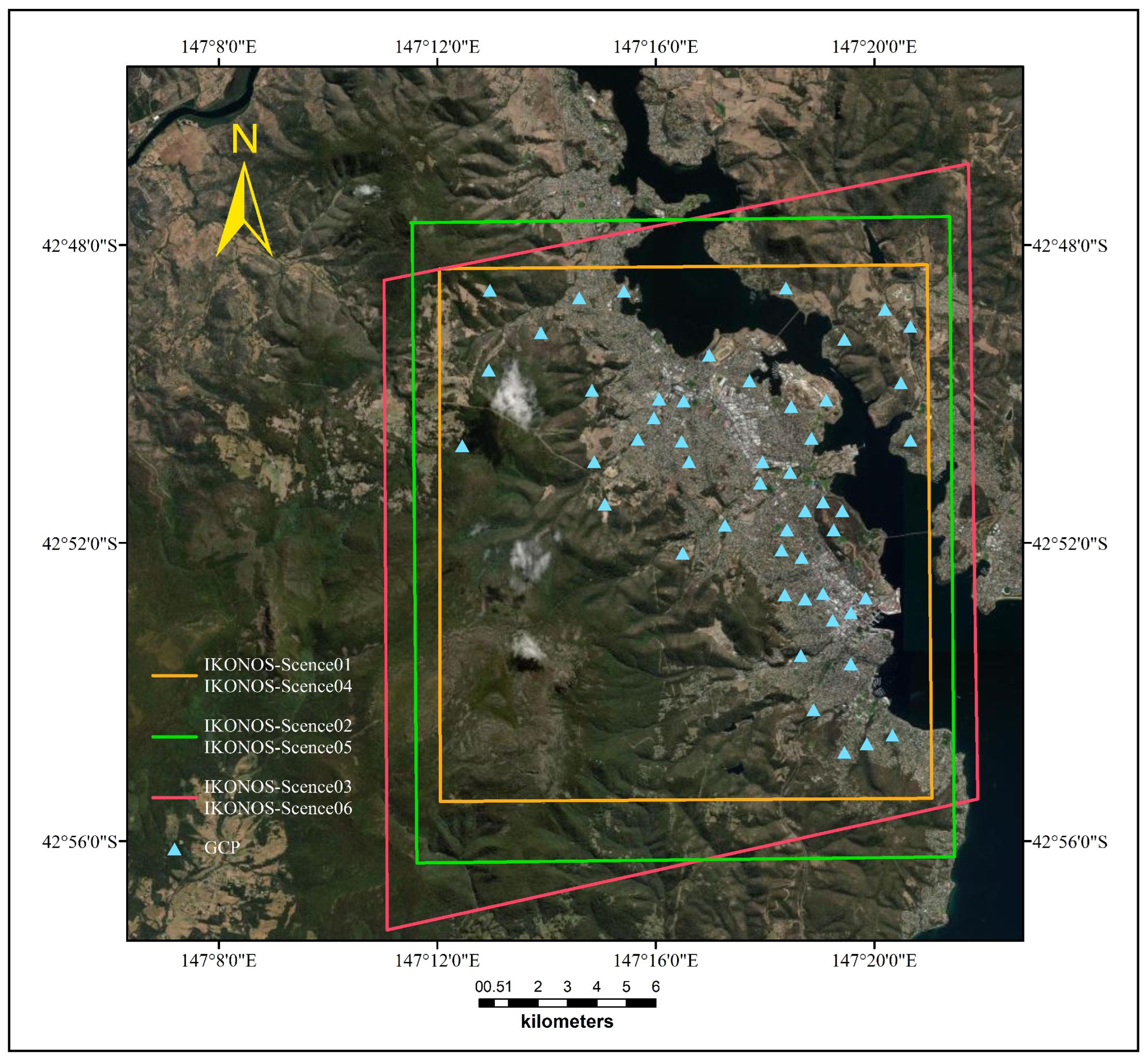
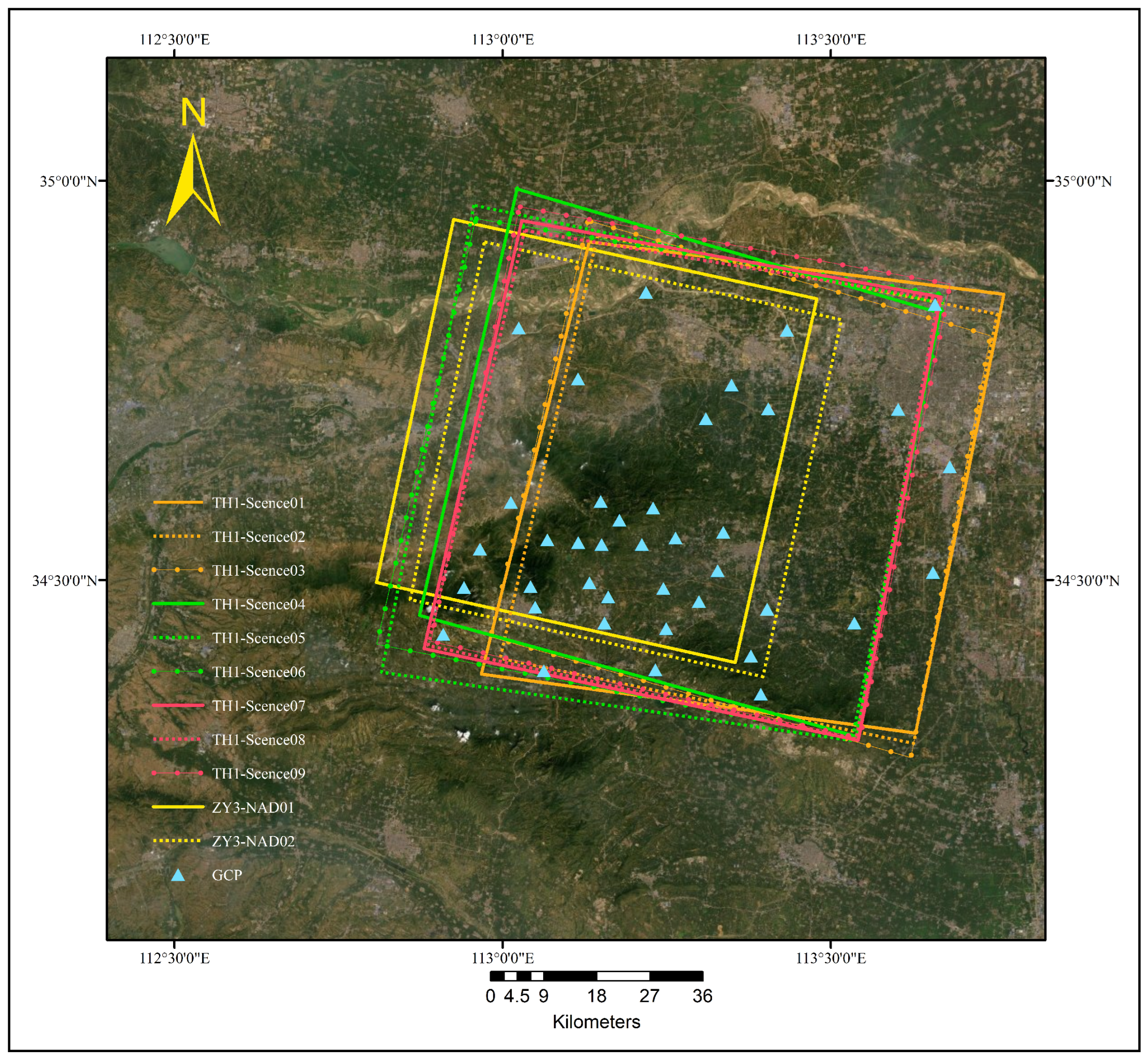
| Set | Image Name | Acquisition Time | Sensor Azimuth (°) | Resolution (m) | Image Size (Pixels) |
|---|---|---|---|---|---|
| 1 | IKONOS-Scence01 | 22 February 2003 00:27:24.8 | 293.7 | 1 | 12,124 × 13,148 |
| IKONOS-Scence02 | 22 February 2003 00:27:03.8 | 329.4 | 1 | 12,124 × 13,148 | |
| 2 | IKONOS-Scence03 | 22 February 2003 00:27:54.3 | 235.7 | 1 | 12,124 × 13,148 |
| IKONOS-Scence04 | 22 February 2003 00:27:24.8 | 293.7 | 4 | 3031 × 3287 | |
| 3 | IKONOS-Scence05 | 22 February 2003 00:27:03.8 | 329.4 | 4 | 3031 × 3287 |
| IKONOS-Scence06 | 22 February 2003 00:27:54.3 | 235.7 | 4 | 3031 × 3287 |
| Set | Image Name | Acquisition Time | Sensor | Resolution (m) | Image Size (Pixels) |
|---|---|---|---|---|---|
| TH1-Scence01 | 27 March 2013 | Forward | |||
| 1 | TH1-Scence02 | 27 March 2013 | Nadir | 5 | 12,000 × 12,000 |
| TH1-Scence03 | 27 March 2013 | Backward | |||
| TH1-Scence04 | 15 June 2013 | Forward | |||
| 2 | TH1-Scence05 | 15 June 2013 | Nadir | 5 | 12,000 × 12,000 |
| TH1-Scence06 | 15 June 2013 | Backward | |||
| TH1-Scence07 | 30 August 2013 | Forward | |||
| 3 | TH1-Scence08 | 30 August 2013 | Nadir | 5 | 12,000 × 12,000 |
| TH1-Scence09 | 30 August 2013 | Backward | |||
| 4 | ZY3-NAD01 | 3 November 2013 | Nadir | 2.1 | 24,525 × 24,410 |
| ZY3-NAD02 | 3 February 2012 | Nadir |
| The Traditional Method | The Direct Method | The Merged Method | |
|---|---|---|---|
| Planimetric | 7.97 | 7.88 | 8.49 |
| Vertical | 4.29 | 4.21 | 3.20 |
| The Traditional Method | The Direct Method | The Merged Method I | The Merged Method II | |
|---|---|---|---|---|
| Planimetric | 7.88 | 7.75 | 8.19 | 7.69 |
| Vertical | 4.72 | 4.61 | 3.12 | 3.07 |
| The Traditional Method | The Direct Method | The Merged Method I | The Merged Method II | The Merged Method III | |
|---|---|---|---|---|---|
| Planimetric | 8 | 7.73 | 8.22 | 6.72 | 7.39 |
| Vertical | 5.19 | 4.58 | 3.43 | 3.12 | 3.18 |
| The Traditional Method | The Direct Method | The Merged Method | |
|---|---|---|---|
| Planimetric | 0.75 | 0.73 | 1.29 |
| Vertical | 0.75 | 0.82 | 0.89 |
| The Traditional Method | The Direct Method | The Merged Method I | The Merged Method II | The Merged Method III | |
|---|---|---|---|---|---|
| Planimetric | 0.74 | 0.84 | 1.28 | 1.14 | 2.26 |
| Vertical | 0.64 | 0.77 | 0.71 | 0.83 | 3.02 |
| IKONOS | TH-1 | |
|---|---|---|
| the direct method | 0.928 | 1.24 |
| the merged method | 0.561 | 0.597 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Z.; Chen, Y.; Zhong, X.; Xie, H.; Liu, Y.; Wang, Z.; Shi, P. Bundled-Images Based Geo-Positioning Method for Satellite Images Without Using Ground Control Points. Remote Sens. 2025, 17, 3289. https://doi.org/10.3390/rs17193289
Ma Z, Chen Y, Zhong X, Xie H, Liu Y, Wang Z, Shi P. Bundled-Images Based Geo-Positioning Method for Satellite Images Without Using Ground Control Points. Remote Sensing. 2025; 17(19):3289. https://doi.org/10.3390/rs17193289
Chicago/Turabian StyleMa, Zhenling, Yuan Chen, Xu Zhong, Hong Xie, Yanlin Liu, Zhengjie Wang, and Peng Shi. 2025. "Bundled-Images Based Geo-Positioning Method for Satellite Images Without Using Ground Control Points" Remote Sensing 17, no. 19: 3289. https://doi.org/10.3390/rs17193289
APA StyleMa, Z., Chen, Y., Zhong, X., Xie, H., Liu, Y., Wang, Z., & Shi, P. (2025). Bundled-Images Based Geo-Positioning Method for Satellite Images Without Using Ground Control Points. Remote Sensing, 17(19), 3289. https://doi.org/10.3390/rs17193289






