From the Moon to Mercury: Release of Global Crater Catalogs Using Multimodal Deep Learning for Crater Detection and Morphometric Analysis
Abstract
Highlights
- First global crater catalog for Mercury (>400 m) produced using a multimodal deep-learning pipeline.
- Extension of YOLOLens to multimodal inputs enables robust crater detection in shadowed and degraded terrains.
- Multimodal learning establishes a scalable approach for planetary crater detection and morphometric studies.
- Cross-planet generalization opens the way to automated crater detection on other planetary bodies.
Abstract
1. Introduction
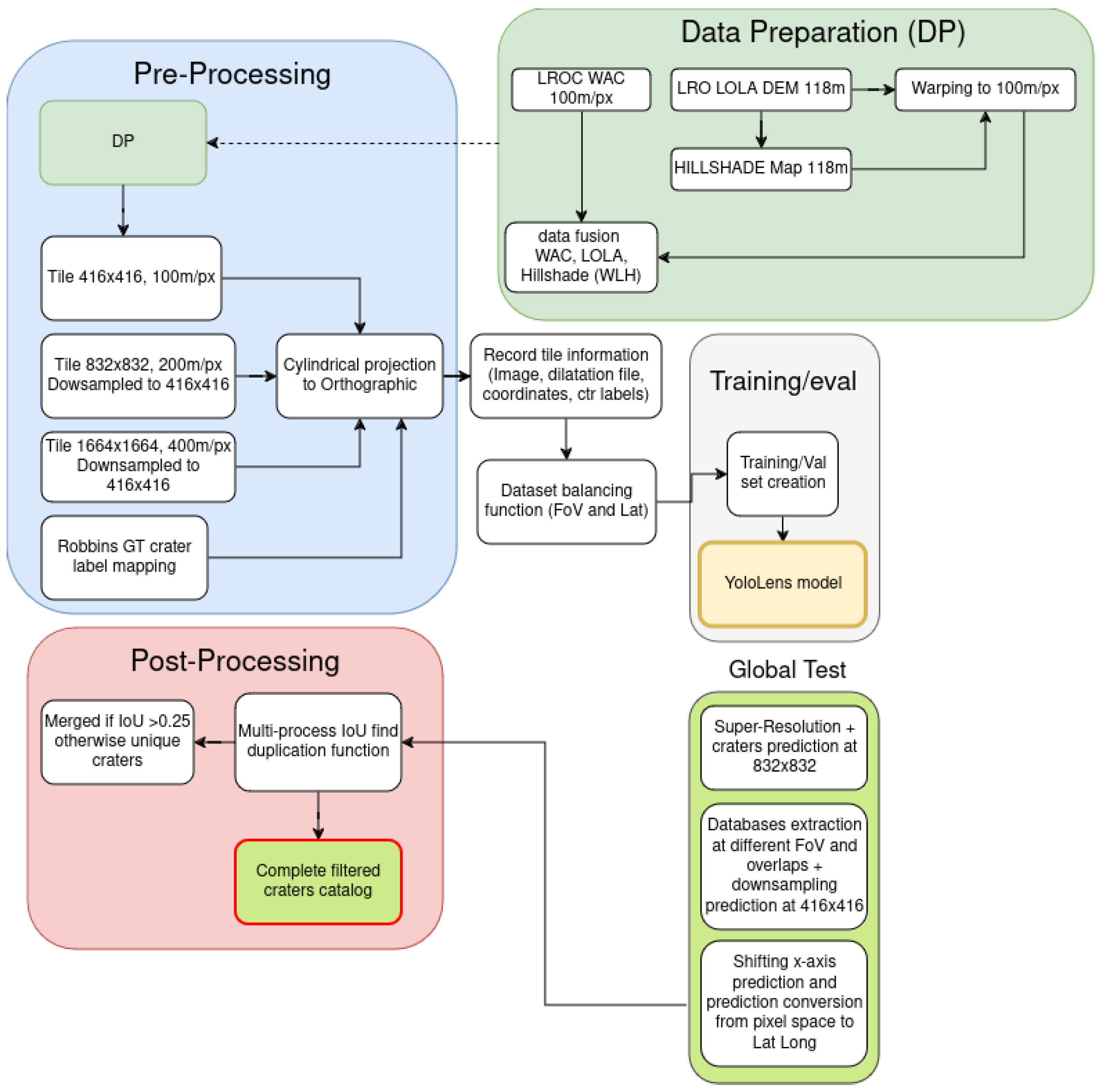
2. Materials and Methods
2.1. Preprocessing and Dataset
Overcoming the Limitations of Imagery in Permanently Shadowed Regions
- LROC WAC Image: This serves as a baseline visual representation, capturing the albedo variations, textures, and subtle patterns suggestive of the crater forms.
- LROC WAC DTM: The DTM directly encodes elevation data. Key aspects beneficial for crater detection include the following:Rim Definition: Pronounced elevation changes at crater rims become starkly visible in the DTM, allowing the model to delineate crater boundaries more confidently, even for degraded or partially obscured craters.Interior Depth: The craters exhibit a distinct bowl-shaped depth profile that the DTM highlights, helping discriminate them from other circular depressions that might appear similar in the WAC image alone.
- LROC WAC Hillshade: Simulates how the terrain would appear when illuminated from a specific angle. Strategically, it emphasizes topographic details, providing a perspective to enhance the robustness of the features.
2.2. The Model
- Super-Resolution Generator: The generator applies super-resolution to the input, producing a high-resolution image:where is the resolution scaling factor, and .
- Object-Detection Model: The high-resolution output is then forwarded to an object-detection model , which performs object-detection and returns a set of predictions:where is the set of detected objects and their corresponding attributes (e.g., class labels, bounding box coordinates, and confidence scores).
- Unified Function: The entire system can be represented as a composite function , where
2.3. Methods for Extraction of Morphometric Parameters
3. Results
3.1. Enhancements to the Lunar Global Catalog: The LU6M371TGT
3.2. Model’s Performance
- Longitude, latitude: These are the crater’s center coordinates in decimal degrees, between and . The format utilizes a two-dimensional coordinate system, with separate values for the x and y coordinates.
- Diameters W, H: These variables represent the horizontal and vertical sides, respectively, of the bounding box of the crater, expressed in kilometers.
- Confidence: This variable measures the certainty level of the crater identification by means of our model. Higher confidence values suggest a greater likelihood that the identified feature is indeed a crater. This variable is vital for assessing the reliability of each crater record.
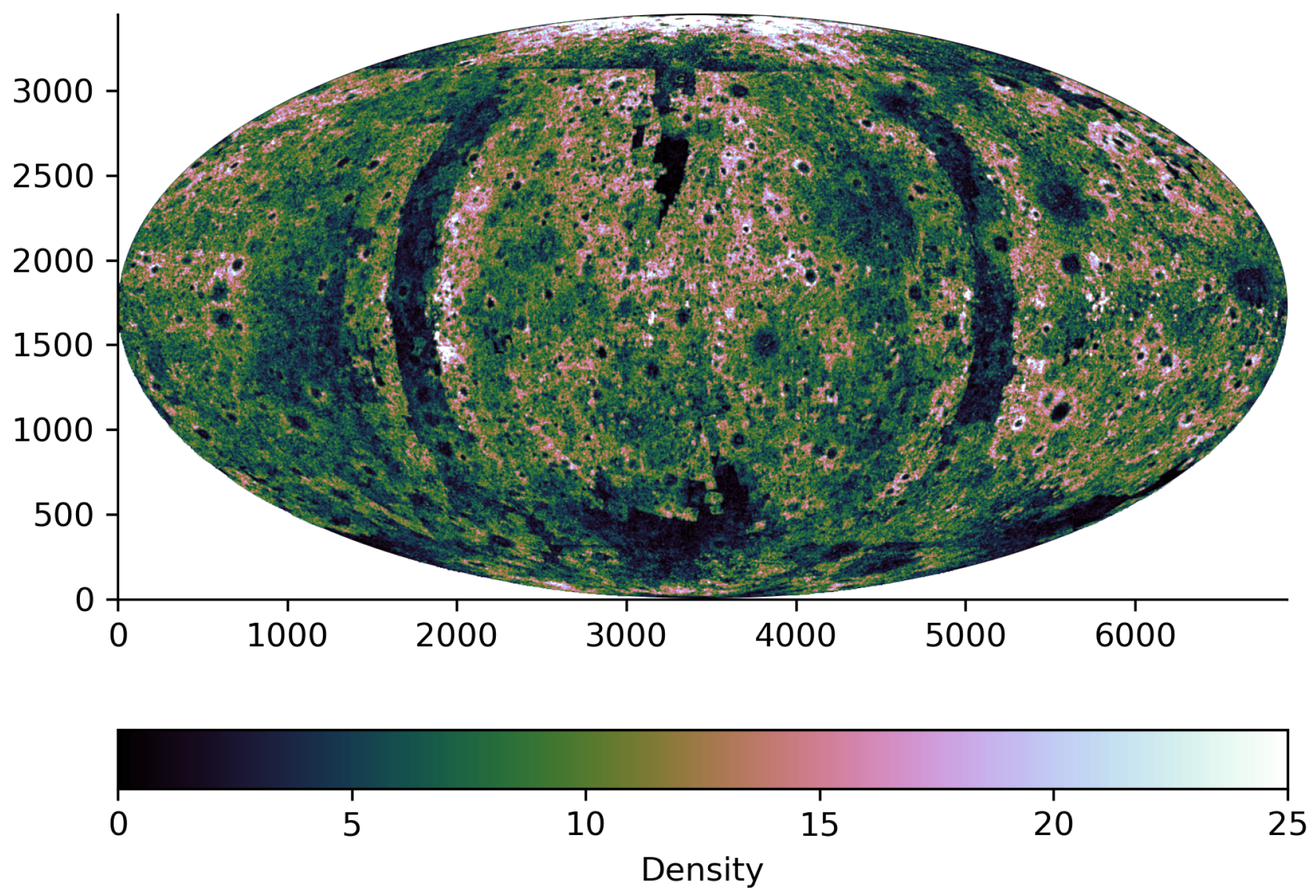
3.3. The Global Mercury Catalog ME6M300TGT
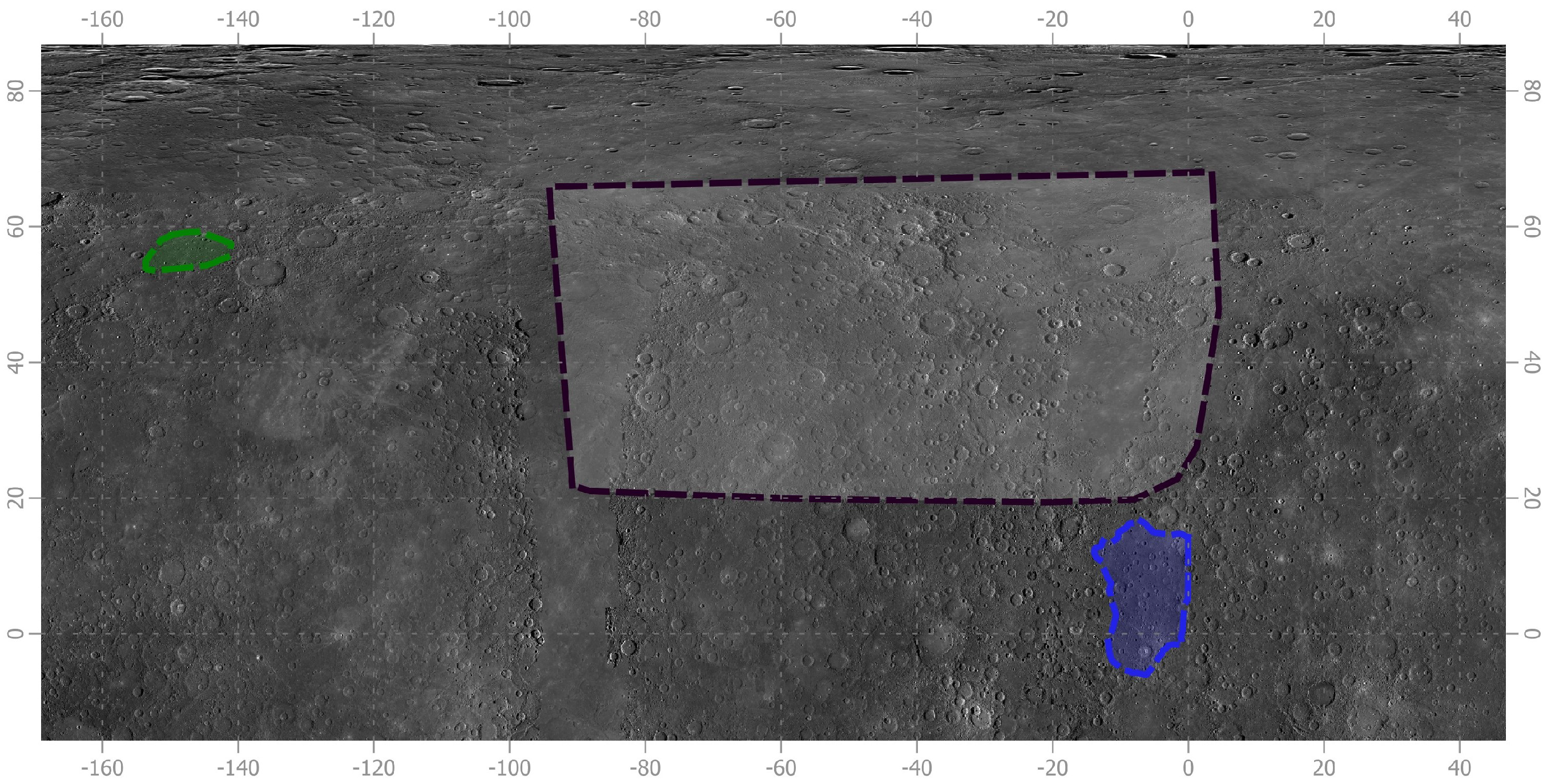
3.3.1. Evaluation of the Crater-Detection Model
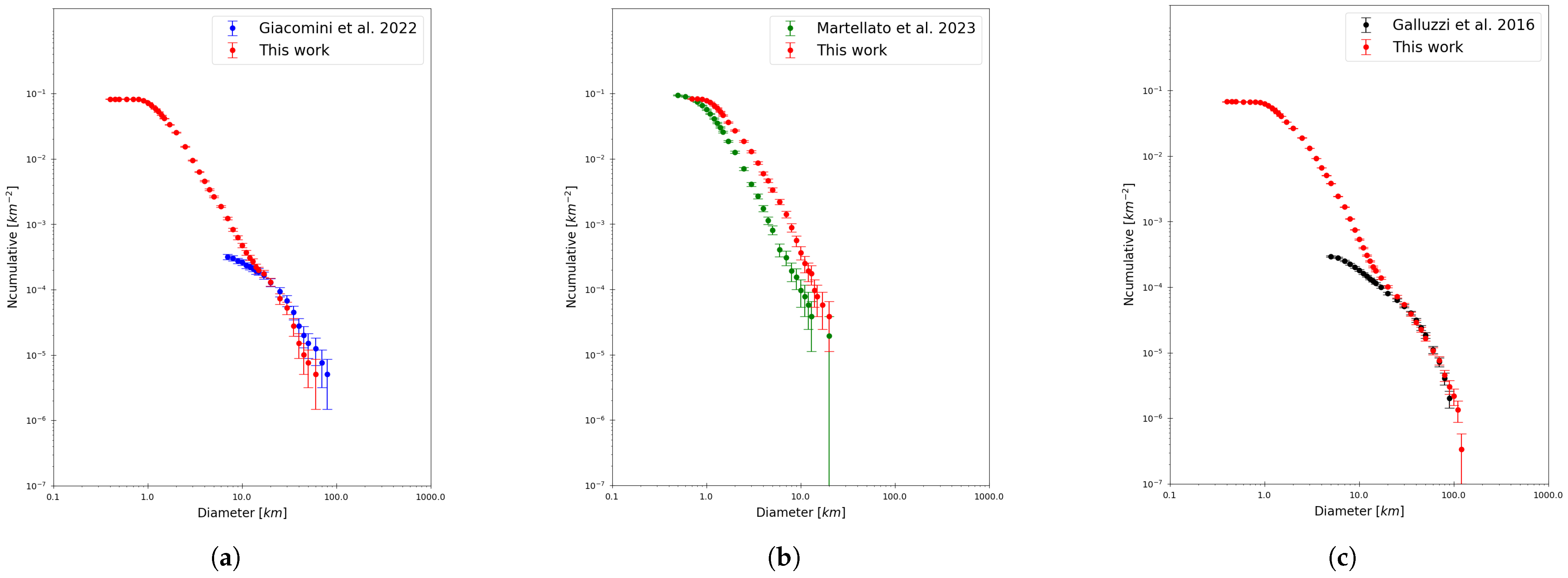
3.3.2. Size-Frequency Distribution Analysis
3.3.3. Comparison with Current Geological Knowledge
Smooth Plains
Intercrater Plains and Other Observations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. YOLOLens Architecture
| Layer Type | Output Shape | Param # |
|---|---|---|
| Conv2d: 1-1 | [−1, 64, 416, 416] | 1792 |
| Sequential: 1-2 (× 23) | [−1, 64, 416, 416] | |
| ResidualResidualDenseBlock: 2-1 | [−1, 64, 416, 416] | |
| ResidualDenseBlock: 3-1 | [−1, 64, 416, 416] | 239,808 |
| ResidualDenseBlock: 3-2 | [−1, 64, 416, 416] | 239,808 |
| ResidualDenseBlock: 3-3 | [−1, 64, 416, 416] | 239,808 |
| Conv2d: 1-3 | [−1, 64, 416, 416] | 36,928 |
| Sequential: 1-4 | [−1, 32, 832, 832] | |
| Conv2d: 2-24 | [−1, 128, 416, 416] | 73,856 |
| LeakyReLU: 2-25 | [−1, 128, 416, 416] | |
| PixelShuffle: 2-26 | [−1, 32, 832, 832] | |
| Sequential: 1-5 | [−1, 64, 832, 832] | |
| Conv2d: 2-27 | [−1, 64, 832, 832] | 18,496 |
| LeakyReLU: 2-28 | [−1, 64, 832, 832] | |
| Sequential: 1-6 | [−1, 64, 832, 832] | |
| Conv2d: 2-29 | [−1, 64, 832, 832] | 36,928 |
| Sequential: 1-7 | [−1, 64, 832, 832] | |
| Conv2d: 2-30 | [−1, 64, 832, 832] | 36,928 |
| LeakyReLU: 2-31 | [−1, 64, 832, 832] | |
| Conv2d: 2-32 | [−1, 128, 832, 832] | 73,856 |
| LeakyReLU: 2-33 | [−1, 128, 832, 832] | |
| Conv2d: 2-34 | [−1, 128, 832, 832] | 147,584 |
| LeakyReLU: 2-35 | [−1, 128, 832, 832] | |
| Conv2d: 2-36 | [−1, 64, 832, 832] | 73,792 |
| Sequential: 1-8 | [−1, 3, 832, 832] | |
| Conv2d: 2-37 | [−1, 64, 832, 832] | 36,928 |
| Conv2d: 2-38 | [−1, 3, 832, 832] | 1731 |
| DetectionModel: 1-9 | [−1, 5, 14196] | |
| Sequential: 2 | ||
| Conv: 3-70 | [−1, 80, 416, 416] | 2320 |
| Conv: 3-71 | [−1, 160, 208, 208] | 115,520 |
| C2f: 3-72 | [−1, 160, 208, 208] | 436,800 |
| Conv: 3-73 | [−1, 320, 104, 104] | 461,440 |
| C2f: 3-74 | [−1, 320, 104, 104] | 3,281,920 |
| Conv: 3-75 | [−1, 640, 52, 52] | 1,844,480 |
| C2f: 3-76 | [−1, 640, 52, 52] | 13,117,440 |
| Conv: 3-77 | [−1, 640, 26, 26] | 3,687,680 |
| C2f: 3-78 | [−1, 640, 26, 26] | 6,969,600 |
| SPPF: 3-79 | [−1, 640, 26, 26] | 1,025,920 |
| Upsample: 3-80 | [−1, 640, 52, 52] | |
| Concat: 3-81 | [−1, 1280, 52, 52] | |
| C2f: 3-82 | [−1, 640, 52, 52] | 7,379,200 |
| Upsample: 3-83 | [−1, 640, 104, 104] | |
| Concat: 3-84 | [−1, 960, 104, 104] | |
| C2f: 3-85 | [−1, 320, 104, 104] | 1,948,800 |
| Conv: 3-86 | [−1, 320, 52, 52] | 922,240 |
| Concat: 3-87 | [−1, 960, 52, 52] | |
| C2f: 3-88 | [−1, 640, 52, 52] | 7,174,400 |
| Conv: 3-89 | [−1, 640, 26, 26] | 3,687,680 |
| Concat: 3-90 | [−1, 1280, 26, 26] | |
| C2f: 3-91 | [−1, 640, 26, 26] | 7,379,200 |
| Detect: 3-92 | [−1, 5, 14196] | 8,718,931 |
Appendix B. Detection Sample over PSR of the Lunar South Pole

References
- Head, J.W.; Chapman, C.R.; Strom, R.G.; Fassett, C.I.; Denevi, B.W.; Blewett, D.T.; Ernst, C.M.; Watters, T.R.; Solomon, S.C.; Murchie, S.L.; et al. Flood volcanism in the northern high latitudes of Mercury revealed by MESSENGER. Science 2011, 333, 1853–1856. [Google Scholar] [CrossRef]
- La Grassa, R.; Cremonese, G.; Gallo, I.; Re, C.; Martellato, E. YOLOLens: A Deep Learning Model Based on Super-Resolution to Enhance the Crater Detection of the Planetary Surfaces. Remote Sens. 2023, 15, 1171. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, B.; Xue, H.; Li, X.; Ma, J. An improved global catalog of lunar impact craters (>1 km) with 3D morphometric information and updates on global crater analysis. J. Geophys. Res. Planets 2021, 126, e2020JE006728. [Google Scholar] [CrossRef]
- Robbins, S.J. A new global database of lunar impact craters > 1–2 km: 1. Crater locations and sizes, comparisons with published databases, and global analysis. J. Geophys. Res. Planets 2019, 124, 871–892. [Google Scholar] [CrossRef]
- Salamunićcar, G.; Lončarić, S.; Mazarico, E. LU60645GT and MA132843GT catalogues of Lunar and Martian impact craters developed using a Crater Shape-based interpolation crater detection algorithm for topography data. Planet. Space Sci. 2012, 60, 236–247. [Google Scholar] [CrossRef]
- Head, J.W., III; Fassett, C.I.; Kadish, S.J.; Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Mazarico, E. Global distribution of large lunar craters: Implications for resurfacing and impactor populations. Science 2010, 329, 1504–1507. [Google Scholar] [CrossRef]
- Povilaitis, R.; Robinson, M.; Van der Bogert, C.; Hiesinger, H.; Meyer, H.; Ostrach, L.R. Crater density differences: Exploring regional resurfacing, secondary crater populations, and crater saturation equilibrium on the moon. Planet. Space Sci. 2018, 162, 41–51. [Google Scholar] [CrossRef]
- Yue, Z.; Michael, G.; Di, K.; Liu, J. Global survey of lunar wrinkle ridge formation times. Earth Planet. Sci. Lett. 2017, 477, 14–20. [Google Scholar] [CrossRef]
- Kneissl, T.; Michael, G.; Platz, T.; Walter, S. Age determination of linear surface features using the Buffered Crater Counting approach–Case studies of the Sirenum and Fortuna Fossae graben systems on Mars. Icarus 2015, 250, 384–394. [Google Scholar] [CrossRef]
- Giacomini, L.; Massironi, M.; Galluzzi, V.; Ferrari, S.; Palumbo, P. Dating long thrust systems on Mercury: New clues on the thermal evolution of the planet. Geosci. Front. 2020, 11, 855–870. [Google Scholar] [CrossRef]
- Hiesinger, H.; Head, J.; Wolf, U.; Jaumann, R.; Neukum, G. Ages and stratigraphy of lunar mare basalts: A synthesis. Recent Adv. Curr. Res. Issues Lunar Stratigr. 2011, 477, 1–51. [Google Scholar]
- Giacomini, L.; Galluzzi, V.; Massironi, M.; Ferranti, L.; Palumbo, P. Geology of the Kuiper quadrangle (H06), Mercury. J. Maps 2022, 18, 246–257. [Google Scholar] [CrossRef]
- Robinson, M.S.; Brylow, S.; Tschimmel, M.e.; Humm, D.; Lawrence, S.; Thomas, P.; Denevi, B.W.; Bowman-Cisneros, E.; Zerr, J.; Ravine, M.; et al. Lunar reconnaissance orbiter camera (LROC) instrument overview. Space Sci. Rev. 2010, 150, 81–124. [Google Scholar] [CrossRef]
- Haruyama, J.; Matsunaga, T.; Ohtake, M.; Morota, T.; Honda, C.; Yokota, Y.; Torii, M.; Ogawa, Y.; Group, L.W. Global lunar-surface mapping experiment using the Lunar Imager/Spectrometer on SELENE. Earth Planets Space 2008, 60, 243–255. [Google Scholar] [CrossRef]
- Kereszturi, A. Polar ice on the moon. In Encyclopedia of Lunar Science; Springer: Cham, Switzerland, 2023; pp. 971–980. [Google Scholar]
- Herrick, R.R.; Curran, L.L.; Baer, A.T. A Mariner/MESSENGER global catalog of mercurian craters. Icarus 2011, 215, 452–454. [Google Scholar] [CrossRef]
- Robbins, S.J. New crater calibrations for the lunar crater-age chronology. Earth Planet. Sci. Lett. 2014, 403, 188–198. [Google Scholar] [CrossRef]
- Robbins, S.J.; Riggs, J.D.; Weaver, B.P.; Bierhaus, E.B.; Chapman, C.R.; Kirchoff, M.R.; Singer, K.N.; Gaddis, L.R. Revised recommended methods for analyzing crater size-frequency distributions. Meteorit. Planet. Sci. 2018, 53, 891–931. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, M.; Xiao, Z.; Cui, J. The minimum confidence limit for diameters in crater counts. Icarus 2020, 341, 113645. [Google Scholar] [CrossRef]
- Zuo, W.; Gao, X.; Wu, D.; Liu, J.; Zeng, X.; Li, C. YOLO-SCNet: A Framework for Enhanced Detection of Small Lunar Craters. Remote Sens. 2025, 17, 1959. [Google Scholar] [CrossRef]
- Zhong, Z.; Lai, J.; Zhong, Y.; Xu, Y.; Cui, F. Enhancing lunar DEM data using super-resolution techniques and optimizing the faster R-CNN network for sub-kilometer crater detection. Icarus 2025, 430, 116483. [Google Scholar] [CrossRef]
- Martinez, L.; Andrieu, F.; Schmidt, F.; Talbot, H.; Bentley, M. Robust automatic crater detection at all latitudes on Mars with deep-learning. Planet. Space Sci. 2025, 260, 106053. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, H.; Yang, S.; Cai, Z. Crater-DETR: A Novel Transformer Network for Crater Detection Based on Dense Supervision and Multiscale Fusion. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5614112. [Google Scholar] [CrossRef]
- Cadogan, P.H. Automated precision counting of very small craters at lunar landing sites. Icarus 2020, 348, 113822. [Google Scholar] [CrossRef]
- Tewari, A.; Verma, V.; Srivastava, P.; Jain, V.; Khanna, N. Automated crater detection from co-registered optical images, elevation maps and slope maps using deep learning. Planet. Space Sci. 2022, 218, 105500. [Google Scholar] [CrossRef]
- Silburt, A.; Ali-Dib, M.; Zhu, C.; Jackson, A.; Valencia, D.; Kissin, Y.; Tamayo, D.; Menou, K. Lunar crater identification via deep learning. Icarus 2019, 317, 27–38. [Google Scholar] [CrossRef]
- La Grassa, R.; Gallo, I.; Landro, N. OCmst: One-class novelty detection using convolutional neural network and minimum spanning trees. Pattern Recognit. Lett. 2022, 155, 114–120. [Google Scholar] [CrossRef]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar]
- Shen, J.; Castan, S. An optimal linear operator for step edge detection. CVGIP Graph. Model. Image Process. 1992, 54, 112–133. [Google Scholar]
- La Grassa, R.; Martellato, E.; Cremonese, G.; Re, C.; Tullo, A.; Bertoli, S. LU5M812TGT: An AI-Powered global database of impact craters > 0.4 km on the Moon. ISPRS J. Photogramm. Remote Sens. 2025, 220, 75–84. [Google Scholar]
- Hawkins, S.E.; Boldt, J.D.; Darlington, E.H.; Espiritu, R.; Gold, R.E.; Gotwols, B.; Grey, M.P.; Hash, C.D.; Hayes, J.R.; Jaskulek, S.E.; et al. The Mercury dual imaging system on the MESSENGER spacecraft. Space Sci. Rev. 2007, 131, 247–338. [Google Scholar] [CrossRef]
- Barker, M.K.; Mazarico, E.; Neumann, G.A.; Smith, D.E.; Zuber, M.T.; Head, J.W.; Sun, X. A New View of the Lunar South Pole from the Lunar Orbiter Laser Altimeter (LOLA). Planet. Sci. J. 2023, 4, 183. [Google Scholar] [CrossRef]
- Barker, M.; Mazarico, E.; Neumann, G.; Zuber, M.; Haruyama, J.; Smith, D. A new lunar digital elevation model from the Lunar Orbiter Laser Altimeter and SELENE Terrain Camera. Icarus 2016, 273, 346–355. [Google Scholar] [CrossRef]
- Archinal, B.A.; A’Hearn, M.F.; Bowell, E.; Conrad, A.; Consolmagno, G.J.; Courtin, R.; Fukushima, T.; Hestroffer, D.; Hilton, J.L.; Krasinsky, G.A.; et al. Report of the IAU working group on cartographic coordinates and rotational elements: 2009. Celest. Mech. Dyn. Astron. 2011, 109, 101–135. [Google Scholar] [CrossRef]
- Mazarico, E.; Rowlands, D.; Neumann, G.; Smith, D.; Torrence, M.; Lemoine, F.; Zuber, M. Orbit determination of the lunar reconnaissance orbiter. J. Geod. 2012, 86, 193–207. [Google Scholar]
- Smith, D.; Zuber, M.; Neumann, G.; Mazarico, E.; Head, J.; Torrence, M.; LOLA Science Team. Results from the Lunar Orbiter Laser Altimeter (LOLA): Global, high resolution topographic mapping of the Moon. In Proceedings of the 42nd Annual Lunar and Planetary Science Conference, The Woodlands, TX, USA, 7–11 March 2011; p. 2350. [Google Scholar]
- Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Lemoine, F.G.; Mazarico, E.; Torrence, M.H.; McGarry, J.F.; Rowlands, D.D.; Head, J.W., III; Duxbury, T.H.; et al. Initial observations from the lunar orbiter laser altimeter (LOLA). Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Tooley, C.R.; Houghton, M.B.; Saylor, R.S.; Peddie, C.; Everett, D.F.; Baker, C.L.; Safdie, K.N. Lunar Reconnaissance Orbiter mission and spacecraft design. Space Sci. Rev. 2010, 150, 23–62. [Google Scholar] [CrossRef]
- Wessel, P.; Smith, W.H.; Scharroo, R.; Luis, J.; Wobbe, F. Generic mapping tools: Improved version released. Eos Trans. Am. Geophys. Union 2013, 94, 409–410. [Google Scholar] [CrossRef]
- Williams, J. DE421 Lunar Orbit, Physical Librations, and Surface Coordinates. 2008. Available online: https://cir.nii.ac.jp/crid/1570572700867074816 (accessed on 10 September 2025).
- Galluzzi, V.; Guzzetta, L.; Ferranti, L.; Di Achille, G.; Rothery, D.A.; Palumbo, P. Geology of the Victoria quadrangle (H02), Mercury. J. Maps 2016, 12, 227–238. [Google Scholar] [CrossRef]
- Susorney, H.C.; Barnouin, O.S.; Ernst, C.M.; Johnson, C.L. Morphometry of impact craters on Mercury from MESSENGER altimetry and imaging. Icarus 2016, 271, 180–193. [Google Scholar] [CrossRef]
- Martellato, E.; Luther, R.; Benkhoff, J.; Da Deppo, V.; Casini, C.; Palumbo, P.; Rotundi, A.; Slemer, A.; Cremonese, G. MESSENGER Grand Finale at Mercury: Surface age and property characterization. In Proceedings of the Mercury Exploration Assessment Group (MExAG) Annual Meeting 2023, Virtual, 1–3 February 2023. [Google Scholar]
- Galluzzi, V.; Giacomini, L.; Guzzetta, L.; Lewang, A.M.; Malliband, C.C.; Mancinelli, P.; Pegg, D.L.; Semenzato, A.; Wright, J.; Ferranti, L.; et al. Geological Mapping of Mercury. Geophys. Res. Abstr. 2019, 21, 1. [Google Scholar]
- Schultz, P.H. Endogenic modification of impact craters on Mercury. Phys. Earth Planet. Inter. 1977, 15, 202–219. [Google Scholar] [CrossRef]
- Krüger, T.; Hergarten, S.; Kenkmann, T. Deriving morphometric parameters and the simple-to-complex transition diameter from a high-resolution, global database of fresh lunar impact craters (D > 3 km). J. Geophys. Res. Planets 2018, 123, 2667–2690. [Google Scholar] [CrossRef]
- Pike, R.J. Geomorphology of impact craters on Mercury. Mercury 1988, 89, 165–273. [Google Scholar]
- Denevi, B.W.; Ernst, C.M.; Meyer, H.M.; Robinson, M.S.; Murchie, S.L.; Whitten, J.L.; Head, J.W.; Watters, T.R.; Solomon, S.C.; Ostrach, L.R.; et al. The distribution and origin of smooth plains on Mercury. J. Geophys. Res. Planets 2013, 118, 891–907. [Google Scholar] [CrossRef]
- Ostrach, L.R.; Robinson, M.S.; Whitten, J.L.; Fassett, C.I.; Strom, R.G.; Head, J.W.; Solomon, S.C. Extent, age, and resurfacing history of the northern smooth plains on Mercury from MESSENGER observations. Icarus 2015, 250, 602–622. [Google Scholar] [CrossRef]
- Caminiti, E.; Doressoundiram, A.; Besse, S.; Wright, J. A spectral study of the Caloris basin on Mercury and the origin of associated volcanic smooth plains. J. Geophys. Res. Planets 2023, 128, e2022JE007685. [Google Scholar] [CrossRef]
- Wu, B.; Wang, Y.; Werner, S.C.; Prieur, N.C.; Xiao, Z. A global analysis of crater depth/diameter ratios on the Moon. Geophys. Res. Lett. 2022, 49, e2022GL100886. [Google Scholar] [CrossRef]
- Klimczak, C.; Watters, T.R.; Ernst, C.M.; Freed, A.M.; Byrne, P.K.; Solomon, S.C.; Blair, D.M.; Head, J.W. Deformation associated with ghost craters and basins in volcanic smooth plains on Mercury: Strain analysis and implications for plains evolution. J. Geophys. Res. Planets 2012, 117. [Google Scholar] [CrossRef]
- Ernst, C.M.; Denevi, B.W.; Barnouin, O.S.; Klimczak, C.; Chabot, N.L.; Head, J.W.; Murchie, S.L.; Neumann, G.A.; Prockter, L.M.; Robinson, M.S.; et al. Stratigraphy of the Caloris basin, Mercury: Implications for volcanic history and basin impact melt. Icarus 2015, 250, 413–429. [Google Scholar] [CrossRef]
- Whitten, J.L.; Head, J.W.; Denevi, B.W.; Solomon, S.C. Intercrater plains on Mercury: Insights into unit definition, characterization, and origin from MESSENGER datasets. Icarus 2014, 241, 97–113. [Google Scholar] [CrossRef]
- Fassett, C.I.; Crowley, M.C.; Leight, C.; Dyar, M.D.; Minton, D.A.; Hirabayashi, M.; Thomson, B.J.; Watters, W.A. Evidence for rapid topographic evolution and crater degradation on Mercury from simple crater morphometry. Geophys. Res. Lett. 2017, 44, 5326–5335. [Google Scholar] [CrossRef]
- Pegg, D.; Rothery, D.; Balme, M.; Conway, S.J.; Malliband, C.; Man, B. Geology of the Debussy quadrangle (H14), Mercury. J. Maps 2021, 17, 718–729. [Google Scholar] [CrossRef]
- Denevi, B.; Ernst, C.; Prockter, L.; Robinson, M.; Spudis, P.; Klima, R.; Murchie, S.; Solomon, S.; Whitten, J.; Povilaitis, R.; et al. The origin of Mercury’s oldest surfaces and the nature of intercrater plains resurfacing. In Proceedings of the 47th Annual Lunar and Planetary Science Conference, The Woodlands, TX, USA, 21–25 March 2016; p. 1624. [Google Scholar]
- Man, B.; Rothery, D.A.; Balme, M.R.; Conway, S.J.; Wright, J.; Pegg, D.L.; Lennox, A.R.; Buoninfante, S. Geology of the Neruda quadrangle (H13), Mercury. J. Maps 2023, 19, 2256353. [Google Scholar] [CrossRef]
- Buoninfante, S.; Galluzzi, V.; Ferranti, L.; Milano, M.; Palumbo, P. Geostructural mapping of the Michelangelo (H-12) quadrangle of Mercury: Relationship between tectonic and crustal structures. In Proceedings of the Europlanet Science Congress 2022, EPSC2022, Granada, Spain, 18–23 September 2022; Volume 811. [Google Scholar]
- Kinczyk, M.; Prockter, L.; Denevi, B.; Ostrach, L.; Skinner, J. A global geological map of Mercury. Mercur. Curr. Future Sci. Inn. Planet 2018, 2047, 6123. [Google Scholar]
- Zuber, M.T.; Smith, D.E.; Phillips, R.J.; Solomon, S.C.; Neumann, G.A.; Hauck, S.A.; Peale, S.J.; Barnouin, O.S.; Head, J.W.; Johnson, C.L.; et al. Topography of the northern hemisphere of Mercury from MESSENGER laser altimetry. Science 2012, 336, 217–220. [Google Scholar] [CrossRef] [PubMed]
- Perry, M.E.; Neumann, G.A.; Phillips, R.J.; Barnouin, O.S.; Ernst, C.M.; Kahan, D.S.; Solomon, S.C.; Zuber, M.T.; Smith, D.E.; Hauck, S.A.; et al. The low-degree shape of Mercury. Geophys. Res. Lett. 2015, 42, 6951–6958. [Google Scholar] [CrossRef]







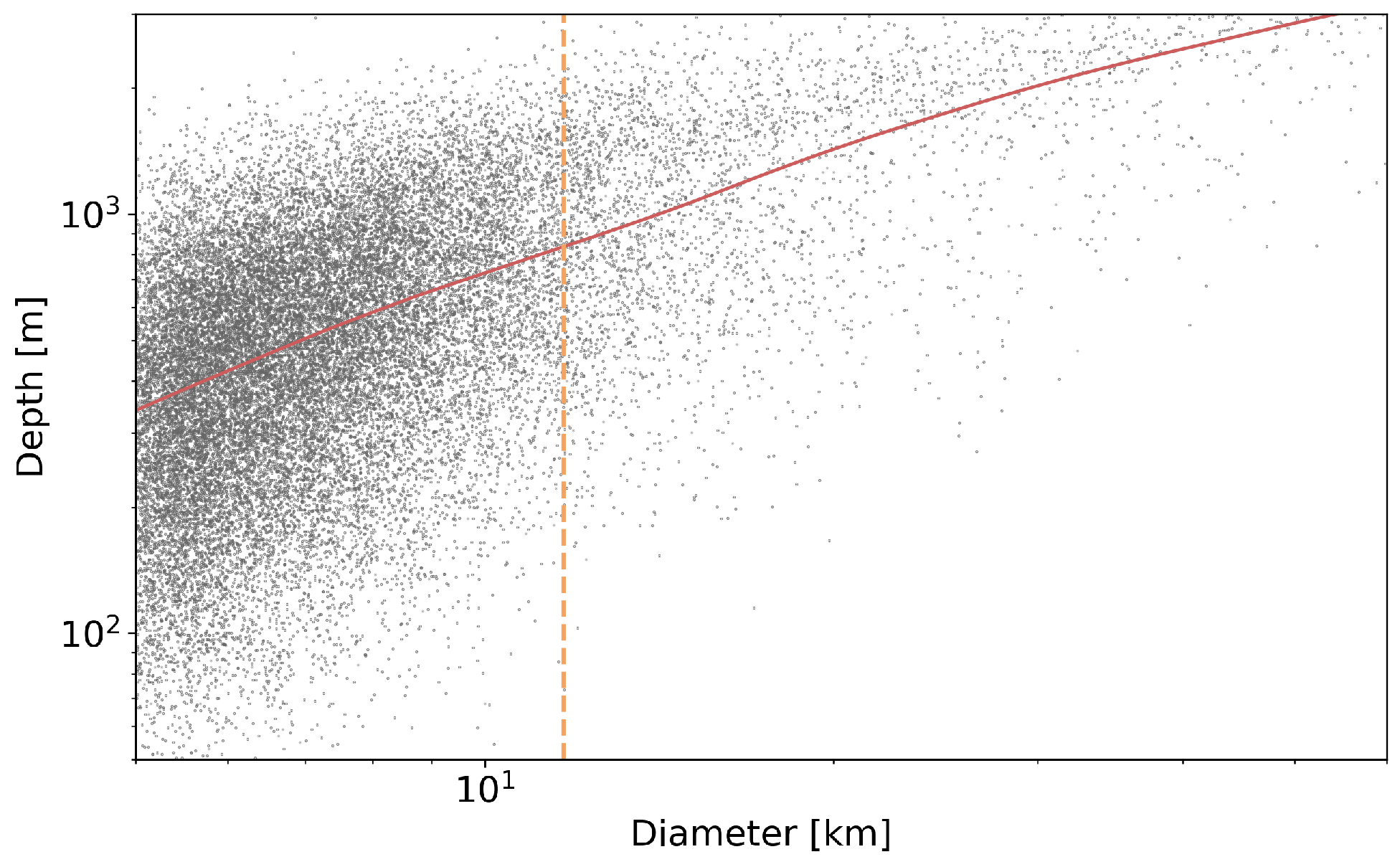


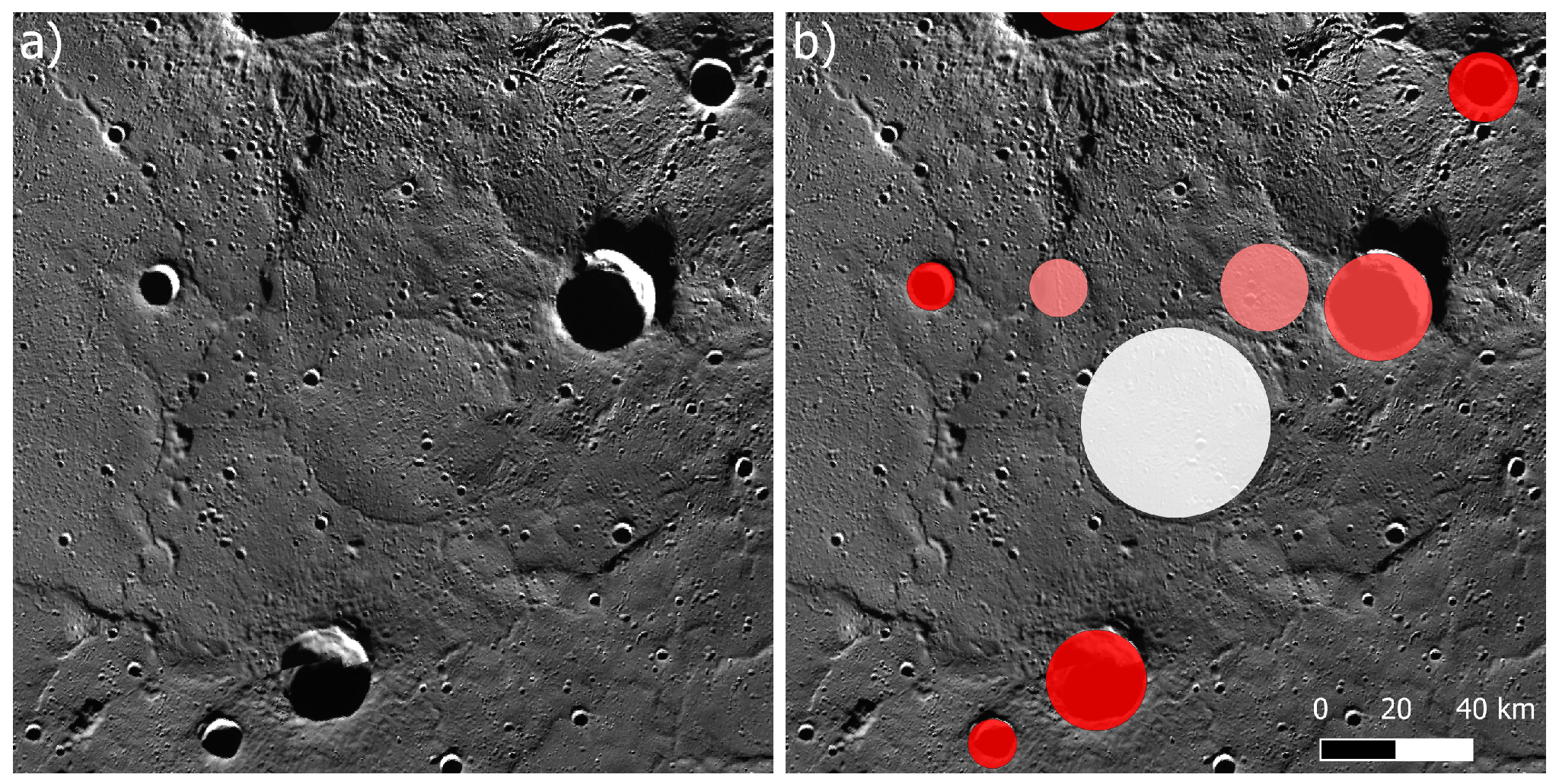
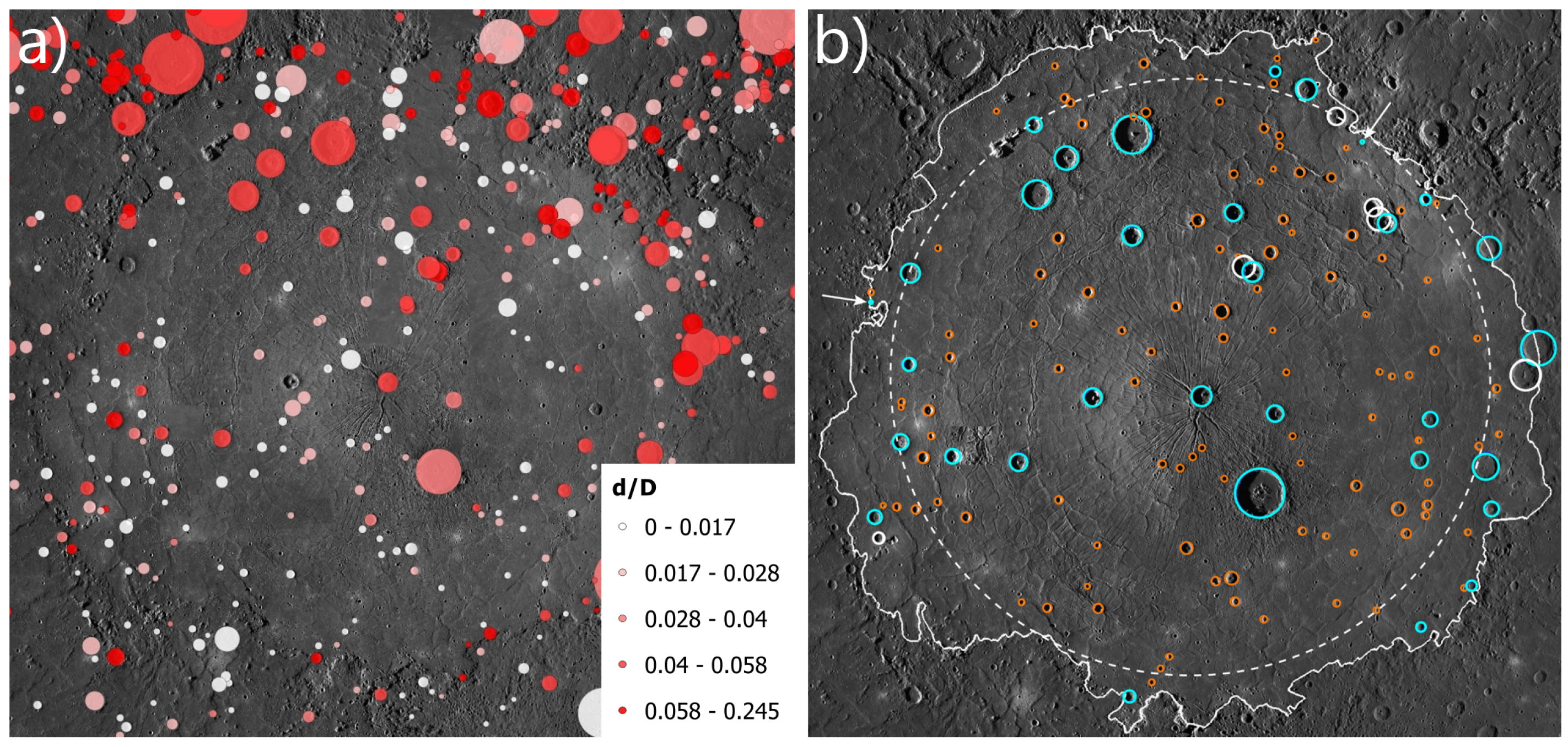


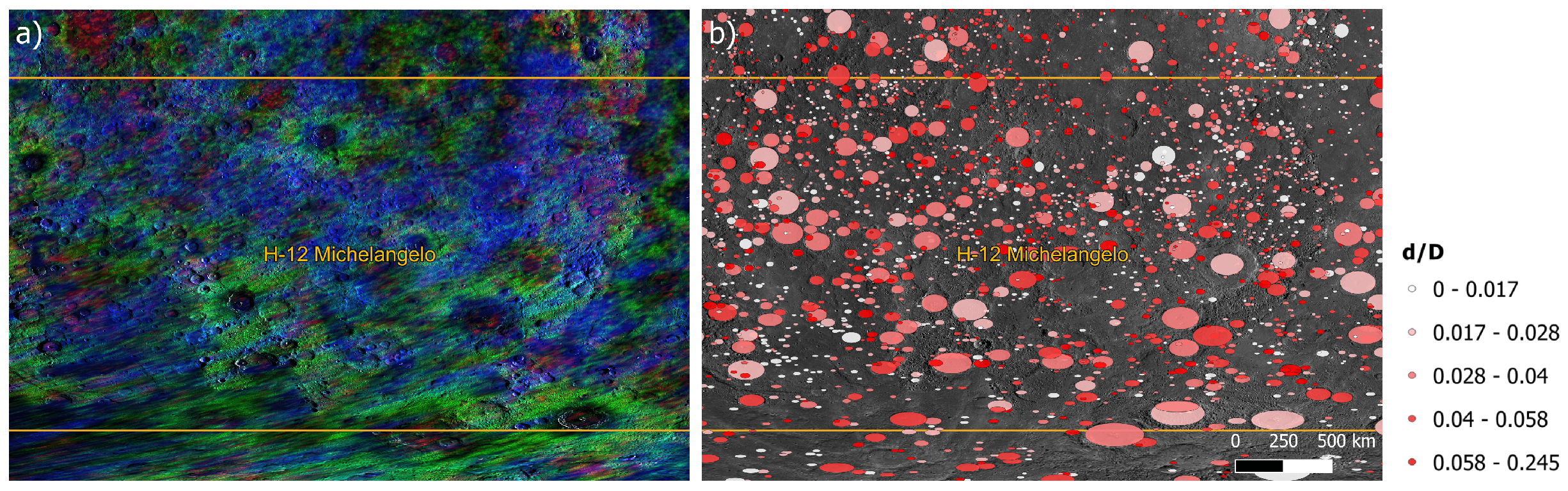
| Window | Latitude Ranges | ||||
|---|---|---|---|---|---|
| m/px | −90 to −80 | −80 to −60 | −60 to 60 | 60 to 80 | 80 to 90 |
| 100 | 1094 | 2267 | 2083 | 2267 | 1024 |
| 200 | 243 | 490 | 517 | 490 | 227 |
| 400 | 43 | 97 | 126 | 97 | 21 |
| South Pole | North Pole | ||||
|---|---|---|---|---|---|
| Range | LU5M812TGT | LU6M371TGT | Range | LU5M812TGT | LU6M371TGT |
| 60.1 | 59.6 | ||||
| 67.8 | 68.2 | ||||
| 77.8 | 74.3 | ||||
| 77.1 | 76.7 | ||||
| Descriptions of Regions | |||||
| : to of latitude | : to of latitude | ||||
| : to of latitude | : to of latitude | ||||
| : to of latitude | : to of latitude | ||||
| : to of latitude | : to of latitude | ||||
| Confidence | Detected Craters | False Positives | True Positives [%] |
|---|---|---|---|
| Southern Highlands (Lat: −45/−40° and Long: 55/60°) | |||
| 0.28 | 1550 (4864) | 17 (54) | 98.90 (98.9) |
| 0.26 | 1625 (5013) | 20 (60) | 98.77 (98.8) |
| 0.22 | 1793 (5294) | 39 (65) | 97.82 (98.77) |
| 0.2 | 1906 (5496) | 55 (76) | 97.11 (98.62) |
| Northern Highlands (Lat: 60/65° and Long: 120/125°) | |||
| 0.5 | 327 (863) | 44 (65) | 86.54 (92.47) |
| 0.4 | 414 (950) | 64 (80) | 84.54 (91.58) |
| 0.3 | 517 (1052) | 90 (93) | 82.59 (91.16) |
| 0.2 | 746 (1223) | 139 (117) | 81.37 (90.43) |
| Diameter Range (km) | ME6M300TGT | Herrick |
|---|---|---|
| <1 | 895,629 | 0 |
| 5,130,837 | 62 | |
| 231,816 | 4150 | |
| 32,388 | 6477 | |
| 6480 | 3646 | |
| 1503 | 1300 | |
| 576 | 553 | |
| 252 | 280 | |
| 6,299,481 | 16,468 |
| Area | Recall (%) | Manually Counted | Matched by YOLOLens | YOLOLens Count |
|---|---|---|---|---|
| 92.0 | 1732 | 1579 | 30,920 | |
| 80.0 | 132 | 106 | 30,017 | |
| 58.0 | 5052 | 2949 | 30,017 | |
| 84.0 | 418 | 352 | 35,905 | |
| 95.7 | 331 | 317 | 493,970 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
La Grassa, R.; Re, C.; Martellato, E.; Tullo, A.; Bertoli, S.; Cremonese, G.; Vergara Sassarini, N.A.; Faletti, M.; Galluzzi, V.; Giacomini, L. From the Moon to Mercury: Release of Global Crater Catalogs Using Multimodal Deep Learning for Crater Detection and Morphometric Analysis. Remote Sens. 2025, 17, 3287. https://doi.org/10.3390/rs17193287
La Grassa R, Re C, Martellato E, Tullo A, Bertoli S, Cremonese G, Vergara Sassarini NA, Faletti M, Galluzzi V, Giacomini L. From the Moon to Mercury: Release of Global Crater Catalogs Using Multimodal Deep Learning for Crater Detection and Morphometric Analysis. Remote Sensing. 2025; 17(19):3287. https://doi.org/10.3390/rs17193287
Chicago/Turabian StyleLa Grassa, Riccardo, Cristina Re, Elena Martellato, Adriano Tullo, Silvia Bertoli, Gabriele Cremonese, Natalia Amanda Vergara Sassarini, Maddalena Faletti, Valentina Galluzzi, and Lorenza Giacomini. 2025. "From the Moon to Mercury: Release of Global Crater Catalogs Using Multimodal Deep Learning for Crater Detection and Morphometric Analysis" Remote Sensing 17, no. 19: 3287. https://doi.org/10.3390/rs17193287
APA StyleLa Grassa, R., Re, C., Martellato, E., Tullo, A., Bertoli, S., Cremonese, G., Vergara Sassarini, N. A., Faletti, M., Galluzzi, V., & Giacomini, L. (2025). From the Moon to Mercury: Release of Global Crater Catalogs Using Multimodal Deep Learning for Crater Detection and Morphometric Analysis. Remote Sensing, 17(19), 3287. https://doi.org/10.3390/rs17193287






