Assessing the Long-Term Changes in the Suspended Particulate Matter in Hangzhou Bay Using MODIS/Aqua Data
Abstract
Highlights
- Long-term MODIS/Aqua data (2003–2024) revealed a significant decline in suspended particulate matter (TSM) in Hangzhou Bay (HZB), linked to reduced sediment discharge from the Yangtze River.
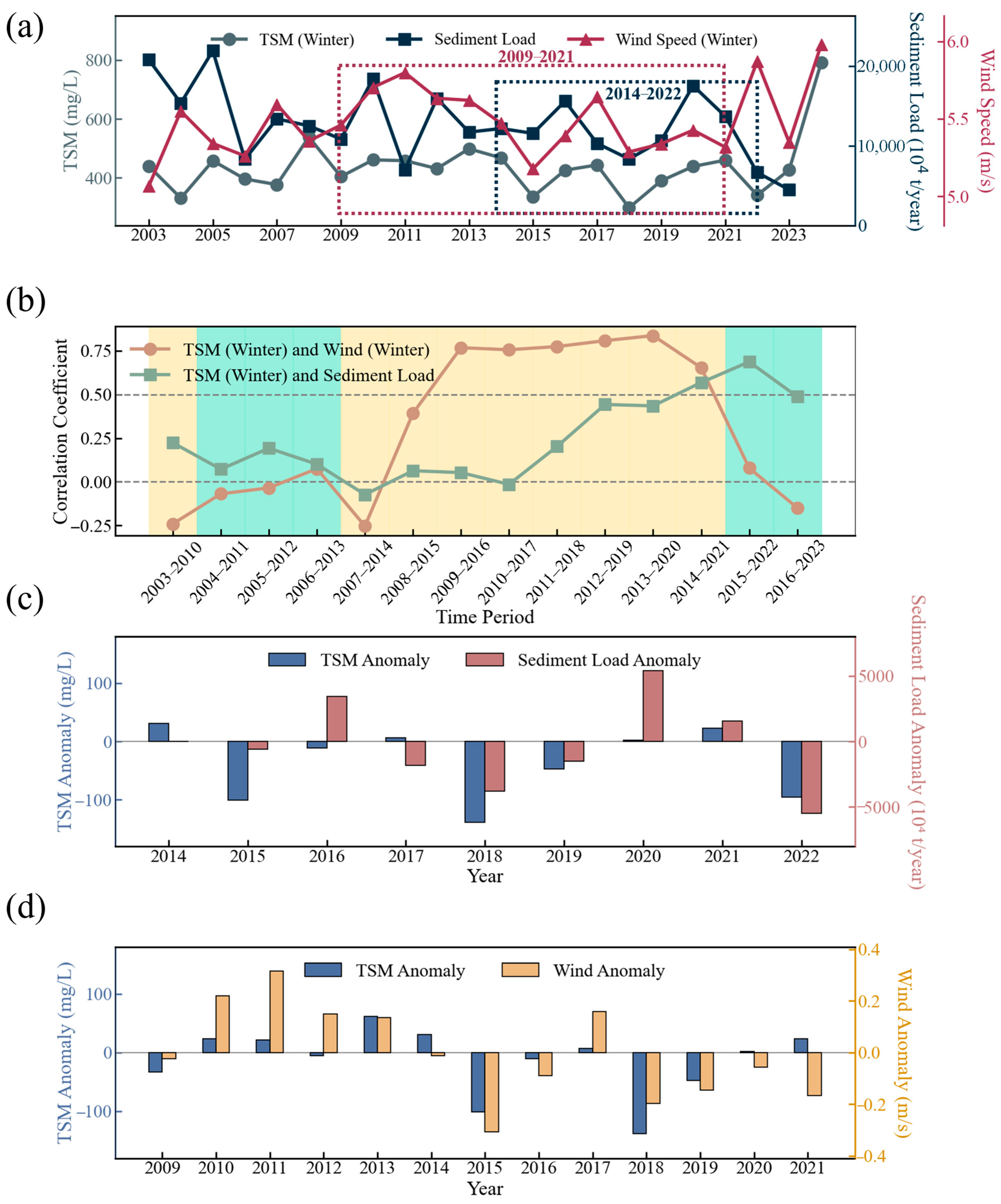
- Interannual TSM variations in winter were associated with Yangtze River sediment discharge and regional wind forcing, with bridge construction causing spatial contrasts across the Hangzhou Bay Bridge and reclamation altering TSM around Yushan Island.
- The results highlight the combined influence of natural factors and human activities on sediment dynamics, revealing significant spatiotemporal changes and regulatory mechanisms of TSM in HZB.
- The findings provide valuable insights into the long-term changes in suspended sediment and water quality in HZB, supporting sustainable water management and effective water strategies.
Abstract
1. Introduction
2. Data and Methods
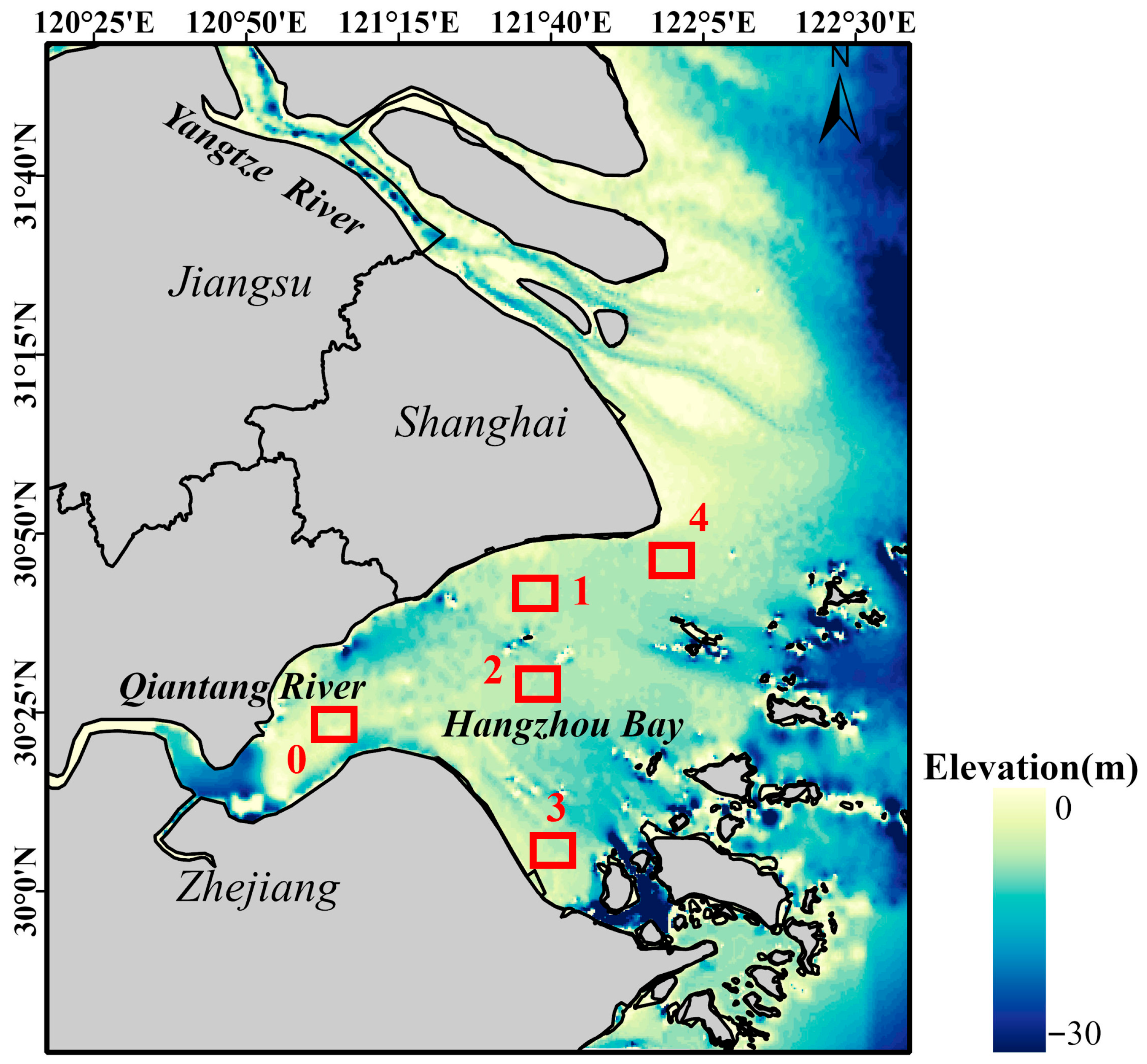
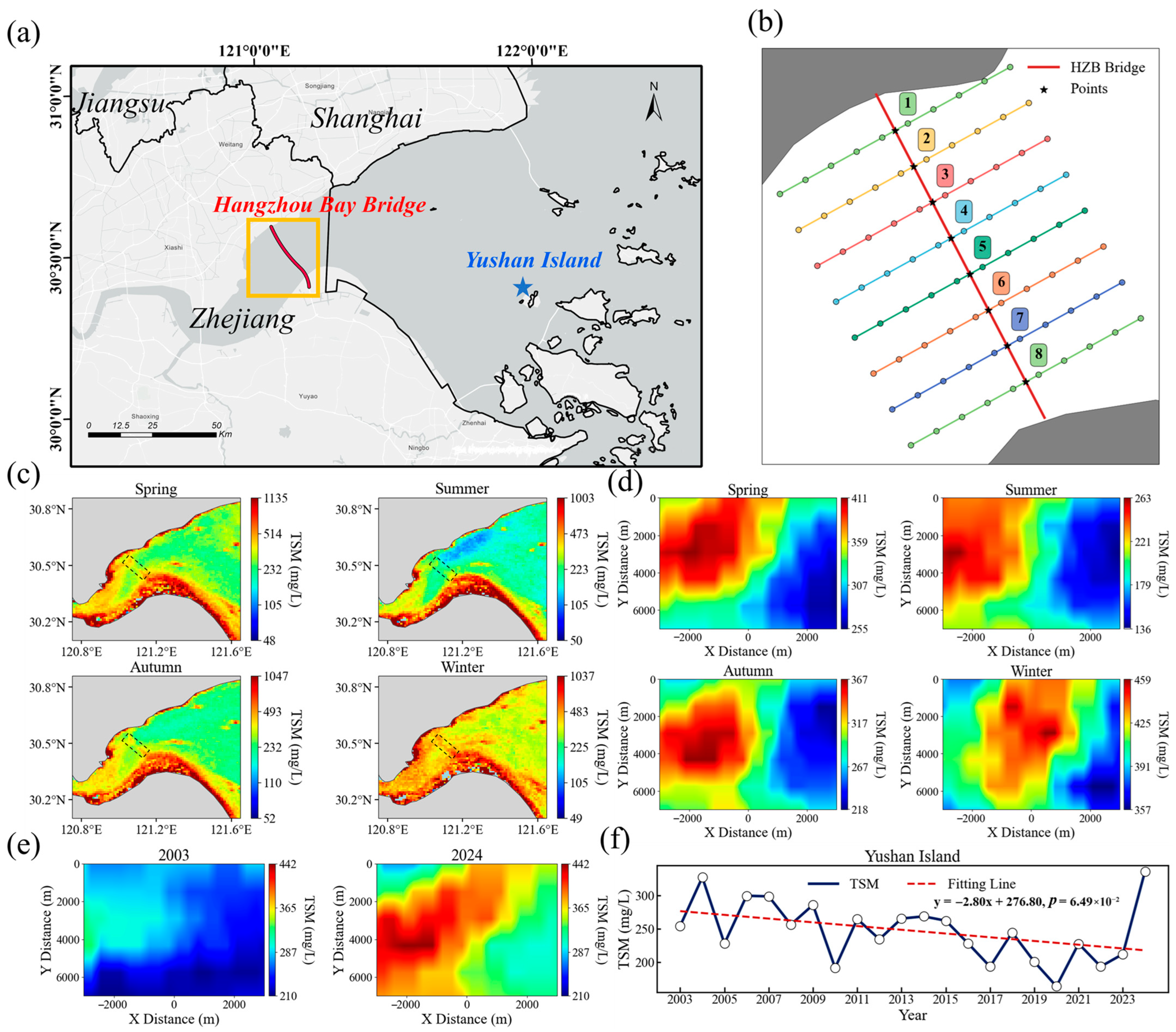
2.1. Study Area
2.2. Data
2.2.1. Satellite Data
2.2.2. In Situ TSM Data
2.2.3. In Situ Data
2.2.4. Environmental Data
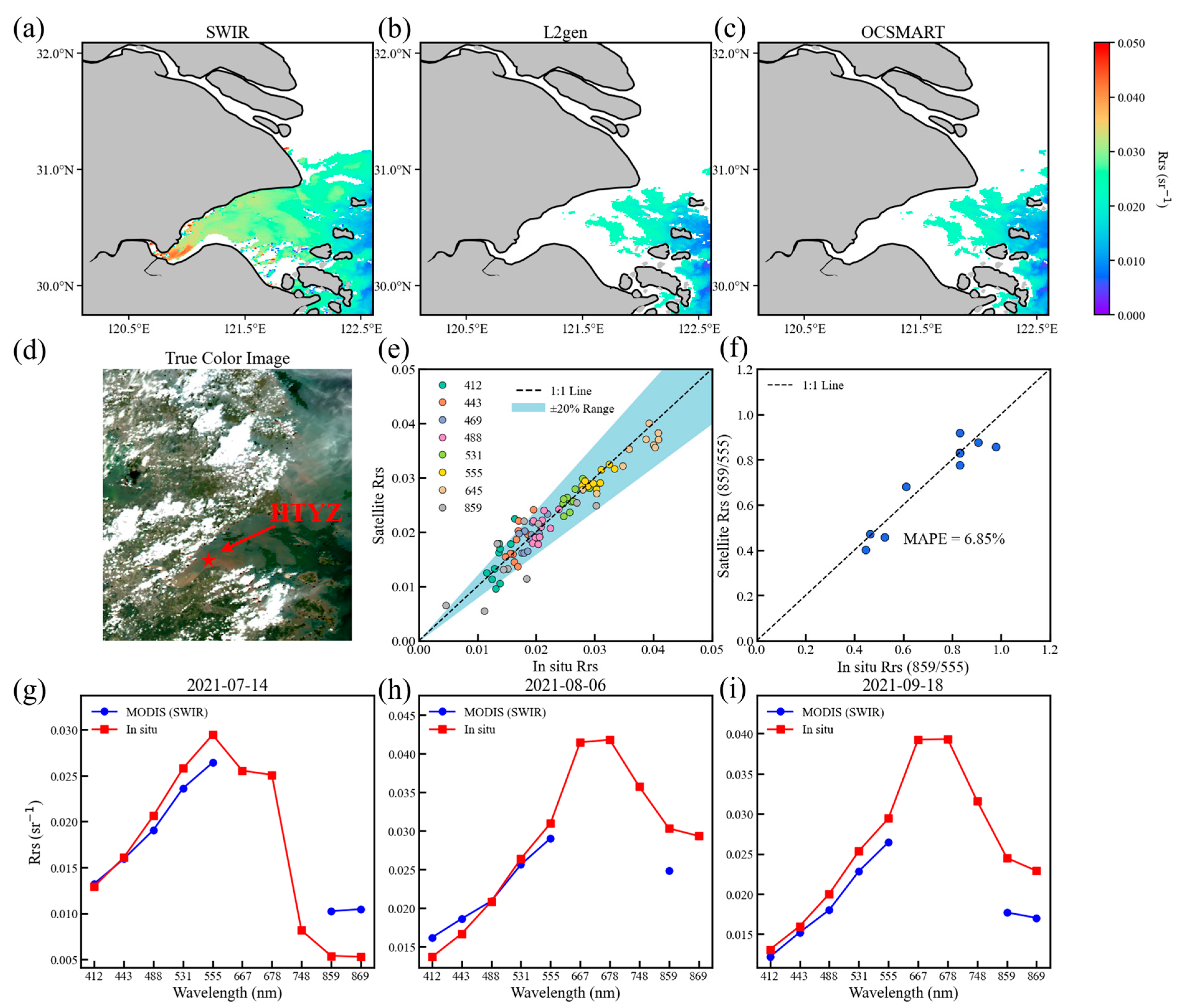
2.3. Atmospheric Correction Method
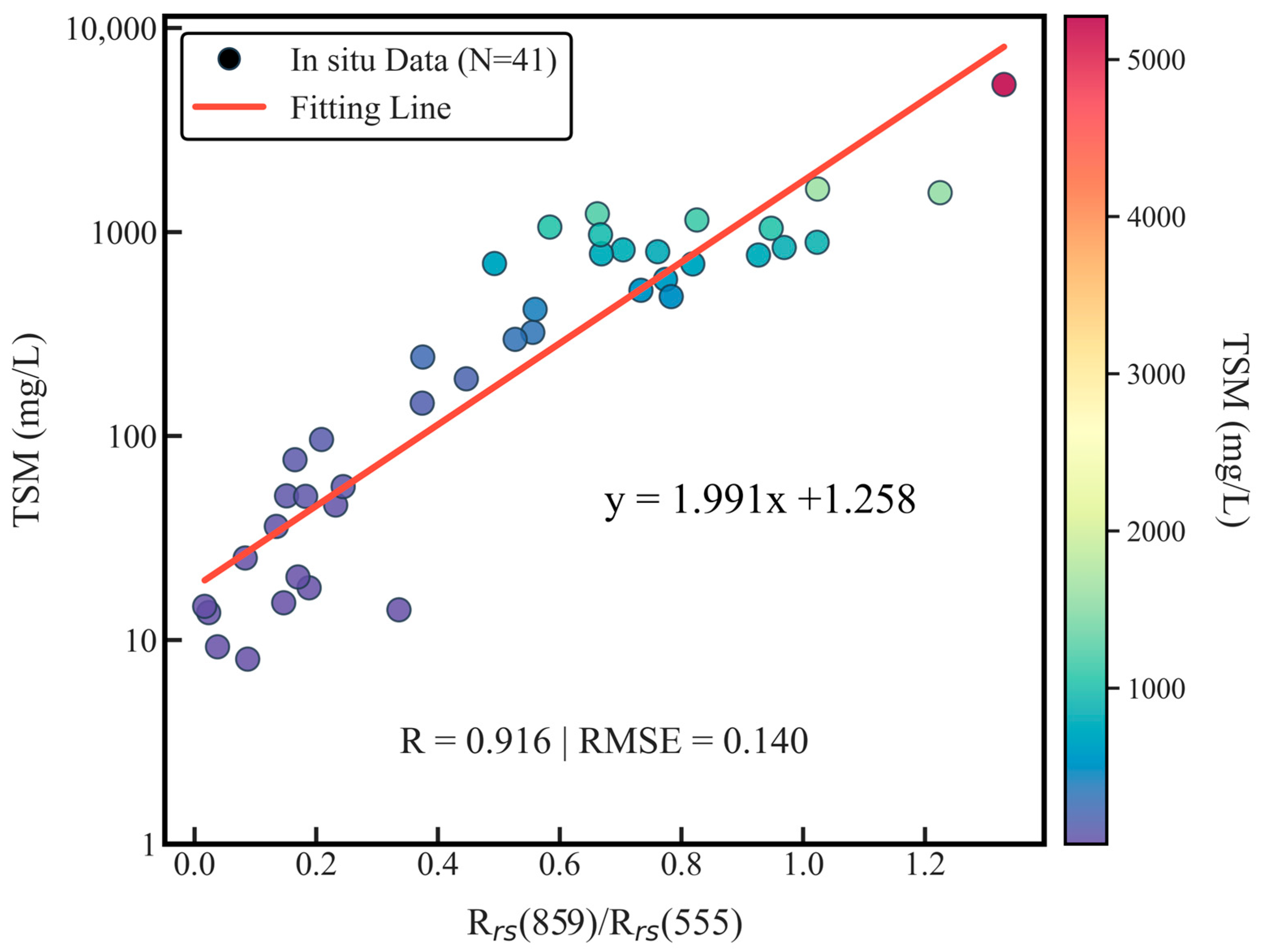
2.4. Description of the TSM Retrieval Algorithm
3. Results
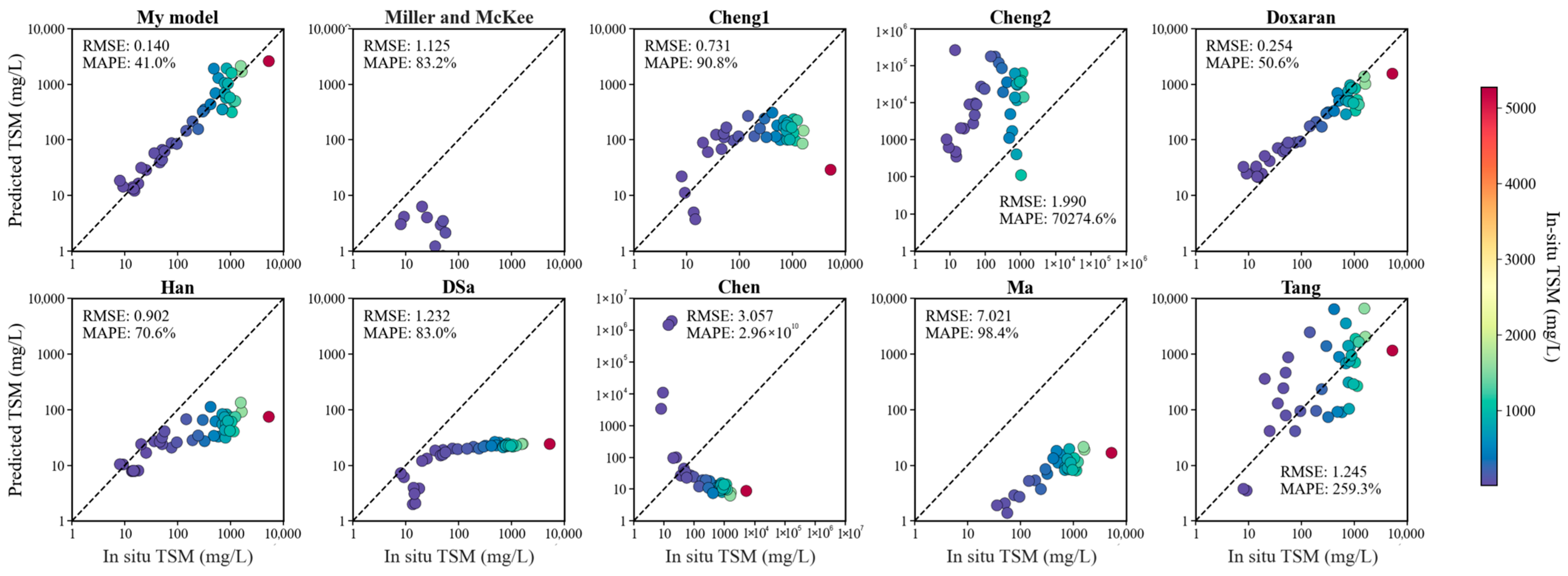
3.1. TSM Retrieval Algorithm Validation
3.2. Spatial Distribution of TSM in HZB
3.2.1. Long-Term Average Spatial Distribution
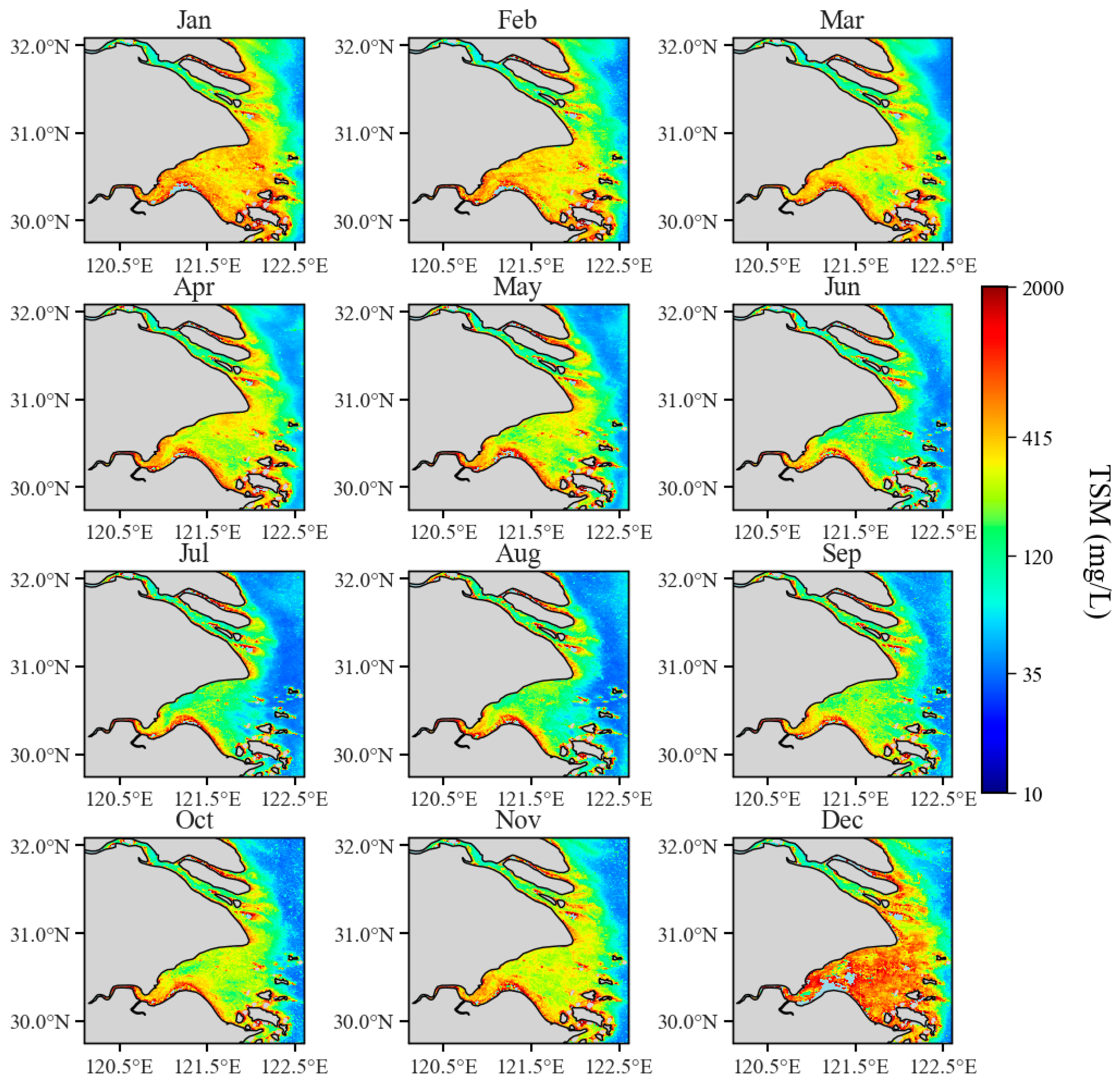
3.2.2. Long-Term Monthly Average Spatial Distribution
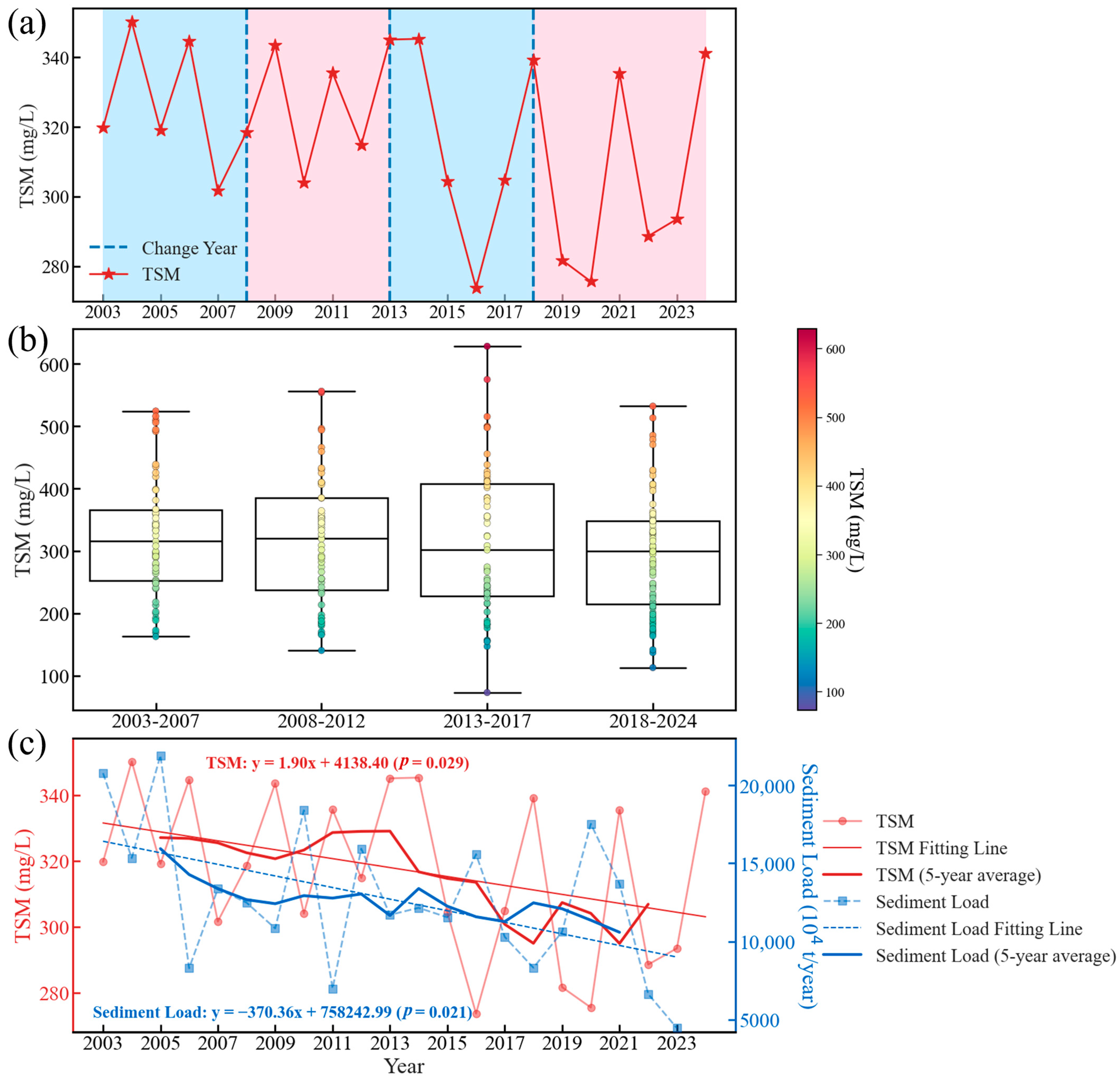
3.3. Long-Term Changes in TSM in HZB
3.3.1. Long-Term Changes in Annual Mean TSM in HZB
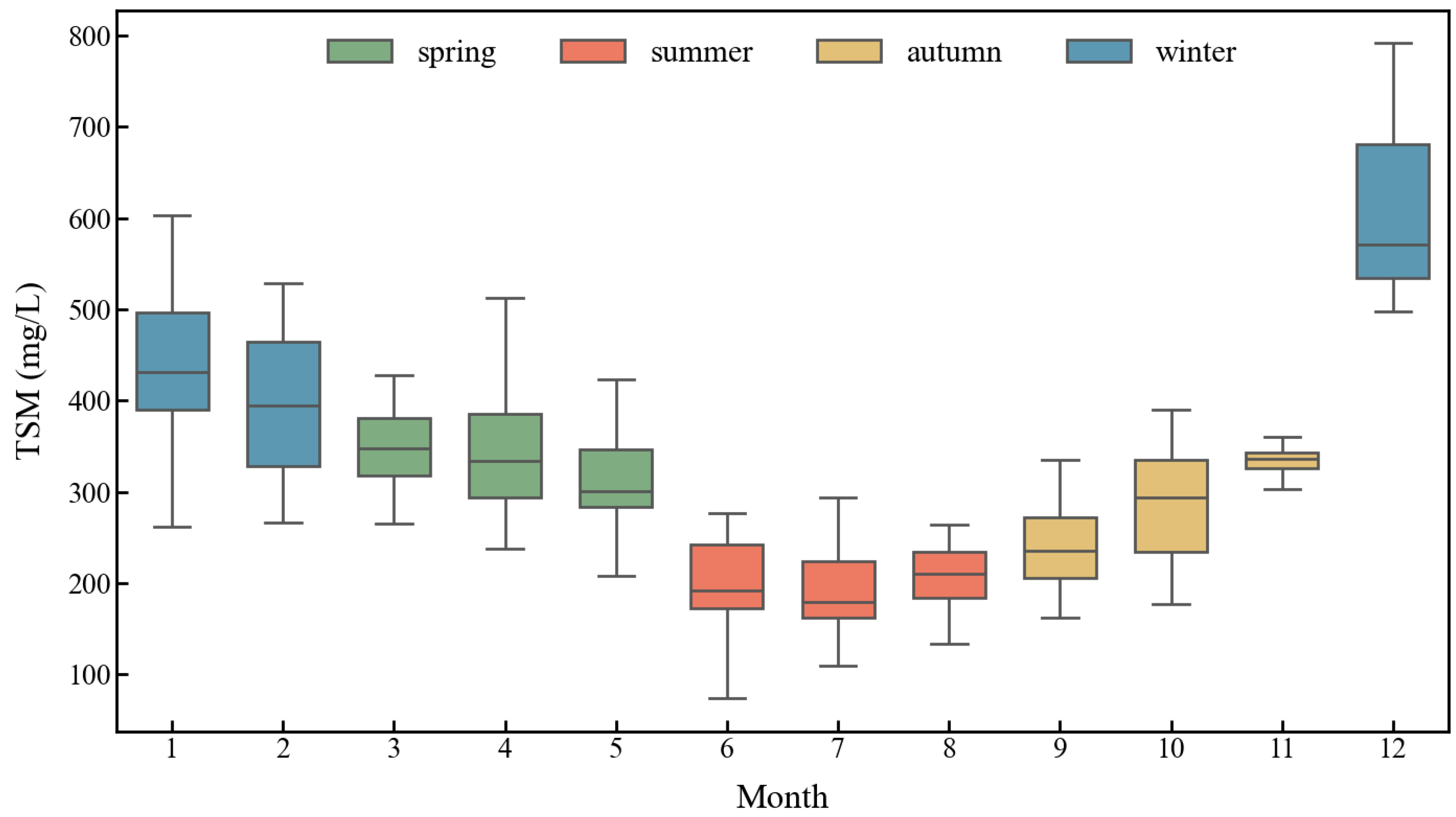
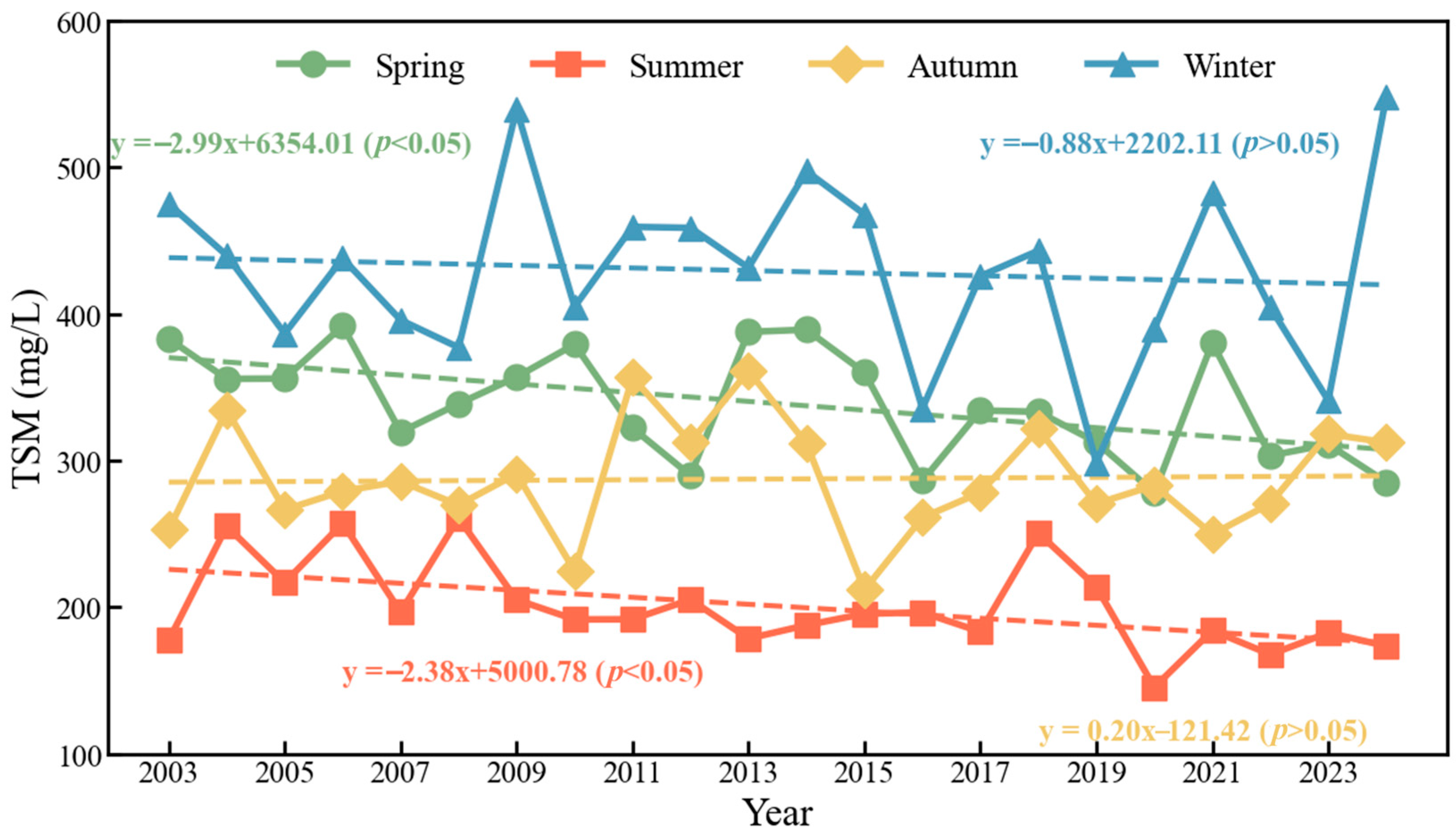
3.3.2. Long-Term Changes in Seasonal Mean TSM in HZB
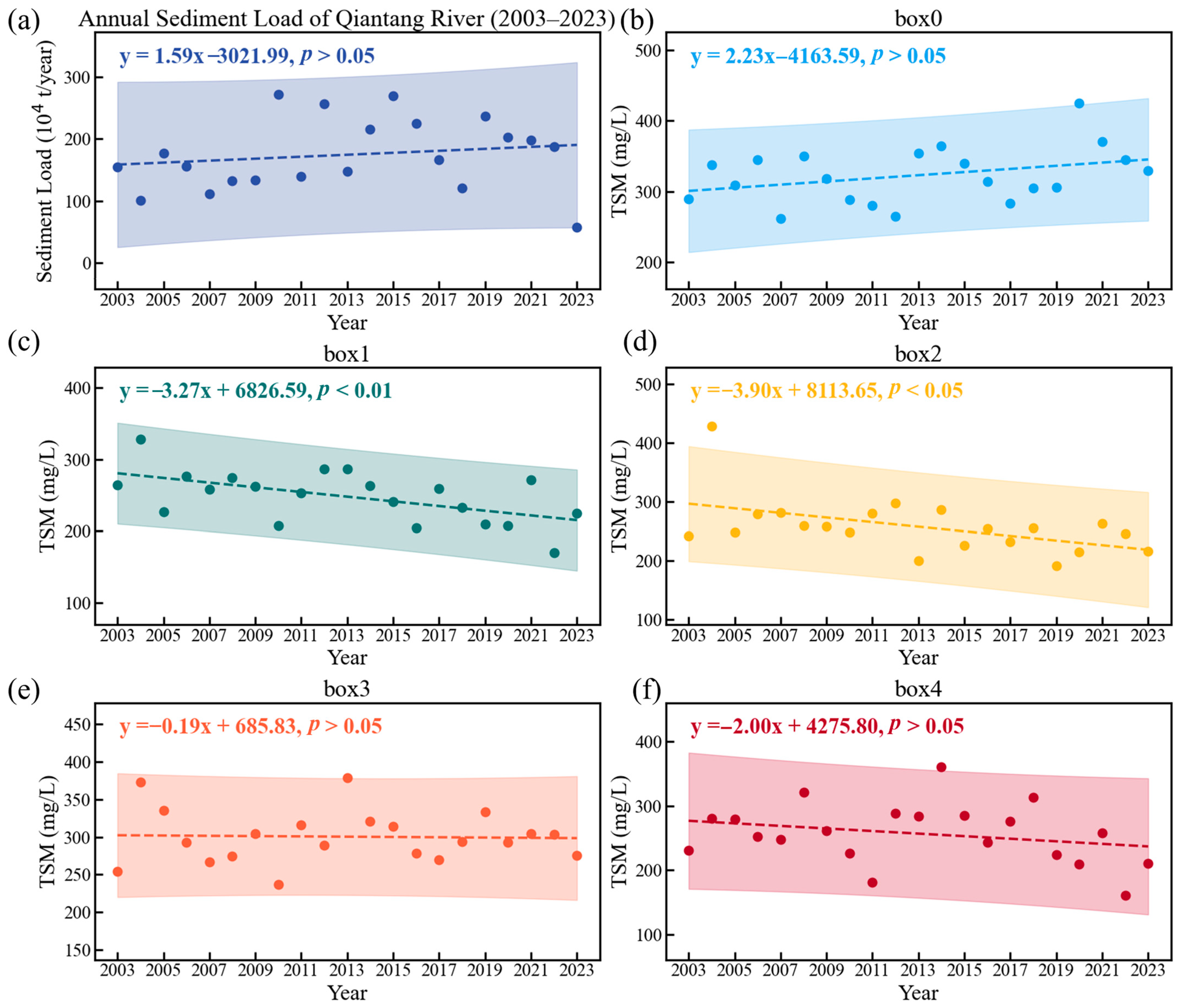
3.3.3. The Rate of TSM Variation in HZB
4. Discussion
4.1. Uncertainties in the Atmospheric Correction Method and theTSM Retrieval Algorithm
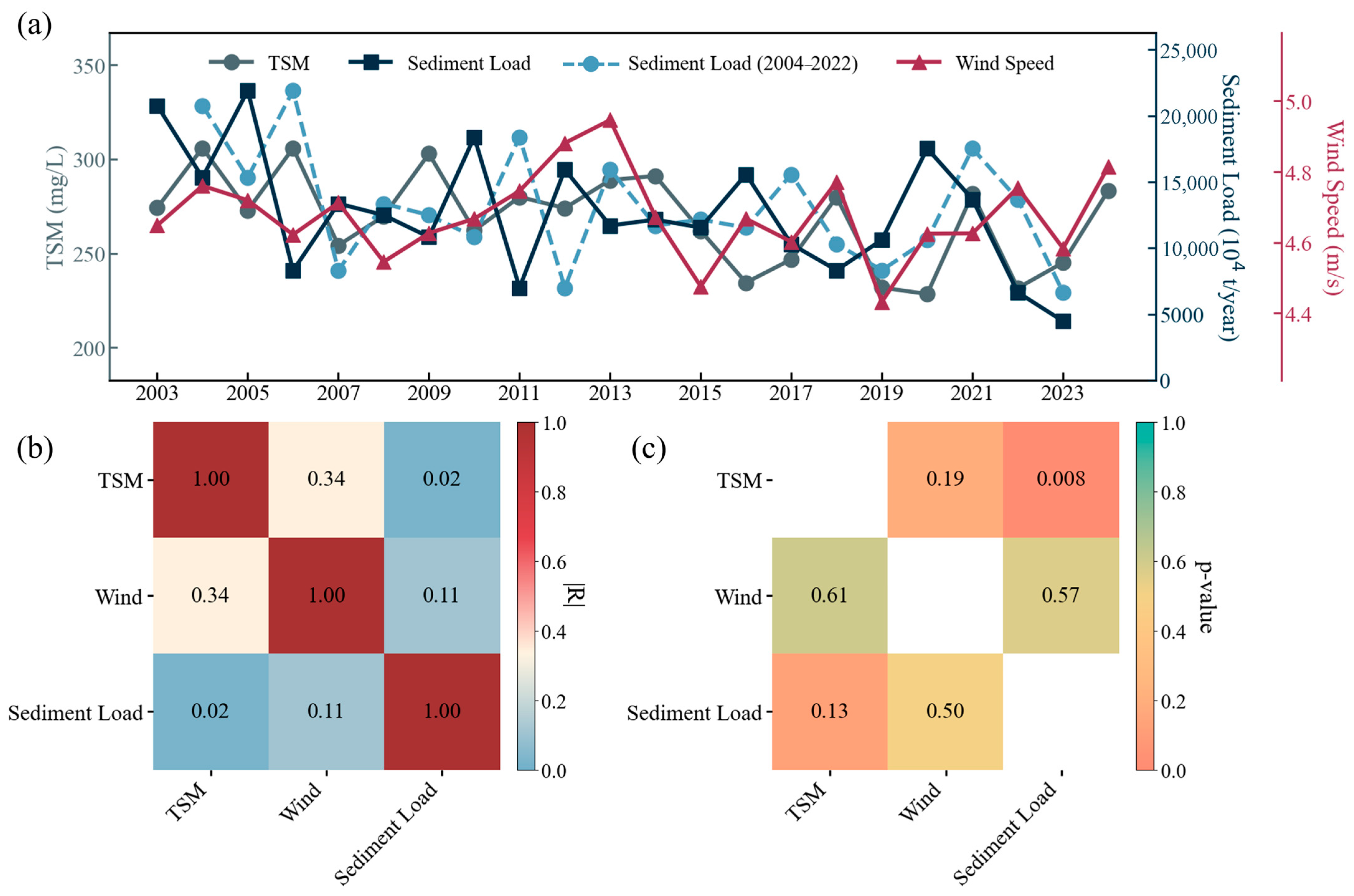
4.2. Factors Influencing TSM Interannual Variations
4.3. Impacts of Human Activities
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yun, C. China River Delta Crisis; Ocean Press: Beijing, China, 2010. [Google Scholar]
- Feng, L.; Hu, C.; Chen, X.; Song, Q. Influence of the Three Gorges Dam on total suspended matters in the Yangtze Estuary and its adjacent coastal waters: Observations from MODIS. Remote Sens. Environ. 2014, 140, 779–788. [Google Scholar] [CrossRef]
- Li, L.; Ye, T.; Zhang, L.; Yao, Y.; Xia, Y. Influences of reclamation location on the water and sediment environment in Hangzhou Bay. J. Harbin Eng. Univ. 2019, 40, 1870–1875. [Google Scholar]
- Fang, Q.; Huang, S.; Xu, X. Analysis of the influence of reclamation engineering group on the accumulated hydrodynamics in the south coast of Hangzhou Bay. Sci. Technol. Eng. 2020, 20, 5338–5344. [Google Scholar]
- Huang, S.; Zhang, Q.; Yan, J. Impact of shoreline changes caused by Hangzhou Bay Reclamation Project on water environment. J. North China Univ. Water Resour. Electr. Power (Nat. Sci. Ed.) 2021, 42, 32–41. [Google Scholar]
- Ministry of Ecology and Environment of China. The Ministry of Ecology and Environment and Six Other Departments Jointly Issued the “Action Plan for the Comprehensive Governance Campaign in Key Sea Areas”. Available online: https://www.gov.cn/xinwen/2022-02/17/content_5674359.htm (accessed on 9 August 2025).
- Ouillon, S.; Douillet, P.; Petrenko, A.; Neveux, J.; Dupouy, C.; Froidefond, J.-M.; Andréfouët, S.; Muñoz-Caravaca, A. Optical algorithms at satellite wavelengths for total suspended matter in tropical coastal waters. Sensors 2008, 8, 4165–4185. [Google Scholar] [CrossRef] [PubMed]
- Güttler, F.N.; Niculescu, S.; Gohin, F. Turbidity retrieval and monitoring of Danube Delta waters using multi-sensor optical remote sensing data: An integrated view from the delta plain lakes to the western–northwestern Black Sea coastal zone. Remote Sens. Environ. 2013, 132, 86–101. [Google Scholar] [CrossRef]
- Constantin, S.; Doxaran, D.; Constantinescu, Ș. Estimation of water turbidity and analysis of its spatio-temporal variability in the Danube River plume (Black Sea) using MODIS satellite data. Cont. Shelf Res. 2016, 112, 14–30. [Google Scholar] [CrossRef]
- Knaeps, E.; Ruddick, K.G.; Doxaran, D.; Dogliotti, A.I.; Nechad, B.; Raymaekers, D.; Sterckx, S. A SWIR based algorithm to retrieve total suspended matter in extremely turbid waters. Remote Sens. Environ. 2015, 168, 66–79. [Google Scholar] [CrossRef]
- Mao, Z.; Chen, J.; Pan, D.; Tao, B.; Zhu, Q. A regional remote sensing algorithm for total suspended matter in the East China Sea. Remote Sens. Environ. 2012, 124, 819–831. [Google Scholar] [CrossRef]
- Nazirova, K.; Alferyeva, Y.; Lavrova, O.; Shur, Y.; Soloviev, D.; Bocharova, T.; Strochkov, A. Comparison of in situ and remote-sensing methods to determine turbidity and concentration of suspended matter in the estuary zone of the mzymta river, black sea. Remote Sens. 2021, 13, 143. [Google Scholar] [CrossRef]
- Wen, Z.; Wang, Q.; Liu, G.; Jacinthe, P.-A.; Wang, X.; Lyu, L.; Tao, H.; Ma, Y.; Duan, H.; Shang, Y. Remote sensing of total suspended matter concentration in lakes across China using Landsat images and Google Earth Engine. ISPRS J. Photogramm. Remote Sens. 2022, 187, 61–78. [Google Scholar] [CrossRef]
- Mohseni, F.; Saba, F.; Mirmazloumi, S.M.; Amani, M.; Mokhtarzade, M.; Jamali, S.; Mahdavi, S. Ocean water quality monitoring using remote sensing techniques: A review. Mar. Environ. Res. 2022, 180, 105701. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Song, K.; Wen, Z.; Liu, G.; Shang, Y.; Lyu, L.; Du, J.; Yang, Q.; Li, S.; Tao, H. Remote sensing of turbidity for lakes in northeast China using Sentinel-2 images with machine learning algorithms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9132–9146. [Google Scholar] [CrossRef]
- Ye, T.; Li, L.; Yao, Y.; Xia, Y.; Guan, W. Inter-Annual Variability of the Turbidity Maximum Zone in Hangzhou Bay Based on Landsat Imagery. Geomat. Inf. Sci. Wuhan Univ. 2019, 44, 1377–1384. [Google Scholar]
- He, X.; Bai, Y.; Pan, D.; Huang, N.; Dong, X.; Chen, J.; Chen, C.T.A.; Cui, Q. Using geostationary satellite ocean color data to map the diurnal dynamics of suspended particulate matter in coastal waters. Remote Sens. Environ. 2013, 133, 225–239. [Google Scholar] [CrossRef]
- Li, P.; Yang, S.; Milliman, J.; Xu, K.; Qin, W.; Wu, C.; Chen, Y.; Shi, B. Spatial, temporal, and human-induced variations in suspended sediment concentration in the surface waters of the Yangtze Estuary and adjacent coastal areas. Estuaries Coasts 2012, 35, 1316–1327. [Google Scholar] [CrossRef][Green Version]
- Shen, F.; Zhou, Y.; Li, J.; He, Q.; Verhoef, W. Remotely sensed variability of the suspended sediment concentration and its response to decreased river discharge in the Yangtze estuary and adjacent coast. Cont. Shelf Res. 2013, 69, 52–61. [Google Scholar] [CrossRef]
- Liu, H. Hydrodynamic problems associated with construction of sea-crossing bridges. J. Hydrodyn. Ser. B 2006, 18, 13–18. [Google Scholar] [CrossRef]
- Pasiok, R.; Stilger-Szydło, E. Sediment particles and turbulent flow simulation around bridge piers. Arch. Civ. Mech. Eng. 2010, 10, 67–79. [Google Scholar] [CrossRef]
- Qiao, S.; Pan, D.; He, X.; Cui, Q. Numerical Study of the Influence of Donghai Bridge on Sediment Transport in the Mouth of Hangzhou Bay. Procedia Environ. Sci. 2011, 10, 408–413. [Google Scholar] [CrossRef]
- Liu, Y. Recent evolution process and influencing factors of Jinshan Trough in Hangzhou Bay. Ph.D. Thesis, East China Normal University, Shanghai, China, 2019. [Google Scholar]
- Gao, A.; Zhao, H.; Yang, S. Seasonal and tidal variations in suspended sediment concentration under the influence of River runoff, tidal current and wind waves-taking the Nanhui headland, the joint area between Changjiang Estuary and Hangzhou Bay as an Example. Adv. Mar. Sci. 2008, 26, 44. [Google Scholar]
- Dan, Y.; Zhifeng, Y.; Wenjie, D. Hourly Variability of Surface Suspended Sediment Concen--tration in Hangzhou Bay in Winter. J. Hangzhou Norm. Univ. (Nat. Sci. Ed.) 2014, 13, 373–379. [Google Scholar]
- Liu, M.; Shen, F.; Ge, J.; Kong, Y. Diurnal variation of suspended sediment concentration in Hangzhou Bay from geostationary satellite observation and its hydrodynamic analysis. J. Sediment Res. 2013, 1, 7–13. [Google Scholar]
- Bai, Y.; He, X.; Pan, D.; Zhu, Q.; Lei, H.; Tao, B.; Hao, Z. The extremely high concentration of suspended particulate matter in Changjiang Estuary detected by MERIS data. In Proceedings of the Remote Sensing of the Coastal Ocean, Land, and Atmosphere Environment, Incheon, Republic of Korea, 11–14 October 2010; pp. 250–257. [Google Scholar]
- Xu, Y.; He, X.; Bai, Y.; Wang, D.; Zhu, Q.; Ding, X. Evaluation of remote-sensing reflectance products from multiple ocean color missions in highly turbid water (Hangzhou bay). Remote Sens. 2021, 13, 4267. [Google Scholar] [CrossRef]
- Bai, R.; He, X.; Bai, Y.; Gong, F.; Zhu, Q.; Wang, D.; Li, T. Atmospheric correction algorithm based on the interpolation of ultraviolet and shortwave infrared bands. Opt. Express 2023, 31, 6805–6826. [Google Scholar] [CrossRef]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 1999, 38, 7442–7455. [Google Scholar] [CrossRef]
- Dai, Q.; Pan, D.; He, X.; Zhu, Q.; Gong, F.; Huang, H. High-Frequency Observation of Water Spectrum and Its Application in Monitoring of Dynamic Variation of Suspended Materials in the Hangzhou Bay. Spectrosc. Spectr. Anal. 2015, 35, 3247–3254. [Google Scholar]
- Fraser, R.S.; Mattoo, S.; Yeh, E.N.; McClain, C. Algorithm for atmospheric and glint corrections of satellite measurements of ocean pigment. J. Geophys. Res. Atmos. 1997, 102, 17107–17118. [Google Scholar] [CrossRef]
- Wang, M.; Bailey, S.W. Correction of sun glint contamination on the SeaWiFS ocean and atmosphere products. Appl. Opt. 2001, 40, 4790–4798. [Google Scholar] [CrossRef]
- Frouin, R.; Schwindling, M.; Deschamps, P.Y. Spectral reflectance of sea foam in the visible and near–infrared: In situ measurements and remote sensing implications. J. Geophys. Res. Ocean. 1996, 101, 14361–14371. [Google Scholar] [CrossRef]
- Gordon, H.R.; Wang, M. Influence of oceanic whitecaps on atmospheric correction of ocean-color sensors. Appl. Opt. 1994, 33, 7754–7763. [Google Scholar] [CrossRef] [PubMed]
- Moore, K.D.; Voss, K.J.; Gordon, H.R. Spectral reflectance of whitecaps: Their contribution to water--leaving radiance. J. Geophys. Res. Ocean. 2000, 105, 6493–6499. [Google Scholar] [CrossRef]
- Gordon, H.R.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: A preliminary algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R. Atmospheric correction of ocean color imagery in the Earth Observing System era. J. Geophys. Res. Atmos. 1997, 102, 17081–17106. [Google Scholar] [CrossRef]
- Gordon, H.R.; Wang, M. Surface-roughness considerations for atmospheric correction of ocean color sensors. 1: The Rayleigh-scattering component. Appl. Opt. 1992, 31, 4247–4260. [Google Scholar] [CrossRef]
- Wang, M. The Rayleigh lookup tables for the SeaWiFS data processing: Accounting for the effects of ocean surface roughness. Int. J. Remote Sens. 2002, 23, 2693–2702. [Google Scholar] [CrossRef]
- Wang, M. A refinement for the Rayleigh radiance computation with variation of the atmospheric pressure. Int. J. Remote Sens. 2005, 26, 5651–5663. [Google Scholar] [CrossRef]
- Deschamps, P.; Herman, M.; Tanre, D. Modeling of the atmospheric effects and its application to the remote sensing of ocean color. Appl. Opt. 1983, 22, 3751–3758. [Google Scholar] [CrossRef]
- Gordon, H.R.; Franz, B.A. Remote sensing of ocean color: Assessment of the water-leaving radiance bidirectional effects on the atmospheric diffuse transmittance for SeaWiFS and MODIS intercomparisons. Remote Sens. Environ. 2008, 112, 2677–2685. [Google Scholar] [CrossRef]
- Gordon, H.R.; Brown, J.W.; Evans, R.H. Exact Rayleigh scattering calculations for use with the Nimbus-7 coastal zone color scanner. Appl. Opt. 1988, 27, 862–871. [Google Scholar] [CrossRef]
- He, X.; Pan, D.; Bai, Y.; Mao, Z.; Gong, F. General exact Rayleigh scattering look-up-table for ocean color remote sensing. In Proceedings of the Remote Sensing of the Marine Environment, Goa, India, 13–17 November 2006; pp. 319–328. [Google Scholar]
- Wang, M.; Shi, W. Estimation of ocean contribution at the MODIS near--infrared wavelengths along the east coast of the US: Two case studies. Geophys. Res. Lett. 2005, 32, L13606. [Google Scholar] [CrossRef]
- Siegel, D.A.; Wang, M.; Maritorena, S.; Robinson, W. Atmospheric correction of satellite ocean color imagery: The black pixel assumption. Appl. Opt. 2000, 39, 3582–3591. [Google Scholar] [CrossRef] [PubMed]
- Stumpf, R.; Arnone, R.; Gould, R.; Martinolich, P.; Ransibrahmanakul, V. A partially coupled ocean-atmosphere model for retrieval of water-leaving radiance from SeaWiFS in coastal waters. NASA Tech. Memo 2003, 206892, 51–59. [Google Scholar]
- Ruddick, K.G.; Ovidio, F.; Rijkeboer, M. Atmospheric correction of SeaWiFS imagery for turbid coastal and inland waters. Appl. Opt. 2000, 39, 897–912. [Google Scholar] [CrossRef]
- He, X.; Bai, Y.; Pan, D.; Tang, J.; Wang, D. Atmospheric correction of satellite ocean color imagery using the ultraviolet wavelength for highly turbid waters. Opt. Express 2012, 20, 20754–20770. [Google Scholar] [CrossRef]
- Wang, M.; Shi, W. The NIR-SWIR combined atmospheric correction approach for MODIS ocean color data processing. Opt. Express 2007, 15, 15722–15733. [Google Scholar] [CrossRef]
- Wang, M.; Son, S.; Shi, W. Evaluation of MODIS SWIR and NIR-SWIR atmospheric correction algorithms using SeaBASS data. Remote Sens. Environ. 2009, 113, 635–644. [Google Scholar] [CrossRef]
- Zhang, M.; Tang, J.; Dong, Q.; Song, Q.; Ding, J. Retrieval of total suspended matter concentration in the Yellow and East China Seas from MODIS imagery—ScienceDirect. Remote Sens. Environ. 2010, 114, 392–403. [Google Scholar] [CrossRef]
- Han, Z.; Jin, Y.; Yun, C. Suspended sediment concentrations in the Yangtze River estuary retrieved from the CMODIS data. Int. J. Remote Sens. 2006, 27, 4329–4336. [Google Scholar] [CrossRef]
- Miller, R.L.; McKee, B.A. Using MODIS Terra 250 m imagery to map concentrations of total suspended matter in coastal waters. Remote Sens. Environ. 2004, 93, 259–266. [Google Scholar] [CrossRef]
- Cheng, Q.; Liu, B.; Li, T.; Zhu, L. Research on remote sensing retrieval of suspended sediment concentration in Hangzhou Bay by GF-1 satellite. Mar. Environ. Sci. 2015, 34, 558–563+577. [Google Scholar]
- Doxaran, D.; Froidefond, J.-M.; Lavender, S.; Castaing, P. Spectral signature of highly turbid waters: Application with SPOT data to quantify suspended particulate matter concentrations. Remote Sens. Environ. 2002, 81, 149–161. [Google Scholar] [CrossRef]
- Han, B.; Loisel, H.; Vantrepotte, V.; Mériaux, X.; Bryère, P.; Ouillon, S.; Dessailly, D.; Xing, Q.; Zhu, J. Development of a semi-analytical algorithm for the retrieval of suspended particulate matter from remote sensing over clear to very turbid waters. Remote Sens. 2016, 8, 211. [Google Scholar] [CrossRef]
- D’Sa, E.J.; Miller, R.L.; McKee, B.A. Suspended particulate matter dynamics in coastal waters from ocean color: Application to the northern Gulf of Mexico. Geophys. Res. Lett. 2007, 34, L23611. [Google Scholar] [CrossRef]
- Chen, X.; Lu, J.; Cui, T.; Jiang, W.; Tian, L.; Chen, L.; Zhao, W. Coupling remote sensing retrieval with numerical simulation for SPM study—Taking Bohai Sea in China as a case. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S203–S211. [Google Scholar] [CrossRef]
- Ma, W.-D.; Wu, C.-Q.; Yin, S.-J.; Wang, C.; Nie, Y.-H.; Lin, H.; Li, J.-R. The remote sensing retrieval of total suspended matter in Xiamen bay. Mar. Environ. Sci. 2016, 35, 770–773+786. [Google Scholar]
- Tang, J.; Wang, X.; Song, Q.; Li, T.; Huang, H.; Ren, J.; Jian, W. Statistical inversion models for case II water color elements in the Yellow Sea and East China Sea. Adv. Mar. Sci. 2004, 22, 7. [Google Scholar]
- Wang, F.; Wang, S.; Wang, X.; Song, L.; Xu, Q.; Zheng, H. Remote sensing retrieval and dynamic driving force analysis of suspended sediment in Hangzhou Bay. J. Huazhong Norm. Univ. 2014, 48, 112–116+135. [Google Scholar]
- Chen, S. Seasonal, neap-spring variation of sediment concentration in the joint area between Yangtze Estuary and Hangzhou Bay. Sci. China Ser. B Chem. 2001, 44, 57–62. [Google Scholar] [CrossRef]
- Bai, Y.; He, X.; Pan, D.; Chen, C.u.A.; Kang, Y.; Chen, X.; Cai, W.u. Summertime Changjiang River plume variation during 1998–2010. J. Geophys. Res. Ocean. 2014, 119, 6238–6257. [Google Scholar] [CrossRef]
- Truong, C.; Oudre, L.; Vayatis, N. Selective review of offline change point detection methods. Signal Process. 2020, 167, 107299. [Google Scholar] [CrossRef]
- Chen, J.; Chen, S.; Ding, P.; Yang, S. Sediment transport along the Nanhui submerged spit of the Yangtze Estuary. Resour. Environ. Yangtze Basin 2001, 10, 166–172. [Google Scholar]
- Chen, J.; Wang, B.; Yu, Z. Developments and Evolution of China’s Coast; Shanghai Scientific & Technical Publishers: Shanghai, China, 1989. [Google Scholar]
- Liu, J.; Liu, J.; He, X.; Chen, T.; Zhu, F.; Wang, Y.; Hao, Z.; Chen, P. Retrieval of total suspended particulate matter in highly turbid Hangzhou Bay waters based on geostationary ocean color imager. In Proceedings of the Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions 2017, Warsaw, Poland, 11–14 September 2017; pp. 105–111. [Google Scholar]
- Cao, P.; Gu, G.; Dong, Y.; Hu, F. Basic characteristics of sediment transport in Hangzhou Bay. J. East China Norm. Univ. 1985, 3, 75–84. [Google Scholar]
- Chen, B.; Liu, J.; Bai, D. Variation of suspended sediment concentretion in offshore Yangtze Estuary. Mar. Geol. Front. 2011, 27, 39–44. [Google Scholar]
- Wu, M.; Xu, J.; Feng, Y. Spacial-temporal distribution of suspended sediment concentration in Hangzhou Bay. J. Sediment Res. 2011, 1, 33–37. [Google Scholar]
- Zuo, S.; Li, B.; Yang, H. Remote sensing analysis on distribution and movement of surface suspended sediment in the Nanhuizui tidal flat, Yangtze Estuary. J. Waterw. Harb. 2010, 31, 384–389. [Google Scholar]
- Zhang, G.; Yang, S.; Yu, Z. Temporal and spatial changes of suspended sediment concentration and resuspension in the Yangtze River Estuary and its adjacent waters. Acta Geogr. Sin. 2004, 59, 260–266. [Google Scholar]
- Yang, X.; Mao, Z.; Huang, H.; Zhu, Q. Using GOCI Retrieval Data to Initialize and Validate a Sediment Transport Model for Monitoring Diurnal Variation of SSC in Hangzhou Bay, China. Water 2016, 8, 108. [Google Scholar] [CrossRef]
- Du, P.; Ding, P.; Hu, K. Simulation of three-dimensional cohesive sediment transport in Hangzhou Bay, China. Acta Oceanol. Sin. 2010, 29, 98–106. [Google Scholar] [CrossRef]
- Zhao, J.; Dai, Z.; Li, J.; Li, W. Study on the characteristics of temporal and spatial changes in properties of surface sediment on near-shore seabed of strong-tide bay: A case from the north bank of Hangzhou Bay in Shanghai. Acta Sedimentol. Sin. 2008, 26, 49–57. [Google Scholar]
- Wang, F.; Zhou, B.; Xu, J.; Song, L.; Wang, X. Application of neural network and MODIS 250 m imagery for estimating suspended sediments concentration in Hangzhou Bay, China. Environ. Geol. 2009, 56, 1093–1101. [Google Scholar] [CrossRef]
- Su, J.; Wang, K. Changjiang river plume and suspended sediment transport in Hangzhou Bay. Cont. Shelf Res. 1989, 9, 93–111. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, G.-a.; Yang, S.; Shi, J.Z. Temporal variations of fine suspended sediment concentration in the Changjiang River estuary and adjacent coastal waters, China. J. Hydrol. 2006, 331, 137–145. [Google Scholar] [CrossRef]
- Hu, Y.; Yu, Z.; Zhou, B.; Li, Y.; Shum, C.K. Tidal-driven variation of suspended sediment in Hangzhou Bay based on GOCI data. Int. J. Appl. Earth Obs. Geoinf. 2019, 82, 101920. [Google Scholar] [CrossRef]
- Sternberg, R.; Larsen, L.; Miao, Y. Tidally driven sediment transport on the East China Sea continental shelf. Cont. Shelf Res. 1985, 4, 105–120. [Google Scholar] [CrossRef]
- Lin, C.-M.; Zhuo, H.-C.; Gao, S. Sedimentary facies and evolution in the Qiantang River incised valley, eastern China. Mar. Geol. 2005, 219, 235–259. [Google Scholar] [CrossRef]
- Baker, C.J. The Laminar Horseshoe Vortex. J. Fluid Mech. 1979, 95, 347–367. [Google Scholar] [CrossRef]
- Unger, J.; Hager, W.H. Down-flow and horseshoe vortex characteristics of sediment embedded bridge piers. Exp. Fluids 2007, 42, 1–19. [Google Scholar] [CrossRef]
- Liu, B.; Cheng, Q.; Zeng, H.; Yang, R. On the suspended sediment concentration distribution and diversity of the waters on both sides of Hangzhou Bay sea-crossing bridge based on GOCI data. J. Hangzhou Norm. Univ. (Nat. Sci. Ed.) 2016, 15, 102–107. [Google Scholar]
- Huang, S.; Liu, J.; Cai, L.; Zhou, M.; Bu, J.; Xu, J. Satellites HY-1C and Landsat 8 combined to observe the influence of bridge on sea surface temperature and suspended sediment concentration in Hangzhou Bay, China. Water 2020, 12, 2595. [Google Scholar] [CrossRef]
- Zhou, M. Research on the Influence of Sea-crossing Bridge and Island on Suspended Sediment Concentration Based on HY-1C. Ph.D. Thesis, Zhejiang Ocean University, Zhoushan, China, 2021. [Google Scholar]
- Sun, X.; Li, C. Influence of Yushan Islands reclamation on growth of south and north deep channels and development of port shoreline. Port Waterw. Eng. 2021, 81–85. [Google Scholar] [CrossRef]
- Gao, Y. Study on Three-dimensional Hydrodynamic and Suspended Sediment Transport and Diffusion Characteristics Before and After Yushan Reclamation Project. Ph.D. Thesis, Zhejiang Ocean University, Zhoushan, China, 2022. [Google Scholar]



| Wavelength (nm) | Number | RMSE () | MAPE (%) |
|---|---|---|---|
| 412 | 10 | 0.00316 | 19.09 |
| 443 | 10 | 0.00274 | 12.56 |
| 469 | 10 | 0.00172 | 8.32 |
| 488 | 10 | 0.00173 | 7.22 |
| 531 | 10 | 0.00135 | 4.73 |
| 555 | 10 | 0.00126 | 3.24 |
| 645 | 10 | 0.00290 | 6.56 |
| 859 | 10 | 0.00402 | 23.60 |
| Author | Equation | |
|---|---|---|
| Miller and McKee [55] | ||
| Cheng1 [56] | ||
| Cheng2 [56] | ||
| Doxaran [57] | ||
| Han [58] | ] | |
| D’Sa [59] | ||
| Chen [60] | ||
| Ma [61] | ||
| Tang [62] |
| Month | Mean | Max | Min |
|---|---|---|---|
| January | 589.80 | 5871.32 | 36.16 |
| February | 566.34 | 5799.39 | 39.53 |
| March | 499.38 | 5785.83 | 29.25 |
| April | 485.98 | 5943.95 | 55.62 |
| May | 469.87 | 5676.12 | 53.56 |
| June | 337.82 | 5853.43 | 22.44 |
| July | 327.10 | 5962.10 | 26.26 |
| August | 353.05 | 5793.73 | 29.49 |
| September | 393.80 | 5929.99 | 25.75 |
| October | 434.61 | 5990.35 | 30.47 |
| November | 477.77 | 5975.67 | 30.42 |
| December | 773.80 | 5994.22 | 38.60 |
| Location | k | p-Value |
|---|---|---|
| box0 | 2.23 | 0.122 |
| box1 | −3.27 | 0.009 ** |
| box2 | −3.90 | 0.021 * |
| box3 | −0.19 | 0.885 |
| box4 | −2.00 | 0.250 |
| Season | k | p-Value |
|---|---|---|
| Spring | −2.99 | 0.014 * |
| Summer | −2.38 | 0.017 * |
| Autumn | 0.20 | 0.879 |
| Winter | −0.88 | 0.685 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; He, X.; Zhao, Y.; Shanmugam, P.; Gong, F.; Li, T.; Jin, X. Assessing the Long-Term Changes in the Suspended Particulate Matter in Hangzhou Bay Using MODIS/Aqua Data. Remote Sens. 2025, 17, 3248. https://doi.org/10.3390/rs17183248
Lu X, He X, Zhao Y, Shanmugam P, Gong F, Li T, Jin X. Assessing the Long-Term Changes in the Suspended Particulate Matter in Hangzhou Bay Using MODIS/Aqua Data. Remote Sensing. 2025; 17(18):3248. https://doi.org/10.3390/rs17183248
Chicago/Turabian StyleLu, Xinyi, Xianqiang He, Yaqi Zhao, Palanisamy Shanmugam, Fang Gong, Teng Li, and Xuchen Jin. 2025. "Assessing the Long-Term Changes in the Suspended Particulate Matter in Hangzhou Bay Using MODIS/Aqua Data" Remote Sensing 17, no. 18: 3248. https://doi.org/10.3390/rs17183248
APA StyleLu, X., He, X., Zhao, Y., Shanmugam, P., Gong, F., Li, T., & Jin, X. (2025). Assessing the Long-Term Changes in the Suspended Particulate Matter in Hangzhou Bay Using MODIS/Aqua Data. Remote Sensing, 17(18), 3248. https://doi.org/10.3390/rs17183248






