Submesoscale Eddies Identified by SWOT and Their Comparison with Mesoscale Eddies in the Tropical Western Pacific
Abstract
Highlights
- SWOT identifies 176 mesoscale eddies (vs. 162 by DUACS) and shows 15% stronger amplitudes.
- The distribution of submesoscale eddies’ abundance, size, and amplitude across the tropical western Pacific.
- Conventional DUACS-based studies underrepresent submesoscale eddies, calling for updated parameterizations in ocean and climate models.
- It is conducive to revealing the potential role of submesoscale eddies in the multi-scale dynamic processes of the ocean.
Abstract
1. Introduction
2. Materials and Methods
2.1. Altimetry Datasets
2.2. Data Processing
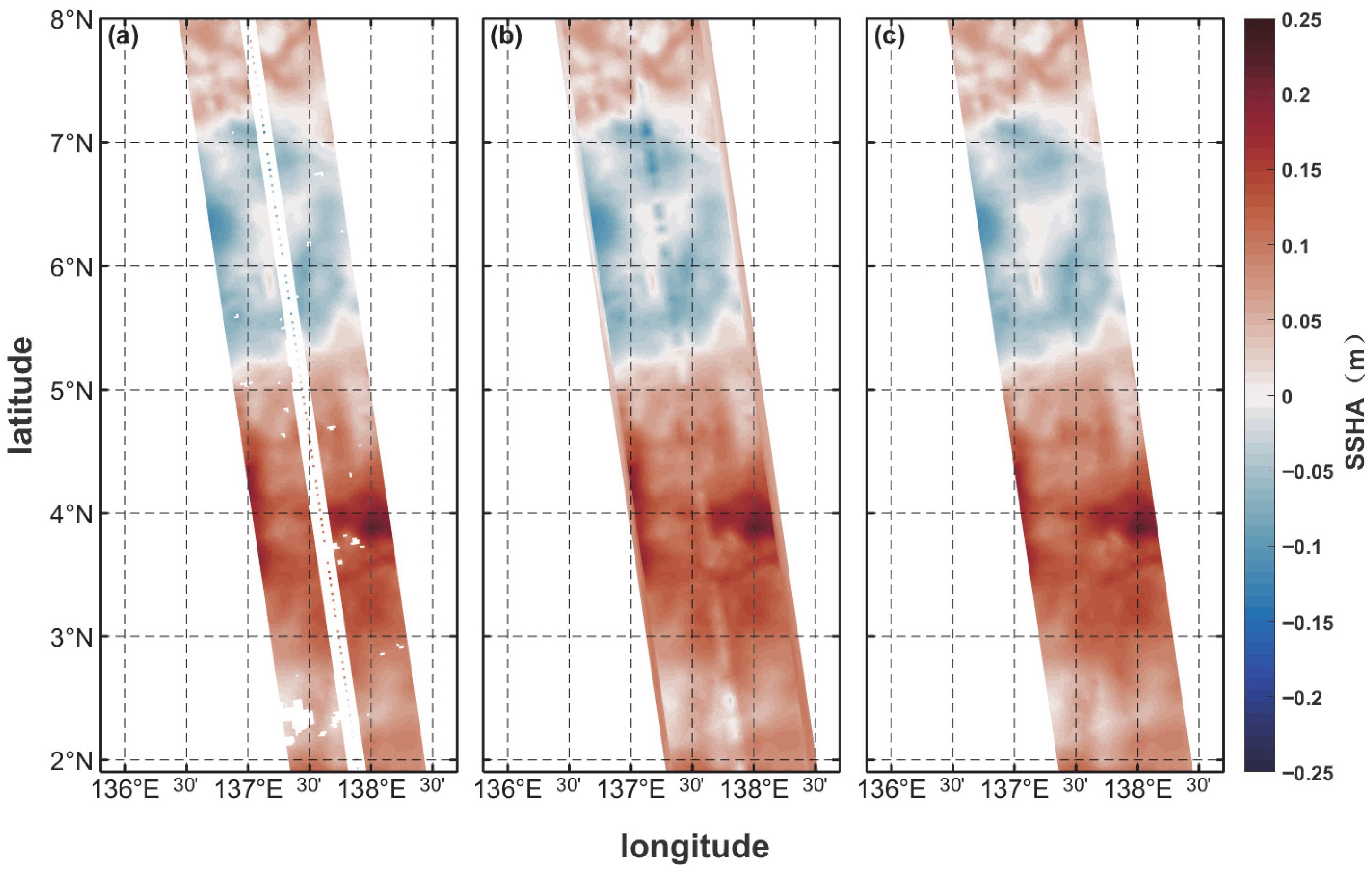
2.2.1. Preprocessing of Single-Orbit Data
2.2.2. Conversion to Gridded Datasets and the Sub-Cycling Strategy
- (1)
- ≤2-day temporal gaps mitigating decorrelation-induced inconsistencies (Figure 2c);
- (2)
- Enhanced cross-orbit data fusion coherence.
2.2.3. Inland Water Detection and Land Masking
2.3. Eddy Detection Methodology
- SLA values are constrained between −100 cm and 100 cm. This threshold aligns with the intensity spectrum of SMEs, filtering out extreme values associated with larger ME or basin-scale phenomena.
- Closed contours must exhibit genuine closure, defined as a continuous loop consisting of at least three discrete points. Additionally, the longitudinal and latitudinal spans of these contours must exceed 0.1°, effectively excluding artifacts generated by noise or subgrid-scale fluctuations.
- The maximum distance between any two points on a closed contour is limited to ensure that the detected features conform to local SME-specific spatial scales (with diameters ranging from 15 km to 80 km depending on the latitude).
- Consistency between eddy core location and contour geometry is rigorously validated. The geometric centroid of each closed contour must lie within its boundaries, and deviations between the centroid and dynamically derived eddy centers are minimized.
- Leveraging the high-resolution capabilities of SWOT, amplitude and radius thresholds are applied: eddies are retained only if their SLA amplitudes exceed 2 cm, and their equivalent radii (calculated from contour areas) surpass 7 km. These thresholds mitigate false detections induced by instrumental noise or small-scale turbulent motions.
2.4. Criteria for Distinguishing ME and SME
3. Results
3.1. Eddies Identified by DUACS
3.1.1. Typical Eddies
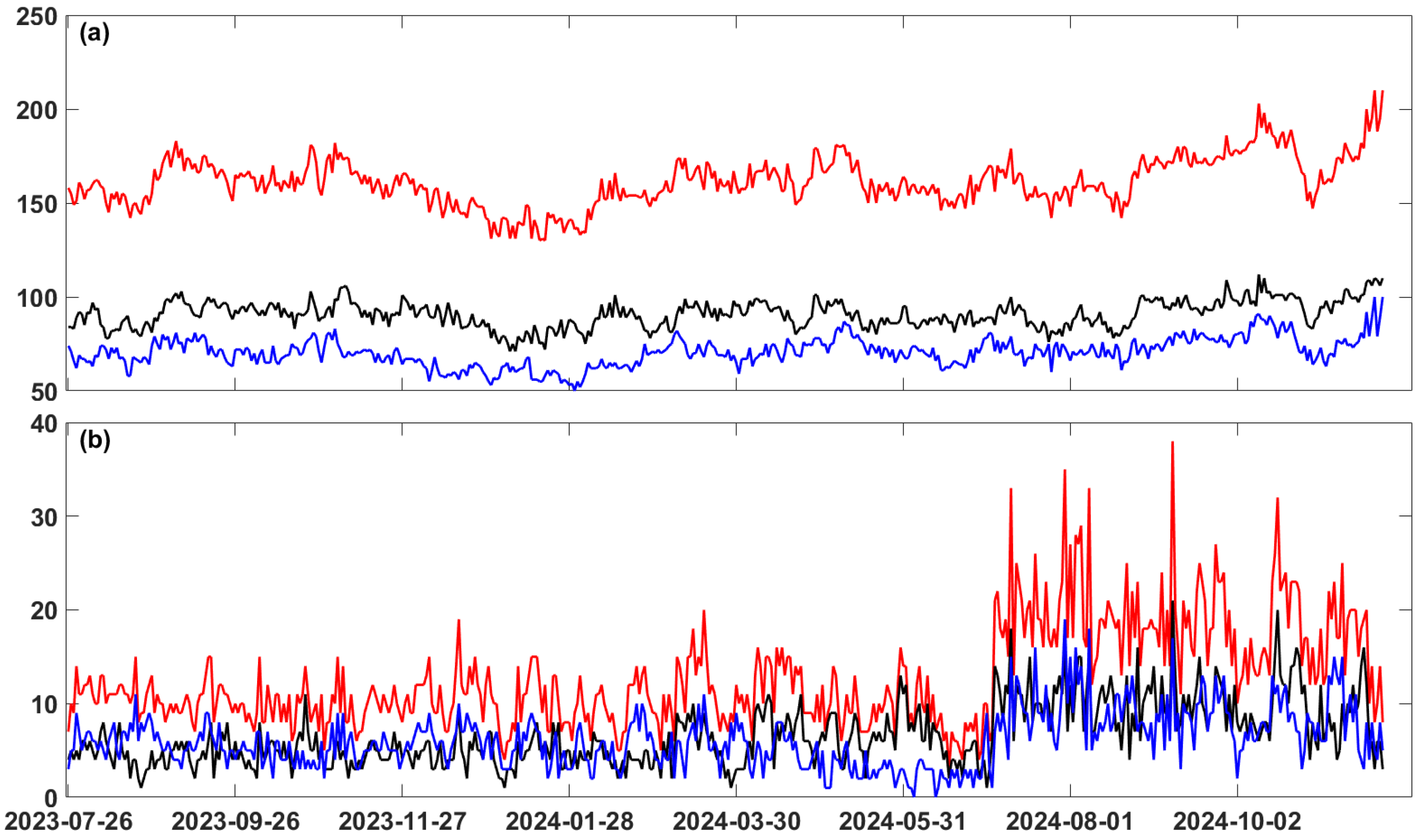
3.1.2. Statistical Characteristics
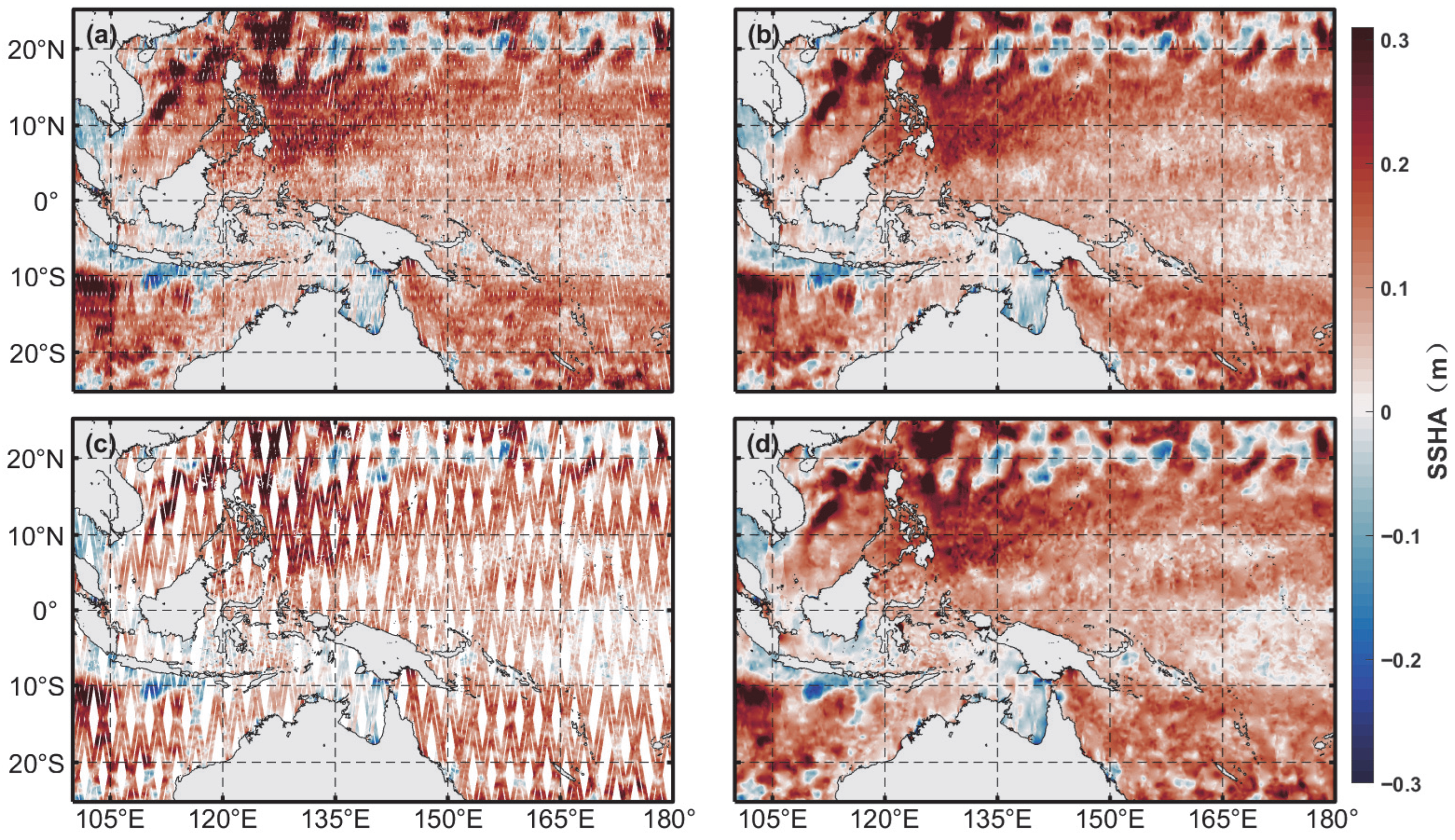
3.2. Eddies Identified by SWOT
3.2.1. Eddies During Commissioning Phase
3.2.2. Eddies During Science Orbit Phase
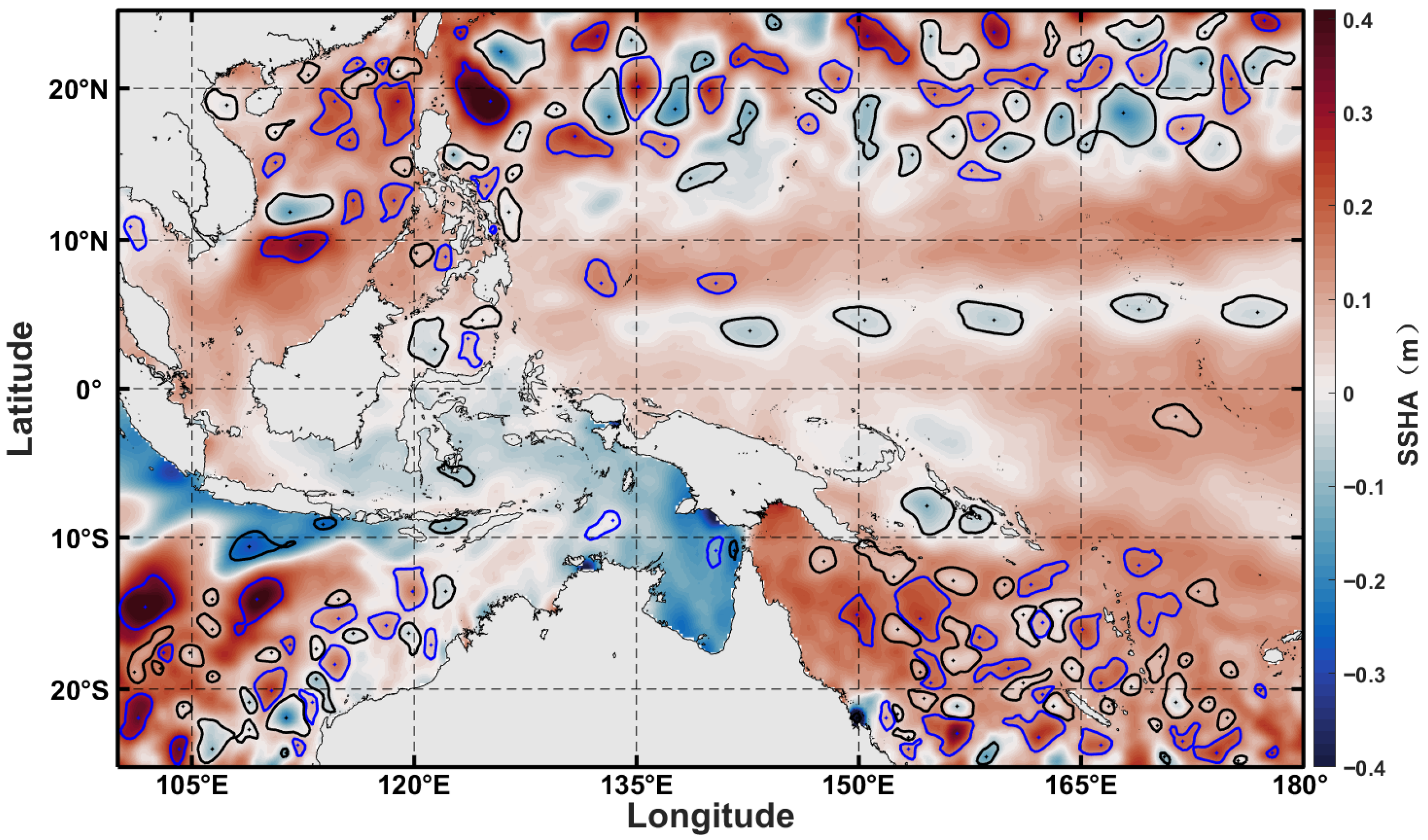
4. Comparative Analysis of SWOT and DUACS in Eddies Detection
4.1. Spatial Distribution
4.2. Comparison of Statistical Characteristics
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Taylor, J.R.; Thompson, A.F. Submesoscale dynamics in the upper ocean. Annu. Rev. Fluid Mech. 2023, 55, 103–127. [Google Scholar] [CrossRef]
- Capet, X.; McWilliams, J.C.; Molemaker, M.J.; Shchepetkin, A.F. Mesoscale to submesoscale transition in the California Current System. Part III: Energy balance and flux. J. Phys. Oceanogr. 2008, 38, 2256–2269. [Google Scholar] [CrossRef]
- Su, Z.; Wang, J.; Klein, P.; Thompson, A.F.; Menemenlis, D. Ocean submesoscales as a key component of the global heat budget. Nat. Commun. 2018, 9, 775. [Google Scholar] [CrossRef]
- Yu, X.; Naveira Garabato, A.C.; Martin, A.P.; Buckingham, C.E.; Brannigan, L.; Su, Z. An annual cycle of submesoscale vertical flow and restratification in the upper ocean. J. Phys. Oceanogr. 2019, 49, 1439–1461. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, X.; Qiu, B.; Zhao, W.; Zhou, C.; Huang, X.; Tian, J. Submesoscale currents in the subtropical upper ocean observed by long-term high-resolution mooring arrays. J. Phys. Oceanogr. 2021, 51, 187–206. [Google Scholar] [CrossRef]
- Qiu, B.; Nakano, T.; Chen, S.; Klein, P. Bi-directional energy cascades in the Pacific Ocean from equator to subarctic gyre. Geophys. Res. Lett. 2022, 49, e2022GL097713. [Google Scholar] [CrossRef]
- Zhang, Z.; Qiu, B. Evolution of submesoscale ageostrophic motions through the life cycle of oceanic mesoscale eddies. Geophys. Res. Lett. 2018, 45, 11,847–11,855. [Google Scholar] [CrossRef]
- Capet, X.; Mcwilliams, J.C.; Molemaker, M.J.; Shchepetkin, A.F. Mesoscale to submesoscale transition in the California Current System. Part I: Flow structure, eddy flux, and observational tests. J. Phys. Oceanogr. 2008, 38, 29–43. [Google Scholar] [CrossRef]
- Chelton, D.B.; DeSzoeke, R.A.; Schlax, M.G.; El Naggar, K.; Siwertz, N. Geographical variability of the first baroclinic Rossby radius of deformation. J. Phys. Oceanogr. 1998, 28, 433–460. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, C.; Liu, Y.; Weisberg, R.H.; Kourafalou, V.H. Submesoscale and mesoscale eddies in the Florida Straits: Observations from satellite ocean color measurements. Geophys. Res. Lett. 2019, 46, 13262–13270. [Google Scholar] [CrossRef]
- Klein, P.; Lapeyre, G. The oceanic vertical pump induced by mesoscale and submesoscale turbulence. Annu. Rev. Mar. Sci. 2009, 1, 351–375. [Google Scholar] [CrossRef]
- McWilliams, J.C. Submesoscale currents in the ocean. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20160117. [Google Scholar] [CrossRef]
- Fox-Kemper, B.; Danabasoglu, G.; Ferrari, R.; Griffies, S.; Hallberg, R.; Holland, M.; Maltrud, M.; Peacock, S.; Samuels, B. Parameterization of mixed layer eddies. III: Implementation and impact in global ocean climate simulations. Ocean Model. 2011, 39, 61–78. [Google Scholar] [CrossRef]
- Mensa, J.A.; Garraffo, Z.; Griffa, A.; Özgökmen, T.M.; Haza, A.; Veneziani, M. Seasonality of the submesoscale dynamics in the Gulf Stream region. Ocean Dyn. 2013, 63, 923–941. [Google Scholar] [CrossRef]
- Piggott, M.; Gorman, G.; Pain, C.; Allison, P.; Candy, A.; Martin, B.; Wells, M. A new computational framework for multi-scale ocean modelling based on adapting unstructured meshes. Int. J. Numer. Methods Fluids 2008, 56, 1003–1015. [Google Scholar] [CrossRef]
- Torres, H.S.; Rodriguez, E.; Wineteer, A.; Klein, P.; Thompson, A.F.; Callies, J.; D’Asaro, E.; Perkovic-Martin, D.; Farrar, J.T.; Polverari, F. Airborne observations of fast-evolving ocean submesoscale turbulence. Commun. Earth Environ. 2024, 5, 771. [Google Scholar] [CrossRef]
- Fu, L.-L.; Ubelmann, C. On the transition from profile altimeter to swath altimeter for observing global ocean surface topography. J. Atmos. Ocean. Technol. 2014, 31, 560–568. [Google Scholar] [CrossRef]
- Beron-Vera, F.J.; Hadjighasem, A.; Xia, Q.; Olascoaga, M.J.; Haller, G. Coherent Lagrangian swirls among submesoscale motions. Proc. Natl. Acad. Sci. USA 2019, 116, 18251–18256. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.L.; Pavelsky, T.; Cretaux, J.F.; Morrow, R.; Farrar, J.T.; Vaze, P.; Sengenes, P.; Vinogradova-Shiffer, N.; Sylvestre-Baron, A.; Picot, N. The surface water and ocean topography mission: A breakthrough in radar remote sensing of the ocean and land surface water. Geophys. Res. Lett. 2024, 51, e2023GL107652. [Google Scholar] [CrossRef]
- Dibarboure, G.; Ubelmann, C.; Flamant, B.; Briol, F.; Peral, E.; Bracher, G.; Vergara, O.; Faugère, Y.; Soulat, F.; Picot, N. Data-driven calibration algorithm and pre-launch performance simulations for the SWOT mission. Remote Sens. 2022, 14, 6070. [Google Scholar] [CrossRef]
- Biancamaria, S.; Lettenmaier, D.P.; Pavelsky, T.M. The SWOT Mission and Its Capabilities for Land Hydrology. In Remote Sensing and Water Resources; Space Sciences Series of ISSI; Springer: Berlin/Heidelberg, Germany, 2016; pp. 117–147. [Google Scholar]
- Archer, M.; Wang, J.; Klein, P.; Dibarboure, G.; Fu, L.-L. Wide-swath satellite altimetry unveils global submesoscale ocean dynamics. Nature 2025, 640, 691–696. [Google Scholar] [CrossRef]
- Zhang, Z.; Miao, M.; Qiu, B.; Tian, J.; Jing, Z.; Chen, G.; Chen, Z.; Zhao, W. Submesoscale eddies detected by SWOT and moored observations in the Northwestern Pacific. Geophys. Res. Lett. 2024, 51, e2024GL110000. [Google Scholar] [CrossRef]
- Morrow, R.; Fu, L.-L.; Ardhuin, F.; Benkiran, M.; Chapron, B.; Cosme, E.; d’Ovidio, F.; Farrar, J.T.; Gille, S.T.; Lapeyre, G. Global observations of fine-scale ocean surface topography with the surface water and ocean topography (SWOT) mission. Front. Mar. Sci. 2019, 6, 232. [Google Scholar] [CrossRef]
- Chaudhary, A.; Agarwal, N.; Sharma, R.; Ojha, S.P.; Kumar, R. Nadir altimetry Vis-à-Vis swath altimetry: A study in the context of SWOT mission for the Bay of Bengal. Remote Sens. Environ. 2021, 252, 112120. [Google Scholar] [CrossRef]
- Morrow, R.; Blurmstein, D.; Dibarboure, G. Fine-scale altimetry and the future SWOT mission. In New Frontiers in Operational Oceanography; GODAE OceanView: London, UK, 2018; pp. 191–226. [Google Scholar] [CrossRef]
- Pujol, M.I.; Faugère, Y.; Taburet, G.; Dupuy, S.; Pelloquin, C.; Ablain, M.; Picot, N. DUACS DT2014: The new multi-mission altimeter data set reprocessed over 20 years. Ocean Sci. 2016, 12, 1067–1090. [Google Scholar] [CrossRef]
- Pujol, M.-I.; Dupuy, S.; Vergara, O.; Sánchez-Román, A.; Faugere, Y.; Prandi, P.; Dabat, M.-L.; Dagneaux, Q.; Lievin, M.; Cadier, E. Refining the resolution of DUACS along track (level 3) altimeter Sea Level products. Earth Syst. Sci. Data Discuss. 2022, 2022, 1–40. [Google Scholar] [CrossRef]
- Tranchant, Y.-T.; Legresy, B.; Foppert, A.; Pena-Molino, B.; Phillips, H.E. SWOT reveals fine-scale balanced motions and dispersion properties in the Antarctic Circumpolar Current. Earth Space Sci. 2025, 12, e2025EA004248. [Google Scholar] [CrossRef]
- Yadidya, B.; Arbic, B.K.; Shriver, J.F.; Zaron, E.D.; Buijsman, M.C.; Carrère, L.; Tchilibou, M.; Uchida, T. Predicting internal tides with a global ocean forecast system: Insights from SWOT CalVal orbit. Geophys. Res. Lett. 2025, 51, e2023GL107232. [Google Scholar] [CrossRef]
- Wang, J.; Fu, L.-L.; Haines, B.; Lankhorst, M.; Lucas, A.J.; Farrar, J.T.; Send, U.; Meinig, C.; Schofield, O.; Ray, R. On the development of SWOT in situ calibration/validation for short-wavelength ocean topography. J. Atmos. Ocean. Technol. 2022, 39, 595–617. [Google Scholar] [CrossRef]
- Du, T.; Jing, Z. Fine-scale eddies detected by SWOT in the kuroshio extension. Remote Sens. 2024, 16, 3488. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S.; Klein, P.; Ubelmann, C.; Fu, L.-L.; Sasaki, H. Reconstructability of three-dimensional upper-ocean circulation from SWOT sea surface height measurements. J. Phys. Oceanogr. 2016, 46, 947–963. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Robinson, S. Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 1991, 23, 601–639. [Google Scholar] [CrossRef]
- Nencioli, F.; Dong, C.; Dickey, T.; Washburn, L.; McWilliams, J.C. A vector geometry–based eddy detection algorithm and its application to a high-resolution numerical model product and high-frequency radar surface velocities in the Southern California Bight. J. Atmos. Ocean. Technol. 2010, 27, 564–579. [Google Scholar] [CrossRef]
- Yongchui, Z.; Ning, W.; Lin, Z.; Kefeng, L.; Haodi, W. The surface and three-dimensional characteristics of mesoscale eddies: A review. Adv. Earth Sci. 2020, 35, 568–580. [Google Scholar] [CrossRef]
- Yiwen, J.; Wenlong, J.; Ji, Y.; Sijing, S.; Yong, L.; Yingbin, D. Comparative Analysis of Ocean Eddy Detection Algorithms Based on Deep Learning in SAR Images. Adv. Mar. Sci. 2024, 42, 137–148. [Google Scholar] [CrossRef]
- Wang, J.; Fu, L.-L.; Torres, H.S.; Chen, S.; Qiu, B.; Menemenlis, D. On the spatial scales to be resolved by the surface water and ocean topography Ka-band radar interferometer. J. Atmos. Ocean. Technol. 2019, 36, 87–99. [Google Scholar] [CrossRef]
- Capet, X.; McWilliams, J.C.; Molemaker, M.J.; Shchepetkin, A.F. Mesoscale to submesoscale transition in the California Current System. Part II: Frontal processes. J. Phys. Oceanogr. 2008, 38, 44–64. [Google Scholar] [CrossRef]
- Chelton, D.B.; Wentz, F.J.; Gentemann, C.L.; de Szoeke, R.A.; Schlax, M.G. Satellite microwave SST observations of transequatorial tropical instability waves. Geophys. Res. Lett. 2000, 27, 1239–1242. [Google Scholar] [CrossRef]
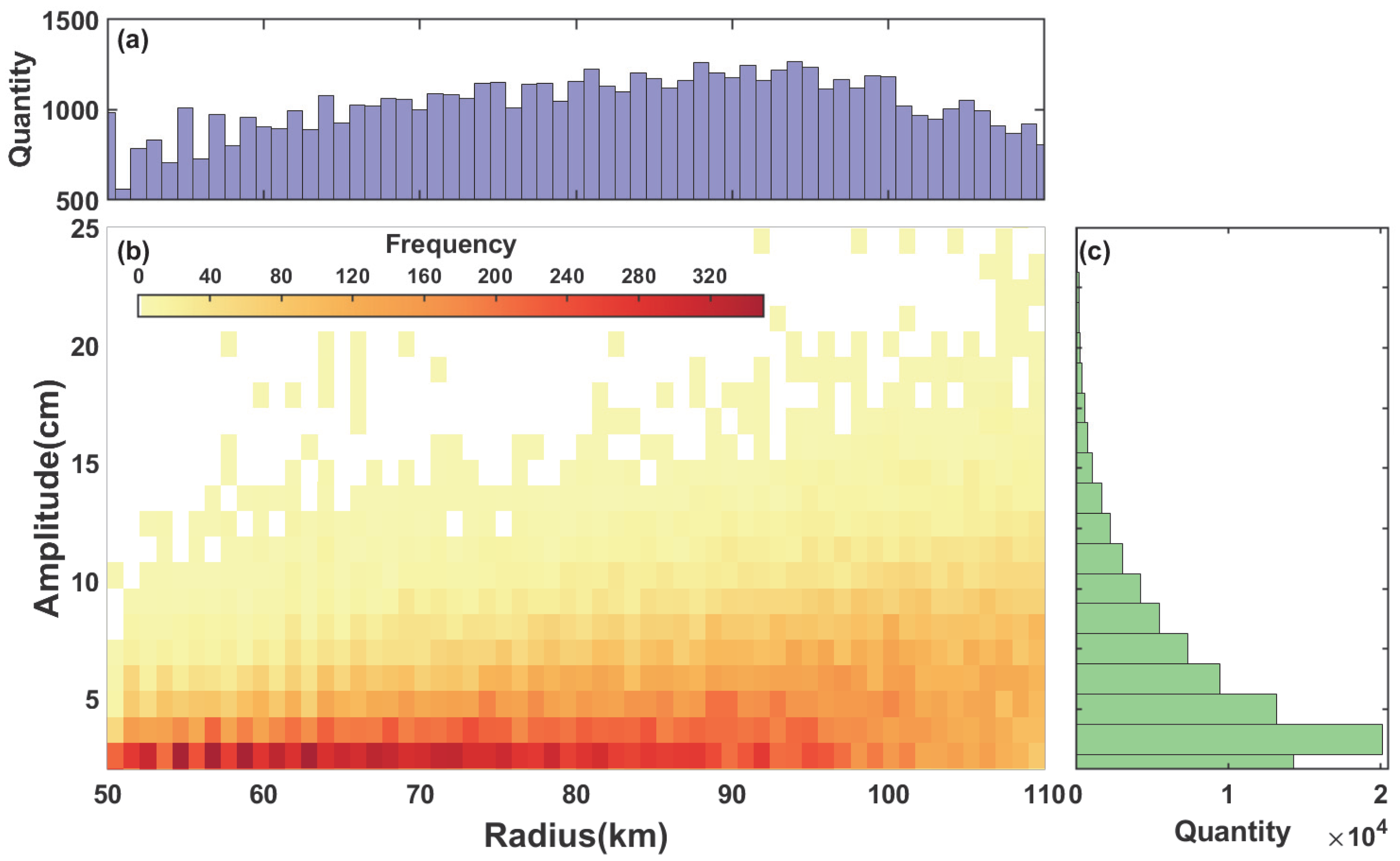
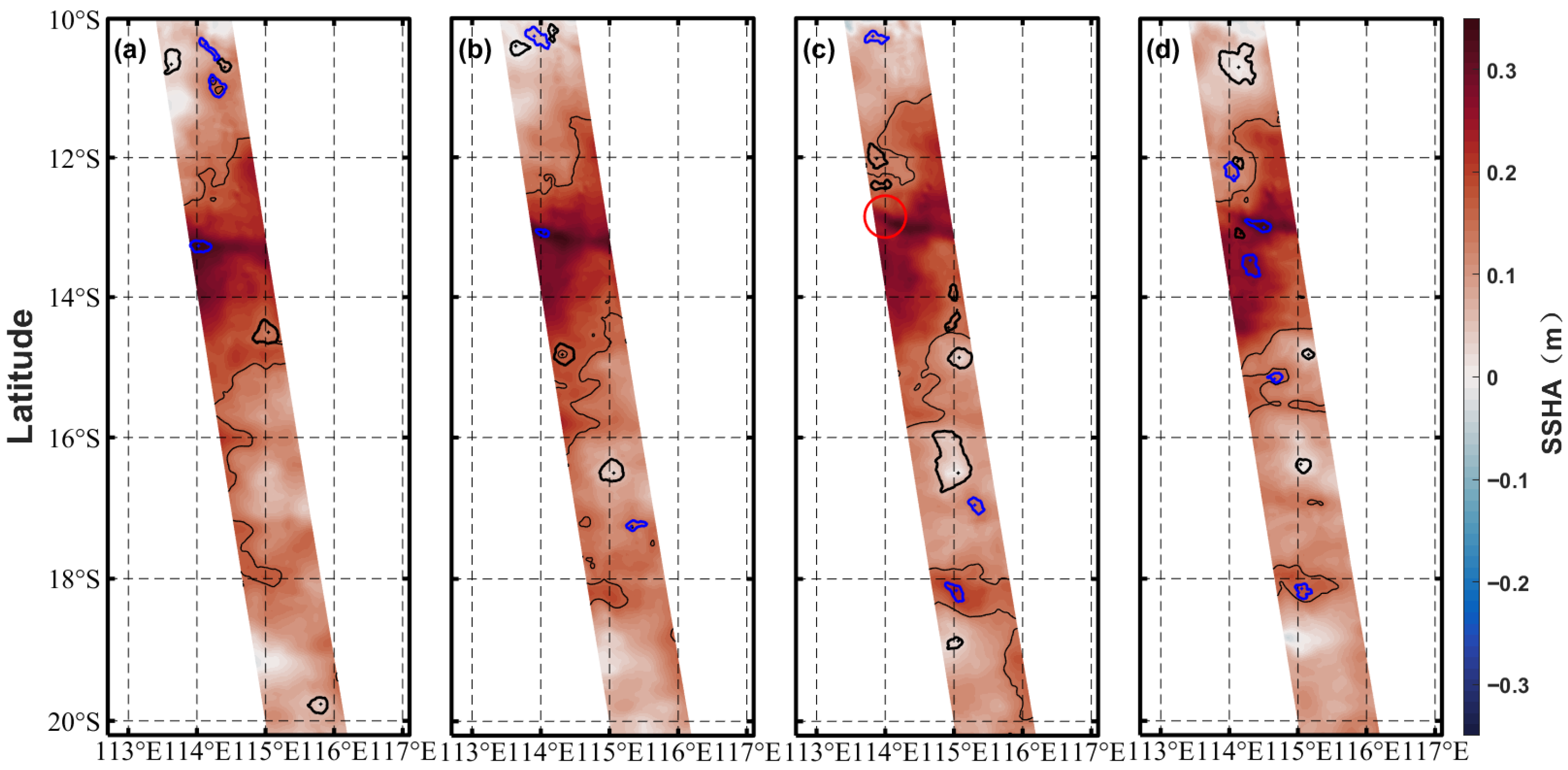
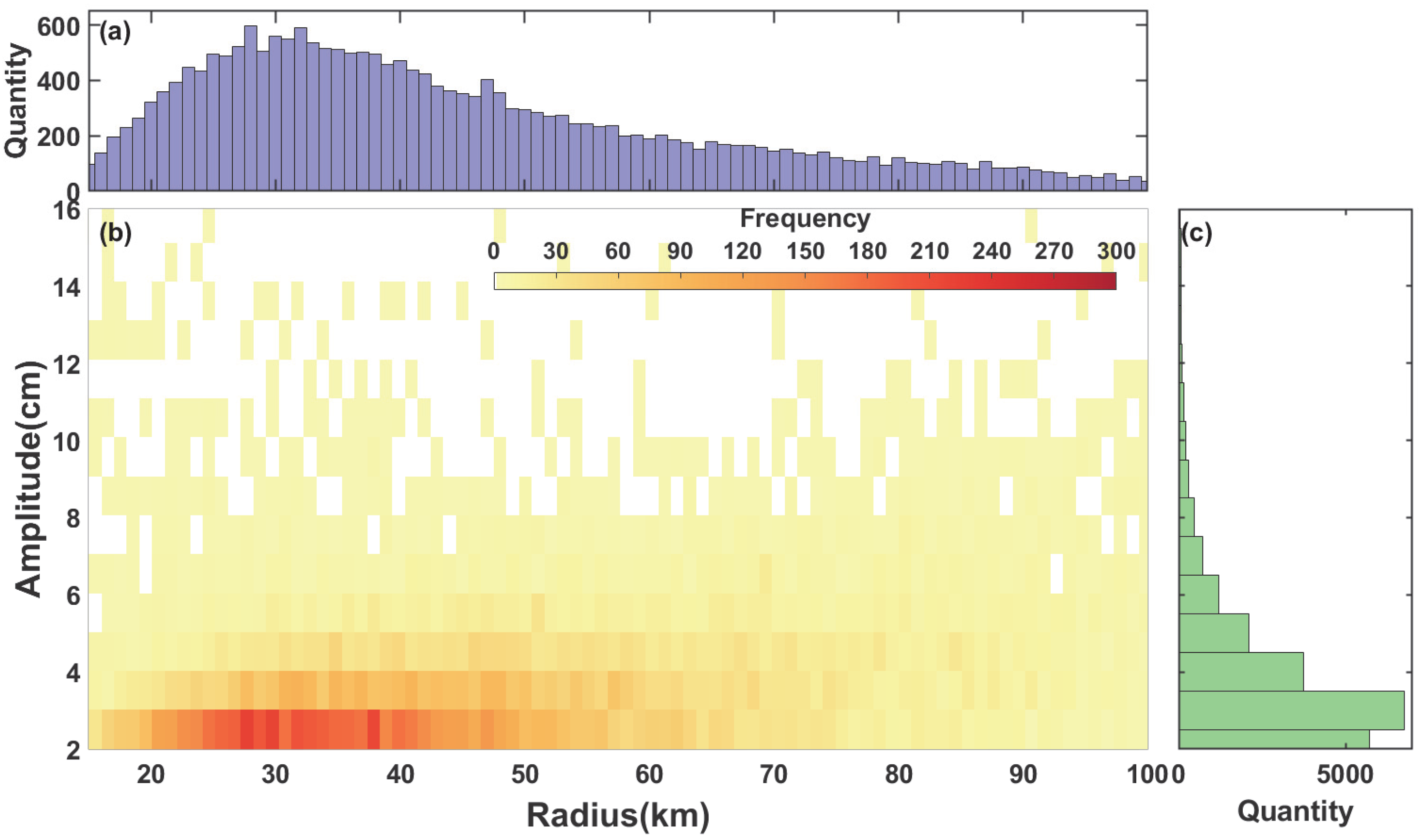
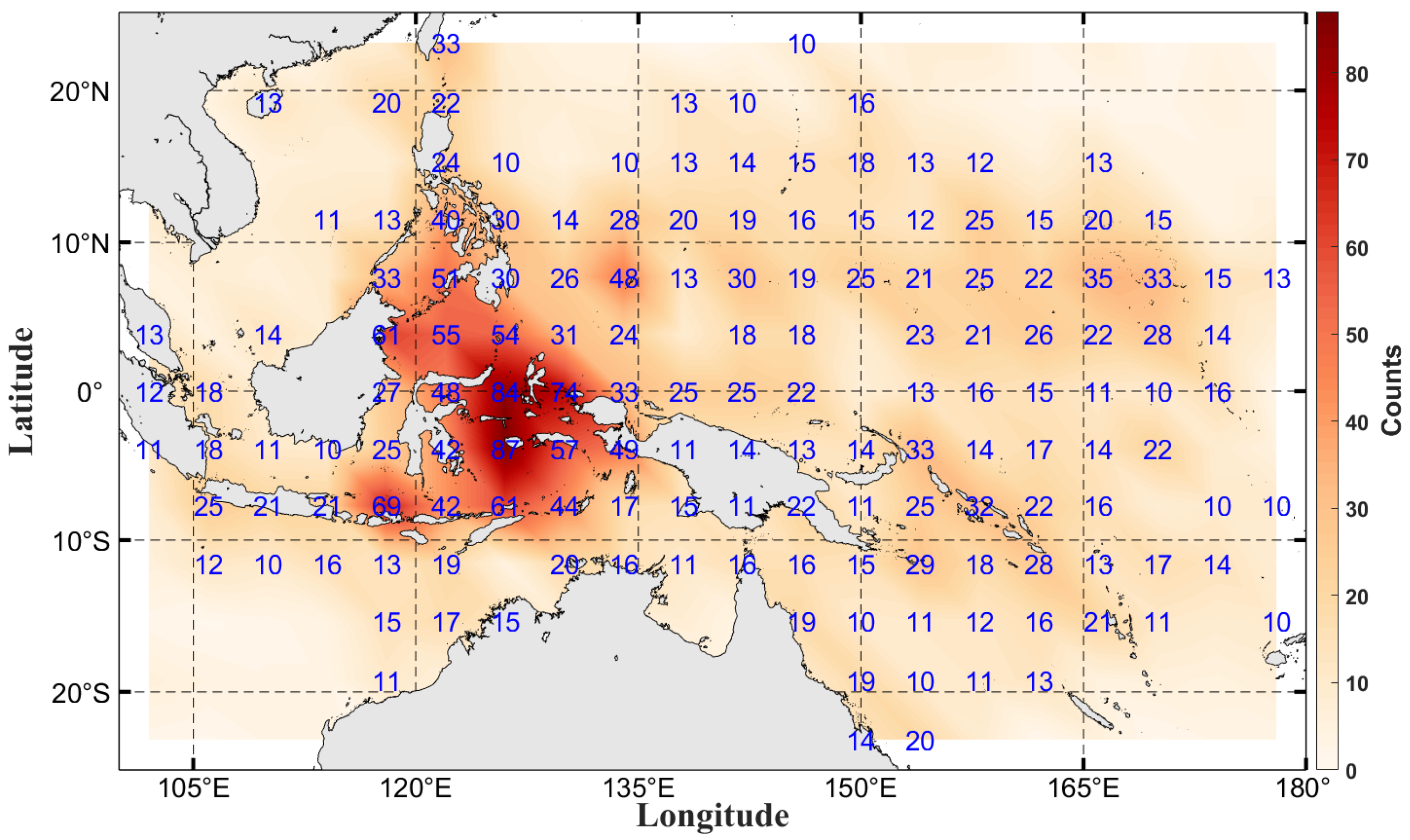
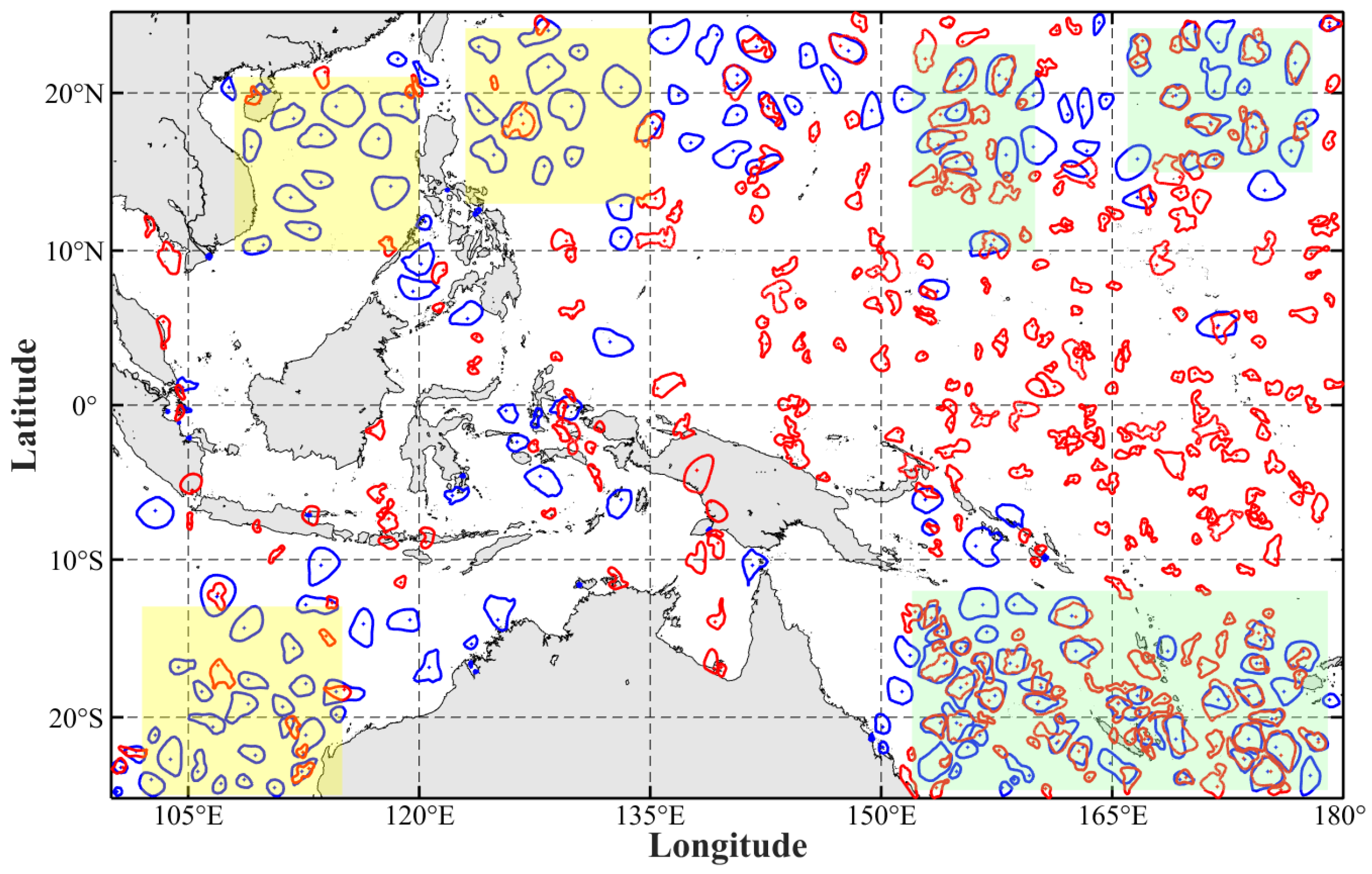
| Region | Min (km) | Max (km) | Mean (km) | R (km) |
|---|---|---|---|---|
| 5°S–5°N | 239 | 252 | 248 | 60 |
| 5°S–10°S, 5°N–10°N | 118 | 205 | 155 | 60 |
| 10°S–15°S, 10°N–15°N | 81 | 110 | 95 | 45 |
| 15°S–20°S, 15°N–20°N | 59 | 81 | 70 | 35 |
| 20°S–25°S, 20°N–25°N | 45 | 63 | 55 | 30 |
| Region | Satellite | Average Number of MEs (units) | Average Number of SMEs (units) | Average Radius of MEs (km) | Average Radius of SMEs (km) | Average Amplitude of MEs (cm) | Average Amplitude of SMEs (cm) |
|---|---|---|---|---|---|---|---|
| 10°S–10°N (60 km) | DUACS | 14 ± 3.69 | 7 ± 3.21 | 94.75 ± 17.21 | 25.20 ± 11.23 | 3.41 ± 0.19 | 3.60 ± 0.55 |
| SWOT | 39 ± 7.93 | 182 ± 22.74 | 76.18 ± 14.08 | 35.01 ± 18.21 | 8.77 ± 0.2 | 4.80 ± 0.75 | |
| DUACS/SWOT | 0.36 | 0.04 | 1.24 | 0.72 | 0.39 | 0.75 | |
| 10°N/S–15°N/S (45 km) | DUACS | 25 ± 4.92 | 3 ± 1.73 | 90.04 ± 19.63 | 24.66 ± 6.33 | 4.37 ± 0.22 | 3.29 ± 0.37 |
| SWOT | 36 ± 5.23 | 53 ± 11.44 | 63.56 ± 16.01 | 30.99 ± 15.02 | 5.18 ± 0.19 | 4.26 ± 0.73 | |
| DUACS/SWOT | 0.70 | 0.05 | 1.42 | 0.80 | 0.84 | 0.77 | |
| 15°N/S–20°N/S (35 km) | DUACS | 56 ± 7.16 | 2 ± 1.43 | 84.03 ± 20.84 | 22.99 ± 3.16 | 4.99 ± 0.23 | 4.04 ± 0.26 |
| SWOT | 54 ± 6.79 | 24 ± 7.32 | 61.92 ± 20.65 | 26.07 ± 10.75 | 5.16 ± 0.2 | 3.27 ± 0.65 | |
| DUACS/SWOT | 1.04 | 0.08 | 1.36 | 0.88 | 0.98 | 1.24 | |
| 20°N/S–25°N/S (30 km) | DUACS | 66 ± 5.97 | 1 ± 0 | 75.49 ± 23.89 | 19.61 ± 2.39 | 6.10 ± 0.23 | 4.30 ± 0.29 |
| SWOT | 48 ± 7.33 | 14 ± 3.48 | 60.05 ± 23.46 | 23.27 ± 8.73 | 5.77 ± 0.2 | 3.44 ± 0.62 | |
| DUACS/SWOT | 1.38 | 0.07 | 1.26 | 0.84 | 1.06 | 1.25 | |
| 0–25°N/S | DUACS | 162 | 13 | 82.36 | 24.17 | 5.22 | 3.67 |
| SWOT | 176 | 273 | 64.91 | 32.84 | 6.13 | 4.49 | |
| DUACS/SWOT | 0.92 | 0.08 | 1.27 | 0.74 | 0.85 | 0.82 |
| Radius | Satellite | Average Number of MEs (units) | Average Number of SMEs (units) | Average Radius of MEs (km) | Average Radius of SMEs (km) | Average Amplitude of MEs (cm) | Average Amplitude of SMEs (cm) |
|---|---|---|---|---|---|---|---|
| 30 km | DUACS | 165 ± 13.79 | 9 ± 3.93 | 81.60 ± 23.19 | 18.38 ± 3.68 | 5.18 ± 0.23 | 3.83 ± 0.33 |
| SWOT | 333 ± 34.94 | 116 ± 18.94 | 53.19 ± 20.03 | 23.05 ± 8.98 | 5.52 ± 0.2 | 4.02 ± 0.6 | |
| DUACS/SWOT | 0.50 | 0.08 | 1.53 | 0.80 | 0.94 | 0.95 | |
| 35 km | DUACS | 162 ± 13.27 | 12 ± 4.7 | 82.33 ± 22.55 | 21.18 ± 4.94 | 5.20 ± 0.23 | 3.83 ± 0.36 |
| SWOT | 278 ± 24.96 | 171 ± 21.77 | 57.40 ± 19.31 | 25.92 ± 11.31 | 5.73 ± 0.2 | 4.15 ± 0.67 | |
| DUACS/SWOT | 0.58 | 0.07 | 1.43 | 0.82 | 0.91 | 0.92 | |
| 45 km | DUACS | 155 ± 12.51 | 19 ± 5.9 | 84.30 ± 21.14 | 28.46 ± 8.58 | 5.29 ± 0.23 | 3.60 ± 0.44 |
| SWOT | 187 ± 21.07 | 262 ± 31.84 | 66.23 ± 17.61 | 30.53 ± 14.72 | 6.4 ± 0.2 | 4.23 ± 0.73 | |
| DUACS/SWOT | 0.83 | 0.07 | 1.27 | 0.93 | 0.83 | 0.85 | |
| 60 km | DUACS | 132 ± 10.9 | 42 ± 7.92 | 89.92 ± 17.67 | 41.71 ± 17.17 | 5.62 ± 0.23 | 3.49 ± 0.58 |
| SWOT | 102 ± 12.54 | 346 ± 37.54 | 78.69 ± 14.67 | 35.57 ± 18.38 | 7.28 ± 0.19 | 4.5 ± 0.75 | |
| DUACS/SWOT | 1.29 | 0.12 | 1.14 | 1.17 | 0.77 | 0.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, L.; Zhang, Y.; Wang, Y.; Hong, M.; Wei, Y.; Qiu, C.; Xia, X. Submesoscale Eddies Identified by SWOT and Their Comparison with Mesoscale Eddies in the Tropical Western Pacific. Remote Sens. 2025, 17, 3242. https://doi.org/10.3390/rs17183242
Cao L, Zhang Y, Wang Y, Hong M, Wei Y, Qiu C, Xia X. Submesoscale Eddies Identified by SWOT and Their Comparison with Mesoscale Eddies in the Tropical Western Pacific. Remote Sensing. 2025; 17(18):3242. https://doi.org/10.3390/rs17183242
Chicago/Turabian StyleCao, Lunyi, Yongchui Zhang, Yang Wang, Mei Hong, Yongliang Wei, Chunhua Qiu, and Xingyue Xia. 2025. "Submesoscale Eddies Identified by SWOT and Their Comparison with Mesoscale Eddies in the Tropical Western Pacific" Remote Sensing 17, no. 18: 3242. https://doi.org/10.3390/rs17183242
APA StyleCao, L., Zhang, Y., Wang, Y., Hong, M., Wei, Y., Qiu, C., & Xia, X. (2025). Submesoscale Eddies Identified by SWOT and Their Comparison with Mesoscale Eddies in the Tropical Western Pacific. Remote Sensing, 17(18), 3242. https://doi.org/10.3390/rs17183242





