Improved Multi-View Graph Clustering with Global Graph Refinement
Abstract
Highlights
- This study proposes a view-specific fusion network (VSFN) that extracts and integrates node attribute and structural information into view-specific representation through a global self-attention mechanism and self-supervised clustering strategy.
- A learnable attention-driven aggregation strategy and cross-view fusion module are adopted to merge view-specific representations for consensus clustering.
- The IMGCGGR method significantly outperforms existing state-of-the-art multi-view graph clustering techniques across various benchmark datasets.
- This approach effectively addresses the issue of insufficient structural extraction in multi-view data while capturing both local and global graph properties, making it suitable for multi-source graph-structured data, multi-sensor fusion and geographic information systems data.
Abstract
1. Introduction
- We propose a novel method called improved multi-view graph clustering with global self-attention (IMGCGGR). In the IMGCGGR, through the view-specific fusion network and cross-view fusion module, the node attribute and structural feature in graph-structured multi-view data can be thoroughly extracted and flexibly integrated. It greatly improves the clustering performance of graph-structured multi-view data.
- We introduce a global self-attention mechanism in the view-specific fusion network to enhance the global properties of structural information. Moreover, to enhance the reliability and capability of view-specific representation, a self-supervised strategy is designed to guide the view-specific clustering distribution assignment. By constructing these modules, the representation learning capability of IMGCGGR can be further improved.
- Extensive experiments on widely used benchmark graph-structured multi-view datasets demonstrate that our proposed IMGCGGR achieves significant improvements against existing state-of-the-art methods.
2. Related Work
2.1. Basic Principles of Multi-View Clustering
2.2. Traditional Multi-View Clustering
2.3. Deep Multi-View Graph Clustering
3. Methods
3.1. Notations and Problem Definition
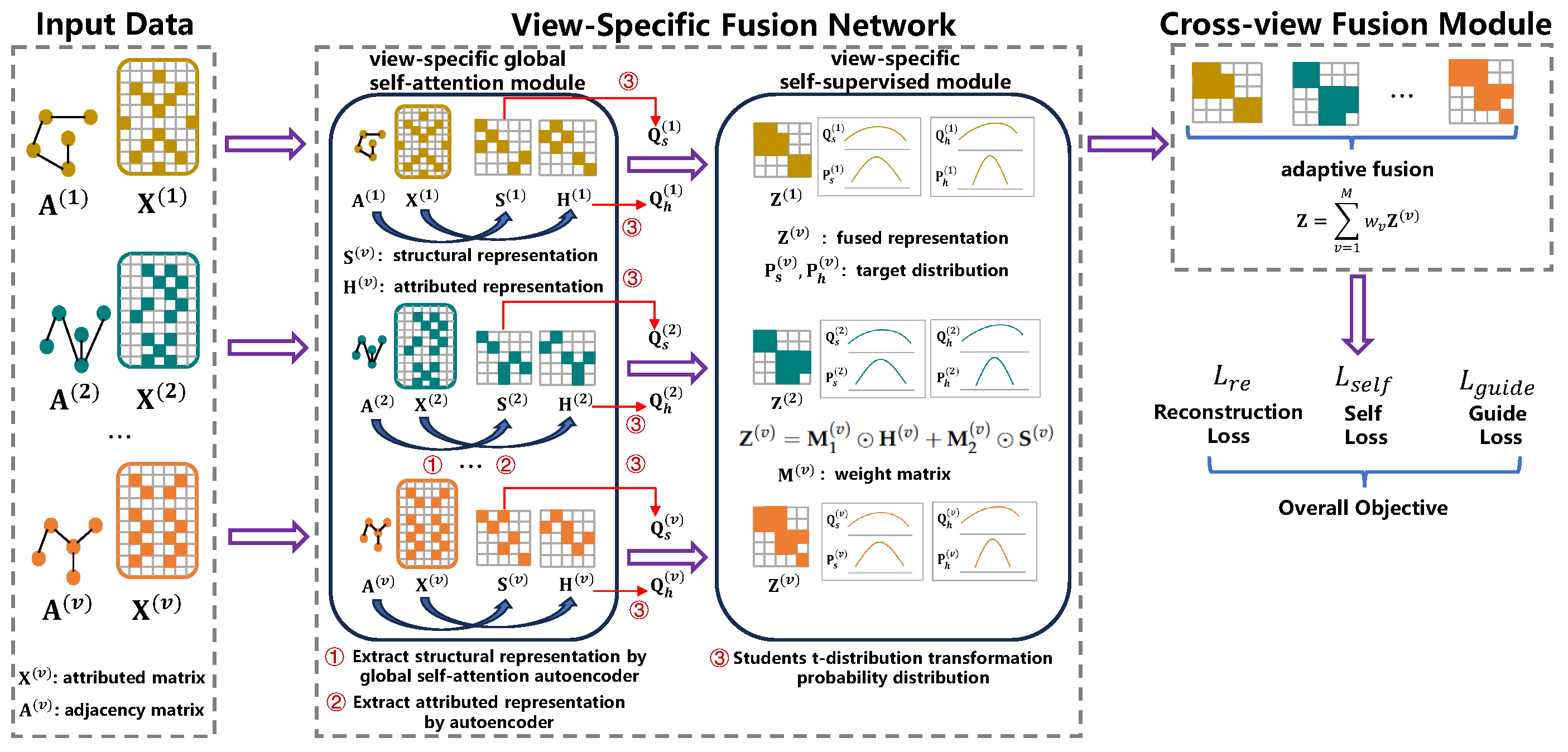
3.2. View-Specific Fusion Network
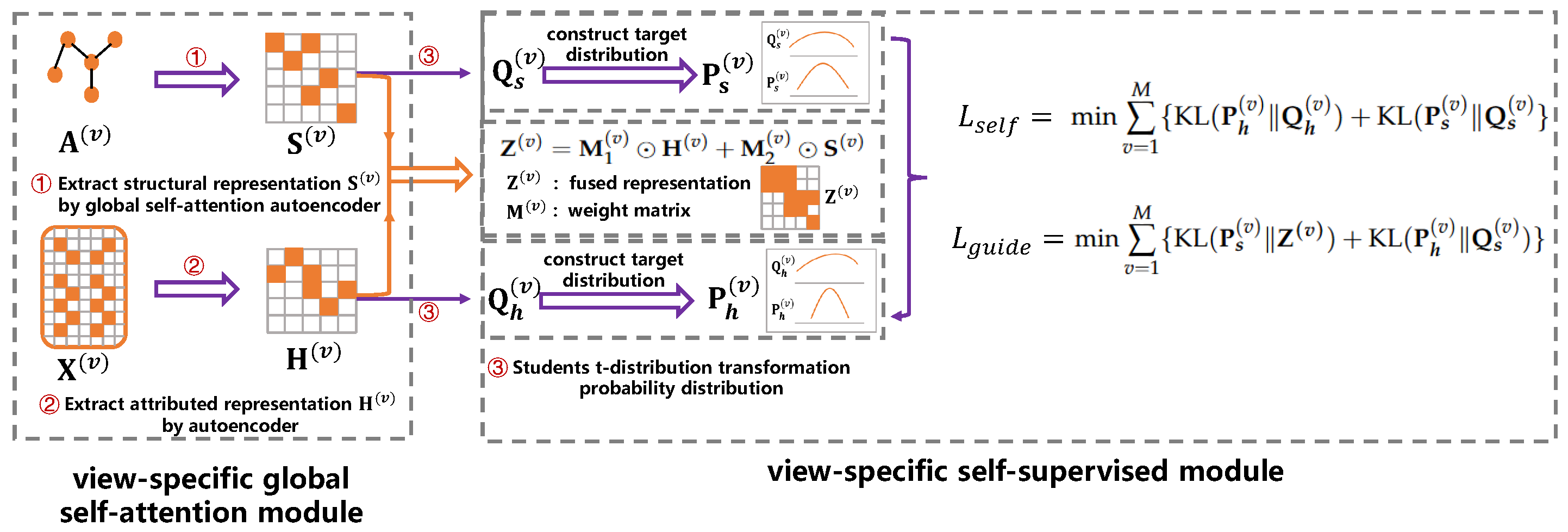
3.2.1. View-Specific Global Self-Attention Module
3.2.2. View-Specific Self-Supervised Module
3.3. Cross-View Fusion Module
| Algorithm 1 Multi-View Graph Clustering with Global Self-Attention |
|
3.4. Complexity Analysis
4. Results
4.1. Experimental Setup
- GMC [28]: It is a representative graph-based MvC algorithm, which derives a unified graph matrix by automatically weighting the graph matrices of each view.
- CGL [29]: It constructs a similarity graph based on consensus graph learning in the spectral embedding space and unifies spectral embedding with low-rank tensor learning into an overall optimization framework.
- CoMSC [30]: It is a representative subspace-based MvC approach, which leverages eigendecomposition to obtain low-redundancy robust data.
- EMVGC [31]: It devises a novel anchor-based multi-view graph clustering framework to achieve global and local structure preservation.
- UPGMC and UPCoMSC [32]: It adopts a unified framework to handle fully and partially unpaired multi-view data, effectively utilizing the structural information from each view to refine cross-view correspondences.
- TSSR [33]: It leverages a low-rank tensor constraint to capture consensus and complementary information among views while preserving the intrinsic relationships of the data.
- EMKIC [34]: It uses the Butterworth filters function to transform the adjacency matrix into a distance matrix.
- MAGCN [20]: It is a representative deep multi-view graph clustering method designed to address the clustering of multi-view graph data, which utilizes two-pathway encoders to map graph embedding features and learn view-consistency information.
- SGCMC [39]: It exploits a self-supervised multi-view graph attention autoencoder to optimize node content reconstruction loss and graph structure reconstruction loss with weighting sharing.
- GMGEC [40]: It devises a graph autoencoder and introduces a multi-view mutual information maximization module to guide the learned common representation.
4.2. Performance Comparison
4.3. Ablation Studies
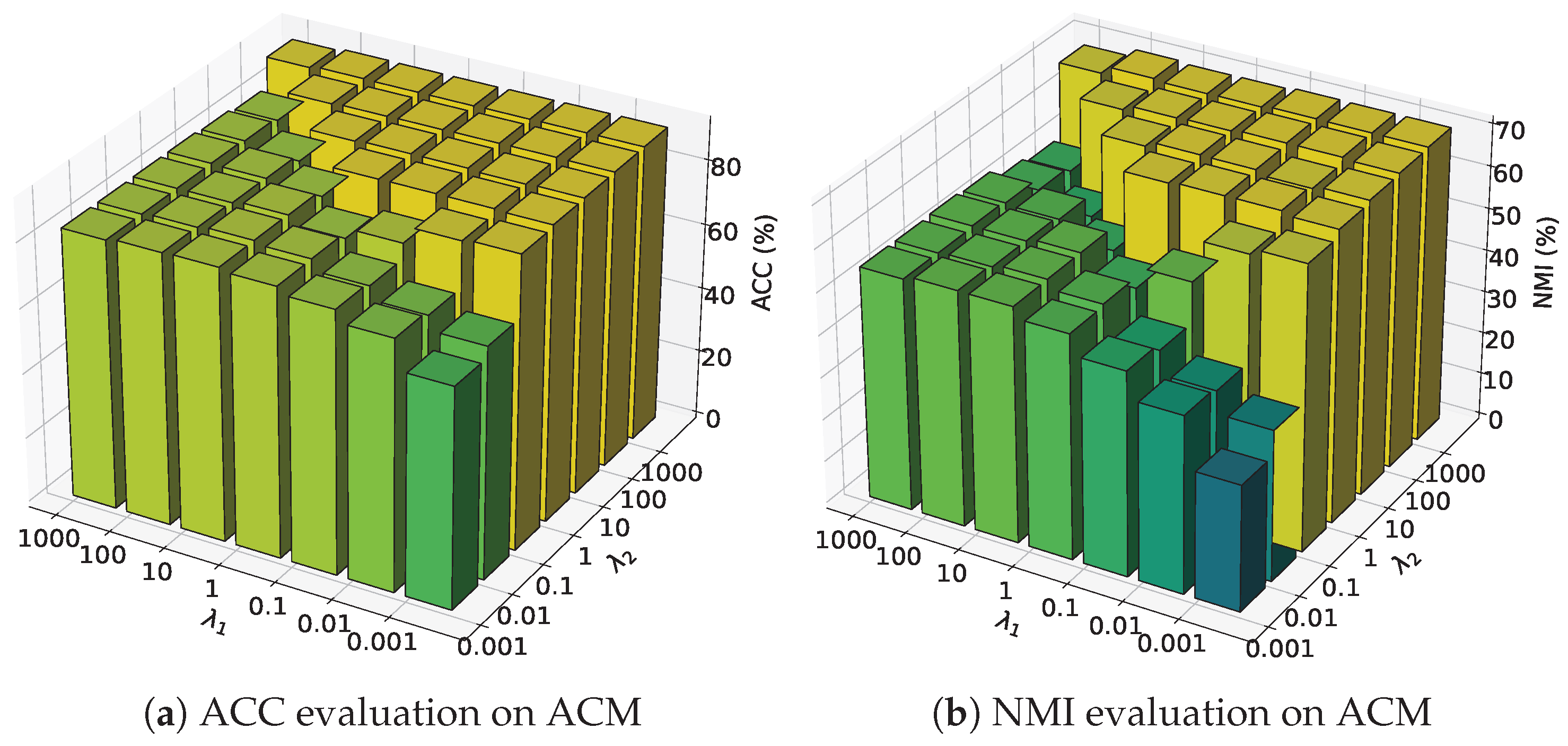
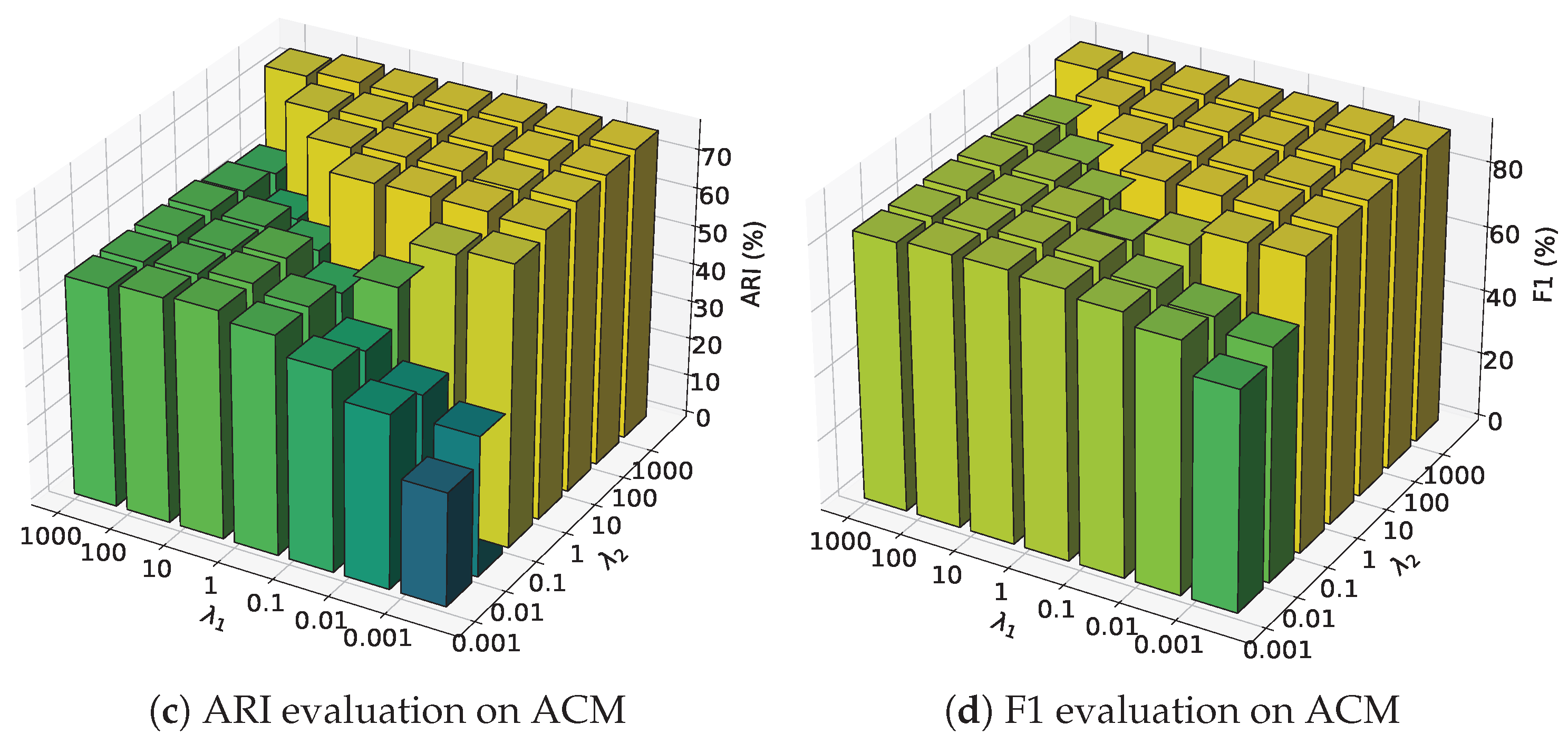
4.4. Hyper-Parameter Sensitivity Analysis
4.5. Running Time
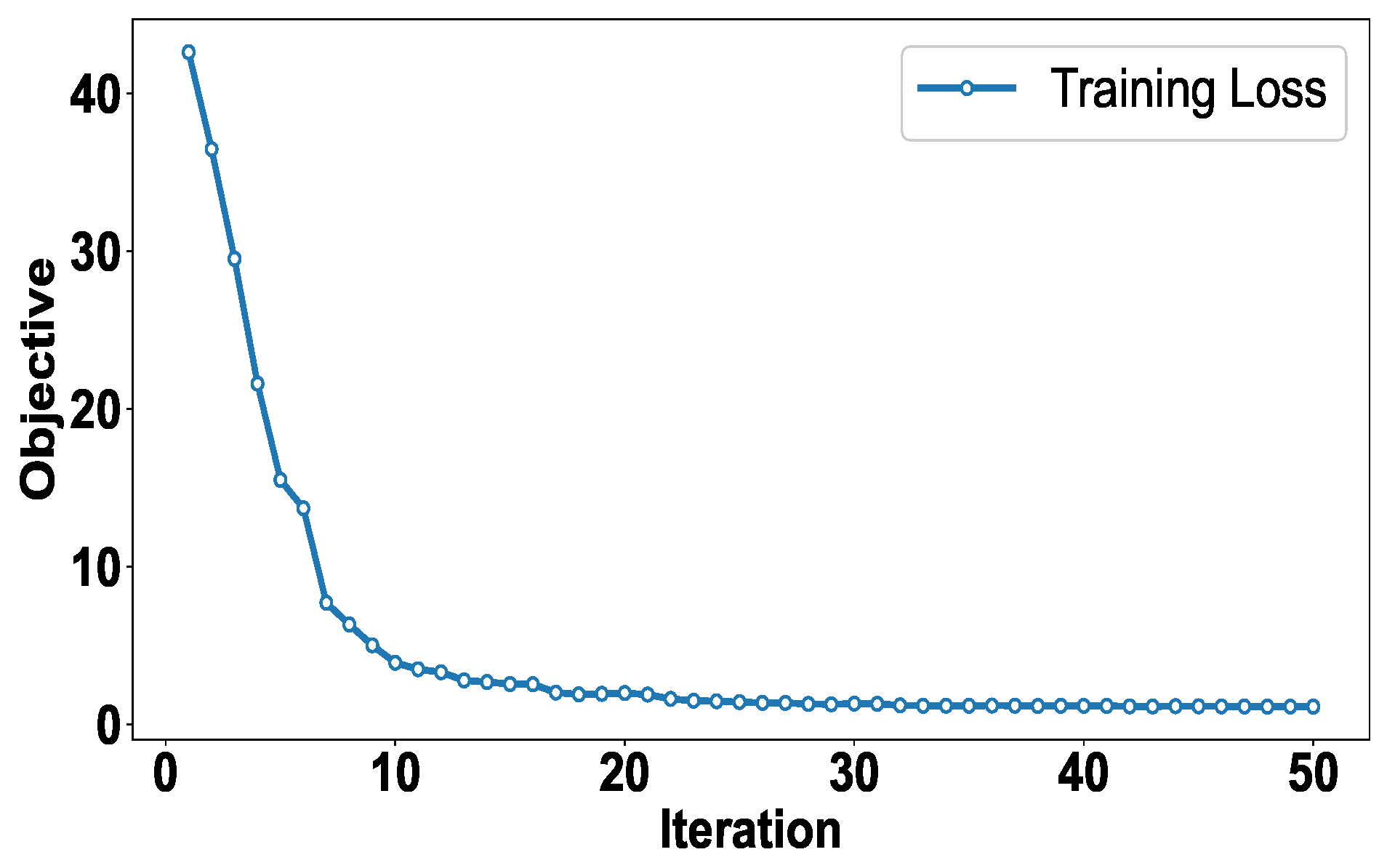
4.6. Convergence Analysis
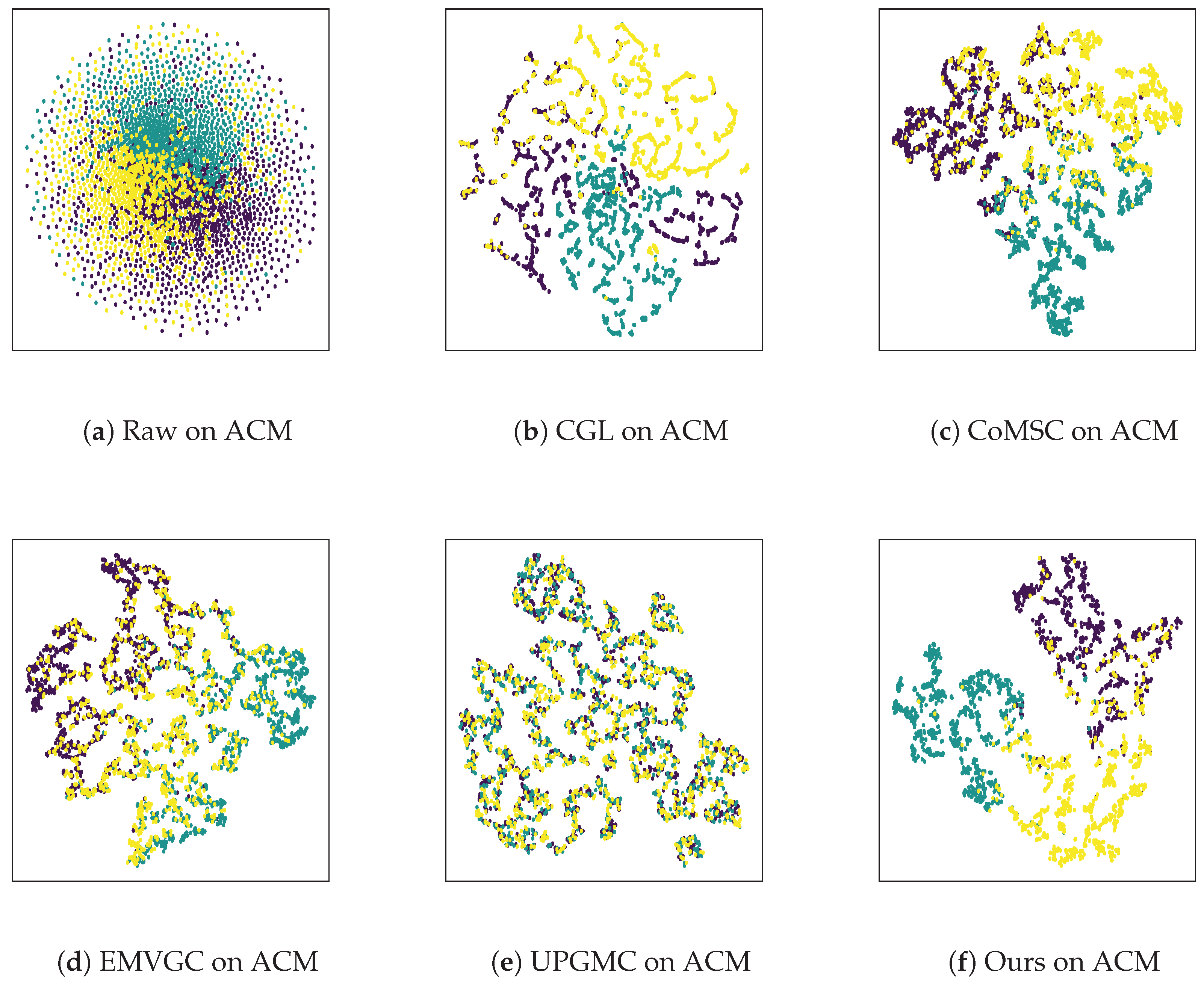
4.7. Visualization Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, W.; Shi, Y.; Huang, X. Multi-View Scene Classification Based on Feature Integration and Evidence Decision Fusion. Remote Sens. 2024, 16, 738. [Google Scholar] [CrossRef]
- Yang, S.; Peng, T.; Liu, H.; Yang, C.; Feng, Z.; Wang, M. Radar Emitter Identification with Multi-View Adaptive Fusion Network (MAFN). Remote Sens. 2023, 15, 1762. [Google Scholar] [CrossRef]
- Yang, X.; Liu, W.; Liu, W. Tensor Canonical Correlation Analysis Networks for Multi-View Remote Sensing Scene Recognition. IEEE Trans. Knowl. Data Eng. 2022, 34, 2948–2961. [Google Scholar] [CrossRef]
- Guan, R.; Li, Z.; Tu, W.; Wang, J.; Liu, Y.; Li, X.; Tang, C.; Feng, R. Contrastive Multiview Subspace Clustering of Hyperspectral Images Based on Graph Convolutional Networks. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5510514. [Google Scholar] [CrossRef]
- Zhao, M.; Meng, Q.; Wang, L.; Zhang, L.; Hu, X.; Shi, W. Towards robust classification of multi-view remote sensing images with partial data availability. Remote Sens. Environ. 2024, 306, 114112. [Google Scholar] [CrossRef]
- Liu, Q.; Huan, W.; Deng, M. A Method with Adaptive Graphs to Constrain Multi-View Subspace Clustering of Geospatial Big Data from Multiple Sources. Remote Sens. 2022, 14, 4394. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, H. Multi-view clustering: A survey. Big Data Min. Anal. 2018, 1, 83–107. [Google Scholar] [CrossRef]
- Su, P.; Liu, Y.; Li, S.; Huang, S.; Lv, J. Robust Contrastive Multi-view Kernel Clustering. In Proceedings of the Thirty-Third International Joint Conference on Artificial Intelligence, Jeju, Republic of Korea, 3–9 August 2024; pp. 4938–4945. [Google Scholar] [CrossRef]
- Liu, J.; Cheng, S.; Du, A. Multi-View Feature Fusion and Rich Information Refinement Network for Semantic Segmentation of Remote Sensing Images. Remote Sens. 2024, 16, 3184. [Google Scholar] [CrossRef]
- Fang, U.; Li, M.; Li, J.; Gao, L.; Jia, T.; Zhang, Y. A Comprehensive Survey on Multi-View Clustering. IEEE Trans. Knowl. Data Eng. 2023, 35, 12350–12368. [Google Scholar] [CrossRef]
- Liu, J.; Liu, X.; Yang, Y.; Liao, Q.; Xia, Y. Contrastive Multi-View Kernel Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 9552–9566. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, Y.; Zhang, D.; Chen, H.; Peng, H.; Pan, S. Towards Unsupervised Deep Graph Structure Learning. In Proceedings of the ACM Web Conference, 2022, WWW ’22, Lyon, France, 25–29 April 2022; pp. 1392–1403. [Google Scholar] [CrossRef]
- Wu, L.; Cui, P.; Pei, J.; Zhao, L.; Guo, X. Graph Neural Networks: Foundation, Frontiers and Applications. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, 2022, KDD ’22, Washington, DC, USA, 14–18 August 2022; pp. 4840–4841. [Google Scholar] [CrossRef]
- Wu, S.; Sun, F.; Zhang, W.; Xie, X.; Cui, B. Graph Neural Networks in Recommender Systems: A Survey. ACM Comput. Surv. 2022, 55, 97. [Google Scholar] [CrossRef]
- Cui, H.; Lu, J.; Ge, Y.; Yang, C. How Can Graph Neural Networks Help Document Retrieval: A Case Study on CORD19 with Concept Map Generation. In Advances in Information Retrieval, Proceedings of the 44th European Conference on IR Research, ECIR 2022, Stavanger, Norway, 10–14 April 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 75–83. [Google Scholar] [CrossRef]
- Zhang, X.M.; Liang, L.; Liu, L.; Tang, M.J. Graph neural networks and their current applications in bioinformatics. Front. Genet. 2021, 12, 690049. [Google Scholar] [CrossRef]
- Xia, W.; Wang, S.; Yang, M.; Gao, Q.; Han, J.; Gao, X. Multi-view graph embedding clustering network: Joint self-supervision and block diagonal representation. Neural Netw. 2022, 145, 1–9. [Google Scholar] [CrossRef]
- Ling, Y.; Chen, J.; Ren, Y.; Pu, X.; Xu, J.; Zhu, X.; He, L. Dual label-guided graph refinement for multi-view graph clustering. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 8791–8798. [Google Scholar] [CrossRef]
- Fan, S.; Wang, X.; Shi, C.; Lu, E.; Lin, K.; Wang, B. One2Multi Graph Autoencoder for Multi-view Graph Clustering. In Proceedings of the Web Conference, 2020, WWW ’20, Taipei, Taiwan, 20–24 April 2020; pp. 3070–3076. [Google Scholar] [CrossRef]
- Cheng, J.; Wang, Q.; Tao, Z.; Xie, D.; Gao, Q. Multi-view attribute graph convolution networks for clustering. In Proceedings of the Twenty-Ninth International Conference on International Joint Conferences on Artificial Intelligence, Yokohama, Japan, 7–15 January 2021; pp. 2973–2979. [Google Scholar] [CrossRef]
- Liu, S.; Liao, Q.; Wang, S.; Liu, X.; Zhu, E. Robust and Consistent Anchor Graph Learning for Multi-View Clustering. IEEE Trans. Knowl. Data Eng. 2024, 36, 4207–4219. [Google Scholar] [CrossRef]
- Ma, H.; Wang, S.; Yu, S.; Liu, S.; Huang, J.J.; Wu, H.; Liu, X.; Zhu, E. Automatic and Aligned Anchor Learning Strategy for Multi-View Clustering. In Proceedings of the 32nd ACM International Conference on Multimedia, 2024, MM ’24, Melbourne, Australia, 28 October–1 November 2024; pp. 5045–5054. [Google Scholar] [CrossRef]
- Wang, F.; Jin, J.; Dong, Z.; Yang, X.; Feng, Y.; Liu, X.; Zhu, X.; Wang, S.; Liu, T.; Zhu, E. View Gap Matters: Cross-view Topology and Information Decoupling for Multi-view Clustering. In Proceedings of the 32nd ACM International Conference on Multimedia, 2024, MM ’24, Melbourne, Australia, 28 October–1 November 2024; pp. 8431–8440. [Google Scholar] [CrossRef]
- Yang, X.; Jiaqi, J.; Wang, S.; Liang, K.; Liu, Y.; Wen, Y.; Liu, S.; Zhou, S.; Liu, X.; Zhu, E. DealMVC: Dual Contrastive Calibration for Multi-view Clustering. In Proceedings of the 31st ACM International Conference on Multimedia, 2023, MM ’23, Ottawa, ON, Canada, 29 October–3 November 2023; pp. 337–346. [Google Scholar] [CrossRef]
- Haris, M.; Yusoff, Y.; Mohd Zain, A.; Khattak, A.S.; Hussain, S.F. Breaking down multi-view clustering: A comprehensive review of multi-view approaches for complex data structures. Eng. Appl. Artif. Intell. 2024, 132, 107857. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, Q.; Fu, H.; Zhu, P.; Cao, X. Latent Multi-view Subspace Clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4333–4341. [Google Scholar] [CrossRef]
- Luo, S.; Zhang, C.; Zhang, W.; Cao, X. Consistent and specific multi-view subspace clustering. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar] [CrossRef]
- Wang, H.; Yang, Y.; Liu, B. GMC: Graph-Based Multi-View Clustering. IEEE Trans. Knowl. Data Eng. 2020, 32, 1116–1129. [Google Scholar] [CrossRef]
- Li, Z.; Tang, C.; Liu, X.; Zheng, X.; Zhang, W.; Zhu, E. Consensus Graph Learning for Multi-View Clustering. IEEE Trans. Multimed. 2022, 24, 2461–2472. [Google Scholar] [CrossRef]
- Liu, J.; Liu, X.; Yang, Y.; Guo, X.; Kloft, M.; He, L. Multiview Subspace Clustering via Co-Training Robust Data Representation. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 5177–5189. [Google Scholar] [CrossRef]
- Wen, Y.; Liu, S.; Wan, X.; Wang, S.; Liang, K.; Liu, X.; Yang, X.; Zhang, P. Efficient Multi-View Graph Clustering with Local and Global Structure Preservation. In Proceedings of the 31st ACM International Conference on Multimedia, 2023, MM ’23, Ottawa, ON, Canada, 29 October–3 November 2023; pp. 3021–3030. [Google Scholar] [CrossRef]
- Wen, Y.; Wang, S.; Liao, Q.; Liang, W.; Liang, K.; Wan, X.; Liu, X. Unpaired Multi-View Graph Clustering with Cross-View Structure Matching. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 16049–16063. [Google Scholar] [CrossRef]
- Cai, B.; Lu, G.F.; Li, H.; Song, W. Tensorized Scaled Simplex Representation for Multi-View Clustering. IEEE Trans. Multimed. 2024, 26, 6621–6631. [Google Scholar] [CrossRef]
- Lu, H.; Xu, H.; Wang, Q.; Gao, Q.; Yang, M.; Gao, X. Efficient Multi-View K-Means for Image Clustering. IEEE Trans. Image Process. 2024, 33, 273–284. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, Z.; Liu, X.; Ding, Y.; Li, F.; Tan, J. Learning Unified Anchor Graph for Joint Clustering of Hyperspectral and LiDAR Data. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 6341–6354. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, T.; Xin, H.; Wang, R.; Nie, F. Multi-view clustering via high-order bipartite graph fusion. Inf. Fusion 2025, 113, 102630. [Google Scholar] [CrossRef]
- Qin, Y.; Qin, C.; Zhang, X.; Feng, G. Dual Consensus Anchor Learning for Fast Multi-View Clustering. IEEE Trans. Image Process. 2024, 33, 5298–5311. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.; Che, H.; Leung, M.F. Tensor-Based Adaptive Consensus Graph Learning for Multi-View Clustering. IEEE Trans. Consum. Electron. 2024, 70, 4767–4784. [Google Scholar] [CrossRef]
- Xia, W.; Wang, Q.; Gao, Q.; Zhang, X.; Gao, X. Self-Supervised Graph Convolutional Network for Multi-View Clustering. IEEE Trans. Multimed. 2022, 24, 3182–3192. [Google Scholar] [CrossRef]
- Wang, Y.; Chang, D.; Fu, Z.; Zhao, Y. Consistent Multiple Graph Embedding for Multi-View Clustering. IEEE Trans. Multimed. 2023, 25, 1008–1018. [Google Scholar] [CrossRef]
- Xiao, S.; Du, S.; Chen, Z.; Zhang, Y.; Wang, S. Dual Fusion-Propagation Graph Neural Network for Multi-View Clustering. IEEE Trans. Multimed. 2023, 25, 9203–9215. [Google Scholar] [CrossRef]
- Guo, X.; Gao, L.; Liu, X.; Yin, J. Improved deep embedded clustering with local structure preservation. In Proceedings of the 26th International Joint Conference on Artificial Intelligence, 2017, IJCAI’17, Melbourne, Australia, 19–25 August 2017; pp. 1753–1759. [Google Scholar]
- Xie, J.; Girshick, R.; Farhadi, A. Unsupervised Deep Embedding for Clustering Analysis. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; Volume 48, pp. 478–487. [Google Scholar]
- Liu, Y.; Zhou, S.; Wang, S.; Guo, X.; Yang, X.; Tu, W.; Liu, X. A survey of deep graph clustering: Taxonomy, challenge, and application. arXiv 2022, arXiv:2211.12875. [Google Scholar]
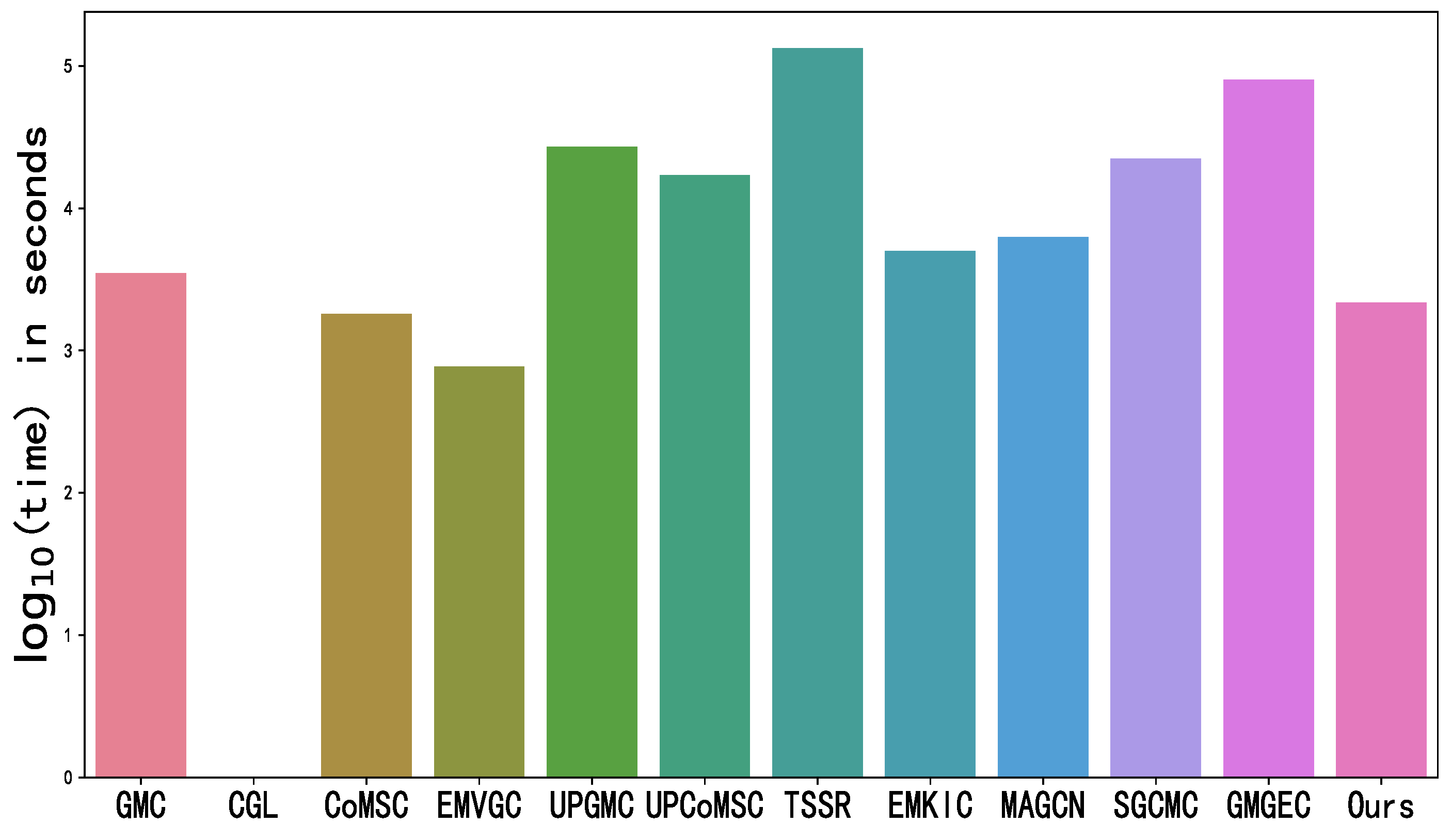
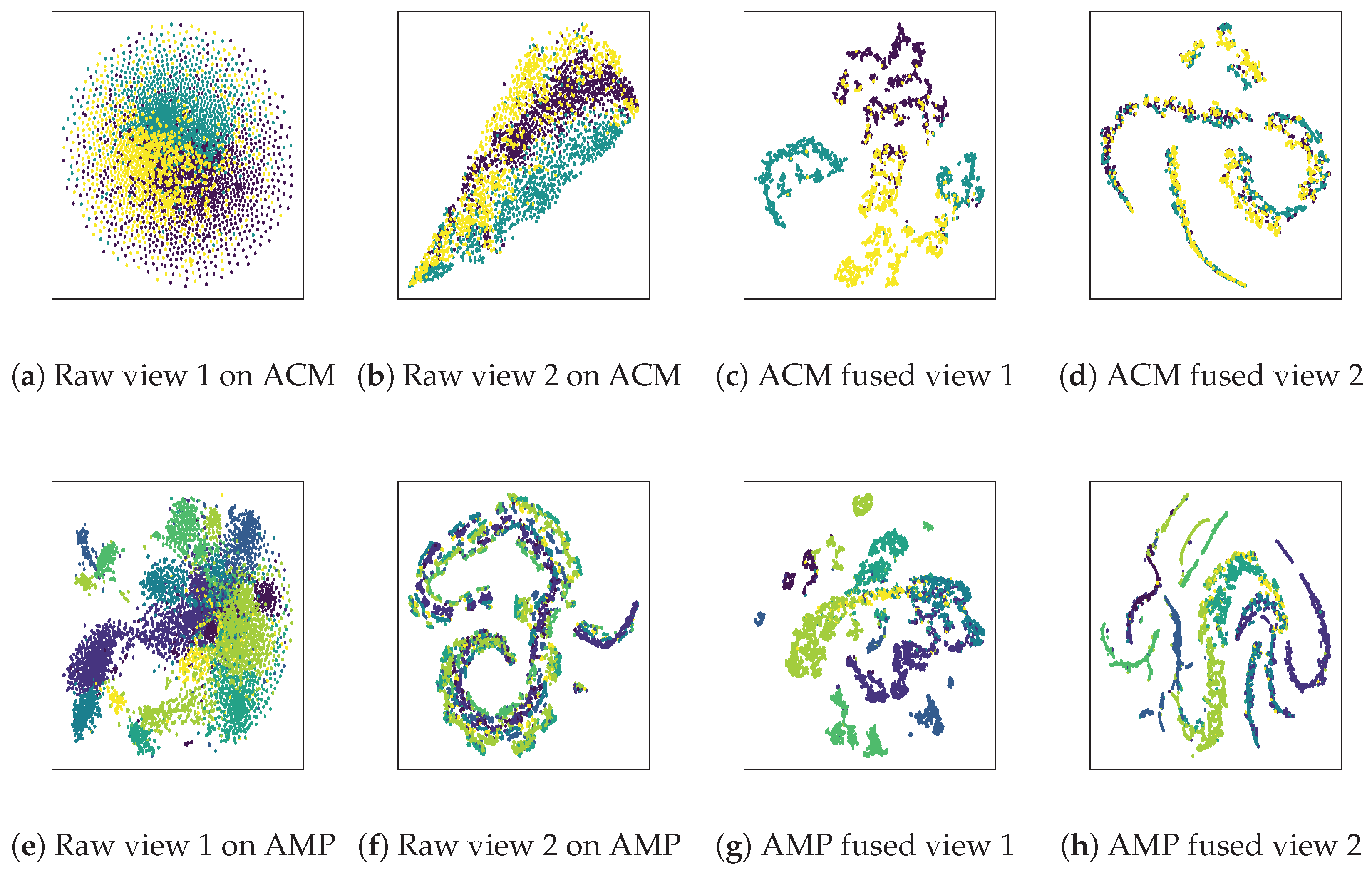
| Notation | Description |
|---|---|
| attribute matrix | |
| undirected original adjacency matrix | |
| renormalized adjacency matrix | |
| reconstructed attribute matrix | |
| reconstructed adjacency matrix | |
| view-specific attributed feature | |
| view-specific structural feature | |
| fused view-specific representation | |
| soft assignment distribution of | |
| soft assignment distribution of | |
| final consensus representation |
| Datasets | Nodes | Dimensions | Classes | Edges | |
|---|---|---|---|---|---|
| ACM | 3025 | 1870 | 3025 | 3 | 13,128 |
| AMP | 7487 | 745 | 7487 | 8 | 119,043 |
| Citeseer | 3327 | 3703 | 3327 | 6 | 4614 |
| Cora | 2708 | 1433 | 2708 | 7 | 5278 |
| DBLP | 4057 | 334 | 4057 | 4 | 3528 |
| Pubmed | 19,717 | 500 | 19,717 | 3 | 44,326 |
| Datasets | Metric | GMC TKDE20 | CGL TMM22 | CoMSC TNNLS22 | EMVGC MM23 | UPGMC TNNLS24 | UPCoMSC TNNLS24 | TSSR TMM24 | EMKIC TIP24 | IMGCGGR Ours |
|---|---|---|---|---|---|---|---|---|---|---|
| ACM | ACC | 35.17 ± 1.12 | 83.42 ± 2.91 | 78.81 ± 2.44 | 46.35 ± 8.94 | 72.03 ± 0.31 | 50.82 ± 20.93 | 40.05 ± 6.63 | 51.78 ± 15.02 | 91.37 ± 0.05 |
| NMI | 0.33 ± 0.02 | 52.32 ± 6.24 | 44.32 ± 3.42 | 7.78 ± 8.79 | 36.62 ± 0.11 | 16.01 ± 22.11 | 4.44 ± 6.97 | 21.97 ± 21.03 | 70.12 ± 0.04 | |
| ARI | 0.04 ± 0.01 | 57.65 ± 6.49 | 48.40 ± 4.37 | 7.84 ± 8.99 | 38.17 ± 0.08 | 17.72 ± 24.79 | 3.97 ± 5.96 | 19.33 ± 19.40 | 76.14 ± 0.09 | |
| F1 | 17.53 ± 0.68 | 83.42 ± 2.93 | 78.79 ± 2.51 | 45.51 ± 9.05 | 71.96 ± 0.23 | 50.70 ± 21.02 | 32.79 ± 13.70 | 48.69 ± 17.75 | 91.38 ± 0.05 | |
| AMP | ACC | 27.22 ± 2.10 | 57.60 ± 7.30 | 27.31 ± 11.86 | 61.09 ± 1.52 | 50.62 ± 16.84 | 16.66 ± 4.12 | 24.74 ± 4.56 | 77.04 ± 0.64 | |
| NMI | 4.06 ± 0.03 | eigs | 46.20 ± 7.19 | 11.06 ± 14.62 | 49.42 ± 0.52 | 37.01 ± 18.29 | 0.27 ± 0.28 | 5.01 ± 6.80 | 66.05 ± 1.24 | |
| ARI | −0.40 ± 0.01 | error | 33.59 ± 8.69 | 7.65 ± 10.60 | 39.12 ± 1.02 | 28.92 ± 14.84 | -0.06 ± 0.13 | 2.08 ± 2.75 | 57.12 ± 0.35 | |
| F1 | 7.81 ± 0.34 | 55.51 ± 7.08 | 23.86 ± 12.88 | 60.49 ± 1.63 | 47.95 ± 16.93 | 12.06 ± 2.07 | 15.61 ± 8.87 | 69.05 ± 3.55 | ||
| Citeseer | ACC | 29.71 ± 5.02 | 42.39 ± 7.25 | 38.67 ± 10.84 | 47.06 ± 0.47 | 43.67 ± 3.35 | 21.20 ± 0.62 | 26.61 ± 7.52 | 66.71 ± 1.81 | |
| NMI | evaluation | 7.52 ± 4.33 | 20.39 ± 6.40 | 15.83 ± 8.87 | 21.68 ± 0.14 | 20.10 ± 3.74 | 0.99 ± 0.54 | 5.39 ± 6.41 | 39.45 ± 1.34 | |
| ARI | error | 5.69 ± 3.37 | 17.27 ± 5.91 | 13.36 ± 8.99 | 20.53 ± 0.09 | 17.48 ± 3.51 | 0.11 ± 0.10 | 4.29 ± 5.31 | 40.40 ± 2.07 | |
| F1 | 24.44 ± 5.22 | 38.47 ± 10.34 | 34.29 ± 15.32 | 44.33 ± 0.56 | 41.07 ± 2.78 | 10.86 ± 3.26 | 20.00 ± 12.22 | 59.22 ± 0.19 | ||
| Cora | ACC | 36.52 ± 2.03 | 41.73 ± 3.33 | 42.81 ± 7.37 | 29.49 ± 4.28 | 41.11 ± 0.23 | 38.27 ± 6.86 | 24.55 ± 5.30 | 30.24 ± 0.01 | 68.54 ± 0.17 |
| NMI | 13.49 ± 0.89 | 24.31 ± 2.19 | 19.89 ± 8.41 | 11.76 ± 4.37 | 18.89 ± 0.27 | 17.33 ± 5.56 | 0.73 ± 0.32 | 0.40 ± 0.01 | 50.46 ± 0.60 | |
| ARI | 2.88 ± 0.01 | 17.84 ± 3.07 | 15.34 ± 6.88 | 6.16 ± 3.07 | 14.70 ± 0.55 | 13.66 ± 5.20 | −0.08 ± 0.38 | −0.02 ± 0.01 | 44.84 ± 0.25 | |
| F1 | 20.67 ± 1.04 | 37.80 ± 4.64 | 36.72 ± 11.52 | 26.68 ± 4.56 | 37.64 ± 1.07 | 35.09 ± 6.07 | 11.99 ± 3.76 | 6.84 ± 0.01 | 60.49 ± 0.22 | |
| DBLP | ACC | 31.73 ± 2.42 | 48.49 ± 12.40 | 37.86 ± 4.12 | 58.49 ± 0.38 | 40.79 ± 10.90 | 26.80 ± 1.17 | 28.06 ± 0.01 | 74.00 ± 1.18 | |
| NMI | eigs | 2.31 ± 1.42 | 17.51 ± 11.16 | 8.43 ± 4.09 | 25.05 ± 0.33 | 11.83 ± 10.20 | 0.19 ± 0.26 | 0.18 ± 0.01 | 40.43 ± 1.53 | |
| ARI | error | 1.94 ± 1.29 | 15.81 ± 10.53 | 5.95 ± 2.90 | 22.12 ± 0.28 | 10.08 ± 8.87 | 0.09 ± 0.21 | 0.23 ± 0.16 | 43.44 ± 1.96 | |
| F1 | 30.50 ± 2.54 | 43.23 ± 20.24 | 36.76 ± 4.73 | 58.18 ± 0.36 | 39.74 ± 11.86 | 26.46 ± 1.28 | 23.86 ± 2.97 | 73.82 ± 1.19 | ||
| Pubmed | ACC | 39.99 ± 0.55 | 58.16 ± 4.30 | 48.78 ± 3.95 | 59.55 ± 0.04 | 49.81 ± 9.79 | 38.96 ± 6.12 | 40.26 ± 4.05 | 63.97 ± 2.41 | |
| NMI | 3.37 ± 0.69 | eigs | 21.24 ± 4.86 | 11.04 ± 3.83 | 22.61 ± 0.04 | 10.35 ± 8.71 | 2.11 ± 2.85 | 1.49 ± 2.75 | 24.09 ± 2.37 | |
| ARI | −1.67 ± 0.34 | error | 19.62 ± 3.83 | 8.84 ± 3.27 | 21.05 ± 0.05 | 9.96 ± 8.51 | 2.35 ± 3.29 | 1.29 ± 2.53 | 23.94 ± 2.49 | |
| F1 | 24.87 ± 0.27 | 57.79 ± 4.64 | 49.34 ± 4.75 | 60.19 ± 0.05 | 46.79 ± 11.83 | 37.07 ± 4.78 | 31.73 ± 10.27 | 63.78 ± 2.92 |
| Datasets | Metric | MAGCN IJCAI21 | SGCMC TMM22 | GMGEC TMM23 | IMGCGGR Ours |
|---|---|---|---|---|---|
| ACM | ACC | 73.02 ± 16.23 | 69.50 ± 11.05 | 40.24 ± 4.90 | 91.37 ± 0.05 |
| NMI | 49.54 ± 21.12 | 37.11 ± 9.76 | 4.10 ± 4.86 | 70.12 ± 0.04 | |
| ARI | 49.24 ± 26.32 | 34.20 ± 14.33 | 2.53 ± 2.84 | 76.14 ± 0.09 | |
| F1 | 68.83 ± 19.66 | 68.77 ± 13.07 | 33.56 ± 10.39 | 91.38 ± 0.05 | |
| AMP | ACC | 31.50 ± 12.08 | 71.20 ± 4.45 | 29.36 ± 3.00 | 77.04 ± 0.64 |
| NMI | 12.09 ± 21.93 | 61.43 ± 1.95 | 18.35 ± 6.46 | 66.05 ± 1.24 | |
| ARI | 7.08 ± 14.55 | 54.32 ± 3.35 | 10.17 ± 3.89 | 57.12 ± 0.35 | |
| F1 | 14.67 ± 17.71 | 61.51 ± 5.99 | 21.58 ± 5.79 | 69.05 ± 3.55 | |
| Citeseer | ACC | 58.01 ± 5.92 | 43.99 ± 5.52 | 31.80 ± 3.20 | 66.71 ± 1.81 |
| NMI | 36.59 ± 3.32 | 28.83 ± 2.67 | 10.26 ± 2.16 | 39.45 ± 1.34 | |
| ARI | 35.54 ± 4.88 | 14.20 ± 4.70 | 6.35 ± 1.53 | 40.40 ± 2.07 | |
| F1 | 48.49 ± 7.28 | 39.21 ± 5.91 | 27.25 ± 3.10 | 59.22 ± 0.19 | |
| Cora | ACC | 64.20 ± 3.28 | 66.67 ± 3.02 | 43.67 ± 5.41 | 68.54 ± 0.17 |
| NMI | 48.65 ± 2.99 | 49.50 ± 1.63 | 28.30 ± 4.94 | 50.46 ± 0.60 | |
| ARI | 43.27 ± 3.11 | 41.63 ± 4.76 | 20.21 ± 5.10 | 44.84 ± 0.25 | |
| F1 | 51.93 ± 5.31 | 54.80 ± 4.99 | 33.35 ± 6.91 | 60.49 ± 0.22 | |
| DBLP | ACC | 40.76 ± 2.66 | 61.23 ± 5.60 | 39.83 ± 4.58 | 74.00 ± 1.18 |
| NMI | 10.06 ± 3.62 | 32.87 ± 3.11 | 8.28 ± 3.32 | 40.43 ± 1.53 | |
| ARI | 4.83 ± 0.96 | 26.02 ± 5.23 | 6.89 ± 2.46 | 43.44 ± 1.96 | |
| F1 | 29.53 ± 5.39 | 57.92 ± 7.73 | 32.49 ± 6.83 | 73.82 ± 1.19 | |
| Pubmed | ACC | 56.59 ± 4.26 | 52.78 ± 9.10 | 38.24 ± 1.43 | 63.97 ± 2.41 |
| NMI | 20.90 ± 4.97 | 17.25 ± 8.88 | 2.10 ± 1.13 | 24.09 ± 2.37 | |
| ARI | 21.19 ± 4.12 | 13.43 ± 11.08 | 1.06 ± 0.98 | 23.94 ± 2.49 | |
| F1 | 43.30 ± 8.82 | 46.64 ± 14.02 | 33.84 ± 3.74 | 63.78 ± 2.92 |
| Dataset | Metrics | noGSA | noSelf | noGuide | noCrossView | IMGCGGR |
|---|---|---|---|---|---|---|
| ACM | ACC | 89.52 ± 0.41 | 41.12 ± 8.80 | 81.73 ± 0.75 | 88.60 ± 0.33 | 91.37 ± 0.05 |
| NMI | 68.30 ± 0.73 | 6.29 ± 8.84 | 52.47 ± 0.52 | 62.78 ± 0.90 | 70.12 ± 0.04 | |
| ARI | 71.96 ± 0.96 | 5.03 ± 9.02 | 55.46 ± 1.53 | 69.04 ± 0.83 | 76.14 ± 0.09 | |
| F1 | 89.35 ± 0.42 | 26.62 ± 11.91 | 81.74 ± 0.70 | 88.65 ± 0.33 | 91.38 ± 0.05 | |
| AMP | ACC | 66.58 ± 5.64 | 26.13 ± 0.03 | 68.23 ± 9.14 | 62.36 ± 1.80 | 77.04 ± 0.64 |
| NMI | 54.23 ± 4.39 | 0.67 ± 0.01 | 58.98 ± 8.79 | 48.70 ± 1.43 | 66.05 ± 1.24 | |
| ARI | 45.84 ± 5.26 | −0.11 ± 0.02 | 49.73 ± 10.82 | 39.81 ± 1.04 | 57.12 ± 0.35 | |
| F1 | 56.09 ± 9.14 | 6.13 ± 0.01 | 57.08 ± 10.69 | 49.28 ± 5.25 | 69.05 ± 3.55 | |
| Citeseer | ACC | 62.45 ± 3.76 | 41.44 ± 5.35 | 53.60 ± 2.23 | 60.77 ± 5.61 | 66.71 ± 1.81 |
| NMI | 37.94 ± 2.51 | 20.95 ± 3.05 | 25.36 ± 2.16 | 36.13 ± 4.58 | 39.45 ± 1.34 | |
| ARI | 36.70 ± 3.58 | 16.97 ± 3.15 | 24.88 ± 2.28 | 34.46 ± 6.41 | 40.40 ± 2.07 | |
| F1 | 58.23 ± 3.29 | 28.25 ± 7.61 | 50.13 ± 1.48 | 56.67 ± 6.25 | 59.22 ± 0.19 | |
| Cora | ACC | 64.02 ± 2.38 | 40.37 ± 3.09 | 61.99 ± 3.08 | 58.81 ± 8.83 | 68.54 ± 0.17 |
| NMI | 46.05 ± 3.37 | 20.81 ± 2.72 | 44.12 ± 3.27 | 39.29 ± 8.70 | 50.46 ± 0.60 | |
| ARI | 38.56 ± 3.52 | 15.27 ± 2.97 | 40.77 ± 4.18 | 34.58 ± 7.33 | 44.84 ± 0.25 | |
| F1 | 53.26 ± 5.92 | 25.69 ± 4.75 | 53.39 ± 4.36 | 48.63 ± 10.82 | 60.49 ± 0.22 | |
| DBLP | ACC | 70.82 ± 2.22 | 40.39 ± 2.16 | 52.72 ± 2.10 | 69.93 ± 2.94 | 74.00 ± 1.18 |
| NMI | 36.77 ± 2.92 | 10.14 ± 2.60 | 20.21 ± 1.56 | 36.16 ± 3.69 | 40.43 ± 1.53 | |
| ARI | 38.27 ± 3.80 | 9.11 ± 2.83 | 18.61 ± 1.55 | 37.57 ± 3.72 | 43.44 ± 1.96 | |
| F1 | 70.81 ± 2.17 | 32.34 ± 2.93 | 50.02 ± 2.00 | 69.51 ± 3.32 | 73.82 ± 1.19 | |
| Pubmed | ACC | 57.58 ± 4.64 | 39.95 ± 0.01 | 58.96 ± 3.22 | 60.09 ± 3.90 | 63.97 ± 2.41 |
| NMI | 21.64 ± 2.04 | 0.02 ± 0.01 | 18.12 ± 2.87 | 21.64 ± 2.03 | 24.09 ± 2.37 | |
| ARI | 21.35 ± 1.37 | 0.01 ± 0.01 | 15.80 ± 2.79 | 21.35 ± 1.37 | 23.94 ± 2.49 | |
| F1 | 56.83 ± 8.20 | 19.04 ± 0.01 | 59.04 ± 3.40 | 56.83 ± 8.20 | 63.78 ± 2.92 |
| Dataset | ||
|---|---|---|
| ACM | 1 | 1 |
| AMP | 1 | 1 |
| Citeseer | 1 | 1 |
| Cora | 1 | 10 |
| DBLP | 1 | 1 |
| Pubmed | 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, L.; Yao, S.; Huang, Y.; Cheng, Y.; Qian, Y. Improved Multi-View Graph Clustering with Global Graph Refinement. Remote Sens. 2025, 17, 3217. https://doi.org/10.3390/rs17183217
Zeng L, Yao S, Huang Y, Cheng Y, Qian Y. Improved Multi-View Graph Clustering with Global Graph Refinement. Remote Sensing. 2025; 17(18):3217. https://doi.org/10.3390/rs17183217
Chicago/Turabian StyleZeng, Lingbin, Shixin Yao, You Huang, Yong Cheng, and Yue Qian. 2025. "Improved Multi-View Graph Clustering with Global Graph Refinement" Remote Sensing 17, no. 18: 3217. https://doi.org/10.3390/rs17183217
APA StyleZeng, L., Yao, S., Huang, Y., Cheng, Y., & Qian, Y. (2025). Improved Multi-View Graph Clustering with Global Graph Refinement. Remote Sensing, 17(18), 3217. https://doi.org/10.3390/rs17183217








