Hierarchical Frequency-Guided Knowledge Reconstruction for SAR Incremental Target Detection
Abstract
Highlights
- We tackle feature representation mismatches in SAR incremental target detection.
- We propose HFKR, a wavelet-guided hierarchical frequency reconstruction method.
- HFKR delivers top performance and stable learning across scenes and multi-step runs.
- HFKR is designed as an independent modular component, which makes it potentially applicable to other domains.
Abstract
1. Introduction
- 1.
- We analyze the impact of sparse target feature distribution and sensitivity to environmental variations in SAR imagery on incremental target detection, highlighting feature representation mismatch as a key factor driving performance degradation across incremental tasks.
- 2.
- We conduct a comprehensive analysis of the correlation between frequency-domain components and hierarchical semantic features in SAR imagery. This analysis demonstrates that frequency-domain representations more clearly capture multi-scale semantic structures, providing essential guidance for the design of our subsequent reconstruction strategy.
- 3.
- Building upon above analysis, we design the HFKR strategy, which integrates frequency-guided decomposition and reconstruction into the feature transfer process. HFKR effectively addresses feature representation mismatch challenges, enhances representation consistency, and significantly improves detection performance in incremental tasks.
2. Related Work
2.1. Incremental Target Classification
2.2. Incremental Target Detection
2.3. Summary and Inspiration to Our Work
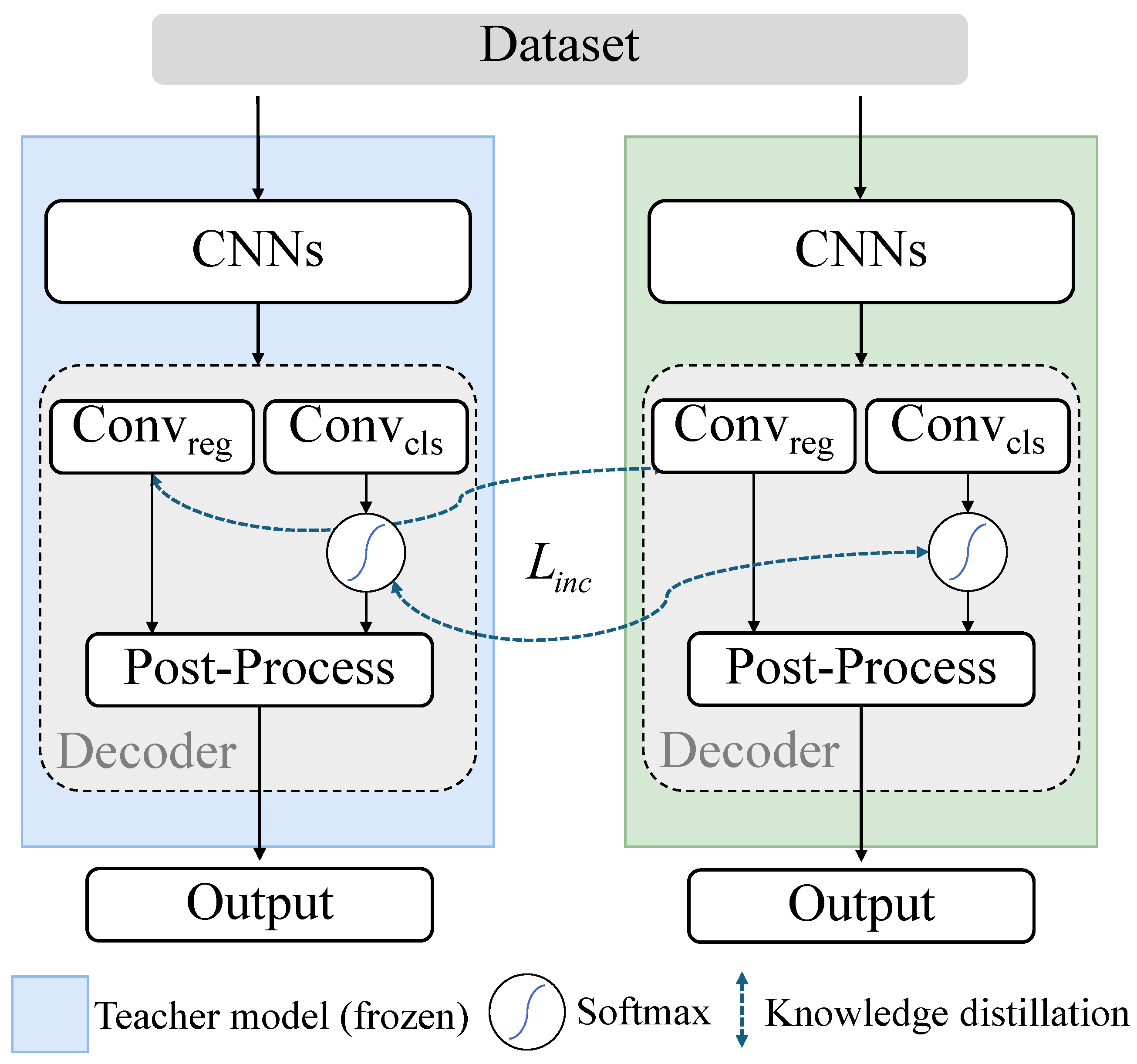
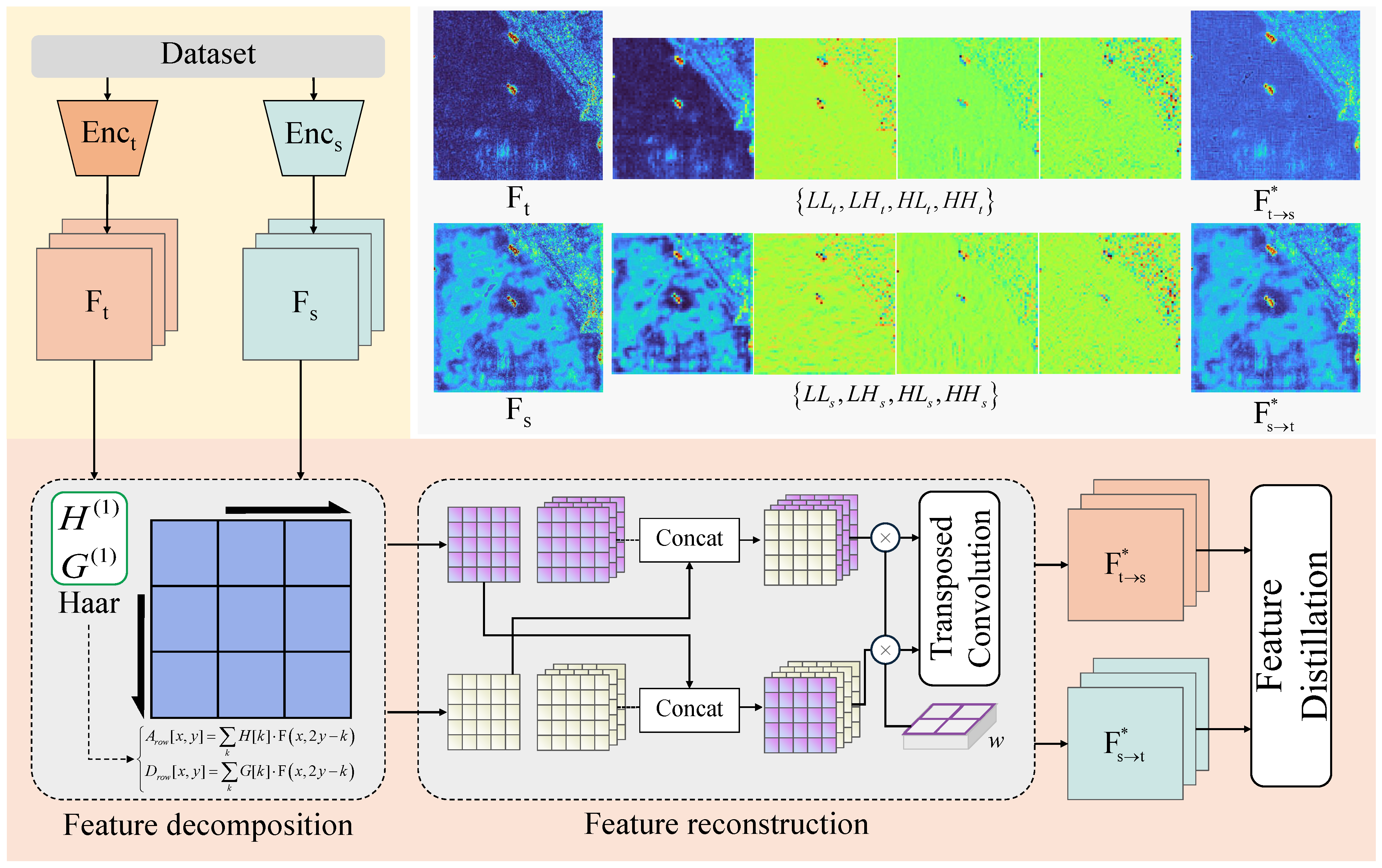
3. Materials and Methods
3.1. Preliminary
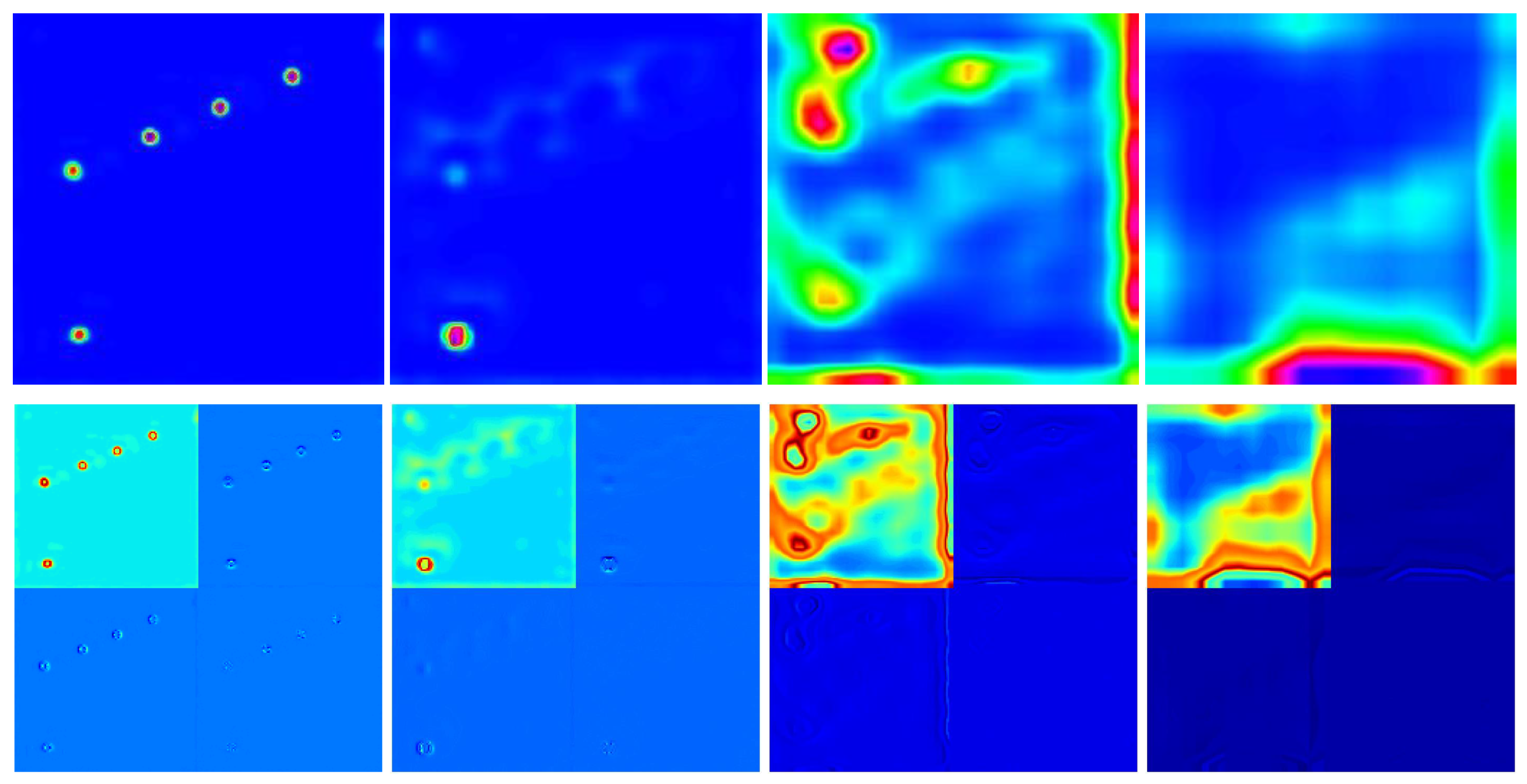
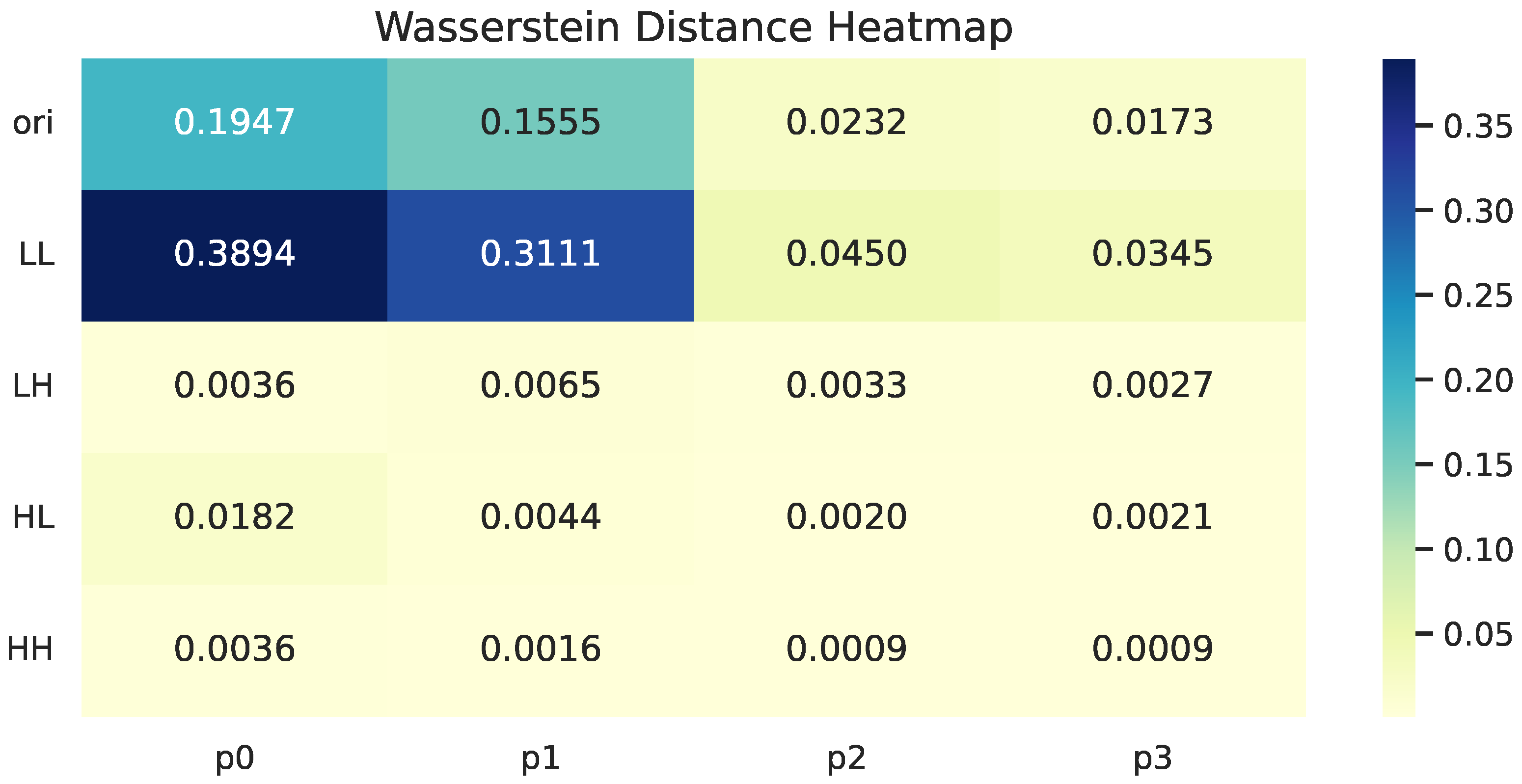
3.2. Frequency Domain-Granularity Feature Correlation
- The multi-scale nature of wavelet transform enables the decomposition of original mixed features into a well-defined hierarchical structure in the frequency domain.
- Low-frequency features capture the spatial relationship between edges and their positions, exhibiting a degree of generalizability; high-frequency features encode fine-grained discriminative details of targets and are more sensitive to variations in target appearance.
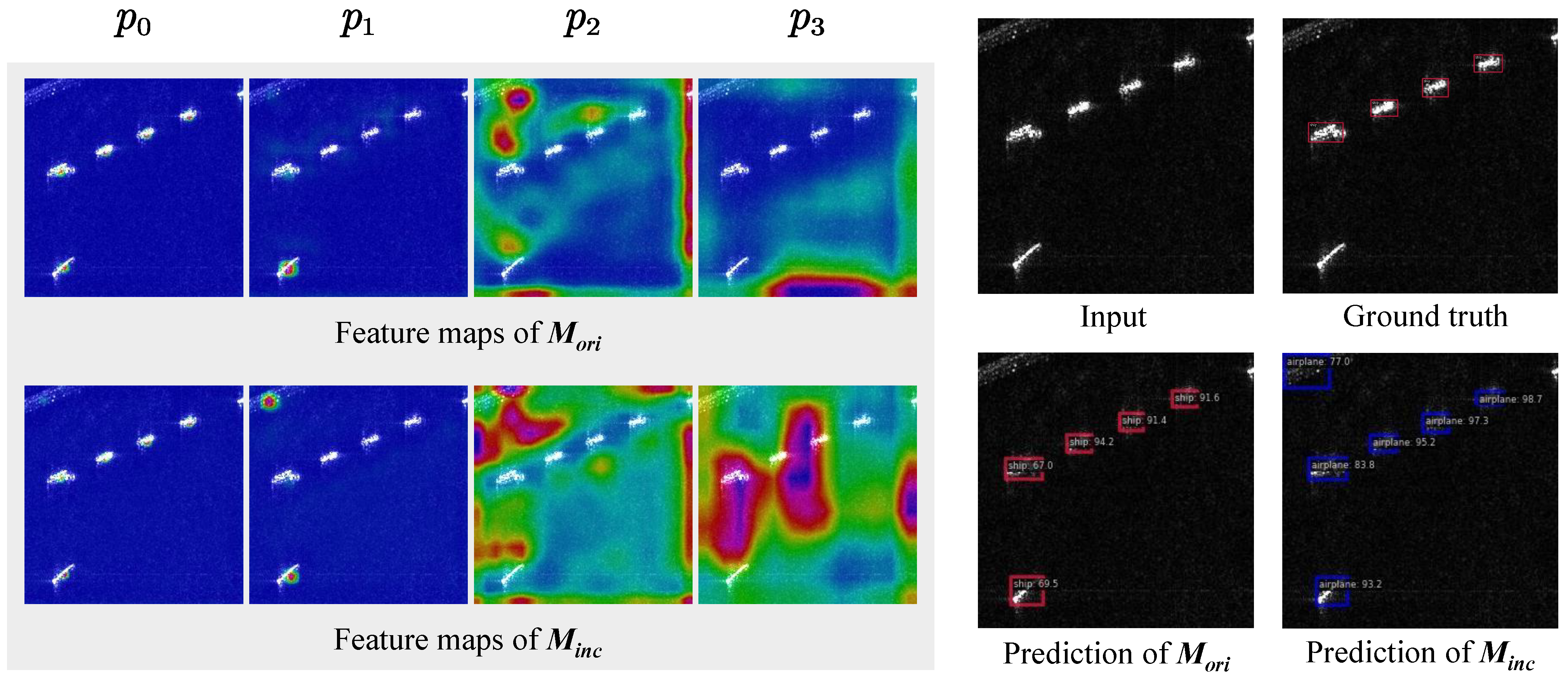
3.3. Hierarchical Frequency-Knowledge Reconstruction (HFKR)
4. Results
4.1. Datasets
4.2. Experimental Settings
4.2.1. Dataset Split
- MSAR dataset partitioning: Ship and bridge are designated as base classes, while oilcan and airplane are treated as incremental classes.
- SARAIRcraft-1.0 dataset partitioning: A220 and A320/321 are designated as base classes. A330 and ARJ21 are introduced in the first increment, Boeing737 and Boeing787 in the second, and the class “other” in the third increment.
4.2.2. Validation Metrics
4.3. Instantiation Under GFL
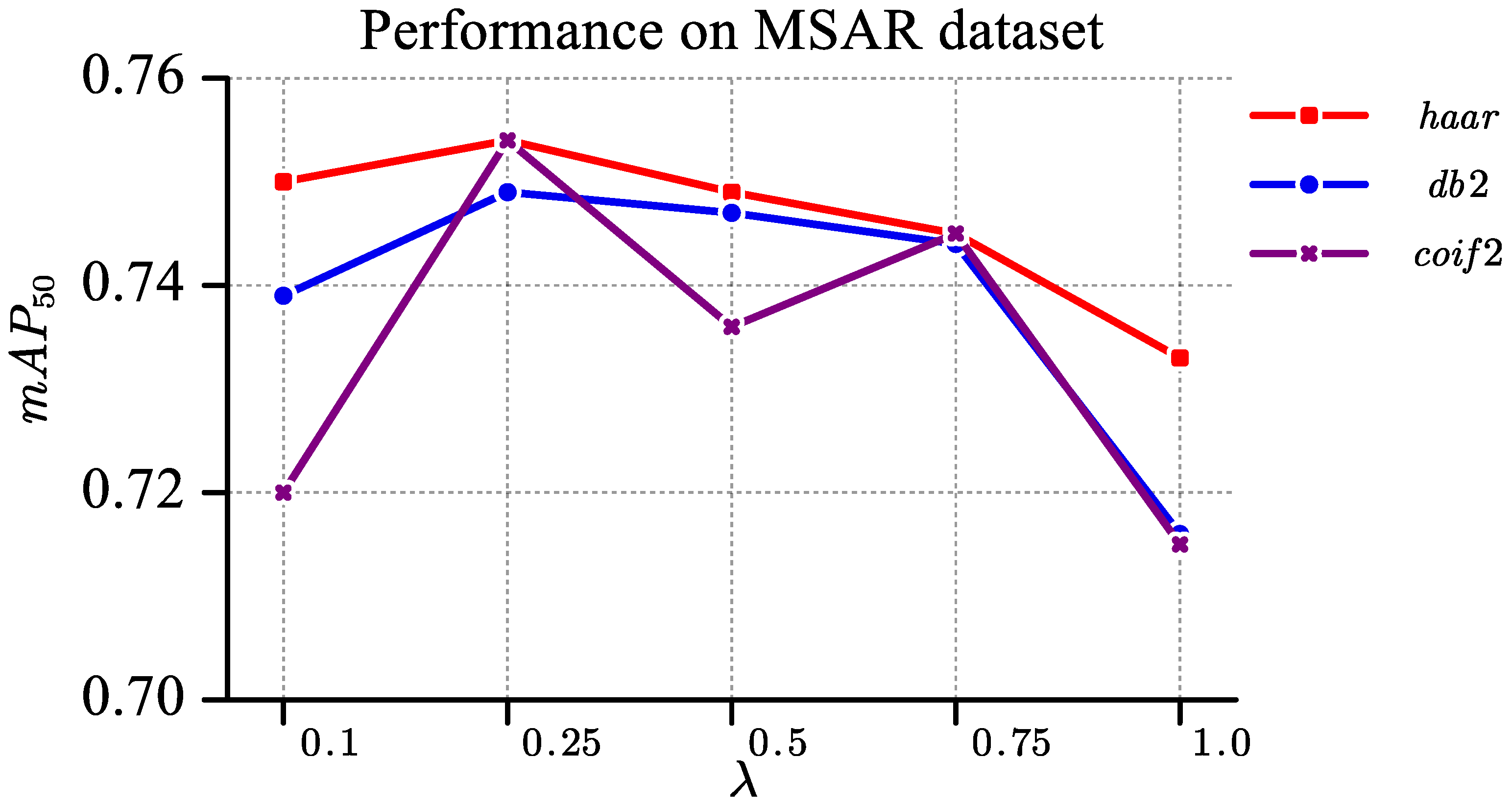
4.4. Ablation Study
4.5. Comparison with Other Methods
- Red: The best effect of current item
- Blue: The second-best effect of current item
- *: Reproduced from the original article (the work was not provided with source code)
- †: Porting its provided source code into the unified framework (GFL).
4.5.1. Experiments on the MSAR Dataset
4.5.2. Experiments on the SARAIRcraft Dataset
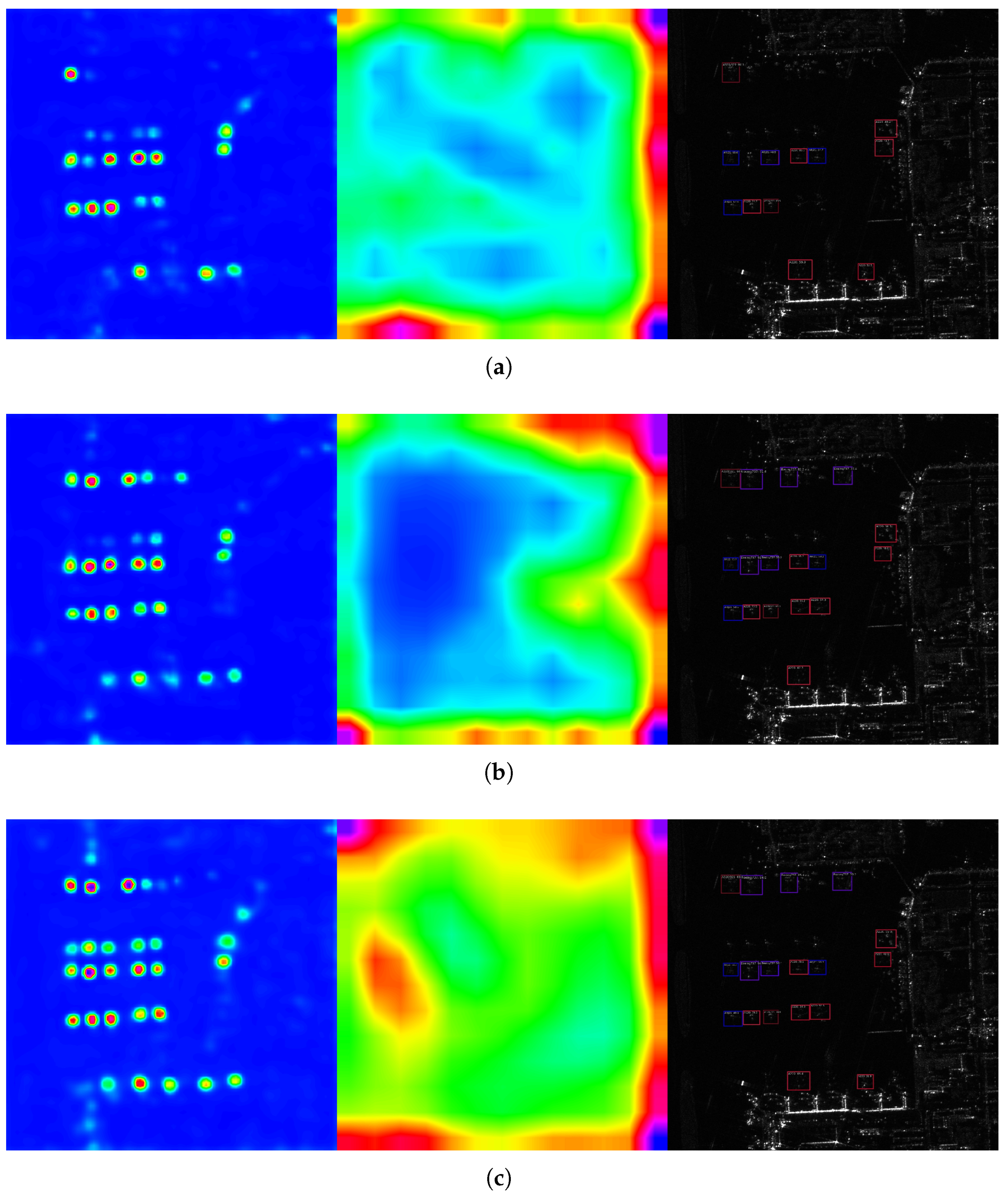
5. Discussion
5.1. Overall Effectiveness
- Fewer airplane samples in MSAR. Airplane has the smallest class size in our split, which weakens calibration and generalization compared with ship.
- Small and clustered targets. Airplane targets are typically small and spatially concentrated, this increases localization ambiguity and makes detection intrinsically harder.
- Bridge size and scene variability. Bridge targets are generally larger than other classes in MSAR and span complex backgrounds (river/urban scenes). Their elongated geometry causes unstable performance in certain scenes despite the larger absolute size.
5.2. Performance Trends
5.3. Potential Applicability to Related Domains
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HFKR | Hierarchical Frequency-Guided Knowledge Reconstruction (Proposed) |
| DWT | Discrete Wavelet Transform |
| IL | Incremental Learning |
| ITD | Incremental Target Detection |
| KD | Knowledge Distillation |
| EMD | Earth Mover’s Distance/Wasserstein Distance |
References
- Dellinger, F.; Delon, J.; Gousseau, Y.; Michel, J.; Tupin, F. SAR-SIFT: A SIFT-like algorithm for SAR images. IEEE Trans. Geosci. Remote Sens. 2014, 53, 453–466. [Google Scholar] [CrossRef]
- Dang, S.; Cao, Z.; Cui, Z.; Pi, Y.; Liu, N. Open Set Incremental Learning for Automatic Target Recognition. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4445–4456. [Google Scholar] [CrossRef]
- Qin, X.; Zhou, S.; Zou, H.; Gao, G. A CFAR detection algorithm for generalized gamma distributed background in high-resolution SAR images. IEEE Geosci. Remote Sens. Lett. 2012, 10, 806–810. [Google Scholar]
- Du, Y.; Du, L.; Guo, Y.; Shi, Y. Semisupervised SAR Ship Detection Network via Scene Characteristic Learning. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–17. [Google Scholar] [CrossRef]
- Zhou, Z.; Cui, Z.; Tang, K.; Tian, Y.; Pi, Y.; Cao, Z. Gaussian meta-feature balanced aggregation for few-shot synthetic aperture radar target detection. ISPRS J. Photogramm. Remote Sens. 2024, 208, 89–106. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, S.; Zhan, R.; Wang, W.; Zhang, J. LMSD-YOLO: A lightweight YOLO algorithm for multi-scale SAR ship detection. Remote Sens. 2022, 14, 4801. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, R.; Ai, J.; Zou, H.; Li, J. Global and Local Context-Aware Ship Detector for High-Resolution SAR Images. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4159–4167. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, X.; Liu, N.; Cao, Z.; Yang, J. Ship detection in large-scale SAR images via spatial shuffle-group enhance attention. IEEE Trans. Geosci. Remote Sens. 2020, 59, 379–391. [Google Scholar] [CrossRef]
- Cui, Z.; Li, Q.; Cao, Z.; Liu, N. Dense Attention Pyramid Networks for Multi-Scale Ship Detection in SAR Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8983–8997. [Google Scholar] [CrossRef]
- Han, S.; Addabbo, P.; Biondi, F.; Clemente, C.; Orlando, D.; Ricci, G. Innovative Solutions Based on the EM-Algorithm for Covariance Structure Detection and Classification in Polarimetric SAR Images. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 209–227. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, T.; Zhang, Z.; Xiong, H. Evaluating the Robustness of Polarimetric Features: A Case Study of PolSAR Ship Detection. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Wang, X.; Cao, Z.; Pi, Y. Semisupervised Classification with Adaptive Anchor Graph for PolSAR Images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Tian, Z.; Wang, W.; Zhou, K.; Song, X.; Shen, Y.; Liu, S. Weighted Pseudo-Labels and Bounding Boxes for Semisupervised SAR Target Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 5193–5203. [Google Scholar] [CrossRef]
- Deng, J.; Wang, W.; Zhang, H.; Zhang, T.; Zhang, J. PolSAR Ship Detection Based on Superpixel-Level Contrast Enhancement. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, L.; Ding, D.; Hu, D.; Kuang, G.; Liu, L. Few-Shot Class-Incremental SAR Target Recognition via Cosine Prototype Learning. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–18. [Google Scholar] [CrossRef]
- Xu, W.; Yuan, X.; Hu, Q.; Li, J. SAR-optical feature matching: A large-scale patch dataset and a deep local descriptor. Int. J. Appl. Earth Obs. Geoinf. 2023, 122, 103433. [Google Scholar] [CrossRef]
- Li, Z.; Hoiem, D. Learning without forgetting. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 2935–2947. [Google Scholar] [CrossRef]
- Dang, S.; Cao, Z.; Cui, Z.; Pi, Y.; Liu, N. Class Boundary Exemplar Selection Based Incremental Learning for Automatic Target Recognition. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5782–5792. [Google Scholar] [CrossRef]
- Li, B.; Cui, Z.; Cao, Z.; Yang, J. Incremental Learning Based on Anchored Class Centers for SAR Automatic Target Recognition. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Rebuffi, S.A.; Kolesnikov, A.; Sperl, G.; Lampert, C.H. icarl: Incremental classifier and representation learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2001–2010. [Google Scholar]
- Shmelkov, K.; Schmid, C.; Alahari, K. Incremental learning of object detectors without catastrophic forgetting. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3400–3409. [Google Scholar]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Peng, C.; Zhao, K.; Lovell, B.C. Faster ilod: Incremental learning for object detectors based on faster rcnn. Pattern Recognit. Lett. 2020, 140, 109–115. [Google Scholar] [CrossRef]
- Peng, C.; Zhao, K.; Maksoud, S.; Li, M.; Lovell, B.C. SID: Incremental learning for anchor-free object detection via Selective and Inter-related Distillation. Comput. Vis. Image Underst. 2021, 210, 103229. [Google Scholar] [CrossRef]
- Feng, T.; Wang, M.; Yuan, H. Overcoming catastrophic forgetting in incremental object detection via elastic response distillation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 9427–9436. [Google Scholar]
- Goodfellow, I.J.; Mirza, M.; Xiao, D.; Courville, A.; Bengio, Y. An Empirical Investigation of Catastrophic Forgetting in Gradient-Based Neural Networks. arXiv 2015, arXiv:1312.6211. [Google Scholar] [CrossRef]
- De Lange, M.; Aljundi, R.; Masana, M.; Parisot, S.; Jia, X.; Leonardis, A.; Slabaugh, G.; Tuytelaars, T. A Continual Learning Survey: Defying Forgetting in Classification Tasks. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 3366–3385. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.; Maire, M.; Belongie, S.J.; Bourdev, L.D.; Girshick, R.B.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. arXiv 2014, arXiv:1405.0312. [Google Scholar] [CrossRef]
- Everingham, M.; Gool, L.V.; Williams, C.K.I.; Winn, J.; Zisserman, A. The Pascal Visual Object Classes (VOC) Challenge. Int. J. Comput. Vis. 2010, 88, 303–338. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, B.; Yu, H.; Chen, J.; Xing, M.; Hong, W. Sparse Synthetic Aperture Radar Imaging From Compressed Sensing and Machine Learning: Theories, applications, and trends. IEEE Geosci. Remote Sens. Mag. 2022, 10, 32–69. [Google Scholar] [CrossRef]
- Zhou, H.; Jayender, J. EMDQ: Removal of Image Feature Mismatches in Real-Time. IEEE Trans. Image Process. 2022, 31, 706–720. [Google Scholar] [CrossRef]
- Lyu, J.; Bai, C.; Yang, J.W.; Lu, Z.; Li, X. Cross-Domain Policy Adaptation by Capturing Representation Mismatch. In Proceedings of Machine Learning Research, Proceedings of the 41st International Conference on Machine Learning (PMLR), Vienna, Austria, 21–27 July 2024; Salakhutdinov, R., Kolter, Z., Heller, K., Weller, A., Oliver, N., Scarlett, J., Berkenkamp, F., Eds.; Microtome Publishing: Brookline, MA, USA, 2024; Volume 235, pp. 33638–33663. [Google Scholar]
- Zhang, T.; Zeng, T.; Zhang, X. Synthetic Aperture Radar (SAR) Meets Deep Learning. Remote Sens. 2023, 15, 303. [Google Scholar] [CrossRef]
- Zhang, P.; Xu, H.; Tian, T.; Gao, P.; Li, L.; Zhao, T.; Zhang, N.; Tian, J. SEFEPNet: Scale Expansion and Feature Enhancement Pyramid Network for SAR Aircraft Detection with Small Sample Dataset. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3365–3375. [Google Scholar] [CrossRef]
- Luo, Z.; Liu, Y.; Schiele, B.; Sun, Q. Class-Incremental Exemplar Compression for Class-Incremental Learning. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 11371–11380. [Google Scholar] [CrossRef]
- Zhang, B.; Luo, C.; Yu, D.; Li, X.; Lin, H.; Ye, Y.; Zhang, B. Metadiff: Meta-learning with conditional diffusion for few-shot learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 16687–16695. [Google Scholar]
- Yang, Y.; Yuan, H.; Li, X.; Lin, Z.; Torr, P.; Tao, D. Neural Collapse Inspired Feature-Classifier Alignment for Few-Shot Class-Incremental Learning. In Proceedings of the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Yu, X.; Dong, F.; Ren, H.; Zhang, C.; Zou, L.; Zhou, Y. Multilevel Adaptive Knowledge Distillation Network for Incremental SAR Target Recognition. IEEE Geosci. Remote Sens. Lett. 2023, 20, 4004405. [Google Scholar] [CrossRef]
- He, J. Gradient Reweighting: Towards Imbalanced Class-Incremental Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 16668–16677. [Google Scholar]
- Li, D.; Tasci, S.; Ghosh, S.; Zhu, J.; Zhang, J.; Heck, L. RILOD: Near real-time incremental learning for object detection at the edge. In Proceedings of the 4th ACM/IEEE Symposium on Edge Computing, New York, NY, USA, 7–9 November 2019; SEC ’19; pp. 113–126. [Google Scholar] [CrossRef]
- Tian, Y.; Cui, Z.; Ma, J.; Zhou, Z.; Cao, Z. Continual Learning for SAR Target Incremental Detection via Predicted Location Probability Representation and Proposal Selection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5211215. [Google Scholar] [CrossRef]
- Feng, H.; Zhang, L.; Yang, X.; Liu, Z. Enhancing class-incremental object detection in remote sensing through instance-aware distillation. Neurocomputing 2024, 583, 127552. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; Cortes, C., Lawrence, N., Lee, D., Sugiyama, M., Garnett, R., Eds.; Curran Associates, Inc.: Nice, France, 2015; Volume 28. [Google Scholar]
- Zhou, X.; Wang, D.; Krähenbühl, P. Objects as points. arXiv 2019, arXiv:1904.07850. [Google Scholar] [PubMed]
- Li, X.; Wang, W.; Wu, L.; Chen, S.; Hu, X.; Li, J.; Tang, J.; Yang, J. Generalized focal loss: Learning qualified and distributed bounding boxes for dense object detection. Adv. Neural Inf. Process. Syst. 2020, 33, 21002–21012. [Google Scholar]
- Kirkpatrick, J.; Pascanu, R.; Rabinowitz, N.; Veness, J.; Desjardins, G.; Rusu, A.A.; Milan, K.; Quan, J.; Ramalho, T.; Grabska-Barwinska, A.; et al. Overcoming catastrophic forgetting in neural networks. Proc. Natl. Acad. Sci. USA 2017, 114, 3521–3526. [Google Scholar] [CrossRef]
- Perez-Rua, J.M.; Zhu, X.; Hospedales, T.M.; Xiang, T. Incremental few-shot object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 13846–13855. [Google Scholar]
- Acharya, M.; Hayes, T.L.; Kanan, C. RODEO: Replay for Online Object Detection. In Proceedings of the British Machine Vision Conference, Virtual, 7–10 September 2020. [Google Scholar]
- Kim, J.; Cho, H.; Kim, J.; Tiruneh, Y.Y.; Baek, S. SDDGR: Stable Diffusion-Based Deep Generative Replay for Class Incremental Object Detection. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 28772–28781. [Google Scholar] [CrossRef]
- Dohare, S.; Hernandez-Garcia, J.F.; Lan, Q.; Rahman, P.; Mahmood, A.R.; Sutton, R.S. Loss of plasticity in deep continual learning. Nature 2024, 632, 768–774. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Y.; Fan, Y.; Jiang, G.; Hu, Q. Reducing Class-wise Confusion for Incremental Learning with Disentangled Manifolds. arXiv 2025, arXiv:2503.17677. [Google Scholar] [CrossRef]
- Tian, Y.; Zhou, Z.; Cui, Z.; Cao, Z. Scene Adaptive SAR Incremental Target Detection via Context-Aware Attention and Gaussian-Box Similarity Metric. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5205217. [Google Scholar] [CrossRef]
- Xiong, S.; Tan, Y.; Wang, G.; Yan, P.; Xiang, X. Learning feature relationships in CNN model via relational embedding convolution layer. Neural Netw. 2024, 179, 106510. [Google Scholar] [CrossRef]
- Xu, M.; Xu, J.; Liu, S.; Sheng, H.; Shen, B.; Hou, K. Stationary Wavelet Convolutional Network with Generative Feature Learning for Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5501613. [Google Scholar] [CrossRef]
- Zhou, F.; Yang, T.; Tan, L.; Xu, X.; Xing, M. DAP-Net: Enhancing SAR target recognition with dual-channel attention and polarimetric features. Vis. Comput. 2025, 41, 7641–7656. [Google Scholar] [CrossRef]
- Zhu, R.; Zhou, J.; Chen, S.; Ding, H. Fast Zero Migration Algorithm for Near-Field Sparse MIMO Array Grating Lobe Suppression. IEEE Trans. Antennas Propag. 2025, 73, 1286–1291. [Google Scholar] [CrossRef]
- Rubner, Y.; Tomasi, C.; Guibas, L.J. The earth mover’s distance as a metric for image retrieval. Int. J. Comput. Vis. 2000, 40, 99–121. [Google Scholar] [CrossRef]
- Cuturi, M. Sinkhorn Distances: Lightspeed Computation of Optimal Transport. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–8 December 2013; Burges, C., Bottou, L., Welling, M., Ghahramani, Z., Weinberger, K., Eds.; Curran Associates, Inc.: Nice, France, 2013; Volume 26. [Google Scholar]


| MSAR | SARAIRcraft | |
|---|---|---|
| Sensor | HS-1, GF-3 | GF-3 |
| Wave Band | c | c |
| Polarization Mode | multi-polarization | single-polarization |
| Resolution | 1 m | 1 m |
| Image Size (pixels) | 256∼2048 | 800∼1500 |
| Number of Images | ship: 26,094 bridge: 1582 oilcan: 1248 airplane: 108 | A220: 2065 A320/321: 939 A330: 290 ARJ21: 713 Boeing737: 1495 Boeing787: 1677 other: 2041 |
| Number of Targets | ship: 39,858 bridge: 1815 oilcan: 12,319 airplane: 6368 | A220: 3730 A320/321: 1771 A330: 309 ARJ21: 1187 Boeing737: 2557 Boeing787: 2645 other: 5264 |
| Number of Images | Number of Targets | |
|---|---|---|
| Ship | 3000 | 4838 |
| Bridge | 1582 | 1815 |
| Oilcan | 950 | 8089 |
| Airplane | 108 | 6368 |
| Wavelet Basis | Low-Pass Filter h | High-Pass Filter g |
|---|---|---|
| haar (db1) | ||
| db2 | ||
| coif2 |
| HFKR | Ship | Bridge | Oilcan | Airplane | Avg |
|---|---|---|---|---|---|
| 73.5 (±0.2) | 73.4 (±0.4) | 93.1 (±0.1) | 43.6 (±0.1) | 70.9 | |
| ✓ | 73.7 (±0.1) | 71.6 (±0.2) | 97.3 (±0.2) | 58.9 (±0.6) | 75.4 |
| Phase | Method | Classes | mAP | Diff (vs. FD) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ship | Bridge | Oilcan | Airplane | Old | New | Avg | Old | New | Avg | ||
| Initial | FD (classes 1–2) | 79.5 | 84 | - | - | - | - | - | - | - | - |
| Inc (2 + 2) | FD (classes 1–4) | 79.1 | 80.6 | 97.4 | 60.9 | 79.8 | 79.2 | 79.5 | - | - | - |
| RILOD * (2019, SEC) [40] | 52.8 | 62.2 | 97.1 | 39.1 | 57.5 | 68.1 | 62.8 | −26.3 | −11.1 | −16.7 | |
| SID † (2021, CVPR) [24] | 73.1 | 79.7 | 89.8 | 4.4 | 76.4 | 45.1 | 61.7 | −3.4 | −34.1 | −17.8 | |
| ERD (2022, CVPR) [25] | 73.6 | 77.1 | 96.0 | 43.6 | 75.4 | 69.8 | 72.6 | −4.4 | −9.4 | −6.9 | |
| IDCOD * (2024, IJON) [42] | 65.0 | 71.0 | 97.7 | 58.6 | 68.0 | 78.2 | 73.1 | −11.8 | −1.0 | −6.4 | |
| Tian (2024, TGRS) [41] | 73.1 | 74.7 | 93.0 | 51.7 | 73.9 | 72.4 | 73.1 | −5.9 | −6.8 | −6.4 | |
| Ours | 73.7 | 71.6 | 97.3 | 58.9 | 72.7 | 78.1 | 75.4 | −7.1 | −1.1 | −4.1 | |
| Phase | Method | Classes | mAP | Diff (vs. FD) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A22 | A32 | A33 | ARJ | B73 | B78 | Other | Old | New | Avg | Old | New | Avg | ||
| Initial | FD (classes 1–2) | 62.3 | 78.2 | - | - | - | - | - | - | - | - | - | - | - |
| Inc (2 + 2) | FD (classes 1–4) | 63.9 | 86.0 | 78.0 | 74.8 | - | - | - | 74.9 | 76.4 | 75.7 | - | - | - |
| RILOD * (2019, SEC) [40] | 50.0 | 68.4 | 73.1 | 60.0 | - | - | 59.2 | 66.6 | 62.9 | −15.7 | −9.8 | −12.8 | ||
| SID † (2021, CVPR) [24] | 54.9 | 81.0 | 77.0 | 59.3 | - | - | - | 67.9 | 68.2 | 68.2 | −7.0 | −8.2 | −7.5 | |
| ERD (2022, CVPR) [25] | 56.6 | 80.9 | 61.4 | 62.0 | - | - | - | 68.8 | 61.7 | 65.2 | −6.1 | −14.7 | −10.2 | |
| IDCOD * (2024, IJON) [42] | 32.3 | 56.9 | 76.4 | 58.8 | - | - | - | 44.6 | 67.6 | 56.1 | −30.3 | −8.8 | −19.6 | |
| Tian (2024, TGRS) [41] | 50.8 | 71.8 | 77.2 | 64.2 | - | - | - | 61.3 | 70.7 | 65.8 | −13.6 | −5.7 | −9.9 | |
| Ours | 62.0 | 81.6 | 75.5 | 66.7 | - | - | - | 71.8 | 71.1 | 71.4 | −3.1 | −5.3 | −4.3 | |
| Inc (4 + 2) | FD (classes 1–6) | 57.8 | 93.9 | 77.2 | 68.4 | 64.1 | 77.8 | - | 74.3 | 71.0 | 73.2 | - | - | - |
| RILOD * (2019, SEC) [40] | 43.1 | 77.9 | 58.5 | 46.5 | 51.2 | 73.0 | - | 56.5 | 62.1 | 58.4 | −17.8 | −8.9 | −14.8 | |
| SID † (2021, CVPR) [24] | 53.9 | 86.9 | 79.5 | 71.8 | 52.6 | 63.3 | - | 73.0 | 57.9 | 68.0 | −1.3 | −13.1 | −5.2 | |
| ERD (2022, CVPR) [25] | 56.8 | 87.5 | 78.0 | 75.6 | 53.1 | 58.9 | - | 74.5 | 56.0 | 68.3 | +0.2 | −15.0 | −4.9 | |
| IDCOD * (2024, IJON) [42] | 44.3 | 82.2 | 68.8 | 54.4 | 61.6 | 72.2 | - | 62.4 | 66.9 | 63.9 | −11.9 | −4.1 | −9.3 | |
| Tian (2024, TGRS) [41] | 50.2 | 84.5 | 79.1 | 64.7 | 61.0 | 70.7 | - | 72.6 | 65.9 | 68.4 | −1.7 | −5.1 | −4.8 | |
| Ours | 52.0 | 87.9 | 77.2 | 75.0 | 56.8 | 74.3 | - | 73.0 | 65.6 | 70.5 | −1.3 | −5.4 | −2.7 | |
| Inc (6 + 2) | FD (classes 1–7) | 66.9 | 89.8 | 77.2 | 81.2 | 65.4 | 77.4 | 79.4 | 76.3 | 79.4 | 76.8 | - | - | - |
| RILOD * (2019, SEC) [40] | 40.3 | 86.2 | 76.9 | 68.8 | 54.1 | 69.3 | 70.4 | 65.9 | 70.4 | 66.6 | −4.5 | −9.0 | −10.2 | |
| SID † (2021, CVPR) [24] | 57.1 | 90.9 | 77.2 | 73.9 | 62.6 | 78.2 | 70.0 | 73.3 | 70.0 | 72.8 | −3.0 | −9.4 | −4.0 | |
| ERD (2022, CVPR) [25] | 59.2 | 94.5 | 77.2 | 72.3 | 64.3 | 77.8 | 66.0 | 74.1 | 66.0 | 73.0 | −2.2 | −13.4 | −3.4 | |
| IDCOD * (2024, IJON) [42] | 41.3 | 84.6 | 58.3 | 67.6 | 46.3 | 52.8 | 74.9 | 58.5 | 74.9 | 60.8 | −17.8 | −4.5 | −16.0 | |
| Tian (2024, TGRS) [41] | 41.9 | 87.2 | 77.2 | 69.9 | 56.3 | 71.8 | 73.1 | 67.4 | 73.1 | 68.2 | −8.9 | −6.3 | −8.6 | |
| Ours | 58.0 | 93.9 | 77.2 | 73.8 | 62.4 | 78.0 | 74.8 | 73.9 | 74.8 | 74.0 | −2.4 | −4.6 | −2.8 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Cui, Z.; Zhou, Z.; Cao, Z. Hierarchical Frequency-Guided Knowledge Reconstruction for SAR Incremental Target Detection. Remote Sens. 2025, 17, 3214. https://doi.org/10.3390/rs17183214
Tian Y, Cui Z, Zhou Z, Cao Z. Hierarchical Frequency-Guided Knowledge Reconstruction for SAR Incremental Target Detection. Remote Sensing. 2025; 17(18):3214. https://doi.org/10.3390/rs17183214
Chicago/Turabian StyleTian, Yu, Zongyong Cui, Zheng Zhou, and Zongjie Cao. 2025. "Hierarchical Frequency-Guided Knowledge Reconstruction for SAR Incremental Target Detection" Remote Sensing 17, no. 18: 3214. https://doi.org/10.3390/rs17183214
APA StyleTian, Y., Cui, Z., Zhou, Z., & Cao, Z. (2025). Hierarchical Frequency-Guided Knowledge Reconstruction for SAR Incremental Target Detection. Remote Sensing, 17(18), 3214. https://doi.org/10.3390/rs17183214





