ESA-MDN: An Ensemble Self-Attention Enhanced Mixture Density Framework for UAV Multispectral Water Quality Parameter Retrieval
Highlights
- An ESA-MDN model is proposed to achieve high-precision modeling of the probability distribution of water quality parameters.
- Data augmentation is accomplished by leveraging the relationship between “multi-point sampling mean and multi-pixel reflectance”, thereby resolving the issue of insufficient sample size.
- ESA-MDN effectively extracts water quality parameters from multispectral data, enabling the generation of spatiotemporal maps critical for identifying pollution sources and guiding emergency responses.
- Data augmentation can effectively increase the sample size, thereby providing more possibilities for improving model accuracy.
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. UAV Imagery Acquisition and Preprocessing
2.3. Water Quality Data Collection and Preprocessing
2.4. Correlation Analysis Between Water Quality Parameters and Spectral Reflectance Values
2.5. Ensemble Self-Attention Enhanced Mixture Density Networks (ESA-MDN) Learning Model
2.6. Model Accuracy Evaluation
3. Results
3.1. Band Combinations and Water Quality Parameters Selection
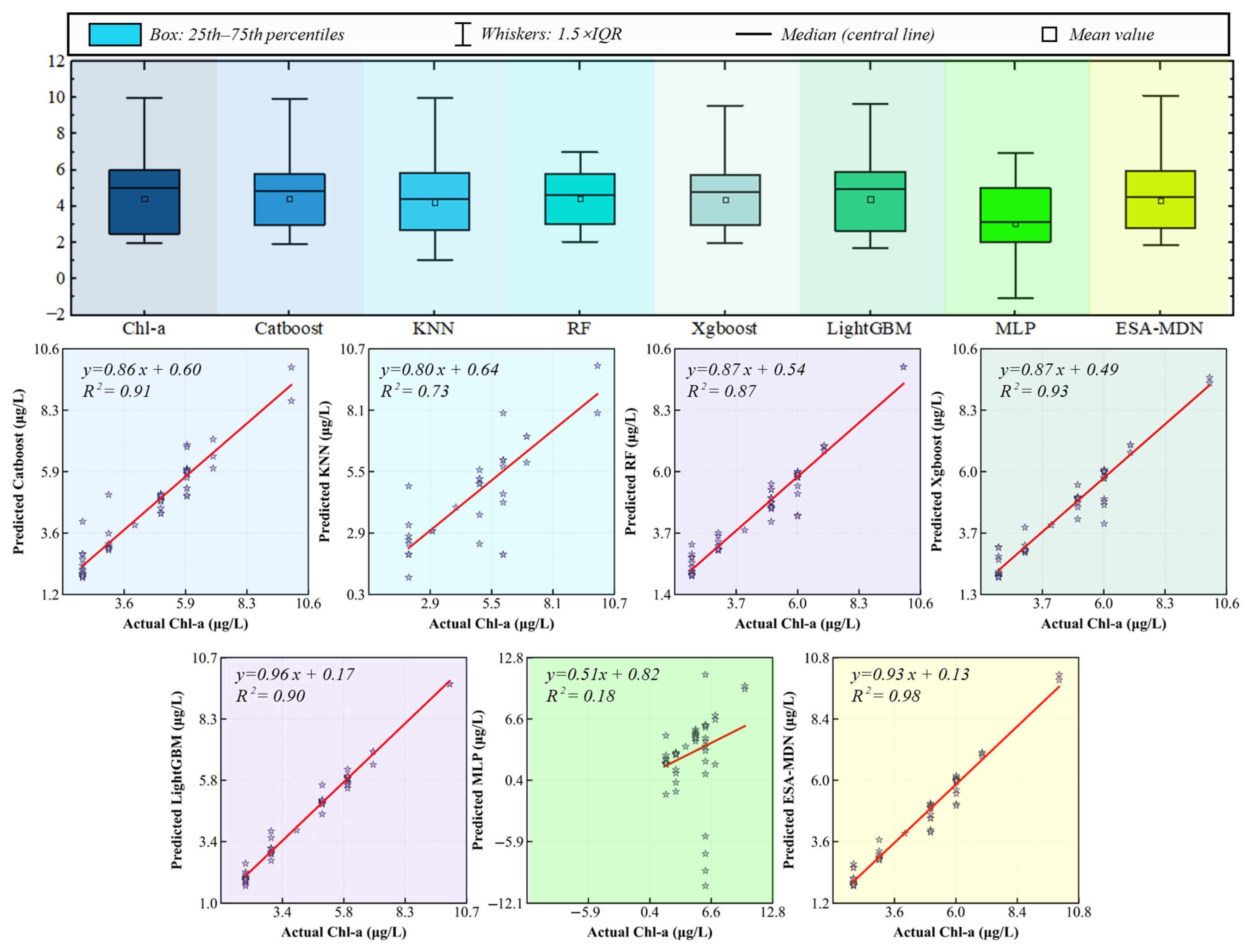
3.2. Chl-a Model Performance Analysis
3.3. TSS Model Performance Analysis
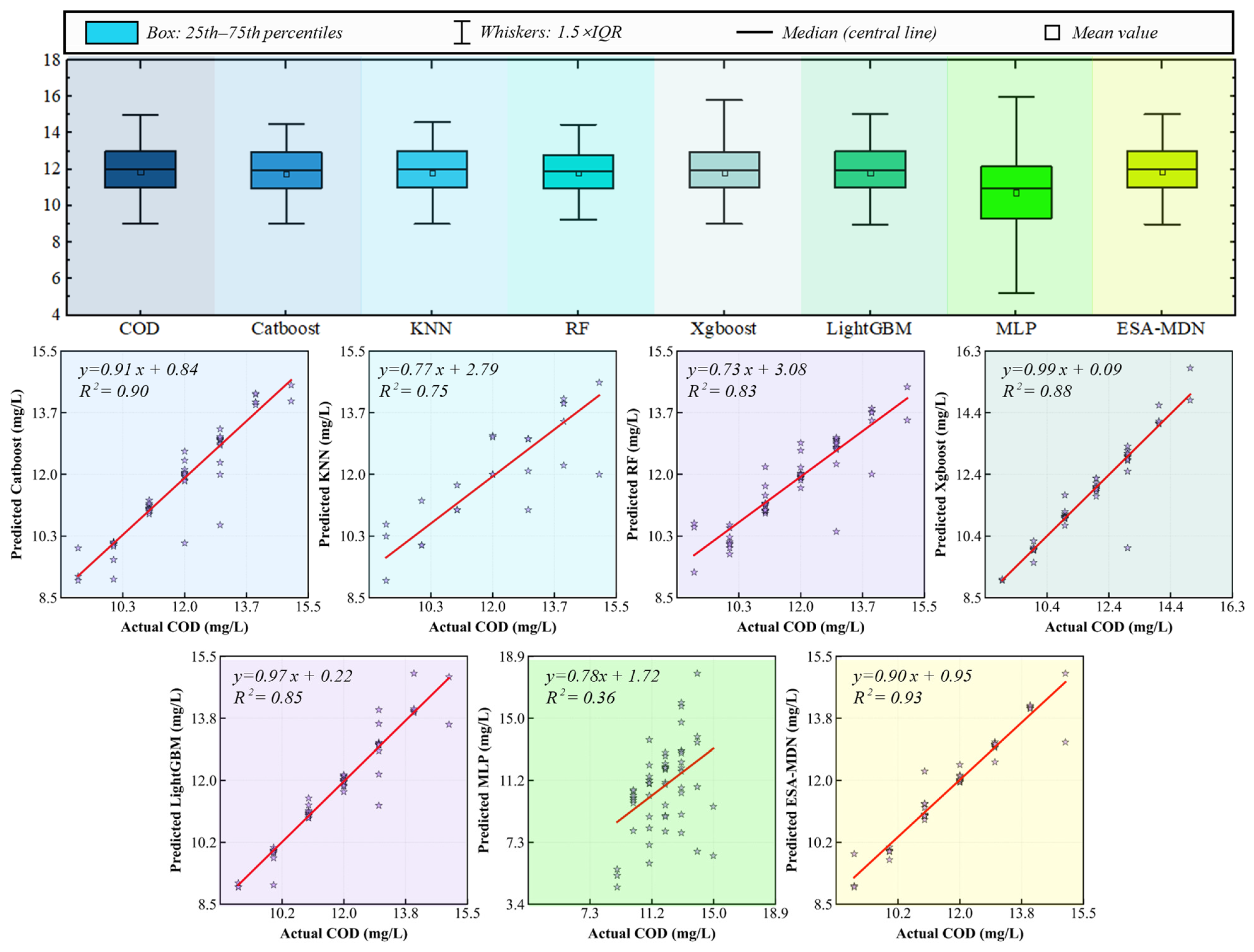
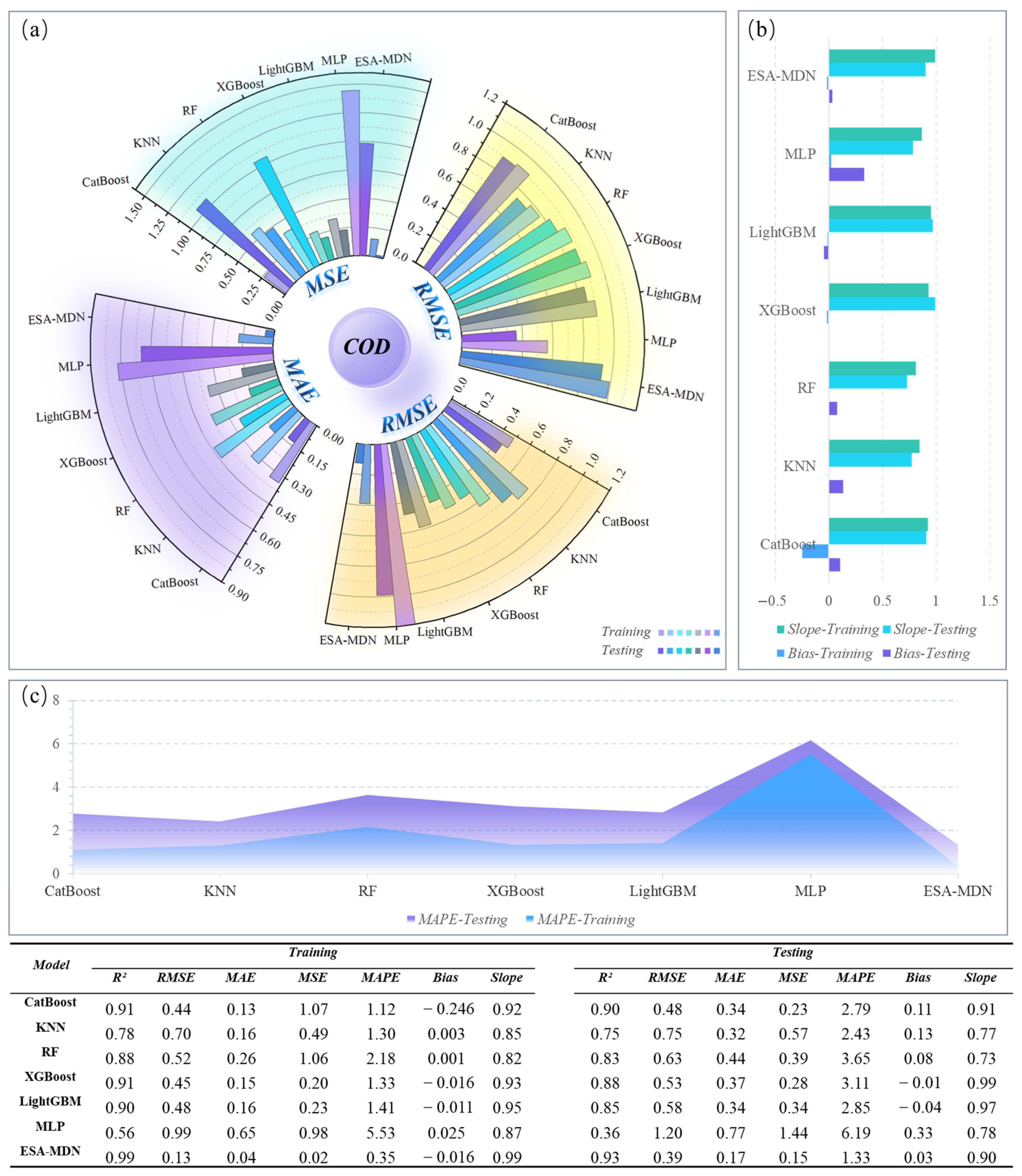
3.4. COD Model Performance Analysis
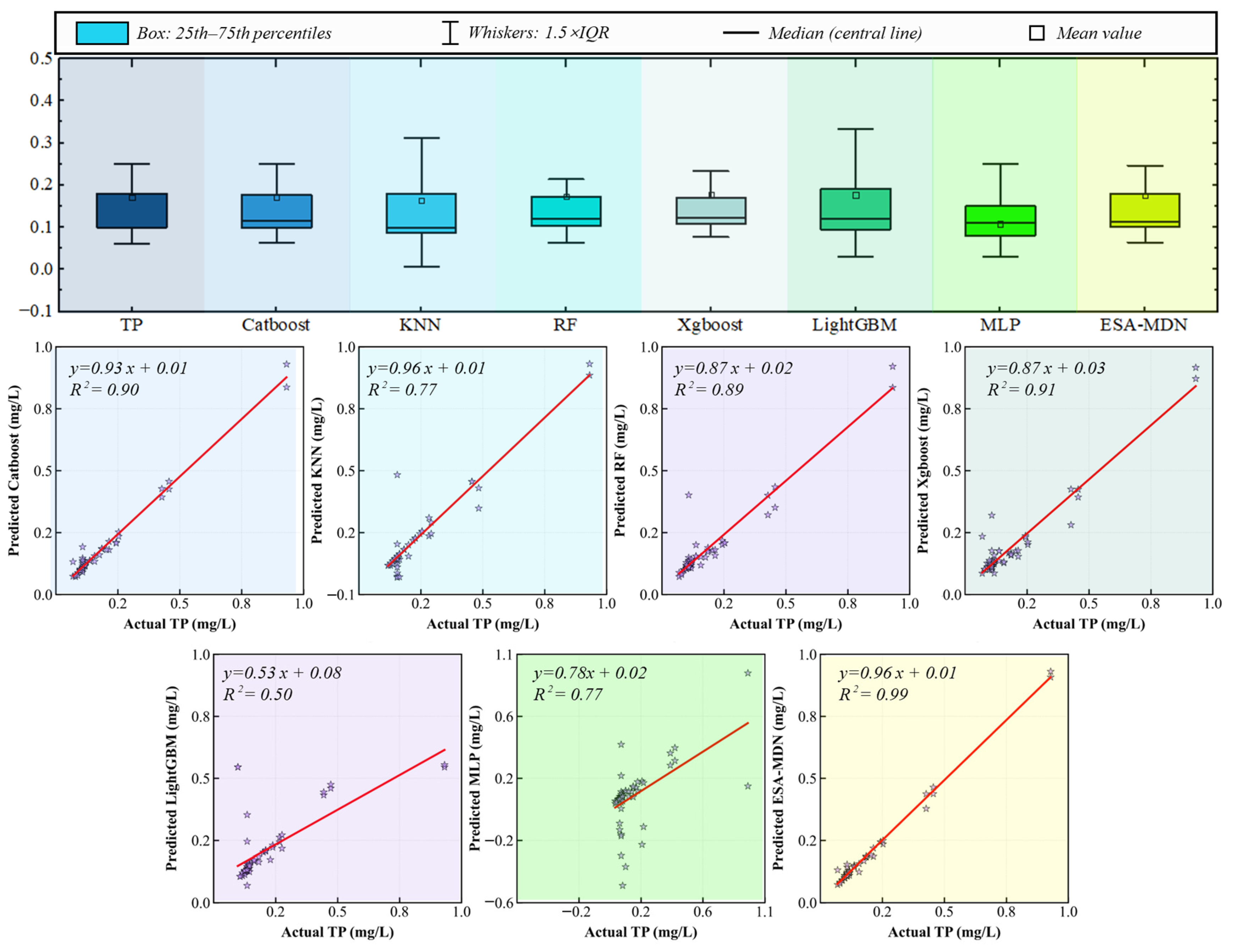
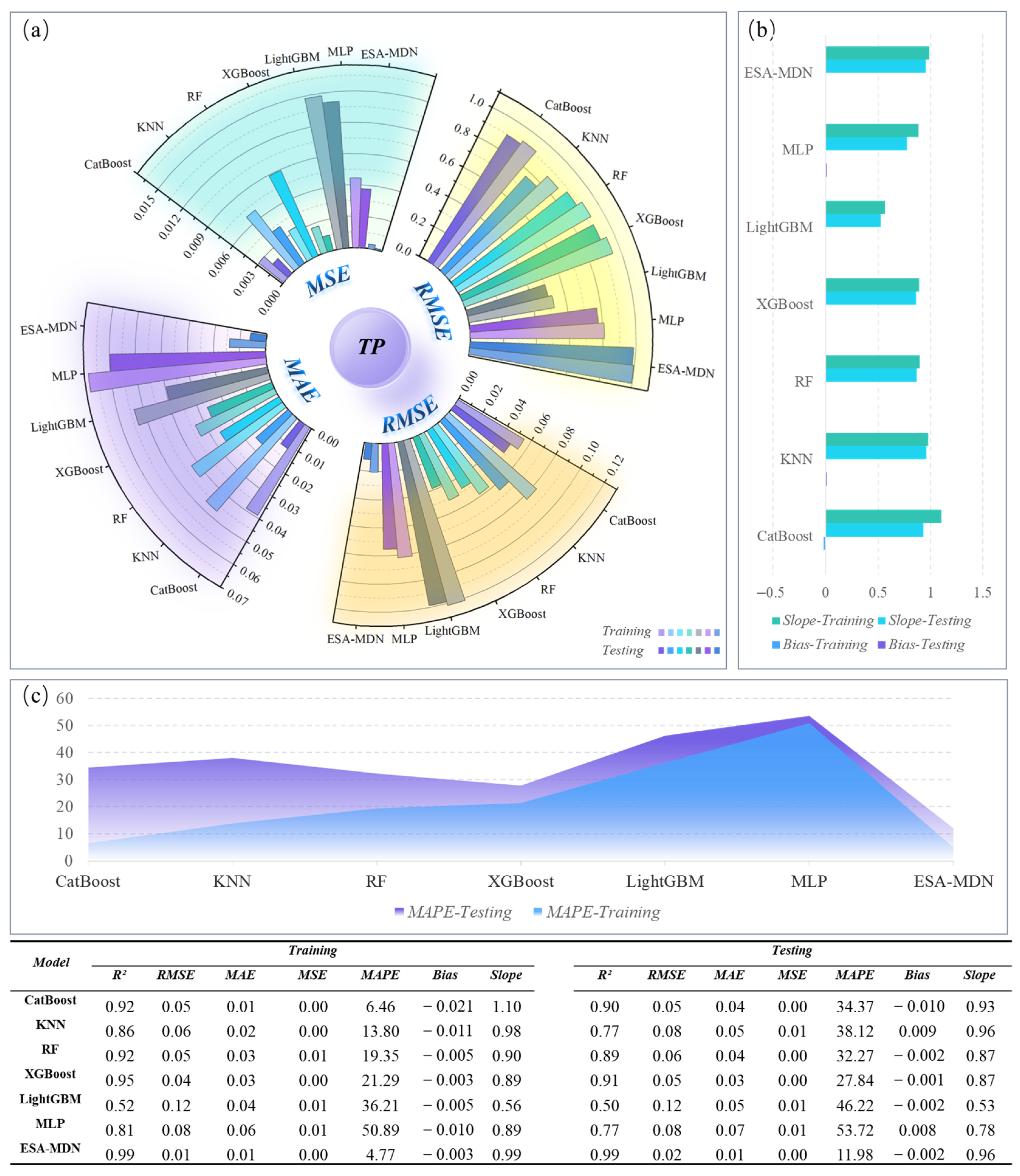
3.5. TP Model Performance Analysis
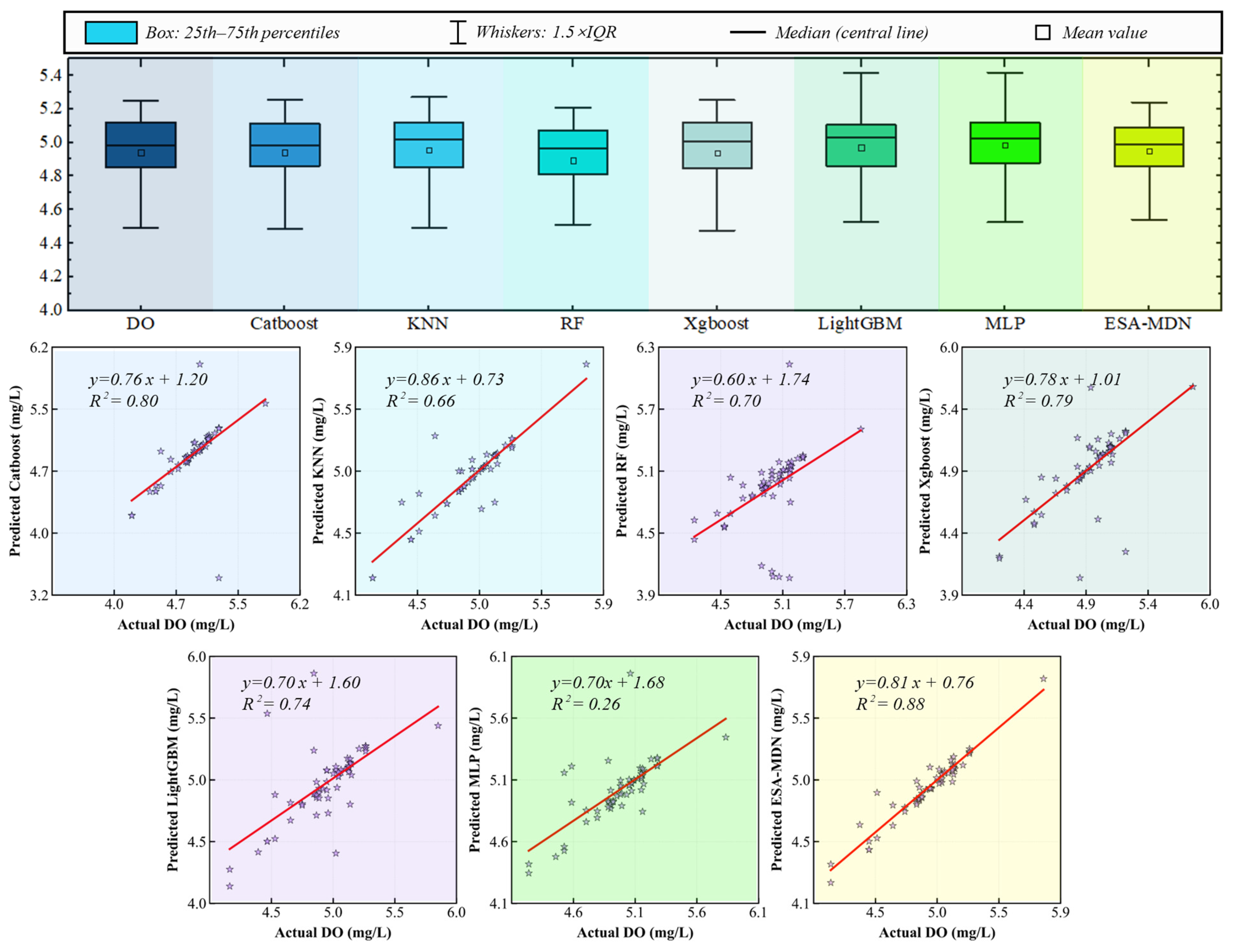
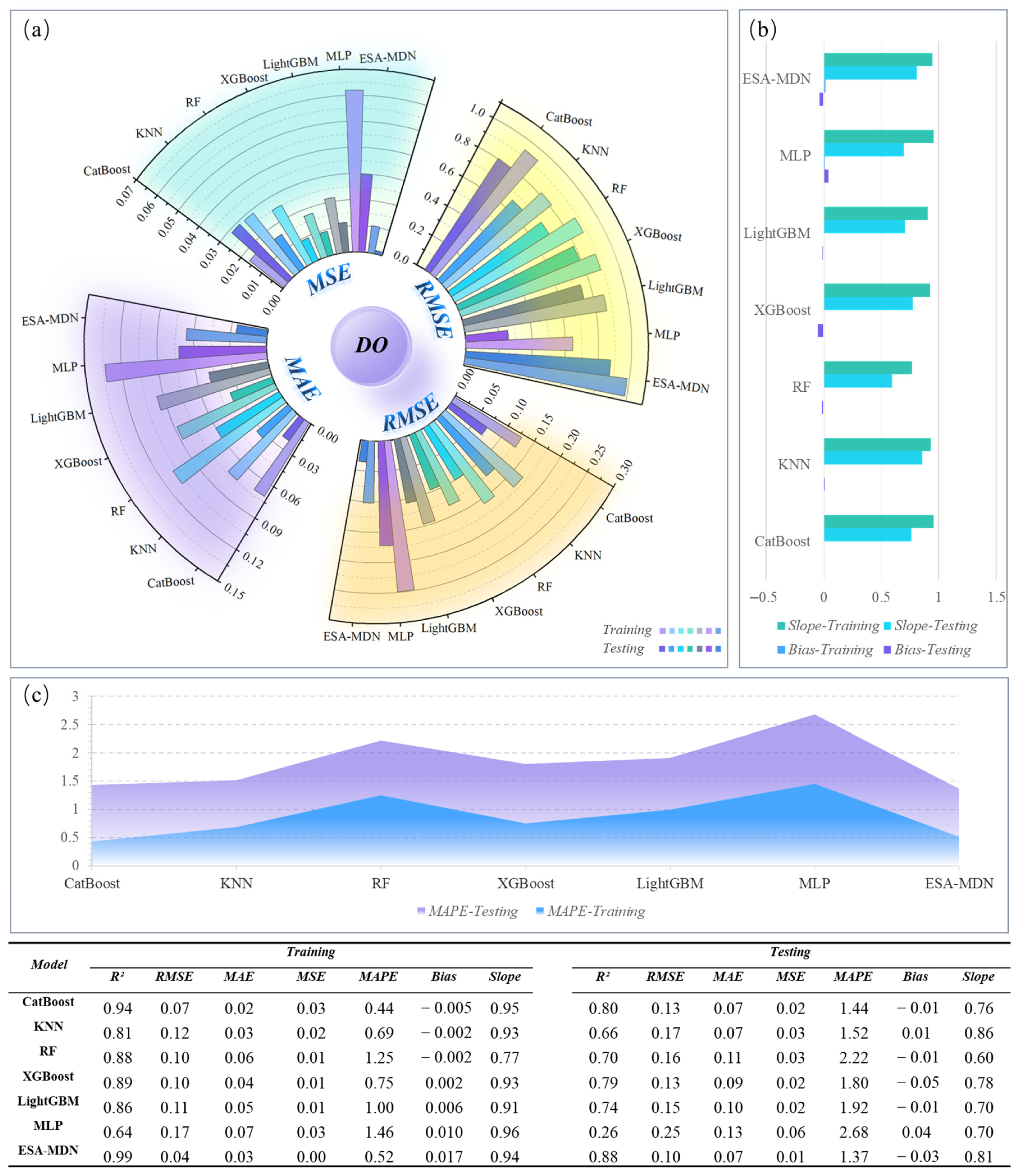
3.6. DO Model Performance Analysis
3.7. Analysis of Spatial Distribution Maps of Water Quality Parameters
4. Discussion
4.1. Potential and Limitations of UAV Multispectral Imagery for Water Quality Inversion
4.2. Advantages and Limitations of Water Quality Data Augmentation Strategies
4.3. Applicability and Limitations of the Model in Water Quality Inversion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Hermes, A.L.; Logan, M.N.; Poulin, B.A.; McKenna, A.M.; Dawson, T.E.; Borch, T.; Hinckley, E.-L.S. Agricultural Sulfur Applications Alter the Quantity and Composition of Dissolved Organic Matter from Field-to-Watershed Scales. Environ. Sci. Technol. 2023, 57, 10019–10029. [Google Scholar] [CrossRef] [PubMed]
- Stets, E.G.; Sprague, L.A.; Oelsner, G.P.; Johnson, H.M.; Murphy, J.C.; Ryberg, K.; Vecchia, A.V.; Zuellig, R.E.; Falcone, J.A.; Riskin, M.L. Landscape Drivers of Dynamic Change in Water Quality of U.S. Rivers. Environ. Sci. Technol. 2020, 54, 4336–4343. [Google Scholar] [CrossRef] [PubMed]
- Roy, S.; Bose, A.; Basak, D.; Chowdhury, I.R. Towards Sustainable Society: The Sustainable Livelihood Security (SLS) Approach for Prioritizing Development and Understanding Sustainability: An Insight from West Bengal, India. Environ. Dev. Sustain. 2023, 26, 20095–20126. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, C.; Carrion, D.; Akbar, A.; Wang, H. Spectro-Environmental Factors Integrated Ensemble Learning for Urban River Network Water Quality Remote Sensing. Water Res. 2024, 267, 122544. [Google Scholar] [CrossRef] [PubMed]
- Rahat, S.H.; Steissberg, T.; Chang, W.; Chen, X.; Mandavya, G.; Tracy, J.; Wasti, A.; Atreya, G.; Saki, S.; Bhuiyan, M.A.E. Remote Sensing-Enabled Machine Learning for River Water Quality Modeling under Multidimensional Uncertainty. Sci. Total Environ. 2023, 898, 165504. [Google Scholar] [CrossRef]
- Wang, H.; Liu, C.; Li, L.; Kong, Y.; Akbar, A.; Zhou, X. High-Precision Inversion of Urban River Water Quality via Integration of Riparian Spatial Structures and River Spectral Signatures. Water Res. 2025, 278, 123378. [Google Scholar] [CrossRef]
- Lu, Q.; Si, W.; Wei, L.; Li, Z.; Xia, Z.; Ye, S.; Xia, Y. Retrieval of Water Quality from UAV-Borne Hyperspectral Imagery: A Comparative Study of Machine Learning Algorithms. Remote Sens. 2021, 13, 3928. [Google Scholar] [CrossRef]
- Jiang, Q.; Xu, L.; Sun, S.; Wang, M.; Xiao, H. Retrieval Model for Total Nitrogen Concentration Based on UAV Hyper Spectral Remote Sensing Data and Machine Learning Algorithms—A Case Study in the Miyun Reservoir, China. Ecol. Indic. 2021, 124, 107356. [Google Scholar]
- Giles, A.B.; Correa, R.E.; Santos, I.R.; Kelaher, B. Using Multispectral Drones to Predict Water Quality in a Subtropical Estuary. Environ. Technol. 2024, 45, 1300–1312. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L. Novel Spectra-Derived Features for Empirical Retrieval of Water Quality Parameters: Demonstrations for OLI, MSI, and OLCI Sensors. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10285–10300. [Google Scholar] [CrossRef]
- Harringmeyer, J.P.; Ghosh, N.; Weiser, M.W.; Thompson, D.R.; Simard, M.; Lohrenz, S.E.; Fichot, C.G. A Hyperspectral View of the Nearshore Mississippi River Delta: Characterizing Suspended Particles in Coastal Wetlands Using Imaging Spectroscopy. Remote Sens. Environ. 2024, 301, 113943. [Google Scholar] [CrossRef]
- Li, J.; Wang, G.; Sun, S.; Ma, J.; Guo, L.; Song, C.; Lin, S. Mapping and Reconstruct Suspended Sediment Dynamics (1986–2021) in the Source Region of the Yangtze River, Qinghai-Tibet Plateau Using Google Earth Engine. Remote Sens. Environ. 2025, 317, 114533. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, D.; Li, L.; Ning, R.; Yu, S.; Gao, N. Application of Remote Sensing Technology in Water Quality Monitoring: From Traditional Approaches to Artificial Intelligence. Water Res. 2024, 267, 122546. [Google Scholar] [CrossRef] [PubMed]
- Binding, C.E.; Pizzolato, L.; Zeng, C. EOLakeWatch; Delivering a Comprehensive Suite of Remote Sensing Algal Bloom Indices for Enhanced Monitoring of Canadian Eutrophic Lakes. Ecol. Indic. 2021, 121, 106999. [Google Scholar] [CrossRef]
- Ji, C.; Zhang, Y.; Nejstgaard, J.C.; Ogashawara, I. Assessment of the Sediment Load in the Pearl River Estuary Based on Land Use and Land Cover Changes. CATENA 2025, 250, 108726. [Google Scholar] [CrossRef]
- Moon, J.; Jung, S.; Suh, S.; Pyo, J. Development of Deep Learning Quantization Framework for Remote Sensing Edge Device to Estimate Inland Water Quality in South Korea. Water Res. 2025, 283, 123760. [Google Scholar] [CrossRef]
- Sagan, V.; Peterson, K.T.; Maimaitijiang, M.; Sidike, P.; Sloan, J.; Greeling, B.A.; Maalouf, S.; Adams, C. Monitoring Inland Water Quality Using Remote Sensing: Potential and Limitations of Spectral Indices, Bio-Optical Simulations, Machine Learning, and Cloud Computing. Earth-Sci. Rev. 2020, 205, 103187. [Google Scholar] [CrossRef]
- Tesfaye, A. Remote Sensing-Based Water Quality Parameters Retrieval Methods: A Review. East Afr. J. Environ. Nat. Resour. 2024, 7, 80–97. [Google Scholar] [CrossRef]
- Cai, X.; Li, Y.; Lei, S.; Zeng, S.; Zhao, Z.; Lyu, H.; Dong, X.; Li, J.; Wang, H.; Xu, J. A Hybrid Remote Sensing Approach for Estimating Chemical Oxygen Demand Concentration in Optically Complex Waters: A Case Study in Inland Lake Waters in Eastern China. Sci. Total Environ. 2023, 856, 158869. [Google Scholar] [CrossRef]
- Chen, S.; Han, L.; Chen, X.; Li, D.; Sun, L.; Li, Y. Estimating Wide Range Total Suspended Solids Concentrations from MODIS 250-m Imageries: An Improved Method. ISPRS J. Photogramm. Remote Sens. 2015, 99, 58–69. [Google Scholar] [CrossRef]
- Ngoc, D.D.; Loisel, H.; Jamet, C.; Vantrepotte, V.; Duforêt-Gaurier, L.; Minh, C.D.; Mangin, A. Coastal and Inland Water Pixels Extraction Algorithm (WiPE) from Spectral Shape Analysis and HSV Transformation Applied to Landsat 8 OLI and Sentinel-2 MSI. Remote Sens. Environ. 2019, 223, 208–228. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Li, X.; Yang, Y.; Ishizaka, J.; Li, X. Global Estimation of Phytoplankton Pigment Concentrations from Satellite Data Using a Deep-Learning-Based Model. Remote Sens. Environ. 2023, 294, 113628. [Google Scholar] [CrossRef]
- Zhang, D.; Shi, K.; Wang, W.; Wang, X.; Zhang, Y.; Qin, B.; Zhu, M.; Dong, B.; Zhang, Y. An Optical Mechanism-Based Deep Learning Approach for Deriving Water Trophic State of China’s Lakes from Landsat Images. Water Res. 2024, 252, 121181. [Google Scholar] [CrossRef]
- Guo, H.; Huang, J.J.; Zhu, X.; Tian, S.; Wang, B. Spatiotemporal Variation Reconstruction of Total Phosphorus in the Great Lakes since 2002 Using Remote Sensing and Deep Neural Network. Water Res. 2024, 255, 121493. [Google Scholar] [CrossRef] [PubMed]
- Xiong, J.; Lin, C.; Cao, Z.; Hu, M.; Xue, K.; Chen, X.; Ma, R. Development of Remote Sensing Algorithm for Total Phosphorus Concentration in Eutrophic Lakes: Conventional or Machine Learning? Water Res. 2022, 215, 118213. [Google Scholar] [CrossRef] [PubMed]
- Gan, M.; Lai, X.; Guo, Y.; Chen, Y.; Pan, S.; Zhang, Y. Floodplain Lake Water Level Prediction with Strong River-Lake Interaction Using the Ensemble Learning LightGBM. Water Resour. Manag. 2024, 38, 5305–5321. [Google Scholar] [CrossRef]
- Mienye, I.D.; Sun, Y. A Survey of Ensemble Learning: Concepts, Algorithms, Applications, and Prospects. IEEE Access 2022, 10, 99129–99149. [Google Scholar] [CrossRef]
- Ehteram, M.; Ahmed, A.N.; Sherif, M.; El-Shafie, A. An Advanced Deep Learning Model for Predicting Water Quality Index. Ecol. Indic. 2024, 160, 111806. [Google Scholar] [CrossRef]
- Tripathy, K.P.; Mishra, A.K. Deep Learning in Hydrology and Water Resources Disciplines: Concepts, Methods, Applications, and Research Directions. J. Hydrol. 2024, 628, 130458. [Google Scholar]
- GB 3838-2002; Environmental Quality Standards for Surface Water. Ministry of Ecology and Environment of the People’s Republic of China: Beijing, China, 2002.
- Mohseni, U.; Pande, C.B.; Pal, S.C.; Alshehri, F. Prediction of Weighted Arithmetic Water Quality Index for Urban Water Quality Using Ensemble Machine Learning Model. Chemosphere 2024, 352, 141393. [Google Scholar] [CrossRef]
- Satish, N.; Anmala, J.; Rajitha, K.; Varma, M.R. A Stacking ANN Ensemble Model of ML Models for Stream Water Quality Prediction of Godavari River Basin, India. Ecol. Inform. 2024, 80, 102500. [Google Scholar] [CrossRef]







| Basic Information on Multispectral Data | |||
|---|---|---|---|
| Collection Time | 8 October 2024 10:00–16:00 | Spatial Resolution | 10 cm |
| UAV Flight Height | 110 m | UAV Flight Frequency | 11 |
| On-site Wind Force | 2–3 | Weather Conditions | Clear and cloudless weather |
| Chl-a | TSS | COD | TP | DO | |
|---|---|---|---|---|---|
| Max | 10 | 9 | 15 | 0.95 | 5.81 |
| Min | 2 | 6 | 9 | 0.06 | 4.2 |
| Mean | 4.33 | 7.73 | 11.87 | 0.17 | 4.95 |
| SD | 2.01 | 1.01 | 1.53 | 0.17 | 0.29 |
| Type | Band Combination Formulas | ||
|---|---|---|---|
| Dual-band Combinations | B1 + B2 | (B1 + B2)/B2 | e(B1 + B2) × B1 |
| B1 − B2 | B1/(B1 − B2) | e(B1 + B2) × B2 | |
| B1 × B2 | B2/(B1 − B2) | e(B1 − B2)/B1 | |
| B1/B2 | B1/(B1 + B2) | e(B1 − B2)/B2 | |
| (B1 − B2)/(B1 + B2) | B2/(B1 + B2) | e(B1 + B2)/B1 | |
| ((B1)2 − (B2)2)/((B1)2 + (B2)2) | eB1 + B2 | e(B1 + B2)/B2 | |
| (B1 − B2) × B1 | eB1 − B2 | e B1/(B1 − B2) | |
| (B1 − B2) × B2 | eB1 × B2 | e B2/(B1 − B2) | |
| (B1 + B2) × B1 | eB1/B2 | e B1/(B1 + B2) | |
| (B1 + B2) × B2 | e(B1 − B2)/(B1 + B2) | e B2/(B1 + B2) | |
| (B1 − B2)/B1 | Log10(1/B1) | ||
| (B1 − B2)/B2 | e(B1 − B2) × B1 | Log10(1/B1) − Log10(1/B2) | |
| (B1 + B2)/B1 | e(B1 − B2) × B2 | Log10(1/B1) + Log10(1/B2) | |
| Three-band combinations | B1 + B2 + B3 | (B1 − B2) × B3 | e B1 × B2 × B3 |
| B1 + B2 − B3 | B1/(B2 + B3) | e (B1 − B2)/B3 | |
| (B1 − B2 + B3)/(B1 + B2 + B3) | B1/(B2 − B3) | e (B1 + B2) × B3 | |
| (B1 − B2 + B3)/(B1 + B2 − B3) | e B1 + B2 + B3 | e (B1 − B2) × B3 | |
| (B1 × B2)/B3 | e B1 + B2 − B3 | e B1/(B2 + B3) | |
| (B1 + B2)/B3 | e (B1 − B2 + B3)/(B1 + B2 + B3) | e B1/(B2 − B3) | |
| B1 × B2 × B3 | e (B1 − B2 + B3)/(B1 + B2 − B3) | Log10(1/B1) + Log10(1/B2) + Log10(1/B3) | |
| (B1 − B2)/B3 | e (B1 × B2)/B3 | Log10(1/B1) − Log10(1/B2) − Log10(1/B3) | |
| (B1 + B2) × B3 | e (B1 + B2)/B3 | Log10(1/B1) − Log10(1/B2) + Log10(1/B3) | |
| Feature Bands | Type | Chl-a | TSS | COD | TP | DO |
|---|---|---|---|---|---|---|
| X1 | Band operation formula | Log10(1/B2) − Log10(1/B4) + Log10(1/B2) | B4 − B2 | B5/(B1 − B3) | B2/(B4 − B3) | (B1 + B4)/B5 |
| Correlation coefficient | 0.38 | 0.42 | 0.31 | 0.70 | 0.31 | |
| p-value | 5.17 × 10−7 | 1.38 × 10−12 | 2.84 × 10−7 | 2.30 × 10−31 | 2.48 × 10−6 | |
| X2 | Band operation formula | Log10(1/B2) − Log10(1/B4) + Log10(1/B3) | (B1 − B2 + B4)/(B1 + B2 + B4) | B2/(B1 − B3) | B1/(B4 − B3) | (B4 − B5 + B1)/(B4 + B5 − B2) |
| Correlation coefficient | 0.37 | 0.38 | 0.31 | 0.70 | 0.31 | |
| p-value | 9.48 × 10−10 | 2.68 × 10−9 | 6.66 × 10−7 | 2.45 × 10−29 | 7.39 × 10−3 | |
| X3 | Band operation formula | B1/(B4 − B3) | (B1 + B4)/B2 | B4/(B1 − B3) | B5/(B4 − B3) | (B2 − B5 + B4)/(B2 + B5 − B4) |
| Correlation coefficient | 0.36 | 0.37 | 0.30 | 0.67 | 0.31 | |
| p-value | 1.34 × 10−9 | 1.18 × 10−10 | 8.05 × 10−7 | 4.57 × 10−27 | 2.86 × 10−3 | |
| X4 | Band operation formula | Log10(1/B2) − Log10(1/B3) + Log10(1/B2) | (B5 − B1) × B1 | B1/(B1 − B3) | B4/(B4 − B3) | (B3 − B5 + B1)/(B3 + B5 − B1) |
| Correlation coefficient | 0.35 | 0.37 | 0.29 | 0.66 | 0.31 | |
| p-value | 9.55 × 10−7 | 2.78 × 10−9 | 2.78 × 10−6 | 4.40 × 10−26 | 6.12 × 10−4 | |
| X5 | Band operation formula | B5/(B4 − B3) | (B5 − B1) × B3 | B3/(B4 − B1) | B4/(B3 − B1) | (B3 − B5 + B2)/(B3 + B5 − B2) |
| Correlation coefficient | 0.35 | 0.37 | 0.29 | 0.38 | 0.30 | |
| p-value | 5.35 × 10−11 | 2.40 × 10−9 | 4.21 × 10−6 | 2.30 × 10−11 | 2.37 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Wang, J.; Jing, Y.; Zhang, S.; Sun, D.; Li, Q. ESA-MDN: An Ensemble Self-Attention Enhanced Mixture Density Framework for UAV Multispectral Water Quality Parameter Retrieval. Remote Sens. 2025, 17, 3202. https://doi.org/10.3390/rs17183202
Yang X, Wang J, Jing Y, Zhang S, Sun D, Li Q. ESA-MDN: An Ensemble Self-Attention Enhanced Mixture Density Framework for UAV Multispectral Water Quality Parameter Retrieval. Remote Sensing. 2025; 17(18):3202. https://doi.org/10.3390/rs17183202
Chicago/Turabian StyleYang, Xiaonan, Jiansheng Wang, Yi Jing, Songjia Zhang, Dexin Sun, and Qingli Li. 2025. "ESA-MDN: An Ensemble Self-Attention Enhanced Mixture Density Framework for UAV Multispectral Water Quality Parameter Retrieval" Remote Sensing 17, no. 18: 3202. https://doi.org/10.3390/rs17183202
APA StyleYang, X., Wang, J., Jing, Y., Zhang, S., Sun, D., & Li, Q. (2025). ESA-MDN: An Ensemble Self-Attention Enhanced Mixture Density Framework for UAV Multispectral Water Quality Parameter Retrieval. Remote Sensing, 17(18), 3202. https://doi.org/10.3390/rs17183202







