A Multi-Feature Fusion Performance Evaluation Method for SAR Deception Jamming
Abstract
Highlights
- An evaluation framework considering brightness variation, edge information, and texture structure was implemented and validated across multiple large-scale deception scenarios.
- Combining three metrics, the framework achieves strong evaluation capability with higher robustness than conventional single-metric methods.
- The study addresses inconsistencies between evaluation results and expert subjective judgment caused by minor distortions.
- The study provides a practical and explainable tool for consistent evaluation of SAR deception jamming imagery.
Abstract
1. Introduction
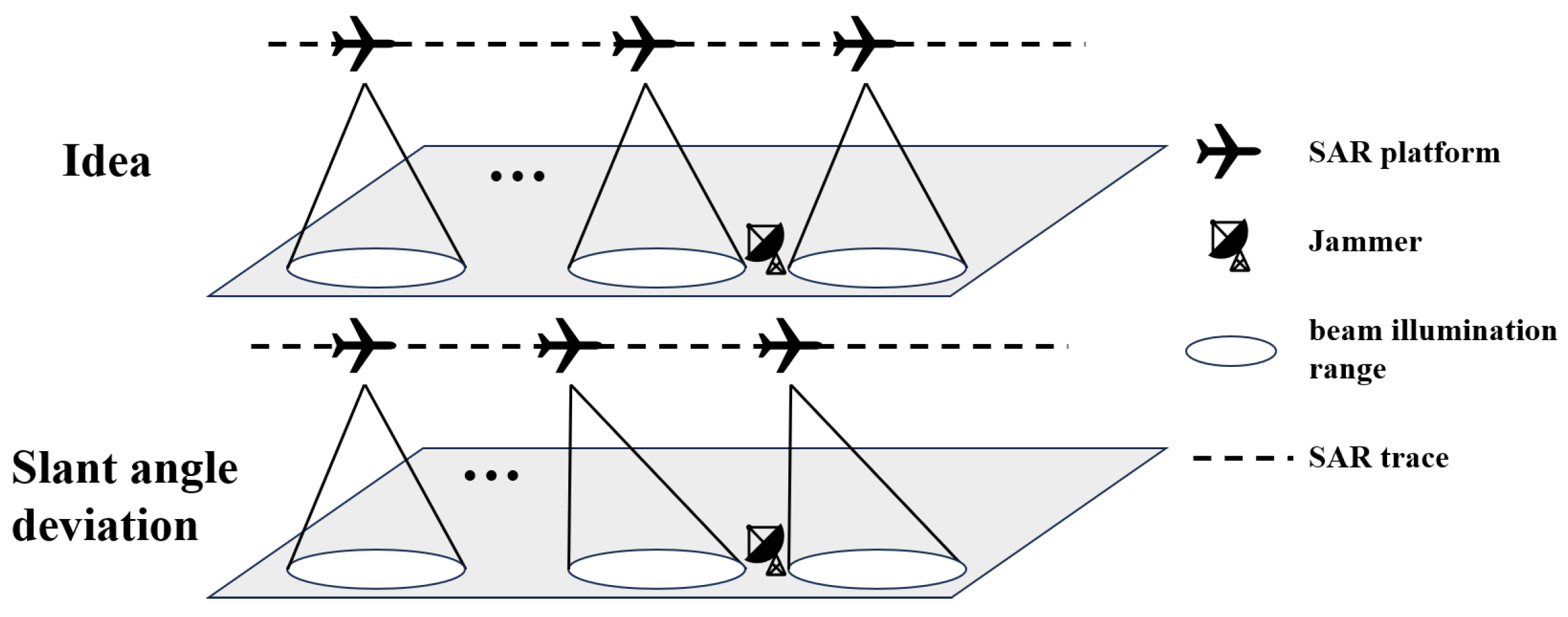
2. Analysis of Deception Jamming Error
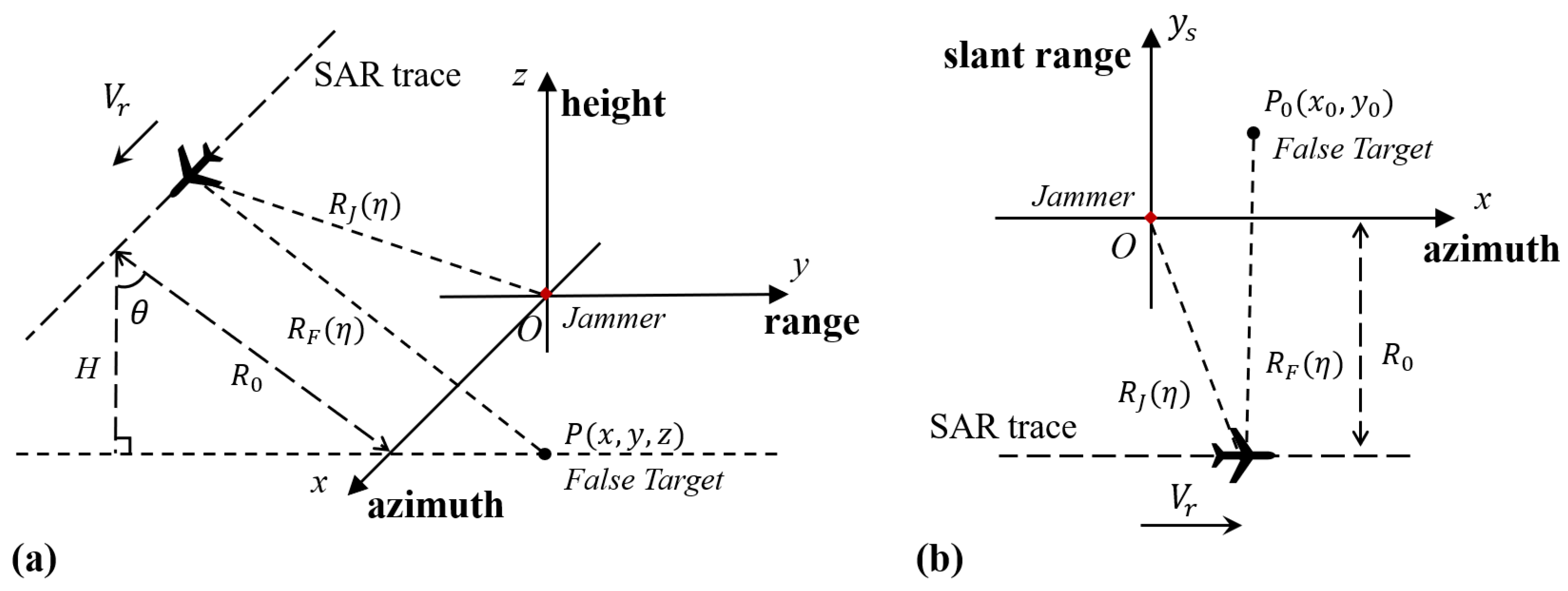
2.1. SAR Jamming Model
2.2. Defocusing
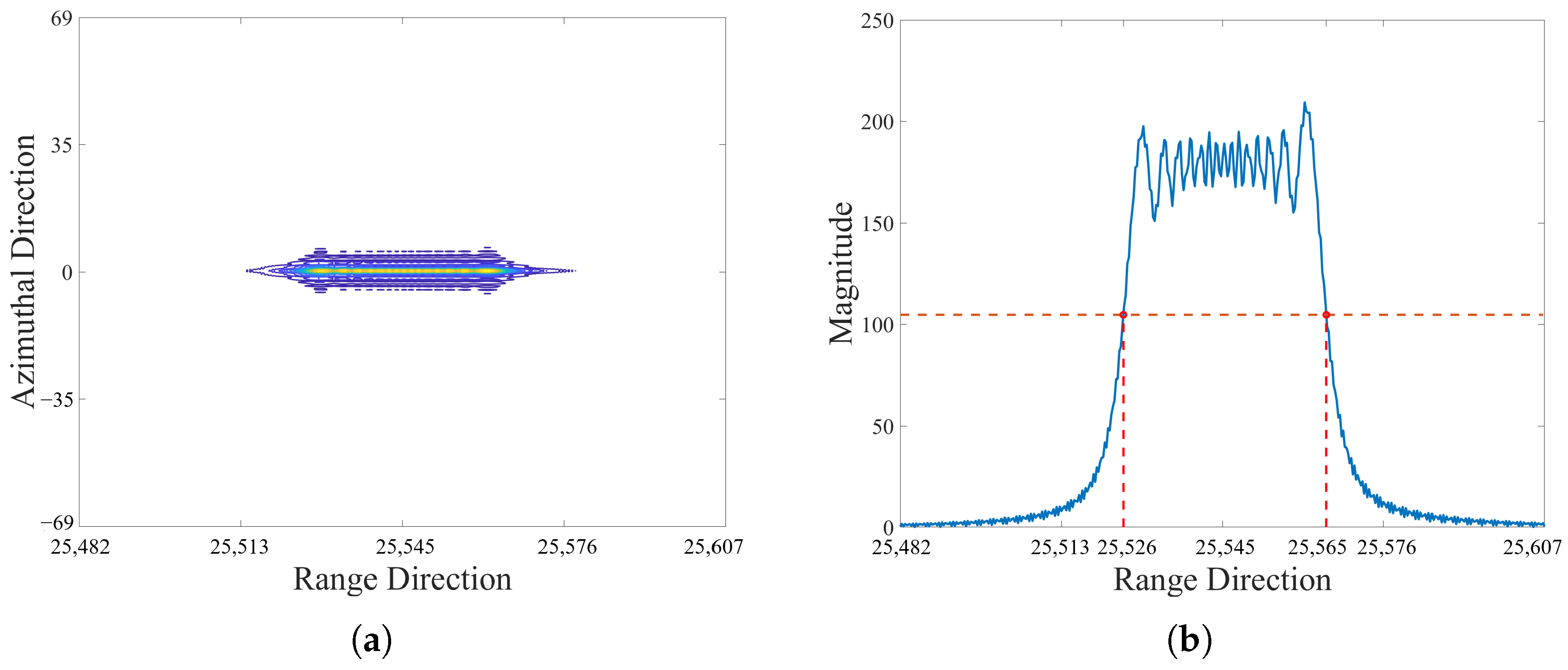
2.2.1. Range Defocusing
2.2.2. Azimuth Defocusing
2.3. Amplitude Variation
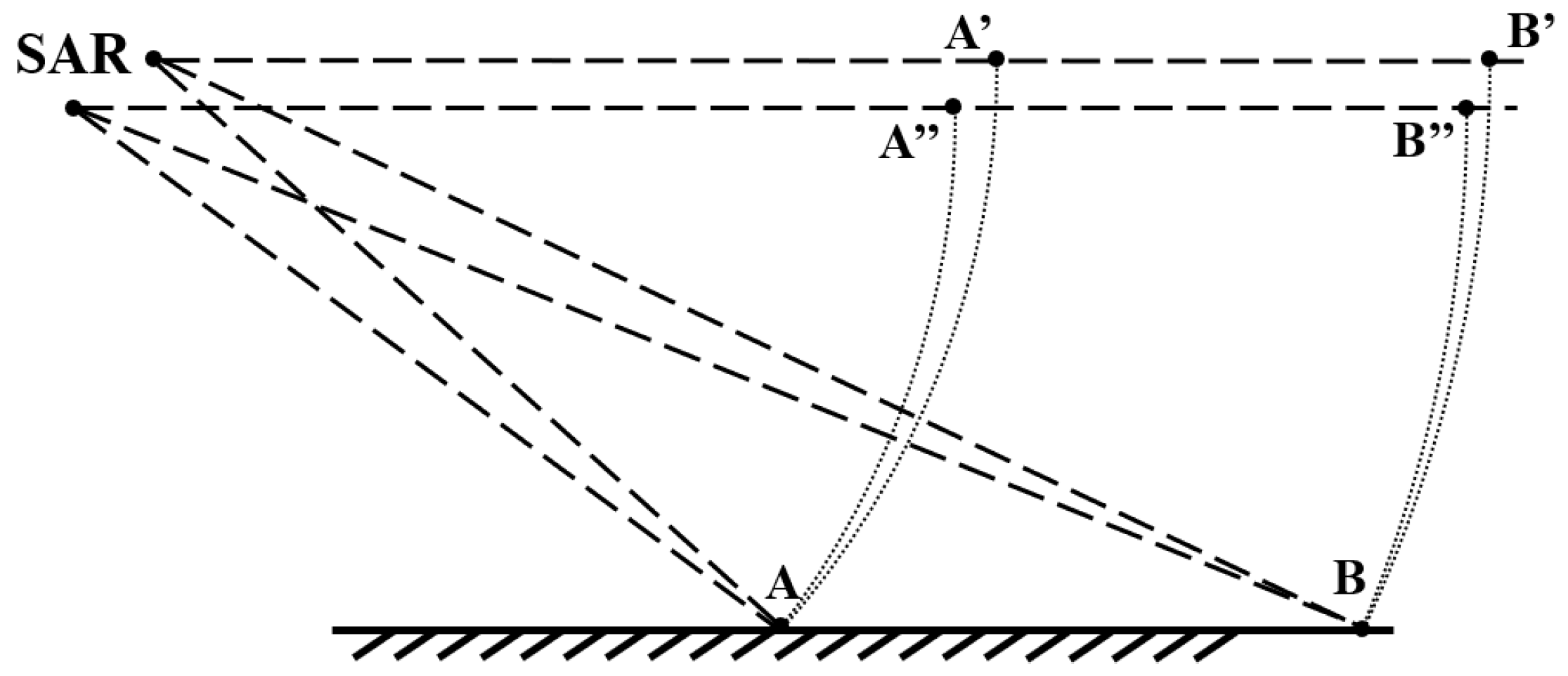
2.4. Distortion
3. Multi-Feature Fusion Framework
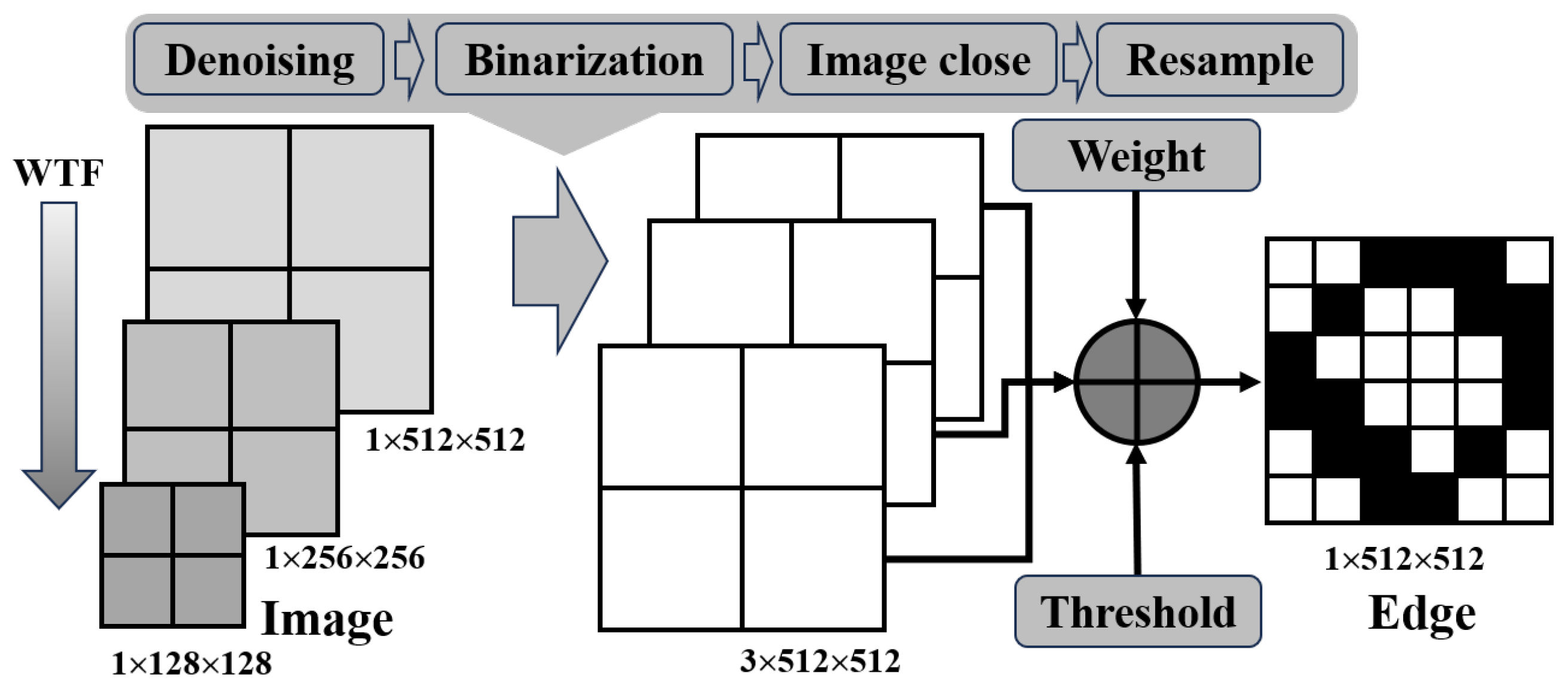
3.1. Contour Similarity Basic Framework
3.2. Modified ENL Difference
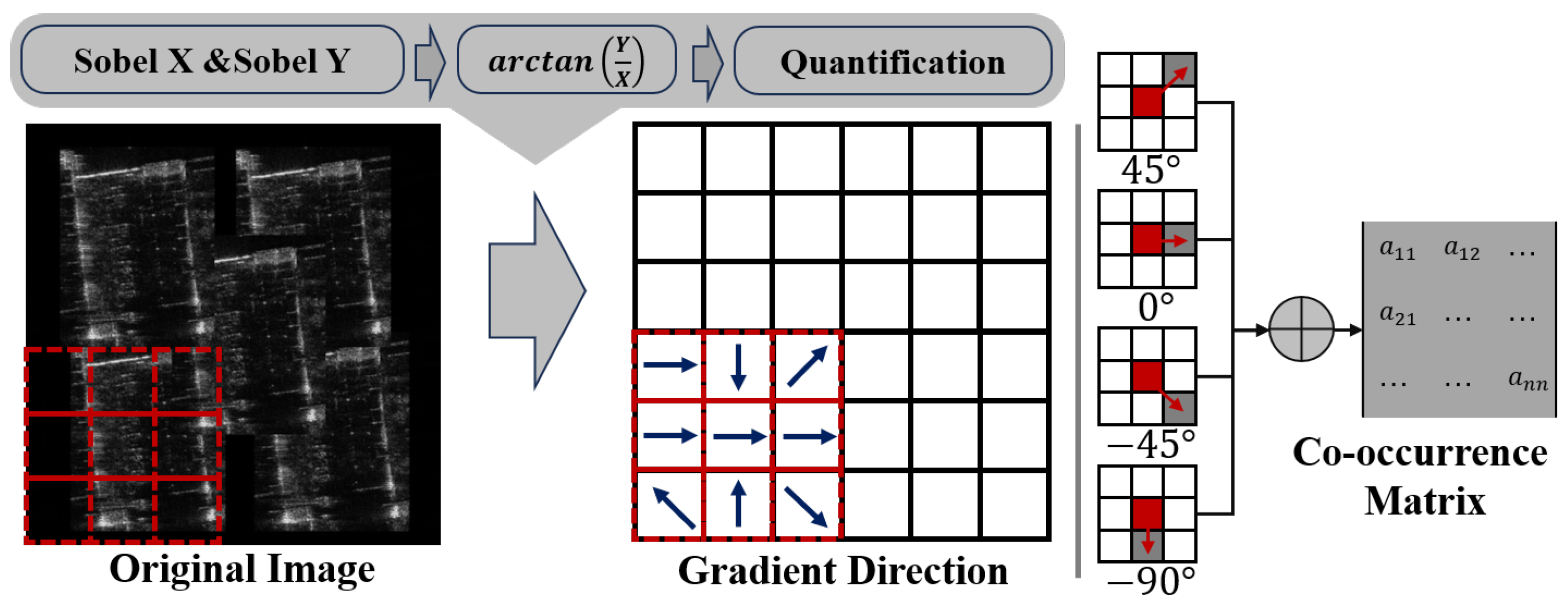
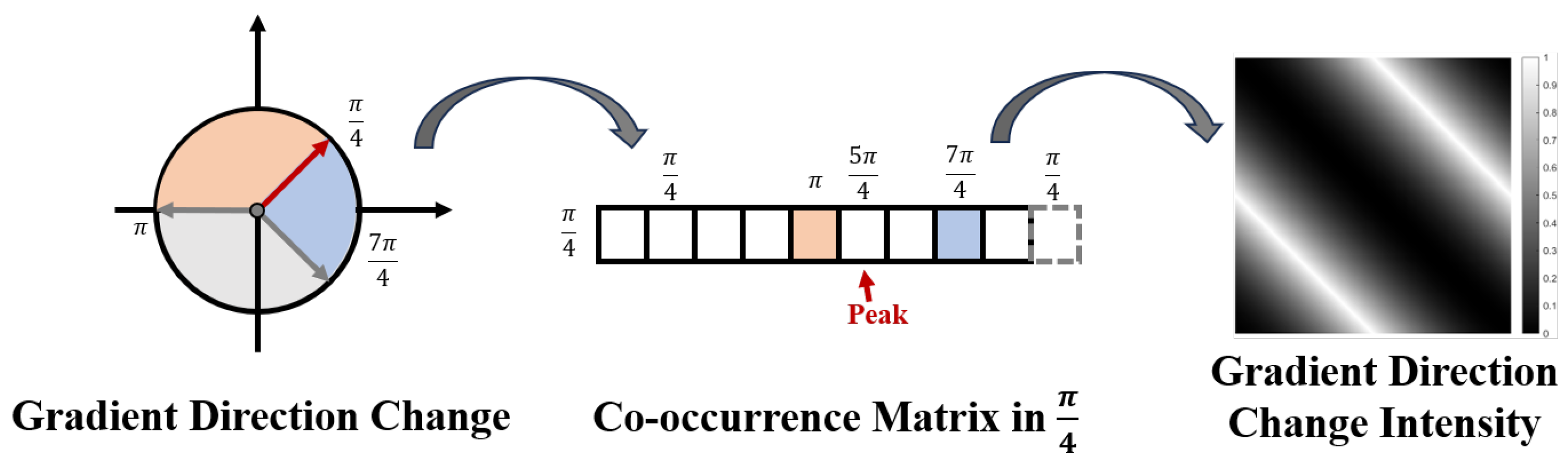
3.3. Gradient Co-Occurrence Matrix
3.4. Feature Fusion
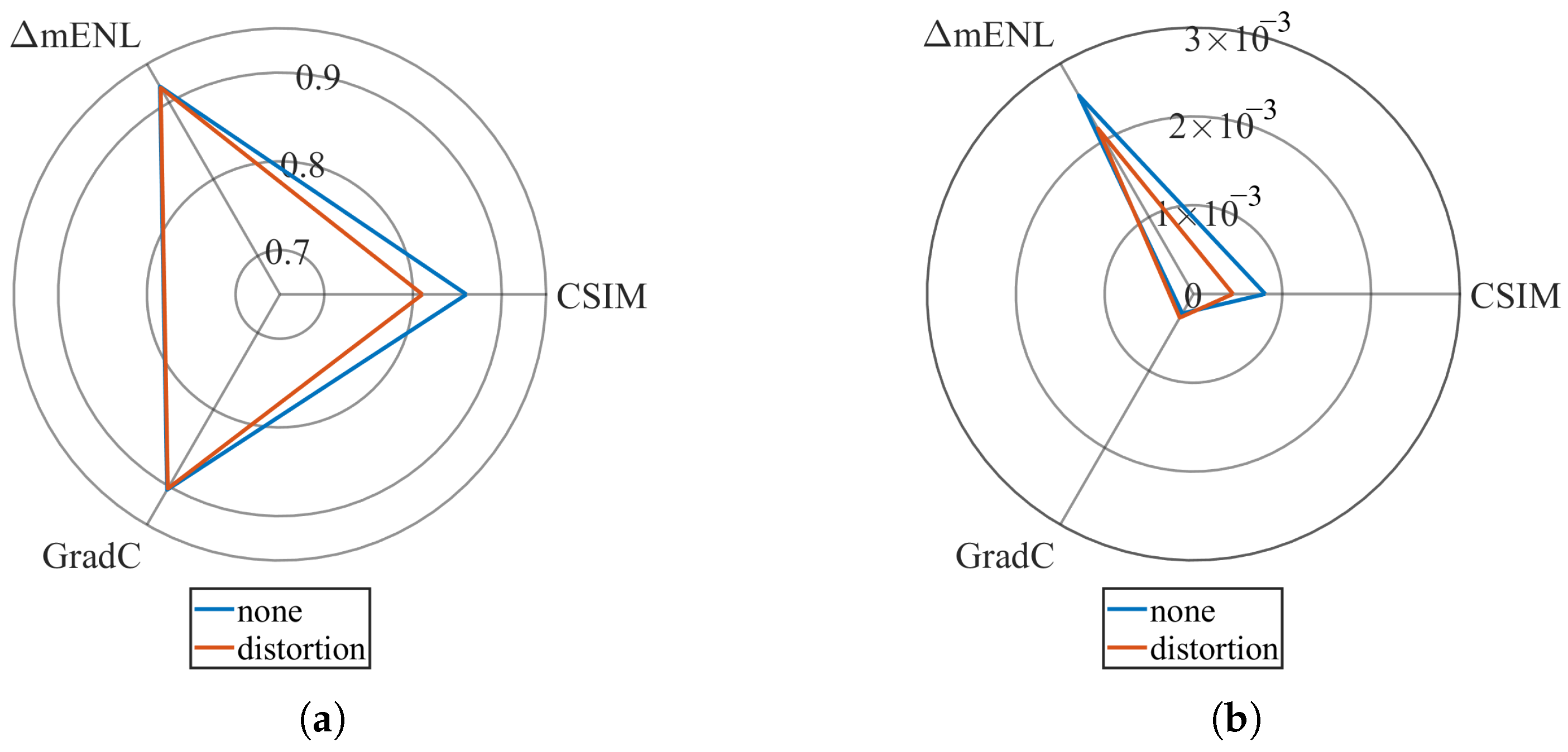
4. Experimental Results
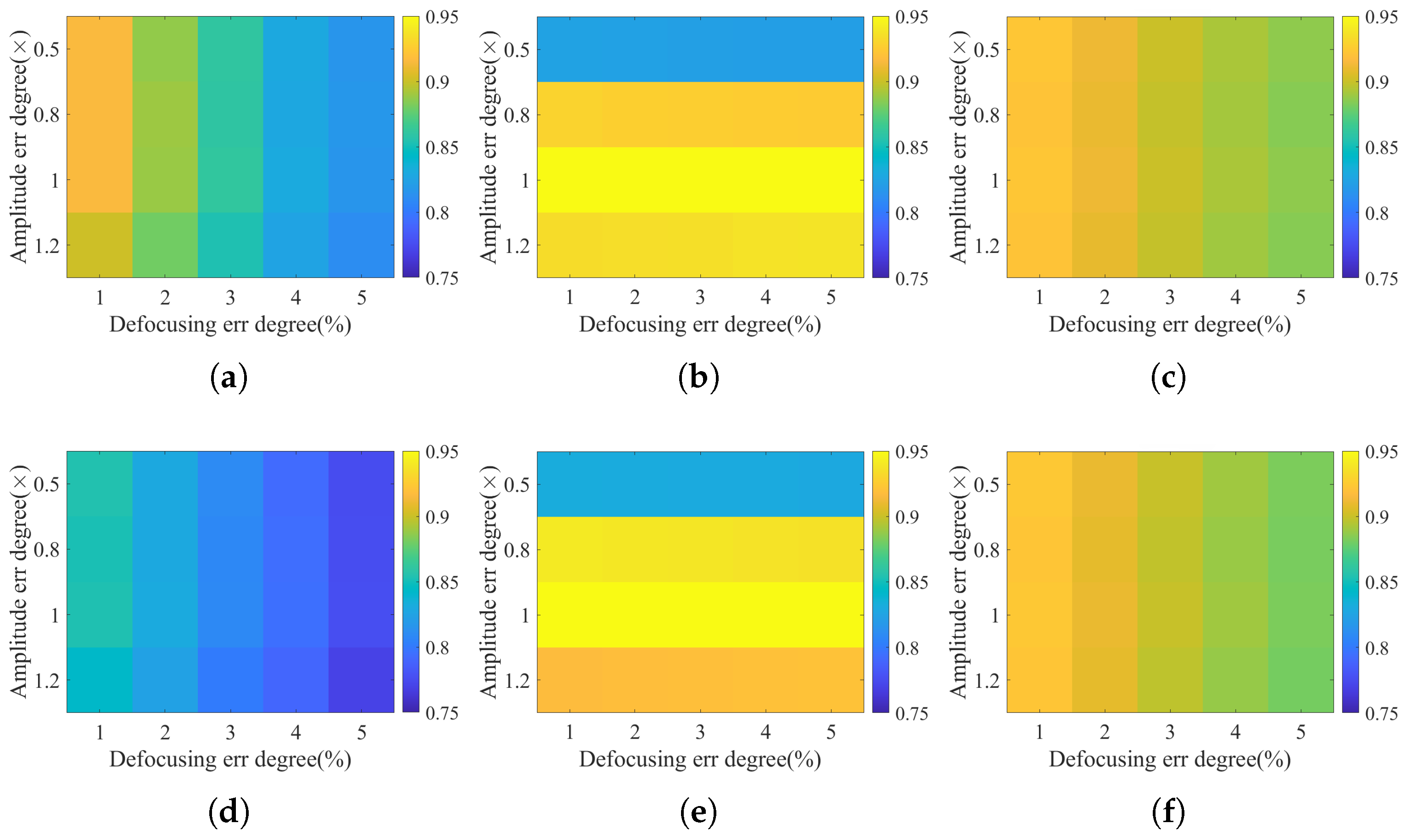
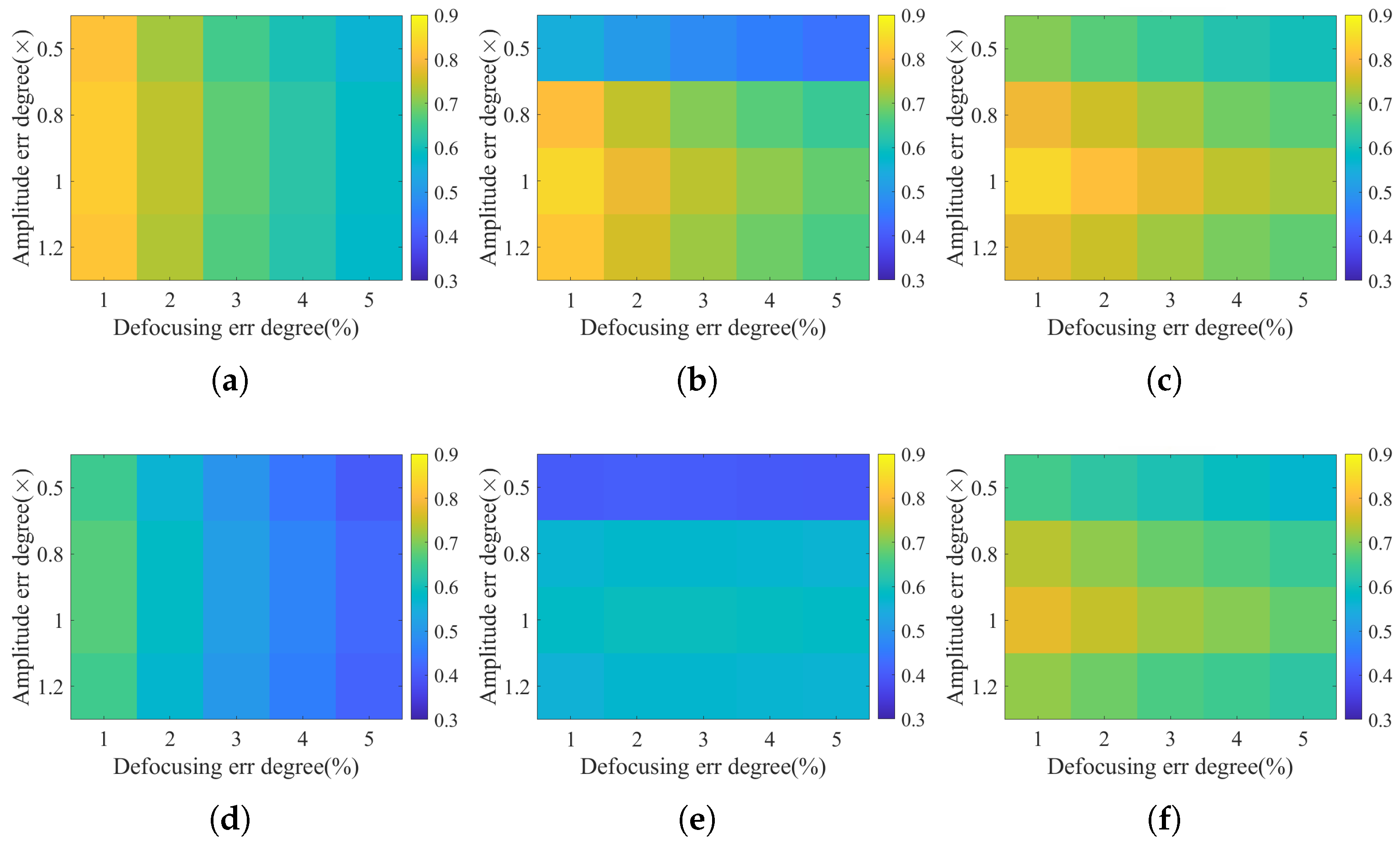
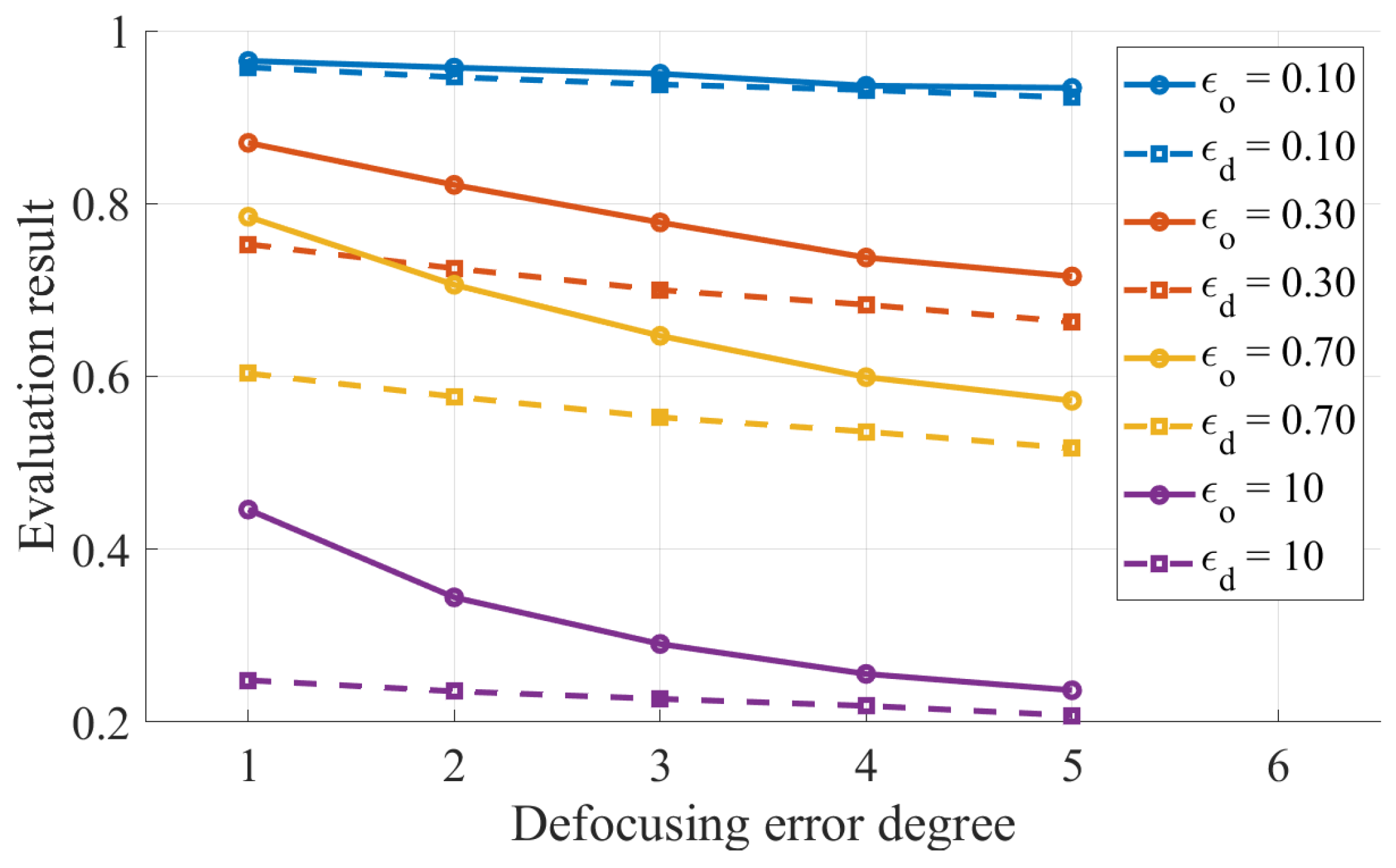
4.1. Error Analysis Experiment
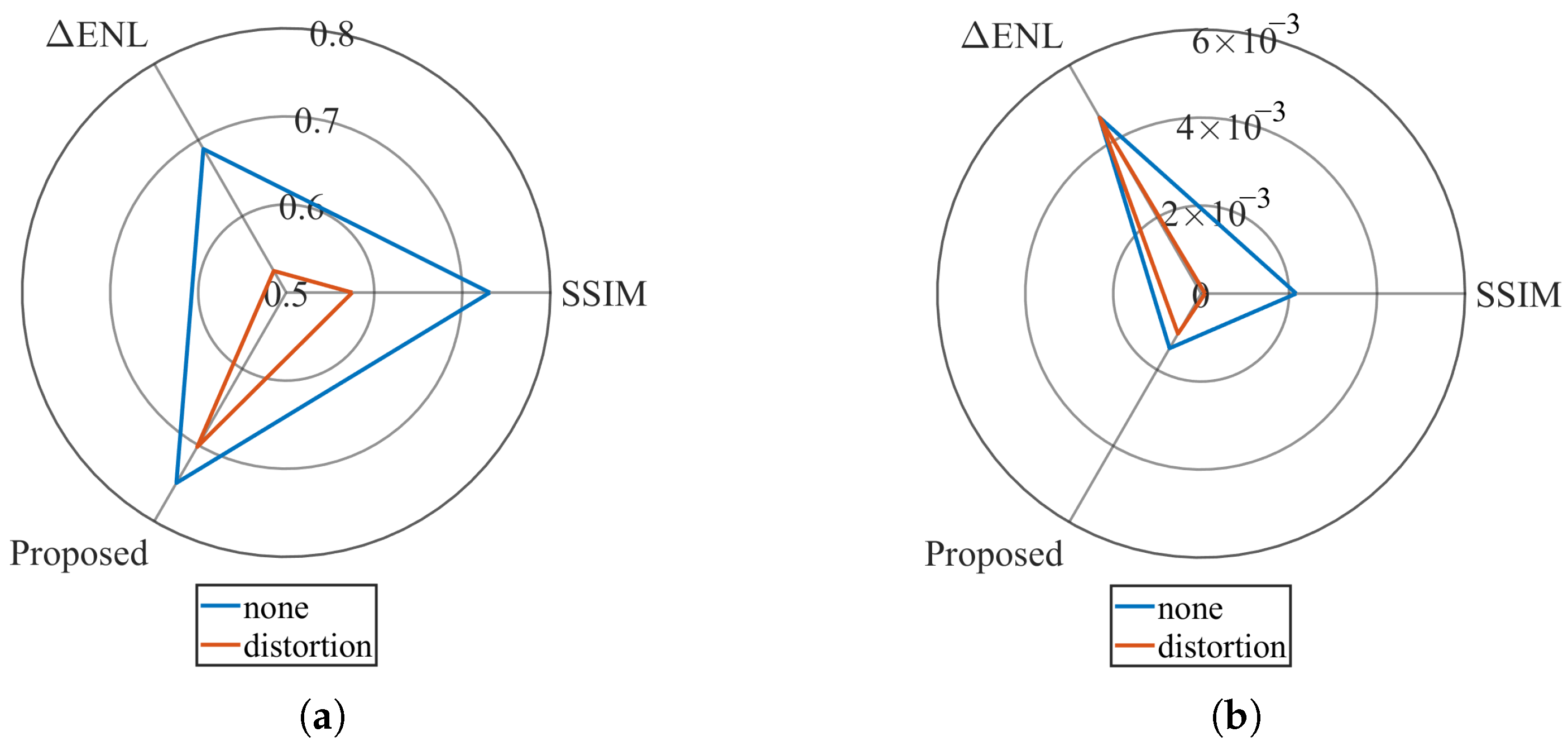
4.2. Simulation Experiment
4.3. Real SAR Jamming Experiment
5. Discussion
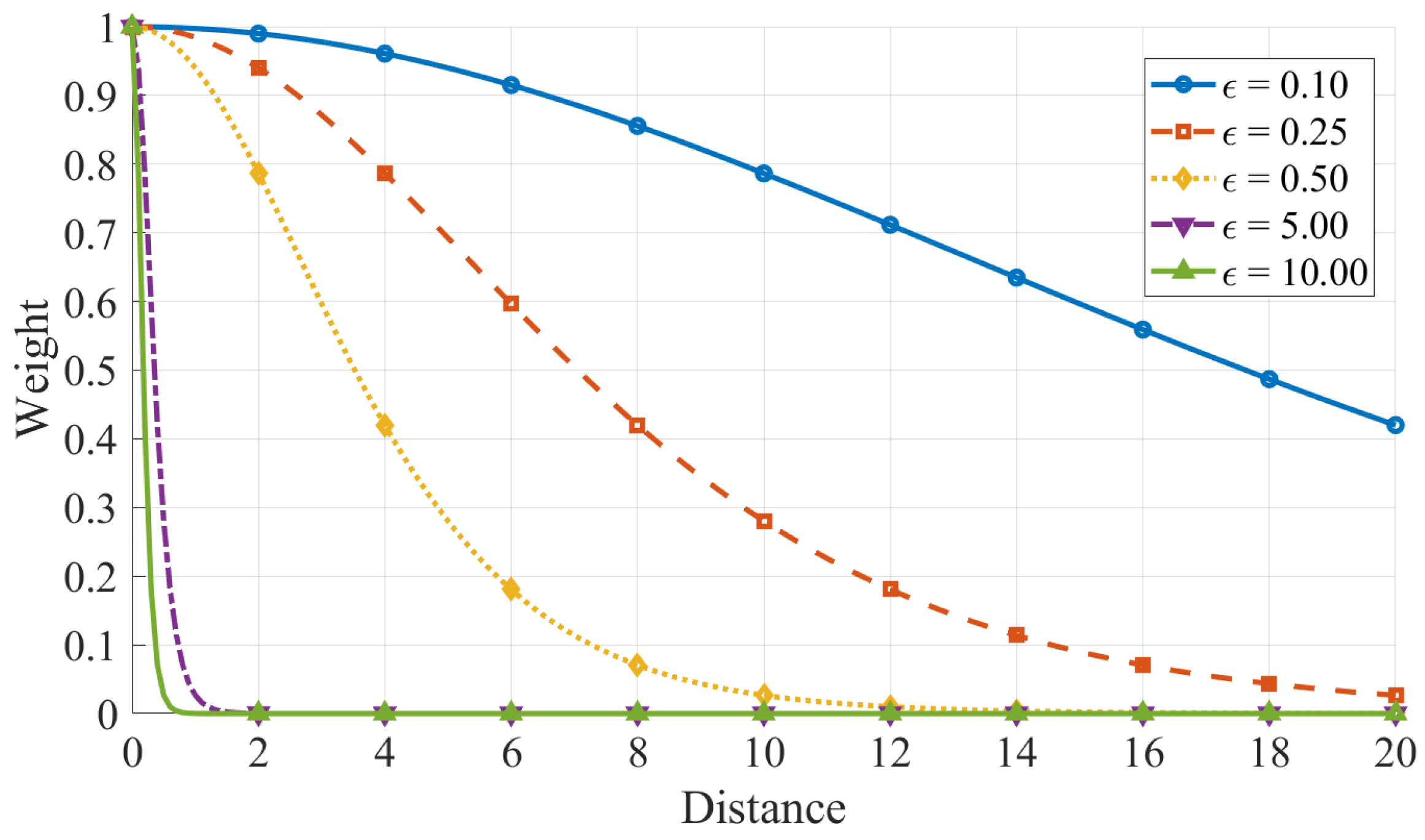
5.1. The Selection of Parameter in CSIM
5.2. Comparison with Traditional Methods
5.3. Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Chan, Y.K.; Koo, V. An introduction to synthetic aperture radar (SAR). Prog. Electromagn. Res. B 2008, 2, 27–60. [Google Scholar] [CrossRef]
- Li, N.-J.; Zhang, Y.-T. A survey of radar ECM and ECCM. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 1110–1120. [Google Scholar] [CrossRef]
- Liu, X.; Wu, Q.; Pan, X.; Wang, J.; Zhao, F. SAR Image Transform Based on Amplitude and Frequency Shifting Joint Modulation. IEEE Sens. J. 2025, 25, 7043–7052. [Google Scholar] [CrossRef]
- Yan, Z.; Guoqing, Z.; Yu, Z. Research on SAR Jamming Technique Based on Man-made Map. In Proceedings of the 2006 CIE International Conference on Radar, Shanghai, China, 16–19 October 2006; pp. 1–4. [Google Scholar] [CrossRef]
- Hanafy, M.; Hassan, H.E.; Abdel-Latif, M.; Elgamel, S. Performance evaluation of deceptive and noise jamming on SAR focused image. In Proceedings of the 11th International Conference on Electrical Engineering ICEENG 2018, Cairo, Egypt, 3–5 April 2018; Volume 11, pp. 1–11. [Google Scholar] [CrossRef]
- Ding, C.; Mu, H.; Shi, Y.; Wu, Z.; Fu, X.; Zhu, R.; Cai, T.; Meng, F.; Wang, J. Dual-polarized and Conformal Time-Modulated Metasurface Based Two-Dimensional Jamming Against SAR Imaging System. IEEE Trans. Antennas Propag. 2025. early access. [Google Scholar] [CrossRef]
- Li, K.; Jiu, B.; Liu, H. Game Theoretic Strategies Design for Monostatic Radar and Jammer Based on Mutual Information. IEEE Access 2019, 7, 72257–72266. [Google Scholar] [CrossRef]
- Wu, X.; Dai, D.; Wang, X.; Lu, H. Evaluation of SAR Jamming Performance. In Proceedings of the 2007 International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, Hangzhou, China, 16–17 August 2007; pp. 1476–1480. [Google Scholar] [CrossRef]
- Li, X.; Zhen, J. Information Theory-Based Amendments of SAR Jamming Effect Evaluation. In Proceedings of the 2012 Sixth International Conference on Internet Computing for Science and Engineering, Zhengzhou, China, 21–23 April 2012; pp. 159–162. [Google Scholar] [CrossRef]
- Quegan, S.; Yu, J.J. Filtering of multichannel SAR images. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2373–2379. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Lee, Y.; Park, J.; Shin, W.; Lee, K.; Kang, H. A study on jamming performance evaluation of noise and deception jammer against SAR satellite. In Proceedings of the 2011 3rd International Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Seoul, Republic of Korea, 26–30 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–3. [Google Scholar]
- Han, G.-Q.; Li, Y.-Z.; Wang, X.-S.; Xing, S.-Q.; Liu, Q.-F. Evaluation of Jamming Effect on SAR Based on Method of Modified Structural Similarity. J. Electron. Inf. Technol. 2011, 33, 711. [Google Scholar] [CrossRef]
- Jiao, S.; Dong, W. SAR Image Quality Assessment Based on SSIM Using Textural Feature. In Proceedings of the 2013 Seventh International Conference on Image and Graphics, Qingdao, China, 26–28 July 2013; pp. 281–286. [Google Scholar] [CrossRef]
- Bu, W. Multi-false-target Jamming Effectiveness Evaluation Based on Analytic Hierarchy Process and Entropy Weight Method. Electron. Inf. Warf. Technol. 2022, 37, 81–85. [Google Scholar]
- Shi, J.; Xue, L.; Zhu, B. Evaluation method of jamming effect on ISAR based on symmetry cross entropy. In Proceedings of the 2009 International Conference on Image Analysis and Signal Processing, Linhai, China, 11–12 April 2009; pp. 402–405. [Google Scholar] [CrossRef]
- Zhu, B.Y.; Xue, L.; Bi, D.P. Evaluation Method of Jamming Effect on ISAR Based on the Similarity of Features. In Proceedings of the 2010 6th International Conference on Wireless Communications Networking and Mobile Computing (WiCOM), Chengdu, China, 23–25 September 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Xing, X.; Chen, Z.; Zou, H.; Zhou, S. A fast algorithm based on two-stage CFAR for detecting ships in SAR images. In Proceedings of the 2009 2nd Asian-Pacific Conference on Synthetic Aperture Radar, Xi’an, China, 26–30 October 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 506–509. [Google Scholar]
- Ai, J.; Yang, X.; Song, J.; Dong, Z.; Jia, L.; Zhou, F. An adaptively truncated clutter-statistics-based two-parameter CFAR detector in SAR imagery. IEEE J. Ocean. Eng. 2017, 43, 267–279. [Google Scholar] [CrossRef]
- El-Darymli, K.; McGuire, P.; Power, D.; Moloney, C. Target detection in synthetic aperture radar imagery: A state-of-the-art survey. J. Appl. Remote Sens. 2013, 7, 071598. [Google Scholar] [CrossRef]
- Zhu, H.; Quan, S.; Xing, S.; Zhang, H.; Ren, Y. Detection-Oriented Evaluation of SAR Dexterous Barrage Jamming Effectiveness. Remote Sens. 2025, 17, 1101. [Google Scholar] [CrossRef]
- Sun, D.; Li, A.; Ding, H.; Wei, J. Detection of DRFM Deception Jamming Based on Diagonal Integral Bispectrum. Remote Sens. 2025, 17, 1957. [Google Scholar] [CrossRef]
- Tang, Z.; Yu, C.; Deng, Y.; Fang, T.; Zheng, H. Evaluation of deceptive jamming effect on SAR based on visual consistency. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 12246–12262. [Google Scholar] [CrossRef]
- Tian, T.; Zhou, F.; Li, Y.; Sun, B.; Fan, W.; Gong, C.; Yang, S. Performance Evaluation of Deception Against Synthetic Aperture Radar Based on Multifeature Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 103–115. [Google Scholar] [CrossRef]
- Zhou, F.; Zhao, B.; Tao, M.; Bai, X.; Chen, B.; Sun, G. A Large Scene Deceptive Jamming Method for Space-Borne SAR. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4486–4495. [Google Scholar] [CrossRef]
- Manzoor, Z.; Ghasr, M.T.; Donnell, K.M. Image distortion characterization due to equivalent monostatic approximation in near field bistatic SAR imaging. In Proceedings of the 2017 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Turin, Italy, 22–25 May 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Cui, R.; Xue, L.; Wang, B. Evaluation method of jamming effect on ISAR based on equivalent number of looks. Syst. Eng. Electron. 2008, 30, 887–888. [Google Scholar]
- Kanopoulos, N.; Vasanthavada, N.; Baker, R. Design of an image edge detection filter using the Sobel operator. IEEE J. Solid-State Circuits 1988, 23, 358–367. [Google Scholar] [CrossRef]
- Gong, M.; Zhou, Z.; Ma, J. Change Detection in Synthetic Aperture Radar Images based on Image Fusion and Fuzzy Clustering. IEEE Trans. Image Process. 2012, 21, 2141–2151. [Google Scholar] [CrossRef]
- Deng, C.X.; Bai, T.T.; Geng, Y. Image edge detection based on wavelet transform and Canny operator. In Proceedings of the 2009 International Conference on Wavelet Analysis and Pattern Recognition, Baoding, China, 12–15 July 2009; pp. 355–359. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]










| Parameter | Symbol | Value |
|---|---|---|
| Velocity | () | 154.2 m/s |
| Bandwidth | (B) | 480 MHz |
| Pulse Width | () | 2.4 μs |
| Carrier Frequency | () | 9.6 GHz |
| SAR Height | (H) | 10,000 m |
| Center Slant Range | () | 25,545 m |
| Squint Angle | () | 0 |
| Error Type | ||||
|---|---|---|---|---|
| Reference | Group 1 | 0 | 0 | 1% |
| Group 2 | 0 | 0 | 2% | |
| Defocusing | Group 3 | 0 | 0 | 3% |
| Group 4 | 0 | 0 | 5% | |
| Group 5 | −20% | 0 | 1% | |
| Amplitude Variation | Group 6 | −50% | 0 | 1% |
| Group 7 | +50% | 0 | 1% | |
| Group 8 | 0 | 0.01 | 1% | |
| Distortion | Group 9 | 0 | 0.03 | 1% |
| Group 10 | 0 | 0.1 | 1% |
| Method | Group 1 | Group 2 | Group 3 | Group 4 |
|---|---|---|---|---|
| Proposed | 0.8453 | 0.8203 | 0.7501 | 0.6673 |
| SSIM | 0.9002 | 0.8337 | 0.7812 | 0.6938 |
| ENL | 0.8682 | 0.7622 | 0.6732 | 0.5350 |
| Method | Group 1 | Group 5 | Group 6 | Group 7 |
|---|---|---|---|---|
| Proposed | 0.8453 | 0.7741 | 0.6538 | 0.6025 |
| SSIM | 0.9001 | 0.8551 | 0.5787 | 0.7933 |
| ENL | 0.8681 | 0.8681 | 0.8556 | 0.7446 |
| Method | Group 1 | Group 8 | Group 9 | Group 10 |
|---|---|---|---|---|
| Proposed | 0.8453 | 0.8373 | 0.8178 | 0.6596 |
| SSIM | 0.9002 | 0.7683 | 0.6717 | 0.4205 |
| ENL | 0.8681 | 0.8652 | 0.8641 | 0.8480 |
| Region | Proposed | SSIM | ENL |
|---|---|---|---|
| False Target with registration | 0.6478 | 0.4603 | 0.8173 |
| False Target without registration | 0.6144 | 0.0163 | 0.9446 |
| Random | 0.1749 | 0.0188 | 0.2591 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Li, L.; Xu, Z.; Liu, G.; Li, G. A Multi-Feature Fusion Performance Evaluation Method for SAR Deception Jamming. Remote Sens. 2025, 17, 3195. https://doi.org/10.3390/rs17183195
Xu H, Li L, Xu Z, Liu G, Li G. A Multi-Feature Fusion Performance Evaluation Method for SAR Deception Jamming. Remote Sensing. 2025; 17(18):3195. https://doi.org/10.3390/rs17183195
Chicago/Turabian StyleXu, Haoming, Liang Li, Zhenyang Xu, Guikun Liu, and Guangyuan Li. 2025. "A Multi-Feature Fusion Performance Evaluation Method for SAR Deception Jamming" Remote Sensing 17, no. 18: 3195. https://doi.org/10.3390/rs17183195
APA StyleXu, H., Li, L., Xu, Z., Liu, G., & Li, G. (2025). A Multi-Feature Fusion Performance Evaluation Method for SAR Deception Jamming. Remote Sensing, 17(18), 3195. https://doi.org/10.3390/rs17183195








