A GRU-Enhanced Kolmogorov–Arnold Network Model for Sea Surface Temperature Prediction Derived from Satellite Altimetry Product in South China Sea
Abstract
1. Introduction
2. Data and Methods
2.1. Study Area and Data
2.2. Model Construction
2.2.1. LSTM
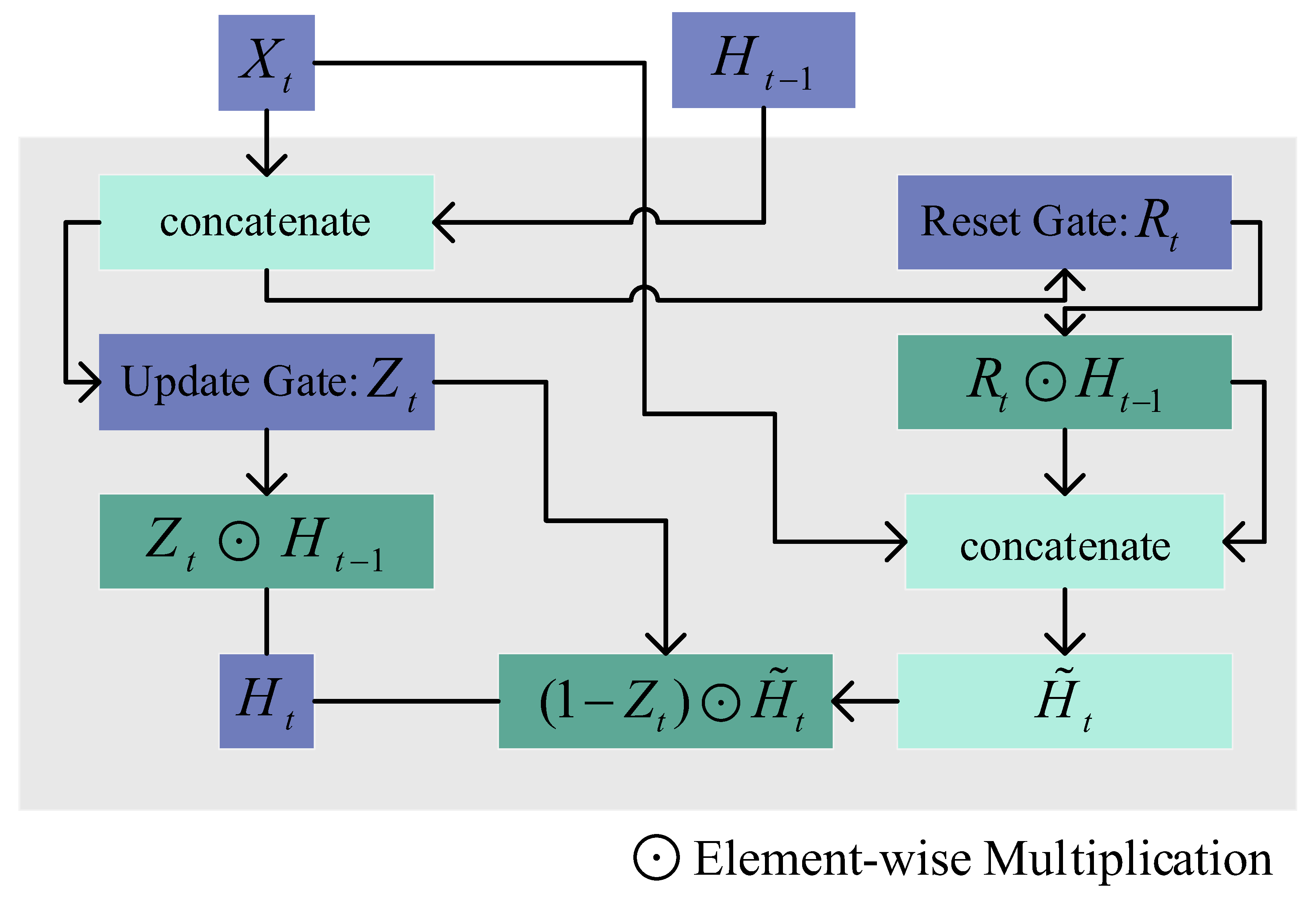
2.2.2. GRU
2.2.3. Transformer
2.2.4. KAN
2.2.5. GRU_EKAN
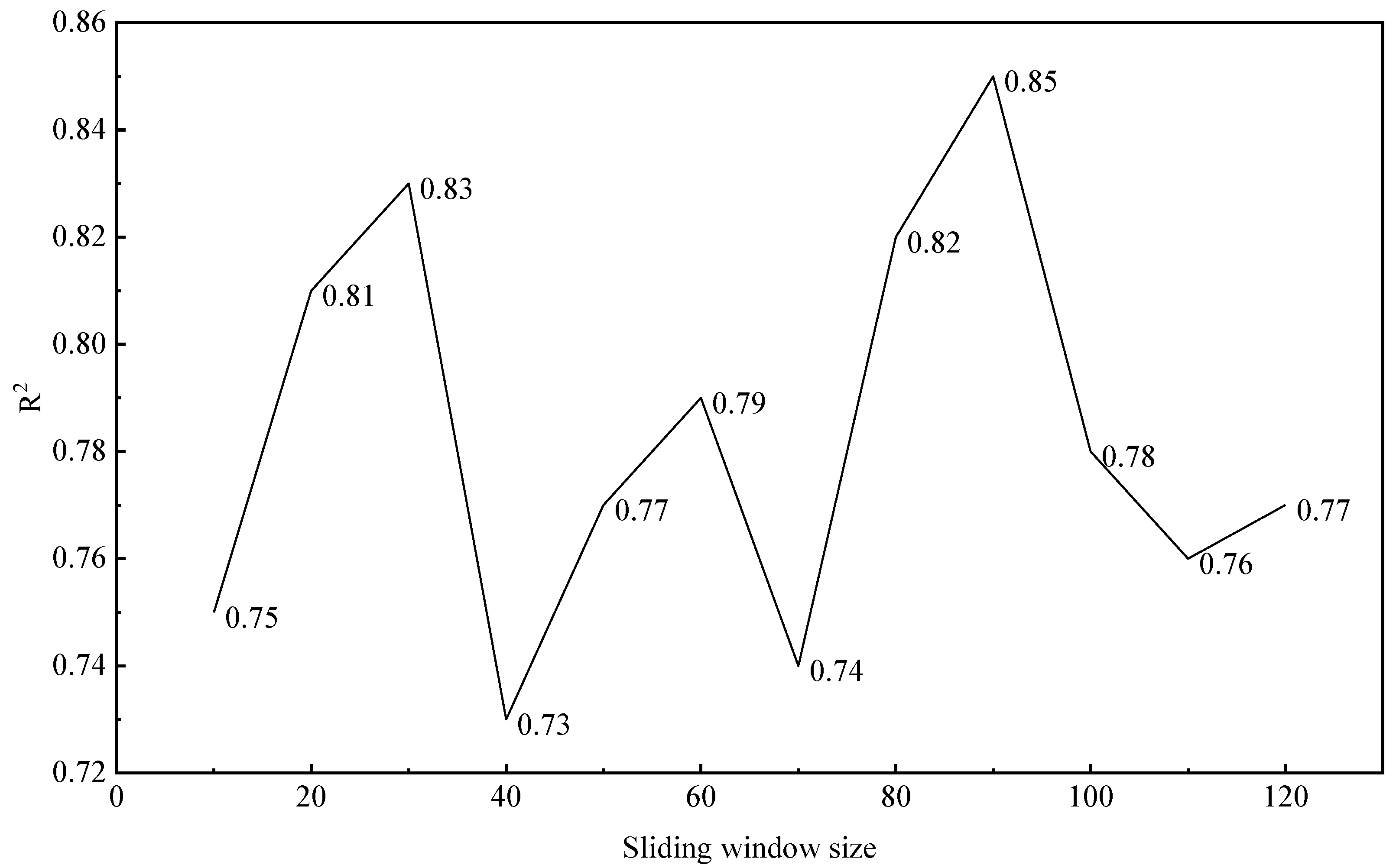
2.3. Model Parameter Settings
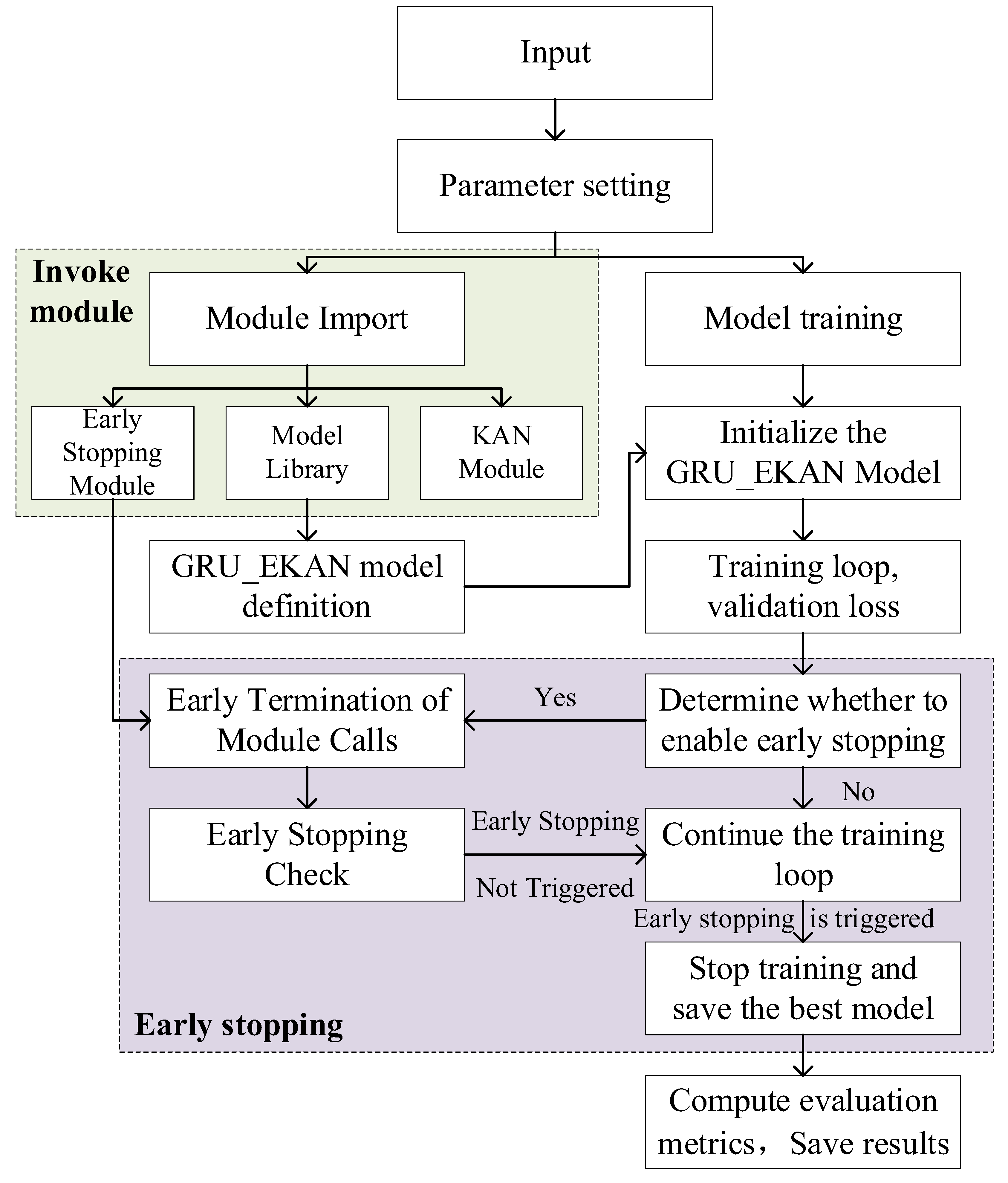
2.4. Model Training Process
3. Results
3.1. Correlation Coefficient Analysis
3.2. Comparison of Model Results
4. Discussion
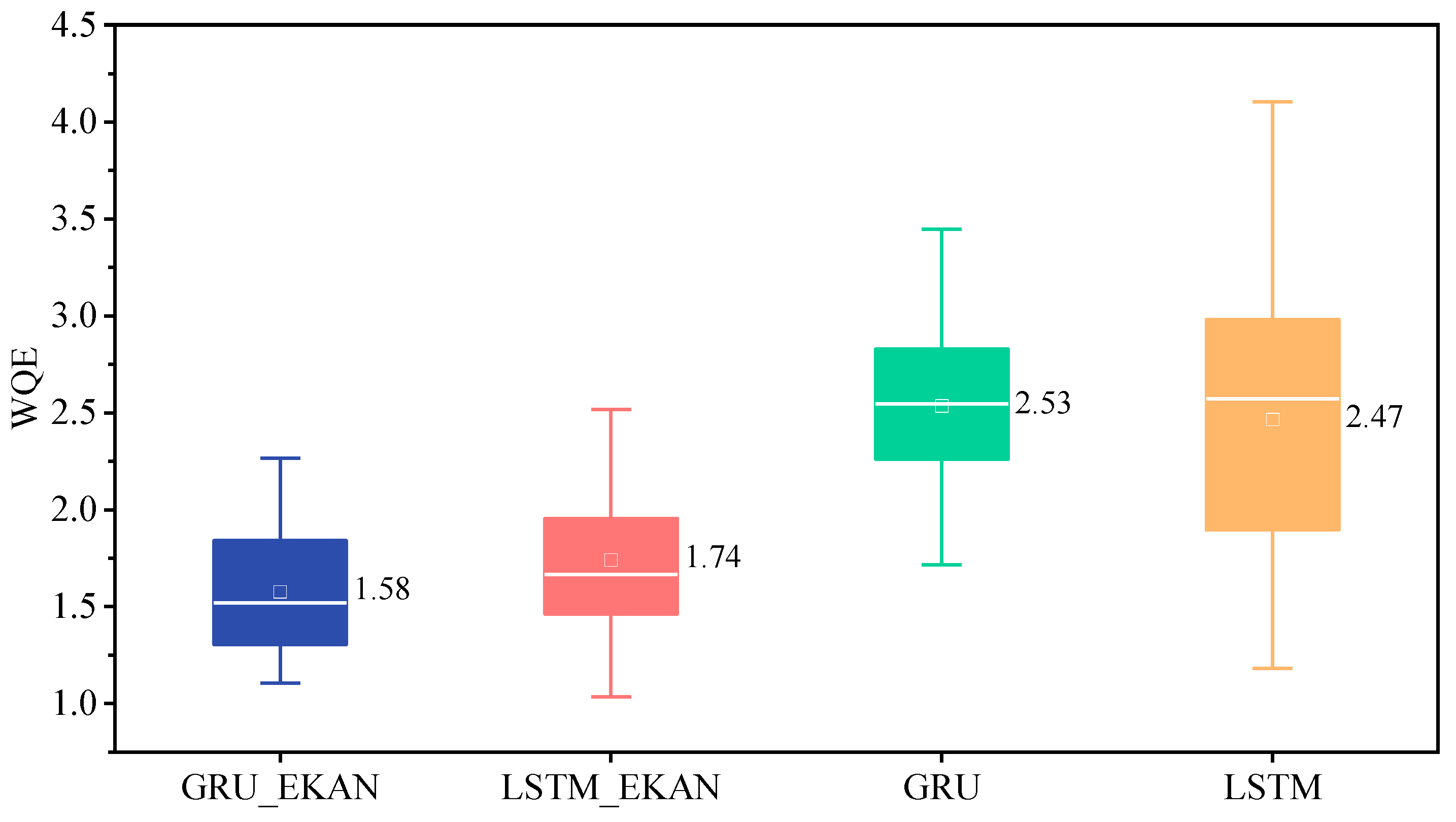
4.1. WQE Index Analysis
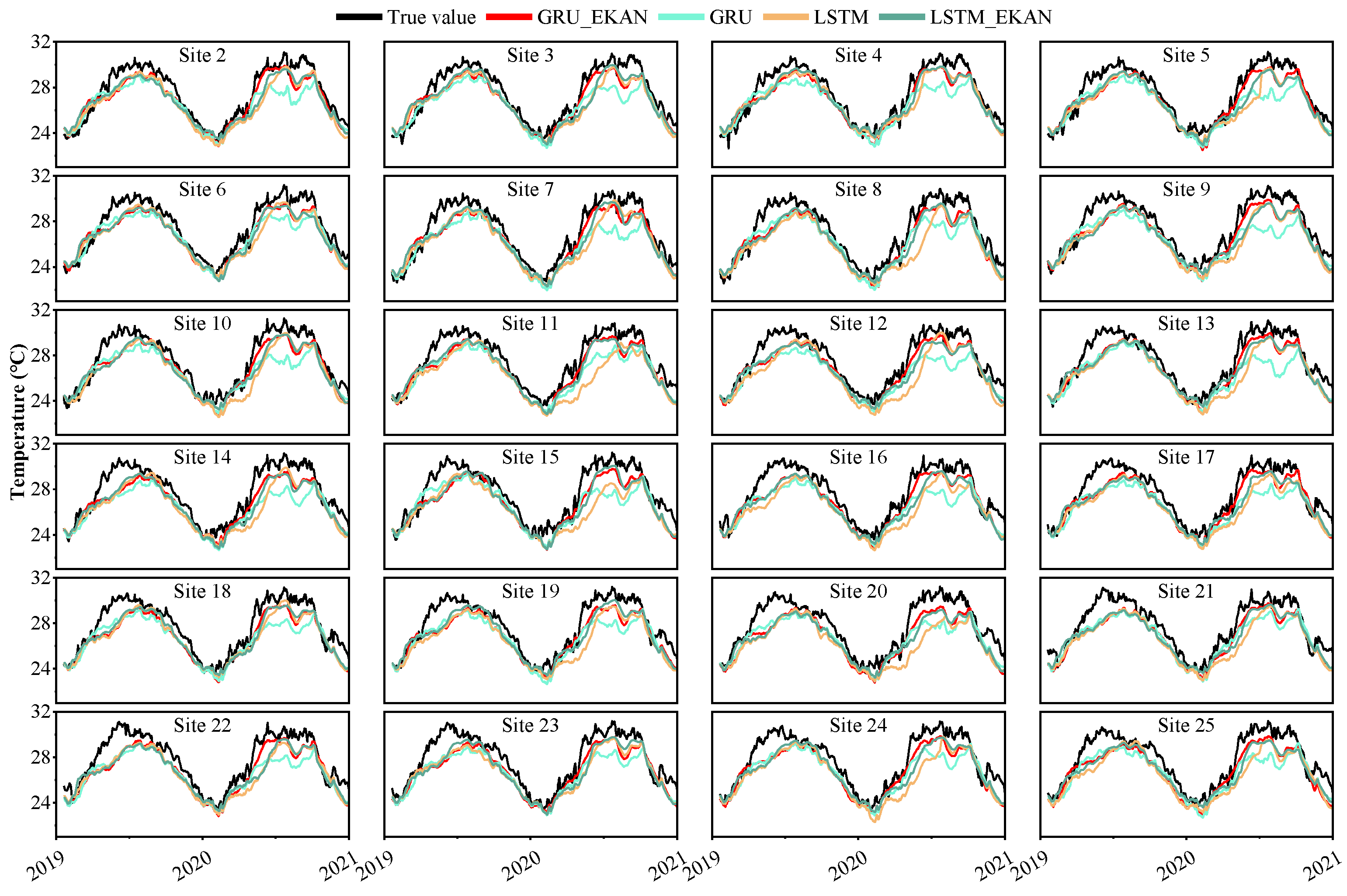
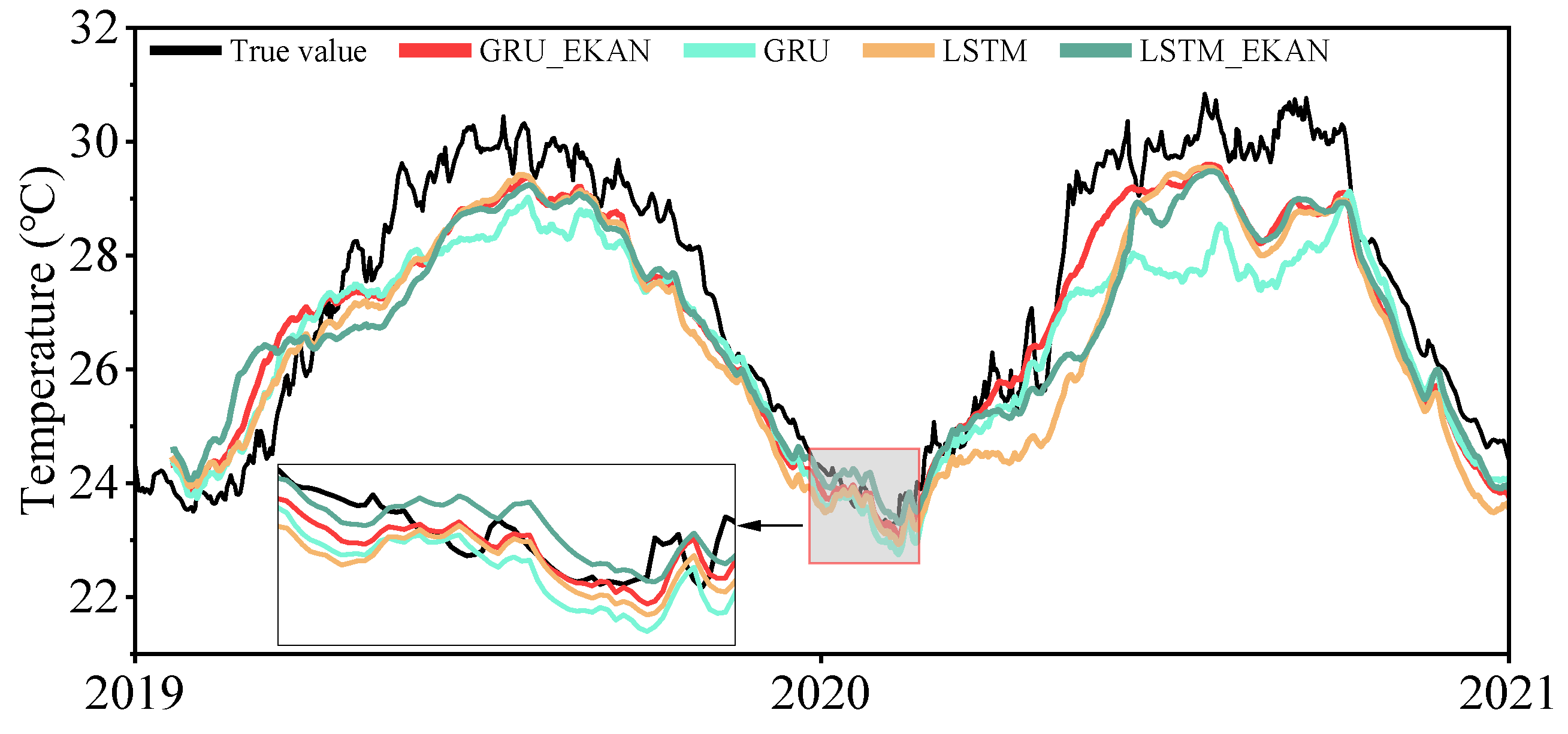
4.2. Comparison Between Predicted Values and True Values
5. Conclusions
- Superior Prediction Accuracy and Robustness: GRU_EKAN delivers high-precision predictions with a consistent average R2 of 0.85, demonstrating substantial improvements over benchmark models: 6% higher than LSTM_EKAN (R2 ≈ 0.80), 25% higher than base GRU (R2 ≈ 0.68), 20% higher than LSTM (R2 ≈ 0.71), and 18% higher than Transformer (R2 ≈ 0.72). Furthermore, GRU_EKAN exhibited exceptional stability across diverse locations, evidenced by its markedly lower prediction volatility (global R2 standard deviation = 0.019) compared to GRU (0.121) and LSTM (0.126).
- Lowest Prediction Errors: GRU_EKAN achieved the best performance across all core error metrics: RMSE = 0.90 °C, MAE = 0.76 °C, MSE = 0.80 °C2. Compared to the base GRU model, this translates to reductions of 31.3% (RMSE), 27.0% (MAE), and 53.2% (MSE). Compared to LSTM, the improvements were 23.1% (RMSE), 19.9% (MAE), and 43.3% (MSE).
- Highest Comprehensive Predictive Quality: The Weighted Quality Evaluation Index (WQE), synthesizing RMSE, MAE, MSE, and MAPE, unequivocally ranked GRU_EKAN as the best model. It achieved the lowest median WQE value (1.58) across all sites, significantly outperforming LSTM_EKAN (1.74), base GRU (2.53), and LSTM (2.47). Critically, GRU_EKAN also demonstrated the greatest reliability under varying conditions, as shown by its smallest fluctuation in WQE performance (range: 0.13), which was far less than other models (e.g., GRU range: 0.52, LSTM_EKAN range: 0.55).
- Enhanced Anomaly Detection Capability: During known SCS temperature anomaly events (2019 and 2020), GRU_EKAN predictions were notably closer to observed values than other models. More importantly, it demonstrated a superior ability to detect the onset of abnormal temperature trends earlier, as evidenced during the May 2019 positive anomaly and the May 2020 marine heatwave. Although deviations increased during peak anomaly periods, GRU_EKAN maintained relatively closer tracking than the alternatives.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Frankignoul, C. Sea Surface Temperature Anomalies, Planetary Waves, and Air-sea Feedback in the Middle Latitudes. Rev. Geophys. 1985, 23, 357–390. [Google Scholar] [CrossRef]
- Deser, C.; Alexander, M.A.; Xie, S.-P.; Phillips, A.S. Sea Surface Temperature Variability: Patterns and Mechanisms. Annu. Rev. Mar. Sci. 2010, 2, 115–143. [Google Scholar] [CrossRef] [PubMed]
- Zheng, F.; Zhu, J. Improved Ensemble-Mean Forecasting of ENSO Events by a Zero-Mean Stochastic Error Model of an Intermediate Coupled Model. Clim. Dyn. 2016, 47, 3901–3915. [Google Scholar] [CrossRef]
- Dong, B.-W.; Sutton, R.T.; Jewson, S.P.; O’Neill, A.; Slingo, J.M. Predictable Winter Climate in the North Atlantic Sector during the 1997–1999 ENSO Cycle. Geophys. Res. Lett. 2000, 27, 985–988. [Google Scholar] [CrossRef]
- Latif, M.; Arpe, K.; Roeckner, E. Oceanic Control of Decadal North Atlantic Sea Level Pressure Variability in Winter. Geophys. Res. Lett. 2000, 27, 727–730. [Google Scholar] [CrossRef]
- Rodwell, M.J.; Rowell, D.P.; Folland, C.K. Oceanic Forcing of the Wintertime North Atlantic Oscillation and European Climate. Nature 1999, 398, 320–323. [Google Scholar] [CrossRef]
- Venzke, S.; Münnich, M.; Latif, M. On the Predictability of Decadal Changes in the North Pacific. Clim. Dyn. 2000, 16, 379–392. [Google Scholar] [CrossRef]
- Chen, Q.; Cai, C.; Chen, Y.; Zhou, X.; Zhang, D.; Peng, Y. TemproNet: A Transformer-Based Deep Learning Model for Seawater Temperature Prediction. Ocean Eng. 2024, 293, 116651. [Google Scholar] [CrossRef]
- He, X.; Montillet, J.-P.; Kermarrec, G.; Shum, C.K.; Fernandes, R.; Huang, J.; Wang, S.; Sun, X.; Zhang, Y.; Schuh, H. Space and Earth Observations to Quantify Present-Day Sea-Level Change. Adv. Geophys. 2024, 65, 125–177. [Google Scholar]
- Usharani, B. ILF-LSTM: Enhanced Loss Function in LSTM to Predict the Sea Surface Temperature. Soft Comput. 2023, 27, 13129–13141. [Google Scholar] [CrossRef]
- Wei, L.; Guan, L. Seven-Day Sea Surface Temperature Prediction Using a 3DConv-LSTM Model. Front. Mar. Sci. 2022, 9, 905848. [Google Scholar]
- Xie, J.; Zhang, J.; Yu, J.; Xu, L. An Adaptive Scale Sea Surface Temperature Predicting Method Based on Deep Learning with Attention Mechanism. IEEE Geosci. Remote Sens. Lett. 2019, 17, 740–744. [Google Scholar] [CrossRef]
- Ham, Y.-G.; Kim, J.-H.; Luo, J.-J. Deep Learning for Multi-Year ENSO Forecasts. Nature 2019, 573, 568–572. [Google Scholar] [CrossRef] [PubMed]
- Wanigasekara, R.; Zhang, Z.; Wang, W.; Luo, Y.; Pan, G. Application of Fast Meemd–Convlstm in Sea Surface Temperature Predictions. Remote Sens. 2024, 16, 2468. [Google Scholar] [CrossRef]
- Dai, H.; He, Z.; Wei, G.; Lei, F.; Zhang, X.; Zhang, W.; Shang, S. Long-Term Prediction of Sea Surface Temperature by Temporal Embedding Transformer with Attention Distilling and Partial Stacked Connection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 4280–4293. [Google Scholar] [CrossRef]
- Dai, H.; Lei, F.; Wei, G.; Zhang, X.; Lin, R.; Zhang, W.; Shang, S. Sea Surface Temperature Prediction by Stacked Generalization Ensemble of Deep Learning. Deep Sea Res. Part Oceanogr. Res. Pap. 2024, 209, 104343. [Google Scholar] [CrossRef]
- Yuan, T.; Zhu, J.; Ren, K.; Wang, W.; Wang, X.; Li, X. Neural Network Driven by Space-Time Partial Differential Equation for Predicting Sea Surface Temperature. In Proceedings of the 2022 IEEE International Conference on Data Mining (ICDM), Orlando, FL, USA, 28 November–1 December 2022; pp. 656–665. [Google Scholar]
- Yang, J.; Huo, J.; He, J.; Xiao, T.; Chen, D.; Li, Y. A DBULSTM-Adaboost Model for Sea Surface Temperature Prediction. PeerJ Comput. Sci. 2022, 8, e1095. [Google Scholar] [CrossRef]
- Du, J.; Nie, J.; Ye, M.; Song, D.; Gao, Z.; Wei, Z. A deep neural networks prediction model for sea surface temperature based on global cross-scale spatial-temporal attention. Chin. J. Mar. Environ. Sci. 2023, 42, 944–954. [Google Scholar]
- He, J.; Yin, S.; Chen, X.; Yin, B.; Huang, X. An Informer-Based Prediction Model for Extensive Spatiotemporal Prediction of Sea Surface Temperature and Marine Heatwave in Bohai Sea. J. Mar. Syst. 2025, 247, 104037. [Google Scholar] [CrossRef]
- Fan, L.-Y.; Cao, Y.-H.; Huang, N.-Y.; Sun, G.-X.; Cao, J.-N.; Liu, C.-X. OTCFM: A Sea Surface Temperature Prediction Method Integrating Multi-Scale Periodic Features. IEEE Access 2024, 12, 108291–108302. [Google Scholar] [CrossRef]
- Chan, J.Y.-L.; Leow, S.M.H.; Bea, K.T.; Cheng, W.K.; Phoong, S.W.; Hong, Z.-W.; Chen, Y.-L. Mitigating the Multicollinearity Problem and Its Machine Learning Approach: A Review. Mathematics 2022, 10, 1283. [Google Scholar] [CrossRef]
- Daoud, J.I. Multicollinearity and Regression Analysis. J. Phys. Conf. Ser. 2017, 949, 012009. [Google Scholar] [CrossRef]
- Zhou, Y.; He, X.; Montillet, J.-P.; Wang, S.; Hu, S.; Sun, X.; Huang, J.; Ma, X. An Improved ICEEMDAN-MPA-GRU Model for GNSS Height Time Series Prediction with Weighted Quality Evaluation Index. GPS Solut. 2025, 29, 113. [Google Scholar] [CrossRef]
- He, X.; Huang, J.; Montillet, J.P.; Wang, S.; Kermarrec, G.; Shum, C.K.; Hu, S.; Wang, F. A Noise Reduction Approach for Improve North American Regional Sea Level Change from Satellite and In Situ Observations. Surv. Geophys. 2025, 47, 1–32. [Google Scholar] [CrossRef]
- Fan, Y.; Hu, S.; Sun, X.; He, X.; Zhang, J.; Jin, W.; Liao, Y. Spatial Variation and Uncertainty Analysis of Black Sea Level Change from Virtual Altimetry Stations over 1993–2020. Remote Sens. 2025, 17, 2228. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the Difficulty of Training Recurrent Neural Networks. In Proceedings of the International Conference on Machine Learning, PMLR, Atlanta, GA, USA, 16–21 June 2013; pp. 1310–1318. [Google Scholar]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations Using RNN Encoder-Decoder for Statistical Machine Translation. arXiv 2014, arXiv:1406.1078. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Kich, V.A.; Bottega, J.A.; Steinmetz, R.; Grando, R.B.; Yorozu, A.; Ohya, A. Kolmogorov-Arnold Networks for Online Reinforcement Learning. In Proceedings of the 2024 24th International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 29 October–1 November 2024; pp. 958–963. [Google Scholar]
- Cybenko, G. Approximation by Superpositions of a Sigmoidal Function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer Feedforward Networks Are Universal Approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. KAN: Kolmogorov-Arnold Networks. arXiv 2025, arXiv:2501.01234. [Google Scholar] [CrossRef]
- Unser, M.; Aldroubi, A.; Eden, M. B-Spline Signal Processing. I. Theory. IEEE Trans. Signal Process. 1993, 41, 821–833. [Google Scholar] [CrossRef]
- Shahrabadi, S.; Adão, T.; Peres, E.; Morais, R.; Magalhães, L.G.; Alves, V. Automatic Optimization of Deep Learning Training through Feature-Aware-Based Dataset Splitting. Algorithms 2024, 17, 106. [Google Scholar] [CrossRef]
- Asuero, A.G.; Sayago, A.; González, A.G. The Correlation Coefficient: An Overview. Crit. Rev. Anal. Chem. 2006, 36, 41–59. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another Look at Measures of Forecast Accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Cameron, A.C.; Windmeijer, F.A. An R-Squared Measure of Goodness of Fit for Some Common Nonlinear Regression Models. J. Econom. 1997, 77, 329–342. [Google Scholar] [CrossRef]
- Nagelkerke, N.J. A Note on a General Definition of the Coefficient of Determination. Biometrika 1991, 78, 691–692. [Google Scholar] [CrossRef]
- Bao, Y. Mechanisms for the abnormally early onset of the South China Sea summer monsoon in 2019. Acta Meteorol. Sin. 2021, 79, 400–413. [Google Scholar]
- Han, T.; Xu, K.; Wang, L.; Liu, B.; Tam, C.-Y.; Liu, K.; Wang, W. Extremely Long-Lived Marine Heatwave in South China Sea during Summer 2020: Combined Effects of the Seasonal and Intraseasonal Variations. Glob. Planet. Change 2023, 230, 104261. [Google Scholar] [CrossRef]


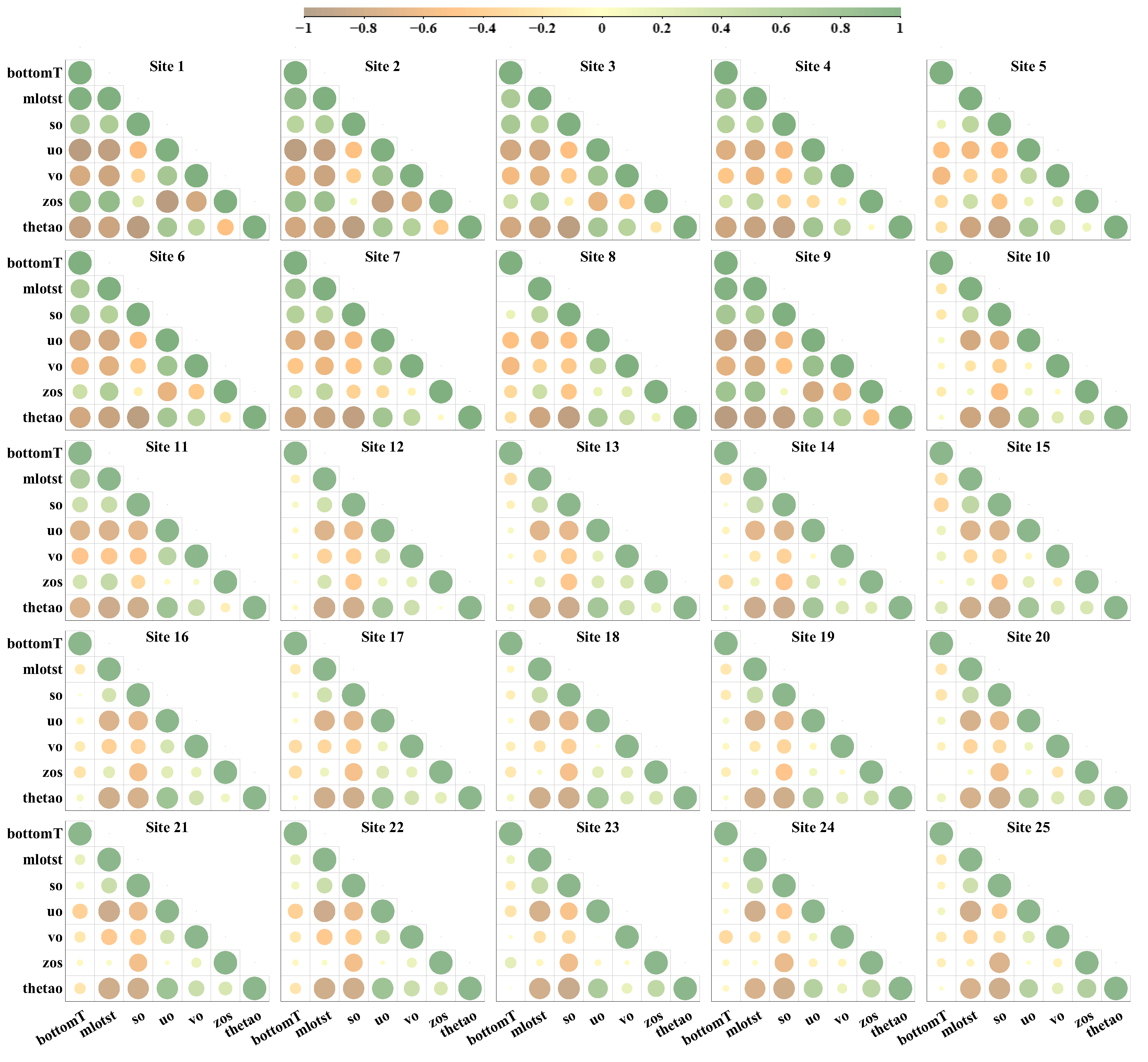
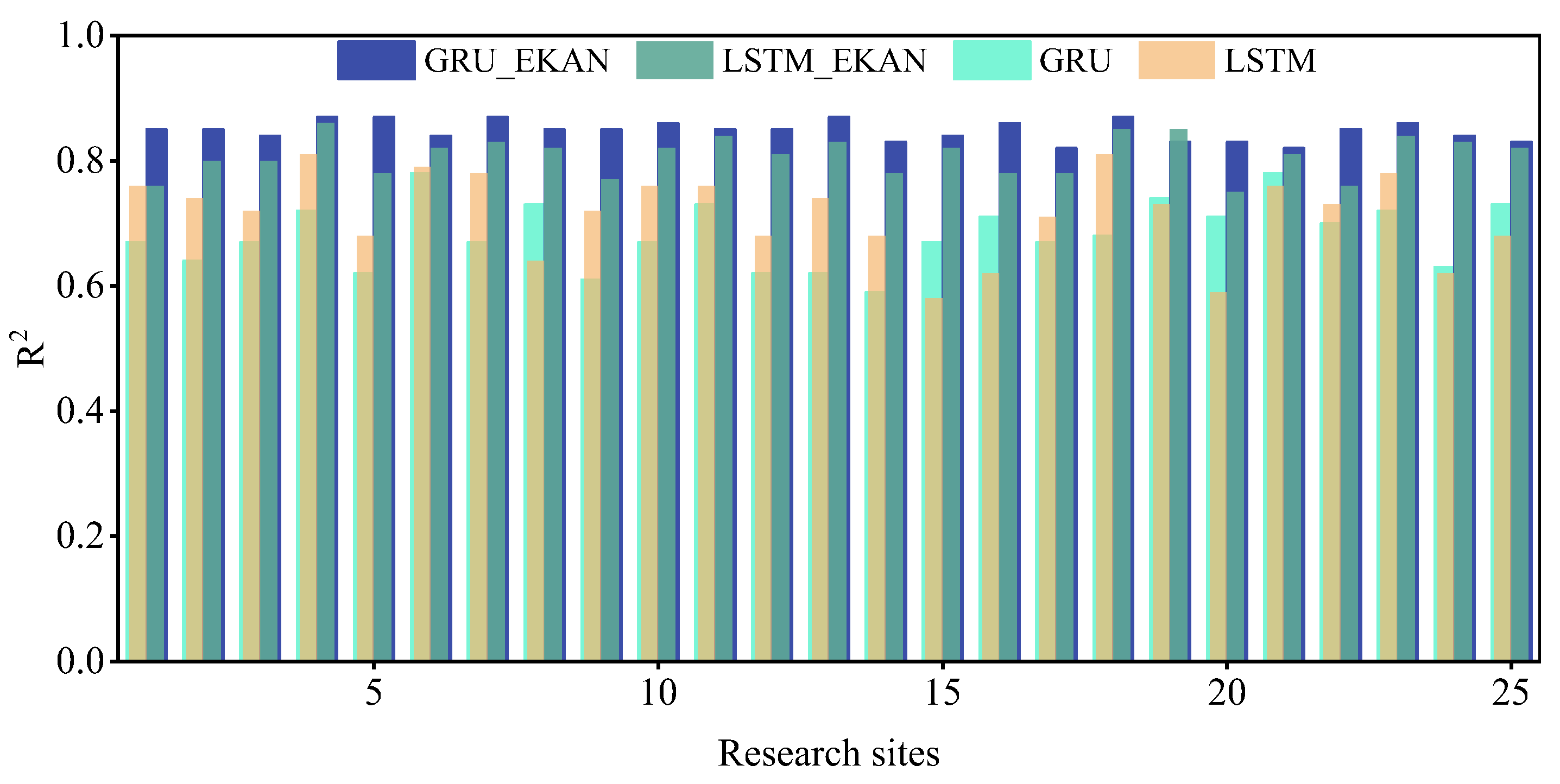

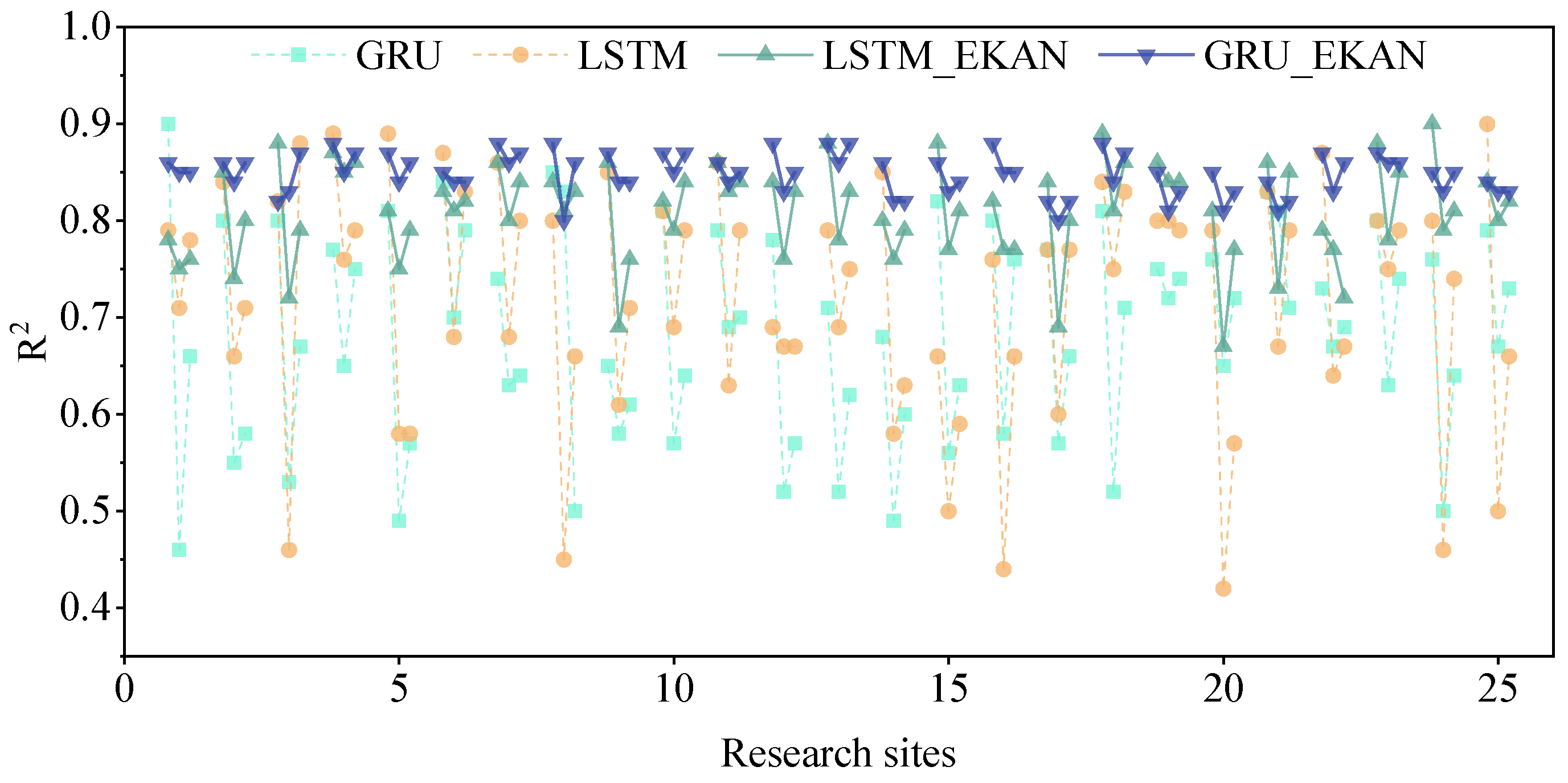
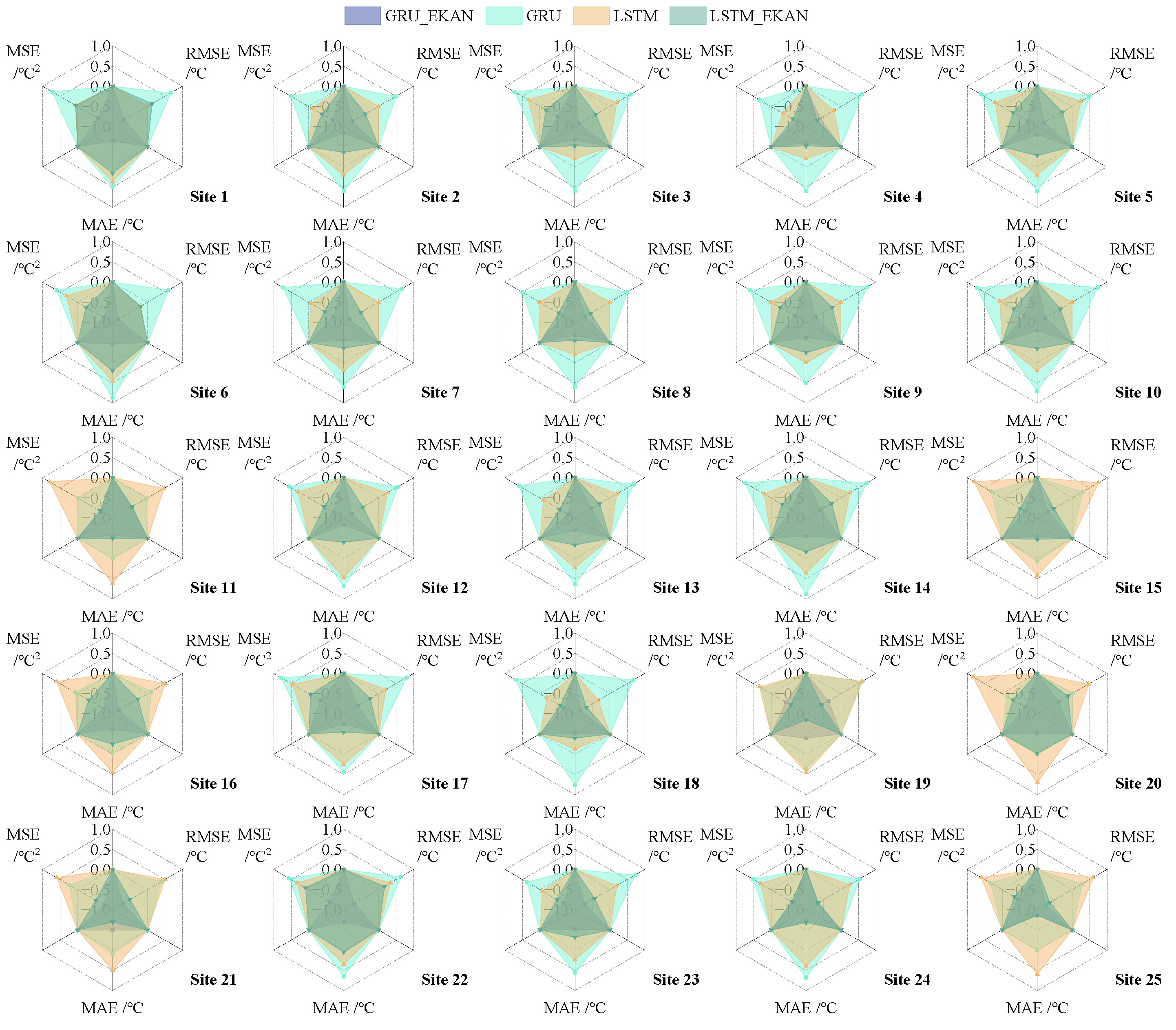
| Parameter | Description | |
|---|---|---|
| bottomT | Sea water potential temperature at sea floor (°C) | Resolution: 1/12° horizontal resolution Data assimilation: reduced-order Kalman filter The correction of large-scale biases in temperature and salinity: 3D-VAR |
| mlotst | Ocean mixed layer thickness defined by sigma theta (m) | |
| so | Sea water salinity (g/kg) | |
| uo | Eastward sea water velocity (m/s) | |
| vo | Northward sea water velocity (m/s) | |
| zos | Sea surface height above geoid (m) | |
| thetao | Sea water potential temperature (°C) |
| Hyperparameter | Model Setting Value | Description |
|---|---|---|
| Training set | 2851 | Training data for model training (January 2011–October 2018) |
| Test set | 713 | Test data for evaluating the performance of the model (October 2018–January 2021) |
| Learning rate | 0.001 | Hyperparameter controls the step size of model parameter update. |
| Hidden size | 64 | The dimension of the hidden layer |
| Input size | 7 | The dimension of the input layer |
| Output size | 1 | The dimension of the output layer |
| Seq len | 90 | The length of each sliding data window |
| Batch size | 32 | The batch input at one time in the time series data |
| Site | Model | MAE | RMSE | MAPE | R2 | WQE |
|---|---|---|---|---|---|---|
| 1 | GRU_EKAN | 0.75 | 0.87 | 2.69% | 0.86 | 1.11 |
| LSTM_EKAN | 0.91 | 1.11 | 3.25% | 0.78 | 1.58 | |
| GRU | 0.99 | 1.23 | 3.48% | 0.72 | 1.85 | |
| LSTM | 0.96 | 1.14 | 3.46% | 0.76 | 1.67 | |
| 2 | GRU_EKAN | 0.73 | 0.91 | 2.62% | 0.85 | 1.15 |
| LSTM_EKAN | 0.86 | 1.02 | 3.08% | 0.81 | 1.39 | |
| GRU | 1.06 | 1.36 | 3.70% | 0.66 | 2.17 | |
| LSTM | 0.96 | 1.13 | 3.45% | 0.76 | 1.64 | |
| 3 | GRU_EKAN | 0.79 | 0.94 | 2.83% | 0.83 | 1.23 |
| LSTM_EKAN | 0.85 | 1.02 | 3.05% | 0.80 | 1.39 | |
| GRU | 1.11 | 1.38 | 3.91% | 0.64 | 2.26 | |
| LSTM | 0.97 | 1.14 | 3.47% | 0.75 | 1.68 | |
| 4 | GRU_EKAN | 0.75 | 0.89 | 2.68% | 0.85 | 1.10 |
| LSTM_EKAN | 0.69 | 0.85 | 2.48% | 0.86 | 1.03 | |
| GRU | 1.03 | 1.27 | 3.60% | 0.69 | 1.94 | |
| LSTM | 0.75 | 0.93 | 2.48% | 0.83 | 1.18 | |
| 5 | GRU_EKAN | 0.72 | 0.90 | 2.59% | 0.84 | 1.16 |
| LSTM_EKAN | 0.86 | 1.03 | 3.06% | 0.79 | 1.46 | |
| GRU | 1.10 | 1.36 | 3.87% | 0.62 | 2.37 | |
| LSTM | 0.96 | 1.13 | 3.39% | 0.71 | 1.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, R.; Huang, Z.; Liang, X.; Zhu, S.; Li, H. A GRU-Enhanced Kolmogorov–Arnold Network Model for Sea Surface Temperature Prediction Derived from Satellite Altimetry Product in South China Sea. Remote Sens. 2025, 17, 2916. https://doi.org/10.3390/rs17162916
Sun R, Huang Z, Liang X, Zhu S, Li H. A GRU-Enhanced Kolmogorov–Arnold Network Model for Sea Surface Temperature Prediction Derived from Satellite Altimetry Product in South China Sea. Remote Sensing. 2025; 17(16):2916. https://doi.org/10.3390/rs17162916
Chicago/Turabian StyleSun, Rumiao, Zhengkai Huang, Xuechen Liang, Siyu Zhu, and Huilin Li. 2025. "A GRU-Enhanced Kolmogorov–Arnold Network Model for Sea Surface Temperature Prediction Derived from Satellite Altimetry Product in South China Sea" Remote Sensing 17, no. 16: 2916. https://doi.org/10.3390/rs17162916
APA StyleSun, R., Huang, Z., Liang, X., Zhu, S., & Li, H. (2025). A GRU-Enhanced Kolmogorov–Arnold Network Model for Sea Surface Temperature Prediction Derived from Satellite Altimetry Product in South China Sea. Remote Sensing, 17(16), 2916. https://doi.org/10.3390/rs17162916






