Estimating Position, Diameter at Breast Height, and Total Height of Eucalyptus Trees Using Portable Laser Scanning
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
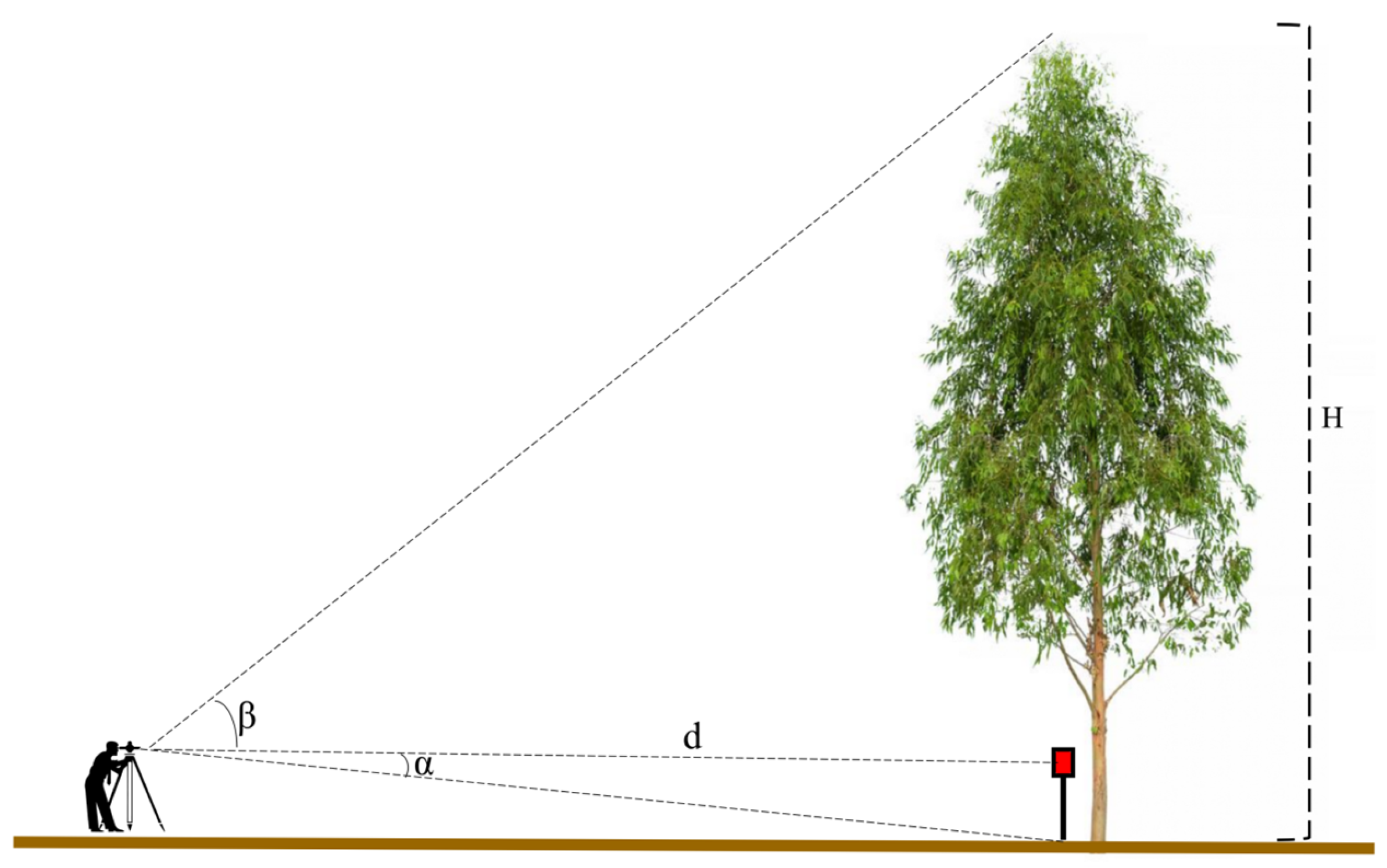
2.2. Tradicional Forest Inventory
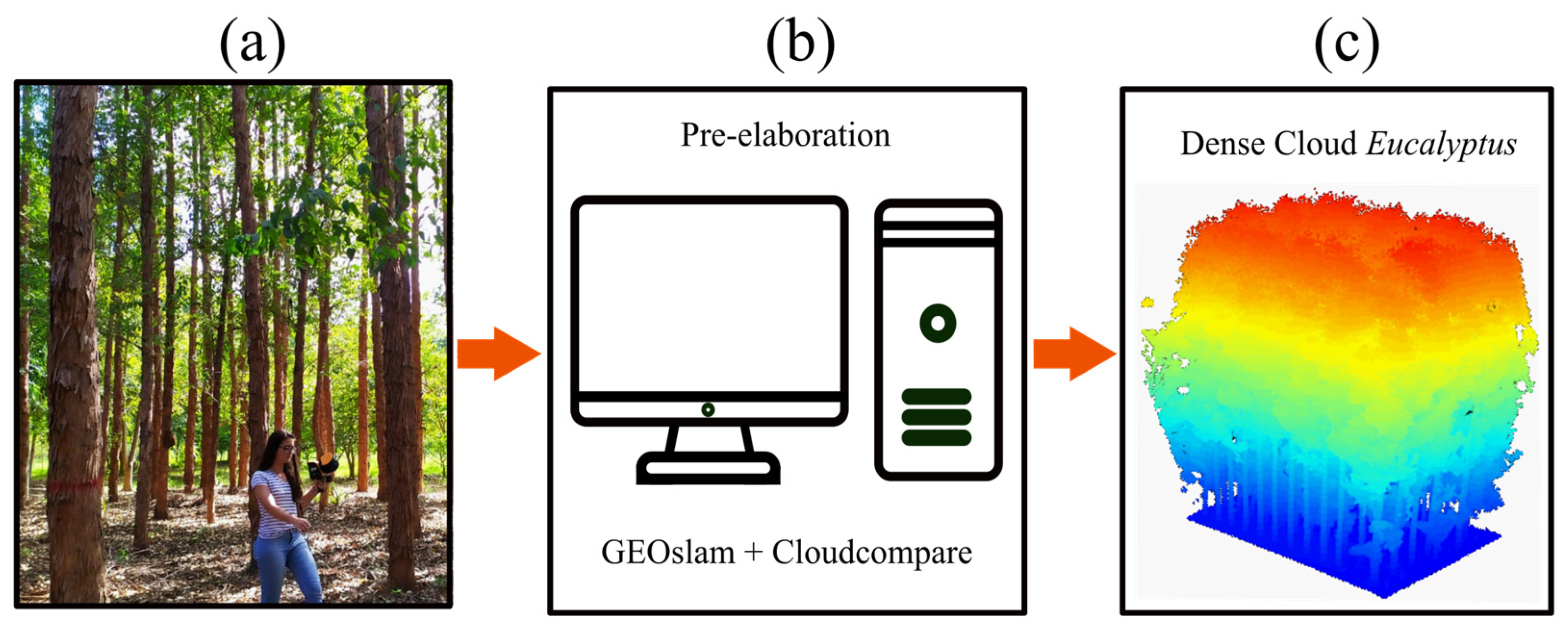
2.3. Portable Laser Scanning (PLS)
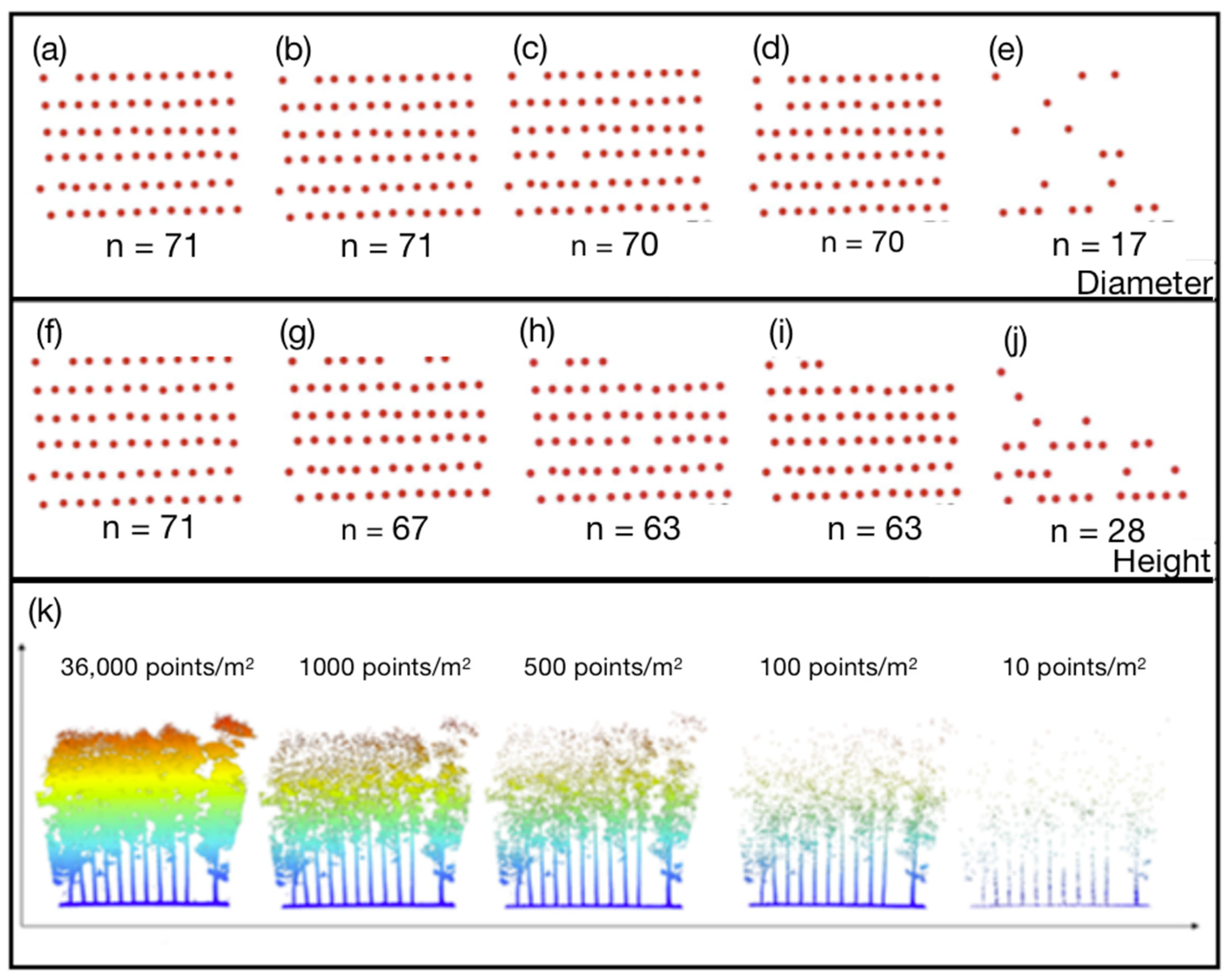
2.3.1. Resampling Point Clouds
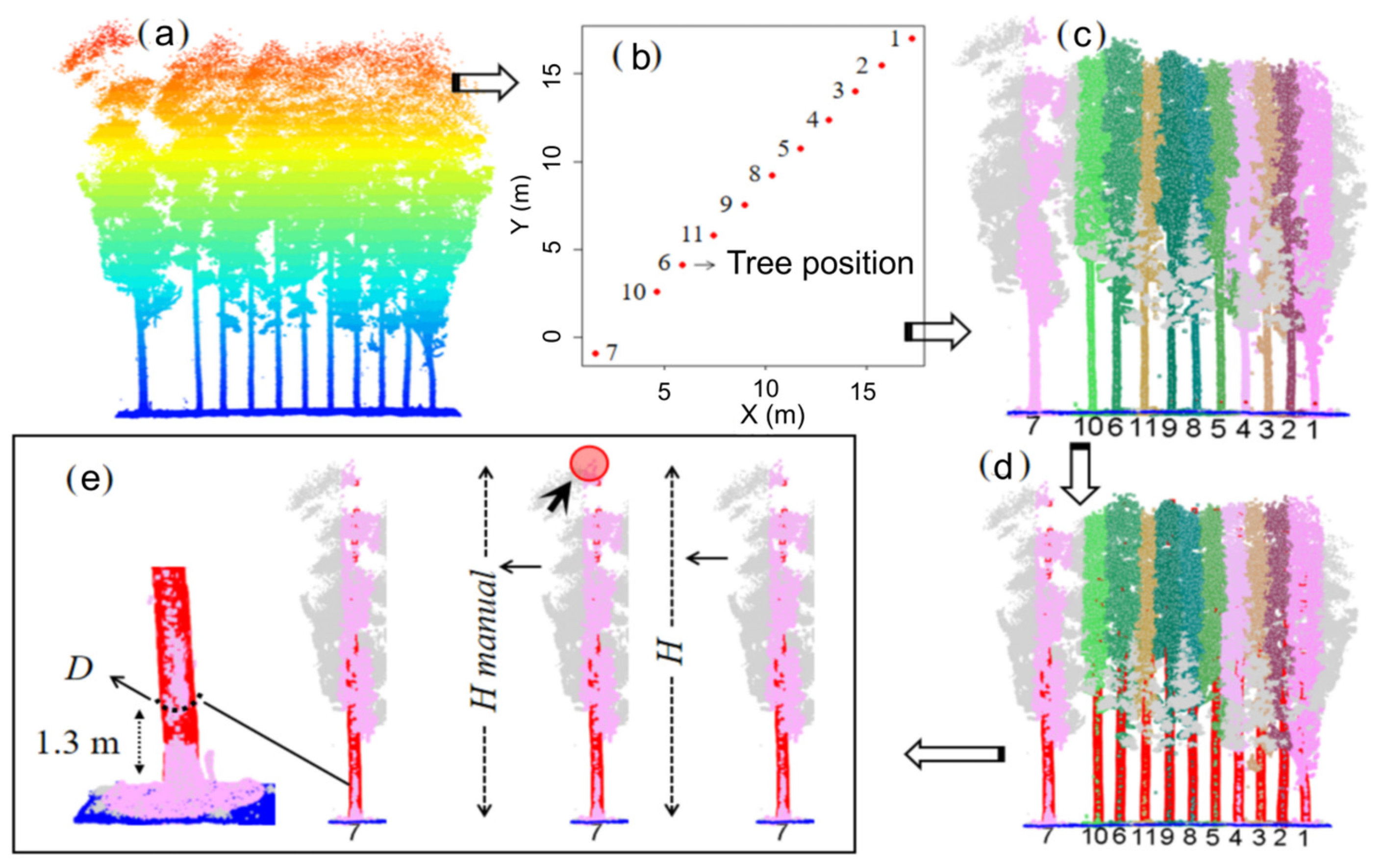
2.3.2. Automatic Tree Detection
2.3.3. Semi-Automatic Tree Height
2.4. Analysis of the DBH and H Estimations
3. Results
3.1. Stem Detection
3.2. DBH Estimation
3.3. Total Height Estimation
4. Discussion
4.1. Stem Detection
4.2. DBH Estimation
4.3. Total Height Estimation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CSF | Cloth simulation filter |
| DBH | Diameter at breast height |
| GNSS | Global Navigation Satellite System |
| H | Total height |
| ICS | Initial Coordinate System |
| IMU | Inertial Measurement Unit |
| LiDAR | Light Detection and Ranging |
| PLS | Portable laser scanner |
| RMSE | Root-mean square error |
| SLAM | Simultaneous Localization and Mapping |
Appendix A
| Returns | Total Height Class | N * | Mean | RMSE | BIAS | |||
|---|---|---|---|---|---|---|---|---|
| Total Station (m) | PLS-SLAM (m) | Abs (m) | % | Abs (m) | % | |||
| Automatic | ||||||||
| 36,000 | All H | 71 | 29.5 | 30.9 (4.75%) | 4.8 | 14.4 | −1.4 | −4.8 |
| 1000 | 67 | 30.1 (2.03%) | 4.0 | 13.7 | 1.2 | 4.0 | ||
| 500 | 63 | 29.6 (0.34%) | 3.9 | 13.5 | −0.1 | −0.5 | ||
| 100 | 63 | 28.2 (−4.41%) | 5.0 | 17.4 | 0.7 | 2.4 | ||
| 10 | 28 | 25.4 (−13.9%) | 8.4 | 28.4 | 5.7 | 18.4 | ||
| 36,000 | H ≤ 31.4 m | 35 | 24.8 | 28.7 (15.7%) | 5.9 | 23.8 | −3.9 | −15.7 |
| 1000 | 34 | 27.8 (12.1%) | 5.3 | 21.6 | −3.1 | −12.6 | ||
| 500 | 33 | 27.5 (10.9%) | 5.1 | 20.4 | −2.6 | −10.4 | ||
| 100 | 34 | 25.9 (3.62%) | 6.1 | 24.7 | −1.2 | −4.8 | ||
| 10 | 13 | 24.5 (−1.21%) | 6.6 | 24.2 | 2.7 | 9.8 | ||
| 36,000 | H > 31.4 m | 36 | 34.0 | 33.0 (8.55%) | 1.3 | 3.9 | 1.0 | 2.9 |
| 1000 | 33 | 32.4 (6.58%) | 1.8 | 5.3 | 1.6 | 4.7 | ||
| 500 | 30 | 32.0 (5.26%) | 2.1 | 6.3 | 1.9 | 5.6 | ||
| 100 | 29 | 31.0 (1.97%) | 3.4 | 9.9 | 2.9 | 8.6 | ||
| 10 | 15 | 26.1 (−14.15%) | 9.7 | 28.2 | 8.4 | 24.3 | ||
| Semi-Automatic | ||||||||
| 36,000 | All H | 71 | 29.5 | 29.0 (−1.69%) | 1.2 | 4.2 | 0.4 | 1.5 |
| 1000 | 28.5 (−3.39%) | 1.7 | 5.6 | 0.9 | 3.2 | |||
| 500 | 28.6 (−3.05%) | 1.7 | 5.6 | 0.9 | 3.0 | |||
| 100 | 28.0 (−5.08%) | 2.4 | 8.0 | 1.5 | 5.1 | |||
| 10 | 25.3 (−14.2%) | 5.0 | 17.1 | 4.2 | 14.2 | |||
| 36,000 | H ≤ 31.4 m | 35 | 24.8 | 25.1 (1.21%) | 1.1 | 4.3 | −0.3 | −1.1 |
| 1000 | 24.7 (−0.40%) | 1.3 | 5.2 | 0.1 | 0.4 | |||
| 500 | 24.8 (−0.00%) | 1.3 | 5.1 | 0.0 | 0.0 | |||
| 100 | 24.6 (−0.81%) | 1.5 | 6.0 | 0.3 | 1.1 | |||
| 10 | 21.5 (−13.3%) | 4.4 | 17.6 | 3.3 | 13.3 | |||
| 36,000 | H > 31.4 m | 36 | 34.0 | 32.9 (−3.24%) | 1.4 | 4.1 | 1.1 | 3.3 |
| 1000 | 32.2 (−5.29%) | 1.9 | 5.7 | 1.8 | 5.2 | |||
| 500 | 32.2 (−5.29%) | 2.0 | 5.8 | 1.8 | 5.2 | |||
| 100 | 31.3 (−7.94%) | 3.0 | 8.7 | 2.7 | 8.0 | |||
| 10 | 28.9 (−15.0%) | 5.6 | 16.4 | 5.1 | 14.9 | |||
References
- Florêncio, G.W.L.; Martins, F.B.; Fagundes, F.F.A. Climate Change on Eucalyptus Plantations and Adaptive Measures for Sustainable Forestry Development across Brazil. Ind. Crops Prod. 2022, 188, 115538. [Google Scholar] [CrossRef]
- Mao, X.; Zheng, H.; Luo, G.; Liao, S.; Wang, R.; Tang, M.; Chen, H. Climate Change Favors Expansion of Three Eucalyptus Species in China. Front. Plant Sci. 2024, 15, 1443134. [Google Scholar] [CrossRef]
- IBÁ, I.B.; De, Á. IBÁ Annual Report 2022; IBÁ: Prague, Czech Republic, 2023. [Google Scholar]
- Shao, J.; Zhang, W.; Mellado, N.; Wang, N.; Jin, S.; Cai, S.; Luo, L.; Lejemble, T.; Yan, G. SLAM-Aided Forest Plot Mapping Combining Terrestrial and Mobile Laser Scanning. ISPRS J. Photogramm. Remote Sens. 2020, 163, 214–230. [Google Scholar] [CrossRef]
- Liu, G.; Wang, J.; Dong, P.; Chen, Y.; Liu, Z. Estimating Individual Tree Height and Diameter at Breast Height (DBH) from Terrestrial Laser Scanning (TLS) Data at Plot Level. Forests 2018, 9, 398. [Google Scholar] [CrossRef]
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest Inventory with Terrestrial LiDAR: A Comparison of Static and Hand-Held Mobile Laser Scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef]
- Pierzchała, M.; Giguère, P.; Astrup, R. Mapping Forests Using an Unmanned Ground Vehicle with 3D LiDAR and Graph-SLAM. Comput. Electron. Agric. 2018, 145, 217–225. [Google Scholar] [CrossRef]
- Mokroš, M.; Vỳbošt’ok, J.; Tomaštík, J.; Grznárová, A.; Valent, P.; Slavík, M.; Merganič, J. High Precision Individual Tree Diameter and Perimeter Estimation from Close-Range Photogrammetry. Forests 2018, 9, 696. [Google Scholar] [CrossRef]
- Chen, S.; Liu, H.; Feng, Z.; Shen, C.; Chen, P. Applicability of Personal Laser Scanning in Forestry Inventory. PLoS ONE 2019, 14, e0211392. [Google Scholar] [CrossRef]
- Hyyppä, E.; Kukko, A.; Kaijaluoto, R.; White, J.C.; Wulder, M.A.; Pyörälä, J.; Liang, X.; Yu, X.; Wang, Y.; Kaartinen, H. Accurate Derivation of Stem Curve and Volume Using Backpack Mobile Laser Scanning. ISPRS J. Photogramm. Remote Sens. 2020, 161, 246–262. [Google Scholar] [CrossRef]
- Durrant-Whyte, H.; Bailey, T. Simultaneous Localization and Mapping: Part I. IEEE Robot. Autom. Mag. 2006, 13, 99–110. [Google Scholar] [CrossRef]
- Bailey, T.; Durrant-Whyte, H. Simultaneous Localization and Mapping (SLAM): Part II. IEEE Robot. Autom. Mag. 2006, 13, 108–117. [Google Scholar] [CrossRef]
- Qian, C.; Liu, H.; Tang, J.; Chen, Y.; Kaartinen, H.; Kukko, A.; Zhu, L.; Liang, X.; Chen, L.; Hyyppä, J. An Integrated GNSS/INS/LiDAR-SLAM Positioning Method for Highly Accurate Forest Stem Mapping. Remote Sens. 2016, 9, 3. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-Time. In Proceedings of the Robotics: Science and Systems, Berkeley, CA, USA, 12–16 July 2014; Volume 2, pp. 1–9. [Google Scholar]
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; Gonçalves, J.D.M.; Sparovek, G. Köppen’s Climate Classification Map for Brazil. Meteorol. Z. 2013, 22, 711–728. [Google Scholar] [CrossRef] [PubMed]
- Instituto Capixaba de Pesquisa, Assistência Técnica e Extensão Rural. Programa de Assistência Técnica e Rural Jerônimo Montero (PROATER 2020–2023); Incaper: Vitória, ES, Brazil, 2020.
- Haglöf Sweden. Haglöf Mantax Blue Caliper; Haglöf Sweden: Stockholm, Sweden, 2021. [Google Scholar]
- Leica Geosystems. Leica FlexLine TS02plus—Data Sheet; Leica Geosystems: St. Gallen, Switzerland, 2022. [Google Scholar]
- GeoSLAM. Zeb Horizon The Ultimate Mobile Mapping Solution; GeoSLAM: Nottingham, UK, 2022. [Google Scholar]
- GeoSLAM. What Is SLAM (Simultaneous Localisation and Mapping)? GeoSLAM: Nottingham, UK, 2022. [Google Scholar]
- CLOUDCOMPARE. CloudCompare (Version 2.13.2) [GLP Software]. 2022. Available online: https://www.cloudcompare.org/ (accessed on 10 April 2025).
- Roussel, J.-R.; Auty, D. lidR: Airborne LiDAR Data Manipulation and Visualization for Forestry Applications, R Package Version 3.1.4; The R Foundation: Vienna, Australia, 2022.
- R Core Team. R: The R Project for Statistical Computing; The R Foundation: Vienna, Australia, 2022. [Google Scholar]
- De Conto, T. TreeLS: Terrestrial Point Cloud Processing of Forest Data; The R Foundation: Vienna, Australia, 2022. [Google Scholar]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Olofsson, K.; Holmgren, J.; Olsson, H. Tree Stem and Height Measurements Using Terrestrial Laser Scanning and the RANSAC Algorithm. Remote Sens. 2014, 6, 4323–4344. [Google Scholar] [CrossRef]
- Tittmann, P.; Shafii, S.; Hartsough, B.; Hamann, B. Tree Detection and Delineation from LiDAR Point Clouds Using RANSAC. In Proceedings of the SilviLaser 2011, Hobart, TAS, Australia, 16–19 October 2011. [Google Scholar]
- de Conto, T.; Olofsson, K.; Görgens, E.B.; Rodriguez, L.C.E.; Almeida, G. Performance of Stem Denoising and Stem Modelling Algorithms on Single Tree Point Clouds from Terrestrial Laser Scanning. Comput. Electron. Agric. 2017, 143, 165–176. [Google Scholar] [CrossRef]
- Heinzel, J.; Huber, M.O. Tree Stem Diameter Estimation from Volumetric TLS Image Data. Remote Sens. 2017, 9, 614. [Google Scholar] [CrossRef]
- Ryding, J.; Williams, E.; Smith, M.J.; Eichhorn, M.P. Assessing Handheld Mobile Laser Scanners for Forest Surveys. Remote Sens. 2015, 7, 1095–1111. [Google Scholar] [CrossRef]
- Cabo, C.; Del Pozo, S.; Rodríguez-Gonzálvez, P.; Ordóñez, C.; González-Aguilera, D. Comparing Terrestrial Laser Scanning (TLS) and Wearable Laser Scanning (WLS) for Individual Tree Modeling at Plot Level. Remote Sens. 2018, 10, 540. [Google Scholar] [CrossRef]
- Gollob, C.; Ritter, T.; Nothdurft, A. Forest Inventory with Long Range and High-Speed Personal Laser Scanning (PLS) and Simultaneous Localization and Mapping (SLAM) Technology. Remote Sens. 2020, 12, 1509. [Google Scholar] [CrossRef]
- Chiappini, S.; Pierdicca, R.; Malandra, F.; Tonelli, E.; Malinverni, E.S.; Urbinati, C.; Vitali, A. Comparing Mobile Laser Scanner and Manual Measurements for Dendrometric Variables Estimation in a Black Pine (Pinus Nigra Arn.) Plantation. Comput. Electron. Agric. 2022, 198, 107069. [Google Scholar] [CrossRef]
- Liang, X.; Kukko, A.; Kaartinen, H.; Hyyppä, J.; Yu, X.; Jaakkola, A.; Wang, Y. Possibilities of a Personal Laser Scanning System for Forest Mapping and Ecosystem Services. Sensors 2014, 14, 1228–1248. [Google Scholar] [CrossRef]
- Jurjević, L.; Liang, X.; Gašparović, M.; Balenović, I. Is Field-Measured Tree Height as Reliable as Believed–Part II, A Comparison Study of Tree Height Estimates from Conventional Field Measurement and Low-Cost Close-Range Remote Sensing in a Deciduous Forest. ISPRS J. Photogramm. Remote Sens. 2020, 169, 227–241. [Google Scholar] [CrossRef]



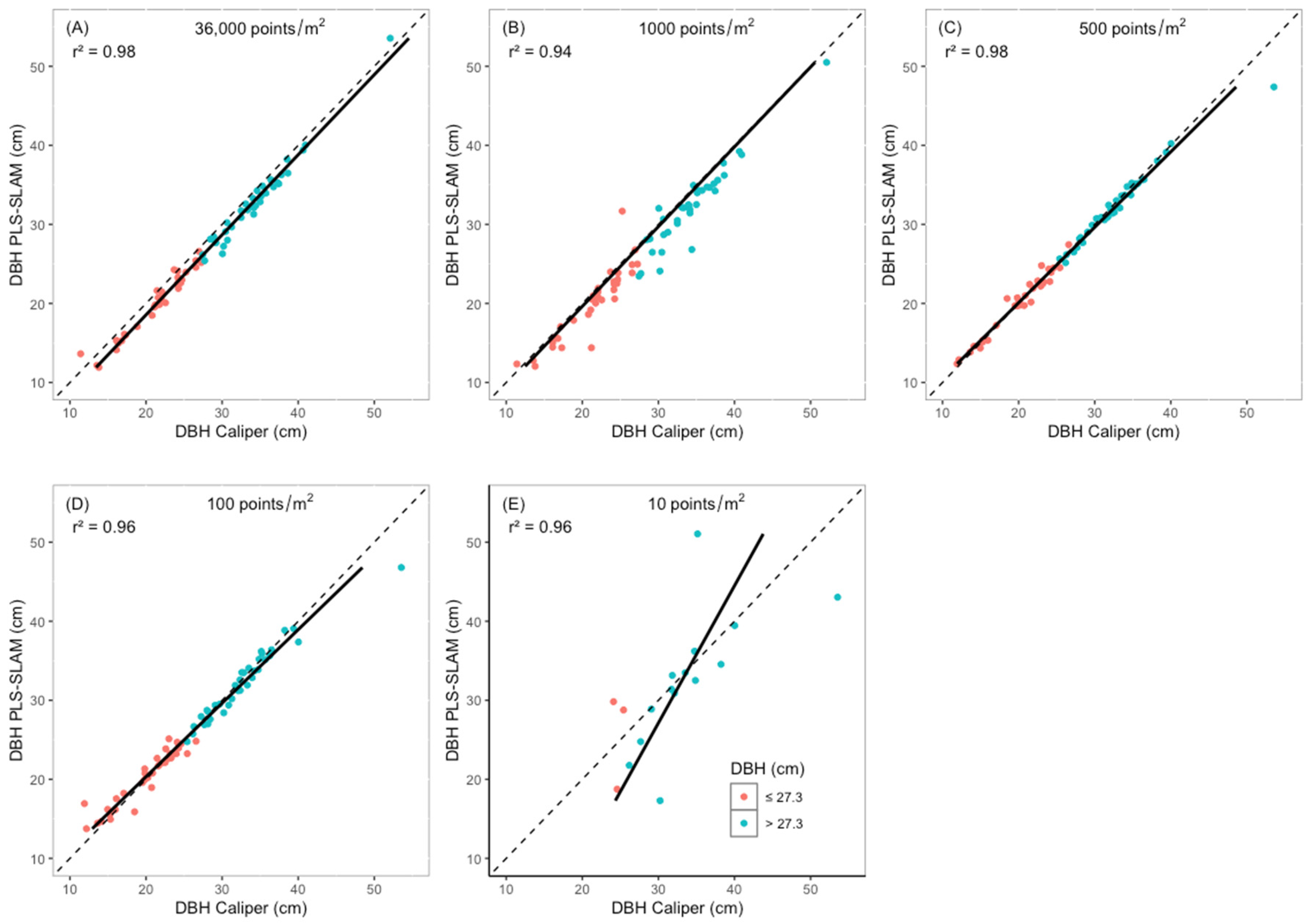
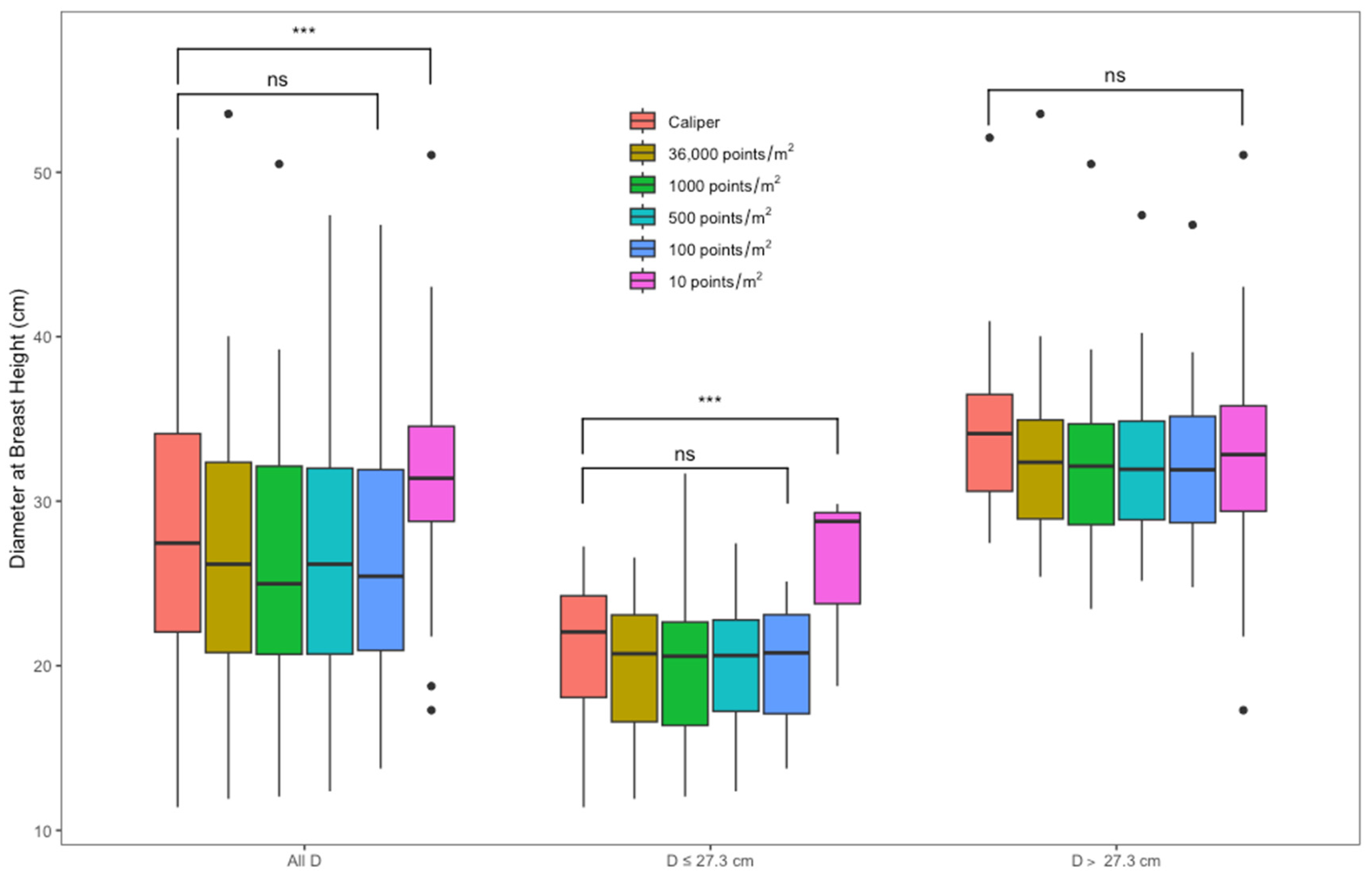

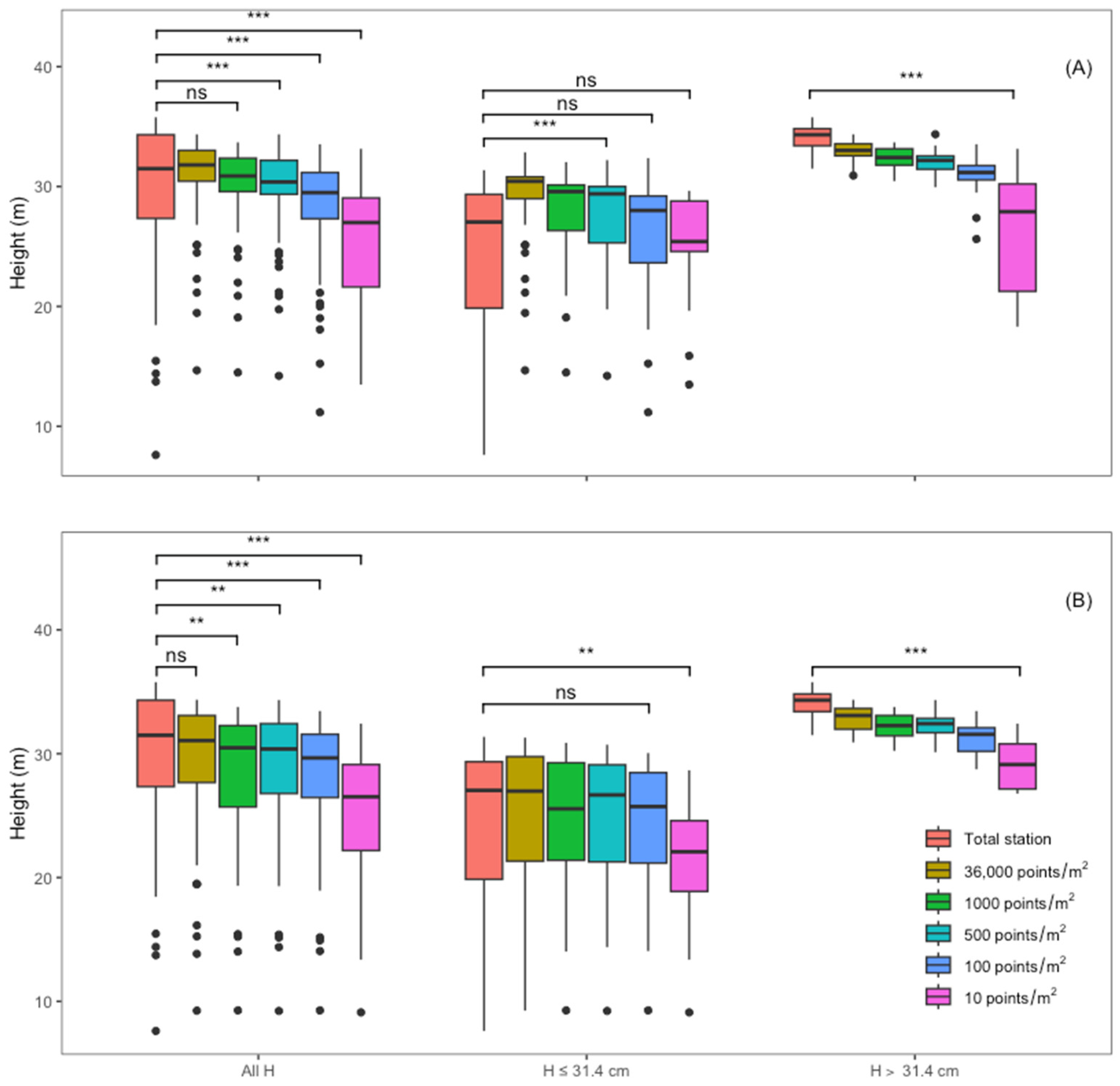
| Returns | Diameter Class | N * | Mean | RMSE | BIAS | |||
|---|---|---|---|---|---|---|---|---|
| Caliper (cm) | PLS-SLAM (cm) | Abs (cm) | % | Abs (cm) | % | |||
| 36,000 | All DBH | 71 | 27.8 | 26.5 (−4.67%) | 1.6 | 5.9 | 1.3 | 4.8 |
| 1000 | 71 | 26.2 (−5.75%) | 2.4 | 9.3 | 1.7 | 5.9 | ||
| 500 | 70 | 26.4 (−5.03%) | 1.9 | 6.8 | 1.5 | 5.5 | ||
| 100 | 70 | 26.4 (−5.03%) | 2.1 | 7.4 | 1.5 | 5.2 | ||
| 10 | 17 | 31.5 (13,3%) | 6.3 | 18.8 | 2.1 | 6.2 | ||
| 36,000 | DBH ≤ 27.3 cm | 35 | 21.3 | 20.1 (−5.63%) | 1.6 | 7.3 | 1.3 | 5.9 |
| 1000 | 35 | 20.1 (−5.63%) | 2.3 | 10.6 | 1.3 | 6.0 | ||
| 500 | 33 | 20.1 (−5.63%) | 1.6 | 7.4 | 1.2 | 5.7 | ||
| 100 | 34 | 20.2 (−5.16%) | 1.8 | 8.7 | 1.0 | 4.5 | ||
| 10 | 3 | 25.8 (−21.1%) | 5.7 | 22.2 | 0.0 | −0.2 | ||
| 36,000 | DBH > 27.3 cm | 36 | 34.1 | 32.7 (−4.11%) | 1.7 | 5.0 | 1.4 | 4.2 |
| 1000 | 36 | 32.1 (−5.86%) | 2.6 | 7.7 | 2.0 | 5.9 | ||
| 500 | 36 | 32.3 (−5.27%) | 2.2 | 6.3 | 1.9 | 5.4 | ||
| 100 | 36 | 32.2 (−5.57%) | 2.3 | 6.6 | 1.9 | 5.6 | ||
| 10 | 14 | 32.8 (−3.81%) | 6.2 | 17.6 | 2.5 | 7.2 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Machado, M.D.; da Silva, G.F.; de Almeida, A.Q.; de Mendonça, A.R.; Martins-Neto, R.P.; Schimalski, M.B. Estimating Position, Diameter at Breast Height, and Total Height of Eucalyptus Trees Using Portable Laser Scanning. Remote Sens. 2025, 17, 2904. https://doi.org/10.3390/rs17162904
Machado MD, da Silva GF, de Almeida AQ, de Mendonça AR, Martins-Neto RP, Schimalski MB. Estimating Position, Diameter at Breast Height, and Total Height of Eucalyptus Trees Using Portable Laser Scanning. Remote Sensing. 2025; 17(16):2904. https://doi.org/10.3390/rs17162904
Chicago/Turabian StyleMachado, Milena Duarte, Gilson Fernandes da Silva, André Quintão de Almeida, Adriano Ribeiro de Mendonça, Rorai Pereira Martins-Neto, and Marcos Benedito Schimalski. 2025. "Estimating Position, Diameter at Breast Height, and Total Height of Eucalyptus Trees Using Portable Laser Scanning" Remote Sensing 17, no. 16: 2904. https://doi.org/10.3390/rs17162904
APA StyleMachado, M. D., da Silva, G. F., de Almeida, A. Q., de Mendonça, A. R., Martins-Neto, R. P., & Schimalski, M. B. (2025). Estimating Position, Diameter at Breast Height, and Total Height of Eucalyptus Trees Using Portable Laser Scanning. Remote Sensing, 17(16), 2904. https://doi.org/10.3390/rs17162904








