Assessing Kernel-Driven Models’ Efficacy in Urban Thermal Radiation Directionality Modeling Using DART-Simulated Scenarios
Abstract
1. Introduction
2. Study Area Materials
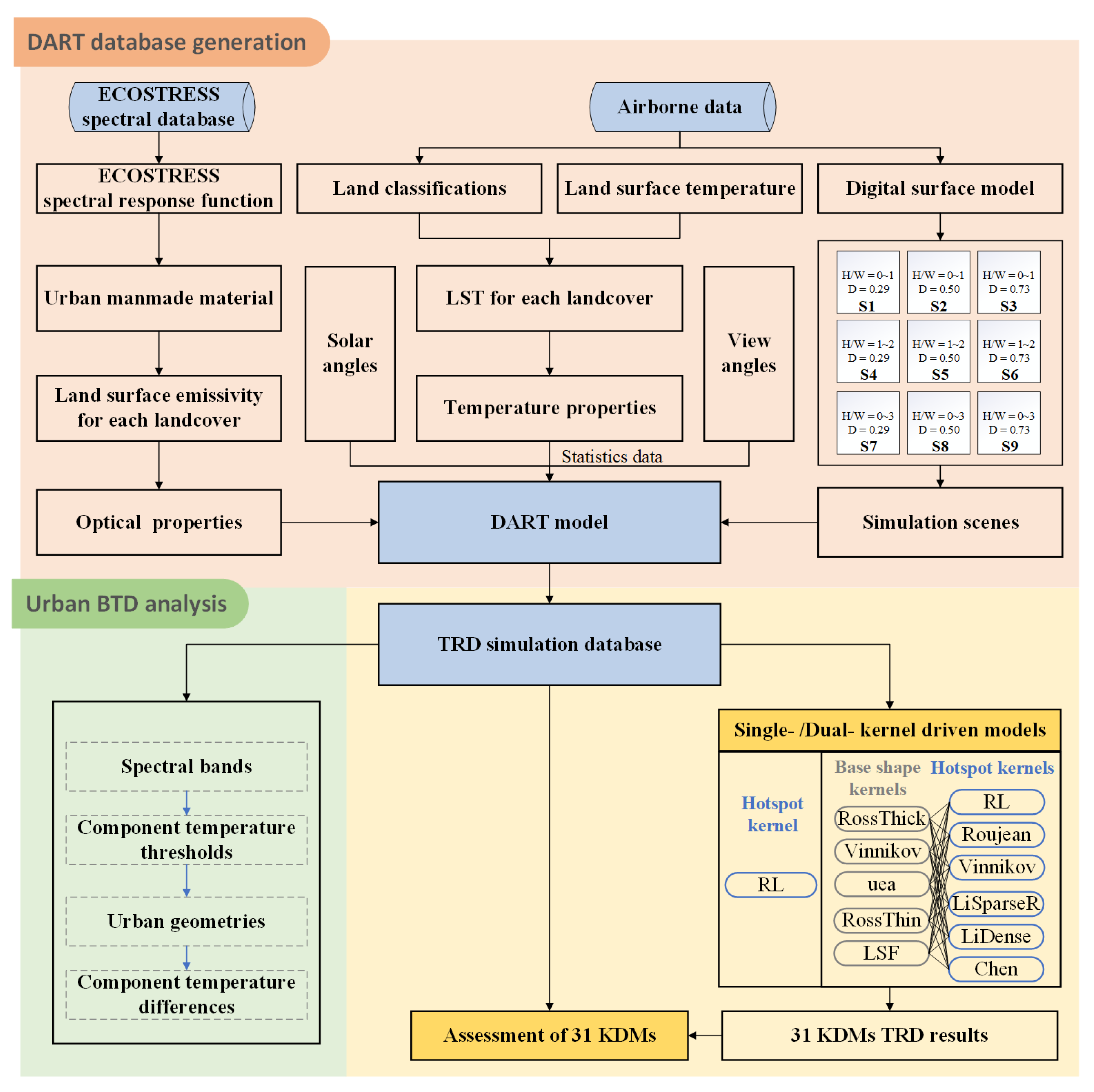
2.1. DART Model
2.2. Airborne LST Data of the DESIREX 2008 Campaign
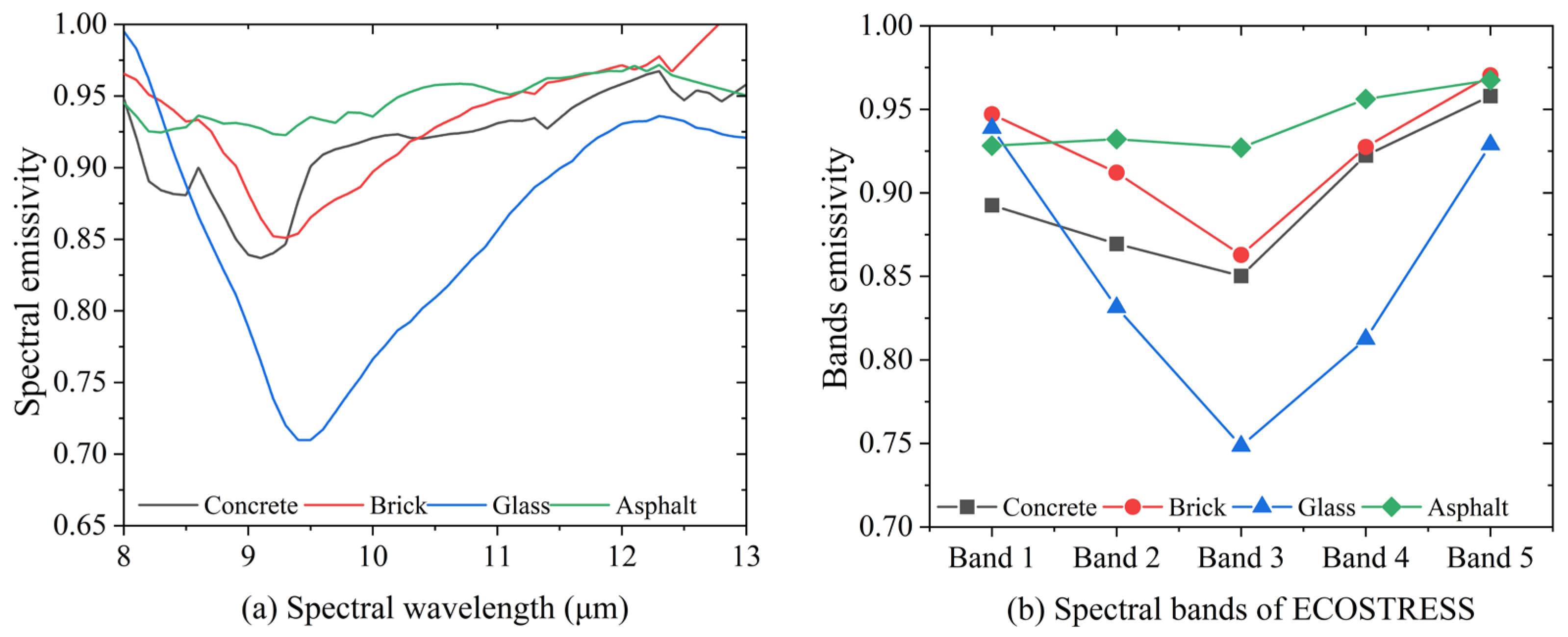
2.3. Spectral Properties
2.4. Simulation Scenarios
3. Kernel-Driven Models
3.1. Base-Shape Kernel
- (1)
- (2)
- Vinnikov kernel [24]
- (3)
- usea kernel [28]
- (4)
- RossThin kernel [55]
- (5)
- LSF kernel [25]
3.2. Hotspot Kernel
- (1)
- (2)
- Roujean kernel [29]
- (3)
- Vinnikov kernel [24]
- (4)
- (5)
- (6)
- Chen kernel [60]
4. Results and Analysis
4.1. Analysis of DART Simulation Dataset
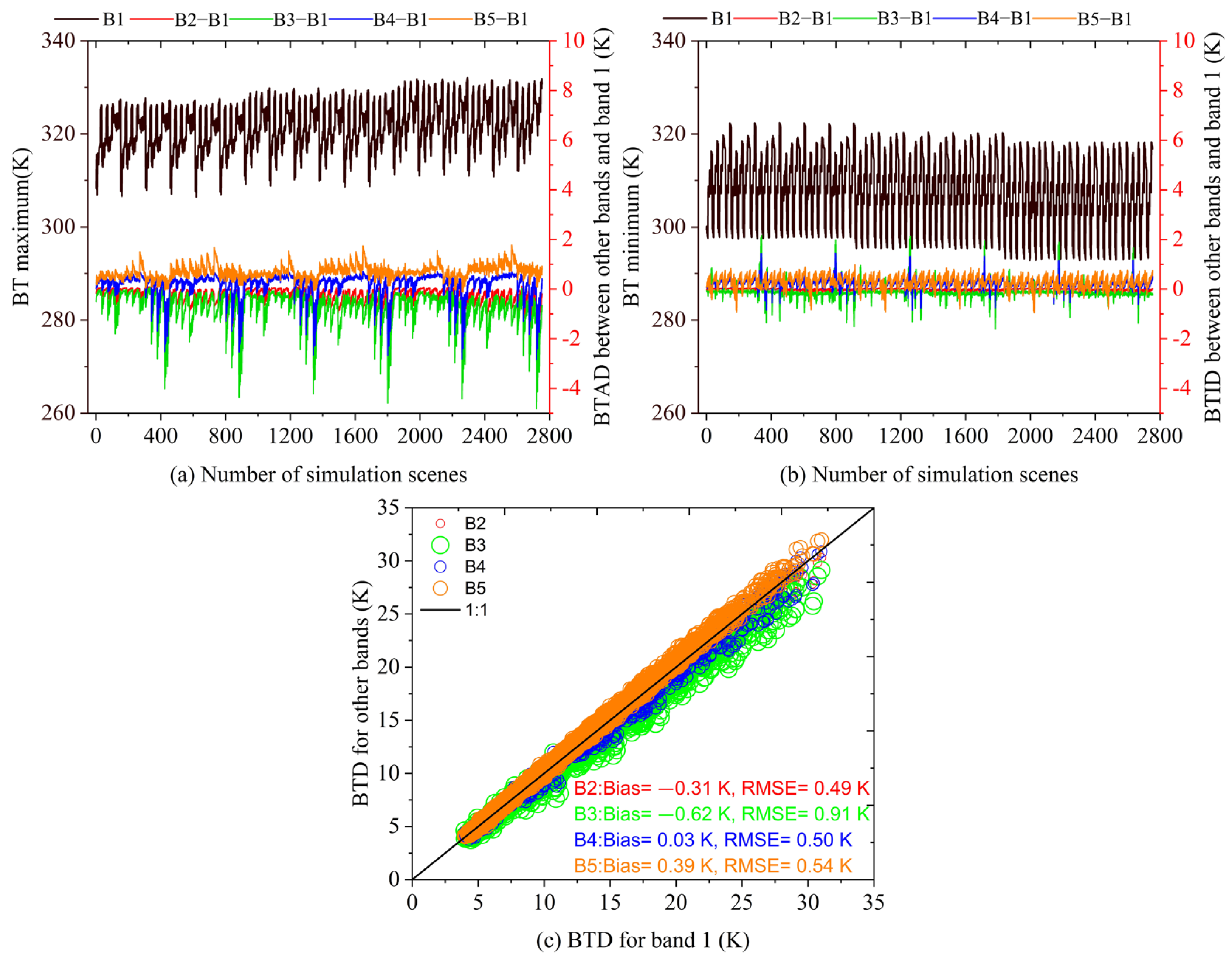
4.1.1. The BTD in Different ECOSTRESS Spectral Bands
4.1.2. The BTD in Different Component Temperature Thresholds
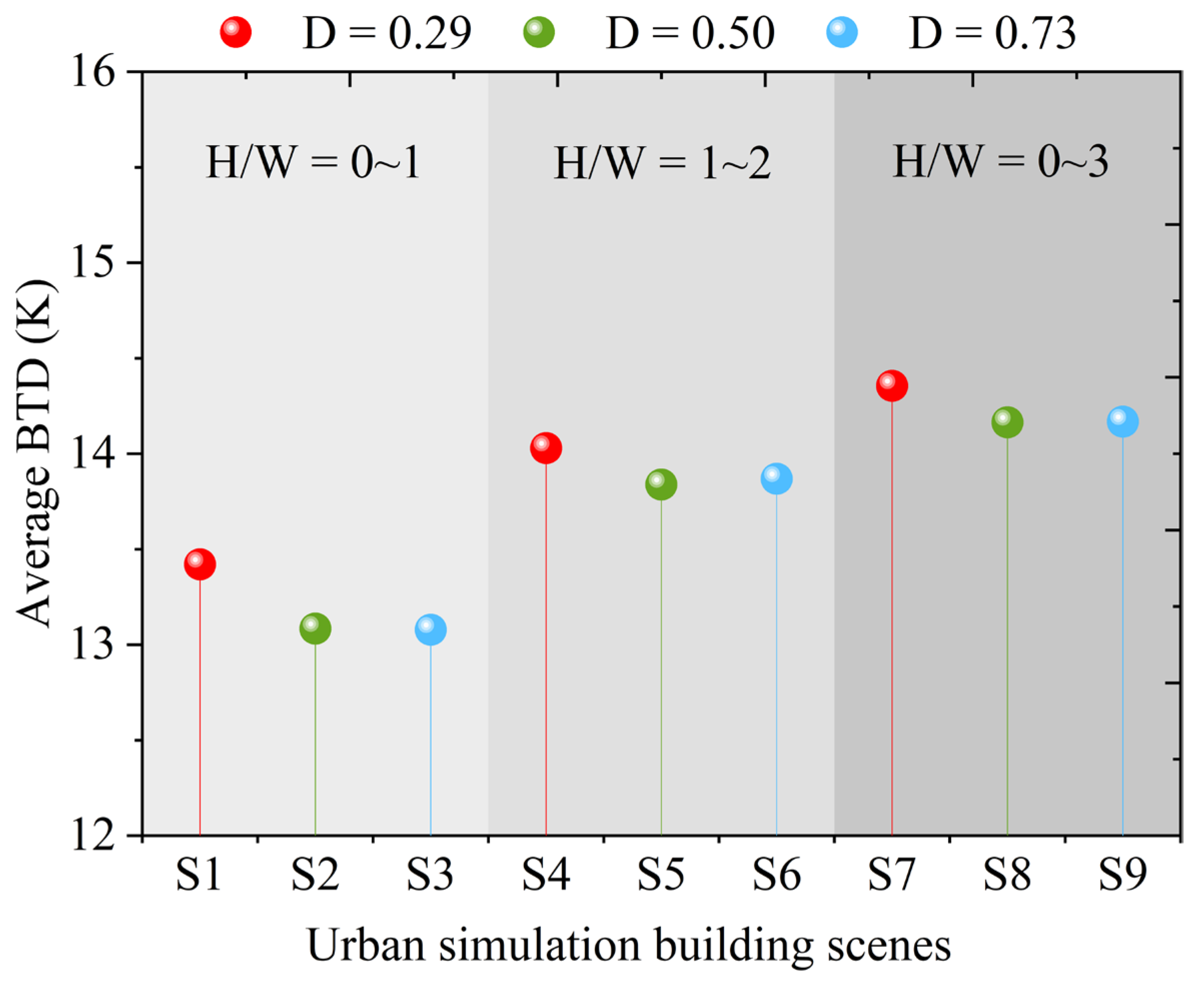
4.1.3. The BTD in Different Urban Geometries
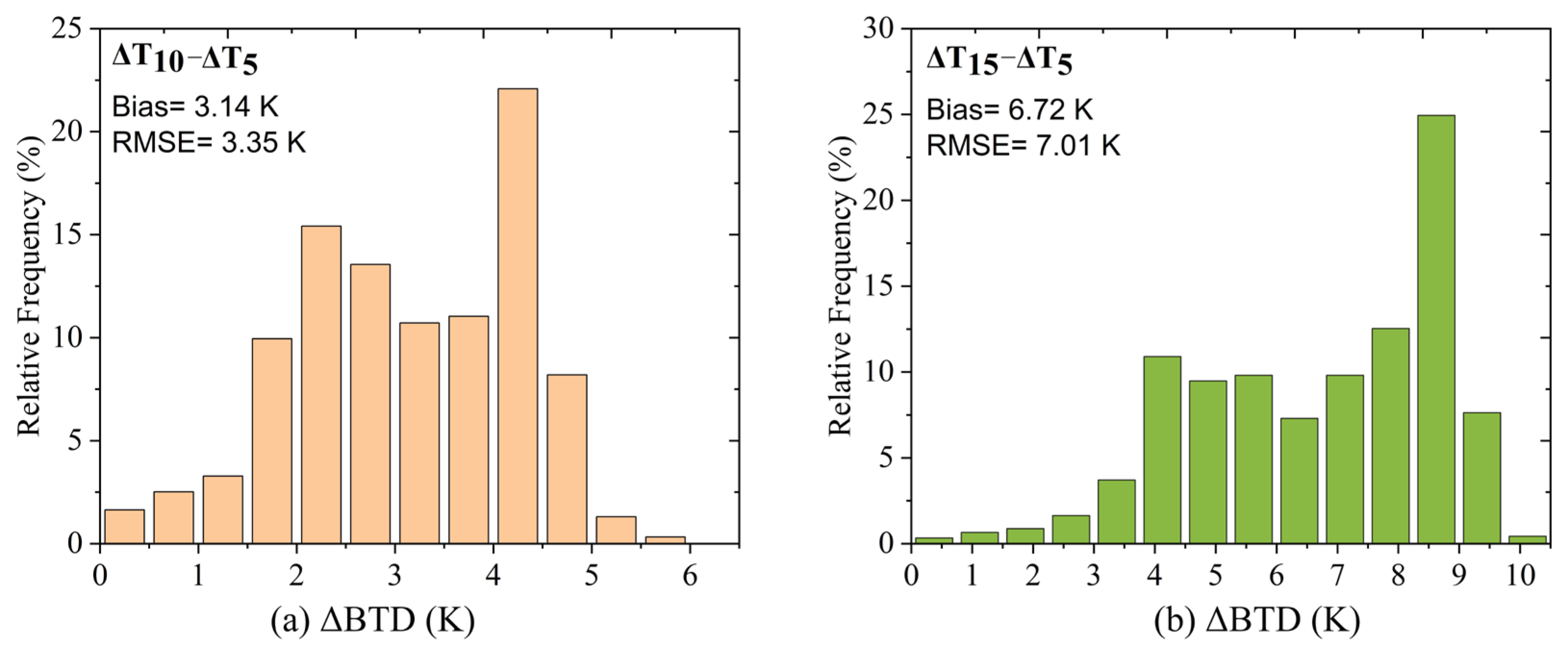
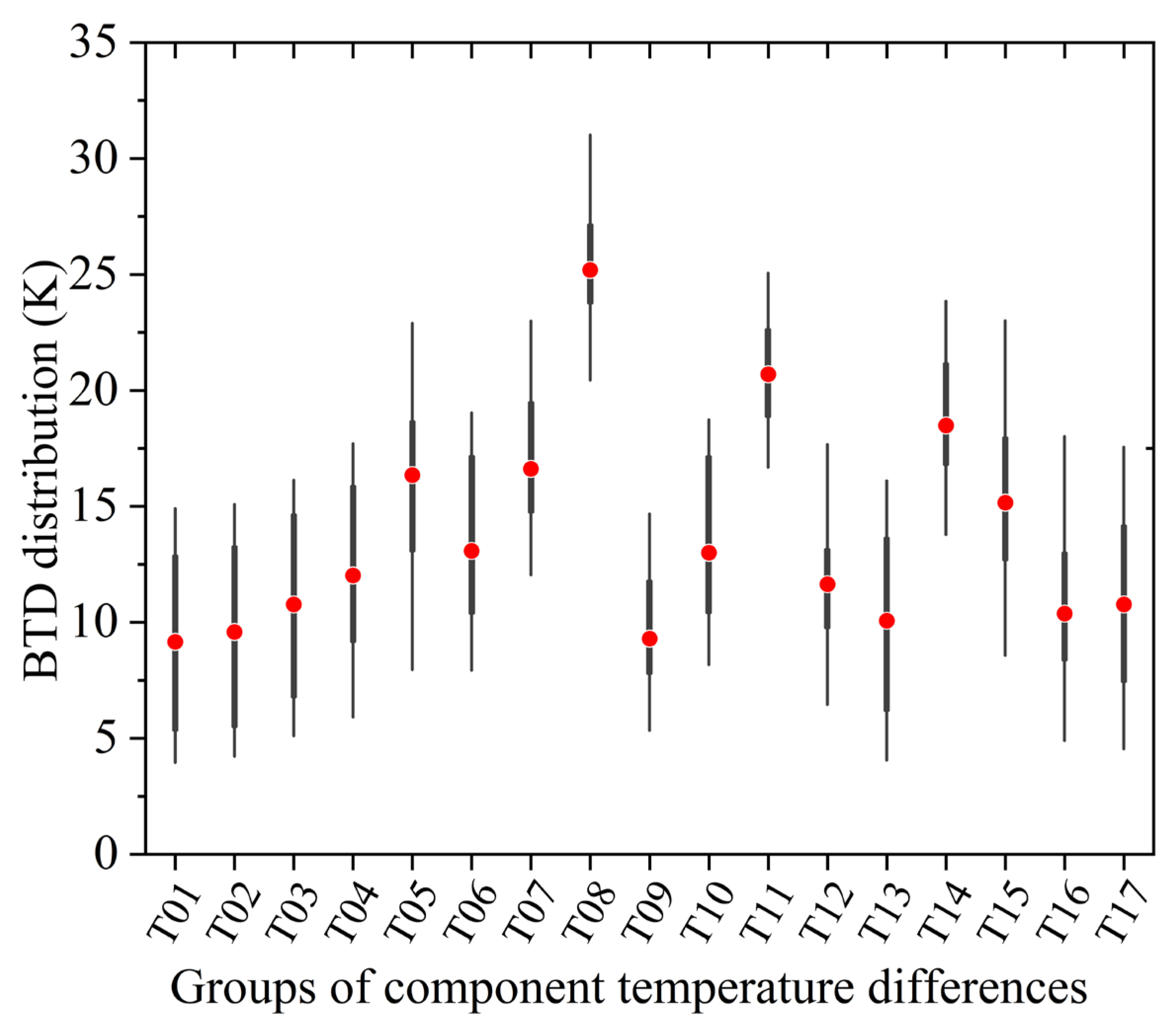
4.1.4. The BTD in Various Component Temperature Differences
4.2. Comparison Between Kernel-Driven Models and DART Simulation TRDs
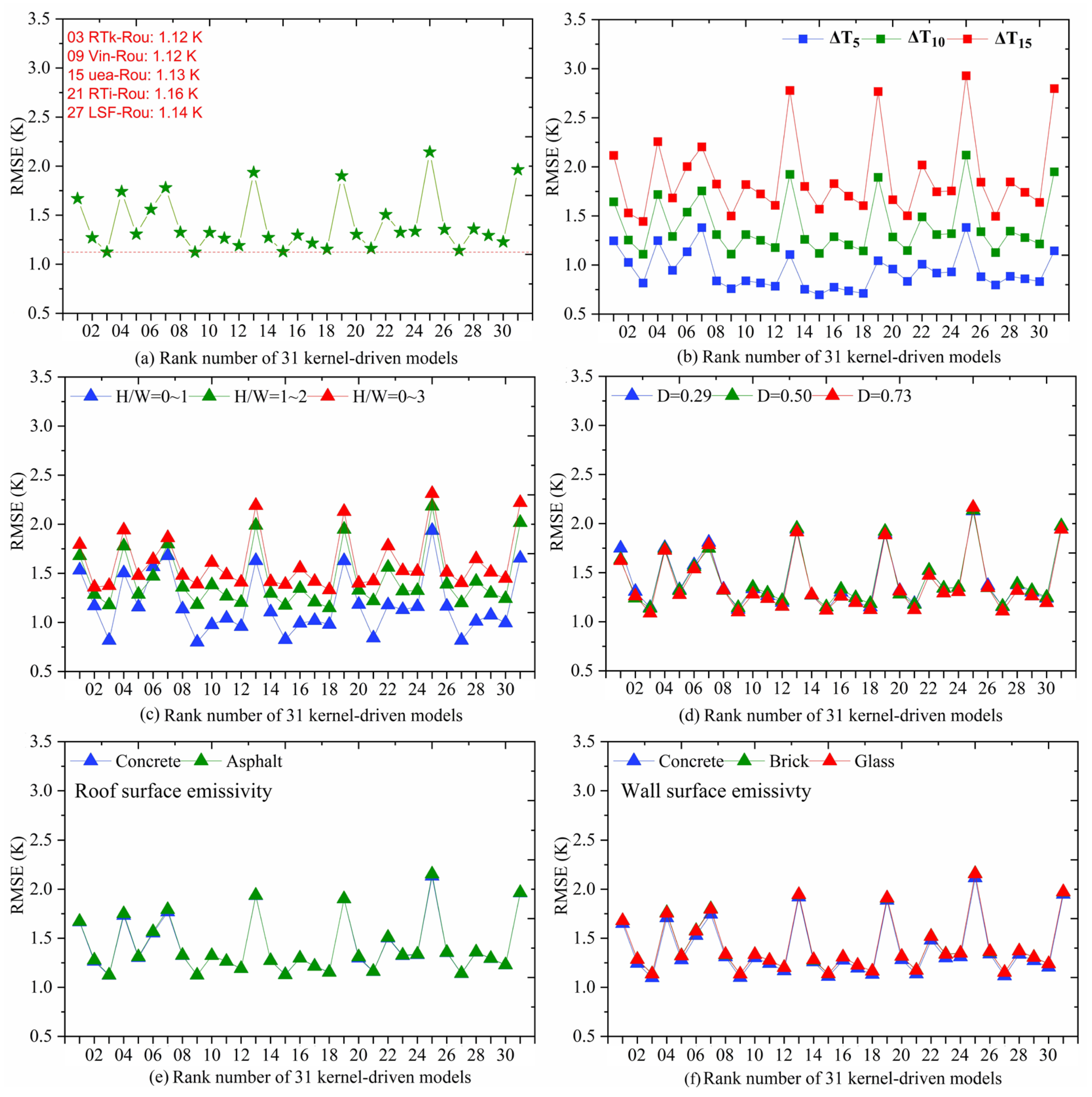
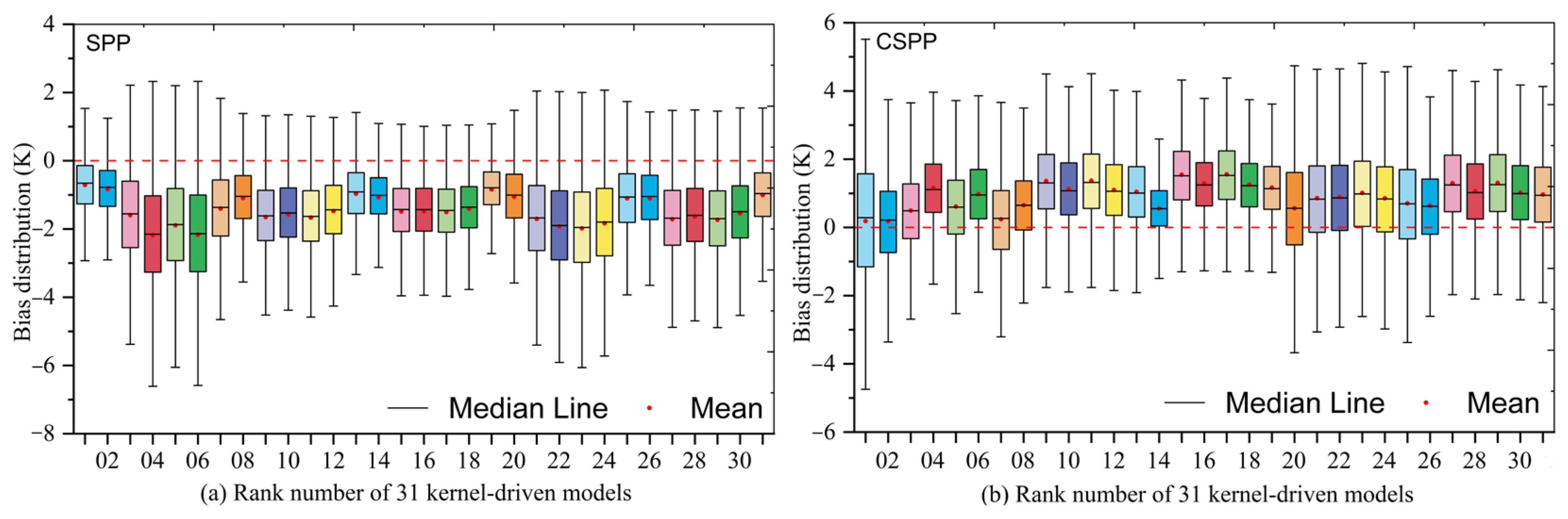
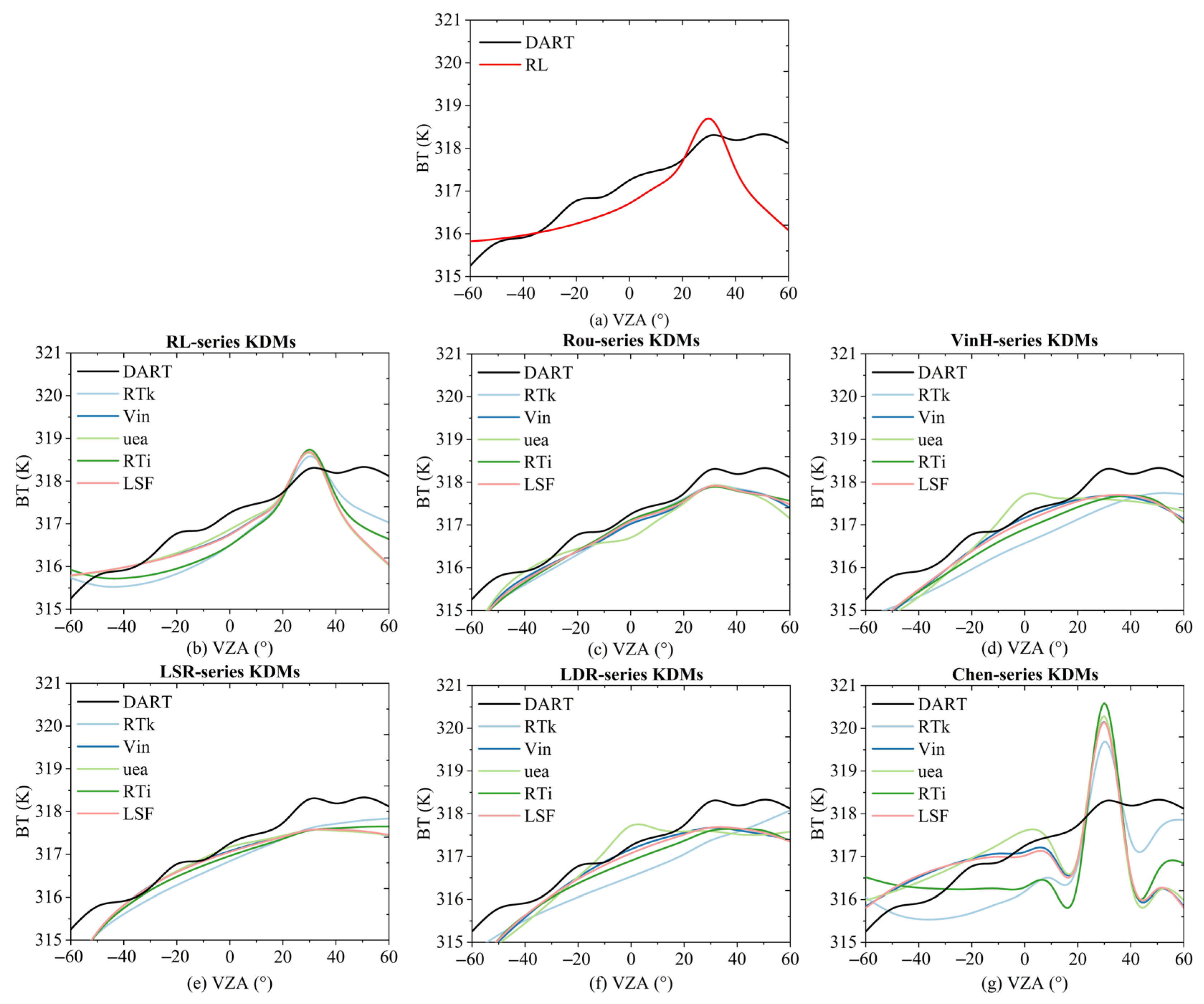
4.2.1. The Performance of Kernel-Driven Models in All Simulations
- (1)
- The magnitude of RMSE increases with the increase in the ΔT from 5 K to 10 K for each KDM, and 31 KDMs are sensitive to various ΔT. The relative magnitude of RMSE in the ΔT is similar to the overall performance for 31 KDMs, but their priority is not completely consistent for each ΔT. The lowest RMSE is 0.70 K for ΔT = 5 K using the uea-Rou dual-kernel model (15). The RTk-Rou dual-kernel model (03) is slightly preferred to other KDMs for ΔT = 10 K and ΔT = 15 K, and its RMSE is 1.11 K and 1.44 K, respectively.
- (2)
- A total of 31 KDMs are sensitive to various H/W. Except for the RTk-LDR dual-kernel model (06), the magnitude of RMSE increases with the increase in the H/W from 0~1 to 0~3. The RMSE minimum is 0.80 K in the Vin-Rou dual-kernel model, and the overall RMSEs of Rou-series KDMS (09, 03, 27, 15, 21) are always smaller than 0.85 K at H/W = 0~1. The RMSE difference between different H/W is higher than 0.60 K in three Vin-series dual-kernel models (28, 10, 12).
- (3)
- The RMSEs for 31 KDMs exhibit comparable values in different building densities, consistent with the overall performance. There is no significant difference between 31 KMDs except for the 0.13 K of RL KDMs in different building densities. As observed in Figure 8d, the higher building densities slightly lead to a smaller RMSE. The optimal performance is the RTk-Rou dual-kernel model (03) with an RMSE of 1.09 K in D = 0.73.
- (4)
- Concrete and asphalt are selected as the building roof material, and their emissivity is 0.893 and 0.928, respectively. As shown in Figure 8e, roof surface emissivity cannot affect the performance of 31 KMDs by more than 0.01 K. In addition, the influence of wall surface emissivity is higher than roof surface emissivity, but their RMSE difference in each KDM is not higher than 0.05 K in Figure 8f. Results indicate that the surface emissivity is not an important parameter for the development of current KMDs when compared with the H/W.
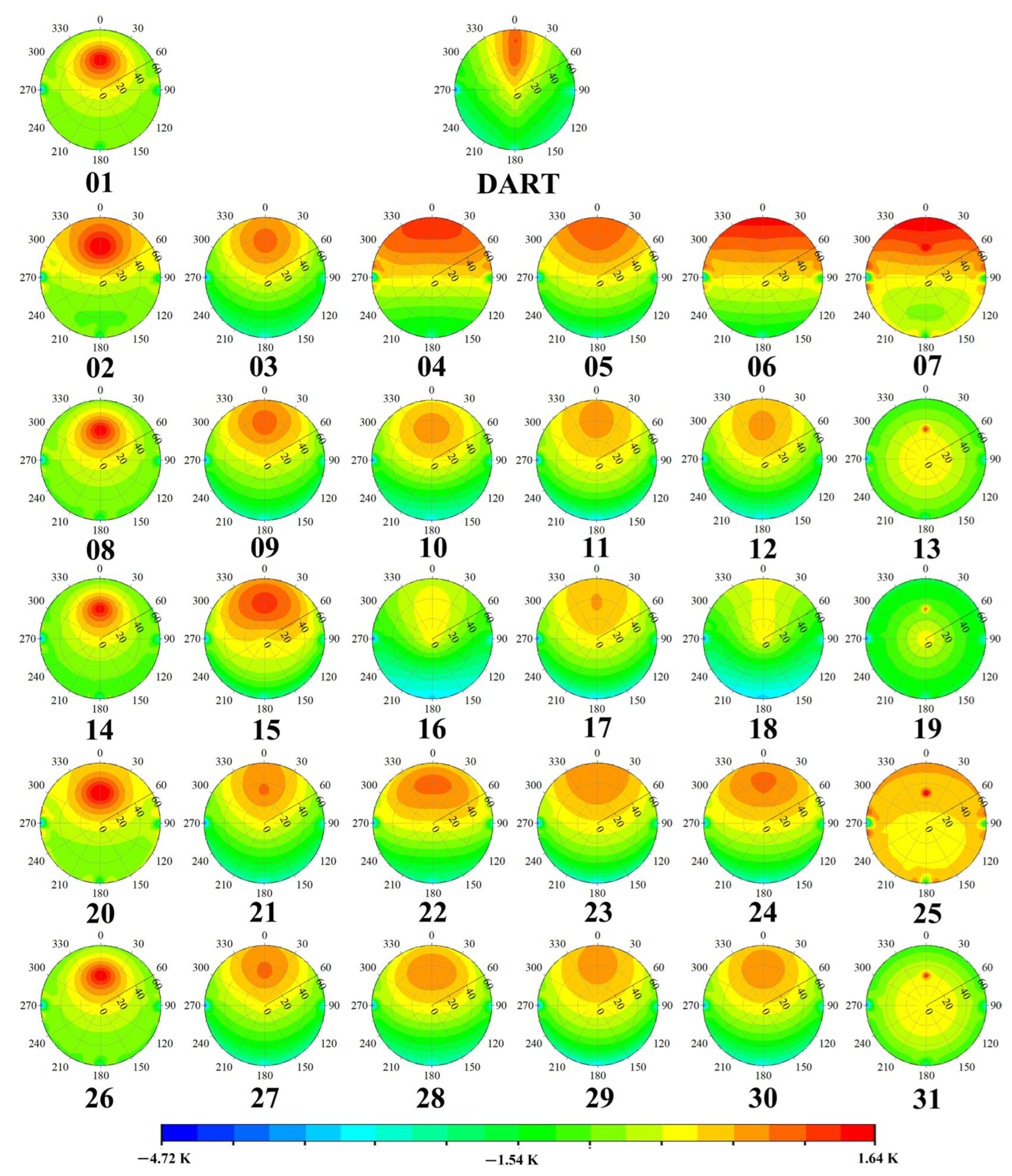
4.2.2. The Performance of Kernel-Driven Models at the Solar Plane
5. Discussion
5.1. The Performance of Multi-Parameter Kernel-Driven Models
5.2. Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hsu, A.; Sheriff, G.; Chakraborty, T.; Manya, D. Disproportionate exposure to urban heat island intensity across major US cities. Nat. Commun. 2021, 12, 2721. [Google Scholar] [CrossRef] [PubMed]
- Imhoff, M.L.; Zhang, P.; Wolfe, R.E.; Bounoua, L. Remote sensing of the urban heat island effect across biomes in the continental USA. Remote Sens. Environ. 2010, 114, 504–513. [Google Scholar] [CrossRef]
- Lazzarini, M.; Marpu, P.R.; Ghedira, H. Temperature-land cover interactions: The inversion of urban heat island phenomenon in desert city areas. Remote Sens. Environ. 2013, 130, 136–152. [Google Scholar] [CrossRef]
- Rajasekar, U.; Weng, Q. Urban heat island monitoring and analysis using a non-parametric model: A case study of Indianapolis. ISPRS J. Photogramm. Remote Sens. 2009, 64, 86–96. [Google Scholar] [CrossRef]
- Ru, C.; Duan, S.-B.; Jiang, X.-G.; Li, Z.-L.; Jiang, Y.Z.; Ren, H.Z.; Leng, P.; Gao, M.F. Land surface temperature retrieval from Landsat 8 thermal infrared data over urban areas considering geometry effect: Method and application. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5000716. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Effects of urban surface geometry on remotely-sensed surface temperature. Int. J. Remote Sens. 1998, 19, 895–920. [Google Scholar] [CrossRef]
- Chen, S.S.; Ren, H.Z.; Ye, X.; Dong, J.Q.; Zheng, Y.T. Geometry and adjacency effects in urban land surface temperature retrieval from high-spatial-resolution thermal infrared images. Remote Sens. Environ. 2021, 262, 112518. [Google Scholar] [CrossRef]
- Ermida, S.L.; Hulley, G.; Trigo, I.F. Introducing emissivity directionality to the temperature-emissivity separation algorithm. Remote Sens. Environ. 2024, 311, 114280. [Google Scholar] [CrossRef]
- Ru, C.; Duan, S.-B.; Jiang, X.-G.; Li, Z.-L.; Huang, C.; Liu, M. An extended SW-TES algorithm for land surface temperature and emissivity retrieval from ECOSTRESS thermal infrared data over urban areas. Remote Sens. Environ. 2023, 290, 113544. [Google Scholar] [CrossRef]
- Ouyang, X.Y.; Sun, Z.C.; Zhou, S.G.; Dou, Y.J. Urban land surface temperature retrieval with high-spatial resolution SDGSAT-1 thermal infrared data. Remote Sens. Environ. 2024, 312, 114320. [Google Scholar] [CrossRef]
- Cao, B.; Liu, Q.H.; Du, Y.M.; Roujean, J.-L.; Gastellu-Etchegorry, J.-P.; Trigo, I.F.; Zhan, W.F.; Yu, Y.Y.; Cheng, J.; Jacob, F.; et al. A review of earth surface thermal radiation directionality observing and modeling: Historical development, current status and perspectives. Remote Sens. Environ. 2019, 232, 111304. [Google Scholar] [CrossRef]
- Fontanilles, G.; Briottet, X.; Fabre, S.; Trémas, T. Thermal infrared radiance simulation with aggregation modeling (TITAN): An infrared radiative transfer model for heterogeneous three-dimensional surface-application over urban regions. Appl. Opt. 2008, 47, 5799–5810. [Google Scholar] [CrossRef] [PubMed]
- Lagouarde, J.-P.; Hénon, A.; Kurz, B.; Moreau, P.; Irvine, M.; Voogt, J.; Mestayer, P. Modelling daytime thermal infrared directional anisotropy over Toulouse city centre. Remote Sens. Environ. 2010, 114, 87–105. [Google Scholar] [CrossRef]
- Lagouarde, J.-P.; Bach, M.; Sobrino, J.A.; Boulet, G.; Briottet, X.; Cherchali, S.; Coudert, B.; Dadou, I.; Dedieu, G.; Gamet, P.; et al. The MISTIGRI thermal infrared project: Scientific objectives and mission specifications. Int. J. Remote Sens. 2013, 34, 3437–3466. [Google Scholar] [CrossRef]
- Zheng, X.P.; Gao, M.F.; Li, Z.-L.; Chen, K.S.; Zhang, X.; Shang, G.F. Impact of 3-D structures and their radiation on thermal infrared measurements in urban areas. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8412–8426. [Google Scholar] [CrossRef]
- Zheng, X.P.; Wang, T.X.; Nerry, F.; Guo, Y.Y.; Huang, Z.H. Thermal infrared radiative transfer modeling in urban areas by considering 3-D structures and sunlit-shadow temperature contrast. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5002217. [Google Scholar] [CrossRef]
- Duffour, C.; Lagouarde, J.-P.; Roujean, J.-L. A two parameter model to simulate thermal infrared directional effects for remote sensing applications. Remote Sens. Environ. 2016, 186, 250–261. [Google Scholar] [CrossRef]
- Lagouarde, J.-P.; Irvine, M. Directional anisotropy in thermal infrared measurements over Toulouse city centre during the CAPITOUL measurement campaigns: First results. Meteorol. Atmos. Phys. 2008, 102, 173–185. [Google Scholar] [CrossRef]
- Hu, T.; Du, Y.M.; Cao, B.; Li, H.; Bian, Z.J.; Sun, D.L.; Liu, Q.H. Estimation of upward longwave radiation from vegetation surfaces considering thermal directionality. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6644–6658. [Google Scholar] [CrossRef]
- Hu, T.; Roujean, J.-L.; Cao, B.; Mallick, K.; Boulet, G.; Li, H.; Xu, Z.H.; Du, Y.M.; Liu, Q.H. Correction for LST directionality impact on the estimation of surface upwelling longwave radiation over vegetated surfaces at the satellite scale. Remote Sens. Environ. 2023, 295, 113649. [Google Scholar] [CrossRef]
- Peng, J.J.; Liu, Q.; Liu, Q.H.; Li, J.H.; Ma, H.Z.; Fang, L. Kernel-driven model fitting of multi-angle thermal infrared brightness temperature and its application. J. Infrared Millim. Waves 2011, 30, 361–365. [Google Scholar] [CrossRef]
- Liu, X.Y.; Tang, B.-H.; Li, Z.-L.; Zhang, X.; Shang, G.F. On the derivation of geometric optical kernels for directional thermal radiation. Earth Space Sci. 2020, 7, e2019EA000895. [Google Scholar] [CrossRef]
- Cao, B.; Roujean, J.-L.; Gastellu-Etchegorry, J.-P.; Liu, Q.H.; Du, Y.M.; Lagouarde, J.-P.; Huang, H.G.; Li, H.; Bian, Z.J.; Hu, T.; et al. A general framework of kernel-driven modeling in the thermal infrared domain. Remote Sens. Environ. 2021, 252, 112157. [Google Scholar] [CrossRef]
- Vinnikov, K.Y.; Yu, Y.Y.; Goldberg, M.D.; Tarpley, D.; Romanov, P.; Laszlo, I.; Chen, M. Angular anisotropy of satellite observations of land surface temperature. Geophys. Res. Lett. 2012, 39, L23802. [Google Scholar] [CrossRef]
- Li, X.W.; Strahler, A.H.; Friedl, M.A. A conceptual model for effective directional emissivity from Nonisothermal surfaces. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2508–2517. [Google Scholar] [CrossRef]
- Ermida, S.L.; Trigo, I.F.; DaCamara, C.C.; Pires, A. A methodology to simulate LST directional effects based on parametric models and landscape properties. Remote Sens. 2018, 10, 1114. [Google Scholar] [CrossRef]
- Ermida, S.L.; Trigo, I.F.; Dacamara, C.C.; Roujean, J.-L. Assessing the potential of parametric models to correct directional effects on local to global remotely sensed LST. Remote Sens. Environ. 2018, 209, 410–422. [Google Scholar] [CrossRef]
- Sun, H.; Chen, Y.H.; Zhan, W.F.; Wang, M.J.; Ma, W. A kernel model for urban surface thermal emissivity anisotropy and its uncertainties. J. Infrared Millim. Waves 2015, 34, 66–73. [Google Scholar]
- Roujean, J.-L.; Leroy, M.; Deschamps, P.-Y. A bidirectional reflectance model of the earth’s surface for the correction of remote sensing data. J. Geophys. Res. 1992, 97, 20455–20468. [Google Scholar] [CrossRef]
- Strahler, A.H.; Jupp, D.L.B. Modeling bidirectional reflectance of forests and woodlands using Boolean models and geometric optics. Remote Sens. Environ. 1990, 34, 153–166. [Google Scholar] [CrossRef]
- Wang, D.D.; Chen, Y.H.; Cui, Y.H.; Sun, H. A geometric model to simulate urban thermal anisotropy for simplified neighborhoods. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4930–4944. [Google Scholar] [CrossRef]
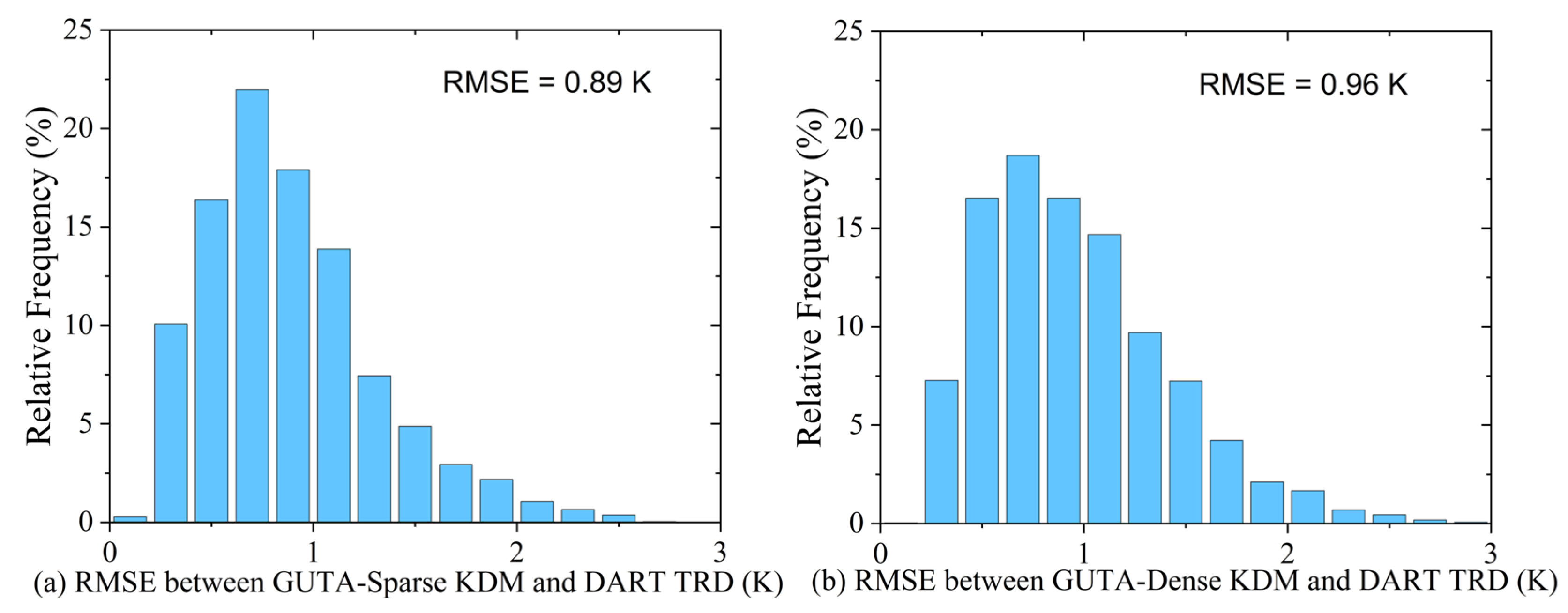
- Wang, D.D.; Chen, Y.H.; Zhan, W.F. A geometric model to simulate thermal anisotropy over a sparse urban surface (GUTA-sparse). Remote Sens. Environ. 2018, 209, 263–274. [Google Scholar] [CrossRef]
- Wang, D.D.; Chen, Y.H. A geometric model to simulate urban thermal anisotropy in simplified dense neighborhoods (GUTA-Dense). IEEE Trans. Geosci. Remote Sens. 2019, 57, 6226–6239. [Google Scholar] [CrossRef]
- Bian, Z.J.; Fan, T.Y.; Roujean, J.-L.; Wang, D.D.; Irvine, W.; Wu, S.B.; Cao, B.; Li, H.; Du, Y.M.; Xiao, Q.; et al. An analytical urban temperature model with building heterogeneity using geometric optical theory. Remote Sens. Environ. 2024, 301, 113948. [Google Scholar] [CrossRef]
- Ran, X.T.; Cao, B.; Qin, B.X.; Bian, Z.J.; Du, Y.M.; Li, H.; Xiao, Q.; Liu, Q.H. Assessment of five thermal infrared kernel-driven models using limited multiangle observations. IEEE Geosci. Remote Sens. Lett. 2022, 19, 7001605. [Google Scholar] [CrossRef]
- Cao, B.; Gastellu-Etchegorry, J.-P.; Du, Y.M.; Li, H.; Bian, Z.J.; Hu, T.; Fan, W.J.; Xiao, Q.; Liu, Q.H. Evaluation of four kernel-driven models in the thermal infrared band. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5456–5475. [Google Scholar] [CrossRef]
- Liu, X.Y.; Tang, B.-H.; Li, Z.-L. Evaluation of three parametric models for estimating directional thermal radiation from simulation, airborne, and satellite data. Remote Sens. 2018, 10, 420. [Google Scholar] [CrossRef]
- Jiang, L.; Zhan, W.F.; Hu, L.Q.; Huang, F.; Hong, F.L.; Liu, Z.H.; Lai, J.M.; Wang, C.G. Assessment of different kernel-driven models for daytime urban thermal radiation directionality simulation. Remote Sens. Environ. 2021, 263, 112562. [Google Scholar] [CrossRef]
- Michel, J.; Hagolle, O.; Hook, S.J.; Roujean, J.-L.; Gamet, P. Quantifying thermal infra-Red directional anisotropy using Master and Landsat-8 simultaneous acquisitions. Remote Sens. Environ. 2023, 297, 113765. [Google Scholar] [CrossRef]
- Chang, Y.; Weng, Q.H.; Voogt, J.A.; Xiao, J.F. Urban thermal anisotropies by local climate zones: An assessment using multi-angle land surface temperatures from ECOSTRESS. Remote Sens. Environ. 2025, 322, 114705. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.-P. 3D modeling of satellite spectral images, radiation budget and energy budget of urban landscapes. Meteorol. Atmos. Phys. 2008, 102, 187–207. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.-P.; Martin, E.; Gascon, F. DART: A 3-D model for simulating satellite images and surface radiation budget. Int. J. Remote Sens. 2004, 25, 73–96. [Google Scholar] [CrossRef]
- Wang, Y.J.; Gastellu-Etchegorry, J.-P. DART: Improvement of thermal infrared radiative transfer modeling for simulating top of atmosphere radiance. Remote Sens. Environ. 2020, 251, 112082. [Google Scholar] [CrossRef]
- Wang, Y.J.; Gastellu-Etchegorry, J.-P. Accurate and fast simulation of remote sensing images at top of atmosphere with DART-Lux. Remote Sens. Environ. 2021, 256, 112311. [Google Scholar] [CrossRef]
- Grau, E.; Durrieu, S.; Fournier, R.; Gastellu-Etchegorry, J.-P.; Yin, T.G. Estimation of 3D vegetation density with Terrestrial Laser Scanning data using voxels. A sensitivity analysis of influencing parameters. Remote Sens. Environ. 2017, 191, 373–388. [Google Scholar] [CrossRef]
- Qin, B.X.; Cao, B.; Roujean, J.-L.; Gastellu-Etchegorry, J.-P.; Bian, Z.J.; Du, Y.M.; Hu, T.; Xiao, Q.; Chen, S.S.; Liu, Q.H. A thermal radiation directionality correction method for the surface upward longwave radiation of geostationary satellite based on a time-evolving kernel-driven model. Remote Sens. Environ. 2023, 294, 113599. [Google Scholar] [CrossRef]
- Oltra-Carrio, R.; Cubero-Castan, M.; Briottet, X.; Sobrino, J.A. Analysis of the performance of the TES algorithm over urban areas. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6989–6998. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Oltra-Carró, R.; Jiménez-Muñoz, J.C.; Julien, Y.; Sòria, G.; Franch, B.; Mattar, C. Emissivity mapping over urban areas using a classification-based approach: Application to the Dual-use European Security IR Experiment (DESIREX). Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 141–147. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Oltra-Carró, R.; Sòria, G.; Jiménez-Muñoz, J.C.; Franch, B.; Hidalgo, V.; Mattar, C.; Julien, Y.; Cuenca, J.; Romaguera, M.; et al. Evaluation of the surface urban heat island effect in the city of Madrid by thermal remote sensing. Int. J. Remote Sens. 2013, 34, 3177–3192. [Google Scholar] [CrossRef]
- Li, Z.-L.; Wu, H.; Duan, S.-B.; Zhao, W.; Ren, H.Z.; Liu, X.Y.; Leng, P.; Tang, R.L.; Ye, X.; Zhu, J.S.; et al. Satellite remote sensing of global land surface temperature: Definition, methods, products, and applications. Rev. Geophys. 2023, 61, e2022RG000777. [Google Scholar] [CrossRef]
- Meerdink, S.K.; Hook, S.J.; Roberts, D.A.; Abbott, E.A. The ECOSTRESS spectral library version 1.0. Remote Sens. Environ. 2019, 230, 111196. [Google Scholar] [CrossRef]
- Zheng, X.P.; Guo, Y.Y.; Zhou, Z.L.; Wang, T.X. Improvements in land surface temperature and emissivity retrieval from Landsat-9 thermal infrared data. Remote Sens. Environ. 2024, 315, 114471. [Google Scholar] [CrossRef]
- Morrison, W.; Grimmond, S.; Kotthaus, S. Simulating satellite urban land surface temperatures: Sensitivity to sensor view angle and assumed landscape complexity. Remote Sens. Environ. 2023, 293, 113579. [Google Scholar] [CrossRef]
- Egbert, D.D. A practical method for correcting bidirectional reflectance variations. In Proceedings of the machine processing of remotely sensed data symposium, West Lafayette, IN, USA, 21–23 June 1977; pp. 178–189. [Google Scholar]
- Wanner, W.; Li, X.; Strahler, A.H. On the derivation of kernels for kernel-driven models of bidirectional reflectance. J. Geophys. Res. 1995, 100, 21077–21089. [Google Scholar] [CrossRef]
- Ross, J.L. The Radiation Regime and Architecture of Plant Stands; Springer: Dordrecht, The Netherlands, 1981. [Google Scholar] [CrossRef]
- Roujean, J.-L. A parametric hot spot model for optical remote sensing applications. Remote Sens. Environ. 2000, 71, 197–206. [Google Scholar] [CrossRef]
- Li, X.W.; Strahler, A.H. Geometric-Optical bidirectional reflectance modeling of discrete crown vegetation canopy: Effect of crown shape and mutual shadowing. IEEE Trans. Geosci. Remote Sens. 1992, 30, 276–292. [Google Scholar] [CrossRef]
- Li, X.W.; Strahler, A.H. Geometric-Optical bidirectional reflectance modeling of a conifer forest canopy. IEEE Trans. Geosci. Remote Sens. 1986, 24, 906–919. [Google Scholar] [CrossRef]
- Chen, J.M.; Cihlar, J. A hotspot function in a simple bidirectional reflectance model for satellite applications. J. Geophys. Res. 1997, 102, 25907–25913. [Google Scholar] [CrossRef]
- Oltra-Carrio, R.; Sobrino, J.A.; Franch, B.; Nerry, F. Land surface emissivity retrieval from airborne sensor over urban areas. Remote Sens. Environ. 2012, 123, 298–305. [Google Scholar] [CrossRef]
- Wang, D.D.; Chen, Y.H.; Hu, L.Q.; Voogt, J.A.; He, X.Y. Satellite-based daytime urban thermal anisotropy: A comparison of 25 global cities. Remote Sens. Environ. 2022, 283, 113312. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.Z.; Yan, G.J.; Wan, Z.M.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Lai, S.X.; Zhao, Y.J.; Fan, Y.F.; Ge, J. Characteristics of daytime land surface temperature in wind corridor: A case study of a hot summer and warm winter city. J. Build. Eng. 2021, 44, 103370. [Google Scholar] [CrossRef]
- Nascimento, A.C.L.; Galvani, E.; Gobo, J.P.A.; Wollmann, C.A. Comparison between air temperature and land surface temperature for the City of São Paulo, Brazil. Remote Sens. 2022, 13, 491. [Google Scholar] [CrossRef]
- Weiland, L.; Rogers, C.A.; Sothe, C.; Arain, M.A.; Gonsamo, A. Satellite-based land surface temperature and soil moisture observations accurately predict soil respiration in temperate deciduous and coniferous forests. Agric. For. Meteorol. 2023, 340, 109618. [Google Scholar] [CrossRef]
- Dash, P.; Göttsche, F.M.; Olesen, F.S.; Fischer, H. Land surface temperature and emissivity estimation from passive sensor data: Theory and practice-current trends. Int. J. Remote Sens. 2002, 23, 2563–2594. [Google Scholar] [CrossRef]
- Wan, Z.M. MODIS Land-Surface Temperature Algorithm Theoretical Basis Document (LST ATBD); NASA/GSFC: Greenbelt, MD, USA, 1999; pp. 1–77.
- Feng, J.-L.; Cai, X.-M.; Chapman, L. Impact of atmospheric conditions and levels of urbanization on the relationship between nocturnal surface and urban canopy heat islands. Q. J. R. Meteorol. Soc. 2019, 145, 3284–3299. [Google Scholar] [CrossRef]
- Huang, F.; Zhan, W.F.; Wang, Z.-H.; Voogt, J.; Hu, L.Q.; Quan, J.L.; Liu, C.; Zhang, N.; Lai, J.M. Satellite identification of atmospheric-surface-subsurface urban heat islands under clear sky. Remote Sens. Environ. 2020, 250, 112039. [Google Scholar] [CrossRef]


| Type | Description | Parameter Setting | 2592 | |||
|---|---|---|---|---|---|---|
| Size | Simulation scene | 70 m × 70 m (0.5 m × 0.5 m × 0.5 m) | ||||
| Wavelength | ECOSTRESS | 8.29 µm, 8.78 µm, 9.20 µm, 10.49 µm, 12.09 µm | ||||
| Solar angle | Zenith angle | 30° | ||||
| Azimuth angle | 0° | |||||
| View angle (310 directions) | Zenith angle | 0~86° | ||||
| Azimuth angle | 0~360° | |||||
| Roofs | Optical properties | Concrete | Asphalt | 2 | ||
| Surface temperature | Troof + 5 K | Troof − 5 K | Troof − 10 K | Troof − 20 K | 4 | |
| Walls | Optical properties | Concrete | Brick | Glass | 3 | |
| Surface temperature | Troof = 321 K ± 5 K, ±10 K, ±15 K | 3 | ||||
| Roads | Optical properties | Asphalt | 1 | |||
| Surface temperature | Troof + 5 K | Troof − 5 K | Troof − 10 K | Troof − 20 K | 4 | |
| Building density | Sroofs/Stotal | 0.29 | 0.50 | 0.73 | 3 | |
| Geometry factor | H/W | 0–1/0.5 | 1–2/1.5 | 0–3/1.5 | 3 | |
| RL | Rou | VinH | LSR | LDR | Chen | |
|---|---|---|---|---|---|---|
| / | 01 | |||||
| RTk | 02 | 03 | 04 | 05 | 06 | 07 |
| VinB | 08 | 09 | 10 | 11 | 12 | 13 |
| uea | 14 | 15 | 16 | 17 | 18 | 19 |
| RTi | 20 | 21 | 22 | 23 | 24 | 25 |
| LSF | 26 | 27 | 28 | 29 | 30 | 31 |
| T01 | T02 | T03 | T04 | T05 | T06 | T07 | T08 | T09 | |
| δT1 (K) | 0 | −5 | 5 | 10 | 20 | −5 | −5 | −5 | 5 |
| δT2 (K) | 0 | −5 | 5 | 10 | 20 | 5 | 10 | 20 | −5 |
| T10 | T11 | T12 | T13 | T14 | T15 | T16 | T17 | ||
| δT1 (K) | 5 | 5 | 10 | 10 | 10 | 20 | 20 | 20 | |
| δT2 (K) | 10 | 20 | −5 | 5 | 20 | −5 | 5 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Li, Z.-L.; Nerry, F. Assessing Kernel-Driven Models’ Efficacy in Urban Thermal Radiation Directionality Modeling Using DART-Simulated Scenarios. Remote Sens. 2025, 17, 2884. https://doi.org/10.3390/rs17162884
Zhu X, Li Z-L, Nerry F. Assessing Kernel-Driven Models’ Efficacy in Urban Thermal Radiation Directionality Modeling Using DART-Simulated Scenarios. Remote Sensing. 2025; 17(16):2884. https://doi.org/10.3390/rs17162884
Chicago/Turabian StyleZhu, Xiaolin, Zhao-Liang Li, and Franҫoise Nerry. 2025. "Assessing Kernel-Driven Models’ Efficacy in Urban Thermal Radiation Directionality Modeling Using DART-Simulated Scenarios" Remote Sensing 17, no. 16: 2884. https://doi.org/10.3390/rs17162884
APA StyleZhu, X., Li, Z.-L., & Nerry, F. (2025). Assessing Kernel-Driven Models’ Efficacy in Urban Thermal Radiation Directionality Modeling Using DART-Simulated Scenarios. Remote Sensing, 17(16), 2884. https://doi.org/10.3390/rs17162884





