Wind Field Retrieval from Fengyun-3E Radar Based on a Backpropagation Neural Network
Abstract
1. Introduction
2. Materials and Methods
2.1. FY-3E Data
2.2. ERA5 Data
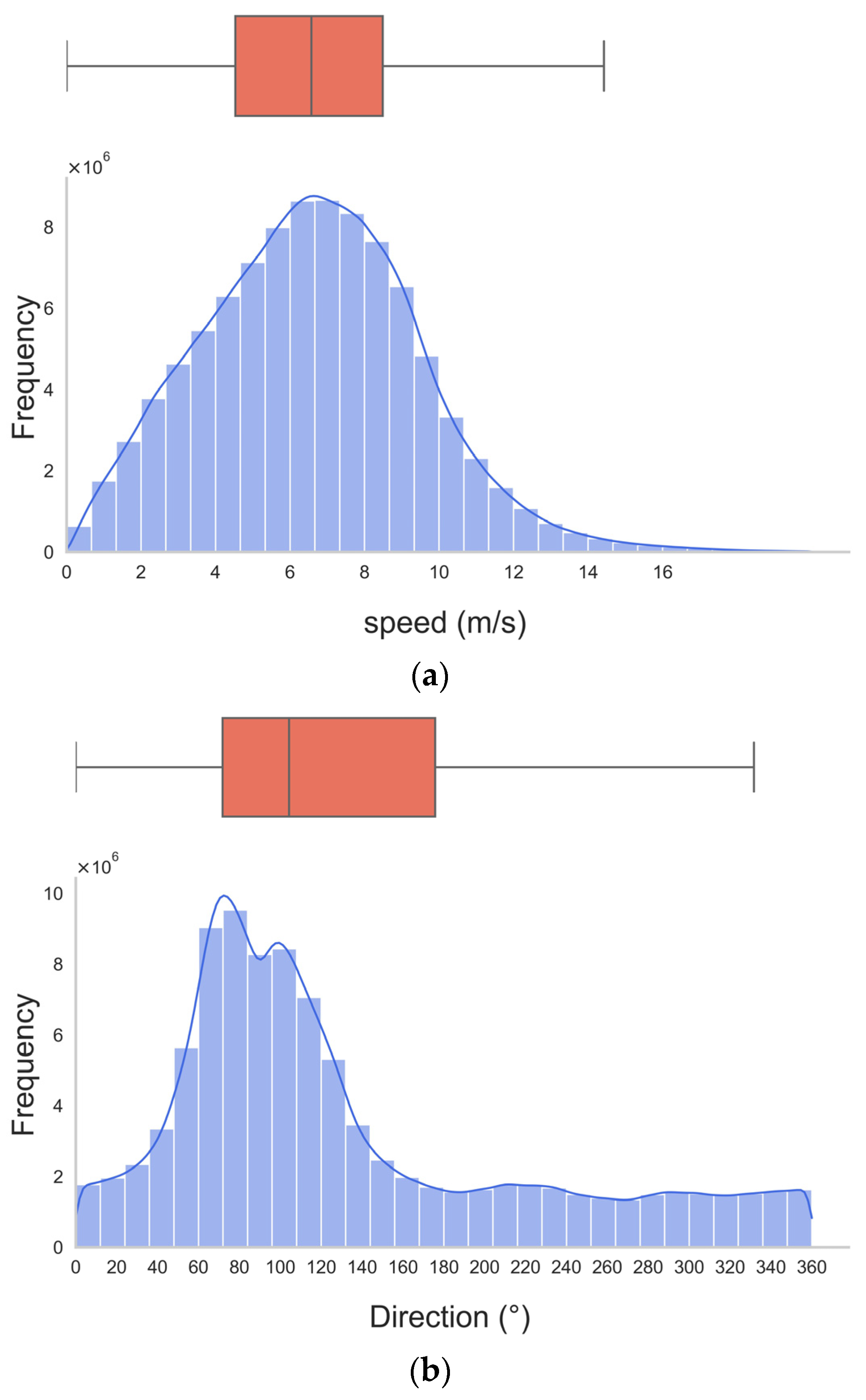
2.3. TAO Data
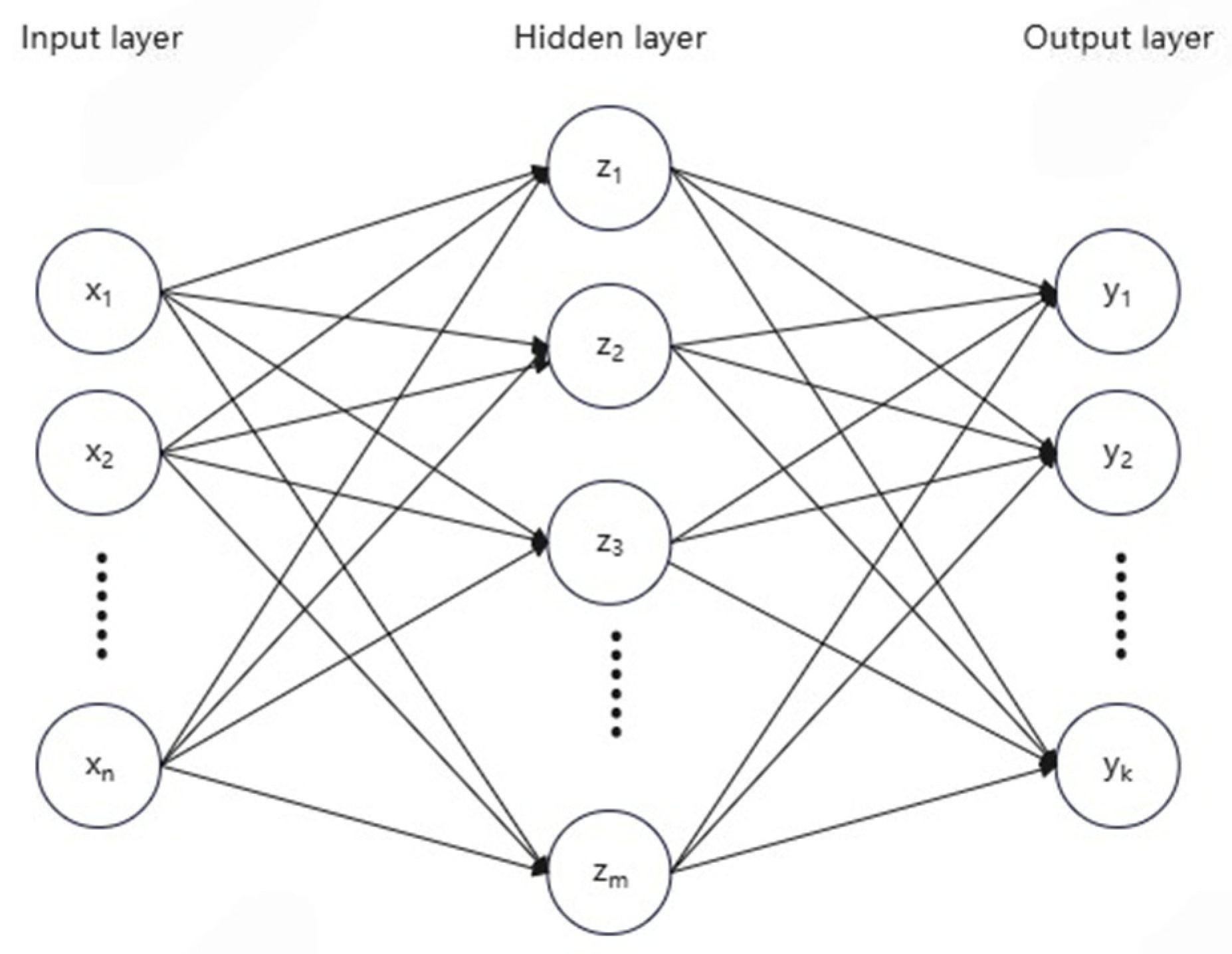
2.4. BP Neural Network
3. Results
3.1. Inversion of Wind Speed Components
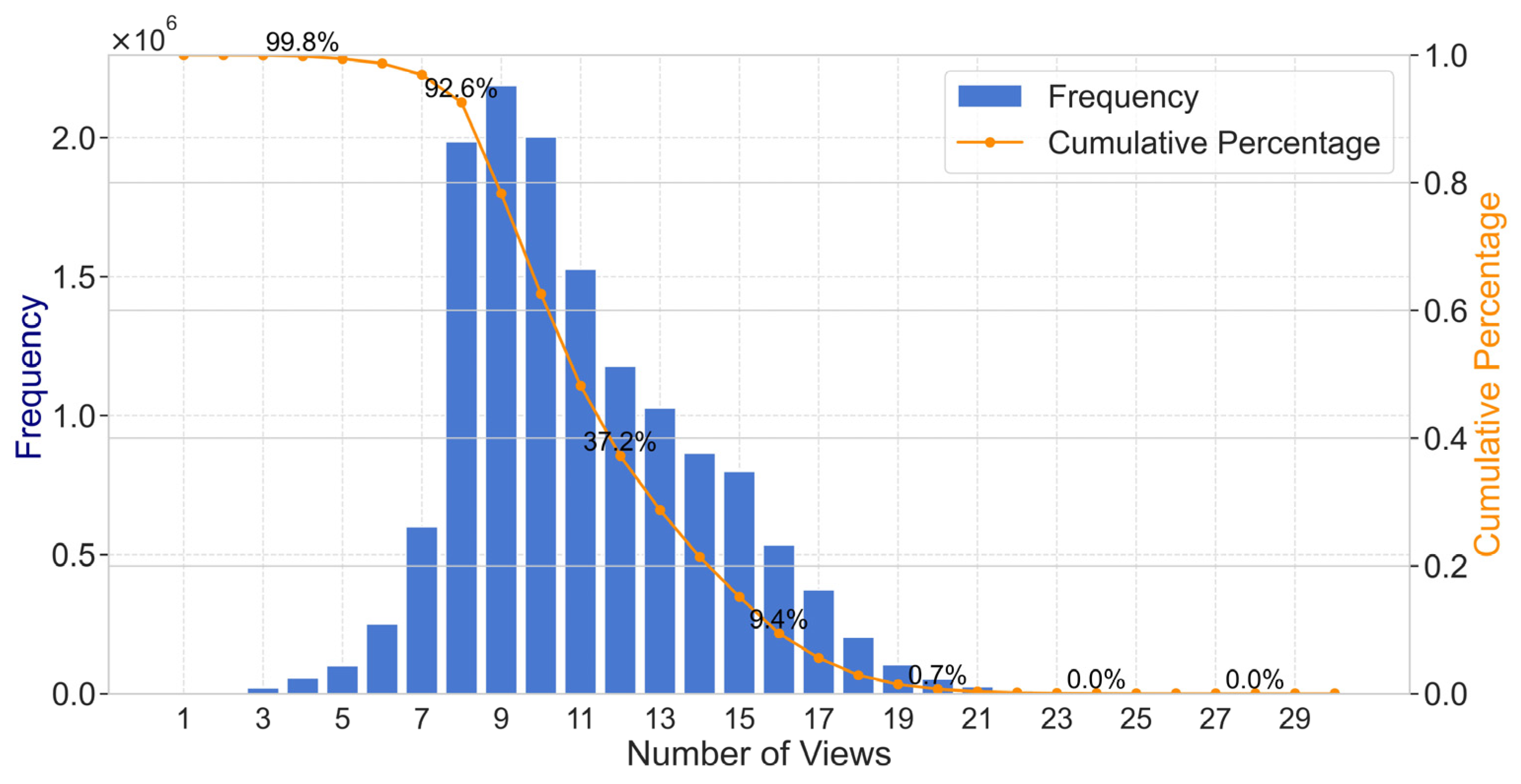
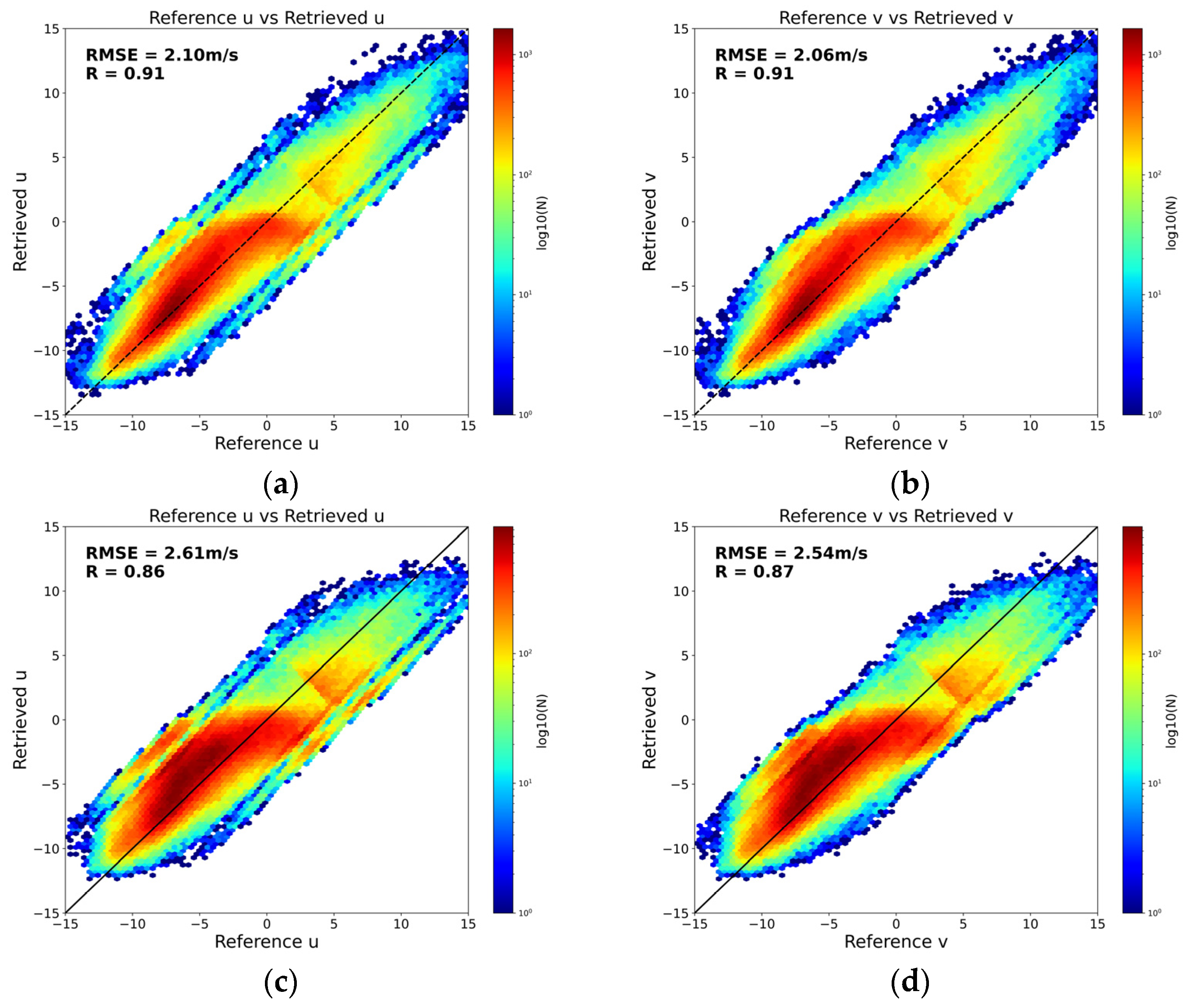
3.1.1. Training Set for Wind Speed Components Model
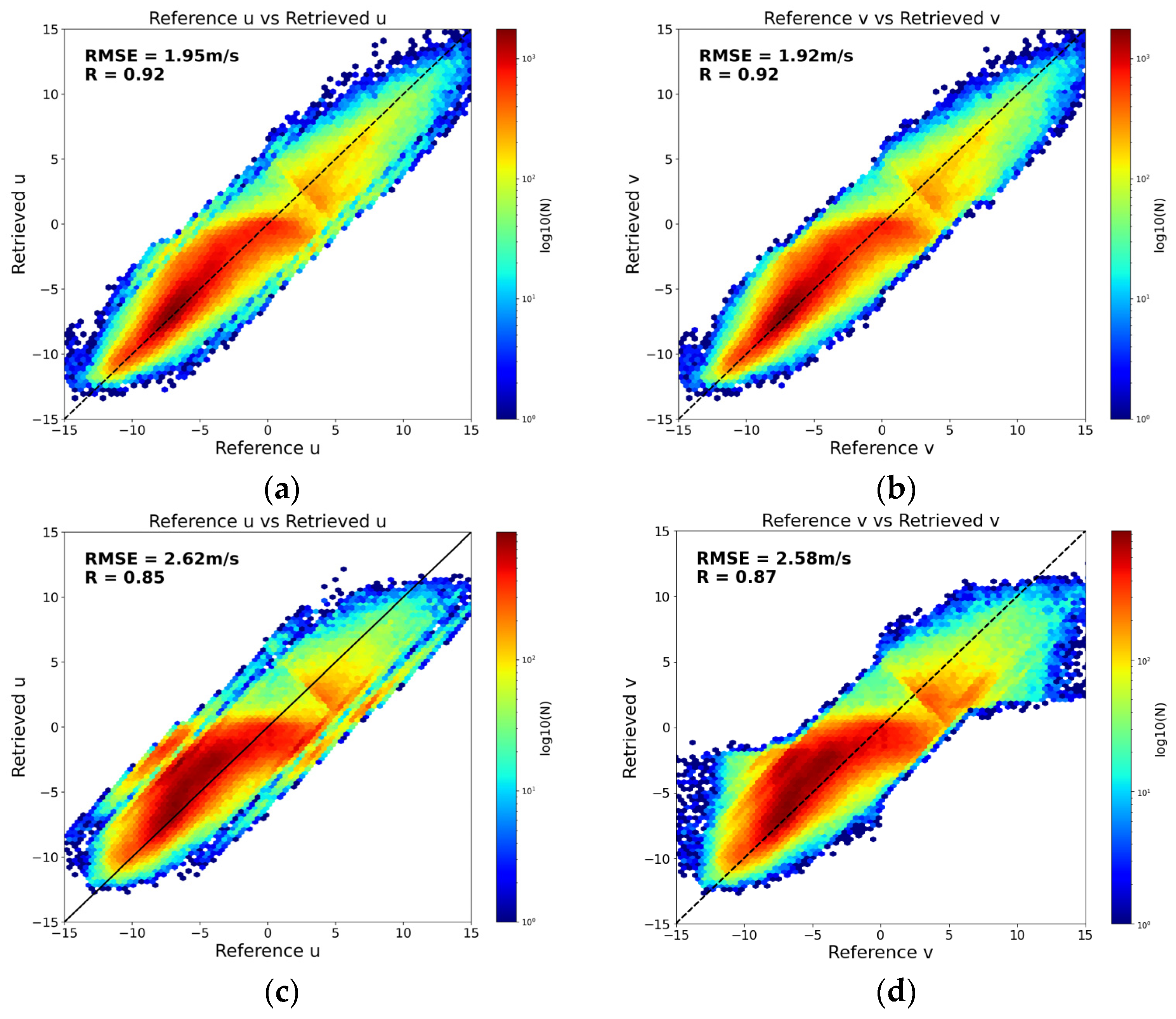
3.1.2. Test Set for Wind Speed Components Model
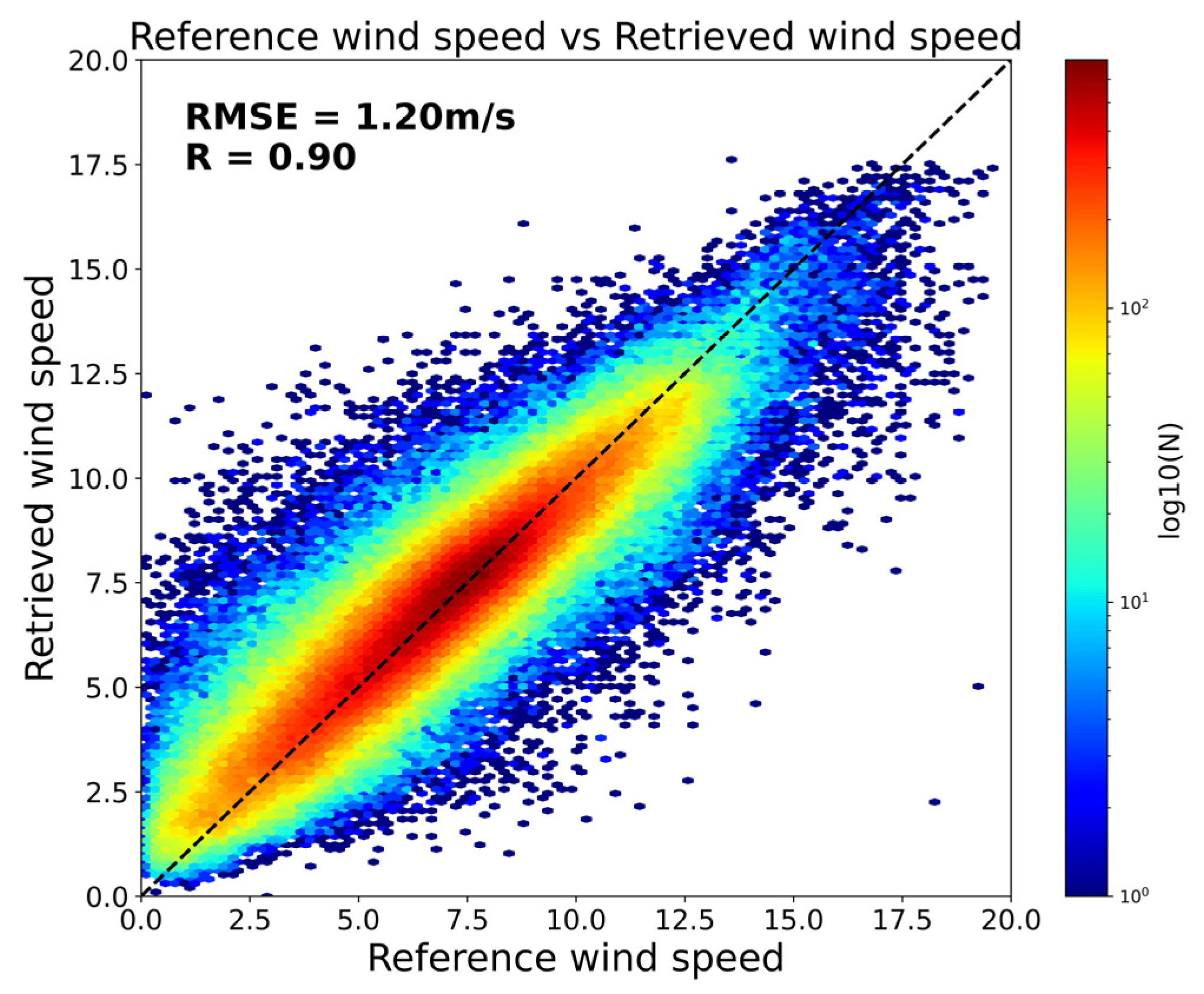
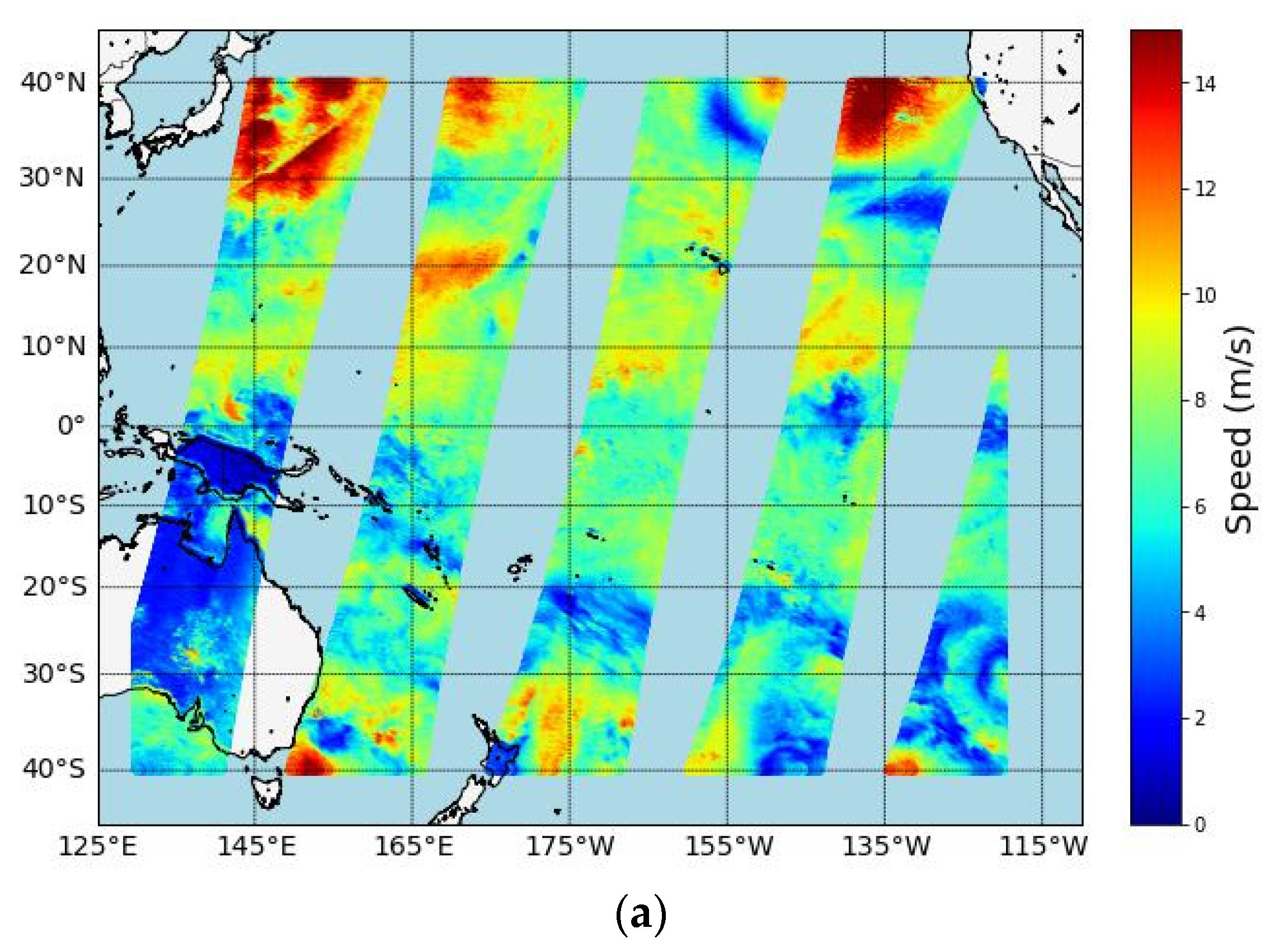
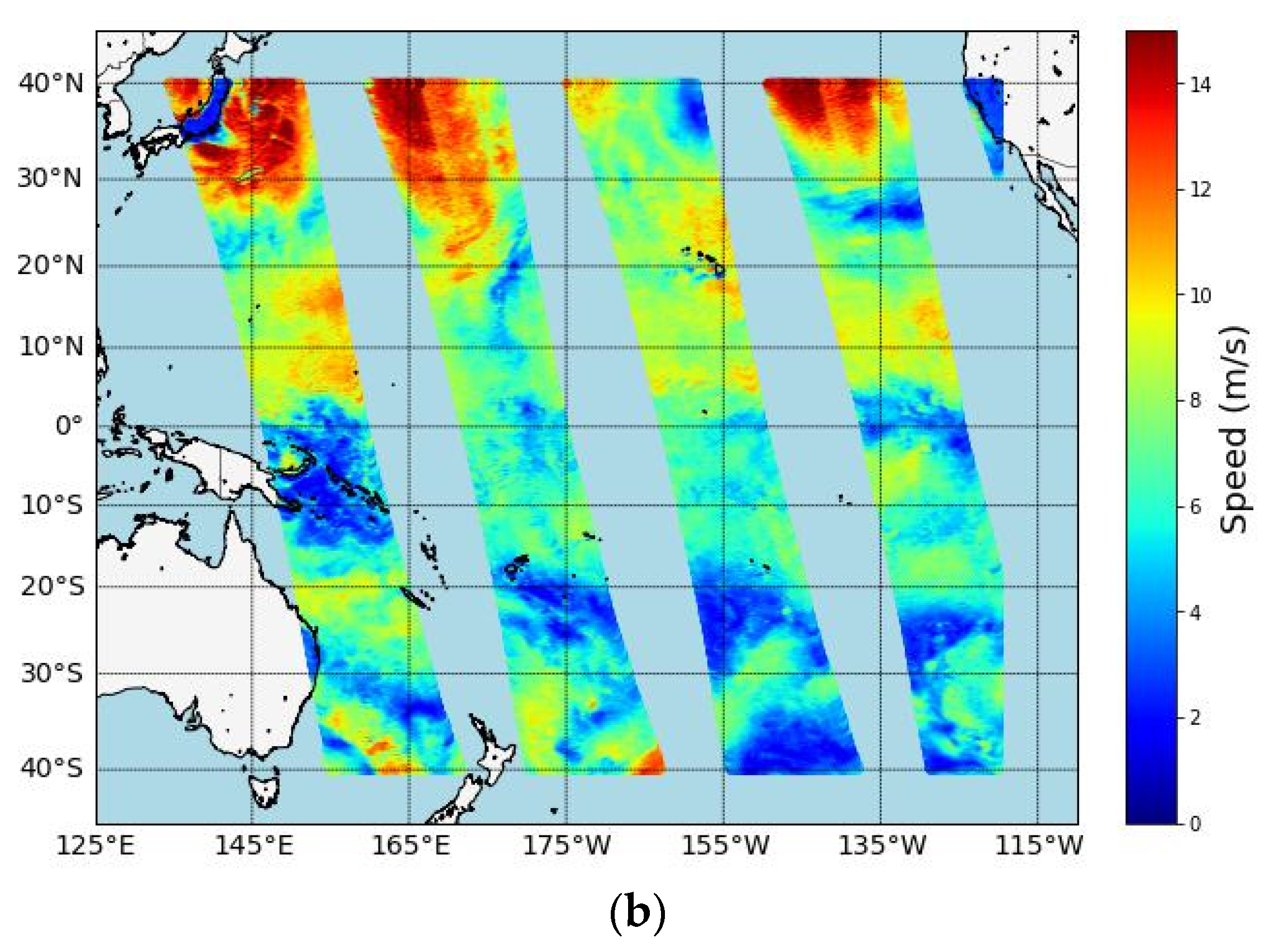
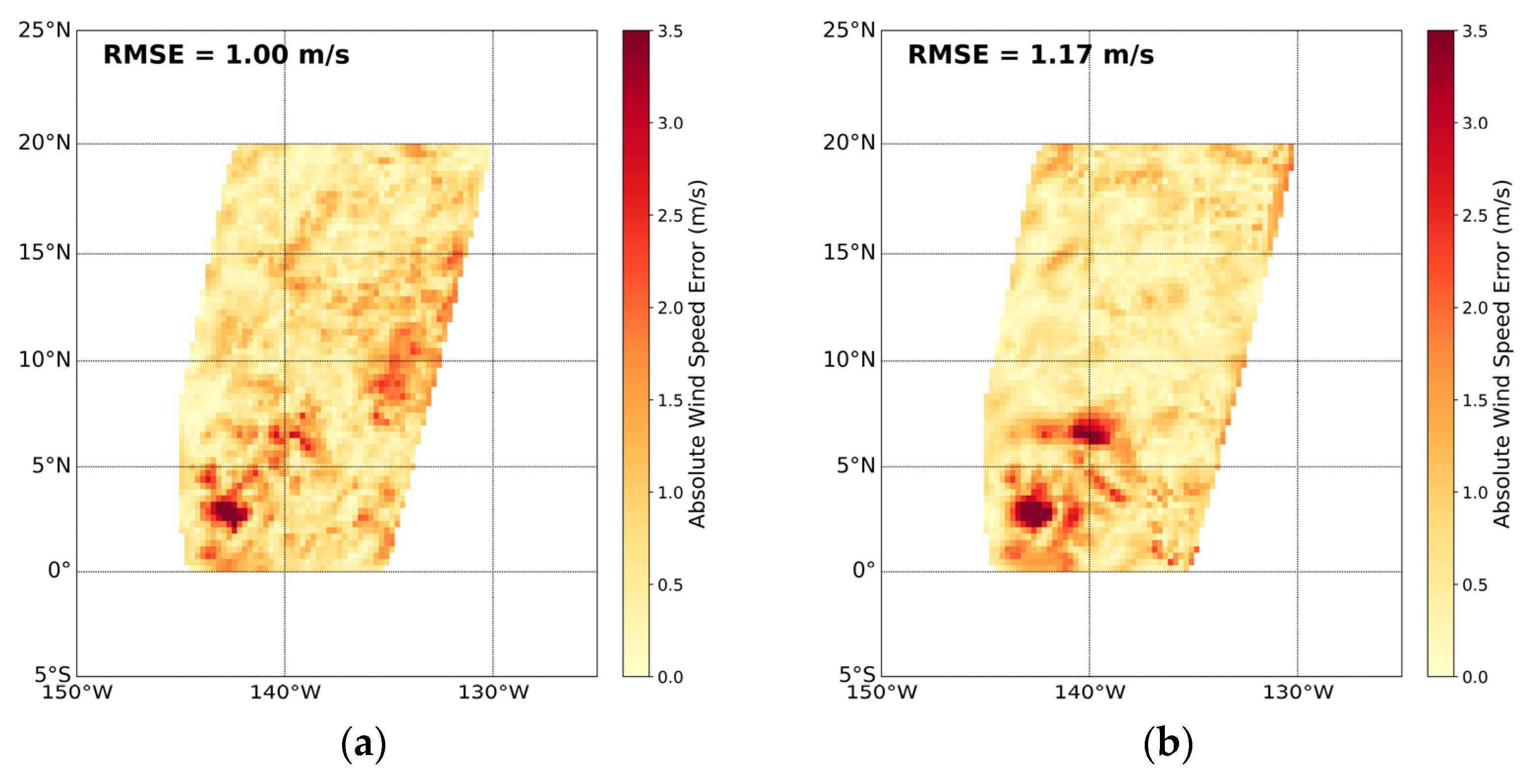
3.2. Validation of Wind Speed
3.2.1. Training Set Validation of Wind Speed
3.2.2. Test Set Validation of Wind Speed
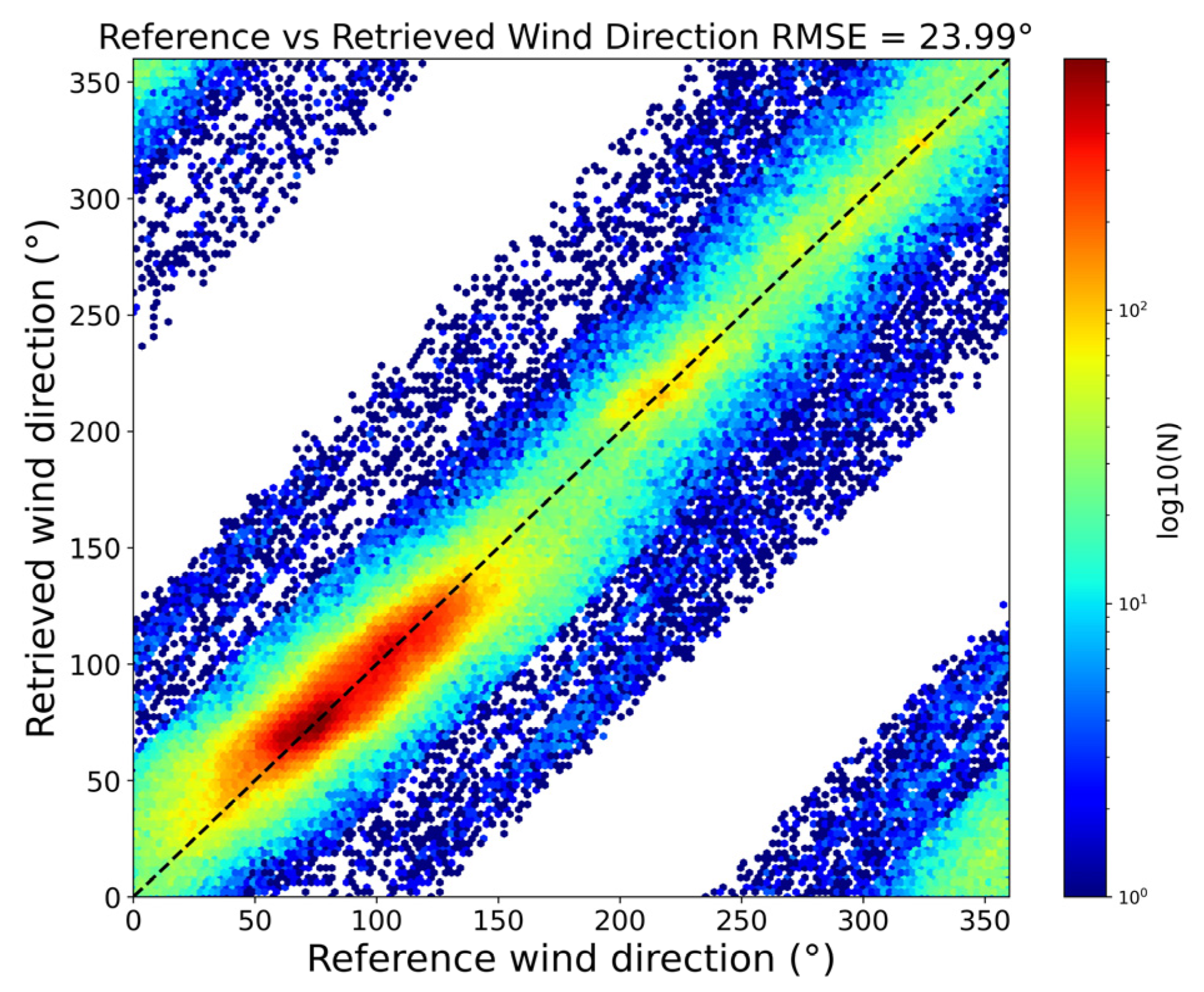
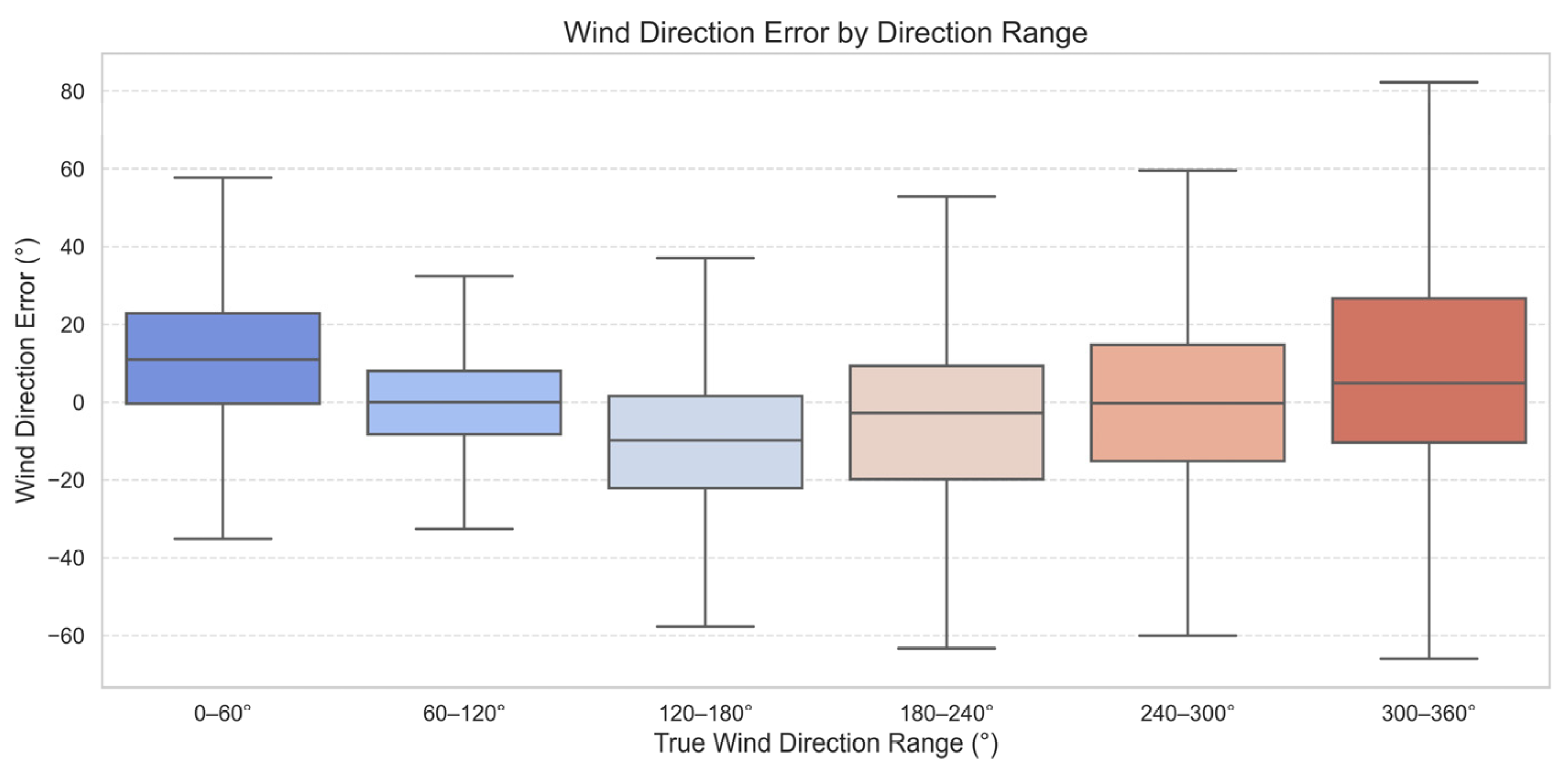
3.3. Validation of Wind Direction
3.3.1. Training Set Validation of Wind Direction
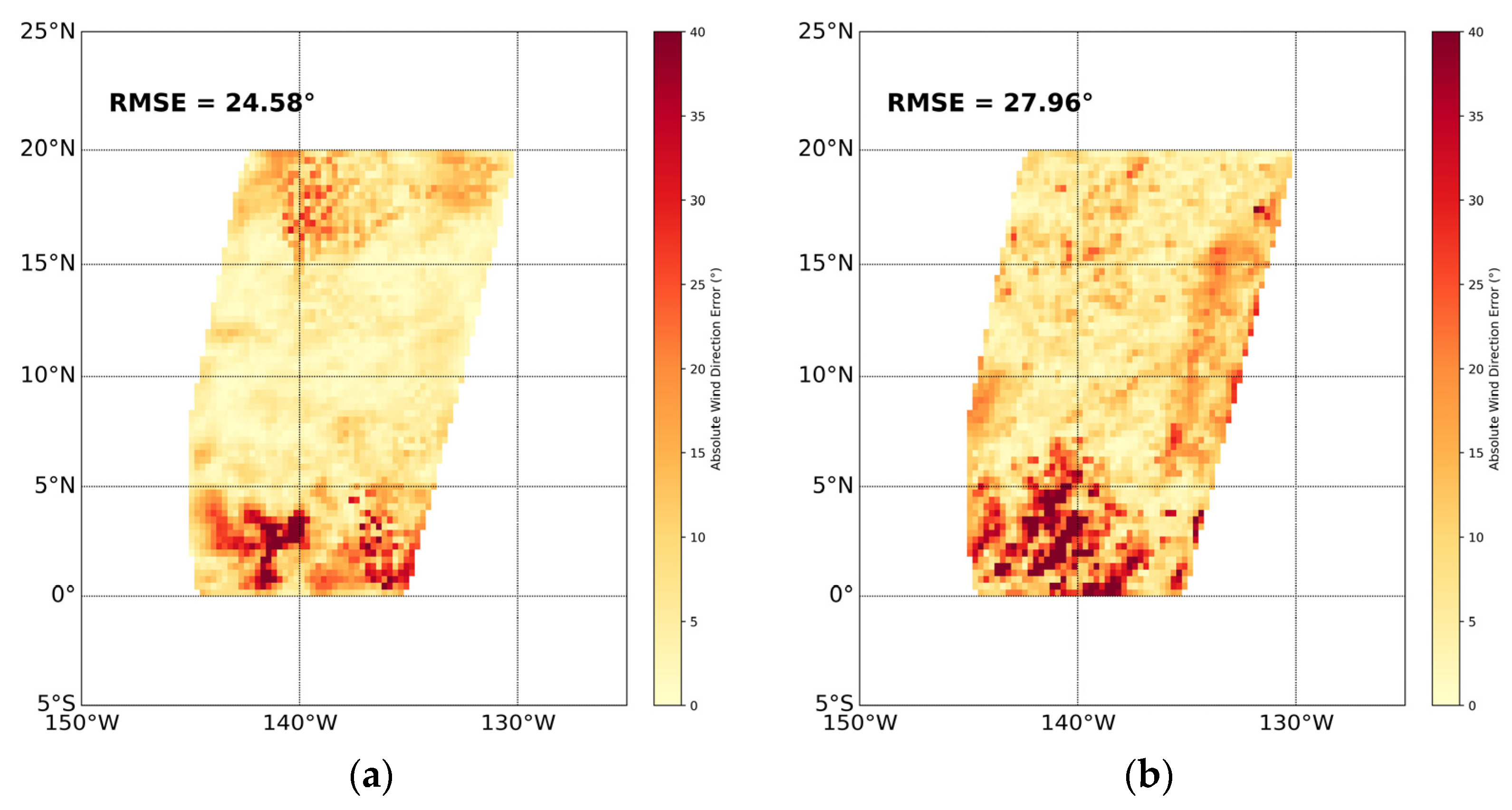
3.3.2. Test Set Validation of Wind Direction
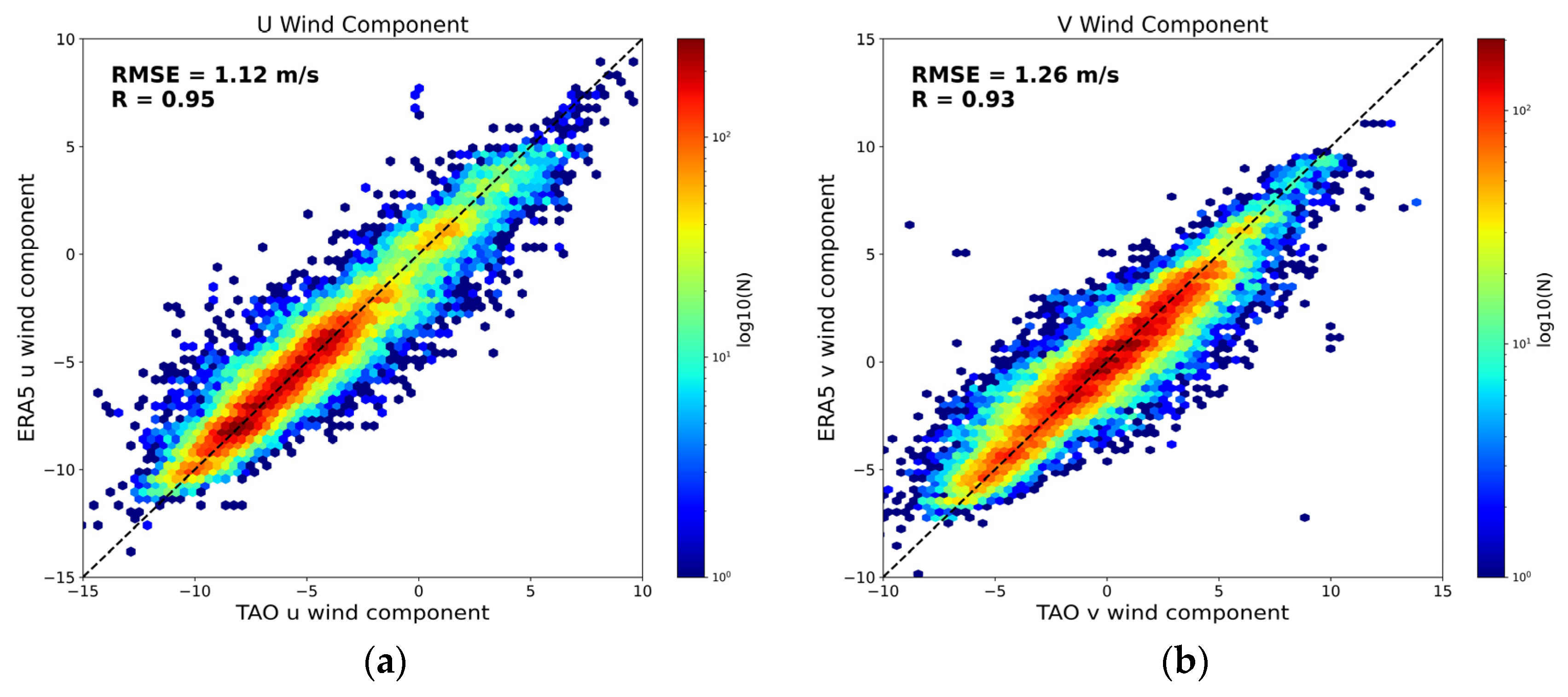
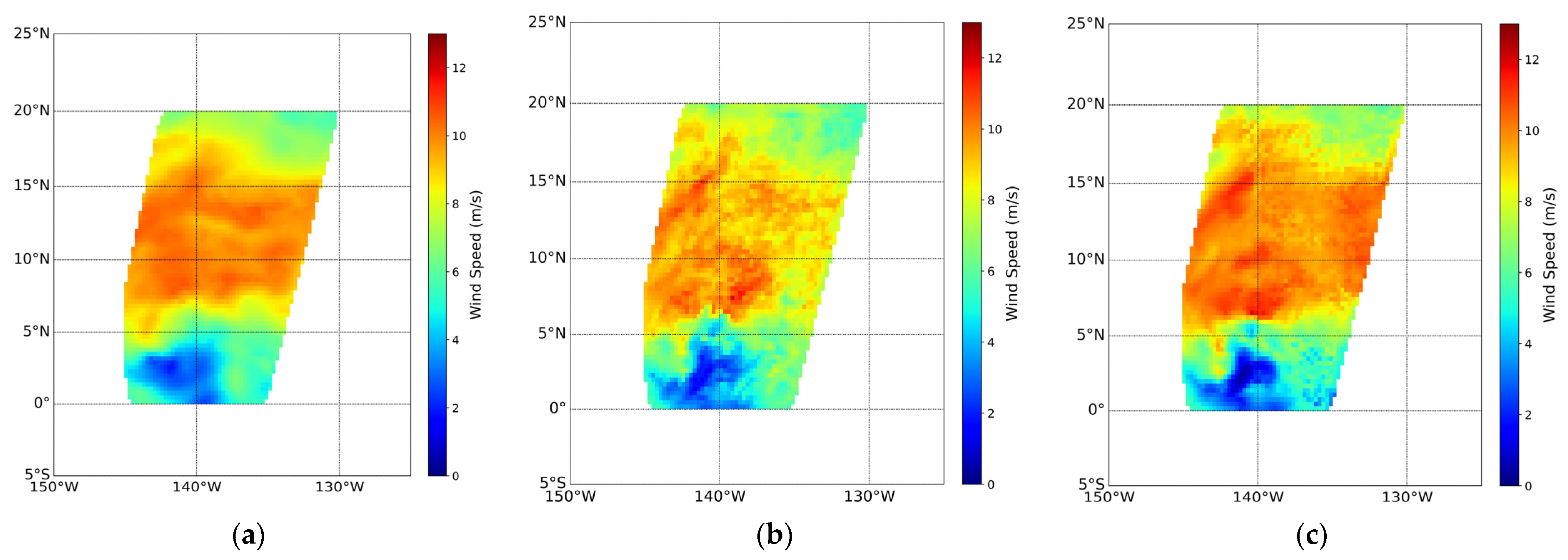
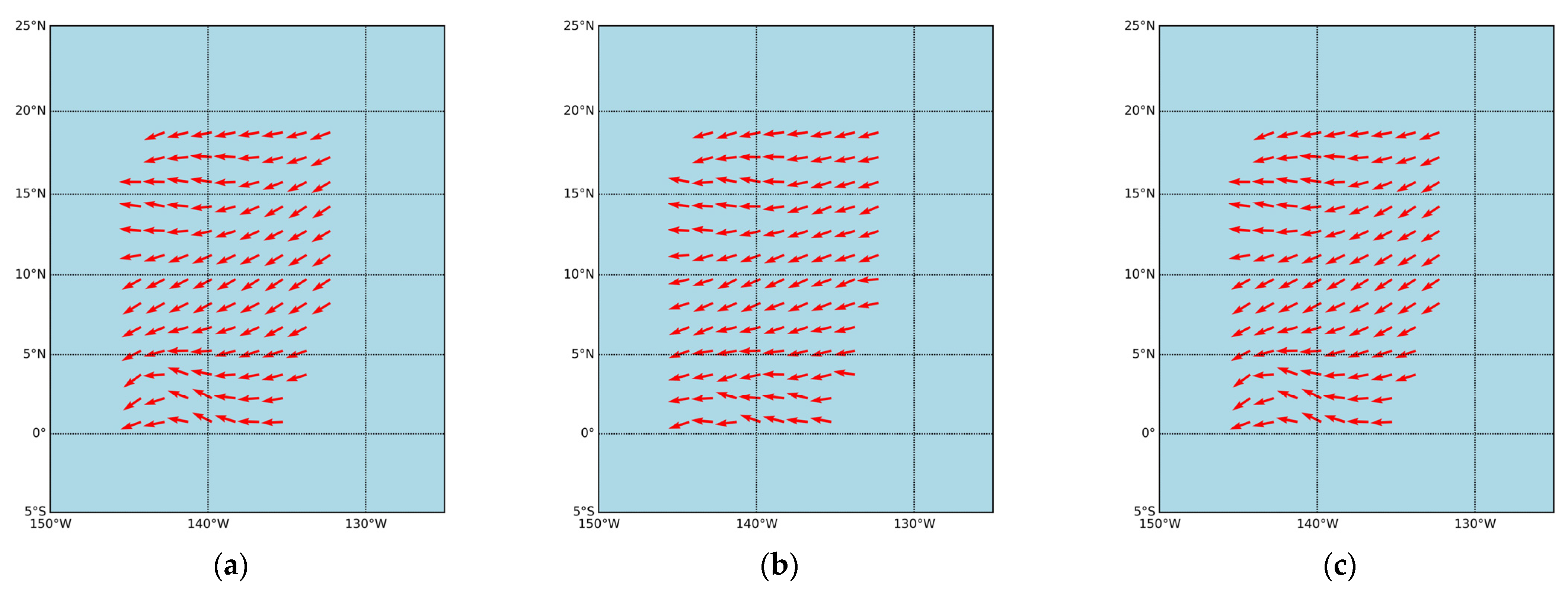
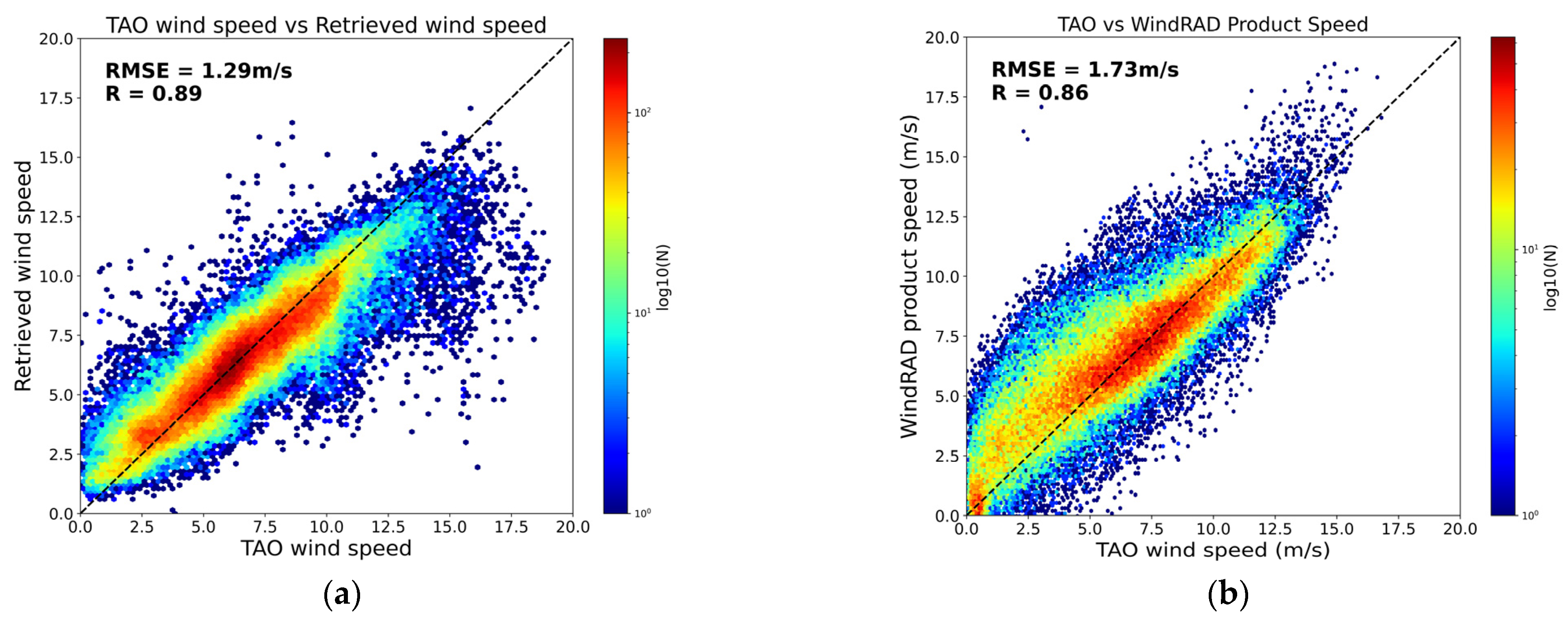
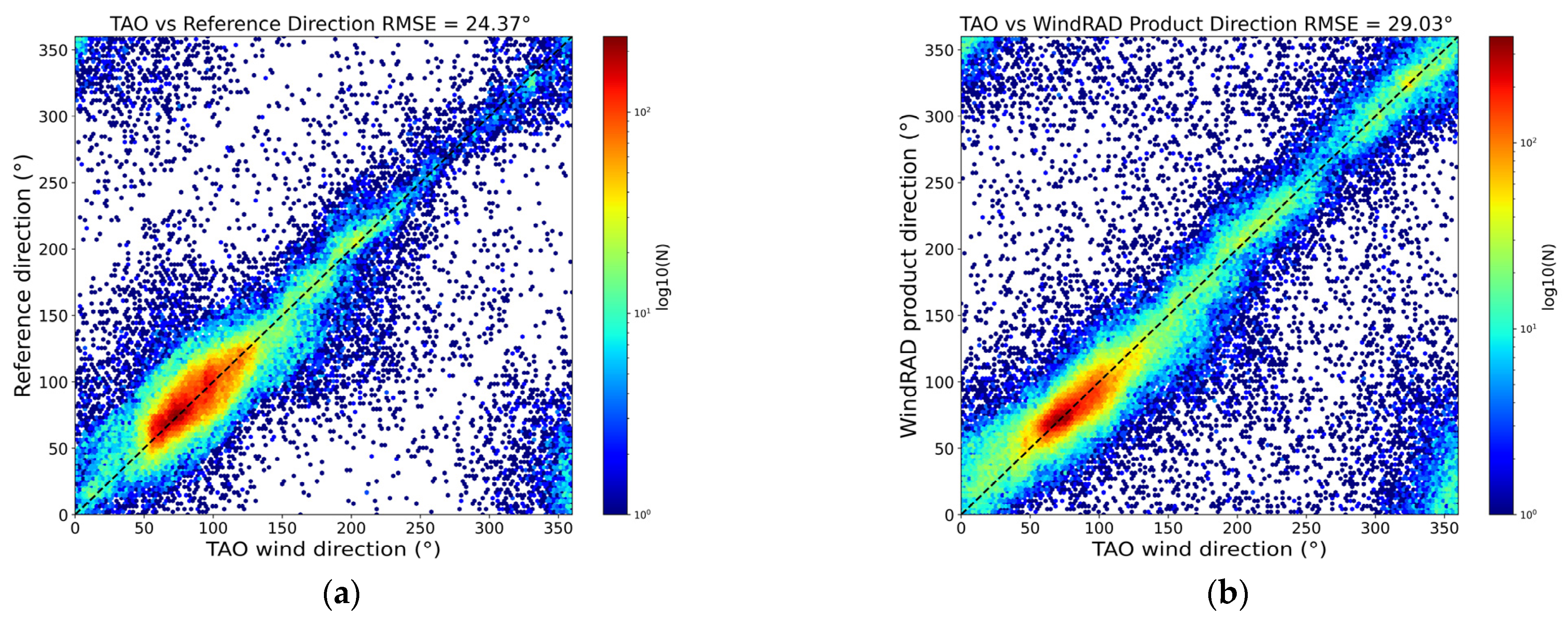
3.4. Validation with TAO Buoy Data
4. Discussion
5. Final Remarks
- (1)
- In this research, observational geometry from four distinct satellite viewing directions was incorporated as input features into a Backpropagation (BP) neural network to estimate ocean surface wind fields. The findings indicate that the BP network effectively learns and represents the intricate nonlinear dependencies between remote sensing observations and wind field characteristics. Compared with conventional retrieval techniques that rely on geophysical model functions (GMFs), the neural network approach demonstrates enhanced adaptability and robustness, especially under complex and variable atmospheric conditions.
- (2)
- Model evaluation metrics demonstrated robust performance, with training set errors measuring 1.20 m/s (wind speed) and 23.99° (direction), while testing set generalization errors reached 1.00 m/s and 24.58°, respectively. These results exhibit superior accuracy compared to the existing literature and operational satellite-derived wind products.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lin, Y.; Oey, L. Global Trends of Sea Surface Gravity Wave, Wind, and Coastal Wave Setup. J. Clim. 2019, 33, 769–785. [Google Scholar] [CrossRef]
- Zheng, C.W.; Li, X.H.; Azorin-Molina, C.; Li, C.Y.; Wang, Q.; Xiao, Z.N.; Yang, S.B.; Chen, X.; Zhan, C. Global Trends in Oceanic Wind Speed, Wind-Sea, Swell, and Mixed Wave Heights. Appl. Energy 2022, 321, 119327. [Google Scholar] [CrossRef]
- Katsaros, K.B.; Vachon, P.W.; Liu, W.T.; Black, P.G. Microwave Remote Sensing of Tropical Cyclones from Space. J. Oceanogr. 2002, 58, 137–151. [Google Scholar] [CrossRef]
- Li, X.; Yang, J.; Wang, J.; Han, G. Evaluation and Calibration of Remotely Sensed High Winds from the HY-2B/C/D Scatterometer in Tropical Cyclones. Remote Sens. 2022, 14, 4654. [Google Scholar] [CrossRef]
- Johnson, J.; Williams, L.; Bracalente, E.; Beck, F.; Grantham, W. Seasat-A Satellite Scatterometer Instrument Evaluation. IEEE J. Ocean. Eng. 1980, 5, 138–144. [Google Scholar] [CrossRef][Green Version]
- Jones, W.L.; Schroeder, L.C.; Boggs, D.H.; Bracalente, E.M.; Brown, R.A.; Dome, G.J.; Pierson, W.J.; Wentz, F.J. The SEASAT-A satellite scatterometer: The geophysical evaluation of remotely sensed wind vectors over the ocean. J. Geophys. Res. Oceans 1982, 87, 3297–3317. [Google Scholar] [CrossRef]
- Singh, S.; Tiwari, R.K.; Sood, V.; Kaur, R.; Prashar, S. The legacy of scatterometers: Review of applications and perspective. IEEE Geosci. Remote Sens. Mag. 2022, 10, 39–65. [Google Scholar] [CrossRef]
- Thompson, T.W.; Weissman, D.E.; Gonzalez, F.I. L-Band Radar Backscatter Dependence upon Surface Wind Stress: A Summary of New SEASAT-1 and Aircraft Observations. J. Geophys. Res. Oceans 1983, 88, 1727–1735. [Google Scholar] [CrossRef]
- Zhong, J.; Huang, S.; Zhang, L. Research on the Development of Surface Wind Retrieval from Microwave Scatterometer. Sci. Meteorol. Sin. 2010, 30, 137–142. [Google Scholar]
- de Kloe, J.; Stoffelen, A.; Verhoef, A.; Improved de Kloe, J.; Stoffelen, A.; Verhoef, A. Improved Use of Scatterometer Measurements by Using Stress-Equivalent Reference Winds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2340–2347. [Google Scholar] [CrossRef]
- Chi, C.Y.; Li, F.K. A Comparative Study of Several Wind Estimation Algorithms for Spaceborne Scatterometers. IEEE Trans. Geosci. Remote Sens. 1988, 26, 115–121. [Google Scholar] [CrossRef]
- Li, Z.; Stoffelen, A.; Verhoef, A. A Generalized Simulation Capability for Rotating-beam Scatterometers. Atmos. Meas. Tech. 2019, 12, 3573–3594. [Google Scholar] [CrossRef]
- Amani, M.; Mohseni, F.; Layegh, N.F.; Nazari, M.E.; Fatolazadeh, F.; Salehi, A. Remote Sensing Systems for Ocean: A Review (Part 2: Active systems). IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1421–1453. [Google Scholar] [CrossRef]
- Wentz, F.J.; Smith, D.K. A Model Function for the Ocean-normalized Radar Cross Section at 14 GHz Derived from NSCAT Observations. J. Geophys. Res. Oceans 1999, 104, 11499–11514. [Google Scholar] [CrossRef]
- Wang, Z.; Zou, J.; Lin, M.; Lin, W.; Zhang, Y.; Li, X.; Feng, Q.; He, Y. Development of A Geophysical Model Function for HY-2 Satellite Microwave Scatterometer Wind Retrievals. Natl. Remote Sens. Bull. 2023, 27, 871–880. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, L.; Ma, C.; Peng, H.; Zhou, W.; Lu, Y. Evaluating the Accuracy of Scatterometer Winds: A Study of Wind Correction Methods Using Buoy Observations. IEEE Trans. Geosci. Remote Sens. 2024, 62, 2007312. [Google Scholar] [CrossRef]
- Liu, S.; Li, Y.; Yang, X.; Zhou, W.; Lv, A.; Jin, X.; Dang, H. Sea Surface Wind Retrieval under Rainy Conditions from Active and Passive Microwave Measurements. Remote Sens. 2022, 14, 3016. [Google Scholar] [CrossRef]
- Li, X.; Lin, W.; Liu, B.; Wang, Z.; Zhang, B.; He, Y. Sea Surface Wind Retrieval Using the Combined Scatterometer and Altimeter Backscatter Measurements of the HY-2B Satellite. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Zhang, P.; Hu, X.; Lu, Q.; Zhu, A.; Lin, M.; Sun, L.; Chen, L.; Xu, N. FY-3E: The First Operational Meteorological Satellite Mission in an Early Morning Orbit. Adv. Atmos. Sci. 2022, 39, 1–8. [Google Scholar] [CrossRef]
- Zhai, X.; Tian, S.; Ye, Y.; Cao, G.; Chen, L.; Xu, N. First Results of Antarctic Sea Ice Classification Using Spaceborne Dual-Frequency Scatterometer FY-3E WindRAD. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- He, Y.; Fang, H.; Li, X.; Fan, G.; He, Z.; Cai, J. Assessment of Spatiotemporal Variations in Wind Field Measurements by the Chinese FengYun-3E Wind Radar Scatterometer. IEEE Access 2023, 11, 128224–128234. [Google Scholar] [CrossRef]
- Chen, K.S.; Tzeng, Y.C.; Chen, P.C. Retrieval of Ocean Winds from Satellite Scatterometer by a Neural Network. IEEE Trans. Geosci. Remote Sens. 1999, 37, 247–256. [Google Scholar] [CrossRef]
- Jian, S.; Wang, Z.; Dou, F.; Yuan, M.; Yin, H.; Liu, L.; Wang, Y.; Hu, X.; Zhang, P. Preliminary Performance of the WindRAD Scatterometer Onboard the FY-3E Meteorological Satellite. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–13. [Google Scholar] [CrossRef]
- Liu, L.; Jin, A.; Jin, A.; Xue, S.; Yao, P.; Dong, G. FY-3E Wind Scatterometer Prelaunch and Commissioning Performance Verification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–12. [Google Scholar] [CrossRef]
- National Satellite Meteorological Center (NSMC). Available online: https://nsmc.org.cn/nsmc/cn/instrument/WindRAD.html. (accessed on 1 May 2025).
- Portabella, M. Wind field retrieval from satellite radar systems. Ph.D. Thesis, University of Barcelona, Barcelona, Spain, 2002. [Google Scholar]
- Trenberth, K.E.; Olson, J.G. An evaluation and intercomparison of global analyses from the National Meteorological Center and the European Centre for Medium Range Weather Forecasts. Bull. Am. Meteorol. Soc. 1988, 69, 1047–1057. [Google Scholar] [CrossRef]
- Cronin, M.F.; Fairall, C.W.; McPhaden, M.J. An Assessment of Buoy-Derived and Numerical Weather Prediction Surface Heat Fluxes in the Tropical Pacific. J. Geophys. Res. 2006, 111, C06038. [Google Scholar] [CrossRef]
- National Data Buoy Center (NDBC). Available online: https://tao.ndbc.noaa.gov/tao/data_download/download_readme.shtml. (accessed on 1 July 2025).
- Thomas, B.R.; Kent, E.C.; Swail, V.R. Methods to Homogenize Wind Speeds from Ships and Buoys. Int. J. Climatol. 2005, 25, 979–995. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, F.; Sun, T.; Xu, B. A Constrained Optimization Method Based on BP Neural Network. Neural Comput. Appl. 2018, 29, 413–421. [Google Scholar] [CrossRef]
- Sadeghi, M.; Asanjan, A.A.; Faridzad, M.; Nguyen, P.; Hsu, K.; Sorooshian, S.; Braithwaite, D. PERSIANN-CNN: Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks–Convolutional Neural Networks. J. Hydrometeorol. 2019, 20, 2273–2289. [Google Scholar] [CrossRef]
- Krasnopolsky, V.M.; Schiller, H. Some Neural Network Applications in Environmental Sciences. Part I: Forward and inverse problems in geophysical remote measurements. Neural Netw. 2003, 16, 321–334. [Google Scholar] [CrossRef]
- Bu, J.; Yu, K.; Zuo, X.; Ni, J.; Li, Y.; Huang, W. GloWS-Net: A Deep Learning Framework for Retrieving Global Sea Surface Wind Speed Using Spaceborne GNSS-R Data. Remote Sens. 2023, 15, 590. [Google Scholar] [CrossRef]
- Rumelhart, D.; Hinton, G.; Williams, R. Learning Representations by Back-propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Wang, X.; Liu, J. Spatially Regularized Leaky ReLU in Dual Space for CNN-based Image Segmentation. Inverse Probl. Imaging 2024, 18, 1320–1342. [Google Scholar] [CrossRef]
- Dubey, S.R.; Singh, S.K.; Chaudhuri, B.B. Activation Functions in Deep Learning: A Comprehensive Survey and Benchmark. Neurocomputing 2022, 503, 92–108. [Google Scholar] [CrossRef]
- Sharma, V.S.; Mahajan, S.; Nayyar, A.; Kant Pandit, A. (Eds.) Deep Learning in Engineering, Energy and Finance: Principals and Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2024. [Google Scholar]
- Tian, Y.; Zhang, Y.; Zhang, H. Recent Advances in Stochastic Gradient Descent in Deep Learning. Mathematics 2023, 11, 682. [Google Scholar] [CrossRef]
- Chen, K.; Dong, X.; Xu, X.; Lang, S. The Study on Oceanic Vector Wind Field Retrieve Technique Based on Neural Networks of Microwave Scatterometer. Remote Sens. Technol. Appl. 2017, 32, 683–690. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A. Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning. J. Artif. Intell. Res. 2017, 31, 4278–4284. [Google Scholar] [CrossRef]
- Kukačka, J.; Golkov, V.; Cremers, D. Regularization for Deep Learning: A taxonomy. arXiv 2017, arXiv:1710.10686. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. 2014. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Dong, X.; Tan, T.; Potter, M.; Tsai, Y.-C.; Kumar, G.; Saripalli, V.R.; Trafalis, T. To Raise or not to Raise: The autonomous learning rate question. Ann. Math. Artif. Intell. 2024, 92, 1679–1698. [Google Scholar] [CrossRef]
- Dai, H.; Peng, X.; Shi, X.; He, L.; Xiong, Q.; Jin, H. Reveal Training Performance Mystery Between TensorFlow and PyTorch in the Single GPU Environment. Sci. China Inf. Sci. 2022, 65, 112103. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Z.Q. Implicit Regularization of Dropout. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 4206–4217. [Google Scholar] [CrossRef] [PubMed]
- Rocha, A.D.; Groen, T.A.; Skidmore, A.K.; Darvishzadeh, R.; Willemen, L. The Naïve Overfitting Index Selection (NOIS): A new method to optimize model complexity for hyperspectral data. ISPRS J. Photogramm. Remote Sens. 2017, 133, 61–74. [Google Scholar] [CrossRef]
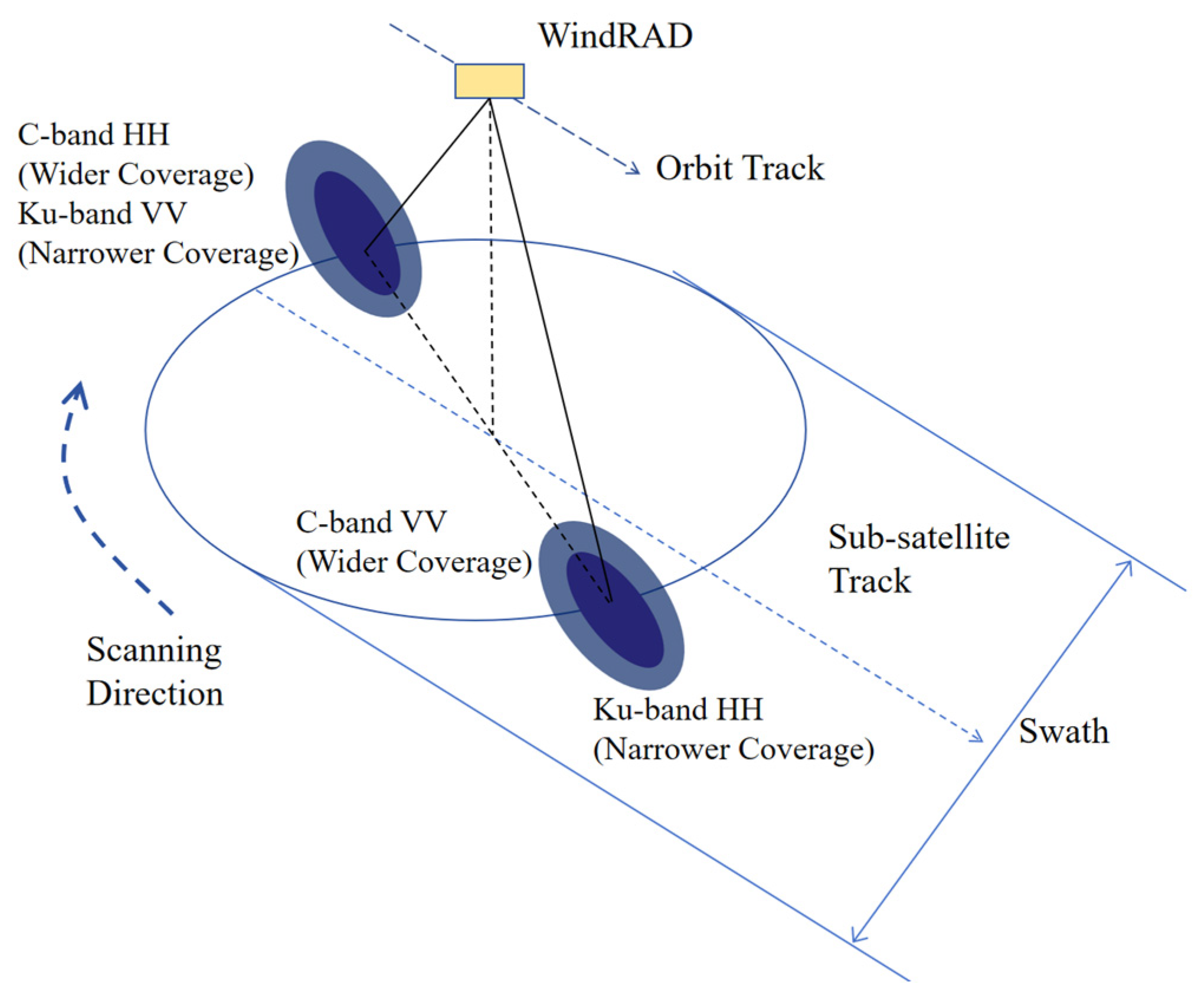

| Parameter | Specification for C Band | Specification for Ku Band |
|---|---|---|
| Spatial resolution | 25 × 0.5 km | 10 × 0.5 km |
| Swath width | >1200 km | |
| Scanning mode | 360° conical scanning | |
| Minimum detectable wind speed | 3 m/s (−26.2 dB) | 3 m/s (−30.8 dB) |
| Radiation resolution 1 | 0.5 dB (far end of swath, wind speed ≥ 5 m/s) 2 1.0 dB (far end of swath, wind speed = 3 m/s) | |
| Parameter Combination | Hidden Layer Neuron Count | Activation Function | ||
|---|---|---|---|---|
| Layer 1 | Layer 2 | Layer 3 | ||
| 1 | 512 | 256 | 128 | Leaky ReLU |
| 2 | 512 | 256 | 128 | Sigmoid |
| 3 | 1024 | 512 | 256 | Leaky ReLU |
| 4 | 1024 | 512 | 256 | Sigmoid |
| Parameter Combination | RMSE for U Wind Component (m/s) | R for U Wind Component | RMSE for V Wind Component (m/s) | R for V Wind Component |
|---|---|---|---|---|
| 1 | 2.10 | 0.91 | 2.06 | 0.91 |
| 2 | 2.61 | 0.86 | 2.54 | 0.87 |
| 3 | 1.95 | 0.92 | 1.92 | 0.92 |
| 4 | 2.62 | 0.85 | 2.58 | 0.87 |
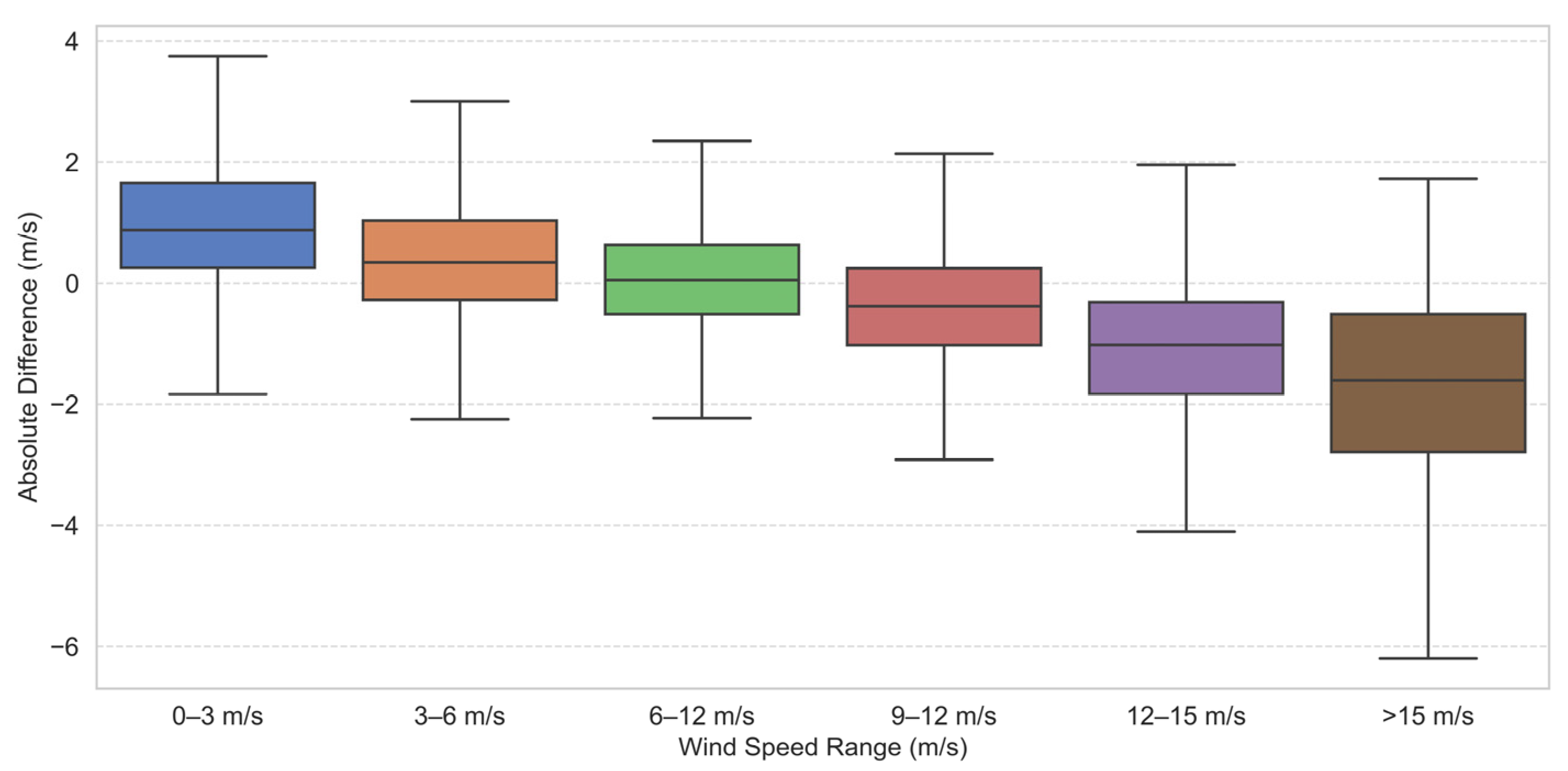
| Wind Speed Range | Mean (m/s) | Standard Deviation (m/s) |
|---|---|---|
| 0–3 m/s | 1.07 | 1.24 |
| 3–6 m/s | 0.42 | 1.12 |
| 6–9 m/s | 0.06 | 0.99 |
| 9–12 m/s | −0.42 | 1.09 |
| 12–15 m/s | −1.14 | 1.30 |
| >15 m/s | −1.84 | 1.73 |
| Wind Direction Range | Mean (°) | Standard Deviation (°) |
|---|---|---|
| 0–60° | 11.61 | 22.54 |
| 60–120° | 0.03 | 16.04 |
| 120–180° | −10.57 | 23.04 |
| 180–240° | −6.51 | 29.72 |
| 240–300° | −0.26 | 31.95 |
| 300–360° | 8.37 | 24.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Pang, F.; Petropoulos, G.P.; Bao, Y.; Xiao, Q.; Wang, Y.; Li, S.; Gao, W.; Wang, T. Wind Field Retrieval from Fengyun-3E Radar Based on a Backpropagation Neural Network. Remote Sens. 2025, 17, 2813. https://doi.org/10.3390/rs17162813
Zhao Z, Pang F, Petropoulos GP, Bao Y, Xiao Q, Wang Y, Li S, Gao W, Wang T. Wind Field Retrieval from Fengyun-3E Radar Based on a Backpropagation Neural Network. Remote Sensing. 2025; 17(16):2813. https://doi.org/10.3390/rs17162813
Chicago/Turabian StyleZhao, Zhengxuan, Fang Pang, George P. Petropoulos, Yansong Bao, Qing Xiao, Yuanyuan Wang, Shiqi Li, Wanyue Gao, and Tianhao Wang. 2025. "Wind Field Retrieval from Fengyun-3E Radar Based on a Backpropagation Neural Network" Remote Sensing 17, no. 16: 2813. https://doi.org/10.3390/rs17162813
APA StyleZhao, Z., Pang, F., Petropoulos, G. P., Bao, Y., Xiao, Q., Wang, Y., Li, S., Gao, W., & Wang, T. (2025). Wind Field Retrieval from Fengyun-3E Radar Based on a Backpropagation Neural Network. Remote Sensing, 17(16), 2813. https://doi.org/10.3390/rs17162813









