Development of a Two-Stage Correction Framework for Satellite, Multi-Source Merged, and Reanalysis Precipitation Products Across the Huang-Huai-Hai Plain, China, During 2000–2020
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Datasets
2.2.1. Satellite Precipitation Products
2.2.2. Multi-Source Merged Precipitation Products
2.2.3. Reanalysis Precipitation Products
2.2.4. Rain Gauge Data
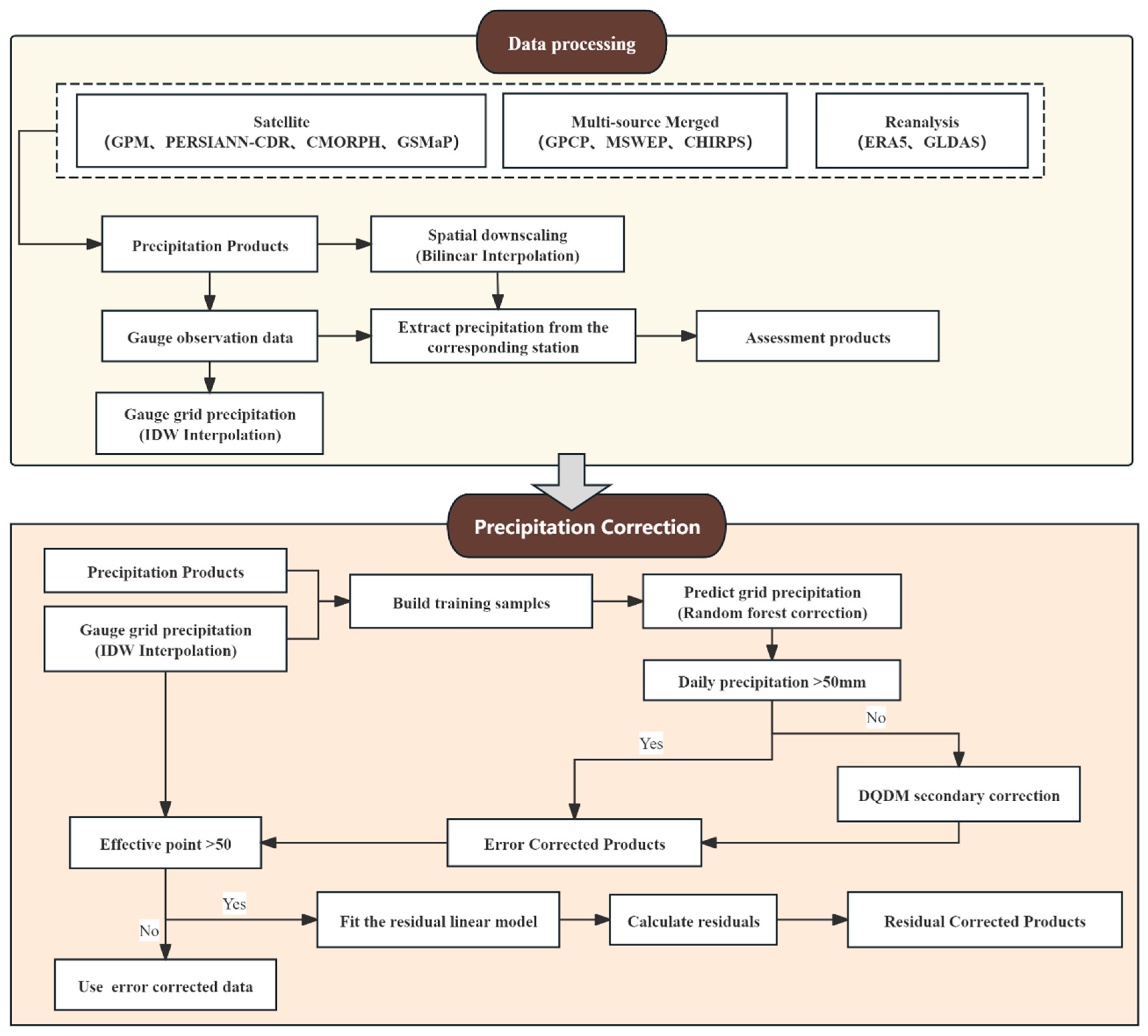
2.3. Methods
2.3.1. Error Correction Stage: RF-DQDM
2.3.2. Residual Correction Stage: Statistical Bias Adjustment
3. Results
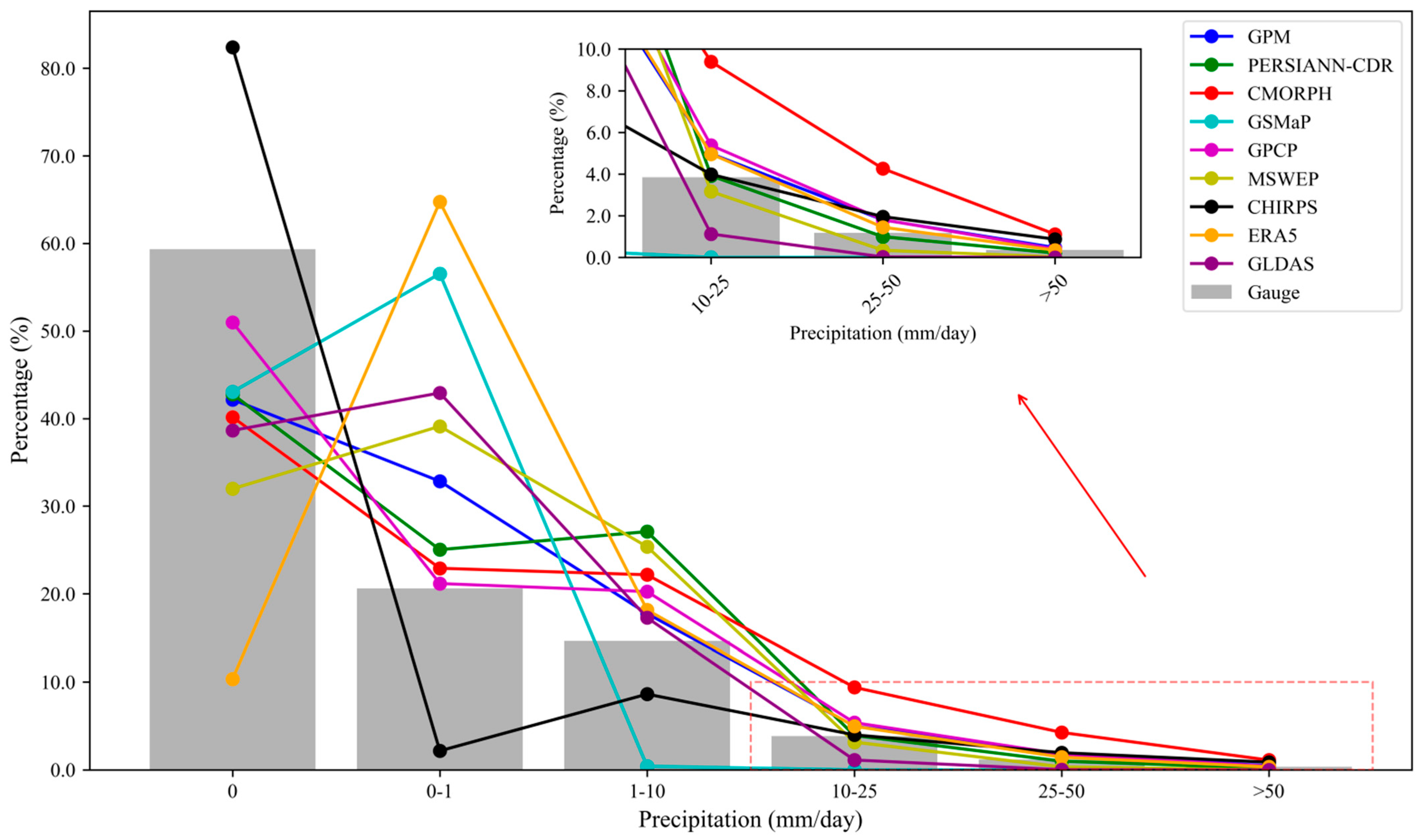
3.1. Precipitation Analysis
3.2. Precipitation Correction
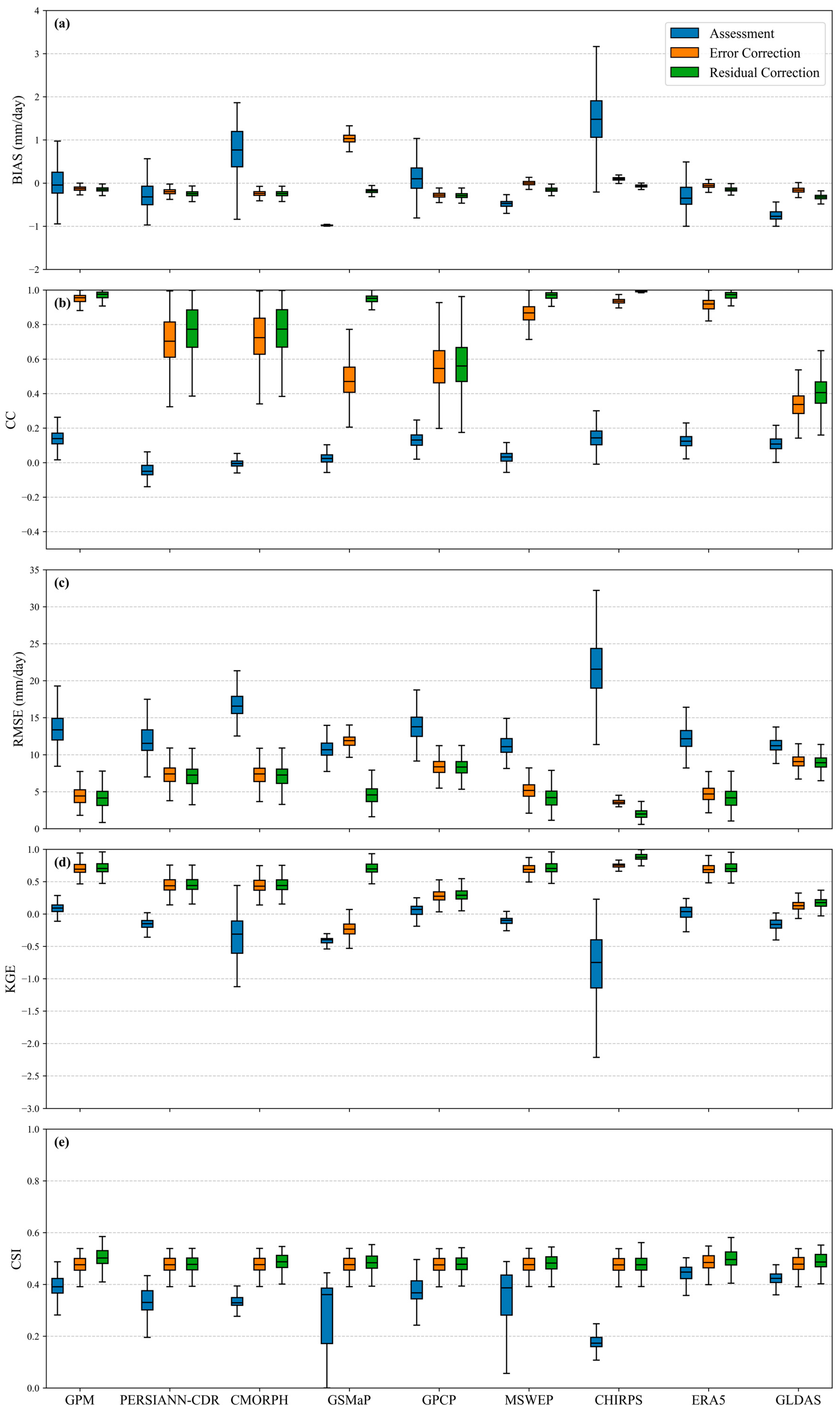
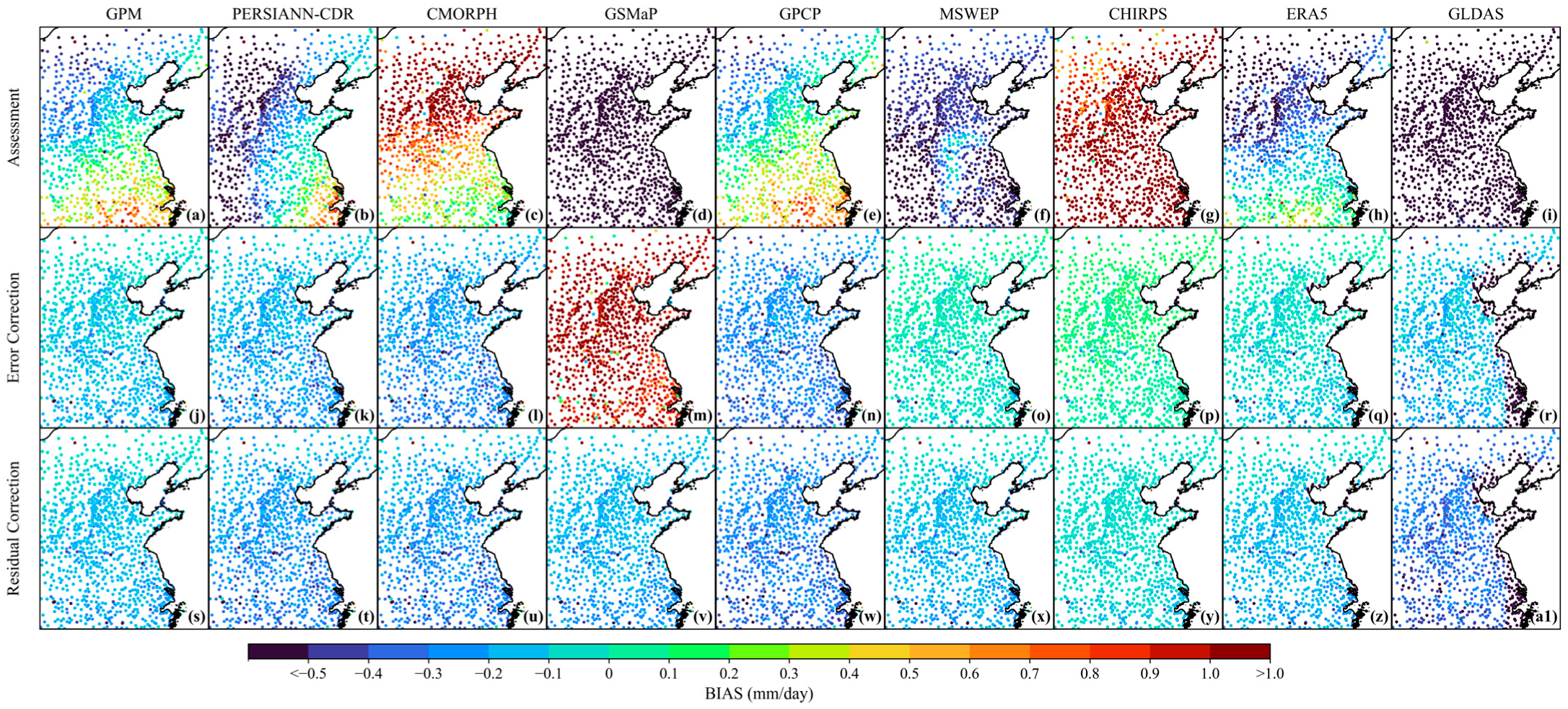
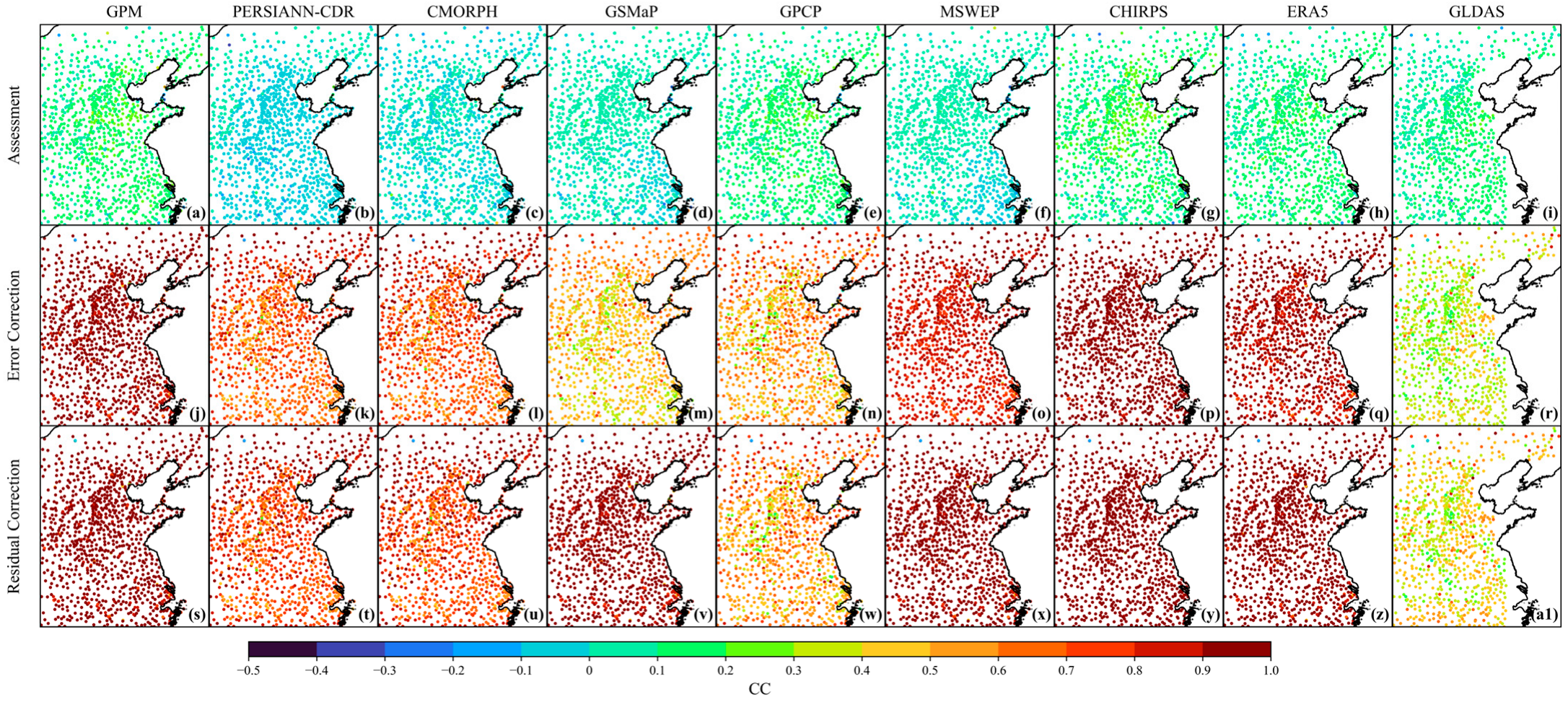
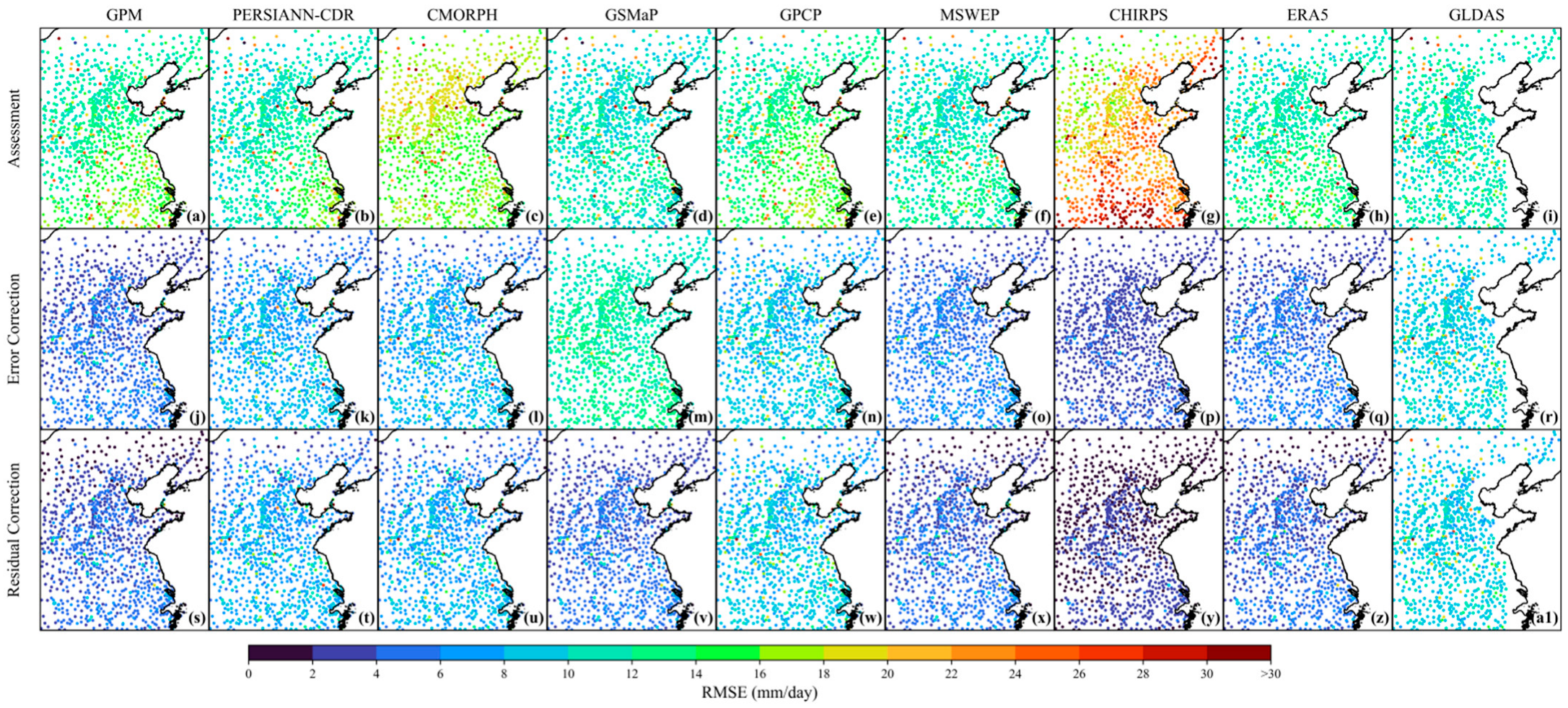
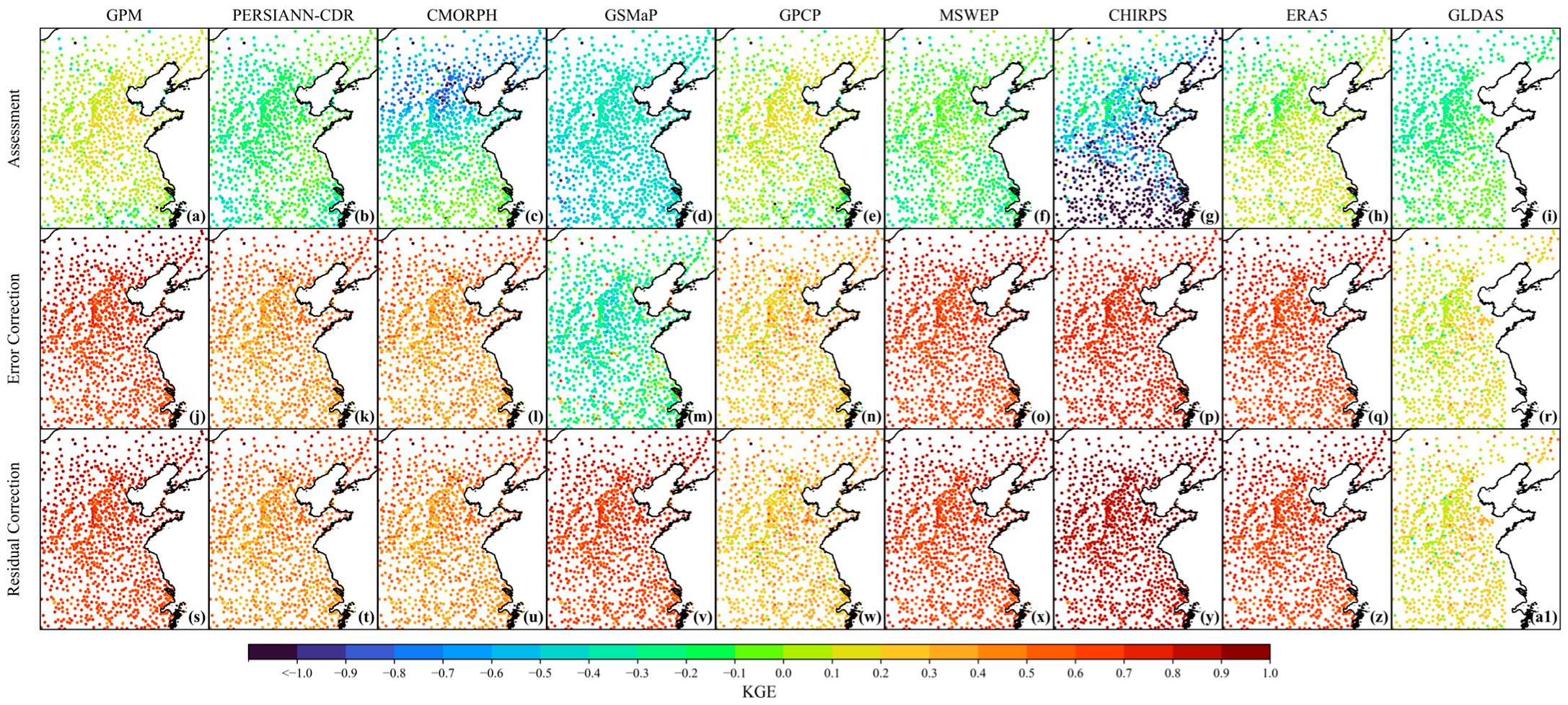
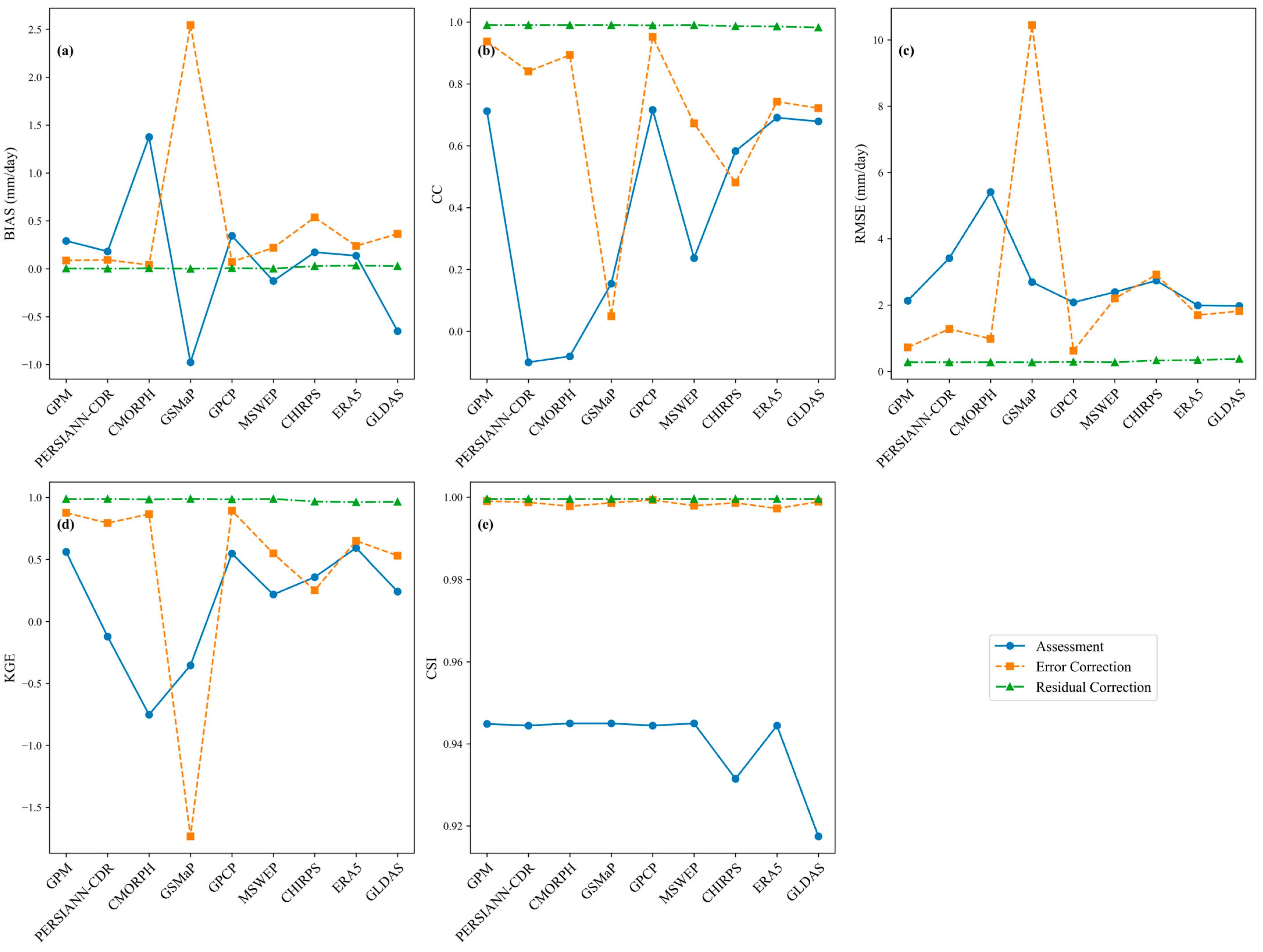
3.2.1. Comparison of Evaluation Metrics
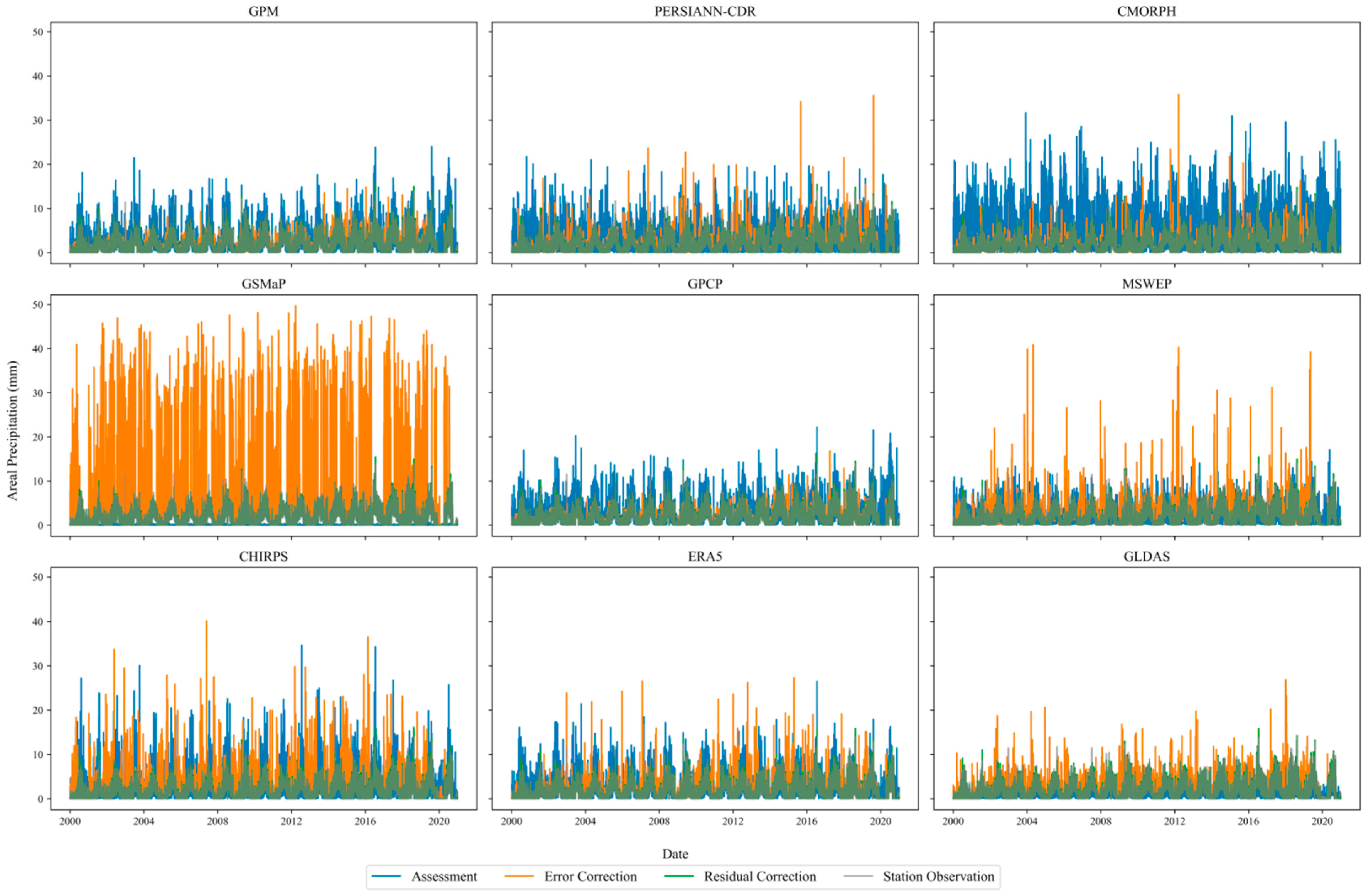
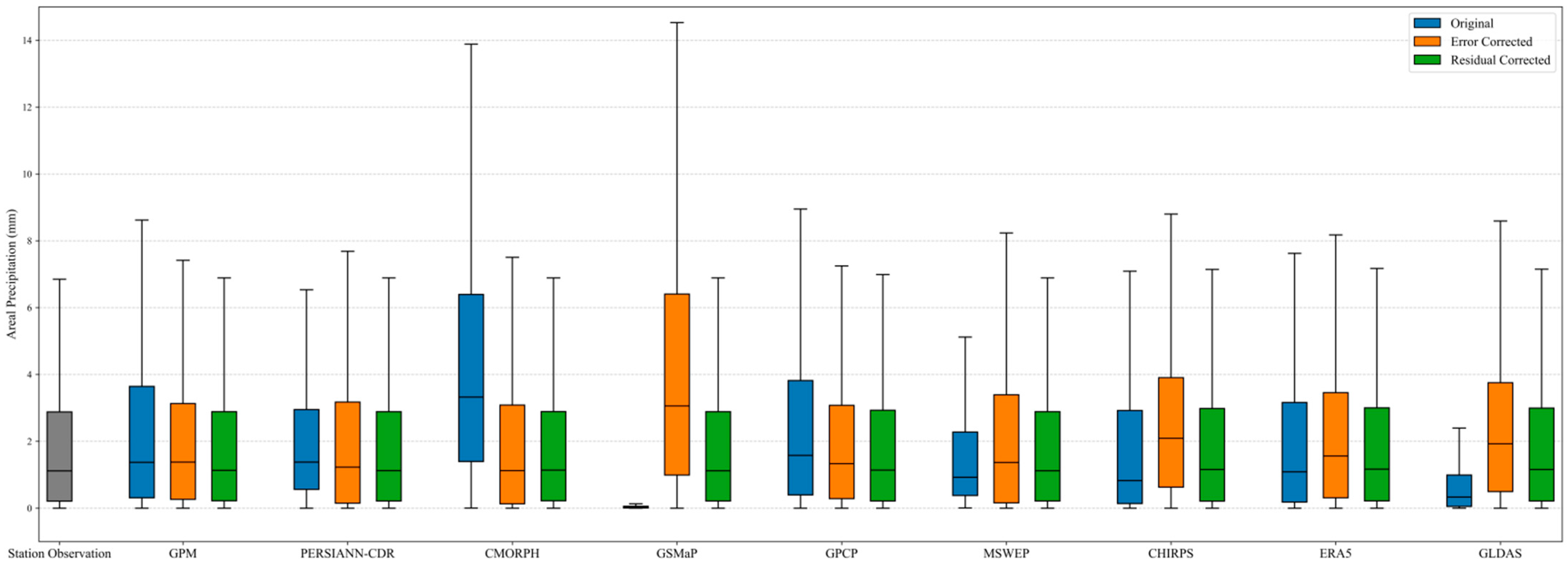
3.2.2. Areal Precipitation Analysis
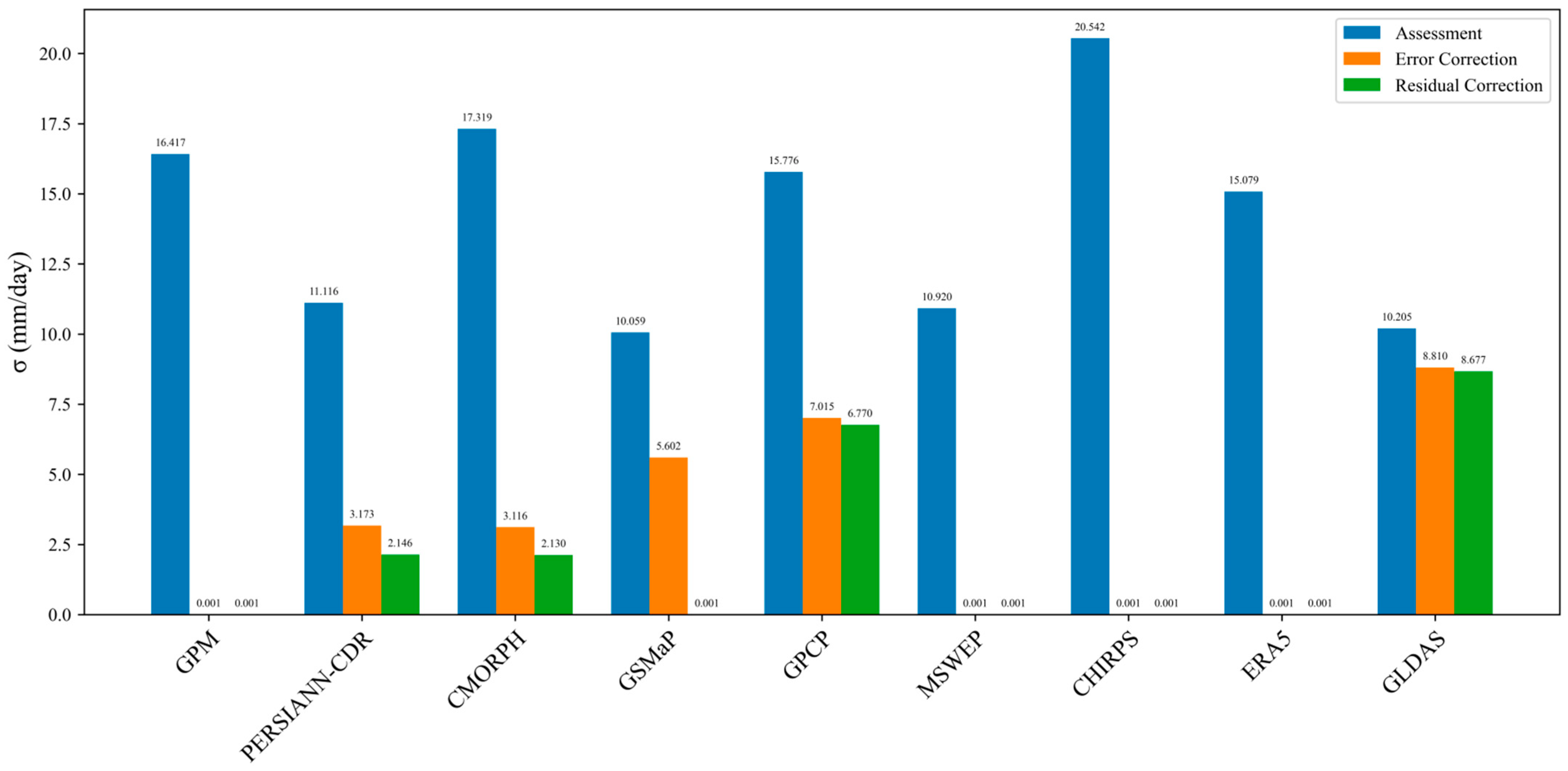
3.2.3. Uncertainty Analysis
4. Discussion
4.1. Divergence in Product Correction Responses
4.2. Spatial Correction and Transferability
4.3. Method Comparison and Performance Evaluation
4.4. Expanded Outlook and Future Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Eltahir, E.A.B.; Bras, R.L. Precipitation recycling. Rev. Geophys. 1996, 34, 367–378. [Google Scholar] [CrossRef]
- Wei, C.; Dong, X.H.; Ma, Y.M.; Gou, J.F.; Li, L.; Bo, H.J.; Yu, D.; Su, B.B. Applicability comparison of various precipitation products of long-term hydrological simulations and their impact on parameter sensitivity. J. Hydrol. 2023, 618, 129187. [Google Scholar] [CrossRef]
- Li, J.; Li, L.; Zhang, T.; Xing, H.; Shi, Y.; Li, Z.; Wang, C.; Liu, J. Flood forecasting based on radar precipitation nowcasting using U-net and its improved models. J. Hydrol. 2024, 632, 130871. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, W.; Chen, Z. Blending gauge, multi-satellite and atmospheric reanalysis precipitation products to facilitate drought monitoring. J. Hydrol. 2025, 647, 132254. [Google Scholar] [CrossRef]
- Yin, J.; Guo, S.; Gu, L.; Zeng, Z.; Xu, C.Y. Blending multi-satellite, atmospheric reanalysis and gauge precipitation products to facilitate hydrological modelling. J. Hydrol. 2020, 593, 125878. [Google Scholar] [CrossRef]
- Zhu, S.; Liu, Z. Comprehensive quantitative assessment of the performance of fourteen satellite precipitation products over Chinese mainland. Clim. Dyn. 2024, 62, 6799–6818. [Google Scholar] [CrossRef]
- Chen, X.; Wang, S.; Hu, Z.; Zhou, Q.; Hu, Q. Spatiotemporal characteristics of seasonal precipitation and their relationships with ENSO in Central Asia during 1901–2013. Acta Geogr. Sin. 2018, 28, 28. [Google Scholar] [CrossRef]
- Yang, X.L.; Song, Z.W.; Wang, H.; Shi, Q.H.; Chu, Q.Q. Spatio-temporal variations of winter wheat water requirement and climatic causes in Huang-Huai-Hai Farming Region. Chin. J. Eco-Agric. 2012, 20, 356–362. [Google Scholar] [CrossRef]
- Wang, Q.; Xia, J.; She, D.; Zhang, X.; Liu, J.; Zhang, Y. Assessment of four latest long-term satellite-based precipitation products in capturing the extreme precipitation and streamflow across a humid region of southern China. Atmos. Res. 2021, 257, 105554. [Google Scholar] [CrossRef]
- Rohith, A.N.; Cibin, R. An extremes-weighted empirical quantile mapping for global climate model data bias correction for improved emphasis on extremes. Theor. Appl. Climatol. 2024, 155, 5515–5523. [Google Scholar] [CrossRef]
- Yao, N.; Ye, J.; Wang, S.; Yang, S.; Lu, Y.; Zhang, H.; Yang, X. Bias correction of the hourly satellite precipitation product using machine learning methods enhanced with high-resolution WRF meteorological simulations. Atmos. Res. 2024, 310, 107637. [Google Scholar] [CrossRef]
- Nan, L.; Yang, M.; Wang, H.; Wang, H.; Dong, N. An Innovative Correction–Fusion Approach for Multi-Satellite Precipitation Products Conditioned by Gauge Background Fields over the Lancang River Basin. Remote Sens. 2024, 16, 1824. [Google Scholar] [CrossRef]
- Meema, T.; Wattanasetpong, J.; Wichakul, S. Integrating machine learning and zoning-based techniques for bias correction in gridded precipitation data to improve hydrological estimation in the data-scarce region. J. Hydrol. 2025, 646, 132356. [Google Scholar] [CrossRef]
- Gan, F.; Diao, X.; Tan, K.; Li, X.; Cao, G.; Zhong, X.; Gao, Y. Error correction for IMERG precipitation estimates based on climatological adjustment combining the dry–wet season division and weight allocation. J. Hydrol. 2023, 624, 129890. [Google Scholar] [CrossRef]
- Li, X.; Li, Z. Assessment of bias correction methods for high resolution daily precipitation projections with CMIP6 models: A Canadian case study. J. Hydrol. Reg. Stud. 2025, 58, 102223. [Google Scholar] [CrossRef]
- Jiyuan, L.; Wenhui, K.; Zengxiang, Z.; Xinliang, X.U.; Yuanwei, Q.; Jia, N.; Wancun, Z.; Shuwen, Z.; Rendong, L.I.; Changzhen, Y. Spatiotemporal characteristics, patterns and causes of land use changes in China since the late 1980s. Acta Geogr. Sin. 2014, 24, 195–210. [Google Scholar]
- Zhang, Q.; Zheng, Y.; Singh, V.P.; Luo, M.; Xie, Z. Summer extreme precipitation in eastern China: Mechanisms and impacts. In Proceedings of the EGU General Assembly 2017, Vienna, Austria, 23–28 April 2017. [Google Scholar]
- Feng, Y.; Qi, Y.; Chen, D.; Li, D.; Li, Z.; Xu, X. Multi-scale analysis of satellite, reanalysis and muti-source precipitation estimates over the Tibetan Plateau. Atmos. Res. 2024, 309, 107484. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, J.; Bao, Z.; Parajka, J.; Wang, G.; Liu, C.; Jin, J.; Tang, Z.; Ning, Z.; Fang, J. A novel error decomposition and fusion framework for daily precipitation estimation based on near-real-time satellite precipitation product and gauge observations. J. Hydrol. 2024, 640, 131715. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H. The JRA-55 Reanalysis: General Specifications and Basic Characteristics. J. Meteorol. Soc. Jpn. 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Menne, M.J.; Durre, I.; Vose, R.S.; Gleason, B.E.; Houston, T.G. An Overview of the Global Historical Climatology Network-Daily Database. J. Atmos. Ocean. Technol. 2011, 29, 897–910. [Google Scholar] [CrossRef]
- Ren, J.; Huang, C.; Hou, J.; Zhang, Y.; Ma, P.; Yang, L. Impact of the combined assimilation of GPM/IMGER precipitation and Himawari-8/AHI water vapor radiance on snowfall forecasts using WRF model and 4Dvar system. Atmos. Res. 2024, 311, 107726. [Google Scholar] [CrossRef]
- Li, X.; Chen, L.; Chen, Y.; Zhang, R.; Zhu, Z.; Yin, H.; Jiang, B. Assessing the use of GPM DPR and IMERG products for Typhoon Mujigae over the southern coastal provinces of China. Atmos. Res. 2025, 315, 107873. [Google Scholar] [CrossRef]
- Xiong, J.; Tang, G.; Yang, Y. Continental evaluation of GPM IMERG V07B precipitation on a sub-daily scale. Remote Sens. Environ. 2025, 321, 114690. [Google Scholar] [CrossRef]
- Salmani-Dehaghi, N.; Samani, N. Development of bias-correction PERSIANN-CDR models for the simulation and completion of precipitation time series. Atmos. Environ. 2021, 246, 117981. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, C.; Yeh, P.J.F.; Li, J.; Hu, B.X.; Feng, P.; Jun, C. Evaluation and comparison of precipitation estimates and hydrologic utility of CHIRPS, TRMM 3B42 V7 and PERSIANN-CDR products in various climate regimes. Atmos. Res. 2022, 265, 105881. [Google Scholar] [CrossRef]
- Tan, M.L.; Santo, H. Comparison of GPM IMERG, TMPA 3B42 and PERSIANN-CDR satellite precipitation products over Malaysia. Atmos. Res. 2018, 202, 63–76. [Google Scholar] [CrossRef]
- Jia, J.; He, Y.; Zhang, B.; Huo, Z.; Tang, Z.; Wang, S.; Yu, H.; Guan, X. Evaluation of hourly summer precipitation products over the Tibetan Plateau: A comparative analysis of IMERG, CMORPH, and TPHiPr. Atmos. Res. 2025, 316, 107955. [Google Scholar] [CrossRef]
- Li, Y.; Yan, H.; Chen, L.; Huang, M.; Shou, W.; Zhu, L.; Zhao, L.; Xing, Y. Performance and uncertainties of five popular satellite-based precipitation products in drought monitoring for different climate regions. J. Hydrol. 2024, 628, 130562. [Google Scholar] [CrossRef]
- Kim, J.; Han, H. Evaluation of the CMORPH high-resolution precipitation product for hydrological applications over South Korea. Atmos. Res. 2021, 258, 105650. [Google Scholar] [CrossRef]
- Wang, H.; Zang, F.; Zhao, C.; Liu, C. A GWR downscaling method to reconstruct high-resolution precipitation dataset based on GSMaP-Gauge data: A case study in the Qilian Mountains, Northwest China. Sci. Total Environ. 2022, 810, 152066. [Google Scholar] [CrossRef] [PubMed]
- Weng, P.; Tian, Y.; Jiang, Y.; Chen, D.; Kang, J. Assessment of GPM IMERG and GSMaP daily precipitation products and their utility in droughts and floods monitoring across Xijiang River Basin. Atmos. Res. 2023, 286, 106673. [Google Scholar] [CrossRef]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D. The Version2 Global Precipitation Climatology Project (GPCP) Monthly Precipitation Analysis (1979 Present). J. Hydrometeorol. 2003, 4, 1147–1167. [Google Scholar] [CrossRef]
- Liu, J.; Shangguan, D.; Liu, S.; Ding, Y.; Wang, S.; Wang, X. Evaluation and comparison of CHIRPS and MSWEP daily-precipitation products in the Qinghai-Tibet Plateau during the period of 1981–2015. Atmos. Res. 2019, 230, 104634. [Google Scholar] [CrossRef]
- Alijanian, M.; Rakhshandehroo, G.R.; Mishra, A.; Dehghani, M. Evaluation of remotely sensed precipitation estimates using PERSIANN-CDR and MSWEP for spatio-temporal drought assessment over Iran. J. Hydrol. 2019, 579, 124189. [Google Scholar] [CrossRef]
- Du, H.; Tan, M.L.; Zhang, F.; Chun, K.P.; Li, L.; Kabir, M.H. Evaluating the effectiveness of CHIRPS data for hydroclimatic studies. Theor. Appl. Climatol. 2024, 155, 1519–1539. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Berrisford, P.; Soci, C.; Bell, B.; Dahlgren, P.; Horányi, A.; Nicolas, J.; Radu, R.; Villaume, S.; Bidlot, J.R.; Haimberger, L. The ERA5 global reanalysis: Preliminary extension to 1950. Q. J. R. Meteorol. Soc. 2021, 147, 4186–4227. [Google Scholar] [CrossRef]
- Chen, H.; Wen, D. Dependency of errors for four global reanalysis and satellite precipitation estimates on four crucial factors. Atmos. Res. 2023, 296, 107076. [Google Scholar] [CrossRef]
- Majidi, F.; Sabetghadam, S.; Gharaylou, M.; Rezaian, R. Evaluation of the performance of ERA5, ERA5-Land and MERRA-2 reanalysis to estimate snow depth over a mountainous semi-arid region in Iran. J. Hydrol. Reg. Stud. 2025, 58, 102246. [Google Scholar] [CrossRef]
- Xu, C.; Wang, W.; Hu, Y.; Liu, Y. Evaluation of ERA5, ERA5-Land, GLDAS-2.1, and GLEAM potential evapotranspiration data over mainland China. J. Hydrol. Reg. Stud. 2024, 51, 101651. [Google Scholar] [CrossRef]
- Besnier, J.; Getirana, A.; Beaudoing, H.; Lakshmi, V. Characterizing the 2019–2021 drought in La Plata River Basin with GLDAS and SMAP. J. Hydrol. Reg. Stud. 2024, 52, 101679. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, B.; Yao, Y.; Yin, J.; Wang, H.; Ran, Q. Jointly using the GLDAS 2.2 model and GRACE to study the severe Yangtze flooding of 2020. J. Hydrol. 2022, 610, 127927. [Google Scholar] [CrossRef]
- Bisht, D.S.; Kumar, D.P.; Amarjyothi, K.; Saha, U. Bias correction of satellite precipitation estimates using Mumbai-MESONET observations: A Random Forest approach. Atmos. Res. 2025, 315, 107858. [Google Scholar] [CrossRef]
- Ma, J.; Wang, G.; Li, H. A variance-upscaling quantile mapping method for gridded precipitation bias correction. J. Hydrol. 2024, 632, 130959. [Google Scholar] [CrossRef]
- Lober, C.; Fayne, J.; Hashemi, H.; Smith, L.C. Bias correction of 20 years of IMERG satellite precipitation data over Canada and Alaska. J. Hydrol. Reg. Stud. 2023, 47, 101386. [Google Scholar] [CrossRef]
- Aghakouchak, A.; Mehran, A.; Norouzi, H.; Behrangi, A. Systematic and random error components in satellite precipitation data sets. Geophys. Res. Lett. 2012, 39, 9406. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; Aghakouchak, A.; Pai, D.S. Error characterization of TRMM Multisatellite Precipitation Analysis (TMPA-3B42) products over India for different seasons. J. Hydrol. 2015, 529, 1302–1312. [Google Scholar] [CrossRef]
- Beck, H.E.; Van Dijk, A.I.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; Roo, A.D. MSWEP: 3-hourly 0.25° global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2016, 21, 589–615. [Google Scholar] [CrossRef]
- Prakash, S. Performance assessment of CHIRPS, MSWEP, SM2RAIN-CCI, and TMPA precipitation products across India. J. Hydrol. 2019, 571, 50–59. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.; Sorooshian, S.; Tan, J.; Xie, P. Reaching for 20 Years with the IMERG Multi-Satellite Products. In Proceedings of the 2020 American Meteorological Society (AMS) Annual Meeting, Boston, MA, USA, 12–16 January 2020. [Google Scholar]
- Kidd, C.; Becker, A.; Huffman, G.J.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D.B. So, how much of the Earth’s surface is covered by rain gauges? Bull. Am. Meteorol. Soc. 2016, 98, 69–78. [Google Scholar] [CrossRef]
- Pradhan, A.; Indu, J. Assessment of SM2RAIN derived and IMERG based precipitation products for hydrological simulation. J. Hydrol. 2021, 603, 127191. [Google Scholar] [CrossRef]
- Mahmoud, M.T.; Al-Zahrani, M.A.; Sharif, H.O. Assessment of global precipitation measurement satellite products over Saudi Arabia. J. Hydrol. 2018, 559, 1–12. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 287–296. [Google Scholar] [CrossRef]
- Sneha, M.R.; Nair, A.; Somasundaram, K. Spatiotemporal bias correction of satellite precipitation products using multimodel techniques over temporally coherent clusters in South Peninsular India. Atmos. Res. 2025, 325, 108244. [Google Scholar]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424, 264–277. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Li, D.; Min, X.; Xu, J.; Xue, J.; Shi, Z. Assessment of three gridded satellite-based precipitation products and their performance variabilities during typhoons over Zhejiang, southeastern China. J. Hydrol. 2022, 610, 127985. [Google Scholar] [CrossRef]
- Wu, X.; Feng, X.; Wang, Z.; Chen, Y.; Deng, Z. Multi-source precipitation products assessment on drought monitoring across global major river basins. Atmos. Res. 2023, 295, 106982. [Google Scholar] [CrossRef]
- Yu, X.; Qian, L.; Wang, W.E.; Hu, X.; Dong, J.; Pi, Y.; Fan, K. Comprehensive evaluation of terrestrial evapotranspiration from different models under extreme condition over conterminous United States. Agric. Water Manag. 2023, 289, 108555. [Google Scholar] [CrossRef]
- Bai, H.; Ming, Z.; Zhong, Y.; Zhong, M.; Kong, D.; Ji, B. Evaluation of evapotranspiration for exorheic basins in China using an improved estimate of terrestrial water storage change. J. Hydrol. 2022, 610, 127885. [Google Scholar] [CrossRef]
- Thakur, C.; Budamala, V.; Kasiviswanathan, K.S.; Teutschbein, C.; Soundharajan, B.-S. Extreme gradient and boosting algorithm for improved bias-correction and downscaling of CMIP6 GCM data across indian river basin. J. Hydrol. Reg. Stud. 2025, 59, 102443. [Google Scholar] [CrossRef]



| Products | Resolution | Coverage | Source | ||
|---|---|---|---|---|---|
| Spatial | Temporal | Spatial | Temporal | ||
| Satellite products | |||||
| GPM | 0.1° | Monthly, Daily | Global | 1998.1–2025.1 | https://disc.gsfc.nasa.gov/datasets?keywords=IMERG&start=1920-01-01&end=2024-09-24&page=1 (accessed on 4 January 2025) |
| PERSIANN-CDR | 0.25° | Monthly, Daily | 60°S–60°N | 1983–2024.10 | https://www.ncei.noaa.gov/data/precipitation-persiann/access/ (accessed on 4 October 2024) |
| CMORPH | 0.25° | Daily | 60°S–60°N | 1998–2024.8 | https://rda.ucar.edu/datasets/d502002/dataaccess/ (accessed on 13 March 2025) |
| GSMaP | 0.1° | Monthly, Daily | Global | 1998.1–2025.7 | https://sharaku.eorc.jaxa.jp/GSMaP/index.htm (accessed on 13 November 2024) |
| Multi-source merged products | |||||
| GPCP | 0.5° | Daily | Global | 1998.1–2024.9 | https://disc.gsfc.nasa.gov/datasets/GPCPDAY_3.3/summary?keywords=GPCP&start=1920-01-01&end=2024-09-24 (accessed on 28 February 2025) |
| MSWEP | 0.1° | Monthly, Daily | Global | 1979–2020 | https://www.gloh2o.org/mswep/ (accessed on 22 November 2024) |
| CHIRPS | 0.05° | Monthly, Daily | 50°S–50°N | 1981–2024 | https://data.chc.ucsb.edu/products/CHIRPS-2.0/global_daily/ (accessed on 21 November 2024) |
| Reanalysis products | |||||
| ERA5 | 0.1° | Monthly, Hourly | Global | 1940–2025.7 | https://cds.climate.copernicus.eu/datasets/reanalysis-era5-land?tab=overview (accessed on 21 May 2025) |
| GLDAS | 1° | Monthly, Hourly | 60°S–90°N | 2000.1–2025.4 | https://disc.gsfc.nasa.gov/datasets?keywords=GLDAS&start=1920-01-01&end=2024-09-24&page=1 (accessed on 1 December 2024) |
| Scores | Equation | Perfect Value |
|---|---|---|
| Bias | 0 | |
| CC | 1 | |
| RMSE | 0 | |
| KGE | 1 | |
| CSI | 1 | |
| Random Err. | ||
| System Err. | ||
| With , | ||
| With , | —precipitation for products; —precipitation for the station observation data |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chao, L.; Deng, Y.; Wang, S.; Ren, J.; Zhang, K.; Wang, G. Development of a Two-Stage Correction Framework for Satellite, Multi-Source Merged, and Reanalysis Precipitation Products Across the Huang-Huai-Hai Plain, China, During 2000–2020. Remote Sens. 2025, 17, 2809. https://doi.org/10.3390/rs17162809
Chao L, Deng Y, Wang S, Ren J, Zhang K, Wang G. Development of a Two-Stage Correction Framework for Satellite, Multi-Source Merged, and Reanalysis Precipitation Products Across the Huang-Huai-Hai Plain, China, During 2000–2020. Remote Sensing. 2025; 17(16):2809. https://doi.org/10.3390/rs17162809
Chicago/Turabian StyleChao, Lijun, Yao Deng, Sheng Wang, Jiahui Ren, Ke Zhang, and Guoqing Wang. 2025. "Development of a Two-Stage Correction Framework for Satellite, Multi-Source Merged, and Reanalysis Precipitation Products Across the Huang-Huai-Hai Plain, China, During 2000–2020" Remote Sensing 17, no. 16: 2809. https://doi.org/10.3390/rs17162809
APA StyleChao, L., Deng, Y., Wang, S., Ren, J., Zhang, K., & Wang, G. (2025). Development of a Two-Stage Correction Framework for Satellite, Multi-Source Merged, and Reanalysis Precipitation Products Across the Huang-Huai-Hai Plain, China, During 2000–2020. Remote Sensing, 17(16), 2809. https://doi.org/10.3390/rs17162809






